Что такое зависимые и независимые события

Теоремы сложения и умножения вероятностей. Зависимые и независимые события Текст научной статьи по специальности «Математика»

Похожие темы научных работ по математике , автор научной работы — Махсуд Тулқин Ўғли Усмонов

Текст научной работы на тему «Теоремы сложения и умножения вероятностей. Зависимые и независимые события»

Теоремы сложения и умножения вероятностей. Зависимые и независимые события

Махсуд Тулкин угли Усмонов maqsudu32@gmail .com Ташкентский университет информационных технологий

Аннотация: В данной статье приведены сведения о теореме сложения и умножения вероятностей событий, а также типовые задачи

Ключевые слова: Теоремы сложения и умножения вероятностей. Зависимые и независимые события.

Addition and multiplication theorems for probabilities. Dependent and independent events

Mahsud Tulgin oglu Usmonov maqsudu32@gmail.com Tashkent University of Information Technologies

Abstract: This article provides information about the theorem of addition and multiplication of the probabilities of events, as well as typical problems

Keywords: Theorems of addition and multiplication of probabilities. Dependent and independent events.

Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или 5, равна сумме вероятностей этих событий:

Аналогичный факт справедлив и для бОльшего количества несовместных событий, например, для трёх несовместных событий s и с :

Следует отметить, что для совместных событий равенство Р(А+В) — Р(Л) + Р(В) буДет неверным, не случайно чуть выше я немного сыронизировал на счёт простоты.

А сейчас возьмём в руки уже знакомое и безотказное орудие труда учёбы —

игральный кубик с полной группой событий 5(5, которые состоят

в том, что при его броске выпадут 1, 2, 3, 4, 5 и 6 очков соответственно.

Рассмотрим событие — в результате броска игральной кости выпадет не менее пяти очков. Данное событие состоит в двух несовместных исходах:

— +В6 (ВЬ1падет 5 или 5 очков). По теореме сложения вероятностей несовместных событий:

6 6 6 3 . вероятность того, что в результате броска игральной кости выпадет не менее пяти очков.

Рассмотрим событие ~ + + + , состоящее в том, что выпадет не более 4 очков и найдем его вероятность. По теореме сложения вероятностей несовместных событий:

По той же теореме, вероятность того, что выпадет нечётное число очков:

«Студент знает ответы на 25 экзаменационных вопросов из 60. Какова вероятность сдать экзамен, если для этого необходимо ответить не менее чем на 2 из 3 вопросов?»

В той задаче мы сначала нашли

сочетаний трёх вопросов), затем вычислили 25 35 25

(количество всех возможных

того, что студент

благоприятствующих исходов и вероятность сдаст экзамен.

Но здесь вместо правила сложений комбинаций в ходу и другая схема рассуждений. Рассмотрим два несовместных события:

л — студент ответит на два вопроса из трёх; 5 — студент ответит на все три вопроса.

Возможно, некоторые читатели ещё не до конца осознали суть несовместности. Вдумаемся ещё раз: студент не может ответить на 2 вопроса из 3 и в то же самое время ответить на все 3 вопроса. Таким образом, события А и 5 — несовместны.

Теперь, пользуясь классическим определением, найдём их вероятности:

Факт успешной сдачи экзамена выражается суммой А+В (ответ на 2 вопроса из 3 или на все вопросы). По теореме сложения вероятностей несовместных событий:

— вероятность того, что студент сдаст экзамен.

Магазин получил продукцию в ящиках с четырех оптовых складов: четыре с 1-го, пять со 2-го, семь с 3-го и четыре с 4-го. Случайным образом выбран ящик для продажи. Какова вероятность того, что это будет ящик с первого или третьего склада.

Решение: всего получено магазином: 4 + 5 + 7 + 4 = 20 ящиков.

В данной задаче удобнее воспользоваться «быстрым» способом оформления без расписывания событий большими латинскими буквами. По классическому определению:

— вероятность того, что для продажи будет выбран ящик с 1-го

20 — вероятность того, что для продажи будет выбран ящик с 3-го

По теореме сложения несовместных событий:

р -Р1+Р1 — 0,2 + 0,35 — 0,55 _ верОЯТНОСТЬ того, что для продажи будет выбран ящик с первого или третьего склада.

Безусловно, задача разрешима и чисто через классическое определение вероятности путём непосредственного подсчёта кол-ва благоприятствующих исходов (4 + 7 = 11), но рассмотренный способ ничем не хуже. И даже чётче.

Зависимые и независимые события

Начнём с независимых событий. События являются независимыми, если вероятность наступления любого из них не зависит от появления/непоявления остальных событий рассматриваемого множества (во всех возможных комбинациях). .. .Да чего тут вымучивать общие фразы:

Теорема умножения вероятностей независимых событий: вероятность совместного появления независимых событий А и 5 равна произведению вероятностей этих событий:

Вернёмся к простейшему примеру 1-го урока, в котором подбрасываются две монеты и следующим событиям:

^ — на 1-й монете выпадет орёл;

^ — на 2-й монете выпадет орёл.

Найдём вероятность события ^^ (на 1-й монете появится орёл и на 2-й монете появится орёл — вспоминаем, как читается произведение событий!). Вероятность выпадения орла на одной монете никак не зависит от результата

броска другой монеты, следовательно, события ^ и ^ независимы. По теореме умножения вероятностей независимых событий:

Аналогично: решка и на 2-й решка;

4 — вероятность того, что на 1-й монете выпадет

вероятность того, что на 1-й монете появится орёл и на 2-й решка;

2 2 4 . вероятность того, что на 1-й монете появится решка и на 2-й орёл.

Заметьте, что события AiA->> AAi образуют полную группу и сумма их вероятностей равна единице:

Теорема умножения очевидным образом распространяется и на бОльшее

количество независимых событий, так, например, если события ^ независимы, то вероятность их совместного наступления равна:

Р(АВС) = Р(А) ■ Р(В) ■ Р(С)

В каждом из трех ящиков имеется по 10 деталей. В первом ящике 8 стандартных деталей, во втором — 7, в третьем — 9. Из каждого ящика наудачу извлекают по одной детали. Найти вероятность того, что все детали окажутся стандартными.

Решение: вероятность извлечения стандартной или нестандартной детали из любого ящика не зависит от того, какие детали будут извлечены из других

ящиков, поэтому в задаче речь идёт о независимых событиях. Рассмотрим следующие независимые события:

^ — из 1-го ящика извлечена стандартная деталь;

из 2-го ящика извлечена стандартная деталь;

3 — из 3-го ящика извлечена стандартная деталь. По классическому определению:

Интересующее нас событие (из 1-го ящика будет извлечена стандартная деталь и из 2-го стандартная и из 3-го стандартная) выражается произведением

По теореме умножения вероятностей независимых событий:

вероятность того, что из трех ящиков будет извлечено по одной стандартной детали. Ответ: 0,504 Зависимые события.

Событие % называют зависимым, если его вероятность ^^ зависит от одного или бОльшего количества событий, которые уже произошли. За примерами далеко ходить не надо — достаточно до ближайшего магазина: X — завтра в 19.00 в продаже будет свежий хлеб.

Вероятность этого события зависит от множества других событий: завезут ли завтра свежий хлеб, раскупят ли его до 7 вечера или нет и т.д. В зависимости от различных обстоятельств данное событие может быть как достоверным

Д^О — ^ ^ так и невозможным ~ 0. Таким образом, событие % является зависимым.

5 — на экзамене студенту достанется простой билет.

Если идти не самым первым, то событие 5 будет зависимым, поскольку

его вероятность будет зависеть от того, какие билеты уже вытянули

Как определить зависимость/независимость событий?

Иногда об этом прямо сказано в условии задачи, но чаще всего приходится проводить самостоятельный анализ. Какого-то однозначного ориентира тут нет, и факт зависимости либо независимости событий вытекает из естественных логических рассуждений.

Чтобы не валить всё в одну кучу, задачам на зависимые события я выделю следующий урок, а пока мы рассмотрим наиболее распространённую на практике связку теорем:

Задачи на теоремы сложения вероятностей несовместных и умножения вероятностей независимых событий

Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка равна 0,8, для второго — 0,6. Найти вероятность того, что:

а) только один стрелок попадёт в мишень;

б) хотя бы один из стрелков попадёт в мишень.

Решение: вероятность попадания/промаха одного стрелка, очевидно, не зависит от результативности другого стрелка.

^ — 1-й стрелок попадёт в мишень;

^ — 2-й стрелок попадёт в мишень.

Найдём вероятности противоположных событий А>А — того, что соответствующие стрелки промахнутся:

а) Рассмотрим событие: 5 — только один стрелок попадёт в мишень. Данное событие состоит в двух несовместных исходах:

1-й стрелок попадёт и 2-й промахнётся

1-й промахнётся и 2-й попадёт.

На языке алгебры событий этот факт запишется следующей формулой:

Сначала используем теорему сложения вероятностей несовместных событий, затем — теорему умножения вероятностей независимых событий:

= 0,8 0,4 + 0,2 0,6 = 0,32 + 0,12 = 0,44 _ верОЯХНОСХЬ того, что будет только ОДНО попадание.

б) Рассмотрим событие: ^ — хотя бы один из стрелков попадёт в мишень.

Прежде всего, вдумаемся — что значит условие «хотя бы один»? В данном

случае это означает, что попадёт или 1-й стрелок (2-й промахнётся) или 2-й (1-й промахнётся) или оба стрелка сразу — итого 3 несовместных исхода.

Способ первый: учитывая готовую вероятность предыдущего пункта, событие с удобно представить в виде суммы следующих несовместных событий:

попадёт кто-то один (событие 5, состоящее в свою очередь из 2 несовместных исходов) или

попадут оба стрелка — обозначим данное событие буквой £>.

Таким образом: С = Б + П

По теореме умножения вероятностей независимых событий:

Р(П) = ДЛА) = ДА) ■ ДА) = 0,3■ о,б = 0,43 _ вероятность Т0Г0; что !_й стрелок

попадёт и 2-й стрелок попадёт.

По теореме сложения вероятностей несовместных событий:

Р(С) = Р(В + 0)=Р(В) + Р(В) = 0,44 + 0,48 =0,92 . вероятность хотя бы одного

попадания по мишени.

Способ второй: рассмотрим противоположное событие: ^ — оба стрелка промахнутся.

По теореме умножения вероятностей независимых событий:

Особое внимание обратите на второй способ — в общем случае он более рационален.

Кроме того, существует альтернативный, третий путь решения, основанный на умолчанной выше теореме сложения совместных событий.

Способ третий: события А>А совместны, а значит, их сумма А+А выражает событие «хотя бы один стрелок попадёт в мишень» теореме сложения вероятностей совместных событий и теореме умножения вероятностей независимых событий:

Выполним проверку: события и — (0, 1 и 2 попадания

соответственно) образуют полную группу, поэтому сумма их вероятностей должна равняться единице:

ДС) + ДЯ) + ВД = 0,08 + 0,44 + 0,48 = 1? чт0 и требовалось проверить.

При основательном изучении теории вероятностей вам встретятся десятки задач милитаристского содержания, и, что характерно, после этого никого не захочется пристрелить — задачи почти подарочные. А почему бы не упростить ещё и шаблон? Сократим запись:

Решение: по условию: ^ — вероятность

соответствующих стрелков. Тогда вероятности их промаха:

а) По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:

только один стрелок попадёт в мишень.

б) По теореме умножения вероятностей независимых событий:

ч = ч^-а = 0,2 0,4 = 0,08 _ верОЯХНОСХЬ того, что оба стрелка промахнутся.

Тогда: р ~ ~ — вероятность того, что хотя бы один из

стрелков попадёт в мишень. 0твет. а) 0,44, 6)0,92

На практике можно пользоваться любым вариантом оформления. Конечно же, намного чаще идут коротким путём, но не нужно забывать и 1-й способ — он хоть и длиннее, но зато содержательнее — в нём понятнее, что, почему и зачем складывается и умножается. В ряде случаев уместен гибридный стиль, когда прописными буквами удобно обозначить лишь некоторые события. Задача 8

Рабочий обслуживает три станка. Вероятность того, что в течение смены первый станок потребует настройки, равна 0,3, второй — 0,75, третий — 0,4. Найти вероятность того, что в течение смены:

а) все станки потребуют настройки;

б) только один станок потребует настройки;

в) хотя бы один станок потребует настройки.

Решение: коль скоро в условии ничего не сказано о едином технологическом процессе, то работу каждого станка следует считать не зависимой от работы других станков.

По аналогии с Задачей №5, здесь можно ввести в рассмотрение события

А’А’ А ^ состоящие в том, что соответствующие станки потребуют настройки в

течение смены, записать вероятности ‘ ‘ 4 ^ ‘ ‘ 4 ^ ‘ , наити

вероятности противоположных событий А’А’А и т д 1-[о с тремя объектами так оформлять задачу уже не очень хочется — получится долго и нудно. Поэтому здесь заметно выгоднее использовать «быстрый» стиль:

По условию: Р1 ~ Р2 ~ Рг ~ — вероятности того, что в течение смены соответствующие станки потребуют настойки. Тогда вероятности того, что они не потребуют внимания:

а) По теореме умножения вероятностей независимых событий:

вероятность того, что в течение смены все три станка потребуют настройки.

б) Событие «В течение смены только один станок потребует настройки» состоит в трёх несовместных исходах:

1) 1-й станок потребует внимания и 2-й станок не потребует и 3-й станок не потребует

2) 1-й станок не потребует внимания и 2-й станок потребует и 3-й станок не потребует

3) 1-й станок не потребует внимания и 2-й станок не потребует и 3-й станок потребует.

По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:

= 0,045 + 0,315 + 0,07 = 0,43

вероятность того, что в течение смены только один станок потребует настройки.

Думаю, сейчас вам должно быть понятно, откуда взялось выражение

в) Вычислим вероятность Рт ~ ~~ того, что станки не

потребуют настройки, и затем — вероятность противоположного события:

того, что хотя бы один станок потребует

Ответ: а) °’09; 6) °’43; в)0’895

Стрелок попадает в цель с одной и той же вероятностью при каждом выстреле. Какова эта вероятность, если вероятность хотя бы одного попадания при трех выстрелах равна 0,973.

Решение: обозначим через р — вероятность попадания в мишень при каждом выстреле.

И таки распишем события

и через # 1 ^ _ вероятность промаха при каждом выстреле.

А — при 3 выстрелах стрелок попадёт в мишень хотя бы один раз;

^ — стрелок 3 раза промахнётся.

По условию ■ ■ ‘ , тогда вероятность противоположного события:

С другой стороны, по теореме умножения вероятностей независимых событий:

ц — ,,/0,027 — 0,3 _ верОЯТНОСТЬ промаха при каждом выстреле.

р ~1 ~ 0,3 ~ — вероятность попадания при каждом выстреле.

В рассмотренной задаче можно поставить дополнительные вопросы о вероятности только одного попадания, только двух попаданий и вероятности трёх попаданий по мишени. Схема решения будет точно такой же, как и в двух предыдущих примерах:

Однако принципиальное содержательное отличие состоит в том, что здесь имеют место повторные независимые испытания, которые выполняются последовательно, независимо друг от друга и с одинаковой вероятностью исходов.

Несмотря на кажущуюся шаблонность примеров, целесообразно ознакомиться с дополнительными задачами на теоремы сложения и умножения вероятностей, которые на самом деле достаточно разнообразны. Кроме того, в предложенном файле прорешаны более трудные задачи с «четырьмя участниками».

На следующем уроке мы разберём задачи с зависимыми событиями, а затем важнейшие следствия рассмотренных теорем — формулу полной вероятности, формулы Байеса и формулу Бернулли, касающуюся независимых испытаний.

1. Киселёв, Андрей Петрович // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969-1978.

2. Андронов И. К., А. П. Киселев. [Некролог], «Математика в школе», 1941, № 2

3. Маргулис А. Я., Андрей Петрович Киселев, «Математика в школе», 1948, № 4

4. Депман И. Я., История арифметики, М., 1959.

5. Моргулис А. Я., Тростников В. Законодатель школьной математики // Наука и жизнь. 1968. № 1

6. Пыльнев-Рогачёв, Лунёва М. И. Служитель «царицы-наук» // Кольцовский сквер. 2002. № 3

1. Kiselev, Andrey Petrovich // Great Soviet Encyclopedia: [in 30 volumes] / Ch. ed. A.M. Prokhorov. — 3rd ed. — M.: Soviet Encyclopedia, 1969-1978.

2. Andronov I.K., A.P. Kiselev. [Obituary], «Mathematics in School», 1941, no.

3. Margulis A. Ya., Andrey Petrovich Kiselev, «Mathematics at school», 1948,

4. Depman I. Ya., History of arithmetic, M., 1959.

5. Morgulis A. Ya., Trostnikov V. Legislator of school mathematics // Science and life. 1968. No. 1

6. Pylnev-Rogachev, Luneva MI Servant of the «queen of sciences» // Koltsovsky square. 2002. No. 3

🎲 Орел или решка? Основы теории вероятностей простыми словами

Теория вероятностей – это раздел математики, изучающий случайные события, их свойства и действия над ними. В этой статье мы рассмотрим ее определение, основы и применение. Плюс три простых задачи с решениями.

❓ Что такое теория вероятностей?

Теория вероятностей использует случайные величины и распределения вероятностей для математической оценки неопределенных ситуаций. Понятие вероятности используется для присвоения числового описания вероятности наступления события. Вероятность можно определить как число благоприятных исходов, деленное на общее число возможных исходов события.

Определение теории вероятностей

Теория вероятностей – это область математики и статистики, которая занимается определением вероятностей, связанных со случайными событиями. Существует два основных подхода к изучению теории вероятностей: теоретический и экспериментальный. Теоретическая вероятность определяется на основе логических рассуждений без проведения экспериментов. В отличие от нее, экспериментальная вероятность определяется на основе исторических данных путем проведения повторных экспериментов.

Пример теории вероятностей

Предположим, нам необходимо определить вероятность выпадения числа 4 при бросании игральной кости. Число благоприятных исходов равно 1. Возможные исходы игральной кости – . Из этого следует, что всего существует 6 исходов. Таким образом, вероятность выпадения 4 при бросании игральной кости, используя теорию вероятности, можно вычислить как 1 / 6 ≈ 0,167.

Основы теории вероятностей

Мы можем понять эту область математики с помощью нескольких основных терминов, напрямую связанных с теорией вероятностей.

Случайный эксперимент

Случайный эксперимент в теории вероятностей – это испытание, которое повторяется несколько раз для получения четко определенного набора возможных результатов. Подбрасывание монеты является примером случайного эксперимента.

Пространство выборки

Пространство выборки можно определить как множество всех возможных исходов, полученных в результате проведения случайного эксперимента. Например, пространство выборки при подбрасывании симметричной монеты (fair coin), стороны которой – это орел и решка.

Событие

Теория вероятностей определяет событие как набор исходов эксперимента, который образует подмножество пространства выборки.

Примеры событий:

1. Независимые – те, на которые не влияют другие события, являются независимыми.
2. Зависимые – те, на которые влияют другие события.
3. Взаимоисключающие – события, которые не могут произойти в одно и то же время.
4. Равновероятные – два или более события, которые имеют одинаковые шансы произойти.
5. Исчерпывающие – это события, которые равны выборочному пространству эксперимента.

Случайная величина

В теории вероятностей случайную переменную можно определить как величину, которая принимает значение при всех возможных исходах эксперимента.

Существует два типа случайных величин:

1. Дискретная случайная величина – принимает точные значения, такие как 0, 1, 2. Описывается кумулятивной функцией распределения и функцией массы вероятности.
2. Непрерывная случайная величина – переменная, которая может принимать бесконечное число значений. Для определения характеристик этой переменной используются кумулятивная функция распределения и функция плотности вероятности.

Вероятность

Вероятность мы можем определить как численную вероятность наступления события. Вероятность того, что событие произойдет, всегда лежит между 0 и 1. Это связано с тем, что число желаемых исходов никогда не может превысить общее число исходов события. Теоретическая вероятность и эмпирическая вероятность используются в теории вероятностей для измерения шанса наступления события.

Формула вероятности P(A): количество благоприятных исходов для A делимое на общее количество возможных исходов.

Условная вероятность

Ситуация, когда необходимо определить вероятность наступления события, притом что другое событие уже произошло.

Обозначается как P(A | B).

Если хочешь подтянуть свои знания по математике, загляни на наш курс «Математика для Data Science», на котором ты:

• Усвоишь специальную терминологию и сможешь читать статьи по Data Science без постоянных обращений к поисковику.
• Подготовишься к успешной сдачи вступительных экзаменов в Школу анализа данных Яндекс.
• Овладеешь математическим аппаратом, который необходим, чтобы стать специалистом в Data Science.

Ожидание

Ожидание случайной величины X можно определить как среднее значение результатов эксперимента, проводимого многократно. Ожидание обозначается как E[X]. Также известно как среднее значение случайной величины.

Дисперсия

Дисперсия – это мера, которая показывает, как распределение случайной величины изменяется относительно среднего значения. Дисперсия определяется как среднее квадратичное отклонение от среднего значения случайной величины. Обозначается как Var[X].

Функция распределения теории вероятностей

Распределение вероятностей или кумулятивная функция распределения – это функция, которая моделирует все возможные значения эксперимента, используя случайную переменную. Распределение Бернулли и биномиальное распределение – это примеры дискретных распределений вероятностей. Например, нормальное распределение представляет собой пример непрерывного распределения.

Массовая функция вероятности

Массовая функция вероятности определяется как вероятность того, что дискретная случайная величина будет в точности равна определенному значению.

Функция плотности вероятности

Функция плотности вероятности – это вероятность того, что непрерывная случайная величина принимает множество возможных значений.

Формулы теории вероятностей

В теории вероятностей существует множество формул, которые помогают рассчитать различные вероятности, связанные с событиями.

Наиболее важные формулы:

1. Теоретическая вероятность: Число благоприятных исходов / Число возможных исходов.
2. Эмпирическая вероятность: Число случаев, когда событие происходит / Общее число испытаний.
3. Правило сложения: P(A ∪ B) = P(A) + P(B) – P(A∩B), где A и B – события.
4. Правило комплементарности: P(A’) = 1 – P(A). P(A’) означает вероятность того, что событие не произойдет.
5. Независимые события: P(A∩B) = P(A) ⋅ P(B).
6. Условная вероятность: P(A | B) = P(A∩B) / P(B). : P(A | B) = P(B | A) ⋅ P(A) / P(B).
7. Массовая функция вероятности: f(x) = P(X = x).
8. Функция плотности вероятности: p(x) = p(x) = dF(x) / dx, где F(x) – кумулятивная функция распределения.
9. Ожидание непрерывной случайной величины: ∫xf(x)dx, где f(x) является МФВ (Массовой функцией вероятности).
10. Ожидание дискретной случайной величины: ∑xp(x), где p(x) – это ФПВ (Функцией плотности вероятности).
11. Дисперсия: Var(X) = E[X2] – (E[X])2.

Применение теории вероятностей

Теория вероятностей используется во многих областях и помогает оценить риски, которые связаны с теми или иными решениями. Некоторые из направлений, где применяют теорию вероятностей:

• В финансовой отрасли теория вероятностей используется для создания математических моделей фондового рынка с целью прогнозирования будущих тенденций. Это помогает инвесторам вкладывать средства в наименее рискованные активы, которые дают наилучший доход.

• В потребительской индустрии теория вероятностей используется для снижения вероятности неудачи при разработке продукта.

• Казино использует теорию вероятностей для разработки азартных игр с максимизацией своей прибыли.

🏋️ Практические задания

Задача 1 : При бросании двух игральных костей, какова вероятность того, что выпадет комбинация, сумма которой будет равна 8?

При бросании двух игральных костей существует 36 возможных исходов. Для получения суммы, равной 8, существует 5 благоприятных исходов: [(2, 6), (6, 2), (3, 5), (5, 3), (4, 4)]. Используя формулы теории вероятностей: Вероятность = Число благоприятных исходов / общее число возможных исходов = 5 / 36. Ответ: Вероятность получения суммы 8 при бросании двух игральных костей равна 5 / 36.

Задача 2 : Какова вероятность вытащить карту королеву из колоды?

Колода карт имеет 4 масти. Каждая масть состоит из 13 карт. Таким образом, общее число возможных исходов = (4) * (13) = 52. Может быть, 4 королевы, по одной из каждой масти. Следовательно, количество благоприятных исходов = 4. Карточная вероятность = 4 / 52 = 1 / 13. Ответ: Вероятность получить королеву из колоды карт равна 1 / 13

Задача 3 : Из 10 человек 3 купили карандаши, 5 купили тетради, а 2 купили и карандаши, и тетради. Если покупатель купил тетрадь, какова вероятность того, что он также купил карандаш?

Используя понятие условной вероятности, P(A | B) = P(A∩B) / P(B). Пусть A – событие, когда люди покупают карандаши, а B – событие, когда люди покупают тетради. P(A) = 3 / 10 = 0,3P(B) = 5 / 10 = 0,5P(A∩B) = 2 / 10 = 0,2. Подставим полученные значения в приведенную формулу, P(A | B) = 0,2 / 0,5 = 0,4. Ответ: Вероятность того, что покупатель купил карандаш, при условии, что он купил блокнот, равна 0,4.

В заключение

• Теория вероятностей – это раздел математики, в котором рассматриваются вероятности случайных событий.
• Понятие вероятности объясняет возможность наступления того или иного события.
• Значение вероятности всегда лежит между 0 и 1.
• В теории вероятностей все возможные исходы случайного эксперимента составляют пространство выборки.
• Теория вероятностей использует такие важные понятия, как случайные величины и кумулятивные функции распределения для моделирования случайного события. Сюда же относится определение различных вероятностей, связанных с этим.

Если хочешь подтянуть свои знания по математике, загляни на наш курс «Математика для Data Science», который включает в себя:

ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Зависимые и независимые события. Теоремы сложения и умножения вероятностей

Событие А называется независимым от события В, если его вероятность не зависит от появления или не появления cобытия В, в противном случае событие А называют зависимым от события В.

Вероятность события А, вычисленная в предположении, что событие В произошло, называется условной вероятностью, обозначается

Теорема сложения несовместных событий. Вероятность появления суммы двух несовместных событий равна сумме вероятностей этих событий

Следствие. Вероятность появления суммы попарно несовместных событий равна сумме вероятностей этих событий

Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Теорема может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий:

Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

Следствие. Вероятность появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

Теорема умножения вероятностей зависимых событий. Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго, при условии, что первое событие произошло

Следствие. Вероятность совместного появления нескольких зависимых событий равна произведению вероятностей одного из них на условные вероятности всех остальных событий, вычисленных в предположении, что все предыдущие события

Теорема о вычислении вероятности появления хотя бы одного события. Вероятность наступления события А, состоящего в появлении хотя бы одного из событий

равна разности между единицей и вероятностью произведения всех противоположных событий

Замечание. Приступая к решению задач на вычисление вероятностей сложных событий, рекомендуется пользоваться следующей схемой:

1) обозначить буквами все события, о которых идет речь в условии задачи;

2) выяснить, совместны или несовместны обозначенные события, зависимы они или независимы;

3) выразить сложное событие, о котором идет речь в вопросе задачи через обозначенные события;

4) выбрать формулу для вычисления нужной вероятности.

Пример 2.1. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что выбранное изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий окажется: а) только одно изделие высшего сорта; б) только два изделия высшего сорта; в) все три изделия высшего сорта.

Пример 2.2.Студент выучил 20 вопросов из 30. Для сдачи зачета необходимо ответить хотя бы на два вопроса из трех заданных. Какова вероятность того, что студент сдаст зачет

совместные и зависимые;

Слагаемые в этом выражении совместны. Запишем это же событие иначе, чтобы слагаемые были несовместны

Тогда будем иметь по теореме сложения несовместных событий и теореме умножения зависимых событий

Пример 2.3. На трех этапах подготовки прибора к работе вероятности появления независимых друг от друга задержек соответственно равны 0,1; 0,06; 0,05. Какова вероятность подготовки изделия к работе без задержек

совместны и независимы;

и по теореме умножения независимых событий

Пример 2.4. Производится наблюдение за группой состоящей из трех одинаковых объектов. Вероятности обнаружения первого, второго и третьего объектов соответственно равны 0,6 0,8 и 0,7. Найти вероятность того, что обнаружен хотя бы один объект

По формуле вычисления вероятности появления хотя бы одного события

Пример 2.5 Над изготовлением изделия работают трое рабочих. Качество изделия при передаче следующему рабочему не проверяется. Вероятности того, что первый, второй и третий рабочий допустят брак, соответственно равны 0,2; 0,15; 0,1. Найти вероятность изготовления изделия без брака

Независимые и зависимые события. Условная вероятность. Теорема умножения вероятностей.

Прежде чем познакомиться с теоремой, введем сопутствующие понятия: зависимые и независимые события. Рассмотрим примеры:

а) Два спортсмена стреляют по мишени. Событие А- попал первый стрелок, вероятность появления этого события Р(А) , В- попал второй стрелок, вероятность Р(В). Появление или не появление события, например, А не повлияет на вероятность появления события В.

б) Бросают два одинаковых кубика. Событие С- выпало 2 очка на первом кубике, вероятность этого события Р(С). Событие Д- 3 очка на втором кубике, вероятность — Р(Д). Появление события Д не повлияет на вероятность появления события С.

В данных примерах описаны независимые события.

Два события А и В называются независимыми, если появление одного из них не изменяет вероятности появления другого.

Рассмотрим другой пример:

В урне 2 белых и 2 черных шара. Событие А- вынут 1 белый шар, событие В- вынут 1 черный шар.

Вероятность их появления при испытании- из урны наудачу вынут один шар, одинакова и равна 1/2. Рассмотрим событие: первым вынут белый шар, т.е. происходит событие А, его вероятность 1/2, затем возвращается в урну и вторым вынимают черный шар, т.е. происходит событие В. Найдем вероятность события В в такой ситуации : Р(В)=2/4=1/2. Итак, появление события А не изменило появление события В.

Теперь изменим условия: вынутый первым белый шар не будем возвращать в урну, тогда вероятность события В будет равна Р(В)=2/3, сравнивая результаты 1/2 и 2/3 можно сделать вывод, что появление события А изменило вероятность появления события В. Такие события называются зависимыми , а вероятность события В, в данном случае называется условной вероятностью и обозначается РА(В), т.е. вероятность события В при условии, что А произошло.

События А и В называются зависимыми, если появление одного из них изменяет вероятность появления другого.

Условной вероятностью РА(В) называется вероятность события В, вычисленная в предположении, что событие А уже произошло.

Теперь познакомимся с теоремами, которые позволяют вычислить вероятность совместного появления двух событий. В первой теореме речь идет о зависимых событиях, во второй- о независимых.

Теорема1: Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое уже произошло, т.е. Р(АВ)= Р(А)РА(В).

Пусть в результате опыта возможны N исходов, из них М благоприятствуют появлению события А, их этихМ- К исходов благоприятствуют событию В. Одновременному появлению событий А и В благоприятствуют L исходов из К.. По классической формуле имеем: Р(АВ)=L/N. Умножим и разделим на М:

Первая дробь- вероятность наступления события А, вторая- вероятность события В, при условии, что А уже произошло, т.е. условная вероятность события В, что и требовалось доказать.

Теорема2: Вероятность произведения двух независимых событий А и В равна произведению их вероятностей Р(АВ)=Р(А)Р(В).

Т.к. события независимые, то верно равенство РА(В)=Р(В), тогда получим Р(АВ)=Р(А)Р(В).

Справедлива обратная теорема:

Если для событий А и В выполняется равенство Р(АВ)=Р(А)Р(В), то эти события независимы.

Пример1. По мишени стреляют три стрелка. Вероятности попадания соответственно равны 0,7; 0,8 и 0,9. Найти вероятность того, что попадут все три.

Пусть событие А- попал 1-й, В- 2-й и С-3-й. Эти события независимые, тогда применяя соответствующую теорему получим, что вероятность совместного появления всех трех событий равна: Р(АВС)=Р(А)Р(В)Р(С)= 0,7·0,8·0,9=0,504.

Пример2. В урне находятся 3 белых, 2 черных и 4 синих шара. Какова вероятность того, что первым будет вынут белый шар, вторым- синий, третьим- черный. Шары не возвращаются.

Решение: Пусть события: А- вынут белый шар, В- вынут синий, С- черный. Вероятность, что первым вынут белый равна

Событие В происходит после события А, при этом условия меняются- общее количество шаров уменьшилось и стало равно 8, поэтому события А и В зависимые и речь идет об условной вероятности события В: РА(В)=4/8=1/2. Событие С происходит после событий А и В , поэтому вероятность его тоже условная Р (АВ – внизу)(С)=2/7. Вероятность же их совместного появления :

CFA — Оценка вероятности независимых и зависимых событий

Рассмотрим концепции независимости и зависимости событий, широко применяющиеся при прогнозировании доходности активов и анализе эффективности вложений на основе прошлых результатов, — в рамках изучения количественных методов по программе CFA.

Большой интерес для инвестиционных аналитиков представляют концепции независимости и зависимости событий.

Эти концепции касаются основных инвестиционных вопросов, связанных с тем, какие финансовые показатели полезны для инвестиционного анализа, можно ли прогнозировать доходность активов и можно ли выбирать лучших управляющих инвестициями на основе их прошлых результатов.

Два события являются независимыми, если возникновение одного события не влияет на вероятность возникновения другого события.

Определение независимых событий.

Два события ( A ) и ( B ) являются независимыми (англ. ‘independent events’), только в том случае, если ( P(A|B) = P(A) ) или, что то же самое, если ( P(B|A) = P(B) ).

Если два события не являются независимыми, они зависимы (англ. ‘dependent events’): вероятность возникновения одного связана с возникновением другого.

Если мы пытаемся прогнозировать одно событие, информация о зависимом событии может быть полезной, но информация о независимом событии будет бесполезна.

Когда два события независимы, правило умножения для вероятностей, представленное Формулой 2, упрощается, потому что тогда ( P(A|B) ) в этом уравнении равно ( P(A) ).

Правило умножения для независимых событий.

Когда два события независимы, совместная вероятность событий ( A ) и ( B ) равна произведению отдельных вероятностей событий ( A ) и ( B ).

( large P(AB) = P(A)P(B) ) (Формула 4)

Поэтому, если нас интересуют два независимых события с вероятностями 0.75 и 0.50 соответственно, вероятность того, что оба события произойдут, равна 0.375 = 0.75(0.50).

Правило умножения для независимых событий обобщается до более чем двух событий; например, если события (A), (B) и (C) являются независимыми событиями, то:

Пример (4). Прибыль на акцию BankCorp.

В качестве аналитика банковской отрасли вы создаете модели для прогнозирования прибыли на акцию (EPS) банков отрасли. Сегодня вы изучаете BankCorp.

Исторические данные показывают, что в 55% последних кварталов EPS BankCorp увеличивалась последовательно, а в 45% кварталов EPS снижалась или оставалась неизменной последовательно.

Последовательные сравнения (англ. ‘sequential comparison’) квартальных EPS — это сравнение EPS данного квартала с непосредственным предыдущим кварталом. Последовательное сравнение отличается от сравнения с тем же кварталом год назад (еще один частый тип сравнения).

На этом этапе вашего анализа вы предполагаете, что изменения в последовательных EPS независимы.

Прибыль на акцию за 2 квартал 2014 года была выше прибыли на акцию за 1 квартал 2014 года.

1. Какова вероятность того, что EPS 3-го квартала будет больше EPS 2-го квартала (положительное изменение в последовательных EPS)?
2. Какова вероятность того, что EPS уменьшится или останется неизменным в следующие 2 квартала?

Решение для части 1:

Исходя из предположения о независимости событий, вероятность того, что EPS за 3 квартал будет больше, чем EPS за 2 квартал, является безусловной вероятностью положительных изменений, равной 0.55.

Тот факт, что EPS за 2 квартал была больше, чем EPS за 1 квартал, не является полезной информацией, поскольку следующее изменение в EPS не зависит от предыдущих изменений.

Решение для части 2:

Вероятность составляет 0.2025 = 0.45(0.45).

В следующем примере показано, насколько сложно соблюсти набор независимых критериев, даже если каждый критерий сам по себе необязательно является строгим.

Пример (5) отбора акций для инвестиций.

Вы разработали схему отбора акций (англ. ‘stock screen’) — набор критериев для выбора акций.

Ваше инвестиционное поле (набор ценных бумаг, из которых вы делаете свой выбор, англ. ‘investment universe’) — это Russell 1000 Index, индекс 1000 акций американских компаний с большой капитализацией.

Ваши критерии отражают различные аспекты проблемы выбора. Вы считаете, что критерии независимы друг от друга, при близком приближении.

Фракция индекса Russell 1000,
соответствующая критерию

Первый критерий оценки

Второй критерий оценки

Критерий охвата аналитика

Критерий рентабельности компании

Критерий финансовой устойчивости компании

Сколько акций, по вашим ожиданиям, пройдут отбор?

Только 23 акции из 1000 соответствуют набору критериев.

Если вы определяете 5 перечисленных в таблице событий (скажем, события (A), (B), (C), (D) и (E) соответственно), — тогда вероятность того, что акция будет соответствовать всем пяти критериям независимо, равна:

Хотя только один из пяти критериев является хотя бы умеренно строгим (самый строгий пропускает 25% акций), вероятность того, что акция может пройти все 5, составляет всего 0.023031, или около 2%.

Размер перечня возможных инвестиций составляет:

0.023031(1,000) = 23.031, или 23 акции.

Область, представляющая большой интерес для управляющих инвестициями и их клиентов, заключается в том, полезны ли записи о прошлых результатах в выявлении постоянных выигрышных и проигрышных управляющих.

В следующем примере показано, как эта проблема связана с концепцией независимости событий.

Пример (6). Условные вероятности и предсказуемость результатов взаимного фонда.

Цель исследования Vidal-Garcia (2013), представленного в Примере (2), состояла в том, чтобы решить вопрос о постоянных выигрышных и проигрышных инвестиционных фондах.

Если статус фонда как выигрышного или проигрышного в течение одного года не зависит от того, будет ли он выигрышным в следующем году, практическая ценность такого рейтинга эффективности сомнительна.

Используя четыре события, определенные в Примере 2, в качестве базовых блоков, мы можем определить следующие события для решения проблемы предсказуемости работы взаимных фондов:

• Фонд — выигрышный в 1-м году И фонд — выигрышный во 2-м году.
• Фонд — выигрышный в 1-м году И фонд — проигрышный во 2-м году.
• Фонд — проигрышный в 1-м году И фонд — выигрышный во 2-м году.
• Фонд — проигрышный в 1-м году И фонд — проигрышный во 2-м году.

В части 4 примера 2 вы рассчитали, что:

P(Фонд — проигрышный во 2 году И Фонд — проигрышный в 1 году) = 0.423.

Если рейтинг в одном году не зависит от рейтинга в следующем году, какое значение вероятности события P(Фонд — проигрышный во 2 году И Фонд — проигрышный в 1 году) вы ожидаете?

Интерпретируйте эмпирическую вероятность 0,423.

По правилу умножения для независимых событий,

P(Фонд — проигрышный во 2 году И Фонд — проигрышный в 1 году) = P (Фонд — проигрышный во 2 году) P (Фонд — проигрышный в 1 году).

Поскольку 50% фондов классифицируются как проигрышные в каждом году, безусловная вероятность того, что фонд будет отмечен как проигрышный в любом году, составляет 0.50.

P (Фонд — проигрышный во 2 году) P (Фонд — проигрышный в 1 году) = 0.50(0.50) = 0.25.

Если статус фонда как проигрышного в течение одного года не зависит от того, является ли он проигрышным в предыдущем году, мы заключаем, что

P(Фонд — проигрышный во 2 году И Фонд — проигрышный в 1 году) = 0,25.

Это априорная вероятность, потому что она вытекает из рассуждений о проблеме.

Вы также можете обосновать, что 4 события, описанные выше, определяют категории и что если фонды случайным образом распределить по четырем категориям, существует вероятность, равная 1/4 на то, что фонд окажется проигрышным в 1 году и во 2 году.

Если бы классификации в 1-м и 2-м годах были зависимыми, распределение фондов по категориям не было бы случайным. Эмпирическая вероятность 0.423 выше 0,25.

Является ли эта очевидная предсказуемость результатом случайности?

Тест, проведенный Vidal-Garcia, показал, что вероятность наблюдения представленных данных, если бы рейтинги 1-го и 2-го года были независимыми, составляла менее 1%.

Что такое зависимые и независимые события

Суммой $A+B$ событий $A$ и $B$ называется событие, состоящее в появлении хотя бы одного из них, то есть могут появиться либо только событие $A$, либо только событие $B$, либо события $A$ и $B$ одновременно.

Пример 21. Два стрелка делают по одному выстрелу в мишень. Событие $A=$ , событие $B=$ . Тогда сумма $A+B$ событий $A$ и $B$ — это попадание в мишень хотя бы одного из этих стрелков.

Пример 22. Подбрасывают две монеты. Событие $C=$ , событие $D=$ . Тогда сумма $C+D$ событий $C$ и $D$ — это появление хотя бы одного герба в двух бросаниях.

Пример 23. Из урны, в которой находятся белые и черные шары, вынимают два шара. Событие $E=$ , событие $F=$ . Тогда сумма $E+F$ событий $E$ и $F$ — это появление хотя бы одного черного шара.

Пример 24. Подбрасывают два раза кубик. Событие $G =$ , событие $H=$ . Тогда сумма $G+H$ событий $G$ и $H$ — это появление хотя бы одной единицы в двух бросаниях кубика.

Теорема. Вероятность суммы несовместных событий равна сумме их вероятностей: $Pleft(A+Bright)=Pleft(Aright)+Pleft(Bright)$, где $A$ и $B$ — несовместные события.

Замечание. Теорема верна и для $n$ попарно несовместных событий.

Произведением $AB$ событий $A$ и $B$ называется событие, состоящее в их одновременном появлении.

Пример 25. Произведение $AB$ событий $A$ и $B$ из примера 21 — это попадание в мишень обоих стрелков.

Пример 26. Произведение $CD$ событий $C$ и $D$ из примера 22 — это выпадение двух гербов.

Пример 27. Произведение $EF$ событий $E$ и $F$ из примера 23 — это то, что оба вынутых шара будут черного цвета.

Пример 28. Произведение $GN$ событий $G$ и $N$ — это выпадение двух единиц при двух бросаниях кубика.

Два события называются зависимыми, если вероятность появления одного из них зависит от появления или непоявления другого. Два события называются независимыми, если вероятность появления одного из них не зависит от появления или непоявления другого.

Пример 29. Из урны, в которой находятся 8 белых и 12 черных шаров, последовательно вынимают два шара и обратно не возвращают. Событие $A=$ , событие $B=$ . Выясним, зависимы ли события $A$ и $B$.

Пусть произошло событие $A$, то есть 1-й вынутый шар черный. Тогда в урне осталось 19 шаров, из них 11 черных. Поэтому вероятность события $B$ равна $Pleft(Bright)=11/19$ (всего 19 вариантов, из них 11 благоприятствуют событию В).

Мы видим, что вероятность появления события $B$ зависит от появления или непоявления события $A$.

Теорема. Вероятность произведения двух независимых событий равна произведению их вероятностей: $Pleft(ABright)=Pleft(Aright)Pleft(Bright)$, где $A$ и $B$ — независимые события.

Пример 30. Система, состоящая из двух работающих независимо друг от друга устройств, функционирует исправно только при одновременной работе этих устройств. Вероятности работы 1-го и 2-го устройств равны соответственно $0,8$ и $0,9$. Какова вероятность функционирования системы в целом?

Так как события $A$ и $B$ независимы (устройства работают независимо друг от друга), то $P$ $=Pleft(ABright)=Pleft(Aright)Pleft(Bright)=0,8times 0,9=0,72$.

Пример 31. Найдем вероятность выпадения двух единиц при двух бросаниях кубика.

$A$ и $B$ — независимые события, так как результаты при втором бросании кубика не зависят от того, что выпало при первом бросании. $Pleft(Aright)=Pleft(Bright)=1/6$. Тогда $Pleft(ABright)=Pleft(Aright)Pleft(Bright)=over >cdot over >=over >$.

Пример 32. По мнению экспертов, надежность предприятий $X$ и $Y$ равна соответственно $0,9$ и $0,7$. Предприятия $X$ и $Y$ функционируют независимо. Определим вероятность того, что оба предприятия не обанкротятся.

Так как события $A$ и $B$ независимы (предприятия $Х$ и $Y$ функционируют независимо), то $P$(оба предприятия не обанкротятся) $=Pleft(ABright)=Pleft(Aright)Pleft(Bright)=0,9cdot 0,7=0,63$.

Условной вероятностью $Pleft(B|Aright)$ называется вероятность события $B$ при условии, что событие $A$ произошло. Тогда для зависимых событий $Pleft(B|Aright)ne Pleft(B|overlineright)$. Для независимых событий $Pleft(B|Aright)=Pleft(B|overlineright)=Pleft(Bright)$.

Пример 33. В примере 29 $Pleft(B|Aright)=$ $P$(2-й вынутый шар черный при условии, что 1-й вынутый шар черный) = $P$(2-й вынутый шар черный 1-й вынутый шар черный) $=11/19$.

Поэтому события $A$ и $B$ зависимы.

Теорема. Для зависимых событий $A$ и $B$ верно следующее: $Pleft(ABright)=Pleft(Aright)Pleft(B|Aright)$.

Пример 34. Вернемся к примерам 29 и 33. Найдем вероятность того, что из урны вынуты два черных шара, то есть найдем вероятность события $AB$. $P$(из урны вынуты два черных шара) $=Pleft(Aright)Pleft(B|Aright)=$ $P$(1-й вынутый шар черный)$times P$(2-й вынутый шар черный при условии, что 1-й вынутый шар черный) $=over >times over >=over >$.

Пример 35. Команде предстоит сыграть полуфинал и, возможно, финал. Вероятность победы в полуфинале сами игроки оценивают в $0,6$, а вероятность победы в финале (при условии победы в полуфинале) — в $0,5$. Какова вероятность, по мнению игроков, того, что команда станет чемпионом?

Событие $A=$ , событие $B=$ . Событие $=$ $=AB$. Тогда $Pleft(ABright)=Pleft(Aright)Pleft(B|Aright)=$ $P$(победа в полуфинале $times $ $P$(победа в финале при условии победы в полуфинале) $=0,6times 0,5=0,3$.

Пример 36. Вероятность получения патента равна $0,7$, а вероятность получения дохода в случае получения патента равна $0,8$. Определим вероятность получения дохода.

Нам известны вероятность $P$(получение патента) $=0,7$ и условная вероятность $P$(получение дохода в случае получения патента) $=0,8$. Тохда $P$(получение дохода) = $P$(получение патента)$times P$(получение дохода в случае получения патента) $0,7cdot 0,8=0,56$.

Теорема. Вероятность суммы двух совместных событий $A$ и $B$ равна сумме их вероятностей без учета вероятности произведения этих событий: $Pleft(A+Bright)=Pleft(Aright)+Pleft(Bright)-Pleft(ABright)$.

Если события $A$ и $B$ несовместны, то $AB$ — невозможное событие. Тогда $Pleft(ABright)=0$.

Пример 37. Найдем вероятность выпадения хотя бы одной единицы при двух бросаниях кубика в примере 31.

Артём Саннников

Пусть есть события A и B, у каждого события есть набор элементарных исходов. Пересечением событий A и B называют то событие, в результате которого произошло и событие A и событие B, то есть случился некоторый элементарный исход, который одновременно принадлежит и событию A и событию B.

События не пересекаются

Если у событий A и B нет пересечения (отсутствует элементарный исход), то такая вероятность равна нулю.

События пересекаются

Если события A и B пересекаются (имеют некоторое общее количество элементарных исходов), то вероятность этого пересечения нельзя рассчитать по какой-то универсальной формуле. Эту вероятность нужно подсчитывать, рассматривая общие элементарные исходы.

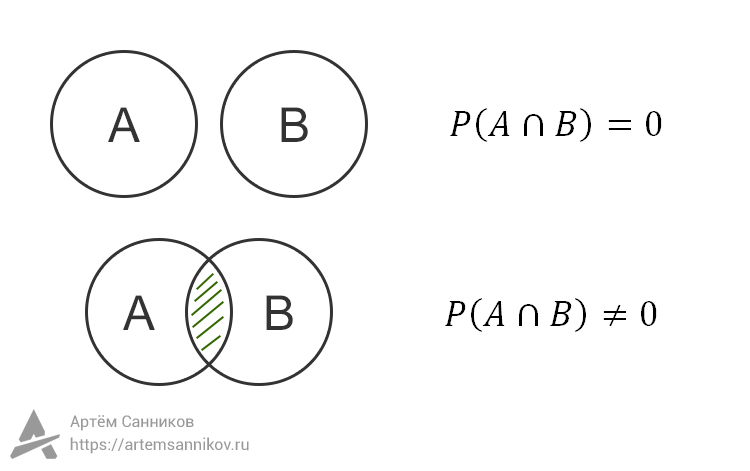
Объединение событий

Объединением событий A и B называют те события, в результате которых произошло или событие A, или событие B, то есть хотя бы одно из двух.

События не пересекаются

Если события A и B не пересекаются, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B).

События пересекаются

Если события A и B пересекаются, то есть у них есть общие элементарные исходы, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B) — вероятность пересечения событий P(A ∩ B)

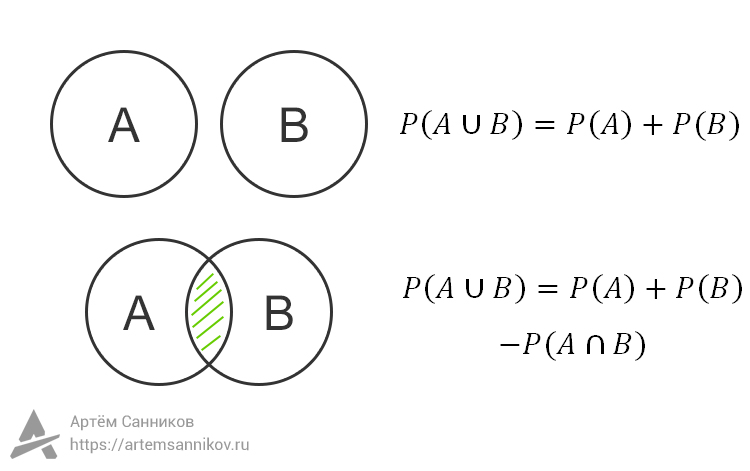
Независимые события

События A и B независимы, если наступление одного события не влияет на другое событие.

Практический пример

Будем рассматривать пример с игральным кубиком, для простоты и анализа нашего эксперимента введём следующие обозначения:

• 1 очко = ω1;
• 2 очка = ω2;
• 3 очка = ω3;
• 4 очка = ω4;
• 5 очков = ω5;
• 6 очков = ω6.

Событие A: выпало > 3 очков

Событие B: выпало нечетное число очков

Чтобы приступить к решению задачи выполняем анализ событий.

Анализ события A: этому событию соответствует три элементарных исхода

Анализ события B: этому событию соответствует три элементарных исхода

После анализа событий приступаем к пошаговому решению.

Рассмотрим теперь пересечение события A и B , то есть у нас должно выпасть > 3 очков и при этом число должно быть нечётное. В этом случае у нас есть один элементарный исход: < ω5>.

Отсюда мы можем посчитать вероятность этого события:

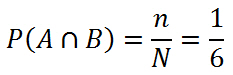
• n – элементарный исход, который удовлетворяет нашим условиям;
• N – общее количество исходов.

Далее рассмотрим объединение событий A и B . В данном случае у нас будет следующий набор элементарных условий

Обратите внимание: у нас отсутствует ω2, так как этот исход не фигурирует ни в событии A, ни в событии B.
Поэтому мы можем сказать, что вероятность объединения в этом случае будет:

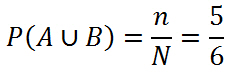
По факту мы решили задачу , но мы можем её решить намного быстрее, если воспользуемся формулой, которую изучили ранее: