Алгебра событий

Теория вероятностей

Теория вероятностей (разг. сокр. “тервер”) — это раздел математики, который занимается анализом случайных событий. С её помощью можно вычислить вероятность события — оно показывает насколько вероятно, что какое-то событие произойдёт. Это число всегда находится в интервале между 0 и 1, где 0 — означает невозможность, а 1 — оно точно произойдёт (достоверное событие).

Например: в мешке есть 6 шаров: 3 красных, 2 жёлтых и 1 синий. Какова вероятность вытащить красный?

Вероятность считается так: количество красных шаров поделить на общее количество шаров в мешке, т. е. 3/6 = 1/2.

Основные формулы теории вероятностей

Теоремы сложения и умножения вероятностей

Применение	Формула
Сложение противоположных событий	P(A) + P(A̅) = 1
Сложение несовместных событий	P(A + B) = P(A) + P(B)
Сложение совместных событий	P(A + B) = P(A) + P(B) — P(AB)
Умножение независимых событий	P(AB) = P(A) × P(B)

Основные формулы вычисления

P(A) = m/n

An m=n!/(n-m)!

Cn m =n!/(m!(n-m)!)

P n = n!

Виды событий

В теории вероятностей события бывают невозможными, случайными и достоверными.

Невозможное событие

Это то, которое уже известно, что в ходе испытания НЕ произойдёт, т. е. вероятность данного события равна нулю. Например: при бросании одной игральной кости (один раз), какова вероятность того, что выпадет 7 очков?

Случайное событие

Это событие может произойти или нет, обычно оно именно случайное. Например: при бросании игральной кости, какова вероятность того, что выпадет чётное число очков?

Достоверное событие

Это то, которое в ходе испытания обязательно произойдёт, т. е. вероятность данного события равна 1. Например: при бросании игральной кости, какова вероятность того, что она не останется в воздухе, а упадёт?

Совместные и несовместные события

Несовместные события — это когда появление одного исключает появление другого (в одном и том же испытании). Например: при бросании одной игральной кости выпадет одновременно и «2» и «3»?

Совместные события могут произойти одновременно. Например: два спортсмена плывут одновременно, два студента сдают экзамен.

Противоположные события

Это два несовместимых события, которые образуют полную группу событий (третьего не существует). Например:

А — при подбрасывании монеты выпадет орёл, A̅ — при подбрасывании монеты выпадет решка;
D — из колоды карт будет извлечена дама, D̅ — из колоды карт будет извлечена не дама.

Логическое ИЛИ означает, что нужно произвести операцию сложения (сумма событий). Т. е. считаем возможность или событие А, или событие В, или оба (одновременно).

Логическое И — операция умножения (произведение событий). Т. е. считаем возможность и событие А, и событие В.

Задачи

Пример 1

В классе 27 учеников. Из них:

17 изучали немецкий язык,

Найти вероятность того, что случайно выбранный ученик изучал хотя бы один язык.

Что мы знаем:

Значит вместе это будет:

(N + A) = (N) + (A) − (N ∙ A) = 17/27 + 6/27 − 2/27 = 21/27 = 7/9.

Пример 2

Лотерейные билеты пронумерованы от 1 до 100. Какова вероятность того, что в выбранном билете будет стоять число больше 40 или чётное число?

Что мы знаем:

P(>40) = 60/100 = 6/10 = 3/5

Логическое ИЛИ означает, что нам нужно произвести операцию сложения (т. е. сумма событий).

Нам понадобится формула сложения совместных событий P(A + B) = P(A) + P(B) — P(AB).

Для этого нам нужно узнать сколько будет P(>40 . Ch), для этого используем формулу P(AB) = P(A) . P(B).

P(>40 . Ch) = P(>40) . P(Ch) = ⅗ . ½ = 3/10

Теперь можем подставить всё в формулу P(A + B) = P(A) + P(B) — P(AB):

P(>40 + Ch) = P(>40) + P(Ch) — P(>40.Ch) = 6/10 + 5/10 — 3/10 = 8/10 = ⅘.

Пример 3

В финале международного турнира по стрельбе из лука участвовали 8 спортсменов: 3 американца, 1 англичанин, 1 немец, 1 француз и 2 русских. Какова вероятность того, что хотя бы один русский попадёт в тройку лучших, учитывая, что все спортсмены имеют равные условия для получения медали (золотой, серебряной и бронзовой).

Что мы знаем:

Когда в вопросе появляется «хотя бы один», можно «пойти от противного» — мы должны найти вероятность того, что этого не произойдёт (на пьедестале русских не будет), а затем вычесть это из 1.

P (никакой русский не выиграет золото) = 6/8 = 3/4

P (никакой русский не выиграет серебро) = 5/7 (убираем золотую медаль)

P (никакой русский не выиграет бронзу) = 4/6 = 2/3 (убираем золотую и серебряную медали)

P (на пьедестале не будет русских) = 3/4 x 5/7 x 2/3 = 30/84 = 5/14

P (хотя бы один русский на пьедестале) = 1 – 5/14 = 14/14 – 5/14 = 9/14.

Кто придумал теорию вероятностей

Основателями теории вероятностей являются два французских математика Блез Паскаль и Пьер Ферма. В 1654 г. французский писатель Антуан Гомбо (известный как Шевалье де Мере), интересовавшийся игрой и азартными играми, вызвал заинтересованность Паскаля насчёт популярной в то время игры в кости.

Кости бросались 24 раза, а вопрос стоял в том, стоит ли ставить деньги на выпадение хотя бы одной «двойной шестёрки». В то время считалось, что это было выгодно, но последующие расчёты показали прямо противоположное.

Алгебра событий

Разъяснить смысл операции суммы событий можно с помощью таблицы 3.1, в которой знак «+» обозначает наступление события, а «−» соответствует ситуации, когда событие не наступило.

Сумма событий A и B

A	B	A+B
+	+	+
+	−	+
−	+	+
−	−	−

Операция суммы событий аналогична операциям объединения множеств и дизъюнкции.

Замечание. Операции суммы событий, как и операции объединения множеств, соответствует союз русского языка «или».

С помощью метода математической индукции операция суммы распространяется на любое число событий.

Определение.Суммой событий A₁, A₂, A₃,… , A_n называется такое событие C, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий A₁, или, A₂,или, A₃,или, …, или A_n.

Пример 3.12.Пусть событие A – попадание в цель первым стрелком, событие B – попадание в цель вторым стрелком. Что представляет собой событие, являющееся суммой этих событий? Что представляет собой событие, противоположное сумме событий A и B?

Суммой событий A и B является событие C, состоящее в попадании в цель хотя бы одним стрелком, т. е. событие C произойдет, если первый стрелок попадет в цель, а второй – не попадет в цель или второй стрелок попадет в цель, а первый – не попадет в цель или оба стрелка попадут в цель.

Событие, противоположное сумме событий A и B, произойдет тогда и только тогда, когда оба стрелка не попадут в цель, т. е. и первый стрелок не попадет в цель и второй стрелок не попадет в цель.

Пример 3.13.Пусть событие A – выпадение двойки на верхней грани игральной кости, событие B – выпадение четверки, C – выпадение шестерки. Что представляет собой событие, являющееся суммой этих событий? Что представляет собой событие, противоположное сумме событий A, B и C?

Суммой событий A, B и C является событие, состоящее в выпадении четного числа на верхней грани игральной кости.

Событие, противоположное сумме событий A, B и C, состоит в выпадении нечетного числа (единицы, или тройки, или пятерки) на верхней грани игральной кости.

Пример 3.14.Рассмотрим опыт с бросанием двух монет. Пусть событие A – выпадение орла и на первой монете и на второй монетах, событие B – выпадение решки на первой монете и орла на второй монете, C – выпадение орла на первой монете и решки на второй монете, D – выпадение решки и на первой и на второй монетах. Что представляет собой событие, состоящее в выпадении хотя бы одного орла?

Событие, состоящее в выпадении хотя бы одного орла, представляет собой сумму событий A, B и C, т. е. A + B + C.

Определение. Произведением событий A и B (A × B) называется такое событие C, которое происходит тогда и только тогда, когда происходят оба события A и B.

Разъяснить смысл операции произведения событий можно с помощью таблицы 3.2, в которой знак «+» обозначает наступление события, а «−» соответствует ситуации, когда событие не наступило.

Произведение событий A и B

A	B	A× B
+	+	+
+	−	−
−	+	−
−	−	−

Операция произведения событий аналогична операциям пересечения множеств и конъюнкции.

Замечание. Операции произведения событий, как и операции пересечения множеств, соответствует союз русского языка «и».

С помощью метода математической индукции операция произведения распространяется на любое число событий.

Определение.Произведением событий A₁, A₂, A₃,… , A_n называется такое событие C, которое происходит тогда и только тогда, когда происходят все события A₁, и A₂, и A₃, и …, и A_n.

Пример 3.15. Пусть событие A – попадание в цель первым стрелком, событие B – попадание в цель вторым стрелком. Что представляет собой событие, являющееся произведением событий A и B? Что представляет собой событие, противоположное произведению событий A и B?

Произведением событий A и B является событие C, которое происходит тогда и только тогда, когда оба стрелка попадают в цель, т. е. и первый стрелок и второй стрелок попадут в цель.

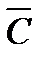
Событие, противоположное произведению событий A и B, произойдет тогда и только тогда, когда хотя бы один стрелок не попадет в цель, т. е. событие произойдет, если первый стрелок попадет в цель, а второй – не попадет в цель или второй стрелок попадет в цель, а первый – не попадет в цель или оба стрелка не попадут в цель.

1.05. Сумма и произведение событий

Таким образом, в теории вероятности знак сложения (+) означает союз «или».

Определение 6. Произведением случайных событий (А1; А2; …АN) называется событие С

А1· А2 ···АN = С, (3.3)

состоящее в появлении Всех перемножаемых событий (и А1, и А2, … и АN).

Таким образом, в теории вероятности знак умножения (·) означает союз «и».

Пример 5. Пусть (А1; А2; А3) – события, состоящее в попадании в мишень первого, второго и третьего стрелков соответственно. Тогда В = А1 + А2 + А3 – событие, состоящее в попадании в мишень Хотя бы одного из стрелков, а С = А1 · А2 ·А3 – событие, состоящее в попадании в мишень Всех трёх стрелков.

Суммы и произведения событий обладают следующими очевидными Свойствами:

1. А+В=В+А – переместительный закон сложения.

2. (А+В)+С=А+(В+С) – сочетательный закон сложения.

3. А·В=В·А – переместительный закон умножения. (3.4)

4. (А·В)·С=А·(В·С) – сочетательный закон умножения.

5. (А+В)·С=А·С+В·С – распределительный закон сложения и умножения.

Свойства (3.4) для случайных событий полностью аналогичны соответствующим свойствам для чисел. Но есть и отличные свойства:

1) А+А=А; 2) А·А=А; 3) (А+В)·А=А; 4) (АВ)·А=АВ. (3.5)

(продумайте эти свойства самостоятельно).

Определение 7. Символом Ā обозначается Событие, противоположное событию А. То есть Ā – это Непоявление события А.

Пример 6. Если событие А – попадание стрелка в мишень, то событие Ā – его промах по мишени. Если А – выпадение орла при бросании монеты, то Ā – выпадение решки. Если А– выпадение пятёрки при бросании игральной кости, то Ā – выпадение любой другой цифры. Если событие А – попадание брошенной точки на одноимённую область А (рис.1.1), то событие Ā – непопадание в эту область. И так далее. Очевидно, что

= 1-, откуда = 1- (3.6)

Последнее равенство (3.6) является ещё одной формулой (в дополнение к формулам (1.1)-(1.4)) для подсчета вероятностей случайных событий. Ею удобно пользоваться в тех случаях, когда вероятность противоположного события Ā найти проще, чем вероятность самого события А.

Пример 7. Бросаются две игральные кости. Найти вероятность того, что хотя бы на одной из них не выпадет шестёрка.

Решение. В данной задаче испытание – это бросание двух костей, а событие А – это невыпадение шестёрки хотя бы на одной из них. Событию А Благоприятствуют, очевидно, много различных исходов испытания (например, 2-5; 3-6; 6-1, и т. д). И лишь один исход (6-6) благоприятствует событию Ā, противоположному событию А (событие Ā – это выпадение двух шестёрок). Так как всех возможных исходов испытания, очевидно, 36, то по классической формуле (1.3)

Значит, по формуле (3.6) получаем:

= 1— = 1 — 1/36 = 35/36.

Событие А (любое) и ему противоположное событие Ā Обладают следующими очевидными свойствами:

1) А+Ā – достоверное событие; P(А+Ā) = 1.

2) А·Ā – невозможное событие; P(А·Ā) = 0. (3.7)

1. Бросаются две игральные кости. Какова вероятность того, что:

А) Сумма выпавших очков будет больше 10?

Б) Сумма выпавших очков будет не больше 10?

2. Бросаются две игральные кости. Какова вероятность того, что

А) Произведение выпавших очков будет чётным?

Б) Произведение выпавших очков будет нечётным?

Ответ: а) 3/4; б) 1/4.

3. Какова вероятность того, что первые три встречные прохожие:

А) Родились в один день?

Б) Родились в разные месяцы?

В) Родились летом?

Г) Хотя бы один из них родился летом?

Д) Никто из них летом не родился?

Ответ: а) 1/144; б) 55/72; в) 1/64; г) 37/64; д) 27/64.

Теоремы сложения и умножения вероятностей: основные задачи

Общая постановка задачи: известны вероятности некоторых событий, а вычислить нужно вероятности других событий, которые связаны с данными событиями. В этих задачах возникает необходимость в таких действиях над вероятностями, как сложение и умножение вероятностей.

Например, на охоте проиведены два выстрела. Событие A — попадание в утку с первого выстрела, событие B — попадание со второго выстрела. Тогда сумма событий A и B — попадание с первого или второго выстрела или с двух выстрелов.

Задачи другого типа. Даны несколько событий, например, монета подбрасывается три раза. Требуется найти вероятность того, что или все три раза выпадет герб, или того, что герб выпадет хотя бы один раз. Это задача на умножение вероятностей.

Сложение вероятностей несовместных событий

Сложение вероятностей используется тогда, когда нужно вычислить вероятность объединения или логической суммы случайных событий.

Сумму событий A и B обозначают A + B или A ∪ B. Суммой двух событий называется событие, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий. Это означает, что A + B – событие, которое наступает тогда и только тогда, когда при наблюдении произошло событие A или событие B, или одновременно A и B.

Больше о сути логической суммы можно узнать в соответствующем месте статьи «Булева алгебра (алгебра логики)».

Если события A и B взаимно несовместны и их вероятности даны, то вероятность того, что в результате одного испытания произойдёт одно из этих событий, рассчитывают, используя сложение вероятностей.

Теорема сложения вероятностей. Вероятность того, что произойдёт одно из двух взаимно несовместных событий, равна сумме вероятностей этих событий:

Например, на охоте произведены два выстрела. Событие А – попадание в утку с первого выстрела, событие В – попадание со второго выстрела, событие (А + В) – попадание с первого или второго выстрела или с двух выстрелов. Итак, если два события А и В – несовместные события, то А + В – наступление хотя бы одного из этих событий или двух событий.

Можно рассчитать как классические, так и статистические вероятности.

Пример 1. В ящике 30 мячиков одинаковых размеров: 10 красных, 5 синих и 15 белых. Вычислить вероятность того, что не глядя будет взят цветной (не белый) мячик.

Решение. Примем, что событие А – «взят красный мячик», а событие В – «взят синий мячик». Тогда событие — «взят цветной (не белый) мячик». Найдём вероятность события А:

События А и В – взаимно несовместные, так как если взят один мячик, то нельзя взять мячики разных цветов. Поэтому используем сложение вероятностей:

Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей — на странице «Различные задачи на сложение и умножение вероятностей».

Теорема сложения вероятностей для нескольких несовместных событий. Если события составляют полное множество событий, то сумма их вероятностей равна 1:

Сумма вероятностей противоположных событий также равна 1:

Противоположные события образуют полное множество событий, а вероятность полного множества событий равна 1.

Вероятности противоположных событий обычно обозначают малыми буквами p и q. В частности,

из чего следуют следующие формулы вероятности противоположных событий:

Пример 2. Цель в тире разделена на 3 зоны. Вероятность того что некий стрелок выстрелит в цель в первой зоне равна 0,15, во второй зоне – 0,23, в третьей зоне – 0,17. Найти вероятность того, что стрелок попадет в цель и вероятность того, что стрелок попадёт мимо цели.

Решение: Найдём вероятность того, что стрелок попадёт в цель:

Найдём вероятность того, что стрелок попадёт мимо цели:

Сложение вероятностей взаимно совместных событий

Два случайных события называются совместными, если наступление одного события не исключает наступления второго события в том же самом наблюдении. Например, при бросании игральной кости событием А считается выпадение числа 4, а событием В – выпадение чётного числа. Поскольку число 4 является чётным числом, эти два события совместимы. В практике встречаются задачи по расчёту вероятностей наступления одного из взаимно совместных событий.

Теорема сложения вероятностей для совместных событий. Вероятность того, что наступит одно из совместных событий, равна сумме вероятностей этих событий, из которой вычтена вероятность общего наступления обоих событий, то есть произведение вероятностей. Формула вероятностей совместных событий имеет следующий вид:

Поскольку события А и В совместимы, событие А + В наступает, если наступает одно из трёх возможных событий: или АВ. Согласно теореме сложения несовместных событий, вычисляем так:

Событие А наступит, если наступит одно из двух несовместных событий: или АВ. Однако вероятность наступления одного события из нескольких несовместных событий равна сумме вероятностей всех этих событий:

Подставляя выражения (6) и (7) в выражение (5), получаем формулу вероятности для совместных событий:

При использовании формулы (8) следует учитывать, что события А и В могут быть:

взаимно независимыми;
взаимно зависимыми.

Формула вероятности для взаимно независимых событий:

Формула вероятности для взаимно зависимых событий:

Если события А и В несовместны, то их совпадение является невозможным случаем и, таким образом, P(AB) = 0. Четвёртая формула вероятности для несовместных событий такова:

Пример 3. На автогонках при заезде на первой автомашине вероятность победить , при заезде на второй автомашине . Найти:

вероятность того, что победят обе автомашины;
вероятность того, что победит хотя бы одна автомашина;

1) Вероятность того, что победит первая автомашина, не зависит от результата второй автомашины, поэтому события А (победит первая автомашина) и В (победит вторая автомашина) – независимые события. Найдём вероятность того, что победят обе машины:

2) Найдём вероятность того, что победит одна из двух автомашин:

Решить задачу на сложение вероятностей самостоятельно, а затем посмотреть решение

Пример 4. Бросаются две монеты. Событие A — выпадение герба на первой монете. Событие B — выпадение герба на второй монете. Найти вероятность события C = A + B .

Умножение вероятностей

Умножение вероятностей используют, когда следует вычислить вероятность логического произведения событий.

При этом случайные события должны быть независимыми. Два события называются взаимно независимыми, если наступление одного события не влияет на вероятность наступления второго события.

Логическим произведением двух событий А и В, обозначаемым А ∩ В, называют событие, которое понимают как одновременное наступление событий А и В. Больше о сути логического произведения можно узнать в соответствующем месте статьи «Булева алгебра (алгебра логики)».

Теорема умножения вероятностей для независимых событий. Вероятность одновременного наступления двух независимых событий А и В равна произведению вероятностей этих событий и вычисляется по формуле:

Пример 5. Монету бросают три раза подряд. Найти вероятность того, что все три раза выпадет герб.

Решение. Вероятность того, что при первом бросании монеты выпадет герб , во второй раз , в третий раз . Найдём вероятность того, что все три раза выпадет герб:

Решить задачи на умножение вероятностей самостоятельно, а затем посмотреть решение

Пример 6. Имеется коробка с девятью новыми теннисными мячами. Для игры берут три мяча, после игры их кладут обратно. При выборе мячей игранные от неигранных не отличают. Какова вероятность того, что после трёх игр в коробке не останется неигранных мячей?

Пример 7. 32 буквы русского алфавита написаны на карточках разрезной азбуки. Пять карточек вынимаются наугад одна за другой и укладываются на стол в порядке появления. Найти вероятность того, что из букв получится слово «конец».

Пример 8. Из полной колоды карт (52 листа) вынимаются сразу четыре карты. Найти вероятность того, что все эти четыре карты будут разных мастей.

Пример 9. Та же задача, что в примере 8, но каждая карта после вынимания возвращается в колоду.

Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей, а также вычислять произведение нескольких событий — на странице «Различные задачи на сложение и умножение вероятностей».

Вероятность того, что произойдёт хотя бы одно из взаимно независимых событий , можно вычислить путём вычитания из 1 произведения вероятностей противоположных событий , то есть по формуле:

Пример 10. Грузы доставляют тремя видами транспорта: речным, железнодорожным и автотранспортом. Вероятность того, что груз будет доставлен речным транспортом, составляет 0,82, железнодорожным транспортом 0,87, автотранспортом 0,90. Найти вероятность того, что груз будет доставлен хотя бы одним из трёх видов транспорта.

Решение. Найдём вероятности противоположных событий – того, что груз не будет доставлен одним из видов транспорта:

Теперь у нас есть всё, чтобы найти требуемую в условии задачи вероятность того, что груз будет доставлен хотя бы одним из трёх видов транспорта:

Решить задачу на умножение вероятностей самостоятельно, а затем посмотреть решение

Пример 11. Из полной колоды карт (52 карты) вынимают одновременно четыре карты. Событие А — среди вынутых карт будет хотя бы одна бубновая. Событие B — среди вынутых карт будет хотя бы одна червонная. Найти вероятность события C = A + B .

Умножение вероятностей взаимно зависимых случайных событий

Если наступление одного события влияет на вероятность наступления второго события, то события называют взаимно зависимыми.

Если события А и В взаимно зависимы, то условной вероятностью называют вероятность события В, принимая, что событие А уже наступило.

Теорема умножения вероятностей взаимно зависимых событий. Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого, то есть вычисляется по формуле:

Пример 12. В ящике 26 лотерейных билетов, из которых 3 с выигрышем. Найти вероятности того, что первый билет будет с выигрышем, вероятность того, что второй билет будет с выигрышем при условии, что первого билета уже нет в ящике и вероятность того, что два взятые подряд билета будут с выигрышем.

Решение. Найдём вероятность того, что первый взятый билет будет с выигрышем:

Найдём вероятность того, что второй взятый билет будет с выигрышем при условии, что первого билета уже нет в ящике:

Найдём теперь вероятность того, что оба взятые подряд билеты будут с выигрышем, т.е. вероятность общего наступления двух зависимых событий, которая является произведением вероятности первого события и условной вероятности второго события:

Действия над событиями

Введем понятие суммы, произведения и разности событий.

Определение. Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из данных событий.

Если А и В — совместные события, то их сумма [1] А + В обозначает наступление или события А, или события В, или обоих событий вместе. Если А и В — несовместные события, то их сумма А + В означает наступление или события А, или события В.

Определение. Произведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий.

Если А, В, С — совместные события, то их произведение [1] АВС означает наступление и события А, и события В, и события С.

Определение. Разностью 1 А — В двух событий А и В называется событие, которое состоится, если событие А произойдет, а событие В не произойдет.

> Пример 1.17а. Победитель соревнования награждается: призом (событие А), денежной премией (событие В), медалью (событие С). Что представляют собой события: а) А + В; б) АВС’, в) АВ — С?

Решение, а) Событие А + В состоит в награждении победителя или призом, или премией, или и тем и другим.

б) Событие АВС состоит в награждении победителя одновременно и призом, и премией, и медалью.
в) Событие АВ — С состоит в награждении победителя одновременно и призом, и премией без выдачи медали. ?

Ниже (параграф 1.12) рассматривается теоретико-множественная трактовка основных понятий теории вероятностей. Здесь же дадим геометрическую интерпретацию основных действий над событиями с помощью диаграмм Венна.

Пусть, например, внутри прямоугольника (рис. 1.3) выбирается наудачу точка (достоверное событие О), и событие А состоит в попадании этой точки в меньший круг (рис. 1.3, а), а событие В — в больший круг (рис. 1.3, 6). Тогда сумма событий А + В означает попадание точки во всю заштрихованную область обоих кругов (рис. 1.3, в), а произведение АВ — в общую часть кругов (рис. 1.3, г). На рис. 1.3, д, е заштрихованные области показывают события А и В, противоположные событиям А и В, а па рис. 1.3, ж и з — разности событий А — В и В — А.

О Пример 1.18. Убедиться в справедливости равенств, выражающих законы де Моргана:

Решение, а) Если событие А + В +. + К состоит в появлении хотя бы одного из данных событий Л, В, . К_у то противоположное событие [3] [4]

Если событие Л представляет собой сумму несовместных событий А_х, Л₂. А_п, т.е. Л = Л, + Л₂ +. + Л„, го говорят, что событие Л распадается на п частных случаев (вариантов) Л,, Л₂. А_п.

Операции сложения и умножения событий обладают следующими с в о й с т в а м и.

1. А + В = В + А— коммутативность сложения.
2. А + (В + С) = (А + В) + С — ассоциативность сложения.
3. АВ = ВА — коммутативность умножения.
4. А(ВС) = (АВ)С — ассоциативность умножения.
5. А + С) = АВ+ АС; А + ВС = (Л + В)(А + С) — законы дистрибутивности.

Последние два свойства иллюстрируются на рис. 1.3, л и м.

Из определения операций над событиями вытекают очевидные равенства:

О Пример 1.18а. Упростить выражения:

а)

Решение, а) Используя приведенные выше свойства операций сложения и умножения событий, получим

Так как то

Теория вероятности формулы и примеры решения задач

События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти. В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).

Зачем нужна теория вероятности

Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.

Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.

В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.

Основные понятия теории вероятности

Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.

Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.

Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.

События А и В называется несовместными, если они не могут произойти одновременно.

Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом .

Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом .

Важным частным случаем является ситуация, когда имеется равновероятных элементарных исходов, и произвольные из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле . Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.

Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов , прямо в условии написано число всех исходов .

Ответ получаем по формуле .

Пример задачи из ЕГЭ по математике по определению вероятности

На столе лежат 20 пирожков — 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?

Решение.

Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть , где А — это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:

Независимые, противоположные и произвольные события

Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.

События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.

Событие B состоит в том, что событие А не произошло, т.е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события,т.е. .

Теоремы сложения и умножения вероятностей, формулы

Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е. .

Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае .

Последние 2 утверждения называются теоремами сложения и умножения вероятностей.

Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.

Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение , которое обозначается символом 6! и читается «шесть факториал».

В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов В нашем случае .

Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение .

В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам

$[ A^{k}_{n}=n cdot (n-1) cdot (n-2) dots cdot(n-k+1)= frac{n!}{(n-k)!} ]$

В нашем случае .

И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину: . В общем случае ответ на этот вопрос дает формула для числа сочетаний из элементов по элементам:

$[ C^{k}_{n}=frac{n cdot (n-1) cdot (n-2) dots (n-k+1)}{1cdot 2 cdot 3 dots cdot k}=frac{n!}{k! cdot (n-k)!}. ]$

В нашем случае .

Примеры решения задач из ЕГЭ по математике на определение вероятности

Задача 1. Из сборника под ред. Ященко.

На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.

.

Задача 2. Из сборника под ред. Ященко.

В каждой партии из 1000 лампочек в среднем 20 бракованных. Найдите вероятность того, что наугад взятая лампочка из партии будет исправной.

Решение: Количество исправных лампочек 1000-20=980. Тогда вероятность того, что взятая наугад лампочка из партии будет исправной:

Вероятность того, что на тестировании по математике учащийся У. верно решит больше 9 задач, равна 0,67. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.

Если мы вообразим числовую прямую и на ней отметим точки 8 и 9, то мы увидим, что условие «У. верно решит ровно 9 задач» входит в условие «У. верно решит больше 8 задач», но не относится к условию «У. верно решит больше 9 задач».

Однако, условие «У. верно решит больше 9 задач» содержится в условии «У. верно решит больше 8 задач». Таким образом, если мы обозначим события: «У. верно решит ровно 9 задач» — через А, «У. верно решит больше 8 задач» — через B, «У. верно решит больше 9 задач» через С. То решение будет выглядеть следующим образом:

.

На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Давайте подумаем какие у нас даны события. Нам даны два несовместных события. То есть либо вопрос будет относиться к теме «Тригонометрия», либо к теме «Внешние углы». По теореме вероятности вероятность несовместных событий равна сумме вероятностей каждого события, мы должны найти сумму вероятностей этих событий, то есть:

Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,29. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Рассмотрим возможные события. У нас есть три лампочки, каждая из которых может перегореть или не перегореть независимо от любой другой лампочки. Это независимые события.

Тогда укажем варианты таких событий. Примем обозначения: — лампочка горит, — лампочка перегорела. И сразу рядом подсчитаем вероятность события. Например, вероятность события, в котором произошли три независимых события «лампочка перегорела», «лампочка горит», «лампочка горит»: , где вероятность события «лампочка горит» подсчитывается как вероятность события, противоположного событию «лампочка не горит», а именно: .

Заметим, что благоприятных нам несовместных событий всего 7. Вероятность таких событий равна сумме вероятностей каждого из событий: .

Еще одну задачку вы можете посмотреть на рисунке:

Таким образом, мы с вами поняли, что такое теория вероятности формулы и примеры решения задач по которой вам могут встретиться в варианте ЕГЭ.

Основы теории вероятностей

Данное введение в теорию вероятностей и математическую статистику ни в коем случае не претендует на полноту изложения. Дается только минимально необходимый материал для трейдеров, работающих на Форексе, фондовой бирже и бинарных опционах.

Данное изложение ведется на достаточно простом языке, понятным для выпусника средней школы, который не изучал эти предметы в ВУЗе. Этот материал также будет полезен тем, кто когда-то знал эти вещи, но подзабыл, и теперь надо очень быстро вспомнить хотя бы основы.

Определения

Теория вероятностей, это раздел математики, который изучает закономерности случайных событий и случайных величин, а также операции над случайными величинами.

Случайное событие, это такое событие, которое может и произойти, и не произойти при выполнении некоторых условий.

Будем считать, что эти условия могут быть воспроизведены неограниченное количество раз.

Испытанием называется каждое воспроизведение этих условий.

Закономерности

Я подкинул монету 10 раз. В результате, орел выпал 7 раз, а решка выпала 3 раза. Получилась разница 7 — 3 = 4.

Я подкинул монету 100 раз. В результате, орел выпал 56 раз, а решка выпала 54 раза. Разница получилась еще больше 56 — 44 = 12.

Я подкинул монету 1000 раз. Теперь, наоборот, орлов выпало меньше, всего 485 раз. А решек выпало 515 раз. Разница стала еще больше, но со знаком минус, так как орлов теперь меньше: 485 — 515 = -30.

Где же закономерность?

10 подбрасываний. 10_2=5. Абсолютные отклонения от 5: орлы 7-5=+2, решки 3-5=-2. Относительные отклонения от 5: орлы +2/5=+0.4, решки -2/5=-0.4.

100 подбрасываний. 100_2=50. Абсолютные отклонения от 50: орлы 56-50=+6, решки 44-50=-6. Относительные отклонения от 50: орлы +6/50=+0.12, решки -6/50=-0.12.

1000 подбрасываний. 1000_2=500. Абсолютные отклонения от 500: орлы 485-500=-15, решки 515-500=+15. Относительные отклонения от 500: орлы -15/500=-0.03, решки +15/500=+0.03.

10 подбрасываний. Отклонение 40%.

100 подбрасываний. Отклонение 12%.

1000 подбрасываний. Отклонение 3%.

Вы можете провести свои испытания, и Вас получатся другие цифры. Но тенденция будет такая же.

Еще одна закономерность будет проявляться в том, что отклонений в пользу большего числа решек будет столько же, сколько отклонений в пользу большего числа орлов. Например, если проводить серию по 10 испытаний, то у меня получилось в первой серии, что орлов больше, чем решек. Но когда я провел 10 таких серий по 10 испытаний, то орлов было больше в семи сериях из 10 серий.

Затем я провел 100 серий по 10 бросаний в каждой. Теперь решек было больше в 55 серий, а орлов было больше в 45 сериях. Хотя по абсолютной величине не получается, чтобы в 50% всех серий было больше отклонений в пользу решек, а в 50% всех серий в пользу орлов, но, тем не менее, относительная разница стремиться к нулю при увеличении числа серий испытаний.

Третья закономерность, это симметрия в отклонениях в пользу решек и в пользу орлов. Если делать много серий испытаний с одинаковыми длинами этих серий, то примерно сколько раз было больше в серии орлов, столько же раз было больше и решек. И чем большее число серий сделать, тем относительная разница между большим выпадением орлов и большим выпадением решек будет стремиться к нулю.

Четвертая закономерность, это распределение отклонений от теоретического. Если провести большое число серий одинаковой длины с подбрасыванием монеты, то можно увидеть, что больше всего будет таких серий, где отклонений от 50% не будет. Поменьше будет таких серий, где отклонений от 50% будет всего на единицу. Еще меньше будет серий, где отклонений от 50% будет на 2. И так далее. Чем больше отклонение от теоретического выпадения 50% решек и 50% орлов, тем реже встречается серия подбрасываний с таким отклонением.

Относительная частота случайного события, это отношение количества случаев появления этого события M к общему числу проведенных испытаний N.

Эксперименты показывают, что при многократном повторении испытаний относительная частота M/N случайного события обладает некоторой устойчивостью. Эта устойчивость относительной частоты объясняется существованием объективных свойств и закономерностей случайного события.

Вероятность и случайная величина

Вероятность, это количественная мера наступления какого-нибудь случайного события.

Вероятность является первичным базовым понятием в математике, и ее нельзя определить через более простые термины и понятия.

Случайная величина, это такая величина, которая принимает те или иные значения с определенными вероятностями.

Вероятность может принимать значение от нуля до единицы (0⩽P⩽1). Ноль означает невозможное событие (P=0). Единица означает достоверное событие, которое обязательно случится (P=1).

Например, Вы держите в руке тяжелую гирю и выпускаете её из рук. С вероятностью P=1 гиря упадет вниз. С вероятностью P=0 гиря зависнет в воздухе как в невесомости.

Еще пример. Вы подбрасываете 6-гранный кубик с пронумерованными гранями. Два очка выпадет с вероятностью P=1/6, то есть примерно в каждом шестом испытании. Пять очков тоже выпадет с вероятностью P=1/6, то есть тоже в каждом шестом испытании.

А теперь более хитрый пример. Вы подбрасываете монету. Вероятность выпадения решки равна вероятности выпадения орла. И та и другая вероятность равна половине (P=1/2).

А может ли монета после подбрасывания встать вертикально на ребро? В прошлом примере мы считали, что это невозможное событие, то есть вероятность такого события P=0. Однако, теоретически такое случайное событие может произойти. Но вероятность такого случайного события очень-очень маленькая. Возможно, более вероятно, что Вам на голову когда-нибудь упадет метеорит, чем Вы увидите, как после подбрасывания, монета встала на своё ребро.

Пусть вероятность того, что монета встанет на своё ребро будет P=0.0000002. (Это на самом деле не так, это число взято только для примера.) Чему тогда равна вероятность выпадения орла?

Эта вероятность уже не будет равной P=0.5, так как сумма вероятности всех возможных событий не может быть равной чему-то больше единицы. В самом деле, если мы подбрасываем монету, то или выпадет решка или выпадет орел или она встанет на ребро. Ничего другого не случится. Значит, вероятность выпадения решки или орла или ребра будет равна единице (P=1). Достоверно произойдет одно из трех событий.

Поэтому, в силу симметрии между решкой и орлом, получаем, что вероятность выпадения орла будет P=0.4999999. И такая же будет вероятность выпадения решки.

0.4999999 + 0.4999999 + 0.0000002 = 1.

А если монета не может становиться на ребро, то

Для 6-гранного кубика вероятность выпадения каждой из его граней P=1/6. Значит, вероятность того, что выпадет хотя бы одна грань (а это достоверное событие, которое обязательно произойдет) будет

1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Дискретные и непрерывные случайные величины

Случайные величины могут быть дискретными и непрерывными.

Дискретная случайная величина, это такая величина, все возможные значения которой образуют конечную или бесконечную последовательность чисел (x₁,x₂. x_n) и принятие ей каждого из указанных значений есть случайное событие, характеризующееся соответствующей вероятностью (P₁,P₂. P_n).

При этом выполняется условие нормировки на единицу, то есть сумма всех этих вероятностей должна быть равна единице.

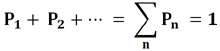
Непрерывная случайная величина, это такая величина, все возможные значения которой целиком заполняют некоторый промежуток и попадание в любой интервал (x₁,x₂) есть случайное событие, характеризующееся соответствующей вероятностью P1⩽x⩽x₂>.

При этом также выполняется условие нормировки на единицу, то есть вероятность достоверного события равна единице.

Генеральная совокупность, это все возможные значения, которые может принимать случайная величина.

Сложение и умножение вероятностей

Для вычисления вероятности сложного события используют вероятности более простых событий и математические действия над ними.

Когда вероятности надо складывать, а когда их надо умножать?

Правило очень простое. Если при формулировке задачи можно использовать союз «ИЛИ«, значит, вероятности надо складывать. Если при формулировке задачи можно использовать союз «И«, значит, вероятности надо умножать. Посмотрим примеры с подбрасыванием 6-гранного кубика.

Какова вероятность того, что, при подбрасывании кубика, выпадет двойка или пятерка?

Используется союз «или». Значит, нужно сложить вероятность выпадения двойки с вероятностью выпадения пятерки.

P = 1/6 +1/6 = 1/3. То есть примерно треть всех подбрасываний кубиков будет приводить к тому, что выпадет или 2 или 5.

Какова вероятность того, что, при подбрасывании двух кубиков, на одном выпадет двойка, а на другом пятерка?

Можно эту задачу переформулировать через союз «и». Какова вероятность того, что, при подбрасывании двух кубиков, на одном выпадет двойка и на другом выпадет пятерка? (Союз «или» совершенно неуместен.)

Значит, нужно перемножить вероятность выпадения двойки и вероятность выпадения пятерки.

P = 1/6 x 1/6 = 1/36. То есть примерно в каждом 36-м случае всех подбрасываний кубиков будет одновременно выскакивать 2 и 5.

Аналогичная задача с таким же решением. Какова вероятность того, что, при двух подбрасываниях одного и того же кубика, один раз выпадет двойка, а второй раз выпадет пятерка? Этот вопрос снова можно переформулировать через союз «и» не меняя сути вопроса. Например, так. Какова вероятность того, что, при двух подбрасываниях одного и того же кубика, выпадет двойка и выпадет пятерка?

Теперь более сложный пример. Какова вероятность того, что, при подбрасывании двух кубиков, сумма очков будет равна четырем?

Сумма очков может быть равной 4, если или выпадает на каждом кубике по 2 очка, или если на одном кубике выпадает 1 очко, а на другом 3 очка. Переформулируем этот вопрос через наши союзы. Какова вероятность того, что, при одновременном подбрасывании двух кубиков, на одном выпадет 2 и на другом выпадет 2 или на одном выпадет 1 и на другом выпадет 3?

Два союза «и» означает, что в формуле будет два умножения. Один союз «или» означает, что в формуле будет одно сложение. Вероятности складываются и умножаются как обычные числа. То есть, если нет скобок, то сначала делается умножение, а потом сложение. Получаем

P = 1/6 x 1/6 + 1/6 x 1/6 = 1/18. То есть примерно в каждом 18-м случае сумма очков на двух кубиках будет равна 4.

Вероятность противоположного события

Противоположное событие, это дополнительное событие. То есть такие события, что появление одного или другого является достоверным событием. Другими словами, сумма противоположных событий равна единице.

Значит, чтобы найти вероятность противоположного события к данному событию, нужно от единицы отнять вероятность данного события.

Например, пусть монета не может становиться на ребро. Значит, при подкидывании монеты может выпасть или орел или решка. Выпадение орла и выпадение решки, это два противоположных события. Если вероятность выпадения орла P=0.5, то вероятность выпадения решки будет 1 — P = 1/2.

А если монета немножко кривая и вероятность выпадения орла P=0.55, то вероятность выпадения решки будет 1 — P = 0.44.

Если подбрасываем 6-гранный кубик, то событие выпадения шестерки будет противоположным событию невыпадения шестерки. А что это за событие такое невыпадение шестерки? Это событие выпадения всего остального, кроме шестерки. То есть это событие выпадения 1 или 2 или 3 или 4 или 5.

Стоят союзы «или». Значит, нужно сложить вероятности выпадения 1, 2, 3, 4, 5 очков.

P = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 5/6. Значит, вероятность выпадения шестерки будет 1 — P = 1 — 5/6 = 1/6, как и должно быть.

Разность вероятностей

Бывает так, что какое-нибудь событие может быть подмножеством другого более широкого события. Это записывается так A⊂B. Здесь событие A является подмножеством события B.

Тогда вероятность наступления события B при ненаступлении событий A будет

Здесь P — вероятность события B, а P — вероятность события A.

Например, при подкидывании кубика событие выпадения шестерки является подмножеством события выпадения четного числа очков. Значит, чтобы найти вероятность выпадения любого четного числа очков, кроме шестерки, надо от вероятности выпадения четного числа очков отнять вероятность выпадения шестерки. Это будет

P <четное6>= P — P = 1/2 — 1/6 = 1/3. (Половина всех номеров четные, поэтому P=1/2.)

Действительно, вероятность выпадения 2 или 4 будет равна 1/6 + 1/6 = 1/3.

Сложение пересекающихся событий

Если есть событие A и событие B, то в общем случае вероятность наступления события A или события B определяется формулой

Здесь P — вероятность одновременного события A и B.

Например, пусть событие A, это выпадение четного числа очков при подбрасывания кубика, а B, это выпадение маленького числа очков, то есть 1, 2 или 3 очка. Вероятность выпадения четного числа P=1/2. Вероятность выпадения маленького числа очков P=1/2. Нужно найти вероятность выпадения или четного числа очков или маленького числа очков.

Просто сложить эти две вероятности нельзя, так как эти два события совместимы. Если выпадет двойка, то значит, что одновременно выпало и четное число очков, и маленькое число очков. Поэтому при простом сложении вероятностей будет дважды учтена вероятность выпадения двойки. Значит, нужно от простой суммы вероятностей отнять вероятность одновременного события. Вероятность выпадения двойки P=1/6. Итак

P = 1/2 + 1/2 — 1/6 = 5/6.

Теория вероятностей:

Случайные процессы:

Сервисы:

Сервис Прогнозирования:

Калькуляторы для Форекса:

Калькуляторы и Симуляторы для Бинарных Опционов:

Мартингейл:

chance.nanoquant.ru © 2008-2022 Lasto Nano CMS | Programming Master Lasto | Memory consumption: 0.75 Mb |
Похожие записи:
Что такое сумма событий
Что такое зависимые и независимые события
Что такое зависимое событие в теории вероятности
$Что такое сумма определение$
Что такое сумма определение
Что такое сумма квадратов чисел
Что такое сумма квадратов