Билет 1. Случайное событие. Определение вероятности (статистическое и классическое). Понятие о совместных и несовместных событиях, зависимых и независимых событиях.
Статистическое определение вероятности – это предел, к которому стремится относительная частота появления данного события при неограниченном возрастании числа испытаний.
Классическое определение вероятности – это отношение числа ожидаемых событий к полному числу возможных в данном опыте событий.
Совместимые события – это события, появление одного из которых не исключает появление другого.
Несовместимые события — это события, появление одного из которых исключает появление другого.
Зависимое событие – это событие, на вероятность которого оказывает влияние исход другого события.
Независимое событие – это событие, на вероятность которого не влияет исход другого события.
Билет 2. Теоремы сложения вероятностей для несовместных и совместных событий.
Теорема сложения вероятностей для несовместных событий:
Вероятность появления какого-либо события из нескольких несовместных равна сумме их вероятностей.
Теорема сложения вероятностей для совместных событий:
Вероятность появления хотя бы одного из нескольких совместных событий равна сомме их вероятностей без вероятности их совместного появления.
Билет 3. Теоремы умножения вероятностей для независимых и зависимых событий. Условные вероятности.
Теорема умножения вероятностей для независимых событий:
Вероятность совместного появления независимых событий равна произведению их вероятностей.
Теорема умножения вероятностей для зависимых событий:
Вероятность появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже наступили.
Условная вероятность – вероятность некоторого события при условии того, что другое событие произошло, либо не произошло.
Например, событие А произойдет при условии реализации события В. В таком случае используют обозначение Р(А/В).
Билет 4. Полная вероятность. Теорема Байеса.
Полная вероятность–это вероятность появления некоторого события В, если известны условные вероятности этого события при наличии некоторых событий Аi (которые попарно несовместны, а их объединение есть достоверное событие):
где n – полное число попарно несовместных событий Ai,
p(Ai) – вероятности каждого из этих событий.
Теорема Байеса определяет условную вероятность p(Ak/B) появления некоторого события Ak при условии того, что некоторое событие B уже наступило; здесь k может принимать любое значение от 1 до n, причём n является числом возможных событий, наступающих в данном опыте. Математическое выражение:

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.



Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
© cyberpedia.su 2017-2020 — Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!
Полная вероятность и формула Байеса
Чтобы вспомнить о сложении и умножении вероятностей и независимых событиях – см. §39 справочника для 9 класса.
Напомним, что два случайных события A и B называют независимыми, если наступление одного из них не изменяет вероятность наступления другого.
Например: при бросании монеты несколько раз каждый следующий бросок совершенно не зависит от предыдущих.
Два случайных события A и B называют зависимыми , если вероятность одного из них зависит от того, произошло или нет другое событие.
Вероятность события B, определенная при условии, что событие A произошло, называется условной вероятностью и обозначается (P(B|A)) или (P_A(B)).
Для условных вероятностей справедливы формулы: $$ P(A|B)=frac
Например:
Рассмотрим урну, в которой находится 3 белых и 3 черных шара.
Мы достаем шары, смотрим на их цвет и не возвращаем их на место. События в последовательности становятся зависимыми.
Пусть событие A=»в 1й раз достаем черный шар»,
Событие B=»во 2й раз достаем белый шар»
Событие C=»во 2й раз достаем черный шар»
После того, как произошло событие A, в урне остается 3 белых и 2 черных шара.
Тогда условная вероятность для события B при условии, что событие A произошло:
(P(B|A)=frac35)
Аналогично, условная вероятность для события C:
(P(B|A)=frac25)
п.2. Вероятность совместного появления событий
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло: $$ P(Awedge B)=P(B)cdot P(A|B)=P(A)cdot P(B|A) $$ Это утверждение также называют теоремой умножения вероятностей .
Например:
Продолжая предыдущий пример, вероятность события ((Awedge B)) – 1й раз достали черный шар и 2й раз белый – равна: $$ P(Awedge B)=P(A)cdot P(B|A)=frac12cdot frac35=0,3 $$ Также, напомним:
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий: $$ P(Awedge B)=P(A)cdot P(B) $$
Например:
Пусть в урне 3 белых и 3 черных шара. Мы достаем шары, смотрим на их цвет и возвращаем их на место. В последовательности наших действий все события будут независимыми. Каждый раз, вероятность достать белый или черный шар будет равна 1/2. Поэтому, в этом случае вероятность события ((Awedge B)) – 1й раз достали черный шар, а 2й раз белый – равна: $$ P(Awedge B)=P(A)cdot P(B)=frac12cdotfrac12=0,25 $$
п.3. Формула полной вероятности
Чтобы вспомнить о несовместных событиях и полной группе событий – см. §39 справочника для 9 класса.
Например:
При подбрасывании монеты события A=«получить орла» и B=«получить решку» — несовместные, т.к. одновременно произойти не могут.
В то же время, эти несовместные события A и B образуют пространство элементарных событий или полную группу (Omega=left\), т.к. ничего другого, кроме орла или решки, получить нельзя. Сумма вероятностей (P(A)+P(B)=frac12+frac12=1), как и положено для полной группы.
Если событие A может произойти только при выполнении одного из событий (B_1,B_2,…,B_k), которые образуют полную группу событий, то вероятность события A определяется по формуле полной вероятности : $$ P(A)=P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+. +P(B_k)P(A|B_k)=sum_^k P(B_i)P(A|B_i) $$
Например:
В 11А и 11Б учится по 35 человек, а в 11В — 30 человек. Будем считать тех, у кого 4 и 5 баллов по алгебре и геометрии, «знатоками математики». Таких учеников в 11А — 10 человек, в 11Б — 7 человек, и в 11В — 3 человека.
Какова вероятность, что произвольно выбранный 11-классник окажется знатоком математики?
Пусть события A=«знаток математики», Bi=«ученик i-го класса», (i=overline)
Составим таблицу:
| i | Класс | К-во учеников |
(P(B_i)) | К-во знатоков |
(P(A|B_i)) | (P(B_i)cdot P(A|B_i)) |
| 1 | 11A | 35 | 35/100=0,35 | 10 | 10/35=2/7 | 0,1 |
| 2 | 11Б | 35 | 35/100=0,35 | 7 | 7/35=1/5 | 0,07 |
| 3 | 11В | 30 | 30/100=0,3 | 10 | 3/30=1/10 | 0,03 |
| Всего | 100 | 1 | 20 | × | 0,2 | |
Получаем полную вероятность (P(A)=sum_^3 P(B_i)cdot P(A|B_i)=0,2)
В данном случае ответ можно получить и проще: 20 знатоков на 100 человек дает (P(A)=0,2).
п.4. Формула Байеса
По данному выше определению полной вероятности событие A случается, если происходит одно из событий полной группы (left\).
Допустим, что событие A случилось. А какова вероятность, что при этом произошло конкретное событие (B_1inleft\)? Т.е., нас интересует условная вероятность (P(B_1|A)).
По теореме об умножении вероятностей: $$ P(Awedge B_1)=P(B_1)cdot P(A|B_1)=P(A)cdot P(B_1|A) $$ Откуда: $$ P(B_1|A)=frac $$ То же самое справедливо для любого события (B_pinleft\). Предположение о том, что случилось событие (B_p), называют гипотезой.
Если событие A может произойти только при выполнении одного из событий полной группы (left\) и событие A случилось, то вероятность гипотезы, что при этом случилось событие (B_pinleft\), определяется формулой Байеса : $$ P(B_p|A)=frac=frac^k P(B_i)P(A|B_i)> $$ Вероятность (P(B_p)) называют априорной вероятностью .
Вероятность (P(B_p|A)) называют апостериорной вероятностью . Случившееся событие A может поменять априорную (предварительную) оценку вероятности события (B_p).
Например:
Продолжим задачу с 11-классниками. Какова вероятность того, что произвольно взятый знаток математики учится в 11Б?
Наши события: A=«знаток математики», B2=«ученик 11Б класса».
Событие A «случилось» — у нас имеется знаток, а событие B2 — это гипотеза про 11Б.
И ответом на поставленный вопрос является вероятность (P(B_2|A)).
Из нашей таблицы: $$ P(B_2)cdot P(A|B_2)=0,07; P(A)=0,2 $$ Получаем: $$ P(B_2|A)=frac=frac=0,35 $$ Т.е. 11Б дает 35% всех знатоков математики в этой школе.
Если сравнить апостериорную вероятность (P(B_2|A)=0,35) с априорной вероятностью (P(B_2)=0,35), они равны. Событие A не повлияло на оценку вклада 11Б в интеллектуальный багаж школы, он находится на среднем уровне.
Теперь найдем вероятность того, что произвольно взятый знаток математики учится в 11А: begin P(B_1|A)=frac=frac=0,5\ P(B_1|A)gt P(B_1) end Вклад 11А по факту (апостериорная вероятность 0,5) оказывается большим, чем ожидалось по количеству учеников (априорная вероятность 0,35). 50% знатоков всей школы – из этого класса.
Наконец, найдем вероятность того, что произвольно взятый знаток математики учится в 11В: begin P(B_3|A)=frac=frac=0,15\ P(B_3|A)lt P(B_3) end Вклад 11В по факту (апостериорная вероятность 0,15) оказывается меньшим, чем ожидалось по количеству учеников (априорная вероятность 0,3). Только 15% знатоков всей школы – из этого класса.
п.5. Примеры
Пример 1. Двигатель работает в трех режимах: нормальном (65% времени), форсированном (25% времени) и холостом. Вероятность поломки в каждом из режимов соответственно равна (p_1=0,1; p_2=0,8; p_3=0,05).
а) найдите вероятность поломки двигателя во время работы;
б) двигатель сломался. Какова вероятность, что он в этот момент работал в форсированном режиме?
а) Пусть событие A=«поломка двигателя», Bi — «работа в i-м режиме», (i=overline)
Необходимо найти полную вероятность (P(A)).
Составим таблицу:
| i | Режим | Часть времени (P(B_i)) |
Вероятность поломки (P(A|B_i)) |
(P(B_i)cdot P(A|B_i)) |
| 1 | Нормальный | 0,65 | 0,1 | 0,065 |
| 2 | Форсированный | 0,25 | 0,8 | 0,2 |
| 3 | Холостой | 0,1 | 0,05 | 0,005 |
| Всего | 1 | × | 0,27 | |
Вероятность поломки (полная вероятность): $$ P(A)=sum_^3 P(B_i)cdot P(A|B_i)=0,27 $$
б) Событие A=«поломка двигателя» произошло. Гипотеза B2 — «работа в форсированном режиме» при фактической поломке имеет вероятность: $$ P(B_2|A)=frac=frac=fracapprox 0,741 $$ Апостериорная вероятность (P(B_2|A)approx 0,741) больше априорной вероятности (P(B_2)=0,25).
Ответ: a) 0,27; б) (fracapprox 0,741)
Пример 2. В состязании лучников участвуют три стрелка. Вероятность попадания в мишень для каждого из них равна 0,3; 0,5 и 0,7. Один из стрелков стреляет и не попадает. Какова вероятность, что это был:
а) первый стрелок;
б) второй стрелок;
в) третий стрелок;
Пусть событие A=«промах», Bi — «выстрел i-го стрелка», (i=overline)
Т.к. стрелять мог любой из стрелков (P(B_i)=frac13) для каждого из них.
Чтобы найти вероятность промаха, нужно от 1 отнять вероятность попадания.
Составим таблицу:
| i | (P(B_i)) | Вероятность промаха (P(A|B_i)) |
(P(B_i)cdot P(A|B_i)) |
| 1 | (frac13) | 1-0,3=0,7 | (frac13cdot 0,7=frac) |
| 2 | (frac13) | 1-0,5=0,5 | (frac13cdot 0,5=frac) |
| 3 | (frac13) | 1-0,7=0,3 | (frac13cdot 0,3=frac) |
| ∑ | 1 | × | 0,5 |
Полная вероятность: $$ P(A)=sum_^3 P(B_i)cdot P(A|B_i)=frac+frac16+frac=0,5 $$ Промах произошел. Находим апостериорные вероятности для каждого стрелка: begin P(B_1|A)=frac=frac=fracapprox 0,467\ P(B_2|A)=frac=frac=fracapprox 0,333\ P(B_3|A)=frac=frac=frac=0,2\ end С точки зрения практической, можно сказать, что «вероятнее всего», это был первый стрелок.
Пример 3. Три фрилансера на площадке выполняют заказы в отношении по количеству 3:4:3. Доля успешно выполненных заказов для каждого из них составляет 98%, 95% и 90%.
а) найдите вероятность успешного выполнения заказа на площадке;
б) найдите вероятность неуспеха на площадке;
в) кто из фрилансеров, вероятнее всего, виноват в неуспешной работе?
Пусть событие A=«успех», Bi — «работа i-го фрилансера», (i=overline)
Составим таблицу успешной деятельности:
| i | (P(B_i)) | Вероятность успеха (P(A|B_i)) |
(P(B_i)cdot P(A|B_i)) |
| 1 | 0,3 | 0,98 | 0,294 |
| 2 | 0,4 | 0,95 | 0,38 |
| 3 | 0,3 | 0,9 | 0,27 |
| ∑ | 1 | × | 0,944 |
Вероятность успешного выполнения (полная вероятность): $$ P(A)=sum_^3 P(B_i)cdot P(A|B_i)=0,944 $$ б) Вероятность неуспеха (противоположное событие): $$ P(overline)=1-P(A)=1-0,944=0,056 $$ в) Составим таблицу неуспешной деятельности:
| i | (P(B_i)) | Вероятность неуспеха (P(overline|B_i)) |
(P(B_i)cdot P(overline|B_i)) |
| 1 | 0,3 | 1-0,98=0,02 | 0,006 |
| 2 | 0,4 | 1-0,95=0,05 | 0,02 |
| 3 | 0,3 | 1-0,9=0,1 | 0,03 |
| ∑ | 1 | × | 0,056 |
Ответ: а) 0,944; б) 0,056; в) третий фрилансер.
Пример 4. Докажите, что если полная вероятность события A равна $$ P(A)=sum_^k P(B_i)cdot P(A|B_i) $$ то вероятность противоположного события равна (P(overline)=1-P(A)).
Теория вероятностей
В этой статье мы расскажем кратко о том, что такое вероятность события. Дадим определение вероятности, введем понятия зависимых и независимых, совместных и несовместных событий. Объясним, что такое сумма событий и произведение событий.
Больше задач – в статье «Задание 2 Профильного ЕГЭ по математике. Теория вероятностей».
Случайным называется событие, которое невозможно точно предсказать заранее. Оно может либо произойти, либо нет. Теория вероятностей изучает случайные события и их закономерности, а также случайные величины и действия над ними.
Благоприятным мы называем исход, способствующий наступлению данного события.
Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.
Очевидно, что вероятность – величина положительная и не может быть больше единицы.
Например, перед экзаменом вы выучили 3 билета из 20. Вероятность вытянуть счастливый билет равна
Вот две простых задачи из вариантов ЕГЭ, где применяется определение вероятности:
1. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Иванов высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Иванову достанется удобное место, если всего в самолёте 300 мест.
В самолете 21+18=30 мест, удобных для Иванова. Всего в самолете 400 мест. Поэтому вероятность того, что пассажир Иванов получит удобное место, равна 30 : 300 = 0,1.
Просто применили определение вероятности.
2. В группе туристов 32 человека. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист К. полетит пятым рейсом вертолёта.
Каждый рейс, в том числе и пятый, перевозит 4 человек из 32. Вероятность полететь пятым рейсом:
События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.
Например, вы бросаете монету. «Выпал орел» и «выпала решка» — несовместные события.
Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.
Вероятность суммы несовместных событий равна сумме их вероятностей.
Вы бросаете игральную кость. Вероятность выпадения «тройки» равна Вероятность выпадения «шестерки» также равна
Вероятность выпадения числа, которое делится на 3,
Произведение двух событий – термин, означающий, что произошло и одно, и другое событие.
События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.
Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.
3. Говорят, что в старину каждый десятый на Руси был Иван, а каждый двадцатый Петр. Если это верно, то кого было больше: Иванов Петровичей или Петров Ивановичей?
Можно по-разному решать эту задачу, и вероятностный подход здесь тоже применим. Посчитаем вероятности двух событий
Событие А. Случайно выбранного мужчину зовут Иван Петрович
Событие В. Мужчину зовут Петр Иванович.
Вероятность быть Иваном Петровичем для жившего в старину россиянина равна Мы перемножили вероятности того, что наш древнерусский житель – Иван и что его отца зовут Петр.
А вероятность оказаться Петром Ивановичем точно такая же:
4. (ЕГЭ) Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с ве-роятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Шахматист А. играет две партии, одну – белыми фигурами, другую – черными. События «выиграть белыми» и «выиграть черными фигурами» независимы. Вероятность того, что шахматист А. выиграет оба раза, равна произведению вероятностей выигрышей в каждой партии: 0,5 · 0,32 = 0,16.
5. (ЕГЭ) В классе 26 человек, среди них два друга — Андрей и Сергей. Класс случайным образом разбивают на 2 группы по 13 человек. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
Пусть Андрей первым занял место в группе (неважно, в какой). И, кроме него, осталось еще 25 человек, среди которых его друг Сергей. Сколько у Сергея шансов оказаться в той же группе, что и Андрей? В группе должно быть 13 человек, то есть Андрей и еще 12. Значит, вероятность того, что Сергей окажется в той же группе, что и Андрей, равна , то есть 0,48.
Следующую задачу можно решить методами комбинаторики – например, с помощью формулы Бернулли. Однако в обычной школе не изучают комбинаторику, и тем не менее эта задача появилась в сборниках для подготовки к ЕГЭ.
6. Монету бросают 10 раз. Во сколько раз событие «Орел выпадет ровно 8 раз» более вероятно, чем событие «Орел выпадет ровно 9 раз»?
Начнем с числа возможных исходов. Если мы бросаем монету, возможных исходов два – орел или решка.
Бросим монету два раза (или две монеты одновременно, все равно). И вот уже 4 возможных исхода:
ОО
ОР
РО
РР
(буквой О обозначен выпавший «орел», буквой «р» — решка.
Каждый следующий бросок монеты увеличивает число возможных исходов в 2 раза (орел или решка).
Для 10 бросков монеты количество возможных исходов, очевидно, равно
По определению, вероятность равна отношению числа благоприятных исходов к общему числу исходов.
Рассмотрим случай, когда орел выпадет ровно 9 раз из 10 бросков монеты. Это значит, что решка выпала ровно 1 раз.
Это могло произойти при первом броске, при втором, при третьем… и, наконец, при десятом, всего 10 благоприятных исходов. Вероятность выпадения решки ровно 1 раз из 10 бросков
Теперь случай, когда орел выпал ровно 8 раз из 10 бросков монеты. Значит, решка выпала ровно 2 раза.
Пронумеруем броски: 1,2,3…10.
Решка могла выпасть в первый и во второй раз. Обозначим эту комбинацию 12.
Могла также выпасть в первый и третий раз, в первый и четвертый… Эти комбинации обозначаем как 13, 14…
Пронумеруем таким образом все благоприятные исходы.
12, 13, 14, 15, 16, 17, 18, 19, 1 10
23, 24, 25, 26, 27, 28, 29, 2 10
34, 35, 36, 37, 38, 39, 3 10
45, 46, 47, 48, 49, 4 10
56, 57, 58, 59, 5 10
9 10
Количество благоприятных исходов равно 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45.
Поделив на , получим, во сколько раз выпадение решки ровно 8 раз более вероятно, чем выпадение решки ровно 9 раз:
Разберем какую-нибудь типовую задачу ЕГЭ по теме «Теория вероятностей». Такую, в которой мы рисуем «дерево» возможных исходов.
7. (ЕГЭ) Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Изобразим все возможные исходы.

По условию, купленное в магазине стекло для автомобильной фары оказалось бракованным. Как это могло получиться?
Стекло сделано либо на первой фабрике, либо на второй. Эти события несовместны.
Вероятность того, что стекло с первой фабрики, равна 0,45.
Вероятность того, что стекло сделано на второй фабрике, равна 0,55.
Первая фабрика выпускает 3% бракованных стекол. Значит, с вероятностью 0,03 стекло, произведенное на первой фабрике, бракованное.
Вторая фабрика выпускает 1% бракованных стекол. Значит, с вероятностью 0,01 сделанное на ней стекло бракованное.
Покупатель купил бракованное стекло. Оно могло быть сделано на первой фабрике и оказалось бракованным. Это означает одновременное наступление, или произведение, двух независимых случайных событий – «стекло сделано на первой фабрике» и «стекло бракованное». Вероятность произведения этих двух событий равна
Или другой случай. Стекло могло быть со второй фабрики и также бракованное. Вероятность одновременного наступления этих двух событий равна События «стекло с первой фабрики» и «стекло со второй фабрики» несовместны – они не могут случиться одновременно.
Вероятность суммы несовместных событий равна сумме вероятностей.
Значит, вероятность купить бракованное стекло равна:
Следующая задача будет интересна и старшеклассникам, и студентам. В самом деле – как быть, если вы пришли на экзамен, выучив всего 20 билетов из 30? Идти отвечать первым? Или вторым? Или предпоследним? В каком случае вероятность вытянуть билет, который ты выучил, будет наибольшей?
8. Экзамен проходит по следующей схеме: если некоторый билет уже был вытянут, то после ответа экзаменатор откладывает его в сторону. Студент выучил 20 билетов из 30. Когда ему выгоднее идти, первым или вторым, чтобы вероятность вынуть выученный билет была больше?
Назовем билеты, которые студент выучил, «счастливыми».
Если студент пошел отвечать первым, вероятность вытянуть «счастливый» билет равна
Если идти отвечать вторым, возможны два случая:
1) Первый билет, который вытянул кто-то другой, был «счастливым», и тогда «счастливых» билетов теперь 19.
2) Первый билет не был «счастливым», и «счастливых» билетов так и осталось 20.
Нарисуем схему возможных исходов, как всегда делаем в подобных задачах:

Вот наш студент идет отвечать вторым. Вероятность вытянуть «счастливый» билет равна Удивительный ответ! Та же самая вероятность! Значит, неважно, первым или вторым идти отвечать, если ты выучил 20 билетов из 30.
Конечно, это были самые простые задачи по теории вероятностей. Такие, которые встречаются на ЕГЭ по математике.
Зависимые и независимые случайные события.
Основные формулы сложения и умножения вероятностей
Понятия зависимости и независимости случайных событий. Условная вероятность. Формулы сложения и умножения вероятностей для зависимых и независимых случайных событий. Формула полной вероятности и формула Байеса.
Теоремы сложения вероятностей
Найдем вероятность суммы событий Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:
Пример 1. Вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12; 45-го — 0,04; 46-го и большего — 0,01. Найти вероятность того, что будет продана пара мужской обуви не меньше 44-го размера.
Решение. Искомое событие ), т. е. событие . События несовместны. Поэтому согласно теореме о сумме вероятностей получаем
Пример 2. При условиях примера 1 найти вероятность того, что очередной будет продана пара обуви меньше 44-го размера.
Решение. События «очередной будет продана пара обуви меньше 44-го размера» и «будет продана пара обуви размера не меньше 44-го» противоположные. Поэтому по формуле (1.2) вероятность наступления искомого события
поскольку , как это было найдено в примере 1.
Теорема 2.1 сложения вероятностей справедлива только для несовместных событий. Использование ее для нахождения вероятности совместных событий может привести к неправильным, а иногда и абсурдным выводам, что наглядно видно на следующем примере. Пусть выполнение заказа в срок фирмой «Electra Ltd» оценивается вероятностью 0,7. Какова вероятность того, что из трех заказов фирма выполнит в срок хотя бы какой-нибудь один? События, состоящие в том, что фирма выполнит в срок первый, второй, третий заказы обозначим соответственно . Если для отыскания искомой вероятности применить теорему 2.1 сложения вероятностей, то получим . Вероятность события оказалась больше единицы, что невозможно. Это объясняется тем, что события являются совместными. Действительно, выполнение в срок первого заказа не исключает выполнения в срок двух других.
Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления).
Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:
Зависимые и независимые события. Условная вероятность
Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.
Пример 3. Монета брошена два раза. Вероятность появления «герба» в первом испытании (событие независимыми в совокупности , если любое из них не зависит от любого другого события и от любой комбинации остальных.
События называются зависимыми , если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события условной вероятностью события .
Условие независимости события , а условие его зависимости — в виде . Рассмотрим пример вычисления условной вероятности события.
Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.
Решение. Обозначим . Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.
Следовательно, вероятность события
Формулы умножения вероятностей
Пусть события Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Пример 5. Три ящика содержат по 10 деталей. В первом ящике — 8 стандартных деталей, во втором — 7, в третьем — 9. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение. Вероятность того, что из первого ящика взята стандартная деталь (событие . Вероятность того, что из второго ящика взята стандартная деталь (событие . Вероятность того, что из третьего ящика взята стандартная деталь (событие ), . Так как события независимые в совокупности, то искомая вероятность (по теореме умножения)
Пусть события и известны. Найдем вероятность произведения этих событий, т. е. вероятность того, что появится и событие Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.
Пример 6. В урне находятся 5 белых шаров, 4 черных и 3 синих. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие ).
Решение. Вероятность появления белого шара при первом испытании . Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, т. е. условная вероятность . Вероятность появления синего шара при третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором — черный, . Искомая вероятность
Формула полной вероятности
Теорема 2.5. Если событие , образующих полную группу несовместных событий, то вероятность события на соответствующую условную вероятность события :
При этом события называются гипотезами, а вероятности — априорными. Эта формула называется формулой полной вероятности.
Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков не одинакова. На первом станке изготовляют 50% всех деталей, на втором — 30%, на третьем — 20%. Вероятность качественной сборки при использовании детали, изготовленной на первом, втором и третьем станке, соответственно 0,98, 0,95 и 0,8, Определить вероятность того, что узел, сходящий с конвейера, качественный.
Решение. Обозначим , и — события, означающие, что детали сделаны соответственно на первом, втором и третьем станке. Тогда
Формула Байеса
Эта формула применяется при решении практических задач, когда событие , образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез . Априорные (до опыта) вероятности известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности . Для гипотезы формула Байеса выглядит так:
Раскрывая в этом равенстве по формуле полной вероятности (2.1), получаем
Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный.
Теория вероятностей для самых маленьких
В этой статье мы рассмотрим основы статистики, полезные изучающим машинное обучение, а также желающим освежить свои знания. Понятия, о которых пойдет речь ниже, встречаются в очень разнообразных контекстах, а также лежат в основе всеми любимого data science. Всегда полезно повторить азы теории, так как зачастую это помогает открыть для себя что-то новое, на что раньше не обращали внимание. Поэтому, начнем.
Вероятности
Зачем нам нужны вероятности, когда мы обладаем таким мощным математическим инструментарием? У нас есть матанализ для работы с функциями на бесконечно малых величинах и оценки их динамики. У нас есть алгебра для решения уравнений, а также десятки других областей математики, с помощью которых мы можем решить едва ли не любую задачу.
Проблема в том, что мы живем в хаотичной вселенной, где точные измерения чаще всего невозможны. Изучая реальные процессы, происходящие в мире, мы хотим понять, какие случайные события влияют на наши эксперименты. Нас окружает неопределенность, и важно уметь «обуздать» и использовать ее в своих целях. Именно в такие моменты в ход идет теория вероятностей и статистика.
В наш век именно эти дисциплины лежат в основе искусственного интеллекта, физики элементарных частиц, обществознания, биоинформатики.
Перед тем как говорить о статистике, необходимо определиться с понятием вероятности. Как ни странно, однозначного ответа нет. Рассмотрим несколько теоретических подходов к определению вероятности.
Частотная вероятность
Представим, что нам дали монету, и мы хотим определить является ли она честной. Как это можно сделать? Подбросим ее несколько раз и запишем как 1, если выпадет орёл, 0 – если выпадет решка. Повторим этот эксперимент 1000 раз, и подсчитаем все 0 и 1. Допустим, по результатам этого утомительного процесса мы насчитали 600 орлов (1) и 400 решек (0). Если мы посчитаем частоту, с которой нам выпадал орёл или решка, мы получим 60% и 40%, соответственно. Эти частоты могут интерпретироваться как вероятности того, что, подбросив монету, нам выпадет орёл или решка. Такой подход к вероятностям называется частотным.
Условные вероятности
Зачастую нам нужно узнать вероятность наступления события при условии, что произошло другое событие. В этом случае, мы указываем условную вероятность события A при условии, что произошло событие B как P (A | B). Рассмотрим это на примере дождя:
- Какова вероятность дождя, если мы слышим раскаты грома?
- Какова вероятность дождя, если на улице солнце?
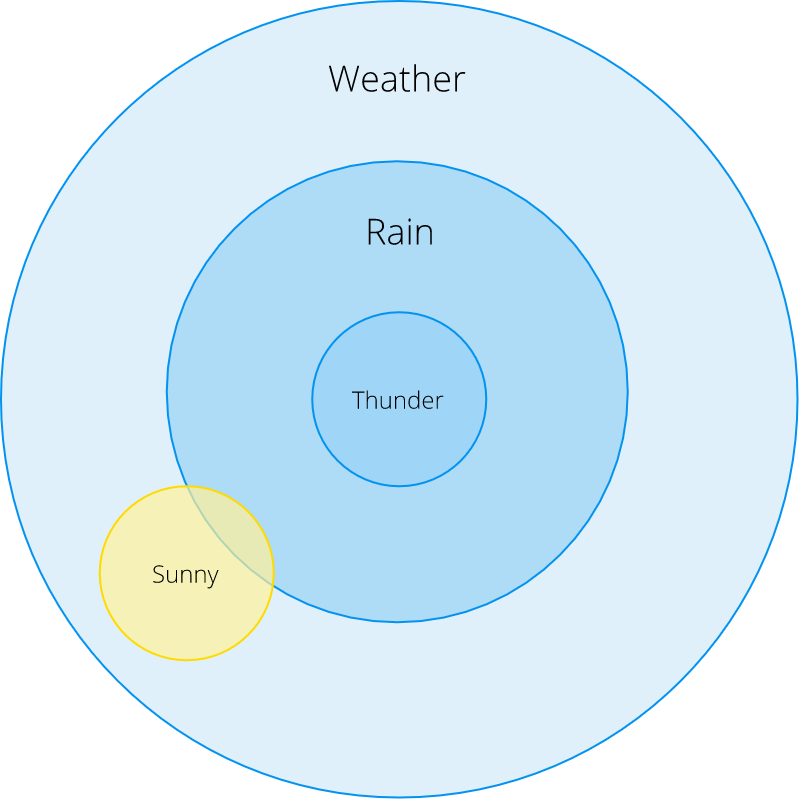
Из этой диаграммы Эйлера мы видим, что P (Дождь | Гром) = 1: дождь идет всегда, когда мы слышим раскаты грома и видим молнии (в реальности это не всегда так, но примем условности для целей нашего примера).
А что насчет P (Дождь | Солнце)? На глаз, эта вероятность достаточно мала, но есть ли способ рассчитать ее точно? Условная вероятность определяется как:
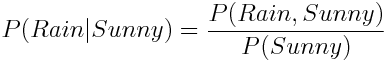
Иными словами, мы должны поделить вероятность наступления обоих событий – Дождя и Солнечной погоды на вероятность события Солнечная погода.
Зависимые и независимые события
События называются независимыми, если вероятность наступления любого из них никак не зависит от наступления других событий. Например, рассмотрим вероятность того, чтобы бросить игральные кости и выкинуть две двойки подряд. Это независимые события. Иными словами,
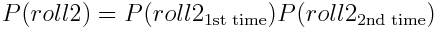
Но почему эта формула работает? Для начала обозначим броски №1 и №2 как A и B, чтобы упростить формулу, а далее перепишем вероятность бросания костей как вероятность появления двух независимых событий:

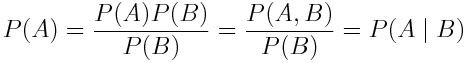
Если формулу выше прочитать справа налево, мы увидим, что P (A | B) = P(A). По сути, это означает, что событие A не зависит от события B. Такая же логика справедлива и в отношении P(B).
Байесовский подход к вероятности
Существует еще один подход к определению вероятностей, который называется Байесовским. Частотный подход к статистике предполагает существование одной оптимальной и конкретной комбинации параметров для модели. Частотная статистика работает с неопределенностью через достаточно сложные для понимания доверительные интервалы (confidence interval). К примеру, 95% доверительный интервал в частотной статистике означает, что если бы мы проводили измерение бесконечное количество раз, то истинное значение параметра попадало бы в этот интервал в 95% случаев. Сбивает с толку, да?
С другой стороны, Байесовская теорема подходит к параметрам с вероятностных позиций и рассматривает их как случайные величины. В Байесовской статистике каждый параметр обладает собственным распределением вероятности, которое отражает, насколько вероятны данные параметры, учитывая имеющиеся в наличии данные. Математически это можно представить как:

В отличие от частотного подхода, Байесовская статистика работает с неопределенностью через достоверные интервалы (credible interval), которые интуитивно понятны. 95% достоверный интервал означает, что значение измеряемого параметра попадает в него с 95% вероятностью.
В этой ветке статистики все крутится вокруг теоремы, позволяющей рассчитать условные вероятности исходя из накопленных знаний:
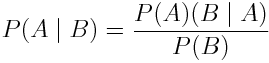
Несмотря на кажущуюся простоту, Теорема Байеса имеет огромную ценность, она применяется в различных областях, и даже существует отдельная ветвь статистики, которая называется Байесовская статистика. Если интересно понять, как выводится эта формула, то вот ссылка на отличный пост, посвященный Теореме Байеса.
Распределения
Распределение вероятностей – это закон, описывающий вероятности наступления всех возможных исходов какой-либо случайной величины, выраженных в виде математической функции. Как и любая функция, распределение может обладать параметрами, позволяющими скорректировать его характеристики.
Когда мы измеряли относительную частоту исходов такого события как подбрасывание монеты, мы на самом деле рассчитали так называемое эмпирическое распределение вероятностей. Многие процессы, отличающиеся неопределенностью, могут быть описаны в терминах распределения вероятностей. Так, например, подбрасывание монеты описывается распределением Бернулли, а если бы мы захотели рассчитать вероятность, что после n попыток выпадет орел, мы можем прибегнуть к Биномиальному распределению.
Для удобства работы с вероятностями введем новое понятие, аналогичное переменной, — случайная переменная. Каждая случайная переменная соответствует определенному распределению. Случайные величины принято обозначать заглавной буквой, а также мы можем использовать символ ~, чтобы обозначить, какому распределению соответствует переменная.

Это означает, что случайная переменная X описывается распределением Бернулли, при этом вероятность успеха (выпадение орла) равна 0,6.
Непрерывное и дискретное распределение вероятностей
Распределения вероятностей бывают двух типов. Дискретное распределение описывает случайные величины, которые принимают конечное число значений, как это было в примере с монетой и распределением Бернулли. Дискретные распределения определяются Функцией распределения масс (Probability Mass Function). Непрерывное распределение описывает непрерывные случайные величины, которые (в теории) могут принимать бесчисленное число значений. Например, когда мы измеряем скорость и ускорение датчиками с высокими шумами. Непрерывные распределения определяются Функцией плотности распределения вероятности (Probability Density Function).
При расчете статистик для дискретного распределения вероятностей применяется суммирование ∑, а для непрерывного – интегралы ∫. Например, математическое ожидание будет иметь следующий вид:


Выборки и статистики
Представим, что мы хотим измерить рост людей в своем городе. Чтобы измерения были независимыми, мы оценивали рост случайных прохожих на улице. Процесс случайного отбора подмножества данных из общей (генеральной) совокупности называется выборкой.
Выборка сама по себе достаточно сложна для понимания. Для того, чтобы описать ее более понятным для человека способом используются статистические показатели – обобщающие математические функции.
С одним таким показателем вы скорее всего уже сталкивались – это арифметическое среднее.
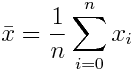
Другой пример – это дисперсия выборки:
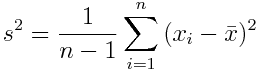
Данная формула характеризует разброс значений в массиве данных относительно среднего.
А если я хочу узнать больше?
Знания статистики могут пригодиться в самых неочевидных ситуациях. Как сказал известный статист Джон Тьюки: «The best thing about being a statistician is that you get to play in everyone’s backyard».
Вот небольшая подборка ресурсов для продолжения изучения математической статистики:
Вычисление вероятности
Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.
Вероятность
Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…
Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться.
Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов.
Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат.
Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом.
По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив.
Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:
- выпадет орел;
- выпадет решка.
Эти два события образуют множество элементарных событий.
Множество элементарных событий — множество всех возможных результатов случайного эксперимента.
В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации.
Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран.
Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности.
Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу.
Вероятность можно обозначить, как P(x), где х — некоторое событие.
Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.
Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.
Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна (P = frac = 1), то есть мы точно выиграем спор.
Однако вероятность не так проста, и даже здесь подготовила ловушку.
Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%.
Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?
Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна
(frac = 0,35)
Выразим в процентах:
0,35 * 100% = 35%
Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ.
Ответ: 0,35
Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой.
Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.
Равновозможные и противоположные события
Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными.
Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие.
Вероятности появления событий равны.
Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий.
Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них.
В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий.
Мы подбросили монету и выпал орел. Следовательно, не выпала решка.
А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными.
Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как (overline).
Заметим, что вероятность события A равняется 12, как и вероятность события (overline). Чему равна их сумма?
Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1.
Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить.
Объединение и пересечение событий
Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим?
Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий.
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег.
Объединение событий обозначается знаком (cup). Объединение событий А и В можно записать как (A cup B).
Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?
Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям.
Пересечение событий обозначается знаком (cap). Пересечение событий А и В можно записать как (A cap B).
Несовместные и совместные события
Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.
Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно.
Несовместные события — такие события, появление одного из которых исключает появление другого.
Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?
Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности.
Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.
Сформулируем определение суммы вероятностей двух несовместных событий.
Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:
(P(A cup B) = P(A) + P(B))
Если существуют несовместные события, то существуют и совместные.
Совместные события — события, наступление одного из которых не исключает наступления другого.
В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят? Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет.
Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”.
Найдем вероятность события А: (frac).
Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна (frac = frac)
Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А.
Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги.
А нужно получить вот такую картину:
Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок.
Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:
(P(A cup B) = P(A) + P(B) — P(A cap B))
В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике.
Независимые и зависимые события
Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем.
Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна (frac = 0,95).
Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?
Ответим на вопрос: зависят ли булочки друг от друга?
Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми.
Независимые события — такие события, появление одного из которых не зависит от появления другого события.
Определим вероятность независимых событий.
Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95.
А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:
(P(A cap B) = P(A) * P(B))
Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025.
В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”.
Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой.
Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого.
Но если автоматы стоят рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого.
Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?
Нужная последовательность может быть в двух случаях:
- сначала вытащат фиолетовый кубик и потом снова фиолетовый;
- сначала вытащат оранжевый кубик, а потом фиолетовый.
Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна (frac). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые.
Вероятность вытащить во второй раз фиолетовый кубик равна (frac * frac = frac = frac).
Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна (frac). В мешке останется шесть кубиков, пять из которых будут фиолетовыми.
Вероятность вытащить во второй раз фиолетовый кубик будет уже равна (frac * frac = frac = frac).
В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы.
Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.
Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.
Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность.
Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:
(P(A cap B) = P(A) * P(B | A))
Формула Бернулли
Рассмотрим случаи, когда испытание повторяется многократно. Для этого еще раз обратимся к игральному кубику. Подбросим кубик 8 раз. Какова вероятность, что цифра 5 выпала ровно три раза?
Пусть p — вероятность, что выпадет цифра 5. Тогда (p = frac).
Теперь возьмем q — противоположное р событие — вероятность, что цифра 5 не выпадет. (q = frac).
Обозначим количество всех бросков за n, а количество выпадения цифры 5 за k.
Чтобы решить задачу, нужно воспользоваться формулой Бернулли.
Множитель (C_n^k) — это число сочетаний. Подробнее узнать про сочетания можно в статье «Основы комбинаторики».
Решим задачу, подставив значения в формулу:
Фактчек
- Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
- События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
- События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A (cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A cup B) = P(A) + P(B) — P(A cap B).
- События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A cap B) = P(A) * P(B | A).
- Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Проверь себя
Задание 1.
Какие события являются несовместными?
- Подбрасывание монетки.
- Брак батареек в одной упаковке.
- “Миша идет” и “Миша стоит”.
- Случайное вытаскивание конфет из вазы.
Задание 2.
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?
Задание 3.
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?
Задание 4.
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут.
Задание 5.
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой.
Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1
Зависимые и независимые события. Условная вероятность. Умножение вероятностей зависимых событий. Примеры
События А, Б, В. называют зависимыми друг от друга, если вероятность появления хотя бы одного из них изменяется в зависимости от появления или непоявления других событий. События называются независимыми, если вероятности появления каждого из них не зависят от появления или непоявления прочих из них.
Условной вероятностью (РA (В)-условная вероятность события В относительно А) называют вероятность события В, вычисленную в предположении, что событие А уже наступило. пример условной вероятности Условная вероятность события В при условии, что событие А уже наступило, по определению, равна РA (В) = Р (АВ) / Р (А) (Р(A)>0).
Умножения вероятностей зависимых событий: вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р (АВ) = Р (А) РA (В)
Пример. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков — конусный, а второй — эллиптический.
Решение:Вероятность того, что первый валик окажется конусным (событие A), Р (А) = 3 / 10. Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик — конусный, т. е. условная вероятность РA (В) = 7 / 9.
По формуле умножения, искомая вероятность Р (АВ) = Р (А) РA (В) = (3 / 10) * (7 / 9) = 7 / 30. Заметим, что, сохранив обозначения, легко найдем: Р (В) = 7 / 10, РB (А) = 3 / 9, Р (В) РB (А) = 7 / 30
Условие независимости событий. Умножение вероятностей независимых событий. Примеры.
Событие В не зависит от события А, если
Р(В/А) = Р(В) т.е. вероятность события В не зависит от того, произошло ли событие А.
В этом случае и событие А не зависит от события В, тоесть свойство независимости событий является взаимным.
Вероятность произведения двух независимых событий равна произведению их вероятностей:
Пример 1: Прибор, работающий в течение времени t, состоит из трех узлов, каждый из которых, независимо от других, может в течение времени t отказать (выйти из строя). Отказ хотя бы одного узла приводит к отказу прибора в целом. За время t надежность (вероятность безотказной работы) первого узла равна p1= 0,8; второго p2 = 0,9 третьего p3 = 0,7. Найти надежность прибора в целом.
Решение. Обозначая:
A – безотказная работа приборов,
A1 — безотказная работа первого узла,
A2— безотказная работа второго узла,
A3 — безотказная работа третьего узла,
откуда по теореме умножения для независимых событий
Пример 2. Найти вероятность совместного появления цифры при одном подбрасывании двух монет.
Решение. Вероятность появления цифры первой монеты (событие А) Р(А) = 1/2; вероятность появления цифры второй монеты (событие В)- Р(В) = 1/2.
События А и В независимы, поэтому искомую вероятность найдем
Р(АВ) = Р(А)Р(В) = 1/2 *1/2 = 1/4
Совместность и несовместность событий. Сложение вероятностей двух совместных событий. Примеры.
Два события называются совместными, если появление одного из них не влияет и не исключает появление другого. Совместные события могут реализоваться одновременно, как, например, появление какого-либо числа на одной кости ни
коим образом не влияет на появление чисел на другой кости. События несовместны, если в одном явлении или при одном испытании они не могут реализоваться одновременно и появление одного из них исключает появление другого (попадание в цель и промах несовместны).
Вероятность появления хотя бы одного из двух совместных событий A или B равна сумме вероятностей этих событий без вероятности их совместного появления:
Пример. Вероятность попадания в мишень для первого спортсмена 0,85, а для второго — 0,8. Спортсмены независимо друг от друга
сделали по одному выстрелу. Найти вероятность того, что в мишень попадет хотя бы один спортсмен?
Решение. Введем обозначения: события А — «попадание первого спортсмена», В — «попадание второго спортсмена», С -«попадание хотя бы одного из спортсменов». Очевидно, А + В = С, причем события А и В совместны. В соответствии с формулой получаем:
P(C) = Р(А) + Р(В) — Р(АВ)
поскольку А и В — независимые события. Подставив данные значения Р(А) = 0,85, Р(В) = 0,8 в формулу для Р( C) , найдем искомую вероятность






