Что такое сумма событий

Основные сведения о сложении и умножении вероятностей

Теория вероятностей — раздел математической науки, изучающий случайные события и величины, их свойства, а также операции, которые можно совершить с ними.

Теорию вероятностей изучают на уроках алгебры в 9 классе.

Для чего нужно знать теорию вероятностей

Базы теории вероятностей необходимо знать каждому для того, чтобы сформировать правильное мировоззрение, для понимания того, что люди живут в вероятностном, случайном мире, в котором происходят самые случайные события, а закономерности проявляются через тысячи случайностей.

Чем сложнее система, тем намного труднее найти закономерности. В данных случаях пользуются вероятностными методиками. Так получается, что теория вероятности крайне актуальна в современном мире как в точных науках, математике, так и в обычной жизни.

Что изучает теория вероятностей

Теория вероятностей занимается изучением объективных закономерностей случайных событий. Считается основной теории для статистики в математике, которая занимается разработкой методик сбора, обработки и описания итогов наблюдений. Посредством наблюдений (например, экспериментов, испытаний) совершается познание процессов реального мира.

Базовыми объектами теории вероятностей являются случайные величины, события, процессы, то есть практически весь мир вокруг человека.

Событие — процесс, который может как произойти, так и нет в случае выполнения конкретного ряда условий, или же в процессе проведения экспериментов.

События бывают невозможные и достоверные. Если в процессе каждого эксперимента происходит какое-то событие, то такое событие называют достоверным. Если в процессе каждого эксперимента какое-то событие в принципе не может совершиться, то такое событие называют невозможным. Если событие не является ни достоверным, ни невозможным, то такое событие называют случайным.

Во многих сферах деятельности человека появляются ситуации, когда конкретные явления способны повторяться бесконечное число раз при одинаковых условиях. При анализе таких простых явлений, как, например, подбрасывание монетки, выброс карты, игральной кости, человек может заметить две особенности, которые присущи данным экспериментам.

1. Не представляется вероятным предсказывать результата будущего исследования по результатам предыдущих экспериментов, какое бы число исследований не было бы проведено.
2. Относительная частота конкретных результатов по мере того, как растет количество попыток, стабилизируется, медленно приближаясь к конкретному пределу.

Приведем пример теории вероятностей на простых примерах. Если в ящике находится 10 шаров, пронумерованных цифрами от 1 до 10, то существует вероятность в 10 % вытянуть шарик с числом 10. Однако более вероятным является случай вытягивания любого другого числа от 1 до 9, потому что данная вероятность — 90 %.

Самое важное понятие в теории вероятности — вероятность. Данное слово, синонимом которому служит слово «шанс», часто используют в жизни. Каждый встречал фразы типа: «Сегодня, вероятно, пойдет дождь», «вероятнее всего, футбольный матч закончится вничью» и т. д. Данные фразы на уровне интуиции оценивают процент вероятности того, будет ли конкретное событие или нет. Математические вероятности придают числовую оценку тому, что может произойти.

Теория вероятности должна учитываться в основе каждой человеческой деятельности. Из-за оценок шансов тех или иных неполадок (например, морского корабля), человек узнает, что может ожидать его в тысячах миль от суши. Возможности войны, экономического кризиса, падения курса валют — все можно вычислить в процентном соотношении. И совершить правильные контрдействия, исходя из данных анализа.

Человеком часто решения принимаются крайне эмоционально. Люди больше боятся погибнуть от нападения акулы, чем утонуть. Шанс погибнуть от того, что на человека нападет акула, составляет лишь 1 к 11,5 миллионам, шанс умереть от данного нападения еще меньше — всего 1 к 264,1 миллионам. В год в США умирает от того, что тонут, примерно 3306 человек, а от нападения акул только 1. Вероятность правит миром, нужно всегда помнить об этом. Они помогают взглянуть человеку на мир с точки зрения случая.

Теорию вероятностей возможно применять во всех сферах человеческой деятельности. Человек разумный обязан стремиться к тому, чтобы мыслить посредством законов вероятностей, что является одной из частей успеха. Если учитывать все законы вероятностей, учитывать неблагоприятные вероятности и предпринимать нужные контрдействия, то возможно упростить собственную жизнь, а также сэкономить временные ресурсы.

Виды событий и примеры

Как уже было сказано выше, существует три вида событий:

1. Достоверные.
2. Невозможные.
3. Случайные.

Достоверное событие — событие, которое должно точно произойти при реализации конкретной совокупности условий S. Примером достоверного события может служить: событие А — «вода располагается в сосуде в жидком состоянии». Оно является достоверным, при условии, что находится при нормальном атмосферном давлении, а также температуре выше 0 °C.

Невозможное событие — событие, которое точно не произойдет (заранее это известно), если будут реализованы конкретные условия. Примером невозможного события может быть: событие А — «вода расположена в сосуде в твердом состоянии» будет невозможным, если она будет находиться при нормальном атмосферном давлении, а также температуре +20 °C.

Случайное событие — событие, которое в процессе реализации условий S, может либо не произойти, либо произойти. Примером случайного события может быть монета, которую бросают. Событие А — «в процессе бросания выпал герб» будет случайным.

Основные теоремы теории вероятностей: сложение, умножение, формула полной вероятности

Операция сложения вероятностей будет означать связку «или», операция умножения вероятностей будет означать связку «и».

Сложение вероятностей

Сумма двух событий A и B будут называть событие A+B. Оно состоит в том, что может наступить или событие B, или событие A, или же оба события в одно и то же время. Если же события являются несовместимыми, последний вариант невозможен, таким образом возможно наступление или события B, или события A.

Это правило может распространяться на большое число слагаемых. Например, событие A 1 + A 2 + A 3 + A 4 + A 5 состоит в том, что может произойти одно из этих событий. Если события являются несовместимыми, то только одно событие может произойти из данной суммы: или событие A 1 , или A 2 и т. д.

Примеров сложения множество: событие B ¯ = B 2 + B 3 + B 4 + B 5 (в процессе броска игральной кости не может выпасть 5 очков) состоит в том, что может выпасть или 1, или 2, или 3, или 4, или 6 очков.

Умножение вероятностей

Произведение двух вероятностей A и B — событие A B , оно состоит в том, что события проявляются совместно. Другими словами, умножение A B будет следующим: в результате некоторых условий может наступить и событие A , и событие B . Это утверждение является справедливым для большого числа событий. Так, например, произведение A 1 A 2 A 3 … A 10 предусматривают, что в конкретных условиях может произойти и событие A 1 , и событие A 2 , и событие A 4 , и событие A 10 .

Приведем пример, в котором подбрасывают две монетки. Существуют следующие вероятности:

• A 1 — на первой монете будет орел;
• A 1 ¯ — на первой монете будет решка;
• A 2 — на второй монете будет орел;
• A 2 ¯ — на второй монете будет решка.

Так получается, что событие A 1 A 1 будет состоять в том, что на монетах (и на первой, и на второй) выпадает орел.

Событие A 2 ¯ × A 2 ¯ — на монетах выпадает решка (и на первой, и на второй).

Событие A 1 A 2 ¯ — на первой монете будет орел, а на второй монете будет решка.

Событие A 1 ¯ A 2 — на первой монете будет решка, а на второй монете будет орел.

Полная группа событий

Зависимое событие A способно произойти только в итоге реализации одной из несовместимых гипотез B 1 , B 2 , B 3 до бесконечности, они образуют полную группу событий. Пусть будут известны вероятности событий P ( B 1 ) , P ( B 2 ) , P ( B 3 ) , … , P ( B ∞ ) , а также соответствующие условные вероятности P b 1 ( A ) , P b 2 ( A ) , P b 3 ( A ) .

Вероятность реализации события A тогда будет равна P ( A ) = P ( B 1 ) × P b 1 ( A ) + P ( B 2 ) × P b 2 ( A ) + ∞ .

Приведенная выше формула является формулой полной вероятности.

В учебниках алгебры она формулируется при помощи теоремы, которую можно доказать очень просто: по алгебре событий A = B 1 A + B 2 A + B 3 A + . . . (случилось событие B 1 и после него случилось событие A или случилось событие B 2 и после него случилось событие A и так до бесконечности).

Из-за того, что гипотезы B 1 , B 2 , B 3 и до бесконечности являются несовместимыми, а событие A является зависимым, то по теореме сложения вероятностей несовместимых событий и теореме умножения вероятностей зависимых событий: P ( A ) = P ( B 1 A + B 2 A + B 3 A + … ) = P ( B 1 A ) + P ( B 2 A ) + P ( B 3 A ) + … = P ( B 1 ) × P b 1 ( A ) + P ( B 2 ) × P b 2 ( A ) + P ( B 3 ) × P b 3 ( A ) + …

Формулы по теории вероятности

События считаются независимыми, если вероятность реализации любого из этих событий не зависит от непоявления/появления других событий из множества событий (в абсолютно всех комбинациях).

Например, в процессе подбрасывания двух монет (возможно и большее число) вероятность того, что выпадет орел или решка на монете, не будет зависеть от того, что выпадает на иных монетах. Вероятность того, что выпадет определенная грань кубика во втором испытании, не зависит от того, какая грань выпадает в первом испытании.

Представим другую ситуацию. Событие A будет зависимым, если вероятность события P(A) будет зависеть от одного или большего числа произошедших событий. Например, A — из неполной колоды человеку сдают карту червовой масти. Вероятность данного события зависит от того, какие карты были извлечены ранее из колоды.

Приведем еще один пример: событие E — на экзамене учащемуся достается легкий билет. Если приходить не первым на экзамен, то событие E будет считаться зависимым, потому что вероятность P(E) будет зависеть от того, какие билеты были вытянуты однокурсниками.

Определить зависимость и независимость события можно двумя способами:

• провести собственный анализ;
• прочитать условия задачи.

Пространство элементарных события — множество разных результатов произвольного эксперимента. Пример: в процессе броска единственной игральной кости пространство элементарных событий буде P = w 1 , w 2 , w 3 , w 4 , w 5 , w 6 , где w будет выпадением очков.

Если невозможно, чтобы события произошли одновременно в одном эксперименте, то такие события называют несовместимыми. К примеру, в процессе бросания монеты не могут в одно время выпасть решка и орел. Самым простым примером несовместимых событий будет пара противоположных событий.

Противоположное событие может произойти тогда, когда событие A не может произойти. Событие, которое противоположно этому, обычно обозначают латинской буквой с чертой наверху. Например, A — студент сдал экзамен, а A ¯ — студент не сдал экзамен.

Умножение вероятностей взаимно зависимых случайных событий

Если наступление события повлияло на вероятность того, что второе событие наступит, то такое событие имеет название взаимно зависимого. Если события A и B взаимно зависимы, то условной вероятностью P a ( B ) будут называть вероятность события B, понимая, что событие A наступило.

Теорема умножения вероятностей взаимно зависимых событий. Вероятность произведения событий будет равна вероятности одного события из двух, умноженной на условную вероятность иного (при том, что есть первое), поэтому вычисляют его по формуле:

P ( A × B ) = P ( A ) × P b ( A ) или же P ( A × B ) = P ( A ) × P a ( B )

Самые важные формулы вероятностей из лекции:

Примеры решений задач с событиями

В ящике находится 26 лотерейных билетов, из них 3 будут с выигрышем. Нужно найти:

• вероятность того, что у первого билета будет выигрыш;
• вероятность того, что у второго билета будет выигрыш (с условием того, что первый билет уже не находится в ящике);
• вероятность того, что оба билета, которые берут подряд, будут выигрышные.

Нужно найти вероятность того, что первый билет выигрышный: P ( A ) = 3 26 = 0 , 115 .

Нужно найти вероятность того, что второй билет выигрышный с условием, что первый билет не находится уже в ящике: P a ( B ) = 2 25 = 0 , 08 .

Нужно найти вероятность того, что два взятых подряд билета будут выигрышными, то есть вероятность общей реализации двух зависимых событий, которая есть произведение вероятности первого события, а также условной вероятности второго события: P ( A ⏜ B ) = P ( A ) × P a ( B ) = 3 26 × 2 25 = 0 , 115 × 0 , 08 = 0 , 0092 .

Ответ: вероятность того, что два взятых подряд билета окажутся выигрышными — 0,0092.

Супермаркет получил поставку в ящиках с четырех разных оптовых складов: четыре ящика получили с первого склада, пять ящиков получили со второго, семь ящиков получили с третьего, четыре получили с четвертого склада. Случайным образом выбрали ящик для того, чтобы продать. Какова вероятность того, что это ящик с третьего или первого склада?

Всего ящиков получили: 4+5+7+4=20 ящиков. В этой задаче можно использовать быстрый метод оформления событий без расписывания латинскими буквами.

Согласно классическому определению: p 1 = 4 20 = 0 , 2 . Это вероятного продажи ящика с первого склада.

p 3 = 7 20 = 0 , 35 — вероятность продажи ящика с третьего склада.

Согласно теореме сложения несовместимых событий, будет p = p 1 + p 3 = 0 , 2 + 0 , 35 = 0 , 55 . Это вероятность продажи ящика с первого или третьего склада.

Ответ: вероятность того, что выбранный для продажи ящик окажется с первого либо третьего склада — 0,55.

Учебник по теории вероятностей

Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записывается как $A subset B$.

События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается очевидно: А = В.

Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.

Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:

Если случайные события $A_1, A_2, . A_n$ образуют полную группу несовместных событий, то имеет место равенство $P(A_1)+P(A_2)+. +P(A_n)=1.$ Такие события (гипотезы) используются при решении задач на полную вероятность.

Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:

Вероятность произведения зависимых событий вычисляется по формуле условной вероятности.

Примеры решений задач с событиями

Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Решение. Обозначим события: А – вынули белый шар из первого ящика,
;

— вынули черный шар из первого ящика,
;

В – белый шар из второго ящика,
;

— черный шар из второго ящика,
.

Нам нужно, чтобы произошло одно из событий или . По теореме об умножении вероятностей
, .
Тогда искомая вероятность по теореме сложения будет
.

Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха, в) хотя бы одного попадания; г) одного попадания.

Пусть А – попадание первого стрелка, ;

В – попадание второго стрелка, .

Тогда — промах первого, ;

Найдем нужные вероятности.

а) АВ – двойное попадание,

б) – двойной промах, .

в) А+В – хотя бы одно попадание,

г) – одно попадание,

Пример. Решить задачу, применяя теоремы сложения и умножения. Мастер обслуживает 3 станка, работающих независимо друг от друга. Вероятность того, что первый станок потребует внимания рабочего в течение смены, равна 0,4, второй — 0,6, третий – 0,3. Найти вероятность того, что в течение смены: а) ни один станок не потребует внимания мастера, б) ровно 1 станок потребует внимания мастера.

Вводим базовые независимые события $A_i$ = (Станок $i$ потребовал внимания рабочего в течение смены), $i=1, 2, 3$. По условию выписываем вероятности: $p_1=0,4$, $p_2=0,6$, $p_3=0,3$. Тогда $q_1=0,6$, $q_2=0,4$, $q_3=0,7$.

Найдем вероятность события $X$=(Ни один станок не потребует внимания в течение смены):

$$ P(X)=Pleft(overline cdot overline cdot overlineright)= q_1 cdot q_2 cdot q_3 = 0,6cdot 0,4 cdot 0,7 = 0,168. $$

Найдем вероятность события $Z$= (Ровно один станок потребует внимания в течение смены):

$$ P(Z)= \ = P(A_1) cdot Pleft(overline right) cdot Pleft(overline right) + Pleft(overlineright) cdot P(A_2) cdot Pleft(overline right) + Pleft(overline right) cdot Pleft(overline right) cdot P(A_3)=\ = p_1 cdot q_2 cdot q_3 + q_1 cdot p_2 cdot q_3 + q_1 cdot q_2 cdot p_3 =\ = 0,4cdot 0,4 cdot 0,7+0,6cdot 0,6 cdot 0,7+0,6cdot 0,4 cdot 0,3 = 0,436. $$

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Вероятность наступления хотя бы одного события

Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий?

Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема. Вероятность появления хотя бы одного из событий $A_1, A_2, . A_n$, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

$$ P(A)=1-Pleft(overlineright)cdot Pleft(overlineright)cdot . cdot Pleft(overlineright)= 1-q_1 cdot q_2 cdot . cdot q_n. $$

Если события $A_1, A_2, . A_n$ имеют одинаковую вероятность $p$, то формула принимает простой вид:

Примеры решений на эту тему

Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события (попадание первого орудия), (попадание второго орудия) и (попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям , и (т. е. вероятности промахов), соответственно равны:

Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События «машина работает» и «машина не работает» (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице:

Отсюда вероятность того, что машина в данный момент не работает, равна

Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.

Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Обозначим через А событие «при n выстрелах стрелок попадает в цель хотя бы один раз». События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула .

Теория вероятностей, формулы и примеры

Есть три группы событий: достоверные, невозможные и случайные. Часть из них можно объяснить при помощи математики и других точных наук. В этом материале расскажем про теорию вероятностей, рассмотрим формулы и примеры решения задач.

О чем эта статья:

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Событие и виды событий

Событие — это базовое понятие теории вероятности. События бывают достоверными, невозможными и случайными.

Достоверным является событие, которое в результате испытания обязательно произойдет. Например, камень упадет вниз.

Невозможным является событие, которое заведомо не произойдет в результате испытания. Например, камень при падении улетит вверх.

Случайным называется событие, которое в результате испытания может произойти, а может не произойти. Например, из колоды карт вытащили туза.

Обычно события обозначают большими латинскими буквами. Например, А — событие, при котором из колоды вытащили туза, D — событие, при котором из колоды вытащили семерку.

Несовместными называются события, в которых появление одного из событий исключает появление другого (при условии одного и того же испытания). Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с черточкой вверху. Например:

A₀ — в результате броска монеты выпадет орел;

Ā₀ — в результате броска монеты выпадет решка.

Полная группа событий — это множество несовместных событий, среди которых в результате отдельно взятого испытания обязательно появится одно из этих событий.

Алгебра событий

Операция сложения событий означает логическую связку ИЛИ, а операция умножения событий — логическую связку И.

Сложение событий

Суммой двух событий A и B называется событие A+B, которое состоит в том, что наступит или событие A, или событие B, или оба события одновременно. В том случае, если события несовместны, последний вариант отпадает, то есть может наступить или событие A, или событие B.

Правило распространяется и на большее количество слагаемых, например, событие A₁ + A₂ + A₃ + A₄ + A₅ состоит в том, что произойдет хотя бы одно из событий A₁, A₂, A₃, A₄, A₅, а если события несовместны — то одно и только одно событие из этой суммы: или событие A₁, или событие A₂, или событие A₃, или событие A₄, или событие A₅.

Событие (при броске игральной кости не выпадет 5 очков) состоит в том, что выпадет или 1, или 2, или 3, или 4, или 6 очков.

Событие B₁,2 = B₁ + B₂ (выпадет не более двух очков) состоит в том, что появится 1 или 2 очка.

Событие B_Ч = B₂ + B₄ + B₆ (будет чётное число очков) состоит в том, что выпадет или 2 , или 4 , или 6 очков.

Умножение событий

Произведением двух событий A И B называют событие AB, которое состоит в совместном появлении этих событий. Иными словами, умножение AB означает, что при некоторых обстоятельствах наступит и событие A, и событие B. Аналогичное утверждение справедливо и для большего количества событий: например, произведение A₁A₂A₃ … A₁₀ подразумевает, что при определенных условиях произойдет и событие A₁, и событие A₂, и событие A₃. и событие A₁₀.

Рассмотрим испытание, в котором подбрасываются две монеты, и следующие события:

A₁ — на 1-й монете выпадет орел;

Ā₁ — на 1-й монете выпадет решка;

A₂ — на 2-й монете выпадет орел;

Ā₂ — на 2-й монете выпадет решка.

событие A₁A₁ состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет орел;

событие Ā₂Ā₂ состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет решка;

событие A₁Ā₂ состоит в том, что на 1-й монете выпадет орел и на 2-й монете решка;

событие Ā₁A₂ состоит в том, что на 1-й монете выпадет решка и на 2-й монете орел.

Классическое определение и формула вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A.

Вероятность достоверного события равна единице.

Вероятность невозможного события равна нулю.

Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Таким образом, вероятность любого события удовлетворяет двойному неравенству 0 ≤ P(A) ≤ 1.

Как решать задачи по теории вероятности

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Вспоминаем основную формулу теории вероятности, которую мы привели выше. Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).

1.2.3. Сложение и умножение событий

Пожалуйста, запомните ВАЖНЕЙШЕЕ ПРАВИЛО, без которого освоить тервер просто нереально:

Сложение событий обозначает логическую связку ИЛИ,
а умножения событий – логическую связку И.

1) Суммой двух событий и называется событие которое состоит в том, что наступит или событие , или событие , или оба события одновременно. В том случае, если событияy несовместны, последний вариант отпадает, то есть может наступить или событие или событие .

Правило распространяется и на бОльшее количество слагаемых, например, событие состоит в том, что произойдёт хотя бы одно из событий , а если события несовместны – то одно и только одно событие из этой суммы: или событие , или событие , или событие , или событие , или .

Событие (при броске игральной кости не выпадет 5 очков) состоит в том, что выпадет 1, или 2, или 3, или 4, или 6 очков.

Все примеры ОСМЫСЛЕННО проговариваем ВСЛУХ!
Это важно.

Событие состоит в том, что выпадет не более двух очков (1 или 2 очка).

Событие состоит в том, что выпадет 2, или 4, или 6 очков (чётное число очков).

Событие заключается в том, что из колоды будет извлечена карта красной масти (черва или бубна), а событие – в том, что будет извлечена «картинка» (валет или дама или король или туз).

Чуть занятнее дело с событиями совместными:

Событие состоит в том, что из колоды будет извлечена трефа или семёрка или семёрка треф. Согласно данному выше определению, хотя бы что-то – или любая трефа или любая семёрка или их «пересечение» – семёрка треф. Легко подсчитать, что данному событию соответствует 12 элементарных исходов (9 трефовых карт + 3 оставшиеся семёрки).

Событие состоит в том, что завтра в 12.00 наступит ХОТЯ БЫ ОДНО из суммируемых совместных событий, а именно:

– будет только дождь / только гроза / только солнце;
– или наступит только какая-нибудь пара событий (дождь + гроза / дождь + солнце / гроза + солнце);
– или все три события появятся одновременно.

То есть, событие включает в себя 7 возможных исходов, которые, к слову, несовместны – по той причине, что любая «погодная комбинация» исключает появление других.

Второй столп алгебры событий:

2) Произведением двух событий и называют событие , которое состоит в совместном появлении этих событий, иными словами, умножение означает, что при некоторых обстоятельствах наступит и событие , и событие . Аналогичное утверждение справедливо и для бОльшего количества событий, так, например, произведение подразумевает, что при определённых условиях произойдёт и событие , и событие , и событие , …, и событие .

Рассмотрим испытание, в котором подбрасываются две монеты (не имеет значения, одновременно или нет) и следующие события:

– на 1-й монете выпадет орёл;
– на 1-й монете выпадет решка;
– на 2-й монете выпадет орёл;
– на 2-й монете выпадет решка.

Тогда:
– событие состоит в том, что на 1-й монете выпадет орёл и на 2-й орёл;
– событие состоит в том, что на 1-й монете выпадет решка и на 2-й решка;
– событие состоит в том, что на 1-й монете выпадет орёл и на 2-й монете выпадет решка;
– событие состоит в том, что на 1-й монете выпадет решка и на 2-й монете выпадет орёл.

Осмысливаем и проговариваем вслух!!

Давайте просуммируем данные события: . Как интерпретировать эту запись? Очень просто – умножение означает логическую связку И, а сложение – ИЛИ. Таким образом, эту сумму легко прочитать понятным человеческим языком: «выпадут два орла или две решки, или на 1-й монете выпадет орёл и на 2-й решка, или на 1-й монете выпадет решка и на 2-й монете орёл ».

Это был пример, когда в одном испытании задействовано несколько объектов, в данном случае две монеты. Другая распространенная в практических задачах схема – это повторные испытания, когда, например, один и тот же игральный кубик бросается 3 раза подряд. В качестве демонстрации рассмотрим следующие события:

– в 1-м броске выпадет 4 очка;
– во 2-м броске выпадет 5 очков;
– в 3-м броске выпадет 6 очков.

Тогда событие состоит в том, что в 1-м броске выпадет 4 очка и во 2-м броске выпадет 5 очков и в 3-м броске выпадет 6 очков.

…понимаю, что разбираются не очень интересные примеры, но это часто встречающиеся в задачах вещи и от них никуда не деться. Помимо монетки, кубика и колоды карт вас поджидают урны с разноцветными шарами, несколько стрелков, стреляющих по мишени, и неутомимый рабочий, который постоянно вытачивает какие-то детали =)

Полную и свежую версию этой книги в pdf-формате ,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

Теорема сложения вероятностей

Определение 4. Суммой двух событий Аи В называют событие С = А +В, которое заключается в наступлении либо события Л, либо события В, либо событий А и В одновременно.

Это определение напоминает определение суммы множеств*, что используется в теоретико-множественном подходе в теории вероятностей. Примеры суммы событий: произведены два выстрела, и события Аи В — попадания при первом и втором выстрелах соответственно; тогда А 4- В — попадание либо при первом выстреле, либо при втором, либо при обоих выстрелах. Если события А и В несовместные, то их сумма — это событие, состоящее в наступлении какого-либо одного из этих событий.

Аналогично определяется сумма нескольких событий, состоящая в наступлении хотя бы одного из этих событий.

Теорема 1.1. Вероятность появления какого-либо из двух несовместных событий равна сумме вероятностей этих событий:

Следствие 1.1. Вероятность появления какого-либо из нескольких попарно несовместных событий равна сумме их вероятностей:

По этой ссылке вы найдёте полный курс лекций по теории вероятности:

Пример 1.

Стрелок стреляет по мишени, разделенной на 4 концентрические зоны. Вероятности попадания в эти зоны соответственно равны 0,4; 0,3; 0,2 и 0,1. Найти вероятность попадания либо в первую, либо во вторую зону.

Решение. Пусть событие А — попадание в первую зону мишени, а событие В — попадание во вторую зону мишени. Эти события несовместны, поэтому применимы теорема 1.1 и формула (1.7) сложения вероятностей. Искомая вероятность

Полная группа событий

Теорема 1.2. Сумма вероятностей событий, образующих полную группу, равна единице:

Возможно вам будут полезны данные страницы:

Пример 2.

На складе готовой продукции находятся изделия, среди которых 5% нестандартных. Найти вероятность того, что при выдаче изделия со склада оно будет стандартным.

Решение:

Вероятность получения нестандартного изделия равна 0,05; события выдачи стандартного и нестандартного изделия образуют полную группу. Следовательно, сумма их вероятностей равна единице, и тогда искомая вероятность равна 0,95.

Противоположные события

Определение 5. Два единственно возможных события, образующих полную группу, называются противоположными.

Если событие обозначено через А, то противоположное ему событие обозначается через . Из теоремы 1.2 следует, что

Например, если при стрельбе по мишени попадание — это событие А, то событие — это промах; сумма их вероятностей равна единице — при выстреле обязательно будет либо попадание, либо промах. То же имеет место и при подбрасывании монеты: обязательно выпадет либо орел, либо решка.

Пример 3.

В магазине имеется 10 телевизоров, из которых 2 неисправных. Найти вероятность того, что среди наугад взятых трех телевизоров будет хотя бы один неисправный.

Решение:

События «среди взятых телевизоров нет ни одного неисправного» и «есть хотя бы один неисправный» — противоположные. Первое из них обозначим через А, а второе — через . Общее число способов, которыми можно взять 3 изделия из 10, равно Число исправных телевизоров равно 8, число способов выборки из них трех изделий равно так что вероятность Искомая вероятность определяется из формулы (1.10):

Предположим, что из этих случаев т благоприятны событию А, а —событию В. Тогда

Так как события А и В несовместны, то нет таких случаев, которые благоприятны и А, и В вместе. Следовательно, событию А В благоприятны случаев и

Подставляя полученные выражения в формулу (3.2.1), получим тождество. Теорема доказана.

Обобщим теорему сложения на случай трех событий.

Обозначая событие буквой D и присоединяя к сумме еще одно событие С, легко доказать, что

Очевидно, методом полной индукции можно обобщить теорему сложения на произвольное число несовместных событий. Действительно, предположим, что она справедлива для событий:

и докажем, что она будет справедлива для событий:

Но так как для п событий мы считаем теорему уже доказанной, то

откуда

что и требовалось доказать.

Таким образом, теорема сложения вероятностей применима к любому числу несовместных событий. Ее удобно записать в виде:

Отметим следствия, вытекающие из теоремы сложения вероятностей.

Следствие 1. Если события образуют, полную группу несовместных событий, то сумма их вероятностей равна единице.

Доказательство. Так как события образуют полную группу, то появление хотя бы одного из них — достоверное событие:

Так как — несовместные события, то к ним приме-

нима теорема сложения вероятностей

что и требовалось доказать.

Перед тем как вывести второе следствие теоремы сложения, определим понятие о «противоположных событиях».

Противоположными событиями называются два несовместных события, образующих полную группу.

Событие, противоположное событию А, принято обозначать А.

Примеры противоположных событий.

1) —попадание при выстреле,

— промах при выстреле;

2) — выпадение герба при бросании монеты,

— выпадение цифры при бросании монеты;

3) — безотказная работа всех элементов технической системы,

— отказ хотя бы одного элемента;

4) — обнаружение не менее двух бракованных изделий в контрольной партии,

— обнаружение не более одного бракованного изделия.

Следствие 2. Сумма вероятностей противоположных событий равна единице.

Это следствие есть частный случай следствия 1. Оно выделено особо ввиду его большой важности в практическом применении теории вероятностей. На практике весьма часто оказывается легче вычислить вероятность противоположного события , чем вероятность прямого события А. В этих случаях вычисляют Р(А) и находят

Рассмотрим несколько примеров с решением на применение теоремы сложения и со следствий.

Пример 4.

В лотерее 1000 билетов; из них на один билет падает выигрыш 500 руб., на 10 билетов — выигрыши по 100 руб., на 50 билетов — выигрыши по 20 руб.. на 100 билетов — выигрыши но 5 руб., остальные билеты невыигрышные. Некто покупает один билет. Найти вероятность выиграть не менее 20 руб.

Решение:

По теореме слбжеиия вероятностей

Пример 5.

Производится бомбометание по трем складам боеприпасов, причем сбрасывается одна бомба. Вероятность попадания в первый склад 0,01; во второй 0,008; в третий 0,025. При попадании в один из складов взрываются все три. Найти вероятность того, что склады будут взорваны.

Решение:

Рассмотрим события:

Так как при сбрасывании одной бомбы события несовместны, то

Пример 6.

Круговая мишень (рис. 3.2.1) состоит из трех зон: /, II и III. Вероятность попадания в первую зону при одном выстреле 0,15, во вторую 0,23, в третью 0,17. Найти вероятность промаха.

Решение:

Обозначим А —промах,

—попадание.

где — попадание соответственно в первую, вторую и третью зоны

, откуда

Как уже указывалось, теорема сложения вероятностей (3.2.1) справедпива ттько для несовместных событий. В случае, когда события А и В совместны» вероятность суммы этих событий выражается формулой

В справедливости формулы (3.2.3) можно наглядно убедиться рассматривая рис. 3.2.2.

Аналогично вероятность суммы трех совместных событий вычисляется по формуле

Справедливость этой формулы также наглядно следует из геометрической интерпретации (рис. 3.2.3).

Методом полной индукции можно доказать общую формулу для вероятности суммы любого числа совместных событий:

где суммы распространяются на различные значения индексов и т. д.

Формула (3.2.4) выражает вероятность суммы любого числа событий через вероятности произведений этих событий, взятых по одному, по два, по три и т. д.

Аналогичную формулу можно написать для произведения событий. Действительно, из рис. 3.2.2 непосредственно ясно, что

Из рис. 3.2.3 видно, что

Общая формула, выражающая вероятность произведения прокз-вольного числа событий через вероятности сумм этих событий, взятых по одному, по два, по три и т. д., имеет вил;

Формулы типа (3.2.4) и (3.2.7) находят практическое применение при преобразовании различных выражений, содержащих вероятности сумм и произведений событий. В зависимости от специфики задачи в некоторых случаях удобнее бывает пользоваться только суммами, а в других только произведениями событий: для преобразования одних в другие и служат подобные формулы.

Пример 7.

Техническое устройство состоит из трех агрегатов: двух агрегатов первого типа — —и одного агрегата второго типа —В. Агрегаты дублируют друг друга: при отказе одного из них происходит автоматическое переключение на второй. Агрегат В не дублирован. Для того чтобы устройство прекратило работу (отказало), нужно, чтобы одновременно отказали оба агрегата или же агрегат В. Таким образом, отказ устройства— событие С — представляется в виде:

где —отказ агрегата — отказ агрегата —отказ агрегата В.

Требуется выразить вероятность события С через вероятности событий, содержащих только суммы, а не произведения элементарных событий .

Вероятность суммы двух событий. Независимость двух событий. Вероятность произведения двух независимых событий

УТВЕРЖДЕНИЕ 1. Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения.

Другими словами, верна формула:

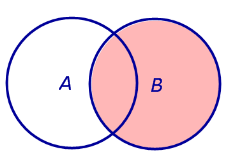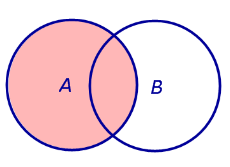
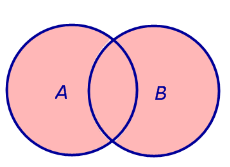
Событие A	Событие B
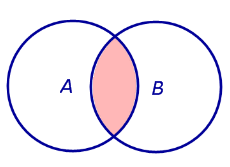Событие A + B	Событие

Событие A

Событие B

Событие A + B

Событие

Проведем доказательство утверждения 1 на примере геометрического определения вероятности.

Если площадь произвольной фигуры F обозначить символом S (F) , то из рисунка 1 легко установить справедливость равенства:

которое словами можно выразить так: «Площадь фигуры A + B равна сумме площадей фигур A и B минус площадь фигуры ».

Если обе части равенства (2) разделить на число S (Ω) , то мы получим равенство

с помощью которых равенство (3) преобразуется к виду (1), что и завершает доказательство утверждения 1.

Доказательство утверждения 1 для классического определения вероятности проводится аналогичным образом, и мы оставляем его читателю в качестве полезного упражнения.

Несовместные события

ОПРЕДЕЛЕНИЕ. Два события A и B называют несовместными, если они не пересекаются.

Другими словами, события A и B несовместны, если

ЗАМЕЧАНИЕ 1. События A и B несовместны в том, и только в том случае, если событие B является подмножеством события , то есть .

ЗАМЕЧАНИЕ 2. События A и B несовместны в том, и только в том случае, если событие A является подмножеством события , то есть .

ЗАМЕЧАНИЕ 3. Если события A и B несовместны, то вероятность их произведения равна нулю.

Другими словами, для несовместных событий A и B верна формула

ЗАМЕЧАНИЕ 4. Если события A и B несовместны, то вероятность суммы событий A + B равна сумме вероятностей событий A и B .

Другими словами, для несовместных событий A и B верна формула

Независимость двух событий. Вероятность произведения двух независимых событий

Два события A и B называют независимыми, если появление одного из этих событий никак не влияет на вероятность появления второго события.

ЗАМЕЧАНИЕ 5. Несовместные события и независимые события – это совершенно разные понятия, и их не следует путать.

Справедливо следующее утверждение.

УТВЕРЖДЕНИЕ 2. Вероятность произведения двух независимых событий равна произведению их вероятностей.

Другими словами, для двух независимых событий A и B верна формула

Проиллюстрируем справедливость формулы (4) на примере.

ПРИМЕР 1. Случайный эксперимент состоит в подбрасывании двух игральных костей. Одна из игральных костей окрашена в синий цвет, другая – в красный. Найти вероятность того, что на синей игральной кости выпадет число 3 , а на красной игральной кости выпадет число 4 .

РЕШЕНИЕ. Сформируем следующую таблицу, в которой записаны все 36 возможных вариантов пар чисел, выпадающих при подбрасывании двух игральных костей. Первая строка таблицы – это числа, выпавшие при бросании синей кости, а первый столбец таблицы – это числа, выпавшие при бросании красной кости. На пересечении строки и столбца указана пара чисел, выпавших на двух костях.

Благоприятным является только один исход, а именно, клетка с результатом 4 , 3 , окрашенная в таблице желтым цветом. Следовательно, вероятность события, состоящего в том, что на синей игральной кости выпадает число 3 , а на красной игральной кости выпадает число 4 , равна .

Теперь рассмотрим случайный эксперимент, описанный в примере 1, с другой стороны. Для этого обозначим буквой A случайное событие, состоящее в том, что на синей игральной кости выпадает число 3 , а буквой B — случайное событие, состоящее в том, что на красной игральной кости выпадает число 4 . События A и B являются независимыми событиями, а их вероятности равны:

Событие состоит в том, что на синей игральной кости выпадет число 3 , а на красной игральной кости выпадет число 4 . Поскольку,

то в рассматриваемом случайном эксперименте по подбрасыванию двух игральных костей формула (4) верна.

ПРИМЕР 2. Два стрелка стреляют по мишени. Первый стрелок поражает мишень с вероятностью 0,9 . Второй стрелок поражает мишень с вероятностью 0,8 . Найти вероятность того, что мишень будет поражена.

РЕШЕНИЕ. Обозначим буквой A случайное событие, состоящее в том, что в мишень попадает первый стрелок, а буквой B обозначим случайное событие, состоящее в том, что в мишень попадает второй стрелок. Тогда событие A + B означает, что мишень поражена, а событие означает, что в мишень попали оба стрелка. По условию

Теоремы сложения и умножения вероятностей

Составитель преподаватель кафедры высшей математики Ищанов Т.Р.

Тeория. Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же опыте; в противном случае события называются совместными.

Пример 1. При бросании игральной кости выпадение 3 очков и 6 очков события несовместные, так как они одновременно не могут произойти в одном и том же опыте.

Пример 2. А — появление четырех очков при бросании игральной кости; В-появление четного числа очков. События А и В совместные, так появление одного из них не исключает появление другого в одном и том же испытании.

Два события называются независимыми, если вероятность появления одного из них не влияет на вероятность появления другого события, в противном случае события зависимы.

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А – деталь годная, В – деталь окрашенная, то АВ – деталь годна и окрашена. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С – появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то «АВС» – выпадение «герба» во всех трех испытаниях.

Условной вероятностью называют вероятность события В, вычисленную в предположении, что событие А уже наступило. Условная вероятность события В при условии, что событие А уже наступило, по определению, равна :

Пример 3. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).

Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность

Этот же результат можно получить по формуле

Найдем вероятность Р (АВ) того, что в первом испытании появится черный шар, а во втором—белый. Общее число исходов — совместного появления двух шаров, безразлично какого цвета, равно числу размещений

Из этого числа исходов событию AВ благоприятствуют исходов. Следовательно,

Искомая условная вероятность

Как видим, получен прежний результат.

Теорема умножения вероятностей (для зависимых событий). Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:

где — вероятность события A_n, вычисленная в предположении, что события A₁, A₂, A₃, . , A_n-1 наступили.

В частности, для трех событий . Заметим, что порядок, в котором расположены события, может быть выбран любым, т. е. безразлично какое событие считать первым, вторым и т.д.

Пример 4. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков — конусный, а второй — эллиптический.

Решение. Вероятность того, что первый валик окажется конусным (событие А), .

Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик— конусный, т. е. условная вероятность .

По теореме умножения, искомая вероятность

Пример 5. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А), при втором — черный (событие В) и при третьем—синий (событие С).

Решение. Вероятность появления белого шара в первом испытании

Вероятность появления черного шара во втором испытании, вычисленная в предположении, что в первом испытании появился белый шар, т. е. условная вероятность

Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что в первом испытании появился белый шар, а во втором — черный, т. е. условная вероятность

Теорема умножения вероятностей (для независимых событий). Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В – попадание при втором выстреле, то А+В – попадание при первом выстреле, или при втором, или в обоих выстрелах. В частности, если два события А и В – несовместные, то А+В – событие, состоящее в появлении одного из этих событий, безразлично какого. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.

Теорема сложения вероятностей (для несовместных событий). Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).

Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Пример 6. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.

Решение Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного шара (событие A) P (A) = 10/30 = 1/3. Вероятность появления синего шара (событие B) P (B) = 5/30 = 1/6. События A и B несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = 1/3 + 1/6 = 0,5.

Пример 7. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую – 0,35.Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.

Решение. Событие A – «стрелок попал в первую область» и B – «стрелок попал во вторую область» — несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = 0,45 + 0,35 = 0,80.

Теорема сложения вероятностей (для совместных событий). Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Для трех событий A, B, C имеем:

Замечание 1. При использовании полученной формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми. Для независимых событий:

Пример 8. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: p1 = 0,7; p2 = 0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А (попадание первого орудия) и В (попадание второго орудия) независимы. Вероятность события АВ (оба орудия дали попадание) Р (АВ)=Р (А)*Р(В) = 0,7*0,8 = 0,56. Искомая вероятность Р(А+В)=Р(А) + Р(В)—Р(АВ) = 0,7 + 0,8 — 0,56=0,94.

Замечание. Так как в настоящем примере события А и В независимые, то можно было воспользоваться формулой . В самом деле, вероятности событий, противоположных событиям А и В, т. е. вероятности промахов, таковы:

Искомая вероятность того, что при одном залпе хотя бы одно орудие даст попадание, равна . Как и следовало ожидать, получен тот же результат.

Для зависимых событий:

Вероятность появления хотя бы одного события.

Теорема. Вероятность появления хотя бы одного из событий A₁, A₂, . A_n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий :

Частный случай. Если события имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий:

Практический материал.

1.(6.4.12) В урне 4 белых и 3 черных шара. Из нее вынимают 2 шара. Найти вероятность того, что оба шара белые. Рассмотреть выборки: а) без возвращения; б) с возвращением.

2. Вероятность наступления некоторого случайного события в каждом опыте одинакова и равна 0,2. Опыты проводятся последовательно до наступления этого события. Определить вероятность того, что: а) придется проводить четвертый опыт; б) будет проведено четыре опыта. Ответ: а) P (A)=0,8 3 ; б) P (B)=0,8 3 ·0,2

3. Три стрелка одновременно стреляют по одной мишени. Вероятности попадания при одном выстреле соответственно равны 0,7; 0,8 и 0,9. Найти вероятности того, что при одновременном залпе этих стрелков в мишени будет: а) только одно попадание; б) хотя бы одно попадание. Ответ: а) 0,092; б) 0,994

4. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8. (Указание: Задача обратная примеру 8). Ответ: 0,7

5. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное. Ответ: 0,18

6. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность. Ответ: 0,432

Похожие записи:

• 

  Что такое зависимые и независимые события

• 

  Что такое сумма событий какие союзы указывают на нее

• 

  Что такое зависимое событие в теории вероятности

• 

  Что такое суть теории

• 

  Что такое сумма определение

• 

  Что такое зависимость между величинами