Виды зависимостей между случайными величинами
Зависимость одной случайной величины от значений, которые принимает другая случайная величина (физическая характеристика), в статистике называется регрессией. Если этой зависимости придан аналитический вид, то такую форму представления изображают уравнением регрессии.
Процедура поиска предполагаемой зависимости между различными числовыми совокупностями обычно включает следующие этапы:
установление значимости связи между ними;
возможность представления этой зависимости в форме математического выражения (уравнения регрессии).
Первый этап в указанном статистическом анализе касается выявления так называемой корреляции, или корреляционной зависимости. Корреляция рассматривается как признак, указывающий на взаимосвязь ряда числовых последовательностей. Иначе говоря, корреляция характеризует силу взаимосвязи в данных. Если это касается взаимосвязи двух числовых массивов xi и yi, то такую корреляцию называют парной.
При поиске корреляционной зависимости обычно выявляется вероятная связь одной измеренной величины x (для какого-то ограниченного диапазона ее изменения, например от x1 до xn) с другой измеренной величиной y (также изменяющейся в каком-то интервале y1 … yn). В таком случае мы будем иметь дело с двумя числовыми последовательностями, между которыми и надлежит установить наличие статистической (корреляционной) связи. На этом этапе пока не ставится задача определить, является ли одна из этих случайных величин функцией, а другая — аргументом. Отыскание количественной зависимости между ними в форме конкретного аналитического выражения y = f(x) — это задача уже другого анализа, регрессионного.
Таким образом, корреляционный анализ позволяет сделать вывод о силе взаимосвязи между парами данных х и у, а регрессионный анализ используется для прогнозирования одной переменной (у) на основании другой (х). Иными словами, в этом случае пытаются выявить причинно-следственную связь между анализируемыми совокупностями.
Строго говоря, принято различать два вида связи между числовыми совокупностями — это может быть функциональная зависимость или же статистическая (случайная). При наличии функциональной связи каждому значению воздействующего фактора (аргумента) соответствует строго определенная величина другого показателя (функции), т.е. изменение результативного признака всецело обусловлено действием факторного признака.
Аналитически функциональная зависимость представляется в следующем виде: y = f(x).
В случае статистической связи значению одного фактора соответствует какое-то приближенное значение исследуемого параметра, его точная величина является непредсказуемой, непрогнозируемой, поэтому получаемые показатели оказываются случайными величинами. Это значит, что изменение результативного признака у обусловлено влиянием факторного признака х лишь частично, т.к. возможно воздействие и иных факторов, вклад которых обозначен как є: y = ф(x) + є.
По своему характеру корреляционные связи — это соотносительные связи. Примером корреляционной связи показателей коммерческой деятельности является, например, зависимость сумм издержек обращения от объема товарооборота. В этой связи помимо факторного признака х (объема товарооборота) на результативный признак у (сумму издержек обращения) влияют и другие факторы, в том числе и неучтенные, порождающие вклад є.
Для количественной оценки существования связи между изучаемыми совокупностями случайных величин используется специальный статистический показатель — коэффициент корреляции r.
Если предполагается, что эту связь можно описать линейным уравне- нием типа y=a+bx (где a и b — константы), то принято говорить о существовании линейной корреляции.
Коэффициент r — это безразмерная величина, она может меняться от 0 до ±1. Чем ближе значение коэффициента к единице (неважно, с каким знаком), тем с большей уверенностью можно утверждать, что между двумя рассматриваемыми совокупностями переменных существует линейная связь. Иными словами, значение какой-то одной из этих случайных величин (y) существенным образом зависит от того, какое значение принимает другая (x).
Если окажется, что r = 1 (или -1), то имеет место классический случай чисто функциональной зависимости (т.е. реализуется идеальная взаимосвязь).
При анализе двумерной диаграммы рассеяния можно обнаружить различные взаимосвязи. Простейшим вариантом является линейная взаимосвязь, которая выражается в том, что точки размещаются случайным образом вдоль прямой линии. Диаграмма свидетельствует об отсутствии взаимосвязи, если точки расположены случайно, и при перемещении слева направо невозможно обнаружить какой-либо уклон (ни вверх, ни вниз).
Если точки на ней группируются вдоль кривой линии, то диаграмма рассеяния характеризуется нелинейной взаимосвязью. Такие ситуации вполне возможны.
Функциональные зависимости отношений и математическое понятие функциональной зависимости
Функциональная зависимость атрибутов отношения напоминает понятие функциональной зависимости в математике. Но это не одно и то же. Для сравнения напомним математическое понятие функциональной зависимости:
Определение 2. Функциональная зависимость (функция) — это тройка объектов , где
— множество (область определения),
— множество (множество значений),
— правило, согласно которому каждому элементу ставится в соответствие один и только один элемент (правило функциональной зависимости).
Функциональная зависимость обычно обозначается как или .
Замечание. Правило может быть задано любым способом — в виде формулы (чаще всего), при помощи таблицы значений, при помощи графика, текстовым описанием и т.д.
Функциональная зависимость атрибутов отношения тоже напоминает это определение. Действительно:
- В качестве области определения выступает домен, на котором определен атрибут (или декартово произведение доменов, если является множеством атрибутов)
- В качестве множества значений выступает домен, на котором определен атрибут (или декартово произведение доменов)
- Правило реализуется следующим алгоритмом — 1) по данному значению атрибута найти любой кортеж отношения, содержащий это значение, 2) значение атрибута в этом кортеже и будет значением функциональной зависимости, соответствующим данному . Определение функциональной зависимости в отношении гарантирует, что найденное значение не зависит от выбора кортежа, поэтому правило определено корректно.
Отличие от математического понятия отношения состоит в том, что, если рассматривать математическое понятие функции, то для фиксированного значения соответствующее значение функции всегда одно и то же. Например, если задана функция , то для значения соответствующее значение всегда будет равно 4. В противоположность этому в отношениях значение зависимого атрибута может принимать различные значения в различных состояниях базы данных. Например, атрибут ФАМ функционально зависит от атрибута Н_СОТР. Предположим, что сейчас сотрудник с табельным номером 1 имеет фамилию Иванов, т.е. при значении детерминанта равного 1, значение зависимого аргумента равно «Иванов». Но сотрудник может сменить фамилию, например на «Сидоров». Теперь при том же значении детерминанта, равного 1, значение зависимого аргумента равно «Сидоров».
Таким образом, понятие функциональной зависимости атрибутов нельзя считать полностью эквивалентным математическому понятию функциональной зависимости, т.к. значение этой зависимости различны при разных состояниях отношения, и, самое главное, эти значения могут меняться непредсказуемо.
Функциональная зависимость атрибутов утверждает лишь то, что для каждого конкретного состояния базы данных по значению одного атрибута (детерминанта) можно однозначно определить значение другого атрибута (зависимой части). Но конкретные значение зависимой части могут быть различны в различных состояниях базы данных.
2НФ (Вторая Нормальная Форма)
Определение 3. Отношение находится во второй нормальной форме (2НФ) тогда и только тогда, когда отношение находится в 1НФ и нет неключевых атрибутов, зависящих от части сложного ключа. (Неключевой атрибут – это атрибут, не входящий в состав никакого потенциального ключа).
Замечание. Если потенциальный ключ отношения является простым, то отношение автоматически находится в 2НФ.
Отношение СОТРУДНИКИ_ОТДЕЛЫ_ПРОЕКТЫ не находится в 2НФ, т.к. есть атрибуты, зависящие от части сложного ключа:
Зависимость атрибутов, характеризующих сотрудника от табельного номера сотрудника является зависимостью от части сложного ключа:
Н_СОТР ФАМ
Н_СОТР Н_ОТД
Н_СОТР ТЕЛ
Зависимость наименования проекта от номера проекта является зависимостью от части сложного ключа:
Н_ПРО ПРОЕКТ
Для того, чтобы устранить зависимость атрибутов от части сложного ключа, нужно произвести декомпозицию отношения на несколько отношений. При этом те атрибуты, которые зависят от части сложного ключа, выносятся в отдельное отношение.
Отношение СОТРУДНИКИ_ОТДЕЛЫ_ПРОЕКТЫ декомпозируем на три отношения — СОТРУДНИКИ_ОТДЕЛЫ, ПРОЕКТЫ, ЗАДАНИЯ.
Отношение СОТРУДНИКИ_ОТДЕЛЫ (Н_СОТР, ФАМ, Н_ОТД, ТЕЛ):
Зависимость атрибутов, характеризующих сотрудника от табельного номера сотрудника:
Алгебраические функциональные зависимости
методическая разработка по алгебре на тему
В публикации представлена логика различия понятия о функциональных зависимостях для учащихся основного общего и среднего (полного) общего образования как переходной этап формирования логики функциональных зависимостей для математических и физических величин при использовании их как методов подхода решения задач по математике, физике и других наук.
Скачать:
| Вложение | Размер |
|---|---|
| algebraicheskie_funktsionalnye_zavisimosti.docx | 21.75 КБ |
Предварительный просмотр:
Алгебраические функциональные зависимости
В п.7 § 2 «Алгебраические выражения и их характеристики» рассматриваются алгебраические выражения, имеющие вид:
у=3х; у=ах 2 +4b; у=0,5х 2 +2;
В алгебре функциональная зависимость имеет определение: «Функцией называют такую зависимость переменной у от переменной х , при которой каждому значению переменной х соответствует единственное значение переменной у», где у – зависимая переменная, х – независимая переменная.
Следует отметить, что в алгебре буквами х и у обозначают множества. Данные множества имеют только числовые (арифметические) значения. Поскольку буквами обозначают не переменные, а множества, значения которых могут быть не только определенными, но и принимать различные значения для х и у , которые зависимы друг от друга (т.е. взаимосвязаны), то правильнее было бы определение: Алгебраической функцией называют алгебраическое выражение, имеющее вид формулы, в которой слева находится множество «у», значение которого зависит от значений множества «х», находящегося справа, т.е. каждому значению множества «х» соответствует единственное значение множества «у». Такие множества называют взаимозависимыми или взаимосвязанными. Для краткости можно сформулировать: Алгебраической функцией называют алгебраическое выражение вида формулы, в которой каждому значению множества «х», находящемуся справа, соответствует единственное значение множества «у», находящемуся слева . Где у – множество с зависимыми значениями, х – множество с независимыми значениями. Примеры конкретных функциональных зависимостей: у=2х; у=0,5х+4; у=0,5х 2 –2 и т.д.
Значения множества «у» определяются (образуются) после арифметических расчетов (вычислений) по предложенной функциональной зависимости после подстановки значений множества «х». Каждому одному значению множества «х» соответствует единственное значение множества «у». Функция связывает задаваемые значения множества «х» со значениями множества «у». Т.е. функция связывает значения двух множеств «х» и «у». Следовательно, значения множеств «х» и «у» связаны. Эту связь кратко обозначают у(х). Под краткой записью у(х) подразумевают запись у=0,5х 2 +2 или у=ах 2 +4b или у=3х и т.д.
Алгебраическая функциональная зависимость – алгебраическое выражение, имеющее вид формулы, у которой с левой стороны от знака равно находится множество, значения которого зависят от задаваемого значения множества, находящегося справа среди других множеств с известными однозначными значениями. На примере для функции у(х) значение функции — это значение множества «х» и значение множества «у». Отсюда вытекает вывод: значение функции у(х) – двухмерно. Т.е. одно значение функции состоит из одного значения множества «х» и связанного с ним одного значения множества «у».
Множество у нельзя называть функцией. Для функции заданной алгебраическим видом у=2х 2 –6 записи вида у=f(х) или f(х)=2х 2 –6 не правильные. Выходит для у=f(х) это (у=у=2х 2 –6), которое является не понятным выражением. Или для f(х)=2х 2 –6 это (у=2х 2 –6=2х 2 –6), которое тоже является непонятным выражением.
Также следует отметить, что выражение у=2х 2 –6, в котором множество «х» имеет не одно конкретное значение, а большое количество различных задаваемых значений и при этом образуется большое количество значений у множества «у», зависящих от «х» не называют формулой, а называют алгебраической функциональной зависимостью. Хотя можно отметить, что алгебраические выражения формула и функциональная зависимость похожи.
Далее говорится, что функция имеет область значений. Но высказывание «Все значения, которые принимает зависимая переменная, образуют область значений функции» – не верное. Как по определению вид зависимости (функция) может иметь одномерную область значений? Нелогично. Одномерные значения имеют в отдельности «буква» х и «буква» у , которыми обозначены числовые множества, связанные функционально. А отсюда следует, что да функция имеет значение и значения, но они не одномерные, а двухмерные. Поэтому область определения функции есть область значений независимой и зависимой переменных для множества «х» и множества «у».
На графике функциональной зависимости значением функции является точка, которая характеризуется двумя мерами (измерениями), значением множества «х» и значением множества «у». А значения (большое число значений) функции образуют множество точек, которые образуют линию, отображающую эту зависимость. Т.е. линия графика отображает множество значений функции, которые являются двумерными т.к. мы имеем две оси ОХ и ОУ (данные суждения см. в следующем параграфе).
Все выше перечисленные понятия полностью соответствуют и суждениям, применяемым в математике, физике и других науках.
1 Какое алгебраическое выражение называют функциональной зависимостью?
2 Что общего и чем отличаются алгебраические выражения вида формулы и функциональной зависимости?
Что такое зависимость в математике
a. При рассмотрении количественной стороны различных процессов мы почти всегда наблюдаем, что переменные величины зависят друг от друга; например, путь проходимый свободно падающим в пустоте телом зависит только от времени, давление в паровом котле зависит только от температуры пара.
Глубина океана в одном пункте постоянна, но в различных пунктах различна, она зависит только от двух переменных — от географической долготы и географической широты места.
Высота растущего дерева зависим от многих переменных — от солнечного освещения, от влажности, от количества питательных веществ в почве и т. д.
Мы видим, что некоторые переменные изменяются независимо, они и называются независимыми переменными или аргументами, другие же от них зависят их называют функциями.
Сама зависимость называется функциональной. Между прочим, функциональная зависимость представляет собой одно из самых важных понятий математики.
b. Следует всегда различать, от какого числа независимых переменных зависит функция. Проще всего поддаются изучению функции одной переменной, ими мы будем заниматься в первую очередь. Изучение функций многих переменных сложнее, но так или иначе сводится к изучению функций одной переменной.
c. Если мы желаем записать математически, что переменная у зависит от , то будем употреблять такое обозначение:
Эта запись читается так:
Не; следует думать, что буква умножается на , она является лишь сокращением слова «функция», а вся запись является сокращенной фразой (2).
Точно так же, если функция U зависит от двух аргументов то эта зависимость обозначается следующим образом:
Здесь буквы f, х и у также не являются сомножителями.
Совершенно ясно, как обозначается функция трех четырех и большего числа аргументов.
Вместо буквы употребляют и другие буквы чаще всего .
d. Записи типа (1) и (3) являются самыми общими обовначениями функций, так как под ними можно понимать какие угодно функции, а потому, имея в руках только эти обозначения, мы ничего не сможем узнать о свойствах этих функций.
Для того чтобы иметь возможность изучать функцию нужно ее задать.
e. Имеется много способов задать функцию, но все они сводятся к трем основным типам:
1) функцию можно задать таблицей ее числовых значений, соответствующих числовым значениям ее аргумента;
2) функцию можно задать графически;
3) функцию можно задать математической формулой.
f. Приведем примеры. Известно, что при вращении махового колеса возникают напряжения, которые стремятся разорвать его обод. Если обод колеса сделан из однородного материала, то напряжения зависят только от скорости вращения. Обозначая скорость через v, а напряжение в ободе через , мы можем записать что
Теория сопротивления материалов дает такую таблицу для значений функции (4), если обод сделан из литой стали:
Здесь v измеряется в метрах в секунду — в ньютонах на квадратный сантиметр.
Большим достоинством табличного способа Зсдания функции является то, что числа таблицы непосредственно могут быть использованы для различных вычислений.
Недостатком является то, что всякая таблица дается не для всех значений аргумента, а через некоторые интервалы, так что, если каких-либо значений функции в таблице нет, то нужно брать более подробную таблицу; если же последней нет, то приходится подбирать нужное число более или менее приблизительног сообразуясь с характером изменения чисел таблицы,
g. Большим недостатком является также и то, что если таблица содержит много чисел, то характер изменения функции уловить трудно. Наконец, третьим недостатком является то, что изучать свойства функции, заданной таблицей, трудно; кроме того, полученные свойства будут неточными.
h. От первых двух недостатков свободен графический способ задания функции.
Чтобы пояснить графический способ рассмотрим такой пример.
Если какой-либо материал подвергнуть растяжению, то сила, необходимая для растягивания, будет зависеть от того, какое растяжение необходимо сделать, т. е. сила есть функция от удлинения. Если удлинение в процентах обозначить через X, а растягивающую силу, которая обычно измеряется в ньютонах на квадратный сантиметр, обозначить через , то
Для различных материалов эта зависимость будет различной. Возьмем координатные оси и будем считать к за абсциссу, а за ординату, тогда для каждой пары их значений получим точку на плоскости.
Все эти точки расположатся на некоторой кривой, которая имеет различный вид для различных материалов. Существуют приборы, которые такие кривые чертят автоматически.
Для мягкой стали мы получим следующую кривую (рис. 31):
k. Как мы видим, действительно графический снособ нагляден и дает значения функции для всех значений аргумента. Но третий недостаток и здесь имеет место. Изучать свойства функции заданной графически, все-таки затруднительно.
l. Теперь покажем способ задания функции формулой Возьмем такой пример. Площадь круга очевидно зависит от радиуса. Если радиус обозначить через я, а площадь через у, то, как известно из геометрии, где — отношение длины окружности к длине диаметра. Мы видим, что зависимость здесь задается математической формулой, поэтому третий способ называется математическим способом. Еще пример: длина гипотенузы прямоугольного треугольника зависит от длин обоих катетов. Если длину гипотенузы обозначить через , а длины катетов через то по теореме Пифагора будем иметь
Так как оба катета мы можем изменять независимо друг от друга, то мы имеем здесь пример функции двух аргументов, заданной математически.
Можно привести еще много примеров функций, заданyых математически, из области различных наук.
m. Математический способ обладает огромным преимуществом перед другими способами задания функций, а именно: к изучению функций, заданных математически, можно привлечь математический анализ.
Помимо того, если необходимо, всегда можно математический способ превратить в табличный. Действительно, мы вправе задать аргументам желательные нам числовые значения и по формуле вычислить сколько угодно значений функции. Таким образом, одна формула заменяет всю таблицу.
n. Математический способ имеет только один недостаток, а именно, формула не дает наглядного представления об изменении функции. Однако этот недостаток мы всегда можем восполнить, так как всегда математический способ задания можно превратить в графический. Это делается так.
o. Если мы имеем функцию одной переменной, то составляем таблицу и каждую пару значений аргумента и функции принимаем за координаты, после этого строим возможно большее число точек. Все полученные точки расположатся на некоторой кривой линии, которая и будет графиком функции. Если мы имеем функцию двух или более аргументов, то и ее можно изобразить графически. Но это уже значительно сложнее, а потому этим вопросом мы займемся несколько позднее.
p. Все сказанное свидетельствует о том, что математический способ задания функций является наиболее выгодным.
Поэтому всегда стремятся, если функция задана таблицей или графиком, выразить ее формулой. Эта задача обычно очень трудная, но чрезвычайно важная для естествознания и технических наук. Без преувеличения можно сказать, что все проблемы механики, естествознания — прикладных наук сводятся к установлению и изучению функциональных зависимостей между теми переменными величинами, с которыми эти дисциплины имеют дело. Бела удается эти функциональные зависимости выразить формулами, то наука приобретает надежный рычаг для приложения всей огромной мощи математического анализа и далеко продвигается в своем развитии.
С другой стороны, математический анализ, получая эту прекрасную пищу, сам растет и совершенствуется.
q. Ввиду того, что перевод на язык формул функциональных зависимостей не является непосредственной задачей математики, мы будем предполагать, что функции уже выражены формулами. Таким образом, в дальнейшем мы будем заниматься только функциями, заданными матетатически.
Прямая и обратная пропорциональные зависимости
Назад Вперёд
Загрузить презентацию (851 кБ)
- Обучающие:
- ввести понятия прямая и обратная пропорциональные зависимости;
- изучить алгоритмы решения задач по теме «Прямая и обратная пропорциональные зависимости»;
- использование для достижения поставленной задачи уже полученные знания;
- развивать умение обобщать, конкретизировать;
- расширение кругозора и развитие интереса к предмету посредством привлечения практико-экономической составляющей.
Аудитория: 6 класс.
I. Организационный момент
II. Мотивация учебной деятельности учащихся
Учитель: Перед Вами молодая семья. Им нужно сделать бюджетный ремонт в ванной комнате. Предлагаю Вам помочь им, используя те знания, которые у Вас есть.
III. Устная работа
Учитель: Проверим Ваши знания».
– Что такое отношение?
– Что показывает отношение?Учитель: Вспомним, если значения двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. Отношением масс, отношением длин и т.д.
– Что такое пропорция?
– Основное свойство пропорции?IV. Актуализация знаний
Учитель: Из каких этапов состоит ремонт в ванной комнате? (спросить детей, выслушать их варианты, повторить, что семья молодая и ремонт бюджетный, совместно придти к следующему плану)
- Покрасить потолок. Купить краску.
- Купить плитку наиболее экономичную.
- Нанять бригаду, которая выполнит работу быстрее.
План постепенно, по мере рассуждений появляется на слайде. После, вывешивается на доске (заранее распечатать каждый этап).
Учитель: 3 кг потолочной краски в среднем стоят 250 рублей. Им необходимо приобрести 9 кг краски. Сколько будет стоить покупка?
Рассуждают дети. Появляется ответ (750 рублей).
Учитель: Посмотрите на схему, заметили ли Вы зависимость?
Масса краски увеличилась в 3 раза, соответственно стоимость то же увеличилась в 3 раза. Показать стрелки.
Обратить внимание на направление стрелок.
Во сколько раз увеличивается масса краски, во столько же раз увеличивается её стоимость, при условии, что цена на товар остается неизменной.Учитель: Значит, отношение значений одной величины и отношение значений другой величины по отношению к друг другу?
Рассуждают дети, приходят к ответу: будут равны.
Учитель: Вывод: Отношения соответствующих значений этих величин равны.
Учитель: Напомните, что такое пропорция? Следовательно, пропорция верна.
Учитель: Первая бригада состоит из 8 человек, они могут выложить плитку за 3 дня. Сколько дней будет выполнять эту же работу вторая бригада, работая с той же производительностью труда, состоящая из 4 человек?
Рассуждают дети, приходят к ответу: 6.
Учитель: Посмотрите на схему, заметили ли Вы зависимость?
Количество человек в бригаде уменьшилось в 2 раза, во столько же раз увеличилась количество дней. Показать стрелки.
Обратить внимание на направление стрелок.
Во сколько раз уменьшается число человек, выполняющих с одинаковой производительностью труда работу, во столько же раз увеличивается время выполнения работы, при условии, что объем работы, которую выполняют бригады одинаковый.Учитель: Значит, отношение значений одной величины и отношение значений другой величины по отношению к друг другу?
Рассуждают дети, приходят к ответу: будут не равны.
Учитель: Значит, отношение значений одной величины и обратное отношение значений другой величины по отношению к друг другу?
Рассуждают дети, приходят к ответу: будут равны.
Учитель: Вывод: Отношение значений одной величины равно обратному отношению соответствующих значений другой величины, следовательно, пропорция верна.
Учитель: Что у нас получилось?
Учитель: Общий вид Вы видите на слайде. Такая шпаргалка есть у каждого (распечатать каждому). Приложение 1. Она поможет вам при решении задач.
Учитель: Сформулируйте тему сегодняшнего урока.
Рассуждают дети, приходят к ответу: «Прямая и обратная пропорциональные зависимости».
Учитель: Открываем тетради, записываем число и тему урока.
Учитель: Перед молодой семьёй стал выбор плитки. Имеется два вида плитки (лучше показать оригиналы, я показывала квадратную плитку с размерами 20 см х 20 см и прямоугольную плитку 25 см х 36 см, размеры написаны на плитке маркером).
Учитель: Размеры меньшей – 20 см х 20 см. Переведите см в дм.
Рассуждают дети, приходят к ответу: 20 см = 2 дм (подписать маркером на плитке).
Учитель: Форма плитки? Найдите площадь плитки.
Рассуждают дети, приходят к ответу: квадрат, S = 4 дм 2 (подписать маркером на плитке).
Учитель: Размеры большей – 25 см х 36 см. Переведите см в дм.
Рассуждают дети, приходят к ответу: 25 см = 2,5 дм; 36 см = 3,6 дм; (подписать маркером на плитке).
Учитель: Форма плитки? Найдите площадь плитки.
Рассуждают дети, приходят к ответу: квадрат, S = 4дм 2 (подписать маркером на плитке).
V. Первичное усвоение новых знаний
№1: Необходимо выложить стены ванной комнаты керамической плиткой. Имеется плитка двух видов: площадью 4 дм 2 и площадью 9 дм 2 . Сколько потребуется плитки площадью 4 дм 2 , если плитки площадью 9 дм 2 требуется 12 упаковок?
Учитель: «Задачи на пропорциональные зависимости решаются с помощью пропорции».
Учитель: Задачи решаются по следующему алгоритму.
Алгоритм:
1. Составить схему.
2. Неизвестное число обозначить за х.
3. Установить вид зависимости между величинами.
4. Записать пропорцию.
5. Найти её неизвестный член.Учитель: Составим схему.
Учитель: Неизвестное число обозначим за х.
Учитель: Установите вид зависимости между величинами.
Учитель: Как составить пропорцию? Используйте шпаргалку.
Пригласить к доске одного ребенка решить пропорцию и записать ответ (27 упаковок).Учитель: Какую плитку выгоднее купить?
Рассуждают дети, приходят к ответу: плитку большей площади.
Учитель: Вернемся к задаче про бригаду. Какую бригаду, выгоднее нанять, если за работу они берут одну и ту же сумму денег?
Рассуждают дети, приходят к ответу: бригаду, состоящую из 8 человек.
VI. Первичная проверка понимания
Учитель: Ребята, какую плитку выгоднее купить мы определили, какую бригаду нанять выбрали. Справились ли мы с поставленной задачей в начале урока?
Учитель: А помогли нам в этом прямая и обратная пропорциональная зависимость. Что показывает прямая пропорциональная зависимость? Обратная? Как составить пропорцию, при решении задач на прямую пропорциональную зависимость? На обратную? А все ли в этом мире находится в пропорциональной зависимости?
Рассуждают дети, приходят к ответу: нет.
Попросить привести примеры, если не получается привести пример: возраст человека и его рост.VII. Первичное закрепление
Выполнить задание (при условии, что есть интернет).
http://learningapps.org/633824 – Прямая и обратная пропорциональная зависимости.
VII. Домашнее задание
VIII. Рефлексия (подведение итогов занятия)
Учитель: Что сегодня Вы узнали на уроке? Спасибо за урок. Молодцы!
Функциональная зависимость
В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое понятие числовой функции, являющееся частным случаем математической функции.
Содержание
Определения
Обозначения
Связанные определения
Свойства
Свойства прообразов и образов
Классы функций
При необходимости можно различать отображения в зависимости от природы множеств X и Y . Если X и Y — числовые множества, такие, как или , то отображение называют функцией. Если X или Y многомерны, например, или , то отображение называют ве́ктор-фу́нкцией. Если X — произвольной природы, а Y — поле, то отображение называют функциона́лом. В специальных случаях используют и другие термины: оператор, функтор, преобразование, морфизм и т. д.
Вариации и обобщения
Функции нескольких аргументов
Определение функции легко обобщить на случай функции многих аргументов.
Пусть даны множества и множество Y , тогда упорядоченное множество всех кортежей » width=»» height=»» /> называется функцией n аргументов тогда и только тогда, когда для любых и из следует, что » width=»» height=»» />. [1]
Примечания
- ↑ Кудрявцев Л. Д. Курс математического анализа. — том 1. — М.: Высшая школа, 1981. — с. 8.
См. также
Литература
- Функция. Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Функциональная зависимость» в других словарях:
функциональная зависимость — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN functional dependence … Справочник технического переводчика
функциональная зависимость — funkcinė priklausomybė statusas T sritis fizika atitikmenys: angl. functional dependence vok. Funktionalabhängigkeit, f rus. функциональная зависимость, f pranc. dépendance fonctionnelle, f … Fizikos terminų žodynas
Функциональная зависимость (программирование) — Функциональная зависимость концепция, лежащая в основе многих вопросов, связанных с реляционными базами данных, включая, в частности, их проектирование. Математически представляет бинарное отношение между множествами атрибутов данного… … Википедия
полная функциональная зависимость — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN fully functional dependence … Справочник технического переводчика
Зависимость — В Викисловаре есть статья «зависимость» Зависимость неоднозначный термин … Википедия
ЗАВИСИМОСТЬ ФУНКЦИОНАЛЬНАЯ — см. ФУНКЦИЯ. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
функциональная характеристика переменного резистора — Ндп. закон изменения сопротивления переменного резистора Зависимость электрического сопротивления переменного резистора от положения подвижного контакта. Примечание Функциональная характеристика может определяться аналогично через выходное… … Справочник технического переводчика
функциональная электроннолучевая трубка — Электроннолучевой прибор, воспроизводящий в аналоговой форме функциональную зависимость между сигналами. [ГОСТ 13820 77] Тематики электровакуумные приборы EN plotting display tube FR tube fonctionnel … Справочник технического переводчика
Функциональная семантико-стилистическая категория, ФССК — – разновидность текстовых категорий (см.), отражающая функционально стилевую дифференциацию речи (типологию текстов). ФССК – это система разноуровневых языковых средств (включая текстовые), объединенных функционально семантически и стилистически… … Стилистический энциклопедический словарь русского языка
Функциональная характеристика переменного резистора — 49. Функциональная характеристика переменного резистора Ндп. Закон изменения сопротивления переменного резистора D. Funktioneller Widerstandsverlauf E. Resistance law F. Loi de variation Зависимость электрического сопротивления переменного… … Словарь-справочник терминов нормативно-технической документации
§3. Функциональные зависимости
Ôункциональные зависимости между величинами могут задаваться различными способами: с помощью формул, графиков, таблиц, словесных описаний. Совершенствованию умений пользоваться этими способами, получать из них необходимую информацию посвящен данный параграф.
1. Понятие функции, способы ее задання

Характерной особенностью функциональной зави-
симости является то, что для каждого допустимого значения одной из переменных она однозначно определяет значения второй переменной. Так, для каждого значе-
ния t по формуле s = 3 t – 1 можно найти лишь одно значение s . Напомним сначала то, что изучалось о функциональных зависимостях ранее.
Пусть заданы две переменные х и у , принимающие числовые значения, и D — множество значений переменной х .
Зависимость между переменными х и у, которая для каждого значения х из D определяет единственное значение у, называется функциональной зависимостью или функцией у от х с областью определения D.
Переменную х в таких зависимостях называют независимой переменной или аргументом , переменную у — зависимой переменной . Функции обычно обозначают латинскими (иногда греческими) буквами — f , g , F , ϕ и т. п.
Функция — от латинского function — действие, выполнение.
Область определения функции f часто обозначают D ( f ). Значение переменной у , которое соответствует х , называют значением функции f в точке х и обозначают f ( х ). Запись « у = f ( х )» означает, что задана функция f . Функциональную зависимость переменной у от х иногда записывают так: у = у ( х ).
Множество значений, которые принимает зависимая переменная у , если х пробегает область определения функции f , называют
множеством значений этой функции и обозначают Е ( f ).
! Фраза «задать функцию у от х » означает сформулировать правило, с помощью которого для каждого допустимого значения переменной х можно найти соответствующее ему значение переменной у .
Существуютразличныеспособызаданняфункции.Вматематике функциональная зависимость чаще всего задается формулами .
Какизвестно, линейнаяфункция задаетсяформулой: y = kx + b , где k и b — некоторые числа, х — аргумент. Например, функции
у =2 х –3(здесь k = 2, b = – 3), у = –0,5 х + 2 (здесь k = – 0,5, b = 2), у = 4 х (здесь k = 4, b = 0), у = 5 (здесь k = 0, b = 5) являются линейными.
Квадратичная функция задается формулой: y = ax 2 + bx + c ,
где a , b , c – некоторые числа, а ≠ 0, х — аргумент. Например, функции у = х 2 , у = 3 х 2 + 1, у = 2 х 2 + х – 4 являются квадратичными. (Укажите для каждой из этих функций, чему равняются коэффициенты a , b , c .)
Обратная пропорциональность задается формулой y = k x ,
где k ≠ 0 — некоторое число, х — аргумент.
Такой способ задания функции называется аналитическим . Заметим, что не всякая зависимость между переменными является функциональной. Например, зависимость между переменными у и х , заданная уравнением х 2 + у 2 = 1, не является функциональной, так как, например, значению х = 0 соответствуют два
значения у : у 1 = –1, у 2 = 1.
! Если функция задана формулой, то при отсутствии дополнительных замечаний или условий считают, что ее областью определения является множество всех значений независимой переменной, при которых эта формула имеет смысл. Её иногда называют естественной областью определения функции.
Функции, их свойства и графики
Так, линейная функция y = kx + b , квадратичная функция y = ax 2 + + bx + c определены при всех значениях х , то есть D ( y ) = (– ∞ ; + ∞ ) .
Обратная пропорциональность y = k x определена при всех зна-
чениях х , кроме х = 0, то есть D ( y ) = (– ∞ ; 0) (0; + ∞ ) . Естественной областью определения функции у = x является промежуток [ 0; + ∞ ) , поскольку извлечение квадратного корня возможно толь-
ко из неотрицательных чисел.
1) область определения функции; x 2 − 1 . Найти:
2) значение функции в точке х = –2;
3) значения аргумента, при которых функция принимает значение 1.
1) Функция определена при всех значениях х , для которых знаменатель дроби не равен нулю, то есть при всех х , кроме х = ±1.
Следовательно, D ( y ) = ( −∞ ; − 1 ) ( − 1;1 ) ( 1; +∞ ) .
2) Значение функции в точке х = – 2 равно:
3) Чтобы найти значения аргумента, при которых функция
принимает значение 1,
решим уравнение 1 =
х 2 – 1 = 3, х 2 = 4, х 1 = – 2,
х 2 = 2. Следовательно, в этих точках фун-
кция принимает значение 1.
Ответ. 1) ( −∞ ; − 1 ) ( − 1;1 ) ( 1; +∞ ) ; 2) 1; 3) – 2; 2.
При решении многих прикладных задач область определения функции устанавливают, исходя из физического или геометрического смысла задачи. Например, если рассматривать зависимость площади квадрата от длины его стороны х , то областью оп-
ределения этой функции будет интервал ( 0; + ∞ ) , так как длина
стороны квадрата может выражаться только положительным числом. В таком случае иногда пишут: y = x 2 , х > 0.
! Обратите внимание на то, что функции y = x 2 и y = x 2 ,
х > 0 различны. У них не только не совпадают области
определения, они также обладают различными свойс-
твами, в чем убедимся впоследствии.
В математике и ее приложениях очень распространен графи-
ческий способ задания функции. Существует много самопи-
шущих приборов, которые вычерчивают кривые, устанавливая
тем самым зависимость между исследуемыми величинами. Так,
сейсмограф вычерчивает график колебания земной коры. По это-
му графику можно, например, изучать силу и характер толчков
С помощью линии, изображен-
ной на рис. 10, можно для каждого
момента времени 0 ≤ t ≤ 12 указать
ры среды Т , то есть эта линия задает
переменными t и Т .
Не всякая линия на координатной плоскости задаёт некоторую
функцию. Чтобы некоторая линия определяла функциональную
зависимость у от х , необходимо и достаточно, чтобы каждая пря-
мая, параллельная оси у , и ось у пересекали эту линию не более
чем в одной точке. Так, линии на рис. 11 определяют функцио-
нальные зависимости у
от х . Линии, изображённые на рис. 12,
не задают функции у от
х , так как можно указать вертикальные
прямые, пересекающие линию в двух точках.

Пример 2. Функция y = f ( x ) задана гра-
фически (рис. 13). Указать:
1) её область определения;
2) её множество значений;
3) значение функции при х = 5;
Функции, их свойства и графики
4) значение аргумента х , при котором функция принимает значе-
1) Областью определения функции яв-
ляется отрезок [–2; 5].
2) Множеством значений функции явля-
ется отрезок [0; 4].
4) Проведем прямую у = 3 и найдем ее
точки пересечения с графиком функции
у = f ( x ) (рис. 14). Это точки с координатами
(0; 3) и (4; 3). Следовательно, значение 3 функция принимает при
Ответ. 1) [–2; 5]; 2) [0; 4]; 3) 4; 4) 0; 4.
На рис. 15 изображена зависимость N ( t ) количест-
ва деталей, изготовленных рабочим, от времени t (в днях).
1) Сколько деталей изготовил рабочий за первые 10 дней?
2) За какие 10 дней — первые или последние — рабочий изгото-
вил больше деталей?
3) За сколько дней рабочий изготовил 50 деталей?
1) Найдем значение функции N ( t ) при t = 10.
Обратите внимание на масштаб по оси t и оси N .
Имеем: N (10) = 40, то есть за первые 10 дней из-
готовлено 40 деталей.
2) За последние десять дней изготовлено
N (30) – N (20) = 80 – 60 = 20 деталей, то есть мень-
ше, чем за первые 10 дней.
3) Необходимо найти значение аргумента, при
дем прямую N = 50 до пересечения с графиком функции N = N ( t ).
Получим, что 50 деталей рабочий изготовил за 15 дней.
Ответ. 1) 40; 2) за первые; 3) 15.
! В рассмотренном примере функция N ( t ) определена для натуральных значений аргумента. Её графиком являетсяконечнаясовокупностьточек.Длянаглядностионисоединены отрезками. Такой приём построения изображения зависимостей будем использовать и в дальнейшем, если он не приводит к недоразумениям.
Кроме аналитического и графического способов задания функций, применяется также табличный способ. В физике и технике час-
то зависимости между переменными фиксируются на шкалах измерительных приборов. В таких случаях функцию задают в виде таблицы, в первой строке которой содержатся значения независимой переменной x 1 , x 2 , x 3 , …, во второй — соответствующие им значения функции. Наиболее распространёнными являются таблицы с постояннымиразностями x 2 – x 1 , x 3 – x 2 . причемзначениеразности называется шагом таблицы. Для таких таблиц независимая переменная принимает значения x 0 , x 0 + h , x 0 + 2 h , . где h — шаг таблицы.Так,приведеннаянижетаблицапоказываетдинамикуизменения объема пассажирских перевозок (в млн. людей) в нашей стране по железным дорогам, начиная с 2000 года.
2000 2001 2002 2003 2004 2005 2006 2007 2008
1,16 1,29 1,77 2,37 3,23 3,81 4,35 4,87 6,17

Функциональные зависимости широко исполь-
зуются на практике. Много процессов и явлений описываются линейной функцией. Например, при равномерном движении пройденный путь прямо пропорционален времени движения; давление газа р при постоянном объеме прямо пропорционально его температуре T : p = cT (законШарля);напряжение U вэлектрическойцеписпостоянным сопротивлением R прямо пропорционально силе тока I : U = RI (закон Ома). Зависимость силы F , действующей на пружину, от
величины ее растяжения х имеет вид F = – kx (закон Гука). Немало физических зависимостей моделируются с помощью
квадратичной функции. Например, закон движения тела вдоль координатнойпрямой поддействиемпостояннойсилы можно предста-
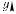
вить в виде: x = x 0 + v 0 t + at 2 2 , зависимость кине-

тической энергии тела W , масса которого равняется m , от скорости движения v выражает-

ся формулой: W = mv 2 2 . Тела, брошенные гори-
зонтально или под углом к горизонту, будут двигаться под действием силы тяжести по
параболическим траекториям (рис. 16, 17). Обратно пропорциональными являются:
— зависимость времени, необходимого на преодоление данного пути, от скорости;
Функции, их свойства и графики
— зависимость между сторонами прямоугольника при заданной площади;
— зависимость между давлением газа и его объемом при постоянной температуре.
Пример 4. При свободном падении тела с достаточно большой высоты с начальной скоростью v 0 = 10 м/с зависимость пройденного
пути от времени t ≥ 0 выражается формулой: s = v 0 t + gt 2 2 , де s — путь, м; t — время, с; g ≈ 10 м/с 2 — ускорение свободного падения.
1) Какой путь пройдет тело за первые 2 с?
2) За какое время тело пройдет 15 м?
1) Чтобы ответить на первый вопрос, нужно вычислить значение функции s при t = 2: s (2) ≈10 2+ 10 2 2 2 = 40 (м).
2) Чтобы ответить на второй вопрос, нужно решить квадратное
уравнение: 10 t + 5 t 2 =15 . Оно имеет два корня: –3 и 1, но условию задачи удовлетворяет только значение t = 1. Следовательно, тело преодолеет 15 м примерно за 1 с.
Ответ. 1) ≈ 40 м; 2) ≈ 1 с.
Пример 5. Некоторая масса газа при температуре 20°С имела объем 107 см 3 , а при 40°С объем равнялся 114 см 3 .
1) Опираясь на закон Гей-Люссака, найти функциональную зависимость объема газа от температуры.
2) Каким будет объем газа при 0°С?
1) По закону Гей-Люссака, объем газа V линейно зависит от температуры t : V = a + bt , где a и b — некоторые числа. Найдем эти числа, используя условие задачи. Так как V (20) = 107, V (40) = 114, то имеем систему уравнений относительно a и b :
107 = a + 20 b , Отсюда: b = 0,35, a = 100. Итак, V = 100 + 0,35 t .114 = a + 40 b .
2) V (0) = 100 + 0,35 0 = 100 (см 3 ). Ответ. 1) V = 100 + 0,35 t ; 2) 100 см 3 .
9 Контрольные вопросы
1°. Какие из следующих зависимостей являются функциональными:
а) каждому двузначному числу ставится в соответствие сумма его цифр;
б) каждому числу, не равному нулю, ставится в соответствие обратное к нему число; в) каждому числу ставится в соответствие целое число, меньшее его?
2°. Какая из линий, изображенных на рис. 18, а)–г), не задаёт функциональную зависимость у от х ?