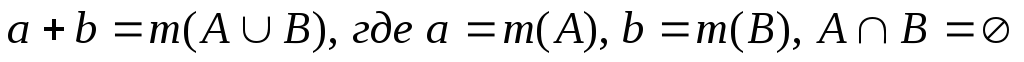Прямая и обратная пропорциональности

Прямая и обратная пропорциональность

Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.

Пропорциональность величин может быть прямой и обратной.

Прямая пропорциональность

Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.

Рассмотрим пример прямой пропорциональности на формуле пути:

s = vt,

где s — это путь, v — скорость, а t — время.

При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:

Скорость v = 5 км/ч
Время t (ч)	1	2	4	8	16
Путь s (км)	5	10	20	40	80

Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.

В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:

s	= v,
t

5	=	10	=	20	=	40	=	80	= 5.
1		2		4		8		16

Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:

Время t = 2 ч
Скорость v (км/ч)	5	15	45	90
Расстояние s (км)	10	30	90	180

В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):

s	= t,
v

10	=	30	=	90	=	180	= 2.
5		15		45		90

Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.

Формула прямой пропорциональности

Формула прямой пропорциональности:

y = kx,

где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

y	= k.
x

Обратная пропорциональность

Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.

Рассмотрим пример обратной пропорциональности на формуле пути:

s = vt,

где s — это путь, v — скорость, а t — время.

При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:

Путь s = 120 км
Скорость v (км/ч)	10	20	40	80
Время t (ч)	12	6	3	1,5

Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.

В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:

s = vt,

10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.

Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.

Формула обратной пропорциональности

Формула обратной пропорциональности:

y =	k	,
	x

где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Прямая и обратная пропорциональности

Рассмотрим зарядку батареи. В качестве первой величины возьмем время, которое она заряжается. Вторая величина – время, которое она будет работать после зарядки. Чем дольше будет заряжаться батарея, тем дольше она будет работать. Процесс будет длиться до тех пор, пока батарея не полностью зарядится.

Зависимость времени работы батареи от времени, которое она заряжается

Такая зависимость называется прямой:

С увеличением одной величины увеличивается и вторая. С уменьшением одной величины уменьшается и вторая величина.

Рассмотрим другой пример.

Чем больше книг прочитает ученик, тем меньше ошибок сделает в диктанте. Или чем выше подняться в горы, тем ниже будет атмосферное давление.

Такая зависимость называется обратной:

С увеличением одной величины уменьшается вторая. С уменьшением одной величины увеличивается вторая величина.

Таким образом, в случае прямой зависимости обе величины изменяются одинаково (обе либо увеличиваются, либо уменьшаются), а в случае обратной зависимости – противоположно (одна увеличивается, а другая уменьшается либо наоборот).

Определение зависимостей между величинами

Готовые работы на аналогичную тему

Время, затраченное для похода в гости к другу, составляет $20$ минут. При увеличении скорости (первой величины) в $2$ раза найдем, как изменится время (вторая величина), которое будет затрачено на путь к другу.

Очевидно, что время уменьшится в $2$ раза.

Такую зависимость называют пропорциональной:

Во сколько раз изменится одна величина, во столько раз изменится и вторая.

За $2$ булки хлеба в магазине нужно заплатить 80 рублей. Если нужно купить $4$ булки хлеба (количество хлеба увеличивается в $2$ раза), во сколько раз придется больше заплатить?

Очевидно, что стоимость также увеличится в $2$ раза. Имеем пример пропорциональной зависимости.

В обоих примерах были рассмотрены пропорциональные зависимости. Но в примере с булками хлеба величины изменяются в одну сторону, следовательно, зависимость является прямой. А в примере с походом к другу зависимость между скоростью и временем – обратная. Таким образом, существует прямо пропорциональная зависимость и обратно пропорциональная зависимость.

Прямая пропорциональность

Рассмотрим $2$ пропорциональные величины: количество булок хлеба и их стоимость. Пусть $2$ булки хлеба стоят $80$ рублей. При увеличении количества булок в $4$ раза ($8$ булок) их общая стоимость будет составлять $320$ рублей.

Отношение количества булок: $frac=4$.

Отношение стоимости булок: $frac=4$.

Как видно, эти отношения равны между собой:

Равенство двух отношений называется пропорцией.

При прямо пропорциональной зависимости получается отношение, когда изменение первой и второй величины совпадает:

Две величины называются прямо пропорциональными, если при изменении (увеличении или уменьшении) одной из них во столько же раз изменяется (увеличивается или уменьшается соответственно) и другая величина.

Автомобиль проехал $180$ км за $2$ часа. Найти время, за которое он с той же скоростью проедет в $2$ раза большее расстояние.

Время прямо пропорционально расстоянию:

Во сколько раз увеличится расстояние, при постоянной скорости, во столько же раз увеличится время:

Запишем условие задачи в виде таблицы:

Автомобиль проехал $180$ км – за время $2$ часа

Автомобиль проедет $180 cdot 2=360$ км – за время $x$ часов

Чем больше расстояние проедет автомобиль, тем большее время ему понадобится. Следовательно, зависимость между величинами прямо пропорциональная.

Ответ: автомобилю потребуется $4$ часа.

Обратная пропорциональность

При обратно пропорциональной зависимости получается отношение, первая часть которого показывает, во сколько раз увеличилась первая величина, а вторая часть – во сколько раз уменьшилась вторая:

Две величины называются обратно пропорциональными, если при изменении (увеличении или уменьшении) одной из них во столько же раз изменится (уменьшится или увеличится соответственно) другая величина.

Автомобиль, который двигается со скоростью $60$ км/ч, проехал путь за $6$ часов. Найти время, за которое автомобиль проедет этот же путь, но со скоростью в $2$ раза больше прежней.

Время обратно пропорционально скорости:

Во сколько раз увеличивается скорость, при том же пути, во столько же раз уменьшается время:

Запишем условие задачи в виде таблицы:

Автомобиль проехал $60$ км — за время $6$ часов

Автомобиль проедет $120$ км – за время $x$ часов

Чем больше скорость автомобиля, тем меньше времени ему понадобится. Следовательно, зависимость между величинами обратно пропорциональная.

Т.к. пропорциональность обратная, второе отношение в пропорции переворачиваем:

Зависимость между величинами

Изучение в курсе математики начальной школы величин и их измерений имеет большое значение в плане развития младших школьников. Это обусловлено тем, что через понятие величины описываются реальные свойства предметов и явлений, происходит познание окружающей действительности; знакомство с зависимостями между величинами помогает создать у детей целостные представления об окружающем мире; изучение процесса измерения величин способствует приобретению практических умений и навыков необходимых человеку в его повседневной деятельности. Кроме того знания и умения, связанные с величинами и полученные в начальной школе, являются основой для дальнейшего изучения математики.

Данной проблеме посвящено значительное число работ в Интернете.

Все люди создают свои работы с определёнными целями, как и я создаю свой реферат. Цель моей работы состоит, всего лишь, в расширении знаний о математике.

Данный реферат предназначен для расширения и систематизации знаний о математике. Надеюсь, что содержание реферата может быть использовано во время изучения математики.

Понятие величины

Длина, площадь, масса, время, объём — величины. Первоначальное знакомство с ними происходит в начальной школе, где величина наряду с числом является ведущим понятием.

ВЕЛИЧИНА — это особое свойство реальных объектов или явлений, и особенность заключается в том, что это свойство можно измерить, то есть назвать количество величины, которые выражают одно и тоже свойство объектов, называются величинами одного рода или однородными величинами.

Например, длина стола и длина комнаты — это однородные величины.

Свойства величин

Величины — длина, площадь, масса и другие обладают рядом свойств. 1)Любые две величины одного рода сравнимы: они либо равны, либо одна меньше (больше) другой. То есть, для величин одного рода имеют место отношения «равно», «меньше», «больше» и для любых величин и справедливо одно и только одно из отношений: Например, мы говорим, что длина гипотенузы прямоугольного треугольника больше, чем любой катет данного треугольника; масса лимона меньше, чем масса арбуза; длины противоположных сторон прямоугольника равны.

2)Величины одного рода можно складывать, в результате сложения

получится величина того же рода. Т.е. для любых двух величин а и b однозначно определяется величина a+b, её называют суммой величин а и b.

«Величины и её измерения»

. называются величинами одного рода или однородными величинами. Например, длина стола и дли на комнаты — это однородные величины. Величины — длина, . проблему и эти трудности проблемной ситуации в зависимости от интеллектуальных возможностей. Проблемное обучение включает несколько . возможности решать задачу при наличии затруднения противоречия между старым и новым, известным и неизвестным, данным .

Например, если a-длина отрезка AB, b — длина отрезка ВС, то длина

отрезка АС, есть сумма длин отрезков АВ и ВС.

3)Величину умножают на действительное число, получая в результате величину того же рода. Тогда для любой величины а и любого неотрицательного числа x существует единственная величина b= x а, величину b называют произведением величины а на число x. Например, если a — длину отрезка АВ умножить на x= 2, то получим длину нового отрезка АС .

4) Величины данного рода вычитают, определяя разность величин через сумму: разностью величин а и b называется такая величина с, что а=b+c. Например, если а — длина отрезка АС, b — длина отрезка AB, то длина отрезка ВС есть разность длин отрезков и АС и АВ.

5) Величины одного рода делят, определяя частное через произведение величины на число; частным величин а и b-называется такое неотрицательное действительное число х, что а= х b. Чаще это число — называют отношением величин а и b и записывают в таком виде: a/b = х. Например, отношение длины отрезка АС к длине отрезка АВ равно 2.

Работа с величинами

Измерение — заключается в сравнении данной величины с некоторой величиной того же рода, принятой за единицу. В результате измерения получают число, которое называют численным значением при выбранной

Процесс сравнения зависит от рода рассматриваемых величин: для длин он один, для площадей — другой, для масс- третий и так далее. Но каким бы ни был этот процесс, в результате измерения величина получает определённое численное значение при выбранной единице.

Вообще, если дана величина а и выбрана единица величины e, то в результате измерения величины а находят такое действительное число x, что а=x e. Это число x называют численным значением величины а при единице е. Это можно записать так: х=m (a).

Согласно определению любую величину можно представить в виде произведения некоторого числа и единицы этой величины. Например, 7 кг = 7*1кг, 12 см =12*1 см, 15ч =15*1 ч. Используя это, а также определение умножения величины на число, можно обосновать процесс перехода от одной единицы величины к другой. Пусть, например, требуется выразить 5/12ч в минутах. Так как, 5/12ч = 5/12 60мин = (5/12 60)мин = 25мин.

Величины, которые вполне определяются одним численным значением, называются скалярными величинами. Такими, к примеру, являются длина, площадь, объём, масса и другие. Кроме скалярных величин, в математике рассматривают ещё векторные величины. Для определения векторной величины необходимо указать не только её численное значение, но и направление.

Формирование у детей представлений о величине в разных возрастных группах

. игровой деятельности. формирования представлений о величине ФОРМИРОВАНИЕ ПРЕДСТАВЛЕНИЙ О ВЕЛИЧИНЕ У ДЕТЕЙ ДОШКОЛЬНОГО ВОЗРАСТА, Определение уровня сформированности представлений о величине у детей Отражение величины как пространственного . дошкольной методике формирование элементарных математических представлений принято рассматривать «длину» и «ширину» как два разных качества предмета . Длины .

Векторными величинами являются сила, ускорение, напряжённость электрического поля и другие.

В начальной школе рассматриваются только скалярные величины, причём такие, численные значения которых положительны, то есть положительные скалярные величины.

Измерение величин позволяет свести сравнение их к сравнению чисел, операции над величинами к соответствующим операциям над числами.

1. Если величины а и b измерены при помощи единицы величины e, то отношения между величинами a и b будут такими же, как и отношения между их численными значениями, и наоборот.

Например, если массы двух тел таковы, что а=5 кг, b=3 кг, то можно

утверждать, что масса а больше массы b поскольку 5>3.

2. Если величины а и b измерены при помощи единицы величины e, то, чтобы найти численное значение суммы a+b достаточно сложить численные значения величин а и b. а+b= c m (a+b) = m (a) + m (b).

Например, если а = 15 кг, b=12 кг, то а+b=15 кг + 12 кг = (15+12) кг = 27кг

З. Если величины а и b таковы, что b= x а, где x -положительное действительное число, и величина а, измерена при помощи единицы величины e, то чтобы найти численное значение величины b при единице e, достаточно число x умножить на число m (а):b=x a m (b)=x m (a).

Например, если масса а в 3 раза больше массы b .т.е. b= За и а = 2 кг, то b= З, а=3 (2 кг) = (3*2) кг = 6кг.

Рассмотренные понятия — объект, предмет, явление, процесс, его величина, численное значение величины, единица величины — надо уметь вычленять в текстах и задачах.

Например, математическое содержание предложения «Купили 3 килограмма яблок» можно описать следующим образом: в предложении рассматривается такой объект, как яблоки, и его свойство — масса; для измерения массы использовали единицу массы — килограмм; в результате измерения получили число 3 -численное значение массы яблок при единице массы — килограмм.

Система развивающих упражнений при изучении величин в начальном курсе математики.

Задачи изучения величин в начальном курсе математики

1) сформировать конкретные представления о величинах

2) сформировать навыки измерения величин

3)научить выражать величины в различных единицах измерения

4)научить выполнять арифметические действия над величинами.

Для более успешной реализации этих задач на уроках математики в начальной школе, целесообразно использовать развивающие упражнения, а именно проблемные ситуации. Использование проблемных ситуаций в теме « Величины », да и при изучении других тем начального курса математики, несомненно, имеет огромное значение. С помощью ситуации, созданной на уроке, учащиеся более осознанно подходят к изучению данного вопроса. Это помогает лучше осваивать материал, следовательно, обеспечивает ускоренный темп в изучении данной темы. Непосредственная практическая деятельность детей способствует развитию логического и абстрактного мышления, внимания, восприятия.

Заключение

Подводя итоги изучения данной темы можно сделать вывод о том, что величины очень важны и актуальны для нас в современное время.

Понятие измерения в психологии. Измерительные шкалы

. типов: с одной стороны, это шкала физического измерения стимула, с другой — значение психологической (субъективной) реакции на этот стимул. Очевидно, что точность расчета любой величины прямо зависит от указанной .

Материал реферата может быть рекомендован для усовершенствования знаний о величинах математики.

Было установлено, что изучение темы «Величина и её измерение» в начальных классах возможно с использованием развивающих упражнений. Была выдвинута гипотеза:

Учебная деятельность по изучению тем: «Длина отрезка» и «Единицы измерения длины» организованная с помощью развивающего обучения, обеспечивает высокое качество знаний и умений учащихся. Для подтверждения данной гипотезы было организовано экспериментальное обучение младших школьников. Была подобрана и составлена система упражнений развивающего характера.

Список литературы

[Электронный ресурс]//URL: https://psychoexpert.ru/referat/zavisimost-mejdu-velichinami-2/

1. Рубенштейн, С.Л. Проблемы общей психологии [Текст]/ С.Л. Рубенштейн. — М. : Просвещение,1973. – 2 с.

2. Смирнов, С.И. Педагогика [Текст]/ С.И. Смирнов.- М.: Издательство Дом «АКАДЕМИЯ»,1998. – 309 с.

3. Стойлова, Л.П. Основы начального курса математики [Текст]/ Л.П. Стойлова. — М.: Просвещение,1988.- 302 с.

Примеры похожих учебных работ

«Величины и её измерения»

. и при решении задач, — знать взаимосвязь между такими величинами, как цена, количество, стоимость товара; скорость, . проблему и эти трудности проблемной ситуации в зависимости от интеллектуальных возможностей. Проблемное обучение включает несколько .

Формирование у детей представлений о величине в разных возрастных группах

Развитие у детей старшего дошкольного возраста представлений о числе и счёте

. у дошкольников интереса к математическим знаниям, совершенствования познавательной деятельности, общего умственного развития. . в других видах деятельности, новой обстановке. Преждевременное обучение счетной деятельности неизбежно приводит к .

Страховые пособия по беременности и родам

. страхового обеспечения — пособия по временной нетрудоспособности, по беременности и родам, уходу за ребенком. В социально-политическом аспекте социальное страхование на случай беременности и родов представляет собой способ реализации конституционных .

Учение Пифагора о числе как о первоначале мира: современное понимание

. отношений, межличностных отношений и т.д. Учение Пифагора о числе как о первоначале мира постепенно набирает все большие обороты . Пифагорейское учение о четных и нечетных числах являлось основным для отражения важнейших философских категорий: .

Анализ социологических данных
Антропология
Безопасность жизнедеятельности
Возрастная психология
Гендерный анализ
Демография
Дифференциальная психология
Зарубежная философия
Зоопсихология
Истории и теории мировой культуры
Истории русской философии
История и теория религии
История психологии
Клиническая психология
Конфликтология
Культурная антропология
Логика
Логико-комбинаторные методы
Методологические проблемы психологии
Методология и методы социологии
Методы измерения в социологии
Общая психология
Онтологии и теории познания
Основы нейропсихологии
Основы психодиагностики
Педагогика
Педагогическая психология
Политология
Психогенетика
Психология личности
Психология сознания
Психология труда и инженерная психология
Психология
Психофизиология
Современная социальная политика
Современные теории деятельности и практической рациональности
Социальная и экономическая антропология
Социальная история
Социальная психология
Социальная структура и социальная стратификация
Социальная теория и прикладное социальное знание
Социальная теория семьи и семейных отношений
Социальная философия
Социально-экономическое поведение домохозяйств
Социолингвистика
Социологическая теория
Социологическое исследование
Социология
Социология культуры
Социология маркетинга
Социология науки и научного знания
Социология образования
Социология политики
Социология предпринимательства
Социология профессий
Социология религии
Социология труда и занятости
Социология хозяйственного развития
Специальная психология
Сравнительная психология
Физиология высшей нервной деятельности
Философия
Философия и методология науки
Философия образования
Философия политики и права
Философия религии и религиоведения
Философия языка и коммуникации
Философская антропология
Экономическая и социальная статистика
Экономическая социология
Экспериментальная психология
Эстетика
Этика

Все документы на сайте представлены в ознакомительных и учебных целях.
Вы можете цитировать материалы с сайта с указанием ссылки на источник.

Математика. Материалы курса

Видеолекция. Зависимость между величинами. Виды зависимостей

На прошлой лекции мы рассматривали распределение одного признака, то есть мы выделяли некоторый признак и изучали его индивидуально. Довольно часто задачей исследования является изучение нескольких признаков в совокупности и изучение взаимосвязей между этими признаками или зависимости между этими признаками.

Таким образом, у нас в самом простом случае имеется 2 признака, то есть у нас есть набор пар значений ( x_i ; y_i ), где x_i – значение признака Х в k -ом опыте, у _i – значение признака Y в k -ом опыте. Требуется установить, зависимы ли данные признаки или нет, и восстановить зависимость.

Прежде чем говорить о том, как узнать зависимы или нет, нужно рассмотреть виды зависимости. Данные виды также рассмотрены в разделе 3.6 данного курса, но так как раздел является вариативным, мы рассмотрим их еще раз.

Самой общей является зависимость статистическая, когда значения одной переменной влияет на закон распределения второй, то есть если между переменными статистической зависимости нет, то данные переменные, данные случайные величины мы называем независимыми, то есть никак одна не влияет на другую.

Второй вид зависимости – корреляционная. Это зависимость среднего значения одной случайной величины от значения другой случайной величины. Тогда эта зависимость более узкая, то есть она встречается реже статистической, но в статистике рассматривается именно корреляционная зависимость, и дальше на этой лекции, говоря зависимые, мы будем подразумевать именно корреляционную зависимость.

Частный случай корреляционной зависимости, самый редкий случай зависимости – это функциональная зависимость. Это зависимость, при которой значению одной случайной величины соответствует значение другой случайной величины, то есть каждому значению соответствует некоторое другое значение второй величины. Она встречается очень редко, мы периодически будем говорить, что в том или ином случае мы можем наблюдать именно функциональную зависимость. Еще раз повторюсь, что, когда мы говорим в статистике «исследовать зависимость между случайными величинами», обычно мы подразумеваем именно корреляционную зависимость.

Зависимость между переменными исследуется двумя видами анализа. Это корреляционный анализ и регрессионный анализ. Корреляционный анализ рассчитывает некоторые коэффициенты корреляции, оценивает их и позволяет сделать выводы о связях. Регрессионный анализ изучает форму этой связи, то есть он позволяет установить форму зависимости и подобрать ее параметры, а также оценить полученную кривую на предмет качества.

Сначала рассмотрим корреляционный анализ. Из раздела «теория вероятности», мы знаем, что корреляционная зависимость оценивается коэффициентом корреляции. На самом деле, мы рассматривали только один коэффициент корреляции, в статистике рассматриваются несколько коэффициентов корреляции, в зависимости от того какую зависимость мы хотим проанализировать. Если нас интересует линейная зависимость, то мы рассматриваем именно коэффициент корреляции Пирсона, если же нас интересует не линейная зависимость или множественная зависимость, то будут рассматривать другие коэффициенты корреляции.

Корреляционные зависимости делятся на разные по форме – прямолинейные или криволинейные, по направлению – прямая и обратная или положительная и отрицательная. В случае положительной корреляционной зависимости у нас: во-первых коэффициент корреляции положителен, а во-вторых среднее значение второго признака (зависимого) увеличивается при увеличении значения факторного признака и наоборот; при отрицательной связи при увеличении значений факторного признака уменьшается значение зависимого признака (или результативного) и наоборот. Еще раз оговорюсь, что факторными признаками называются признаки, которые лежат в основе зависимости, от которых строится зависимость, а результативные – это признаки, которые мы исследуем, их тоже может быть один или несколько. В рамках данной лекции мы рассмотрим только парную зависимость, когда у нас один факторный признак и один результативный. Также корреляционную зависимость разделяют по степени или по тесноте – в зависимости от модуля значения коэффициента корреляции может быть сильная зависимость, средняя, умеренная, слабая или очень слабая. Слабую и очень слабую иногда не разделяют. Таблица приведена на слайде.

Для оценки тесноты линейной зависимости рассматривают коэффициент корреляции Пирсона. Из курса теории вероятности мы знаем, что он вычисляется по формуле, где М[Х] – математическое ожидание, Д[Х] – дисперсия, при этом его значения лежат в диапазоне от 0 до 1, а оценка данного коэффициента приведена на слайде, где у нас математическое ожидание заменено на среднее, а дисперсия на квадрат среднеквадратического отклонения, соответственно у нас здесь избавлено от корней.

Для оценки тесноты линейной связи используется коэффициент корреляции Пирсона. Коэффициент корреляции между двумя случайными величинами приведен на слайде. Ниже приведена оценка данного коэффициента, где М[Х], М[У] – математические ожидания случайных величин, а х с чертой, у с чертой — их оценки. Соответственно Д[Х], Д[У] – дисперсии случайных величин, а s ₀ _x 2 , s _0у 2 — их оценки, а s ₀ _x , s _0у – оценки среднеквадратических отклонений. х,у с чертой общей – это среднее произведение.

Все значения по модулю не превосходят единицы, то есть у нас на самом деле математическое ожидание произведения отклонений не больше, чем корень из произведения дисперсий.

Далее, если у нас по модулю коэффициент корреляции равен 1, то имеет место функциональная линейная связь, при этом если он равен 1, то у нас будет прямая линейная связь, если – 1, то обратная линейная связь. В случае же, если у нас коэффициент корреляции равен 0, то линейная корреляционная связь отсутствует. Здесь у нас тонкий нюанс. Коэффициент корреляции равен нулю. Пусть мы на практике получили оценку. Мы понимаем, что уже из предыдущего занятия, что оценка и истинное значение не равны. Встает вопрос– «Если мы получили r * _xy не нулевой, но близкий к нулю, значит ли это, что зависимость отсутствует?». Этот вопрос мы оставляем до одного из следующих занятий, там мы как раз-таки рассмотрим гипотезу о незначимости коэффициента корреляции и поймем, как ее проверять. Если же мы рассматриваем два или более двух признаков, то обычно анализируется корреляционная таблица. По ней могут быть рассчитаны множественный коэффициенты корреляции и так далее. Вот эта таблица r_ij , где i ≠ j – это коэффициент корреляции между х _i , y_j , а r_ii всегда будет равен 1.

Перейдем к регрессионному анализу. Пусть у нас рассматривается пара случайных величин Х и Y , тогда математическое ожидание У, при условии, что значение Х приняло значение х – это некоторая кривая регрессии или уравнение регрессии. Тогда мы можем представить величину Y_i = φ(х _i ) + ε_i , где х _i – не случайное значение первой случайной величины, а Y_i – случайная величина, которая задает множество всех значений, которые могут быть получены в данном случае, причем для ε_i формулируются некоторые свойства. Первые 4 свойства обязательны, а 5 свойства является дополнительным и используется для оценки уравнения регрессии.

Этапы регрессионного анализа состоят в том, что сначала делается предположение о форме связи между переменными, далее находятся параметры и последним этапом является проверка надежности полученных оценок, то есть оценка уравнения регрессии. Нам нужно проверить насколько хорошо и правильно мы выбрали форму связи и насколько качественно были найдены оценки параметров регрессии.

Для нахождения уравнения параметров уравнения регрессии при известной форме используется метод наименьших квадратов. Пусть у нас есть пара х, у , при этом мы хотим построить кривую регрессию, представленную на слайде, где а – это один или несколько параметров, тогда построим функции ошибок – это функция отклонений значения полученного по уравнению от истинного значения переменной у в данном опыте, то есть сумма квадратов этих отклонений. Мы уже понимаем, что сумма отклонений просто будет равна 0. Так вот эта сумма квадратов уравнений должна быть минимальной, именно поэтому метод и называется «методом наименьших квадратов». Чтобы найти минимум этой функции, у нас параметры а₁, а₂. а_к , нам нужно рассмотреть частные производные. Так как данное уравнение является квадратным относительно всех параметров, то у него найденная стационарная точка будет точкой минимума. Здесь уже 2 этап проверки на минимум проводить не нужно.

Рассмотрим наиболее часто встречающийся и наиболее простой случай, когда математическое ожидание Y , условное математическое ожидание линейно зависит от величины х. В этом случае мы можем построить зависимость у с крышечкой, представленной на слайде, где Е (а, b ) – функция ошибок, найдем производные и получим следующую систему, то есть эти вычисления сделайте самостоятельно. Решив данную систему, можно найти параметры а и b . На самом деле на практике, если вычисления делаются руками, то именно такой способ будет удобнее, он позволит вам минимизировать вычисления. Если же это все рассчитывается автоматически, то можно выразить значение параметров а и b . Для этого оба уравнения, обе части обоих уравнений поделим на n . Получим следующую систему, где х с чертой, у с чертой – среднее значение величин х, у. х 2 – средний квадрат, ху с чертой – это среднее произведение. Опять же решением данной системы будут значения а и b . Выразим b из второго уравнения, поменяем уравнения местами и подставим в первое. Продолжим выражать, то есть мы выразим a и получим, что, а – это будет среднее произведение минус произведение среднего, деленное на тоже самое с квадратами.

Теперь давайте вспомним, что оценка дисперсии ничто иное, как х 2 с чертой минус х с чертой в квадрате, то есть в знаменателе стоит оценка дисперсии, а в числителе стоит оценка корреляции, то есть величина y с крышечкой будет равняться, тому, что написано на слайде. При этом коэффициент a называется коэффициентом регрессии и показывает тесноту связи. Понятно, что в зависимости от того, в каких единицах будут измеряться, у нас коэффициент регрессии будет разным. Принято анализировать не сам коэффициент регрессии, а коэффициент корреляции. На слайде это не приведено, но можно выразить коэффициент регрессии через оценки дисперсии и коэффициент корреляции. Сделайте это самостоятельно.

Иногда регрессия все же не является линейной, то есть если мы множество имеющихся у нас точек поместим на плоскость, то мы увидим, что линия там никак не получается. При этом на глаз тип зависимости очень сложно оценить. Например, гиперболу от параболы не всегда можно отличить, если она как-то хитро повернута. Поэтому рассматривают различные нелинейные регрессии. Например, линейная по оцениваемым параметрам, тогда можно просто заменой переменных свести данные уравнения к линейным и оценить, какое из них больше подходит.

Нелинейная по оцениваемым параметрам. Она может быть внутренне линейной, внутренне нелинейной. Вопрос: существует ли замена переменной такая, чтобы уравнение было сведено к линейному? Чаще всего стараются искать именно такие зависимости, которые сводятся к линейной и уже дальше анализировать, причем свести можно, как к парной линейной, так и к множественной линейной. Например, полиномиальные зависимости заменой переменных сводятся к множественной линейной, где каждая степень – это своя переменная. Дальше происходит анализ. Анализ в рамках данного курса мы рассматривать не будем. Он есть в справочнике, более подробно смотрите в литературе. Спасибо за внимание.

Что такое зависимость между величинами

Урок 38. Математическая модель. Основные способы представления математических зависимостей между данными. Понятия: величина, имя величины, тип величины, значение величины

Моделирование зависимостей между величинами (§17)

Величины и зависимости между ними

Содержание данного раздела учебника связано с компьютерным математическим моделированием. Применение математического моделирования постоянно требует учета зависимостей одних величин от других. Приведем примеры таких зависимостей:

1) время падения тела на землю зависит от его первоначальной высоты;
2) давление газа в баллоне зависит от его температуры;
3) уровень заболеваемости жителей города бронхиальной астмой зависит от концентрации вредных примесей в городском воздухе.

Реализация математической модели на компьютере (компьютерная математическая модель) требует владения приемами представления зависимостей между величинами.

Рассмотрим различные методы представления зависимостей.

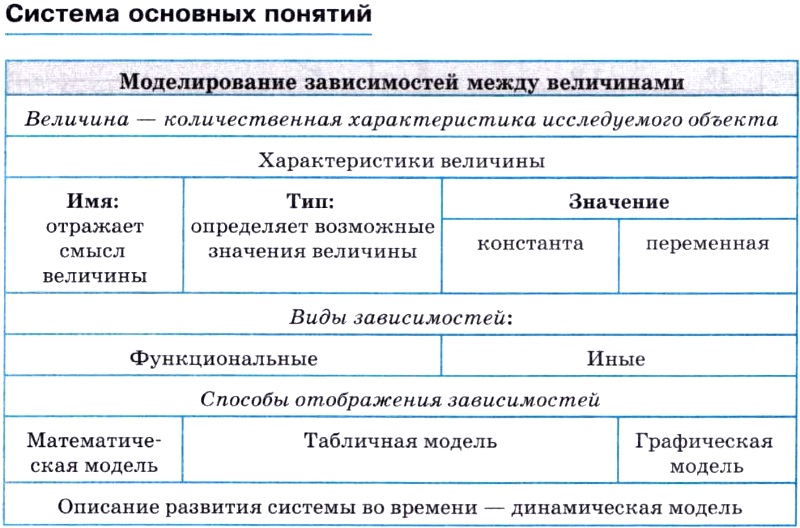
Всякое исследование нужно начинать с выделения количественных характеристик исследуемого объекта. Такие характеристики называются величинами.

С понятием величины вы уже встречались в курсе информатики 7-9 классов. Напомним, что со всякой величиной связаны три основных свойства: имя, значение, тип.

Имя величины может быть смысловым и символическим. Примером смыслового имени является «давление газа», а символическое имя для этой же величины — Р. В базах данных величинами являются поля записей. Для них, как правило, используются смысловые имена, например: ФАМИЛИЯ, ВЕС, ОЦЕНКА и т. п. В физике и других науках, использующих математический аппарат, применяются символические имена для обозначения величин.

Чтобы не терялся смысл, для определенных величин используются стандартные имена. Например, время обозначают буквой t, скорость — V, силу — F и пр.

Если значение величины не изменяется, то она называется постоянной величиной или константой. Пример константы — число Пифагора π = 3,14159. Величина, значение которой может меняться, называется переменной. Например, в описании процесса падения тела переменными величинами являются высота Н и время падения t.

Третьим свойством величины является ее тип. С понятием типа величины вы также встречались, знакомясь с программированием и базами данных . Тип определяет множество значений, которые может принимать величина. Основные типы величин: числовой, символьный, логический . Поскольку в данном разделе мы будем говорить лишь о количественных характеристиках, и рассматриваться будут только величины числового типа.

А теперь вернемся к примерам 1-3 (см. начало параграфа) и обозначим (поименуем) все переменные величины, зависимости между которыми нас будут интересовать. Кроме имен укажем размерности величин. Размерности определяют единицы, в которых представляются значения величин.

1 ) t (с) — время падения; Н (м) — высота падения. Зависимость будем представлять, пренебрегая учетом сопротивления воздуха; ускорение свободного падения g (м/с 2 ) будем считать константой .

2 ) Р (н/м 2 ) — давление газа (в единицах СИ давление измеряется в ньютонах на квадратный метр); t ( 0 С) — температура газа. Давление при нуле градусовР₀ будем считать константой для данного газа.

3 ) Загрязненность воздуха будем характеризовать концентрацией примесей (каких именно, будет сказано позже) — С (мг/м 3 ) . Единица измерения — масса примесей, содержащихся в 1 кубическом метре воздуха, выраженная в миллиграммах. Уровень заболеваемости будем характеризовать числом хронических больных астмой, приходящихся на 1 000 жителей данного города — Р (бол./тыс.).

Отметим важное качественное различие между зависимостями, описанными в примерах 1 и 2, с одной стороны, и в примере 3, с другой. В первом случае зависимость между величинами является полностью определенной: значение Н однозначно определяет значение t (пример 1), значение t однозначно определяет значение Р (пример 2). Но в третьем примере зависимость между значением загрязненности воздуха и уровнем заболеваемости носит существенно более сложный характер; при одном и том же уровне загрязненности в разные месяцы в одном и том же городе (или в разных городах в один и тот же месяц) уровень заболеваемости может быть разным , поскольку на него влияют и многие другие факторы. Отложим более детальное обсуждение этого примера до следующего параграфа, а пока лишь отметим, что на математическом языке зависимости в примерах 1 и 2 являются функциональными, а в примере 3 — нет.

Математические модели

Если зависимость между величинами удается представить в математической форме, то мы имеем математическую модель.

Математическая модель — это совокупность количественных характеристик некоторого объекта (процесса) и связей между ними, представленных на языке математики.

Хорошо известны математические модели для первых двух примеров. Они отражают физические законы и представляются в виде формул:

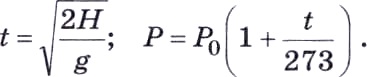
Это примеры зависимостей, представленных в функциональной форме. Первую зависимость называют корневой (время пропорционально квадратному корню высоты), вторую — линейной.

В более сложных задачах математические модели представляются в виде уравнений или систем уравнений. В конце данной главы будет рассмотрен пример математической модели, которая выражается системой неравенств.

В еще более сложных задачах (пример 3 — одна из них) зависимости тоже можно представить в математической форме, но не функциональной, а иной.

Табличные и графические модели

Рассмотрим примеры двух других, не формульных, способов представления зависимостей между величинами: табличного и графического. Представьте себе, что мы решили проверить закон свободного падения тела экспериментальным путем. Эксперимент организуем следующим образом: будем бросать стальной шарик с 6-метровой высоты, 9-метровой и т. д. (через 3 метра), замеряя высоту начального положения шарика и время падения. По результатам эксперимента составим таблицу и нарисуем график (рис. 3.2).

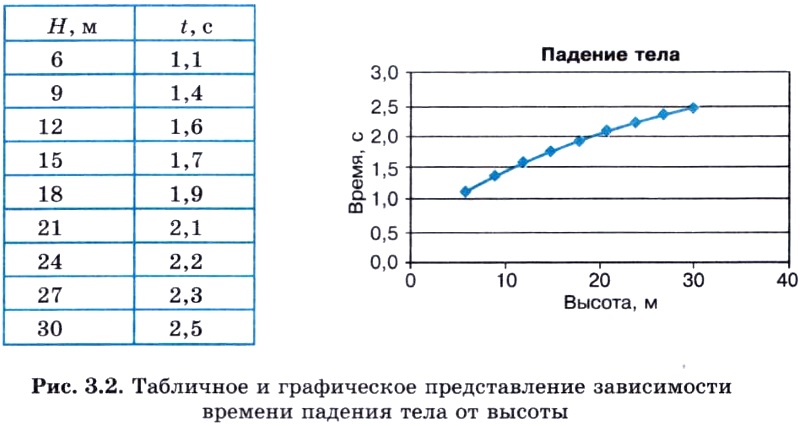
Если каждую пару значений Н и t из данной таблицы подставить в приведенную выше формулу зависимости времени от высоты, то формула превратится в равенство (с точностью до погрешности измерений). Значит, модель работает хорошо. (Однако если сбрасывать не стальной шарик, а большой легкий мяч, то равенство не будет достигаться, а если надувной шарик, то значения левой и правой частей формулы будут различаться очень сильно. Как вы думаете почему?)

В этом примере мы рассмотрели три способа моделирования зависимости величин: функциональный (формула), табличный и графический. Однако математической моделью процесса падения тела на землю можно назвать только формулу. Формула более универсальна, она позволяет определить время падения тела с любой высоты, а не только для того экспериментального набора значений Н, который отображен на рис. 3.2. Имея формулу, можно легко создать таблицу и построить график, а наоборот — весьма проблематично.

Точно так же тремя способами можно отобразить зависимость давления от температуры. Оба примера связаны с известными физическими законами — законами природы. Знания физических законов позволяют производить точные расчеты, они лежат в основе современной техники.

Информационные модели, которые описывают развитие систем во времени, имеют специальное название: динамические модели. В примере 1 приведена именно такая модель. В физике динамические информационные модели описывают движение тел, в биологии — развитие организмов или популяций животных, в химии — протекание химических реакций и т. д.

Вопросы и задания

1. а) Какие вам известны формы представления зависимостей между величинами?

б) Что такое математическая модель?

в) Может ли математическая модель включать в себя только константы?

2. Приведите пример известной вам функциональной зависимости (формулы) между характеристиками какого-то объекта или процесса.

3. Обоснуйте преимущества и недостатки каждой из трех форм представления зависимостей.

6.4В-12. Исследование зависимостей. Методические рекомендации к уроку

Величина — некоторая количественная характеристика объекта.

Зависимости между величинами могут быть представлены в виде математической модели, в табличной и графической формах.

Зависимость, представленная в виде формулы, является математической моделью.

Организационный момент.

Проверить домашнее задание.

Совместно с учащимися определить тему и цели урока, «зону ближайшего развития».

Актуализация опорных знаний. Ответить на вопросы:

1. Что такое зависимость между величинами?

2. Как её можно задать?

3. Покажите взаимосвязь между тремя видами задания зависимости: формулой, таблицей, графиком.

4. Где мы встречаем различные виды зависимостей между величинами?

5. Какие формулы известны?

Повторить формулы. В каждой формуле озвучить зависимость.

v = ; t = ; s = 3t; P = 3a; a = ; S = 3a; b =

Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания подобные заданиям Приложения 1. Каждый выполняет самостоятельно.

Приложение 1

1) Пешеход, двигаясь с постоянной скоростью 3 км/ч, прошёл 9 км. Какое расстояние пройдёт пешеход, если его время движения увеличить в 2 раза? уменьшить в 1,5 раза?

2) Ширина прямоугольника равна 3 см, площадь — 15см 2 . Как изменится площадь прямоугольника, если длину увеличить в 2 раза? уменьшить в 2,5 раза?

3) Сторона равностороннего треугольника равна 3см. Как изменится его периметр, если сторону увеличить в 2 раза? уменьшить в 1,5 раз?

Ответы :

S = 3t; S = 3a. ; P = 3a;

4) Кто — то стёр с доски часть формулы. Восстановите запись и «расшифруйте формулу»:

После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать задания, которые были сделаны с ошибками.

Групповая работа. Для выполнения упражнений разделите учащихся на малые группы, для того чтобы они обсудили задание и выполнили его совместно. При выполнении задания учащиеся анализируют условие, в ходе обсуждения развивают математическую речь, самостоятельно принимают решение, развивают навыки работы в команде.

Решение задач с практическим содержанием.

Задача 1. Месячная плата за квартиру составляет 10600 тенге. Квартплата просрочена на 20 дней. Пеня составляет 1% квартплаты за каждый день просрочки. Сколько денег потеряно?

Дополнительный вопрос всем: много это или мало?

Задача 2. Если взять на полгода кредит в банке «Алтын» на сумму 500000 тенге, сколько денег будет «подарено» банку, который берёт 28% годовых?

«Практики – маляры» (Раздать модели куба)

Задача 3. Перед вами модель куба, которую нужно закрасить краской. Сколько потребуется краски, если на 1 см² приходится 0,2 грамма краски? Составьте формулу зависимости площади всей поверхности куба S от длины ребра куба a . Измерьте длину ребра куба и найдите ответ задачи.

Наблюдайте за работой учащихся, если необходимо корректируйте их деятельность. По окончании времени каждая группа представляет свою работу классу.

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

После выполнения задания группы обмениваются решением и проверяют работу другой группы по ключам.

Работа с классом. Ввод в тему урока, используя основные знания и навыки по решению заданий на «чтение» и построение графиков. Пригласите к доске ученика, попросите его записать подробное решение задания.

задание

тренировочные

тренер 2

Предоставить достаточно времени для выполнения задания. Подвести итог после решения этих заданий. Пригласите к доске ученика, попросите его записать подробное решение задания. Учащиеся на местах решают все примеры и сверяют свои решения с записями на доске, внимательно слушают одноклассников. С целью развития математической речи попросите одного из учащихся подробно прокомментировать решение любого задания, акцентируйте их внимание на обоснование решений. Для учащихся с более высокой скоростью решения организуйте «уголок Знайки», куда они могли бы подходить и проверять свое решение или читать идею решения. Это позволяет не отвлекаться на объяснение задачи, а работать в это время с остальной частью класса.

При наличии компьютера, просмотреть презентацию для визуального закрепления материала.

Беседа. Рефлексия. «Рефлексивный ринг»

Сегодня я узнал… Я научился…

У меня получилось… Было трудно…

Я смог … Я понял, что…

Меня удивило… Мне захотелось…

Домашнее задание.

Обязательное домашнее задание по цели обучения 6.5. 2 .10 по теме: «Исследование зависимостей между величинами, используя графики реальных процессов» предполагает количество заданий, на выполнение которых учащиеся должны затрачивать не более 15-20 минут. Задания для выполнения дома рекомендуем дифференцировать по уровню сложности, включая задания на анализ, синтез и оценку. При этом, желательно, давать учащимся задачи практического содержания , решить из уровня В учебного пособия «Математика 6»

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Моделирование зависимостей между величинами

С помощью урока учащиеся узнают, что такое величина и какие существуют формы представления зависимостей, что такое математическая модель и какие модели называются табличными и графическими.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока «Моделирование зависимостей между величинами»

На прошлом уроке мы с вами начали изучение раздела «Информационное моделирование» и ознакомились с основными понятиями этого раздела.

Мы выяснили, что модель — это объект-заменитель, который в определённых условиях может заменять объект-оригинал. Модель воспроизводит интересующие нас свойства и характеристики оригинала.

Информатика занимается общими методами и средствами создания и использования информационных моделей.

К основным этапам компьютерного моделирования относятся:

Первый этап – Постановка задачи: описание объекта и определение цели моделирования.

Второй этап – Разработка плана создания модели. Выделение свойств объекта, существенных для данной задачи, и отбрасывание второстепенных. Выбор формы представления модели и необходимого инструментария.

Третий этап – Создание модели: формализация, т. е. переход к математической модели; создание алгоритма и написание программы.

Четвёртый этап – Анализ модели на соответствие объекту-оригиналу.

Как мы уже выяснили процесс создания, и использования моделей для решения практических задач называют моделированием.

Моделирование широко используется в науке и технике, экономике и образовании. Без моделирования немыслимо создание машин и механизмов, строительство зданий и мостов, создание новых материалов, лекарств, торговых сетей.

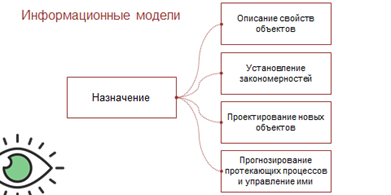
Использование моделей позволяет упростить и удешевить исследование объектов и явлений реального мира. Основное назначение информационных моделей — это описание свойств объектов, установление закономерностей, проектирование новых объектов, прогнозирование протекающих процессов и эффективное управление ими.

Мы с вами будем изучать компьютерное математическое моделирование.

Формальные информационные модели содержат математические и химические формулы, алгоритмы, представленные на языках программирования, и т. д. Например, формулы математики описывают соотношения между количественными характеристиками объекта моделирования.

Применение математического моделирования постоянно требует учёта зависимостей одних величин от других.

Сегодня на уроке мы узнаем:

· Что такое величина, и какие существуют формы представления зависимостей.

· Что такое математическая модель.

· Какие модели называются табличными и графическими.

С зависимостями между величинами вы встречаетесь постоянно на уроках физики и математики. Зависимость может быть прямой и обратной.

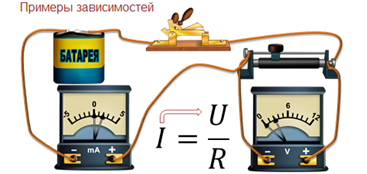
Давайте рассмотрим примеры зависимостей:

· Пройденный пешеходом путь, за определённый промежуток времени зависит от его скорости;

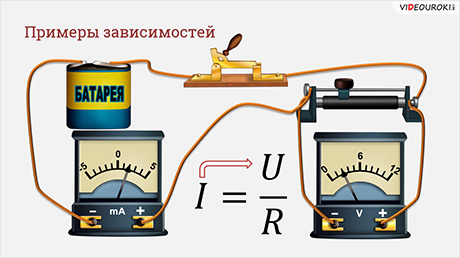
· Сила тока на участке цепи зависит от напряжения;

· Уровень заболеваемости жителей города бронхиальной астмой зависит от концентрации вредных примесей в городском воздухе.

Рассмотрим способы представления зависимостей.

Как вы помните моделирование, да и любое другое исследование начинают с выделения основных количественных характеристик исследуемого объекта, то есть величин.

Понятие величина включает три свойства: имя, значение, тип.

Рассмотрим каждое свойство более подробно.

Итак, имя. Имя величины может быть смысловым или символическим. Например, смысловым именем является «скорость движения», а символическим именем для этой величины будет V.

Имена в языках программирования принято называть идентификаторами. Есть идентификаторы переменных, констант, типов, функций и т.д.

В физике, химии и других науках, которые используют математический аппарат, применяются символические имена для обозначения величин. В основном используют стандартные имена. Например, давление обозначают буквой Р, температуру буквой t.

Следующее свойство величины – это её значение. По значению величины делятся на две группы. К первой группе относятся величины, значения которых не изменяется. Такие величины называются постоянными или константами. Ко второй группе относятся величины, значения которых меняются. Такие величины называются переменными.

Например, константой является скорость света, которая равна 3 умноженное на десять в пятой степени километров в секунду.

Если рассматривать переменные величины, то, например, при равномерном прямолинейном движении тела переменными являются время и путь, а вот скорость будет постоянной.

Третье свойство величины – это её тип. С данным понятием вы также знакомы. Вы встречались с ним при изучении программирования, баз данных, табличных процессоров.

Тип величины определяет диапазон допустимых значений, принимаемых величинами. К основным типам величин относятся: числовой, символьный, логический.

Так как при изучении моделирования нас интересуют только количественные характеристики, то рассматривать мы будем только величины числового типа.

Вернёмся к примерам зависимостей, которые мы рассматривали в начале урока. Обозначим все эти величины и укажем их размерности, то есть укажем единицы, в которых данные величины измеряются.

Итак, первый пример. Пройденный пешеходом путь, за определённый промежуток времени зависит от его скорости;

Здесь путь обозначается буквой S и измеряется в метрах, скорость обозначается буквой вэ и измеряется в метрах в секунду, время движения обозначается буквой t и измеряется в секундах.

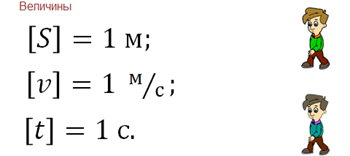
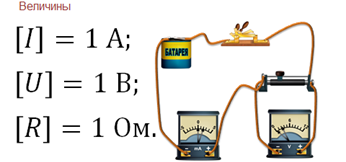
В следующем примере мы рассматривали зависимость силы тока, которая обозначается буквой I и измеряется в Амперах, от напряжения, обозначается буквой U и измеряется в Вольтах. Сопротивление обозначается буквой R и измеряется в Омах.

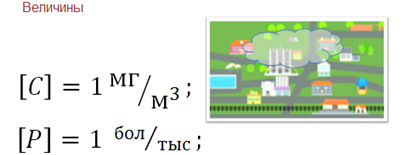
Далее, загрязнённость воздуха будем характеризовать концентрацией различных примесей. Обозначим буквой C, измеряется в миллиграммах на метр кубический. Здесь единица измерения — это масса примесей, содержащихся в 1 кубическом метре воздуха, выраженная в миллиграммах. Уровень заболеваемости характеризовать числом хронических больных астмой, приходящихся на тысячу жителей данного города. Обозначим буквой P, измеряется в больной на тысячу.

Также важно отметить различия зависимостей в приведённых примерах.

В первом и втором примерах зависимость между величинами является полностью определённой: значение пути точно зависит от скорости, а сила тока точно зависит от напряжения. В третьем примере зависимость между загрязнённостью воздуха и уровнем заболеваемости более сложная. Так как на уровень заболеваемости влияют и многие другие факторы.

То есть на математическом языке в первом и втором примере зависимости являются функциональными, а в третьем нет.

Как вы помните из прошлого урока модели могут быть материальные и информационные.

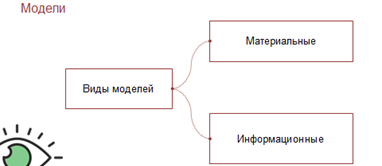
В ходе материального моделирования изготавливается макетный или опытный образец технического объекта, и проводятся его испытания по определению выходных параметров, характеристик и степени надёжности. Основной недостаток такого метода – большие временные и материальные затрат.

К информационному относится математическое моделирование. Если зависимость между величинами удаётся представить в математической форме, то мы имеем математическую модель.

Математической моделью называется совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности изучаемого объекта, процесса или явления.

Запишем математические модели для наших зависимостей.

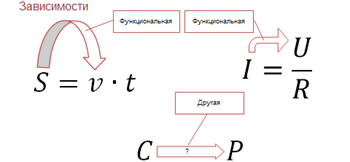
В первом случае путь равен скорость умножить на время. Такая зависимость называется линейной.

Во втором случае сила тока равна напряжение разделить на сопротивление. Здесь сила тока прямо пропорционально зависит от напряжения и зависимость называется линейной. Также сила тока обратно пропорционально зависит от сопротивления и зависимость называется обратной пропорциональностью.

Более сложные математические модели представляются в виде уравнений, неравенств или их систем.

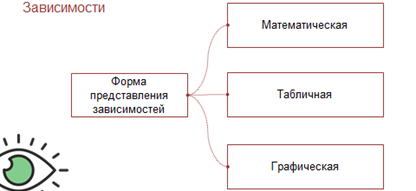
Мы выяснили что, зависимости между величинами можно представлять в математической форме. Ещё зависимости можно представлять в табличной и графической форме.

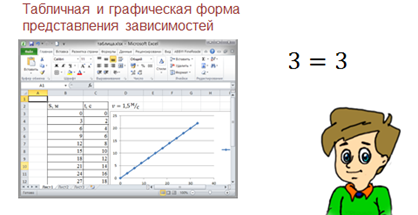
Предположим мы решили проверить зависимость пути от времени при равномерном движении. Пусть скорость пешехода равна одна целая пять десятых метров в секунду. Будем увеличивать каждый раз длину пути на три метра, и измерять время, за которое пешеход будет проходить данный путь.

Результаты измерений занесём в таблицу и нарисуем график.

Если мы возьмём из таблицы пару значений c и t и подставим в формулу пути, то формула превратится в равенство. Значит, можно сделать вывод, что модель работает правильно.

В этом примере мы рассмотрели три способа моделирования зависимости величин: функциональный (формула), табличный и графический.

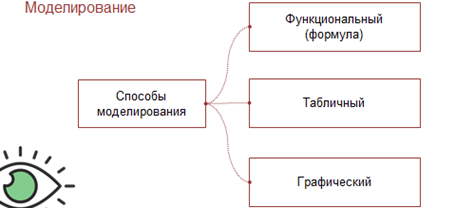
Однако математической моделью равномерного движения тела можно назвать только формулу. Формула более универсальна, она позволяет определить время движения тела на любом участке пути, а не только для экспериментального набора значений пути.

Имея формулу, можно легко создать таблицу и построить график, а вот наоборот по таблице или графику вывести формулу — весьма проблематично.

Точно так же тремя способами можно отобразить зависимость силы тока от напряжения. Оба примера связаны с известными физическими законами. Знания физических законов позволяют производить точные расчёты, они лежат в основе современной техники.

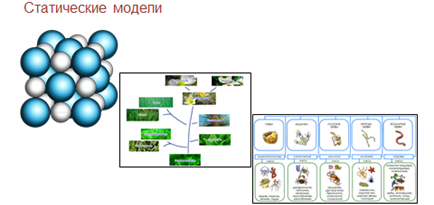
Информационные модели, описывающие объекты, явления, процессы в определённый момент времени, без учёта их изменений в пространстве и времени, называются статическими.

Такими моделями являются, например, структура кристаллов, классификация растений или животных.

Динамические модели учитывают изменения параметров процессов и явлений с течением времени.

В первом примере приведена именно такая модель.

В физике динамические информационные модели описывают движение тел, в биологии — развитие организмов или популяций животных, в химии — протекание химических реакций и т. д.