Что такое задача регрессии

Регрессия (Regression)

В теории вероятности и математической статистике это зависимость математического ожидания случайной величины от одной или нескольких других случайных величин.

В отличие от чисто функциональной зависимости y = f ( x ) , где каждому значению независимой переменной x соответствует единственное значение зависимой переменной y , регрессионная зависимость предполагает, что каждому значению переменной x могут соответствовать различные значения y , обусловленные случайной природой зависимости.

Если некоторому значению величины x i соответствует набор значений величин y i 1 , y i 2 , … , y i n , то зависимость средних арифметических:

¯ y i = y i 1 + y i 2 + ⋯ + y i n n i

от x i и является регрессией в статистическом понимании данного термина.

Типичным примером регрессионной зависимости может быть зависимость между ростом и весом человека. В большинстве случае вес пропорционален росту, но фактически большой рост не всегда означает большой вес. Иными словами, у роста, например, 175 см. может наблюдаться несколько значений веса, скажем 69, 78 и 86 кг. Тогда зависимость между ростом и средним значением указанных весов будет являться регрессионной.

Изучение регрессии в теории вероятностей основано на том, что случайные величины X и Y , имеющие совместное распределение вероятностей, связаны статистической зависимостью: при каждом фиксированном значении X = x , величина Y является случайной величиной с определённым (зависящим от значения x ) условным распределением вероятностей.

Регрессия величины Y по величине X определяется условным математическим ожиданием Y , вычисленным при условии, что X = x : E ( Y | x ) = u ( x ) .

Уравнение y = u ( x ) называется уравнением регрессии, а соответствующий график — линией регрессии Y по X . Точность, с которой уравнение Y по X отражает изменение Y в среднем при изменении x , измеряется условной дисперсией D величины Y , вычисленной для каждого значения X = x : D ( Y | x ) = D ( x ) .

Если D ( x ) = 0 при всех значениях x , то можно достоверно утверждать, что Y и X связаны строгой функциональной зависимостью Y = u ( X ) . Если D ( x ) = 0 при всех значениях x и u ( x ) не зависит от x , то говорят, что регрессионная зависимость Y по X отсутствует.

Линии регрессии обладают следующим замечательным свойством: среди всех действительных функций f ( X ) минимум математического ожидания E [ Y — f ( X ) ] 2 достигается для функции f ( x ) = u ( X ) .

Это означает, что регрессия Y по X даёт наилучшее в указанном смысле представление величины Y по величине X . Это свойство позволяет использовать регрессию для предсказания величины Y по X .

Иными словами, если значение Y непосредственно не наблюдается и эксперимент позволяет регистрировать только X , то в качестве прогнозируемого значения Y можно использовать величину Y = u ( X ) .

Наиболее простым является случай, когда регрессионная зависимость Y по X линейна, т.е. E ( Y | x ) = b 0 + b 1 x , где b 0 и b 1 – коэффициенты регрессии. На практике обычно коэффициенты регрессии в уравнении y = u ( x ) неизвестны, и их оценивают по наблюдаемым данным.

Регрессия широко используется в аналитических технологиях при решении различных бизнес-задач, таких как прогнозирование (продаж, курсов валют и акций), оценивание различных бизнес-показателей по наблюдаемым значениям других показателей (скоринг), выявление зависимостей между показателями и т.д.

В Loginom существует специализированный обработчик логистическая регрессия, с помощью которого можно оценивать вероятность того, что событие наступит для конкретного объекта испытания (больной/здоровый, возврат кредита/дефолт и т.д.). И обработчик линейная регрессия, который может использоваться для решения различных задач, например, прогнозирования и численного предсказания.

Логистическая регрессия является традиционным статистическим инструментом для расчета коэффициентов (баллов) скоринговой карты на основе накопленной кредитной истории. Подробнее в статье «Логистическая регрессия и ROC-анализ — математический аппарат».

О прикладном применении логистической регрессии в двух областях — диагностика заболеваний и оценка кредитоспособности физических лиц узнайте в статье «Применение логистической регрессии в медицине и скоринге».

Что такое регрессия?

Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и так далее.

Регрессия решает проблему единого представления данных анализа для каждого работника. Причём опыт, образование, роль и город – это независимые переменные при зависимой от них зарплате.

Таким же способом можно установить математическую зависимость между ценами домов в определённой области, количеством комнат, расстоянием от центра и т. д.

Регрессия рассматривает некоторое явление и ряд наблюдений. Каждое наблюдение имеет две и более переменных. Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.

Другими словами, вам нужно найти функцию, которая отображает зависимость одних переменных или данных от других.

Зависимые данные называются зависимыми переменными, выходами или ответами.

Независимые данные называются независимыми переменными, входами или предсказателями.

Обычно в регрессии присутствует одна непрерывная и неограниченная зависимая переменная. Входные переменные могут быть неограниченными, дискретными или категорическими данными, такими как пол, национальность, бренд, etc.

Общей практикой является обозначение данных на выходе – ?, входных данных – ?. В случае с двумя или более независимыми переменными, их можно представить в виде вектора ? = (?₁, …, ?ᵣ), где ? – количество входных переменных.

Когда вам нужна регрессия?

Регрессия полезна для прогнозирования ответа на новые условия. Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.

Где она вообще нужна?

Регрессия используется во многих отраслях: экономика, компьютерные и социальные науки, прочее. Её важность растёт с доступностью больших данных.

Линейная регрессия

Линейная регрессия – одна из важнейших и широко используемых техник регрессии. Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.

Постановка проблемы

Линейная регрессия некоторой зависимой переменной y на набор независимых переменных x = (x₁, …, xᵣ), где r – это число предсказателей, предполагает, что линейное отношение между y и x: y = 𝛽₀ + 𝛽₁x₁ + ⋯ + 𝛽ᵣxᵣ + 𝜀. Это уравнение регрессии. 𝛽₀, 𝛽₁, …, 𝛽ᵣ – коэффициенты регрессии, и 𝜀 – случайная ошибка.

Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как b₀, b₁, …, bᵣ. Они определяют оценочную функцию регрессии f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.

Для каждого результата наблюдения i = 1, …, n, оценочный или предсказанный ответ f(xᵢ) должен быть как можно ближе к соответствующему фактическому ответу yᵢ. Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.

Для получения лучших весов, вам нужно минимизировать сумму остаточных квадратов (SSR) для всех результатов наблюдений: SSR = Σᵢ(yᵢ − f(xᵢ))². Этот подход называется методом наименьших квадратов.

Простая линейная регрессия

Простая или одномерная линейная регрессия – случай линейной регрессии с единственной независимой переменной x.

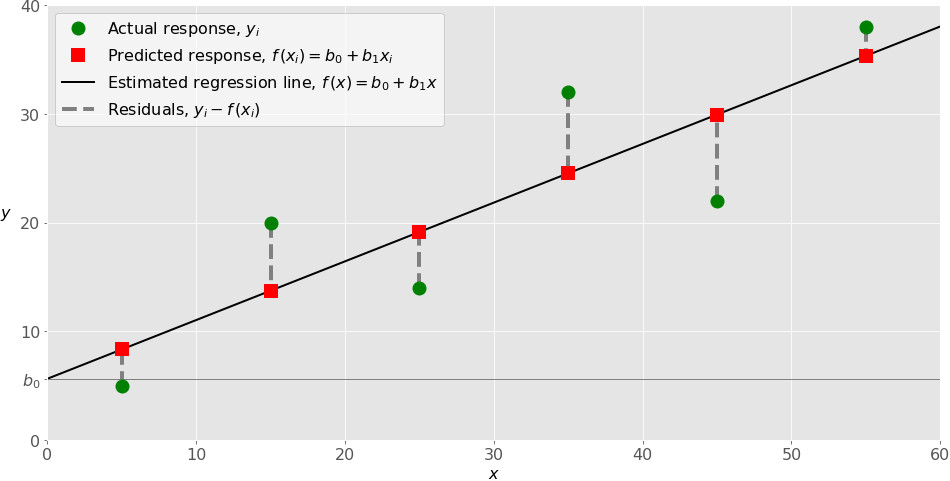
Реализация простой линейной регрессии начинается с заданным набором пар (зелёные круги) входов-выходов (x-y). Эти пары – результаты наблюдений. Наблюдение, крайнее слева (зелёный круг) имеет на входе x = 5 и соответствующий выход (ответ) y = 5. Следующее наблюдение имеет x = 15 и y = 20, и так далее.

Оценочная функция регрессии (чёрная линия) выражается уравнением f(x) = b₀ + b₁x. Нужно рассчитать оптимальные значения спрогнозированных весов b₀ и b₁ для минимизации SSR и определить оценочную функцию регрессии. Величина b₀, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось y. Это значение расчётного ответа f(x) для x = 0. Величина b₁ определяет наклон расчетной линии регрессии.

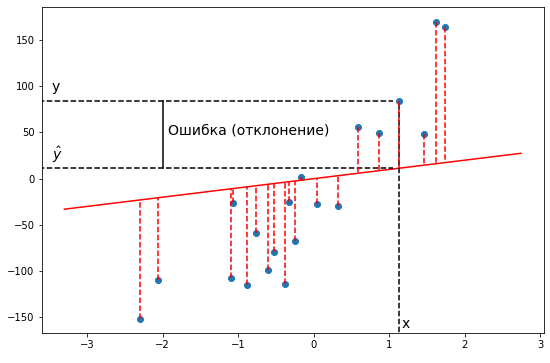
Предсказанные ответы (красные квадраты) – точки линии регрессии, соответствующие входным значениям. Для входа x = 5 предсказанный ответ равен f(5) = 8.33 (представленный крайним левыми квадратом).

Остатки (вертикальные пунктирные серые линии) могут быть вычислены как yᵢ − f(xᵢ) = yᵢ − b₀ − b₁xᵢ для i = 1, …, n. Они представляют собой расстояния между зелёными и красными пунктами. При реализации линейной регрессии вы минимизируете эти расстояния и делаете красные квадраты как можно ближе к предопределённым зелёным кругам.

Реализуйте линейную регрессию в Python

Пришло время реализовать линейную регрессию в Python. Всё, что вам нужно, – подходящие пакеты, функции и классы.

Пакеты Python для линейной регрессии

NumPy – фундаментальный научный пакет для быстрых операций над одномерными и многомерными массивами. Он облегчает математическую рутину и, конечно, находится в open-source.

Незнакомы с NumPy? Начните с официального гайда.

Пакет scikit-learn – это библиотека, широко используемая в машинном обучении. Она предоставляет значения для данных предварительной обработки, уменьшает размерность, реализует регрессию, классификацию, кластеризацию и т. д. Находится в open-source, как и NumPy.

Начните знакомство с линейными моделями и работой пакета на сайте scikit-learn.

Простая линейная регрессия со scikit-learn

Начнём с простейшего случая линейной регрессии.

Следуйте пяти шагам реализации линейной регрессии:

1. Импортируйте необходимые пакеты и классы.
2. Предоставьте данные для работы и преобразования.
3. Создайте модель регрессии и приспособьте к существующим данным.
4. Проверьте результаты совмещения и удовлетворительность модели.
5. Примените модель для прогнозов.

Это общие шаги для большинства подходов и реализаций регрессии.

Шаг 1: Импортируйте пакеты и классы

Первым шагом импортируем пакет NumPy и класс LinearRegression из sklearn.linear_model :

Теперь у вас есть весь функционал для реализации линейной регрессии.

Фундаментальный тип данных NumPy – это тип массива numpy.ndarray . Далее под массивом подразумеваются все экземпляры типа numpy.ndarray .

Класс sklearn.linear_model.LinearRegression используем для линейной регрессии и прогнозов.

Шаг 2 : Предоставьте данные

Вторым шагом определите данные, с которыми предстоит работать. Входы (регрессоры, x) и выход (предиктор, y) должны быть массивами (экземпляры класса numpy.ndarray ) или похожими объектами. Вот простейший способ предоставления данных регрессии:

Теперь у вас два массива: вход x и выход y. Вам нужно вызвать .reshape() на x, потому что этот массив должен быть двумерным или более точным – иметь одну колонку и необходимое количество рядов. Это как раз то, что определяет аргумент (-1, 1).

Вот как x и y выглядят теперь:

Шаг 3: Создайте модель

На этом шаге создайте и приспособьте модель линейной регрессии к существующим данным.

Давайте сделаем экземпляр класса LinearRegression , который представит модель регрессии:

Эта операция создаёт переменную model в качестве экземпляра LinearRegression . Вы можете предоставить несколько опциональных параметров классу LinearRegression :

• fit_intercept – логический ( True по умолчанию) параметр, который решает, вычислять отрезок b₀ ( True ) или рассматривать его как равный нулю ( False ).
• normalize – логический ( False по умолчанию) параметр, который решает, нормализовать входные переменные ( True ) или нет ( False ).
• copy_X – логический ( True по умолчанию) параметр, который решает, копировать ( True ) или перезаписывать входные переменные ( False ).
• n_jobs – целое или None (по умолчанию), представляющее количество процессов, задействованных в параллельных вычислениях. None означает отсутствие процессов, при -1 используются все доступные процессоры.

Наш пример использует состояния параметров по умолчанию.

Пришло время задействовать model . Сначала вызовите .fit() на model :

С помощью .fit() вычисляются оптимальные значение весов b₀ и b₁, используя существующие вход и выход (x и y) в качестве аргументов. Другими словами, .fit() совмещает модель. Она возвращает self — переменную model . Поэтому можно заменить две последние операции на:

Эта операция короче и делает то же, что и две предыдущие.

Шаг 4: Получите результаты

После совмещения модели нужно убедиться в удовлетворительности результатов для интерпретации.

Вы можете получить определения (R²) с помощью .score() , вызванной на model :

.score() принимает в качестве аргументов предсказатель x и регрессор y, и возвращает значение R².

model содержит атрибуты .intercept_ , который представляет собой коэффициент, и b₀ с .coef_ , которые представляют b₁:

Код выше показывает, как получить b₀ и b₁. Заметьте, что .intercept_ – это скаляр, в то время как .coef_ – массив.

Примерное значение b₀ = 5.63 показывает, что ваша модель предсказывает ответ 5.63 при x, равном нулю. Равенство b₁ = 0.54 означает, что предсказанный ответ возрастает до 0.54 при x, увеличенным на единицу.

Заметьте, что вы можете предоставить y как двумерный массив. Тогда результаты не будут отличаться:

Как вы видите, пример похож на предыдущий, но в данном случае .intercept_ – одномерный массив с единственным элементом b₀, и .coef_ – двумерный массив с единственным элементом b₁.

Шаг 5: Предскажите ответ

Когда вас устроит ваша модель, вы можете использовать её для прогнозов с текущими или другими данными.

Получите предсказанный ответ, используя .predict() :

Применяя .predict() , вы передаёте регрессор в качестве аргумента и получаете соответствующий предсказанный ответ.

Вот почти идентичный способ предсказать ответ:

В этом случае вы умножаете каждый элемент массива x с помощью model.coef_ и добавляете model.intercept_ в ваш продукт.

Вывод отличается от предыдущего примера количеством измерений. Теперь предсказанный ответ – это двумерный массив, в отличии от предыдущего случая, в котором он одномерный.

Измените количество измерений x до одного, и увидите одинаковый результат. Для этого замените x на x.reshape(-1) , x.flatten() или x.ravel() при умножении с помощью model.coef_ .

На практике модель регрессии часто используется для прогнозов. Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:

Здесь .predict() применяется на новом регрессоре x_new и приводит к ответу y_new . Этот пример удобно использует arange() из NumPy для генерации массива с элементами от 0 (включительно) до 5 (исключительно) – 0, 1, 2, 3, и 4.

Основы линейной регрессии

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).

Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).

Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

• a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
• b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
• a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Метод наименьших квадратов

Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.

Предположения линейной регрессии

Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.

Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:

• Между и существует линейное соотношение: для любых пар данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.

• Остатки нормально распределены с нулевым средним значением;

• Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин Если нанести остатки против предсказанных величин от мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением то это допущение не выполняется;

Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).

Аномальные значения (выбросы) и точки влияния

«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).

Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.

И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).

При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.

Гипотеза линейной регрессии

При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.

Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на

Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:

Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента

— оценка дисперсии остатков.

Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.

Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :

где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия

Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.

Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)

Оценка качества линейной регрессии: коэффициент детерминации R 2

Из-за линейного соотношения и мы ожидаем, что изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.

Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.

Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.

Разность представляет собой процент дисперсии который нельзя объяснить регрессией.

Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.

Применение линии регрессии для прогноза

Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).

Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.

Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.

Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.

Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.

Простые регрессионные планы

Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид

а регрессионное уравнение с использованием P для X1 выглядит как

Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:

а уравнение примет вид

Y = b 0 + b 1 P 2

Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.

Пример: простой регрессионный анализ

Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.

Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.

Задача исследования

Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.

Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.

Просмотр результатов

Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.

На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p

Распределение переменных

Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .

Рис. 6. Гистограмма переменной Pt_Poor.

Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.

Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.

Диаграмма рассеяния

Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.

Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.

Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.

Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p

На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.

Регрессия как задача машинного обучения

Источник: Analytics Vidhya.

Задача регрессии — это одна из основных задач машинного обучения. И хотя, большинство задач на практике относятся к другому типу — классификации, мы начнем знакомство с машинным обучением именно с регрессии. Регрессионные модели были известны задолго до появления машинного обучения как отрасли и активно применяются в статистике, эконометрике, математическом моделировании. Машинное обучение предлагает новый взгляд на уже известные модели. И этот новый взгляд позволит строить более сложные и мощные модели, чем классические математические дисциплины.

Задача регрессии относится к категории задач обучения с учителем. Это значит, что в наборе данных, который используется для обучения, должен иметь определенную структуру. Обычно, наборы данных для машинного обучения представляют собой таблицу, в которой по строкам перечислены разные объекты наблюдений или измерений. В столбцах — различные характеристики, или атрибуты, объектов. А на пересечении строк и столбцов — значение данной характеристики у данного объекта. Обычно один атрибут (или переменная) имеет особый характер — именно ее значение мы и хотим научиться предсказывать с помощью модели машинного обучения. Эта характеристика объекта называется целевая переменная. И если эта целевая переменная выражена числом (а точнее, некоторой непрерывной величиной) — то мы говорим о задаче регрессии.

Задачи регрессии на практике встречаются довольно часто. Например, предсказание цены объекта недвижимости — классическая регрессионная задача. В таких проблемах атрибутами выступают разные характеристики квартир или домов — площадь, этажность, расположение, расстояние до центра города, количество комнат, год постройки. В разных наборах данных собрана разная информация И, соответственно, модели тоже должны быть разные. Другой пример — предсказание цены акций или других финансовых активов. Или предсказание температуры завтрашним днем.

Во всех таких задачах нам нужно иметь данные, которые позволят осуществить такое предсказание. Да, “предсказание” — это условный термин, не всегда мы говорим о будущих событиях. Регрессионные модели используют информацию об объектах в обучающем наборе данных, чтобы сделать вывод о возможном значении целевой переменной. И для этого нужно, чтобы ее значение имело какую-то зависимость от имеющихся у нас атрибутов. Если построить модель предсказания цены акции, но на вход подать информацию о футбольных матчах — ничего не получится. Мы предполагаем, что в наборе данных собраны именно те атрибуты объектов, которые имеют влияние на на значение целевой переменной. И чем больше это предположение выполняется, тем точнее будет потенциально наша модель.

Немного поговорим о терминах. Набор данных который мы используем для обучения модели называют датасетом (dataset) или обучающей выборкой (training set). Объекты, которые описываются в датасете еще называют точками данных (data points). Целевую переменную еще называют на статистический манер зависимой переменной (dependent variable) или результативной, выходной (output), а остальные атрибуты — независимыми переменными (dependent variables), или признаками (features), или факторами, или входными переменными (input). Значения одного конкретного атрибута для всех объектов обучающей выборки часто представляют как вектор этого признака (feature vector). А всю таблицу всех атрибутов называют матрицей атрибутов (feature matrix). Соответственно, еще есть вектор целевой переменной, он не входит в матрицу атрибутов.

С точки зрения информатики, регрессионная модель — это функция, которая принимает на вход значения атрибутов какого-то конкретного объекта и выдает на выходе предполагаемое значение целевой переменной. В большинстве случаев мы предполагаем, что целевая переменная у нас одна. Если стоит задача предсказания нескольких характеристик, то их чаще воспринимают как несколько независимых задач регрессии на одних и тех же атрибутах.

Мы пока ничего не говорили о том, как изнутри устроена регрессионная модель. Это потому, что она может быть какой угодно. Это может быть математическое выражение, условный алгоритм, сложная программа со множеством ветвлений и циклов, нейронная сеть — все это можно представить регрессионной моделью. Единственное требование к модели машинного обучения — она должна быть параметрической. То есть иметь какие-то внутренние параметры, от которых тоже зависит результат вычисления. В простых случаях, чаще всего в качестве регрессионной модели используют аналитические функции. Таких функций бесконечное количество, но чаще всего используется самая простая функция, с которой мы и начнем изучение регрессии — линейная функция.

Так же надо сказать, что иногда регрессионные модели подразделяют на парную и множественную регрессии. Парная регрессия — это когда у нас всего один атрибут. Множественная — когда больше одного. Конечно, на практике парная регрессия почти не встречается, но на примере такой простой модели мы поймем основные концепции машинного обучения. Плюс, парную регрессию очень удобно и наглядно можно изобразить на графике. Когда у нас больше двух переменных, графики уже не особо построишь, и модели приходится визуализировать иначе, более косвенно.

1. Регрессия — это задача машинного обучения с учителем, которая заключается в предсказании некоторой непрерывной величины.
2. Для использования регрессионных моделей нужно, чтобы в датасете были характеристики объектов и “правильные” значения целевой переменной.
3. Примеры регрессионных задач — предсказание цены акции, оценка цены объекта недвижимости.
4. Задача регрессии основывается на предположении, что значение целевой переменной зависит от значения признаков.
5. Регрессионная модель принимает набор значений и выдает предсказание значения целевой переменной.
6. В качестве регрессионных моделей часто берут аналитические функции, например, линейную.

Линейная регрессия с одной переменной

Функция гипотезы

Напомним, что в задачах регрессии мы принимаем входные переменные и пытаемся получить более-менее достоверное значение целевой переменной. Ведь любая функция, даже самая простая линейная может выдавать совершенно разные значения для одних и тех же входных данных, если в функции будут разные параметры. Поэтому, любая регрессионная модель — это не какая-то конкретная математическая функция, а целое семейство функций. И задача алгоритма обучения — подобрать значения параметров таким образом, чтобы для объектов обучающей выборки, для которых мы уже знаем правильные ответы, предсказанные (или теоретические, вычисленные из модели) значения были как можно ближе к тем, которые есть в датасете (эмпирические, истинные значения).

Парная, или одномерная (univariate) регрессия используется, когда вы хотите предсказать одно выходное значение (чаще всего обозначаемое $y$), зависящее от одного входного значения (обычно обозначается $x$). Сама функция называется функция гипотезы.

В случае парной линейной регрессии функция гипотезы имеет следующий общий вид:

[hat = h_b (x) = b_0 + b_1 x]

Обратите внимание, что это похоже на уравнение прямой. Эта модель соответствует множеству всех возможных прямых на плоскости. Когда мы конкретизируем модель значениями параметров (в данном случае — $b_0$ и $b_0$), мы получаем конкретную прямую. И наша задача состоит в том, чтобы выбрать такую прямую, которая бы лучше всего “легла” в точки из нашей обучающей выборки.

в данном случае, мы пытаемся подобрать функцию h(x) таким образом, чтобы отобразить данные нам значения x в данные значения y.

Допустим, мы имеем следующий обучающий набор данных:

входная переменная x	выходная переменная y
0	4
1	7
2	7
3	8

Мы можем составить случайную гипотезу с параметрами $ b_0 = 2, b_1 = 2 $. Тогда для входного значения $ x=1, y=4 $, что на 3 меньше данного. Задача регрессии состоит в нахождении таких параметров функции гипотезы, чтобы она отображала входные значения в выходные как можно более точно, или, другими словами, описывала линию, наиболее точно ложащуюся в данные точки на плоскости (x, y).

1. Модель машинного обучения — это параметрическая функция
2. Задача обучения состоит в том, чтобы подобрать параметры модели таким образом, чтобы она лучше всего описывала обучающие данные.
3. Парная линейная регрессия работает, если есть всего одна входящая переменная.

Функция ошибки

Мы можем измерить точность нашей функции гипотезы, используя функцию ошибки. Для этого требуется средняя (фактически чуть усложненная версия среднего арифметического) всех результатов вычисления гипотезы с входами x по сравнению с фактическим выходом y.

По сути своей, это половина среднего квадрата разницы между прогнозируемым и фактическим значением выходной переменной.

Эту функцию называют «функцией квадрата ошибки» или «среднеквадратичной ошибкой» (mean squared error, MSE). Среднее значение уменьшено вдвое для удобства вычисления градиентного спуска, так как производная квадратичной функции будет отменять множитель 1/2.

Теперь мы можем конкретно измерить точность нашей предсказывающей функции по сравнению с правильными результатами, которые мы имеем, чтобы мы могли предсказать новые результаты, которых у нас нет.

Если мы попытаемся представить это наглядно, наш набор данных обучения будет разбросан по плоскости x-y. Мы пытаемся подобрать прямую линию, которая проходит через этот разбросанный набор данных. Наша цель — получить наилучшую возможную линию. Лучшая линия будет такой, чтобы средние квадраты вертикальных расстояний рассеянных точек от линии были наименьшими. В лучшем случае линия должна проходить через все точки нашего набора данных обучения. В таком случае значение J будет равно 0.

1. Функция ошибки нужна для того, чтобы отличать хорошие модели от плохих.
2. Функция ошибки показывает численно, насколько модель хорошо описывает данные.
3. Аргументами функции ошибки являются параметры модели, ошибка зависит от них.
4. Само значение функции ошибки не несет никакого смысла, оно используется только в сравнении.
5. Цель алгоритма машинного обучения — минимизировать функцию ошибки, то есть найти такой набор параметров модели, при которых ошибка минимальна.
6. Чаще всего используется так называемая L2-ошибка — средний квадрат отклонений теоретических значений от эмпирических.

Метод градиентного спуска

Таким образом, у нас есть наша функция гипотезы, и у нас есть способ оценить, насколько хорошо конкретная гипотеза вписывается в данные. Теперь нам нужно подобрать параметры в функции гипотезы. Вот где приходит на помощь метод градиентного спуска.

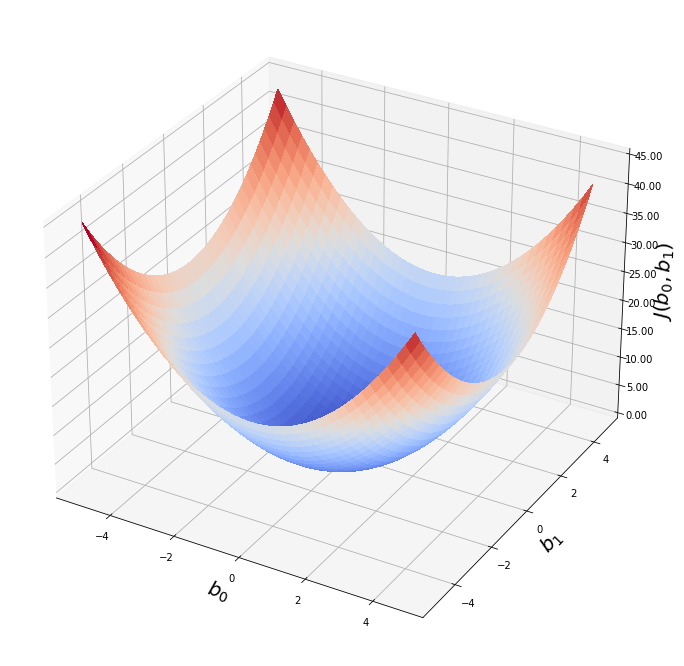
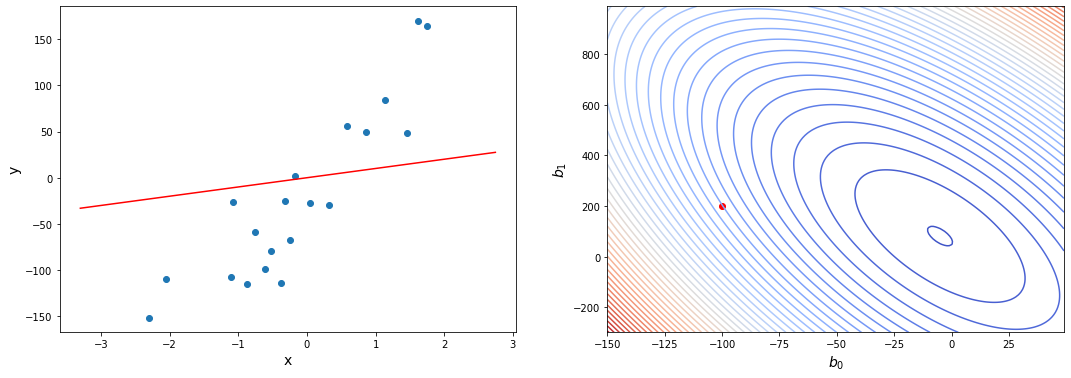
Представьте себе, что мы нарисуем нашу функцию гипотезы на основе ее параметров b₀ и b₁ (фактически мы представляем график функции стоимости как функцию оценок параметров).

Отложим b₀ на оси x и b₁ на оси y, с функцией стоимости на вертикальной оси z. Точки на нашем графике будут результатом функции стоимости, используя нашу гипотезу с этими конкретными параметрами.

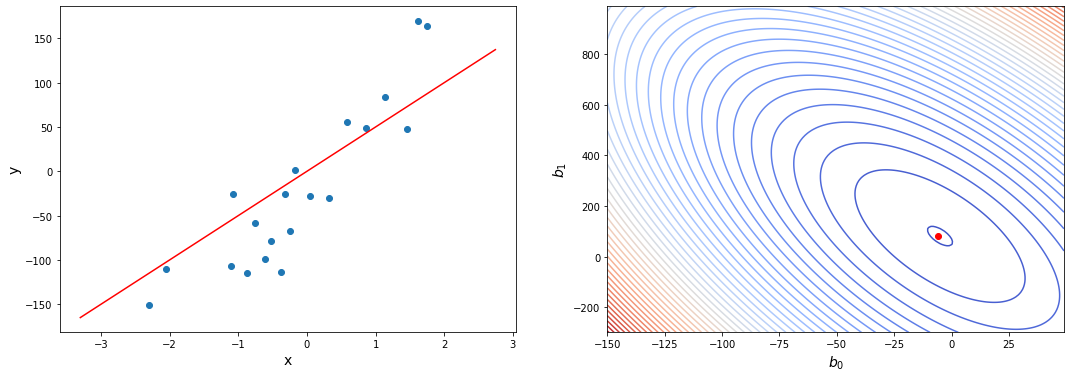
Мы будем знать, что нам удалось подобрать оптимальные параметры, когда наша функция стоимости находится в самом низу на нашем графике, то есть когда ее значение является минимальным.

То, как мы это делаем — это используя производную (касательную линию к функции) нашей функции стоимости. Наклон касательной является производной в этой точке, и это даст нам направление движения в сторону самого крутого уменьшения значения функции. Мы делаем шаги вниз по функции стоимости в направлении с самым крутым спусками, а размер каждого шага определяется параметром α, который называется скоростью обучения.

Алгоритм градиентного спуска:

повторяйте до сходимости:

где j=0,1 — представляет собой индекс номера признака.

Алгоритм градиентного спуска для парной линейной регрессии:

повторяйте до сходимости:

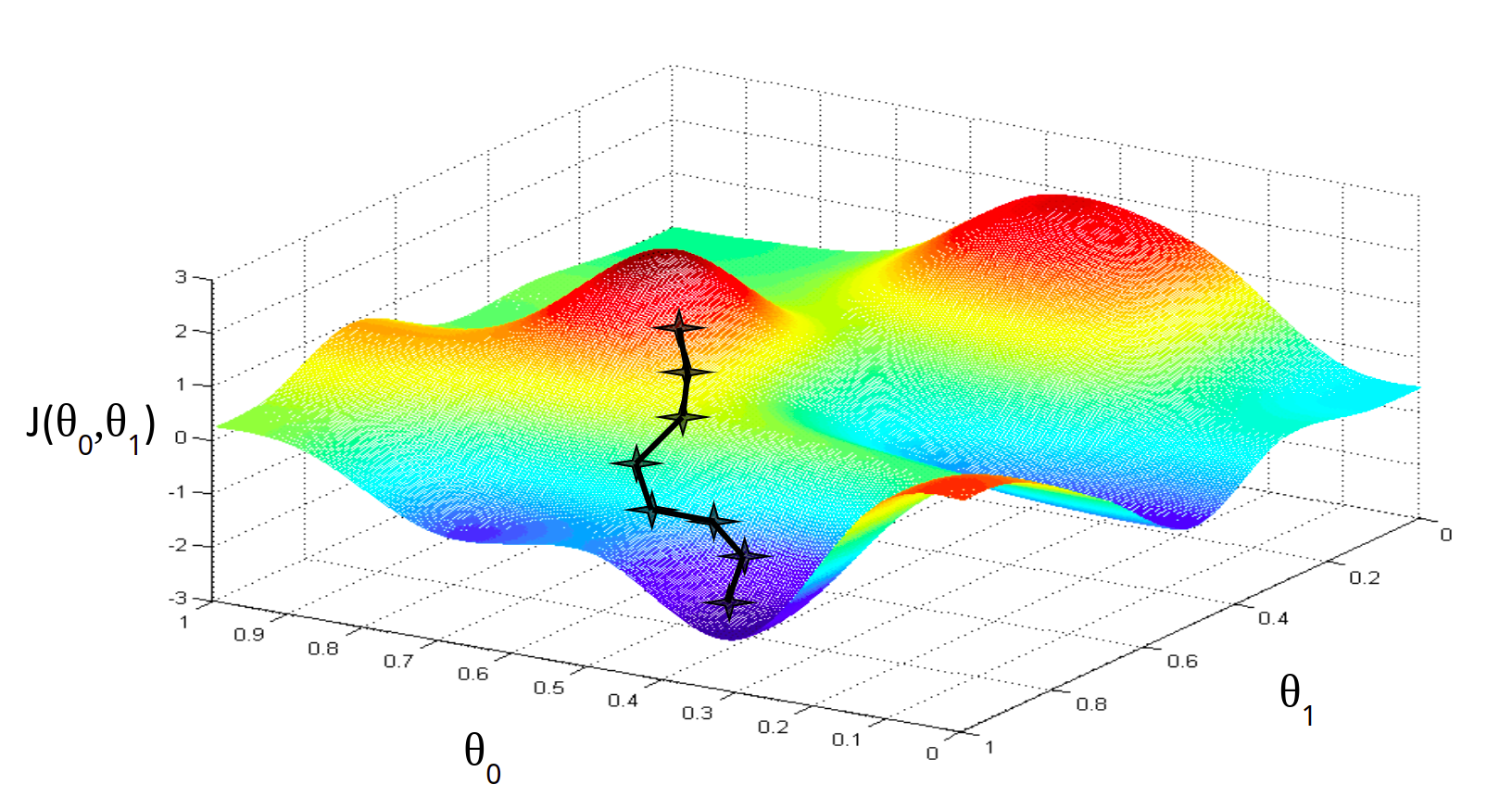
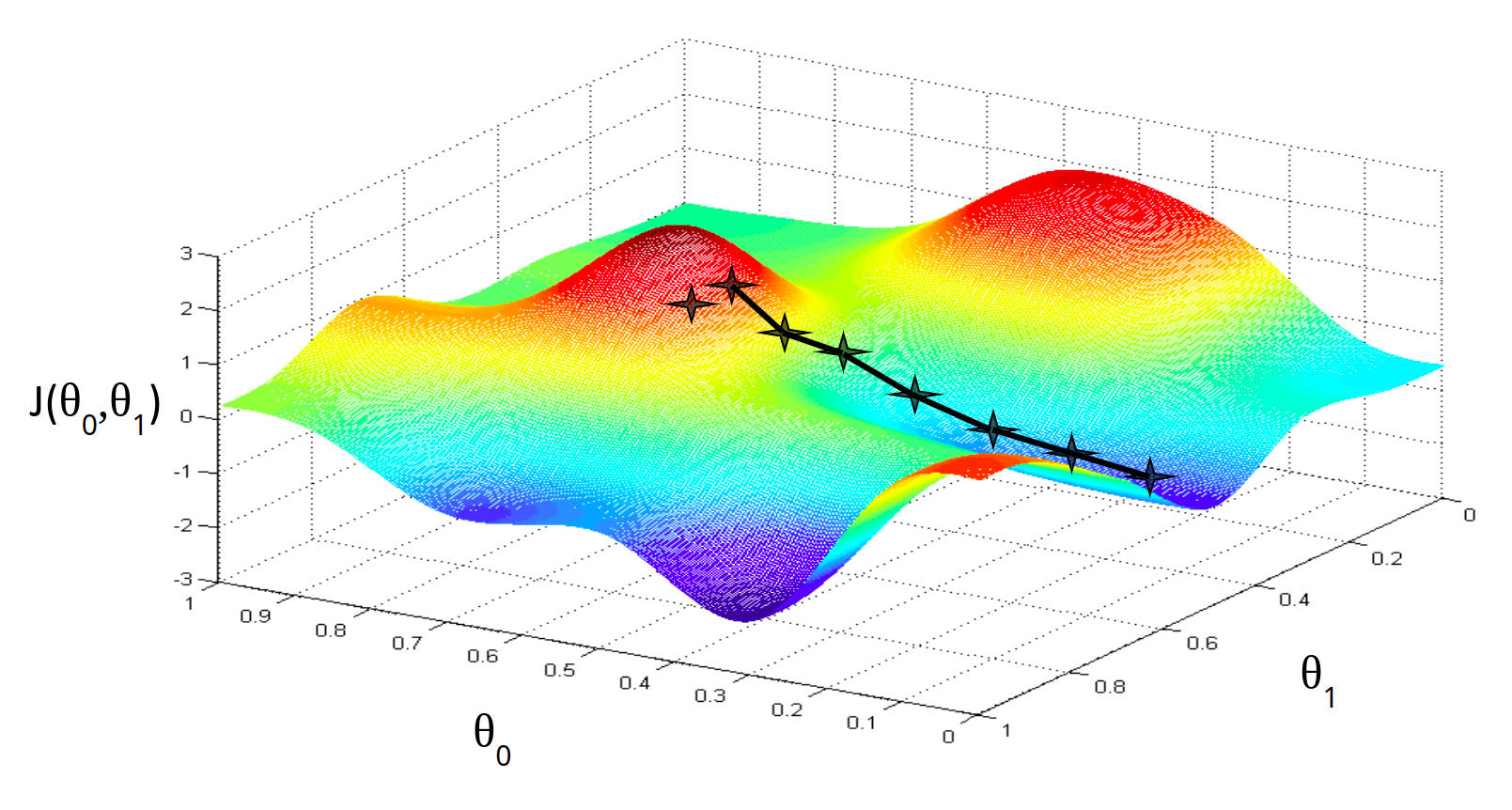
1. Метод градиентного спуска нужен, чтобы найти минимум функции, если мы не можем ее вычислить аналитически.
2. Это численный итеративный алгоритм локальной оптимизации.
3. Для запуска градиентного спуска нужно знать частную производную функции ошибки.
4. Для начала мы берем произвольные значения параметров, затем обновляем их по данной формуле.
5. Доказано, что этот метод сходится к локальному минимуму.
6. Если функция ошибки достаточно сложная, то разные начальные точки дадут разный результат.
7. Метод градиентного спуска имеет свой параметр — скорость обучения. Обычно его подстаивают автоматически.
8. Метод градиентного спуска повторяют много раз до тех пор, пока функция ошибки не перестанет значимо изменяться.

Линейная регрессия с несколькими переменными

Множественная линейная регрессия

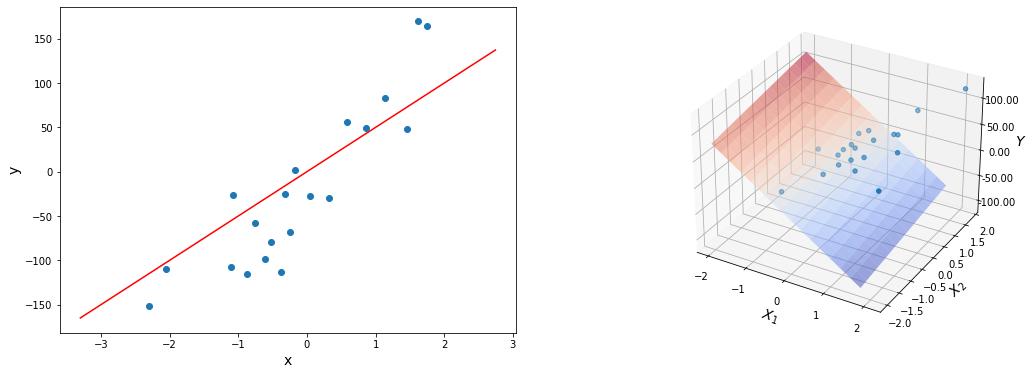
Линейная регрессия с несколькими переменными также известна как «множественная линейная регрессия». Введем обозначения для уравнений, где мы можем иметь любое количество входных переменных:

$ x^ $- вектор-столбец всех значений признаков i-го обучающего примера;

$ x_j^ $ — значение j-го признака i-го обучающего примера;

m — количество примеров в обучающей выборке;

n — количество признаков;

X — матрица признаков;

b — вектор параметров регрессии.

Заметим, что в будущем для удобства примем, что $ x_0^ = 1 $ для всех i. Другими словами, мы для удобства введем некий суррогатный признак, для всех наблюдений равный единице. это сильно упростит математические выкладки, особенно в матричной форме.

Теперь определим множественную форму функции гипотезы следующим образом, используя несколько признаков:

Используя определение матричного умножения, наша многопараметрическая функция гипотезы может быть кратко представлена в виде: h(x) = B X.

Для множественной регрессии функция ошибки от вектора параметров b выглядит следующим образом:

Или в матричной форме:

[J(b) = frac (X b — vec)^T (X b — vec)]

Метод градиентного спуска для множественной регрессии определяется следующими уравнениями:

повторять до сходимости:

[b_0 := b_0 — alpha frac sum_^ (h_b(x^) — y^) cdot x_0^] [b_1 := b_1 — alpha frac sum_^ (h_b(x^) — y^) cdot x_1^] [b_2 := b_2 — alpha frac sum_^ (h_b(x^) — y^) cdot x_2^] [. ]

Или в матричной форме:

1. Множественная регрессия очень похожа на парную, но с большим количеством признаков.
2. Для удобства и однообразия, почти всега обозначают $x_0 = 1$.
3. Признаки уже образуют матрицу, поэтому уравнения множественной регрессии часто приводят в матричной форме, так короче.
4. Алгоритм градиентного спуска для множественной регресси точно такой же, как и для парной.

-3 . Однако на практике трудно выбрать это пороговое значение. Было доказано, что если скорость обучения α достаточно мала, то J(b) будет уменьшаться на каждой итерации. 3. Суррогатные признаки Мы можем улучшить наши функции и форму нашей функции гипотез несколькими способами. Мы можем объединить несколько признаков в один. Например, мы можем объединить x1 и x2 в новый признак x3, взяв x1⋅x2. —>

Полиномиальная регрессия

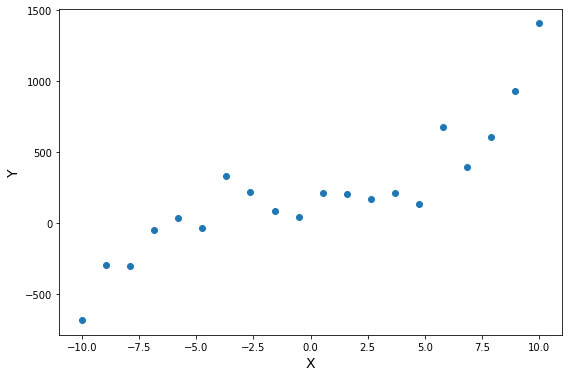
Наша функция гипотезы не обязательно должна быть линейной (прямой), если это не соответствует данным.

Мы можем изменить поведение или кривую нашей функции гипотезы, сделав ее квадратичной, кубической или квадратной корневой функцией (или любой другой формой).

Например, если наша функция гипотезы $ hat = h_b (x) = b_0 + b_1 x $, то мы можем добавить еще один признак, основанный на x1, получив квадратичную функцию

или кубическую функцию

В кубической функции мы по сути ввели два новых признака: $ x_2 = x^2, x_3 = x^3 $. Точно таким же образом, мы можем создать, например, такую функцию:

Одна важная вещь, о которой следует помнить, заключается в том, что если вы выбираете свои функции таким образом, масштабирование признаков становится очень важным. Например, если x имеет диапазон 1 — 1000, тогда диапазон x 2 становится 1 — 1000000, а диапазон x 3 становится 1 — 1000000000.

[hat = h_b (x) = b_0 + b_1 x_1 + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2 + b_6 x_1^3 + b_7 x_2^3 + b_7 x_1^2 x_2 + b_8 x_1 x_2^2]

Источник: Wikimedia.

1. Данные в датасете не всегда располагаются так, что их хорошо может описывать линейная функция.
2. Для описания нелинейных зависимостей нужна более сложная, нелинейная модель.
3. Чтобы не изобретать алгоритм обучения заново, можно просто ввести в модель суррогатные признаки.
4. Суррогатный признак — это новый признак, который считается из существующих атрибутов.
5. Чаще всего используют полиномиальную регрессию — это когда в модель вводят полиномиальные признаки — степени существующих атрибутов.
6. Обычно берут все комбинации факторов до какой-то определенной степени полинома.
7. Полиномиальная регрессия может аппроксимировать любую функцию, нужно только подобрать степень полинома.
8. Чем больше степень полиномиальной регрессии, тем она сложнее и универсальнее, но вычислительно сложнее (экспоненциально).

3 ) по сравнению с O(n 2 ) у градиентного спуска. Поэтому довольно медленно работает при больших n. 2. Требует вычисления обратной матрицы. В некоторых случаях матрица $X^T X$ может быть вырожденной, что затруднит использование нормального уравнения. —>

Пример регрессионного анализа

Основная цель регрессионного анализа состоит в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения.
Задачи регрессионного анализа:
а) Установление формы зависимости. Относительно характера и формы зависимости между явлениями, различают положительную линейную и нелинейную и отрицательную линейную и нелинейную регрессию.
б) Определение функции регрессии в виде математического уравнения того или иного типа и установление влияния объясняющих переменных на зависимую переменную.
в) Оценка неизвестных значений зависимой переменной. С помощью функции регрессии можно воспроизвести значения зависимой переменной внутри интервала заданных значений объясняющих переменных (т. е. решить задачу интерполяции) или оценить течение процесса вне заданного интервала (т. е. решить задачу экстраполяции). Результат представляет собой оценку значения зависимой переменной.

Парная регрессия — уравнение связи двух переменных у и х : y=f(x), где y — зависимая переменная (результативный признак); x — независимая, объясняющая переменная (признак-фактор).

• полиномы разных степеней y=a+b₁·x+b₂·x 2 +b₃·x 3 +ε
• равносторонняя гипербола .

y=a·x b ·ε
• показательная y=a·b x ·ε y=e a+b·x ·ε

Можно воспользоваться готовыми формулами, которые вытекают из этой системы:

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_xy для линейной регрессии (-1≤r_xy≤1):

и индекс корреляции p_xy — для нелинейной регрессии (0≤p_xy≤1):

Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:
.
Допустимый предел значений A — не более 8-10%.
Средний коэффициент эластичности Э показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:
.

Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
∑(y- y )²=∑(y_x— y )²+∑(y-y_x)²
где ∑(y- y )² — общая сумма квадратов отклонений;
∑(y_x— y )² — сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
∑(y-y_x)² — остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R 2 :

Коэффициент детерминации — квадрат коэффициента или индекса корреляции.

F-тест — оценивание качества уравнения регрессии — состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера. F_факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
,
где n — число единиц совокупности; m — число параметров при переменных х.
F_табл — это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a — вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.
Если F_табл < F_факт, то Н_о — гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F_табл > F_факт, то гипотеза Н_о не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н_о о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
; ; .
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

Сравнивая фактическое и критическое (табличное) значения t-статистики — t_табл и t_факт — принимаем или отвергаем гипотезу Н_о.
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством

Если t_табл < t_факт то H_o отклоняется, т.е. a , b и r_xy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если t_табл > t_факт то гипотеза Н_о не отклоняется и признается случайная природа формирования а, b или r_xy.
Для расчета доверительного интервала определяем предельную ошибку D для каждого показателя:
Δ_a=t_табл·m_a, Δ_b=t_табл·m_b.
Формулы для расчета доверительных интервалов имеют следующий вид:
γ_a=a±Δ_a; γ_a=a-Δ_a; γ_a=a+Δ_a
γ_b=b±Δ_b; γ_b=b-Δ_b; γ_b=b+Δ_b
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение y_p определяется путем подстановки в уравнение регрессии y_x=a+b·x соответствующего (прогнозного) значения x_p. Вычисляется средняя стандартная ошибка прогноза m_yx:
,
где
и строится доверительный интервал прогноза:
γ_yx=y_p±Δ_yp; γ_yxmin=y_p-Δ_yp; γ_yxmax=y_p+Δ_yp
где Δ_yx=t_табл·m_yx.

Пример решения

Задача №1 . По семи территориям Уральского района За 199Х г. известны значения двух признаков.
Таблица 1.

Район	Расходы на покупку продовольственных товаров в общих расходах, %, у	Среднедневная заработная плата одного работающего, руб., х
Удмуртская респ.	68,8 + N/2	45,1 – K/2
Свердловская обл.	61,2 + M/2	59,0 – N/2
Башкортостан	59,9 + K/2	57,2 – M/2
Челябинская обл.	56,7 + N/2	61,8 – K/2
Пермская обл.	55,0 + K/2	58,8 – N/2
Курганская обл.	54,3 + M/2	47,2 – K/2
Оренбургская обл.	49,3 + K/2	55,2 – M/2

Требуется: 1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной (предварительно нужно произвести процедуру линеаризации переменных, путем логарифмирования обеих частей);
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации A и F-критерий Фишера.

Решение (Вариант №1)

Для расчета параметров a и b линейной регрессии y=a+b·x (расчет можно проводить с помощью калькулятора).
решаем систему нормальных уравнений относительно а и b:
По исходным данным рассчитываем ∑y, ∑x, ∑y·x, ∑x², ∑y²:

y	x	yx	x 2	y 2	yx	y-yx	Ai
l	68,8	45,1	3102,88	2034,01	4733,44	61,3	7,5	10,9
2	61,2	59,0	3610,80	3481,00	3745,44	56,5	4,7	7,7
3	59,9	57,2	3426,28	3271,84	3588,01	57,1	2,8	4,7
4	56,7	61,8	3504,06	3819,24	3214,89	55,5	1,2	2,1
5	55,0	58,8	3234,00	3457,44	3025,00	56,5	-1,5	2,7
6	54,3	47,2	2562,96	2227,84	2948,49	60,5	-6,2	11,4
7	49,3	55,2	2721,36	3047,04	2430,49	57,8	-8,5	17,2
Итого	405,2	384,3	22162,34	21338,41	23685,76	405,2	0,0	56,7
Ср. знач. (Итого/n)	57,89 y	54,90 x	3166,05 x·y	3048,34 x²	3383,68 y²	X	X	8,1
s	5,74	5,86	X	X	X	X	X	X
s 2	32,92	34,34	X	X	X	X	X	X

a= y -b· x = 57.89+0.35·54.9 ≈ 76.88

Уравнение регрессии: у = 76,88 — 0,35х. С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %-ных пункта.
Рассчитаем линейный коэффициент парной корреляции:

Связь умеренная, обратная.
Определим коэффициент детерминации: r²_xy=(-0.35)=0.127
Вариация результата на 12,7% объясняется вариацией фактора х. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения y_x. Найдем величину средней ошибки аппроксимации A :

В среднем расчетные значения отклоняются от фактических на 8,1%.
Рассчитаем F-критерий:

Полученное значение указывает на необходимость принять гипотезу Н₀ о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.
1б. Построению степенной модели y=a·x b предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
lg y=lg a + b·lg x
Y=C+b·Y
где Y=lg(y), X=lg(x), C=lg(a).

Рассчитаем С и b:

C= Y -b· X = 1.7605+0.298·1.7370 = 2.278126
Получим линейное уравнение: Y=2.278-0.298·X
Выполнив его потенцирование, получим: y=10 2.278 ·x -0.298
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата. По ним рассчитаем показатели: тесноты связи — индекс корреляции p_xy и среднюю ошибку аппроксимации A .

Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимосвязь.

1в. Построению уравнения показательной кривой y=a·b x предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:
lg y=lg a + x·lg b
Y=C+B·x
Для расчетов используем данные таблицы.

Таблица

Y	x	Yx	Y 2	x 2	yx	y-yx	(y-yx)²	Ai
1	1,8376	45,1	82,8758	3,3768	2034,01	60,7	8,1	65,61	11,8
2	1,7868	59,0	105,4212	3,1927	3481,00	56,4	4,8	23,04	7,8
3	1,7774	57,2	101,6673	3,1592	3271,84	56,9	3,0	9,00	5,0
4	1,7536	61,8	108,3725	3,0751	3819,24	55,5	1,2	1,44	2,1
5	1,7404	58,8	102,3355	3,0290	3457,44	56,4	-1,4	1,96	2,5
6	1,7348	47,2	81,8826	3,0095	2227,84	60,0	-5,7	32,49	10,5
7	1,6928	55,2	93,4426	2,8656	3047,04	57,5	-8,2	67,24	16,6
Итого	12,3234	384,3	675,9974	21,7078	21338,41	403,4	-1,8	200,78	56,3
Ср. зн.	1,7605	54,9	96,5711	3,1011	3048,34	X	X	28,68	8,0
σ	0,0425	5,86	X	X	X	X	X	X	X
σ 2	0,0018	34,339	X	X	X	X	X	X	X

Значения параметров регрессии A и В составили:

A= Y -B· x = 1.7605+0.0023·54.9 = 1.887
Получено линейное уравнение: Y=1.887-0.0023x. Произведем потенцирование полученного уравнения и запишем его в обычной форме:
y_x=10 1.887 ·10 -0.0023x = 77.1·0.9947 x
Тесноту связи оценим через индекс корреляции p_xy:

Связь умеренная.
A =8,0%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах. Показательная функция чуть хуже, чем степенная, описывает изучаемую зависимость.

1г. Уравнение равносторонней гиперболы линеаризуется при замене:. Тогда y=a+b·z. Для расчетов используем данные таблицы.

y	z	yz	z 2	y 2	yx	y-yx	(y-yx)²	Ai
1	68,8	0,0222	1,5255	0,000492	4733,44	61,8	7,0	49,00	10,2
2	61,2	0,0169	1,0373	0,000287	3745,44	56,3	4,9	24,01	8,0
3	59,9	0,0175	1,0472	0,000306	3588,01	56,9	3,0	9,00	5,0
4	56,7	0,0162	0,9175	0,000262	3214,89	55,5	1,2	1,44	2,1
5	55	0,0170	0,9354	0,000289	3025,00	56,4	-1,4	1,96	2,5
6	54,3	0,0212	1,1504	0,000449	2948,49	60,8	-6,5	42,25	12,0
7	49,3	0,0181	0,8931	0,000328	2430,49	57,5	-8,2	67,24	16,6
Итого	405,2	0,1291	7,5064	0,002413	23685,76	405,2	0,0	194,90	56,5
Среднее значение	57,9	0,0184	1,0723	0,000345	3383,68	X	X	27,84	8,1
σ	5,74	0,002145	X	X	X	X	X	X	X
σ 2	32,9476	0,000005	X	X	X	X	X	X	X

Значения параметров регрессии а и b составили:

По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи: py_xy=0.3944 (по сравнению с линейной, степенной и показательной регрессиями). A остается на допустимом уровне: 8,1%.

где Fтабл = 6,6 > Fфакт, при α =0,05.
Следовательно, принимается гипотеза Н₀ о статистически незначимых параметрах этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.

Что такое регрессионный анализ?

Научитесь выстраивать процессы для роста бизнеса и увеличения прибыли.

Регрессионный анализ — это набор статистических методов оценки отношений между переменными. Его можно использовать для оценки степени взаимосвязи между переменными и для моделирования будущей зависимости. По сути, регрессионные методы показывают, как по изменениям «независимых переменных» можно зафиксировать изменение «зависимой переменной».

Зависимую переменную в бизнесе называют предиктором (характеристика, за изменением которой наблюдают). Это может быть уровень продаж, риски, ценообразование, производительность и так далее. Независимые переменные — те, которые могут объяснять поведение выше приведенных факторов (время года, покупательная способность населения, место продаж и многое другое).

Регрессионный анализ включает несколько моделей. Наиболее распространенные из них: линейная, мультилинейная (или множественная линейная) и нелинейная.

Как видно из названий, модели отличаются типом зависимости переменных: линейная описывается линейной функцией; мультилинейная также представляет линейную функцию, но в нее входит больше параметров (независимых переменных); нелинейная модель — та, в которой экспериментальные данные характеризуются функцией, являющейся нелинейной (показательной, логарифмической, тригонометрической и так далее).

Чаще всего используются простые линейные и мультилинейные модели.

Регрессионный анализ предлагает множество приложений в различных дисциплинах, включая финансы. Кстати, регрессионный анализ можно проводить с помощью языка R. Сделать первые шаги в освоении этого языка поможет наш открытый курс « Аналитика с SQL и R ».

Рассмотрим поподробнее принципы построения и адаптации результатов метода.

Предположения линейной модели

Линейный регрессионный анализ основан на шести фундаментальных предположениях:

1. Переменные показывают линейную зависимость;
2. Независимая переменная не случайна;
3. Значение невязки (ошибки) равно нулю;
4. Значение невязки постоянно для всех наблюдений;
5. Значение невязки не коррелирует по всем наблюдениям;
6. Остаточные значения подчиняются нормальному распределению.

Построение простой линейной регрессии

Простая линейная модель выражается с помощью следующего уравнения:

Y = a + bX

• Y — зависимая переменная
• X — независимая переменная (объясняющая)
• а – свободный член (сдвиг по оси OY)
• b – угловой коэффициент. Он указывает на поведение кривой (убывает или возрастает, угол между с осью)

a и b называют коэффициентами линейной регрессии. В их нахождении и заключается основная задача.

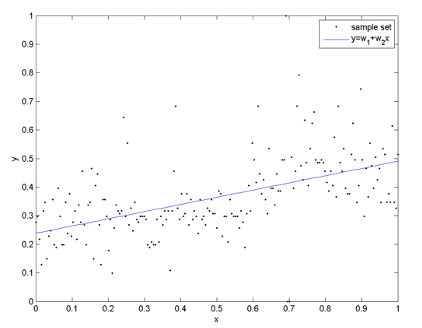
Рис.1. Линия линейной регрессии

Если в нашей задаче присутствуют несколько факторов: x₁, x₂, x₃, от которых, мы полагаем, зависит y, то нужно использовать множественную регрессию, описываемую уравнением:

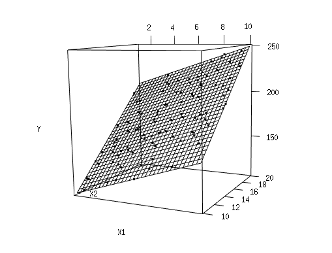
Рис.2. Множественная регрессия

Существует много способов определить коэффициенты a и b. Но самым простым и надежным является метод наименьших квадратов (можно научно доказать, что это лучший способ).

Идея метода: мы имеем значения y – числовой ряд или набор данных. Необходимо построить функцию регрессии Y=a + bX так, чтобы выражение (Y – y) 2 было минимальным. (Y – y) 2 – ошибка, которую мы хотим минимизировать. Минимизируется функционал благодаря подбору коэффициентов a и b.

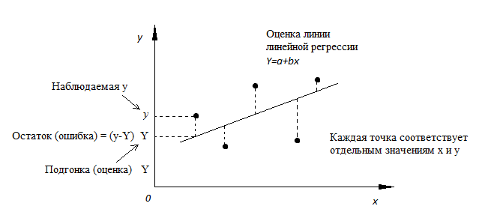
Рис. 3. Линия линейной регрессии.
Пунктиром изображено расстояние y – Y для каждой точки.

Ключевым фактором применения любой статистической модели является правильное понимание предметной области и ее бизнес-приложения.

Линейная регрессия — это довольно простой, но мощный инструмент, который может существенно облегчить работу аналитика при изучении поведения потребителей; факторов, влияющих на производительность и окупаемость; улучшит понимание бизнес процессов в целом.

Примеры использования линейной регрессии

Прогнозирование показателей

Данную модель можно использовать для обнаружения тенденций и составления прогнозов. Предположим, продажи компании росли на протяжении двух лет. Путем проведения линейного анализа данных о ежемесячных продажах компания могла бы спрогнозировать продажи в будущие месяцы.

Оценка эффективности маркетинга

Линейная регрессия также может использоваться для оценки эффективности маркетинга, рекламных кампаний и ценообразования. Чтобы компания «XYZ» оценила качественную отдачу от средств, потраченных на маркетинг определенного бренда, достаточно построить график линейной регрессии и посмотреть, как связаны затраты с прибылью.

Прелесть линейной регрессии в том, что она позволяет улавливать отдельные воздействия каждой маркетинговой кампании, а также контролировать факторы, которые могут повлиять на продажи.

В реальных сценариях обычно существует несколько рекламных кампаний, которые проводятся в один и тот же период времени. Предположим, что две кампании запускаются на телевидении и радио параллельно. Построенная модель может уловить как изолированное, так и комбинированное влияние одновременного показа этой рекламы.

Оценка риска

Модель линейной регрессии хорошо работает для расчета рисков в сфере финансов или страхования. К примеру, компания по страхованию автомобилей может построить линейную регрессию, чтобы составить таблицу выплат по страховке, используя отношение прогнозируемых исков к заявленной страховой стоимости. Основными факторами в такой ситуации являются характеристики автомобиля, данные о водителе или демографическая информация. Результаты такого анализа помогут в принятии важных деловых решений.

Обнаружение важных факторов

В индустрии кредитования финансовая компания заинтересована в минимизации рисков. Поэтому ей важно понять пять основных факторов, вызывающих неплатежеспособность клиента. На основе результатов регрессионного анализа компания могла бы выявить эти факторы и определить варианты EMI (Equated Monthly Installment – фиксированный платеж, произведенный заемщиком кредитору в течение оговоренного срока), чтобы минимизировать дефолт среди сомнительных клиентов.

Ценообразование активов

Еще модель линейной регрессии находит свое применение в ценообразовании активов. «Модель оценки долгосрочных активов» описывает связь между ожидаемой доходностью и риском инвестирования в ценную бумагу. Это помогает инвесторам оценивать целесообразность инвестиций и доходность их портфеля.

Вывод

Несмотря на то, что линейная регрессия имеет довольно жесткие ограничения, поскольку она может работать только тогда, когда зависимая переменная имеет непрерывный характер и имеется линейная зависимость между переменными, модель является самым известным методом анализа и прогнозирования.

Мы привели самые популярные примеры использования данной модели в бизнесе и финансах. Естественно, чтобы глубоко понять, как его использовать в той или иной ситуации, нужно погрузиться в метод поподробнее – самостоятельно «пощупать» все его слабые и сильные стороны; посмотреть, как модель ведет себя на уникальных данных и так далее. Это очень интересный и важный процесс – именно поэтому индустрия Data Science сейчас находится на таком подъеме!

Линейная регрессия в машинном обучении

Линейная регрессия ( Linear regression ) — модель зависимости переменной x от одной или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости.

Линейная регрессия относится к задаче определения «линии наилучшего соответствия» через набор точек данных и стала прос тым предшественником нелинейных методов, которые используют для обучения нейронных сетей. В этой статье покажем вам примеры линейной регрессии.

Применение линейной регрессии

Предположим, нам задан набор из 7 точек (таблица ниже).

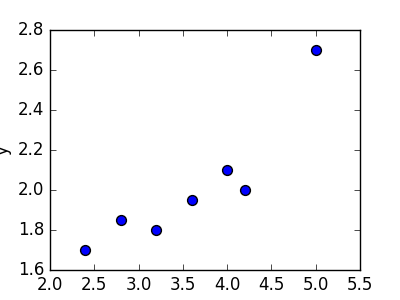
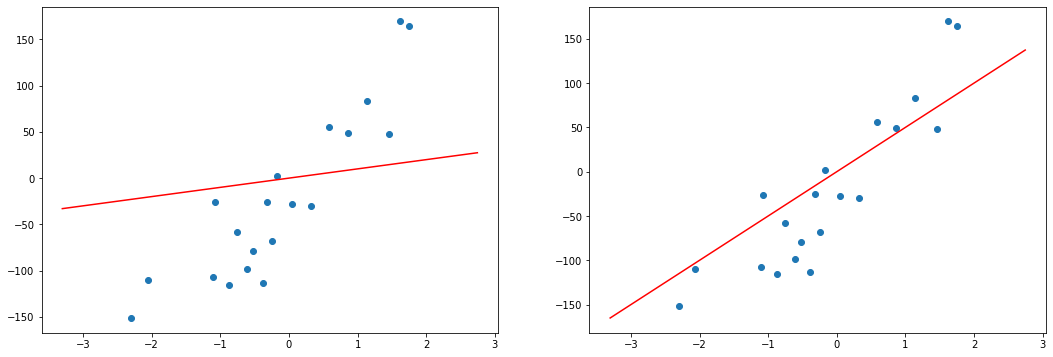
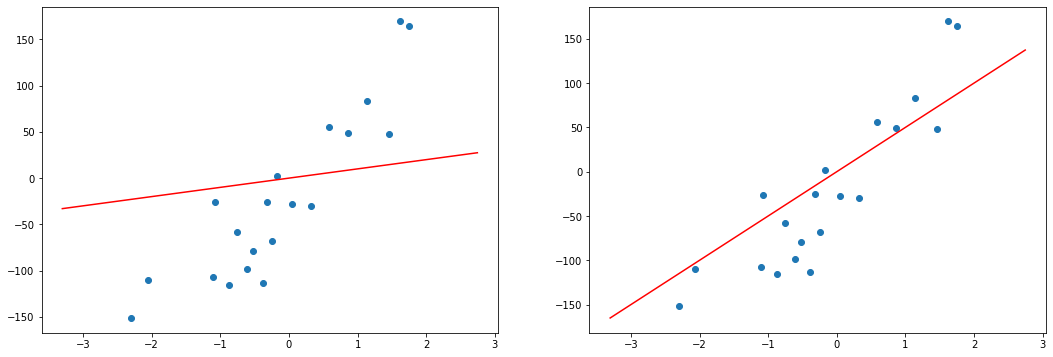
Цель линейной регрессии — поиск линии, которая наилучшим образом соответствует этим точкам. Напомним, что общее уравнение для прямой есть f (x) = m⋅x + b, где m — наклон линии, а b — его y-сдвиг. Таким образом, решение линейной регрессии определяет значения для m и b, так что f (x) приближается как можно ближе к y. Попробуем несколько случайных кандидатов:

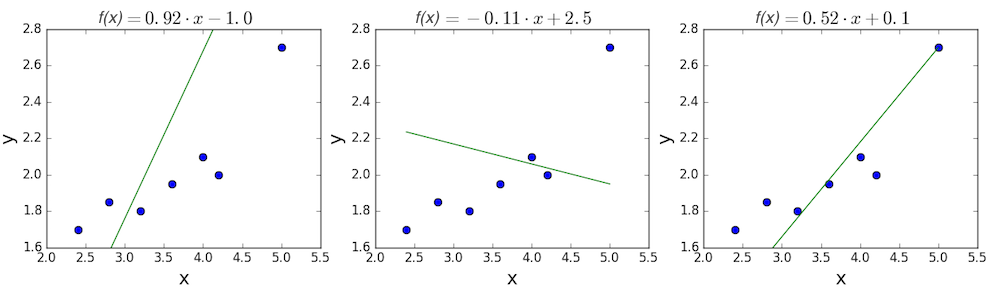
Довольно очевидно, что первые две линии не соответствуют нашим данным. Третья, похоже, лучше, чем две другие. Но как мы можем это проверить? Формально нам нужно выразить, насколько хорошо подходит линия, и мы можем это сделать, определив функцию потерь.

Функция потерь — метод наименьших квадратов

Функция потерь — это мера количества ошибок, которые наша линейная регрессия делает на наборе данных. Хотя есть разные функции потерь, все они вычисляют расстояние между предсказанным значением y( х) и его фактическим значением. Например, взяв строку из среднего примера выше, f(x)=−0.11⋅x+2.5, мы выделяем дистанцию ошибки между фактическими и прогнозируемыми значениями красными пунктирными линиями.

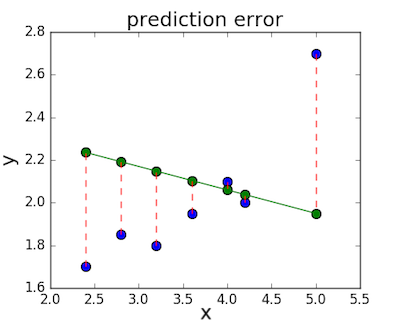
Одна очень распространенная функция потерь называется средней квадратичной ошибкой (MSE). Чтобы вычислить MSE, мы просто берем все значения ошибок, считаем их квадраты длин и усредняем.

Вычислим MSE для каждой из трех функций выше: первая функция дает MSE 0,17, вторая — 0,08, а третья — 0,02. Неудивительно, что третья функция имеет самую низкую MSE, подтверждая нашу догадку, что это линия наилучшего соответствия.

Рассмотрим приведенный ниже рисунок, который использует две визуализации средней квадратичной ошибки в диапазоне, где наклон m находится между -2 и 4, а b между -6 и 8.

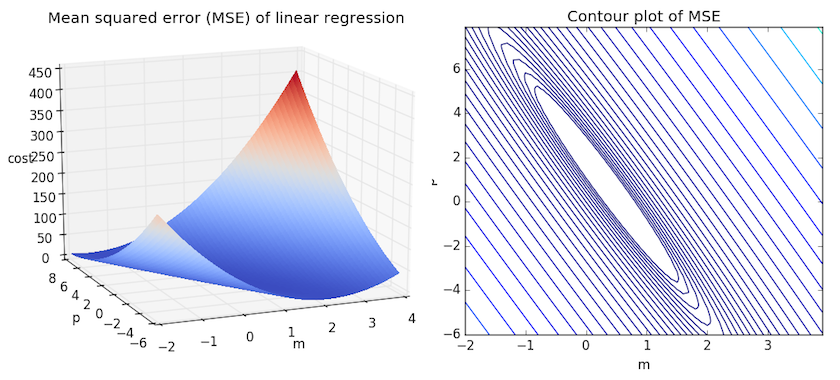
Слева: диаграмма, изображающая среднеквадратичную ошибку для -2≤m≤4, -6≤p≤8 Справа: тот же рисунок, но визуализирован как контурный график, где контурные линии являются логарифмически распределенными поперечными сечениями высоты.

Глядя на два графика, мы видим, что наш MSE имеет форму удлиненной чаши, которая, по-видимому, сглаживается в овале, грубо центрированном по окрестности (m, p) ≈ (0.5, 1.0). Есл и мы построим MSE линейной регрессии для другого датасета, то получим аналогичную форму. Поскольку мы пытаемся минимизировать MSE, наша цель — выяснить, где находится самая низкая точка в чаше.

Больше размерностей

Вышеприведенный пример очень простой, он имеет только одну независимую переменную x и два параметра m и b. Что происходит, когда имеется больше переменных? В общем случае, если есть n переменных, их линейная функция может быть записана как:

Один трюк, который применяют, чтобы упростить это — думать о нашем смещении «b», как о еще одном весе, который всегда умножается на «фиктивное» входное значение 1. Другими словами:

Добавление измерений, на первый взгляд, ужасное усложнение проблемы, но оказывается, постановка задачи остается в точности одинаковой в 2, 3 или в любом количестве измерений. Существует функция потерь, которая выглядит как чаша — гипер-чаша! И, как и прежде, наша цель — найти самую нижнюю часть этой чаши, объективно наименьшее значение, которое функция потерь может иметь в отношении выбора параметров и набора данных.

Итак, как мы вычисляем, где именно эта точка на дне? Распространенный подход — обычный метод наименьших квадратов, который решает его аналитически. Когда есть только один или два параметра для решения, это может быть сделано вручную, и его обычно преподают во вводном курсе по статистике или линейной алгебре.

Проклятие нелинейности

Увы, обычный МНК не используют для оптимизации нейронных сетей, поэтому решение линейной регрессии будет оставлено как упражнение, оставленное читателю. Причина, по которой линейную регрессию не используют, заключается в том, что нейронные сети нелинейны.

Различие между линейными уравнениями, которые мы составили, и нейронной сетью — функция активации (например, сигмоида, tanh, ReLU или других).

Эта нелинейность означает, что параметры не действуют независимо друг от друга, влияя на форму функции потерь. Вместо того, чтобы иметь форму чаши, функция потерь нейронной сети более сложна. Она ухабиста и полна холмов и впадин. Свойство быть «чашеобразной» называется выпуклостью, и это ценное свойство в многопараметрической оптимизации. Выпуклая функция потерь гарантирует, что у нас есть глобальный минимум (нижняя часть чаши), и что все дороги под гору ведут к нему.

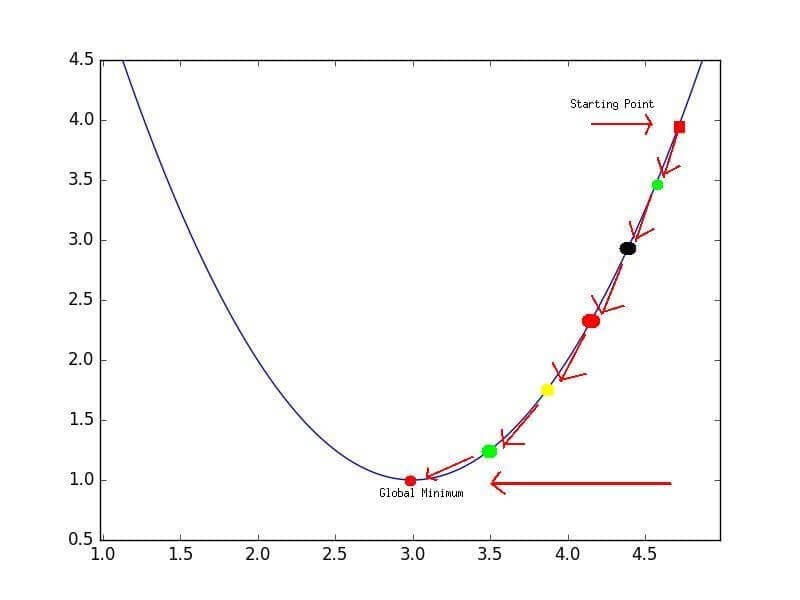
Минимум функции

Но, вводя нелинейность, мы теряем это удобство ради того, чтобы дать нейронным сетям гораздо большую «гибкость» при моделировании произвольных функций. Цена, которую мы платим, заключается в том, что больше нет простого способа найти минимум за один шаг аналитически. В этом случае мы вынуждены использовать многошаговый численный метод, чтобы прийти к решению. Хотя существует несколько альтернативных подходов, градиентный спуск остается самым популярным методом.