Урок 7: Масштаб, соотношение чисел.

Тема 11 Причинность, регрессия, корреляция

Исследование объективно существующих связей между социально-экономическими явлениями и процессами является важнейшей задачей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие основное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения ‑ это такая связь явлений и процессов, когда изменение одного из них ‑ причины ведет к изменению другого ‑ следствия.

Финансово-экономические процессы представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении этих процессов необходимо выявлять главные, основные причины, абстрагируясь от второстепенных.

В основе первого этапа статистического изучения связи лежит качественный анализ, связанный с анализом природы социального или экономического явления методами экономической теории, социологии, конкретной экономики.

Второй этап – построение модели связи, базируется на методах статистики: группировках, средних величинах, и так далее.

Третий, последний этап ‑ интерпретация результатов, вновь связан с качественными особенностями изучаемого явления. Статистика разработала множество методов изучения связей. Выбор метода изучения связи зависит от познавательной цели и задач исследования.

Признаки по их сущности и значению для изучения взаимосвязи делятся на два класса.

Признаки, обуславливающие изменения других, связанных с ними признаков, называются факторными, или просто факторами.

Признаки, изменяющиеся под действием факторных признаков, называются результативными.

В статистике различают функциональную и стохастическую зависимости.

Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.

Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем, при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.

Связи между явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению.

Таблица 11.1. ‑ Количественные критерии оценки тесноты связи

Величина показателя связи

По направлению выделяют связь прямую и обратную.

Прямая ‑ это связь, при которой с увеличением или с уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного признака.

Пример. Так, рост объемов производства способствует увеличению прибыли предприятия.

В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака, то есть обратная ‑ это связь, при которой с увеличением или с уменьшением значений одного признака происходит уменьшение или увеличение значений другого признака.

Пример. Так, снижение себестоимости единицы производимой продукции влечет за собой рост рентабельности.

По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные.

Если статистическая связь между явлениями может быть приблизительно выражена уравнением прямой линии, то ее называют линейной связью вида:

Если же связь может быть выражена уравнением какой-либо кривой, то такую связь называют нелинейной или криволинейной, например:

11.3

Для выявления наличия связи, ее характера и направления в статистике используются методы: приведения параллельных данных; графический; аналитических группировок; корреляции, регрессии.

Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере.

Графически взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат ‑ результативного. Каждое пересечение линий, проводимых через эти оси, обозначаются точкой. При отсутствии тесных связей имеет место беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.

В статистике принято различать следующие виды зависимостей:

Парная корреляция ‑ связь между двумя признаками (результативным и факторным, или двумя факторными).
Частная корреляция ‑ зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков.
Множественная корреляция ‑ зависимость результативного и двух или более факторных признаков, включенных в исследование.

Корреляционный анализ имеет своей задачей количественное определение тесноты и направления связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).

Теснота связи количественно выражается величиной коэффициентов корреляции, которые, давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» факторных признаков при построении уравнения множественной регрессии. Знаки при коэффициентах корреляции характеризуют направление связи между признаками.

Регрессия тесно связана с корреляцией и позволяет исследовать аналитическое выражение взаимосвязи между признаками.

Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой или результативным признаком), обусловлено влиянием одной или нескольких независимых величин (факторных признаков).

Одной из проблем построения уравнений регрессии является их размерность, то есть определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным. Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет получить модель, быстрее и качественнее реализуемую. В то же время, построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс.

При построении моделей регрессии должны соблюдаться требования:

Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями.
Возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей.
Все факторные признаки должны иметь количественное (числовое) выражение.
Наличие достаточно большого объема исследуемой совокупности (в последующих примерах в целях упрощения изложения материала это условие нарушено, т.е. объем очень мал).
Причинно-следственные связи между явлениями и процессами должны описываться линейной или приводимой к линейной форме зависимостью.
Отсутствие количественных ограничений на параметры модели связи.
Постоянство территориальной и временной структуры изучаемой совокупности.

Соблюдение данных требований позволяет построить модель, наилучшим образом описывающую реальные социально-экономические явления и процессы.

Парная регрессия на основе метода наименьших квадратов позволяет получить аналитическое выражение связи между двумя признаками: результативным и факторным.

Определить тип уравнения можно, исследуя зависимость графически, однако существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, то это свидетельствует о том, что связь между ними линейная, а при обратной связи ‑ гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная регрессия.

Оценка параметров уравнений регрессии ( и — в уравнении параболы второго порядка) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели , при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:

11.4

где п ‑ объем исследуемой совокупности (число единиц наблюдения).

В уравнениях регрессии параметр а_о показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков. Коэффициент регрессии а₁ показывает, на сколько в среднем изменяется значение результативного признака при увеличении факторного признака на единицу собственного измерения. x_i – теоретические значения результативного признака; y_i – наблюдаемые значения факторного признака.

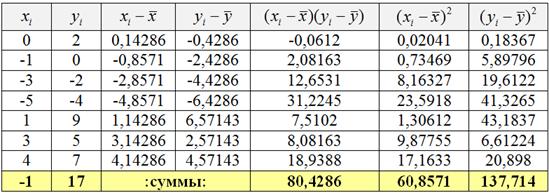
Пример. Имеются данные по 10 однотипным предприятиям о выпуске продукции (х) в тыс.ед. и о расходе условного топлива (у) в тоннах (графы 1 и 2 табл. 17).

Требуется найти уравнение зависимости расхода топлива от выпуска продукции (или уравнение регрессии у по х) и измерить тесноту зависимости между ними. Для этого представим данные в табл. 11.2 (вместе с расчетными столбцами).

Таблица 11.2 – Расчет показателей для нахождения уравнения регрессии

Необходимые для решения суммы рассчитаны выше в таблице. Подставим их в уравнение и решим систему.

Получив искомое уравнение регрессии можно утверждать, что с увеличение выпуска продукции на тыс. ед., расход топлива возрастет в среднем на 0,547 тонны.

* Если параметры уравнения найдены верно, то

Измерение тесноты (силы) и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака и одного (при изучении парных зависимостей) или нескольких (множественных зависимостей) факторных признаков.

Линейный коэффициент корреляции (К. Пирсона) характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.

В теории разработаны и на практике применяются различные модификации формулы расчета данного коэффициента.

Для измерения тесноты зависимости между у и х применяют линейный коэффициент корреляции, который может быть рассчитан по любой из нижеприведенных формул:

11.8

Таблица 11.3 – Оценка линейного коэффициента корреляции

Значение линейного коэффициента связи	Характеристика связи	Интерпретация связи
г = 0	отсутствует	–
0	прямая	с увеличением х увеличивается у
-1	обратная	с увеличением х уменьшается у и наоборот
г=1	функциональная	каждому значению факторного признака строго соответствует одно значение результативного признака

Пример вычисления коэффициента корреляции

Найдем коэффициент корреляции по данным табл. 11.2., используя формулы (11.6‑11.8):

Пример вычисления формула 11.6

Пример вычисления формула 11.7

Пример вычисления формула 11.8

Линейный коэффициент корреляции может принимать по модулю значения от 0 до 1 (знак + при прямой зависимости и знак – при обратной зависимости).

Найденный коэффициент корреляции означает, что характер связи между исследуемыми признаками прямой.

По степени тесноты связи между признаками (одним из критериев оценки служит коэффициент корреляции) различают связи:

пояснение характера корреляц связи

Следовательно, 0,7≤0,96≤ 1 , значит, связь в данном примере сильная (с увеличением выпуска продукции увеличивается расход топлива).

Термин “корреляция” впервые применил французский палеонтолог Ж. Кювье, который вывел “закон корреляции частей и органов животных” (этот закон позволяет восстанавливать по найденным частям тела облик всего животного). В статистику указанный термин ввел в 1886 году английский биолог и статистик Френсис Гальтон (не просто связь – relation, а “как бы связь” – co-relation). Однако точную формулу для подсчёта коэффициента корреляции разработал его ученик – математик и биолог – Карл Пирсон (1857 – 1936).

Корреляционным называется исследование, проводимое для подтверждения или опровержения гипотезы о статистической связи между несколькими (двумя и более) переменными. В психологии переменными могут выступать психические свойства, процессы, состояния и др.

Контрольные задания.

По данным статистических сборников постройте таблицу: по 10 однотипным предприятиям с данными о численности персонала, выпуске продукции, расходах; данных о прожиточном минимуме и средней заработной плате и т.п.; найдите уравнение зависимости (или уравнение регрессии) и измерьте тесноту связи между показателями.

Масштаб, соотношение чисел

Ученики шестого класса заинтересовались картой мира. Ребята, на перемене, стоя у доски, долго рассматривали океаны, материки, горные вершины, пустыни. После, перешли к изучению обозначений и символов, нанесенных на карту. Вдруг, Макар заметил, в верхнем правом углу рассматриваемого изображения, имеются непонятные цифры – 1:20 000 000. Мальчик спросил у одноклассников, что обозначает странная надпись на карте. Школьники не смогли дать ответ на вопрос Макара. В этот момент прозвенел звонок, в класс вошел учитель. Мальчик поднял руку и задал свой вопрос. Учитель объяснил детям, что цифры на карте обозначают масштаб, то есть, отношение размера рисунка к реальному размеру. Проще говоря, запись 1:20 000 000 показывает, что отрезок в 1см на карте соответствует отрезку 20 000 000 см на местности. И посоветовала ребятам внимательно изучить тему отношения и пропорции на сайте «100urokov.ru». Сегодня на уроке рассмотрим, на простых и понятных примерах, как найти отношение двух чисел, как звучит определение пропорции, что такое прямая и обратная пропорциональная зависимость, и что скрывается за непонятным словом «масштаб».

План урока:

Отношение двух чисел

На уроке математики ребята выполняли самостоятельную работу. На решение самостоятельных заданий Наталья Ивановна выделила 15 минут, после чего попросила сдать тетради на проверку. Подумайте, какую часть урока заняла самостоятельная работа?

Чтобы дать ответ на данное задание, давайте вспомним, какую продолжительность имеет обычный урок? Всем известно, что стандартный урок длится 45 минут. Получается, из 45 минут только 15 дети решали самостоятельную работу. Следовательно, нужно выяснить, какая часть целого урока потрачена на самостоятельную работу. В арифметике для вычисления части от числа или определения во сколько раз одно число больше другого существует специальное понятие «Отношение чисел»:

Исходя из рассмотренного определения, необходимо составить отношение длительности самостоятельной работы к длительности целого урока. Таким образом, ответим на главный вопрос задачи. Запишем отношение (частное) двух чисел:

15/45 – данную дробь можно сократить, разделив числитель и знаменатель на 15.

Выходит, что на самостоятельную работу класс потратил 1/3 всего урока.

Важно помнить, что числовое значение отношения чисел останется прежним, если каждый компонент отношения умножить или разделить на одно и то же число.

Давайте, составляющие отношения 6/7 умножим на 2, то есть на дробь 2/2.

6/7 × 2/2 (числитель умножаем на числитель, знаменатель на знаменатель);

6×2/7×2 = 12/14 – при сокращении на 2, получим исходную дробь.

Следовательно, числовое значение дроби не изменилось – 6/7 = 12/14.

При составлении отношений с использованием различных чисел и величин, важно помнить, что отношение будет верным, если все компоненты отношения выражены в одинаковых единицах измерения.

Разберем на примере.

В вазочке находился один килограмм конфет. Бабушка отсыпала 300 граммов сладостей в пакет. Определите, какую часть всех конфет отсыпала бабушка?

Чтобы ответить на главный вопрос задачи нужно составить отношение массы отсыпанных конфет к общей массе сладостей: 300 граммов/1 килограмм. Сразу определить числовое значение отношения не можем, составляющие имеют разные единицы измерения массы – грамм и килограмм. Выразим один килограмм в граммах:

1кг = 1000 грамм

Теперь определим, какую часть составили отсыпанные сладости:

Бабушка отсыпала 3/10 всех сладостей в пакет.

Запомни!

Если a и b числовые значения или значения, выраженные в одной и той же величине, тогда:

отношение a/b, будет равно частному a и b;
при условии, что a>b, отношение a/b говорит, во сколько раз a больше, чем b;
при условии, что a

Определение пропорции

Руководитель детского хореографического кружка, для пошива костюмов своим воспитанникам, приобрел в магазине тканей 10 метров шелка, на сумму 420 рублей. Но купленной ткани не хватило. Какую сумму нужно потратить, чтобы купить еще 5 метров такого же материала?

Данную задачу можно решить двумя способами. Рассмотрим каждый из них подробно.

По условию нам известно, что 10 метров материала, стоит 420 рублей. Отсюда можно узнать цену одного метра. Для этого, общую сумму(420) необходимо разделить на количество приобретенной ткани(10):

420 : 10 = 42 рубля стоит один метр ткани.

Зная цену одного метра ткани, можно узнать стоимость пяти метров. Для этого стоимость одного метра (42), умножаем на количество таких метров (5):

42 × 5 = 210 рублей необходимо, для покупки 5 метров материала.

Этот способ известен еще из начальной школы. Но далеко не все задачи такого вида можно решить первым способом.

В этом случае используют второй способ решения задач такого вида.

Вначале, запишем краткое условие.

Теперь нужно подумать. В нашем случае, количество материала уменьшается, следовательно,уменьшается стоимость покупки. Обозначим цену пяти метров материала – х.

Для решения задач такого вида в математике существует специальное определение – «Пропорция»

Используя рассмотренное определение, подумаем, как составить пропорцию из чисел? Формировать пропорцию будем, опираясь на краткую запись условия задачи – десять относится к пяти как четыреста двадцать к иксу:

Пропорция составлена и возникает вопрос, как вычислить неизвестный компонент?

Для вычисления неизвестной составляющей пропорции существует правило, которое называется «Основное свойство пропорции»:

Определим крайние и средние члены в составленном равенстве:

Крайними членами пропорции будут числа 10, х.

Средними членами пропорции будут числа 5, 420.

Запишем равенство произведений крайних и средних членов в составленной пропорции:

10х = 5 × 420 – высчитываем произведение;

10х = 2100 – решаем как обычное уравнение;

Выходит, 210 рублей необходимо для приобретения пяти метров материала.

Вот так на примере решения задачи мы разобрали новое определение. Запомните, пожалуйста, все правила и поиск неизвестного компонента в любых отношениях и пропорциях будет для вас только развлечением!

Продолжаем дальше знакомиться с пропорцией.

Прямая и обратная пропорциональная зависимость.

Рассмотрим ситуацию, в которой оказывается каждый, попадая в магазин.

Витя пришел в магазин за покупками. В кошельке ребенка лежало 300 рублей. Витя купил хлеб, молоко, масло, заплатил за товар. Денег у мальчика стало меньше. После посещения кондитерского отдела, где он купил карамель, пирожные, рулет денег стало совсем мало. Делаем вывод: чем больше покупок делает мальчик, тем меньше денег у него остается.

Значит, количество денег в нашем кошельке и количество покупок имеют обратно пропорциональную зависимость и являются обратно пропорциональными величинами.

А если взять ситуацию с оплатой за пользование водой и электроэнергией

Чем больше воды/электроэнергии мы используем, тем больше должны заплатить. В таком случае величины кубы воды/киловатты электроэнергии и денежные единицы называются прямо пропорциональными и имеют прямую пропорциональную зависимость.

Масштаб

Мама с Арсением решили нарисовать путь, который проходит мальчик, идя из дома в школу. Ребенок заволновался: «Как можно на листке бумаги нарисовать 450 метров пути?». Мама успокоила сына и рассказала, что именно для таких случаев и используется определение масштаба карты.

Рассмотрим решение задачи с использованием масштаба.

Расстояние на карте от Москвы до Киева составляет пять сантиметров. Вычислите, сколько километров от Москвы до Киева, если масштаб карты 1:15 000 000.

В первую очередь, нужно понимать, что масштаб 1:15 000 000 показывает, что 1 см карты содержит 15 000 000 сантиметров или 150 километров на местности.

Чтобы ответить на главный вопрос задачи,составим пропорцию. Для этого, расстояние на местности от Москвы до Киева примем за х:

Помним, произведение крайних членов пропорции равно произведению средних. Имеем:

Выходит, 750 километров – расстояние от Москвы до Киева.

Расчеты оказались верными. Вся справочная литература говорит о том, что расстояние Москва – Киев составляет примерно 755 км!

Теперь вы совершенно самостоятельно можете рассчитать абсолютно любое расстояние, имея под рукой линейку и карту!

Интересно!

С пропорциями мы сталкиваемся, ежедневно, ежеминутно. Все в нашем мире пропорционально. Любая вещь, предмет, техника, животные, растения – все имеет свои пропорции! Мы можем любоваться красивой архитектурой – благодаря пропорциям, наслаждаться цветками роз или ромашек – тоже не без участия пропорций. Природа создает все в строгой пропорциональности. В случае, когда пропорции отсутствуют, вещь или предмет нам кажутся неправильными. Ведь даже в нашем теле все имеет свои пропорции:

Быть одержимым числами — это нормально?

В любом грамотном обществе числа — это аспект, от которого нам не уйти. Они везде: на дверях домов, на номерных знаках машин, при составлении декларации о доходах .

Но они не просто написаны. Они также присутствуют в нашем сознании в виде любимых чисел, которые вызывают у нас страх или предпочтение при выполнении каких-либо действий, например, дважды проверять, закрыта ли входная дверь.

Все это — часть повседневной жизни многих людей. Однако есть те, кому кажется, что цифры взяли под контроль их жизнь, и они даже задаются вопросом: Нормально ли зацикливаться на цифрах?. Попробуем ответить на этот вопрос.

Статья по теме: «Обсессивно-компульсивное расстройство (ОКР): что это такое и как оно проявляется?»

Зацикленность на числах — это нормально или это проблема?

Числа — это фундаментальный аспект нашей жизни, независимо от того, насколько мы отвращаемся к математике. Они повсюду, как буквы, образующие слова. Независимо от нашей профессии или хобби, в какой-то момент дня мы должны видеть цифры, чтобы позвонить, посчитать деньги, заплатить, составить отчет о доходах или любую другую деятельность, в которой нам приходится иметь дело с числовыми значениями. аспекты.

Но они не только написаны, но и находятся в наших умах. У всех нас есть какое-то поведение и мышление, связанное с числами. Классический пример — два или три раза проверять дверь, чтобы убедиться, что она правильно закрыта. Другой может быть необходимость купить в супермаркете четыре пачки тунца, ни одну больше и ни одну меньше.

Такое поведение легко оправдать. Имеет смысл дважды проверить, была ли дверь закрыта, проверить, действительно ли дверь закрыта. Пакеты с тунцом могут быть просто потому, что считается, что это точное количество, которого хватит на неделю или до следующей покупки. Но давайте посмотрим правде в глаза, во многих случаях это происходит потому, что мы предпочитаем эти суммы. Проблема в том, что мы говорим не о двух или трех, а о 50, 60, 130 .

Также может случиться так, что мы одержимы самим числом, то есть символом и тем, что оно представляет.. В определенном смысле это нормально, что у нас есть любимое число и другое, которое мы связываем с неудачей, точно так же, как есть те, у кого есть любимый цвет. Культура имеет очень большой вес в этих выборах. Например, в Испании и других европейских странах 13 — это число неудач, а 7, 9 или 11 — это число, которое считается удачей.

Наличие любимого или несчастливого числа не очень важно, пока оно не станет навязчивой идеей. Избегать любой ценой входа в дверь с номером 13 или желать, чтобы наш номер телефона имел, да или да, 7 — это аспекты, которые, какими бы незначительными они ни казались, ограничивают жизнь тех, кто страдает от этой навязчивой идеи. Что, если нас пригласят в дом под номером 13? Мы не вошли? Что мы говорим тем, кто нас пригласил?

Глядя на эти небольшие вводные примеры, нетрудно привыкнуть к мысли, что, хотя мыслить числами, как символом, так и выполнять X действий, — это нормально, но с некоторыми ограничениями. Если мы зайдем слишком далеко, если мысли о числах станут навязчивой идеей, сильно ограничивающей нашу жизнь, у нас возникнет проблема. Нормально проверять дверь дважды, это не так, если мы проверяем все 10 раз перед выходом из дома. Это называется арифмоманией, тесно связанной с ОКР.

Вам может быть интересно: «Что такое навязчивая идея? Причины, симптомы и лечение»

ОКР и арифмомания

Обсессивно-компульсивное расстройство (ОКР) — это тревожное расстройство, характеризующееся навязчивыми, повторяющимися и постоянными мыслями, которые вызывают беспокойство, опасения, страх и беспокойство в дополнение к повторяющемуся поведению.Среди основных характеристик ОКР мы обычно находим такие аспекты, как беспокойство по поводу гигиены, порядка и симметрии, двойное закрытие двери . аспекты, которые могут быть включены в навязчивые идеи или компульсии.

Между наиболее распространенные навязчивые идеи, связанные с ОКР у нас есть: страх заражения, страх причинить вред другим или того, что в результате действия или бездействия будут причинены вреда близким, навязчивые идеи сексуального содержания, забота о здоровье, потребность в порядке и симметрии, чрезмерная религиозность .

Что касается навязчивых действий, мы можем обнаружить повторяющееся поведение, такое как мытье рук или чистка зубов, открытие или закрытие дверей, прикосновение к предмету руками, постукивание ногами по полу, размещение предметов в определенном порядке или проверка того, как обстоят дела с ними. они должны быть (двери закрыты, электроприборы отключены . ). Также при навязчивых действиях мы находим повторяющиеся мысли, такие как молитва, подсчет чисел или тихое повторение слов снова и снова.

Одержимость цифрами называется арифмоманией. По сути, это обсессивно-компульсивное расстройство, но с особой одержимостью числами. Люди с этим расстройством очень нуждаются в подсчете своих действий или предметов в их окружении, чтобы убедиться, что они их считали или выполняли такое поведение определенное количество раз. Также может случиться так, что у пациента развивается сложная психическая система, в которой он присваивает значения или числа людям, объектам и событиям, навязчиво ища отношения между ними, чтобы сделать их связными.

Люди с этим расстройством могут вести подсчет, который можно вести громко или тихо, и даже могут проводить более одного счета одновременно (например, подсчет уличных фонарей, красных автомобилей и собак). Этот счет дает им безопасность, и если они этого не сделают, они могут начать думать, что случится что-то плохое., в том же духе, что и остальная ТОС.

Некоторые примеры одержимости числами

Упоминание всех случаев арифмомании, связанных как с навязчивыми идеями, так и с компульсиями, даст нам список, если количество чисел бесконечно. Есть навязчивые идеи абсолютно любым числом, переходящие во всевозможные принуждения. Если что-то характеризует ОКР, так это то, что каждый человек, страдающий этим, имеет разные патологические мысли и поведение., а одержимость чем-то столь же обширным, как числа, делает его еще более разнообразным. Вот несколько примеров одержимости числами.

1. Нечетные и четные числа.

Кажется, есть особая одержимость нечетными и четными числами, одних считали удачливыми, в то время как другие приносили дурные предзнаменования. Обычно удачу приносят пары. Одно из наиболее распространенных объяснений состоит в том, что, поскольку это пары, их всегда можно разделить на два, и это очень хорошо, согласно логике человека, одержимого этими типами ценностей.

2. Предпочтение или боязнь простых чисел

Простые числа — это числа, которые можно разделить только на одно и на себя. Некоторые из них — 1, 2, 3, 5, 7, 11, 13, 17, 19 . Поскольку эти числа настолько уникальны, их можно рассматривать как особо выгодные или, наоборот, числа, которые приносят очень много неудач.

3. Проверяйте вещи с помощью шаблона.

В рамках этого принуждения мы можем постоянно проверять, отключили ли двери, свет, сигнализацию . включение и выключение несколько раз, всегда следуя одному образцу. Например, откройте и закройте кран по схеме 1, 2, 3, 4 (открыть и закрыть; открыть, открыть и закрыть; открыть, открыть, открыть и закрыть; открыть, открыть, открыть, открыть и закрыть), думая, что Иначе случится что-то плохое.

4. Число активатор и дезактиватор тревоги.

Бывают случаи, когда люди связывают одно число с тревогой, а другое — как своего рода «анксиолитик» для того же симптома. Например, ассоциируя число 3 со стрессом, а 7 как расслабление, когда вы видите первое число (проходя через портал с номером 3, видите номерной знак с этим номером . ), вы должны произнести 7 раз «семь». .

5. Число, которое не может отсутствовать изо дня в день.

Одержимость числа, которое должно быть в вашей жизни. Например, быть одержимым 3, просить номер в отеле с этим или кратным числом, всегда имея 3 блока .

6. Прикасайтесь к предметам обеими руками определенное количество раз.

Есть люди, которым нужно одинаковое количество раз прикоснуться к чему-либо обеими руками, когда они случайно коснулись чего-то одной из них. Например, идете по улице и случайно дотронетесь правой рукой до фонарного столба. Это заставляет человека трогать фонарный столб три раза левой рукой и еще два раза — правой..

7. Подсчитайте буквы слов.

Одержимость числами связана не только с числами. Он также экстраполируется на буквы, которые иногда рассматриваются как двойники цифр. Например, бывают случаи, когда люди ненавидят определенное число, скажем 4, и избегают использования каждого слова, в котором столько букв, избегая таких слов, как «любовь», «просто», «индейка» . с «Филией», «индивидуалкой», «галлиновой» .

Это может быть особенно проблематично, если число, которого боятся, очень мало. (от 1 до 3), поскольку наиболее часто используемые слова в любом языке обычно самые короткие, включая грамматические частицы (например, de, el, en, . ). Поскольку человек не может их использовать, его язык может стать очень трудным для понимания или использовать слова и выражения, которые делают его язык очень великим.

8. Двигайтесь со скоростью, оканчивающейся на определенное число.

Это особенно опасно. Человек чувствует необходимость ехать со скоростью, оканчивающейся на одну и ту же цифру, или превышать или превышать ограничение скорости X километров.

9. Подсчитайте шаги.

Идите постоянно, считая шаги. Например, считать шаги от 1 до 10., убедившись, что по прибытии в пункт назначения вы выполнили шаг 10 последнего подсчета.

10. Сложные математические операции.

Некоторые люди с ОКР выполняют действительно сложные арифметические операции всех видов, которые мы можем себе представить, просто потому, что они сталкиваются с определенными значениями.

Приведем наглядный пример этого: идите по улице и посмотрите номера номерных знаков автомобилей, добавьте их цифры и добавьте еще одну операцию, например 1 + 1 + 1 + 1 + 1, а затем номер наш номер телефона и DNI, присвоить значение букве DNI и умножить его на полученный результат.

вывод

Зацикленность на числах — довольно распространенное явление, но с точки зрения здоровья и качества жизни это ненормально. Одно дело иметь любимое число или иметь какое-то ежедневное хобби, а другое — заправлять постель X раз, верить, что, думая о числе 3, будет очень плохой день, или начать заниматься. арифметика по простому факту встретить числа на улице.

Что Синдром, связанный с обсессивно-компульсивным расстройством, арифмомания — это заболевание, лечение которого должен выполнять профессионал. Это может быть связано с серьезным вмешательством в повседневную жизнь пострадавшего, поскольку он может тратить много времени на компульсии, чтобы успокоить свое беспокойство. Кроме того, по мере усугубления расстройства человек будет все больше отключаться от окружающей среды, он не поймет, почему у него такая одержимость цифрами.

19. Линейный коэффициент корреляции

Эта тема планировалась более 10 лет назад и вот, наконец, я здесь…. И вы здесь! И это замечательно! Даже не то слово. Это корреляционно.

О корреляции речь зашла в статьях в статьях об аналитической и комбинационной группировке, в результате чего перед нами нарисовались некоторые эмпирические показателями корреляции (прочитайте хотя бы «по диагонали»!). И сейчас на очереди линейный коэффициент корреляции, популярный настолько, что по умолчанию под коэффициентом корреляции понимают именно его. …Да, всё верно – существует довольно много разных коэффициентов корреляции. Однако всему своё время.

Материал данной темы состоит из двух уровней:

– начального, для всех – вплоть до студенток психологических и социологических факультетов, школьников, бабушек, дедушек, etc и

– продвинутого, где я разберу более редкие задачи, а некоторые даже не буду разбирать

В результате вы научитесь БЫСТРО решать типовые задачи (видео прилагается) и для самых ленивых есть калькуляторы. И пока не запамятовал, хочу порекомендовать корреляционно-регрессионный анализ для ваших научных работ и практических исследований – наряду со статистическими гипотезами, это самая настоящая находка в плане новизны и творческих изысканий.

Оглавление:

то было для «чайников», для начала достаточно…

…и в этот момент я благоговейно улыбаюсь – как здорово, что все мы здесь сегодня собрались:

Имеются выборочные данные по студентам: – количество прогулов за некоторый период времени и – суммарная успеваемость за этот период:

И сразу обращаю внимание, что в условии приведены несгруппированные данные. Помимо этого варианта, есть задачи, где изначально дана комбинационная таблица, и их мы тоже разберём. Сначала одно, затем другое.

1) высказать предположение о наличии и направлении корреляционной зависимости признака-результата от признака-фактора и построить диаграмму рассеяния;

2) анализируя диаграмму рассеяния, сделать вывод о форме зависимости;

3) найти уравнение линейной регрессии на , выполнить чертёж;

4) вычислить линейный коэффициент корреляции, сделать вывод;

5) вычислить коэффициент детерминации, сделать вывод,

и позже будет ещё 5-6 пунктов для продвинутых читателей (см. конец урока).

Решение:

1) Прежде всего, повторим, что такое корреляционная зависимость. Очевидно, что чем больше студент прогуливает, тем более вероятно, что у него плохая успеваемость. Но всегда ли это так? Нет, не всегда. Успеваемость зависит от многих факторов. Один студент может посещать все пары, но все равно учиться посредственно, а другой – учиться неплохо даже при достаточно большом количестве прогулов. Однако общая тенденция состоит в том, что с увеличением количества прогулов средняя успеваемость студентов будет падать. Такая нежёсткая зависимость и называется корреляционной.

По своему направлению зависимость бывает прямой («чем больше, тем больше») и обратной («чем больше, тем меньше»). В данной задаче мы высказали предположение о наличии обратной корреляционной зависимости – успеваемости студентов от – количества их прогулов. И что немаловажно, обосновали причинно-следственную связь (читать всем. ) между признаками.

Проверить выдвинутое предположение проще всего графически, и в этом нам поможет:

диаграмма рассеяния

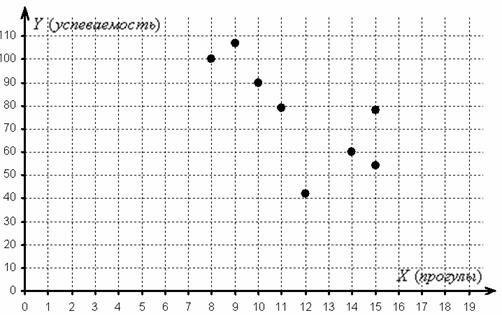
– это множество точек в декартовой системе координат, абсциссы которых соответствуют значениям признака-фактора , а ординаты – соответствующим значениям признака-результата . Минимальное количество точек должно равняться пяти-шести, в противном случае рассматриваемая задача превращается в профанацию. И мы «вписываемся в рамки» – объём выборки равен восьми студентам:

Обратите, кстати, внимание как раз на тот момент, что при одном и том же количестве прогулов (15) двое студентов имеют существенно разные результаты.

2) По диаграмме рассеяния хорошо видно, что с увеличением числа прогулов успеваемость преимущественно падает, что подтверждает наличие обратной корреляционной зависимости успеваемости от количества прогулов. Более того, почти все точки «выстроились» примерно по прямой, что даёт основание предположить, что данная зависимость близкА к линейной.

И здесь я анонсирую дальнейшие действия: сейчас нам предстоит найти уравнение прямой, ТАКОЙ, которая проходит максимально близко к эмпирическим точкам, а также оценить тесноту линейной корреляционной зависимости – насколько близко расположены эти точки к построенной прямой.

Технически существует два пути решения:

– сначала найти уравнение прямой и затем оценить тесноту зависимости;
– сначала найти тесноту и затем составить уравнение.

В практически задачах чаще встречается второй вариант, но я начну с первого, он более последователен. Построим:

3) уравнение линейной регрессии на

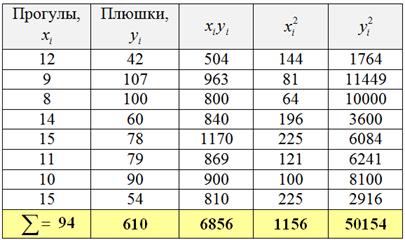
Это и есть та самая оптимальная прямая , которая проходит максимально близко к эмпирическим точкам. Обычно её находят методом наименьших квадратов, и мы пойдём знакомым путём. Заполним расчётную таблицу:

Обратите внимание, что в отличие от задач урока МНК у нас появился дополнительный столбец , он потребуется в дальнейшем, для расчёта коэффициента корреляции.

Коэффициенты функции найдём из решения системы:

Сократим оба уравнения на 2, всё попроще будет:

Систему решим по формулам Крамера:
, значит, система имеет единственное решение.

И проверка forever, подставим полученные значения в левую часть каждого уравнения исходной системы:

в результате получены соответствующие правые части, значит, система решена верно.

Таким образом, искомое уравнение регрессии:

Данное уравнение показывает, что с увеличением количества прогулов («икс») на 1 единицу суммарная успеваемость падает в среднем на 6,0485 – примерно на 6 баллов. Об этом нам рассказал коэффициент «а». И обратите особое внимание, что эта функция возвращает нам средние (среднеожидаемые) значения «игрек» для различных значений «икс».

Почему это регрессия именно « на » и о происхождении самого термина «регрессия» я рассказал чуть ранее, в параграфе эмпирические линии регрессии. Если кратко, то полученные с помощью уравнения средние значения успеваемости («игреки») регрессивно возвращают нас к первопричине – количеству прогулов. Вообще, регрессия – не слишком позитивное слово, но какое уж есть.

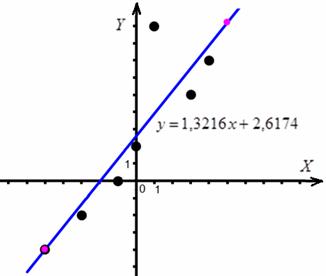
Найдём пару удобных точек для построения прямой:

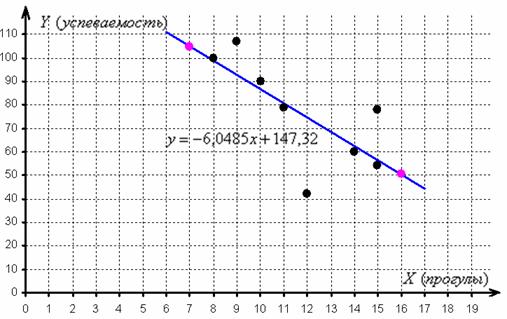
отметим их на чертеже (малиновый цвет) и проведём линию регрессии:

Говорят, что уравнение регрессии аппроксимирует (приближает) эмпирические данные (точки), и с помощью него можно интерполировать (оценить) неизвестные промежуточные значения, так при количестве прогулов среднеожидаемая успеваемость составит балла.

И, конечно, осуществимо прогнозирование, так при среднеожидаемая успеваемость составит баллов. Единственное, нежелательно брать «иксы», которые расположены слишком далеко от эмпирических точек, поскольку прогноз, скорее всего, не будет соответствовать действительности. Например, при значение может вообще оказаться невозможным, ибо у успеваемости есть свой фиксированный «потолок». И, разумеется, «икс» или «игрек» в нашей задаче не могут быть отрицательными.

Второй вопрос касается тесноты зависимости. Очевидно, что чем ближе эмпирические точки к прямой, тем теснее линейная корреляционная зависимость – тем уравнение регрессии достовернее отражает ситуацию, и тем качественнее полученная модель. И наоборот, если многие точки разбросаны вдали от прямой, то признак зависит от вовсе не линейно (если вообще зависит) и линейная функция плохо отражает реальную картину.

Прояснить данный вопрос нам поможет:

4) линейный коэффициент корреляции

Этот коэффициент как раз и оценивает тесноту линейной корреляционной зависимости и более того, указывает её направление (прямая или обратная). Его полное название: выборочный линейный коэффициент пАрной корреляции Пирсона

– «выборочный» – потому что мы рассматриваем выборочную совокупность;
– «линейный» – потому что он оценивает тесноту линейной корреляционной зависимости;
– «пАрной» – потому что у нас два признака (бывает хуже);
– и «Пирсона» – в честь английского статистика Карла Пирсона, это он автор понятия «корреляция».

И в зависимости от фантазии автора задачи вам может встретиться любая комбинация этих слов. Теперь нас не застанешь врасплох, Карл.

Линейный коэффициент корреляции вычислим по формуле:
, где: – среднее значение произведения признаков, – средние значения признаков и – стандартные отклонения признаков. Числитель формулы имеет особый смысл, о котором я расскажу, когда мы будем разбирать второй способ решения.

Осталось разгрести всё это добро Впрочем, все нужные суммы уже рассчитаны в таблице выше. Вычислим средние значения:

Стандартные отклонения найдём как корни из соответствующих дисперсий, вычисленных по формуле:

Таким образом, коэффициент корреляции:

И расшифровка: коэффициент корреляции может изменяться в пределах и чем он ближе по модулю к единице, тем теснее линейная корреляционная зависимость – тем ближе расположены точки к прямой, тем качественнее и достовернее линейная модель. Если либо , то речь идёт о строгой линейной зависимости, при которой все эмпирические точки окажутся на построенной прямой. Наоборот, чем ближе к нулю, тем точки рассеяны дальше, тем линейная зависимость выражена меньше. Однако в последнем случае зависимость всё равно может быть! – например, нелинейной или какой-нибудь более загадочной. Но до этого мы ещё дойдём. А у кого не хватит сил, донесём

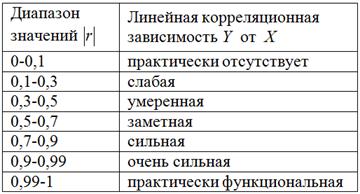
Для оценки тесноты связи будем использовать уже знакомую шкалу Чеддока:

При этом если , то корреляционная связь обратная, а если , то прямая.

В нашем случае , таким образом, существует сильная обратная линейная корреляционная зависимость – суммарной успеваемости от – количества прогулов.

Линейный коэффициент корреляции – это частный аналог эмпирического корреляционного отношения. Но в отличие от отношения, он показывает не только тесноту, но ещё и направление зависимости, ну и, конечно, здесь определена её форма (линейная).

5) Коэффициент детерминации

– это частный аналог эмпирического коэффициента детерминации – есть квадрат коэффициента корреляции:

– коэффициент детерминации показывает долю вариации признака-результата , которая обусловлена воздействием признака-фактора .

В нашей задаче:
– таким образом, в рамках построенной модели успеваемость на 51,74% зависит от количества прогулов. Оставшаяся часть вариации успеваемости (48,26%) обусловлена другими причинами.

! Примечание: но это не является какой-то «абсолютной истиной», это всего лишь оценка в рамках построенной модели.

Задание выполнено

Но точку ставить рано. Теперь второй способ решения, в котором мы сначала находим коэффициент корреляции, а затем уравнение регрессии.

Линейный коэффициент корреляции вычислим по формуле:
, где – стандартные отклонения признаков .

Член в числителе называют корреляционным моментом или коэффициентом ковариации (совместной вариации) признаков, он рассчитывается следующим образом: , где – объём статистической совокупности, а – средние значения признаков. Данный коэффициент показывает, насколько согласованно отклоняются пАрные значения от своих средних в ту или иную сторону. Формулу можно упростить, в результате чего получится ранее использованная версия, без подробных выкладок: . Но сейчас мы пойдём другим путём.

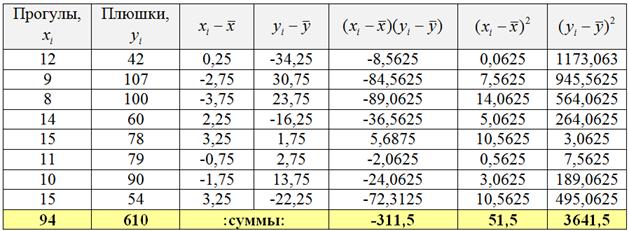
Заполним расчётную таблицу:

При этом сначала рассчитываем левые нижние суммы и средние значения признаков:
и только потом заполняем оставшиеся столбцы таблицы. О том, как быстро выполнить эти вычисления в Экселе, будет видео ниже!

Вычислим коэффициент ковариации:
.

Стандартные отклонения вычислим как квадратные корни из дисперсий:

Таким образом, коэффициент корреляции:

И если нам известны значения , то коэффициенты уравнения регрессии легко рассчитать по следующим формулам:

Таким образом, искомое уравнение:

Теперь смотрим ролик о том, как это всё быстро подсчитать и построить:

Как вычислить коэффициент корреляции и найти уравнение регрессии? (Ютуб)

Если под рукой нет Экселя, ничего страшного, разобранную задачу не так трудно решить в обычной клетчатой тетради. А если Эксель есть и времени нет, то можно воспользоваться моим калькулятором. Да, вы можете найти аналоги в Сети, но, скорее всего, это будет не совсем то, что нужно

Какой способ решения выбрать? Ориентируйтесь на свой учебный план и методичку. По умолчанию лучше использовать 2-й способ, он несколько короче, и, вероятно, потому и встречается чаще. Кстати, если вам нужно построить ТОЛЬКО уравнение регрессии, то уместен 1-й способ, ибо там мы находим это уравнение в первую очередь.

Следующая задача много-много лет назад была предложена курсантам местной школы милиции (тогда ещё милиции), и это чуть ли не первая задача по теме, которая встретилась в моей профессиональной карьере. И я безмерно рад предложить её вам сейчас, разумеется, с дополнительными пунктами:)

В результате независимых опытов получены 7 пар чисел:

…да, числа могут быть и отрицательными.

По данным наблюдений вычислить линейный коэффициент корреляции и детерминации, сделать выводы. Найти параметры линейной регрессии на , пояснить их смысл. Изобразить диаграмму рассеяния и график регрессии. Вычислить , что означают полученные результаты?

Из условия следует, что признак , очевидно, зависит от (ибо кто ж делает бессвязные опыты). Однако помните, что корреляционная зависимость и причинно-следственная связь – это не одно и то же! (прочитайте, если до сих пор не прочитали!). Поэтому, если в задаче просто предложены два числовых ряда (без контекста), то можно говорить лишь о зависимости корреляционной, но не о причинно-следственной.

Все данные уже забиты в Эксель, и вам осталось аккуратно выполнить расчёты. В образце я решил задачу вторым, более распространённым способом. И, конечно же, выполните проверку первым путём.

Следует отметить, что в целях экономии места я специально подобрал задачи с малым объёмом выборки. На практике обычно предлагают 10 или 20 пар чисел, реже 30, и максимальная выборка, которая мне встречалась в студенческих работах – 100. …Соврал малость, 80.

И сейчас я вас приглашаю на следующий урок, назову его Уравнение линейной регрессии, где мы рассчитаем и найдём всё то же самое – только для комбинационной группировки. Плюс немного глубже копнём уравнения регрессии (их два).

Решения и ответы:

Пример 68. Решение: вычислим суммы и средние значения признаков , и заполним расчётную таблицу:

Вычислим коэффициент ковариации:
.
Вычислим средние квадратические отклонения:

Вычислим коэффициент корреляции:
, таким образом, существует сильная прямая корреляционная зависимость от.

Вычислим коэффициент детерминации:
– таким образом, 77,19% вариации признака обусловлено изменением признака . Остальная вариация (22,81%) обусловлена другими факторами.

Вычислим коэффициенты линейной регрессии :

Таким образом, искомое уравнение регрессии:

Данное уравнение показывает, что с увеличением значения «икс» на одну единицу «игрек» увеличивается в среднем примерно на 1,32 единицы (смысл коэффициента «а»).

При среднеожидаемое значение «игрек» составит примерно 2,62 ед. (смысл коэффициента «бэ»).

Найдём пару точек для построения прямой:

и выполним чертёж:

Вычислим:
– среднеожидаемое значение «игрек» при (интерполированный результат);
– среднеожидаемое значение «игрек» при (спрогнозированный результат).

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Zaochnik.com – профессиональная помощь студентам,

cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys

Расчет вероятности выпадения чисел

Меня зовут Иван Мельников! Я – выпускник вуза НТУ «ХПИ», инженерно-физический факультет, специальность «Прикладная математика», счастливый семьянин и просто поклонник игр на удачу. С детства я увлекался лотереями. Мне всегда было интересно, по каким законам выпадают те или иные шары. С 10 лет я записываю результаты лотерей и после анализирую данные.

В моей книге «Секреты Везения или Пошаговый Алгоритм Выигрыша в Лотерее» я хочу поделиться с вами наблюдениями, накопленными годами, а также выводами, которые я смог сделать с помощью своего образования. Играйте по моей системе и уже совсем скоро вы превратите азартную игру в стабильный доход!

Математические шансы на победу

Простой расчет с факториалами

Самыми распространенными в мире лотереями являются игры на везение типа «5 из 36» и «6 из 45». Рассчитаем шанс выигрыша в лотерее банально по теории вероятности.

Пример расчета возможности получения джекпота в лотерею «5 из 36»:

Необходимо число свободных ячеек поделить на количество возможных комбинаций. То есть первую цифру можно выбрать из 36, вторую – из 35, третью – из 34 и так далее.

Следовательно, вот формула:

Количество возможных комбинаций в лотерее типа «5 из 36» = (36*35*34*33*32) / (1*2*3*4*5) = 376 992

Шанс выигрыша составляет 1 к почти 400 000.

Давайте проделаем то же самое для лотереи типа «6 к 45».

Количество возможных комбинаций = «6 из 45» = (45*44*43*42*41*40) / (1*2*3*4*5*6) = 9 774 072.

Соответственно, шанс выигрыша составляет практически 1 к 10 млн.

Согласно давно уже известной теории у каждого шара в каждом следующем розыске есть абсолютно равный шанс выпасть по сравнению с другими.

Но не все так просто, даже согласно теории вероятности. Рассмотрим подробнее на примере подбрасывания монетки. Первый раз у нас выпал орел, тогда в следующий раз вероятность выпадения решки гораздо выше. Если орел выпал еще раз, то в следующий раз ожидаем решку с еще большей вероятностью.

С шарами, выходящими из лототронов, приблизительно та же история, но несколько сложнее и с более существенным количеством переменных. Если один шар выпал 3 раза, а другой – 10, то вероятность выпадения первого шара будет выше, чем у второго. Стоит отметить, что данный закон старательно нарушают организаторы некоторых лотерей, которые меняют лототроны время от времени. В каждом новом лототроне появляется новая последовательность.

Еще некоторые организаторы используют отдельный лототрон для каждого шара. Таким образом, необходимо рассчитывать вероятность выпадения каждого шара в каждом отдельном лототроне. Это с одной стороны немного облегчает задачу, с другой – усложняет.

Но это всего лишь теория вероятности, которая, как выяснилось, не очень-то и работает. Давайте посмотрим, какие есть секреты, основанные на сухой науке и статистических данных, накопленных за не одно десятилетие.

Почему не работает теория вероятности?

Первое, о чем стоит поговорить, — это калибровка лототронов. Ни один из лототронов не откалиброван идеально.

Второй нюанс – диаметры лотерейных шаров также не являются одинаковыми. Даже отличие на малейшие доли миллиметров играют роль в частоте выпадения того или иного шара.

Третья деталь – разный вес шаров. Опять же отличие может казаться вовсе не существенным, но оно также влияет на статистику, притом, значительно.

Если рассматривать статистику номеров, выигравших в лотерею типа «6 из 45», то можно заметить интересный факт: сумма цифр, на которые ставили игроки, колеблется между 126 и 167.

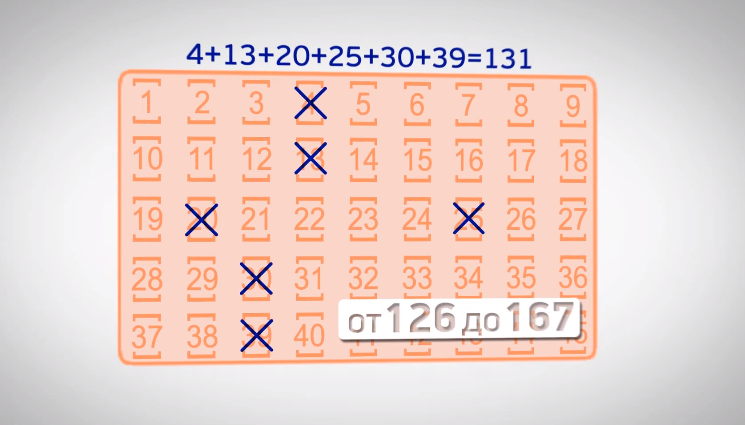
С суммой выигрышных лотерейных цифр для «5 из 36» немного другая история. Здесь выигрышные цифры составляют сумму в 83-106.

Как думаете, какие цифры чаще есть в выигрышных билетах? Четные? Нечетные? Скажу вам с полной уверенностью, что в лотереях «6 из 45» этих цифр поровну.

А вот как быть с «5 из 36»? Ведь нужно выбрать всего 5 шариков, четных и нечетных не может быть равное количество. Так вот. Проанализировав результаты розыгрышей лотерей данного типа четырех последних десятилетий, могу заявить, что незначительно, но все-таки чаще, в выигрышных комбинациях появляются нечетные цифры. Особенно, те, которые содержат в себе цифру 6 или 9. Например, 19, 29, 39, 69 и так далее.

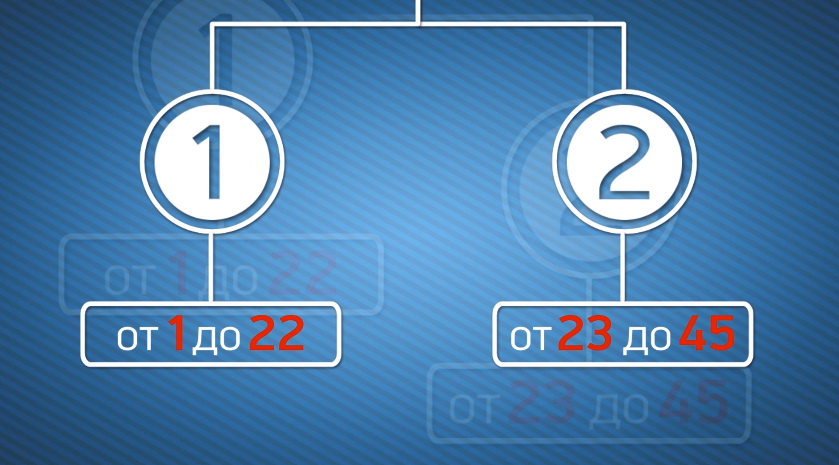
Для лотереи типа «6 к 45» числа условно делим на 2 группы – от 1 до 22 и от 23 до 45. Следует отметить, что в выигрышных билетах отношение чисел, принадлежащих к группе, 2 к 4. То есть либо в билете будет 2 числа из группы от 1 до 22 и 4 числа из группы от 23 до 45 либо наоборот (4 числа из первой группы и 2 из второй).

Я пришел к аналогичному выводу, анализируя статистику лотерей типа «5 из 36». Только в данном случае немного иначе дробятся группы. Давайте первой обозначим группы, в которую входят цифры от 1 до 17, а второй – ту, куда помещаются оставшиеся числа от 18 до 35. Отношение цифр из первой группы ко второй в выигрышных комбинациях в 48% случаем равно 3 к 2, а в 52% случаев – наоборот, 2 к 3.

Стоит ли ставить на цифры из прошедших розыгрышей?

Доказано, что в 86% случаев в новом розыгрыше повторяется число, которое уже было в предыдущих розыгрышах. Поэтому просто необходимо следить за розыгрышами интересующей вас лотереи.

Последовательные цифры. Выбирать или не выбирать?

Шанс на то, что выпадут сразу 3 последовательные цифры, очень низок, и составляет менее 0,09%. А если вы хотите поставить сразу на 5 или 6 последовательных чисел, шанса практически нет. Поэтому выбирайте разные цифры.

Числа с единым шагом: победа или проигрыш?

Не стоит ставить на числа, которые идут в единой последовательности. Например, однозначно не нужно выбирать шаг 2 и с этим шагом делать ставку. 10, 13, 16, 19, 22 – однозначно проигрышная комбинация.

Больше одного билета: да или нет?

Лучше играть раз в 10 недель по 10 билетам, чем раз в неделю по одному. А также играйте группами. Можно выиграть большой денежный приз и разделить его между несколькими людьми.

Статистика всемирных лотерей

Одна из самых популярных в мире лотерей проводилась по следующему принципу: необходимо выбрать 5 чисел из 56, а также 1 из 46 для так называемого золотого шара.

За 5 угаданных шаров и 1 верно названный золотой счастливчик получает джекпот.

Содержание статьи

Как рассчитать теорию вероятности в лотерее
Самые крупные выигрыши в лотереи в истории
Как выиграть в лотерею при помощи маятника

Теория и термины

В мире постоянно проводится множество лотерей с самыми различными правилами, условиями победы, призами, однако существуют общие принципы расчета вероятности выигрыша, которые можно адаптировать под условия той или иной конкретной лотереи. Но для начала желательно определиться с терминологией.

Итак, вероятность – это вычисленная оценка возможности того, что произойдет определенное событие, которая чаще всего выражается в форме отношения числа желаемых событий к общему числу исходов. Например, вероятность выпадения «орла» при подбрасывании монетки – один к двум.

Исходя из этого, очевидно, что вероятность выигрыша – это соотношение количества выигрышных комбинаций к числу всех возможных. Однако нельзя забывать, что критерии и определения понятия «выигрыш» тоже могут быть разными. К примеру, в большинстве лотерей используется такое определение как «класс выигрыша». Требования к выигрышу третьего класса ниже, чем к выигрышу первого, поэтому вероятность выигрыша первого класса самая низкая. Как правило, таким выигрышем является джек-пот.

Еще один значимый момент в расчетах заключается в том, что вероятность двух связанных событий вычисляется путем перемножения вероятностей каждого из них. Проще говоря, если вы подбросите монетку два раза, то вероятность выпадения «орла» каждый раз будет равна один к двум, но шанс, что «орел» выпадет оба раза, составит лишь один к четырем. В случае с тремя подбрасываниями шанс вообще упадет до одного к восьми.

Расчет шансов

Таким образом, для расчета шанса выигрыша джек-пота в абстрактной лотерее, где нужно верно угадать несколько выпавших значений из определенного числа шаров (например, 6 из 36), нужно рассчитать вероятность выпадения каждого из шести шаров и перемножить их между собой. Учтите, что с уменьшением числа шаров, оставшихся в барабане, вероятность выпадения нужного шара меняется. Если для первого шара вероятность того, что выпадет нужный, равна 6 к 36, то есть, 1 к 6, то для второго шанс составит 5 к 35 и так далее. В данном примере вероятность того, что билет окажется выигрышным составит 6x5x4x3x2x1 к 36x35x34x33x32x31, то есть 720 к 1402410240, что будет равно 1 к 1947792.

Несмотря на такие пугающие числа, люди регулярно выигрывают в лотереи по всему миру. Не забывайте, что даже если вы не возьмете главный приз, существуют еще выигрыши второго и третьего классов, вероятность получить которые намного выше. Кроме того, очевидно, что наилучшей стратегией является покупка нескольких билетов одного тиража, так как каждый дополнительный билет кратно увеличивает ваши шансы. Например, если купить не один билет, а два, то и вероятность победы будет в два раза больше: два из 1,95 миллиона, то есть примерно 1 к 950 тысячам.

Вероятность или шанс угадать комбинацию, развёрнутую ставку, группу чисел —
в зависимости от количества выбранных номеров, для лотерей 5 из 36, 6 из 45, 7 из 49, 6 из 49, 4 из 20, Рапидо —
смотрим по этой ссылке

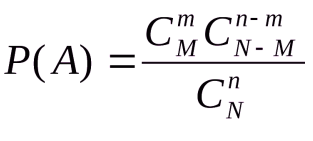
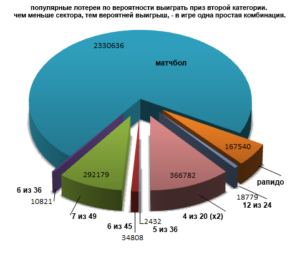
Вероятности в популярных лотереях

5 из 36, 6 из 45, 7 из 49, 6 из 36, 4 из 20, Матчбол, Рапидо

На этом графике хорошо видно количество комбинаций. Чем меньше сектора,
тем вероятней джек пот, на одну простую комбинацию.

В лотереях 5 из 36 и Рапидо самое малое количество комбинаций — практически не видно на фоне остальных. Если учитывать призовой фонд, то в лотереях Рапидо, 4 из 20, — он самый большой (67% призового фонда), следовательно, выигрыши в низших категория будут чаще, если это можно назвать «выигрышем»… — на дистанции «слив» всё равно обеспечен, если, конечно, не «словится» суперприз! Тем не менее, чем больше возврат при длительной игре, тем больше можно ставить комбинаций, тем вероятней суперприз.

По вероятности выиграть суперприз, лотерея 5 из 36 считается лучшей из всех (без дополнительного), — сейчас «приз», который может достигать десятков миллионов. Далее по популярности у игроков следует лотерея 6 из 45, в которой шансы 1 на 8 миллионов комбинаций.
Лотерея 6 из 45 отличается ещё от остальных неплохой выплатой за приз второй категории, по такому параметру (вероятность-выплата)

Сравним популярные лотереи по вероятности выиграть приз второй категории.
Чем меньше сектора, тем вероятней выигрыш, — в игре одна простая комбинация.

При выборе лотереи желательно учитывать потенциальную выплату за приз второй категории, угадать который более реально. Для этого нужно просмотреть выплаты на сайте лотерей. Вероятность второй категории лучше не превышать 1: 100 000. В этом плане, например, лотереи 7 из 49 и 4 из 20 выглядят не очень привлекательно, у них вероятность второй категории практически сравнима с первой категорией приза лотереи 5 из 36 (1: 376 992). В какую лотерею играть, решает каждый сам!

Найти зависимость/вывести формулу среди ряда чисел

Как найти формулу, чтобы можно было на график вывести зависимость
У меня есть кофицент который меняется со временем его ставлю на На хочу видеть зависимость.

вывести формулу для ряда чисел
Вывести формулу для ряда чисел: 0, 1, 1, 6, 6, 15, 15, 28, 28, 44, 44, и т.д

Найти среди ряда чисел наименьшее и все остальные уменьшить на 1
4. Ввести с клавиатуры N чисел (N также вводится с клавиатуры). Найти среди них наименьшее; все.

Сообщение от _Murchik_

Могу для начала предложить упростить задание,
здесь опущены первые числа, ибо они дублируются
вторыми числами. В этом ряде уже не сами числа, а
степени числа 2.

1 2 1 || 2 3 1 || 2 3 2 || 3 4 1 || 2 3 2 || 3 4 2 || 3 4 3 || 4 5 1 || 2 3 2 || 3 4 2 || 3 4 3 || 4 5 2 || 3 4 3

Имеем
2 2 4 2 || 4 4 8 2 || 4 4 8 4 || 8 8 16 2 || 4 4 8 4 || 8 8 16 4 || 8 8 16 8 || 16 16 32 2 || 4 4 8 4 || 8 8 16 4 || 8 8 16 8 || 16 16 32 4 || 8 8 16 8
Если рассмотреть неразбитую последовательность
2 2 4 2 4 4 8 2 4 4 8 4 8 8 16 2 4 4 8 4 8 8 16 4 8 8 16 8 16 16 32 2 4 4 8 4 8 8 16 4 8 8 16 8 16 16 32 4 8 8 16 8
, то можно увидеть закономерность
2 (+) 2 (=) 4,
следующее число 2 — непонятно из каких соображений берется, но получаем
2 (в уме умножаем на 2 =) 4 (+) 4 (=) 8
следующее число 2 — непонятно из каких соображений берется, но получаем
2 (в уме умножаем на 2 =) 4 (+) 4 (=) 8
следующее число 4 — непонятно из каких соображений берется, но получаем
4 (в уме умножаем на 2 =) 8 (+) 8 (=)16
.
8 (в уме умножаем на 2 =) 16 (+) 16 (=) 32
4 (в уме умножаем на 2 =) 8 (+) 8 (=)16
Возможно, правильнее разделить исходную последовательность так (по крайней мере выглядит непротиворечиво)
2 2 4 || 2 4 4 8 || 2 4 4 8|| 4 8 8 16|| 2 4 4 8|| 4 8 8 16|| 4 8 8 16|| 8 16 16 32|| 2 4 4 8|| 4 8 8 16|| 4 8 8 16|| 8 16 16 32|| 4 8 8 16|| 8 16 16 32;

Добавлено через 8 минут
Другими словами, каждый четвертый член выбирается непонятно как, два следующих равны его удвоенному значению, а третий равен их сумме.

Лучший ответ

Сообщение было отмечено _Murchik_ как решение

Решение

Непонятно что значит найти закон…
Закон это функция от порядкового номера комбинации?
Функция от знания значения некого элемента найти другие?
Похоже ТС фиолетово =).
Если отбросить все первые элементы, убрать дубли, отсортировать то остается такое:
2,3,4 эл.

2 4 2
4 8 2
4 8 4
8 16 2
8 16 4
8 16 8
16 32 2
16 32 4
Это значит невозможно определить 4 элемент для всех.

Значит, остается варианты:
1)использовать значения прошлых илии следующих элементов.
2)функция рендомно выбирает из возможных
4 элемента ABCD
Задать A.
B=A
C=A+A
D=выбрать из
Если A=2 то 2
Если A=4 или 16 то случайно из 2,4.
Если A=8 то случайно из 2,4,8.

3)Сделать функцию от порядкового номера комбинации.
Можно через полином или тригонометрический ряд Фурье или просто список case даст
номер комбинации – значение 4 элемента.

2 эл. R
3 эл. G
4 эл. B
Полином почему то 12 степени фиолетовый.

Возможно закономерность в последовательности все-таки есть
2 (+) 2 (=) 4 — четверка на третьей позиции встречается 1 раз, значит далее ставится двойка
2 (в уме умножаем на 2 =) 4 (+) 4 (=) 8 Восьмерка на третьей позиции встречается 1 раз, 2 1 2 (в уме умножаем на 2 =) 4 (+) 4 (=) 8. Восьмерка на третьей позиции встречается 2 раза, 2 2 < 8 значит далее ставится четверка
4 (в уме умножаем на 2 =) 8 (+) 8 (=)16. Шестнадцать на третьей позиции встречается 1 раз, 2 1 2 (в уме умножаем на 2 =) 4 (+) 4 (=) 8 Восьмерка на третьей позиции встречается 3 раза, 2 2 >= 8 значит далее ставится 8/2 = 4
.
4 (в уме умножаем на 2 =) 8 (+) 8 (=)16 Шестнадцать на третьей позиции встречается 6 раз, 2 6 >= 16 значит далее ставится 16/2=8
Далее можно попытаться экстраполировать данный ряд
8 (в уме умножаем на 2 =) 16 (+) 16 (=) 32. Тридцать два на третьей позиции встречается 3 раза, 2 3 .
2 2 4 || 2 4 4 8 || 2 4 4 8|| 4 8 8 16|| 2 4 4 8|| 4 8 8 16|| 4 8 8 16|| 8 16 16 32|| 2 4 4 8|| 4 8 8 16|| 4 8 8 16|| 8 16 16 32|| 4 8 8 16|| 8 16 16 32 || 8 16 16 32 || 16 32 32 64 || 2 4 4 8 .

Что такое зависимость чисел

ну с натуральным рядом вы погорячились) Он с 1 начинается. Вы когда перекличку на физре делаете, вы с 0 начинаете?)

y =a*x^n + b*x^(n-1) +..+m*x^2+z

нахождение a,b,c. зю. сводится к решению системы уравнений. Подумайте сами как.
По заданым n координатам напишите n СЛАУ. Решите. Ваша формула будет в итоге описывать каждое число которое вы ввели. Будет многочлен n-ой степени. Если вы математический гений, круче перельмана, то сможете данный многочлен P(x) Маклорена, сложить в конечную функцию))) Что наврядли.

1,2,3,4,5,6,7. Думаете это ряд типа Sn=n? А вот и нет, я щас захочу и введу где нибудь после семерки, допустим двойку.

Поэтому ряд нужно задавать в явном виде.

Например, надо ставить программу для определения зависимости в каком то числовом ряде используя уравнение y = a*x^3+b*x^2+c*x+d, что означает подбор значений a,b,c,d в соответствии со значениями
x — номер расположения числа в ряду
y — значение функции для данного x при найденных a,b,c,d

y = a*x^3+b*x^2+c*x+d

Эта формула будет справедлива только для первых 4 чисел вашей последовательности.
Смотри пример в лоб.
1, 4, 11, 2, 9.
Ищем формулу задающую данную последовательность
1=a*n1^4+b*n1^3+c*n1^2+d*n1+e
4=a*n2^4+b*n2^3+c*n2^2+d*n2+e
11=a*n3^4+b*n3^3+c*n3^2+d*n3+e
.
9=a*n5^4+b*n5^3+c*n5^2+d*n5+e

Где ni — натуральный ряд(1,2,3,4,5). те n1=1, n2=2,n3=3.
Решите слау и получите коэффициенты a,b,c,d,e для вашего уравнения.

это был вопрос? изо скажите честно, вы просто тупо пропустили мой ответ?

Где ni — натуральный ряд(1,2,3,4,5). те n1=1, n2=2,n3=3.
Решите слау и получите коэффициенты a,b,c,d,e для вашего уравнения.

Предполагается что в заданном ряде чисел точно имеется зависимость, а мы её определяем. Можно найти зависимость не только на первых четырех 4 чисел, но и для любых других четырёх чисел. Не надо изначально рассматривать хаотичные ряды чисел. Напрмер, уравнение параболы можно найти по трех любым точкам, принадлежащим этой параболе.

1)Если вы про школьную параболу, то такая парабола непрерывна и определена на всех Х, и так же существует ее рациональные и иррациональные значения.
2)A(1,1), B(2,2), C(3,3) — напишите мне уравнение параболы(нет такой параболы которая показывала бы распределение натуральных чисел на ней.)
3)А(1,2), В(2,3), С(3,2.99) — и вот это тоже
4)Ряд — это явно заданная последовательность н-ных частичный сумм.
Никогда ряд не задается 5-10 числами!
Пройдете это на первому курсе, а так же, что делить на ноль можно, и корень из отриц. числа тоже извлекаем. просто не забегайте вперед.

Уважаемый MyLastHit прошу Вас определить простейшую зависимость в ряде чисел 0, 3, 15, 42, 90, 165, 273, 420.
Эта зависимость точно сушествует и не имеет такие крайние исключения, которые Вы указываете, типа A(1,1), B(2,2), C(3,3) не парабола и на 0 можно делить (непонятно зачем Вы об этом говорите).
Указанная бесконечность не ограничивается . 5-10 числами. — она бесконечна и реально существует, только требуется определить зависимость y = a1*x^n + a2*x^m + a3*x^p + a4*x^t +. составив соответствующую программу для определения степеней n,m,p,t.
и a1,a2,a3,a4. при x,y — переменных. Убедительная просьба не отвлекаться на демонстрацию Ваших глубоких познаний в математике и на убеждения меня в том, что я тупой.

Убедительная просьба не отвлекаться на демонстрацию Ваших глубоких познаний в математике и на убеждения меня в том, что я тупой.

Я не говорю ничего подобного вам. Может я не так выражаюсь, но если вы знаете что такое много член тейлора/маклорена или просто многочлен n-ой степени, то смотрите то что я вам уже написал http://programmersforum.ru/showpost. 71&postcount=5. Ну поймите Вы, что допустим вы вводите и считываете с клавиатуры 1,2,3,4,5 и всё.
Программа дальше сама должна понять что это An=n? Вдруг это на самом деле последовательность задана например An=[n*0.1]+n? Эта формула тоже верна, но распределение чисел будет таково:
1,2,3,4,5,6,7,8,9,11,12,13,14,15,16,17,18,19,22,24.
И это только один из вариантов множества формул.

Я ещё раз попробую объяснить, чего я хочу добиться.
Имеется два ряда чисел:
y = 0, 3, 15, 42, 90, 165, 273, 420. ;
x = 0, 1, 2, 3, 4, 5, 6, 7, 8. ;
необходимо найти зависимость между x и y имеющуюю вид:
y = a1*x^n + a2*x^m + a3*x^p + a4*x^t +. составив соответствующую программу для определения степеней n,m,p,t.
и a1,a2,a3,a4.
Обычным способом определена искомая зависимость
y = x^3 + (3/2)*x^2 + (1/2)*x, то есть определены
n = 3
m = 2
p = 1

a1 = 1, a2 = 3/2, a3 = 1/2
Задача такая: Как с помощью программы определять n,m,p,t.
и a1,a2,a3,a4.