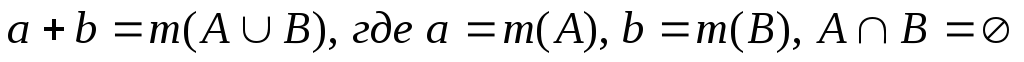Формулы сокращённого умножения. Неполный квадрат суммы и разности

Сумма квадратов и квадрат суммы

Выражение (a + b) 2 – это квадрат суммы чисел a и b. По определению степени выражение (a + b) 2 представляет собой произведение двух многочленов (a + b)(a + b). Следовательно, из квадрата суммы мы можем сделать выводы, что

т. е. квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Из правила следует, что общая формула квадрата суммы, без промежуточных преобразований, будет выглядеть так:

Многочлен a 2 + 2ab + b 2 называется разложением квадрата суммы.

Так как a и b обозначают любые числа или выражения, то правило даёт нам возможность сокращённым путём возводить в квадрат любое выражение, которое может быть рассмотрено как сумма двух слагаемых.

Пример. Возвести в квадрат выражение 3x 2 + 2xy.

Решение: чтобы не производить дополнительных преобразований, воспользуемся формулой квадрата суммы. У нас должна получиться сумма квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

Теперь, пользуясь правилами умножения и возведения в степень одночленов, упростим получившееся выражение:

Квадрат разности

Выражение (a – b) 2 – это квадрат разности чисел a и b. Выражение (a – b) 2 представляет собой произведение двух многочленов (a – b)(a – b). Следовательно, из квадрата разности мы можем сделать выводы, что

т. е. квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Из правила следует, что общая формула квадрата разности, без промежуточных преобразований, будет выглядеть так:

Многочлен a 2 – 2ab + b 2 называется разложением квадрата разности.

Это правило применяется к сокращённому возведению в квадрат выражений, которые могут быть представлены как разность двух чисел.

Пример. Представьте квадрат разности в виде трёхчлена:

Решение: используя формулу квадрата разности, находим:

Теперь преобразуем выражение в многочлен стандартного вида:

Разность квадратов

Выражение a 2 – b 2 – это разность квадратов чисел a и b. Выражение a 2 – b 2 представляет собой сокращённый способ умножения суммы двух чисел на их разность:

т. е. произведение суммы двух чисел на их разность равно разности квадратов этих чисел.

Из правила следует, что общая формула разности квадратов выглядит так:

Это правило применяется к сокращённому умножению таких выражений, которые могут быть представлены: одно – как сумма двух чисел, а другое – как разность тех же чисел.

Пример. Преобразуйте произведение в двучлен:

(5a 2 + 3)(5a 2 – 3) = (5a 2 ) 2 – 3 2 = 25a 4 – 9

В примере мы применили формулу разности квадратов справа налево, то есть, нам дана была правая часть формулы, а мы преобразовали её в левую:

На практике все три рассмотренные формулы применяются и слева направо, и справа налево, в зависимости от ситуации.

Докажем, что при любых значениях a и b верно равенство

( a + b ) 2 = a 2 + b 2 + 2 a b

или ( a + b ) 2 = a 2 + 2 a b + b 2 .

( a + b ) 2 = ( a + b ) ( a + b ) = a 2 + a b + a b + b 2 = a 2 + b 2 + 2 a b .

Если в эту формулу вместо a и b подставить какие-нибудь выражения,
то опять получится тождество.

Квадрат суммы двух выражений равен сумме квадратов этих выражений
плюс удвоенное произведение первого и второго выражений.

Докажем, что при любых значениях a и b верно равенство

( a − b ) 2 = a 2 + b 2 − 2 a b

или ( a − b ) 2 = a 2 − 2 a b + b 2 .

( a − b ) 2 = ( a − b ) ( a − b ) = a 2 − a b − a b + b 2 = a 2 + b 2 − 2 a b .

Квадрат разности двух выражений равен сумме квадратов этих выражений
минус удвоенное произведение первого и второго выражений.

1) = d 4 + 9 c 2 − 6 c d 2

2) = 3 c 2 + d 4 − 6 c d 2

3) = 3 c 2 + d 4 + 6 c d 2 Неверно. Не кликай на пустое поле. ( 0 , 2 a − 0 , 3 ) 2 =

1) = 0 , 04 a 2 − 0 , 12 a + 0 , 09

2) = 0 , 4 a 2 − 1 , 2 a + 0 , 9

3) = 0 , 4 a 2 − 0 , 12 a + 0 , 9 Неверно. Неверно. Неверно. Не кликай на пустое поле. (

x 4 + 2 x 2 y 3 + y 6

3) = y 6 + x 2 y 3 +

x 4 Неверно. Неверно. Неверно. Не кликай на пустое поле. Неверно. Неверно. (

Формулы сокращённого умножения

При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.

Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.

a 2 + b 2 = (a + b) 2 — 2ab — сумма квадратов;

a 2 — b 2 = (a + b)(a — b) — разность квадратов;

(a + b) 2 = a 2 + 2ab + b 2 — квадрат суммы;

(a — b) 2 = a 2 — 2ab + b 2 — квадрат разности;

a 3 + b 3 = (a + b)(a 2 — ab + b 2 ) — сумма кубов;

a 3 — b 3 = (a — b)(a 2 + ab + b 2 ) — разность кубов;

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 — куб суммы;

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3 — куб разности.

Обратите внимание, что a и b в формулах сокращённого умножения могут быть как числами, так и выражениями.

Разложение формул сокращенного умножения

Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.

Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:

a 2 + b 2 = (a + b) 2 — 2ab.

Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b) 2 — 2ab = (a + b)(a + b) — 2ab = a 2 + ab + ab + b 2 — 2ab = a 2 + b 2 .

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:

a 2 — b 2 = (a + b)(a — b).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)(a — b) = a 2 — ab + ab — b 2 = a 2 — b 2 .

Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

(a + b) 2 = a 2 + 2ab + b 2 .

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a + b) 2 = (a + b)(a + b) = a 2 + ab + ab + b 2 = a 2 + 2ab + b 2 .

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:

(a — b) 2 = a 2 — 2ab + b 2 .

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b) 2 = (a — b)(a — b) = a 2 — ab — ab + b 2 = a 2 — 2ab + b 2 .

Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:

a 3 + b 3 = (a + b)(a 2 — ab + b 2 ).

(a + b)(a 2 — ab + b 2 ) = a 3 — a 2 b + ab 2 + a 2 b — ab 2 + b 3 = a 3 + b 3 .

Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:

a 3 — b 3 = (a — b)(a 2 + ab + b 2 ).

(a — b)(a 2 + ab + b 2 ) = a 3 + a 2 b + ab 2 — a 2 b — ab 2 — b 3 = a 3 — b 3 .

Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 .

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a + b) 3 = (a + b)(a + b) 2 = (a + b)(a 2 + 2ab + b 2 ) = a 3 + 2a 2 b + ab 2 + a 2 b + 2ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3 .

Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3 .

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b) 3 = (a — b)(a — b) 2 = (a — b)(a 2 — 2ab + b 2 ) = a 3 — 2a 2 b + ab 2 — a 2 b + 2ab 2 — b 3 = a 3 — 3a 2 b + 3ab 2 — b 3 .

Неполный квадрат суммы

a 2 + 2ab + b 2

это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:

a 2 + ab + b 2 ,

которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.

Неполный квадрат разности

a 2 — 2ab + b 2

это квадрат разности, который также называется полным квадратом разности относительно выражения:

a 2 — ab + b 2 ,

которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.

Сокращенное умножение: правила, формулы

Знакомство с сокращенным умножением начинается впервые в седьмом классе. Тема непростая: нужно выучить наизусть много формул. Но зато вы сможете быстрее решать задачки без ошибок. Проверим?

О чем эта статья:

Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

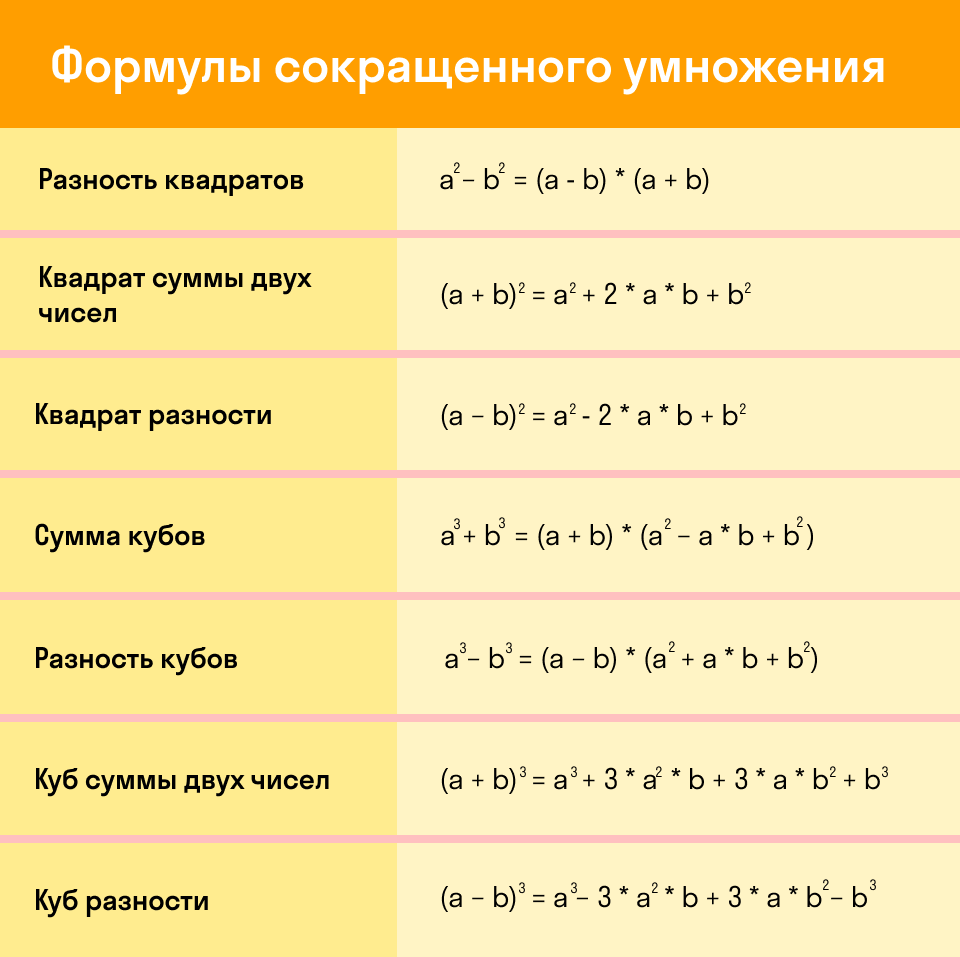
Формулы сокращенного умножения

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

Разность квадратов двух выражений равна произведению их разности и их суммы.
Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.

Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.

Доказательство формул сокращенного умножения

Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a 2 — b 2 = (a — b) * (a + b).

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a 2 — b 2 .

Важно знать, что разность квадратов не равна квадрату разности: a 2 — b 2 ≠ (a — b) 2 .

Докажем, что a 2 — b 2 = (a — b) * (a + b).

a 2 — b 2 = a 2 — b 2 + ab — ab

(a 2 — a * b) + (a * b — b 2 ) = a *(a — b) + b *(a — b)

Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
Результат доказательства: a 2 — b 2 = (a — b) * (a + b)
Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a 2 — b 2 , нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a 2 — b 2 .

Остальные ФСУ можно доказать аналогичным методом.

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).

Для четных показателей можно записать так:

a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).

Для нечетных показателей:

a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Что сделать: вычислить квадрат произведения (55 + 10) 2 .

Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с 3 – 8.

Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).

Задание 3

Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).

Как решаем:

Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y 2 + 7 * y * x — 7 * y * x — x 2 = 49 * y 2 — x 2 .
Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y) 2 — x 2 = 49 * y 2 — x 2 .

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей

Формулы сокращенного умножения и другие полезные алгебраические тождества

a^2-b^2=(a-b)(a+b)

1) Разность квадратов

a^2+2ab+b^2=(a+b)^2

2) Квадрат суммы

a^2-2ab+b^2=(a-b)^2

3) Квадрат разности

a^3+b^3=(a+b)(a^2-ab+b^2)

4) Сумма кубов

a^3-b^3=(a-b)(a^2+ab+b^2)

5) Разность кубов

Комментарий репетитора по математике:
Перед вами базовый школьный комплект формул, изучаемый в 7 классе по всем программам. Наибольшая доля задач в учебниках приходится на применение первых трех формул.
Трехчлены и называются неполными квадратами суммы и разности соответственно

Из методики репетитора по заучиванию названий: Примите к сведению, что названия всех формул даются по самой короткой их части. Например, в формуле разность квадратов это левая часть, а в формуле квадрат суммы — правая. В начале названия формулы указывается последнее действие в этой короткой части. Например, в формуле разность квадратов -это разность, а в формуле квадрат суммы — это квадрат.

Дополнительные формулы, изучаемые в математических классах:

(a+b)^3=a^3+3a^2b+3ab^2+b^3

6) Куб суммы

(a-b)^3=a^3-3a^2b+3ab^2-b^3

7) Куб разности

(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc

Квадрат суммы трех чисел

Комментарий репетитора по математике: Если в последней формуле поставить знак минус, например перед b или c (или сразу оба знака), то в правой части знак минус появится перед тем удвоенным произведением, которое эту букву содержит (или два минуса дадут снова плюс).

Другие полезные алгебраические тождества:

a^2+b^2=(a+b)^2-2ab

выражение суммы квадратов двух чисел через их сумму

a^2+b^2=(a-b)^2+2ab

выражение суммы квадратов двух чисел через их разность

Комментарий репетитора по математике: Эти тождества часто используются составителями конкурсных задач по математике (в том числе и на ЕГЭ) для того, чтобы замаскировать в уравнениях и неравенствах замену переменной. Если в вашем задании присутствует сумма квадратов двух выражений попробуйте перейти к сумме или к разности.

(a+b)^n=C_n^0a^n + C_n^1a^<n-1>
Бином Ньютона b + C_n^2a^b^2+. +C_n^ka^b^k+. +C_n^nb^n» />
<img decoding= (n) (1) (2) (3) (4) (5) (6) (7) (S_1) (1) (3) (6) (10) (15) (21) (28) (S_2) (1) (5) (14) (30) (55) (91) (140) (S_2/S_1) (1) (5/3) (7/3) (3) (11/3) (13/3) (5)

Теперь нетрудно заметить закономерность: с увеличением (n) на 1 частное увеличивается на (2/3), то есть это частное равно ((2n+1)/3). Вместе с формулой для суммы (1+2+ldots+n) это дает (гипотетический) ответ

С суммами кубов дело обстоит даже проще, чем с квадратами — глядя на таблицу естественно предположить, что (S_3=S_1^2), то есть

Заметно сложнее угадать формулу для суммы четвертых степеней. В отличие от предыдущих случаев, у (S_4(n)) практически не видно общих делителей с (S_1(n)) (кроме двойки). Зато можно заметить, что 14 и 98 делятся на 7, 55 и 979 — на 11. Посмотрим на отношение (S_4/S_2):

(n)	(1)	(2)	(3)	(4)	(5)	(6)
(S_2)	(1)	(5)	(14)	(30)	(55)	(91)
(S_4)	(1)	(17)	(98)	(354)	(979)	(2275)
(S_4/S_2)	(1)	(17/5)	(7)	(59/5)	(89/5)	(25)

Видно, что после домножения этого отношения на 5 получится последовательность целых чисел: 5, 17, 35, 59, 89, 125. Тут уже нельзя сказать, что разность соседних чисел неизменна. Но если выписать эти разности: 12, 18, 24, 30. то закономерность сразу становится видной!

Таким образом, гипотеза состоит в том, что

Итак, стало понятно, какие должны быть ответы, но как их доказать?

И что вообще значит, что какое-то выражение (P(n)) дает формулу для суммы (1^2+ldots+n^2)?

Это значит, что (P(1)=1), (P(2)=P(1)+2^2), . (P(n)=P(n-1)+n^2). То есть все сводится к быть может утомительному, но прямолинейному вычислению:

Аналогичным образом (говоря формально — по индукции) можно доказать найденные выше формулы для (S_3(n)) и (S_4(n)).

Послесловие

Геометрическое доказательство формулы

Геометрическое доказательство формулы для суммы (1+2+ldots+n)

Видимо наиболее наглядный способ вычислить сумму (1+2+ldots+n) — геометрический: об этой сумме можно думать как о треугольном числе, то есть площади «пиксельного» (составленного из единичных квадратиков) равнобедренного прямоугольного «треугольника» со стороной (n). Из двух таких треугольников легко составить прямоугольник размера (ntimes(n+1)), откуда и получается ответ (n(n+1)/2) (половина площади прямоугольника).

Пирамидка, составленная из квадратов

Пирамидка, составленная из квадратов со стороной (1), (2), …, (n)

Подобным образом можно вычислить и сумму (1^2+2^2+ldots+n^2): ее можно проинтерпретировать как объем пирамиды из кубиков (нижний слой которой состоит из (n^2) кубиков, следующий — из ((n-1)^2) кубиков и т. д.), после чего сложить из шести таких пирамид параллелепипед (ntimes(n+1)times(2n+1)). Как это сделать, можно посмотреть на сайте «Математические этюды».

Есть геометрические доказательства и у позволяющего вычислить сумму кубов замечательного равенства (1^3+2^3+ldots+n^3=(1+2+ldots+n)^2). Одно из них можно посмотреть на youtube-канале Think Twice, см. также подборку «доказательств без слов» в «Кванте» №11 за 2017 год.

Заметим, однако, что формула для суммы четвертых степеней не раскладывается (в отличие от предыдущих) на простые линейные множители. Видимо из-за этого ее не получается найти методами геометрического суммирования и открыта она была примерно на 1000 лет позже, чем формула для суммы кубов (известная уже в античности).

Чтобы продвинуться дальше, полезно задуматься, что мы вообще надеемся увидеть в качестве ответа. Не любое алгебраическое выражение можно разложить на достаточно простые множители, но всегда можно, наоборот, раскрыть все скобки и привести подобные. В изученных нами случаях получаются следующие многочлены от (n):

Практически сразу возникает гипотеза, что вообще для любого (k) сумма (1^k+2^k+ldots+n^k) равна многочлену от (n), который начинается с (frac1n^) (в этом выражении изучавшие математический анализ сразу узнают первообразную того, что мы суммируем), дальше идет (frac12n^k) и члены еще меньших степеней.

С алгебраической точки зрения это очень естественный переход — но самого языка алгебры, «выражений с буквами» и преобразования таких выражений, не существовало до работ Франсуа Виета (конца XVI века)! А до появления такого языка описанную выше гипотезу практически невозможно не то что доказать — сформулировать.

В первой половине XVII века Иоганн Фаульхабер смог найти формулы для сумм (1^k+2^k+ldots+n^k) до (k=17) (интересную попытку реконструкции рассуждений Фаульхабера опубликовал Дональд Кнут). Вот несколько из таких формул:

Коэффициенты при (n^) и при (n^) обсуждались выше. Подумав некоторое время вы наверняка угадаете формулу для коэффициентов при (n^) и (n^), а быть может, — и для коэффициента при (n^).

Страница из книги «Ars Conjectandi» Якова Бернулли

Возникает надежда на общую (работающую для произвольного (k)) формулу для (S_k(n)). И такую формулу нашел в конце XVII века Якоб Бернулли. В нее входит последовательность так называемых чисел Бернулли ((B^0=1), (B^1=1/2), (B^2=1/6), . ), а саму формулу можно записать символически очень коротко:

Понимать эту запись следует следующим образом. Нужно раскрыть формально в выражении ((n+B)^) скобки, после чего начать воспринимать (B^m) не как степень переменной (B), а как (m)-е число Бернулли. Например:

Если поверить в эту (крайне странную, на первый взгляд) процедуру, то будет ясно и как вычислять числа Бернулли: при подстановке (n=1) получается равенство (1=frac-B^>), позволяющее найти (B^k), если числа Бернулли с меньшими номерами уже известны. В таблице ниже приведены несколько первых чисел Бернулли.

(m)	(0)	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)
(B^m)	(1)	(frac12)	(frac16)	(0)	(-frac1)	(0)	(frac1)	(0)	(-frac1)	(0)	(frac5)	(0)	(-frac)	(0)	(frac76)

Замечательным образом те же самые числа Бернулли возникают и в квадратурных формулах для вычисления приближенных значений интегралов, и при вычислении бесконечных сумм типа (1+frac14+frac19+frac1+ldots=frac6) (то есть значений знаменитой дзета-функции), и в комбинаторике, и в теории чисел, и в топологии.

Литература по теме:
1) Д. Пойа. Математика и правдоподобные рассуждения (М.: Наука, 1975). — Мало где можно прочитать не о конкретной области математики, а о том, как вообще решать новую для себя математическую задачу. Подсказки и решение выше по существу следуют главе 7 этой замечательной книги.
2) Интервью с академиком И. М. Гельфандом // Квант, 1989, № 1, стр. 3–12. — В приведенном выше решении сделана попытка объяснить, как некоторые формулы для сумм степеней мог бы искать любой человек. Интересующимся математикой может быть интересно прочитать, как такую задачу решал в школьные годы один из выдающихся математиков XX века (собственно про это — небольшой фрагмент на стр. 8–9, но все интервью интересное).
3) В. С. Абрамович. Суммы одинаковых степеней натуральных чисел // Квант, 1973, № 5, стр. 22–25. — Можно прочитать доказательство формулы для суммы степеней (из конца послесловия), использующее, по сути, только бином Ньютона.
4) Г. А. Мерзон. Алгебра, геометрия и анализ сумм степеней последовательных чисел // Математическое просвещение, сер. 3, вып. 21 (2017), стр. 104–118. — Подробная статья о разных взглядах на задачу о суммировании степеней.
5) Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика (М.: Мир, 1998). — В учебнике, написанном по лекциям знаменитого Дональда Кнута, обсуждается и задача о суммировании степеней, и числа Бернулли.

Таблица формул сокращенного умножения 👍🐱‍💻

Таблица формул сокращенного умножения - www.studik.kiev.ua

Формулы сокращённого умножения используются для возведения чисел в степень, а также умножения этих чисел и различных выражений. Не редко такие формулы сокращающего умножения помогают вычислять примеры быстрее и компактней.

Нас ищут по таким запросам:

Квадрат суммы;
Формулы сокращённого умножения примеры;
Все формулы сокращённого умножения;
Формулы сокращённого умножения видео;
Как быстро выучить формулы сокращённого умножения;
Задание на формулы сокращённого умножения;
Задание на формулы сокращённого умножения ВНО;
Алгебра 7 класс формулы сокращённого умножения;
Теорема Виета;
Табличка сокращённого умножения;
Тригонометрические формулы.

В этой статье рассмотрим самые популярные формулы сокращённого умножения. Затем сгруппируем формулы в табличку и рассмотрим некоторые примеры использования формул сокращающего умножения.

Таблица №1. Примеры использования формул сокращающего умножения для 7 класса

Как сократить формулы сокращённого умножения?

Квадрат суммы двух чисел:

В алгебре приведение целого выражения к стандартному виду многочлена осуществляется с помощью формул сокращённого умножения.

(a+b) 2 =(a+b)(a+b)=a 2 +2ab+b 2 =a 2 +ab+ab+b 2 =a 2 +2ab+b 2 (квадрат суммы двух чисел)

Выражение (a+b) 2 — это квадрат суммы чисел a и b. По определению степени выражение (a+b) 2 представляет собой произведение двух многочленов (a+b)(a+b). Следовательно, из квадрата суммы мы можем сделать выводы, что

Многочлен a 2 +2ab+b 2 называется разложением квадрата суммы.

Пример. Возвести в квадрат выражение 3x 2 +2xy.

Решение: для того чтобы нам не производить лишних преобразований, воспользуемся формулой квадрата суммы двух чисел. У нас должна получиться сумма квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

А сейчас, используя правило умножения и возведения в степень одночленов, упростим это выражение:

Квадрат разности двух чисел:

(a — b) 2 = a 2 — 2ab + b 2 (квадрат разности двух чисел)

Выражение (a—b) 2 — это квадрат разности чисел a и b. Выражение (a—b) 2 представляет собой произведение двух многочленов (a—b)(a—b). Следовательно, из квадрата разности мы можем сделать выводы, что

Многочлен a 2 -2ab+b 2 называется разложением квадрата разности.

Пример. Представьте квадрат разности двух чисел в виде трёхчлена:

Решение: используя формулу квадрата разности двух чисел находим:

Теперь преобразуем выражение в многочлен стандартного вида:

Разность квадратов двух чисел

a 2 -b 2 =(a+b)(a-b) (разность квадратов двух чисел)

Выражение a 2 —b 2 — это разность квадратов чисел a и b. Выражение a 2 —b 2 представляет собой сокращённый способ умножения суммы двух чисел на их разность:

т. е. произведение суммы двух чисел на их разность равно разности квадратов этих чисел.

Из правила следует, что общая формула разности квадратов выглядит так:

Это правило применяется к сокращённому умножению таких выражений, которые могут быть представлены: одно — как сумма двух чисел, а другое — как разность тех же чисел.

Пример. Преобразуйте произведение в двучлен:

В примере мы применили формулу разности квадратов справа налево, то есть нам дана была правая часть формулы, а мы преобразовали её в левую:

При решении практических примеров в алгебре зачастую применяют формулы сокращённого умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители. На практике первые три формулы применяются как слева направо, так и справа налево, в зависимости от конкретной ситуации.

Формулы сокращённого умножения частенько называют тождествами сокращённого умножения. И здесь нет ничего удивительного, так как каждое равенство представляет собой тождество.

Сумма квадратов двух чисел бывает двух типов:

a 2 +b 2 =(a+bi)(a-bi)

OR.

(1) a 2 +b 2 =(a+b) 2 -2ab (сумма двух квадратов)

a²+b²=(a-b)²+2ab

Другие формулы сокращённого умножения:

(a+b-c) 2 =a 2 +b 2 +c 2 +2ab-2ac-2bc

Куб суммы двух чисел

(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3 (куб суммы двух чисел)

Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго плюс куб второго числа.

(a+b) 3 = a 3 +3a 2 b+3ab 2 +b 3

Пример выражения:

a) (m+2n) 3 =m 3 +3·m 2 ·2n+3·m·(2n) 2 +(2n) 3 =m 3 +6m 2 n+12mn 2 +8n 3

б) (3x+2y) 3 =(3x) 3 +3·(3x) 2 ·2y+3·3x·(2y) 2 +(2y) 3 =27x 3 +54x 2 y+36xy 2 +8y 3

Куб разности двух чисел

(a-b) 3 =a 3 -3a 2 b+3ab 2 -b 3 (куб разности двух чисел)

Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе число плюс утроенное произведение первого числа на квадрат второго числа минус куб второго числа.

(a-b) 3 =a 3 -3a 2 b+3ab 2 -b 3

Пример выражения:

а) (2x–y) 3 =(2x) 3 -3·(2x) 2 ·y +3·2x·y 2 –y 3 =8x 3 –12x 2 y+6xy 2 –y 3

б) (x–3n) 3 =x 3 -3·x 2 ·3n+3·x·(3n) 2 –(3n) 3 =x 3 –9x 2 n+27xn 2 –27n 3

Сумма кубов двух чисел

a 3 + b 3 = (a + b)(a 2 — ab + b 2 ) (сумма кубов)

Сумма кубов двух чисел равна произведению суммы самих чисел на неполный квадрат их разности.

a 3 +b 3 = (a+b)(a 2 –ab+b 2 )

Пример выражения:

a) 125 + 8x 3 = 5 3 + (2x) 3 = (5 + 2x)(5 2 — 5·2x + (2x) 2 ) = (5 + 2x)(25 – 10x + 4x 2 )

б) (1 + 3m)(1 – 3m + 9m 2 ) = 1 3 + (3m) 3 = 1 + 27m 3

Разность кубов двух чисел

a 3 — b 3 = (a — b)(a 2 + ab + b 2 ) (разность кубов)

Разность кубов двух чисел равна произведению разности самих чисел на неполный квадрат их суммы.

a 3 -b 3 = (a-b)(a 2 +ab+b 2 )

Пример выражения:

а) 64с 3 – 8 = (4с) 3 – 2 3 = (4с – 2)((4с) 2 + 4с·2 + 2 2 ) = (4с – 2)(16с 2 + 8с + 4)

б) (3a – 5b)(9a 2 + 15ab + 25b 2 ) = (3a) 3 – (5b) 3 = 27a 3 – 125b 3

Формула для нахождения четвертой степени суммы двух чисел имеет вид:

(a + b) 4 = a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4

Формула для нахождения четвертой степени разности двух чисел имеет вид:

(a — b) 4 = a 4 — 4a 3 b + 6a 2 b 2 — 4ab 3 + b 4

Данные формулы сокращённого умножения доказываются путём раскрытия скобок и приведения подобных слагаемых .

Таблица формул сокращённого умножения для учеников 7 классов

Рассмотрим семь основных формул сокращённого умножения, которые изучают ученики на уроках алгебры в 7 классе:

Таблица формул сокращенного умножения

Таблица формул сокращённого умножения

Произведение суммы двух чисел на их разность равно разности квадратов этих чисел:

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа:

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа:

Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго плюс куб второго числа:

Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго числа:

Выражение в алгебре принято называть неполным квадратом разности. Если умножить сумму двух чисел на неполный квадрат разности этих чисел, то получим формулу суммы кубов.

Сумма кубов двух чисел равна произведению суммы этих чисел на их неполный квадрат разности:

Выражение в алгебре, принято называть неполным квадратом суммы. Если умножить разность двух чисел на неполный квадрат суммы этих чисел, то получим формулу разности кубов.

Разность кубов двух чисел равна произведению разности этих чисел на их неполный квадрат суммы:

Группа формул: сумма степеней

Группа формул «Сумма степеней» составляет Таблицу 2. Эти формулы можно получить, выполняя вычисления в следующем порядке:

(x + y) 2 = (x + y)(x + y) ,
(x + y) 3 = (x + y) 2 (x + y) ,
(x + y) 4 = (x + y) 3 (x + y)

Группу формул «сумма степеней» можно получить также с помощью треугольника Паскаля и с помощью бинома Ньютона, которым посвящены специальные разделы нашего справочника.

Таблица 2. – Сумма степеней

Название формулы	Формула
Квадрат (вторая степень) суммы	(x + y) 2 = x 2 + 2xy + y 2
Куб (третья степень) суммы	(x + y) 3 = x 3 + 3x 2 y + 3xy 2 + y 3
Четвертая степень суммы	(x + y) 4 = x 4 + 4x 3 y + 6x 2 y 2 + 4xy 3 + y 4
Пятая степень суммы	(x + y) 5 = x 5 + 5x 4 y + 10x 3 y 2 + 10x 2 y 3 + 5xy 4 + y 5
Шестая степень суммы	(x + y) 6 = x 6 + 6x 5 y + 15x 4 y 2 + 20x 3 y 3 + 15x 2 y 4 + 6xy 5 + y 6

Общая формула для вычисления суммы

с произвольным натуральным значением n рассматривается в разделе «Бином Ньютона» нашего справочника.

Разность степеней

Если в формулах из Таблицы 2 заменить y на – y , то мы получим группу формул «Разность степеней» (Таблица 3.):

Таблица 3. – Разность степеней

Название формулы	Формула
Квадрат (вторая степень) разности	(x – y) 2 = x 2 – 2xy + y 2
Куб (третья степень) разности	(x – y) 3 = x 3 – 3x 2 y + 3xy 2 – y 3
Четвертая степень разности	(x – y) 4 = x 4 – 4x 3 y + 6x 2 y 2 – 4xy 3 + y 4
Пятая степень разности	(x – y) 5 = x 5 – 5x 4 y + 10x 3 y 2 – 10x 2 y 3 + 5xy 4 – y 5
Шестая степень разности	(x – y) 6 = x 6 – 6x 5 y + 15x 4 y 2 – 20x 3 y 3 + 15x 2 y 4 – 6xy 5 + y 6

Квадрат многочлена

Следующая формула применяется достаточно часто и называется «Квадрат многочлена» :

Квадрат многочлена формула

Что бы возвести многочлен в квадрат необходимо сложить его члены в квадрате и удвоенные произведения его членов попарно взятых.

Квадрат многочлена

Примеры квадрата многочлена

1. (1 + 2 + 3 + 4) 2 =
1 2 + 2 2 + 3 2 + 4 2 + 2 • 1 • (2 + 3 + 4) + 23 • (3 + 4) + 2 • 3 • 4 =
1 + 4 + 9 + 16 + 2 • 1 • 9 + 2 • 2 • 7 + 24 =
30 + 18 + 28 + 24 = 100 ;
a = 1 ;
b = 2 ;
c = 3 ;
d = 4 ;
2. (2 + 3 + 4 + 5) 2 =
2 2 + 3 2 + 4 2 + 5 2 + 2 • 2 • 3 + 2 • 2 • 4 + 2 • 2 • 5 + 2 • 3 • 4 + 2 • 3 • 5 + 2 • 4 • 5 =
4 + 9 + 16 + 25 + 12 + 16 + 20 + 24 + 30 + 40 = 196 ;
a = 2 ;
b = 3 ;
c = 4 ;
d = 5 ;
3. (5 + 6 + 7 + 2 =
5 2 + 6 2 + 7 2 + 8 2 + 2 • 5 • 6 + 2 • 5 • 7 + 2 • 5 • 8 + 2 • 6 • 7 + 2 • 6 • 8 + 2 • 7 • 8 =
25 + 36 + 49 + 64 + 60 + 70 + 80 + 84 + 96 + 112 = 676 ;
a = 5 ;
b = 6 ;
c = 7 ;
d = 8 ;

Формулы сокращённого умножения

При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения. Всего таких формул семь. Их все необходимо знать наизусть.

Следует также помнить, что вместо « a » и « b » в формулах могут стоять как числа, так и любые другие алгебраические многочлены.

Разность квадратов

Запомните!

Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.

a 2 − b 2 = (a − b)(a + b)

15 2 − 2 2 = (15 − 2)(15 + 2) = 13 · 17 = 221
9a 2 − 4b 2 с 2 = (3a − 2bc)(3a + 2bc)

Квадрат суммы

Запомните!

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

(a + b) 2 = a 2 + 2ab + b 2

Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик. Поясним на примере:

Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.
112 = 100 + 1
Запишем сумму чисел в скобки и поставим над скобками квадрат.
112 2 = (100 + 12) 2
Воспользуемся формулой квадрата суммы:
112 2 = (100 + 12) 2 = 100 2 + 2 · 100 · 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544

Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.

(8a + с) 2 = 64a 2 + 16ac + c 2

Предостережение!

Квадрат разности

Запомните!

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.

(a − b) 2 = a 2 − 2ab + b 2

Также стоит запомнить весьма полезное преобразование:

Формула выше доказывается простым раскрытием скобок:

(a − b) 2 = a 2 −2ab + b 2 = b 2 − 2ab + a 2 = (b − a) 2

Куб суммы

Запомните!

Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Как запомнить куб суммы

Запомнить эту «страшную» на вид формулу довольно просто.

Выучите, что в начале идёт « a 3 ».
Два многочлена посередине имеют коэффициенты 3 .
Вспомним, что любое число в нулевой степени есть 1 . (a 0 = 1, b 0 = 1) . Легко заметить, что в формуле идёт понижение степени « a » и увеличение степени « b ». В этом можно убедиться:
(a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3

Предостережение!

Куб разности

Запомните!

Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.

(a − b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Запоминается эта формула как и предыдущая, но только с учётом чередования знаков « + » и « − ». Перед первым членом « a 3 » стоит « + » (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять « − », затем опять « + » и т.д.

(a − b) 3 = + a 3 − 3a 2 b + 3ab 2 − b 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Сумма кубов

Не путать с кубом суммы!

Запомните!

Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.

a 3 + b 3 = (a + b)(a 2 − ab + b 2 )

Сумма кубов — это произведение двух скобок.

Первая скобка — сумма двух чисел.
Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:
(a 2 − ab + b 2 )
Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.