Что такое сумма правило

2. Правила суммы и произведения

В комбинаторике, которая возникла раньше теории множеств, правило нахождения числа элементов объединения двух непересекающихся конечных множеств называют правилом суммы и формулируют в таком виде:

Если объект а можно выбрать т способами, а объект b – k способами (не такими, как а), то выбор «либо а, либо в» можно осуществить т + k способами.

Задача 1. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?

Решение. По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу суммы, можно осуществить 5 + 4 = 9 способами.

Правило нахождения числа элементов декартова произведения двух множеств называют в комбинаторике правилом произведения и формулируют в таком виде:

Если объект а можно выбрать т способами, а объект b – k способами, то пару (а, b) можно выбрать m  k способами.

Замечание. Правило суммы и произведения, сформулированные для двух объектов можно обобщить и на случай t.

Задача 2. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать пару плодов, состоящую из яблока и апельсина?

Решение. По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе пары (яблоко, апельсин), то ее, согласно правилу произведения, можно выбрать 5  4 = 20 способами.

Задача 3. Сколько всего двузначных чисел можно составить из цифр 7, 4 и 5 при условии, что они в записи числа не повторяются?

Решение. Чтобы записать двузначное число, надо выбрать цифру десятков и цифру единиц. Согласно условию на месте десятков в записи числа может быть любая из цифр 7, 4 и 5. Другими словами, выбрать цифру десятков можно тремя способами. После того, как цифра десятков определена для выбора цифры единиц остаются две возможности, поскольку цифры в записи числа не должны повторятся. Так как любое двузначное число – это упорядоченная пара, состоящая из цифры десятков и цифры единиц, то ее выбор, согласно правилу произведения, можно осуществить 3  2 = 6 способами.

Задача 4. Сколько трехзначных чисел можно составить, используя цифры 7, 4 и 5?

Решение. В данной задаче рассматриваются трехзначные числа, так как цифры в записи этих чисел могут повторяться, то цифру сотен, цифру десятков и цифру единиц можно выбирать тремя способами каждую. Поскольку запись трехзначного числа представляет собой каждую. Поскольку запись трехзначного числа представляет собой упорядоченный набор из трех элементов, то, согласно правилу произведения, его выбор можно осуществить 27 способами, так как 3  3  3 = 27.

Задача 5. Сколько всего четырехзначных чисел можно составить из цифр 0 и 3?

Решение. Запись четырехзначного числа представляет собой упорядоченный набор (кортеж) из четырех цифр. Первую цифру – цифру тысяч можно выбрать только одним способом, так как запись числа не может начинаться с нуля. Цифрой сотен может быть либо нуль, либо три, т.е. два способа выбора. Сколько же способов выбора имеется для цифры десятков и цифры единиц.

Итак, цифру тысяч можно выбрать одним способом, цифру сотен – двумя, цифру единиц двумя. Чтобы узнать сколько всего четырехзначных чисел можно составить из цифр 0 и 3, согласно правилу произведения, способы выбора каждой цифры надо перемножить: 1 2  2  2 = 8.

Таким образом, имеем 8 четырехзначных чисел.

Задача 6. Сколько трехзначных чисел можно записать, используя цифры 0, 1, 3, 6, 7 и 9, если каждая из них может быть использована в записи только один раз?

Решение. Так как запись числа не может начинаться с нуля, то цифру сотен можно выбрать пятью способами; выбор цифры десятков можно осуществить также пятью способами, поскольку цифры в записи числа не должны повторятся, а одна из шести данных цифр будет уже использована для записи сотен; после выбора двух цифр (для записи сотен и десятков) выбрать цифру единиц из данных шести можно четырьмя способами. Отсюда, по правилу произведения, получаем, что всего трехзначных чисел (из данных шести цифр) можно образовать 100: 5  5  4 = 100.

Правило суммы и правило произведения

Пусть множество A состоит из n элементов, а множество B состоит из m элементов. При этом множества не пересекаются, A ∩ B = ∅.
Тогда общий набор, множество A ∪ B состоит из n + m элементов.
Выбрать один элемент a ∈ A ИЛИ b ∈ B можно n + m способами.

Например:
На подносе лежит 5 слив и 4 абрикоса.
Сколькими способами можно выбрать фрукт с подноса?
Всего фруктов: 5 + 4 = 9. Значит – 9 способов.

п.2. Правило произведения

Пусть множество A состоит из n элементов, а множество B состоит из m элементов. При этом множества не пересекаются, A ∩ B = ∅.
Тогда множество всех возможных упорядоченных пар (a, b) = A · B состоит из n · m элементов.
Выбрать упорядоченную пару a ∈ A И b ∈ B можно n · m способами.

Например:
Сколько всего двузначных четных чисел?
В двузначном числе на первом месте могут быть цифры , n = 9
В двузначном четном числе на втором месте могут быть цифры , m = 5
Всего nm = 9 · 5 = 45 чисел.

п.3. Исключение «двойного учета» для неупорядоченных пар

При составлении пар порядок бывает неважен: (a, b) или (b, a), – главное, составить пару. В таком случае, например, пары (1; 2) и (2; 1) – одно и то же.
Поэтому правило произведения для неупорядоченных пар:

Пусть множество A состоит из n элементов, а множество B состоит из m элементов. При этом множества не пересекаются, A ∩ B = ∅.
Тогда множество всех возможных неупорядоченных пар (a, b) ≡ (b, a) состоит из (mathrm>) элементов.
Выбрать неупорядоченную пару a ∈ A И b ∈ B можно (n · m)/2 способами.

Например:
В саду поспевает 7 видов фруктов. Было решено сварить компот из любых двух фруктов. Сколько всего различных компотов можно сварить?
Первый фрукт можно выбрать n = 7 способами.
Второй фрукт можно выбрать m = 6 способами.
В данном случае 2 фрукта образуют неупорядоченную пару – неважно, в каком порядке их бросать в кастрюлю. Поэтому (mathrm=21>).
Ответ: 21 различных компотов.

п.4. Примеры

Пример 1. О 4-значном пин-коде карты известно, что первая и последняя цифры у него одинаковые, вторая и третья – разные, и не равны первой цифре.
Сколько всего вариантов такого пин-кода?

В начале и в конце одновременно используются цифры , n = 10
На второй позиции могут использоваться все цифры, кроме уже использованной на первом месте, m = 9
На третьей позиции могут использоваться все цифры, кроме уже использованных на первом и втором месте, k = 8
По правилу произведения общее количество наборов: N = nmk = 10·9·8 = 720.
Ответ: 720 вариантов.

Пример 2. Сколько всего 3-значных чисел, у которых ровно две цифры.
а) семёрки; б) нули?

а) Варианты расстановки семёрок:
77x, x ≠ 7 – таких чисел 9
7×7, x ≠ 7 – таких чисел также 9
x77, x ≠ 7 – таких чисел 8 (слева не может стоять 0)
По правилу суммы: 9 + 9 + 8 = 26

б) Вариант расстановки нулей только x00, x ≠ 0 – таких чисел 9
Других вариантов нет.
Ответ: а) 26 чисел; б) 9 чисел.

Пример 3. На экзамене будет 5 задач по 5 разным темам. Каждая задача берется из списка, в котором 8 задач по теме. Вася умеет решать по 3 задачи из каждой темы.
Сколько всего вариантов билетов может быть на экзамене?
Сколько существует вариантов билетов, за которые Вася получит 5 баллов?
Сколько существует вариантов билетов, в которых Вася не решит ни одной задачи?

В экзамене по каждой теме n = 8 вариантов выбора задачи. По правилу произведения всего возможно N = 8 5 = 32768 вариантов билетов.
Вася готов решать k = 3 задачи по каждой теме. По правилу произведения всего он сможет полностью решить K = 3 5 = 243 вариантов.
Вася не готов решать m = 8 – 3 = 5 задач по каждой теме. По правилу произведения всего он вообще не сможет решить M = 5 5 = 3125 вариантов.
Ответ: 32768; 243; 3125.

Пример 4. Каких пятизначных чисел больше: тех, что не делятся на 5, или таких, у которых ни первая, ни вторая слева цифры – не пятёрки?

Сколько всего пятизначных чисел? На первом месте – 9 вариантов цифр, на четырёх последующих – по 10 вариантов. Итого: N = 9 · 10 4 = 90000 чисел.
Признак делимости на 5: последняя цифра 5 или 0.
Количество чисел с последней цифрой 5: M₁ = 9 · 10 3 · 1 = 9000.
Аналогично, с последним 0: M₂ = 9 · 10 3 · 1 = 9000.
Итого, чисел, которые не делятся на 5:
M = N – (M₁ + M₂) = 90000 – 2 · 9000 = 72000.
Сколько всего пятизначных чисел, у которых ни первая, ни вторая слева цифры – не пятёрки? На первом месте – 8 вариантов цифр, на втором – 9 вариантов. На остальных – по 10 вариантов.
Итого: K = 8 · 9 · 10 3 = 72000 чисел.
Получаем: M = K – искомых чисел поровну.
Ответ: их поровну.

Пример 5*. На глобусе проведено 17 параллелей и 24 меридиана. На сколько частей разделена поверхность глобуса?

Возьмём неразмеченный глобус. Проведем экватор.
Поверхность глобуса разделилась на 2 части.
Добавим еще одну параллель. Поверхность разделилась на 3 части.
Мы видим, что n параллелей делит поверхность на N = n + 1 частей.
Соответственно, для 17 параллелей, N = 18 частей.

Опять берём неразмеченный глобус. Проведем меридиан.
Поверхность глобуса разделилась на 2 части.
Добавим ещё один меридиан. Поверхность разделилась на 4 части.
Мы видим, что m меридианов делит поверхность на M = 2m частей.
Соответственно, для 24 меридианов, M = 48 частей.
Общее количество частей по правилу произведения (с исключением «двойного учета», т.к. нам всё равно: мы сначала проводили параллели, а потом – меридианы, или наоборот): (mathrm=frac=432>).
Ответ: 432 части.

Комбинаторика: основные правила и формулы.

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

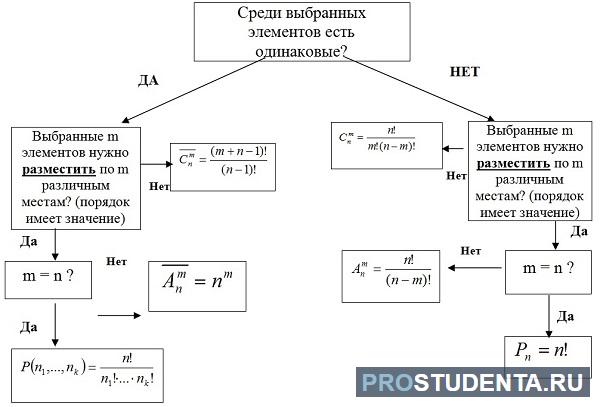
Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

.

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

.

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

.

Перестановки без повторений. Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

Правила суммы и произведения

Комбинаторика представляет собой область математики, занимающейся подсчётом элементов конечных множеств. Общие задачи подсчета элементов некоторого множества связаны с выборкой некоторого числа элементов из заданного базисного множества. Такие задачи полезно делить на типы в зависимости от того, как выбираются элементы: с повторением или без повторений, с учетом порядка выбора или без оного. Мы выведем формулы для каждого из перечисленных типов задач

Начнем с формулировки ряда простых задач.

Задача 1. В небольшой кондитерской к концу рабочего дня осталось несколько пирожных: четыре ванильных, два шоколадных и три фруктовых. Один покупатель собирается купить пирожные перед закрытием кондитерской. Сколько вариантов выбора существует, если покупатель может купить 1, 2, 3 пирожных?

Первая задача решается простым подсчетом. Поскольку все пирожные различны, мы просто можем сложить их количества. Это дает 4 + 2 + 3 = 9 пирожных, из которых покупатель может сделать выбор. Во втором случае 9*8=72 варианта выбора пирожных, в третьем 9*8*7= 504, если не важно какие именно пирожные выбирать!

Эти задачи иллюстрируют два фундаментальных правила пересчета.

Правило суммы гласит, что если А и В — несвязанные события, и существует n₁ возможных исходов события A, и n₂ возможных исходов события B, то возможное число исходов события «А или B» равно сумме n₁ + n₂ .

Правило произведения утверждает, что если дана последовательность к событий с n₁ возможными исходами первого, n₂ — второго, и т. д., вплоть до n_k возможных исходов последнего, то общее число исходов последовательности k событий равно произведению n₁ * n₂*…* n_k.

Задача 2. Сколько существует трехзначных чисел, начинающихся с 3 или 4? Трехзначные числа, о которых идет речь в задаче, разбиваются на два непересекающихся класса. К одному из них относятся числа, начинающиеся с 3, а ко второму — с 4. Для подсчета чисел в первом классе заметим, что существует один возможный исход для первой цифры (она должна быть равна 3), 10 исходов для второй и 10 исходов для последней цифры.

По правилу произведения получаем, что всего чисел в первом классе насчитывается ровно 1*10*10 = 100. Аналогично можно подсчитать количество чисел во втором классе. Оно тоже равно 100. Наконец, по правилу суммы получаем, что существует 100 + 100 = 200 трехзначных чисел, начинающихся с 3 или 4.

Задача 3. Государственный регистрационный знак легкового автомобиля состоит из трех цифр и трех букв русского алфавита (не считая кода города). Будем считать, что в номере можно задействовать любую последовательность букв и цифр. Сколько различных автомобильных номеров может выдать ГИБДД?

Решение. Каждую из трех букв номера можно выбрать из 33 букв алфавита. По правилу произведения число различных последовательностей из трех букв равно 33*33*33 = 35937. Аналогично, число последовательностей трех цифр равно 10*10*10 = 1000. Наконец, поскольку каждый из автомобильных номеров состоит из трех букв и трех цифр, правило произведения дает искомый ответ: 35937000 различных автомобильных номеров может выдать ГИБДД.

Задача 4. Ребенку предложили мешок с конфетами трех наименований: «Мишка на севере» (А), «Карамель» (В) и «Шоколад» (С). Сколькими способами ребенок может выбрать две конфеты из мешка?

На этот вопрос можно дать несколько ответов в зависимости от уточнения его формулировки. Ставя задачу, мы не уточнили, можно ли брать конфеты одного наименования или нет. Например, можно ли взять две конфеты «Мишка на севере», т.е. АА. Кроме того, имеет ли значение порядок выбора? Иными словами, отличается ли выбор АВ от ВА или нет?

Таким образом, мы имеем четыре разных уточнения формулировки.

1. Повторения разрешены и порядок выбора существенен. В этом случае у нас есть 9 возможностей: АА, АВ, АС, АВ, ВВ, ВС, С А, С В и СС.

2. Запрещено брать конфеты одного наименования, но порядок существенен. В этой ситуации — 6 случаев: АВ, АС, В А, ВС, С А и СВ.

3. Повторения разрешены, но порядок выбора не имеет значения. Тогда ответ — тоже 6 возможностей: АА, АВ, АС, ВВ, ВС и СС.

4. И, наконец, если нельзя брать одинаковые конфеты, а порядок не имеет значения, то у ребенка есть только три варианта выбора: АВ, АС и ВС.

Чтобы различать на терминологическом уровне тип конкретной задачи, введем несколько определений.

Начнем со вспомогательных терминов. Предположим, что мы берем элементы x₁, x₁, . x_k из множества X мощности k ( число элементов в множестве равно k). Каждый такой набор принято называть выборкой объема k из n элементов или, иначе, (n, k)-выборкой. Выборка называется упорядоченной, если порядок следования элементов в ней задан. При этом две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются разными. Если же порядок следования элементов в выборке не имеет значения, то выборка называется неупорядоченной.

Теперь введем основные термины в соответствии с типом уточнений, приведенных выше.

• (n, k)-размещением с повторениями называется упорядоченная (n, k)-выборка, элементы в которой могут повторяться;

• (n, k)-размещением без повторений называется упорядоченная (n, k)-выборка, элементам в которой повторяться запрещено;

• неупорядоченная (n, k)-выборка с повторяющимися элементами называется (n, k)-сочетанием с повторениями

• неупорядоченная (n, k)-выборка без повторяющихся элементов называется (n, k)-сочетанием без повторений.

Подсчитаем количество всех различных (n, k)-размещений с повторениями. На первое место выборки мы можем поставить любой из n элементов множества. Поскольку повторения разрешены, то на второе место мы опять можем поставить любой элемент из этого же множества, и т. д. Поскольку у нас k мест в выборке, то опираясь на правило произведения, получаем, что число всех (n, k)-размещений с повторениями равно n k .

Задача 5. Целые числа в компьютере представляются строчкой из N двоичных знаков. Первый из них отведен на знак (+ или -), а остальные N — 1 отвечают за модуль целого числа. Сколько различных целых чисел может использовать компьютер?

Решение. Двоичная цифра это 0 или 1. Для записи числа используется N таких цифр. Заметим, что двоичные строки, представляющие числа, могут иметь повторяющиеся цифры, и порядок их следования, естественно, существенен для данной задачи. Поэтому мы имеем дело с (2, N)-размещениями с повторениями. По выведенной формуле получаем, что общее количество таких строк равно 2 N .

Практически всегда различные размещения изображают различные числа, за исключением двух строк: -000000…00 и + 000000…00, которые изображают 0. Значит, компьютер может оперировать (2 N — 1) целыми числами.

Для числа всех (n, k)-размещений без повторений зафиксировано специальное обозначение P(n, k).Подсчитаем это число. На первое место выборки мы можем поставить любой из n элементов. Поскольку здесь нам не разрешены повторения, то для второго места мы можем выбрать любой из (n- 1) оставшихся элементов. На третье — из (n- 2) и так далее, вплоть до k-го места, куда можно написать любой из (n-k +1) элементов. Теперь применим правило произведения. Имеем Р(n, k) = n(n-1)(n — 2) … (n-k +1).

Для сокращения записи напомним, что произведение всех натуральных чисел от 1 до n включительно называется n факториал и обозначается символом n!. Выразим Р(n, k)

число различных (n, k)- размещений без повторений.

Число всех (n, k)- сочетаний без повторений обозначается символом С(n, k). Оно связано с числом (n, k)- размещений без повторений Р(n, k) формулой

Задача 6. По меню в ресторане можно выбрать ровно три из семи главных блюд. Сколькими способами Вы можете сделать заказ?

Решение. Здесь мы имеем дело с (7, 3)-сочетаниями без повторений.

Итак, у Вас есть 35 возможностей для различных заказов.

Исследуем, это сочетания с повторениями. Напомним, что это выборки, в которых порядок не важен, а вот повторы элементов допускаются. Поскольку порядок в наших выборках значения не имеет, а повторы разрешены, мы можем сгруппировать вместе одинаковые элементы, разделив группы какими-нибудь метками.

Предположим, например, что мы сделали выборку, состоявшую из пяти букв, каждая из которых может быть одной из а, 6^ и е.

Выборку, состоящую из двух «а», одной «б» и двух «в», можно записать как аа|б|вв, а выборка из одной буквы «а» и четырех букв «в» будет выглядеть так: а||вввв. Договоримся, что слева от первой метки либо стоят буквы «а», либо ничего, справа от второй метки — либо «в», либо ничего, а буквы «б», если они присутствуют в выборке, стоят между метками. Таким образом, можно считать, что мы всегда смотрим на семь ячеек (пять букв и две метки), причем различные выборки будут отличаться ячейками, в которых стоят метки. Значит, число всех таких сочетаний с повторениями совпадает с количеством способов, которыми мы можем поместить две метки в семь ячеек. Осталось понять, что это количество есть не что иное, как число всех (7, 2)- сочетаний без повторений, т. е. равно С(7, 2). Действительно, первую метку можно поставить в любую из семи ячеек, а вторую — в любую из шести, поскольку одна ячейка уже занята. Это дает нам 7 * 6 возможностей. Поменяв расставленные метки местами, мы получим то же самое заполнение ячеек. Стало быть, 7*6 нужно разделить на 2. Итак, количество способов равно

Возвращаясь к общему случаю (n, k)-сочетаний без повторений (k объектов из n данных), заметим, что нам потребуется n-1 метка и k объектов. Таким образом, у нас будет (n- 1) + k ячеек для заполнения. Значит, число (n, k)-сочетаний без повторений совпадает с количеством способов размещения (n- 1) метки в (n+k-1) ячейку. Итак, общее число (n, k)-сочетаний без повторений равно

В таблице запишем все формулы для подсчета количества выборок k элементов из n-элементного множества, которые мы вывели сегодня.

Законы математики

В каждой семье свои законы: сладкое — после супа, игры — после приборки. Но если с родителями можно договориться об исключениях, то правила точных наук оспорить никак нельзя. В этой статье узнаем, какие законы есть в математике.

О чем эта статья:

Переместительный закон сложения

Начнем изучать основные законы математики со сложения натуральных чисел.

Переместительный закон сложения

От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:

m + n = n + m

Переместительный закон сложения работает для любых чисел.

Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.

Приведем пример с весами, которые используют продавцы в магазинах.

Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.

При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.

Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:

Формула переместительного закона для обыкновенных дробей:

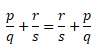
Чтобы сложить две дроби с одинаковым знаменателем, нужно сложить числители, а знаменатель оставить прежним. Вот так:

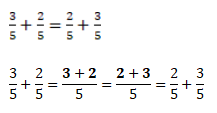
Сочетательный закон сложения

Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.

Сочетательный закон сложения: два способа

1. Результат сложения нескольких слагаемых не зависит от порядка действий.
2. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.

Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.

Рассмотрим сумму из трех слагаемых:

Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:

• 1 + 3 + 4 = (1 + 3) + 4 = 4 + 4 = 8

Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:

• 1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8

В обоих случаях получается один и тот же результат — что и требовалось доказать.

Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:

• (1 + 3) + 4 = 1 + (3 + 4)
• 8 = 8

Отразим сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Формула сочетательного закона для обыкновенных дробей:

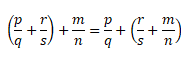
Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.

Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.

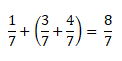
Значит, сочетательный закон справедлив и для обыкновенных дробей.

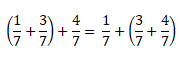
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Переместительный закон умножения

С каждым новым правилом решать задачки по математике все интереснее.

Переместительный закон умножения

От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.

Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:

В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.

Переместительный закон умножения с помощью переменных выглядит так:

a * b = b * a

Сочетательный закон умножения

Рассмотрим еще один полезный закон в математике.

Сочетательный закон умножения

Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.

Другими словами, умножайте числа в любом порядке — как вам больше нравится.

Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:

• 2 * 3 = 6
• 6 * 4 = 24
• 2 * 3 * 4 = 24

А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:

• 3 * 4 = 12
• 2 * 12 = 24
• 2 * 3 * 4 = 24

Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.

• (2 * 3) * 4 = 2 * (3 * 4)
• 6 * 4 = 2 * 12
• 24 = 24

Для любых натуральных чисел a, b и c верно равенство:

a * b * с = (a * b) * с = a * (b * с)

Пример

Вычислить: 5 * 6 * 7 * 8.

Это выражение можно вычислять в любом порядке. Вычислим слева направо:

5 * 6 * 7 * 8 = 1680

Распределительный закон умножения

Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:

Распределительный закон умножения

• Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
• Чтобы сумму чисел умножить на число, нужно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:

Сначала выполним действие в скобках:

В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:

Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:

• (3 + 5) * 2 = 3 * 2 + 5 * 2
• 3 * 2 = 6
• 5 * 2 = 10
• 6 + 10 = 16

Отразим распределительный закон умножения с помощью переменных:

(a + b) * c = a * c + b * c

Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.

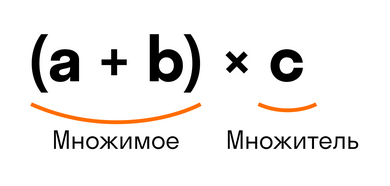
Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.

Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:

c * (a + b) = c * a + c * b

Пример 1

Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:

5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25

Пример 2

Найти значение выражения 2 * (5 + 2).

Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:

2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14

Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.

Пример 3

Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:

4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16

Распределительный закон умножения для суммы обыкновенных дробей:

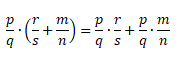
Распределительный закон умножения для разности обыкновенных дробей:

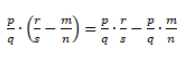
Проверим справедливость этого закона:

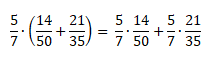
Посчитаем, чему равна левая часть равенства.

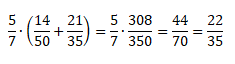
Теперь посчитаем, чему равна правая часть равенства.

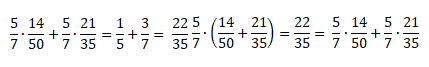
Так мы доказали справедливость распределительного закона.

Задания для самопроверки

Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать

Задание 1. Найти значение выражения: 8 * (1 + 6).

Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).

Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).

Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).

Задание 5. Применить распределительный закон умножения: 13 * (3 + + 5 * (4 + 2)

Комбинаторика — основные понятия и формулы с примерами

Комбинаторика — раздел математики. Основные понятия и формулы комбинаторики как науки применяются во всех сферах жизни.

Неудивительно, что она включена в программу 11 класса, а также во вступительные испытания во многих ВУЗах РФ. Ее основы лежат в прикладном искусстве многих сфер деятельности человека.

Ее история насчитывает более 6 веков. Первые комбинаторные задачи появились в трудах философов и математиков Средневековья.

Представители того научного мира пытались найти методы решения таких задач, их базовые правила и понятия, утвердить уникальные формулы и уравнения для тех, кто ещё не встречался с ними. Такая информация в наше время называется информацией «для чайников».

Попытаемся разобраться в аспектах этой области науки: каковы элементы, свойства, правила, методы и основное ее применение в нашей жизни? Конечно, всю область в одной статье невозможно охватить. Поэтому ниже будет представлено всё самое основное.

Что такое комбинаторика в математике

Суть этого термина дают книги прошлых лет: это раздел математики, занимающийся операциями со множеством элементов.

В интернете есть учебники по информатике и математике для детей, школьников, сборники материалов и задач для начинающих, где в доступном виде объяснена «занимательная» комбинаторика. Нужно твердо выяснить, как решать подобные задачи.

В младших классах задачи на эту тему решают на дополнительных кружках, а в школах с углубленным изучением математики — на основных уроках. К тому же, задачи по комбинаторике включены в олимпиады всех уровней.

Основные понятия

1. Элемент – любой объект или явление, входящий в искомое множество.
2. Сочетание – подмножества, находящиеся в произвольном порядке в исходном множестве.
3. Перестановка – элементы во множестве находятся в строго определенном порядке.
4. Размещение – упорядоченные подмножества в исходном множестве.

Правило произведения

Является одним из основных правил при решении таких задач и звучит так:

При выборе элемента А из n способов и выборе элемента В из m способов верно утверждение, что выбрать пару А и В одновременно можно n*m способами.

Рассмотрим на конкретных примерах.

Задача №1.

В коробке лежит 2 мяча и 6 скакалок. Сколько существует способов достать 1 мяч и 1 скакалку?

Ответ прост: 2 * 6 = 12.

Задача №2.

Есть 1 кубик, 2 шарика, 3 цветка и 4 конфеты. Сколькими способами можно вытянуть кубик, шарик, цветок и конфету?

Решение аналогично: 1 * 2 * 3 * 4 = 24.

Причем левую часть можно записать гораздо проще: 4!

! в данном случае является не знаком препинания, а факториалом. С помощью него можно вычислить более сложные варианты и решать трудные задачи (существуют разные формулы, но об этом позже).

Задача №3.

Сколько двузначных чисел можно составить из 2 цифр?

Задача №4.

Сколько десятизначных чисел можно составить из 10 цифр?

Правило суммы

Тоже является базовым правилом комбинаторики.

Если А можно выбрать n раз, а В — m раз, то А или В можно выбрать (n + m) раз.

Задача №5.

В коробке лежат 5 красных, 3 желтых, 7 зеленых, 9 черных карандашей. Сколько есть способов вытащить 1 любой карандаш?

Ответ: 5 + 3 + 7 + 9 = 24.

Сочетания с повторениями и без повторений

Под этим термином понимают комбинации в произвольном порядке из множества n по m элементов.

Число сочетаний равно количеству таких комбинаций.

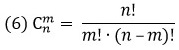
Задача №6.

В коробке находится 4 разных фрукта. Сколькими способами можно достать одновременно 2 разных фрукта?

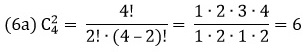
Где 4! – комбинация из 4 элементов.

С повторениями чуть сложней, комбинации считаются по такой формуле:

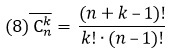
Задача №7.

Возьмем тот же самый случай, но при условии, что один фрукт возвращается в коробку.

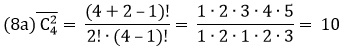
Размещения с повторениями и без повторений

Под этим определением понимают набор m элементов из множества n элементов.

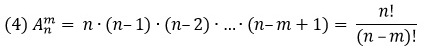
Задача №8.

Из 3 цифр надо выбрать 2, чтобы получались разные двузначные числа. Сколько вариантов?

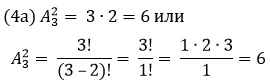
А как же быть с повторениями? Здесь каждый элемент может размещаться несколько раз! В таком случае общая формула будет выглядеть следующим образом:

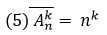
Задача №9.

Из 12 букв латинского алфавита и 10 цифр натурального ряда надо найти все варианты составления автомобильного кода региона.

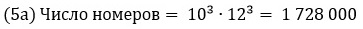
Перестановки с повторениями и без повторений

Под этим термином понимают все возможные комбинации из n элементного множества.

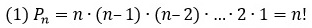
Задача №10.

Сколько возможных пятизначных чисел можно составить из 5цифр? А шестизначных из 6 цифр? Семизначных из 7 цифр?

Решения, согласно вышеприведенной формуле, следующие:

А как же быть с повторениями? Если в таком множестве есть одинаковые по своей значимости элементы, то перестановок будет меньше!

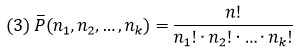
Задача №11.

В коробке есть 3 одинаковых карандаша и одна ручка. Сколько перестановок можно сделать?

Ответ прост: 4! / (3! * 1!) = 4.

Комбинаторные задачи с решениями

Примеры всех возможных типов задач с решениями были даны выше. Здесь попробуем разобраться с более сложными случаями, встречающимися в нашей жизни.

Типы задач	Что требуется найти	Методы решения
Магический квадрат	Фигура, в которой сумма чисел в рядах и столбцах должна быть одинакова (его разновидность – латинский квадрат).	Рекуррентные соотношения. Решается подобная же задача, но с гораздо меньшим множеством элементов по известным правилам и формулам.
Задача размещения	Стандартная производственная задача (например, в лоскутной технике) — найти возможные способы разложения количества продуктов в ячейки в определенном порядке.	Включения и исключения. Как правило, применяется при доказательстве различных выражений.
Задачи про торговцев	Суть — найти все возможные пути прохождения людей из пункта А в пункт В.	Траектории. Для этого вида задач характерно геометрическое построение возможных способов решения.

Заключение

Стоит изучать эту науку, поскольку в век быстрой модернизации технологий потребуются специалисты, способные предоставить различные решения тех или иных практических задач.

Правило суммы

Если элемент A можно выбрать m способами, а элемент B можно выбрать k способами, то выбор элемента A или B можно осуществить m + k способами.

Правило суммы можно перефразировать на теоретико-множественном языке. Обозначим через | A | число элементов множества A, через A B — объединение множеств A и B, через AxB — декартово произведение множеств A и B. Тогда для непересекающихся множеств A и B выполняется равенство:

Обобщением правила суммы является правило произведения.

Если элемент A можно выбрать m способами, а после каждого выбора элемента A элемент B можно выбрать k способами, тогда, упорядоченную пару элементов (A, B) можно выбрать m*k способами.

Правило произведения можно распространить на выбор последовательности (x1, x2, …, xn) произвольной конечной длины n.

На теоретико-множественном языке правило произведения формулируется так: | Aх B | = | A | | B |.

Назовём множество, содержащее n элементов, n-множеством.

Последовательность (x1, x2, …, xk ) длины k без повторяющихся элементов из элементов данного n-множества назовём k-размещением.

Обозначим символом число размещений из n по k элементов (от фран. «arrangement» — размещение). Используя правило произведения, вычислим число .

Пусть произвольное размещение длины k имеет вид:

Элемент x1 можно выбрать n способами. После каждого выбора x1 элемент x2 можно выбрать

• (n — 1) способами. После каждого выбора элементов x1 и x2 элемент x3 можно выбрать (n — 2) способами, и т.д. После каждого выбора элементов x1 , x2, …, xk-1 элемент xk можно выбрать
• (n — (k — 1)) = (n — k + 1) способами. Тогда, по правилу произведения, последовательность
• (x1; x2; , …, xk ) можно выбрать числом способов, равным

n(n — 1)(n — 2) … (n — k + 1) = (1.1)

Произведение в левой части равенства (1.1) умножим и разделим на (n — k)!, получим:

Если в форуме (1.2) k = n, то есть число Pn перестановок из n элементов

Pn = n! (от «permutation»- перестановка).

k-подмножество данного n-множества называется k-сочетанием.

Обозначим через число k-сочетаний из данных n элементов. Формулу для числа получим, рассуждая следующим образом. Если каждое сочетание упорядочить всеми возможными способами, то получим все k-последовательностей из n элементов, без повторений, то есть все k-размещения.

Предполагая, что n и k — целые положительные числа и 0!=1, сформулируем основные свойства сочетаний.

Основные свойства сочетаний.

1. Условились, что

Сочетания и размещения широко используются при вычислении классической вероятности случайных событий.

Пример. В корзине находятся 20 орехов, из которых 7 грецких. Наудачу выбирают 5 орехов. Найти вероятность того, что среди выбранных орехов содержатся 2 грецких.

Решение. Число исходов опыта . Случайное событие A — среди пяти выбранных орехов содержатся 2 грецких ореха. Число исходов, благоприятствующих событию A, равно: . Искомая вероятность .

• 1. Найти вероятность того, что случайно выбранное 5-значное (десятичное) число не содержит цифры 5.
• 2. Предприятие располагает 5 вакансиями для мужчин, 5 вакансиями для женщин и 4 вакансиями для работников любого пола. В отдел кадров предприятия обратилось 20 человек, среди которых 12 мужчин и 8 женщин. Сколькими способами предприятие может заполнить имеющиеся вакансии?
• 3. В классе 25 учеников, из которых 13 юношей и 12 девушек. Сколькими способами 25 учеников могут встать в шеренгу так, чтобы юноши после удаления из строя девушек, оказались построенными по росту; аналогично девушки после удаления из строя юношей оказались построенными по росту?

В современной литературе наиболее употребителен для обозначения числа k-сочетаний из n элементов символ , n называют верхним индексом, k — нижним индексом.

Используя свойства сочетаний 1, 2, 4, составим таблицу1.

Таблица 1.Треугольник Паскаля

Заметим, что Блез Паскаль называл числовой треугольник, начало которого содержится в таблице1, арифметическим. Паскаль посвятил свойствам арифметического треугольника основополагающий «Трактат об арифметическом треугольнике» (1654). Справедливости ради, стоит упомянуть, что биномиальные коэффициенты были хорошо известны в Азии за много веков до рождения Паскаля. В Италии треугольник Паскаля называют треугольником Тартальи.

Сочетания имеют многочисленные интерпретации и приложения. Сочетания являются биномиальными коэффициентами в разложении бинома

В этой интерпретации индексы могут принимать вещественные значения. Используя свойства биномиальных коэффициентов (при разных ограничениях на выбор верхних и нижних индексов), доказано громадное число комбинаторных тождеств, составивших самостоятельный раздел комбинаторной математики. В частности, из формулы 1.4 при x = 1, получим

x = -1, n > 0, получим , продифференцировав равенство 1.4, получим при x = 1, и т.д.

Существует тесная связь между подмножествами множества и разложениями целого (положительного) числа. Разложение n есть представление числа n в виде упорядоченной суммы положительных целых чисел. Например, существует восемь разложений числа 4, именно:

• 1+1+1+1 3+1
• 2+1+1 1+3
• 1+2+1 2+2
• 1+1+2 4

Если разложение содержит в точности k слагаемых, то говорят, что имеет k частей и называется k-разложением. Для k-разложения числа n: a1 + a2 + …+ an — определим

Эта формула устанавливает биекцию между всеми k-разложениями числа n и (k — 1)-подмножествами (n — 1)-множества.

Следовательно, существует k-разложений числа n и 2n-1 разложений числа n. Биекцию часто схематично изображают строкой, состоящей из n точек и k — 1 разделяющей вертикальной черты. Точки разделились по k линейно упорядоченным «купе»; числа точек в «купе» соответствуют слагаемым в k-разложении числа n. Например, строка | | | | | соответствует разложению 1+2+1+1+3+2. Другая проблема, тесно связанная с разложениями, есть задача подсчёта числа N(n,k) решений уравнения

x1 + x2 + …+ xk = n (1.6)

Неотрицательные целые решения уравнения 1.6 называются слабыми k-разложениями числа n. Число неотрицательных целых решений уравнения 1.6 равно числу положительных решений уравнения

y1 + y2 + … + yk = n + k,

то есть числу k-разложений числа n + k. Таким образом, N(n,k) = .

Если k-сочетание содержит повторяющиеся элементы, то такое k-сочетание называют

k-мультимножеством. Число всех k-сочетаний с повторениями из данного n-элементного множества обозначим через , где

Сочетание можно интерпретировать, как распределение элементов n-множества S между двумя категориями, первая из которых содержит k элементов, вторая содержит n — k элементов. Обобщим это представление. Пусть (a1, a2, …, am)- последовательность неотрицательных целых чисел, сумма которых равна n. Рассмотрим m категорий C1, C2, … Cm.

Обозначим символом (1.8)

число способов распределения n элементов среди категорий C1, C2, … Cm так, чтобы категории Ci принадлежало точно ai элементов. Тогда