Что такое заданное множество

Множества: понятие, определение, примеры

Людям постоянно приходится иметь дело с различными совокупностями предметов, что повлекло за собой возникновение понятия числа, а затем и понятия множества, которое является одним из основных простейших математических понятий и не поддается точному определению. Нижеследующие замечания имеют своей целью пояснить, что такое множество , но не претендуют на то, чтобы служить его определением.

Множеством называется собрание, совокупность, коллекция вещей, объединенных по какому-либо признаку или по какому-либо правилу. Понятие множества возникает путем абстракции. Рассматривая какую-либо совокупность предметов как множество, отвлекаются от всех связей и соотношений между различными предметами, составляющими множества, но сохраняют за предметами их индивидуальные черты. Таким образом, множество, состоящее из пяти монет, и множество, состоящее из пяти яблок, — это разные множества. С другой стороны, множество из пяти монет, расположенных по кругу, и множество из тех же монет, положенных одна на другую, — это одно и то же множество.

Приведем несколько примеров множеств. Можно говорить о множестве песчинок, составляющих кучу песка, о множестве всех планет нашей солнечной системы, о множестве всех людей, находящихся в данный момент в каком-либо доме, о множестве всех страниц этой книги. В математике тоже постоянно встречаются различные множества, например множество всех корней заданного уравнения, множество всех натуральных чисел, множество всех точек на прямой и т. д.

Математическая дисциплина, изучающая общие свойства множеств, т. е. свойства множеств, не зависящие от природы составляющих их предметов, называется теорией множеств. Эта дисциплина начала бурно развиваться в конце XIX и начале XX в. Основатель научной теории множеств — немецкий математик Г. Кантор.

Работы Кантора по теории множеств выросли из рассмотрения вопросов сходимости тригонометрических рядов. Это весьма обычное явление: очень часто рассмотрение конкретных математических задач ведет к построению весьма абстрактных и общих теорий. Значение таких абстрактных построений определяется тем, что они оказываются связанными не только с той конкретной задачей, из которой они выросли, но имеют приложения и в ряде других вопросов. В частности, именно так обстоит дело и с теорией множеств. Идеи и понятия теории множеств проникли буквально во все разделы математики и существенно изменили ее лицо. Поэтому нельзя получить правильного представления о современной математике, не познакомившись с элементами теории множеств. Особенно большое значение имеет теория множеств для теории функций действительного переменного.

Множество считается заданным, если относительно любого предмета можно сказать, принадлежит он множеству или не принадлежит. Иными словами, множество вполне определяется заданием всех принадлежащих ему предметов. Если множество состоит из предметов , записывается в виде

принадлежит «, или » есть элемент «. Если же предмет не принадлежит множеству , то пишут: могут сами быть множествами, однако, во избежание противоречий, приходится требовать, чтобы само множество не было одним из своих собственных элементов: Множество, не содержащее ни одного элемента, называется пустым множеством . Например, множество всех действительных корней уравнения

Если для двух множеств и каждый элемент множества является также элементом множества , то говорят, что входит в есть часть , что есть подмножество или что содержится в ; это записывается в виде

Ясно, что всегда . Удобно считать, что пустое множество есть часть любого множества.

Два множества равны , если они состоят из одних и тех же элементов. Например, множество корней уравнения и множество правила действий над множествами .

Объединение или сумма множеств

Пусть имеются множества . Объединением или суммой этих множеств называется множество , состоящее из всех элементов, принадлежащих хотя бы одному из «слагаемых»

Пересечение множеств

Пересечением или общей частью множеств . называется множество , состоящее из всех тех элементов, которые принадлежат одновременно всем множествам .

Ясно, что , и если , то .

Если пересечение множеств и пусто: , то говорят, что эти множества не пересекаются .

Для обозначения операции суммы и пересечения множеств употребляют также знаки есть сумма множеств , a — их пересечение.

Читателю рекомендуется доказать, что сумма и пересечение множеств связаны обычным распределительным законом

Разность множеств

Разностью двух множеств и называется множество всех тех элементов из , которые не принадлежат :

Нетрудно показать, что всегда

Таким образом, правила действий над множествами значительно отличаются от обычных правил арифметики.

Конечные и бесконечные множества

Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же число элементов множества неограниченно, то такое множество называется бесконечным. Например, множество всех натуральных чисел бесконечно.

Рассмотрим два каких-либо множества и и поставим вопрос о том, одинаково или нет количество элементов в этих множествах.

Если множество конечно, то количество его элементов характеризуется некоторым натуральным числом — числом его элементов. В этом случае для сравнения количества элементов множеств и достаточно сосчитать число элементов в , число элементов в и сравнить полученные числа. Естественно также считать, что если одно из множеств и конечно, а другое бесконечно, то бесконечное множество содержит больше элементов, чем конечное.

Однако, если оба множества и бесконечны, то путь простого счета элементов ничего не дает. Поэтому сразу возникают такие вопросы: все ли бесконечные множества имеют одинаковое количество элементов, или же существуют бесконечные множества с большим и меньшим количеством элементов? Если верно второе, то каким способом можно сравнивать между собой количество элементов в бесконечных множествах? Этими вопросами мы теперь и займемся.

Взаимно однозначное соответствие множеств

Пусть снова и — два конечных множества. Как узнать, какое из этих множеств содержит больше элементов, не считая числа элементов в каждом множестве? Для этого будем составлять пары, объединяя в пару один элемент из и один элемент из . Тогда, если какому-нибудь элементу из не найдется парного к нему элемента из , то в больше элементов, чем в . Поясним это рассуждение примером.

Пусть в зале находится некоторое число людей и некоторое число стульев. Чтобы узнать, чего больше, достаточно попросить людей занять места. Если кто-нибудь остался без места, значит, людей больше, а если, скажем, все сидят и заняты все места, то людей столько же, сколько стульев. Описанный способ сравнения количества элементов во множествах имеет то преимущество перед непосредственным счетом элементов, что он без особых изменений применяется не только к конечным, но и к бесконечным множествам.

Рассмотрим множество всех натуральных чисел

Какое множество содержит больше элементов? На первый взгляд кажется, что первое. Однако мы можем образовать из элементов этих множеств пары, как указано ниже.

и ни один элемент не остается без пары. Правда, мы могли бы также образовать пары и так:

остаются без пар. С другой стороны, мы могли бы составить пары и так:

Таким образом, если множества и бесконечны, то различным способам образования пар соответствуют разные результаты. Если существует такой способ образования пар, при котором у каждого элемента и каждого элемента имеется парный к нему элемент, то говорят, что между множествами и можно установить взаимно однозначное соответствие . Например, между рассмотренными выше множествами и можно установить взаимно однозначное соответствие, как
это видно из табл. 1.

Если между множествами и можно установить взаимно однозначное соответствие, то говорят, что они имеют одинаковое количество элементов или равномощны . Если же при любом способе образования пар некоторые элементы из всегда остаются без пар, то говорят, что множество содержит больше элементов, чем , или что множество имеет большую мощность, чем .

Таким образом, мы получили ответ на один из поставленных выше вопросов: как сравнивать между собой количество элементов в бесконечных множествах. Однако это нисколько не приблизило нас к ответу на другой вопрос: существуют ли вообще бесконечные множества. имеющие различные мощности? Чтобы получить ответ на этот вопрос, исследуем некоторые простейшие типы бесконечных множеств.

Счетные множества. Если можно установить взаимно однозначное соответствие между элементами множества и элементами множества всех натуральных чисел

счетно . Иными словами, множество счетно, если все его элементы можно занумеровать посредством натуральных чисел, т. е. записать в виде последовательности

Таблица 1 показывает, что множество всех четных чисел счетно (верхнее число рассматривается теперь как номер соответствующего нижнего числа).

Счетные множества это, так сказать, самые маленькие из бесконечных множеств: во всяком бесконечном множестве содержится счетное подмножество.

Если два непустых конечных множества не пересекаются, то их сумма содержит больше элементов, чем каждое из слагаемых. Для бесконечных множеств это правило может и не выполняться. В самом деле, пусть есть множество всех четных чисел, — множество всех нечетных чисел и — множество всех натуральных чисел. Как показывает таблица 4, множества и счетны. Однако множество Таблица 4

качественно отличны от свойств конечных множеств. Переход от конечного к бесконечному сопровождается в полном согласии с известным положением диалектики — качественным изменением свойств.

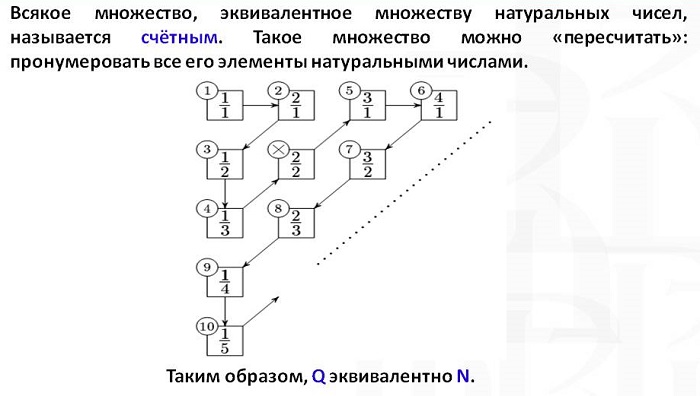
Докажем, что множество всех рациональных чисел счетно . Для этого расположим все рациональные числа в такую таблицу:

Множества мощности континуума

Если можно установить взаимно однозначное соответствие между элементами множества и точками отрезка имеет мощность континуума . В частности, согласно этому определению, само множество точек отрезка имеет мощность континуума. Здесь взаимно однозначное соответствие устанавливается геометрически, посредством проектирования.

Нетрудно показать, что множества точек любого интервала — имеют мощность континуума.

Значительно более интересен такой факт: множество точек квадрата Теория множеств Множества Формулы Алгебра Теория 25573

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Понятие множества. Способы задания множеств.

Данная тема содержит немало терминологии, поэтому я добавлю содержание темы, которое позволит легче ориентироваться в материале.

Начнём с того, что же, собственно, понимать под словом «множество». На интуитивном уровне под множеством понимают некую совокупность объектов, именуемых элементами множества. Например, можно говорить о множестве груш на столе, множестве букв в слове «множество» и так далее. Георг Кантор (немецкий математик, основатель современной теории множеств) писал, что под «множеством я понимаю вообще всё то многое, которое возможно мыслить как единое, т.е. такую совокупность определённых элементов, которая посредством одного закона может быть соединена в одно целое». Некоторое время понятие множества, введённое Кантором, полагалось довольно очевидным и не требующим дополнительных пояснений. Казалось, что появление работ Больцано, а затем и Кантора в конце 19 — начале 20 века, положит конец многим вопросам (например, окончательно разрешит апории Зенона, разрешит проблему бесконечности и т.д.) и станет началом новой математики. Гениальный немецкий математик Давид Гильберт отмечал, что «Никто не изгонит нас из рая, созданного Кантором».

Однако появление парадоксов (Рассел, Бурали-Форти) положило конец «канторовскому раю». Одна из формулировок парадокса Рассела, известная под названием «парадокс брадобрея» звучит так: в некотором селе брадобрей бреет тех и только тех жителей села, которые не бреются сами. Кто же тогда бреет самого брадобрея? Допустим, он бреет себя самостоятельно. Т.е. он принадлежит к тем жителям села, которые бреются сами, – а ведь согласно условию этих жителей брадобрей не имеет права брить. Следовательно, допущение о том, что брадобрей бреется сам, приводит к противоречию. Попробуем иначе: пусть брадобрей не бреется сам. Если он сам не бреется, то согласно условию его обязан брить брадобрей – вновь противоречие! Были предприняты попытки разрешить противоречия теории множеств, предложенной Кантором. Саму канторовскую теорию множеств математики назвали «наивной». Целью многих математических трудов стало построение такой системы аксиом, в которой подобные парадоксы были бы невозможны. Но задача оказалась не столь уж проста. На данный момент, насколько мне известно, единой аксиоматики теории множеств нет. Наиболее распространенной считается система аксиом Цермело-Френкеля (ZFC), в которой особняком стоит так называемая «аксиома выбора». Есть и вариации этой системы: например, автор B-метода Жан-Раймонд Абриал предложил типизированную теорию множеств, на основании которой создал формальный метод разработки программ.

Обозначение множеств. Принадлежность элемента множеству. Пустое множество.

Обычно множества записываются в фигурных скобках. Например, множество всех гласных букв русского алфавита будет записано так:

А множество всех целых целых чисел, больших 8, но меньших 15, будет таким:

Множество может вообще не содержать ни одного элемента. В этом случае его именуют пустым множеством и обозначают как $varnothing$.

Чаще всего в математической литературе множества обозначаются с помощью больших букв латинского алфавита. Например:

Есть и устоявшиеся обозначения определённых множеств. Например, множество натуральных чисел принято обозначать буквой $N$; множество целых чисел – буквой $Z$; множество рациональных чисел – буквой $Q$; множество всех действительных чисел – буквой $R$. Есть и иные устоявшиеся обозначения, но к ним мы станем обращаться по мере необходимости.

Множество, которое содержит конечное количество элементов, именуют конечным множеством. Если множество содержит бесконечное количество элементов, его называют бесконечным.

Например, указанное выше множество $A=$ – конечное множество, ибо содержит 4 элемента (т.е. конечное число элементов). Множество натуральных чисел $N$ является бесконечным. Вообще говоря, мы не всегда можем сразу с уверенностью сказать, бесконечно некое множество или нет. Например, пусть $F$ – множество простых чисел.

Что такое простое число: показатьскрыть

Простыми числами именуют такие натуральные числа большие 1, которые делятся лишь на 1 или на самое себя. Например, 2, 3, 5, 7 и так далее. Для сравнения: число 12 не является простым числом, так как оно делится не только на 12 и 1, а ещё и на иные числа (например, на 3). Число 12 является составным.

Возникает вопрос: бесконечно множество $F$ или нет? Существует ли наибольшее простое число? Для ответа на этот вопрос понадобилась целая теорема, доказанная Эвклидом, о том, что множество простых чисел – бесконечно.

Под мощностью множества для конечных множеств понимают количество элементов данного множества. Мощность множества $A$ обозначается как $|A|$.

Например, так как конечное множество $A=$ содержит 4 элемента, то мощность множества $A$ равна 4, т.е. $|A|=4$.

Если нам известно, что некий объект $a$ принадлежит множеству $A$, то записывают это так: $ain A$. Например, для вышеуказанного множества $A$ можно записать, что $5in A$, $-9in A$. Если же объект $a$ не принадлежит множеству $A$, то обозначается это следующим образом: $anotin A$. Например, $19notin A$. Кстати, сказать, элементами множеств могут быть и иные множества, например:

Элементами множества $M$ являются числа -9, 1, 0, а также множество $ < a,; g>$ и пустое множество $varnothing$. Вообще, для упрощения восприятия множество можно представлять как портфель. Пустое множество – пустой портфель. Эта аналогия пригодится чуть далее.

Подмножество. Универсальное множество. Равенство множеств. Булеан.

Множество $A$ называют подмножеством множества $B$, если все элементы множества $A$ являются также элементами множества $B$. Обозначение: $Asubseteq B$.

Например, рассмотрим множества $K=< -9,5>$ и $T=$. Каждый элемент множества $K$ (т.е. -9 и 5) является также элементом множества $T$. Следовательно, множество $K$ есть подмножество множества $T$, т.е. $Ksubseteq T$.

Так как все элементы любого множества $A$ принадлежат самому множеству $A$, то множество $A$ является подмножеством самого множества $A$. Пустое множество $varnothing$ является подможеством любого множества. Т.е. для произвольного множества $A$ верно следующее:

$$Asubseteq A; ; varnothingsubseteq A.$$

Введём ещё одно определение – универсальное множество.

Универсальное множество (универсум) $U$ обладает тем свойством, что все иные множества, рассматриваемые в данной задаче, являются его подмножествами.

Иными словами, универсум содержит в себе элементы всех множеств, которые рассматриваются в рамках некоей задачи. Например, рассмотрим такую задачу: проводится опрос студентов некоей академгруппы. Каждому студенту предлагается указать мобильных операторов РФ, сим-карты которых он использует. Данные этого опроса можно представить в виде множеств. Например, если студент Василий использует сим-карты от МТС и Life, то можно записать следующее:

Подобные множества можно составить для каждого студента. Универсумом в этой модели будет множество, в котором перечислены все операторы России. В принципе, в качестве универсума можно взять также множество, в котором перечислены все операторы СНГ, а также множество всех мобильных операторов мира. И это не будет противоречием, ибо любой оператор России входит в множество операторов как СНГ, так и всего мира. Итак, универсум определяется только в рамках некоей конкретной задачи, при этом зачастую можно рассмотреть несколько универсальных множеств.

Множества $A$ и $B$ называются равными, если они состоят из одних и тех же элементов. Иными словами, если каждый элемент множества $A$ является также элементом множества $B$, и каждый элемент множества $B$ является также элементом множества $A$, то $A=B$.

Определение равенства множеств можно записать и по-иному: если $Asubseteq B$ и $Bsubseteq A$, то $A=B$.

Рассмотрим пару множеств: первое будет $$, а второе – $$. Каждый элемент первого множества (т.е. $Delta$ и $k$) является также элементом второго множества. Каждый элемент второго множества (т.е. $k$ и $Delta$) является также элементом второго множества. Вывод: $=$. Как видите, порядок записи элементов в множестве роли не играет.

Рассмотрим ещё пару множеств: $X=$ и $Y=$. Каждый элемент множества $X$ является также элементом множества $Y$; каждый элемент множества $Y$ является также элементом множества $X$. Следовательно, $=$. С учётом подобных равенств в теории множеств принято одинаковые элементы не повторять в записи дважды. Например, множество цифр числа 1111111555559999 будет таким: $$. Есть, конечно, исключения: так называемые мультимножества. В записи мультимножеств элементы могут повторяться, однако в классической теории множеств повторения элементов не допускаются.

Используя понятие равенства множеств, можно классифицировать подмножества.

Если $Asubseteq B$, при этом $Aneq B$, то множество $A$ называют собственным (строгим) подмножеством множества $B$. Также говорят, что множество $A$ строго включено в множество $B$. Записывают это так: $A subset B$.

Если же некое подмножество множества $A$ совпадает с самим множеством $A$, то это подмножество называют несобственным. Иными словами, множество $A$ является несобственным подмножеством самого множества $A$.

Например, для рассмотренных выше множеств $K=< -9,5>$ и $T=$ имеем: $Ksubseteq T$, при этом $Kneq T$. Следовательно, множество $K$ является собственным подмножеством множества $T$, что записывается как $Ksubset T$. Можно сказать и так: множество $K$ строго включено в множество $T$. Запись $Ksubset T$ более конкретна, нежели $Ksubseteq T$. Дело в том, что записывая $Ksubset T$ мы гарантируем, что $Kneq T$. В то время как запись $Ksubseteq T$ не исключает случая равенства $K=T$.

Примечание относительно терминологии: показатьскрыть

Вообще говоря, тут есть некая путаница в терминологии. Приведённое выше определение несобственных множеств принято в американской и части отечественной литературы. Однако в другой части отечественной литературы есть несколько иная трактовка понятия несобственных множеств.

Если $Asubseteq B$, при этом $Aneq B$ и $Aneq varnothing$, то множество $A$ называют собственным (строгим) подмножеством множества $B$. Также говорят, что множество $A$ строго включено в множество $B$. Записывают это так: $A subset B$. Множества $B$ и $varnothing$ именуются несобственными подмножествми множества $B$.

Иными словами, пустое множество в такой трактовке исключается из собственных подмножеств и переходит в разряд несобственных. Выбор терминологии – дело вкуса.

Множество всех подмножеств некоего множества $A$ называют булеаном или степенью множества $A$. Обозначается булеан как $P(A)$ или $2^A$.

Пусть множество $A$ содержит $n$ элементов. Булеан множества $A$ содержит $2^n$ элементов, т.е.

Рассмотрим пару примеров на использование введённых выше понятий.

Из предложенного списка выберите те утверждения, которые являются верными. Ответ аргументируйте.

1. Нам заданы два множества: $$ и $$. Каждый элемент первого множества является также элементом второго множества. Следовательно, первое множество есть подмножество второго, т.е. $\subseteq $. Утверждение первого пункта – верное.
2. В первом пункте мы выяснили, что $\subseteq $. При этом данные множества не равны между собой, т.е. $\neq $. Значит, множество $$ является собственным (в иной терминологии строгим) подмножеством множества $$. Этот факт записывается как $\subset $. Итак, утверждение второго пункта истинно.
3. Множество $$ не является элементом множества $$. Утверждение третьего пункта ложно. Для сравнения: утверждение $\in , 6 >$ истинно.
4. Пустое множество является подможеством любого множества. Поэтому утверждение $varnothing subseteq varnothing$ истинно.
5. Утверждение ложно. Множество $varnothing$ не содержит элементов, а множество $$ содержит один элемент, посему равенство $varnothing=$ неверно. Чтобы это было нагляднее, можно обратиться к той аналогии, что я описал выше. Множество – это портфель. Пустое множество $varnothing$ – пустой портфель. Множество $$ – портфель, внутри которого лежит пустой портфель. Естественно, что пустой портфель и непустой портфель, внутри которого нечто есть – разные портфели
6. Пустое множество не содержит элементов. Ни единого. Поэтому утверждение $varnothing in varnothing$ ложно. Для сравнения: утверждение $varnothingin$ истинно.
7. Множество $A$ содержит 4 элемента, а именно: 9, -5, 8 и $$. Поэтому мощность множества $A$ равна 4, т.е. $|A|=4$. Следовательно, утверждение о том, что $|A|=5$ – ложно.

Ответ: Утверждения в пунктах №1, №2, №4 – истинны.

Записать булеан множества $A=$.

Множество $A$ содержит 3 элемента. Иными словами: мощность множества $A$ равна 3, $|A|=3$. Следовательно, множество $A$ имеет $2^3=8$ подмножеств, т.е. булеан множества $A$ будет состоять из восьми элементов. Перечислим все подмножества множества $A$. Напомню, что пустое множество $varnothing$ является подмножеством любого множества. Итак, подмножества таковы:

Напомню, что подмножество $$ является несобственным, так как совпадает с множеством $A$. Все остальные подмножества – собственные. Все записанные выше подмножества являются элементами булеана множества $A$. Итак:

Булеан найден, остаётся лишь записать ответ.

Способы задания множеств.

Первый способ – это простое перечисление элементов множества. Естественно, такой способ подходит лишь для конечных множеств. Например, с помощью данного способа множество первых трёх натуральных чисел будет записано так:

Часто в литературе можно встретить обозначения такого характера: $T=$. Здесь множество задаётся не перечислением элементов, как кажется на первый взгляд. Перечислить все чётные неотрицательные числа, которые и составляют множество $T$, невозможно, ибо этих чисел бесконечно много. Запись вида $T=$ допускается только тогда, когда не вызывает разночтений.

Второй способ – задать множество с помощью так называемого характеристического условия (характеристического предиката) $P(x)$. В этом случае множество записывается в таком виде:

Запись $$ читается так: «множество всех элементов $x$, для которых высказывание $P(x)$ истинно». Что именно значит словосочетание «характеристическое условие» проще пояснить на примере. Рассмотрим такое высказывание:

$$P(x)=»x; – ;натуральное; число,; последняя; цифра; которого ;равна; 7″$$

Подставим в это высказывание вместо $x$ число 27. Мы получим:

$$P(27)=»27; – ;натуральное; число,; последняя; цифра; которого ;равна; 7″$$

Это истинное высказывание, так как 27 действительно является натуральным числом, последняя цифра которого равна 7. Подставим в это высказывание число $frac$:

$$Pleft(fracright)=»frac; – ;натуральное; число,; последняя; цифра; которого ;равна; 7″$$

Это высказывание ложно, так как $frac$ не является натуральным числом. Итак, для некоторых объектов $x$ высказывание $P(x)$ может быть ложно, для некоторых – истинно (а для некоторых вообще не определено). Нас будут интересовать лишь те объекты, для которых высказывание $P(x)$ будет истинно. Именно эти объекты и образуют множество, заданное с помощью характеристического условия $P(x)$ (см. пример №3).

Третий способ – задать множество с помощью так называемой порождающей процедуры. Порождающая процедура описывает, как получить элементы множества из уже известных элементов или неких иных объектов (см. пример №4).

Записать множество $A=$ перечислением элементов.

Множество $A$ теперь задано с помощью перечисления элементов.

Описать элементы множества $M$, которое задано такой порождающей процедурой:

1. $3in M$;
2. Если элемент $xin M$, то $3xin M$.
3. Множество $M$ – является подмножеством любого множества $A$, удовлетворяющего условиям №1 и №2.

Давайте пока оставим в покое условие №3 и посмотрим, какие элементы входят в множество $M$. Число 3 туда входит согласно первому пункту. Так как $3in M$, то согласно пункту №2 имеем: $3cdot 3in M$, т.е. $9in M$. Так как $9in M$, то согласно пункту №2 получим: $3cdot 9in M$, т.е. $27in M$. Так как $27in M$, то по тому же пункту №2 имеем: $81in M$. Короче говоря, построенное множество 3, 9, 27, 81 и так далее – это натуральные степени числа 3.

$$3^1=1; ; 3^2=9; ; 3^3=27; ; 3^4=81;; ldots$$

Итак, кажется, что искомое множество задано. И выглядит оно так: $<3,9,27,81,ldots >$. Однако действительно ли условия №1 и №2 определяют только это множество?

Рассмотрим множество всех натуральных чисел, т.е. $N$. Число 3 – натуральное, посему $3in N$. Вывод: множество $N$ удовлетворяет пункту №1. Далее, для любого натурального числа $x$ множество $N$ содержит также и число $3x$. Например, 5 и 15, 7 и 21, 13 и 39 и так далее. Значит, множество $N$ удовлетворяет условию №2. И, кстати сказать, не только множество $N$ удовлетворяет условиям №1 и №2. Например, множество всех нечётных натуральных чисел $N_1=$ тоже подходит под условия пунктов №1 и №2. Как же указать, что нам нужно именно множество $<3,9,27,81,ldots >$?

Вот тут на помощь приходит пункт №3. Говоря огрублённо, он означает, что множество $M$ – наименьшее из всех возможных множеств. Так как множества $N$ и $<3,9,27,81,ldots >$ удовлетворяют пунктам №1 и №2, но $Nnsubseteq <3,9,27,81,ldots >$, то множество $N$ не удовлетворяет третьему пункту. Аналогично, так как $N_1nsubseteq <3,9,27,81,ldots >$, то множество $N_1$ также не удовлетворяет пункту №3. Можно показать (если это необходимо, отпишите мне на почту, я распишу подробнее), что всем трём пунктам удовлетворяет лишь множество $<3,9,27,81,ldots >$, т.е.

Обычно при задании множества с помощью таких правил (которые часто называют рекурсивными или индуктивными) третий пункт подразумевается, но не оговаривается явно. Но нужно иметь его в виду.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Множество и его элементы. Подмножества

Что такое «множество», мы понимаем интуитивно. В этом смысле это понятие первично, так же как «точка» или «плоскость».

Создатель теории множеств Г.Кантор описывал множество как «многое, мыслимое нами как единое».

Приведём примеры множеств:

Множество людей в салоне самолёта

Множество деревьев в парке

Множество планет Солнечной системы

Множество электронов в атоме

Множество натуральных чисел

Множество «синих-синих презелёных красных шаров»

Конечное, бесконечное и пустое множества

Людей в салоне самолёта легко посчитать, это множество конечно.

С деревьями в парке, планетами и электронами – сложней. Скорее всего, мы не сможем назвать точное количество элементов этих множеств в данный момент времени. Однако, и эти множества конечны.

Натуральное число – это идеальный объект, абстракция. Множество натуральных чисел бесконечно. Как оказалось, человек может оперировать и абстракциями, и бесконечностями.

Можно себе представить даже то, «чего на свете вообще не может быть». Поскольку таких объектов нет, их множество будет пустым. Пустое множество является частью любого другого множества.

Конечные множества

Бесконечные множества

Пустые множества

Помидоры на грядке

Числа (натуральные, рациональные, действительные и т.д.)

Количество рациональных чисел на отрезке [0;1]

Полосатые летающие слоны

Все точки пересечения двух параллельных прямых на плоскости

Способы задания множеств

1) Перечисление – в списке задаются все элементы множества.

Множество всех континентов Земли:

Множество букв слова «математика»:

Множество натуральных чисел меньших 5:

2) Характеристическое свойство – указывается особенность элементов множества.

A = $$ — множество всех действительных положительных x

B = $$ — множество всех натуральных n, кратных 5

C = $$ – множество всех действительных точек координатной плоскости (x,y), расстояние от которых до начала координат не больше 1 (круг с центром в начале координат, радиусом 1).

D = – множество всех материков планеты Земля

3) Графическое изображение – визуальное моделирование с помощью различных диаграмм (круги Эйлера, интервалы, графики и т.п.)

Подмножества

Множество A называют подмножеством множества B (A $subseteq$ B), если всякий элемент множества A также является элементом множества B:

$$ A subseteq B iff (a in Bbb A Rightarrow a in Bbb B) $$

Говорят, что B содержит A, или B покрывает A.

Пустое множество является подмножеством любого множества.

Знак $subseteq$ является аналогом $ge$, т.е. «нестрогим» неравенством. Это значит, что множества A и B могут и совпадать (любое множество является подмножеством самого себя).

Между множествами можно также ввести отношение «строгое подмножество», $A subset B$, в котором B заведомо «шире» множества A (аналог строгого неравенства $lt$).

Примеры подмножеств:

Множество людей является подмножеством приматов, живущих на Земле.

Множество натуральных чисел меньших 5 является подмножеством натуральных чисел меньших $10: A = , B = , A subseteq B$

Множество квадратов является подмножеством прямоугольников.

Множество полосатых летающих слонов – как пустое множество — является подмножеством чего угодно: приматов, чисел, прямоугольников. Что удобно для размышлений о смысле всего.

Множество всех подмножеств данного множества A называют булеаном или степенью множества A.

Булеан конечного множества из n элементов содержит $2^n$ элементов:

Примеры

Пример 1. Запишите данное множество с помощью перечисления элементов:

Задано множество целых чисел, квадрат которых меньше 5. Перечисляем:

Задано множество целых чисел, модуль которых не больше 3. Перечисляем:

Задано множество рациональных чисел, являющихся корнями уравнения

(x-1)(2x+5) = 0. Перечисляем:

Задано множество натуральных чисел, входящих в полуинтервал $9 lt n le 12$.

Пример 2. Запишите данное множество с помощью характеристического свойства:

а) Множество всех натуральных чисел меньше 10

б) Множество всех действительных чисел, кроме 0

в) Множество всех точек с целыми координатами, принадлежащих прямой y = 2x+1

г) Множество всех целых решений уравнения $x^3+x^2+4 = 0$

Пример 3. Изобразите на графике в координатной плоскости данное множество:

Задано конечное множество точек, которое можно представить перечислением:

Задано бесконечное множество точек, принадлежащих данной гиперболе $y = frac$ в данном интервале $-4 le x le -1$. На графике:

Пример 4. Укажите и запишите с помощью перечисления одно из непустых конечных подмножеств для данного множества:

Множество — виды, операции и примеры решения

Мы каждый день сталкиваемся с большим количеством одинаковых предметов, но не задумываемся о том, как называется совокупность этих объектов. Это множество — математическая единица, подчиняющаяся определенным законам и правилам, обладающая разными свойствами и функциями.

• Что такое множество в математике и как оно обозначается
• Множество натуральных чисел
• Множество целых чисел
• Множество рациональных чисел
• Операции над множествами
• Свойства операций над множествами

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A₁, A₂ и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a₁, a₂ и т. д.

Границы совокупности обозначаются фигурными скобками < >.

А = – А состоит из четырех элементов.

Записать совокупность Z согласных букв в слове «калькулятор»:

Z = , повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = , а Є N – элемент «а» принадлежит N.

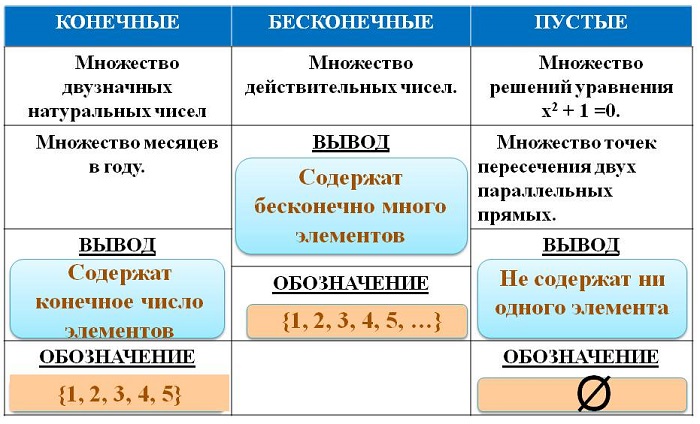
Выделяют три вида множеств:

конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);

бесконечные — не являющиеся конечными (например, числовые);

пустые (обозначаются Ø) – не имеющие элементов.

Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.

Пример: А = и В = – все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = и В = , тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

Множество натуральных чисел

К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.

Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.

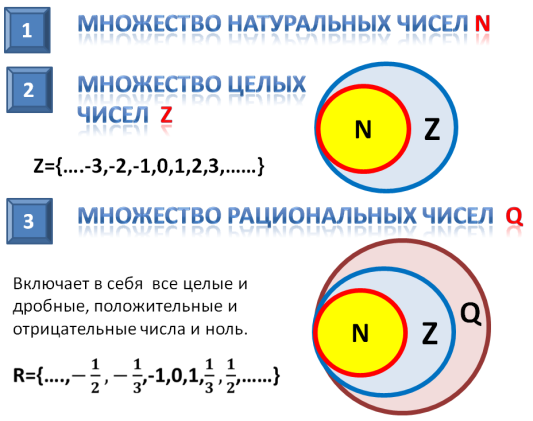
Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

5 = 5/1 = 10/2 = 25/5;

0,45 = 45/100 = 9/20.

Следовательно, N и Z являются подмножествами Q.

Операции над множествами

Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.

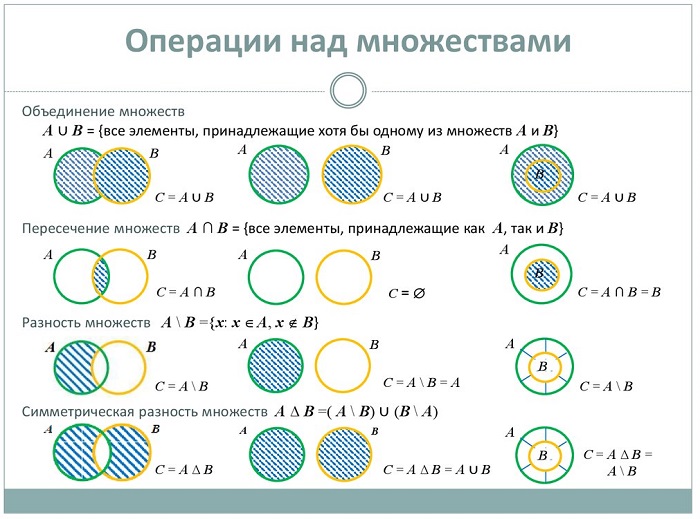
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.

Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.

Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.

В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.

Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:

Объединение

Пересечение

Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.

Свойства операций над множествами

Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:

умножения S ∩ D = D ∩ S;

сложения S ∪ D = D ∪ S.

Ассоциативность – сочетательные законы:

умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);

сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).

Дистрибутивность – законы распределения:

умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);

умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);

сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).

Транзитивность — законы включения:

если S ⊆ Fи F ⊆ J, то S ⊆ J;

если S ⊆ F и F ⊆ S, то S = F.

Идемпотентность объединения и пересечения:

О других свойствах операций можно узнать из картинки:

Счетные и несчетные множества

Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.

Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.

В случае, когда бесконечное множество равномощно натуральному ряду чисел, оно называется счетным, а если оно не равномощно — несчетным. Другими словами, счетная единица — это совокупность, которую мы можем представить в виде последовательности чисел по порядковым номерам.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.

Теория множеств — достаточно широкая тема, которая требует глубокого изучения. Она затрагивает начальный курс математики, изучается в среднем звене школьной программы по алгебре. Высшая математика, математический анализ, логика – рассматривают законы, теоремы, аксиомы множеств, на которых основаны фундаментальные знания науки.

Множество

математики, в частности, теории множеств и [1] [2] . Также возможно косвенное определение через аксиомы теории множеств. Множество может быть пустым и упорядоченным и неупорядоченным, конечным и счётным или наивной , так и в аксиоматической теориях множеств любой объект обычно считается множеством.

Содержание

История понятия

Основы теории конечных и бесконечных множеств были заложены Бернардом Больцано, который сформулировал некоторые из её принципов.

С 1872 года по 1897 год (главным образом в 1872—1884 годы) Георг Кантор опубликовал ряд работ, в которых были систематически изложены основные разделы теории множеств, включая теорию точечных множеств и теорию трансфинитных чисел (кардинальных и порядковых). В этих работах он не только ввёл основные понятия теории множеств, но и обогатил математику рассуждениями нового типа, которые применил для доказательства теорем теории множеств, в частности впервые к бесконечным множествам. Поэтому общепризнано, что теорию множеств создал Георг Кантор. В частности определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты назвал , обозначил >» width=»» height=»» />. Если некоторое множество >» width=»» height=»» />, то » width=»» height=»» /> назвал характеристическим свойством множества » width=»» height=»» />.

Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.

Так как теория множеств фактически используется как основание и язык всех современных математических теорий в 1908 году теория множеств была аксиоматизирована независимо Бертраном Расселом и Эрнстом Цермело . В дальнейшем многие исследователи пересматривали и изменяли обе системы, в основном сохранив их характер. До сих пор они всё ещё известны как теория типов Рассела и теория множеств Цермело. Впоследствии теорию множеств Кантора стало принято называть наивной теорией множеств , а вновь построенную — аксиоматической теорией множеств .

В практике, сложившейся с середины XX века множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются Элемент множества

Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами — элемент множества » width=»» height=»» />, то записывают » width=»» height=»» /> («» width=»» height=»» /> принадлежит » width=»» height=»» />»). Если » width=»» height=»» /> не является элементом множества » width=»» height=»» />, то записывают » width=»» height=»» /> («» width=»» height=»» /> не принадлежит » width=»» height=»» />»). В отличие от .

Некоторые виды множеств и сходных объектов

Специальные множества

— множество, не содержащее ни одного элемента.
• парадоксом Рассела данное понятие трактуется в настоящее время как «множество, включающее все множества, участвующие в рассматриваемой задаче». , вполне упорядоченное множество — множество, на котором задано отношение порядка.

Сходные объекты

• Вектор — элемент линейного пространства, содержащий конечное число элементов некоторого поля в качестве координат. Порядок имеет значение, элементы могут повторяться. — функция одного натурального переменного. Представляется как бесконечный набор элементов (не обязательно различных), порядок которых имеет значение.
• функцией. Иными словами, относительно элементов нечёткого множества можно говорить «в какой мере» они в него входят, а не просто, входят они в него или нет.

По иерархии

• Множество множеств (в частности, булеан — множество всех подмножеств данного множества).
• Надмножество

Отношения между множествами

Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество М состоит из чисел 1; 2; 3, то его обозначают так: М = . Тот факт, что число 2 входит в это множество (является элементом данного множества М), записывается с помощью специального значка ∈ следующим образом: 2 ∈ М; а то, что число 5 не входит в это множество (не является элементом данного множества), записывается так: 5 ∉ М.

Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество.

Например: множество простых делителей числа 1 — пустое множество.

Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом ∅, множество всех натуральных чисел — буквой N, множество всех целых чисел — буквой Z, множество всех рациональных чисел — буквой Q, а множество всех действительных чисел — буквой R.

Множества бывают конечными и бесконечными в зависимости от того, какое количество элементов они содержат. Так, множества А = и M = — конечные, потому что содержат конечное число элементов, а множества N, Z, Q, R — бесконечные.

Множества задают или с помощью перечисления их элементов (это можно сделать только для конечных множеств), или с помощью описания, когда задается правило (характеристическое свойство), которое позволяет определить, принадлежит или нет данный объект рассматриваемому множеству. Например, А = (множество задано перечислением элементов), B — множество всех четных целых чисел (множество задано характеристическим свойством всех элементов множества). Последнее множество иногда записывают так: B = или так: B = ∈ Z> — здесь после вертикальной черточки записано характеристическое свойство*.

В общем виде запись множества с помощью характеристического свойства можно обозначить так: A = , где P (x) — характеристическое свойство. Например, = < –1, 1>, ∈ R и x2 + 1 = 0> = ∅.

1. Равенство множеств. Пусть А — множество всех цифр трехзначного числа 312, то есть A = , а B — множество всех натуральных чисел, меньших четырех, то есть B = . Поскольку эти множества состоят из одних и тех же элементов, то они считаются равными. Это записывают так: A = B. Для бесконечных множеств таким способом (сравнивая все элементы) установить их равенство невозможно. Поэтому в общем случае равенство множеств определяется следующим образом.

Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества.

Из приведенного определения равенства множеств следует, что в множестве одинаковые элементы не различаются. Действительно, например, = , поскольку каждый элемент первого множества (1 или 2) является элементом второго множества и, наоборот, каждый элемент второго множества (1 или 2) является элементом первого. Поэтому, записывая множество, чаще всего каждый его элемент записывают только один раз.

Если каждый элемент множества A является элементом множества B, то говорят, что множество A является подмножеством множества B.

Это записывают следующим образом: A ⊂ B.

Например, ⊂ , N ⊂ Z (поскольку любое натуральное число — целое), Z ⊂ Q (поскольку любое целое число — рациональное), Q ⊂ R (поскольку любое рациональное число — действительное).

Полагают, что всегда ∅ ⊆ A, то есть пустое множество является подмножеством любого множества.

Иногда вместо записи A ⊂ B используется также запись A ⊆ B.

Сопоставим определение равенства множеств с определением подмножества. Если множества А и В равны, то: 1) каждый элемент множества А является элементом множества В, следовательно, А — подмножество В (A ⊆ B); 2) каждый элемент множества В является элементом множества А, следовательно, В — подмножество А (B ⊆ A). Таким образом,

два множества равны тогда и только тогда, когда каждое из них является подмножеством другого.

Иногда соотношения между множествами удобно иллюстрировать с помощью кругов (которые часто называют кругами Эйлера–Венна). Например, рисунок 1 иллюстрирует определение подмножества, а рисунок 2 — отношения между множествами N, Z, Q, R.

Похожие записи:

• 

  Что такое зависимость между числами

• 

  Что такое суть разговора

• 

  Что ответить девушке на вопрос за что ты меня любишь

• 

  Что такое задача в математике определение

• 

  Что такое загадка определение для детей дошкольного возраста

• 

  Что такое задача для дошкольников как объяснить