Обучение дошкольников решению простых арифметических задач
Решение простых арифметических задач уместно сочетать с формированием представлений об образовании числа, состава числа из двух меньших чисел. Так, например, на этапе работы по образованию числа «2» воспитатель дает детям «задачу»: «На полянке был один зайчик, к нему прискакал еще один зайчик. Сколько зайчиков стало на полянке?» А на этапе формирования представлений об образовании числа «4» дети уже сами по аналогии с задачей воспитателя составят свою — например, про белочек: «На полянке было три белочки, прибежала еще одна белочка. Сколько белочек стало на полянке?»
Алгоритм обучения простым арифметическим задачам
Образование числа, состав числа из двух меньших чисел
2
3
4
5
6
7
8
9
Готовые задачи дает педагог
Составление задач детьми по аналогии с задачами педагога
Формирование представлений об условии задачи
Формирование представлений о вопросе задачи
Формирование представлений о структуре задачи
Формирование представлений о решении
Рассмотрим содержание таблицы 1 подробнее.
П.1. Сначала педагог дает детям готовые задачи на полной предметной наглядности. Здесь тоже работает свой алгоритм усложнения (см. Таблица 2).
Таблица 2
Алгоритм решения готовых задач на полной предметной наглядности
Усложнение в использовании наглядности
Образование числа, состав числа из двух меньших чисел
2
3
4
5
6
7
8
9
С опорой на деятельность с игрушками, предметами
С опорой на сюжетные картинки
С опорой на предметные картинки
С опорой на схемы
Без опоры на наглядность
Во время игр или иной детской деятельности воспитатель в форме задачи комментирует действия детей с игрушками, предметами: «У Коли был один кубик. Настя дала ему еще один кубик. Сколько стало кубиков у Коли?». С этой целью в группе можно использовать самые разные игровые и бытовые ситуации: посадили кукол на диван, поставили чашки на стол, покатали ежиков в машинке, слепили снежки, застегнули пуговицы, посадили луковицы и пр. Самое главное, чтобы в задачах отражался конкретный, понятный ребенку сюжет, и предметы (игрушки) были максимально простыми для восприятия.
Постепенно к этому приему добавляется следующий (П 2). Детям предлагается по аналогии с задачами педагога составить свою. (см. Таблица 3).
Таблица 3
Усложнение в составлении задач детьми по аналогии с задачами педагога
Усложнение в составлении задач
Образование числа, состав числа из двух меньших чисел
2
3
4
5
6
7
8
9
С опорой на действия с игрушками, предметами
С опорой на сюжетные картинки
С опорой на предметные картинки
С опорой на схемы
Без опоры на наглядность
По сюжетным картинкам детям легче составлять задачу, т.к. в них подсказано действие (мальчики слепили снеговика). Но предметные картинки позволяют активизировать жизненный опыт детей, включить воображение. Например, на картинке изображены четыре тюльпана и один тюльпан. В детских задачах эти тюльпаны сажают, покупают, продают, дарят, поливают, срезают, ставят в вазу, рисуют, вырезают, вышивают и пр.
С опорой на схемы (например, схема состава числа пять из двух меньших чисел) составлять задачи еще сложнее. Поэтому на первом этапе детям можно к ним давать схематичное изображение мышки, цыпленка, рыбки, кораблика, домика, жука и пр., чтобы помочь разнообразить содержание задач.
П.3. Формирование представлений об условии задачи (условие задачи — это то, что мы знаем).
Цель: понимание смысла количественных изменений (добавили – стало больше, убавили – стало меньше, а также; пришел – ушел, дал (он) – дали (ему), подошли – отошли, подарил (он) – подарили (ему), взял – отдал, взял (он) — взяли (у него), подняли – опустили, принесли – унесли, прилетели – улетели и др. — Больше стало или меньше? Значит, будем прибавлять или вычитать?).
Формируем у детей понимание того, что в задаче обязательны два числовых исходных данных. Обсуждаем, чем задача отличается от рассказа?
Чем задача отличается от загадки?
Загадываем: Один говорит, два глядят, а двое слушают. Или: Четыре братца под одной крышей живут. Это задачи?
П.4. Формирование представлений о вопросе задачи (что не знаем, но хотим узнать).
Цель: раскрыть арифметическое значение вопроса задачи, дифференциация понятий стало – осталось. Здесь помогут задачи-шутки, например: В автобусе ехало пять пассажиров. На остановке зашел еще один пассажир. Как звали водителя?
Необходимо соблюдать последовательность в усложнении содержания задач:
- Простые задачи на сложение
- Простые задачи на вычитание
- Прямые и обратные задачи (слышится прибавить, а надо вычитать)
- Задачи на понятие разностных отношений (Леша вылепил 6, а Коля — на 1 больше. Сколько вылепил Коля?)
Таким образом, можно выделить требования к задачам для дошкольников:
- Простота сюжета
- Краткость и конкретность изложения
- Динамика содержания
- Ярко выраженные количественные отношения между объектами
Особо надо отметить задачи в стихах. Часто в них многословность отвлекает детей от количественных изменений, не позволяет понять динамику (прибавление – убавление). Так, вместо задачи:
«У домика утром
Два зайца сидели
И дружно веселую песенку
Пели.
Один убежал,
А второй вслед глядит.
Сколько у домика
Зайцев сидит?»
лучше сказать: «У домика сидели два зайца. Один убежал. Сколько зайцев осталось у домика?».
Методика обучения дошкольников составлению и решению задач.
материал по математике (подготовительная группа)
Данный материал поможет педагогам при обучению решения и составления задач дошкольниками по ФЭМП.
Скачать:
| Вложение | Размер |
|---|---|
| metodika_obucheniya_resheniyu_zadach_po_matematike.docx | 22.82 КБ |
Предварительный просмотр:
Методика обучения дошкольников составлению и решению задач
1. Значение обучения решению арифметических задач в умственном развитии дошкольников
2. Виды арифметических задач
3. Этапы и методические приемы обучения решению задач
4. Типичные ошибки детей при составлении задач
5. Наглядные пособия по обучению детей составлению и решению задач
1. Значение. В процессе математического и общего развития детей дошкольного возраста существенное место занимает обучение их решению и составлению простых арифметических задач. В детском саду проводится подготовительная работа по формированию у детей уверенных навыков вычислений при сложении и вычитании однозначных чисел с целью подготовки их к обучению в начальной школе. Если в школе обучение вычислениям ведется при решении примеров и арифметических задач, то в практике работы дошкольных учреждений принято знакомить детей с арифметическими действиями и простейшими приемами вычисления на основе простых задач, в условии которых отражаются реальные, в основном игровые и бытовые ситуации. В условии задачи указываются связи между данными числами, а также между данными и искомыми. Эти связи и определяют выбор арифметического действия. Установив эти связи, ребенок довольно легко приходит к пониманию смысла арифметических действий и значения понятий «прибавить» , «вычесть» , «получится» , «останется» . Решая задачи, дети овладевают умением находить зависимости между величинами.
Вместе с тем задачи являются одним из средств развития у детей логического мышления, смекалки, сообразительности. В работе с задачами совершенствуются умения проводить анализ и синтез, обобщать и конкретизировать, раскрывать основное, выделять главное в тексте задачи и отбрасывать несущественное, второстепенное. При решении задач ребенок должен научиться рассуждать, доказывать, аргументировать свои действия, должен понять, какие числовые данные с какими должны вступать во взаимодействие, что нужно сложить, а что нужно вычесть. Именно эта, часто скрытая в задаче сторона, должна стать явной для ребенка.
Важно, чтобы содержание задачи соответствовало реальной жизни, так как это воспитывает у детей вдумчивое отношение к фактам, учит критически анализировать их, помогает усвоению логических связей и количественных отношений… Работа над задачами приучает детей к дисциплинированному поведению, вниманию, то есть обеспечивает воспитательно-образовательный эффект.
2. Виды арифметических задач, используемые в работе с дошкольниками
Простые задачи, т. е. задачи, решаемые одним действием (сложением или вычитанием, принято делить на следующие группы.
К первой группе относятся простые задачи, при решении которых дети усваивают конкретный смысл каждого из арифметических действий, т. е. какое арифметическое действие соответствует той или иной операции над множествами (сложение или вычитание) . Это задачи на нахождение суммы двух чисел и на нахождение остатка (На дереве сидело две птички, прилетела еще одна. Сколько птичек стало на дереве).
Ко второй группе относятся простые задачи, при решении которых надо осмыслить связь между компонентами и результатами арифметических действии. Это задачи на нахождение неизвестных компонентов («Нина вылепила из пластилина несколько грибков и мишку, а всего она вылепила 8 фигур. Сколько грибков вылепила Нина?»).
К третьей группе относятся простые задачи, связанные с понятием разностных отношений :
а) увеличение числа на несколько единиц («Леша вылепил 6 морковок, а Костя на одну больше. Сколько морковок вылепил Костя?»);
б) уменьшение числа на несколько единиц («Маша вымыла 4 чашки, а Таня на одну чашку меньше. Сколько чашек вымыла Таня?»).
В зависимости от используемого для составления задач наглядного материала они делятся на
1. Особенность задач-драматизаций состоит в том, что содержание их непосредственно отражает жизнь самих детей, т. е. то, что они только что делали или обычно делают (пример) . В задачах-драматизациях наиболее наглядно раскрывается их смысл. Дети начинают понимать, что в задаче всегда отражается конкретная жизнь людей. Задачи этого вида особенно ценны на первом этапе обучения: дети учатся составлять задачи про самих себя, рассказывать о действиях друг друга, ставить вопрос для решения, поэтому структура задачи на примере задач-драматизаций наиболее доступна детям.
2. Особое место в системе наглядных пособий занимают задачи-иллюстрации с картинками или игрушками. Если в задачах-драматизациях все предопределено, то в задачах-иллюстрациях при помощи игрушек создается простор для разнообразия сюжетна, эти задачи развивают воображение, стимулируют, память и умение самостоятельно придумывать задачи, а, следовательно, подводят к решению и составле-нию устных задач.
Требования к картинкам : простота сюжета, динамизм содержания и ярко выраженные количественные отношения между объектами (пример) .
3. Последовательные этапы и методические приемы в обучении решению арифметических задач
Обучение дошкольников решению задач проходит через ряд взаимосвязанных между собой этапов.
Первый этап — подготовительный.
Основная цель этого этапа — организовать систему упражнений по выполнению операций над множествами (объединение множеств, выделение части множества. С помощью операций над множествами раскрывается отношение «часть — целое» , доводится до понимания смысл выражений «больше на.» , «меньше на.» .
Учитывая наглядно-действенный и наглядно-образный характер мышления детей, работа над множествами проводится на конкретных предметах (отсчитать и положить на карточку шесть грибов, а затем добавить еще 1 гриб. «Сколько всего стало грибов? Почему их стало семь? К шести грибам прибавили 1 (показывает на предметах) и получили семь. На сколько стало больше грибов?»
Второй этап Основная его цель — учить детей составлять задачи и подводить к усвоению их структуры.
Подводить к пониманию структуры задачи лучше всего на задачах-драматизациях. Воспитатель знакомит детей со словом задача и при разборе составленной задачи подчеркивает необходимость числовых данных и вопросов : «Что известно?» , «Что нужно узнать?» .
На этом этапе обучения составляются такие задачи, в которых вторым слагаемым или вычитаемым является число 1 (для чего это нужно) . Это важно учитывать, чтобы не затруднять детей поиском способов решения задачи. Прибавить или вычесть число 1 они могут на основе имеющихся у них знаний об образовании последующего или предыдущего числа.
Например, воспитатель просит ребенка, принести и поставить в стакан семь флажков, а в другой — один флажок. Эти действия и будут содержанием задачи, которую составляет воспитатель. Текст задачи произносится так, чтобы было четко отделено условие, вопрос и числовые данные. Составленную задачу повторяют двое-трое детей. Воспитатель при этом должен следить, чтобы дети не забывали числовые данные, правильно формулировали вопрос.
При обучении дошкольников составлению задач важно показать, чем отличается задача от рассказа, загадки, подчеркнуть значение и характер вопроса.
Для усвоения значения и характера вопроса в задаче можно применить такой прием : к условию задачи, составленной детьми, ставится вопрос не арифметического характера («С одной стороны стола поставили двух девочек, а с другой стороны одного мальчика.» «Как зовут этих детей?» ). Дети замечают, что задача не получилась. Далее можно предложить им самим поставить такой вопрос, чтобы было понятно, что это задача. Следует отметить, что вопрос в задаче обязательно начинается со слова сколько.
Чтобы показать отличие задачи от рассказа и подчеркнуть значение чисел и вопроса в задаче, воспитателю следует предложить детям рассказ, похожий на задачу. В рассуждениях по содержанию рассказа отмечается, чем отличается рассказ от задачи.
Чтобы научить детей отличать задачу от загадки, воспитатель подбирает такую загадку, где имеются числовые данные. Например : «Два кольца, два конца, а посередине гвоздик» . Вместе с детьми рассуждаем, что в этой загадке описываются ножницы и решать ничего не надо, в загадке необходимо догадаться о каком предмете идет речь, а в задаче узнать о количестве, сколько получится или останется предметов.
Закрепляя эти знания можно предложить детям преобразовать загадку или рассказ в задачу.
Также, продолжая учить детей составлять задачи, нужно особо подчеркнуть необходимость числовых данных. Например, воспитатель предлагает следующий текст задачи: «Лене я дала гусей и уток. Сколько птиц я дала Лене?» В обсуждении этого текста выясняется, что такой задачи решить нельзя, так как не указано, сколько было дано гусей и сколько – уток, детям предлагается исправить ошибку.
Чтобы убедить детей в необходимости наличия не менее двух чисел в задаче, можно предложить детям задачу, выпустив при этом одно числовое данное : «Сережа держал в руках четыре воздушных шарика, часть из них улетела. Сколько шариков осталось у Сережи?» Дети приходят к выводу, что такую задачу решить невозможно, так как в ней не указано, сколько шариков улетело, опять детям предлагается исправить ошибку.
После таких упражнений можно подвести детей к пониманию составных частей задачи. Основными элементами задачи являются условие и вопрос. В условии содержатся отношения между числовыми данными. Анализ условия подводит к пониманию известных данных (условие это то, что нам известно) и к поискам неизвестного (вопрос) . Этот поиск идет в процессе решения задачи. Детям надо объяснить, что решать задачу — это значит понять и рассказать, какие действия нужно выполнить с данными числами, чтобы получить ответ.
Таким образом, структура задачи включает четыре компонента :
Наглядно структуру задачи дошкольником хорошо представить в виде наглядной модели «ПИРАМИДКА» , где каждое звено пирамидки обозначает компонент задачи, если выпустили один из компонентов, то пирамидка не соберется, детям будет видно, что они допустили ошибку.
Выяснив структуру задачи, следует перейти к выделению в ней отдельных частей. Дошкольников следует поупражнять в повторении простейшей задачи в целом и отдельных ее частей. Можно предложить одним детям повторить условие задачи, а другим поставить в этой задаче вопрос.
Формулируя вопрос, дети, как правило, употребляют слова : стало, осталось (стоит обратить внимание, что при постановке вопроса, дети часто употребляют ошибочно слово «стало» , как в задачах на сложение, так и на вычитание). Следует показывать им, что формулировка вопроса в задачах на сложение может быть разной, в вопросе можно употреблять глаголы, отражающие действия по содержанию задачи (Прилетели, купили, выросли, гуляют, играют и т. д.) .
Когда дети научатся правильно формулировать вопрос, можно перейти к следующей задаче этого этапа — учить анализировать задачи, устанавливать отношения между данными и искомым, выбор арифметического действия. (Например, «На площадке гуляли 3 мальчика, 1 ушел домой. Сколько осталось мальчиков?» Назовите условие задачи, что нам известно? Назовите вопрос (что надо узнать) . Если 1 мальчик ушел, мальчиков стало больше или меньше? Если стало меньше, то надо прибавить или вычесть)
Следует помнить, что обучающее значение задач на сложение и вычитание состоит не столько в том, чтобы получить ответ, а в том, чтобы научить анализировать задачу и в результате этого правильно выбрать нужное арифметическое действие.
Итак, на втором этапе работы над задачами дети должны:
а) научиться составлять задачи;
б) понимать их отличие от рассказа и загадки;
в) понимать структуру задачи;
г) уметь анализировать задачи, устанавливая отношения между данными и искомыми.
Важно при решении задач обращать внимание на правильную и полную формулировку ответа на вопрос задачи.
По теме: методические разработки, презентации и конспекты

Консультация для педагогов ДОУ «Методика обучения дошкольников решению задач»
В процессе математического и общего развития детей дошкольного возраста существенное место занимает обучение их решению и составлению простых арифметических задач. В детском саду проводится подготовит.

Конспект ООД по образовательной области «Познавательное развитие» в подготовительной группе «На помощь к Буратино» (обучение составлению и решению задач на сложение в пределах 10)
Открытый показ на семинаре школы молодого педагога «Ступеньки» за 2014 -2015 г.

Методика обучения дошкольников составлению логических рассказов по серии картинок

Методика обучения дошкольников составлению логических рассказов по серии картинок

Составление и решение задач на сложение для дошкольников (по картинкам)
ЦЕЛЬ:учить детей составлять и решать задачи на сложение, выделяя их составные части (условие, вопрос, решение, ответ).Развивать мышление, внимание и речь.

Конспект Непосредственной образовательной деятельности по ФЭМП «Обучение детей составлению и решению арифметических задач»
Дать детям представление об арифметической задаче.

Занятие по ФЭМП для старших дошкольников «Составление и решение задач с опорой на сюжетные картинки»
Закреплять навыки детей составлять и решать задачи с опорой на сюжет картинки.
Математические задачи игры для дошкольников
Составление и решение задач. Игры-задачи для детей дошкольного возраста
Когда ребенок освоит простейшие приемы сложения и вычитания, вы можете перейти к составлению и решению простейших задач.
Как составлять и решать задачи. Главными составляющими задачи являются условие и вопрос. Размышляя над условием, ребенок выделяет известные величины и стремится найти неизвестные. Поиск неизвестных величин и есть решение задачи. Решить задачу — значит понять и рассказать, какие действия с данными числами надо выполнить, чтобы получить ответ. Любая задача состоит из условия, вопроса, решения и ответа. Ребенок должен научиться выделять эти основные части задачи. Вы можете тренировать его следующим образом: вы повторяете условие задачи, а ребенок формулирует вопрос, например:
Задача 1. Вы рассказываете условие задачи: «На ветке сидели 3 сороки. Затем прилетели еще 2». А ребенок формулирует вопрос: «Сколько теперь стало сорок?». Вопрос сформулирован правильно, но стоит пояснить, что вместо слов «стало теперь» лучше подобрать глагол, отражающий содержание задачи: «Сколько сорок сидит на ветке?» Всегда старайтесь использовать глаголы, называющие действия, присутствующие в содержании задач.
Хорошей практикой являются игры-задачи, составленные на основании выполненных действий.
Игра-задача 1. Поставьте в одну вазу 3 гвоздики, а в другую 1. Предложите малышу описать ваши действия: «Маша поставила в одну вазу 3 гвоздики, а в другую 1 гвоздику». Описывая ваши действия, ребенок уже составляет условие задачи. Обратите его внимание на этот факт: «Это и есть условие задачи. Что нам известно из условия? Что в одной вазе стоит 3 гвоздики, а в другой 1». Запишите эти данные цифрами или выложите карточками: 3+1. «Что же нам надо узнать?» — пусть ребенок подскажет вам ответ: «Сколько всего гвоздик в обеих вазах». Решаем задачу: 3+1=4. Пусть малыш запишет решение или выложит его предметными карточками.
Аналогично анализируем задачу на вычитание.
Игра-задача 2. Предложите ребенку расставить на столе 5 чашек, а затем уберите 1. Предложите ему самостоятельно составить условие задачи, описав действия, свои и ваши: Оля расставила на стол 5 чашек, а мама убрала одну».
Итак, это условие задачи. Из него известно, что было 5 чашек на столе. А одну убрали. Что же требуется узнать, что неизвестно в задаче? Пусть ребенок сформулирует вопрос самостоятельно: «Сколько чашек осталось на столе?» Запишите данные цифрами и решите задачу: 5-1=4.
Описывая математические действия, дети, как правило, используют бытовые слова: стало, будет, отнять, прибавить. Старайтесь закрепить в речи ребенка математические термины: сложить, вычесть, получится, равняется.
Необходимо научить ребенка правильно формулировать математические действия. Для начала предложите ему задачи с одними и теми же числами на разные действия.
Задача 1. У Маши было 3 апельсина. Один она съела. Сколько апельсинов осталось? Что нужно сделать, чтобы узнать, сколько осталось апельсинов?
Предполагаемый ответ: «Из трех апельсинов вычесть один». Запишите цифрами решение и ответ: 3-1=2. Осталось два апельсина.
Задача 2. Лене дали 3 яблока и 1 грушу. Сколько всего фруктов у Лены? Что нужно сделать, чтобы узнать, сколько всего у Лены фруктов.
Правильный ответ: «Нужно сложить три и один. Получится 4. Всего у Лены фруктов 4.»
Хорошо также потренироваться решать задачи внешне похожие, но требующие выполнения разных арифметических действий.
Задача 1. На крыше сидело три голубя. Один улетел. Сколько голубей осталось на крыше? Решение: 3-1=2.
Задача 2. На крыше сидело 3 голубя. Прилетел еще один. Сколько теперь голубей на крыше?
Вопрос, помогающий ребенку сформулировать арифметическое действие, сначала вы будете задавать конкретно и близко к содержанию задачи: «Что надо сделать, чтобы узнать, сколько голубей сидит на крыше?» Когда ребенок научится без труда формулировать арифметические действия, вы будете задавать вопрос общего вида: «Что нужно сделать, чтобы решить эту задачу?»
Мы рассмотрели в качестве примера самые простые задачи, решение которых поможет вашему ребенку понять смысл арифметических действий — сложения и вычитания. Это были задачи на нахождение суммы двух чисел и нахождение остатка. Немного сложнее задачи на нахождение неизвестного компонента.
Задача 1. Найти первое слагаемое при известной сумме и втором слагаемом.
Вера нарисовала несколько кружков и 1 треугольник. Всего она нарисовала 5 фигур. Сколько кружков она нарисовала?
Задача 2. Найти второе слагаемое, если известна сумма и первое слагаемое. Миша вырезал из бумаги один квадрат и несколько треугольников. Всего он вырезал 7 фигур. Сколько треугольников вырезал Миша?
Задача 3. Найти уменьшаемое, если известны вычитаемое и разность.
У Антона было несколько груш. Одну он отдал Тане. У него осталось три груши. Сколько груш было у Антона?
Задача 4. У Оли было 7 конфет. Она отдала Ире несколько. У нее осталось пять конфет. Сколько конфет Оля отдала Ире?
Еще одна разновидность несложных задач, которые полезно научиться решать ребенку— задачи, связанные с разностными отношениями.
Задача 1. Увеличение числа. Юля съела 2 пирожных, а Вова на одно больше. Сколько пирожных съел Вова?
Задача 2. Уменьшение числа. Вика вымыла три чашки, а Катя на одну меньше. Сколько чашек вымыла Катя?
Еще одним важным звеном в математической подготовке ребенка является умение ребенка читать цифровую запись арифметических действий и составлять задачи по этой записи, например: 3+1=4. К трем яблокам прибавить одно яблоко. Получится 4 яблока.
Вы можете превратить составление задач по числовому примеру в интересную и увлекательную игру, представив их как задачи-драматизации. Содержание таких задач отражает жизнь вашего ребенка и его окружающих
Разнообразьте сюжеты задач драматизаций, используя события и предметы окружающей реальности. Героями этих задач вы можете сделать вашего ребенка и себя, полюбившихся персонажей мультфильмов, привлечь наиболее интересные для малыша образы и темы.
Задачи-картинки. Вы можете самостоятельно нарисовать такие картинки вместе с вашим ребенком, придумав их сюжет. Количественное соотношение предметов на картинке должно быть ярко выражено. Например, на картинке изображены 3 самоката и один велосипед. К одной такой картинке можно придумать 1—2 варианта задач. Можно также использовать предметные картинки, иллюстрируя ими цифровую запись задачи.
Ярким наглядным пособием к составлению и решению задач может стать самостоятельно приготовленное тематическое панно. Вы можете использовать любую картинку достаточно крупного размера: натюрморт, пейзаж с изображением лесной поляны, пляжа, стадиона, городской улицы. В панно делают надрезы, в которые затем вставляют фигурные изображения предметов, задействованных в условии задачи. Соответственно, это могут быть фигурки зверей, птиц, растений, спортсменов, машин. Такое оформление задач позволит поддержать интерес ребенка к занятиям, сделать их интересными и веселыми.
Методика обучения дошкольников умению решать задачи
Автор: Демидова Ольга Владимировна
Должность: воспитатель
Учебное заведение: МБДОУ №51
Населённый пункт: Московская область, Сергиево-Посадский рн, Г.Хотьково
Наименование материала: Реферат
Тема: Методика обучения дошкольников умению решать задачи
Раздел: дошкольное образование
«Омутнинский колледж педагогики, экономики и права»
МДК 03.04. «Теория и методика математического развития»
Тема: «Методика обучения дошкольников составлять и решать
арифметические задачи»
Выполнила: Демидова
Ольга Владимировна
Специальность 44.02.01
Дошкольное образование,
курс 5 , группа 6
Московская область, Сергиево-Посадский р-н, г.Хотьково
Значение обучения решению арифметических задач в умственном развитии
Виды арифметических задач………………………………………………6 стр
Этапы и методические приемы обучения решению задач………………9 стр
Особенности понимания старшими дошкольниками арифметической
Список использованной литературы………………………………………19 стр
важное место. Это вызвано целым рядом причин: началом школьного обучения
обучения более интенсивным, стремлением родителей в связи с этим как можно
раньше научить ребенка узнавать цифры, считать, решать задачи.
Знакомство с величиной, формой, пространственным ориентированием
начинается у ребенка очень рано, уже с младенческого возраста. Он на каждом
шагу сталкивается с тем, что нужно учитывать величину и форму предметов,
правильно ориентироваться в пространстве, считать.
Умение решать разнообразные математические задачи –это необходимое
обучения. В процессе решения проблемной ситуации взрослый учит ребенка,
незнакомые условия. Нередко для получения ответа требуется открытие нового
способа: в этом случае ребенок может идти путем опытных проб. Особое
ответам. Анализируя вместе с детьми путь решения и вывод, который был
сделан, взрослый помогает им понять ошибочность решения и подводит к
способу нового поиска.
Важно, чтобы содержание задачи соответствовало реальной жизни,
Значение обучения решению арифметических задач в умственном
развитии дошкольников
В современном обществе все больше внимания уделяется обучению,
воспитанию и развитию подрастающего поколения. Особая роль в образовании
личности (П. П. Блонский, Л.С. Выготский, А. Н. Леонтьев, Д. Б. Эльконин и
др. ).Огромное значение в образовании, развитии, социальной адаптации и
математических представлений у дошкольников.
возраста существенное место занимает обучение их решению и составлению
простых арифметических задач. В детском саду проводится подготовительная
сложении и вычитании однозначных чисел с целью подготовки их к обучению в
начальной школе. Если в школе обучение вычислениям ведется при решении
которых отражаются реальные, в основном игровые и бытовые ситуации. В
условии задачи указываются связи между данными числами, а также между
действия. Установив эти связи, ребенок довольно легко приходит к
«прибавить», «вычесть», «получится», «останется».
Решая задачи, дети овладевают умением находить зависимости между
Песталоцци, К. Д. Ушинский, М. Монтесори, Ф. Н. Блехер, А. М. Леушина, В.
И. Логинова. Л. Н. Вахрушева и др.). Разработаны многочисленные программы
развития и воспитания детей в дошкольных учреждениях, в которых отражены
представлений: «Детский сад – дом радости» (И. М. Крылова, В. Т. Иванова),
«Радуга» (Т. Н. Доронова, С. Г. Якобсон и др.), «Развитие» (Л. А. Венгер и др.),
«Детство» (В. И. Логинова, Т. И. Бабаева, Н.А. Ноткина и др.). Формирование
Вместе с тем задачи являются одним из средств развития у детей
логического мышления, смекалки, сообразительности. В работе с задачами
совершенствуются умения проводить анализ и синтез, обобщать и
конкретизировать, раскрывать основное, выделять главное в тексте задачи и
отбрасывать несущественное, второстепенное. При решении задач ребенок
должен научиться рассуждать, доказывать, аргументировать свои действия,
взаимодействие, что нужно сложить, а что нужно вычесть. Именно эта, часто
скрытая в задаче сторона, должна стать явной для ребенка.
Математика проникает почти во все области деятельности человека, что
связи с этим стало жизненно необходимым усовершенствовать математическую
подготовку подрастающего поколения.
Решение задач – это работа несколько необычная, а именно умственная
работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо
помощью которых выполняется эта работа. Значит, для того чтобы научиться
решать задачи, надо разобраться в том, что собой они представляют, как они
устроены, из каких составных частей они состоят, каковы инструменты, с
помощью которых производится решение задач. Каждая задача – это единство
условия и цели. Если нет одного из этих компонентов, то нет и задачи. Это
составляют одно целое.
Математическая задача – это связанный лаконический рассказ, в котором
неизвестные значения величин, зависимые от данных и связанные с ними
определенными соотношениями, указанными в условии.
Виды арифметических задач
арифметических задач: простые задачи, т.е. задачи, решаемые одним действием
(сложением или вычитанием),
принято делить на
задачи-драматизации , задачи-иллюстрации и устные задачи.
К первой группе относятся простые задачи, при решении которых дети
усваивают конкретный смысл каждого из арифметических действий, т. е.
множествами (сложение или вычитание). Это задачи на нахождение суммы двух
чисел и на нахождение остатка . (На дереве сидело две птички, прилетела еще
одна. Сколько птичек стало на дереве?).
Ко второй группе относятся простые задачи, при решении которых надо
вылепила из пластилина несколько грибков и мишку, а всего она вылепила 8
фигур. Сколько грибков вылепила Нина?»).
К третьей группе
относятся простые задачи, связанные с понятием
а) увеличение числа на несколько единиц («Леша вылепил 6 морковок, а
Костя на одну больше. Сколько морковок вылепил Костя?»);
б) уменьшение числа на несколько единиц («Маша вымыла 4 чашки, а
Таня на одну чашку меньше. Сколько чашек вымыла Таня?»).
раскрывается новый смысл арифметических действий, но с ними, как правило,
элементарному пониманию отношений между компонентами и результатами
арифметических действий – сложения и вычитания.
В принципе оба вида задач (простые и составные) доступны детям
подготовительной группы, но в известной последовательности. Сначала следует
арифметических действий и усвоения способов решения допустимо решение
и задач второго вида, но с начала с облегченными числовыми данными (когда
второе слагаемое или вычитаемое является единицей).
материала они делятся на :
непосредственно отражает жизнь самих детей, т.е. то, что они только что делали
или обычно делают . В задачах-драматизациях наиболее наглядно раскрывается
их смысл. Дети начинают понимать, что в задаче всегда отражается конкретная
жизнь людей. Умение вдумываться в соответствие содержания задачи реальной
Задачи этого вида особенно ценны на первом этапе обучения: дети
учатся составлять задачи про самих себя, рассказывать о действиях друг друга,
ставить вопрос для решения, поэтому структура задачи на примере задач-
драматизаций наиболее доступна детям.
Особое место в системе наглядных пособий занимают задачи-
иллюстрации с картинками или игрушками. Если в задачах-драматизациях все
предопределено, то в задачах-иллюстрациях при помощи игрушек создается
разнообразия сюжетна, эти
задачи развивают воображение,
следовательно, подводят к решению и составлению устных задач.
Основные требования к ним: простота сюжета, динамизм содержания и ярко
картине нарисованы три легковых и одна грузовая машина. С этими данными
можно составить 1-2 варианта задач.
Задачи-картинки могут иметь и более динамичный характер. Например,
дается картина-панно с фоном озера и берега; на берегу нарисован лес. На
изображении озера, берега и леса сделаны надрезы, в которые можно вставить
небольшие контурные изображения разных предметов. К картине прилагаются
наборы таких предметов, по 10 штук каждого вида: утки, грибы, зайцы, птицы и
т. д. Таким образом, тематика и здесь предопределена, но числовые данные и
содержание задачи можно в известной степени варьировать (утки плавают,
выходят на берег и др.) так же, как создавать различные варианты задач о
грибах, зайцах, птицах.
рисунку вазы с пятью яблоками и одним яблоком на столе около вазы дети
могут составить задачи на сложение и вычитание.
арифметической задачи и ее структуры.
Устные задачи. Предшествующая работа создает условия для перехода к
составлению задач без опоры на наглядный материал (устные задачи). Спешить
с составлением устных задач не следует. Дети, как правило, легко схватывая
схему задачи, начинают ей подражать и подчас искажают правду жизни, не
понимая логики количественных отношений, которые являются основой задачи.
Первые устные задачи дает детям воспитатель. В качестве переходной
ступеньки к решению устных задач может быть использован такой прием:
воспитатель рассказывает детям задачу и предлагает им изобразить условие с
помощью кружков, квадратов или отложить косточки на счетах.
Этапы и методические приемы обучения решению задач
Что же значит « решить задачу?» Как правило, на этот вопрос отвечают
следующим образом: «Решить задачу – это найти к ней правильный ответ». Но
это не совсем так. Решить задачу – это значит: разобраться в ее условии,
выделить, какие величины в задаче известны, какую надо найти, как они между
действия, записать соответствующий пример, вычислить его и записать ответ.
Таким образом, решение задачи включает в себя следующие элементы:
анализ условия задачи, выделение известных величин и той, которую
краткая запись условия задачи;
разбор задачи, правильный выбор арифметического действия;
Наглядно структуру задачи дошкольником хорошо представить в виде
компонент задачи, если выпустили один из
компонентов, то пирамидка не
соберется, детям будет видно, что они допустили ошибку.
взаимосвязанных между собой этапов.
организовать систему упражнений по выполнению операций над множествами.
Так, подготовительный к решению задач на сложение являются упражнения по
проводятся для подготовки детей к решению задач на вычитание.
Учитывая наглядно – действенный и наглядно – образный характер
которых являются конкретные предметы. Подобные упражнения проводятся и
на выделение части множества. В качестве наглядной основы для понимания
отношений между частями и целым могут применяться диаграммы Эйлера –
Венна, в которых эти отношения изображают графически.
На втором этапе нужно учить детей составлять задачи и приводить к
усвоению их структуры. Детей учат устанавливать связи между данными и
арифметическое действие. Приводить к пониманию структуры задачи лучше
всего на задачах – драматизациях.
На этом этапе обучения составляются такие задачи, в которых вторым
слагаемым или вычитаемым является число 1. Это важно учитывать, чтобы не
затруднять детей поиском способов решения задачи. Прибавить или вычесть
последующего или предыдущего числа. Текст задачи произносится так, чтобы
было четко отделено условие, вопрос и числовые данные. Составленную задачу
повторяют двое или трое детей. Воспитатель при этом должен следить, чтобы
Как обучить детей решению задач по математике в ДОУ

Раннее развитие детей — один из главных принципов современного общества. Особую роль в этом процессе играет система дошкольного образования. Именно на занятиях в детском саду формируются первичные математические представления, которые создают фундамент интеллектуального развития, а также познавательной и творческой деятельности ребенка.
Когда можно начинать решать задачи по математике с дошкольником
Ребенок использует математические навыки на протяжении всей своей жизни. Раннее изучение математики не означает, что нужно браться за учебники вместо игры. Еще до того, как они пойдут в школу, большинство детей развивают умения складывать и вычитать посредством повседневных взаимодействий. Например, когда мы кладем печенье в банку, сумма увеличивается (сложение); когда мы вынимаем печенье из банки, сумма уменьшается (вычитание).

Дети сортируют предметы по цвету
Вся наша жизнь пронизана математикой и маленькому ребенку будет гораздо проще, если он начнет как можно раньше с ней знакомиться. Исследования педагогов и психологов показали, что мозг детей уже в два года способен решать простейшие задания по математике.
Изучение математических основ в детском саду начинается в младшей группе, где у малышей формируют элементарные представления об этом предмете. Например, детям предлагают задания на подбор и объединение различных предметов по общему признаку.
Цели обучения малыша решению задач
Решать математические задания полезно для развития у дошкольников сообразительности и логического мышления. Во время работы формируются умения анализировать, соединять, уточнять, акцентировать внимание на главном и исключать второстепенное.
Обратите внимание! Главным видом математической деятельности в первом классе является обучение вычитанию и сложению.
Очень важно провести в детском саду своевременную подготовку и помочь освоить вычисление, составляя и решая арифметические задачи. Благодаря этой работе дети учатся понимать смысл арифметических действий и сознательно к ним прибегать.
Виды задач по математике в ДОУ
В дошкольных учреждениях дети учатся решать задания в одно действие. Их подразделяют на три группы:
Первая группа включает в себя задания, во время решения которых изучаются значения арифметических действий.
Во вторую группу входят основанные на понимании взаимосвязей частей и результата вычислений.
Виды заданий на поиск неизвестных частей:
- найти первое слагаемое;
- найти второе слагаемое;
- найти уменьшаемое;
- найти вычитаемое;
Третья группа состоит из простых задач, основанных на определении разности отношений:
- увеличить число на несколько единиц;
- уменьшить число на несколько единиц;
Аналогично задания делят еще на два вида: задачи-драматизации и задачи-иллюстрации. Тип задач определяется исходя из используемого наглядного материала. У каждого вида есть свои отличительные особенности, они помогают развивать умение подбирать для сюжета жизненный и игровой материал, логически мыслить.
В сюжете задачи-драматизации содержится жизнь самих детей, то, чем они занимаются или только что делали. В таком типе заданий наглядно представлен их смысл. Благодаря решению таких задач дети начинают осознавать, что в них всегда отражена реальная жизнь людей.
Во время решения задачи-драматизации важно научить детей замечать многообразие связей и количественных отношений.
Обратите внимание! Очень важно решать подобные задания на начальном моменте обучения. Потому что дети пробуют придумывать задачи о себе, а также описывать деятельность друг друга и учатся формулировать вопрос.
Задачи-иллюстрации – важный вид заданий в системе наглядных пособий. Большое разнообразие сценариев создается при помощи игрушек. Они помогают фантазировать, тренировать память, учат детей придумывать задачи и подводят тем самым к составлению и решению устных задач.
Наглядные материалы довольно часто используют для иллюстрирования задач. Легкость сюжета, динамичность содержания и очевидные количественные отношения между предметами – главные требования к материалу.

Наглядный материал для счета
Создать задачу-картинку воспитатель вполне может самостоятельно. Наглядные пособия помогают легче усвоить смысл арифметических заданий и их структуру.
Задачи образовательные, воспитательные, развивающие в ДОУ по ФГОС
Постановка цели и задач организованной образовательной деятельности заключается в следующих принципах:
- Цель одна;
- Триединство задач: образовательная, развивающая и воспитательная направленность;
- Образовательные задачи ориентированы на привлечение детей к творческому процессу, на организацию групповой и индивидуальной видов деятельности, на выявление умений и способностей детей работать самостоятельно по теме организованной образовательной деятельности;
- Развивающие задачи по ФГОС в ДОУ ориентированы на усовершенствование навыков мышления, памяти, воображения, внимания;
- Воспитательные задачи в ДОУ на занятиях ориентированы на способность понимать учебную задачу и самостоятельно ее исполнять;
- Формулировка всех видов заданий обязательно должна начинаться с глагола, а также соответствовать программным задачам.
Интересные и развивающие математические задачи
У дошкольников формируются основные знания, необходимые им для последующего обучения в школе. Часто возникает вопрос: как научить ребенка решать задачи по математике перед поступлением в 1 класс. Есть несколько основных приемов, которые позволят детям легко решать математические задания:
- Внимательно прочитать условие и выделить несколько этапов: условие, вопрос, решение, ответ.
- Составить план-схему для нахождения неизвестного. Маленьким детям проще использовать рисунки и схемы, примеры из жизни.
- Сделать акцент на вопросе задания: что именно нужно найти и что уже известно.
- Для успешного освоения арифметических действий приучите ребенка постоянно практиковать навык решения задач.
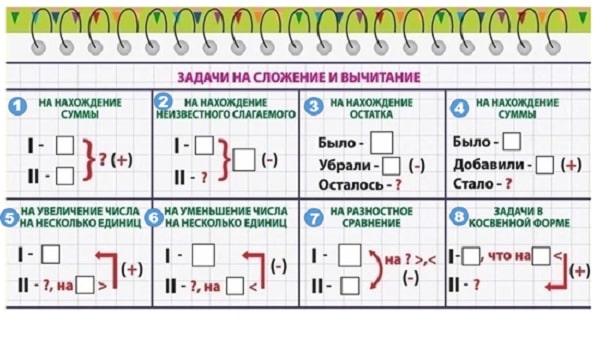
Схемы решения задач
Математика – сложная наука, она может привести к некоторым трудностям в период обучения в школе. Не каждый ребенок характеризуется математическим складом ума, и очень важно в период подготовки детей к школе развить интерес к этому предмету и заложить базовые математические представления.
Для занятий с дошкольниками предпочтительнее использовать интересные и развивающие задания, способные пробудить тягу к предмету.
Задания для малышей по математике
Счет до 5. Детям раздаются карточки с изображением предметов и последовательностью чисел от 1 до 5. Необходимо посчитать, например, птиц и обвести получившееся число в кружок.
Птицы и последовательность чисел от 1 до 5
Закрашиваем клетки. Детям предлагаются карточки с заданием. На них изображены клеточки и указано количество, которое необходимо закрасить. Например, изображено пять клеток, а требуется закрасить три.
Количественное сравнение предметов. На карточках изображены предметы, например, чашки. Справа три, а слева одна. В задании просят указать, где больше чашек.
Задания по математике для старшей группы
Задание на сравнение. Детям раздаются листы с рисунками и соответствующие им числовые примеры. Они должны подобрать к каждой картинке правильный пример.
Складывание фигур. Детям в группе раздаются палочки и бланки с изображением предметов, к примеру, гриб, очки, качели и т.п. Ребенку необходимо собрать эти фигуры из палочек, ориентируясь на образец.
Изображение предметов для складывания палочками
Посчитай фигуры. На бланке изображены геометрические фигуры и детям предлагается сосчитать, сколько на картинке квадратов, треугольников или иных фигур, из которых состоит предложенное задание.
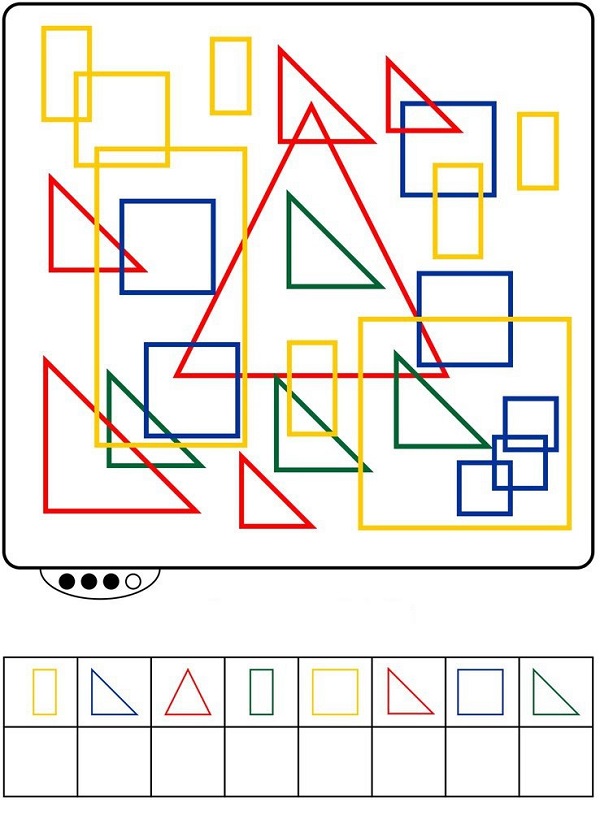
Геометрические фигуры для счета
Обучающие задачи в детском саду по ФГОС
Обучающие задания для детей по математике направлены на актуализацию знаний и самостоятельное закрепление изученного материала.
Отлично подойдут детские задачки по математике:
Сложи игрушки. Дети должны сложить определенное количество игрушек, которое назвал воспитатель. Таким образом тренируются навыки предметного счета, развивается способность сохранять в памяти нужное число и находить к нему требуемое количество предметов.
Определи фигуру. Малышам раздается наглядный печатный материал с изображением различных фигур разных цветов. Воспитатель называет фигуру и просит детей обвести ее пальчиком и произнести название.
Образовательные задачи в детском саду по ФГОС также направлены на закрепление ранее изученного материала. Например, закрепление состава чисел.

Методический материал по математике в ДОУ
Самое важное в обучении детей объяснить им отличия между задачей и повестью. Нужно отработать основные признаки задачи: выделить характер и смысл вопроса, важность существования как минимум двух чисел в условии.
Обратите внимание! Сделать упор на значимость чисел и вопроса в задаче можно, прочитав детям рассказ аналогичный задаче и отметив в тексте рассказа его основные отличия от задачи.
Еще один важный момент – научить различать задачи и загадки. Для этого следует выбрать загадку, в которой есть числа. К примеру: «Семь ребят по лесенке, заиграли песенки». «Что это: задача или загадка?» Дети отвечают, что загадка. Тогда воспитателю стоит возразить: «В тексте есть числа. Все-таки в загадке представлено описание нот и ее не нужно решать».
Для лучшего понимания смысла и типа вопроса можно использовать такой способ. Предложите детям самостоятельно составить задачу, например: «Сложили в ящик трех плюшевых зайчиков и двух мишек», задать не арифметический вопрос: «Какого цвета игрушки?». Дети должны заметить, что с таким вопросом задача не получилась, нужно предложить им сформулировать свои вопросы и отметить, что все они начинаются со слова сколько.
Также необходимо сделать акцент на необходимости числовых данных. Нужно прочитать детям текст: «Оля взяла со стола треугольники и круги. Сколько фигур взяла Оля?». Во время обсуждения опять выяснится, что текст не является задачей, так как не содержит числовые данные: сколько кругов и квадратов.
В свою очередь нужно объяснить детям важность наличия как минимум двух чисел в условии. Для этого специально пропускают одно из числовых данных: «У Нины в корзинке лежит семь пирожков с капустой и несколько с яблоком. Сколько всего пирожков у Нины?»
Дети должны прийти к заключению, что нет решения, потому что не известно, сколько пирожков с яблоком. Затем текст нужно изменить и прочитать его снова: «У Нины в корзинке лежит семь пирожков с капустой и три с яблоком. Сколько всего пирожков у Нины?». Дети лучше понимают необходимость наличия двух чисел в условии, если им приводить конкретные примеры из жизни.
Обратите внимание! Главной целью в обучении дошкольников решению арифметических задач является знакомство с основными арифметическими действиями. Также дети учатся рассуждать, выполнять логические операции, анализировать их, выделять известное и неизвестное и, как следствие, лучше понимать структуру задачи.
Обучение дошкольников решению примеров формирует у них начальные представления о математике и способствует подготовке к школе.
Научите детей решать задачи

Обучение сложению и вычитанию – одна из основных задач математической работы в первом классе. В детском саду проводят главным образом подготовительную работу.
Дети осваивают вычисление, составляя и решая арифметические задачи. Работа эта позволяет понять смысл арифметических действий и сознательно к ним прибегать, устанавливать взаимосвязи между величинами.
Дошкольники решают простые задачи в одно действие, главным образом прямые, т.е. такие, где арифметическое действие с предметами (добавили — стало больше, убавили- стало меньше). Это задачи на нахождение суммы и остатка. Учет прибавлять и вычитать с начало число 1, потом число 2, а затем 3.
Этапы обучения решению задач.
На первом этапе необходимо научить детей составлять задачи и помочь им осознать, что в содержании задач находит отражение окружающая жизнь.
Они усваивают структуру задачи, выделяют условие и вопрос, осознают особое значение числовых данных. Помимо этого, они учатся решать задачи, сознательно выбирать и формулировать действие сложения или вычитания, вникать в смысл того, к каким количественным изменениям проводят практические действия с предметами, о которых говорится в задаче (больше или меньше стало или осталось).
Дети учатся давать полный, развернутый ответ на вопрос задачи. Числовой материал в этот период либо ограничивают первым пятком, либо в пределах второго пятка прибавляют или вычитают 1.
На втором этапе дети учатся не только обоснованно выбирать действие сложения или вычитания, но и правильно пользоваться приемами присчитывания и отсчитывания по 1, прибавляя или вычитая сначала число 2, а позже 3.
Обучение детей составлению задач.
Для того, чтобы дети научились выделять числовые данные задачи, практические действия и понимать смысл количественных изменений, к которым они приводят, необходима полная предметная наглядность.На первом занятий воспитатель дает детям общее представление о задаче, учит практически составлять условие и ставить вопрос к ней. Основное внимание уделяют пониманию детьми смысла количественных изменений, к которым приводят те или иные действия с предметами. Соединили 2 группы предметов: к одной группе добавили другую – становится больше предметов чем было. Отделили столько-то предметов, убавили – предметов стало меньше, чем было.
Первые 1-2 задачи составляет воспитатель, описывая в них те действия, которые дети выполнили по его указанию:
«Сережа поставил на стол 3 матрешки, Вера принесла еще 1 матрешку. Сколько всего матрешек принесли Вера и Сережа?»
Важно привлечь внимание детей к количественным отношениям между числовыми данными задачи: Сколько матрешек Сережа поставил на стол? Сколько матрешек принесла Вера? Больше или меньше стало матрешек после того, как Вера принесла еще 1?
Сколько всего матрешек принесли Вера и Сережа? Больше или меньше у нас получилось матрешек, чем поставил Сережа? Почему?
Воспитатель говорит, что я составила задачу, а вы ее решили. Теперь мы будем учиться составлять и решать задачи.
Вспоминают задачу, которую только что решили. Воспитатель объясняет, как составлена задача: «Сначала рассказано о том, сколько матрешек поставил на стол Сережа, и сколько матрешек принесла Вера, а затем поставлен вопрос, сколько всего матрешек принесли Сережа и Вера. (4 матрешки).
Решив задачу, вы правильно ответили на вопрос. Важно отметить необходимость давать точный, развернутый ответ на вопрос задачи. Если ребенок упускает что-либо, например, говорит лишь о количестве предметов ( 4 матрешки), воспитатель замечает, что непонятно, о каких матрешках идет речь. Полезно давать задания одновременно всем детям, предлагать придумать задачу о том, что они сделали: « На верхнюю полоску положите 5 кружков, а на нижнюю 1 кружок». Расскажите о том, что вы сделали. Это то, что мы знаем. А что надо узнать? Какой вопрос надо задать? На первых двух занятиях дети должны научиться элементарно анализировать задачи.
Знакомство со структурой задачи.
Со структурой задачи дети знакомятся на 2 или 3 занятии: они узнают, что в задаче есть условие и вопрос, особо подчеркивается наличие в условии задачи не менее 2 чисел. Воспитатель предлагает показать все то, о чем он будет говорить. Слева на карточку положили 6 флажков, а справа- 1 флажок. Сколько всего флажков положили на карточку? Составили задачу. Давайте повторим задачу и отделим то, что мы знаем, от того, что не знаем. Что мы знаем? 6 флажков лежат слева и 1 флажок справа. Это мы знаем. Это условие задачи. Что же в задаче спрашивается? Сколько всего флажков на карточке? Этого не знаем. Это то, что надо узнать. Это вопрос задачи. В каждой задаче есть условие и вопрос. Повторим нашу задачу.
Так составляется 2-3 задачи. Каждый раз воспитатель предлагает одному ребенку повторить условие задачи, а другому – вопрос, уточняет из каких двух частей состоит задача.
Можно – один ребенок рассказывает условие, другой ставит вопрос, третий дает ответ на вопрос задачи.
Важно раскрыть арифметическое значение вопроса задачи. С этой целью, рассматривая очередную задачу, воспитатель специально сосредотачивает внимание ребят на характере вопроса. Например, дети рассказали условие задачи: « У Оли было 4 шара, а Дима подарил ей еще 1 шар. Это условие задачи, это то, что мы знаем».
А что нового можно узнать о шарах? Оказывается, можно узнать много: и какого цвета шары, большие они или маленькие. Но главное, надо узнать их общее количество. Так какой вопрос надо поставить к задаче? Дети ставят вопрос об общем количестве шаров. Вопрос задачи начинается с вопроса «Сколько?»
Необходимо подчеркнуть значение числовых данных задачи. С этой целью рекомендуется такой прием: рассказывая об условии задачи, воспитатель опускает одно из чисел или оба числа и спрашивает: « Можно ли решить задачу?». Дети практически убеждаются в том, что в условии задачи должно быть не менее 2 чисел. (В вазе стояло несколько цветов. Я поставила еще несколько. Сколько цветов стало в вазе?). После того, как дети научатся составлять задачи без наглядного материала, для закрепления знаний о структуре задачи полезно сравнить ее с рассказом загадкой.
Можно использовать задачи- драматизации, задачи-иллюстрации и устные задачи, которые дети решают без опоры на наглядный материал.
Мой детский сад
Более 15 лет работы сайта «Мой детсад». Авторы – профессиональные учителя со всего СНГ. Более 2 000 уникальных методик для детского сада и школы. Суммарно сайт оценило около 100 000 воспитателей. В итоге более 1 млн. счастливых детей.
Загадки, задачи-шутки, занимательные вопросы в обучении детей математики

Автор: Волкова Наталья Владимировна, воспитатель, Муниципальное бюджетное дошкольное образовательное учреждение – детский сад N25 «Ромашка», г.Верхний Тагил.
Из многообразия математических игр и развлечений детям в дошкольном возрасте доступны и интересны загадки и задачи-шутки.
В загадках математического содержания анализируется предмет с количественной, пространственной, временной точки зрения, подмечены простейшие математические отношения.
Загадки математического содержания:
У кого одна нога, да и та без башмака? (гриб).Много рук, нога – одна (дерево).
На одной ноге кружится, беззаботна, весела. В пестрой юбке танцовщица, музыкальная … (юла).На длинной ножке, застыв до поры, отдыхает палочка после игры (единица). Два конца, два кольца, а посредине гвоздик. (Ножницы.)
Есть у каждого лица два красивых озерца. Между ними есть гора. Назови их, детвора. (глаза). Два глядят, да двое слушают (глаза и уши).У него два колеса и седло на раме, две педали есть внизу, крутят их ногами (велосипед). Два коня у меня, два коня. По воде они возят меня, а вода тверда, словно каменная! (коньки). две полоски на снегу оставляю на бегу.
Я лечу от них стрелой, а они опять за мной (лыжи).Двое в небе ходят кругом, но не видятся друг с другом (солнце и луна).Есть спина, а не лежит никогда. Есть четыре ноги, а не ходят .
Сам всегда стоит, а всем сидеть велит (стул).
Возле леса на опушке
трое их живет в избушке.
Там три стула и три кружки,
три кровати, три подушки.
Угадайте без подсказки,
кто герои этой сказки? (Машенька и три медведя).
У него глаза цветные, не глаза, а три огня, он по очереди ими сверху смотрит на меня (светофор). Четыре ноги, а ходить не может. (Стол.)Четыре братца под одной крышей стоят (стол).Под крышей четыре ножки, а на крыше суп да ложки (стол).На четыре ноги надевали сапоги. Перед тем как надевать, четыре стали обувь надувать (шины). Шевелились у цветка все четыре лепестка. Я сорвать его хотел, он вспорхнул и улетел (бабочка). Кто в году четыре раза переодевается? (Земля) В году у дедушки четыре имени (зима, весна, лето, осень). Ежегодно приходят к нам в гости: один седой, другой молодой, третий скачет, а четвертый плачет (времена года).У двух матерей по пяти сыновей, одно имя всем (пальцы).
Пять братцев в одном домике живут. (варежка.) И жужжит, и летит, есть шесть ног, но без копыт. (жук) Пять щенят, да мама-лайка. Ты попробуй, сосчитай-ка! (шесть) Есть семь братьев: годами равные, именами разные (дни недели). Цифру восемь ,цифру восемь на носу всегда мы носим, цифра восемь плюс крючки –получаются … (очки)12 братьев друг за другом ходят, друг друга не находят. (Месяцы.)Сто одёжек, а все без застёжек (капуста).Сидит дед во сто шуб одет, кто его раздевает, тот слезы проливает. (Лук.)Ног нет, а хожу, рта нет, а скажу: когда спать, когда вставать. (Часы.) Овальная лягушка, но вовсе не зверушка, а овощ-молодец –зелёный … (Огурец.) Небо, будто синий дом, есть одно оконце в нём: словно круглое оконце в небесах сверкает …(Солнце.)
Задачи-шутки – это занимательные игровые задачи с математическим смыслом. Для их решения надо в большей мере проявить находчивость, смекалку, понимание юмора, нежели познания в математике. Построение, содержание, вопрос в этих задачах необычны. Они лишь косвенно напоминают математическую задачу.
Задачи-шутки:
- Сидят три кошки, против каждой кошки две кошки, много ль всех? (Три.)
- Шел один, нашел пять рублей; трое пойдут, много ли найдут? (пять рублей.)
- Из какой посуды нельзя ничего съесть? (Из пустой)
- У животного 2 правые ноги, 2 левые, 2 ноги спереди, 2 сзади. Сколько у него ног?
- Сколько орехов в пустом стакане? (Ни сколько)
- В вазе стояло 3 тюльпана и 7 нарциссов. Сколько тюльпанов стояло в вазе? (В вазе было 3 тюльпана)
- По морю плыли 9 акул. Они увидели косяк рыб и нырнули в глубину. Сколько плавало акул? (9 акул , только они нырнули )
- На столе лежало 4 яблока. Одно из них разрезали пополам и положили на стол. Сколько яблок на столе? (4 яблока)
- 7 мальчиков расчистили по 1 дорожке в саду. Сколько дорожек расчистили мальчики?( 7 дорожек)
- У бабушки Даши внучка Маша, кот Пушок, собака Дружок. Сколько у бабушки внуков?
- Над рекой летели птицы: голубь, щука, 2 синицы, 2 стрижа и 5 угрей. Сколько птиц? Ответь скорей.
- Горело 7 свечей. 2 свечи погасили. Сколько свечей осталось? (2.)
- Летела стая гусей. Один гусь впереди, два – сзади. Один гусь между двумя и три гуся рядом. Сколько гусей в стае? (3)
- Сестра старше брата на 5 лет. На сколько лет она будет старше брата через 7 лет?
- Одно яйцо варят 4 минуты. Сколько минут надо варить 6 яиц? (4 мин)
- Когда козе исполнится 6 лет, что будет? (Ей пойдет седьмой год)
- На столе стоят три стакана с вишней. Костя съел один стакан вишни и поставил пустой стакан на стол. Сколько стаканов осталось? (3 стакана)
Занимательные математические вопросы способствуют развитию у детей смекалки и находчивости, учат детей анализировать, выделять главное, сравнивать.
При формировании пространственных и временных представлений помогают логические концовки.
– Если Саша вышел из дома раньше Сережи, то Сережа… (вышел позже Саши.)
– Если сестра старше брата, то брат… (младше сестры.)
– Если правая рука справа, то левая… (слева.)
– Если стол выше стула, то стул… (ниже стола.) и др.
Очень нравятся детям задачи в стихотворной форме.
Задачи в стихах:
1.На крыльце сидит щенок,
Греет свой пушистый бок.
Прибежал еще один
И уселся рядом с ним. (Сколько стало щенят?)
2.На плетень взлетел петух.
Повстречал еще там двух.
Сколько стало петухов?
У кого ответ готов? (3)
3.Ежик осенью по лесу шел,
На обед он грибочков нашел:
Два – под березой,
Один – у осины,
Сколько их будет
В плетеной корзине? (3)
4.Под кустами у реки
Жили майские жуки:
Дочка, сын, отец и мать.
Кто их может сосчитать?
5.У стены стоят кадушки,
В каждой кадушке по 1 лягушке
Если было 5 кадушек,
Сколько было в них лягушек?
6.Хозяйка однажды с базара пришла.
Хозяйка с базара домой принесла:
Картошку, капусту,
Морковку, горох,
Петрушку и свеклу… ОХ!
Сколько всего овощей принесла хозяйка?(6)
7. На большом диване в ряд
Куклы Танины сидят:
Два медведя, Буратино,
И веселый Чипполино,
И котенок, и слоненок…
Помогите вы Танюшке
Сосчитать свои игрушки!
8. Потеряла крольчиха крольчат.
А крольчата лежат и молчат.
Один – за ветлой,
Два – за метлой,
Один – под листом,
Двое – под кустом.
Как детей поскорее найти
Их у мамы чуть больше 5? (6)
9.Четыре спелых груши
На веточке качалось
Две груши снял Павлуша,
А сколько груш осталось?
Такие задачи делают счет наиболее интересным для ребят. Дети и сами не замечают, как в процессе игры, они осваивают необходимые навыки счета. А практика показывает, что знания и умения, приобретенные в игровой деятельности, более прочные, устойчивые, осознанные и вызывают интерес к действиям с числами. Применять и закреплять математические знания можно во время других занятий и разнообразных игр.
Назначение загадок и задач-шуток, занимательных вопросов состоит в приобщении детей к активной умственной деятельности, выработке умения выделять главные, существенные свойства, математические отношения, замаскированные внешними несущественными данными.Они могут быть использованы воспитателем в процессе разговоров, бесед, наблюдений с детьми за какими-либо явлениями, т. е. в том случае, когда создается необходимая для этого ситуация.
Занимательный математический материал является хорошим средством воспитания у детей уже в дошкольном возрасте интереса к математике, к логике и доказательности рассуждений, желания проявлять умственное напряжение, сосредоточивать внимание на проблеме.
Методически правильно подобранный и к месту использованный занимательный материал (загадки, задачи-шутки, занимательные вопросы) способствует развитию логического мышления, наблюдательности, находчивости, быстроты реакции, интереса к математическим знаниям, формированию поисковых подходов к решению любой задачи.