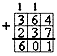
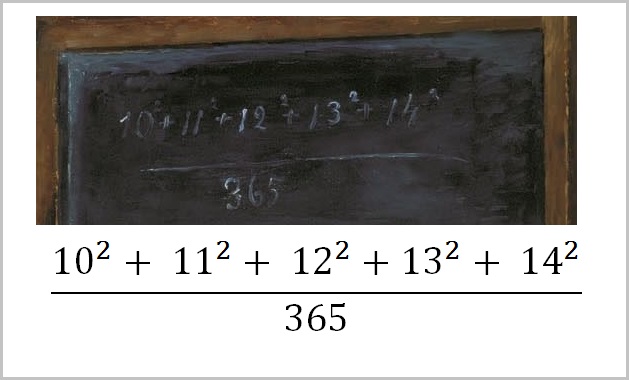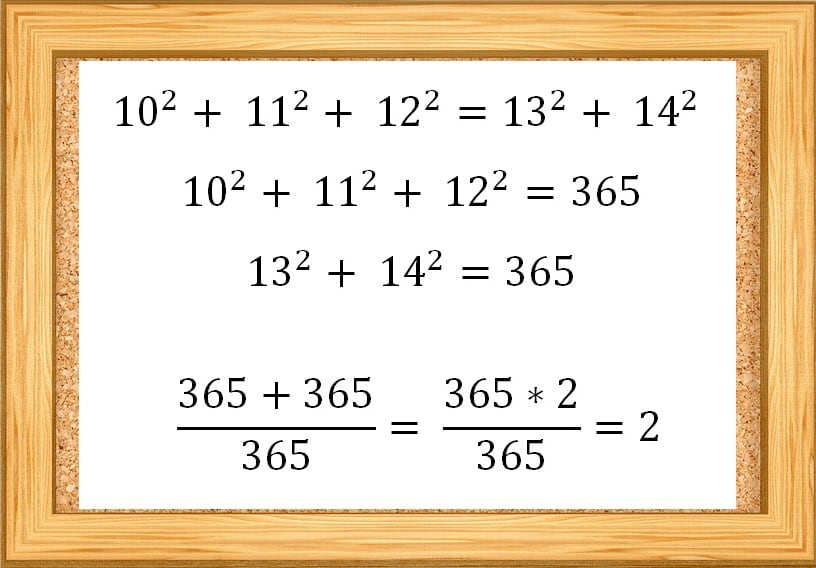Сумма квадратов простых чисел
Теорема Ферма — Эйлера или теорема о представлении простых чисел в виде суммы двух квадратов гласит [1] :
Любое простое число p = 4 n + 1 , где n — натуральное число, представимо в виде суммы квадратов двух натуральных чисел.
где p — простое число.
В иностранной литературе это утверждение часто называют рождественской теоремой Ферма, так как она стала известна из письма Пьера Ферма, посланного 25 декабря 1640 года.
Из этого утверждения при помощи тождества Брахмагупты выводится общее утверждение:
Натуральное число представимо в виде суммы двух квадратов (целых чисел) тогда и только тогда, когда любое простое число вида 4 k + 3 входит в его разложение на простые множители в чётной степени.
Иногда именно этот факт подразумевается под теоремой Ферма — Эйлера.
Содержание
История [ править | править код ]
Впервые это утверждение обнаружено у Альбера Жирара в 1632 году. Пьер Ферма объявил в своём письме к Мерсенну (1640), что он доказал данную теорему, однако доказательство не привёл. Через 20 лет в письме к Каркави (от августа 1659 года) Ферма намекает, что доказательство основывается на методе бесконечного спуска.
Первое опубликованное доказательство методом бесконечного спуска было найдено Леонардом Эйлером между 1742 и 1747 годами. Позднее доказательства, основанные на иных идеях, дали Жозеф Лагранж, Карл Гаусс, Герман Минковский, Якобшталь и Дон Цагир. Последним приведено доказательство, состоящее из одного предложения [2] .
Доказательства [ править | править код ]
Одно из самых коротких доказательств придумано немецким математиком Доном Цагиром [3] :
имеет ровно одну неподвижную точку (а именно ( 1 , 1 , k ) , так как p = 4 k + 1 — простое), так что | S | нечётно и инволюция ( x , y , z ) → ( x , z , y ) ightarrow (x,z,y)> также имеет неподвижную точку.
Также есть доказательство через теорему Вильсона, придуманное Акселем Туэ [4] .
Материалы в помощь студентам и научным работникам
Министерство общего и профессионального образования

Имени Ярослава Мудрого.
Кафедра «Прикладная математика и информатика».
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В ВИДЕ СУММЫ ДВУХ
КВАДРАТОВ И В ВИДЕ
Преподаватель:
Неустроев Н.В.
Студент группы № 3311
ТЕОРЕМА ФЕРМА-ЭЙЛЕРА 5
Доказательство (Лагранжа) 5
Единственность представления простого
числа в виде суммы двух квадратов 6
КОЛИЧЕСТВО представЛЕНИЙ ЧИСЛА в виде суммы двух
квадратов 8
ПРЕДСТАВЛЕНИЕ ЧИСЛА В ВИДЕ 9
ВВЕДЕНИЕ Быть может, потомство будет признательно мне за то, что я показал ему, что Древние знали не все.
Пьер Ферма Лишь один математик удостоился того, что имя его стало нарицательным. Если произносится слово «ферматист», значит, речь идет о человеке, одержимом до безумия какой-то несбыточной идеей. Но это слово ни в какой мере не может быть отнесено к самому Пьеру Ферма (1601–1665), одному из самых светлых умов Франции. Ферма – человек удивительной судьбы: один из величайших математиков всех времен, он не был, в современной терминологии, «профессиональным» математиком. По профессии Ферма был юристом. Он получил великолепное гуманитарное образование и был выдающимся знатоком искусства и литературы. Всю жизнь он проработал на государственной службе, последние 17 лет был советником местного парламента в Тулузе. К математике его влекла бескорыстная и возвышенная любовь (это иногда случается с людьми), и именно эта наука дала ему все, что может дать человеку любовь: упоение красотой, наслаждение и счастье. В те годы не было еще математических журналов, и Ферма почти ничего не напечатал при жизни. Но он много переписывался со своими современниками, и посредством этой переписки некоторые его достижения становились известными. Пьеру Ферма повезло с детьми: сын обработал архив отца и издал его.»Я доказал много исключительно красивых теорем», – сказал как-то Ферма. Особенно много красивых фактов удалось ему обнаружить в теории чисел, которую, собственно, он и основал. В бумагах и в переписке Ферма было сформулировано немало замечательных утверждений, о которых он писал, что располагает их доказательством. И постепенно, год за годом, таких недоказанных утверждений становилось все меньше и меньше. И наконец, осталось только одно. Хорошо известно, что квадраты некоторых чисел можно разложить в сумму двух квадратов. Таков египетский треугольник со сторонами 3, 4 и 5: 3 2 +4 2 =5 2 . Можно описать все целочисленные решения уравнения x 2 +y 2 =z 2 . Это было сделано Диофантом, греческим математиком, жившим (вероятно) в III веке нашей эры, во второй книге его трактата «Арифметика» (до нас дошли 6 книг из 13). На полях около решения Диофанта Ферма написал: «Нельзя разложить куб на два куба, ни квадрато-квадрат (т. е. четвертую степень числа) на два квадрато-квадрата, ни вообще никакую степень выше квадрата и до бесконечности нельзя разложить на две степени с тем же показателем. Я открыл этому поистине чудесное доказательство, но эти поля для него слишком узки». Иначе говоря, уравнение x n +y n =z n при натуральном n>2 в целых числах неразрешимо.
В бумагах Ферма было найдено доказательство этого утверждения для n=4 (это единственное подробное доказательство теоремы из теории чисел, обнаруженное в бумагах Ферма). Для n=3 теорему Ферма доказал Эйлер в 1768 году. В течение XIX века для доказательства теоремы Ферма были предприняты огромные усилия. Особенных успехов добился немецкий математик Куммер. После его работ теорема Ферма оказалась доказанной для всех простых n (а доказать ее только для них), меньших 100, кроме 37, 59 и 97. В нашем веке теорема Ферма была доказана для простых чисел, меньших 100,000 , но окончательное решение так и не было найдено.
В 1908 году любитель математики Вольфскель завещал 100,000 марок тому, кто докажет теорему Ферма. Это стало бедствием для математиков многих стран. Потекли сотни и тысячи писем с доказательствами теоремы Ферма. Как правило, они содержали элементарные ошибки, но на их нахождение тратились немалые силы многих математиков.
Во время Первой мировой войны эта премия обесценилась. Поток псевдодоказательств сократился, но не иссяк.
И уже казалось, что эта проблема перейдет через новую грань веков, но все-таки пять лет тому назад английский математик Уайлс «залатал последнюю дыру» в своем доказательстве этой великой теоремы, с которым он впервые предстал перед математическим миром в 1993 году.
Мир признал: Великая теорема Ферма доказана!
Однако, тем, кто интересуется математикой, имя Ферма говорит очень многое независимо от его Великой теоремы. Он был, без всякого сомнения, одним из самых проницательных умов своего времени – времени Гигантов. Его по праву считают основоположником теории чисел, он внес огромный вклад в зарождающиеся новые направления, определившие последующее развитие науки: математический анализ, аналитическую геометрию. Мы признательны Ферма за то, что он приоткрыл для нас мир, полный красоты и загадочности.
Следующая теорема, несомненно, принадлежит к числу высших достижений математики XVII–XVIII веков.
Взгляните на несколько первых нечетных простых чисел:
3, 5, 7, 11, 13, 17, 19, .
Числа 5, 13, 17 представимы в виде суммы двух квадратов: 5=2 2 +1 2 , 13=2 2 +3 2 , 17=1 2 +4 2 , а остальные числа (3, 7, 11, 19) этим свойством не обладают. Можно ли объяснить этот феномен? Ответ на этот вопрос дает следующая теорема:
Теорема: Для того, чтобы нечетное простое число было представимо в виде суммы двух квадратов, необходимо и достаточно, чтобы оно при делении на 4 давало в остатке 1.
Доказательство (Лагранжа)
Это доказательство опирается на следующую лемму Вильсона : если p — простое число, то число (p-1)!+1 делится на p .
Чтобы не отвлекаться на доказательство этого вспомогательного факта, продемонстрирую лишь основную идею этого доказательства на примере простого числа 13. Для любого числа x , 2 x 11 , найдется такое число y , 2 y 11 , что x* y при делении на 13 дае в остатке 1. Действительно,
(13-1)!=12!=(2* 7)(3* 9)(4* 10)(5* 8)(6* 11)* 12,
и при этом все произведения в скобках при делении на 13 дают в остатке 1, а значит, 12! при делении на 13 даст в остатке 12 , откуда (для выбранного нами числа 13 ) следует утверждение леммы Вильсона.
Из леммы Вильсона извлечем такое следствие: если p=4n+1 , где n — натуральное число, то ((2n)!) 2 +1 делится на p . Действительно, из леммы Вильсона следует, что (4n)!+1 делится на p , и теперь необходимое утверждение вытекает из следующей выкладки:

(4n)!+1=(2n)!(2n+1)*. *(4n)+1=
=(2n)!(p-2n)(p-2n-1)*. *(p-1)+1=
=(2n)!(-1) 2n (2n)!+pk+1 ((2n)!) 2 +1(mod p).

Обозначим (2n)! через N . Мы доказали, что N 2 -1(mod p) .
Теперь нам предстоит преодолеть основную трудность. Рассмотрим все пары целых чисел (m,s) , такие что 0 m [ ] , 0 s [ ] , через [ ] обозначена целая часть числа — наибольшее целое число, не превосходящее . Число таких пар ([ ]+1) 2 >p . Значит, по крайней мере для двух различных пар (m >1> ,s >1> ) и (m >2> ,s >2> ) остатки от деления m >1> +Ns >1> и m >2> +Ns >2> на p одинаковы, т. е. число a+Nb , где a=m >1> -m >2> , b=s >1> -s >2> , будет делиться на p . При этом |a| [ ] , |b| [ ] . Но тогда число a 2 -N 2 b 2 =(a+Nb)(a-Nb) делится на p , и значит, учитывая, что N 2 -1(mod p) , получим, что a 2 +b 2 делится на p , т. е. a 2 +b 2 =rp , где r — натуральное число ( r 0 , ибо иначе пары были бы одинаковы). С другой стороны, a 2 +b 2 2[ ] 2 , т. е. r=1 , и значит, a 2 +b 2 =p . Теорема доказана.
Вопрос о представлении чисел в виде суммы двух квадратов исчерпывается следующим утверждением:
Натуральное число представимо в виде суммы двух квадратов целых чисел тогда и только тогда, когда все простые сомножители вида 4k+3 входят в разложение этого числа на простые сомножители с четными показателями.
Единственность представления простого числа в виде суммы двух квадратов По теореме Ферма-Эйлера любое простое число р, которое при делении на 4 дает остаток 1, представимо в виде суммы двух квадратов. Осталось доказать, что такое представление единственно с точностью до порядка слагаемых. Теорема: Никакое простое число не может быть представлено в виде суммы квадратов двух целых чисел существенно разными (т. е. не получающимися один из другого перестановкой слагаемых) способами.
Доказательство. Если бы простое число p имело два существенно разных представления, p = a 2 + b 2 = c 2 + d 2 , то разложения p = (a + bi)(a – bi) = (c + di)(c – di) представляют собой противоречие . Можно обойтись в доказательстве теоремы 9 и без комплексных чисел. Предположим, что простое число p двумя существенно разными (т. е. отличающимися не только порядком слагаемых) способами разложено в сумму квадратов натуральных чисел:
p = a 2 + b 2 = c 2 + d 2 .
Тогда и Следовательно, a 2 c 2 = (-b 2 )(-d 2 )(mod p), т. е. число a 2 c 2 – b 2 d 2 кратно p. (Если рассуждения со сравнениями по модулю p непривычны и потому подозрительны, можно получить то же самое, рассматривая тождество a 2 c 2 – b 2 d 2 = a 2 (c 2 + d 2 ) – (a 2 + b 2 )d 2 ).)
Поскольку число p простое, из делимости произведения (ac + bd)(ac – bd) на p следует, что один из множителей кратен p. Если число ac + bd кратно p, то воспользуемся формулой (1):
p 2 = (ac + bd) 2 + (ad – bc) 2 .

Если то противоречие очевидно, ибо первое слагаемое (ac + bd) 2 кратно p 2 и потому не меньше p 2 . Если же ad – bc = 0, то ad = bc. Поскольку как числа a и b, так и числа c и d взаимно просты, имеем a = c и d = b.
Случай, когда ac – bd кратно p, можно рассмотреть аналогично, воспользовавшись формулой p 2 = (ac – bd) 2 + (ad + bc) 2 .
Итак, простое число нельзя двумя существенно разными способами представить в виде суммы квадратов двух натуральных чисел. Число, единственным образом представимое в виде суммы квадратов двух натуральных чисел, не всегда является простым: 10 = 1 2 + 3 2 , 25 = 3 2 + 4 2 . Легко сформулировать условия, при которых число имеет единственное представление в виде суммы двух квадратов. Однако боле целесообразной представляется следующая задача, описанная далее.
Натуральное число представимо в виде суммы двух квадратов целых чисел тогда и только тогда, когда все простые сомножители вида 4k+3 входят в разложение этого числа на простые сомножители с четными показателями.
Единственность представления простого числа в виде суммы двух квадратов По теореме Ферма-Эйлера любое простое число р, которое при делении на 4 дает остаток 1, представимо в виде суммы двух квадратов. Осталось доказать, что такое представление единственно с точностью до порядка слагаемых. Теорема: Никакое простое число не может быть представлено в виде суммы квадратов двух целых чисел существенно разными (т. е. не получающимися один из другого перестановкой слагаемых) способами.
Доказательство. Если бы простое число p имело два существенно разных представления, p = a 2 + b 2 = c 2 + d 2 , то разложения p = (a + bi)(a – bi) = (c + di)(c – di) представляют собой противоречие . Можно обойтись в доказательстве теоремы 9 и без комплексных чисел. Предположим, что простое число p двумя существенно разными (т. е. отличающимися не только порядком слагаемых) способами разложено в сумму квадратов натуральных чисел:
p = a 2 + b 2 = c 2 + d 2 .
Поскольку число p простое, из делимости произведения (ac + bd)(ac – bd) на p следует, что один из множителей кратен p. Если число ac + bd кратно p, то воспользуемся формулой (1):
p 2 = (ac + bd) 2 + (ad – bc) 2 .
Случай, когда ac – bd кратно p, можно рассмотреть аналогично, воспользовавшись формулой p 2 = (ac – bd) 2 + (ad + bc) 2 .
Итак, простое число нельзя двумя существенно разными способами представить в виде суммы квадратов двух натуральных чисел. Число, единственным образом представимое в виде суммы квадратов двух натуральных чисел, не всегда является простым: 10 = 1 2 + 3 2 , 25 = 3 2 + 4 2 . Легко сформулировать условия, при которых число имеет единственное представление в виде суммы двух квадратов. Однако боле целесообразной представляется следующая задача, описанная далее.
КОЛИЧЕСТВО представЛЕНИЙ ЧИСЛА в виде суммы двух квадратов
В III веке нашей эры греческий математик Диофант не только знал, что число 65 представимо двумя способами, но и объяснял это тем, что 65 является произведением чисел 13 и 5, каждое из которых — сумма двух квадратов. Комплексных чисел Диофант не знал, иначе он непременно выписал бы разложения 5 = (2 + i)(2 – i), 13 = (3 + 2i)(3 – 2i и продолжил бы свои объяснения следующим образом:
65 = (2 + i)(3 + 2i) . (2 – i)(3 – 2i) = (4 + 7i) . (4 – 7i) =
= 4 2 + 7 2 = (2 + i)(3 – 2i) . (2 – i)(3 + 2i)=
= (8 – i) . (8 + i) = 8 2 + 1 2 .
По-разному группируя множители, получаем два разных разложения!
Следующий пример — число 25. 25 — наименьшее число, двумя способами представимое в виде суммы квадратов двух целых чисел. Оба эти разложения легко получить, по- разному группируя множители:
25 = (2 + i) 2 . (2 – i) 2 = (3 + 4i) . (3 – 4i) =
= 3 2 + 4 2 = (2 + i)(2 – i) . (2 + i)(2 – i) =
= 5 . 5 = 5 2 + 0 2 .
Последнийпример — число 5746. Как мы хорошо знаем, всякому представлению 5746 = a 2 + b 2 соответствует разложение 5746 = (a + bi)(a – bi) на сопряженные множители. Поэтому разложим рассматриваемое число сначала на простые натуральные, а затем и на простые гауссовы множители:
5746 = 2 . 13 2 . 17 = (1 + i)(1 – i)(3 + 2i) 2 (3 – 2i) 2 (4 + i)(4 – i).
Теперь мы должны из нескольких этих множителей составить a + bi, да так, чтобы произведение остальных множителей равнялось a – bi. Этонетрудносделать:
a + bi = (1 + i)(3 + 2i) 2 (4 + i) = -45 + 61i,
a – bi = (1 – i)(3 – 2i) 2 (4 – i) = -45 – 61i.
При этом, разумеется, 45 2 + 61 2 = 2025 + 3721 = 5746. Легко найти и еще два варианта:
a + bi = (1 + i)(3 + 2i)(3 – 2i)(4 + i) = 39 + 65i
a + bi = (1 + i)(3 – 2i) 2 (4 + i) = 75 – 11i.
Они приводят к представлениям 39 2 + 65 2 = 1521 + 4225 = 5746 и 75 2 + 11 2 = 5625 + 121 = 5746. Никаких других представлений нет
Аналогично можно найти число представлений в виде суммы двух квадратов любого натурального числа
Итак, количество представлений числа m в виде суммы квадратов двух целых чисел равно [((a1 + 1) . . . (ar + 1) + 1)/2]. (Если число сомножителей равно О, то произведение считается равным 1. Представления, отличающиеся порядком слагаемых, не различаются.
ПРЕДСТАВЛЕНИЕ ЧИСЛА В ВИДЕ
Теорема: положительное нечетное число представимо в виде
Число таких представлений равно 2v, где v-число решений сравнения
Доказательство. Если нечетное N не имеет простых делителей вида 8n+5 и 8n+7, то сравнение (2) имеет решения, т.е. v<>0 (не равно нулю). Тогда получаем, что число форм с дискриминантом D=-8, таких, что 0
Сумма квадратов всех целых чисел
Сумма квадратов чисел — математическое выражение, для которого не существует формулы сокращенного умножения. На практике иногда требуется быстро прикинуть сумму нескольких квадратов, однако без математических хитростей такое выражение подсчитать достаточно трудно.
Формулы сокращенного умножения
Для упрощения расчетов в математике используются специальные формулы сокращенного умножения, которые, по сути, представляют собой частные случаи бинома Ньютона. При помощи таких формул легко вручную подсчитать, например, квадрат суммы или разности вида:
(a ± b) 2 = a 2 ± 2ab + b 2
Существует множество формул для решения подобных выражений, и дело не ограничивается квадратами. При помощи формул легко подсчитать куб разности или сумму многочленов n-ной степени. Мы легко можем подсчитать даже выражение (a + b + c) 3 , однако формулы сокращенного умножения для простого выражения как:
в учебниках по математике вы не найдете. Естественно, она есть для комплексных чисел, тех самых, с которыми мы знакомимся в университетском курсе математического анализа. Выглядит эта формула достаточно жутко:
a 2 + b 2 = (a + ib) × (a — ib),
где i – легендарная мнимая единица, которая рассчитывается как квадратный корень из минус единицы.
В школьных примерах продвинутые ребята негласно используют формулу, которая не входит в пантеон формул сокращенного умножения:
a 2 + b 2 = (a + b) 2 − 2ab.
Эта формула идеально подходит только для вычисления суммы квадратов двух целых чисел. Но что делать, если на практике требуется сложить сумму нескольких квадратов или рациональных чисел? Здесь на сцене появляется наша программа.
Наша программа позволяет сложить сколько угодно квадратов целых и рациональных чисел. Для вычислений вам потребуется ввести числа в ячейку, отделив их пробелом. Десятичные дроби записываются и с точкой, и с запятой. Рациональные числа записываются через / (слэш). Итак, вы можете подсчитать сумму нескольких квадратных чисел, но для чего это вообще нужно?
Рассмотрим примеры работы калькулятора
Разложение на квадраты
Зачем складывать квадраты целых чисел? Почему бы не складывать их кубы или 33-е степени? Эти вопросы встают перед каждым математиком, занимающимся теорией чисел. Разложение целых чисел на сумму двух квадратов — классическая задача теории чисел, за которой стоит исследование делимости. В целом задача эта обратна теме данной статьи: вопрос ставится таким образом, что математик должен вычислить, раскладывается ли данное число на сумму двух квадратов. Некоторые ученые идут дальше и пытаются раскладывать числа на суммы квадратов последовательных чисел. Мы же просто попробуем сложить некоторые квадраты и посмотрим, что получится в результате. Итак, введем в калькулятор следующие пары чисел:
- 5 и 0 = 25;
- 1 и 4 = 25;
- 8 и 1 = 64;
- 4 и 7 = 64.
Как видите, разные пары чисел дают один и тот же результат. Кроме того, сами числа 25 и 64 являются квадратами 5 и 8 соответственно. Магия теории чисел, которую трудно применить в каких-нибудь бытовых расчетах.
Гипотенуза 5-мерного тетраэдра
Представим еще менее реальную задачу. Пятимерный тетраэдр или 5-мерный симплекс — это обобщение треугольника для пятимерного пространства. Такие причудливые идеи используются в квантовой физике, теории относительности и барицентрическом исчислении, но для решения некоторых задач от вас не потребуется глубоких знаний высшей математики. К примеру, гипотенуза пятимерного тетраэдра рассчитывается по достаточно простой формуле:
f 2 = a 2 + b 2 + c 2 + d 2 ,
где a, b, c, d – стороны симплекса.
Для решения такой задачки достаточно ввести четыре значения в форму онлайн калькулятора и вычислить квадратный корень из результата. Допустим, стороны симплекса в условных единицах имеют следующие значения: 1, 2.3, 3/5, 0,85. Введем этим данные в ячейку через пробел и получим 7,3725. Теперь вычислим квадратный корень и выясним, что гипотенуза пятимерного симплекса равна 2,715.
Заключение
Сумма квадратов нескольких чисел — нестандартная задача, которая вряд ли встретится в обычных бытовых расчетах, как-то вычисление диаметра дачного ограждения или площади пиццы. Для нетривиальных математических расчетов вам пригодится наша программа, которая быстро вычислит сумму квадратов сколько угодно большого количества целых и рациональных чисел.
Решение формулы суммы квадратов двух чисел
Мамарахмонов Н.М., Мамарахмонов М.Х. Решение формулы суммы квадратов двух чисел // Universum: технические науки : электрон. научн. журн. 2020. № 8(77). URL: https://7universum.com/ru/tech/archive/item/10642 (дата обращения: 29.08.2022).
АННОТАЦИЯ
В настоящей статье нами впервые предложено решение формулы сокращенного произведения, которая может широко применена в решении различных математических задач, равенств и неравенств, а также для упрощения сложных алгебраических выражений, имеющих широкое практическое применение в науке и технике.
ABSTRACT
In this article, we first proposed a solution to the abbreviated product formula, which can be used in solving various mathematical problems, equalities and inequalities, as well as to simplify complex algebraic expressions that have wide practical applications in science and technology.
Ключевые слова: формулы сокращенного произведения, сумма квадратов двух чисел.
Keywords: formulas of short multiplication, sum of squares two numbers.
Известно, что при решении задач во всех разделах математики очень часто используют формулы сокращенного произведения (ФСУ) [1. 163-182, 2. 115, 3. 134]. Эти формулы удачно используются при упрощении сложных математических выражений, при решении алгебраических, тригонометрических уравнений, неравенств, геометрических задач, учебных и научных проблем различной сложности. Ниже приведены официально всем известные ФСУ в табличном виде, из учебников Алгебры для 7 класса:
Таблица 1.
Формулы сокращенного умножения
Формула
Название
(a+b) 2 =a 2 +2ab+b 2
Квадрат суммы двух чисел
(a-b) 2 =a 2 -2ab+b 2
Квадрат разности двух чисел
Square of difference
(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3
Куб суммы двух чисел
(a-b) 3 =a 3 -3a 2 b+3ab 2 -b 3
Куб разности двух чисел
Cube of difference
a 3 +b 3 =(a+b)(a 2 -ab+b 2 )
Сумма кубов двух чисел
a 3 -b 3 =(a-b)(a 2 +ab+b 2 )
Разность кубов двух чисел
Difference of cubes
a 2 -b 2 =(a-b)(a+b)
Разность квадратов двух чисел
Difference of squares
a 2 +b 2 = ?
Сумма квадратов двух чисел (Примечание: не разлагающаяся на члены) [8]
Sum of squares (Note: not expands) [8,10]
Наглядно видно из таблицы 1, что приведенные в ней формулы 1, 2; 3, 4; 5, 6; 7, 8 являются формулами-парами, которые отличаются нежели только со знаками у отдельных членов в левой части равенства. Однако, решение для урувнения формулой a 2 +b 2 (8) до настоящего времени ни в официальных источниках, также в учебной и научной литературе не была приведена [1-7]. Тому можно убедиться после ознакомления в электронных интернет учебниках на английском, так и на других языках. В них формула (8) указана как “not expands” – «не разлагающаяся на члены» [8-10]. Также, во всех учебниках для средних образовательных школ по математике, так и в пособиях для ВУЗов Узбекистана, России и Европейских стран, написанные на узбекском, английком, так и на русском языках, формула (8), до настоящего времени обозначается как, “не разлагающаяся на члены”.
В настоящей статье нами впервые предложена конкретное решение для формулы (8), для разложения суммы квадратов двух чисел на многочлены. Она имеет решение следующего вида:
/Mamarakhmonov.files/image001.png)
(8)
Доказательство. Результат последовательного произведения многочленов в правой части формулы (8), должны равняться сумме квадратов двух чисел, в левой части равенства. Для этого применяем правила последовательного умножения для многочленов к выражениям в скобках, в правой части равенства:
/Mamarakhmonov.files/image002.png)
Примечание. Члены с одинаковыми абсолютными значениями, но с различными знаками взаимно сокращаются, как показано ниже:
/Mamarakhmonov.files/image003.png)
;
/Mamarakhmonov.files/image004.png)
;
/Mamarakhmonov.files/image005.png)
В результате упрощения получим результат сумму квадратов двух чисел, идентичный, что в левой части равенства a 2 +b 2 .
Конец доказательства.
Предложенная нами формула для суммы квадратов двух чисел (8) является инновационной, новой и имеет в дальнейшем практическое применение как в математике, информатике, ИТ, в точных науках в целом, так и в других отраслях науки и техники.
Разложение числа на сумму квадратов
Теорема Ферма — Эйлера или теорема о представлении простых чисел в виде суммы двух квадратов гласит [1] :
Любое простое число p = 4 n + 1 , где n — натуральное число, представимо в виде суммы квадратов двух натуральных чисел.
где p — простое число.
В иностранной литературе это утверждение часто называют рождественской теоремой Ферма, так как она стала известна из письма Пьера Ферма, посланного 25 декабря 1640 года.
Из этого утверждения при помощи тождества Брахмагупты выводится общее утверждение:
Натуральное число представимо в виде суммы двух квадратов (целых чисел) тогда и только тогда, когда любое простое число вида 4 k + 3 входит в его разложение на простые множители в чётной степени.
Иногда именно этот факт подразумевается под теоремой Ферма — Эйлера.
Содержание
История [ править | править код ]
Впервые это утверждение обнаружено у Альбера Жирара в 1632 году. Пьер Ферма объявил в своём письме к Мерсенну (1640), что он доказал данную теорему, однако доказательство не привёл. Через 20 лет в письме к Каркави (от августа 1659 года) Ферма намекает, что доказательство основывается на методе бесконечного спуска.
Первое опубликованное доказательство методом бесконечного спуска было найдено Леонардом Эйлером между 1742 и 1747 годами. Позднее доказательства, основанные на иных идеях, дали Жозеф Лагранж, Карл Гаусс, Герман Минковский, Якобшталь и Дон Цагир. Последним приведено доказательство, состоящее из одного предложения [2] .
Доказательства [ править | править код ]
Одно из самых коротких доказательств придумано немецким математиком Доном Цагиром [3] :
имеет ровно одну неподвижную точку (а именно ( 1 , 1 , k ) , так как p = 4 k + 1 — простое), так что | S | нечётно и инволюция ( x , y , z ) → ( x , z , y ) ightarrow (x,z,y)> также имеет неподвижную точку.
Также есть доказательство через теорему Вильсона, придуманное Акселем Туэ [4] .
Сумма квадратов чисел — математическое выражение, для которого не существует формулы сокращенного умножения. На практике иногда требуется быстро прикинуть сумму нескольких квадратов, однако без математических хитростей такое выражение подсчитать достаточно трудно.
Формулы сокращенного умножения
Для упрощения расчетов в математике используются специальные формулы сокращенного умножения, которые, по сути, представляют собой частные случаи бинома Ньютона. При помощи таких формул легко вручную подсчитать, например, квадрат суммы или разности вида:
(a ± b) 2 = a 2 ± 2ab + b 2
Существует множество формул для решения подобных выражений, и дело не ограничивается квадратами. При помощи формул легко подсчитать куб разности или сумму многочленов n-ной степени. Мы легко можем подсчитать даже выражение (a + b + c) 3 , однако формулы сокращенного умножения для простого выражения как:
в учебниках по математике вы не найдете. Естественно, она есть для комплексных чисел, тех самых, с которыми мы знакомимся в университетском курсе математического анализа. Выглядит эта формула достаточно жутко:
a 2 + b 2 = (a + ib) × (a — ib),
где i – легендарная мнимая единица, которая рассчитывается как квадратный корень из минус единицы.
В школьных примерах продвинутые ребята негласно используют формулу, которая не входит в пантеон формул сокращенного умножения:
a 2 + b 2 = (a + b) 2 − 2ab.
Эта формула идеально подходит только для вычисления суммы квадратов двух целых чисел. Но что делать, если на практике требуется сложить сумму нескольких квадратов или рациональных чисел? Здесь на сцене появляется наша программа.
Наша программа позволяет сложить сколько угодно квадратов целых и рациональных чисел. Для вычислений вам потребуется ввести числа в ячейку, отделив их пробелом. Десятичные дроби записываются и с точкой, и с запятой. Рациональные числа записываются через / (слэш). Итак, вы можете подсчитать сумму нескольких квадратных чисел, но для чего это вообще нужно?
Рассмотрим примеры работы калькулятора
Разложение на квадраты
Зачем складывать квадраты целых чисел? Почему бы не складывать их кубы или 33-е степени? Эти вопросы встают перед каждым математиком, занимающимся теорией чисел. Разложение целых чисел на сумму двух квадратов — классическая задача теории чисел, за которой стоит исследование делимости. В целом задача эта обратна теме данной статьи: вопрос ставится таким образом, что математик должен вычислить, раскладывается ли данное число на сумму двух квадратов. Некоторые ученые идут дальше и пытаются раскладывать числа на суммы квадратов последовательных чисел. Мы же просто попробуем сложить некоторые квадраты и посмотрим, что получится в результате. Итак, введем в калькулятор следующие пары чисел:
- 5 и 0 = 25;
- 1 и 4 = 25;
- 8 и 1 = 64;
- 4 и 7 = 64.
Как видите, разные пары чисел дают один и тот же результат. Кроме того, сами числа 25 и 64 являются квадратами 5 и 8 соответственно. Магия теории чисел, которую трудно применить в каких-нибудь бытовых расчетах.
Гипотенуза 5-мерного тетраэдра
Представим еще менее реальную задачу. Пятимерный тетраэдр или 5-мерный симплекс — это обобщение треугольника для пятимерного пространства. Такие причудливые идеи используются в квантовой физике, теории относительности и барицентрическом исчислении, но для решения некоторых задач от вас не потребуется глубоких знаний высшей математики. К примеру, гипотенуза пятимерного тетраэдра рассчитывается по достаточно простой формуле:
f 2 = a 2 + b 2 + c 2 + d 2 ,
где a, b, c, d – стороны симплекса.
Для решения такой задачки достаточно ввести четыре значения в форму онлайн калькулятора и вычислить квадратный корень из результата. Допустим, стороны симплекса в условных единицах имеют следующие значения: 1, 2.3, 3/5, 0,85. Введем этим данные в ячейку через пробел и получим 7,3725. Теперь вычислим квадратный корень и выясним, что гипотенуза пятимерного симплекса равна 2,715.
Заключение
Сумма квадратов нескольких чисел — нестандартная задача, которая вряд ли встретится в обычных бытовых расчетах, как-то вычисление диаметра дачного ограждения или площади пиццы. Для нетривиальных математических расчетов вам пригодится наша программа, которая быстро вычислит сумму квадратов сколько угодно большого количества целых и рациональных чисел.
| ru_mathresearch [ tramsm ] |
Каждое целое неотрицательное число можно разложить в сумму из 4 квадратов целых чисел.
Это известное утверждение. Но мне хочется узнать сколькими способами можно разложить в сумму 3 квадратов целых чисел известное мне натуральное число? А может быть известно что-то о распределении чисел, которые не представляются в виде суммы 3 квадратов?
P.S. Я не специалист в теории числе и смежных областях. Поэтому даже не представляю, насколько сложны данные вопросы.
P.S.S. В принципе, мне интересно так же, сколькими способами натуральное число раскладывается в сумму двух квадратов целых чисел. Или хотя бы условия, когда нат. число не раскладывается в сумму 2 квадратов.
| Comments: |
| From: rus4 2008-05-19 04:11 pm (UTC) |