Сумма всех натуральных чисел: 1 2 3 4 … / Хабр

Натуральные числа

Натуральными числами называются числа, предназначенные для счета предметов. Для записи натуральных чисел используются 10 арабских цифр (0–9), положенных в основание общепринятой для математических расчетов десятичной системы счисления.

Последовательность или ряд натуральных чисел

Натуральные числа составляют ряд, начинающийся с 1 и охватывающий множество всех положительных целых чисел. Такая последовательность состоит из чисел 1,2,3, … . Это означает, что в натуральном ряду:

Есть наименьшее число и нет наибольшего.
Каждое следующее число больше предыдущего на 1 (исключение – сама единица).
При стремлении к бесконечности числа растут неограниченно.

Иногда в ряд натуральных чисел вводят и 0. Это допустимо, и тогда говорят о расширенном натуральном ряде.

Классы натуральных чисел

Каждая цифра натурального числа выражает определенный разряд. Самая последняя – это всегда количество единиц в числе, предыдущая перед ней – количество десятков, третья от конца – количество сотен, четвертая – количество тысяч и так далее.

в числе 276: 2 сотни, 7 десятков, 6 единиц
в числе 1098: 1 тысяча, 9 десятков, 8 единиц; разряд сотен здесь отсутствует, поскольку выражен нулем.

Для больших и очень больших чисел можно увидеть устойчивую тенденцию (если исследовать число справа налево, то есть от последней цифры к первой):

три последних цифры в числе – это единицы, десятки и сотни;
три предыдущие – это единицы, десятки и сотни тысяч;
три стоящие перед ними (т.е.7-я, 8-я и 9-я цифры числа, считая от конца) – это единицы, десятки и сотни миллионов и т.д.

То есть всякий раз мы имеем дело с тремя цифрами, означающими единицы, десятки и сотни более крупного наименования. Такие группы формируют классы. И если с первыми тремя классами в повседневной жизни приходится иметь дело более или менее часто, то другие следует перечислить, потому что далеко не все помнят наизусть их названия.

2-й класс – тысяча
3-й класс – миллион
4-й класс – миллиард (либо биллион);
5-й класс – триллион;
6-й класс – квадриллион;
7-й класс – квинтиллион;
8-й класс – секстиллион;
9-й класс – септиллион.

Сложение натуральных чисел

Сложение натуральных чисел представляет собой арифметическое действие, позволяющее получить число, в котором содержится столько же единиц, сколько имеется в складываемых числах вместе.

Знаком сложения является знак «+». Складываемые числа называются слагаемыми, получаемый результат – суммой. Пример:

Многозначные числа, которые прибавлять в уме затруднительно, принято складывать в столбик . Для этого числа записывают одно под другим, выравнивая по последней цифре, то есть пишут разряд единиц под разрядом единиц, разряд сотен под разрядом сотен и так далее. Далее нужно попарно сложить разряды. Если сложение разрядов происходит с переходом через десяток, то этот десяток фиксируется как единица над разрядом слева (то есть следующим за ним) и суммируется вместе с цифрами этого разряда.

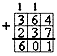
Если в столбик складывается не 2, а больше чисел, то при суммировании цифр разряда избыточным может оказаться не 1 десяток, а несколько. В этом случае на следующий разряд переносится количество таких десятков.

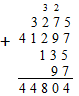
Вычитание натуральных чисел

Вычитание – это арифметическое действие, обратное сложению, которое сводится к тому, что по имеющейся сумме и одному из слагаемых нужно найти другое – неизвестное слагаемое. Число, из которого вычитают, называется уменьшаемым; число, которое вычитают, – вычитаемым. Результат вычитания называют разностью. Знак, которым обозначают действие вычитания, является «–».

При переходе к сложению вычитаемое и разность превращаются в слагаемые, а уменьшаемое – в сумму. Сложением обычно проверяют правильность выполненного вычитания, и наоборот.

Здесь 74 – уменьшаемое, 18 – вычитаемое, 56 – разность.

Обязательным условием при вычитании натуральных чисел является следующее: уменьшаемое обязательно должно быть больше вычитаемого. Только в этом случае полученная разность тоже будет натуральным числом. Если действие вычитания осуществляется для расширенного натурального ряда, то допускается, чтобы уменьшаемое было равно вычитаемому. И результатом вычитания в этом случае будет 0.

Примечание: если нулю равно вычитаемое, то операция вычитания не изменяет величины уменьшаемого.

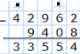
Вычитание многозначных чисел обычно производят в столбик. Записывают при этом числа так же, как и для сложения. Вычитание выполняется для соответствующих разрядов. Если же оказывается, что уменьшаемое меньше вычитаемого, то берут единицу из предыдущего (находящегося слева) разряда, которая после переноса, естественно, превращается в 10. Эту десятку суммируют с цифрой уменьшаемого данного разряда и после этого производят вычитание. Далее при вычитании следующего разряда обязательно учитывают, что уменьшаемое стало на 1 меньше.

Произведение натуральных чисел

Произведение (или умножение) натуральных чисел – это арифметическое действие, представляющее собой нахождение суммы произвольного количества одинаковых слагаемых. Для записи действия умножения используют знак «·» (иногда «×» или «*»). Например: 3·5=15.

Действие умножение незаменимо при необходимости складывать большое количество слагаемых. Например, если нужно число 4 прибавить 7 раз, то перемножить 4 на 7 проще, нежели выполнять такое сложение: 4+4+4+4+4+4+4.
Числа, которые перемножают, называются множителями, результат умножения – произведением. Соответственно, термин «произведение» может в зависимости от контекста выражать собой как процесс умножения, так и его результат.
Многозначные числа перемножают в столбик. Для этого числа записывают так же, как и для сложения и вычитания. Рекомендуется первым (выше) записывать то из 2-х чисел, которое длиннее. В этом случае процесс умножения будет более простым, а следовательно, более рациональным.
При умножении в столбик выполняют последовательное умножение цифры каждого из разрядов второго числа на цифры 1-го числа, начиная с его конца. Найдя первое такое произведение, записывают цифру единиц, а цифру десятков держат в уме. При умножения цифры 2-го числа на следующую цифру 1-го числа к произведению прибавляют ту цифру, которую держат в уме. И снова записывают цифру единиц полученного результата, а цифру десятков запоминают. При умножении на последнюю цифру 1-го числа полученное таким способом число записывают полностью.
Результаты умножения цифры 2-го разряда второго числа записывают вторым рядом, сместив его на 1 клетку вправо. И так далее. В итоге будет получена «лесенка». Все получившиеся ряды цифр следует сложить (по правилу сложения в столбик). Пустые клетки при этом нужно считать заполненными нулями. Полученная сумма и есть конечное произведение.

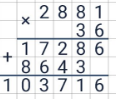
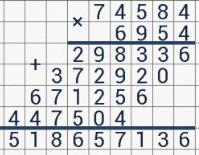
Произведение любого натурального числа на 1 (или 1 на число) равно самому числу. Например: 376·1=376; 1·86=86.
Когда один из множителей либо оба множителя равны 0, то и произведение равно 0. Например: 32·0=0; 0·845=845; 0·0=0.

Деление натуральных чисел

Делением называют арифметическое действие, с помощью которого по известному произведению и одному из множителей может быть найдет другой – неизвестный – множитель. Деление является действием, обратным умножению, и используется для проверки правильности выполненного умножения (и наоборот).

Число, которое делят, называют делимым; число, на которое делят, – делителем; результат деления называется частным. Знаком деления является «:» (иногда, реже – «÷»).

Здесь 48 – делимое, 6 – делитель, 8 – частное.

Не все натуральные числа можно поделить между собой. В этом случае выполняют деление с остатком. Заключается оно в том, что для делителя подбирается такой множитель, чтобы его произведение на делитель было бы числом, максимально близким по значению к делимому, но меньшим него. Делитель умножают на этот множитель и вычитают его из делимого. Разность и будет остатком от деления. Произведение делителя на множитель называют неполным частным. Внимание: остаток обязательно должен быть меньше подобранного множителя! Если остаток больше, то это означает, что множитель подобран неверно, и его следует увеличить.

Подбираем множитель для 7. В данном случае это число 5. Находим неполное частное: 7·5=35. Вычисляем остаток: 38-35=3. Поскольку 3

Многозначные числа делят в столбик. Для этого делимое и делитель записывают рядом, отделив делитель вертикальной и горизонтальной чертой. В делимом выделяют первую цифру или несколько первых цифр (справа), которые должны представлять собой число, минимально достаточное для деления на делитель (то есть это число должно быть больше делителя). Для этого числа подбирают неполное частное, как описано в правиле деления с остатком. Цифру множителя, использованного для нахождения неполного частного, записывают под делителем. Неполное частное записывают под числом, которое делили, выровняв его по правому краю. Находят их разность. Сносят следующую цифру делимого, вписав ее рядом с этой разностью. Для полученного числа снова находят неполное частное, записав цифру подобранного множителя, рядом с предыдущей под делителем. И так далее. Такие действия производят до тех пор, пока не закончатся цифры делимого. После этого деление считается завершенным. Если делимое и делитель делятся нацело (без остатка), то последняя разность даст нуль. В противном случае будет получено число остатка.

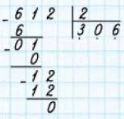
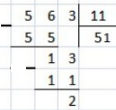
Возведение в степень

Возведение в степень – это математическое действие, заключающееся в перемножении произвольного количества одинаковых чисел. Например: 2·2·2·2.

Такие выражения записываются в виде: a x ,

где a – перемножаемое само на себя число, x – количество таких множителей.

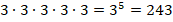
Простые и составные натуральные числа

Всякое натуральное число, кроме 1, можно разделить как минимум на 2 числа – на единицу и на само себя. Исходя из этого критерия, натуральные числа разделяют на простые и составные.

Простыми считаются числа, которые делятся только на 1 и на само себя.

Числа, которые делятся более чем на эти 2 числа, называют составными.

Единица, делящаяся исключительно на саму себя, не относится ни к простым, ни к составным.

Простыми являются числа: 2, 3, 5, 7, 11, 13, 17, 19 и т.д. Примеры составных чисел: 4 (делится на 1,2,4), 6 (делится на 1,2,3,6), 20 (делится на 1,2,4,5,10,20).

Всякое составное число можно разложить на простые множители. Под простыми множителями при этом понимаются его делители, являющиеся простыми числами.

Пример разложения на простые множители:

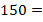
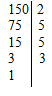
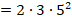
Делители натуральных чисел

Под делителем понимают число, на которое можно без остатка разделить данное число.

В соответствии с этим определением, простые натуральные числа имеют 2 делителя, составные – больше 2 делителей.

Многие числа имеют общие делители. Общим делителем называется число, на которое данные числа делятся без остатка.

У чисел 12 и 15 общий делитель 3
У чисел 20 и 30 общие делители 2,5,10

Особое значение имеет наибольший общий делитель (НОД). Это число, в частности, полезно уметь находить для сокращения дробей. Для его нахождения требуется разложить данные числа на простые множители и представить его как произведение их общих простых множителей, взятых в наименьших своих степенях.

Требуется найти НОД чисел 36 и 48.

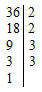
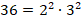
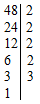
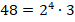
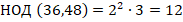
Делимость натуральных чисел. Признаки делимости.

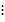
Далеко не всегда представляется возможным «на глазок» определить, делится ли одно число на другое без остатка. В таких случаях полезным оказывается соответствующий признак делимости, то есть правило, по которому за считанные секунды можно определить, можно ли разделить числа без остатка. Для обозначения делимости используется знак «».

Признак делимости на 2 или 5. На 2 или 5 делятся числа, у которых последняя цифра является числом, делящимся соответственно на 2 или 5. Примеры: 4928 делится на 2; 1365 делится на 5; 1220 делится и на 2, и на 5.
Признак делимости на 3 или 9. На эти числа делятся числа, сумма цифр которых формирует число, делящееся соответственно на 3 или 9. Примеры: 831 ( ) делится на 3; 1422 ( ) делится на 9; 3942 (3+9+4+2=18) делится и на 3, и на 9.
Признак делимости на 4 или 25. Эти числа являются делителями для тех чисел, у которых последние две цифры нули или представляют собой число соответственно делящееся на 4 или на 25. Примеры: 1300 делится и на 4, и на 25; 35616 делится на 4; 8650 делится на 25.
Признак делимости на 8 или 125. Этот признак подобен предыдущему с тем отличием, что 3 последние цифры делимого числа должны быть нулями либо представлять собой число, делящееся соответственно на 8 либо 125. Примеры: 64250 делится на 125; 15048 делится на 8; 192500 делится на 8, и на 125.
Признак делимости на 10. На 10 делятся числа, оканчивающиеся 0.
Признак делимости на 7 или 11 или 13. На 7,11,13 делятся числа, у которых разность между числом, выраженным 3-мя последними цифрами, и числом, состоящим из всех остальных цифр (или наоборот), без изменения порядка записи цифр, делится соответственно на 7 или 11 или 13. Примеры: 49105 ( ) делится на 7; 82104 ( ) делится на 11; 284245 ( ) делится на 13.

Наименьшее общее кратное

Наименьшее общее кратное (обозначается НОК) представляет собой наименьшее число, которое делится на каждое из заданных. НОК может быть найден для произвольного набора натуральных чисел.

НОК, как и НОД, имеет значительный прикладной смысл. Так, именно НОК нужно находить, приводя обыкновенные дроби к общему знаменателю.

НОК определяется путем разложения заданных чисел на простые множители. Для его формирования берется произведение, состоящее из каждого из встречающихся (хотя бы для 1 числа) простых множителей, представленных в максимальной степени.

Требуется найти НОК чисел 14 и 24.

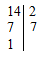
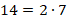
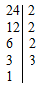
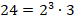
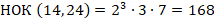
Среднее арифметическое

Средним арифметическим произвольного (но конечного) количества натуральных чисел является сумма всех этих чисел, разделенная на количество слагаемых:

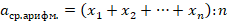
Среднее арифметическое представляет собой некоторое усредненное значение для числового множества.

Сумма всех натуральных чисел: 1 + 2 + 3 + 4 +…

Чему равна сумма этого бесконечного ряда? Перед тем, как читать дальше, дайте себе минуту на размышления. Если вы до этого не встречались с подобным рядом, а тема численных рядов в целом не слишком вам близка, то ответ на этот вопрос будет для вас большим сюрпризом.

Этот, на первый взгляд, совершенно противоречащий интуиции результат, тем не менее может быть строго доказан. Но прежде, чем говорить о доказательстве, нужно сделать отступление и вспомнить основные понятия.

Начнём с того, что «классической» суммой ряда называется предел частичных сумм ряда, если он существует и конечен. Подробности можно найти в википедии и соответствующей литературе. Если конечный предел не существует, то ряд называется расходящимся.

Например, частичная сумма первых k членов числового ряда 1 + 2 + 3 + 4 +… записывается следующим образом

Нетрудно понять, что эта сумма неограниченно растёт при стремлении k к бесконечности. Следовательно, исходный ряд является расходящимся и, строго говоря, не имеет суммы. Существует, однако, множество способов присвоить конечное значение расходящимся рядам.

Ряд 1+2+3+4+… далеко не единственный из расходящихся рядов. Возьмём, например, ряд Гранди

который тоже расходится, но известно, что метод суммирования Чезаро позволяет присвоить этому ряду конечное значение 1/2. Суммирование по Чезаро заключается в оперировании не частичными суммами ряда, а их арифметическими средними. Позволив себе порассуждать в вольном стиле, можно сказать, что то частичные суммы ряда Гранди осцилируют между 0 и 1, в зависимости от того какой член ряда является последним в сумме (+1 или -1), отсюда и значение 1/2, как арифметическое среднее двух возможных значений частичных сумм.

Другим интересным примером расходящегося ряда является знакопеременный ряд 1 — 2 + 3 — 4 +. , частичные суммы которого также осцилируют. Суммирование методом Абеля позволяет присвоить данному ряду конечное значение 1/4. Отметим, что метод Абеля является, своего рода, развитием метода суммирования по Чезаро, поэтому результат 1/4 несложно осмыслить с точки зрения интуиции.

Здесь важно отметить, что методы суммирования не являются трюками, которые придумали математики, чтобы как-то совладать с расходящимися рядами. Если вы примените суммирование по Чезаро или метод Абеля к сходящемуся ряду, то ответ, который дают эти методы, равен классической сумме сходящегося ряда.

Ни суммирование по Чезаро, ни метод Абеля, однако, не позволяют работать с рядом 1 + 2 + 3 + 4 +. т. к. средние арифметические частичных сумм, равно как и средние арифметические средних арифметических, расходятся. Кроме того, если значения 1/2 или 1/4 ещё как-то можно принять и соотнести с соответствующими рядами, то -1/12 сложно связать с рядом 1 + 2 + 3 + 4 +. представляющим собой бесконечную последовательность положительных целых чисел.

Существует несколько способов прийти к результату -1/12. В этой заметке я лишь кратко остановлюсь на одном из них, а именно регуляризации дзета-функцией. Введём дзета-функцию

Подставляя s = -1, получим исходный числовой ряд 1+2+3+4+…. Проделаем над этой функцией ряд несложных математических действий

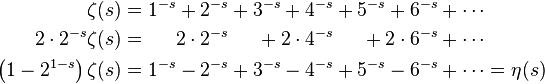
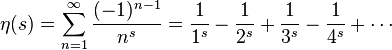
При значении s = -1 эта-функция становится уже знакомым нам рядом 1 — 2 + 3 — 4 + 5 -… «сумма» которого равна 1/4. Теперь мы можем легко решить уравнение

Интересно, что этот результат находит своё применение в физике. Например, в теории струн. Обратимся к стр. 22 книги Joseph Polchinski «String Theory»:

Если для кого-то теория струн не является убедительным примером в силу отсутствия доказательств множества следствий этой теории, то можно также упомянуть, что похожие методы фигурируют в квантовой теории поля при попытке рассчитать эффект Казимира.

Чтобы два раза не ходить, ещё пара интересных примеров с дзета-функцией

Для тех, кто захочет получить больше информации по теме отмечу, что написать данную заметку я решил после перевода соответствующей статьи на википедии, где в разделе «Ссылки» вы сможете найти массу дополнительного материала, в основном на английском языке.

Натуральные числа

Изучение математики начинается с натуральных чисел и действий с ними. Но интуитивно мы уже многое знаем с малых лет. В этой статье познакомимся с теорией и научимся правильно записывать и произносить сложные числа.

О чем эта статья:

Определение натурального числа

Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.

Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.

Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.

Наименьшее натуральное число: единица (1).
Наибольшее натуральное число: не существует. Натуральный ряд бесконечен.
У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7 и т. д.
Множество всех натуральных чисел принято обозначать латинской буквой N.

Какие операции возможны над натуральными числами

сложение:
слагаемое + слагаемое = сумма;
умножение:
множитель × множитель = произведение;
вычитание:
уменьшаемое − вычитаемое = разность.

Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!

Десятичная запись натурального числа

В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.

Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.

Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.

077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.

Количественный смысл натуральных чисел

Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.

Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».

Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.

Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:

🍌🍌🍌	3 предмета («три»)
🍌🍌🍌🍌	4 предмета («четыре»)
🍌🍌🍌🍌🍌	5 предметов («пять»)
🍌🍌🍌🍌🍌🍌	6 предметов («шесть»)
🍌🍌🍌🍌🍌🍌🍌	7 предметов («семь»)
🍌🍌🍌🍌🍌🍌🍌🍌	8 предметов («восемь»)
🍌🍌🍌🍌🍌🍌🍌🍌🍌	9 предметов («девять»)

Основная функция натурального числа — указать количество предметов.

Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.

Однозначные, двузначные и трехзначные натуральные числа

Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.

Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.

По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.

Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.

Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.

Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.

Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.

Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.

Многозначные натуральные числа

Многозначные натуральные числа состоят из двух и более знаков.

1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.

Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.

Сколько всего натуральных чисел?

Однозначных 9, двузначных 90, трехзначных 900 и т.д.

Свойства натуральных чисел

Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:

множество натуральных чисел	бесконечно и начинается с единицы (1)
за каждым натуральным числом следует другое	оно больше предыдущего на 1
результат деления натурального числа на единицу (1)	само натуральное число: 5 : 1 = 5
результат деления натурального числа самого на себя	единица (1): 6 : 6 = 1
переместительный закон сложения	от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4
сочетательный закон сложения	результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4)
переместительный закон умножения	от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4
сочетательный закон умножения	результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 ×
распределительный закон умножения относительно сложения	чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6
распределительный закон умножения относительно вычитания	чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5
распределительный закон деления относительно сложения	чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + : 3 = 9 : 3 + 8 : 3
распределительный закон деления относительно вычитания	чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2

Разряды натурального числа и значение разряда

Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.

Разряд — это позиция, место расположения цифры в записи натурального числа.

У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.

Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.

Низший (младший) разряд многозначного натурального числа — разряд единиц.

Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.

Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.

Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.

Десятичная система счисления

Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.

Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.

Вопрос для самопроверки

Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:

Урок 10 Бесплатно Сложение натуральных чисел и его свойства

Натуральные числа для вас являются привычными и давно знакомыми.

С детства считая предметы или указывая их порядковые номера, вы использовали натуральные числа.

С натуральными числами можно производить основные математические операции: складывать, вычитать, умножать, делить, сравнивать.

На этом занятии мы поговорим об операции сложения натуральных чисел, рассмотрим, как можно проиллюстрировать сложение чисел на координатном луче.

Определим основные свойства сложения и научимся применять их при решении задач.

Продемонстрируем свойства сложения с помощью координатного луча.

Научимся группировать и округлять натуральные числа при сложении.

Сложение натуральных чисел

Первым делом вспомним, что называют числовым рядом натуральных чисел и как он выглядит.

Натуральный ряд- это неограниченная последовательность натуральных чисел, расположенных в порядке их возрастания (каждое число стоит на своем месте).

У меня есть дополнительная информация к этой части урока!

В конце XIX века в работах итальянского математика Дж. Пеано были сформулированы аксиомы — истинные утверждения, которые не требуют доказательств, для множества натуральных чисел:

1. Единица- это натуральное число, которое непосредственно не следует ни за каким натуральным числом

2. За каждым натуральным числом следует одно и только одно натуральное число

3. Каждое натуральное число, отличное от единицы, следует за одним и только одним натуральным числом

Таким образом, в натуральном ряду каждое последующее число больше предыдущего на единицу.

Если не известно какое-либо число из натурального ряда, его можно определить прибавлением к предыдущему числу единицы.

Найдем в натуральном ряду, изображенном на картинке, пропущенное число, которое следует за числом три.

Прибавим к тройке единицу и получим следующее за тройкой число, равное четырем.

Получим натуральный ряд:

Попробуем сложить числа 2 и 3, действуя по аналогии с предыдущим примером.

К числу 2 прибавим три раза по единице.

К числу 2 прибавим единицу — получим число 3. К числу 3 прибавим единицу — получим число 4. К 4 прибавим единицу — получим число 5.

В результате сложения чисел 2 и 3 получили число 5.

Данный способ сложения натуральных чисел легко представить на маленьких числах.

Рассмотрим пример, в котором необходимо сложить два больших числа:

Маша прочитала за первый день 25 страниц рассказа, за второй день она прочитала 35 страниц.

Чтобы определить общее число страниц, которые прочитала маша, можно было бы пересчитать все страницы по одной, отсчитывая сначала 25 страниц, затем еще 35.

Времени на решение поставленной задачи было бы затрачено много, да и запись решения такого примера получилась бы очень громоздкой.

Чтобы освободится от пересчета объектов, используют операцию сложения.

Сложение- это арифметическое действие, в результате которого происходит объединение исчисляемых объектов в единое целое.

Результат операции сложения называется суммой (от латинского — итог, общее количество).

В общем виде операция сложения выглядит так:

Для записи сложения используют математический знак плюс «+», который находится между складываемыми числами.

Складываемые числа называют слагаемыми.

Операция сложения и результат сложения соединяются знаком равно «=».

У меня есть дополнительная информация к этой части урока!

Знак равенства «=» в математике- это символ, который пишется между идентичными по своему значению выражениями.

Знак равенства обозначался в разные времена по-разному.

В античной математике знак равенства обозначали в виде слова (например, est и egale).

В качестве обозначения знака равенства пытались использовать первые буквы слова «равный» на различных языках.

Долгое время использовали аббревиатуру «ае» от латинского слова aegualis- «равный».

Знак равенства в том виде, в котором мы его знаем сейчас, предложил математик Роберт Рекорд в 1557 году.

Этот знак он изобразил в виде двух горизонтальных отрезков, стоящих на одинаковом расстоянии друг от друга «=».

Продолжительное время знак равенства не приживался, свое распространение он получил только столетие спустя, так как многие именитые ученые использовали в своих трудах в качестве знака равенства аббревиатуру «ае», продолжительное время знаком равно «=» обозначали совсем иное математическое понятие- параллельные прямые

Решение нашей задачи будет выглядеть так:

Найдем сумму страниц, прочитанных Машей за два дня.

25 + 35 = 60 (страниц)

Эта запись читается так: «Сумма 25 (двадцати пяти) и 35 (тридцати пяти) равняется 60 (шестидесяти) или «25 (двадцать пять) плюс 35 (тридцать пять) равно 60 (шестьдесят)»

Сложение небольших натуральных чисел легко представить на координатном луче.

Найдем сумму чисел 2 и 4.

Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О (0) и единичным отрезком 1 деление = 1 единица.

Известно, что любому числу координатного луча соответствует одна единственная точка.

Выполним сложение натуральных чисел 2 и 4 на координатном луче:

Отметим на координатном луче число 2

К числу 2 прибавим 4, т.е. переместим точку А(2) на 4 единичных отрезка вправо, окажемся в точке В (6)

Следовательно, сумма чисел 2 и 4 равна 6

2 + 4 = 6

Ответ: 6

Пройти тест и получить оценку можно после входа или регистрации

Свойства сложения натуральных чисел

Рассмотрим свойства сложения натуральных чисел.

1. Переместительное свойство сложения.

Чтобы лучше понять переместительное свойство сложения натуральных чисел, рассмотрим задачу:

В вазу для фруктов положили 4 яблока и 3 груши, в результате в вазе оказалось 7 фруктов.

Представим другую ситуацию: в вазу для фруктов положили сначала 3 груши, затем 4 яблока, общее количество фруктов в вазе стало равным 7.

В первом и во втором случае общее количество фруктов, которые положили в вазу, одинаковое.

Таким образом, если сложить 4 яблока и 3 груши, то получится такой же результат, как при сложении 3 груш и 4 яблок.

4 + 3 = 7

3 + 4 = 7

4 + 3 = 3 + 4

Продемонстрируем рассмотренный пример на координатном луче.

Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О (0) и единичным отрезком (1 деление = 1 единица).

Первый вариант задачи: 4 + 3

Отметим точку C (4) на координатном луче, отложив 4 единичных отрезка вправо от точки О (0).

К числу 4 прибавим число 3, т.е. переместим точку С(4) на 3 единичных отрезка вправо, получим точку D(7), следовательно, сумма 4 + 3 = 7

Второй вариант задачи: 3 + 4

Отметим точку Е (3) на координатном луче, отложив 3 единичных отрезка вправо от точки О (0).

К числу 3 прибавим число 4, т.е. переместим точку E (3) на 4 единичных отрезка вправо, получим точку F (7), следовательно, сумма 3 + 4 = 7

Cформулируем переместительное свойство сложения.

От перестановки слагаемых сумма не меняется.

В общем виде данное свойство выглядит так:

2. Сочетательное свойство сложения натуральных чисел.

Рассмотрим данное свойство на примере.

В овощной салат нарезали 2 огурца, затем добавили 1 луковицу и 3 томата.

Рассмотрим другую ситуацию: в салат положили сначала 2 огурца и луковицу, а затем добавили 3 томата.

В первом и во втором случае для приготовления салата было использовано 6 овощей (2 огурца, 1 луковица, 3 томата).

Таким образом, результат сложения числа 2 с суммой чисел 1 и 3 равен результату сложения суммы чисел 2 и 1 с числом 3

2 + (1 + 3) = (2 + 1) + 3

Сочетательное свойство сложения звучит так:

Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить к нему первое слагаемое, а потом к полученной сумме второе.

Последовательность действий при суммировании не важна.

В общем виде сочетательное свойство сложения выглядит так:

Изобразим рассмотренный пример на координатном луче.

Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком (1 деление = 1 единица).

Первый вариант задачи: 2 + (1 + 3) = 2 + 4 = 6 (к числу 2 прибавили сумму двух чисел 1 и 3).

Второй вариант задачи: (2 + 1) + 3 = 3 + 3 = 6 (к числу 2 прибавили сначала единицу, затем к тому что получилось прибавили второе число равное 3).

Отметим точку С (2) на координатном луче (два огурца).

Решение первого варианта задачи: к двум прибавить сумму 1 + 3 = 4 (одна луковица и три томата), т.е. отложить в правую сторону от точки С (2) 4 единичных отрезка, остановимся в точке D c координатой, равной 6 (общее количество овощей в салате).

Решение второго варианта задачи: к числу 2 (число обозначающее количество огурцов в салате) прибавить сначала 1 (количество луковиц), т.е. от точки С (2) отложить на координатном луче вправо один единичный отрезок.

Затем к полученному результату прибавить число 3 (число обозначающее количество томатов), т.е. от точки Е (3) отступить 3 единичных отрезка вправо, — остановимся в точке D c координатой равной 6 (общее количество овощей в салате).

В первом и во втором варианте в результате всех производимых действий мы оказывались в точке D (6), следовательно, общее количество овощей в салате в первом и во втором варианте задачи одинаковое и равно шести.

3. Свойство сложения нуля с натуральным числом и натурального числа с нулем.

Представим, что в пустую корзину положили 6 яблок.

Это значит в корзине находилось ноль яблок и в нее помещают 6 яблок.

Понятно, что в результате в вазе оказалось 6 яблок.

0 + 6 = 6

При сложении нуля с каким-либо числом всегда получается это самое число.

Аналогичная ситуация будет складываться, если в корзине находилось 6 яблок и в нее больше ничего не положили, то в корзине останется прежнее число яблок.

Если к числу прибавлять ноль (т.е. ничего не прибавлять), то получится исходное число.

6 + 0 = 6

Сумма двух слагаемых, если одно из слагаемых равно нулю, будет всегда равна другому слагаемому.

Рассмотрим, как выглядит данное свойство на координатном луче.

6 + 0 = 6

К 6 прибавить 0, значит, точку с координатой 6 переместить на 0 единичных отрезков, т.е. оставить точку на том же месте.

0 + 6 = 6

К 0 прибавить 6, значит, от точки О (0) отложить вправо 6 единичных отрезков, полученная точка с координатой 6 является суммой чисел 0 и 6

Переместительное и сочетательное свойство сложения используют для упрощения вычисления математических выражений.

В выражениях со скобками первым действием выполняют то, которое стоит в скобках.

Когда в записи суммы нет скобок, то сложение выполняют по порядку слева направо.

При вычислении суммы, состоящей из трех и более слагаемых, удобно использовать сразу переместительное и сочетательное свойство сложения, группируя слагаемые, объединяя их по определенному признаку с помощью скобок.

Группировать числа лучше так, чтобы в сумме эти числа давали круглое число (число, оканчивающееся на ноль), с такими числами легче выполнять математические операции.

Пример:

Дано выражение 15 + 23 + 35 + 17

Найдем сумму чисел удобным способом.

Проще решить данное выражение, объединив с помощью скобок слагаемые так, чтобы в сумме они давали круглые числа.

Используя переместительное и сочетательное свойство сложения, переставим местами слагаемые и сгруппируем их.

Ответ: 90

У меня есть дополнительная информация к этой части урока!

Круглые числа легче сложить друг с другом.

Пример:

Существует правило: сумма чисел не изменяется, если к одному из слагаемых прибавить несколько единиц, а из другого слагаемого вычесть такое же количество единиц.

Найдем сумму чисел 49 и 13

Увеличим слагаемое 49 на одну единицу; таким образом, округлим его до 50

Но, увеличивая одно слагаемое на одну единицу, необходимо второе слагаемое уменьшить на одну единицу для сохранения равенства.

Уменьшим число 13 на одну единицу.

49 + 1 = 50

13 — 1 = 12

Получаем следующее выражение:

50 + 12 =62

Ответ: 62.

Данный прием округления особенно удобно использовать при устных вычислениях.

Суммирование методом Рамануджана: 1 + 2 + 3 + … + ∞ = −1/12?

+7 926 604 54 63 address

«Что ты несёшь? Этого не может быть!»

Моя мама.

В качестве эпиграфа я взял то, что сказала мне мама, узнав от меня об этой маленькой математической аномалии. И это именно аномалия. В конце концов, это противоречит основам логики. Как может сумма натуральных чисел равняться не только отрицательной величине, но ещё и отрицательной дроби? Что за дребедень?

Прежде чем начать: мне указали на то, что в данной статье слово «сумма» я использую в нетрадиционном смысле, ибо все ряды, о которых я говорю, не стремятся естественным образом к определённому числу. Так что речь идёт о другом типе сумм, а именно о суммировании методом Чезаро. Для всех, кто интересуется математикой: суммирование по Чезаро присваивает значения некоторым бесконечным суммам, которые не сходятся в обычном смысле. Согласно Википедии, «сумма Чезаро определяется как предел последовательности средних арифметических первых n частичных сумм ряда при n, стремящемся к бесконечности». Добавлю, что в данной статье используется понятие счётной бесконечности, то есть идёт речь о таком бесконечном множестве чисел, при котором, имея достаточно времени, можно сосчитать до любого числа множества. Это позволяет мне применять в уравнениях некоторые обычные математические свойства, такие как коммутативность (аксиома, которую я использую на протяжении всей статьи).

Сриниваса Рамануджан Айенгор (1887—1920), выдающийся индийский математик

Сриниваса Рамануджан Айенгор (1887—1920), выдающийся индийский математик.

Для тех из вас, кто незнаком с рядом, известным как суммирование методом Рамануджана (Сриниваса Рамануджан (Srinivasa Ramanujan) — выдающийся индийский математик), объясняю: такое суммирование означает, что, складывая все натуральные числа, то есть 1, 2, 3, 4 и так далее, вплоть до бесконечности, вы получите результат −1/12. Ага, −0,08333333333.

суммирование рамануджана

Вы не верите мне? Читайте дальше, и узнаете, как я доказываю это путём доказательства истинности двух одинаково безумных утверждений:

1. 1 − 1 + 1 − 1 + 1 − 1 … = 1/2

2. 1 − 2 + 3 − 4 + 5 − 6 … = 1/4

Прежде всего, расскажу о главном — о волшебном преобразовании, без которого невозможны доказательства двух данных утверждений.

Возьмём ряд A, который представляет собой бесконечное повторение 1 − 1 + 1 − 1 + 1 − 1. Я запишу это так:

A = 1 − 1 + 1 − 1 + 1 − 1 …

Теперь маленький трюк: вычту А из 1.

1 − A = 1 − (1 − 1 + 1 − 1 + 1 − 1 …)

Пока всё правильно? Настало время перейти к волшебству. Упростив правую часть уравнения, я получаю кое-что весьма странное:

1 − A = 1 − 1 + 1 − 1 + 1 − 1 + 1 …

Не правда ли, что-то такое уже было? Подсказываю: это A. Да, в правой части уравнения оказался ряд, с которого мы начали. Теперь я могу заменить всю правую часть на букву A, немного поупражняться в применении алгебры средней школы — и опля!

Эта маленькая прелесть — ряд Гранди, названный в честь итальянского математика, философа и священника Гвидо Гранди (Guido Grandi). Вот и всё, что есть интересного в этом ряде, и, хотя лично для меня он самый замечательный, с ним не связано никаких крутых историй или открытий. Однако именно он позволяет построить доказательство для многих интересных вещей, включая очень важное для квантовой механики и даже для теории струн уравнение. Но об этом чуть позже. А пока перейдём к доказательству утверждения №2: 1 − 2 + 3 − 4 + 5 − 6 … = 1/4.

Приступим к делу так же, как и выше. Пусть мы имеем ряд B: В = 1 − 2 + 3 − 4 + 5 − 6 … Теперь с этим можно поиграть. Для начала вычтем B из A. По правилам математики мы получаем следующее:

A − B = (1 − 1 + 1 − 1 + 1 − 1 …) − (1 − 2 + 3 − 4 + 5 − 6 …)

A − B = (1 − 1 + 1 − 1 + 1 − 1 …) − 1 + 2 − 3 + 4 − 5 + 6 …

Затем слегка перемешаем элементы, чтобы получился ещё один интересный паттерн.

A − B = (1 − 1) + (−1 + 2) + (1 − 3) + (−1 + 4) + (1 − 5) + (−1 + 6) …

A − B = 0 + 1 − 2 + 3 − 4 + 5 …

И снова мы пришли к ряду, с которого начали, а поскольку нам уже известно, что A = 1/2, мы, используя основы алгебры, можем завершить доказательство нашего второго умопомрачительного факта.

Вуаля! У данного уравнения нет эффектного названия, ибо известно оно давно, и за долгие годы многие математики сумели выполнить его доказательство, что, однако не помешало им считать это уравнение парадоксальным. Как бы то ни было, оно будоражило умы учёных и даже помогло Эйлеру более широко подойти к решению «базельской проблемы», а также привело к исследованию важных математических функций, таких как дзета-функция Римана.

А теперь вишенка на торте, которую вы так долго ждали, — гвоздь программы. Первые шаги похожи на те, которые мы делали раньше: возьмём ряд C = 1 + 2 + 3 + 4 + 5 + 6 …, а дальше, как вы, возможно, догадались, вычтем C из B.

B − C = (1 − 2 + 3 − 4 + 5 − 6 …) — (1 + 2 + 3 + 4 + 5 + 6)

Поскольку математика по-прежнему безупречна, поменяем некоторые числа местами, чтобы получить кое-что знакомое, но, вероятно, не то, о чём вы подумали.

В − С = (1 − 2 + 3 − 4 + 5 − 6 …) − 1 − 2 − 3 − 4 — 5 − 6 …

В − С = (1 − 1) + (−2 − 2) + (3 − 3) + (−4 − 4) + (5 − 5) + (−6 − 6) …

B − C = 0 − 4 + 0 − 8 + 0 − 12 …

Это не то, что вы ожидали, верно? Но сейчас вы не сможете удержаться от возгласа «Вау!», ибо я готов выполнить ещё один, последний трюк, который стоит того, чтобы им восхищаться. Возможно, вы заметили, что все числа с правой стороны кратны числу −4. Следовательно, мы можем вынести этот постоянный множитель за скобки — и вновь прийти к тому, с чего начали!

В − С = −4 (1 + 2 + 3) …

А поскольку, как мы выяснили ранее, B = 1/4, получаем наш волшебный результат:

1/−12 = C, или C = −1/12.

Теперь объясню, почему этот результат важен. Во-первых, он используется в теории струн. Увы, в её первоначальной версии (в теории бозонных струн), а не в версии Стивена Хокинга (Stephen Hawking). К сожалению, теория бозонных струн несколько устарела, и сегодня учёные предпочитают суперсимметричную теорию струн, но исходная теория всё ещё используется для понимания суперструн, которые являются неотъемлемыми элементами вышеупомянутой обновлённой теории струн.

Во-вторых, суммирование по методу Рамануджана оказало большое влияние на развитие общей физики, особенно при осмыслении явления, известного как эффект Казимира. Хендрик Казимир (Hendrik Casimir) предсказал, что две незаряженные проводящие пластины, помещённые в вакуум, будут притягиваться друг к другу из-за присутствия виртуальных частиц, порождаемых квантовыми флуктуациями. Моделируя количество энергии между пластинами, Казимир использовал то самое уравнение, истинность которого мы только что доказали. Вот почему этот результат такой важный.

Итак, вы познакомились с открытым в начале 1900-х годов суммированием по методу Рамануджана, которое, хоть и прошло сто лет, всё ещё играет важную роль при решении проблем во многих областях физики и которое, если заключать пари с несведущими людьми, всё ещё может приносить победу.

P.S. Если у вас не пропал интерес к безумному уравнению Рамануджана и вы хотите узнать больше, то у меня есть для вас ссылка на беседу с двумя физиками. Они пытаются объяснить данное уравнение и показать его полезность и значимость. Это красиво, коротко и очень интересно.

Из серии рассказов на математические темы «Канторовский рай» («Cantor’s Paradise»).

Почему сумма всех натуральных чисел равна -1/12?

Когда мы складываем числа, увеличивая каждый последующий член на одно и то же положительное значение, мы будем получать все больше и больше значений с каждым новым термином. Например, сумма всех натуральных чисел от 1 до 10 будет 55, от 1 до 100 будет 5050, и из-за увеличения верхнего предела сумма станет больше. Логично предположить, что сумма чисел от 1 до бесконечности дает бесконечно большое число, но если мы произведем вычисления, мы получим значение -1/12. Одно дело, если мы получаем некое конечное число со знаком плюс, хотя это вызывает диссонанс, другое дело, когда мы получаем дробь со знаком минус, что кажется совершенно абсурдным, потому что как мы можем получить отрицательное число, складывая положительные числа? . В этой статье мы рассмотрим, как математики вообще достигли такого значения.

Почему сумма всех натуральных чисел равна -1/12?

Для этого стоит сначала проанализировать внешний вид некоторых других сумм. Начнем с этого: 1-1 + 1-1 + 1-1…. Это бесконечная сумма чередующихся единиц и единицы минус один. Если бы мы знали, каким знаком заканчивается данный числовой ряд, то у нас не было бы проблем сказать, каково его окончательное значение, но этот ряд бесконечен. Для удобства мы обозначили этот набор чисел буквой A. Для расчета суммы после первого элемента вставляем знак минус, как показано на рисунке ниже. Поскольку ряд чисел бесконечен, выражение в скобках также будет суммой A, и после обычных алгебраических вычислений мы получим, что A = 1/2, точнее, 1-1 + 1-1 + 1-1 + 1.. = 1/2

Почему сумма всех натуральных чисел равна -1/12?

Теперь подсчитываем следующую строку: 1-2 + 3-4 + 5-6 + 7-8 +… Назовем эту строку номером B и теперь добавляем к ней уже посчитанную строку A = ½, но добавляем начальную из второго элемента как это, как показано на диаграмме ниже. Тогда получаем, что из единицы вычитается тот же ряд B. После обычных алгебраических действий получаем B=¼

Почему сумма всех натуральных чисел равна -1/12?

И, наконец, этот же ряд является суммой всех натуральных чисел, обозначим его X. X = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +… Вычтем вышеупомянутый ряд из это чисел B = ¼. В результате получаем: 1-1 + 2 + 2 + 3-3 + 4 + 5-5 + 6 + 6 + 7-7 . и для простоты перепишем его как на изображении ниже. В результате получается, что наша сумма всех натуральных чисел X будет вычтена ¼ будет равна 4 + 8 + 12 + 16… Сумма всех чисел будет кратна четырем, из которых мы просто положили 4 между скобками, а в скобках мы получаем 1 + 2 + 3 + 4…, то есть ту же строку, что и X, ну после упрощений, показанных ниже, мы получаем X = -1 / 12, так как X = 1 + 2 + 3 + 4 + 5 + 6…, сумма всех натуральных чисел равна -1/12.

Почему сумма всех натуральных чисел равна -1/12?

При этом интересно отметить, что этот факт о сумме чисел используется во многих статьях по физике, особенно в квантовой механике, например, многие статьи по теории струн работают с ним, а также благодаря ему эффект Казимира . Конечно, можно и стоит подвергнуть сомнению тот факт, что сумма всех натуральных чисел равна отрицательному числу, и, возможно, это недостаток методов подсчета рядов, но тот факт, что число -1/12 используется во многих научных исследованиях статьи, и это работает, говорит о многом.

Автор: Владислав Кигим. Под редакцией Федора Карасенко.

Поднимите вверх, чтобы увидеть больше статей о космосе и науке в вашей ленте!

Подпишитесь на мой канал здесь, а также на мои каналы в Telegram и YouTube. Там вы можете прочитать большое количество интересных материалов и задать свой вопрос. Вы можете оказать финансовую поддержку нашему каналу через patreon.

Натуральные числа. Ряд натуральных чисел.

История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.

Натуральные числа – это числа которые мы используем при счете предметов.

Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….

Нуль не относится к натуральным числам.

Все натуральные числа или назовем множество натуральных чисел обозначается символом N.

Таблица натуральных чисел.

Таблица натуральных чисел от 1 до 100

Натуральный ряд.

Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.

Свойства натурального ряда:

Наименьшее натуральное число – единица.
У натурального ряда следующее число больше предыдущего на единицу. (1, 2, 3, …) Три точки или троеточие ставятся в том случае, если закончить последовательность чисел невозможно.
Натуральный ряд не имеет наибольшего числа, он бесконечен.

Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5

Пример №2:
Нуль является натуральным числом?
Ответ: нет.

Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.

Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.

Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.

Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.

Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.

Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.

Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.