Что такое задача коши для дифференциального уравнения
Pers.narod.ru. Обучение. Лекции по численным методам. Численное решение обыкновенных дифференциальных уравнений
5. Численное решение обыкновенных дифференциальных уравнений
Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:
, где x – независимая переменная, — i-ая производная от искомой функции. n — порядок уравнения. Общее решение ОДУ n–го порядка содержит n произвольных постоянных , т.е. общее решение имеет вид .
Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.
Ясно, что при n=1 можно говорить только о задачи Коши.
Примеры постановки задачи Коши:
Примеры краевых задач:
Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений.
Численные методы решения задачи Коши для ОДУ первого порядка
Постановка задачи. Найти решение ОДУ первого порядка
на отрезке при условии
При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом , расчетными узлами служат точки промежутка [x0, xn].
Целью является построение таблицы
т.е. ищутся приближенные значения y в узлах сетки.
Интегрируя уравнение на отрезке , получим
Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка
то получим явную формулу Эйлера:
Зная , находим , затем т.д.
Геометрическая интерпретация метода Эйлера:
Пользуясь тем, что в точке x0 известно решение y(x0) = y0 и значение его производной , можно записать уравнение касательной к графику искомой функции в точке : . При достаточно малом шаге h ордината этой касательной, полученная подстановкой в правую часть значения , должна мало отличаться от ординаты y(x1) решения y(x) задачи Коши. Следовательно, точка пересечения касательной с прямой x = x1 может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую , которая приближенно отражает поведение касательной к в точке . Подставляя сюда (т.е. пересечение с прямой x = x2), получим приближенное значение y(x) в точке x2: и т.д. В итоге для i–й точки получим формулу Эйлера.
Явный метод Эйлера имеет первый порядок точности или аппроксимации.
Если использовать формулу правых прямоугольников: , то придем к методу
Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения по известному значению требуется решать уравнение, в общем случае нелинейное.
Неявный метод Эйлера имеет первый порядок точности или аппроксимации.
Модифицированный метод Эйлера: в данном методе вычисление состоит из двух этапов:
Данная схема называется еще методом предиктор – корректор (предсказывающее – исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.
Методы Рунге – Кутта: идея построения явных методов Рунге–Кутты p–го порядка заключается в получении приближений к значениям y(xi+1) по формуле вида
Здесь an, bnj, pn, – некоторые фиксированные числа (параметры).
При построения методов Рунге–Кутты параметры функции (an, bnj, pn) подбирают таким образом, чтобы получить нужный порядок аппроксимации.
Схема Рунге – Кутта четвертого порядка точности:
Пример. Решить задачу Коши:
Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта.
IX. Обыкновенные диференциальные уравнения. Задача Коши
1. Основные определения.Обыкновенным дифференциальным уравнением называется уравнение, которое содержит производные от искомой функции y(x):
где x-независимая переменная, (n)-порядок производной. Наивысший порядок n, входящий в это уравнение называется порядком дифференциального уравнения.
Общее решение дифференциального уравнения имеет вид:
где с1. сn — произвольные постоянные. Их количество определяется порядком дифференциального уравнения. Если значения c1. cn — известны и соответственно равны , то получаем частное решение: . Значения определяются из условий, которые называются дополнительными условиями для данного дифференциального уравнения.
В зависимости от способа задания дополнительных условий для данного дифференциального уравнения существуют два различных типа задач: задача Коши и краевая задача. Дополнительные условия задаются значениями функции и ее производных при некоторых значениях переменной x, т.е. в некоторых точках отрезка, где требуется найти решение.
2. Задача Коши для дифференциального уравнения первого порядка. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями, а точка x=x0, в которой они задаются — начальной точкой.
Рассмотрим задачу Коши для дифференциального уравнения первого порядка:
с начальным условием .
Решением дифференциального называется функция y(x), которая при подстановке его в уравнение, превращает последнее в тождество. График решения дифференциального уравнения называется интегральной кривой. Общее решение уравнения имеет вид: y=j(x,c1). Данному решению соответствует бесконечное семейство интегральных кривых с параметром c1. С помощью начальных условий y(x0)=y0 из этого семейства выделяется одна конкретная интегральная кривая, которая является частным решением.
Пусть выбраа произвольная интегральная кривая и на ней точка с координатами (xi,yi). В этой точке имеем: , где ai угол наклона касательной к интегральной кривой в заданной точке xi (Рис.9).
Величина называется угловым коэффициентом. Угловой коэффициент в узле xi равен тангенсу угла наклона касательной к интегральной кривой, проходящей через точку (xi,yi).
3. Методы Эйлера решения задачи Коши.На отрезке [a,b] вводится равномерная сетка: xi, i=0,1. n; с шагом h=xi+1-xi, при этом x0=a и xn=b. Сетка рассматривается как переменная величина xh, которая изменяется дискретным образом с шагом h между узлами. Набор значений функции yi=y(xi), i=0,1. n; в узлах xi называется сеточной функцией и обозначается как yh. Решение задачи Коши состоит в нахождении значений сеточной функции удовлетворяющей дифференциальному уравнению и заданным начальным условиям.
а) простой метод Эйлера первого порядка точности по шагу h.Для аппроксимации первой производной используем правую разность . В итоге получим формулу метода Эйлера для решения дифференциального уравнения:
В узле xi вычисляется угловой коэффициент ki, с помощью которого вычисляется значение сеточной функции yi+1 в узле xi+1.
Так как значение y0 задано граничным условием: y0=y(x0), то приведенное соотношее позволяет определить значение сеточной функции yi во всех последующих узлах начиная с первого;
б) метод Эйлера-Коши второго порядка точности по шагу h. Расчетная формула данного метода имеет вид:
На первом этапе, в соответствии с методом Эйлера первого порядка точности, с помощью углового коэффициента ) вычисляется грубое приближение искомой функции в узле xi+1=xi+h. Затем ,в этом узле с помощью значений вычисляется угловой коэффициент . Далее определяется усредненный угловой коэффициент , который служит для вычисления значения yi+1=yi+h×ki;
в) усовершенствованный метод Эйлера второго порядка точности по шагу h. Расчетная формула данного метода имеет вид:
С помощью углового коэффициента: в узле вычисляется приближенное значение . Далее вычисляется угловой коэффициент в этом узле. С помощью этого коэффициента вычисляется значение .
4. Метод Рунге — Кутты четвертого порядка точности. Наиболее известным из методов Рунге-Кутты является классический 4-этапный метод четвертого порядка точности, расчетные формулы которого имеют вид:
В начале один за другим вычисляются угловые коэффициенты . Далее определяется угловойт , с помощью которого находится значение сеточной функции в узле .
Варианты задания №12
Используя указанный метод на отрезке [a,b] с шагом h=0,2 численно решить дифференциальное уравнение при заданном начальном условии.
Понятие о дифференциальном уравнении. Задача Коши
Определение 1. Уравнение, содержащее независимую переменную, функцию от этой независимой переменной и ее производные различных порядков, называется дифференциальным уравнением.
Определение 2. Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.
Дифференциальное уравнение n-го порядка имеет вид
F(x,y,y‘,y», …, y (n) )=0.
Определение 3. Дифференциальное уравнение n-го порядка называется линейным, если неизвестная функция и все ее производные входят в него в первой степени. Общий вид линейного дифференциального уравнения n-го порядка:
a0(x)y ( n ) + a1(x)y ( n -1) + . + an-1(x)y (1) + an(x)y = f(x). (1)
Определение 4. Линейное дифференциальное уравнение (1) называется однородным, если f(x) º 0, и неоднородным — в противном случае.
Примеры дифференциальных уравнений:
y» — sin x y’ + (cos x) y = tg x — линейное,
sin y’ — cos y = ctg x — нелинейное,
y»’ — y’ = 0- линейное,
(y IV ) 2 — 3y»’ + y = 1 — нелинейное.
Определение 5. Решением дифференциального уравнения называется любая функция y = j(x), при подстановке которой в уравнение будет получено тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения, график решения называют интегральной кривой.
Пример 1. y’ — f(x) = 0 , Пример 2. y» = 0,
y = ò f(x)dx + C. y = C1x + C2.
Определение 6. Решение дифференциального уравнения n-го порядка, содержащее n произвольных постоянных, называется общим решением дифференциального уравнения.
Определение 7. Если в результате интегрирования дифференциального уравнения получена зависимость между y и x, из которой не удается явно выразить y через x (т.е. неизвестная функция задана неявно), то данную зависимость называют общим интегралом дифференциального уравнения.
Определение 8. Решение, полученное из общего при конкретных значениях произвольных постоянных, называется частным решением.
Пример. y» + y = 0.
y = C1cos x + C2sin x — общее решение.
у1 = 3cos x —2sin x — частное решение.
Задача Коши
Материал из Википедии — свободной энциклопедии
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла)дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).
Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при , а решение отыскивается при .
От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.
Основные вопросы, которые связаны с задачей Коши, таковы:
1. Существует ли (хотя бы локально) решение задачи Коши?
2. Если решение существует, то какова область его существования?
3. Является ли решение единственным?
4. Если решение единственно, то будет ли оно корректным, то есть непрерывным (в каком-либо смысле) относительно начальных данных?
Говорят, что задача Коши имеет единственное решение, если она имеет решение и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки имеет поле направлений, совпадающее с полем направлений . Точка задаёт начальные условия.
| Содержание [убрать] · 1 Различные постановки задачи Коши · 2 Теоремы о разрешимости задачи Коши для ОДУ · 3 См. также · 4 Литература |
[править]Различные постановки задачи Коши
§ ОДУ первого порядка, разрешённое относительно производной

§ Система ОДУ первого порядка, разрешённая относительно производных (нормальная система -го порядка)
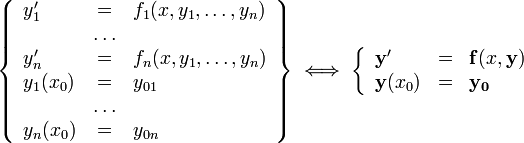
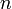
§ ОДУ -го порядка, разрешённое относительно старшей производной
Решение задачи Коши

задача Коши, или начальная задача, ставится следующим образом: среди всех решений уравнения (2) найти такое решение

в котором функция у(х) принимает заданное числовое значение Уо при заданное числовом значении х0 независимой переменной х, т. е.
где и — заданные числа, так что решение (36) удовлетворяет условию:
При этом число называется начальным значением искомой функции, а число — начальным значением независимой переменной. В целом же числа и называются начальными данными решения (36), а условие (38) —начальным условием этого решения.
По этой ссылке вы найдёте полный курс лекций по высшей математике:

Задачу Коши геометрически можно сформулировать так: среди всех интегральных кривых уравнения (2)’найти tj (рис. 6), которая проходит через заданную точку

Будем говорить, что задача Коши с начальными условиями (38) имеет единственное решение, если существует та кое число , что в интервале — определено решение такое, что и не существует решения, определенного в этом же интервале и не совпадающего с решением хотя бы в одной точке интервала
отличной от точки В противном случае, т. е. когда задача Коши с начальным условием (38) имеет не одно решение или же совсем не имеет решений, мы будем говорить, что в точке нарушается единственность решения задачи Коши.
Возможно вам будут полезны данные страницы:
Вопрос о единственности решения задачи Коши представляет исключительный интерес как для самой теории дифференциальных уравнений, так и для ее многочисленных приложений, ибо, зная, что решение задачи Коши единственно, мы, найдя решение, удовлетворяющее заданным начальным условиям, уверены, что других решений, удовлетворяющих тем же начальным условиям, нет.
В вопросах естествознания эго приводит к тому, что мы получаем вполне определенный, единственный закон явления, определяемый только дифференциальным уравнением и начальным условием. Иллюстрацией сказанного может служить хотя бы пример 1, рассмотренный во введении.
Заметим, что в простейшем случае задача Коши встречается нам уже в интегральном исчислении, именно там, по существу, доказывается, что если функция f(x) непрерывна в интервале (а, Ь),то единственным решением уравнения
принимающим значение принадлежит интервалу —любое заданное число, является функция*

Эго решение определено ео всем интервале (а, Ь).
Из формулы (40) легко усмотреть характер зависимости решения рассматриваемой задачи Коши как от независимой переменной, так и от начальных данных.

Прежде всего из курса анализа известно, что решение (40) является непрерывно дифференцируемой** функцией от независимой переменной х. Геометрически это означает, что через точку проходит одна и только одна интегральная кривая. Эта интегральная кривая гладкая***. Она пересекается со всякой -прямой, параллельной оси Оу, не более чем в одной точке.

Из формулы (40) видно также, что решение задачи К о ш и дл я простейшего дифференциального уравнения (39) я в-ляется непрерывной и даже непрерывно дифференцируемой функцией начальных данных
Особые случаи задачи Коши. При постановке задачи Коши с начальными данными мы неявно предполагали, что числа х0 и уо конечны и что правая часть уравнения (2) определена и конечна в точке , т. е. уравнение (2) задает в точке определенное направление поля, причем последнее не параллельно оси Оу. Если правая часть уравнения (2) обращается в точке в бесконечность, то следует рассматривать перевернутое уравнение (.
и искать решение (рис. 7), удовлетворяющее начальному условию: . Единственная «особенность» решения этой задачи Коши состоит только в том, что в точке касательная к интегральной кривой параллельна оси Оу.

Совсем другое положение мы будем иметь, если в точке правая часть уравнения (2) по определена. Предположим, что f(x, у) обращается в точке в неопределенность вида Тогда обычная постановка задачи Коши теряет смысл, так как через точку не проходит ни одна интегральная кривая.
В этом случае задача Коши ставится так:
найти решение вида [или обладающее свойством (28) [или (29)], т. е. найти решение, примыкающее к точке
Здесь, так же как и в основном случае задачи Коши, возникают вопросы существования и единственности решения.
Кроме того, здесь возникают и дополнительные вопросы:
1) имеют ли решения, примыкающие к точке , определенную касательную в этой точке? Дело в том, что само уравнение (2) в этом случае не предписывает никакого определенного направления касательной в такой точке ;
2) если интегральные кривые примыкают к точке с определенными направлениями касательной, то каковы эти направления? Сколько кривых входит по данному направлению? В примерах 3 и 4, рассмотренных в п. 4, все интегральные кривые уравнения (30) примыкают к точке (0,0) (где правая часть обращается в о — неопределенность вида ), имея в ней каждая свою касательную, в то время как ни одна из интегральных кривых уравнения (34) не примыкает к точке (0,0), так что для этого уравнения задача Коши с начальными данными не имеет ни одного решения.

В некоторых случаях возникает необходимость искать решения , удовлетворяющие условиям:

Указанные выше особые случаи задачи Коши исследуются в аналитической теории дифференциальных уравнений и в качественной теории дифференциальных уравнений. Во всех случаях задачи Коши наряду с вопросами существования и единственности возникают /вопросы о свойствах решения задачи Коши как функции независимой переменной (аналитический вид, дифференциальные и геометрические свойства и особенности «поведения во всей области существования) и как функции начальных данных. Рассмотрение этих вопросов составляет одну из основных задач теории дифференциальных уравнений.
Достаточное условие существования решения задачи Коши
Предположим, что правая часть уравнения (2) определена и непрерывна в некоторой области G изменения х и у. Тогда, как уже отмечалось раньше (п. 4), уравнение (2) определяет некоторое поле направлений, причем в силу только что сделанного предположения о непрерывности правой части уравнения (2) это ноле направлений непрерывно, так что направления в двух достаточно близких точках разнятся сколь угодно мало. Заметим, что из сделанного предположения о непрерывности


правой части уравнения (2) следует, что всякое решение этого уравнения (если оно существует) будет непрерывно дифференцируемым, так что всякая интегральная кривая будет гладкой. Всякая интегральная кривая, как уже было сказано в п. 4., обладает чем свойством, что в каждой ее точке направление карательной совпадает с направлением поля, определяемым дифференциальным уравнением в этой точке. Попытаемся, пользуясь этим свойством интегральной кривой, найти решение задачи Коши для уравнения (2) с начальными данными из области G.
Возьмем п области G некоторую точку (рис  Наклон поля в этой точке равен Проведем через точку -прямую с угловим коэффициентом
Наклон поля в этой точке равен Проведем через точку -прямую с угловим коэффициентом
На этой прямой возьмем любую точку , принадлежащую области G, и через нее прощую области G, и через нее проведем прямую с угловым коэффициентом, равным наклону поля в этой точке, т. е. На последней прямой возьмем любую точку принадлежащую области G, и проведем через нее прямую с угловым коэффициентом и т. д. Такое же построение можно сделать и влево от точки . Построенная ломаная линия называется ломаной Эйлера.
Ясно, что можно построить бесчисленное множество ломаных Эйлера, проходящих через точку — Каждая из этих ломаных с достаточно короткими звеньями дает некоторое представление об интегральной кривой, проходящей через точку если эта интегральная кривая существует. Естественно ожидать, что .мы можем построить последовательность ломаных Эйлера, имеющую своим пределом (когда длины всех звеньев ломаной стремятся к пулю, а их число стремится к бесконечности) интегральную кривую, проходящую через точку Л<о(хо, Уо).
Можно доказать*, что при сделанном предположении относительно f(x, у) это действительно имеет место, так что для существования непрерывно дифференцируемого решения задачи Коши для уравнения (2) достаточно предположить, что его правая часть непрерывна в окрестности начальных данных (теорема Пеано).
Заметим, однако, что нс исключена возможность существования нескольких последовательностей ломаных Эйлера, проходящих через точку , каждая из которых стремится к своей интегральной кривой, так что в общем случае, нет оснований ожидать, что мы получим единственную интегральную кривую, проходящую через точку . Более того, как показал М. Л. Лаврентьев**, единственность решения может нарушаться даже во всех точках непрерывности правой части уравнения (2).
Таким образом, теорема Пеано есть только теорема существования решения задачи Коши. Единственности решения она не гарантирует.
Достаточные условия существования и единственности решения задачи Коши
Поставим вопрос: каким условиям достаточно подчинить правую часть уравнения (2) в окрестности начальных данных чтобы через точку проходила одна и только одна интегральная кривая этого уравнения» В общем виде этот вопрос мы рассматриваем в гл. V, где пр* некоторых предположениях относительно правой части уравнения (2) мы доказываем существование и единственность решения задачи Коши и показываем, что свойства решения задачи Коши вполне определяются свойствами правой части уравнения (2) и начальными данным и. Сейчас мы приведем без дока-загельства основную теорему существования и единственности (теорему Пикара) для уравнения (2) в упрощенной формулировке.
Теорема. Пусть дано уравнение (2),

и поставлено начальное условие (38),


Предположим, что функция определена в некоторой замкнутой ограниченной области (рис. 9)



с точкой внутри (а и b — заданные положительные числа) и удовлетворяет в ней следующим двум условиям.

У 1. Функция непрерывна и следовательно, ограничена, т. е.

где М—постоянное положительное число, а(х, у) — любая точка области R;
II. Функция f(x, у) имеет ограничейную частную производную по аргументу у, т. е.:

где К — постоянное положительное число, а (х, у)—любая точка области R.
При этих предположениях уравнение (2) имеет единственное решение (36),

удовлетворяющее начальному условию (38). Это решение определено и непрерывно дифференцируемо в некоторой окрестности начального значения х0 независимой переменной х, а именно оно заведомо определено в интервале


где h есть наименьшее из чисел
Из этой теоремы, в частности, следует, что если правая часть уравнения (2) есть полином относительно х и у или любая другая функция, определенная и непрерывная относительно х и у вместе с частной производной по у при всех значениях х и у, то через любую точку проходит одна и только одна интегральная кривая, ибо во всяком прямоугольнике R с центром в точке (х0, уо) оба условия теоремы Пикара будут очевидно выполнены. В этом случае вся плоскость (х, у) будет заполнена не пересекающимися и не касающимися друг друга гладкими интегральными кривыми.
Примеры с решением
Пример 1.
Пусть дано уравнение

и поставлено начальное условие:

Так как правая часть уравнения (45) есть полином относительно х и у, то решение с любыми начальными условиями, в том числе и с начальным условием (46), существует и единственно.
Оценим область определения решения с начальным условием (46).
С этой целью построим прямоугольник R с центром в точке (0, 0),

причем в качестве а и b можно взять любые положительные числа. Будем иметь:

Отсюда видно, что h зависит от выбора чисел а к &*. В частности, при а = b — 1, получим:


Поэтому уравнение (45) имеет единственное решение, заведомо определенное в интервале и удовлетворяющее начальному условию (46). это решение непрерывно дифференцируемо.
С геометрической точки зрения полученный результат означает, что уравнение (45) имеет только одну интегральную кривую, проходящую через начало координат, причем эта интегральная кривая гладкая.
Этот результат приобретает особое значение, если принять во внимание, что уравнение (45) не интегрируется пи в элементарных функциях, пи в квадратурах от элементарных функций, в чем мы убедимся в п. 51. Установленный факт существования и единственноеги решения дает нам основание пытаться искать его другими методами и в том числе находить это решение приближенно.
Пример 2.
Найти решение уравнения

удовлетворяющее начальному условию:


Так как правая часть уравнения (50) вместе с ее частной производной по непрерывна при всех х и у, то через каждую точку плоскости (х, у) проходит единственная интегральная кривая. Это же будет иметь место и в начале координат. Но легко заметить, что у = 0 (ось Ох) есть решение уравнения (50) и это решение проходит через начало координат, так чго оно и будет искомым решением. В силу только что установленной единственности решения уравнение (50) не имеет других решений, проходящих через начало координат.
* Наибольшим значением h будет

Вообще, если в уравнении (2) функция f(x, у) удовлетворяет обоим условиям теоремы Пикара в некоторой окрестности заданной точки (х0, у0) и такова, что , то единственным решением этого уравнения, проходящим через точку , будет прямая


Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
В случае копирования материалов, указание web-ссылки на сайт natalibrilenova.ru обязательно.
Задача Коши. Теорема Коши. Понятие общего решения.
Уравнение (5) всегда можно записать в дифференциалах, где переменные x и y равноправны:
P ( x , y ) dx + Q ( x , y ) dy = 0.
Здесь P ( x , y ) и Q ( x , y ) − известные функции, заданные в
причем P 2 ( x , y ) + Q 2 ( x , y ) ≠ 0.
и ydy − xdx = 0 − это записи одного и
того же уравнения, но первое задано на плоскости R 2
0 X , а второе – без начала координат.
Примеры показывают, что дифференциальные уравнения первого порядка имеют бесчисленное множество решений.
Пример. y ′ = 2 x y = x 2 + C – семейство интегральных кривых.
Определение4. Нахождение решения y =ϕ ( x ), или x =ψ ( y ) уравнения (5) или (6) , для которого при заданных начальных условиях ( x 0 , y 0 ) D выполняется равенство y 0 = ϕ ( x 0 ) или x 0 =ψ ( y 0 ), называется решением задачи Коши для начальных условий ( x 0 , y 0 ) D .
Таким образом, геометрическое
содержание задачи Коши состоит в нахождении интегральной кривой, проходящей через заданную точку
M 0 ( x 0 , y 0 ) D .
В некоторых случаях решение задачи Коши является не единственным. Следующая теорема указывает одно из достаточных условий, которое гарантирует существование и единственность решения задачи Коши.
проф. Дымков М. П. 7
функция f ( x , y )
в открытой области D R 2 . Тогда найдется интервал
дифференциального уравнения y ′ = f ( x , y ),
удовлетворяющее условию y ( x 0 ) = y 0 , ( x 0 , y 0 ) D .
ВНИМАНИЕ! Отметим, что приведенная теорема носит локальный характер, т.е. она обеспечивает существование и единственность решения лишь в окрестности точки x 0 . При
нарушении условий теоремы через точку M 0 могут проходить несколько интегральных кривых.
Две различные функции y = ( x + C ) 3 и y ≡ 0 решения ДУ.
© БГЭУ Лекция № 7 Дифференциальные уравнения проф. Дымков М. П. 8
Определение5. Пусть в некоторой области D R 2 задано дифференц и альное уравнение (5) и для любого замкнутого множества D D выполнены условия теоремы Коши. Тогда однопараметрическое семейство функций
непрерывно дифференцируемых по x и непрерывных по C называется общим решением уравнения (5) в области D , если:
1) функция y =ϕ ( x , C ) является решением (5) для любого фиксированного C из некоторой области G R , где x ( a , b );
2) для любых начальных условий ( x 0 , y 0 ) D существует
C 0 G такое, что y 0 = ϕ ( x 0 , C 0 ).
Таким образом, общее решение дает возможность решить задачу Коши для любых начальных условий
( x 0 , y 0 ) D , где в D имеет место теорема Коши.
Определение 6 . Любое решение, полученного из общего при фиксированном значении C 0 G , называется частным решением.
Пусть функция y = ϕ ( x ) – решение задачи Коши. Тогда график этой функции называется интегральной линией или интегральной кривой, которая проходит через точку ( x 0 , y 0 ). Интегральная кривая в рассматриваемой точке имеет касательную, угловой коэффициент которой равен
tg α = y ′ ( x 0 ) = ϕ′ ( x 0 ) = f ( x 0 , ϕ ( x 0 )).
Таким образом, в каждой точке области D можно установить положение касательной к графику решения уравнения, проходящему через эту точку.
проф. Дымков М. П.
Можно себе представить, что в каждой
точке области D построен короткий отрезок касательной к интегральной кривой, проходящей через эту точку. Тогда получится чертеж, который называется
полем направлений , задаваемым Поле направлений
Таким образом, каждое дифференциальное уравнение вида задает на плоскости XY в области D поле направлений.
Интегральные линии этого уравнения касаются направления, задаваемого полем в этой точке.
Если в уравнении y ′ = f ( x , y ) положим y ′ = k , где k − fix , то линии вида f ( x , y ) = k называются изоклинами, так как точки этих кривых имеют одинаковый наклон поля k .
k = 0 y ′ = 0 α = 0 0 x = 0
k = 1 y ′ = 1 α = 45 0 x = 1
k = − 1 y ′ = − 1 α = 135 0 x = − 1
проф. Дымков М. П. 10
1. Дифференциальные уравнения первого порядка с разделяющимися переменными.
Дифференциальное уравнение первого порядка y ′ = f ( x , y ) или P ( x , y ) dx + Q ( x , y ) dy = 0 называется уравнением с разделяющимися переменными, если его можно записать в виде:
Что такое задача коши для дифференциального уравнения
Напомним, что решением обыкновенного дифференциальною уравнения первою порядка
называется дифференцируемая функция которая при подстановке в уравнение (14.1) обращает его в тождество. График решения дифференциального уравнения называют интегральной кривой. Процесс нахождения решений дифференциального уравнения принято называть интегрированием этого уравнения.
Исходя из геометрического смысла производной у заметим, что уравнение (14.1) задает в каждой точке плоскости переменных значение тангенса угла а наклона (к оси касательной к графику решения, проходящего через эту точку. Величину далее будем называть угловым коэффициентом (рис. 14.1). Если теперь в каждой точке задать с помощью некоторого вектора направление касательной, определяемое значением то получится так называемое поле
направлений (рис. 14.2, а). Таким образом, геометрически задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной (рис. 14.2, б). Для того, чтобы выделить из семейства решений дифференциального уравнения (14.1) одно конкретное решение, задают начальное условие
Здесь — некоторое фиксированное значение аргумента величина, называемая начальным значением. Геометрическая интерпретация использования начального условия состоит в выборе из семейства интегральных кривых той кривой, которая проходит через фиксированную точку
Задачу нахождения при решения дифференциального уравнения (14.1), удовлетворяющего начальному условию (14.2), будем называть задачей Коши. В некоторых случаях представляет интерес поведение решения при всех Однако чаще ограничиваются определением решения на конечном отрезке
2. Разрешимость задачи Коши.
Пусть множество точек удовлетворяющих условию это множество будем называть полосой.
Приведем одну из теорем о разрешимости задачи Коши. Теорема 14.1. Пусть функция определена и непрерывна в полосе Предположим также, что она удовлетворяет условию Липшица
для всех и произвольных некоторая постоянная (постоянная Липшица).
Тогда для каждою начальною значения существует единственное решение задачи Коши (14.1), (14.2), определенное на отрезке
Замечание 1. Для дифференцируемых по у функций условие (14.3) выполняется тогда и только тогда, когда для всех справедливо неравенство
Поэтому условие (14.4) можно также называть условием Липшица. Замечание 2. Теорема 14.1 остается справедливой, если в ее формулировке условие Липшица (14.3) заменить менее ограничительным односторонним условием Липшица
Подчеркнем, что входящая в это условие постоянная а может иметь произвольный знак.
Для дифференцируемых по у функций условие (14.5) выполняется тогда и только тогда, когда для всех , справедливо неравенство
Ясно, что для функций, удовлетворяющих условию Липшица с постоянной одностороннее условие заведомо выполнено с постоянной
Пример 14.1. Функция удовлетворяет условию Липшица с постоянной так как Отсюда следует, что решение задачи Коши существует и единственно на любом отрезке
Пример 14.2. Функция не удовлетворяет условию Липшица, поскольку и модуль этой величины не ограничен. В то же время одностороннее условие (14.6) выполняется с постоянной Следовательно, можно утверждать, что решение задачи Коши существует и единственно на любом отрезке
Пример 14.3. Функция не удовлетворяет одностороннему условию (14.6), так как частная производная не ограничена сверху.
Поэтому вопрос о разрешимости задачи. Коши требует дополнительного исследования.
Отметим следующий полезный результат, указывающий на зависимость степени гладкости решения задачи Коши от степени гладкости правой части дифференциального уравнения.
Теорема 14.2. Пусть функция непрерывно дифференцируема раз в полосе Тогда если функция у является на отрезке решением задачи Коши (14.1), (14.2), то она непрерывно дифф еренцируема раз на этом отрезке.
Это утверждение непосредственно вытекает из возможности дифференцирования тождества не менее чем раз.
В дальнейшем функции будем предполагать дифференцируемыми столько раз, сколько потребуется при рассмотрении соответствующих численных методов.
3. Устойчивость решения задачи Коши на конечном отрезке.
Этот вопрос весьма важен для понимания особенностей методов численного интегрирования дифференциальных уравнений. Рассмотрим сначала процесс распространения погрешностей, внесенных в начальные значения. Пусть у — возмущенное начальное значение, погрешность, а решение соответствующей задачи Коши
Вычтем из уравнения (14.1) уравнение (14.7) и воспользуемся формулой конечных приращений Лагранжа:
где некоторое промежуточное между и значение. В результате получим, что погрешность удовлетворяет дифференциальному уравнению
и начальному условию
Решение задачи (14.8), (14.9) выражается формулой
Таким образом, величина
играет в задаче Коши роль коэффициента роста ошибки.
Заметим, что знак производной оказывает существенное влияние на поведение погрешности Если то величина а вместе с ней и модуль погрешности монотонно возрастают. При этом соответствующие интегральные кривые расходятся. Иллюстрацией такого поведения погрешности может служить рис. 14.3, а. Иначе ведет себя погрешность в случае Здесь и с ростом t монотонно убывают, а соответствующие интегральные кривые сближаются. Ошибка, внесенная в начальное значение, имеет тенденцию к затуханию (рис. 14.3, б). В случае, когда производная незнакопостоянна, поведение погрешности может быть более сложным.
Важно отметить, что в любом случае выполнение одностороннего условия Липшица (14.5) гарантирует, что коэффициент роста ошибки окажется ограниченным, если задача решается на конечном отрезке В самом деле, в этом случае
и поэтому для всех где
Таким образом, при выполнении условия а справедлива оценка
выражающая устойчивость на конечном отрезке решения задачи Коши по начальным значениям.
4. Модельное уравнение.
Наиболее простым образом ведет себя погрешность в случае, когда решается линейное уравнение
с постоянным коэффициентом А. В этом случае погрешность удовлетворяет уравнению и выражается формулой
Поскольку функция не влияет на характер распространения погрешности, при изучении устойчивости по начальным значениям естественно ограничиться случаем и рассматривать уравнение
Уравнение (14.13) часто называют модельным уравнением. Оно играет важную роль при исследовании свойств численных методов решения задачи Коши.
Как следует из формулы (14.12), модуль погрешности решения уравнения (14.13) изменяется в раз за интервал времени Поэтому величину иногда называют временной постоянной или постоянной времени модельного уравнения (14.13). Если же параметр А является комплексным числом, то временной постоянной называют величину
В случае, когда рассматривается распространение малого возмущения, внесенного в решение уравнения в малой окрестности точки значение коэффициента в уравнении (14.8) оказывается близко к постоянной Поэтому при справедливо приближенное равенство Это означает, что поведение погрешности для уравнения моделирует локальное распространение погрешности для общего уравнения (14.1). Роль временной постоянной играет здесь величина Так как ее значение меняется с изменением точки t то ее называют локальной временной постоянной. Если же функция
может принимать комплексные значения, то формула для имеет вид
5. Устойчивость по правой части.
Будет ли решение задачи Коши устойчивым не только по отношению к погрешности задания начального значения, но и к погрешностям задания правой части уравнения? Положительный ответ на этот вопрос дает следующая теорема.
Теорема 14.3. Пусть выполнены условия теоремы 14.1. Далее, пусть решение задачи (14.1), (14.2), решение задачи
Тогда справедлива оценка
выражающая устойчивость на конечном отрезке решения задачи Коши по начальным значениям и правой части. Здесь
Замечание. Величина играет в задаче Коши роль оценки числа обусловленности. Если в теореме 14.1 условие Липшица (14.3) заменить односторонним условием (14.5), то оценка (14.16) будет выполнена с постоянной определенной формулой (14.10).
6. Устойчивость решения на неограниченном промежутке.
При решении самых разнообразных прикладных задач особый интерес представляет изучение описываемых дифференциальными уравнениями процессов на больших временных отрезках. В такой ситуации недостаточно наличия у задачи Коши свойства устойчивости на конечном отрезке. Если входящая в неравенство (14.16) величина может неограниченно расти с ростом то это означает, что допускается неограниченный при рост погрешностей. Как следствие, при достаточно больших такая задача является плохо обусловленной и найти ее решение на отрезке с приемлемой точностью оказывается невозможно.
Пример 14.4. Рассмотрим задачу Коши Ее решением, как нетрудно проверить, является функция
Внесем в начальное значение погрешность, заменив условие условием Решением соответствующей задачи служит уже функция . Погрешность с ростом t быстро увеличивается и, как видно из рис. 14.4, уже при не очень больших значение становится неприемлемо большим.
Для того чтобы обусловленность задачи Коши не ухудшалась с ростом в силу замечания 1 к теореме 14.3 достаточно потребовать, чтобы правая часть уравнения удовлетворяла неравенству для всех и произвольных у. Более того, можно доказать, что при выполнении условия справедлива следующая оценка:
Предположим, что на каждом отрезке произвольное) неравенство (14.6) выполнено с некоторой постоянной Тогда решение определено для всех Пусть решение уравнения (14.7), отвечающее произвольному начальному значению у. Назовем решение задачи Коши (14.1), (14.2) устойчивым по Ляпунову, если справедлива оценка где постоянная К не зависит от Если дополнительно известно, что при то решение называется асимптотически устойчивым.
Замечание 1. Решения модельного уравнения (14.13) с вещественным параметром А устойчивы по Ляпунову тогда и только
тогда, когда и асимптотически устойчивы тогда и только тогда, когда Этот вывод легко следует из формулы (14.12). Если же параметр комплексное число, то из той же формулы следует, что Поэтому решения модельного уравнения устойчивы по Ляпунову тогда и только тогда, когда , и асимптотически устойчивы тогда и только тогда, когда
Замечание 2. Для решения задачи Коши (14.1), (14.2) (как вытекает из неравенства (14.11) и формулы грубым достаточным условием устойчивости по Ляпунову служит выполнение неравенства 4 0. Следствием выполнения условия с постоянной является асимптотическая устойчивость решения.
Задача Коши для обыкновенного дифференциального уравнения первого порядка

где х — независимая переменная; у(х) — искомая неизвестная функция этой переменной; у'(х) — производная искомой функции.
Будем рассматривать уравнение, разрешенное относительно неизвестной функции:


или в другой записи
Если некоторая функция

обращает это уравнение в тождество, то эта функция называется решением дифференциального уравнения (4.1). Сама процедура решения дифференциального уравнения называется интегрированием дифференциального уравнения.
Поскольку при интегрировании функций возникает произвольная постоянная, то в общем случае решением дифференциального уравнения (4.1) является семейство функций

называемое общим интегралом или общим решением. Придавая произвольной постоянной различные значения, получают различные частные решения дифференциального уравнения.
Решить следующее дифференциальное уравнение:

Решение. Легко видно, что общим решением является функция

Действительно, подставив это выражение в заданное уравнение,

которое является тождеством при любых значениях С.
Для определения конкретного значения постоянной задают значение искомой функции в некоторой наперед заданной точке х0, т.е.

Например, если для предыдущего примера потребовать, чтобы в точке х = 0 искомая функция равнялась нулю (у(0) = 1), то частным решением уравнения будет функция

Задача Коши для уравнения (4.1) состоит в требовании нахождения его решения при выполнении условия (4.4), которое называется начальным условием. Ее иногда называют начальной задачей, поскольку к ней приходят при описании некоторых динамических систем, начальное состояние которых задано и требуется описать состояние в более поздний момент.
Это одна из самых простых задач, связанных с решением дифференциальных уравнений. Вместе с тем полученные при изучении задачи Коши результаты в значительней мере используются и при решении более сложных задач.
Результатом численного решения задачи Коши являются совокупности приближенных значений искомой функции

в наперед заданных точках некоторого отрезка [а; Ъ]:

Совокупность всех этих точек (узловых точек) называют сеткой. Если узлы отстоят друг от друга на одинаковом расстоянии, то сетка называется равномерной, а величина h = (b-a)/n — шагом сетки.
Вопрос о существовании и единственности решения задачи Коши разрешает следующая теорема.
Теорема 4.1. Если функция f(x, у) в формуле (4.1) непрерывна

вместе со своей частной производной в некоторой обла
сти D, то при любых начальных данных (х0, у0) е D задача Коши имеет единственное решение.
Погрешность полученных результатов оценивают величиной

Сама постановка задачи Коши подсказывает возможный метод решения: если известно решение в данной точке, то в следующей точке приближенное решение можно выразить так:

Весь вопрос в том, как определять величину Ду,. Методов выбора этой величины разработано весьма много (см., например, работы [3, 4]).

Как уже отмечалось, большинство одношаговых методов построено на разложении функции в ряд Тейлора. Известно, что если функцию ср(х) разложить в окрестности точки х0 в ряд Тейлора
то в большинстве практических случаев можно ожидать, что отрезок этого ряда в близких к х0 точках даст некоторое приближение к точному (неизвестному нам) решению, которое равно сумме всего ряда Тейлора (конечно, при условии его сходимости к этой функции).
Метод Эйлера. Запишем разложение искомой функции по формуле Тейлора с остаточным членом в форме Лагранжа, оставляя только линейные относительно h члены и принимая во внимание соотношения (4Л) и (4.4). Получим


где х0 2 (см. формулу (4.5)). После п шагов, поскольку ?, погрешность возрастет в п раз.

Таким образом, метод Эйлера имеет первый порядок точности относительно h. Это означает, что если шаг уменьшить, например, в пять раз, то точность решения задачи Коши возрастет также в пять раз.
С геометрической точки зрения метод Эйлера сводится к замене неизвестной функции на шаге h отрезком касательной (рис. 4.1).

Рис. 4.1. Метод Эйлера
Метод Рунге — Кутты. К наиболее распространенным методам относится метод Рунге — Кутты четвертого порядка. По существу здесь сохраняются пять первых членов разложения искомой функции в ряд Тейлора. На равномерной сетке с шагом h вычислительная схема этого метода такова:


где

Точность этого метода имеет порядок 4, т.е. при уменьшении шага, например, в пять раз точность решения увеличится в 625 раз. Рассмотрим следующий пример.
Решить уравнение у’ = 2х 2 +2у при начальном условии у(0) = 1 на отрезке [0; 1], выбрав шаг h = 0,1 (заметим, что точное аналитическое решение имеет вид у(х) = 1,5е 2лг -х 2 -х-0,5).
Решение. С использованием метода Эйлера первые два шага дадут следующий результат:

Применим метод Рунге — Кутты.

Первый шаг: