что такое слагаемое в математике 5 класс определение
СЛАГАЕМОЕ — СЛАГАЕМОЕ, слагаемого, ср. 1. Название числа, которое складывается с другим в арифметическом действии сложения (мат.). Взять два слагаемым три раза. Сумма есть результат сложения слагаемых. 2. перен. То, что вместе с чем нибудь другим образует… … Толковый словарь Ушакова
СЛАГАЕМОЕ — СЛАГАЕМОЕ, ого, ср. 1. Число или выражение, к рое складывается с другим (с другими). 2. перен. Составная часть, вместе с другими образующая целое. Слагаемые успеха. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
слагаемое — член суммы — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы член суммы EN summand … Справочник технического переводчика
СЛАГАЕМОЕ — любой из элементов, над которым производится операция (см.) … Большая политехническая энциклопедия
слагаемое — narys statusas T sritis fizika atitikmenys: angl. summand; term vok. Glied, n rus. слагаемое, n; член, m pranc. terme, m … Fizikos terminų žodynas
Слагаемое — ср. 1. Число, которое складывается с одним или несколькими другими при сложении. 2. Составная часть какого либо целого. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
слагаемое — слаг аемое, ого … Русский орфографический словарь
слагаемое — Р. слага/емого … Орфографический словарь русского языка
слагаемое — ого; ср. 1. Матем. Число или выражение, которое складывается с другим (другими). От перестановки мест слагаемых сумма не изменяется. 2. То, из чего слагается, составляется что л., составная часть какого л. целого. Слагаемые успеха. Слагаемые… … Энциклопедический словарь
слагаемое — ого; ср. 1) матем. Число или выражение, которое складывается с другим (другими). От перестановки мест слагаемых сумма не изменяется. 2) То, из чего слагается, составляется что л., составная часть какого л. целого. Слагаемые успеха. Слагаемые… … Словарь многих выражений
слагаемое
Смотреть что такое «слагаемое» в других словарях:
СЛАГАЕМОЕ — СЛАГАЕМОЕ, слагаемого, ср. 1. Название числа, которое складывается с другим в арифметическом действии сложения (мат.). Взять два слагаемым три раза. Сумма есть результат сложения слагаемых. 2. перен. То, что вместе с чем нибудь другим образует… … Толковый словарь Ушакова
СЛАГАЕМОЕ — СЛАГАЕМОЕ, ого, ср. 1. Число или выражение, к рое складывается с другим (с другими). 2. перен. Составная часть, вместе с другими образующая целое. Слагаемые успеха. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
слагаемое — член суммы — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы член суммы EN summand … Справочник технического переводчика
СЛАГАЕМОЕ — любой из элементов, над которым производится операция (см.) … Большая политехническая энциклопедия
слагаемое — narys statusas T sritis fizika atitikmenys: angl. summand; term vok. Glied, n rus. слагаемое, n; член, m pranc. terme, m … Fizikos terminų žodynas
Слагаемое — ср. 1. Число, которое складывается с одним или несколькими другими при сложении. 2. Составная часть какого либо целого. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Слагаемое — … Википедия
слагаемое — слаг аемое, ого … Русский орфографический словарь
слагаемое — Р. слага/емого … Орфографический словарь русского языка
слагаемое — ого; ср. 1) матем. Число или выражение, которое складывается с другим (другими). От перестановки мест слагаемых сумма не изменяется. 2) То, из чего слагается, составляется что л., составная часть какого л. целого. Слагаемые успеха. Слагаемые… … Словарь многих выражений
СЛАГАЕМОЕ
Смотреть что такое «СЛАГАЕМОЕ» в других словарях:
СЛАГАЕМОЕ — СЛАГАЕМОЕ, слагаемого, ср. 1. Название числа, которое складывается с другим в арифметическом действии сложения (мат.). Взять два слагаемым три раза. Сумма есть результат сложения слагаемых. 2. перен. То, что вместе с чем нибудь другим образует… … Толковый словарь Ушакова
слагаемое — член суммы — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы член суммы EN summand … Справочник технического переводчика
СЛАГАЕМОЕ — любой из элементов, над которым производится операция (см.) … Большая политехническая энциклопедия
слагаемое — narys statusas T sritis fizika atitikmenys: angl. summand; term vok. Glied, n rus. слагаемое, n; член, m pranc. terme, m … Fizikos terminų žodynas
Слагаемое — ср. 1. Число, которое складывается с одним или несколькими другими при сложении. 2. Составная часть какого либо целого. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Слагаемое — … Википедия
слагаемое — слаг аемое, ого … Русский орфографический словарь
слагаемое — Р. слага/емого … Орфографический словарь русского языка
слагаемое — ого; ср. 1. Матем. Число или выражение, которое складывается с другим (другими). От перестановки мест слагаемых сумма не изменяется. 2. То, из чего слагается, составляется что л., составная часть какого л. целого. Слагаемые успеха. Слагаемые… … Энциклопедический словарь
слагаемое — ого; ср. 1) матем. Число или выражение, которое складывается с другим (другими). От перестановки мест слагаемых сумма не изменяется. 2) То, из чего слагается, составляется что л., составная часть какого л. целого. Слагаемые успеха. Слагаемые… … Словарь многих выражений
Сложение натуральных чисел
Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!
Сумма чисел – это такое число, которое получается после объединения всех единиц других данных натуральных чисел.
Слагаемые – это числа, над которыми мы выполняем действие сложения. Иными словами, это те числа, количество единиц которых мы объединяем в новом числе.
Арифметическое действие – это нахождение нового числа при помощи двух или нескольких других данных чисел.
В курсе математики 5 класса изучаются основные арифметические действия – сложение, вычитание, умножение и деление.
Сложение – это арифметическое действие, которое выполняется для получения суммы нескольких чисел.
Или другими словами:
Сложение – это действие увеличения числа на количество единиц, содержащихся в другом числе.
Сумма – это результат действия сложения.
Компоненты действия сложения для двух слагаемых:
Компоненты сложения для трех слагаемых:
Рисунок 1. Сумма двух чисел на координатном луче.
Основные свойства суммы натуральных чисел
Переместительный закон сложения
Сумма двух или нескольких чисел от изменения порядка сложения слагаемых не меняется.
Это значит, что значение суммы не зависит от порядка выполнения действия сложение.






Сочетательный закон сложения
Сумма нескольких чисел не поменяется, если некоторые слагаемые заменить их суммой.
Это значит, что мы можем группировать слагаемые как угодно, а также выполнять действия сложения в любом порядке.
Например, если в нашем примере мы заменим слагаемые 2 и 3 их суммой, то результат останется такой же, как и при обычном сложении слагаемых:
или
Для прибавления суммы некоторых чисел к числу или некоторого числа к сумме чисел, нужно сложить это число с одним из слагаемых суммы, а получившийся результат сложить последовательно с остальными слагаемыми.
Пример 1. Прибавление числа к сумме чисел:
Можно сразу вычислить сумму чисел в скобках и сложить ее с первым слагаемым:
325 +( 12 + 64 + 5 ) = 325 +81 = 406
Также можно использовать правило прибавления слагаемого и суммы. Результат при этом не поменяется
Пример 2. Прибавление суммы чисел к другому числу:
Можно сразу вычислить сумму чисел в скобках и сложить ее со вторым слагаемым
( 54 + 240 + 189 )+ 37 = 483+ 37 = 520
Или можно использовать правило прибавления суммы чисел к числу. Результат останется тот же.
Изменение суммы чисел с изменением слагаемых
При увеличении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже увеличится на это же число (на это же количество единиц).
При уменьшении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже уменьшится на это же число (на это же количество единиц).
Эти два свойства справедливы и в обратную сторону. То есть, если увеличить или уменьшить сумму на какое-то число, тогда для сохранения равенства нужно соответственно увеличить или уменьшить одно из слагаемых.
Простой пример увеличения суммы при увеличении слагаемого: у вас есть 700 рублей; 200 рублей лежит в левом кармане, а 500 – в правом. Вы нашли на улице 300 рублей и положили их в левый карман, после чего там стало 200+300=500 рублей. Таким образом, всего у вас оказалось 500+500=1000 рублей, то есть, сумма всех ваших денег увеличилась на 300 рублей.
Попробуйте самостоятельно придумать примеры для всех трех правил.
Сложение однозначных чисел
Сложение двух однозначных чисел выполняется так: одно число увеличивается на количество единиц другого числа. То есть, единицы одного числа присоединяются к единицам другого числа.
Сложение многозначного числа с однозначным
Чтобы найти сумму многозначного числа и однозначного, можно действовать двумя способами. Оба они основаны на свойствах суммы чисел. Рассмотрим их на примерах.
То есть, мы проделываем такие действия:
88+5 = 80+8+5 = 80+13 = 80+10+3 = 90+3=93.
То есть, ход вычисления был такой:
88+5 = 88+2+3 = 90+3 = 93.
Сложение в столбик многозначных чисел
Сложение в столбик – это способ нахождения суммы чисел путем их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим).
Итак, допустим, что нам нужно найти сумму : 5728+803





После нахождения суммы чисел методом сложения столбиком, записываем результат решения в исходном строчном примере:
5728+803 = 6531
Сложение в столбик нескольких многозначных чисел
Рассмотрим пример: 12044+28609+1358
Сложив простые единицы, мы получим 21, то есть, 2 десятка и 1 единицу. Записываем под чертой в разряде единиц цифру 1, а 2 отмечаем «в уме».





Нам остается только записать результат в начальном примере:
12044+28609+1358
Значение слова «слагаемое»

1. Мат. Число или выражение, которое складывается с другим (другими).
2. То, из чего слагается, составляется что-л., составная часть какого-л. целого. Существование комбината немыслимо без основных слагаемых — сырья, топлива и воды. Паустовский, Кара-Бугаз.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
СЛАГА’ЕМОЕ, ого, ср. 1. Название числа, к-рое складывается с другим в арифметическом действии сложения (мат.). Взять два слагаемым три раза. Сумма есть результат сложения слагаемых. 2. перен. То, что вместе с чем-н. другим образует какое-н. целое; то, из чего слагается что-н. (книжн.).
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
слага́емое I
1. матем. число или выражение, которое складывается с другим (другими)
2. то, что вместе с чем-нибудь другим образует какое-нибудь целое; то, из чего слагается что-нибудь
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: спонтанность — это что-то нейтральное, положительное или отрицательное?
Сумма разрядных слагаемых натурального числа
Представленная статья посвящена интересной теме о натуральных числах. Для того, чтобы выполнять некоторые действия, необходимо представлять исходные выражения как сложение нескольких чисел – другим языком, раскладывать числа по разрядам. Обратный процесс также очень важен для решения упражнений и задач.
В данном разделе детально рассмотрим типичные примеры для лучшего усвоения информации. Мы также научимся преобразовывать натуральные числа и записывать их в другом виде.
Каким образом можно разложить число по разрядам?
Исходя из названия статьи, можно сделать вывод, что этот параграф посвящен таким математическим терминам, как «сумма» и «слагаемые». Перед тем, как приступить к изучению данной информации, следует подробно изучить тему, чтобы иметь понятие о натуральных числах.
Приступим к работе и рассмотрим основные понятия о разрядных слагаемых.
Разрядные слагаемые – это определенные числа, которые состоят из нулей и единственной цифры, отличной от нуля. Натуральные числа 5 , 10 , 400 , 200 относятся к данной категории, а числа 144 , 321 , 5 540 , 16 441 – не относятся.
Количество разрядных слагаемых у представленного числа равняется тому числу, сколько цифр, отличных от нуля, содержится в записи. Если представить число 61 как сумму разрядных слагаемых, так как 6 и 1 отличаются от 0 . Если разложить число 55050 как сумму разрядных слагаемых, то оно представлено как сумма 3 слагаемых. Три пятерки, представленные в записи, отличны от нуля.
Следует помнить, что все разрядные слагаемые числа содержат разное количество знаков в своей записи.
Сумма разрядных слагаемых натурального числа равна этому числу.
Перейдем к понятию разрядных слагаемых.
Разрядные слагаемые– это такие натуральные числа, в записи которых содержится цифра, отличная от нуля. Количество чисел должно быть равно количеству цифр, не равных нулю. Все слагаемые числа могут записываться с различным количеством знаков. Если мы раскладываем число по разрядам, то сумма слагаемых числа всегда будет равна этому числу.
Проанализировав понятие, можно сделать вывод, что однозначные и многозначные числа (полностью состоящие из нулей за исключением первой цифры) нельзя представить в качестве суммы. Это происходит потому, что данные числа сами будут разрядными слагаемыми для каких-то чисел. За исключением данных чисел, все остальные примеры могут раскладываться на слагаемые.
Как раскладывать числа?
Чтобы разложить число как сумму разрядных слагаемых, необходимо вспомнить, что натуральные числа связаны с количеством некоторых предметов. В записи числа разряды зависят от количества единиц, десятков, сотен, тысяч и так далее. Если вы возьмем, например, число 58 , то может отметить, что он отвечает 5 десяткам и 8 единицам. Число 134 400 соответствует 1 сотне тысяч, 3 десяткам тысяч, 4 тысячам и 4 сотням. Можно представить эти числа в виде равенств – 50 + 8 = 58 и 134 400 = 100 000 + 30 000 + 4 000 + 400 . В данных примерах мы наглядно увидели, как можно разложить число в виде разрядных слагаемых.
Смотря на этот пример, мы сможем любое натуральное число представить в виде суммы разрядных слагаемых.
Приведем еще один пример. Представим натуральное число 25 в виде суммы разрядных слагаемых. Число 25 соответствует 2 десяткам и 5 единицам, поэтому 25 = 20 + 5 . А вот сумма 17 + 8 не является суммой разрядных слагаемых числа 25 , так как в ней не может быть двух чисел, состоящих из одинакового количества знаков.
Мы разобрали основные понятия. Разрядные слагаемые получили свое название из-за того, что каждое принадлежит к определенному разряду.
Как найти натуральное число, если известна сумма разрядных слагаемых?
Для того, чтобы разобрать данный пример, проанализируем обратную задачу. Представим, что нам известна сумма разрядных слагаемых. Нам необходимо найти данное натуральное число.
Например, сумма 200 + 30 + 8 разложено по разрядам числа 238 , а сумма 3 000 000 + 20 000 + 2 000 + 500 соответствует натуральному числу 3 022 500 . Таким образом, мы легко можем определить натуральное число, если нам известна его сумма резервных слагаемых.
Еще один способ нахождения натурального числа – это сложение в столбцах разрядных слагаемых. Данный пример не должен вызвать у вас сложности во время выполнения. Поговорим об этом подробнее.

Необходимо определить исходное число, если известна сумма разрядных слагаемых 200 000 + 40 000 + 50 + 5 . Перейдем к решению. Необходимо записать числа 200 000 , 40 000 , 50 и 5 для сложения в столбик:
Осталось сложить числа по столбцам. Для этого нужно помнить, что сумма нулей равна нулю, а сумма нулей и натурального числа равна этому натуральному числу.
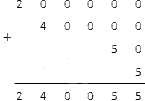
Получаем:
Выполнив сложение, мы получим натуральное число 240 055 , сумма разрядных слагаемых которого имеет вид 200 000 + 40 000 + 50 + 5 .
Поговорим еще об одном моменте. Если мы научимся раскладывать числа и представлять их в виде суммы разрядных слагаемых, то мы также сможем представлять натуральные число в виде суммы слагаемых, не являющихся разрядными.
Разложение по разрядам числа 725 будет представлено как 725 = 700 + 20 + 5 , а сумму разрядных слагаемых 700 + 20 + 5 можно представить как ( 700 + 20 ) + 5 = 720 + 5 или 700 + ( 20 + 5 ) = 700 + 25 , или ( 700 + 5 ) + 20 = 705 + 20 .
Иногда сложные вычисления можно немного упростить. Рассмотрим еще небольшой пример для закрепления информации.
Выполним вычитание чисел 5 677 и 670 . Для начала представим число 5677 в виде суммы разрядных слагаемых: 5 677 = 5 000 + 600 + 70 + 7 . Выполнив действие, мы можем сделать вывод, что. сумме ( 5 000 + 7 ) + ( 600 + 70 ) = 5 007 + 670 . Тогда 5 677 − 670 = ( 5 007 + 670 ) − 670 = 5 007 + ( 670 − 670 ) = 5 007 + 0 = 5 007 .
Сумма разрядных слагаемых натурального числа
Для того, чтобы выполнить некоторые действия над натуральными числами необходимо представить эти числа в виде суммы разрядных составляющих или, как говорят, разложить натуральные числа на цифры. Не менее важен и обратный процесс, который заключается в записи натурального числа в виде суммы разрядных составляющих.
Как найти натуральное число, если известна его подобная сумма?
Для того, чтобы проделывать некоторые действия, нужно представлять начальные выражения в виде сложенных чисел – другим языком, необходимо разложить числа по разрядам. Противоположный процесс также безгранично важен при решении задач и упражнений.
Разрядные слагаемые – это такие числа, которые состоят исключительно из нулей и единственной цифры, отличной от нуля. Такие натуральные числа, как 5, 20, 400, 100, принадлежат данной категории, а числа 55, 213, 680, 324, 458, 25, 694, 25 и другие – не относятся.
Число разрядных слагаемых у некоторого числа равно тому числу, сколько цифр содержатся в записи. Представление числа 61 в виде суммы разрядных слагаемых, станет выглядеть как 6 и 1, они отличаются от 0. Когда есть необходимость разложить 55050 как сумму слагаемых разрядов, оно будет представлено в виде трех слагаемых. Три пятерки, что присутствуют в записи, отличны от нуля.
Необходимо помнить, что каждое разрядное слагаемое содержит отличное от других количество знаков в собственной записи.
Сумма разрядных слагаемых числа, принадлежащего к классу натуральных, обязательно эквивалентна данному числу.
Натуральные числа, в записи которых присутствует цифра, что отлична от нуля, называются разрядными слагаемыми.
Количество чисел обязано быть равно количеству тех цифр, которые не равных нулю. Каждое слагаемое может быть записано с разным количеством знаков. Если необходимо разложить по разрядам, то при сложении получившихся цифр, мы получим число равно данному числу.
При анализе понятия, можно сформулировать вывод, что многозначные и однозначные числа, которые полностью состоят из нулей за исключением первой цифры, нельзя представлять в виде суммы. Это происходит в том случае, когда такие числа сами будут разрядными слагаемыми для каких-то чисел.
Исключая данные числа, все остальные примеры могут раскладываться на слагаемые.
Правила разложения чисел
Чтобы разложить число на сумму разрядных слагаемых, необходимо вспомнить, что каждое натуральное число связано с количеством определенных элементов. При записи числа разложение зависит от числа единиц, десятков, сотен, тысяч и т.д. К примеру, если взять число 937, то можно увидеть, что ему соответствует 9 сотен, 3 десятка и 7 единиц. Число 245 500 соответствует 2 сотням тысяч, 4 десяткам тысяч, 5 тысячам и 5 сотням. Эти числа можно представить в виде равенств — 900 + 30 + 8 = 938 и 245 500 = 200 000 + 40 000 + 5 000 + 500. В данных примерах можно наглядно увидеть, как число можно разделить на сумму цифр. Рассматривая этот пример, мы можем представить всевозможное натуральное число в виде суммы его разрядных членов. Вот еще один пример. Представим натуральное число 724 как сумму составляющих цифр. 724 равно 7 сотням, 2 десяткам и 4 единицам, поэтому 724 = 700 + 20 + 4. Однако сумма 312 + 412 не является суммой составляющих цифр числа 724, потому что нельзя иметь два числа, которые состоят из одинакового количества цифр. Мы уже рассматривали ключевое понятие. Разрядные слагаемые названы так потому, что они принадлежат к конкретному разряду.
Нет времени решать самому?
Наши эксперты помогут!
Примеры задач
Пример 1. Известна сумма разрядов, как же найти само число?
Чтобы решить этот пример, давайте рассмотрим обратную задачу. Представим, что мы знаем сумму слагаемых цифр. Нам нужно найти заданное натуральное число.
Например, сумма 300 + 40 + 9 равна 349, а сумма 30 000 + 3 000 + 600 + 20 + 7 соответствует натуральному числу 33627. Поэтому легко определить натуральное, если вы знаете сумму его вспомогательных слагаемых.
Другой способ найти натуральное — сложить столбцы сумм цифр. Этот пример не должен вызвать у вас затруднений. Рассмотрим его более подробно.
Пример 2. Нужно найти исходное число, когда дана сумма разрядных концов 300 000 + 50 000 + 2000+ 400 + 40 + 7.
Далее приступим к решению. Необходимо записать числа 300 000, 50 000, 2000, 400, 40, 7 сложить в столбик: осталось лишь сложить все числа в столбик. Важно помнить о том, что сумма нулей равна нулю и что сумма нулей и натурального числа равна натуральному числу.
Таким образом, выполнив сумму, мы получаем натуральное — 352447, сумма цифр которого равна 300 000 + 50 000 + 2000 + 400 + 40 + 7.
Поговорим еще об одном методе. Если мы научились делить числа и преобразовывать их в виде суммы понятий с цифрами, мы также можем представлять данные числа в виде некоторой суммы без цифр.
Пример 3. Разложение числа 5825 представляется как 49565 = 40000 + 9000 + 500 + 60 + 5, а сумма разрядных компонентов 5000 + 800 + 20 + 5 может быть представлена как (40000 + 9000) + (500 + 60) + 5 = 49565 или (40000 + 9000 + 500 + 60) + 5 = 49565 или 40000 + (9000 + 500 + 60) + 5 = 49565 и многие другие способы. Иногда сложные расчеты можно немного упростить. Приведем еще один небольшой пример для наилучшего закрепления представленной информации.
Пример 4. Вычтите числа 67838 и 780. Сначала представим — 67838 как сумму разрядных компонентов: 67838 = 60000 + 7000 + 800 + 30 + 8. Выполнив операцию, можно сделать вывод, что сумма (60000+7000)+ (800 + 30 +  = 67000 + 838. Тогда 67838 — 780 = (67000 + 838) — 780 = 67000 + (838 — 780) = 67000 + 58 = 67058.
= 67000 + 838. Тогда 67838 — 780 = (67000 + 838) — 780 = 67000 + (838 — 780) = 67000 + 58 = 67058.
Стоит рассмотреть обратную задачу более подробно. Считайте, что у нас есть сумма разрядных составляющих натурального числа, и нам нужно найти это число.
Например, сумма 300+20+9 является разложением разрядных чисел 329, а сумма разрядных слагаемых вида 3 000 000 + 40 000 + 4 000 + 500 соответствует натуральному числу 3 044 500.
То есть 600 + 20 + 9 = 629, а 3 000 000 + 30 000 + 4 000 + 500 = 3 034 500.
Чтобы найти положительное число по известной сумме разрядных слагаемых, можно сложить эти разрядные слагаемые в столбик (при необходимости обратитесь к материалу по сложению целых положительных чисел в столбик). Рассмотрим решение этого примера.
Найдите целое положительное, если сумма разрядных составляющих равна 200 000 + 40 000 + 50 + 5.
Запишите числа 200 000, 40 000, 50 и 5 так, как того требует метод сложения в столбик:
Осталось только сложить все эти числа в столбик:
Под горизонтальной чертой мы получили искомое натуральное число.
В заключение мы хотели бы обратить ваше внимание еще на один момент. Умение раскладывать натуральные числа на цифры и умение выполнять обратное действие позволяет представить натуральное в виде суммы слагаемых, которые не являются разрядными.
Например, разрядное сложение целых положительных чисел 643 имеет следующий вид 643 = 600 + 40 + 3, а сумма разрядных слагаемых 700 + 20 + 5 в силу свойств сложения целых положительных чисел может быть представлена как (600 + 40) + 5 = 640 + 3 или 600+(40 + 3) = 600 + 43, или (600 + 3) + 40 = 603 + 40.
Возникает логичный вопрос: «Для чего это нужно? Ответ на него прост: в некоторых случаях это может упростить вычисления.
Пример 4. Вычтем целые положительные числа 5 799 и 790.
Сначала представим вычитаемое как сумму разрядных компонентов: 5 799 = 5 000 + 700 + 90 + 9.
Легко увидеть, что сумма разрядных компонентов равна сумме (5000 + 9) + (700 + 90) = 5009 + 790.
Тогда 5 799 — 790 = (5 009 + 790) — 790 = 5 009 + (790 — 790) =5 009 + 0=5 009.
Многозначные числа. Единицы разрядов и классов. Сумма разрядных слагаемых.
Существуют в математике огромное количество натуральных чисел. Они все разные. Например, 2, 67, 354, 1009. Рассмотрим подробно эти числа.
Натуральное число 2 состоит из одной цифры, поэтому такое число называют, однозначным числом. Еще пример однозначных чисел: 3, 5, 8.
Натуральное число 67 состоит из двух цифр, поэтому такое число называют, двузначным числом. Пример двузначных чисел: 12, 35, 99.
Трехзначные числа состоят из трех цифр, например: 354, 444, 780.
Четырехзначные числа состоят из четырёх цифр, например: 1009, 2600, 5732.
Двузначные, трехзначные, четырехзначные, пятизначные, шестизначные и т.д. числа, называются, многозначными числами.
Разряды чисел.
Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.
Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой первого разряда.
Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда. Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.
Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. 10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.
Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 – третий разряд сотен.
Такой разбор числа называется разрядным составом числа.
Классы.
Многозначные числа разбивают на группы по три цифры справа налево. Такие группы цифр называют классам. Первый класс справа называется классом единиц, второй называется классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов, пятый – классом триллионов, шестой – классом квадриллионов, седьмой – классом квинтиллионов, восьмой – классом секстиллионов.
Класс единиц – первый класс справа с конца три цифры состоит из разряда единиц, разряда десятков и разряда сотен.
Класс тысяч – второй класс состоит из разряда: единиц тысяч, десятков тысяч и сотен тысяч.
Класс миллионов – третий класс состоит из разряда: единиц миллионов, десятков миллионов и сотен миллионов.
Разберем пример:
У нас есть число 13 562 006 891.
Это число имеет 891 единиц в классе единиц, 6 единиц в классе тысяч, 562 единиц в классе миллионов и 13 единиц в классе миллиардов.
Таблица разрядов и классов.
Чтобы прочитать натуральное число 13562006891 нужно справа отметить по три цифры класса 13 562 006 891 и прочитать число единиц каждого класса слева направо:

13 миллиардов 562 миллионов 6 тысяч 891.
Сумма разрядных слагаемых.
Любое натурально число имеющее различные разряды можно разложить на сумму разрядных слагаемых. Рассмотрим пример:
Число 4062 распишем на разряды.
4 тысяч 0 сотен 6 десятков 2 единиц или по-другому можно записать
4062=4 ⋅1000+0 ⋅100+6 ⋅10+2
Следующий пример:
26490=2 ⋅10000+6 ⋅1000+4 ⋅100+9 ⋅10+0
Вопросы по теме:
Назовите первые четыре класса в записи натуральных чисел?
Ответ: класс единиц, класс тысяч, класс миллионов, класс миллиардов.
Как читают многозначные числа?
Ответ: многозначные числа читают слева направо. Разбивают число по 3 цифры с конца на классы, называют все цифры, кроме нуля. Цифра 0 в записи числа означают отсутствие разряда.
Какие цифры могут стоять в любом разряде числа, кроме высшего?
Ответ: 0, 1, 2, 3, 4. 5, 6, 7, 8, 9.
Какие цифры могут стоять в высшем разряде числа?
Ответ: 1, 2, 3, 4. 5, 6, 7, 8, 9.
Что такое сумма разрядных слагаемых?
Ответ: Это разложение натурального числа на разряды и суммирование их.
Сколько десятков в сотне?
Ответ: в сотне 10 десятков.(10+10+10+10+10+10+10+10+10+10=100)
Сколько сотен в тысячи?
Ответ: в тысячи 10 сотен. (100+100+100+100+100+100+100+100+100+100=1000)
Сколько десятков в тысячи?
Ответ: в тысячи 100 десятков.
Сколько тысяч в миллионе?
Ответ: в миллионе 1000 тысяч.
Примеры на задачи.
Пример №1:
Запишите и прочитайте число: а) пятизначное б) шестизначное.
Ответ: а) 35 100 (тридцать пять тысяч сто) б) 803 273 (восемьсот три тысячи двести семьдесят три)
Пример №2:
Сколько натуральных чисел: а) однозначных б) двузначных?
Ответ: а) однозначных натуральных чисел 10 (0, 1, 2, 3, 4. 5, 6, 7, 8, 9), б) двузначных натуральных чисел 90 (10, 11, 12, …,99)
Пример №3:
В записи числа 10398 назовите цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч, …
Ответ: 8 – разряд единиц, 9 – разряд десятков, 3 – разряд сотен, 0 – разряд тысяч, 1 – разряд десятков тысяч.
Пример №4:
Напишите наименьшее трехзначное число и наибольшее пятизначное число.
Ответ: 100 и 99999.
Пример №5:
Запишите число 56976 в виде суммы разрядных слагаемых:
Ответ: 56976=50000+6000+900+70+6=5⋅10000+6⋅1000+9⋅100+7⋅10+6
You may also like:

Десятичные дроби. Разряды и классы десятичных дробей.

Нужен репетитор по математике (алгебре) или геометрии?

Сравнение неправильных дробей правила и примеры.

Деление дробей. Правила. Примеры.
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Свежие записи
- Решение линейных уравнений с одной переменной.
- Определение числовой функции. Область определения функции. Область значения функции.
- Определение функции. Способы задания функции.
- Десятичные дроби. Разряды и классы десятичных дробей.
- Что такое уравнение и корни уравнения? Как решить уравнение?
Пожалуйста отключите блокировку рекламы или добавьте сайт в исключения блокировщика, если желаете чтобы проект развивался.
Урок математики в 1-м классе «Слагаемые. Сумма»
Назад Вперёд
Класс: 1.
Дидактическая цель: познакомить учащихся с компонентами сложения, способствовать развитию вычислительных навыков.
Тип урока: Изучение нового материала.
Планируемые результаты:
Предметные:
- знать название чисел при сложении;
- уметь употреблять новые понятия математической речи;
- совершенствовать вычислительные навыки;
- формировать умение решать простые задачи;
- выбирать различные способы чтения математических выражений.
Метапредметные УУД:
- использование имеющихся знаний;
- исследование учебной задачи;
- установление логических, причинно-следственных связей,
- применение знаково-символической схемы.
- умение слушать и вступать в диалог;
- умение правильно выражать свои мысли;
- умение контролировать и корректировать действия других обучающихся;
- оформление своей мысли в устной речи;
- обоснование своего ответа;
- умение ориентироваться в своей системе знаний.
- уметь самостоятельно планировать и выполнять свои действия на знакомом учебном материале;
- выполнять действия в сотрудничестве с учителем по предложенному плану;
- самостоятельно выстраивать план действий по решению учебной задачи изученного вида.
Личностные УУД:
- самооценка своих возможностей;
- формирование положительного отношения к учению.
Планируемые результаты (метапредметные универсальные учебные действия):
- Регулятивные: научится оценивать результат своей работы на уроке.
- Познавательные: владеть общими приемами решения задач, выполнения заданий и вычислений; использовать простейшие таблицы и схемы для решения конкретных задач.
- Коммуникативные: слушать и вступать в диалог, участвовать в коллективном обсуждении.
Личностные: положительно относиться к школе, учению; проявлять познавательные потребности и учебные мотивы; соблюдать организованность, дисциплинированность на уроке, действовать согласно памятке обращения с учебными пособиями, наглядным материалом.
Планируемые результаты (метапредметные универсальные учебные действия):
- Регулятивные: научится оценивать результат своей работы на уроке.
- Познавательные: владеть общими приемами решения задач, выполнения заданий и вычислений; использовать простейшие таблицы и схемы для решения конкретных задач.
- Коммуникативные: слушать и вступать в диалог, участвовать в коллективном обсуждении.
Личностные: положительно относиться к школе, учению; проявлять познавательные потребности и учебные мотивы; соблюдать организованность, дисциплинированность на уроке, действовать согласно памятке обращения с учебными пособиями, наглядным материалом.
Методы: частично-поисковый.
Формы организации познавательной деятельности: фронтальная, индивидуальная, парная.
Средства обучения: компьютер, учебники, тетради.
Этап урока
Содержание урока
1. Мотивация (самоопределение) к учебной деятельности
Организация урока, проверка готовности к уроку; называть числа в порядке их следования при счете.
Начинаем урок математики. Сегодня у нас на уроке гости. Поздороваемся, улыбнёмся друг другу.
Раз, два, три, четыре, пять —
Все умеем мы считать.
Раз! Подняться потянуться. (Под счет учителя дети выполняют потягивания.)
Два! Согнуться, разогнуться. (Наклоны. Повороты туловища.)
Три! ;В ладоши три хлопка,
Головою три кивка. (Движения головой.)
На четыре — руки шире. (Хлопки в ладоши.)
Пять — руками помахать. (Движения руками.)
Шесть — за парту тихо сесть. (Прыжки. Ходьба на месте.)
Семь, восемь – лень отбросим!
Слайд 1.
Прочитаем тему нашего урока. Знакомы ли вам эти слова? Кто догадался, какова цель нашего урока?
2. Актуализация знаний
Слайд 2.
Ребята, к нам пришла срочная телеграмма!
«В нашей сказке нет порядка!
Помогите нам ребята»
— Поможем? Только какой сказке помогать? Это надо отгадать! Какие числа прозвучали в нашей физкультминутке?
Слайд 3.
— Назовите их по порядку слева направо и обратно.
— Запишите их.
— Ответы на мои вопросы обводим простым карандашом.
(делает каждый, один на доске)
1.Закрепить последовательность чисел, предыдущее, последующее число, состав чисел, увеличение и уменьшение чисел.
1 2 3 4 5 6 7 8
— какое число стоит между числами 5 и 7?
— какое число больше 7 на 1?
— 8 – это 6 и …?
— 9 – это 5 и …?
— уменьшить 6 на 1.
— число, следующее за числом 2.
— какое число надо прибавить к 9, чтобы получить 10?
Слайд 4.
— Какое число не выделили? (7)
А вот и оно! Число 7 – ключик к нашему сказочному домику. Как он называется? (теремок)
Вспомним кто первый в нём поселился.
Слайд 5.
— Первая поселилась мышка, но сейчас она не может попасть в теремок! Она не знает состав числа 7, а мы? Поможем?(делает каждый , один на доске)
Слайд 6.
Стала мышка жить в теремке.
Слайд 7.
— Физкультминутка.
По реке плывет кораблик.
Он плывет издалека.
На кораблике четыре
Очень храбрых моряка.
У них ушки на макушке,
У них длинные хвосты,
И страшны им только кошки,
Только кошки да коты!
3. Постановка учебной задачи.
1. Закрепить понятие «числовое равенство»;
2. Умение читать математическую запись, числовые равенства;
3. Развитие математической речи.
4. Подведение к теме урока
Ай-да Лиса мастерица!
Вяжет всем рукавицы.
Извязала три клубка,
Два ещё лежат пока.
У кого ответ готов:
Сколько у неё клубков? (5)
— Составьте числовое равенство (1у доски, остальные в тетради).
Слайд 9.
3+2=5
— Как можно прочитать это числовое равенство?
1). к трем прибавить два, получится пять;
2). Три увеличить на два получится пять;
3). три плюс два получится пять).
— Эту запись ещё можно прочитать используя термины. Прочитайте. (ответа нет)
— Почему не получается? (не хватает знаний)
— Каких знаний не хватает? (знаний математических терминов)
— Значит, какая цель урока? (познакомиться с новыми математическими терминами, узнать как прочитать числовое равенства, используя математическую терминологию).
— Верно, будучи внимательными на уроке в конце – вы сможете обязательно прочесть это числовое равенство;
Пока лиса не может пройти в теремок.
4. Изучение нового материала
Поиск решения проблемы.
Практическая работа:
познакомить с новыми математическими терминами: «слагаемые», «сумма»
Слайд 10.
А вот и зайчик.
— Зайчик пошел в огород, сорвал и положил в корзину 2 кочана капусты. Нарисуем ниже в тетради столько же кругов.(один у доски)
— Потом он дошел до грядки с морковью, сорвал и положил в корзину три морковки. Нарисуйте столько же треугольников.
— Что делал зайчик с овощами? (складывал в корзину)
— какое действие он выполнял? (сложение)
— Что он складывал? ( 2 кочана капусты и 3 морковки)
— Как это записать? ( 2+3)
— Как же назвать эти числа на математическом языке?
— В древнерусском языке слово «слагать слагать» означало «соединять». Люди слагали песни, стихи, т.е. соединяли слова, чтобы получить какие-либо произведения.
— Мы с вами на уроках математики тоже слагаем, соединяем числа. И числа эти получили свои имена! Кто догадается, какие?
— Числа, которые мы складываем, на математическом языке называются СЛАГАЕМЫМИ.
Слайд 11.
— Назовите первое слагаемое. (2)
— Назовите второе слагаемое. (3)
— Сколько овощей в корзине у зайчика? (5)
— Сколько фигур у вас на столе? (5)
— Дополните свою запись. (2+3=5)
Слайд 12.
— Как можно назвать число 5? (ответ, то, что получилось, результат)
— В математике все эти слова заменяют одним словом — сумма.
Слайд 13.
— С какими новыми терминами познакомились? (сумма, первое, второе слагаемое)
— Прочитайте запись, используя новые слова :
(первое слагаемое 2, второе слагаемое 3, сумма 5)
— чтение хором, в паре.
Зайчик заскочил в домик. Сейчас мы сможем и Лисе помочь.
Решение проблемы
Вывод
— Вернемся, к записи: 3+2=5
— Сможем ли мы прочесть теперь числовое равенство, используя новые математические термины. (да)
— Прочитаем. (первое слагаемое 2, второе слагаемое 3, сумма 5)
— Почему нам удалось это сделать? (появились новые знания, достигли цели урока).
Лисичка может зайти в теремок
Физминутка
Слайд 14.
Бабочка
Маленькая гусеница по листу ползёт
Листик как конфеточку целый день грызёт
Наконец наелась, кокон там свила
Всю зиму до весны, как куколка спала
А весной проснулась, надоело спать
Превратилась в бабочку, чтоб везде летать.
5. Закрепление изученного материала
1. Работа с учебником. С.86, №1.
Закрепление нового знания: называние «слагаемых», «Сумма», нахождение, умение записывать суммы
2.Работа в тетради.
1.формировать умение определять «слагаемое»,
2.формирование вычислительных навыков;
3.формирование умений взаимопроверки.
Слайд 15.
Помогаем Лягушке ( работа в парах)
— Найдите задание №1.
— работаем в паре, назвать друг другу первое и второе слагаемые, записать эти суммы в тетрадь, найти их значение.( Проверка на доске по одному с каждого ряда).
Слайд 16.
Помогаем Волку
Запишите под диктовку (один у доски):
— найти сумму 7 и 2
— первое слагаемое 4, второе 3. Найти сумму.
— даны числа 4 и 5. Запишите две суммы с этими числами.
Молодцы. Помогли героям сказки справиться с заданиями.
Волк и лягушка могут зайти в теремок.
3.
1.формирование умения составлять суммы;
2.формировать умение записывать цифры;
3.Закрепить понятие «числовое равенство»
Слайд 17.
Помогаем Медведю решить задачу
Медведь заготовил на зиму 6 больших бочек с мёдом и 2 маленьких. Сколько всего бочек с мёдом заготовил на зиму Медведь?
— о чем прочитанный рассказ?
— что известно? Было 6 больших бочки и ещё 2 маленьких
Изобразим бочки кружочками: 6 кружочков размером с клеточку и 2 поменьше.
— что нужно узнать? Сколько всего бочек с мёдом заготовил Медведь?
— какое арифметическое действие следует выполнить, чтобы ответить на поставленный вопрос? Сложение.
— почему так считаете? Потому что надо найти сколько всего.
— запишите решение. Прочитайте
6+2=8(к)
Ответ: 8 книг.
Записываем решение в тетради и на доске.
И медведь может пройти в теремок. Всем помогли.
5. Итог, рефлексия
1.формирование умений самоанализа, анализа деятельности учителя;
2.закрепление новых понятий «слагаемое», «сумма».
— С какими новыми словами мы познакомились? (сумма, первое слагаемое, второе слагаемое)
— Что называется слагаемыми? (числа, которые складываем)
— Что называется суммой? (ответ и выражение)
Подведем сейчас итог,
Чему нас научил урок.
Если вы со мной согласны,
То в ладоши хлопайте,
Ну, а если не согласны,
руку поднимайте.
1.Это неравенство 2 < 4
2. Это сумма 3 — 1
3. Это сумма 7+3
4. Первое слагаемое 7
5. Второе слагаемое 4
6. Второе слагаемое 3
Слайд 19.
— Если вы довольны уроком, считаете, что на отлично поняли новую тему урока, нарисуйте зелёный смайлик.
— Если вы довольны своей работой на уроке, но можете работать активнее, нарисуйте жёлтый смайлик.
— Если вы ничего не поняли на уроке, и вам понадобится помощь учителя, чтобы он опять объяснил тему урока, нарисуйте красный смайлик.
Герои сказки Теремок благодарят вас за помощь и угощают вас конфетами.
Ребята, спасибо за урок!
Сумма разрядных слагаемых
Для всех тех кто хочет научится быстро считать и уметь быстро решать примеры в уме мы дадим очень полезный навык. Для того чтобы ваш счет был не только на телефоне или калькуляторе, вам может пригодится ряд советов из этой статьи. Вы сможете быстро считать прямо в уме.
О чем эта статья:
- Сумма разрядных слагаемых
- Разряды и классы чисел
- Примеры
Сумма разрядных слагаемых
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:
- Число 35 состоит из 3 десятков и 5 единиц
35 = 3 десятка + 5 единиц = 3*10 = 30 + 5 = 35.
30 — разрядное слагаемое; 5 — разрядное слагаемое.
- Число 86 состоит из 8 десятков и 6 единиц
86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86
80 — разрядное слагаемое; 5 — разрядное слагаемое.
- Число 356 состоит из 3 сотен, 5 десятков и 6 единиц
356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300+50+6 = 356.
300, 50, 6 — разрядные слагаемые.
Разряды и классы чисел
Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.
В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами .

Названия классов многозначных чисел:
- первый — класс единиц,
- второй — класс тысяч,
- третий — класс миллионов,
- четвёртый — класс миллиардов,
- пятый — класс триллионов,
- шестой — класс квадриллионов,
- седьмой — класс квинтиллионов,
- восьмой — класс секстиллионов.
Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:
- 345 466 129 350 вместо 345466129350
Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.
Разряд — это место, которое занимает цифра в записи многозначного числа.
Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду .
- Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.
Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.
Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.
- 10 единиц = 1 десяток;
- 10 десятков = 1 сотня;
- 10 сотен = 1 тысяча;
- 10 тысяч = 1 десяток тысяч;
- 10 десятков тысяч = 1 сотня тысяч;
- 10 сотен тысяч = 1 миллион.
Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.
Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.
- Например, нужно сказать, сколько сотен в числе 5689.
Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. 5689 — на третьем месте в классе единиц стоит цифра 6, значит в числе есть 6 сотен. Следующая влево цифра — 5 (тысячи). 1 тысяча = 10 сотен. 5 тысяч = 50 сотен. Всего в числе 56 сотен.
Если в разряде стоит цифра 0, то это означает отсутствие единиц, десятков, сотен и т.д., в зависимости от того, где именно содержится цифра.
Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.
В такой ситуации можете выполнить подробный разбор числа.
- Разберем число 6 057 386
Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть
6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.
Из чего состоит это число? Из:
- шести единиц миллионов (6 * 1 000 000);
- пяти десятков тысяч (5 * 10 000);
- семи единиц тысяч (7 * 1000);
- трех сотен (3 * 100);
- восьми десятков (8 * 10);
- шести единиц (6).
Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.
Определите, сколько единиц в числе 5 068 252.
Расписав таким образом число, мы выяснили, что в числе 5 068 252: 5 единиц класса миллионов (3 класс); 68 единиц класса тысяч (2 класс); 252 единицы класса единиц (1 класс).
Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.
Примеры
Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.
Представьте в виде суммы разрядных слагаемых:
-
- 84 610
84 610 = 8 * 10 000 + 4 * 1 000 + 6 * 100 + 10
84 610 = 80 000 + 4 000 + 600 + 10.
-
- 45 317
45 317 = 4 * 10 000 + 5 * 1000 + 3 * 100 + 17
45 317 = 40 000 + 5 000 + 300 + 17.
-
- 56 789
56 789 = 5 * 10 000 + 6 * 1000 + 7 * 100 + 8 * 10 + 9
56 789 = 50 000 + 6 000 + 700 + 80 + 9.
-
- 345 677
345 677 = 3 * 100 000 + 4 * 10 000 + 5 * 1000 + 6 * 100 + 7 * 10 + 7
345 677 = 300 000 + 40 000 + 5 000 + 600 + 70 + 7.
-
- 687 543
687 543 = 6 * 100 000 + 8 * 10 000 + 7 * 1000 + 5 * 100 + 4 * 10 + 3
687 543 = 600 000 + 80 000 + 7 000 + 500 + 40 + 3.
- 877 589
877 589 = 8 * 100 000 + 7 * 10 000 + 7 * 1000 + 5 * 10 + 8 * 10 + 9
877 589 = 800 000 + 70 000 + 7 000 + 500 + 80 + 9.
Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.
Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.
-
- 4 895 634
4 895 634 = 4 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 5 * 1000 + 6 * 100 + 3 * 10 + 4
4 895 634 = 4 000 000 + 800 000 + 90 000 + 5 000 + 600 + 30 +4.
-
- 8 675 349
8 675 349 = 8 * 1 000 000 + 6 * 100 000 + 7 * 10 000 + 5 * 1000 + 3 * 100 + 4 * 10 + 9
8 675 349 = 8 000 000 + 600 000 + 70 000 + 5 000 + 300 + 40 + 9.
-
- 77 897 125
77 897 125 = 7 * 10 000 000 + 7 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 7 * 1000 + 1 * 100 + 2 * 10 + 5
77 897 125 = 70 000 000 + 7 000 000 + 800 000 + 90 000 + 7 000 + 100 + 20 + 5.
- 656 734 212
656 734 212 = 6 * 100 000 000 + 5 * 10 000 000 + 6 * 1 000 000 + 7 * 100 000 + 3 * 10 000 + 4 * 1000 + 2 * 100 + 1 * 10 + 2
656 734 212 = 600 000 000 + 50 000 000 + 6 000 000 + 700 000 + 30 000 + 4 000 + 200 + 10 + 2.
Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.
Копирование информации с сайта greednews.su разрешено только при использовании активной гипер ссылки на новость, спасибо за то что цените наши авторские права!
Разрядные слагаемые в математике

Число — это математическое понятие для количественного описания чего-либо или его части, служит также для сравнения целого и частей, расположения по порядку. Понятие числа изображается знаками или цифрами в различном сочетании. В настоящее время почти везде используются цифры от 1 до 9 и 0. Цифры в виде семи латинских букв применения почти не имеют и рассматриваться здесь не будут.
[block >Натуральные числа

При счёте: «один, два, три… сорок четыре» или расстановке по очереди: «первый, второй, третий… сорок четвёртый» используются естественные числа, которые называются натуральными. Вся эта совокупность называется «ряд натуральных чисел» и обозначается латинской буквой N и не имеет конца, ведь всегда есть число ещё больше, и са́мого большого просто не существует.
Разряды и классы чисел
Разряды
Отсюда видно, что разрядом числа является его позиция в цифровой записи, причём любое значение можно представлять через разрядные слагаемые в виде nnn = n00 + n0 + n, где n — любая цифра от 0 до 9.
Один десяток является единицей второго разряда, а одна сотня — третьего. Единицы первого разряда называются простыми, все остальные являются составными.
Для удобства записи и передачи применяется группировка разрядов в классы по три в каждом. Между классами для удобства чтения допускается ставить пробел.
Классы

Первый — единиц, содержит до 3 знаков:
- 200 + 10 +3 = 213.
Двести тринадцать содержит в себе следующие разрядные слагаемые: две сотни, один десяток и три простых единиц.
Сорок пять состоит из четырёх десятков и пяти простых единиц.
[block > Второй — тысяч, от 4 до 6 знаков:- 679 812 = 600 000 + 70 000 + 9 000 + 800 +10 + 2.

Эта сумма состоит из следующих разрядных слагаемых:
- шестьсот тысяч;
- семьдесят тысяч;
- девять тысяч;
- восемьсот;
- десять;
- два;
- 3 456 = 3000 + 400 +50 +6.
Здесь отсутствуют слагаемые выше четвёртого разряда.

Третий — миллионов, от 7 до 9 цифр:
Это число содержит девять разрядных слагаемых:
- 800 миллионов;
- 80 миллионов;
- 7 миллионов;
- 200 тысяч;
- 10 тысяч;
- 3 тысячи;
- 6 сотен;
- 4 десятка;
- 4 единицы;
- 7 891 234.
В этом числе нет слагаемых выше 7 разряда.
[block > Четвёртый — миллиардов, от 10 до 12 цифр:Пятьсот шестьдесят семь миллиардов восемьсот девяносто два миллиона двести тридцать четыре тысячи девятьсот семьдесят шесть.
Разрядные слагаемые 4 класса читаются слева направо:
- единицы сотен миллиардов;
- единицы десятков миллиардов;
- единицы миллиардов;
- сотен миллионов;
- десятков миллионов;
- миллионов;
- сотен тысяч;
- десятков тысяч;
- тысяч;
- простые сотни;
- простые десятки;
- простые единицы.
Нумерация разряда числа производится начиная с меньшего, а чтение — с большего.
[block > При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса; девятого, восьмого и седьмого третьего и самого́ третьего класса; также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.
Пятый — триллионов, от 13 до 15 знаков.
- 487 789 654 427 241.
Четыреста восемьдесят семь триллионов семьсот восемьдесят девять миллиардов шестьсот пятьдесят четыре миллиона четыреста двадцать семь двести сорок один.
Шестой — квадриллионов, 16—18 цифр.
- 321 546 818 492 395 953;
Триста двадцать один квадриллион пятьсот сорок шесть триллионов восемьсот восемнадцать миллиардов четыреста девяносто два миллиона триста девяносто пять тысяч девятьсот пятьдесят три.
Седьмой — квинтиллионов, 19—21 знак.
- 771 642 962 921 398 634 389.
Семьсот семьдесят один квинтиллион шестьсот сорок два квадриллиона девятьсот шестьдесят два триллиона девятьсот двадцать один миллиард триста девяносто восемь миллионов шестьсот тридцать четыре тысячи триста восемьдесят девять.
Восьмой — секстиллионов, 22—24 цифры.
- 842 527 342 458 752 468 359 173
Восемьсот сорок два секстиллиона пятьсот двадцать семь квинтиллионов триста сорок два квадриллиона четыреста пятьдесят восемь триллионов семьсот пятьдесят два миллиарда четыреста шестьдесят восемь миллионов триста пятьдесят девять тысяч сто семьдесят три.
Можно просто различать классы по нумерации, к примеру, число 11 класса содержит в себе при написании от 31 до 33 знаков.
Но на практике запись такого количества знаков неудобна и чаще всего приводит к ошибкам. Поэтому при операциях с такими величинами производится сокращение количества нулей путём возведения в степень. Ведь значительно проще написать 10 31 , чем приписывать тридцать один ноль к единице.
[block >
[block > [block > - 77 897 125
- 8 675 349
- 4 895 634
- 687 543
- 345 677
- 56 789
- 45 317
- 84 610






