Что такое задача в геометрии

Геометрия с нуля

В 21 веке, несмотря на активное развитие науки, у многих школьников Российской Федерации такая наука, как геометрия вызывает все больше затруднений, а какая-то часть детей и вовсе не может решать простейшие геометрические задачи. Поэтому необходимо признать тот факт, что восприятие у нового поколения совершенно иное, и дело тут вовсе не в их деградации. Дети все также хотят развиваться: читают книги, смотрят научные фильмы и проводят эксперименты. Но самое главное, чего они не хотят, так это заучивать то, чего не понимают. На основе этого утверждения как раз и будет построена моя программа.

Представим, что перед нами сидит человек, который вообще не представляет, что такое геометрия. А именно так и выглядит бОльшая часть детей приходящих в 7 класс. Этот человек не в состоянии накладывать треугольники друг на друга и тем более не может делать из этого какие-то выводы. Поэтому сначала его нужно долго и упорно знакомить его с геометрией, чтобы в итоге он понял, насколько она проста и полюбил ее.

Разделение на уровни

• Базовый уровень: школьник знает(не обязательно наизусть) и понимает простейшие теоремы, а также решает незамысловатые задачи;
• Средний уровень: школьник умеет доказывать теоремы и решать задачи, используя доказательства;
• Высокий уровень: школьник знает сложные теоремы и умеет решать сложные задачи.

Именно эти три пункта будут подробно описаны в статье.

Базовый уровень (простейшая теория и задачи)

— понятие точки, прямой, луча, отрезка, угла, фигуры и т.д.

Прежде всего, школьник должен понять, с чем он будет иметь дело на протяжении ближайших трех лет, поэтому начинать необходимо с вводного курса. Не надо давать детям сложные задачи, а их надо просто познакомить с геометрией.

— углы (по градусам)

Углам нужно уделить особое внимание, потому что далеко не все дети могут в пространстве могут отличить тупой угол от прямого. Кроме того, максимум внимания нужно уделить развернутому углу, потому что на нем будет основан следующий пункт.

— смежные углы

Многим детям тяжело запомнить существующее определение смежных углов, и именно в большинстве случаев начинаются первые проблемы с геометрией. Поэтому мною будет предложено новое определение смежных углов: “Смежные углы – это углы, полученные в результате деления развернутого угла на две части.” Если уделить должное время развернутому углу, то получится сэкономить время на объяснении свойства смежных углов, т.к. оно итак будет понятно.

— вертикальные углы

Вертикальные углы, также как и смежные, имеют весьма непростое определение, которое можно заменить ан более просто. Достаточно ограничиться следующим: “Вертикальные углы-это углы между пересекающимися прямыми.”, а далее просто постараться разобрать как можно больше примеров, связанных с вертикальными и смежными углами.

— перпендикулярные прямые

Этой теме я не стану уделять много внимания, т.к. он итак понятен большинству школьников.

— параллельные прямые

Вместо равенства треугольников гораздо лучше рассматривать параллельные прямые, т.к., помимо получения новой информации, дети закрепляют старую, используя вертикальные и смежные углы при решении задач на параллельные прямые. Объяснять данную тему проще с признака, основанного на внутренних односторонних углах, т.к. единственное, что запоминают дети после шестого класса, это что сумма углов треугольника равна 180 градусам. Опираясь на это можно представить, что прямые пересекутся и образуют с секущей треугольник, сумма углов которого равна 180 градусам. А после этого показать детям вариант, при котором треугольника не будет, т.е. когда внутренние односторонние углы заберут градусную меру третьего угла треугольника. После этого остальные признаки доказать уже будет не так и сложно. Самое главное, не надо заставлять детей учить первые доказательства, т.к. они должны их понять.

— биссектриса, высота и медиана

После всех предыдущих тем, ребенок будет понимать, что такое углы и уметь с ними работать, а также будет знаком с прямыми, отрезками, фигурами и прочим. В этот момент ему уже можно давать более-менее сложные темы, которые ему в дальнейшем будут постоянно пригождаться. В определениях ничего менять не стоит, т.к. они итак максимально доступны. Единственное, что нужно обязательно сделать, так это убедиться в том, что ребенок может провести биссектрисы, медианы и высоты в любой фигуре и из любой вершины!

— треугольники *(при объяснении свойств треугольников можно и нужно опираться на признаки равенства)

Теперь, когда школьник со знаком с основами, можно приступать к рассмотрению фигур. Начать лучше всего с треугольников, т.к. именно они используются в большинстве задач. Здесь необходимо рассмотреть все виды треугольников с их свойствами. Объяснить ребенку откуда что берется, опять же не заставляя это заучивать. Но определения и свойства школьник должен знать, т.к. именно на этапе прохождения свойств фигур, мы можем начинать спрашивать с ребенка теорию. Теперь он уже полноценно вовлечен в процесс.

— четырехугольники *(при объяснении свойств четырехугольников можно и нужно опираться на признаки равенства)

Здесь я бы хотела представить Вашему вниманию увлекательный процесс эволюции параллелограмма, который детям запомнить гораздо проще, чем определения из учебника:

Здесь рассмотрены только те свойства, которые способен легко усвоить школьник на базовом уровне.

Кроме того, сюда же необходимо включить и трапецию со всеми ее свойствами и разновидностями.

Таким образом, мы сможем закрепить параллельные прямые и понять, откуда что берется в четырехугольниках.

В этой теме необходимо рассмотреть разные виды многоугольников и сумму углов n-угольника.

— теорема Пифагора

Тема, которую итак все прекрасно понимают, поэтому ничего усложнять не надо.

Здесь я опять же хочу предложить удобную схему, которую необходимо объяснять с помощью бумажных фигурок.

Трапеция опять же рассматривается отдельно.

— подобие и первый признак подобия

Рассматривается исключительно в ознакомительных целях, чтобы детям легче было понимать начала тригонометрии.

— средние линии треугольника и трапеции

Средние линии лучше рассматривать вместе, потому что так они лучше усваиваются.

В самом начала тригонометрии, школьникам стоит напомнить о том, что такое соотношения, а после очень много времени посвятить самим определениям синуса, косинуса, тангенса и котангенса, чтобы школьники понимали, откуда взялись эти странные английские буквы. Затем необходимо рассмотреть множество задач, в которых они будут использоваться. Удобнее всего давать задачи на теорему Пифагора и площади. Желательно уже на базовом уровне ознакомить детей с таблицей, т.к. сейчас они уже максимально близки к среднему и уровню и способны усваивать информацию средней сложности.

— окружность и круг

И, наконец, последняя тема на базовом уровне. Здесь необходимо напоминать детям обо всем, что связано с окружностью и кругом, начиная с определений, т.к. никто уже ничего не помнит из курса 6 класса. А также стоит рассмотреть свойство касательной, вписанный и центральный углы, и свойство гипотенузы прямоугольного треугольника.

На этом базовый курс окончен. У рядового школьника достаточно базовых знаний, на которые он мог бы опираться при решении задач, с использованием доказательств. Пришла пора поближе с ними познакомиться.

Средний уровень (доказательства)

Расписывать программу для среднего уровня смысла нет, т.к. на этом этапе ребенок готов усваивать практически любую информацию и способен аргументированно решать задачи на доказательства. Единственное, что стоит сделать, так это перечислить темы среднего уровня:

— соотношения между сторонами и углами;

— признаки равенства треугольников;

— признаки подобия треугольников;

— четыре замечательные точки;

— вписанная и описанная окружности.

Этого вполне достаточно для доказательств средней степени сложности.

Высокий уровень (сложные доказательства и решение сложных задач)

К сожалению, немногие могут достичь высокого уровня, но каждый должен хотя бы попытаться. Опять же, нет смысла все подробно расписывать, поэтому будут перечислены лишь темы:

— углы при окружности;

Из всего вышесказанного можно сделать следующий вывод: прогресс любого школьника основан на его базовых знаниях. Если они есть, то их необходимо лишь грамотно развивать. Поэтому, прежде всего, необходимо упростить получение базовых знаний и сделать их максимально доступными для всех школьников без исключения.

Примечание: векторы в статье не учтены, т.к. являются дополнением ко всему вышесказанному.

Как решать задачи по геометрии. Часть 1

Геометрия… Страшное слово для бесчисленного множества учеников. Они знают свойства фигур и выучили определения и теоремы, но задачи по геометрии все равно остаются какой-то китайской грамотой.

Это про тебя? Тогда ты попал туда, куда нужно!

Проблема подавляющего большинства учеников в том, что они не умеют обдумывать задачу по геометрии. Их этому не научили (ну, или они не захотели научиться, когда была возможность). Именно в этой статье, я объясню саму технологию обдумывания и, в конечном счете, нахождения решения ПРАКТИЧЕСКИ ЛЮБОЙ задачи по геометрии.

Сразу оговорюсь — без знания теории в геометрии никак. В смысле, вообще никак, от слова «совсем». Чтоб тебе было полегче при чтении этой статьи, я буду внутри решений задач в скобках курсивом указывать используемые свойства и теоремы. Но помни: если вдруг в знании теории у тебя пробел – закрытие его за тобой! Бери учебник и читай. Причем главные вещи – заучивай (или понимай). Знать теорию – обязательно!

Ты играл когда-нибудь в квесты? Неважно в реальной жизни или в компьютере. Во всех квестах принцип один – у тебя есть что-то (вещи, знания, навыки) и есть цель (раскрыть какую-нибудь тайну, найти некий предмет, «спасти принцессу» и т.д.). При этом путь к цели – неизвестен. И зачем нужны эти самые имеющиеся у тебя «вещи, знания, навыки» – тоже непонятно. Что делать? Как достичь цели?

Известно как: использовать то, что есть, и искать, куда это применить, чтоб продвинуться к цели. То есть, делать шаги от своего текущего местонахождения – к цели. При этом понятно, что некоторые шаги будут вести нас не туда, куда надо, а совсем даже в тупик. А иногда мы будем находить вещи или информацию, вроде бы напрямую к цели не ведущие, но как выяснится в дальнейшем – необходимую.

Более того, порой можно логически двигаться и наоборот – от цели к твоей текущей позиции. Например, если нужно «спасти принцессу из замка», то понятно, что, скорее всего, надо будет как-то попасть в замок. А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт. Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.

К чему весь этот разговор? Решение задачи по геометрии это точно такой же «квест», только математический . Вдумайся: у нас всегда есть некоторые исходные данные и есть то, что нужно найти (или доказать – разницы на самом деле практически нет). И наша задача – построить логическую цепочку от исходных данных к цели. Строительным материалом при этом у нас будут данные (исходные и полученные при рассуждениях), а также теоремы и свойства.

Ладно, давай уже конкретный пример разберем.

Задача. В треугольнике (ABC) из точки (B) проведена высота (BH). Найти длину отрезка (AH), если известно, что сторона (AC; =; 14) см и угол (A) равен углу (C).

Так. С чего начинается решение геометрической задачи? Ну, а с чего начинается решение квеста? Правильно, осматриваемся по сторонам, изучаем, что у нас есть и куда нас жизнь закинула.

В геометрии это означает:

1. построить чертежа выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
2. выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.

Хорошо. Значит, текущая ситуация у нас такова:

Давайте потихоньку развеивать туман. Нам известно, что углы (А) и (С) равны, а это значит, что треугольник (АВС) – равнобедренный с основанием АС (теория – «признак равнобедренного треугольника: равенство углов при одной из сторон. Она и является основанием»). Это новая информация, новые данные, изначально неизвестные. Делаем шаг.

Отлично. Теперь смотрим, что у нас есть еще? Еще у нас есть информация, что (BH) – высота. А раз треугольник (ABC) – равнобедренный, то значит (BH) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.

А что мы знаем про медиану? Она делит противоположную сторону на две равные части (определение медианы: отрезок, соединяющий вершину треугольника с серединой противоположной стороны). Но тогда получается, что точка (H) делит сторону (AC) пополам. То есть (AH = HC).

Стоп. Так у нас же есть длина стороны (AC)! И если мы знаем, что точка (H) делит сторону (AC) пополам, значит, (AH) равен половине (AC)! Таким образом, получаем, что (AH = AC/2 = 14/2=7) см.

Готово. Ответ получен.

Естественно, такие конструкции с «пятном тумана» рисовать каждый раз не нужно, эта схема показывает логическую цепочку решения у нас в голове. А записывается примерно так:

Геометрические задачи и методы их решения с примерами

Геометрия — это наука о пространственной форме и количественных характеристиках предметов реального мира. Прочие свойства предметов изучают другие дисциплины. Если при изучении предмета учитывать только пространственную форму и размеры, то получим абстрактный объект, называемый геометрической фигурой.

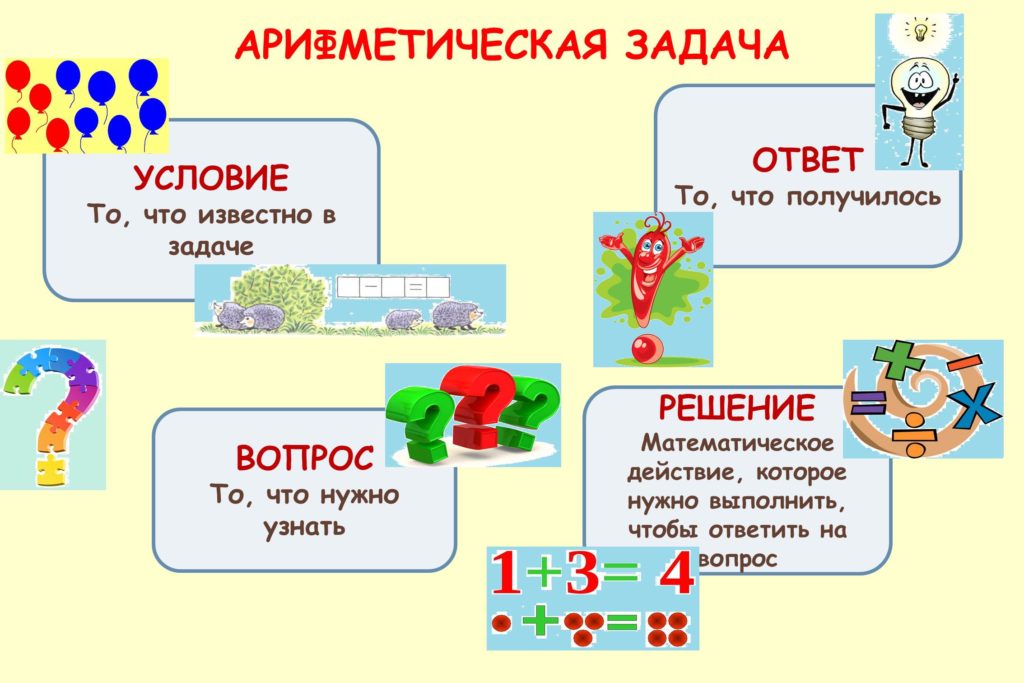
Слово «геометрия» — греческого происхождения и в переводе означает землеизмерение. Геометрию, изучаемую в школе, называют евклидовой по имени древнегреческого ученого Евклида. Геометрия состоит из двух частей: планиметрии и стереометрии. Планиметрия изучает свойства фигур на плоскости, а стереометрия — в пространстве (рис. 1).

Чтобы отличать геометрические фигуры друг от друга, их свойства описывают в виде утверждения, которое называют определением. Однако, определить вес геометрические фигуры невозможно. Некоторые из них, первоначальные, вынуждены принять без определения. Принимаем их за неопределяемые, начальные (основные) геометрические фигуры. Логическое построение геометрии осуществляют в следующем порядке: 1. Вначале принимают основные (начальные) геометрические фигуры без определения; 2. Принимают основные свойства этих фигур без доказательств;

3. Определяют другие геометрические фигуры через основные фигуры и их свойства, а затем доказывают свойства этих фигур и утверждений, истинность которых устанавливается путем доказательств, опираясь на известные.

Такое построение науки называют аксиоматическим построением. Свойства фигур, принятые без доказательства, называют аксиомами.

В планиметрии, которую мы изучали до сих пор основными геометрическими фигурами были точка и прямая. Их приняли без определения. Но определили отрезок, луч, треугольник и другие геометрические фигуры. Точно так же следующие свойства (утверждения) мы принимаем без доказательств в качестве аксиом:

I. Аксиомы принадлежности

1.1. Какова бы ни была прямая на плоскости, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

1.2. Через любые две точки можно провести прямую, и притом только одну.

II. Аксиомы расположения

2.1. Из трех точек, лежащих на прямой, одна и только одна лежит между двумя другими.

2.2. Любая прямая делит плоскость на две части: на две полуплоскости.

III. Аксиомы измерения

3.1. Любой отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

3.2. Любой угол имеет определенную градусную меру, большую нуля. Градусная мера развернутого угла равна 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

IV. Аксиомы откладывания

4.1. На любом луче от его начальной точки можно отложить единственный отрезок, равный данному.

4.2. От любого луча в определенную полуплоскость можно отложить единственный угол, равный данному, не развернутому углу.

4.3. Для любого треугольника существует единственный равный ему треугольник в заданном расположении относительно данного луча.

V. Аксиома параллельности

5.1. На плоскости через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

Вывод некоторого утверждения с помощью логических размышлений называют доказательством. Утверждение, верность которого установлена с помощью доказательства, называют теоремой. Обычно теорема состоит из условия и заключения. В первой части теоремы — условии объясняют что задано. А во второй части — заключении формулируют что требуется доказать.

Доказать теорему — эго значит, используя ее условие, опираясь на принятые и доказанные ранее свойства, рассуждая, привести к правильности предложения, сформулированного в заключении.

Уточнение условия и заключения теоремы — разъясняет ее, облегчает понимание и доказательство теоремы.

Древнегреческий ученый Платон отмстил удивительную закономерность в геометрии: из свойств, изученных и доказанных ранее, логически размышляя и обдумывая, можно получить новые свойства. Следовательно, используя эти удивительные возможности, можно формулировать остальные свойства в виде теорем, которые доказывают с помощью логических размышлений, аксиом, а также свойств, доказанных до этого.

В процессе размышления запрещается использование недоказанных свойств, даже если их правильность очевидна.

Таким образом, если рассматривать геометрию как одно здание, начальные понятия и аксиомы составляют его фундамент. Кирпичи, уложенные на этом фундаменте — это новые определяемые понятия и свойства, доказанные в виде теорем.

В формировании геометрии в качестве самостоятельной науки большой вклад внесли древнегреческие ученые. Например, Гиппократ Хиосский дал разъяснения о первых геометрических понятиях. Наибольший вклад в этой области принадлежит великому древнегречеcкому ученому Евклиду (356-300 годы до нашей эры). Его основной труд «Начала» содержит планиметрию, стереометрию и некоторые вопросы теории вероятностей, кроме того, алгебру, основы теории отношений, способы вычисления площадей и объемов и также элементы теории пределов. Евклид в «Началах» собрал все достижения древнегреческих математиков того времени и создал основу для дальнейшего развития математики.

«Начала» состоят из 13 книг и содержат переработанные труды древнегреческих ученых V — IV веков до нашей эры. В нем приведены 23 определения, 5 постулатов и 9 аксиом. В этом труде даны правильные определения прямоугольника, квадрата и окружности. Для точки и прямой приведены следующие определения: «Точка-это то, что не имеет частей», «Линия-это длина без ширины».

В «Началах» приведены 9 аксиом — высказывания, принятые без доказательства. Также приведены следующие 5 математических умозаключений (постулатов), позволяющие осуществлять геометрические построения:

I. Через любые две точки можно провести только одну прямую.

II. Отрезок прямой можно бесконечно продолжить.

III. Из любой точки можно построить окружность произвольныго радиуса.

IV. Все прямые углы равны между собой.

V. Если две прямые, лежащие в одной плоскости, пересеченные третьей, образуют внутренние углы, сумма которых меньше двух прямых углов, то при продолжении вышеупомянутых прямых они пересекутся с той стороны, где сумма углов меньше двух прямых углов.

Упомянутый труд получил огромную славу и признание. Особенно V постулат стал причиной большой научной дискуссии. Если обозначить внутренние углы в V постулате а и (3 (рис. 1), а прямые а и b, то по смыслу этого постулата а+(3

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Образовательный портал

Процесс обучения, являясь составной частью целостного педагогического процесса, в современной школе должен быть направлен на формирование всесторонне и гармонически развитой личности.
Обобщённый опыт обучения школьников основам наук, в частности математики, показывает, что для обеспечения единого подхода к учащимся, к выбору методов и средств учебной работы учитель должен придерживаться положений, носящих универсальный характер.
В связи с этим в дидактике разработаны принципы, которые рассматриваются как важнейшие требования к организации процесса обучения, его содержанию, формам и методам.
В методической литературе выделяется следующая система общих принципов дидактики:
научности;
сознательности, активности, самостоятельности;
систематичности и последовательности;
доступности;
наглядности;
индивидуального подхода;
прочности знаний. Но если рассматривать методику обучения математике, то среди частных дидактических принципов следует выделить принцип обучения через задачи.
Данная статья представляет собой попытку показать, что принцип обучения через задачи является одним из наиболее важных, в свете реализации требований ФГОС.
Идея использования этого принципа не нова. Ещё в конце 19 века известный русский методист С.И. Шохор-Троцкий выступил как изобретатель «методы целесообразных задач». Под этой «методой» он понимал построение курса математики из систематически подобранных задач. В 1908г. в Москве вышла его книга, посвящённая этой проблеме, «Геометрия на задачах». Усвоение математики, по мысли Шохор-Троцкого, должно происходить не с помощью зазубривания книжных истин или объяснений учителя, а посредством более или менее самостоятельной работы ученика над искусно подобранными задачами.
Практического применения идеи С.И. Шохор-Троцкого в то время не получили, но сейчас эта тема весьма актуальна: необходимо повышать эффективность уроков математики, добиваться развития познавательных интересов учащихся, способствовать приобретению ими навыков самообразования.
Осознанное использование на уроках принципа обучения через задачи возможно только тогда, когда учитель чётко представляет значение и роль задач в процессе обучения, развития, воспитания, поскольку эти процессы взаимосвязаны между собой. Необходимо знать различные методы решения задач, способы организации обучения решению математических задач. В качестве примера можно привести опыт передовых педагогов, который в большинстве своём носит элементы проблемного обучения и подтверждает тесную взаимосвязь проблемности урока и принципа обучения через задачи.
Вместе с тем следует иметь в виду, что дидактические принципы, выражая определённые закономерности обучения, не являются раз и навсегда установленными. Они постоянно углубляются, видоизменяются, в соответствии с задачами, которые ставит перед школой современное общество.
Данная работа является попыткой проанализировать использование принципа обучения через задачи в процессе преподавания геометрии.
Примерно половина уроков математики в средней школе отводится на решение задач. Таким образом, обучение математике, в частности геометрии, осуществляется и при решении задач. Обучая, мы преследуем три основные цели: знать, понимать, уметь применять. Обучение математике невозможно разделить на теорию и практику: решая задачи, мы усваиваем теорию. Ошибаются и те, кто считает решение задач самостоятельной целью: задачи это средство обучения, цель не в ответе, а в процессе решения. Выделим и рассмотрим несколько видов задач, условно классифицировав их по дидактическим целям, поставленным перед этими задачами.
1. Задачи и овладение математическими символами.
С помощью задач можно добиться более осознанного овладения математическими символами. Ведь одной из целей обучения математике является освоение математического языка, а следовательно и математической символики. На начальных этапах изучения геометрии это особенно важно, так как необходимо научить школьников правильному употреблению геометрических символов. Обучаем, раскрывая роль и назначение символов при решении задач. Правильное применение символики при записи решений и условий задач имеет существенное значение в обучении школьников использовать её.
Часто символьная запись используется при формулировке краткой записи условия задачи. Например, задача:
Отрезок ВС параллелен плоскости β. Из точки В к плоскости β опущен перпендикуляр ВА. Через точку С проведён отрезок CD параллельно ВА до пересечения с плоскостью β в точке D. Определить вид четырёхугольника ABCD.
Рис.1 (см. приложение)
Символьная запись акцентирует внимание учащихся на важных моментах в условии задачи, позволяет перевести её текст на математический язык.
Необходимо следить за грамотностью применения символов. Например:
Таблица 1. (см. приложение)
2. Задачи, предшествующие изучению нового материала.
Изучение теории – один из наиболее трудных, с методической точки зрения, вопросов преподавания математики. Дело в том, что обычная методика объяснения нового теоретического материала имеет существенные недостатки, связанные прежде всего с
пассивностью обучаемых, деятельность которых часто сводится к слушанию учителя и переписыванию с доски. Повысить активность учащихся при изучении теории можно попытаться с помощью специально подобранных задач. Такие задачи должны подготавливать учащихся к доказательству теорем, актуализировать уже пройденный, но необходимый для усвоения нового, материал.
Например, при организации усвоения теорем задачи играют не последнюю роль.
Важными моментами в работе с теоремой являются: 1) ознакомление с фактом, отражённым в теореме; 2) усвоение формулировки теоремы; 3) ознакомление с методом доказательства; 4) доказательство теоремы; 5) применение теоремы.
Каждый из этих этапов может быть осуществлён с помощью задач. Например, теорема:
В любом треугольнике против большей стороны, лежит больший угол.
Этап знакомства с формулировкой теоремы можно осуществить посредством выполнения задач на построение треугольников, измерения величин их углов и длин сторон. А затем соотнесение зависимостей между сторонами треугольников и величинами противолежащих им углов. Задача:
Измерить с помощью транспортира и линейки углы и стороны данных треугольников. Записать полученные значения. Какая зависимость существует между длинами сторон и величинами противолежащих им углов данных треугольников?
Рис.2 (см. приложение)

В целях облегчения запоминания громоздких формулировок целесообразно поэлементное усвоение содержания формулировки теоремы. Для этого формулировку «разбиваем» на отдельные части, после чего каждая из частей отрабатывается при выполнении задач. Например, теорема:
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Разбиваем формулировку на части:
Если две стороны и угол между ними одного треугольника

равны соответственно двум сторонам и углу между ними другого треугольника,

то такие треугольники равны.

Предлагаем следующее задание:
Рис.3 (см. приложение)

Выделить на рисунке равные треугольники.
Можно предложить учащимся работу в паре с использованием готового слайда презентации или интерактивной доски.

I ученик (читает теорему по частям)	II ученик (называет элементы треугольника и выделяет их )
Если две стороны и угол между ними одного треугольника	AD, DB и
равны соответственно двум сторонам и углу между ними другого треугольника	KC, CL и
то такие треугольники равны	Δ ABD = Δ KLC

Далее можно предложить несколько задач следующего типа. Задача: какие из данных треугольников равны?
Рис.4 (см. приложение)

Важно постоянно обращать внимание учащихся на соответствие называемых сторон и углов.
С помощью задач часто удаётся ознакомить учащихся с идеей доказательства, иногда и доказать теорему, вовлечь учащихся в доказательство теоремы. Рассмотрим, например, теорему Пифагора.
Формулировку теоремы учащимся заранее не сообщаем, необходимо чтобы они сами пришли к ней. Просто решаем задачу.
Задача: Дан квадрат ABCD с длиной стороны a+b. На его сторонах отмечены точки M, N, P, K так, чтобы каждый раз чередовались отрезки длиной a и b. Найти площадь четырёхугольника MNPK.

Рис.5 ( см. приложение)

Рис.6 ( см. приложение).

После того, как доказано равенство треугольников, работу с задачей продолжим в ином направлении. Рассмотрим четырёхугольник MBNF.

Вполне возможно, что учащиеся сделают (пусть и с помощью учителя) вывод о том, что параллельные прямые отсекают от сторон угла равные отрезки. А затем можно задать вопрос: «А при каком условии это происходит?» и переходим непосредственно к теореме Фалеса.
Следует отметить и такой факт: подготовительные задачи особенно полезны в тех случаях, когда при изучении нового материала используются непривычные для учащихся рассуждения, которыми «с ходу» овладеть довольно трудно. А подготовительные задачи позволяют сформировать у учащихся некоторый опыт в проведении таких рассуждений и тем самым облегчить усвоение теорем.
О задачах можно говорить долго, ценность их на уроках геометрии
велика, особенно если система задач подобрана правильно в соответствии с целью и задачами урока. С помощью задач можно, например, проиллюстрировать приложение изученного материала, проконтролировать уровень усвоения теории.
Математика имеет существенное преимущество перед другими школьными предметами в том, что она с помощью задач на каждом уроке может касаться самых разнообразных явлений природы и окружающей жизни, что позволяет расширять интересы учащихся.

Классификации геометрических задач

В методической литературе приняты следующие условные классификации геометрических задач.

1. По специфике языка. В курсе геометрии основной школы часто решаются текстовые задачи, т.е. те задачи, условие которых представлено преимущественно на естественном языке. Примером такого рода задачи из задач, рассмотренных в предыдущем пункте, может служить задача о хордах круга. Как видно из этого примера, кроме естественного здесь может использоваться и геометрический язык.

Иногда решаются и сюжетные геометрические задачи, то есть те, в которых присутствует фабула. В них описан «некоторый жизненный сюжет (явление, событие, процесс) …» [22. С. 3]. Чаще всего это геометрические задачи с практическим содержанием. Таковой является, например, последняя задача предыдущего пункта.

Сюжетные геометрические задачи играют значительную роль в процессе обучения, т.к. при их решении решается одна из важнейших задач всего курса математики – обучение методу моделирования и, в первую очередь, перевод естественного языка на язык математический, что иногда представляет значительную трудность.

Абстрактные задачи (с использованием только геометрического языка) встречаются гораздо реже. Иллюстрацией такого рода задач могут служить две задачи на готовых чертежах в первом из рассмотренных в предыдущем пункте примере.

2. По характеру рассматриваемых в геометрической задаче объектов они подразделяются на чисто геометрические задачи и практические задачи.

В чисто геометрических задачах речь идет только о геометрических фигурах вне связи их с конкретными объектами окружающего мира. Именно такие задачи составляют основное содержание задачного материала современных учебников геометрии. Приведенные в предыдущем пункте задачи, кроме последней, являются чисто геометрическими.

В практических задачах основными объектами являются предметы окружающего мира. Например, последняя задача предыдущего пункта относится к практическим. Эти задачи помогают учащимся узнавать в предметах окружающего мира знакомые геометрические фигуры, использовать те или иные свойства этих фигур и тем самым осознавать возможности практического применения геометрии. Более того, практические задачи играют большую роль в формировании общих компетенций. Задач с практическим содержанием в учебниках обычно недостаточно. Большую помощь в насыщении курса планиметрии такого рода задачами может оказать пособие для учителя [Апанасовы].

3. По отношению к теории [23. Оборот титула] или по уровню проблемности [11. С. 102] геометрические задачи делятся на стандартные и нестандартные[3] задачи.

Геометрические задачи, для решения которых в школьном курсе имеются готовые алгоритмы или эти алгоритмы непосредственно следуют из определений или теорем, называют стандартными.

Примеры.Первый пример.Стандартными являются геометрические задачи, в которых теоремы могут служить алгоритмами решения. Так, теорема о средней линии трапеции служит алгоритмом для решения задач нахождения длины средней линии трапеции по ее основаниям. Последовательность шагов алгоритма для решения таких задач проста:

1) устанавливаем длину оснований трапеции;

2) находим их полусумму. Это и будет длина средней линии.

Второй пример.Все так называемые элементарные задачи на построение являются стандартными. 

4. Наиболее распространенная классификация, которая обычно используется и в работе с учащимися, – это классификация, основанием которой является характер требований задачи. В соответствии с этим основанием геометрические задачи условно классифицируются на задачи: 1) на вычисление, 2) на доказательство, 3) на построение (конструктивные задачи).

Заметим, что эта классификация, несмотря на очень широкое ее распространение, достаточно условна: задача на вычисление часто является и задачей на доказательство, так как требует обоснования; одним из очень существенных этапов решения задачи на построение является доказательство; во многих задачах сочетается построение, вычисления и измерение. Все же эта классификация облегчает рассмотрение особенностей каждого вида геометрических задач.

5. В методической литературе специально выделяются так называемые “задачи на готовых чертежах”. Далее мы кратко их охарактеризуем. Функции этих задач не столько математические, сколько методические.

6. Методический характер носит и классификация, основой которой является характер использования задачи на уроке. В соответствии с этой классификацией можно выделить:

– задачи на раскрытие содержания новых понятий,

– задачи на применение отдельной теоремы, формулы и др.;

– комбинированные задачи: на применение нескольких теорем, формул и т.д.

Некоторые примеры такого рода задач приведены в пункте 1.2.

Рассмотрим методику использования в процессе обучения наиболее интересных с методической точки зрения классов геометрических задач.

Основы геометрии

Понять геометрию с нуля — это непросто. Но, чем дальше, тем интереснее. Новые знания можно применить везде: в школе на уроках, дома во время ремонта и даже на прогулке. В этой статье рассказали про основы геометрии для начинающих.

О чем эта статья:

Идеальные объекты

Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.

Математика занимается объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Базовые геометрические объекты

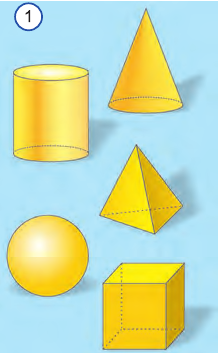
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.

Точка — это идеальный математический объект, у которого нет длины и ширины.

Отрезок — это часть прямой, у которого есть начало и конец.

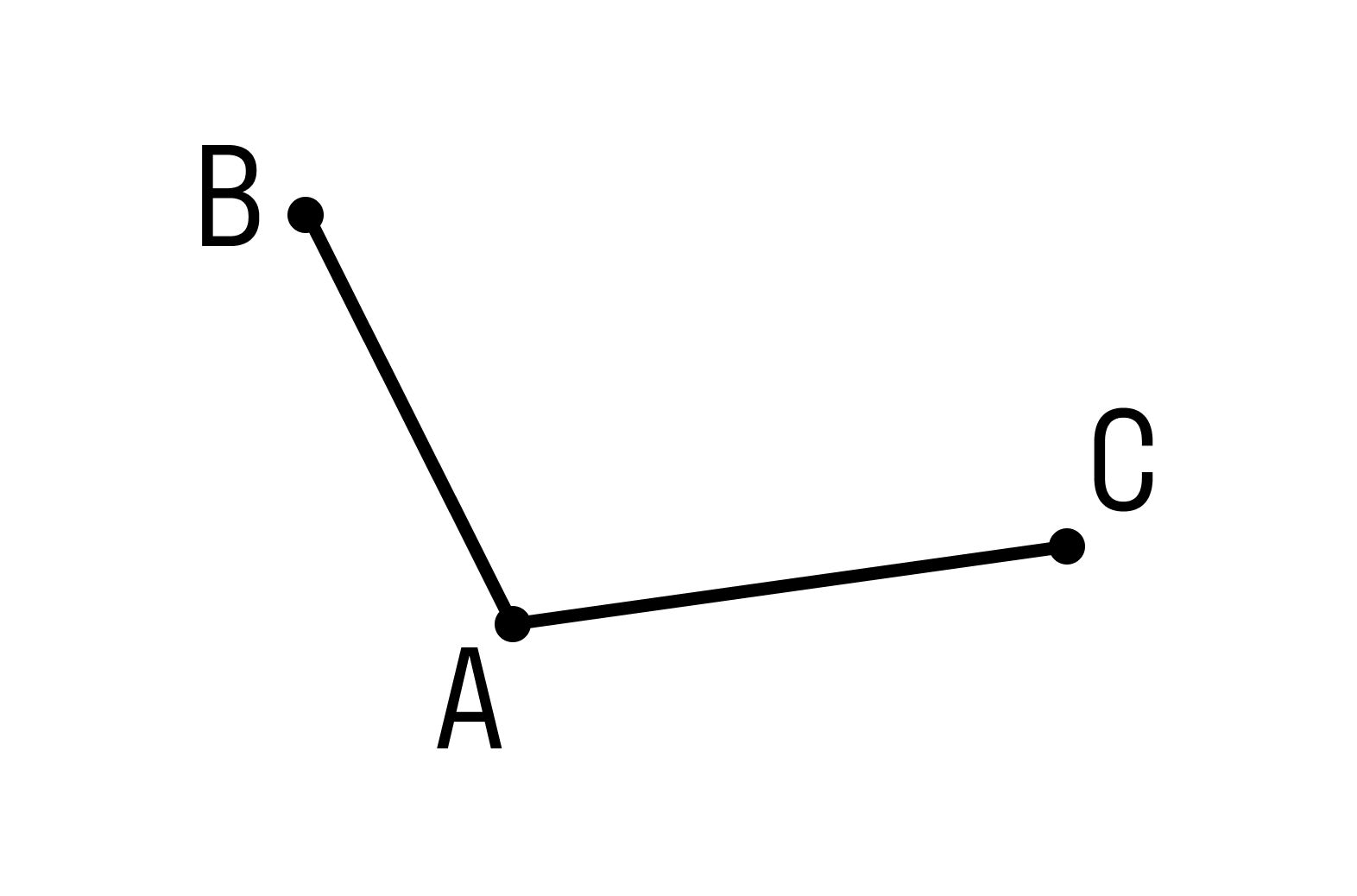
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.

Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.

Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.

Обозначать прямые принято малыми латинскими буквами (a, b, c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).

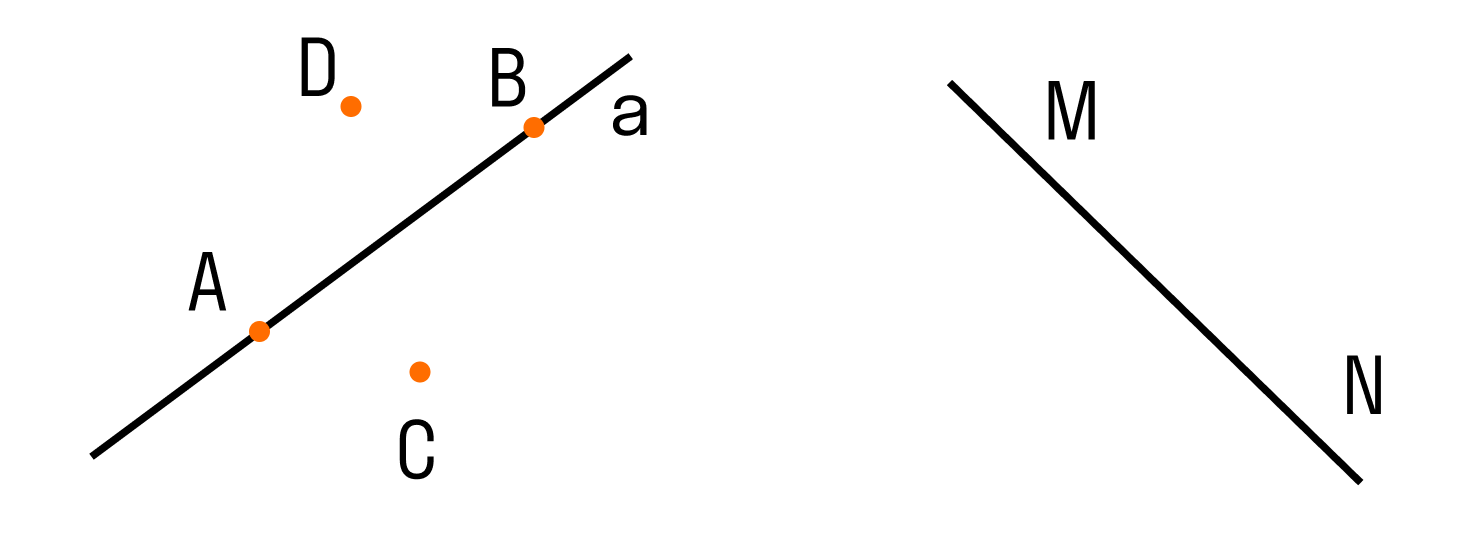
Два варианта расположения точек относительно прямой:

Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).

Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).

Если рассмотреть две прямые, то возможны два варианта их расположения:

Прямые пересекаются, то есть имеют одну общую точку.

Для записи пересекающихся прямых используют специальный знак — ∩, то есть a∩b (читают: прямая a пересекает прямую b). Чтобы обозначить точку пересечения прямых, пишут a∩b = O (читается: прямая a пересекается с прямой b в точке O).

Для записи не пересекающихся прямых используют специальный знак — , то есть m n (читают: прямая m не пересекает прямую n). В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||.

Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.

На рисунке точка О разбивает прямую АВ на две части:

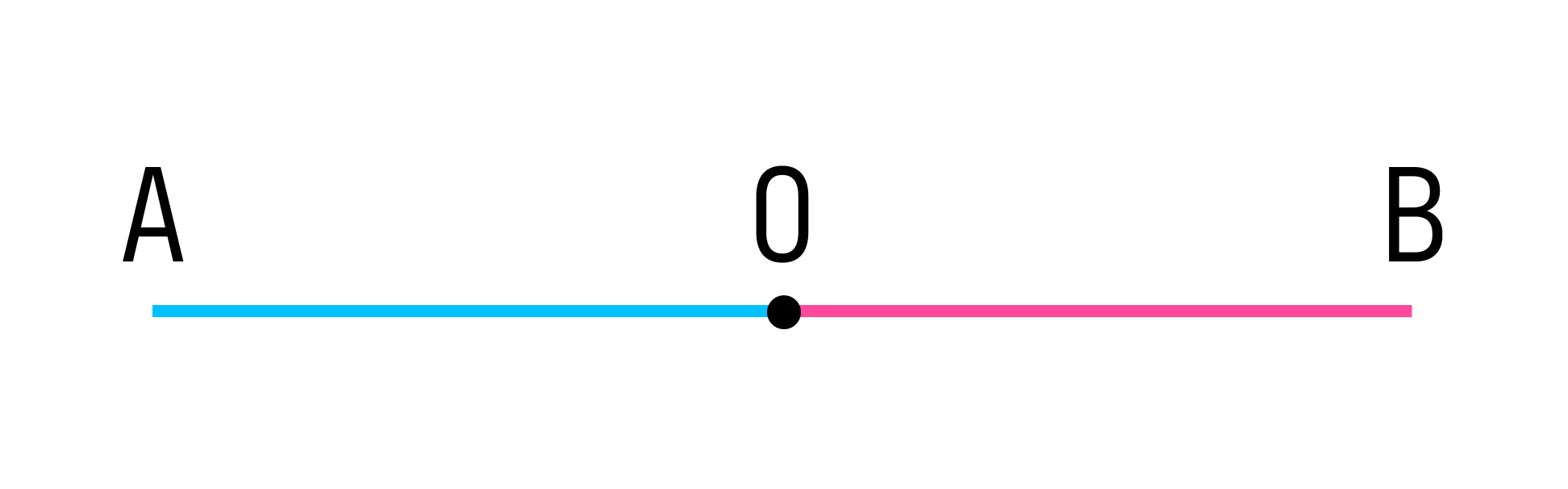
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.

Назовем получившиеся лучи:

Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.

Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.

Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.

Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости

Комбинации простейших объектов

Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).

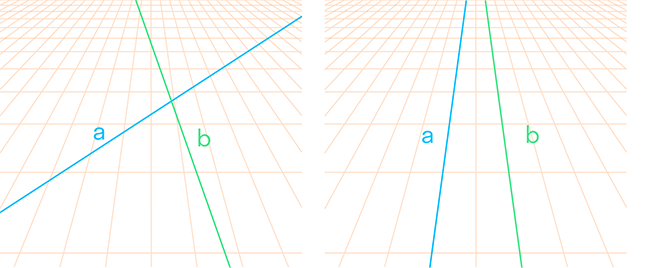
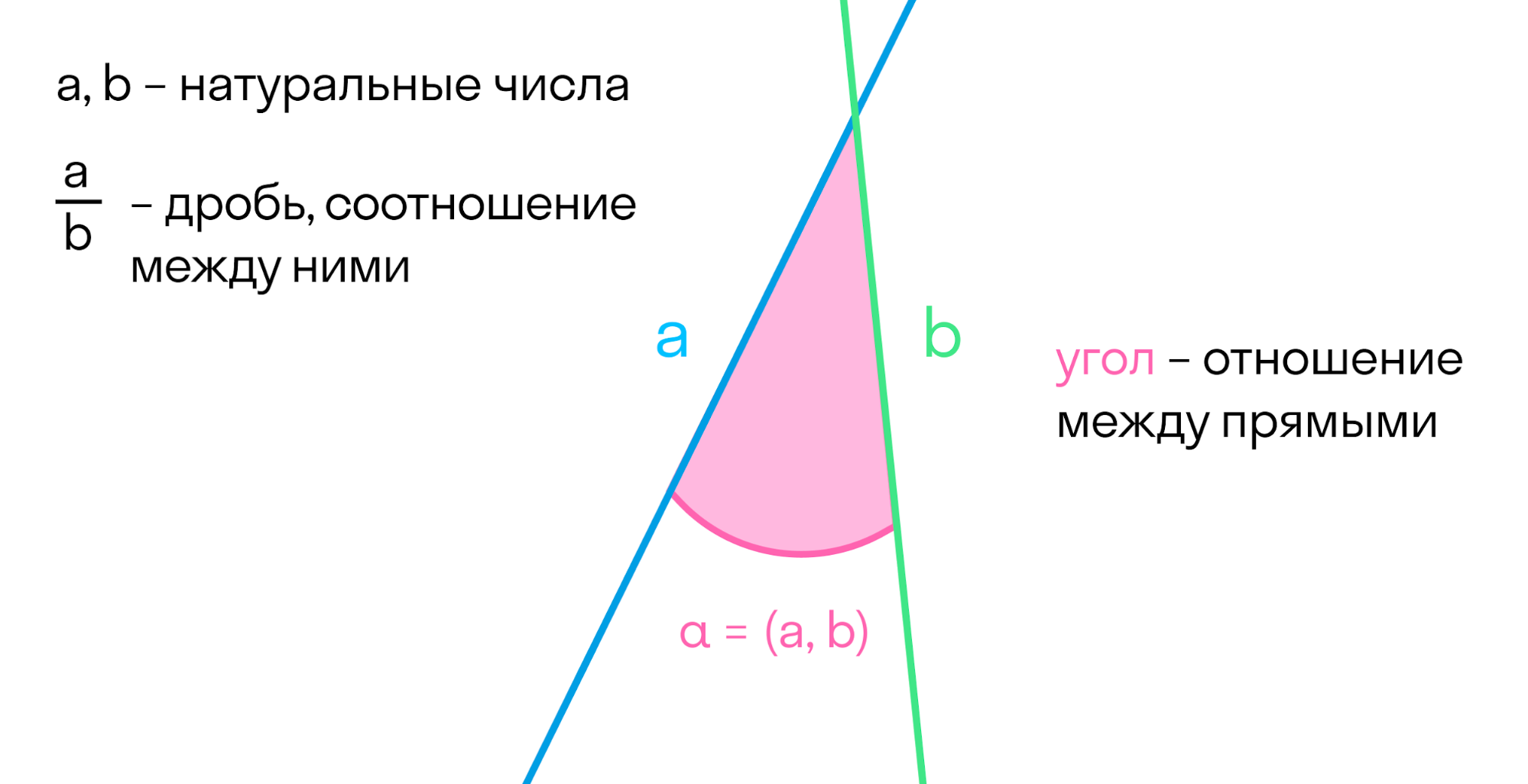
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.

Точно так же мы изучали множества, а после — отношения между множествами, функции.

Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.

Максимальный угол – это полный оборот, он составляет 360 градусов.

Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.

Есть разные виды углов, выделим самые часто встречающиеся:

Если градусная мера угла меньше 90° — угол острый.

Если градусная мера угла равна 90° — угол прямой.

Если градусная мера угла больше 90°, но меньше 180° — угол тупой.

Если градусная мера угла равна 180° — угол развернутый.

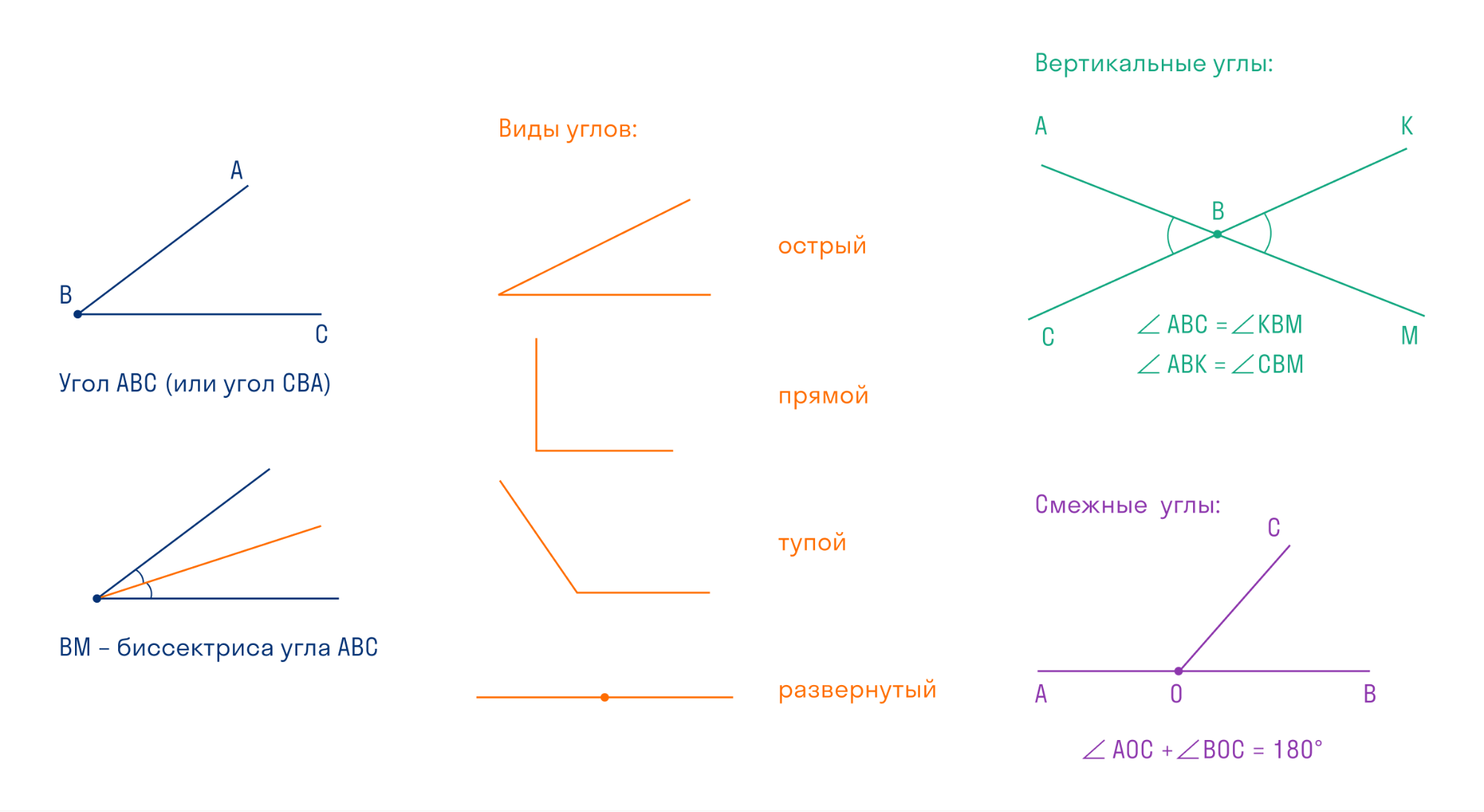
Общая точка, из которой исходят лучи, называется вершиной угла, а лучи — сторонами угла.

Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.

Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.

Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.

А теперь посмотрим на взаимное расположение трех прямых.

Первый случай: все три прямые параллельны.

Второй случай: две прямые параллельны, а третья их пересекает.

Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.

Треугольник

Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.

Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.

Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.

Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:

две стороны и угол между ними;

два угла и сторону;

Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!

Свойства треугольников

Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.

Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.

Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.

Неравенство треугольника

Сумма любых двух сторон треугольника больше его третьей стороны.

Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.

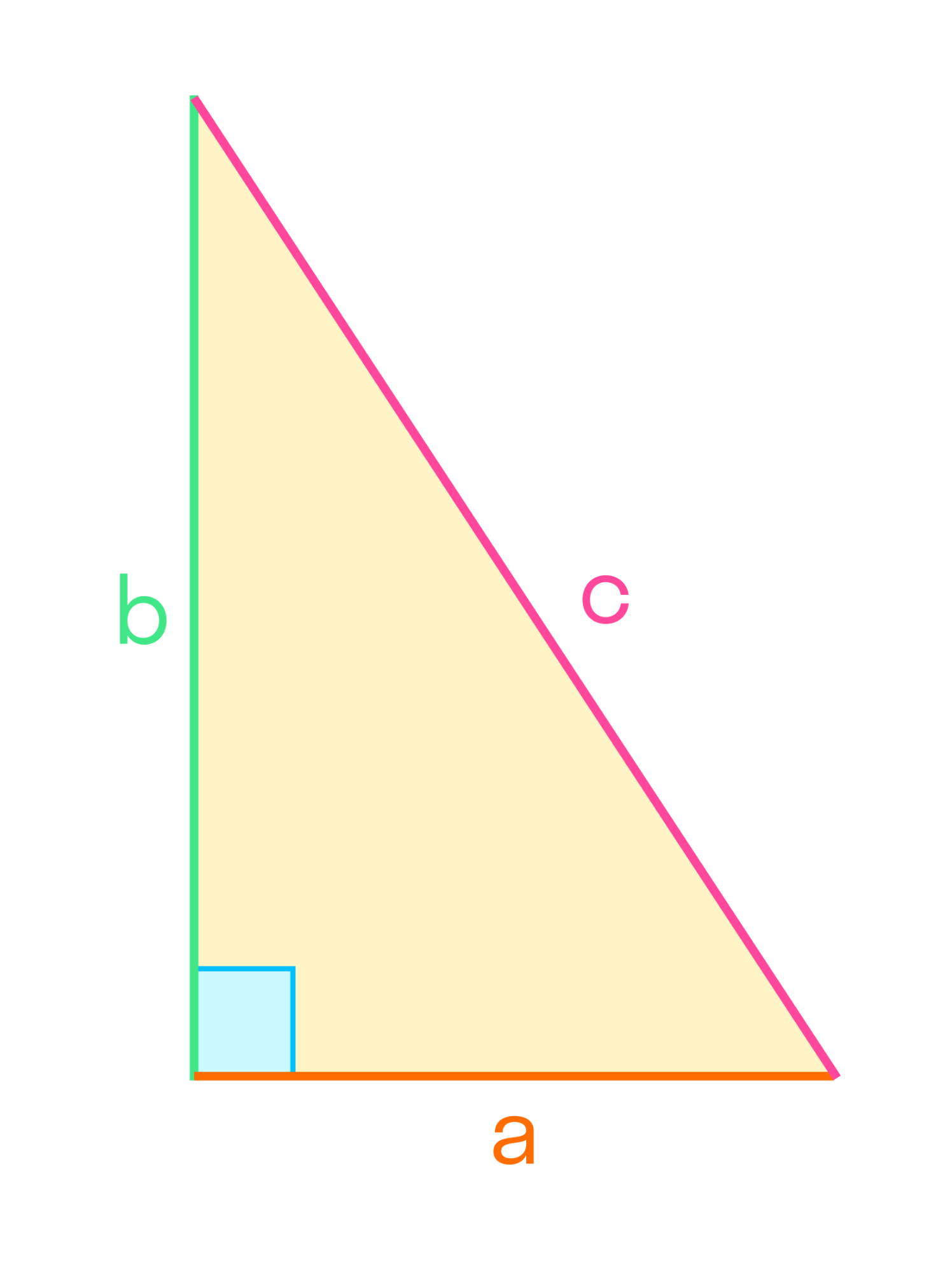
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.

Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.

Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.

От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃

Четырехугольники

Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.

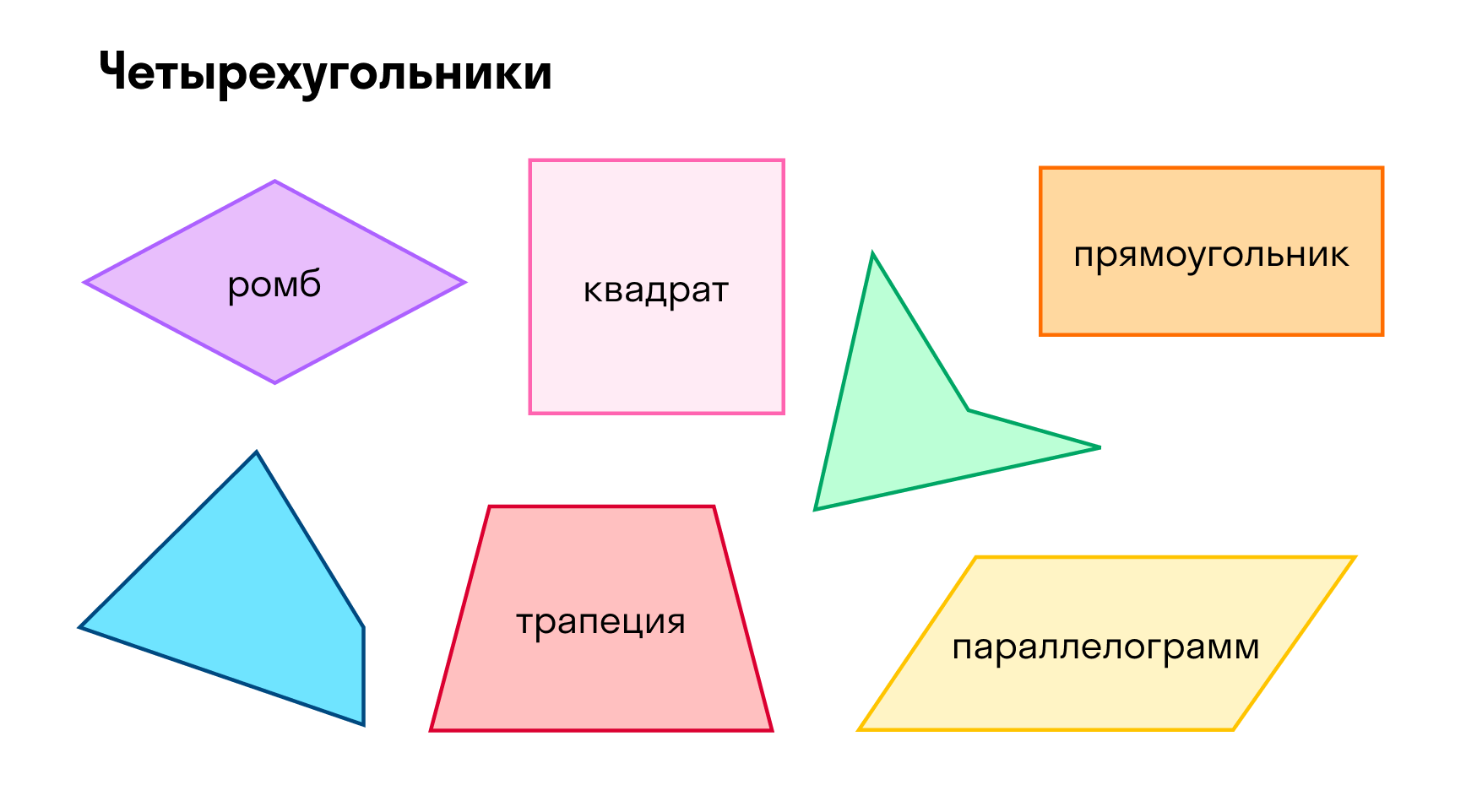
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.

Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:

Окружность

Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.

Практическая сторона геометрии

Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.

Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.

А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.

Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.

Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.

Почему изучать геометрию сложно: некоторые правила придется учить наизусть.

Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.

Как научиться решать задачи по геометрии?

Любой студент или школьник должен запомнить одну простую истину – можно решить любую задачу, какой бы трудной она не казалась на первый взгляд. Ведь задачи составляют для закрепления теоретических знаний и отработки определенных практических навыков, следовательно, для того, чтобы их решали, а не в целях третирования учащихся.

Разумеется, есть такие сверхсложные варианты задач, которые пытаются разрешить столетиями. Однако их количество не так уж и велико, да и награда за найденное решение будет больше «пятерки» за контрольную работу или экзамен. Встретить нечто подобное в школьной программе невозможно.

Следовательно, для того, что бы научиться решать задачи по геометрии необходимо иметь желание, усидчивость и тренированные мозги и воображение. Других путей освоить эту интересную область математики не существует, мы не берем в расчет решебники со 2 по 11 класс и всевозможные ГДЗ, очень сильно облегчающие жизнь студенту. Однако, получив все необходимые навыки и тщательно проштудировав теорию, можно приблизиться к пониманию того, что существует определенная методика решения задач по геометрии, способная упростить процесс решения любой задачи. Для этого необходимо всегда выполнять следующие действия:

1. Изучив условие задачи, сразу же займитесь составление чертежа. Без толковой схемы затруднительно решить даже простую задачу, а сложную – практически невозможно. При этом не жадничайте, экономить место в тетради вы будете в другом случае. Визуализация условия задачи по геометрии требует максимально возможного объема на тетрадном листе. Чем крупнее чертеж, тем нагляднее и доступнее будут решение задачи.

2. Построив чертеж или схему, нанесите на нее все известные данные – прямые и косвенные (которые можно получить путем промежуточных вычислений). Поверьте, решение задачи может «всплыть» сразу же после того, как вы сделаете эту нехитрую работу.

3. Не полагайтесь во всем на интуицию и пространственное воображение, без знания теоретической базы серьезных результатов вам не достигнуть. При этом можно не забираться в дебри формулировок, а запомнить и осмыслить несколько десятков распространенных формул и правил.

4. Помните о небольших хитростях: о задачах, которые решаются методом «первого и второго треугольника», об использовании центра окружности в соответствующих случаях (всегда соединяйте «интересные» точки вписанных и описанных фигур с центром окружности), о правилах суммы углов треугольника и прочих несложных способах вычисления промежуточных величин, которые помогут в поиске искомого значения.

5. Всегда записывайте «полет» вашей мысли. После трех-четырех связок вы можете потерять нить рассуждений и потратить значительное время на попытки вспомнить уже принятое решение. После решения задачи обязательно проверьте себя. Это поможет избежать досадных ошибок, которые могли ускользнуть от вашего внимания, увлеченного удачными поисками варианта решения задачи.

В заключение несколько слов о неудачах и патовых ситуациях, когда все потуги учащегося не приводят к положительным результатам. Для выхода из тупика используйте несколько простых действий:

Во-первых, переверните схему задачи. Посмотрите на чертеж буквально «под другим углом». Вероятно, вы что-то упустили или не заметили, и решение может прийти само собой.

Во-вторых, отложите «затруднительную» задачу в сторону, отвлекитесь на другое дело. Через десять минут мозг «перезагрузится», «накатанная» схема, которая привела вас в тупик, забудется и можно начинать искать новый путь к решению задачи.

В-третьих, примените тактическую хитрость. Вспомните, что вы проходите по программе на данный момент. На контрольной работе вам, как правило, будут задавать задачи с четкой привязкой к изученной теории. Постарайтесь заново оценить условие с точки зрения именно «последних» теоретических материалов. Например, если вы занимались изучением хорды или биссектрисы, постарайтесь «по максимуму» заполнить чертеж именно этими элементами.

Решаем задачи по геометрии

Любой студент или школьник должен запомнить одну простую истину – можно решить любую задачу, какой бы трудной она не казалась на первый взгляд. Ведь задачи составляют для закрепления теоретических знаний и отработки определенных практических навыков, следовательно, для того, чтобы их решали, а не в целях третирования учащихся.

Разумеется, есть такие сверхсложные варианты задач, которые пытаются разрешить столетиями. Однако их количество не так уж и велико, да и награда за найденное решение будет больше «пятерки» за контрольную работу или экзамен. Встретить нечто подобное в школьной программе невозможно.

Следовательно, для того, что бы научиться решать задачи по геометрии необходимо иметь желание, усидчивость и тренированные мозги и воображение. Других путей освоить эту интересную область математики не существует, мы не берем в расчет решебники со 2 по 11 класс и всевозможные ГДЗ, очень сильно облегчающие жизнь студенту. Однако, получив все необходимые навыки и тщательно проштудировав теорию, можно приблизиться к пониманию того, что существует определенная методика решения задач по геометрии, способная упростить процесс решения любой задачи. Для этого необходимо всегда выполнять следующие действия:

1. Изучив условие задачи, сразу же займитесь составление чертежа. Без толковой схемы затруднительно решить даже простую задачу, а сложную – практически невозможно. При этом не жадничайте, экономить место в тетради вы будете в другом случае. Визуализация условия задачи по геометрии требует максимально возможного объема на тетрадном листе. Чем крупнее чертеж, тем нагляднее и доступнее будут решение задачи.

2. Построив чертеж или схему, нанесите на нее все известные данные – прямые и косвенные (которые можно получить путем промежуточных вычислений). Поверьте, решение задачи может «всплыть» сразу же после того, как вы сделаете эту нехитрую работу.

3. Не полагайтесь во всем на интуицию и пространственное воображение, без знания теоретической базы серьезных результатов вам не достигнуть. При этом можно не забираться в дебри формулировок, а запомнить и осмыслить несколько десятков распространенных формул и правил.

4. Помните о небольших хитростях: о задачах, которые решаются методом «первого и второго треугольника», об использовании центра окружности в соответствующих случаях (всегда соединяйте «интересные» точки вписанных и описанных фигур с центром окружности), о правилах суммы углов треугольника и прочих несложных способах вычисления промежуточных величин, которые помогут в поиске искомого значения.

5. Всегда записывайте «полет» вашей мысли. После трех-четырех связок вы можете потерять нить рассуждений и потратить значительное время на попытки вспомнить уже принятое решение. После решения задачи обязательно проверьте себя. Это поможет избежать досадных ошибок, которые могли ускользнуть от вашего внимания, увлеченного удачными поисками варианта решения задачи.

В заключение несколько слов о неудачах и патовых ситуациях, когда все потуги учащегося не приводят к положительным результатам. Для выхода из тупика используйте несколько простых действий:

Во-первых, переверните схему задачи. Посмотрите на чертеж буквально «под другим углом». Вероятно, вы что-то упустили или не заметили, и решение может прийти само собой.

Во-вторых, отложите «затруднительную» задачу в сторону, отвлекитесь на другое дело. Через десять минут мозг «перезагрузится», «накатанная» схема, которая привела вас в тупик, забудется и можно начинать искать новый путь к решению задачи.

В-третьих, примените тактическую хитрость. Вспомните, что вы проходите по программе на данный момент. На контрольной работе вам, как правило, будут задавать задачи с четкой привязкой к изученной теории. Постарайтесь заново оценить условие с точки зрения именно «последних» теоретических материалов. Например, если вы занимались изучением хорды или биссектрисы, постарайтесь «по максимуму» заполнить чертеж именно этими элементами.

Как научиться решать задачи по геометрии?

Дорогие ребята, Вы начали изучать геометрию. Это новая для вас дисциплина, и вы поначалу можете испытывать трудности в её освоении. Не пугайтесь: пройдет некоторое время, и вы научитесь с легкостью решать любые геометрические задачи. Для приобретения необходимого навыка нужно лишь приложить немного усилий. Итак, как решать задачи по геометрии?

Вам понадобится: учебник, тетрадь, ручка, карандаш, линейка, транспортир, циркуль, ластик.

1. Внимательно прочитайте условие задачи.
2. Сделайте чертеж.
3. Отметьте на чертеже то, что вам дано: длины сторон, величины углов. Если в условии задачи сказано, что какие-то отрезки равны, поставьте на них одинаковые штрихи. Равные по величине углы отмечайте одинаковыми дужками: одинарными, двойными, волнистыми. Углы разных величин выделяйтеразными дужками.
4. Исследуйте фигуры, представленные в задаче. Вспомните их определения и свойства.
5. Определите тему, к которой относится ваша задача. Освежите в голове теоретический материал по этой теме, повторите основные теоремы.
6. Рассмотрите примеры решения задач по этой теме. В задачах, приводимых в учебнике в качестве примеров, часто рассматриваются принципиальные вопросы, которые вы должны знать.
7. Если вы чувствуете себя в теме достаточно уверенно, приступайте к решению задачи. Начните с того, что требуется найти или доказать. Подумайте, каким путем это можно сделать. То есть, решайте задачу «с конца».
8. Если вы не видите путей решения задачи, попробуйте найти хоть что-нибудь, используя имеющиеся данные. Возможно, так к вам придет идея, как решать задачу.

Полезные советы: не увлекайтесь «устными» доказательствами. Записывайте решение задачи как можно более подробно, если не оговорено иное. Некоторые вещи могут казаться вам очевидными, но всё равно прописывайте их. Так у вас будет отрабатываться навык, вы лучше запомните идею.

Рекомендации от учителя математики Е.В.Жалыбиной

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

© cyberpedia.su 2017-2020 — Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!