Урок геометрии по теме «Сумма углов многоугольника». 9-й класс
Михайло Васильевич Ломоносов, сказал: “ Неусыпный труд препятствия преодолевает”. Я надеюсь, что сегодня на уроке наш с вами труд поможет нам преодолеть все препятствия.
1. Актуализация опорных знаний. (Фронтальный опрос.)
– Сформулируйте определение многоугольника, назовите его основные элементы.
– Определение выпуклого многоугольника.
– Приведите примеры известных вам четырехугольников, которые являются выпуклыми многоугольниками.
– Можно ли треугольник считать выпуклым многоугольником?
– Что такое внешний угол выпуклого многоугольника?
2. Постановка проблемы (выход на тему урока).
Устная фронтальная работа.
Найдите сумму углов данных многоугольников (Слайды 5–6)
– треугольника; прямоугольника:
– трапеции; произвольного семиугольника.
В случае затруднения учитель задает вопросы:
– Сформулируйте определение трапеции.
– Назовите основания трапеции.
– Что можно сказать о паре углов А и Д, каким свойством они обладают?
– Можно ли еще назвать на чертеже пару внутренних односторонних улов?
– Смогли вы найти сумму углов семиугольника? Какой возникает вопрос? (Существует ли формула для нахождения суммы углов произвольного многоугольника?)
Итак, ясно, что наших знаний на сегодня не достаточно для решения этой задачи.
Каким образом можно сформулировать тему нашего урока? – Сумма углов выпуклого многоугольника.
3. Решение проблемы. Чтобы ответить на поставленный вопрос, давайте проведем небольшое исследование.
Мы уже знаем теорему о сумме углов треугольника. Можем ли мы ее каким либо образом применить?
– Что для этого надо сделать? (Разбить многоугольник на треугольники.)
– А каким образом многоугольник можно разбить на треугольники? Подумайте над этим, обсудите и предложите свои самые удачные варианты.
Идет работа в группах, каждая группа работает за отдельным компьютером, на котором установлена программа “Geo Gebra”.
По окончании работы учитель выводит на экран результаты работы групп. (Слайд 7)

– Давайте проанализируем предложенные варианты и попробуем выбрать самый оптимальный для нашего исследования.
Определимся с критериями отбора: что мы хотим получить в результате разбиения? (Сумма всех углов построенных треугольников должна быть равна сумме углов многоугольника.)
– Какие варианты можно сразу отбросить? Почему?
(Вариант 1, так как сумма углов всех треугольников не равна сумме углов многоугольника.)
– Какой вариант годиться больше всего? Почему? (Вариант 3.)
Как получили этот вариант? (Провели диагонали из одной вершины многоугольника
| чертеж | n – количество вершин многоугольника | Количество диагоналей, проведенных из одной вершины | Количество полученных треугольников |
 |
4 | ||
 |
5 | ||
 |
6 | ||
 |
7 | ||
| n |
– Попробуем установить зависимость между количеством вершин многоугольника, количеством диагоналей, которые можно провести из одной вершины и количеством получаемых при этом треугольников.
Каждая группа получает таблицу, которую должны заполнить в процессе исследования.
После обсуждения в группах дети формулируют полученные выводы:
из одной вершины n-угольника можно провести n – 3 диагонали, (так как диагональ нельзя провести к самой выбранной вершине и к двум соседним). При этом получим n – 2 треугольника.
Следовательно, сумма углов выпуклого многоугольника равна 180 0 (n-2).
– Вернемся к предложенным вариантам разбиения многоугольника на треугольники.
Можно ли использовать для доказательства этой теоремы вариант, предложенный на рисунке 4?
– Сколько треугольников получается при таком разбиении? (п штук)
– На сколько отличается сумма углов всех треугольников от суммы углов многоугольника? (На 360 0 )
– Каким образом можно сосчитать сумму углов многоугольника в этом случае?
(180п – 360 = 180 п – 180х2 = 180(п -2) )(Слайд 
– Удовлетворяет ли главному требованию, которое мы предъявляли к разбиению, вариант, предложенный на рисунке 2? (Да.)
– Почему не целесообразно его использование для нахождения суммы углов многоугольника? (Тяжелее подсчитать количество получаемых треугольников.)
Ну а теперь вернемся к задаче, которую мы не смогли решить вначале урока.
(Дети устно считают сумму углов семиугольника и еще два аналогичных упражнения.) (Слайд 9 и 10)
4. Применение полученных знаний.
Мы вывели формулу для нахождения суммы внутренних углов выпуклого многоугольника. А теперь поговорим о сумме внешних углов многоугольника, взятых по одной при каждой вершине.
Итак, задача: что больше: сумма внешних углов, взятых по одному при каждой вершине, у выпуклого шестиугольника или у треугольника? (Слайд 11)

Дети высказывают свои предположения. Учитель предлагает провести исследование для решения этого вопроса.
Каждая группа получает задание для самостоятельного решения.
1) Найдите сумму внешних углов, взятых по одному при каждой вершине, у правильного треугольника.
2) – У треугольника, градусные величины углов которого равны соответственно 70 0 , 80 0 и 30 0 .
1) Найдите сумму внешних углов, взятых по одному при каждой вершине, у прямоугольника.
2) – У четырехугольника, внутренние углы которого равны соответственно 70 0 , 80 0 и 120 0 и 90 0 .
1) Найдите сумму внешних углов, взятых по одному при каждой вершине, у правильного шестиугольника.
2) – У шестиугольника, внутренние углы которого равны соответственно 170 0 , 80 0 и 130 0 , 100 0 , 70 0 , 170 0.
После окончания работы дети сообщают свои результаты, учитель заносит их в таблицу и демонстрирует на экране. (Слайд 12)

Итак, какой вывод можно сделать из полученных результатов? (Сумма внешних углов, взятых по одному при каждой вершине, у любого многоугольника равна 360 0. )
А теперь давайте попробуем доказать этот факт для любого н-угольника.
Если возникают трудности, коллективно обсуждается план доказательства:
1. Обозначить внутренние углы многоугольника через α, β, γ и т.д.
2. Выразить через введенные обозначения градусные меры внешних углов
3. Составить выражение для нахождения суммы внешних углов многоугольника
4. Преобразовать полученное выражение, использовать полученную ранее формулу для суммы внутренних углов многоугольника.
Доказательство записывается на доске:
(180 – α) + (180 – β) + (180 – γ) + …= 180 п – (α+ β +γ + …) = 180 п – 180(п – 2) = 360
Далее демонстрируется видео: как можно проиллюстрировать этот факт с помощью картонной модели. (Слайд 13)
5. Закрепление изученного материала. Решение задач.
Задача 1. Существует ли выпуклый многоугольник с такими внутренними углами: 45 0 , 68 0 , 73 0 и 56 0 ? Объясните свой ответ.
Проведем доказательство от противного. Если у выпуклого многоугольника четыре острых внутренних угла то среди его внешних углов четырех тупых, откуда следует, что сумма всех внешних углов многоугольника больше 4*90 0 = 360 0 . Имеем противоречие. Утверждение доказано.
В выпуклом многоугольнике три угла по 80 градусов, а остальные – 150 градусов. Сколько углов в выпуклом многоугольнике?
Так как: для выпуклого n-угольника сумма углов равна 180°(n – 2), то 180(n – 2)=3*80 + x*150, где 3 угла по 80 градусов нам даны по условию задачи, а количество остальных углов нам пока неизвестно, значит, обозначим их количество через x.
Однако из записи в левой части мы определили количество углов многоугольника как n, поскольку из них величины трех углов мы знаем по условию задачи, то очевидно, что x=n-3.
Таким образом, уравнение будет выглядеть так: 180(n – 2) = 240 + 150(n – 3)
Решаем полученное уравнение
180n – 360 = 240 + 150n – 450
180n – 150n = 240 + 360 – 450
6. Подведение итогов урока.
Итак, давайте подведем итоги. Сформулируйте свои вопросы для ребят из другой группы по материалам сегодняшнего урока.
Какой вопрос вы считаете наиболее удачным?
Обсудите степень участия каждого члена группы в коллективной работе, назовите самых активных.
Чья работа в группе была самой результативной?
7. Домашнее задание:
В многоугольнике три угла по 113 градусов, а остальные равны между собой и их градусная мера – целое число. Найти количество вершин многоугольника.
Многоугольники
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.1).
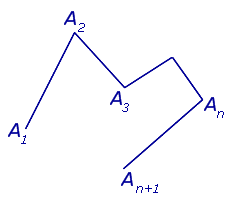
Определение 1 . Ломаной линией с n звеньями называют фигуру L , составленную из отрезков (1), то есть фигуру, заданную равенством
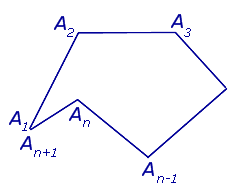
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).
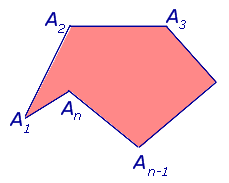
Определение 2 . Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией без самопересечений (рис. 3). Отрезки, составляющие ломаную линию ( звенья ), называют сторонами многоугольника. Концы отрезков называют вершинами многоугольника.
Определение 3 . Многоугольник называют n – угольником , если он имеет n сторон.
Таким образом, многоугольник, имеющий 3 стороны, называют треугольником , многоугольник, имеющий 4 стороны, называют четырёхугольником и т.д.
Определение 4 . Периметром многоугольника называют сумму длин всех сторон многоугольника.
Величину, равную половине периметра, называют полупериметром .
Диагонали n — угольника
Число диагоналей n – угольника равно
| Диагональ многоугольника |
Число диагоналей n – угольника равно
Внешний угол многоугольника
Определение 5 . Два угла называют смежными , если они имеют общую сторону, и их сумма равна 180° (рис.1).

Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
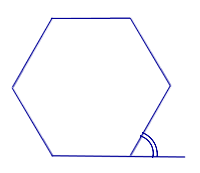
Свойства углов треугольника
Сумма углов треугольника равна 180°
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
| Углы треугольника |
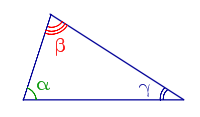 |
Сумма углов треугольника равна 180°


Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
Свойства углов многоугольника
Сумма углов многоугольника равна
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°
| Углы n – угольника |
Сумма углов многоугольника равна
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°
Свойства углов правильного n – угольника
Все углы правильного n – угольника равны
Все внешние углы правильного
n – угольника равны
| Углы правильного n – угольника |
 |
Все углы правильного n – угольника равны
Все внешние углы правильного
n – угольника равны
Доказательства свойств углов многоугольника
Теорема 1 . В любом треугольнике сумма углов равна 180° .
Доказательство . Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
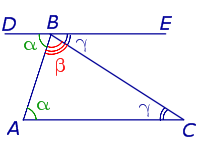
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE . Поскольку углы ABD , ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180° . Теорема доказана.
Теорема 2 . Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Доказательство . Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
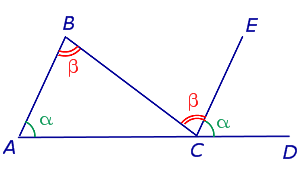
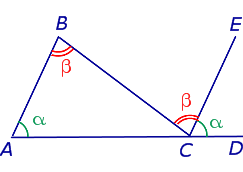
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC . Теорема доказана.
Замечание . Теорема 1 является следствием теоремы 2.
Теорема 3 . Сумма углов n – угольника равна
Доказательство . Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
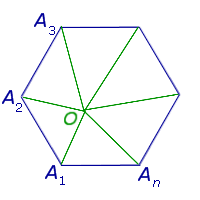
Получим n треугольников:
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O . Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
Теорема 4 . Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° .
Чему равна сумма углов выпуклого многоугольника

В 8 классе на уроках геометрии в школе ученики впервые знакомятся с понятием выпуклого многоугольника. Очень скоро они узнают, что эта фигура обладает очень интересным свойством. Какой бы сложной она ни была, сумма всех внутренних и внешних углов выпуклого многоугольника принимает строго определенное значение. В данной статье репетитор по математике и физике рассказывает о том, чему равна сумма углов выпуклого многоугольника.
Сумма внутренних углов выпуклого многоугольника
| Сумма внутренних углов выпуклого многоугольника равна , где — количество сторон многоугольника. |
Как доказать эту формулу?
Прежде чем перейти к доказательству этого утверждения, вспомним, какой многоугольник называется выпуклым. Выпуклым называется такой многоугольник, который целиком находится по одну сторону от прямой, содержащей любую его сторону. Например такой, который изображен на этом рисунке:
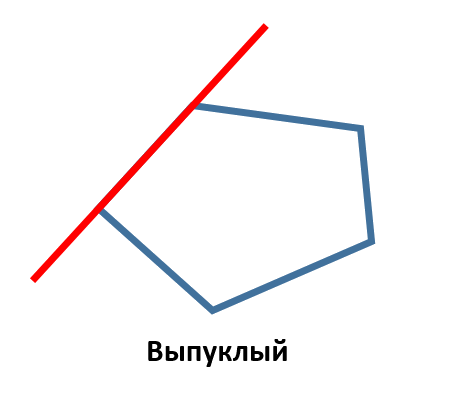
Если же многоугольник не удовлетворяет указанному условию, то он называется невыпуклым. Например, такой:
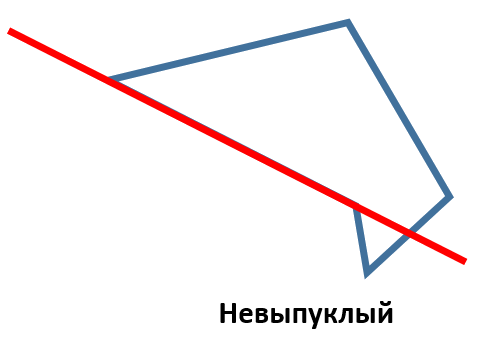
Сумма внутренних углов выпуклого многоугольника равна , где — количество сторон многоугольника.
Доказательство этого факта основано на хорошо известной всем школьникам теореме о сумме углов в треугольнике. Уверен, что и вам эта теорема знакома. Сумма внутренних углов треугольника равна .
Идея состоит в том, чтобы разбить выпуклый многоугольник на несколько треугольников. Сделать это можно разными способами. В зависимости от того, какой способ мы выберем, доказательства будут немного отличаться.
1. Разобьём выпуклый многоугольник на треугольники всеми возможными диагоналями, проведёнными из какой-нибудь вершины. Легко понять, что тогда наш n-угольник разобьётся на треугольника:
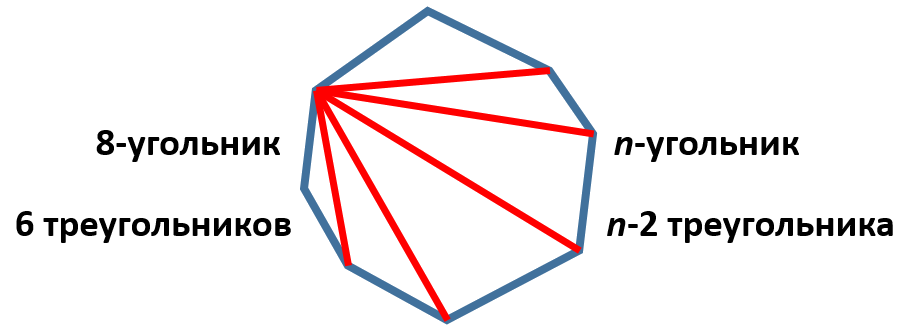
Причём сумма всех углов всех получившихся треугольников равна сумме углов нашего n-угольника. Ведь каждый угол в получившихся треугольниках является частичной какого-то угла в нашем выпуклом многоугольнике. То есть искомая сумма равна .
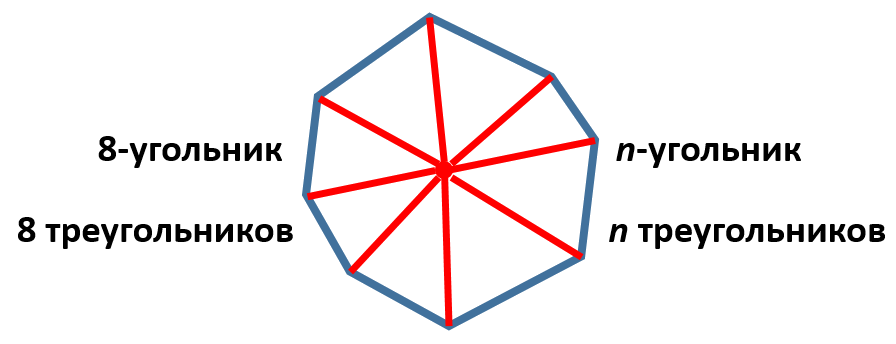
2. Можно также выбрать точку внутри выпуклого многоугольника и соединить её со всеми вершинами. Тогда наш n-угольник разобьется на треугольников:
![]()
Причём сумма углов нашего многоугольника в этом случае будет равна сумме всех углов всех этих треугольников за вычетом центрального угла, который равен . То есть искомая сумма опять же равна .
Сумма внешних углов выпуклого многоугольника
Зададимся теперь вопросом: «Чему равна сумма внешних углов выпуклого многоугольника?» Ответить на этот вопрос можно следующим образом. Каждый внешний угол является смежным с соответствующим внутренним. Поэтому он равен :
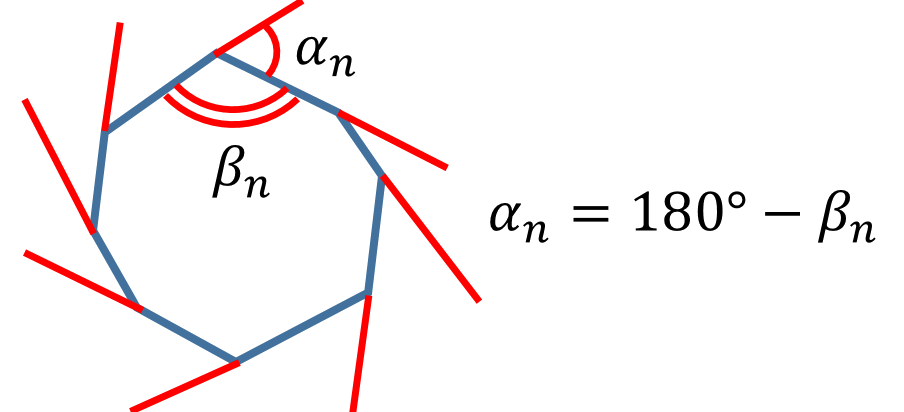
Тогда сумма всех внешних углов равна . То есть она равна .
То есть получается весьма забавный результат. Если отложить последовательно друг за другом все внешние углы любого выпуклого n-угольника, то в результате заполнится ровно вся плоскости.
Этот интересный факт можно проиллюстрировать следующим образом. Давайте пропорциональном уменьшать все стороны какого-нибудь выпуклого многоугольника до тех пор, пока он не сольётся в точку. После того, как это произойдёт, все внешние углы окажутся отложенными один от другого и заполнят таким образом всю плоскость.
Интересный факт, не правда ли? И таких фактов в геометрии очень много. Так что учите геометрию, дорогие школьники!
Материал о том, чему равна сумма углов выпуклого многоугольника, подготовил репетитор по геометрии, Сергей Валерьевич
Многоугольники
Никогда не было интересно, почему в треугольнике 180 градусов?
А в других фигурах сколько? Да постой, положи транспортир!
Сейчас ты узнаешь много нового о такой, казалось бы, простой теме, как многоугольники.
Многоугольники — коротко о главном
Многоугольник – это замкнутая линия, которая образовывается, если взять ( displaystyle n) каких-либо точек ( displaystyle >,text< >>,text< >…,~>) и соединить их последовательно отрезками.
- Точки ( displaystyle >,~>,text< >…,~>) — вершины многоугольника.
- Отрезки ( displaystyle >>,~ >>,text< >…,text< >>>) – стороны многоугольника.
![]()
Многоугольник с ( displaystyle n) сторонами называют ( displaystyle n)-угольником.
Например: многоугольник c ( displaystyle 4) сторонами называют четырехугольником, многоугольник с ( displaystyle 6) сторонами — шестиугольником и так далее по аналогии.
![]()
![]()
Выпуклый многоугольник – многоугольник лежащий по одну сторону от любой прямой, соединяющей его соседние вершины.
![]()
Сумма внутренних углов выпуклого n-угольника равна ( displaystyle 180<>^circ cdot (n-2)) или ( displaystyle _>+_>+text< >…~+_>), где ( displaystyle _>) – внутренний угол многоугольника.
Правильный выпуклый многоугольник – многоугольник все стороны и внутренние углы которого равны.
Внутренний угол правильного ( displaystyle n)-угольника равен ( displaystyle alpha =fraccdot 180<>^circ ).
Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.
![]()
Центры вписанной в правильный многоугольник окружности и окружности, описанной около него, совпадают.
Если многоугольник такой, что в него можно вписать окружность, то его площадь выражается формулой: ( displaystyle S=pr), где ( displaystyle p=frac>>+>>+…+>>>).
Многоугольник — подробнее
Многоугольник – это замкнутая линия, которая образовывается, если взять ( displaystyle n) каких-либо точек ( displaystyle >,text< >>,text< >…,~>) и соединить их последовательно отрезками.
- Точки ( displaystyle >,~>,text< >…,~>) — вершины многоугольника.
- Отрезки ( displaystyle >>,~ >>,text< >…,text< >>>) – стороны многоугольника.
![]()
При этом смежные стороны (имеющие общую вершину) не должны лежать на одной прямой, а несмежные стороны не должны иметь общих точек (то есть не должны пересекаться).
Многоугольник с ( displaystyle n) сторонами называют ( displaystyle n)-угольником.
Произвольные многоугольники
Давай-ка нарисуем, какие бывают многоугольники.
![]()
А теперь вопрос: какой из этих многоугольников выпадает из ряда?
Посмотри внимательно на второй многоугольник — он отличается от всех остальных. Чем же?
Это не выпуклый многоугольник. Это, конечно, математическое название, но с человеческой интуицией не расходится.
Ну вот, а мы будем рассматривать только выпуклые многоугольники, то есть такие, как 1),3),4) и т.п.
Итак, основной факт:
В любом многоугольнике сумма внутренних углов равна ( displaystyle 180^o(n-2)), где буква «( displaystyle n)» означает число углов многоугольника.
![]()
Давай сразу к примерам:
Четырехугольник
![]()
Пятиугольник
![]()
Шестиугольник
![]()
Ах да, про треугольник забыли.
Треугольник
![]()
Сумма углов многоугольника. Доказательство.
А теперь давай все-таки разберемся, откуда же взялась формула суммы углом многоугольника ( displaystyle 180^circ(n-2)).
Понимаешь, приемчик, который мы сейчас применим, часто оказывается полезным при решении разных задач.
Несмотря на то, что теорема о сумме углов многоугольника верна для всякого многоугольника, доказательство красивое и простое только для выпуклых многоугольников.
Итак, давай разделим многоугольник на треугольники.
Вот так: из одной точки проведем все диагонали, что можно. Сколько их будет? Считаем:
Всего вершин: ( displaystyle n)
Из вершины ( displaystyle B) можем провести диагонали во все вершины, кроме:
- Самой вершины B
- Вершины A
- Вершины C
![]()
Значит всего диагоналей ( displaystyle (n-3)). А на сколько треугольников распался наш многоугольник?
Представь себе: на ( displaystyle n-2). Порисуй, посчитай – удостоверься, что треугольников оказывается ровно на один больше.
Итак, у нас ровно ( displaystyle n-2) треугольника. И сумма углов многоугольника просто равна сумме углов треугольников, на которые мы разбили многоугольник.
Чему равна сумма углов треугольника? Помнишь? Конечно ( displaystyle 180<>^circ ).
Ну вот, ( displaystyle n-2) треугольника, в каждом по ( displaystyle 180<>^circ ), значит:
Сумма углов многоугольника равна ( displaystyle 180<>^circ )( displaystyle (n-2))
Что же из этого может оказаться полезным? Два момента:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Правильные многоугольники
Многоугольник называется правильным, если все его углы и все его стороны равны.
Так, например: квадрат – правильный четырехугольник, а вот прямоугольник – нет, хоть и все углы у него равные, и ромб – нет, хоть и все стороны равны. Нужно непременно, чтобы все углы и все стороны были равны.
Первый вопрос:
А можно ли найти величину одного (а значит и всех) угла правильного многоугольника?
Давай посмотрим на примере.
Пусть есть, скажем, правильный восьмиугольник:
Сумма всех его углов равна ( displaystyle 180<>^circ left( 8-2 right)=1080<>^circ ).
А сколько всего углов? Восемь конечно, и они все одинаковые.
![]()
Значит любой угол, скажем ( displaystyle angle A) можно найти:
( displaystyle angle A=frac^circ >=135<>^circ ).
Что мы еще должны знать?
Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.
При этом центры этих окружностей совпадают.
Смотри, как это выглядит!
![]()
И более того, всегда можно посчитать соотношение между радиусом вписанной и описанной окружностей.
Давай опять на примере восьмиугольника.
Посмотри на ( displaystyle Delta OKG). В нем ( displaystyle OK=r,OG=R.)
Значит, ( displaystyle frac=sin angle x) – и это не только в восьмиугольнике!
Чему же равен в нашем случае ( displaystyle angle x)?
Ровно половине ( displaystyle angle G), представь себе!
Значит ( displaystyle angle x=frac^circ >=67,5<>^circ ).
Смешно? Но так и есть! Поэтому для восьмиугольника ( displaystyle frac=sin 67,5<>^circ ).
Может возникнуть еще один вопрос: а можно ли посчитать углы «около» точки ( displaystyle O)?
И тот же ответ: конечно можно!
Опять рассмотрим наш восьмиугольник. Вот мы хотим найти ( displaystyle angle alpha) (то есть ( displaystyle angle HOG)).
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
И так можно все находить не только для восьмиугольника, но и для любого правильного многоугольника.
Бонус. Вебинар из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 6. Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.
Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
![]()
Алексей Шевчук — ведущий курсов
Добавить комментарий Отменить ответ
3 комментария
![]()
Даша :
Як разбить чатырох угольник так, чтоб палучился трохвугольник и чатырохвугольник
![]()
Алексей Шевчук :
Даша, например, можно провести отрезок из вершины в середину противоположной стороны.
![]()
Александр Кель :
Некоторые комментарии прошлых лет к этой статье:
Сергей
19 февраля 2018
Просто огромное спасибо. Хоть что-то начал понимать.
Александр (админ)
19 февраля 2018
Просто огромное пожалуйста. Очень приятно слышать от вас такие слова.
Вероника
18 марта 2020
Спасибо большое, а то на карантине приходится самим разбирать темы!
Александр (админ)
18 марта 2020
Отлично, Вероника! Круто, что ты сама пытаешься разобраться с математикой! Этот навык ой как пригодится в будущем. Я всегда говорю: «В жизни репетитора и учителя рядом не будет». И я рад, что наш скромный сайт в этом помогает. Удачи на экзаменах! Все будет хорошо!
Сима
01 июля 2020
Блин, действительно очень круто изложили. А главное- понятно и просто. Начала подготовку к егэ, в следующем году сдавать. Очень помогли разобраться с этой темой! Спасибо)
Александр (админ)
01 июля 2020
Блин, Сима, до чертиков приятно слышать такие слова! Если начала подготовку к ЕГЭ, то будь на связи, мы сейчас делаем крутейший курс подготовки к ЕГЭ, где вот так вот просто все будет объяснять Алексей Шевчук.
Чему равна сумма углов?
Просто мне нужно объяснить. Но не просто объяснить, а чтобы ещё стало понятно!
Е. Гришковец «Одновременно»
Разговор покупателя с продавцом в магазине «Ткани».
— Здравствуйте! Я шью дома и сама делаю выкройки. Для этого использую угольник с различными углами. Мне нужны чаще всего 90, 60 и 45 градусов, но они у меня в разных угольниках. Приходится перекладывать. Нет ли у вас угольника, в котором были бы именно эти углы?
— Вы знаете, среди тех, что я вижу, нет, но вы заходите, такие должны на днях привезти.
— Большое спасибо, обязательно зайду.

Для математического уха разговор выглядит комично. То, что сумма углов треугольника равна 180°, знают даже школьники, не очень увлечённые математикой. А что такое 180° и почему именно 180? Ясно, скажет умный школьник, это половина от 360, то есть полного оборота.
Невозможно точно сказать, почему окружность была разбита на 360 одинаковых частей и когда это произошло. То ли это персы придумали, у которых год длился 360 дней, то ли вавилоняне, которым удобно было делить окружность на 6 равных частей с помощью равностороннего треугольника.
Была, правда, попытка ввести более логичную, с точки зрения современных представлений о счёте, шкалу для угловых мер. Она делила окружность на 400 равных частей — градов. В этой шкале величина прямого угла равнялась 100 градам. Однако шкала эта не прижилась. Трудно одним желанием изменить пятитысячелетнюю историю цивилизации. Да впрочем, какая разница, в чём мерить, хоть в попугаях, главное — понять, что угол — это некоторая доля от полного оборота.
Почему же сумма углов любого треугольника равна в точности половине полного оборота? Давайте представим себе, что у нас есть три прожектора. Каждый освещает внутренность некоторого угла до бесконечности (жить мы будем временно в двумерном мире). Если мы, стоя в одной точке, включим три прожектора (зелёный, розовый и жёлтый на рисунке), сумма «световых углов» которых равна 180°, и направим их без наложений освещаемой площади, то осветим ровно половину нашего двумерного пространства.

Теперь рассмотрим произвольный треугольник и в вершинах его поставим трёх помощников (Али, Бен и Сирил по буквам вершин, но можно попросить Анну, Варвару и Светлану), доверив им по прожектору. Каждый помощник должен осветить внутренность треугольника лучами света, которые выходят из вершины и продолжаются до бесконечности. Таким образом, каждый прожектор будет освещать внутренность своего угла и не будет освещать внутренность такого же угла, вертикального выбранному. При этом каждая точка плоскости либо попадёт внутрь освещённого угла, либо не будет освещена, попав в вертикальный угол к углу треугольника. Точки же самого треугольника будут освещены трижды. Теперь давайте посмотрим на нашу частично освещённую плоскость с большой высоты (мы-то, как люди трёхмерные, имеем на это право). Если закрыть глаза на небольшой участок перекрытия внутри треугольника, то нетрудно понять, что мы осветили «ровно» половину плоскости. Из чего и можно заключить, что сумма углов произвольного треугольника равна 180°!


Если наше маленькое жульничество внутри треугольника режет глаз, давайте отойдём далеко-далеко от плоскости и забудем, что где-то стоят наши помощники. Нарисуем окружность огромного радиуса с центром где-то внутри треугольника. Какая часть окружности освещена? Ровно (почти) половина. И чем больше радиус нашей окружности, тем меньше будут отличаться освещённая и тёмная части окружности. Ведь каждой светлой дуге будет в пару поставлена такая же тёмная.
Не будем останавливаться на сумме углов треугольника, а попробуем развить эту идею. Самое естественное продолжение — четырёхугольник. Нетрудно понять, что четыре помощника, выполняя аналогичное задание, осветят всю плоскость, что значит: сумма углов четырёхугольника равна 360°. Стоп! Давайте не торопиться, отойдём подальше. Что мы видим? Ужас! Некоторые точки плоскости вообще не освещены. Всё пропало? Не будем паниковать преждевременно. Продолжим наши прямые до бесконечности. На рисунке серым цветом закрашена неосвещённая часть плоскости. Посмотрим внимательно на вертикальный с ней угол. Он освещён, конечно, но освещён дважды! А значит, и здесь всё сходится. Так и должно быть, ведь четырёхугольник можно просто разрезать на два треугольника. Думаем дальше.

Нарисуем пятиконечную звёздочку (не обязательно правильную). Теперь позовём пять фонарщиков, поставим их в вершинах «лучиков» нашей звёздочки, и пусть каждый освещает внутренность того угла, в котором стоит. Соответственно, вертикальный угол освещён не будет. Что мы видим? Картина почти такая же, как у треугольника. Половина плоскости светлая, половина тёмная, а значит, сумма углов пятиконечной звезды равна 180°!
При этом мы нигде не пользовались какими-то особенностями формы этой звёздочки. Более того, а где мы считали количество углов? Давайте внимательно посмотрим на 7-конечную звезду. А потом на 2021-конечную (нарисовать непросто, а представить можно). Что изменится для суммы? Да ничего — половина светлого, половина тёмного. Правда, для большого числа углов нужно «правильно» рисовать звёздочку. Например, для семиугольной конструкции можно привести два примера. Подсчитайте самостоятельно сумму для «более тупоугольной» звёздочки.

Теперь давайте немного развернём наших фонарщиков и дадим им задание осветить один из своих внешних углов. Для начала позовём четверых, поставим их в вершинах выпуклого четырёхугольника. Нетрудно понять, что они осветят всё, кроме самого четырёхугольника. Удаляясь от них, мы поймём, что сумма внешних углов выпуклого четырёхугольника равна 360°.

Также при достаточном удалении мы забудем о количестве помощников, а когда вспомним, поймём, что это совершенно неважно. Сколько бы их ни было, плоскость будет освещена полностью и без перекрытий. Из этого следует чрезвычайно важный и удивительный вывод: сумма внешних углов выпуклого многоугольника равна 360°!
Продолжая применять этот метод, можно получить и другие формулы для суммы углов. То есть если внимательно посмотреть на количество перекрытий, можно вывести формулу для суммы углов выпуклого многоугольника. Но даже без вывода становится понятно, почему сумма внутренних углов зависит от их количества, а сумма внешних нет. Попробуйте развить эту идею на случай невыпуклых многоугольников. Можно, немного поломав голову, найти сумму внутренних углов, а вот для суммы внешних надо сначала понять: что такое внешний угол невыпуклого многоугольника? Успехов в вашем исследовании!

P. S. А угольник 45°, 60° и 90°, оказывается, существует! Это специальный портновский угольник — треугольник, в котором сделаны треугольные дырки с другими углами. И речь в магазине «Ткани», оказывается, совсем не шла о сумме углов треугольника.
Сумма углов многоугольника
В основном курсе геометрии доказывается, что сумма углов выпуклого n-угольника равна 180° (n-2). Оказывается, что это утверждение справедливо и для невыпуклых многоугольников.
Теорема 3. Сумма углов произвольного n-угольника равна 180° (n — 2).
Доказательство. Разобьем многоугольник на треугольники, проведением диагоналей (рис. 11). Число таких треугольников равно n-2, и в каждом треугольнике сумма углов равна 180°. Поскольку углы треугольников составляют углы многоугольника, то сумма углов многоугольника равна 180° (n — 2).

Рассмотрим теперь произвольные замкнутые ломаные, возможно с самопересечениями A1A2…AnA1 (рис. 12, а). Такие самопересекающиеся ломаные будем называть звездчатыми многоугольниками (рис. 12, б-г).
Зафиксируем направление подсчета углов против часовой стрелки. Заметим, что углы, образованные замкнутой ломаной, зависят от направления ее обхода. Если направление обхода ломаной меняется на противоположное, то углами многоугольника будут углы, дополняющие углы исходного многоугольника до 360°.
Если M — многоугольник, образован простой замкнутой ломаной, проходимой в направлении по часовой стрелке (рис. 13, а), то сумма углов этого многоугольника будет равна 180° (n — 2). Если же ломаная проходится в направлении против часовой стрелки (рис. 13, б), то сумма углов будет равна 180° (n + 2).

Таким образом, общая формула суммы углов многоугольника, образованного простой замкнутой ломаной, имеет вид = 180° (n 2), где — сумма углов, n — число углов многоугольника, «+» или «-» берется в зависимости от направления обхода ломаной.
Наша задача состоит в том, чтобы вывести формулу суммы углов произвольного многоугольника, образованного замкнутой (возможно самопересекающейся) ломаной. Для этого введем понятие степени многоугольника.
Степенью многоугольника называется число оборотов, совершаемой точкой при полном последовательном обходе его сторон. Причем обороты, совершаемые в направлении против часовой стрелки, считаются со знаком «+», а обороты по часовой стрелке — со знаком «-».
Ясно, что у многоугольника, образованного простой замкнутой ломаной, степень равна +1 или -1 в зависимости от направления обхода. Степень ломаной на рисунке 12, а равна двум. Степень звездчатых семиугольников (рис. 12, в, г) равна соответственно двум и трем.
Аналогичным образом понятие степени определяется и для замкнутых кривых на плоскости. Например, степень кривой, изображенной на рисунке 14 равна двум.

Для нахождения степени многоугольника или кривой можно поступать следующим образом. Предположим, что, двигаясь по кривой (рис. 15, а), мы, начиная с какого-то места A1, совершили полный оборот, и попали в ту же точку A1. Удалим из кривой соответствующий участок и продолжим движение по оставшейся кривой (рис. 15,б). Если, начиная с какого-то места A2, мы снова совершили полный оборот и попали в ту же точку, то удаляем соответствующий участок кривой и продолжаем движение (рис. 15, в). Считая количество удаленных участков со знаками «+» или «-», в зависимости от их направления обхода, получим искомую степень кривой.
Теорема 4. Для произвольного многоугольника имеет место формула
где — сумма углов, n — число углов, m — степень многоугольника.
Доказательство. Пусть многоугольник M имеет степень m и условно изображен на рисунке 16. M1, …, Mk — простые замкнутые ломаные, проходя по которым, точка совершает полные обороты. A1, …, Ak — соответствующие точки самопересечения ломаной, не являющиеся ее вершинами. Обозначим число вершин многоугольника M, входящих в многоугольники M1, …, Mk через n1, …, nk соответственно. Поскольку, помимо вершин многоугольника M, к этим многоугольникам добавляются еще вершины A1, …, Ak, то число вершин многоугольников M1, …, Mk будет равно соответственно n1+1, …, nk+1. Тогда суммы их углов будут равны 180° (n1+12), …, 180° (nk+12). Плюс или минус берется в зависимости от направления обхода ломаных. Сумма углов многоугольника M0, оставшегося от многоугольника M после удаления многоугольников M1, …, Mk, равна 180° (n-n1- …-nk+k2). Суммы углов многоугольников M0, M1, …, Mk дают сумму углов многоугольника M и в каждой вершине A1, …, Ak дополнительно получим 360°. Следовательно, имеем равенство
180° (n1+12)+…+180° (nk+12)+180° (n-n1- …-nk+k2)=+360°k.
= 180° (n2…2) = 180° (n+2m),
где m — степень многоугольника M.

В качестве примера рассмотрим вычисление суммы углов пятиконечной звездочки (рис. 17, а). Степень соответствующей замкнутой ломаной равна -2. Поэтому искомая сумма углов равна 180.
Ломаная
Ломаной линией, или короче, ломаной, называется конечная последовательность отрезков, такая, что один из концов первого отрезка служит концом второго, другой конец второго отрезка служит концом третьего и т.д. При этом соседние отрезки не лежат на одной прямой. Эти отрезки называют звеньями ломаной.

Виды ломаной
Ломаная может пересекать сама себя, коснуться сама себя, налегать на себя. Если таких особенностей нет, то такая ломаная называется простой.




Многоугольники
Определение
Простая замкнутая ломаная вместе с частью плоскости, ограниченной ею, называется многоугольником.

Замечание
В каждой вершине многоугольника его стороны задают некоторый угол многоугольника. Он может быть как меньше развернутого, так и больше развернутого.

Свойство
У каждого многоугольника есть угол, меньший $180^circ$.
Доказательство

Пусть дан многоугольник $P$.
Проведем какую-нибудь прямую, не пересекающую его. Будем перемещать ее параллельно в сторону многоугольника. В некоторый момент мы впервые получим прямую $a$, имеющую с многоугольником $P$ хотя бы одну общую точку. От этой прямой многоугольник лежит по одну сторону (при этом некоторые его точки лежат на прямой $a$).
На прямой $a$ лежит хотя бы одна вершина многоугольника. В ней сходится две его стороны, расположенные по одну сторону от прямой $a$ (считая и тот случай, когда одна из них лежит на этой прямой). А значит, при этой вершине угол меньше развернутого.
Определение
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону. Если многоугольник не является выпуклым, его называют невыпуклым.


Замечание
Выпуклый многоугольник является пересечением полуплоскостей, ограниченных прямыми, которые содержат стороны многоугольника.

Свойства выпуклого многоугольника
Отрезок, соединяющий любые две точки выпуклого многоугольника (в частности, любая его диагональ), содержится в этом многоугольнике.
Доказательство
Докажем первое свойство

Возьмем любой угол $A$ выпуклого многоугольника $P$ и его сторону $a$, идущую из вершины $A$. Пусть $l$ – прямая, содержащая сторону $a$. Так как многоугольник $P$ выпуклый, то он лежит по одну сторону от прямой $l$. Следовательно, и его угол $A$ лежит по одну сторону от этой прямой. Значит угол $A$ меньше развернутого угла, то есть меньше $180^circ$.
Докажем второе свойство

Возьмем любые две точки $A$ и $B$ выпуклого многоугольника $P$. Многоугольник $P$ является пересечением нескольких полуплоскостей. Отрезок $AB$ содержится в каждой из этих полуплоскостей. Поэтому он содержится и в многоугольнике $P$.
Определение
Диагональю многоугольника называется отрезок, соединяющий его несоседние вершины.

Теорема (о количестве диагоналей n-угольника)
Количество диагоналей выпуклого $n$-угольника вычисляется по формуле $dfrac$.
Доказательство

Из каждой вершины n-угольника можно провести $n-3$ диагонали (нельзя провести диагональ в соседние вершины и в саму эту вершину). Если посчитать все такие возможные отрезки, то их будет $ncdot(n-3)$, так как вершин $n$. Но каждая диагональ будет посчитана дважды. Таким образом, количество диагоналей n-угольника равно $dfrac$.
Теорема (о сумме углов n-угольника)
Сумма углов выпуклого $n$-угольника равна $180^circ(n-2)$.

Доказательство
Рассмотрим $n$-угольник $A_1A_2A_3ldots A_n$.
Возьмём внутри этого многоугольника произвольную точку $O$.
Сумма углов всех треугольников $A_1OA_2$, $A_2OA_3$, $A_3OA_4$, $ldots$, $A_OA_n$ равна $180^circcdot n$.
C другой стороны эта сумма складывается из суммы всех внутренних углов многоугольника и полного угла $angle O=angle 1+angle 2+angle 3+ldots=360^circ$.
Тогда сумма углов рассматриваемого $n$-угольника равна $180^circcdot n-360^circ=180^circcdot(n-2)$.
Теорема
Сумма углов невыпуклого $n$-угольника равна $180^circ(n-2)$.

Теорема (о сумме внешних углов выпуклого n-угольника)
Сумма внешних углов выпуклого $n$-угольника равна $360^circ$.

Доказательство
Внешний угол при вершине $A_1$ равен $180^circ-angle A_1$.
Сумма всех внешних углов равна:
$sumlimits_(180^circ-angle A_n)=ncdot180^circ — sumlimits_A_n=ncdot180^circ — 180^circcdot(n-2)=360^circ$.






