Что такое многоугольник в математике — виды, свойства и примеры фигур с названиями
— геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной. Если граничная ломаная не имеет точек самопересечения, многоугольник называется
простым
[1]. Например, треугольники и квадраты — простые многоугольники, а пятиконечная звезда — нет.
Вершины ломаной называются вершинами
многоугольника, а её звенья —
сторонами
многоугольника. Число сторон многоугольника совпадает с числом его вершин[2].
Правильный тринадцатиугольник — многоугольник с 13 углами и 13 вершинами.
Варианты определений[ | ]
Существуют три различных варианта определения многоугольника; последнее определение является наиболее распространённым[1].
- Плоская замкнутая ломаная — наиболее общий случай;
- Плоская замкнутая ломаная без самопересечений, любые два соседних звена которой не лежат на одной прямой;
- Часть плоскости, ограниченная замкнутой ломаной без самопересечений — плоский многоугольник
; в этом случае сама ломаная называется
контуром
многоугольника.
Существуют также несколько вариантов обобщения данного определения, допускающие бесконечное число звеньев ломаных, несколько несвязных граничных ломаных, ломаные в пространстве, произвольные отрезки непрерывных кривых вместо отрезков прямых и др.[1]
Свойства углов правильного n – угольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы правильного n – угольника | Все углы правильного n – угольника равны | |
| Внешние углы правильного n – угольника | Все внешние углы правильного n – угольника равны |
| Углы правильного n – угольника |
| Все углы правильного n – угольника равны |
| Внешние углы правильного n – угольника |
| Все внешние углы правильного n – угольника равны |
Связанные определения[ | ]
Основной источник: [2]
- Вершины многоугольника называются соседними
, если они являются концами одной из его сторон. - Стороны многоугольника называются смежными
, если они прилегают к одной вершине. - Общая длина всех сторон многоугольника называется его периметром
. - Диагоналями
называются отрезки, соединяющие несоседние вершины многоугольника. - Углом
(или
внутренним углом
) плоского многоугольника при данной вершине называется угол между двумя сторонами, сходящимися в этой вершине. Угол может превосходить 180 ∘ > в том случае, если многоугольник невыпуклый. Число углов простого многоугольника совпадает с числом его сторон или вершин. - Внешним углом
выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В случае невыпуклого многоугольника
внешний угол
— разность между 180 ∘ > и внутренним углом, он может принимать значения от − 180 ∘ > до 180 ∘ > . - Перпендикуляр, опущенный из центра вписанной окружности правильного многоугольника на одну из сторон, называется апофемой.
Свойства углов многоугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы n – угольника | Сумма углов многоугольника равна Посмотреть доказательство |
|
| Внешние углы n – угольника | Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° |
Виды многоугольников и их свойства[ | ]
Основной источник: [2]
- Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и так далее. Многоугольник с n вершинами называется n -угольником
.
Многоугольник, вписанный в окружность Многоугольник, описанный около окружности
- Выпуклый многоугольник
— это многоугольник, который лежит по одну сторону от любой прямой, содержащей его сторону (то есть продолжения сторон многоугольника не пересекают других его сторон). Существуют и другие эквивалентные определения выпуклого многоугольника. Выпуклый многоугольник всегда простой, то есть не имеет точек самопересечения. - Выпуклый многоугольник называется правильным
, если у него равны все стороны и все углы, например равносторонний треугольник, квадрат и правильный пятиугольник. Символ Шлефли правильного n -угольника равен < n >> . - Многоугольник, у которого равны все стороны и все углы, но который имеет самопересечения, называется правильным звёздчатым многоугольником
, например, пентаграмма и октаграмма. - Многоугольник называется вписанным
в окружность, если все его вершины лежат на одной окружности. Сама окружность при этом называется описанной, а её центр лежит на пересечении серединных перпендикуляров к сторонам многоугольника. Любой треугольник является вписанным в некоторую окружность. - Многоугольник называется описанным
около окружности, если все его стороны касаются некоторой окружности. Сама окружность при этом называется вписанной, а её центр лежит на пересечении биссектрис углов многоугольника.. Любой треугольник является описанным около некоторой окружности. - Выпуклый четырёхугольник называется внеописанным
около окружности, если продолжения всех его сторон (но не сами стороны) касаются некоторой окружности.[3] Окружность при этом называется вневписанной. Вневписанная окружность существует также и у произвольного треугольника.
Простейшие четырёхугольники
Любой многоугольник, который состоит из четырёх углов, называют четырёхугольным. Он относится к простейшим геометрическим телам. Если о нём ничего не известно, его считают произвольным, то есть фигурой, у которой нет особенных углов или сторон. В другом случае четырёхугольники имеют собственные названия.
Наиболее часто приходится сталкиваться со следующими видами:
- прямоугольник — четырёхугольник, у которого все углы прямые, то есть равняются 900;
- ромб — фигура с четырьмя сторонами одинаковой длины;
- квадрат — многоугольник, удовлетворяющий одновременно условиям ромба и прямоугольника.

Для всех этих видов характерно, что каждая из фигур имеет 2 пересекающиеся диагонали. Причём точка их соприкосновения делит отрезок на 2 равные части. Кроме этого, для прямоугольника и квадрата длина одной диагонали равна другой. Если у четырёхугольного прямоугольника обозначить стороны a и b, противоположные им грани также будут a и b.
Каждый отрезок, образующий многоугольник, имеет свою длину. При их сложении получается периметр фигуры. Для его обозначения используют заглавную латинскую букву P. Например, если есть многоугольник, образованный сторонами AB, BC, CA, его периметр будет равняться: Pabc = AB + BC + CA. Можно обратить внимание, что количество углов соответствует числу сторон, складываемых для нахождения P. Это важный параметр, позволяющий оценить размер фигуры.
Из-за особенностей прямоугольника формулу для расчёта периметра можно переписать так: P = 2*(a + b). В то же время площадь такой фигуры находится путём простого перемножения примыкающих сторон: S = a*b. Параметры квадрата можно вычислить, зная длину только одной стороны. Всё дело в том, что длины отрезков, из которых он состоит, равны друг другу, поэтому для квадрата периметр находится как P = 4*a, а площадь: S = a*a = a2.
Прямая четырёхугольная фигура является частным случаем ромба. А значит, что все формулы, указанные для квадрата, справедливы и при применении к нему. Следует отметить, что площадь ромба может быть найдена и как половина произведения его диагоналей.
Общие свойства[ | ]
Теорема о сумме углов многоугольника[ | ]
Сумма внутренних углов простого плоского n -угольника равна[4] 180 ∘ ( n − 2 ) (n-2)> . Сумма внешних углов не зависит от числа сторон и всегда равна 360 ∘ . .>
Число диагоналей[ | ]
- Число диагоналей всякого n -угольника равно n ( n − 3 ) 2 >> .
Площадь[ | ]
Пусть < ( X i , Y i ) >, i = 1 , 2 , . . . , n ,Y_)>,i=1,2,…,n> — последовательность координат соседних друг другу вершин n -угольника без самопересечений . Тогда его площадь вычисляется по формуле Гаусса:
S = 1 2 | ∑ i = 1 n ( X i + X i + 1 ) ( Y i − Y i + 1 ) | >left|sum limits _^(X_+X_)(Y_-Y_)right|> , где ( X n + 1 , Y n + 1 ) = ( X 1 , Y 1 ) ,Y_)=(X_,Y_)> .
Если даны длины сторон многоугольника и азимутальные углы сторон, то площадь многоугольника может быть найдена по формуле Саррона [5].
Площадь правильного n -угольника вычисляется по одной из формул[6]:
где a — длина стороны многоугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
Квадрируемость фигур[ | ]
С помощью множества многоугольников определяется квадрируемость и площадь произвольной фигуры на плоскости. Фигура F называется квадрируемой
Свойства углов треугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы треугольника | Сумма углов треугольника равна 180° α + β + γ = 180° |
Примечания[ | ]
- ↑ 123
Многоугольник // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 749—752. - ↑ 123
Элементарная математика, 1976, с. 383—384. - Картаслов.ру
- Элементарная математика, 1976, с. 499.
- Хренов Л. С.
Вычисление площадей многоугольников по способу Саррона // Математическое просвещение. 1936. Выпуск 6. С. 12—15 - Элементарная математика, 1976, с. 503—504.
Теорема об углах
Многоугольники бывают выпуклые и вогнутые. Чтобы узнать, какой из них приходится рассматривать в том или ином случае, можно сделать следующее. Через каждую сторону провести прямую. Если по отношению к любой из них фигура будет лежать в одной полуплоскости относительно неё, многоугольник считается выпуклым, в ином случае — вогнутым.
Для первого типа существуют важные соотношения. Пусть имеется произвольный многоугольник. Интерес представляет сумма всех его углов. Посчитать её можно следующим образом. Нужно взять любую вершину и соединить её со всеми оставшимися прямой линией. В результате получится несколько треугольников. Затем нужно посчитать их количество. Например, в шестиугольнике их будет 4, восьмиугольнике — 6. Это число легко находится, так как существует правило, согласно которому в любой n-угольной фигуре можно построить n-2 треугольника.
В каждом треугольнике сумма углов равняется 180 градусов. Отсюда следует, что искомая сумма будет равняться 1800 * (n — 2). Например, для восьмиугольного она равняется 180 * (8 — 2) = 10800. Для многоугольника можно вести понятие внешнего угла.
К любой вершине можно построить 2 таких смежных угла. Если взять каждый из них, то их сумма будет равняться: a1 + a2 +…+ an = 3600. Доказать это можно так. Угол a1 равняется (180 — ∠A1), a2 = (180 — ∠A2) и так далее. Таких слагаемых будет n штук. Тогда можно записать, 180 * n — 180 * (n — 2) = 180 * 2 = 360. Таким образом, сумма всех внешних углов равняется 3600.
Лучше всего понять сказанное можно, рассмотрев пример, рассчитанный на учащихся средней школы. Пусть есть правильный шестиугольник. Нужно определить его угол. У такой фигуры все стороны, а значит и углы равны. Для начала следует определить их сумму. Она будет равняться 180 * (4−2) = 1800 * 4 = 7200. Но так как это шестиугольник, результат необходимо поделить на 6. Таким образом, искомый угол правильной фигуры будет равняться 120 градусам.
Как вычислить сумму внутренних углов
Соавтор(ы): David Jia. Дэвид Джиа — репетитор и основатель частной репетиторской компании LA Math Tutoring в Лос-Анджелесе, Калифорния. Имеет более 10 лет преподавательского опыта, работает с учащимися всех возрастов и классов над разными предметами, а также занимается конультированием по поступлению в колледж и подготовкой к SAT, ACT, ISEE и другим тестам. Набрав максимальные 800 баллов за SAT по математике и 690 — по английскому языку, получил стипендию Дикинсона в Университете Майами, который окончил со степенью бакалавра делового администрирования. Кроме того, был инструктором в обучающих онлайн-видео компаний, выпускающих учебники, таких как Larson Texts, Big Ideas Learning и Big Ideas Math.
Количество просмотров этой статьи: 35 319.
Многоугольник – это любая замкнутая фигура с тремя и более сторонами, которые представляют собой прямые отрезки. Каждая вершина многоугольника содержит как внутренний, так и внешний угол (изнутри и снаружи фигуры, соответственно). Для решения разных геометрических задач полезно знать, как соотносятся эти углы. В частности, необходимо уметь вычислять сумму внутренних углов многоугольника. Это можно сделать по формуле или через разбиение многоугольника на треугольники.

- Цифра «180» – это сумма углов треугольника, а n − 2 – это число треугольников, на которые можно разбить многоугольник. Таким образом, формула вычисляет сумму углов треугольников, на которые можно разбить многоугольник. [2] X Источник информации
- Этот метод применим к правильным и неправильным многоугольникам. Суммы внутренних углов правильного и неправильного многоугольников с одинаковым число сторон равны. Все углы правильного многоугольника равны. [3] X Источник информации Углы неправильного многоугольника имеют разные значения, но их сумма равна сумме углов правильного многоугольника.

- Например, если дан шестиугольник, то число сторон равно 6.

-
В нашем примере n = 6 , так как у шестиугольника 6 сторон. Таким образом, формула запишется так:
S = ( 6 − 2 ) × 180

- В нашем примере:
S = ( 6 − 2 ) × 180
S = ( 4 ) × 180
S = ( 4 ) × 180 = 720
Таким образом, сумма внутренних углов шестиугольника равна 720 градусов.

- Например, нужно вычислить сумму внутренних углов шестиугольника. Нарисуйте шестиугольник.

- Вершина – это точка, в которой сходятся две стороны многоугольника.

- Выбранную вершину не нужно соединять со смежными ей вершинами, так как они соединены сторонами многоугольника.
- Например, в случае шестиугольника выбранную вершину нужно соединить с тремя другими вершинами, чтобы получить 4 треугольника.

- В нашем примере шестигранник разбивается на 4 треугольника. Таким образом, 4 × 180 = 720 , то есть сумма внутренних углов шестиугольника равна 720 градусов.
- Проверьте ответ при помощи транспортира, измерив каждый угол вручную. Для этого аккуратно нарисуйте прямые стороны многоугольника.
- Как доказать теорему о сумме углов треугольника
Дополнительные статьи














- ↑http://www.mathsisfun.com/geometry/interior-angles-polygons.html
- ↑http://www.bbc.co.uk/schools/gcsebitesize/maths/geometry/polygonsrev4.shtml
- ↑http://www.bbc.co.uk/schools/gcsebitesize/maths/geometry/polygonsrev3.shtml
Об этой статье
Соавтор(ы): David Jia. Дэвид Джиа — репетитор и основатель частной репетиторской компании LA Math Tutoring в Лос-Анджелесе, Калифорния. Имеет более 10 лет преподавательского опыта, работает с учащимися всех возрастов и классов над разными предметами, а также занимается конультированием по поступлению в колледж и подготовкой к SAT, ACT, ISEE и другим тестам. Набрав максимальные 800 баллов за SAT по математике и 690 — по английскому языку, получил стипендию Дикинсона в Университете Майами, который окончил со степенью бакалавра делового администрирования. Кроме того, был инструктором в обучающих онлайн-видео компаний, выпускающих учебники, таких как Larson Texts, Big Ideas Learning и Big Ideas Math. Количество просмотров этой статьи: 35 319.
8 класс. Геометрия. Многоугольники.
В курсе геометрии мы изучаем свойства геометрических фигур и уже рассмотрели простейшие из них: треугольники и окружности. При этом мы обсуждали и конкретные частные случаи этих фигур, такие как прямоугольные, равнобедренные и правильные треугольники. Теперь пришло время поговорить о более общих и сложных фигурах – многоугольниках.
С частным случаем многоугольников мы уже знакомы – это треугольник (см. Рис. 1).

Рис. 1. Треугольник
В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник (см. Рис. 2), т.е. фигуру с пятью углами.

Рис. 2. Пятиугольник. Выпуклый многоугольник
Определение.Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.
Определение.Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят кмногоугольнику.
Иными словами, например, когда говорят о пятиугольнике , имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т.е. точка тоже относится к пятиугольнику (см. Рис. 2).
Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).
Определение. Периметр многоугольника – сумма длин сторон многоугольника.
Теперь надо познакомиться с видами многоугольников. Они делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на Рис. 2, является выпуклым, а на Рис. 3 невыпуклым.

Рис. 3. Невыпуклый многоугольник
2. Выпуклые и невыпуклые многоугольники
Определение 1. Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми являются все остальные многоугольники.

Легко представить, что при продлении любой стороны пятиугольника на Рис. 2 он весь окажется по одну сторону от этой прямой, т.е. он выпуклый. А вот при проведении прямой через в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
Но существует и другое определение выпуклости многоугольника.
Определение 2. Многоугольник называется выпуклым, если при выборе любых двух его внутренних точек и при соединении их отрезком все точки отрезка являются также внутренними точками многоугольника.

Демонстрацию использования этого определения можно увидеть на примере построения отрезков на Рис. 2 и 3.
Определение. Диагональю многоугольника называется любой отрезок, соединяющий две не соседние его вершины.
3. Теорема о сумме внутренних углов выпуклого n-угольника
Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольника и теорема о сумме внешних углов выпуклого многоугольника. Рассмотрим их.
Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).
, где – количество его углов (сторон).
Доказательство 1. Изобразим на Рис. 4 выпуклый n-угольник.

Рис. 4. Выпуклый n-угольник
Из вершины проведем все возможные диагонали. Они делят n-угольник на треугольника, т.к. каждая из сторон многоугольника образует треугольник, кроме сторон, прилежащих к вершине . Легко видеть по рисунку, что сумма углов всех этих треугольников как раз будет равна сумме внутренних углов n-угольника. Поскольку сумма углов любого треугольника – , то сумма внутренних углов n-угольника:

, что и требовалось доказать.
Доказательство 2. Возможно и другое доказательство этой теоремы. Изобразим аналогичный n-угольник на Рис. 5 и соединим любую его внутреннюю точку со всеми вершинами.


Мы получили разбиение n-угольника на n треугольников (сколько сторон, столько и треугольников). Сумма всех их углов равна сумме внутренних углов многоугольника и сумме углов при внутренней точке, а это угол . Имеем:

, что и требовалось доказать.
По доказанной теореме видно, что сумма углов n-угольника зависит от количества его сторон (от n). Например, в треугольнике , а сумма углов . В четырехугольнике , а сумма углов – и т.д.
4. Теорема о сумме внешних углов выпуклого n-угольника
Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).
, где – количество его углов (сторон), а , …, – внешние углы.
Доказательство. Изобразим выпуклый n-угольник на Рис. 6 и обозначим его внутренние и внешние углы.

Рис. 6. Выпуклый n-угольник с обозначенными внешними углами

Т.к. внешний угол связан со внутренним как смежные, то и аналогично для остальных внешних углов. Тогда:

.

В ходе преобразований мы воспользовались уже доказанной теоремой о сумме внутренних углов n-угольника .

Из доказанной теоремы следует интересный факт, что сумма внешних углов выпуклого n-угольника равна от количества его углов (сторон). Кстати, в отличие от суммы внутренних углов.
Далее мы более подробно будем работать с частным случаем многоугольников – четырехугольниками. На следующем уроке мы познакомимся с такой фигурой, как параллелограмм, и обсудим его свойства.
Многоугольники
Многоугольник — это геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной. Если граничная ломаная не имеет точек самопересечения, многоугольник называется простым.
Содержание:
Общее понятие многоугольника
На рисунке 2.111 изображена замкнутая ломаная L с произвольным числом звеньев; эта ломаная разбивает множество не принадлежащих ей точек плоскости на две части. Их называют внутренней и внешней областями относительно этой ломаной. На рисунке 2.111 внутренняя область закрашена.
Две любые точки, лежащие в одной и той же области, можно соединить отрезком или ломаной, не пересекающей данную замкнутую ломаную (рис. 2.112). Для точек разных областей этого сделать нельзя.

Во внешней области найдется прямая, которая вся расположена в этой области. Во внутренней области такой прямой нет.
Определение. Объединение замкнутой ломаной и ее внутренней области называют многоугольником.
Саму ломаную называют границей многоугольника, а ее внутреннюю область — внутренней областью многоугольника. Звенья границы многоугольника называют сторонами многоугольника, а вершины — вершинами многоугольника.
Треугольник — это самый простой многоугольник, имеющий наименьшее число вершин и сторон — три. Далее идут четырехугольники. Они бывают различными (рис. 2.113).
Многоугольники с большим числом сторон (пятиугольники, шестиугольники и т.д.) уже не имеют столько разновидностей, как четырехугольники. Есть только различия в длинах их сторон и величине углов.
Отрезок, соединяющий две несоседние вершины многоугольника, называют его диагональю.


На рисунке 2.114 изображены диагонали АС и AD пятиугольника ABCDE.
В геометрии различают выпуклые и невыпуклые многоугольники.
Определение. Многоугольник называют выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону.
На рисунке 2.115 изображен невыпуклый многоугольник, а на рисунке 2.116 — выпуклый многоугольник, исходя из данного определения.
Углы многоугольника
Пусть дан многоугольник. Рассмотрим его вершину А и два луча АВ и AD, выходящие из вершины А и содержащие стороны АВ и AD данного многоугольника (рис. 2.117). Два луча с общим началом, как известно, задают два угла.
Тот из углов, которому принадлежит сам многоугольник ABCD, называют его внутренним углом (рис. 2.118).
Для краткости внутренним углом многоугольника иногда называют и величину этого угла. Ясно, что у каждого -угольника есть внутренних углов (иногда слово «внутренний» опускают).
Можно доказать две теоремы о свойствах внутренних углов выпуклых многоугольников.

Теорема 24. У выпуклого многоугольника каждый угол меньше 180°.
Теорема 25. Сумма внутренних углов выпуклого -угольника равна ( — 2)180°.
Параллелограмм
Определение. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны, т. е. лежат на параллельных прямых.
На рисунке 2.119 четырехугольник ABCD — параллелограмм, у него АВ || DC и ВС || AD.
Используя определение параллелограмма и другие знания, можно доказать свойства параллелограмма:
— сумма внутренних углов параллелограмма равна 4d;
— каждая диагональ параллелограмма делит его на два равных треугольника.
Можно доказать теорему о центре симметрии параллелограмма — еще одно свойство параллелограмма.
Теорема 26. Середина диагонали параллелограмма является его центром симметрии.
Из теоремы 26 можно получить следующие следствия.
Следствие 1. Противоположные стороны параллелограмма попарно равны.
Следствие 2. Противоположные углы параллелограмма попарно равны.
Признаки параллелограмма отвечают на вопрос: что надо знать о четырехугольнике, чтобы утверждать, что он является параллелограммом?
Теорема 27. Четырехугольник является параллелограммом, если он имеет две пары равных противоположных сторон.
Теорема 28. Четырехугольник является параллелограммом, если его диагонали, пересекаясь, делятся пополам.
Теорема 29. Четырехугольник является параллелограммом, если две его противоположные стороны равны и параллельны.
Используя свойства параллелограммов, можно доказать очень важную теорему геометрии — теорему Фалеса.
Теорема 30 (теорема Фалеса). Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Используя теорему Фалеса, можно легко разделить любой отрезок на любое число равных отрезков.
Пример 1.
Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найдите стороны параллелограмма.
Решение:
Из условия задачи имеем:
1. ABCD — параллелограмм.
2. Периметр параллелограмма равен 122 см.
3. ВС больше CD на 25 см.
4. Найдите стороны параллелограмма.
При решении этой задачи может помочь так называемый алгебраический метод. Его суть в следующем.
5. Обозначим одну сторону параллелограмма х, другую — у.

6. Получим систему: (1, 2, 3, 5).
7. Решая эту систему, получим х = 43, у = 18.
8. Стороны параллелограмма равны 18 и 43 см (5, 7).

Пример 2.
Разделите отрезок OA на пять равных отрезков.
Решение:
Из условия задачи имеем:
1. Отрезок OA (дан) (рис. 2.120).

2. Проведем через точку О луч и отложим на нем последовательно пять равных отрезков (рис. 2.121):


3. Проведем прямую и через точки — четыре прямые, параллельные этой прямой (рис. 2.122).
4. Эти прямые разделяют отрезок OA на пять равных отрезков (1, 2, 3, теорема 30).

Прямоугольник и квадрат
Определение. Прямоугольник — это параллелограмм, у которого все углы прямые.
Определение. Квадрат — это прямоугольник, у которого все стороны равны.
Прямоугольник обладает следующими свойствами:
— серединные перпендикуляры к сторонам прямоугольника являются его осями симметрии (рис. 2.123);
— у прямоугольника есть две оси симметрии (рис. 2.124);
— диагонали прямоугольника равны.

Справедлива следующая теорема:
Теорема 31. Около прямоугольника всегда можно описать окружность.
Так как квадрат является прямоугольником (по определению), то у него есть две оси симметрии — серединные перпендикуляры к его сторонам; можно также доказать, что диагонали квадрата также являются его осями симметрии (рис. 2.125).

Пример 1.
Сторона прямоугольника равна 4 см и образует с диагональю угол 60°. Найдите эту диагональ.
Решение:
Из условия задачи имеем:
1. ABCD — прямоугольник.
2. ВС = 4 см. (рис. 2.126)

3.
5. — прямоугольный, в нем катет ВС = 4 см, a По свойству катета, лежащего в прямоугольном треугольнике против угла 30°, (1, 2, 3).

Определение. Параллелограмм, все стороны которого равны, называют ромбом.
На рисунке 2.127 изображен параллелограмм ABCD, у которого АВ = ВС = CD = DA. По определению этот параллелограмм является ромбом.
Так как ромб — параллелограмм, то он обладает всеми свойствами параллелограмма. Кроме того, у ромба есть и другие свойства.
Теорема 32. Прямая, содержащая диагональ ромба, является его осью симметрии (рис. 2.128).

Используя теорему 32, можно доказать следующие следствия — свойства ромба.
Следствие 1. Диагонали ромба делят его углы пополам.
Следствие 2. Диагонали ромба взаимно перпендикулярны.
Квадрат является ромбом, поэтому он обладает свойствами как прямоугольника, так и ромба.
Пример:
Найдите углы ромба, если основание перпендикуляра, опущенного из вершины тупого угла, делит сторону ромба пополам.
Решение:
Из условия задачи имеем:

2. AKCD. (рис. 2.129)
4. Найдите углы ромба.

5. АВ = ВС = DC = DA (1, определение ромба).
Нужно использовать данные п. 2 и 3. Это подсказывает дополнительное построение:
6. Проведем диагональ ромба BD (рис. 2.130).


7. — равнобедренный с основанием BD (5, 6, определение равнобедренного треугольника).

8. — равнобедренный с основанием AD (2, 3, признак равнобедренного треугольника).

9. — равносторонний (7,8).

10. (9).
11. (1,10).
Трапеция
Определение. Четырехугольник, две стороны которого параллельны, а две другие не параллельны, называется трапецией.
На рисунке 2.131 изображена трапеция ABCD. Параллельные стороны трапеции называют ее основаниями, а непараллельные — боковыми сторонами (на рис. 2.131 ВС и AD — основания, АВ и CD — боковые стороны).
Определение. Если боковые стороны трапеции равны, то трапеция называется равнобедренной.
На рисунке 2.132 АВ = CD, значит, трапеция равнобедренная.

Определение. Трапецию, один из углов которой прямой, называют прямоугольной.
На рисунке 2.133 угол К прямой, значит, трапеция KLMN прямоугольная.
Определение. Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.

На рисунке 2.134 точки М и N — середины боковых сторон трапеции. Значит, MN — средняя линия ABCD.
Средняя линия трапеции обладает некоторыми свойствами: средняя линия трапеции параллельна основаниям, а длина ее равна полусумме длин оснований.
Пример:
Докажите, что середины сторон равнобедренной трапеции являются вершинами ромба.
Решение:
Из условия задачи имеем:
1. ABCD — равнобедренная трапеция, АВ = DC.
2. М, N, Р, К — середины сторон трапеции ABCD.
3. MNPK — четырехугольник.
4. MNPK — ромб (требуется доказать).
Чтобы доказать, что MNPK — ромб, нужно доказать, что MN || КР, МК || NP и что MN = NP =
= РК = КМ. Как это сделать? Помогает п. 2 и понятие средней линии треугольника.

5. Проведем диагонали АС и BD трапеции (построение) (рис. 2.136).

7. MN || AC, (5, теорема 7).

8. КР || AC, (5,теорема 7).
9. MN || КР и MN = КР (7, 8). Аналогично получаем, что МК || NP и МК = NP. Учитывая п. 6, задача решена.
Правильные многоугольники
Определение. Многоугольник, у которого все стороны равны и все углы равны, называют правильным.
На рисунке 2.137 изображены правильные треугольник, четырехугольник, пятиугольник, шестиугольник, восьмиугольник и десятиугольник.

По теореме 25 о сумме внутренних углов многоугольников можно вычислить величину каждого угла правильных многоугольников: для правильного треугольника — 60°, для правильного четырехугольника (квадрата) — 90°, для правильного пятиугольника — 108°, для правильного шестиугольника — 120°.
Пользуясь этим методом, можно узнать величину каждого угла любого правильного -угольника при любом . Кроме того, можно решить и обратную задачу: зная сумму углов правильного многоугольника, можно найти число его сторон.
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
В случае копирования материалов, указание web-ссылки на сайт natalibrilenova.ru обязательно.
Чему равна сумма углов. Чему равна сумма углов выпуклого многоугольника
Треугольник представляет собой многоугольник, имеющий три стороны (три угла). Чаще всего стороны обозначают маленькими буквами, соответствующими заглавным буквам, которыми обозначают противоположные вершины. В данной статье мы ознакомимся с видами этих геометрических фигур, теоремой, которая определяет, чему равняется сумма углов треугольника.
Виды по величине углов
Различают следующие виды многоугольника с тремя вершинами:
- остроугольный, у которого все углы острые;
- прямоугольный, имеющий один прямой угол, при его образующие, называют катетами, а сторона, которая размещена противоположно прямому углу, именуется гипотенузой;
- тупоугольный, когда один ;
- равнобедренный, у которого две стороны равные, и называются они боковыми, а третья — основанием треугольника;
- равносторонний, имеющий все три равные стороны.

Свойства
Выделяют основные свойства, которые характерны для каждого вида треугольника:
- напротив большей стороны всегда располагается больший угол, и наоборот;
- напротив равных по величине сторон находятся равные углы, и наоборот;
- у любого треугольника есть два острых угла;
- внешний угол больше по сравнению с любым внутренним углом, не смежным с ним;
- сумма каких-либо двух углов всегда меньше 180 градусов;
- внешний угол равняется сумме остальных двух углов, которые не межуют с ним.
Теорема о сумме углов треугольника
Теорема утверждает, что если сложить все углы данной геометрической фигуры, которая расположена на евклидовой плоскости, то их сумма будет составлять 180 градусов. Попробуем доказать данную теорему.
Пускай у нас есть произвольный треугольник с вершинами КМН.

Через вершину М проведем КН (еще эту прямую называют прямой Евклида). На ней отметим точку А таким образом, чтоб точки К и А были расположены с разных сторон прямой МН. Мы получаем равные углы АМН и КНМ, которые, как и внутренние, лежат накрест и образовываются секущей МН совместно с прямыми КН и МА, которые являются параллельными. Из этого следует, что сумма углов треугольника, расположенных при вершинах М и Н, равняется размеру угла КМА. Все три угла составляют сумму, которая равна сумме углов КМА и МКН. Поскольку данные углы являются внутренними односторонними относительно параллельных прямых КН и МА при секущей КМ, их сумма составляет 180 градусов. Теорема доказана.
Следствие
Из выше доказанной теоремы вытекает следующее следствие: любой треугольник имеет два острых угла. Чтобы это доказать, допустим, что данная геометрическая фигура имеет всего один острый угол. Также можно предположить, что ни один из углов не является острым. В этом случае должно быть как минимум два угла, величина которых равна или больше 90 градусов. Но тогда сумма углов будет больше, чем 180 градусов. А такого быть не может, поскольку согласно теореме сумма углов треугольника равна 180° — не больше и не меньше. Вот это и нужно было доказать.
Свойство внешних углов
Чему равна сумма углов треугольника, которые являются внешними? Ответ на этот вопрос можно получить, применив один из двух способов. Первый заключается в том, что необходимо найти сумму углов, которые взяты по одному при каждой вершине, то есть трех углов. Второй подразумевает, что нужно найти сумму всех шести углов при вершинах. Для начала разберемся с первым вариантом. Итак, треугольник содержит шесть внешних углов — при каждой вершине по два.

Каждая пара имеет равные между собой углы, поскольку они являются вертикальными:
Кроме этого, известно, что внешний угол у треугольника равняется сумме двух внутренних, которые не межуются с ним. Следовательно,
∟1 = ∟А + ∟С, ∟2 = ∟А + ∟В, ∟3 = ∟В + ∟С.
Из этого получается, что сумма внешних углов, которые взяты по одному возле каждой вершины, будет равна:
∟1 + ∟2 + ∟3 = ∟А + ∟С + ∟А + ∟В + ∟В + ∟С = 2 х (∟А + ∟В + ∟С).
С учетом того, что сумма углов равняется 180 градусам, можно утверждать, что ∟А + ∟В + ∟С = 180°. А это значит, что ∟1 + ∟2 + ∟3 = 2 х 180° = 360°. Если же применяется второй вариант, то сумма шести углов будет, соответственно, большей в два раза. То есть сумма внешних углов треугольника будет составлять:
∟1 + ∟2 + ∟3 + ∟4 + ∟5 + ∟6 = 2 х (∟1 + ∟2 + ∟2) = 720°.
Прямоугольный треугольник
Чему равняется сумма углов прямоугольного треугольника, являющихся острыми? Ответ на этот вопрос, опять же, вытекает из теоремы, которая утверждает, что углы в треугольнике в сумме составляют 180 градусов. А звучит наше утверждение (свойство) так: в прямоугольном треугольнике острые углы в сумме дают 90 градусов. Докажем его правдивость.

Пускай нам дан треугольник КМН, у которого ∟Н = 90°. Необходимо доказать, что ∟К + ∟М = 90°.
Итак, согласно теореме о сумме углов ∟К + ∟М + ∟Н = 180°. В нашем условии сказано, что ∟Н = 90°. Вот и получается, ∟К + ∟М + 90° = 180°. То есть ∟К + ∟М = 180° — 90° = 90°. Именно это нам и следовало доказать.
В дополнение к вышеописанным свойствам прямоугольного треугольника, можно добавить и такие:
- углы, которые лежат против катетов, являются острыми;
- гипотенуза треугольна больше любого из катетов;
- сумма катетов больше гипотенузы;
- катет треугольника, который лежит напротив угла 30 градусов, в два раза меньше гипотенузы, то есть равняется ее половине.
Как еще одно свойство данной геометрической фигуры можно выделить теорему Пифагора. Она утверждает, что в треугольнике с углом 90 градусов (прямоугольном) сумма квадратов катетов равняется квадрату гипотенузы.
Сумма углов равнобедренного треугольника
Ранее мы говорили, что равнобедренным называют многоугольник с тремя вершинами, содержащий две равные стороны. Известно такое свойство данной геометрической фигуры: углы при его основании равны. Докажем это.
Возьмем треугольник КМН, который является равнобедренным, КН — его основание.

От нас требуется доказать, что ∟К = ∟Н. Итак, допустим, что МА — это биссектриса нашего треугольника КМН. Треугольник МКА с учетом первого признака равенства равен треугольнику МНА. А именно по условию дано, что КМ = НМ, МА является общей стороной, ∟1 = ∟2, поскольку МА — это биссектриса. Используя факт равенства этих двух треугольников, можно утверждать, что ∟К = ∟Н. Значит, теорема доказана.
Но нас интересует, какова сумма углов треугольника (равнобедренного). Поскольку в этом отношении у него нет своих особенностей, будем отталкиваться от теоремы, рассмотренной ранее. То есть мы можем утверждать, что ∟К + ∟М + ∟Н = 180°, или 2 х ∟К + ∟М = 180° (поскольку ∟К = ∟Н). Данное свойство доказывать не будем, поскольку сама теорема о сумме углов треугольника была доказана ранее.
Кроме рассмотренных свойств об углах треугольника, имеют место и такие немаловажные утверждения:
- в которая была опущена на основание, является одновременно медианой, биссектрисой угла, который находится между равными сторонами, а также его основания;
- медианы (биссектрисы, высоты), которые проведены к боковым сторонам такой геометрической фигуры, равны.
Равносторонний треугольник
Его еще называют правильным, это тот треугольник, у которого равны все стороны. А поэтому равны также и углы. Каждый из них составляет 60 градусов. Докажем это свойство.
Допустим, что у нас есть треугольник КМН. Нам известно, что КМ = НМ = КН. А это значит, что согласно свойству углов, расположенных при основании в равнобедренном треугольнике, ∟К = ∟М = ∟Н. Поскольку согласно теореме сумма углов треугольника ∟К + ∟М + ∟Н = 180°, то 3 х ∟К = 180° или ∟К = 60°, ∟М = 60°, ∟Н = 60°. Таким образом, утверждение доказано.

Как видно из выше приведенного доказательства на основании теоремы, сумма углов как и сумма углов любого другого треугольника, составляет 180 градусов. Снова доказывать эту теорему нет необходимости.
Существуют еще такие свойства, характерные для равностороннего треугольника:
- медиана, биссектриса, высота в такой геометрической фигуре совпадают, а их длина вычисляется как (а х √3) : 2;
- если описать вокруг данного многоугольника окружность, то ее радиус будет равен (а х √3) : 3;
- если вписать в равносторонний треугольник окружность, то ее радиус будет составлять (а х √3) : 6;
- площадь этой геометрической фигуры вычисляется по формуле: (а2 х √3) : 4.
Тупоугольный треугольник
Согласно определению один из его углов находится в промежутке от 90 до 180 градусов. Но учитывая то, что два остальных угла данной геометрической фигуры острые, можно сделать вывод, что они не превышают 90 градусов. Следовательно, теорема о сумме углов треугольника работает при расчете суммы углов в тупоугольном треугольнике. Получается, мы смело можем утверждать, опираясь на вышеупомянутую теорему, что сумма углов тупоугольного треугольника равна 180 градусам. Опять-таки, данная теорема не нуждается в повторном доказательстве.
Доказательство
Пусть ABC» — произвольный треугольник. Проведем через вершину B прямую, параллельную прямой AC (такая прямая называется прямой Евклида). Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC .Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD . Поэтому сумма углов треугольника при вершинах B и С равна углу ABD .Сумма всех трех углов треугольника равна сумме углов ABD и BAC . Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB , то их сумма равна 180°. Теорема доказана.
Следствия
Из теоремы следует, что у любого треугольника два угла острые. Действительно, применяя доказательство от противного , допустим, что у треугольника только один острый угол или вообще нет острых углов. Тогда у этого треугольника есть, по крайней мере, два угла, каждый из которых не меньше 90°. Сумма этих углов не меньше 180°. А это невозможно, так как сумма всех углов треугольника равна 180°. Что и требовалось доказать.
Обобщение в симплекс теории
Где -угол между i и j гранями симплекса.
Примечания
- На сфере сумма углов треугольника всегда превышает 180°, разница называется сферическим избытком и пропорциональна площади треугольника.
- В плоскости Лобачевского сумма углов треугольника всегда меньше 180°. Разность также пропорциональна площади треугольника.
См. также
Wikimedia Foundation . 2010 .
Смотреть что такое «Теорема о сумме углов треугольника» в других словарях:
Свойство многоугольников в евклидовой геометрии: Сумма углов n угольника равна 180°(n 2). Содержание 1 Доказательство 2 Замечание … Википедия
Теорема Пифагора одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 … Википедия
Теорема Пифагора одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 Формулировки 2 Доказательства … Википедия
Теорема косинусов обобщение теоремы Пифагора. Квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними. Для плоского треугольника со сторонами a,b,c и углом α… … Википедия
У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия
Стандартные обозначения Треугольник простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника … Википедия
Древнегреческий математик. Работал в Александрии в III в. до н. э. Главный труд «Начала» (15 книг), содержащий основы античной математики элементарной геометрии, теории чисел, общей теории отношений и метода определения площадей и объёмов,… … Энциклопедический словарь
— (умер между 275 и 270 до н. э.) древнегреческий математик. Сведения о времени и месте его рождения до нас не дошли, однако известно, что Евклид жил в Александрии и расцвет его деятельности приходится на время царствования в Египте Птолемея I… … Большой Энциклопедический словарь
Геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов… … Энциклопедия Кольера
Сумма внутренних углов треугольника равна 180 0 . Это одна из основополагающих аксиом геометрии Эвклида. Именно эту геометрию изучают школьники. Геометрию определяют наукой, изучающей пространственные формы реального мира.
Что побудило древних греков разработать геометрию? Потребность измерять поля, луга — участки земной поверхности. При этом древние греки приняли, что поверхность Земли горизонтальная, плоская. С учетом этого допущения и создавались аксиомы Эвклида, в том числе и о сумме внутренних углов треугольника в 180 0 .
Под аксиомой понимается положение, не требующее доказательства. Как это нужно понимать? Высказывается пожелание, устраивающее человека, и далее оно подтверждается иллюстрациями. Но все, что не доказано — вымысел, то, чего нет в реальности.
Принимая земную поверхность горизонтальной, древние греки автоматически приняли форму Земли плоской, но она другая — сферическая. Горизонтальных плоскостей и прямых линий в природе вообще нет, потому что гравитация искривляет пространство. Прямые линии и горизонтальные плоскости имеются только в мозгу головы человека.
Поэтому, геометрия Эвклида, объясняющая пространственные формы вымышленного мира, является симулякром — копией, не имеющей оригинала.
Одна из аксиом Эвклида гласит, что сумма внутренних углов треугольника равна 180 0 . На самом деле в реальном искривленном пространстве, или на сферической поверхности Земли, сумма внутренних углов треугольника всегда больше 180 0 .
Рассуждаем так. Любой меридиан на глобусе пересекается с экватором под углом 90 0 . Чтобы получить треугольник, нужно от меридиана отодвинуть другой меридиан. Сумма углов треугольника между меридианами и стороной экватора составит 180 0 . Но еще останется угол у полюса. В итоге сумма всех углов и составит больше 180 0 .
Если на полюсе стороны пересекутся под углом 90 0 , то сумма внутренних углов такого треугольника будет 270 0 . Два меридиана, пересекающиеся с экватором под прямым углом в этом треугольнике, будет параллельными друг другу, а на полюсе, пересекающиеся друг с другом под углом 90 0 , станут перпендикулярами. Получается, две параллельные линии на одной плоскости не только пересекаются, но могу на полюсе быть перпендикулярами.
Конечно, стороны такого треугольника будут не прямыми линиями, а выпуклыми, повторяющими сферическую форму земного шара. Но, именно такой реальный мир пространства.
Геометрию реального пространства с учетом его кривизны в середине XIX в. разработал немецкий математик Б. Риман (1820-1866). Но об этом школьникам не говорят.
Итак, эвклидова геометрия, принимающая форму Земли плоской с горизонтальной поверхностью, чего на самом деле нет, представляет собой симулякр. Ноотик — геометрия Римана, учитывающая кривизну пространства. Сумма внутренних углов треугольника в ней больше 180 0 .
Как найти внешний угол многоугольника
Внутренний угол многоугольника – это угол, образованный двумя смежными сторонами многоугольника. Например, ∠ABC является внутренним углом.

Внешний угол многоугольника – это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например, ∠LBC является внешним углом.

Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.
Сумма внутренних углов
Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.
где s – это сумма углов, 2d – два прямых угла (то есть 2 · 90 = 180°), а n – количество сторон.
Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:
Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).
где s – это сумма внешних углов, 4d – четыре прямых угла (то есть 4 · 90 = 360°).
Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:

Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n — 2):
Что такое внешний угол многоугольника? Сколько внешних углов у многоугольника? Чему равна сумма внешних углов многоугольника?
Внешним углом многоугольника называется угол, смежный с его внутренним.углом.

Например, угол 1 — внешний угол при вершине A1 многоугольника
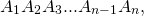
так как он смежный с его внутренним углом A2A1An.

Угол 2 также является смежным углу A2A1An.
А значит, ∠2 — внешний угол при вершине A1.

Таким образом, при каждой вершине многоугольника есть два равных между собой внешних угла.
У n-угольника n вершин, значит, всего внешних углов у n-угольника 2n.
Поскольку оба внешних угла при одной вершине равны, говоря о сумме внешних углов n-угольника, рассматривают внешние углы, взятые по одному при каждой вершине.
(о сумме внешних углов выпуклого многоугольника)
Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360º.

Дано :
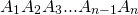
∠1, ∠2, ∠3, …, ∠n — внешние углы при вершинах
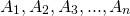
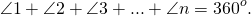
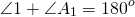
Аналогично, сумма внешнего и внутреннего углов при каждой вершине n — угольника равна 180º.
Значит, сумма всех внутренних углов многоугольника и всех его внешних углов (взятых по одному при каждой вершине) равна 180º∙n.
Следовательно, сумма всех внешних углов
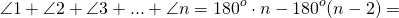
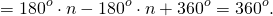
Что и требовалось доказать .
2 Comments
Вроде бы ошибка в написании условия.Вы хотите доказать,что сумма внешних углов = 180 градусов.
| Определение многоугольника |
| Диагонали n – угольника |
| Внешний угол многоугольника |
| Свойства углов треугольника |
| Свойства углов многоугольника |
| Свойства углов правильного n – угольника |
| Доказательства теорем о свойствах углов многоугольника |
Определение многоугольника
Рассмотрим n отрезков
| [A1 A2], [A2 A3], … , [An An +1] | (1) |
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.1).
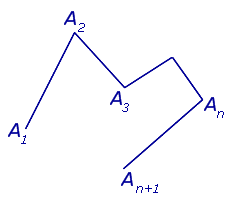
Определение 1 . Ломаной линией с n звеньями называют фигуру L , составленную из отрезков (1), то есть фигуру, заданную равенством
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).
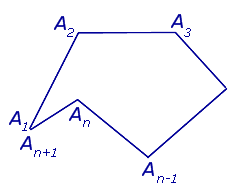
Определение 2 . Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией без самопересечений (рис. 3). Отрезки, составляющие ломаную линию ( звенья ), называют сторонами многоугольника. Концы отрезков называют вершинами многоугольника.
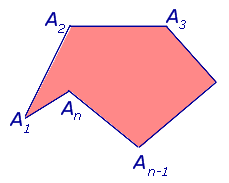
Определение 3 . Многоугольник называют n – угольником , если он имеет n сторон.
Таким образом, многоугольник, имеющий 3 стороны, называют треугольником , многоугольник, имеющий 4 стороны, называют четырёхугольником и т.д.
Определение 4 . Периметром многоугольника называют сумму длин всех сторон многоугольника.
Величину, равную половине периметра, называют полупериметром .
Диагонали n — угольника
| Фигура | Рисунок | Описание |
| Диагональ многоугольника |
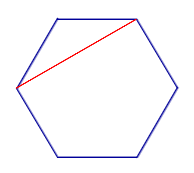 |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |
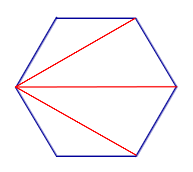 |
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |
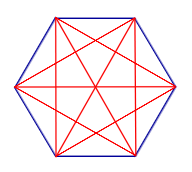 |
Число диагоналей n – угольника равно
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника

Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника

Число диагоналей n – угольника равно
Внешний угол многоугольника
Определение 5 . Два угла называют смежными , если они имеют общую сторону, и их сумма равна 180° (рис.1).

Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
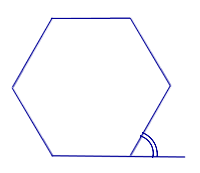
Свойства углов треугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы треугольника | 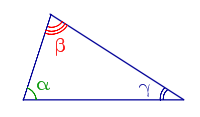 |
Сумма углов треугольника равна 180°
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
Сумма углов треугольника равна 180°


Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
Свойства углов многоугольника
Сумма углов многоугольника равна
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°
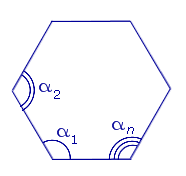
Сумма углов многоугольника равна
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°
Свойства углов правильного n – угольника
Все углы правильного n – угольника равны
Все внешние углы правильного
n – угольника равны

Все углы правильного n – угольника равны
Все внешние углы правильного
n – угольника равны
Доказательства свойств углов многоугольника
Теорема 1 . В любом треугольнике сумма углов равна 180° .
Доказательство . Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
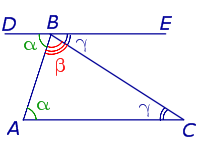
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE . Поскольку углы ABD , ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180° . Теорема доказана.
Теорема 2 . Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Доказательство . Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
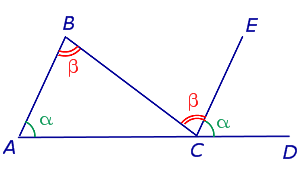
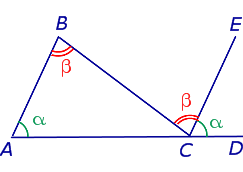
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC . Теорема доказана.
Замечание . Теорема 1 является следствием теоремы 2.
Теорема 3 . Сумма углов n – угольника равна
Доказательство . Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
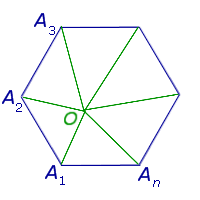
Получим n треугольников:
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O . Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
Теорема 4 . Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° .
Многоугольник, выпуклый многоугольник, четырехугольник
В геометрии многоугольниками называют плоские замкнутые фигуры, состоящие из нескольких прямых отрезков. Суммарная длина всех сторон называется периметром.
Поговорим подробнее о видах многоугольников и их характеристиках.
Многоугольник — это замкнутая ломаная линия.
Многоугольник — это простое понятие: Если в замкнутой ломаной линии соседние стороны имеют общую точку и любые две стороны не являются продолжением друг друга, то фигура называется многоугольником.
При изучении темы, что такое многоугольники, применяются следующие термины:
- Вершины многоугольника.
- Стороны замкнутой ломаной.
- Углы, образованные между смежными сторонами.
- Отрезки между несмежными вершинами называются диагоналями.
- Сумма длин всех сторон фигуры является периметром.
- Внутренние углы между соседними сторонами. Число углов равно числу сторон и вершин.
Наименования данных фигур зависят от количества сторон:
- Треугольник – это 3 стороны.
- Четырехугольник имеет 4 стороны.
- Пятиугольник – это 5 сторон и пр.
Все фигуры имеют буквенные обозначения, необходимо правильно проставлять их при вершинах.
Например, обозначение пятиугольника ABCDE будет выглядеть так:

В этом пятиугольнике вершинами являются точки: A, B, C, D и E.
Отрезки: AB, BC, CD, DE и EA являются сторонами пятиугольника.
Виды многоугольников
Различают несколько видов этих фигур: выпуклые, вогнутые, правильные и неправильные.
Какие многоугольники называются выпуклыми и невыпуклыми (вогнутыми)? Чтобы определить, какой многоугольник называется выпуклым, достаточно знать его определение.
Если стороны, при продолжении до прямой линии, не пересекают плоскость, то это выпуклый многоугольник.

Определение невыпуклого многоугольника: если при продолжении сторон прямые линии пересекают плоскость фигуры, то она является вогнутой.
Что такое правильные многоугольники
Выпуклые многоугольники, у которых все стороны и все углы равны, называются правильными.
На рисунке показан правильный многоугольник.

Как найти периметр многоугольника и определить диагонали
Периметром многоугольника называется сумма длин его сторон.
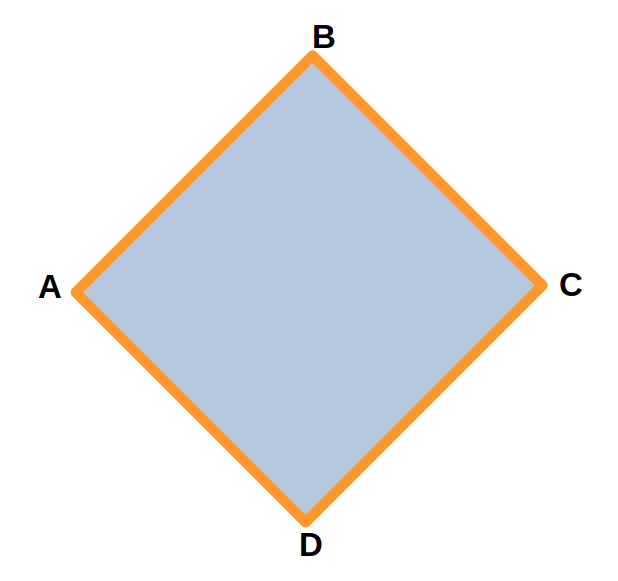
Для четырехугольника ABCD периметр будет равен сумме его сторон: AB + BC + CD + DA.
Задание: Длина одной стороны четырехугольника ABCD равна 3 см. Требуется найти периметр четырехугольника.
Решение: AB + BC + CD + DA = 3 + 3 + 3 + 3 = 12 см
Ответ: периметр четырехугольника ABCD равен 12 см.
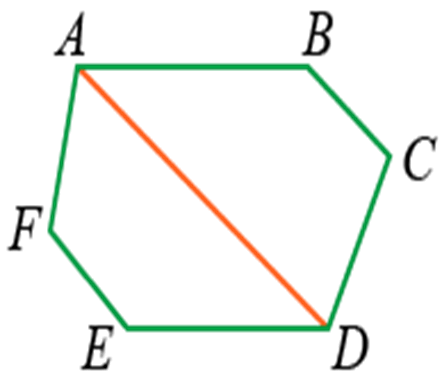
Диагональю многоугольника является отрезок, который соединяет вершины противоположных углов.
Например, отрезок AD будет являться диагональю фигуры ABCDEF:
Свойство треугольников: если треугольник не имеет углов с общими сторонами, диагональ он иметь не может.
Если из вершин провести несколько диагоналей, то они разделят фигуру на несколько треугольников:
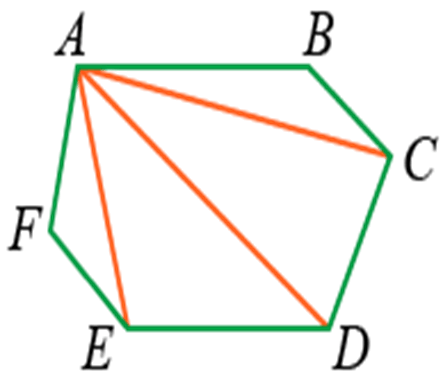
Количество треугольников будет на 2 меньше, чем число сторон:
Если t — количество треугольников, а n — количество сторон, то формула будет выглядеть так: t = n – 2.
Разделение многоугольника диагоналями на несколько треугольников помогает быстро найти площадь.
Чтобы найти площадь многоугольника, нужно разделить его на треугольники, затем найти их площадь и сложить полученные результаты.
Сумма углов выпуклого многоугольника
Научимся находить сумму углов выпуклого четырёхугольника, не только внешних, но и внутренних. Но сначала определим, какие углы называются внутренними углами выпуклого многоугольника.
Внутренним называется угол между смежными сторонами.
Например, ∠ABC является внутренним для ABCDEF.

Внешним называют угол между стороной фигуры и линейным продолжением близлежащего отрезка.
Например, ∠LBC является внешним углом для ABCDEF.
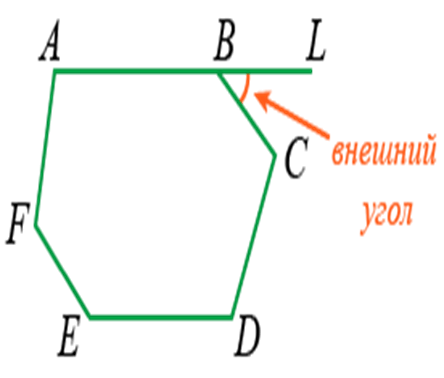
Правило: сумма углов выпуклого многоугольника всегда равно числу его сторон. Это определение относится ко всем углам.
Это значит, чтобы найти количество углов, достаточно посчитать количество всех его сторон. Значит сумма углов четырехугольника будет равна четырем.
Сумма внутренних углов
Правило для нахождения суммы углов гласит: чтобы найти сумму всех внутренних углов выпуклого многоугольника, нужно умножить уменьшенное на 2 количество его сторон на 180°.
Обозначения выглядят следующим образом:
- сумма углов – s;
- число сторон – n;
- два прямых угла (2 · 90 = 180°) – 2d.
Формула многоугольника для нахождения суммы углов: s = 2d · (n – 2).
Найти сумму углов также можно с помощью деления фигуры на треугольники. Она будет равна сумме углов всех треугольников (180° · n).
Пример:
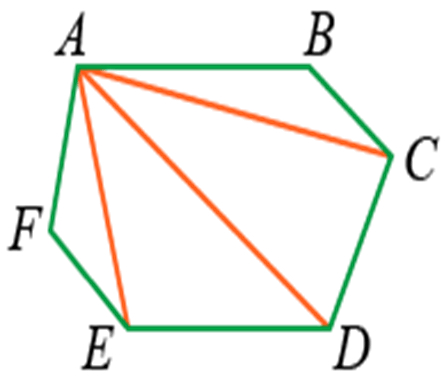
Если у фигуры 4 треугольника, то сумму всех углов находим по следующей формуле: s = 2d (n — 2) = 180 · 4 = 720°.
Это означает, что сумма внутренних углов – это постоянная величина, которая зависит от количества его сторон.
- Август 2022 (1639)
- Декабрь 2020 (3)
- Апрель 2020 (433)






