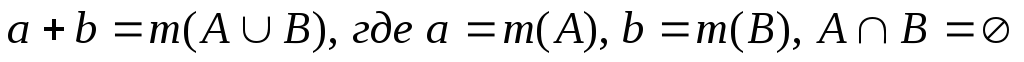Что такое сумма чисел 2 класс математика

Слагаемые. Сумма — ЧИСЛА ОТ 1 ДО 10. СЛОЖЕНИЕ И ВЫЧИТАНИЕ

Учащиеся научатся читать равенства, используя математическую терминологию (слагаемые, сумма); планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями ее выполнения; определять наиболее эффективные способы достижения результата; оценивать себя, границы своего знания и незнания; работать в паре и оценивать товарища.

Содержимое публикации

Слагаемые. Сумма — ЧИСЛА ОТ 1 ДО 10. СЛОЖЕНИЕ И ВЫЧИТАНИЕ

Цель: познакомить с понятиями “слагаемые”, “сумма”.

Планируемые результаты: учащиеся научатся читать равенства, используя математическую терминологию (слагаемые, сумма); планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями ее выполнения; определять наиболее эффективные способы достижения результата; оценивать себя, границы своего знания и незнания; работать в паре и оценивать товарища.

I. Организационный момент

II. Актуализация знаний

1. Задачи-шутки

• Стоя на одной ноге, гусь весит 2 кг. Сколько он будет весить, стоя на двух ногах? (2 кг.)

• Я шел, пятачок нашел. С другом пойдем — сколько найдем? (Нельзя ответить.)

• Вова за 1 ч поймал 5 рыбок. Сколько рыбок он поймает за 2 ч? (Нельзя ответить.)

• Шли 2 друга в школу. Навстречу им шли еще 2 друга. Сколько друзей шло в школу? (2)

2. Устный счет

• от 1 до 10 и обратно;

• от 1 до 10 через один (без хлопков);

• от 1 до 10 через два: 1, два хлопка, 4, два хлопка и т. д.

— Решите цепочки, покажите ответы.

Игра “Веселый мяч”

(Учитель кидает мяч и говорит вопрос или задание. Отвечает тот, кто поймал мяч.)

• К 4 прибавь 2. (6.)

• Какое число на 2 меньше, чем 8? (6.)

• Уменьши 10 на 1. (9.)

• Какое число больше 5 на 2? (7.)

• Увеличь 7 на 2. (9.)

III. Самоопределение к деятельности

Ай да белка-мастерица!

Вяжет детям рукавицы.

Извязала три клубка,

Два еще лежат пока.

У кого ответ готов:

Сколько у нее клубков? (5.)

— Как вы узнали? (3 + 2 = 5.)

— Как можно эту запись прочитать по-разному? (К 3 прибавить 2 — получится 5, 3 увеличить на 2 — получится 5, 3 да еще 2 — будет 5.)

— Можно ли по-другому прочитать запись?

На этот вопрос вы сможете ответить в конце урока.

(Запись учитель оставляет на доске.)

IV. Работа по теме урока

Практическая работа

(У учителя корзина и муляжи овощей, с помощью которых он демонстрирует все действия зайчика.)

— Зайчик пошел в огород, сорвал и положил в корзину 2 кочана капусты. Положите на парту столько же кругов.

— Потом он дошел до грядки с морковью, сорвал и положил в корзину 3 морковки. Положите столько же треугольников.

— Что делал зайчик с овощами? (Складывал в корзину.)

— Какое действие он выполнял? (Сложение.)

— Что он складывал? (2кочана капусты и 3морковки.)

— Как это записать? (2 + 3.)

— Числа, которые мы складываем, на математическом языке называются слагаемыми.

— Назовите первое слагаемое. (2.)

— Назовите второе слагаемое. (3.)

— Сколько овощей в корзине у зайчика? (5.)

— Сколько фигур у вас на столе? (5.)

— Дополните свою запись. (2 + 3 = 5.)

— Как можете назвать число 5? (Ответ, то, что получилось, результат и т. д.)

В математике все эти слова заменяют одним словом — сумма. (Учитель записывает слово “сумма” на доске, учащиеся читают его хором.)

— Прочитайте запись, используя слова “слагаемое” и “сумма”. (Первое слагаемое 2, второе слагаемое 3, сумма 5.)

— Как можно прочитать запись на доске еще одним способом? (Первое слагаемое 3, второе слагаемое 2, сумма 5.)

V. Физкультминутка

В норке спал хорек зимой,

Но проснулся он с весной.

Вверх он лапки потянул,

Головой своей кивнул.

И помчался он вприпрыжку,

Словно озорной мальчишка.

VI. Закрепление изученного материала

1. Работа по учебнику

— Откройте учебник на с. 86. Прочитайте, что мы сегодня должны узнать на уроке.

— Кто уже запомнил, как называются числа при сложении? (Слагаемые, сумма.)

— Прочитайте правило и скажите, что нового вы узнали. (Сумма — это не только результат, но и выражение.)

— Прочитайте выражение 4 + 3 = 7 по-разному. (Первое слагаемое 4, второе слагаемое 3, сумма 7. Сумма чисел 4 и 3 равна 7.)

— Кто сможет прочитать выражение? (Первое слагаемое 4, второе слагаемое 2, сумма 6.)

(Второе выражение хором читают мальчики, третье — девочки.)

2. Работа в тетради с печатной основой

— Откройте тетрадь на с. 32. Прочитайте первое задание.

— Что такое слагаемые? (Числа, которые складываем.)

— Какие равенства подчеркнули? Прочитайте их с ответом.

— Прочитайте следующее задание. Выполните его.

— Какое равенство составили к первому рисунку? (5 + 1 = 6.)

— Какое равенство составили ко второму рисунку? (7 — 1 = 6.)

— Составьте рассказы по рисункам.

(Остальные задания учащиеся выполняют самостоятельно. Самооценка с помощью “Светофора”.)

3. Работа по учебнику

— Решите примеры, пользуясь числовым рядом.

(Учащиеся подробно объясняют решение: говорят, с какого деления начинают движение, в какую сторону и сколько шагов делают, около какой точки остановились, называют ответ.)

— Прочитайте задачу. Что известно в задаче? (У Васи было 6 книг. Ему подарили еще 2 книги.)

— Что нужно узнать? (Сколько книг стало у Васи.)

— Что обозначено зелеными квадратами? (Сколько книг было.)

— Что обозначено желтыми квадратами? (Сколько книг подарили.)

— Ответьте на вопрос задачи. (У Васи стало 8 книг.)

— Как вы узнали? (6 + 2 = 8.)

— Прочитайте запись разными способами.

— Прочитайте задачу. Что известно в задаче? (У Лены было 3собачки. Она подарила подруге 1 собачку.)

— Что нужно узнать? (Сколько собачек осталось у Лены.)

— Объясните схему. (Было 3 собачки — они обозначены кругами. Лена подарила 1 собачку — 1 круг зачеркнули. Осталось 2 собачки.)

— Как это записать? (3 — 1 = 2.)

— Ответьте на вопрос задачи. (У Лены осталось 2 собачки.)

VII. Рефлексия

(“Проверь себя” (учебник, с. 87).)

— Посмотрите на рисунок и скажите, кто ошибся. (Зайчик.)

— В чем его ошибка? (Знак + показывает, что нужно двигаться вправо.)

— Оцените свои знания с помощью “Светофора”.

VIII. Подведение итогов урока

— Какие математические термины вы сегодня узнали? (Слагаемое, сумма.)

— Что называем слагаемыми? (Числа, которые складываем.)

— Что называем суммой? (Ответ и выражение.)

Домашнее задание (по желанию)

Международный конкурс детского рисунка на свободную тему «В ВИХРЕ ЯРКИХ КРАСОК »

Международный конкурс изобразительного искусства, декоративно-прикладного творчества и фотографии ко Всемирному дню моря «МОРСКИЕ ПРОСТОРЫ »

Всероссийский патриотический конкурс художественного слова «ЧИТАЮ О ТЕБЕ, МОЯ РОССИЯ! » к Дню народного единства

Если вам понравилась статья, лучший способ сказать cпасибо — это поделиться ссылкой со своими друзьями в социальных сетях

• Предыдущая работа
• Следующая работа

Также вас может заинтересовать

• Разное по математике для «Компетентностно-ориентированные задания и тесты на уроках математики как средства формирования ключевых компетентностей учащихся» Математика
• Планирование по математике для 6 класса «Рабочая программа для обучающихся 6 класса по предмету «Математика»» Математика
• Конспект занятия по математике для дошкольников «Конспект НОД для детей старшего дошкольного возраста по ФЭМП «Путешествие к волшебнику Магнолику»» Математика
• Разное по математике для дошкольников «Методическая разработка. Тема: «Дидактическая игра как средство формирования количественных представлений у детей младшего дошкольного возраста».» Математика
• Презентации по математике для 5 класса «Математический диктант» Математика

Адрес: 197371, Санкт-Петербург, Испытателей пр. д.39 лит.А оф.С-3-20к. ИНН 7840447816 КПП 781401001 ОГРН 1117847081153. Ограничение по возрасту: 6+

Сложение

Числа идут слева направо, по порядку, как при счёте.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Посмотри на числовой ряд, по которому идёт заяц.

Какое действие выполняет заяц?

Прибавляет число 2.

К какому числу он прибавляет число 2?

К числу 4.

Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.

В какую сторону пойдёт зайчик?

Вправо, потому что у него на табличке знак +.

Сколько шагов вправо сделает заяц?

2, потому что ему нужно прибавить 2.

На каком делении остановится заяц?

На числе 6.

Когда прибав­ляем, становится больше.

Чем правее, тем числа больше.

4 + 2 = 6

Рассмотрим еще один пример.

Какое действие выполняет заяц?

Прибавляет число 5.

К какому числу он прибавляет число 5?

К числу 3. Мы поставили зайчика на число 3.

В какую сторону он пойдёт?

Вправо, потому что у него на табличке знак +.

Сколько шагов вправо сделает зайчик? 5.

На каком делении он остановится? На числе 8.

3 + 5 = 8

Как называются числа при сложении?

Первое слагаемое и второе слагаемое.

Результат называется суммой.

Представь части домика как слагаемые и сумму.

Как найти неизвестное слагаемое

Второе слагаемое неизвестно.

Рассмотри рисунок и догадайся, как его можно найти.

Нужно из суммы вычесть первое слагаемое.

Неизвестно первое слагаемое.

Как его можно найти?

Нужно из суммы вычесть второе слагаемое.

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

Проверка сложения

Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.

Именно эта связь между суммой и слагаемыми используют для проверки вычислений.

Например, 35 + 7 = 42.

Правильно ли произведено вычисление? Можно проверить так:

42 — 7 = 35, мы из суммы вычли одно из слагаемых и получили ВТОРОЕ слагаемое. Значит, вычисление произведено верно и пример решен правильно.

Перестановка слагаемых

Сделаем запись к рисунку.

3 + 2 = 5

Сделаем запись к этому рисунку.

2 + 3 = 5

Теперь рассмотрим обе записи к рисункам:

3 + 2 = 5

3 — первое слагаемое

2 — второе слагаемое

2 + 3 = 5

2 — первое слагаемое

3 — второе слагаемое

Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.

Это переместительный закон сложения, который гласит:

От перестановки мест слагаемых сумма не меняется.

Сочетательный закон сложения

Рассмотрим пример: (37 + 29) + 1 = . (читаем: к сумме чисел 37 и 29 прибавить

1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.

Сумму чисел 29 и 1 возьмем в скобки.

37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)

Что такое вычислить сумму чисел

Сумма чисел — это простое (базовое) математическое решение, выражающееся в увеличении исходного числа на заданное.

Визуально операцию суммирования можно представить следующим образом — положите на стол одно яблоко, а затем положите ещё два яблока. Итого получится три яблока. Это и есть сумма чисел яблок.

1 + 2 + 3 + 4 + 5 = 15

Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлено определение суммы чисел и самый простой онлайн калькулятор расчета расчета суммы чисел.

Вычислить сумму чисел до данного

Напишите функцию sumTo(n) , которая вычисляет сумму чисел 1 + 2 + . + n .

Сделайте три варианта решения:

1. С использованием цикла.
2. Через рекурсию, т.к. sumTo(n) = n + sumTo(n-1) for n > 1 .
3. С использованием формулы арифметической прогрессии.

Пример работы вашей функции:

P.S. Какой вариант решения самый быстрый? Самый медленный? Почему?

P.P.S. Можно ли при помощи рекурсии посчитать sumTo(100000) ?

Решение с помощью цикла:

Решение через рекурсию:

Решение по формуле: sumTo(n) = n*(n+1)/2 :

P.S. Надо ли говорить, что решение по формуле работает быстрее всех? Это очевидно. Оно использует всего три операции для любого n, а цикл и рекурсия требуют как минимум n операций сложения.

Вариант с циклом – второй по скорости. Он быстрее рекурсии, так как операций сложения столько же, но нет дополнительных вычислительных затрат на организацию вложенных вызовов. Поэтому рекурсия в данном случае работает медленнее всех.

Определение суммы чисел

Суммой $s$ (лат. summa — итог, общее количество) чисел $a_, a_, dots, a_ $ называется результат суммирования этих чисел: $s=a_+a_+ldots+a_ $ . В частности, если складывается два числа $a$ и $b$, то

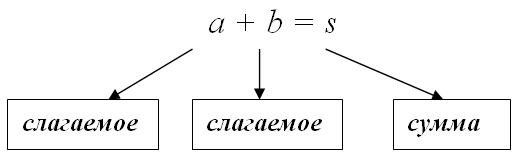
Задание. Найти сумму чисел:

1) $12$ и $15$ 2) $1,1 ; 2,2 ; 3,3$ и $4,4$

Ответ.

Свойства суммы чисел

Коммутативность: $n+m=m+n$

На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.

Дистрибутивность по отношению к умножению

$$(n+m) cdot k=n cdot k+m cdot k$$

Задание. Найти сумму чисел удобным способом:

1) $15+17+13$ ; 2) $34+22+16+18$

Решение. По свойствам сложения имеем

Ответ. 1) $15+17+13=45$

При сложении больших чисел или десятичных дробей используется сложение в столбик.

Задание. Найти сумму чисел удобным способом:

1) $1562+13827$ ; 2) $34,71+356,161$

Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом. В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:

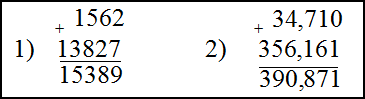
Ответ. 1) $1562+13827=15389$

Сложение рациональных дробей производится по правилу

Задание. Найти сумму чисел:

Решение. Вычислим первую сумму используя правило сложения рациональных чисел

Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим

Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим правило сложение рациональных дробей

Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком. Полученное частное запишем в целую часть, а остаток от деления в числитель.

Сумма чисел

Назад Вперёд

1. Создать условия для усвоения понятия “сумма чисел”, учить детей записывать суммы и находить их значения.
2. Создать условия для развития ума, воли, чувств, памяти, мышления.
3. Воспитывать трудолюбие, творческое отношение к учению, труду, жизни.

Оборудование: интерактивная доска, презентация к уроку, учебные принадлежности, репа.

1. Организация класса.

2. Мобилизирующий этап.

Слайд 2. 5 > 2; 2 < 5; 5 + 2.

Учитель. Что вы видите на доске?

Дети. Математические записи.

У. Прочитайте. Чем они похожи?

Д. В каждой записи есть число 2 и 5.

У. Найдите “лишнюю” запись. Она подскажет вам тему урока.

3. Сообщение темы урока детьми. Обозначение целей.

Д. “Лишняя” запись 5 + 2, т.к. это сумма. Тема урока “Сумма чисел”. Будем работать с суммами чисел.

У. Молодцы! Будем учиться записывать суммы чисел, находить их значения, узнавать компоненты действия сложения. Запишите, пожалуйста, в своих тетрадях число и “классная работа”.

4. Введение в тему.

У. Кто может сказать? Что такое сумма чисел?

Д. Я могу сказать! Если между числами стоит знак сложения “ +”, запись называют суммой чисел. Например: 4 + 3, 8 + 1, 7 + 2 и т.д.

Слайд 3. СУММА ЧИСЕЛ

5. Минутка чистописания.

У. Для чистописания возьмём число, которое указывает на количество букв в слове СУММА.

Д. Это число 5. Натуральное, однозначное, соседи числа 4 и 6.

Слайд 4. Анимированная демонстрация написания цифры 5. После показа дети записывают цифры 5 через клетку в своих тетрадках. Все стараются. Каждому хочется написать так же красиво!

6. Работа по теме.

У. Итак, сумма “лишняя”. Как назвать остальные записи? Слайд 2

Д. Неравенства.

У. Задайте следующий вопрос.

Д. Что такое неравенство? Неравенство – это математическая запись со знаком “ >” или “

У. Как назвать знаки “ >”, “

Д. Знаки сравнения.

У. На сколько 5 > 2?

Д. На 3. Слайд 5 3

У. На сколько 2 < 5?

Д. На 3. Слайд 5 3 3

У. Поставьте между числами знак сравнения. (Ученик выходит к доске и вписывает между числами знак “=”)

У. Что получилось?

Д. Равенство.

У. Задайте вопрос.

Д. Что такое равенство?

Д. Равенство – это математическая запись со знаком “=”. Слайд 5 3 = 3

Учитель стирает знак равенства между числами 3 и 3.

У. Как обозначают действие сложения?

Д. Сложение обозначают знаком “+”. Ученик пишет “+” между числами 3 и 3, читает запись. Слайд 5 3 + 3.

У. Как называют числа 3,3 в этой записи?

Д. Слагаемые.

У. Что такое слагаемые?

Д. Слагаемые – это числа, которые складывают.

У. Как превратить эту запись в равенство, ничего не стирая?

Д. Найти и записать значение суммы 3 + 3 = 6. 6 – это значение суммы.

У. Вернёмся к началу урока. (Слайд 2.) Выпишите сумму, найдите её значение.

У. Подчеркни красным цветом первое слагаемое, синим второе, зелёным сумму, жёлтым значение суммы, простым карандашом – равенство. Затем ученик выполняет подчёркивания у доски, а дети проверяют.

7. Физкультминутка.

У. Молодцы, ребята. Хорошо потрудились. А теперь давайте отдохнём.

Изображение животных открывается по строчкам: 6 коров, 4 зайца, 5 жуков.

У. Сколько видите коров, столько сделайте хлопков
Сколько зайчиков весёлых, столько сделайте наклонов
Сколько здесь у нас жуков, столько сделайте рывков.
Руки вверх вы поднимите и немножко потрясите.

У. Запомните: сколько коров, зайцев, жуков изображено на доске. (Изображение животных исчезает.) Садитесь, пожалуйста.

8. Работа с натуральным рядом чисел.

У. Запишите числа по памяти в таком порядке: сколько видели коров, сколько зайцев, жуков. Прочитайте свою запись.

У. Молодцы! Расположите числа в порядке увеличения. (Проверка: 4, 5, 6)

У. Можно ли эту запись назвать натуральным рядом чисел? (Слайд

Д. Нет. Натуральный ряд чисел начинается с числа 1. Каждое следующее число в натуральном ряду больше предыдущего на 1. Этот ряд можно назвать отрезком натурального ряда.

У. Что нужно сделать, чтобы получился натуральный ряд чисел? Ученик отвечает и дописывает числа 1, 2, 3 на доске, ставит многоточие. (Проверка: 1, 2, 3, 4, 5, 6, …..)
У. Запишите сумму самого маленького натурального числа и числа, которое стоит на седьмом месте в натуральном ряду. Найди значение суммы. (Проверка: 1 + 7 = Молодцы!

9. Составление сумм по иллюстрации к сказке “Репка”.

У. Посмотрите на экран. (Слайд 9) Иллюстрацию к какой сказке видите?

Д. Это иллюстрация к русской народной сказке “Репка”.

У. Чему учит эта сказка?

Д. Сказка учит трудолюбию. Учит тому, что справляться со сложной работой лучше дружно и вместе.

У. Репа – это фрукт или овощ? (Учитель показывает детям репу)

У. Что вы знаете об этом овоще? (За неделю до урока я предложила детям узнать о репе как можно больше. Ребята спрашивали у взрослых, искали информацию в справочниках и энциклопедиях.)

Д. Репа – полезный овощ .Содержит много витаминов. В репе в 2 раза больше витамина С, чем в лимоне, апельсине и капусте.

У. В нашем крае тоже выращивают репку. (Слайд 10: фото репы на грядке.) Вот так она растёт на грядке!

У. (Возвращаемся к слайду 9) Предложите задание по рисунку, учитывая тему урока.

Д. Составить суммы, подходящие к рисунку.

У. Подумайте и запишите столько сумм сколько сможете. Найдите их значения. Проверка: дети читают свои суммы и объясняют, что обозначают числа в записях.

У. Молодцы! Хорошо потрудились!

10. Физкультминутка.

Дети вместе с учителем выполняют движения под музыку (Слайд 9, мелодия песни “Ехал Ваня на коне” в Слайде 9), в соответствии со словами:

Выросла репка
Огромная да крепкая,
Румяная красавица,
Как ни тяни не тянется!

11. Задание на группировку.

У. А над тем полем, где выросла репка, летают бабочки. Рассмотрите их внимательно. (Слайд 11)

Д. Какие они красивые!

У. На какие группы их можно разбить?

Д. На розовые и фиолетовые. На большие и маленькие.

У. Задание. Девочки записывают суммы, подходящие к фиолетовым и розовым бабочкам.

Мальчики – к большим и маленьким. Найдите значения сумм.

Проверяем. Девочки: 5 + 3, 3 + 5. Мальчики: 6 + 2, 2 + 6.

У. Что заметили?

Д. Значения сумм одинаковые. Бабочек всего 8.

У. Молодцы, ребята! Мне очень понравилось с вами работать. А теперь нарисуйте в тетрадях свою бабочку и раскрасьте её в соответствии с вашим настроением.

12. Подведение итога.

У. Наш урок подходит к концу. По какой теме мы работали? Что вы теперь умеете делать?

Д. Мы работали по теме “Сумма чисел”. Теперь мы умеем записывать разные суммы и находить их значения.

У. Как вы думаете: почему мы смогли справиться с такими трудными заданиями?

Сумма (математика)

Су́мма (лат. summa — итог, общее количество), результат сложения величин (чисел, функций, векторов, матриц и т. д. ). Общими для всех случаев являются свойства коммутативности, ассоциативности, а также дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение определено), то есть выполнение соотношений:

• а + b = b + a
• а + (b + с) = (а + b) + с
• (а + b) с = ас + bc
• с (а + b) = ca + cb

В теории множеств суммой (или объединением) множеств называется множество, элементами которого являются все элементы слагаемых множеств, взятые без повторений.

Содержание

Определенная сумма

Часто для краткости сумму n слагаемых a_k, a_k+1, …, a_N обозначают заглавной греческой буквой Σ (сигма):

Это обозначение называют определённой (конечной) суммой по i от k до N.

Для удобства вместо ^Na_i» width=»» height=»» /> иногда пишут ^<>a_i» width=»» height=»» />, где — некоторое соотношение для , таким образом ^<>a_i» width=»» height=»» /> это конечная сумма всех , где

Свойства определённой суммы

Примеры

Уметь быстро решать примеры в уме — навык полезный. Конечно, под рукой всегда есть смартфон, но куда приятнее и эффективнее — вычислять самостоятельно и гордиться собой. Есть много фишек, чтобы упростить устный счет: разрядные слагаемые — одна из них.

О чем эта статья:

Сумма разрядных слагаемых

Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:

Число 35 состоит из 3 десятков и 5 единиц

35 = 3 десятка + 5 единиц = 30 + 5

30 — разрядное слагаемое; 5 — разрядное слагаемое.

Число 86 состоит из 8 десятков и 6 единиц

86 = 8 десятков + 6 единиц = 80 + 6

80 — разрядное слагаемое; 6 — разрядное слагаемое.

Число 356 состоит из 3 сотен, 5 десятков и 6 единиц

356 = 3 сотни + 5 десятков + 6 единиц = 300 + 50 + 6

300, 50, 6 — разрядные слагаемые.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Разряды и классы чисел

Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.

В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.

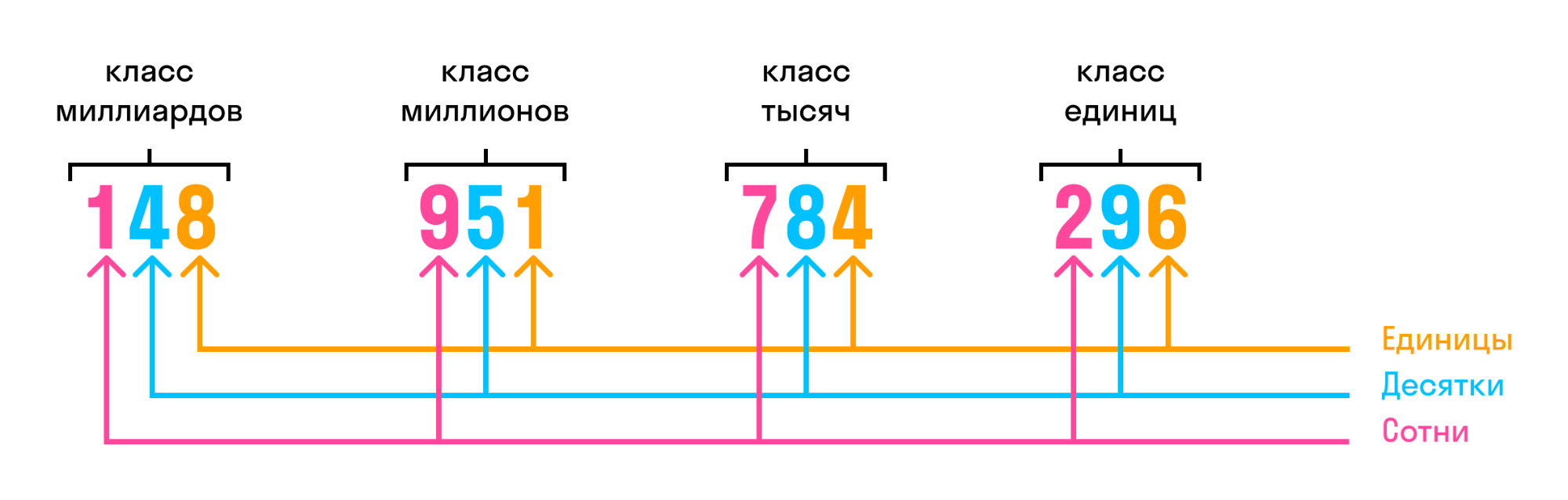
Названия классов многозначных чисел:

первый — класс единиц,

второй — класс тысяч,

третий — класс миллионов,

четвёртый — класс миллиардов,

пятый — класс триллионов,

шестой — класс квадриллионов,

седьмой — класс квинтиллионов,

восьмой — класс секстиллионов.

Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:

345 466 129 350 вместо 345466129350

Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.

Разряд — это место, которое занимает цифра в записи многозначного числа.

Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.

• Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.

Разрядные единицы — это единицы, десятки, сотни, тысячи, десятки тысяч, сотни тысяч, миллионы и т. д.

Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.

10 единиц = 1 десяток;

10 десятков = 1 сотня;

10 сотен = 1 тысяча;

10 тысяч = 1 десяток тысяч;

10 десятков тысяч = 1 сотня тысяч;

10 сотен тысяч = 1 миллион.

Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.

Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.

Например, нужно сказать, сколько сотен в числе 5689.

Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. Мысленно вычеркиваем разряды правее сотен, остается две цифры: 56. Значит, в числе 5689 56 сотен.

Если в разряде стоит цифра 0 — это означает отсутствие единиц данного разряда.

Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.

В такой ситуации можете выполнить подробный разбор числа.

Разберем число 6 057 386

Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть

6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.

Из чего состоит это число? Из:

шести единиц миллионов (6 * 1 000 000);

пяти десятков тысяч (5 * 10 000);

семи единиц тысяч (7 * 1000);

трех сотен (3 * 100);

восьми десятков (8 * 10);

Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.

Определите, сколько единиц каждого разряда в числе 5 068 252.

1. Определяем сколько всего единиц в числе.

2. Определяем количество десятков.
Записываем число без первого разряда (единицы).

3. Определяем количество сотен.
Записываем число без первого
и второго разрядов (десятки и сотни).

4. Определяем количество единиц тысяч.
Записываем число без первого, второго,
третьего разрядов (единицы, десятки, сотни).

5. Определяем количество десятков тысяч.
Записываем число без первого, второго, третьего,
четвертого разрядов (единицы, десятки, сотни, единицы тысяч).

6. Определяем количество сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
сотен и единиц.

7. Определяем количество единиц миллионов.

Записываем число без сотен тысяч, десятков тысяч,
единиц тысяч, сотен, десятков, единиц.

Расписав таким образом число, мы выяснили, что в числе 5 068 252 содержится 5 миллионов, 50 сотен тысяч, 506 десятков, 5068 тысяч, 50 682 сотни, 506 825 десятка, 5 068 252 единицы.

А если разобрать число по классам, то можно сказать, что число 5 068 252 содержит 5 единиц класса миллионов (третий класс), 68 единиц класса тысяч (второй класс), 252 единицы класса единиц (первый класс).

Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.

Примеры

Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.

Представьте в виде суммы разрядных слагаемых:

84 610 = 8 × 10 000 + 4 × 1 000 + 6 × 100 + 1 × 10

84 610 = 80 000 + 4 000 + 600 + 10.

45 317 = 4 × 10 000 + 5 × 1000 + 3 × 100 + 1 × 10 + 7 × 1

45 317 = 40 000 + 5 000 + 300 + 10 + 7.

56 789 = 5 × 10 000 + 6 × 1000 + 7 × 100 + 8 × 10 + 9 × 1

56 789 = 50 000 + 6 000 + 700 + 80 + 9.

345 677 = 3 × 100 000 + 4 × 10 000 + 5 × 1000 + 6 × 100 + 7 × 10 + 7 × 1

345 677 = 300 000 + 40 000 + 5 000 + 600 + 70 + 7.

687 543 = 6 × 100 000 + 8 × 10 000 + 7 × 1000 + 5 × 100 + 4 × 10 + 3 × 1

687 543 = 600 000 + 80 000 + 7 000 + 500 + 40 + 3.

877 589 = 8 × 100 000 + 7 × 10 000 + 7 × 1000 + 5 × 10 + 8 × 10 + 9 × 1

877 589 = 800 000 + 70 000 + 7 000 + 500 + 80 + 9.

Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.

4 895 634 = 4 × 1 000 000 + 8 × 100 000 + 9 × 10 000 + 5 × 1000 + 6 × 100 + 3 × 10 + 4 × 1

4 895 634 = 4 000 000 + 800 000 + 90 000 + 5 000 + 600 + 30 + 4.

8 675 349 = 8 × 1 000 000 + 6 × 100 000 + 7 × 10 000 + 5 × 1000 + 3 × 100 + 4 × 10 + 9 × 1

8 675 349 = 8 000 000 + 600 000 + 70 000 + 5 000 + 300 + 40 + 9.

77 897 125 = 7 × 10 000 000 + 7 × 1 000 000 + 8 × 100 000 + 9 × 10 000 + 7 × 1000 + 1 × 100 + 2 × 10 + 5 × 1

77 897 125 = 70 000 000 + 7 000 000 + 800 000 + 90 000 + 7 000 + 100 + 20 + 5.

656 734 212 = 6 × 100 000 000 + 5 × 10 000 000 + 6 × 1 000 000 + 7 × 100 000 + 3 × 10 000 + 4 × 1000 + 2 × 100 + 1 × 10 + 2 × 1

656 734 212 = 600 000 000 + 50 000 000 + 6 000 000 + 700 000 + 30 000 + 4 000 + 200 + 10 + 2.

Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.

Разрядные слагаемые — правило и примеры разложения чисел

Числа относятся к главным математическим понятиям. Они обозначаются цифрами от 0 до 9 в различных сочетаниях и позволяют количественно описать что-либо, сравнить целое и части, расположить по порядку и так далее. Для выполнения некоторых действий требуется разложить исходное выражение на определенные составляющие: представить его в виде сложения нескольких чисел, которые называются разрядными слагаемыми.

• Натуральные числа и их классификация
• Особенности разложения
• Упражнения для тренировки

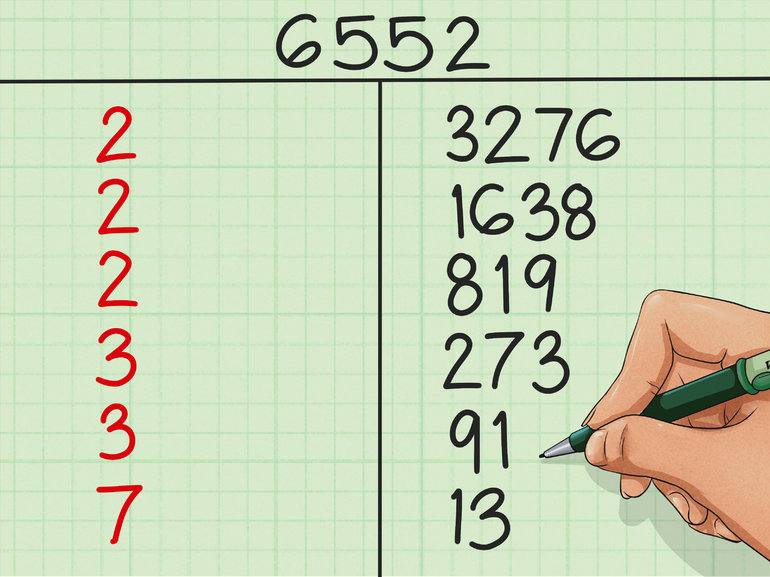
Натуральные числа и их классификация

Натуральными называют естественные величины, которые используются для счета (цифры и их комбинации: 1, 2, 3, 4, 5 и так далее), а также для расстановки по очереди (порядковые числительные: первый, второй, третий, четвертый и так далее). В совокупности они образуют так называемый ряд натуральных чисел. Его обозначением служит латинская буква N.

Главной особенностью этого ряда считается его бесконечность. Она обусловлена тем, что самого большого числа не существует. У любой составляющей ряда есть «старшие товарищи» — величины, которые по своему значению больше.

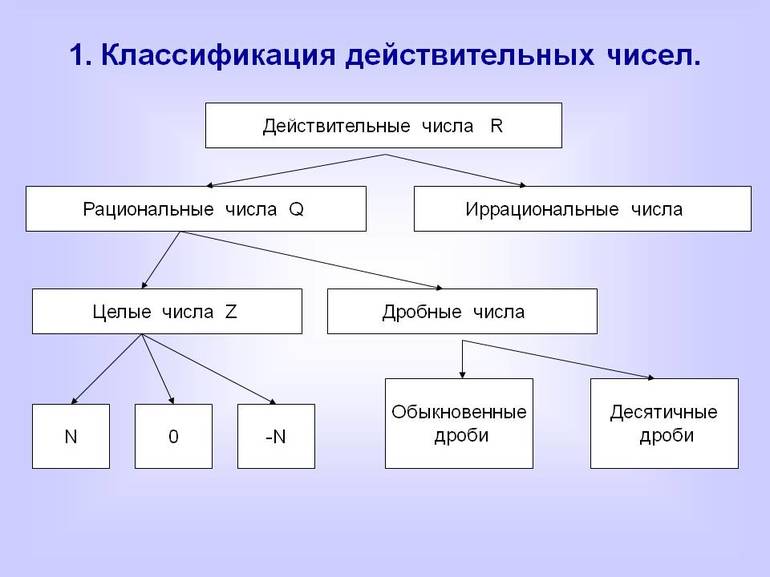
Распределение по категориям

Составляющие ряда натуральных чисел подразделяются на разряды и классы. Каждая из этих категорий неразрывно связана с другими. Разрядная классификация состоит из следующих групп (в скобках приведены слагаемые, соответствующие каждому разряду):

• единицы (1, 2, …, 9);
• десятки (10, 20, …, 90);
• сотни (100, 200, …, 900);
• тысячи (1000, 2000, …, 9000) и так далее.

Разряд числа — это положение, которое оно занимает в цифровой записи. Таким образом, любое числовое значение можно представить посредством разрядных слагаемых по математической формуле следующего вида: nnnn = n000 + n00 + n0 + n, где n означает любую цифру от 0 до 9. Для наглядного примера стоит разбить на составляющие число 4698 = 4000 + 600 + 90 + 8. Получается, что оно состоит из четырех разрядов, отображенных соответствующими составляющими:

• 4000 (четыре тысячи) — это первое слагаемое;
• 600 (шесть сотен) — второе;
• 90 (девять десятков) — третье;
• 8 (восемь простых единиц) — четвертое.

Разряд первого слагаемого называют высшим. Цифра, которой он обозначается, всегда больше нуля. Количество разрядов числа, как и количество его разрядных составляющих, всегда соответствует количеству в нем цифр, отличных от 0. Например, число 7052 состоит из трех разрядов, несмотря на свою четырехзначность. Это связано с тем, что в его составе отсутствуют сотни. Его слагаемые — семь тысяч, пять десятков и две простых единицы (7000 + 50 + 2 = 7052).

Разрядные составляющие — это натуральные числа, содержащие только одну цифру, отличную от нуля. Примеры разрядных слагаемых: 7, 30, 200, 4000 и тому подобные. Числа такого вида, как 12, 21, 475, 3500 и так далее, не могут быть отнесены к этой категории. Они подлежат математическому разложению на составляющие.

Название разрядных слагаемых обусловлено принадлежностью каждого из них к определенному разряду. Тысяча считается единицей четвертого разряда, сотня — единицей третьего разряда, десяток — второго, единица — первого. То есть нумерация разрядов начинается от наименьшей составляющей. Единицы первого разряда называются простыми, так как они однозначные. Составляющие прочих разрядов относятся к составным.

Каждый разряд состоит из десяти единиц, но обозначаться он может только девятью, так как десятая единица обеспечивает переход на следующий более высокий разряд. Не может быть разрядной составляющей типа десяти сотен — эта единица обозначается как одна тысяча.

Комплектация разрядов

В целях упрощения записи представления числа через разрядные составляющие единицы разрядов принято группировать в классы. В состав каждого из них входит три разряда:

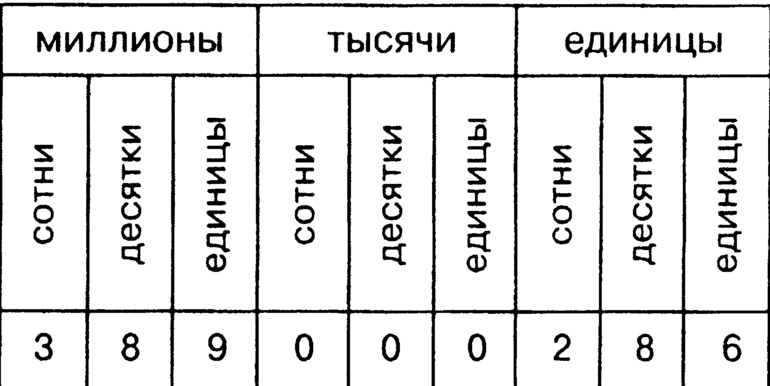
Для удобства между классами разрешается ставить пробел. Особенно это необходимо для представлений очень больших величин (от миллиона), чтобы они не выглядели бесконечным набором цифр, и в процессе их разложения не возникло путаницы. На классы число разбивается строго по три цифры справа налево.

Первый класс — это единицы. Он включает от одного до трех разрядов. Это значит, что к нему относятся все натуральные числа от 1 до 999. Второй класс — это тысячи. В него входят от четырех до шести разрядов. То есть единицы, принадлежащие к этому классу, есть во всех величинах от 1000 и больше. Дальнейшее распределение по классам:

• третий — миллионы (с седьмого по девятый разряды);
• четвертый — миллиарды (с десятого по двенадцатый);
• пятый — триллионы (с тринадцатого по пятнадцатый);
• шестой — квадриллионы (с шестнадцатого по восемнадцатый);
• седьмой — квинтиллионы (с девятнадцатого по двадцать первый) и так далее.

Распределение по классовым и разрядным категориям отображено в таблице:

Особенности разложения

Чтобы лучше понять, что такое разрядные слагаемые в математике и как их использовать, стоит подробно рассмотреть процесс разложения натуральных величин на эти составляющие. В основе большинства задач с разрядными слагаемыми лежит разложение натурального числа, то есть его представление в виде суммы разрядов через сложение количеств всех разрядных единиц.

Преобразить в сумму разрядных слагаемых можно каждую натуральную величину составного типа, то есть многозначную (двузначную, трехзначную и так далее). Чтобы разложить число на разрядные слагаемые корректно, необходимо соблюдать основные правила. Первое — нули не учитываются в разрядном составе числа. Второе — слагаемые записываются в порядке старшинства, то есть от старшего к младшему — вначале тысячи, затем сотни и десятки, последними фиксируются простые единицы.

Разрядный состав можно записать в трех вариантах разбора:

• базовый — простое сложение: 852768 = 800 000 + 50 000 + 2000 + 700 + 60 + 8;
• подробный — сложение с умножением единиц разряда на их количество: 852768 = 8*100 000 + 5*10 000 + 2*1000 + 7*100 + 6*10 + 8*1.
• словесный — текстовая расшифровка: 852768 = восемь сотен тысяч, пять десятков тысяч, две тысячи, семь сотен, шесть десятков, восемь простых единиц.

Вне зависимости от выбранного способа разложить число на составляющие по разрядам не составит особого труда. Конечно, чем больше число, тем выше риск запутаться и совершить ошибку. Упражняться лучше сперва на двузначных числах, а затем постепенно повышать разрядность.

Упражнения для тренировки

Для лучшего усвоения материала стоит разобрать несколько тренировочных упражнений. Несколько примеров, какими бывают математические задания по этой теме:

• 75 = 70 + 5;
• 324 = 300 + 20 + 4;
• 8434 = 8000 + 400 + 30 + 4;
• 68 486 = 60 000 + 8000 + 400 + 80 + 6;
• 575 783 = 500 000 + 70 000 + 5000 + 700 + 80 + 3;
• 8 633 087 = 8 000 000 + 600 000 + 30 000 + 3000 + 80 + 7.

Нередки упражнения с обратным процессом, то есть такие, в которых нужно найти число по его составляющим:

• 500 + 60 + 5 = 565;
• 8000 + 300 + 4 = 8304;
• 900 000 + 50 000 + 7000 + 80 + 2 = 957 082.

Стоит отметить, что не все задачи с разрядными составляющими решаются путем сложения. Многие упражнения содержат прием их вычитания. Но сложными такие задания кажутся только на первый взгляд. Их суть проста. В скобках приводятся составляющие двух чисел — уменьшаемого и вычитаемого. Требуется найти их разность: (500 + 40 + 1) — (400 + 20) = (100 + 20 + 1) = 121.

Процессы разложения чисел по разрядам и обратного сложения имеют огромное значение для решения различных математических задач и упражнений. Очень важно уметь быстро раскладывать числа любой величины по разрядному составу. Это умение поможет в устном счете и оперировании многозначными числами.

Изучение натуральных чисел и разрядного состава входит в базовую программу по математике. Этот материал проходится учащимися в начальных классах школы.