Что такое сумма разрядных чисел в математике

Урок математики по теме: «Понятие о разрядных слагаемых» (система Л.В. Занкова). 2-й класс

ЦЕЛЬ: создать условия для введения понятия “разрядные слагаемые”.

1. Учить представлять числа в виде суммы разрядных слагаемых.
2. Систематизировать и углубить знания учащихся о натуральных числах.
3. Формировать вычислительные навыки учащихся, навык распознавания геометрических фигур.

1. Организационный момент.

Учитель: Ребята, давайте проверим вашу готовность к уроку. Решите задачу:

Из-за куста торчало 8 ушек. Это спрятались зайчики . Сколько их?

Учитель: Как рассуждали?

Тимур : я считал по 2 – 2 да еще 2 будет 4 ушка. Это 2 зайчика. Еще 2 да еще 2 , еще 2 зайчика. Всего 4 зайчика.

Учитель: А сколько у них лапок?

Артем: 16. Я считал так – 4+4 =8, 8+4=12, 12+4=16.

Учитель: А сколько у них хвостиков?

Учитель: Как рассуждали?

Дети: Всего ведь было 4 зайчика, значит, и хвостиков у них было 4.

Учитель: А кто охотится на зайчиков?

2. Актуализация знаний. Работа с числами.

Учитель: Сегодня к нам на урок пришла лиса, да необычная. Она сегодня поможет нам сделать открытие. Посмотрите ,в лапах она держит какой-то секрет. Она приготовила вам задание. Прочитайте числа: 4,1,6,3.

Учитель: Что могут обозначать эти числа на рисунке?

3 — ромашки на платье лисы.

1 — пятиугольник, 1 цветок в лапе лисы.

6 — треугольников и маленьких, и больших…

Учитель: А где на рисунке , Артем, ты нашел такую фигуру? Сможешь показать? (Артем выходит к доске, начинает считать…Насчитывает 9 сторон.)

Учитель: Как же называется такая фигура?

Ксюша : 1 — овал. Это ротик у лисы.

Полина: 1 — треугольник.

Полина : На мордочке у лисы нос.

Учитель: Я правильно тебя поняла….Ты говорила о коричневом треугольнике?

Учитель: А может еще какие то числа можно найти на рисунке?

Дети: 2 — желтых круга, 2 — оранжевых…

Учитель: Что вы можете сказать об этих числах?

Дети: Числа натуральные. Числа однозначные. Числа расположены не по порядку. Пропущены числа…..Если числа вставить, то получится натуральный ряд.

Учитель: Дети , вы согласны с Артемом? Назовите числа, в каком порядке они будут идти?

( На доске делается запись 1,2,3,4,5,6)

Учитель: Эта запись является натуральным рядом чисел?

Алина : Это отрезок натурального ряда чисел.

Учитель: А как сделать так, чтобы эта запись стала натуральным рядом чисел?

Настя :Нужно поставить точки.

Алина: Это будет обозначать, что числа будут идти дальше.

Учитель: О каком признаке натурального ряда вы говорили?

Настя: О бесконечности.

Учитель: Ребята, легко было выполнять задания? А хотите задание посложнее?

Учитель: Используя данные числа составьте и запишите в тетрадь двузначные числа , в которых десятков больше , чем единиц. Как поняли?

Артем: Я буду составлять числа, в которых десятков больше , чем единиц.

Учитель: Приступайте. ( Дети выполняют задание в тетрадях и на доске.)

В результате проверки появляется запись: 65, 64, 61, 54, 51, 41.

Учитель: Есть другие варианты выполнения задания?

Даша: Да .Я записала числа 66, 11,44, 33.

Учитель: Ребята, что скажете о работе Даши?

Дети: Даша, ты использовала в записи одинаковые цифры, а задание было другое.

Учитель: Чем эти числа отличаются от этих?

Дети: В них есть десятки и единицы. В записи две цифры.

Учитель: Подчеркните цифры в разряде десятков одной чертой, а в разряде единиц – двумя чертами. (На доске прикрепляется карточка — разряд десятков, разряд единиц)

Учитель: Как вы думаете, это все, что мы знаем о двузначных числах? А хотите узнать? А зачем вам это надо?

Дети: — Мы будем учиться складывать двузначные числа. Это нам пригодится.

— У меня брат решает такие примеры,в которых ……. надо умножить на ………. . Сначала надо узнать все про такие числа.

— Или у вас делают ремонт. Вам надо рассчитаться.

Учитель: Как будем это делать?

Дети: Вы нам задание приготовили.

3.Изучение нового материала. Введение понятия разрядные слагаемые.

Учитель: Постарайтесь догадаться, какое число пропущено. Раздаю листы, только по первым партам, а их всего 6.)

Ой, ребята, как быть? Листов то у меня только 6, а вас много . Как быть?

Дети: давайте работать в группах…( На листах даны равенства с, в которых пропущены слагаемые. В нескольких равенствах слагаемые разрядные. Для одной группы, в которой более слабые учащиеся, все равенства записаны в виде суммы разрядных слагаемых).

54+…=61	60 +…=61
60 + …=64	60 +…=64
59 +…=63	60 +…=63
40 + …= 43	40 +…= 41
37 + ….=41	40 +…=43
27 +…=31	30 +…= 31

Учитель: Проверьте правильность выполнения.

Учитель: А кто заметил, какая группа выполнила задание раньше всех? ( Закончила работу раньше всех, как раз та группа, в которой уч-ся слабее.)

Учитель: Как вы думаете, почему?

Дети: У них равенства легче.

Учитель: А это как?

Дети: Там десятки и единицы, поэтому легче было искать пропущенные числа.

Учитель: Я правильно вас поняла, что первое слагаемое – это десятки, а второе – единицы? Что обозначает I слагаемое? А II слагаемое? Попробуйте придумать название таким слагаемым…

Дети совещаются в группах.

Учитель: Какие варианты у вас получились?

Дети: -Мы просто назвали десятки и единицы.

— Мы не смогли придумать.

— Мы назвали разрядные слагаемые.

Учитель: Как вы думаете, а как проверить правильность ваших ответов? Откройте учебник на с.25 , найдите на странице название таких слагаемых…. (Дети читают жужжащим чтением).

Учитель: Кто сможет прочитать?

Учитель: Давайте проверим, а что же нам лисичка принесла… (Переворачивается карточка, на ней запись – РАЗРЯДНЫЕ СЛАГАЕМЫЕ.)

Учитель: А кто догадался , по какой теме мы сегодня работаем?

Учитель: Покажите с помощью карточек разрядные слагаемые чисел 39 и 93.

4. Физминутка. Проводится упражнение на внимание “Парта” ( Если учитель перед движением называет слово ПАРТА, то учащиеся выполняют действие, а если слово не названо или названо какое-то другое, то уч-ся движение не выполняют.)

5. Закрепление понятия разрядные слагаемые.

Учитель: Может дело в числах — они для вас легкие, и вы легко справились с заданием? С другими числами справитесь? Выполните п.4 задания № 60.

Учитель: Что будете делать?

Учитель: Мне тоже хочется поработать, я выполню задание вместе с вами на доске.(На доске делаю запись, в которой делается “ловушка”)

Учитель: Сверьте свою работу с образцом.

Учитель: Что–то лисичка наша загрустила. Может из-за задания? Как вы думаете, что нужно сделать? (Слева и справа от лисицы расположены карточки с выражениями .Например: 80+12, 32+4, 50+8, 42+10, 60+6, 50+ 14, 70+5, 80+7)

Дети: Найти суммы разрядных слагаемых.

ВЗАИМОПРОВЕРКА. После выполнения задания карточки с суммами разрядных слагаемых убираются.

Учитель: А что можно сделать с оставшимися выражениями?

Предполагаемые ответы детей: Можно найти значения суммы., а можно изменить слагаемые так, чтобы они стали разрядными. Проверка выполняется по образцу.

6.Подведение итогов урока.

Учитель: Над какой темой работали на уроке?

Какое задание было самым интересным?

Учитель: Раз были трудности, предлагаю вам выполнить дома задание (оно записано заранее , но закрыто листом):

Что такое разрядные слагаемые?

Представленная статья посвящена интересной теме о натуральных числах. Для того, чтобы выполнять некоторые действия, необходимо представлять исходные выражения как сложение нескольких чисел – другим языком, раскладывать числа по разрядам. Обратный процесс также очень важен для решения упражнений и задач.

В данном разделе детально рассмотрим типичные примеры для лучшего усвоения информации. Мы также научимся преобразовывать натуральные числа и записывать их в другом виде.

Сумма разрядных слагаемых натурального числа, в виде суммы разрядных слагаемых

Каким образом можно разложить число по разрядам?

Исходя из названия статьи, можно сделать вывод, что этот параграф посвящен таким математическим терминам, как «сумма» и «слагаемые». Перед тем, как приступить к изучению данной информации, следует подробно изучить тему, чтобы иметь понятие о натуральных числах. Приступим к работе и рассмотрим основные понятия о разрядных слагаемых.

Разрядные слагаемые – это определенные числа, которые состоят из нулей и единственной цифры, отличной от нуля. Натуральные числа 5, 10, 400, 200относятся к данной категории, а числа 144, 321, 5 540, 16 441 – не относятся.

Количество разрядных слагаемых у представленного числа равняется тому числу, сколько цифр, отличных от нуля, содержится в записи. Если представить число 61 как сумму разрядных слагаемых, так как 6 и 1 отличаются от .

Если разложить число 55050 как сумму разрядных слагаемых, то оно представлено как сумма 3 слагаемых. Три пятерки, представленные в записи, отличны от нуля. Следует помнить, что все разрядные слагаемые числа содержат разное количество знаков в своей записи.

Сумма разрядных слагаемых натурального числа равна этому числу. Перейдем к понятию разрядных слагаемых.

Разрядные слагаемые– это такие натуральные числа, в записи которых содержится цифра, отличная от нуля. Количество чисел должно быть равно количеству цифр, не равных нулю. Все слагаемые числа могут записываться с различным количеством знаков. Если мы раскладываем число по разрядам, то сумма слагаемых числа всегда будет равна этому числу.

Проанализировав понятие, можно сделать вывод, что однозначные и многозначные числа (полностью состоящие из нулей за исключением первой цифры) нельзя представить в качестве суммы.

Это происходит потому, что данные числа сами будут разрядными слагаемыми для каких-то чисел. За исключением данных чисел, все остальные примеры могут раскладываться на слагаемые.

Как раскладывать числа?

Чтобы разложить число как сумму разрядных слагаемых, необходимо вспомнить, что натуральные числа связаны с количеством некоторых предметов. В записи числа разряды зависят от количества единиц, десятков, сотен, тысяч и так далее.

Если вы возьмем, например, число 58, то может отметить, что он отвечает 5 десяткам и 8 единицам. Число 134 400 соответствует 1 сотне тысяч, 3 десяткам тысяч, 4тысячам и 4 сотням.

Можно представить эти числа в виде равенств – 50+8=58 и 134 400=100 000+30 000+4 000+400. В данных примерах мы наглядно увидели, как можно разложить число в виде разрядных слагаемых. Смотря на этот пример, мы сможем любое натуральное число представить в виде суммы разрядных слагаемых.

Приведем еще один пример. Представим натуральное число 25 в виде суммы разрядных слагаемых. Число 25 соответствует 2 десяткам и 5 единицам, поэтому 25=20+5. А вот сумма 17+8 не является суммой разрядных слагаемых числа 25, так как в ней не может быть двух чисел, состоящих из одинакового количества знаков.

Мы разобрали основные понятия. Разрядные слагаемые получили свое название из-за того, что каждое принадлежит к определенному разряду.

Как найти натуральное число, если известна сумма разрядных слагаемых?

Для того, чтобы разобрать данный пример, проанализируем обратную задачу. Представим, что нам известна сумма разрядных слагаемых. Нам необходимо найти данное натуральное число.

Например, сумма 200+30+8 разложено по разрядам числа 238, а сумма 3 000 000+20 000+2 000+500 соответствует натуральному числу 3 022 500. Таким образом, мы легко можем определить натуральное число, если нам известна его сумма резервных слагаемых.

Еще один способ нахождения натурального числа – это сложение в столбцах разрядных слагаемых. Данный пример не должен вызвать у вас сложности во время выполнения. Поговорим об этом подробнее.

Пример 1

Необходимо определить исходное число, если известна сумма разрядных слагаемых 200 000+40 000+50+5. Перейдем к решению. Необходимо записать числа 200 000, 40 000, 50 и 5 для сложения в столбик:

Осталось сложить числа по столбцам. Для этого нужно помнить, что сумма нулей равна нулю, а сумма нулей и натурального числа равна этому натуральному числу.

Выполнив сложение, мы получим натуральное число 240 055, сумма разрядных слагаемых которого имеет вид 200 000+40 000+50+5. Поговорим еще об одном моменте. Если мы научимся раскладывать числа и представлять их в виде суммы разрядных слагаемых, то мы также сможем представлять натуральные число в виде суммы слагаемых, не являющихся разрядными.

Пример 2

Разложение по разрядам числа 725 будет представлено как 725=700+20+5, а сумму разрядных слагаемых 700+20+5 можно представить как (700+20)+5=720+5 или 700+(20+5)=700+25, или (700+5)+20=705+20. Иногда сложные вычисления можно немного упростить. Рассмотрим еще небольшой пример для закрепления информации.

Пример 3

Выполним вычитание чисел 5 677 и 670. Для начала представим число 5677 в виде суммы разрядных слагаемых: 5 677=5 000+600+70+7. Выполнив действие, мы можем сделать вывод, что. сумме (5 000+7)+(600+70)=5 007+670. Тогда 5 677−670=(5 007+670)−670=5 007+(670−670)=5 007+0=5 007.

Что такое разрядные слагаемые

Разрядные слагаемые – это сумма чисел с разной разрядностью. Возьмем на примере, число 86. Разложим данное число на десятки и единицы. Получаем: 86 = 80 + 6 = 8 * 10 + 6 * 1. Отсюда видим, что число 86 состоит из 8 десятков и 6 единиц. Это и есть разрядные слагаемые.

Числа 1, 10, 100, 1000 и так далее – это разрядные единицы. Запишем разделение разрядных слагаемых:

• Числа от 1 и до 9 – это единицы;
• Числа 10, 20, … , 90 – это десятки;
• Число 100, 200, … , 900 – это сотни и так далее.

Любое натуральное число можно разделить на разрядные слагаемые и записать в виде суммы. Примеры разрядных слагаемых:

• 892 = 800 + 90 + 2;
• 1695 = 1000 + 600 + 90 + 5;
• 45 = 40 + 5.

Рассмотрим пример определения разрядных слагаемых числа 92586

Сначала, разложим число 92586 на разрядные слагаемые и получим:

• 92 586 = 90000 + 2000 + 500 + 80 + 6 = 9 * 10 000 + 2 * 1 000 + 5 * 100 + 8 * 10 + 6 * 1.

Запишем, из чего состоит число 92 586:

• Из 9 десятков тысяч 9 * 10 000;
• Из 2 единиц тысяч 2 * 1000;
• Из 5 сотен 5 * 100;
• Из 8 десятков 8 * 10;
• Из 6 единиц 6 * 1.

Сделаем вывод, что любое число можно разделить на разрядные слагаемые. Разрядные слагаемые помогают при решении более сложных примеров и задач.

Разрядное слагаемое — это любое натуральное многозначное число, которое можно представить в виде суммы разрядных слагаемых. Разложить число на разрядные слагаемые значит разделить число на разряды: единицы, десятки, сотни, тысячи, десятки тысяч и так далее.

Примеры разложения чисел на разрядные слагаемые:123 = 100 + 20 + 3, где 100 — сотни, 20 — десятки, а 3 — единицы.Более сложный пример с большим числом разрядов:16 458 = 10 000 + 6 000 + 400 + 50 + 8, здесь 10 000 — десятки тысяч, 6 000 — тысячи, 400 — сотни, 50 — десятки, 8 — единицы.

Разрядные слагаемые. Диагонали прямоугольника

Сегодня на уроке узнаем о свойствах диагоналей прямоугольника, научимся заменять многозначные числа суммой разрядных слагаемых, находить общее число единиц какого-либо разряда в этих числах.

План урока:

Разрядные слагаемые

Начнем урок с небольшой разминки, повторим многозначные числа. Прочитайте внимательно высказывания, и если согласны с ними, то рисуйте в тетради , если не согласны, то ставьте такой знак: .

• v В числе 601 – 6 сотен и 1 десяток.
• v Число 986 больше, чем 968.
• v В числе 509 отсутствуют единицы.
• v В каждом их этих чисел по 5 десятков: 543, 357, 405.
• v В числе 920.001 отсутствуют единицы первого класса.
• v 899 меньше 900 на 1.
• v В числе 405.000 отсутствуют единицы первого класса.
• v Если к 3 сотням добавить 5 десятков, то получится число 350.
• v При записи числа 5 миллионов используем девять нулей.
• v Если число 148 увеличить на 1 сотню, получим число 158.

Проверь себя.

Ребята, если в многозначном числе есть единицы разных разрядов, его можно заменить суммой разрядных слагаемых.

Например, при записи числа 1.536.185 используем 7 цифр, поэтому сумма будет состоять из семи слагаемых:

В виде суммы это число запишем так:

1.536.185 = 1.000.000 + 500.000 + 30.000 + 6.000 + 100 + 80 + 5

Ребята, сколько потребуется цифр для записи числа, если наивысший разряд этого числа – сотни тысяч? Воспользуемся таблицей разрядов.

По таблице видим, что для записи числа будем использовать 6 цифр.

Попробуйте самостоятельно заменить суммой разрядных слагаемых шестизначные числа 230.449 и 341.509 и понаблюдать, сколько слагаемых у вас получится.

Проверь себя.

Как вы думаете, почему получилось только 5 слагаемых?

В числе 230.449 отсутствуют единицы тысяч, на месте этого разряда стоит 0 (нуль), а в числе 341.509 отсутствуют десятки. Поэтому разрядных слагаемых получилось только 5.

А теперь попробуем «собрать» число из разрядных слагаемых. Поиграем в игру «Собери число».

Нахождение общего количества единиц какого-либо разряда в данном числе

Чтобы определить, сколько всего в числе единиц какого-то разряда, нужно хорошо знать место разряда. Давайте разберемся в этом вопросе на примере числа 2.675

Не забываем, что называть разряды нужно справа налево.

В числе 2.675 на первом месте – единицы, на втором – десятки, на третьем – сотни, а на четвертом – единицы тысяч. Определим, сколько всего единиц в этом числе. Выделим скобочкой сверху все цифры, захватывая единицы.

Свойства диагоналей прямоугольника, квадрата

Вспомним, что такое прямоугольник, и является ли квадрат прямоугольником.

Четырехугольники, у которых все углы прямые называются прямоугольниками. Среди прямоугольников можно выделить такие, у которых все стороны равны. Это квадраты.

А что такое «диагональ»?

Обозначим вершины фигур буквами.

Соединим отрезком вершины прямоугольника из верхнего угла в нижний. Место пересечения отрезков тоже обозначим буквой.

• Поставьте ножку циркуля в точку пересечения диагоналей и сравните по длине все отрезки, которые получились при пересечении.
• Длины диагоналей можно сравнить с помощью циркуля или измерить по линейке.
• А вот свойство квадрата о прямых углах, которые получаются при пересечении диагоналей, проверьте с помощью угольника. Вот так:

Ребята, вооружитесь ножницами! Проверим еще одно свойство прямоугольника. Вырежем из бумаги в клетку любой прямоугольник, согнем его из уголка в уголок и разрежем по линии сгиба (по диагонали). У нас получилось два треугольника. Наложите треугольники друг на друга. Сделайте вывод: равны ли треугольники?

Логические задачи

Великий ученый Михаил Васильевич Ломоносов говорил, что математику нужно любить, потому что она приводит ум в порядок. А вы, ребята, любите математику? Не пасуете перед трудными логическими задачами? Давайте попробуем разобрать несколько интересных сложных задач. Есть над чем подумать! Не спешите заглянуть в правильные ответы!

ЗАДАЧА

Учитель математики Иван Васильевич уже на пенсии. К нему в гости часто приходят школьники. Однажды ребята спросили учителя, сколько ему лет. На что Иван Васильевич хитро улыбнулся и сказал: «Будет ровно 100, если я проживу еще половину того, что уже прожил и еще один год». Подумайте и ответьте, сколько лет Ивану Васильевичу.

В решении этой задачи будем двигаться в обратную сторону от числа 100.

Сначала отнимем «еще один год».

Иван Васильевич сказал, что проживет еще половину того, что уже прожил. Значит, схематически это выглядит так:

Мы получили 3 равные части.

99 : 3 = 33(года) – составляют одну часть.

Нам нужно найти две таких части.

33 ∙ 2 = 66 (лет) – Ивану Васильевичу.

Следующую задачу попробуйте решить самостоятельно.

ЗАДАЧА

Однажды разбойники нашли под старым дубом клад в большом железном сундуке. Сундук был закрыт на замок с кодом из четырех цифр. Разбойники долго бились над расшифровкой кода, но так и не смогли открыть сундук. Ребята, попробуйте расшифровать комбинацию кодового замка и открыть сундук.

• все цифры кода в сумме дают 17;
• третья цифра на 3 больше, чем первая;
• вторая цифра на 2 больше, чем четвертая;
• вторая цифра – 3.

Проверь себя.

Итак, начнем подбирать цифры для кодового замка. Их четыре: обозначим точками.

Нам нужно выполнить еще два условия: набрать в сумме 17, третья цифра на 3 больше, чем первая.

3 + 1 = 4 – сумма известных цифр.

17 – 4 = 13 – сумма неизвестных цифр.

Две оставшиеся цифры должны дать в сумме 13, и обязательно третья цифра больше первой. Рассмотрим три варианта:

4 и 9 (не подходит, 9>4 на 5)

5 и 8 (подходит, 8>5 на 3)

6 и 7 (не подходит, 7>6 на 1)

Правильный ответ:

Ребята, понравились логические задачи? Они не имеют стандартного решения. Размышляйте, используйте для решения таких задач схемы, чертежи, таблицы, рисунки. У вас обязательно все получится.

Что такое сумма разрядных слагаемых в математике?

Любое натуральное число можно записать в виде суммы разрядных слагаемых. Числа 900, 90 и 9 — разрядные слагаемые. . Сумма разрядных слагаемых — это запись многозначного числа в виде сложения количеств его разрядных единиц. Примеры.

Что такое разрядные слагаемые второй класс?

Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Например, число «64» состоит из 6 десятков и 4 единиц. Числа «60» и «4» называются разрядными слагаемыми. называется разложением числа на разрядные слагаемые или суммой разрядных слагаемых.

Как записать в виде суммы разрядных слагаемых?

Количество разрядных слагаемых данного натурального числа должно быть равно количеству цифр в записи данного числа, отличных от цифры 0. Например, натуральное число 59 можно представить в виде суммы двух разрядных слагаемых, так как в записи этого числа участвуют две цифры (5 и 9), отличные от 0.

Какие числа нельзя представить в виде суммы разрядных слагаемых?

Однозначные и многозначные числа (полностью состоящие из нулей за исключением первой цифры) нельзя представить в качестве суммы. Это следует из того, что данные числа сами будут разрядными слагаемыми для каких-то чисел. За исключением данных чисел, все остальные примеры могут раскладываться на слагаемые.

Что такое сумма разрядных слагаемых 4 класс?

Сумма разрядных слагаемых – это представление многозначного числа в виде суммы его разрядов. Сравнение чисел – определение большего или меньшего числа.

Что значит записать число в виде суммы разрядных слагаемых?

Любое натуральное число можно записать в виде суммы разрядных слагаемых. Сумма разрядных слагаемых — это запись многозначного числа в виде сложения количеств его разрядных единиц. .

В каком классе проходят разрядные слагаемые?

2-й класс ЦЕЛЬ: создать условия для введения понятия “разрядные слагаемые”. ЗАДАЧИ: Учить представлять числа в виде суммы разрядных слагаемых.

Какое число записано как сумма разрядных слагаемых 200 80?

Какое число записано как сумма разрядных слагаемых 200 + 80? Варианты ответов: 820; 280; 208.

Какое число записано как сумма разрядных слагаемых 300 2?

Какое число записано как сумма разрядных слагаемых 300 + 2? Варианты ответов: 320; 302; 323.

Как это разложить по разрядам?

Как разложить натуральное число по разрядам

Двигаясь слева направо берём поочерёдно по одной цифре. Оставшиеся цифры заменяем на нули. Сумма разрядных слагаемых числа равна этому числу.

Какому числу равна сумма разрядных слагаемых?

Сумма разрядных слагаемых натурального числа равна этому числу.

Что такое сумма слагаемых?

Числа при сложении называются слагаемыми. Результат сложения – сумма.

Сколько единиц в разряде сотен числа 40 560?

5 единиц в разряде сотен числа 40560.

Что это такое слагаемое?

Слагаемые — это два числа, которые прибавляются друг к другу. В результате чего получается их сумма. . Здесь, например число 2 — первое слагаемое (или «левое» слагаемое), а число 1 — второе (или «правое» слагаемое). Число три — их сумма.

Что такое разряды?

Разряд — это место, на котором в записи числа стоит цифра. Разряд единиц — это самый наименьший разряд, на которым заканчивается любое натуральное число. Разряд десятков — это разряд, который стоит перед разрядом единиц. Разряд сотен — это разряд, который стоит перед разрядом десятков.

Чем можно заменить число в котором есть единицы разных разрядов?

Число, в котором есть единицы разных разрядов, можно заменить суммой разрядных слагаемых.

Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых

Ну-ка проверь, дружок,
Ты готов начать урок?
Всё ль на месте, всё ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку «5».
Тут затеи и задачки,
Игры, шутки, всё для вас!
Пожелаем все удачи –
За работу, в добрый час!

Этап подготовки учащихся к активному сознательному усвоению знаний

Ребята, сегодня у нас будет необычный урок.

Представьте, что вы выросли и стали президентом фирмы. Давайте посмотрим, справитесь ли вы с такой должностью. Для этого придется, как следует потрудиться. Вот первое испытание.

Устный счёт

Президенту фирмы нужно хорошо разбираться в числах, попробуйте выполнить следующие задания.

Задание

Запишите числа цифрами:
двести сорок тысяч семьсот
тринадцать тысяч восемьсот пять
пять тысяч пять
восемьсот три тысячи двенадцать
три тысячи тридцать три
двести пятнадцать тысяч пятьсот двадцать четыре

240 700, 13 805, 5 005, 803 012, 3 033, 215 524.

Задание

Расположите прибыль, полученную фирмой за шесть месяцев, в порядке возрастания.

57002, 31635, 60040, 43 802, 60400, 49 850.

31 635, 43 802, 49 850, 57 002, 60 040, 60 400.

Задание

Ваш секретарь подготовила вам доклад для выступления на совете директоров.

Запишите числа, которые вы должны озвучить на предстоящем совете.

Запишите число, в котором 145 ед. 2 класса и 326 ед. 1 класса.

Запишите число, в котором 7 ед. 2 класса и 5 ед. 1 класса.

Запишите число, в котором 428 ед. 2 класса, а единицы 1 класса отсутствуют.

Запишите число, в котором 18 ед. 2 класса, 347 ед. 1 класса.

Запишите число, которое следует за числом 9 999

Запишите число, в котором 304 ед. 2 класса, 24 ед. 1 класса.

А теперь прочитайте записанные вами числа на совете директоров.

145 326, 7005, 428 000, 18 347, 10 000, 304 024.

Давайте ещё раз повторим:

Сто сорок пять тысяч триста двадцать шесть, семь тысяч пять, четыреста двадцать восемь тысяч, восемнадцать тысяч триста сорок семь, десять тысяч, триста четыре тысячи двадцать четыре.

Задание

Конкуренты часто скрывают информацию о своих достижениях. Сможете ли вы сами догадаться об их успехах?

Назовите пропущенное число в каждой строчке.

В числе 9754 всего ……. сотен.
В числе 925045 всего …….. тысяч.
В числе 500530 всего ……… десятков.

Сколько всего сотен в числе девять тысяч семьсот пятьдесят четыре?
В числе девять тысяч семьсот пятьдесят четыре всего девяносто семь сотен.

Сколько всего тысяч в числе девятьсот двадцать пять тысяч порок пять?
В числе девятьсот двадцать пять тысяч сорок пять всего девятьсот двадцать пять тысяч.

Сколько всего десятков в числе пятьсот тысяч пятьсот тридцать?
В числе пятьсот тысяч пятьсот тридцать всего пятьдесят тысяч пятьдесят три десятка.

Объяснение нового материала

Генеральному директору нужно иметь смекалку. Сегодня на уроке мы будем говорить о том, как представить многозначное число в виде суммы разрядных слагаемых.

Такую работу вы уже выполняли с трехзначными числами. Представьте число сто двадцать восемь в виде суммы разрядных слагаемых

Правильно, число сто двадцать восемь состоит из суммы разрядных слагаемых ста, двадцати и восьми.

Многозначные числа заменяются суммой разрядных слагаемых аналогично. Посмотрите на следующую запись. Число четыреста двадцать семь тысяч девятьсот сорок можно представить в виде суммы разрядных слагаемых – это четыреста тысяч, двадцать тысяч, семь тысяч, девятьсот и сорок. При раскладывании числа помним, что в каждом классе по три разряда. Каждый класс записывается при помощи трёх цифр.

Чтобы представить число в виде суммы разрядных слагаемых, нужно:

1. Определить количество разрядных слагаемых (по количеству цифр отличных от нуля).
2. Потом определить количество нулей в каждом разрядном слагаемом.
3. Записать сумму разрядных слагаемых.

Этап усвоения новых знаний

Задание

Если вы обладаете хорошей смекалкой, то без труда замените суммой разрядных слагаемых следующие числа.

725 368 = 700 000+ 20 000 + 5 000 + 300 + 60 + 8

45 200 = 40 000 + 5 000 + 200

390 020 = 300 000 + 90 000 + 20

500 068 = 500 000 + 60 + 8

610 707 = 600 000 + 10 000 + 700 + 7

Задание

У вашей фирмы есть конкуренты. Им очень не нравится, что вам сопутствует удача и вы лидируете среди других фирм. Они решили вам навредить и затерли числа в отчете. Сможете ли вы восстановить документ?

Вставьте пропущенные числа:

408 690 = 400 000 + … + 600 + 90

200 097 = 200 000 + … + 7

560 448 = … + 60 000 + … + 40 + 8

384 794 = 300 000 + 80 000 + … + 700 + 90 + …

62 058 = … + 2 000 + … + 8

408 690 = 400 000 + 8 000 + 600 + 90

200 097 = 200 000 + 90 + 7

560 448 = 500 000 + 60 000 + 400 + 40 + 8

384 794 = 300 000 + 80 000 + 4 000 + 700 + 90 + 4

62 058 = 60 000 + 2 000 + 50 + 8

В первом выражении вставляем число 8 000.

Во втором выражении пропущено число 90

В третьем выражении пропущены числа 500 000 и 400.

В четвертом числовом выражении пропущены числа 4 000 и 4.

В пятом числовом выражении пропущены числа 60 000 и 50.

Молодцы, ребята, вы быстро справились с такой сложной задачей

Этап усвоения новых знаний

Президенту фирмы нужно хорошо разбираться в бухгалтерской отчетности. Посмотрим, справитесь ли вы со следующим заданием.

Напишите, какие числа представлены в виде суммы разрядных слагаемых.

700 000 + 50 000 + 2 =

80 000 + 6 000 + 30 + 7 =

900 000 + 4 000 + 800 + 90 + 3=

200 000 + 2 000 + 8 =

Молодцы, ребята! Хорошо поработали.

Задание

Следующее задание. Бухгалтер допустил ошибки в вычислениях. Ваша задача найти и исправить ошибки.

450 680 = 400 000 + 500 000 + 600 + 80

950 200 = 90 000 + 50 000 + 200

38 405 = 30 000 + 800 + 40 + 5

603 010 = 60 000 + 3 000 + 100

84 811 = 800 000 + 4 000 + 800 + 10 + 1

450 680 = 400 000 + 50 000 + 600 + 80

950 200 = 900 000 + 50 000 + 200

38 405 = 30 000 + 8 000 + 400 + 5

603 010 = 600 000 + 3 000 + 10

84 811 = 80 000 + 4 000 + 800 + 10 + 1

Задание

А теперь посчитайте выручку из разных филиалов. Я думаю, вы знаете, что филиал – это ваша фирма, расположенная в другом месте и осуществляющая ту же деятельность. Сотрудники филиалов представили отчеты, в которых допущены ошибки. Найдите и исправьте ошибки.

800 000 + 30 000 + 400 + 50 + 2 = 803 452

50 000 + 7 000 + 800 + 10 = 507 810

600 000 + 40 000 + 900 + 1 = 640 091

30 000 + 4 000 + 20 = 34 200

4 000 + 600 + 30 + 7 = 40 637

Давайте еще раз вспомним, какими качествами должен обладать директор фирмы.

Он должен владеть грамотной речью.

Задание

Прочитайте многозначные числа.

Шестьсот восемьдесят девять тысяч восемьсот, пятьдесят две тысячи четыреста десять, семьсот тысяч четыре, триста одна тысяча двести сорок семь, восемьсот тысяч шестьдесят.

Задание

Директор фирмы должен уметь сравнивать свою прибыль с прибылью конкурентов.

510 924 501 024

415 670 415 760

а + 3150 а + 3 015

510 924 501 024

415 670 415 760

а + 3150 а + 3 015

Задание

Директор фирмы должен уметь распределить зарплату между работниками. Для этого выполните следующее задание. Представьте числа в виде суммы разрядных слагаемых.

602 420 = 600 000 + 2 000 + 400 + 20

700 043 =700 000 + 40 + 3

86 480 = 80 000 + 6 000 + 400 + 80

301 071= 300 000 + 1 000 + 70 + 1

И конечно, директор фирмы должен уметь хорошо считать. Найдите сумму разрядных слагаемых.

400 000 + 50 000 + 300 + 8 =

80 000 + 2 000 + 100 + 6 =

500 000 + 7 000 + 80 + 3 =

90 000 + 9 000 + 900 + 9 =

70 000 + 4 000 + 1 =

Если вы справились со всеми заданиями без ошибок, то когда вырастете, сможете стать директорами фирм.

Ребята, давайте вспомним, как правильно представить число в виде суммы разрядных слагаемых.

Для этого нужно определить количество разрядных слагаемых (по количеству цифр отличных от нуля).

Разрядные слагаемые в математике

Число — это математическое понятие для количественного описания чего-либо или его части, служит также для сравнения целого и частей, расположения по порядку. Понятие числа изображается знаками или цифрами в различном сочетании. В настоящее время почти везде используются цифры от 1 до 9 и 0. Цифры в виде семи латинских букв применения почти не имеют и рассматриваться здесь не будут.

Натуральные числа

При счёте: «один, два, три… сорок четыре» или расстановке по очереди: «первый, второй, третий… сорок четвёртый» используются естественные числа, которые называются натуральными. Вся эта совокупность называется «ряд натуральных чисел» и обозначается латинской буквой N и не имеет конца, ведь всегда есть число ещё больше, и са́мого большого просто не существует.

Разряды и классы чисел

Разряды

Отсюда видно, что разрядом числа является его позиция в цифровой записи, причём любое значение можно представлять через разрядные слагаемые в виде nnn = n00 + n0 + n, где n — любая цифра от 0 до 9.

Один десяток является единицей второго разряда, а одна сотня — третьего. Единицы первого разряда называются простыми, все остальные являются составными.

Для удобства записи и передачи применяется группировка разрядов в классы по три в каждом. Между классами для удобства чтения допускается ставить пробел.

Классы

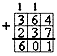
Первый — единиц, содержит до 3 знаков:

• 200 + 10 +3 = 213.

Двести тринадцать содержит в себе следующие разрядные слагаемые: две сотни, один десяток и три простых единиц.

Сорок пять состоит из четырёх десятков и пяти простых единиц.
Второй — тысяч, от 4 до 6 знаков:

• 679 812 = 600 000 + 70 000 + 9 000 + 800 +10 + 2.

Эта сумма состоит из следующих разрядных слагаемых:

1. шестьсот тысяч,
2. семьдесят тысяч,
3. девять тысяч,
4. восемьсот,
5. десять,
6. два,

• 3 456 = 3000 + 400 +50 +6.

Здесь отсутствуют слагаемые выше четвёртого разряда.

Третий — миллионов, от 7 до 9 цифр:

Это число содержит девять разрядных слагаемых:

1. 800 миллионов,
2. 80 миллионов,
3. 7 миллионов,
4. 200 тысяч,
5. 10 тысяч,
6. 3 тысячи,
7. 6 сотен,
8. 4 десятка,
9. 4 единицы,

• 7 891 234.

В этом числе нет слагаемых выше 7 разряда.
Четвёртый — миллиардов, от 10 до 12 цифр:

• 567 892 234 976,

Пятьсот шестьдесят семь миллиардов восемьсот девяносто два миллиона двести тридцать четыре тысячи девятьсот семьдесят шесть.

Разрядные слагаемые 4 класса читаются слева направо:

1. единицы сотен миллиардов,
2. единицы десятков миллиардов,
3. единицы миллиардов,
4. сотен миллионов,
5. десятков миллионов,
6. миллионов,
7. сотен тысяч,
8. десятков тысяч,
9. тысяч,
10. простые сотни,
11. простые десятки,
12. простые единицы.

Нумерация разряда числа производится начиная с меньшего, а чтение — с большего.
При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:

• 400 000 000 004,

Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса, девятого, восьмого и седьмого третьего и самого́ третьего класса, также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.

Пятый — триллионов, от 13 до 15 знаков.

• 487 789 654 427 241.

Четыреста восемьдесят семь триллионов семьсот восемьдесят девять миллиардов шестьсот пятьдесят четыре миллиона четыреста двадцать семь двести сорок один.

Шестой — квадриллионов, 16—18 цифр.

• 321 546 818 492 395 953,

Триста двадцать один квадриллион пятьсот сорок шесть триллионов восемьсот восемнадцать миллиардов четыреста девяносто два миллиона триста девяносто пять тысяч девятьсот пятьдесят три.

Седьмой — квинтиллионов, 19—21 знак.

• 771 642 962 921 398 634 389.

Семьсот семьдесят один квинтиллион шестьсот сорок два квадриллиона девятьсот шестьдесят два триллиона девятьсот двадцать один миллиард триста девяносто восемь миллионов шестьсот тридцать четыре тысячи триста восемьдесят девять.

Восьмой — секстиллионов, 22—24 цифры.

• 842 527 342 458 752 468 359 173

Восемьсот сорок два секстиллиона пятьсот двадцать семь квинтиллионов триста сорок два квадриллиона четыреста пятьдесят восемь триллионов семьсот пятьдесят два миллиарда четыреста шестьдесят восемь миллионов триста пятьдесят девять тысяч сто семьдесят три.

Можно просто различать классы по нумерации, к примеру, число 11 класса содержит в себе при написании от 31 до 33 знаков.

Но на практике запись такого количества знаков неудобна и чаще всего приводит к ошибкам. Поэтому при операциях с такими величинами производится сокращение количества нулей путём возведения в степень. Ведь значительно проще написать 10 31, чем приписывать тридцать один ноль к единице.

Разрядное слагаемое в математике. Сумма разрядных слагаемых

Уровень владения приемами устных и письменных вычислений напрямую зависит от усвоения детьми вопросов нумерации чисел. На изучение указанной темы в каждом классе начальной школы отводится определенное количество часов. Как показывает практика, для отработки навыков не всегда бывает достаточно того времени, которое предусмотрено программой.

Понимая всю важность вопроса, опытный учитель обязательно будет включать в каждый урок упражнения, связанные с нумерацией чисел. Кроме того, он учтет виды этих заданий и последовательность их предъявления ученикам.

Требования программы

Для понимания того, к чему необходимо стремиться самому педагогу и его воспитанникам, первый должен четко знать требования, которые выдвигает программа по математике в целом и в вопросах нумерации в частности.

• Ученик должен уметь образовать любые числа (понимать, как это делается) и называть их – требование, которое относится к устной нумерации.
• Изучая письменную нумерацию, дети должны научиться не только записывать числа, но и сравнивать их. При этом они опираются на знание поместного значения цифры в записи числа.
• С понятиями «разряд», «разрядная единица», «разрядное слагаемое» дети знакомятся во втором классе. Начиная с этого же времени термины вводятся в активный словарь школьников. Но учитель употреблял их на уроках математики еще в первом классе, до изучения понятий.
• Знать названия разрядов, записывать число в виде суммы разрядных слагаемых, использовать на практике такие единицы счета, как десяток, сотня, тысяча, воспроизводить последовательность любого отрезка натурального ряда чисел – это тоже требования программы к знаниям учеников начальной школы.

Как использовать задания

Предлагаемые ниже группы заданий помогут учителю в полной мере сформировать умения, которые в итоге приведут к желаемым результатам в области развития вычислительных навыков учеников.

Упражнения могут использоваться на уроках во время устного счета, повторения пройденного материала, в момент изучения нового. Их можно предлагать для домашних заданий, во внеклассной работе. На материале упражнений учитель может организовать групповые, фронтальные и индивидуальные формы деятельности.

Многое будет зависеть от арсенала приемов и методов, которыми владеет учитель. Но регулярность использования заданий и последовательность отработки навыков – главные условия, которые приведут к успеху.

Образуем числа

Ниже приведены примеры упражнений, направленных на отработку понимания образования чисел. Их необходимое количество будет зависеть от уровня развития учеников класса.

1. Используя рисунок, расскажите, как образовалось число. Прочитайте его (2 сотни, 4 десятка, 3 единицы). Число изображено геометрическими фигурами, например, большими и маленькими треугольниками, точками.
2. Запишите и прочитайте числа. Изобразите их при помощи геометрических фигур. (Учитель читает: «2 сотни, 8 десятков, 6 единиц». Дети слушают задание, затем последовательно выполняют его).
3. Продолжите запись по образцу. Прочитайте числа и изобразите их с помощью модели. (4 сот. 8 ед. = 4 сот. 0 дес. 8 ед. = 408; 3 сот. 4 ед. = … сот. … дес. … ед. = …).

Называем и записываем числа

1. Упражнения этого вида включают задания, где требуется назвать числа, представленные геометрической моделью.
2. Назовите числа, набрав их на полотне: 967, 473, 285, 64, 3985. Сколько в них содержится единиц каждого разряда?

3. Прочитайте текст и запишите каждое числительное цифрами: на семи … машинах перевезли одну тысячу пятьсот двенадцать … ящиков с помидорами. Сколько понадобится таких машин, чтобы перевезти две тысячи восемьсот восемь … таких же ящиков?

4. Запишите числа цифрами. Величины выразите в мелких единицах: 8 сот. 4 ед. = …; 8 м 4 см = …; 4 сот. 9 дес. =…; 4 м 9 дм = …

Читаем и сравниваем числа

1. Прочитайте вслух числа, которые состоят из: 41 дес. 8 ед.; 12 дес.; 8 дес. 8 ед.; 17 дес.

2. Прочитайте числа и подберите к ним соответствующее изображение (на доске в одном столбике записаны различные числа, а в другом — в произвольном порядке изображены модели этих чисел, ученики должны установить их соответствие.)

3. Сравните числа: 416 … 98; 199 … 802; 375 … 474.

4. Сравните величины: 35 см … 3 м 6 см; 7 м 9 см … 9 м 3 см

Работаем с разрядными единицами

1. Выразите в разных разрядных единицах: 3 сот. 5 дес. 3 ед. = … сот. … ед. = … дес. … ед.

2. Заполните таблицу:

Единицы 3 разряда

Единицы 2 разряда

Единицы 1 разряда

3. Выпишите числа, где цифра 2 обозначает единицы первого разряда: 92; 502; 299; 263; 623; 872.

4. Запишите трехзначное число, где количество сотен равно трем, а единиц — девяти.

Сумма разрядных слагаемых

1. Прочитай записи на доске: 480; 700 + 70 + 7; 408; 108; 400 + 8; 777; 100 + 8; 400 + 80. В первом столбике расположи трехзначные числа, сумма разрядных слагаемых должна находиться во втором столбике. Соедини стрелкой сумму с ее значением.
2. Прочитай числа: 515; 84; 307; 781. Замени суммой разрядных слагаемых.
3. Запиши пятизначное число, в котором будет три разрядных слагаемых.
4. Запиши шестизначное число, содержащее одно разрядное слагаемое.

Изучаем многозначные числа

1. Найдите и подчеркните трехзначные числа: 362, 7; 17; 107; 1001; 64; 204; 008.
2. Запишите число, у которого 375 единиц первого класса и 79 единиц второго класса. Назовите наибольшее и наименьшее разрядное слагаемое.
3. Чем схожи и отличаются друг от друга числа каждой пары: 8 и 708; 7 и 707; 12 и 112?

Применяем новую счетную единицу

1. Прочитайте числа и скажите, сколько десятков в каждом из них: 571; 358; 508; 115.
2. Сколько сотен содержится в каждом записанном числе?
3. Разбейте числа на несколько групп, обосновав свой выбор: 10; 510; 940; 137; 860; 86; 832.

Поместное значение цифры

1. Из цифр 3; 5; 6 составьте все возможные варианты трехзначных чисел.
2. Прочитайте числа: 6; 16; 260; 600. Какая цифра повторяется в каждом из них? Что она обозначает?
3. Найдите сходство и отличие, сравнив числа между собой: 520; 526; 506.

Умеем считать быстро и правильно

В задания этого вида должны включаться упражнения, в которых требуется определенное количество чисел расставить в порядке убывания или возрастания. Можно предложить детям восстановить нарушенный порядок следования чисел, вставить пропущенные, убрать лишние числа.

Находим значения числовых выражений

Используя знания нумерации, ученики без затруднений должны находить значения выражений типа: 800 – 400; 500 – 1; 204 + 40. При этом полезно будет постоянно спрашивать детей, что они заметили, выполняя действие, просить назвать их то или иное разрядное слагаемое, обращать их внимание на положение одной и той же цифры в числе и т. д.

Все упражнения разделены на группы для удобства их использования. Каждая из них может быть дополнена учителем по своему усмотрению. Заданиями такого вида очень богата наука математика. Разрядные слагаемые, которые помогают освоить состав любого многозначного числа, должны занять особое место в подборе заданий.

Если данный подход к изучению нумерации чисел и их разрядного состава будет использоваться учителем на протяжении всех четырех лет обучения в начальной школе, то положительный результат обязательно проявится. Дети будут легко и без ошибок выполнять арифметические вычисления любого уровня сложности.

Умение быстро анализировать ситуацию, просчитывать варианты развития и составлять единое изображение реальности — это одно из ключевых умений высокоэффективных людей. Личностное развитие невозможно без интеллектуального, чему способствует быстрый .

В математике довольно часто используют формулы сокращенного умножения. Рассмотрим подробно основные из них, а также примеры с комментариями.

Устный счет на уроках математики — любимый вид деятельности учеников начальной школы.Возможно, это является заслугой учителей, которые стремятся разнообразить этапы урока, где включен устный счет.Что дает детям этот вид работы, кроме повышенного .

Сумма кубов — это формула сокращенного умножения, позволяющая сократить несколько операций при упрощении математических выражений.

У каждой группы людей, объединившихся по какому-либо признаку, рано или поздно образовывается собственный лексикон, позволяющий поддерживать разговор на общие темы без длинных ненужных пояснений. Так называемые анимешники, то есть поклонники аниме, .

Скрытый «режим бога» в Windows 7 теперь доступен и для вас! Коротко и предельно понятно в статье рассказывается, как активировать код доступа к инженерному меню операционной пресловутой системы от Microsoft.

В курсе информатики особое место уделяется такому понятию, как системы счисления. Как правило, на него выделяют несколько уроков или практических занятий с целью не только усвоить основные понятия темы, изучить виды систем счисления, но и познакомиться с двоичной, восьмеричной и шестнадцатеричной арифметикой.

В данной статье мы расскажем о том, как хранятся данные в компьютере, в частности, о распределении числовых данных в ячейках памяти.

Двоичная система счисления, несмотря на кажущуюся простоту, оказалась наиболее эффективной в современной вычислительной технике.

Математика выделилась из общей философии в VI-V веках до н. э., и с этого момента началось ее победное шествие по миру. Каждый этап развития вносил что-то новое – элементарный счет эволюционировал, преображался в дифференциальное и интегральное исчисление, сменялись века, формулы становились все запутаннее, и настал тот момент, когда «началась самая сложная математика – из нее исчезли все числа». Но что же лежало в основе?