Что такое сумма чисел в математике

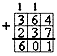
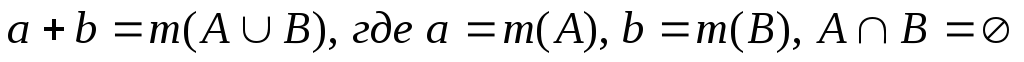Чему равна сумма чисел от 1 до 10?

Сумма первых десяти натуральных чисел, то есть от 1 до 10, равна 55.

Точно так же, что такое математика? Сумма результат сложения. Например, сложение 1, 2, 3 и 4 дает записанную сумму 10. (1) Суммируемые числа называются слагаемыми или иногда слагаемыми.

Чему равна сумма чисел от 1 до 9? Пошаговое объяснение:

Похожие страницы:Блог

Какие есть 3 вида налогов?

Как найти среднюю точку между двумя точками?

Как вы делаете кадровые прогнозы?

Как найти начальную скорость, зная только время?

45 это правильный ответ.

Какова сумма от 1 до 25? Следовательно, сумма счетных чисел от 1 до 25 включительно равна 325.

Во-вторых, каковы суммы 6?

Как найти сумму и упростить?

тогда Как вы делаете сумму в математике? Чай символ Σ (сигма) обычно используется для обозначения суммы нескольких терминов. Этот символ обычно сопровождается индексом, который варьируется, чтобы охватить все термины, которые необходимо учитывать в сумме. Например, сумму первых целых чисел можно представить следующим образом: 1 2 3 ⋯.

Какая сумма 3?

Какие суммы 4?

Число	Повторяющийся цикл суммы кратных цифр
2	2,4,6,8,1,3,5,7,9 <>
3	3,6,9,3,6,9,3,6,9 <>
4	4,8,3,7,2,6,1,5,9 <>
5	5,1,6,2,7,3,8,4,9 <>

Как найти сумму 25?

Таким образом, сумма членов от 1 до 50 равна 1275.

Чему равна сумма 1 30? Итак, сумма от 1 до 30 равна 465.

Какие суммы 8?

Какова сумма ответов 4 и 5?

4 + 5 = 9. Это твой ответ, мой друг.

Чему равна сумма +6 и 8? Сумма 6 и 8 в основном означает 6 + 8 . Это оценивается до 14 .

Что такое формула упрощения? Упрощение или упрощение дробей означает упрощение сложного математического выражения для получения однозначного или прямого ответа. Чтобы понять это ясно, давайте решим следующий пример.
.

БОДМАС правила
B	Скобка (скобки решаются в порядке (), <> и [] соответственно.
M	Умножение
A	Дополнение
S	вычитание

Как найти сумму и разность в математике?

Как вы находите упрощение? Чтобы упростить математическое выражение без круглых скобок, вы соблюдать порядок действий, то есть PEMDAS (круглые скобки, экспоненты, умножение, деление, сложение, вычитание). Поскольку в выражении нет скобок, вы можете начать проверку выражения на экспоненты. Если это так, сначала упростите это.

Как посчитать сумму в Excel?

Выберите ячейку рядом с числами, которые вы хотите суммировать, нажмите Автосумма на вкладку «Главная», нажмите «Ввод», и все готово. Когда вы нажимаете «Автосумма», Excel автоматически вводит формулу (которая использует функцию СУММ) для суммирования чисел.

Как вы читаете формулу суммирования? Ряд может быть представлен в компактной форме, называемой суммированием или сигма-нотацией. Греческая заглавная буква ∑ используется для обозначения суммы. Ряд 4+8+12+16+20+24 можно представить как 6∑n = 14n . Выражение читается как сумма 4n при изменении n от 1 до 6.

Что означает ∑?

Символ ∑ указывает суммирование и используется как сокращенное обозначение суммы терминов, следующих за шаблоном.

Какие суммы 5?

Что такое итоговый пример?

Сумма 6 и 9, например, равна 15, а сумма 4 х и 5 х равна 9 х. 1. 1. Определение суммы общая сумма, которую вы получите, сложив несколько вещей, или общая сумма чего-то, что существует, или общая сумма денег, которые у вас есть. 4 является примером суммы 2+2.

Сложение натуральных чисел

Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!

Как вы уже знаете, любое натуральное число представляет собой единицу или собрание нескольких единиц. Так вот, мы можем взять несколько чисел и объединить все единицы, которые их составляют, в одно большое собрание. Число, которое получилось в результате этого объединения, называется суммой .

Сумма чисел – это такое число, которое получается после объединения всех единиц других данных натуральных чисел.

Слагаемые – это числа, над которыми мы выполняем действие сложения. Иными словами, это те числа, количество единиц которых мы объединяем в новом числе.

Арифметическое действие – это нахождение нового числа при помощи двух или нескольких других данных чисел.

В курсе математики 5 класса изучаются основные арифметические действия – сложение, вычитание, умножение и деление.

Сложение – это арифметическое действие, которое выполняется для получения суммы нескольких чисел.

Или другими словами:

Сложение – это действие увеличения числа на количество единиц, содержащихся в другом числе.

Сумма – это результат действия сложения.

На записи действие сложения обозначается знаком + ( плюс ). То есть, если записано 3+2+5 , то это означает, что нам нужно найти сумму этих трех чисел: 3, 2 и 5. Сумма записывается обычно справа от слагаемых после знака = ( равно ): 3+2+5 = 10.

Сумма чисел состоит (слагается, складывается, – можно говорить по-разному) из двух или более слагаемых. Понятно, что сумма всегда больше любого ее слагаемого .

Слагаемые – это не что иное, как состав числа , обозначающего сумму этих слагаемых.

Компоненты действия сложения для двух слагаемых:

Компоненты сложения для трех слагаемых:

Действие сложения можно выполнить всегда . Действительно, так как натуральный ряд бесконечен, то мы всегда можем любые числа этого ряда объединить в другое, какое угодно большое число.

Действие сложения всегда имеет единственный результат . Действительно, если мы, к примеру, отметим на координатном луче с началом в точке O и единичным отрезком 1 см отрезок OA длиной 5 см , а потом построим еще один отрезок AB длиной 7 см , то у нас получится только единственный отрезок OB длиной 12 см .

Рисунок 1. Сумма двух чисел на координатном луче.

Основные свойства суммы натуральных чисел

Есть два основных закона суммы , из которых следуют остальные ее свойства:

• переместительный закон сложения,
• сочетательный закон сложения.

Переместительный закон сложения

Сумма двух или нескольких чисел от изменения порядка сложения слагаемых не меняется.
Это значит, что значение суммы не зависит от порядка выполнения действия сложение.

Например, в каком бы порядке мы ни складывали числа 2 , 3 и 5 , результат неизменно будет 10 :

Сочетательный закон сложения

Сумма нескольких чисел не поменяется, если некоторые слагаемые заменить их суммой.
Это значит, что мы можем группировать слагаемые как угодно, а также выполнять действия сложения в любом порядке.

Например, если в нашем примере мы заменим слагаемые 2 и 3 их суммой, то результат останется такой же, как и при обычном сложении слагаемых:

То же самое будет, если мы заменим слагаемые 3 и 5 , или 2 и 5 их суммами:

или

или

Из этих законов вытекает правило прибавления слагаемого к сумме или суммы к слагаемому .

Для прибавления суммы некоторых чисел к числу или некоторого числа к сумме чисел, нужно сложить это число с одним из слагаемых суммы, а получившийся результат сложить последовательно с остальными слагаемыми.

Пример 1. Прибавление числа к сумме чисел:

Можно сразу вычислить сумму чисел в скобках и сложить ее с первым слагаемым:

325 +( 12 + 64 + 5 ) = 325 +81 = 406

Также можно использовать правило прибавления слагаемого и суммы. Результат при этом не поменяется

325 + 12 = 337;
337+ 64 = 401;
401+ 5 = 406
или
325 + 64 = 389;
389+ 12 = 401;
401+ 5 = 406 .

Пример 2. Прибавление суммы чисел к другому числу:

Можно сразу вычислить сумму чисел в скобках и сложить ее со вторым слагаемым

( 54 + 240 + 189 )+ 37 = 483+ 37 = 520

Или можно использовать правило прибавления суммы чисел к числу. Результат останется тот же.

54 + 37 = 91;
91+ 240 = 331;
331+ 189 = 520
или
240 + 37 = 277;
277+ 54 = 331;
331+ 189 = 520 .

Изменение суммы чисел с изменением слагаемых

Чтобы понять, как изменится сумма чисел , если изменить одно или несколько ее слагаемых, нужно вспомнить, что сумма представляет собой собрание всех единиц , из которых состоят слагающие ее числа. Поэтому, легко можно понять, что:

При увеличении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже увеличится на это же число (на это же количество единиц).

При уменьшении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже уменьшится на это же число (на это же количество единиц).

Эти два свойства справедливы и в обратную сторону. То есть, если увеличить или уменьшить сумму на какое-то число, тогда для сохранения равенства нужно соответственно увеличить или уменьшить одно из слагаемых.

Если увеличить одно из слагаемых на какое-то число (на какое-то количество единиц), а другое уменьшить на это же число (на это же количество единиц), то в результате сумма не поменяется .

Простой пример увеличения суммы при увеличении слагаемого: у вас есть 700 рублей; 200 рублей лежит в левом кармане, а 500 – в правом. Вы нашли на улице 300 рублей и положили их в левый карман, после чего там стало 200+300=500 рублей. Таким образом, всего у вас оказалось 500+500=1000 рублей, то есть, сумма всех ваших денег увеличилась на 300 рублей.

Попробуйте самостоятельно придумать примеры для всех трех правил.

Сложение однозначных чисел

Сложение двух однозначных чисел выполняется так: одно число увеличивается на количество единиц другого числа. То есть, единицы одного числа присоединяются к единицам другого числа.

Например, для нахождения суммы 5+2 нужно к числу 5 присоединить 2 единицы. Тогда получим 5+2=7 . А если нужно к числу 7 прибавить число 8 , или другими словами, найти сумму 7+8 , то после присоединения к 7 единиц числа 8 получим 1 десяток единиц и еще 5 единиц , то есть, число 15 .

Сложение однозначных чисел – это первый и очень важный шаг в освоении этого арифметического действия. Если хорошо выучить все результаты сложения однозначных чисел между собой , тогда вы сможете намного быстрее складывать в уме любые числа.

Сложение многозначного числа с однозначным

Чтобы найти сумму многозначного числа и однозначного, можно действовать двумя способами. Оба они основаны на свойствах суммы чисел. Рассмотрим их на примерах.

Допустим, нам нужно найти сумму чисел 88 и 5 .

Представим число 88 в виде суммы 80+8 и прибавим к ней число 5 . После этого, найдем сумму однозначных чисел 8 и 5 , получится 13 . Прибавим этот результат к числу 80 . Число 13 – это 10+3 , поэтому мы к 8 десяткам прибавляем 1 десяток, получаем 9 десятков, или число 90 , а к нему прибавляем еще 3 (оставшиеся от числа 13 ), и получим 93 .

То есть, мы проделываем такие действия:

88+5 = 80+8+5 = 80+13 = 80+10+3 = 90+3=93.

Замечаем, что если к 88 прибавить 2 , то получим полный десяток , то есть, число 90 . Тогда представляем число 5 в виде суммы 2+3 ; число 2 складываем с 88 , получаем замеченное нами ранее число 90 . Добавляем к нему оставшееся число 3 , и получаем результат 93 .

То есть, ход вычисления был такой:

88+5 = 88+2+3 = 90+3 = 93.

Сложение в столбик многозначных чисел

Сумма многозначных чисел удобно вычисляется, если использовать так называемое сложение в столбик .

Сложение в столбик – это способ нахождения суммы чисел путем их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим).

Этот способ простой, и он помогает не запутаться во время вычисления, не допустить ошибки. Но, чтобы складывать быстро, как я и говорил раньше, вам нужно очень хорошо знать все попарные суммы однозначных чисел .

Итак, допустим, что нам нужно найти сумму : 5728+803

Запишем их друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел , т.е. единицы под единицами, десятки под десятками и т.д. После этого, под вторым слагаемым проводим горизонтальную черту, а между слагаемыми ставим знак действия, т.е. плюс. У нас получилась такая запись:

Теперь нам нужно сложить между собой единицы каждого разряда , начиная с первого: сперва простые единицы, потом десятки единиц, потом сотни единиц и т.д. Результаты этих сложений записываем под чертой в том разряде, единицы которого мы складывали.

Начинаем с простых единиц: 8+3=11 . У нас получилось число 11 , то есть, 1 десяток и 1 единица. 1 единицу мы записываем под чертой в разряде единиц, а 1 получившийся десяток нужно будет дополнительно прибавить к сумме единиц разряда десятков . Чтобы не забыть совершить это действие, мы пишем над цифрами разряда десятков маленькую цифру 1 или ставим там точку.

Про подобное действие обычно говорят: « один пишем, один в уме » , то есть, оставляем в памяти, чтобы не забыть добавить при следующем действии.

Далее переходим к десяткам. У первого слагаемого 2 единицы разряда десятков , а у второго 0 , поэтому: 2+0=2 . Мы помним, что после сложения простых единиц у нас образовался дополнительно 1 десяток , поэтому к этому результату добавляем еще единицу: 2+1=3 . У нас получилось 3 десятка , поэтому записываем цифру 3 под чертой в разряде десятков .

Следующими идут сотни: 7+8=15 . Первым делом проверяем, не нужно ли нам дополнительно добавлять единицу ? В нашем случае нет, потому что на предыдущем шаге при сложении десятков мы получили однозначное число . Поэтому, пишем под чертой в разряде сотен цифру 5 . И у нас получилось дополнительно 10 сотен , то есть, 1 тысяча единиц. Значит, нам нужно отметить эту получившуюся 1 тысячу как дополнительную , поставив маленькую цифру 1 над цифрами разряда тысяч.

В разряде тысяч у первого слагаемого стоит цифра 5 , а у второго ничего не стоит. Но мы помним, что при отсутствии разрядов в начале числа (слева) нули не пишутся , но подразумевается, что в этих разрядах по 0 единиц. Поэтому мы находим сумму 5+0=5 , т.е. 5 единиц разряда тысяч и добавляем к ней дополнительную 1 единицу тысяч, полученную после сложения разрядов сотен. 5+1=6 . Записываем эту цифру под чертой в разряде тысяч .

После нахождения суммы чисел методом сложения столбиком, записываем результат решения в исходном строчном примере:

5728+803 = 6531

Сложение в столбик нескольких многозначных чисел

Этим способом так же легко можно найти сумму нескольких многозначных чисел .

Рассмотрим пример: 12044+28609+1358

Сложив простые единицы, мы получим 21, то есть, 2 десятка и 1 единицу. Записываем под чертой в разряде единиц цифру 1, а 2 отмечаем «в уме».

Сложив десятки этих трех чисел , мы получим 4+0+5=9 единиц разряда десятков. Добавив 2 десятка единиц, которые у нас были «в уме», получаем 11 , то есть, 10 десятков и ещё 1 десяток . Под чертой мы записываем цифру 1 в разряде десятков , а так как 10 десятков – это не что иное как 1 сотня , то мы отмечаем «единицу в уме», то есть, ставим над всеми тремя числами в разряде сотен маленькую цифру 1 .

Теперь складываем 0 сотен первого числа , 6 сотен второго и 3 сотни третьего . Получается 9 сотен. Добавляем 1 сотню, которая была «в уме» после сложения всех десятков, и у нас выходит 10 сотен , то есть, 1 тысяча единиц. Значит, под чертой в разряде сотен мы пишем 0 (так как у нас не получилось ни одной единицы сотен , только десяток сотен), а над всеми числами в разряде тысяч отмечаем дополнительную 1 тысячу.

В разряде тысяч мы находим сумму 2+8+1 , это будет 11 тысяч единиц , добавляем 1 тысячу, которая получилась после сложения сотен. Получаем 12 тысяч единиц, то есть, 10 тысяч и 2 тысячи. Цифру 2 пишем в разряде тысяч единиц под чертой, а единицу десятка тысяч (наши 10 тысяч единиц) отмечаем сверху в соответствующем разряде.

Нам осталось сложить десятки тысяч единиц: 1+2+0=3 десятка тысяч , и прибавить к результату 1 десяток тысяч, получившийся после прошлого шага. У нас вышло 4 десятка тысяч, поэтому в этом разряде под чертой мы пишем цифру 4 .

Нам остается только записать результат в начальном примере:

12044+28609+1358

Хочу обратить внимание, что при сложении в столбик все шаги (сложение единиц каждого разряда) совершаются последовательно в одной записи . Я расписывал их отдельными только для лучшего понимания сути процесса сложения. И конечно же, не нужно выделять каждый разряд отдельным цветом. В случае рассмотренных выше примеров все решение выглядит так:

math serfer .narod.ru

В математике для записи сумм, содержащих много слагаемых, или в случае, когда число слагаемых обозначено буквой, применяется следующая запись:

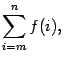
которая расшифровывается так

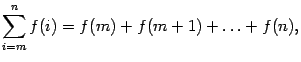( 14 .1)

где — функция целочисленного аргумента. Здесь символ (большая греческая буква «сигма») означает суммирование. Запись внизу символа суммирования показывает, что переменная, которая меняет свои значения от слагаемого к слагаемому, обозначена буквой и что начальное значение этой переменной равно . Запись вверху обозначает последнее значение, которое принимает переменная .

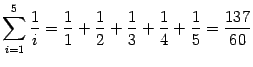
1) .

2) . Так как в правой части стоит сумма геометрической прогрессии с первым членом равным и знаменателем прогрессии равным , то эту сумму легко найти

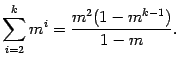
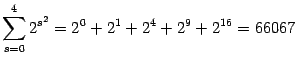
3) .

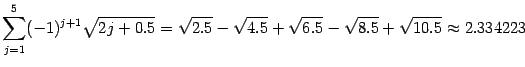
4) .

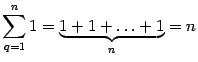
5) .

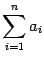
В курсе линейной алгебры чаще всего будут встречаться суммы вида . Здесь переменная с индексом рассматривается как функция от своего индекса. Поэтому

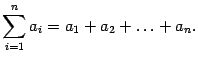
С помощью знака суммы формулу (10.1) скалярного произведения векторов можно записать так:

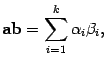( 14 .2)

где для трехмерного пространства , для плоскости .

Для единообразия будем считать, что

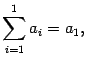
и говорить, что это сумма, содержащая одно слагаемое.

Замечание 14 . 1 Буква, стоящая внизу под знаком суммы (индекс суммирования), не влияет на результат суммирования. Важно лишь, как от этого индекса зависит суммируемая величина. Например,

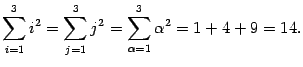
в правой части никакой буквы нет, значит, и результат от не зависит.

Предложение 14 . 1 Множитель, не зависящий от индекса суммирования, может быть вынесен за знак суммы:

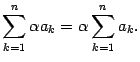
Доказательство этого предложения предоставляется читателю.

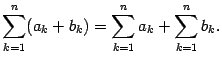( 14 .3)

Это предложение является частным случаем следующего утверждения.

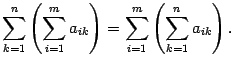( 14 .4)

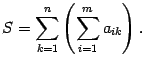
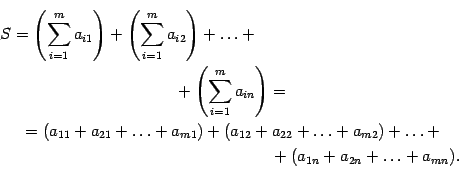
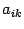
Раскроем скобки в правой части этого равенства. Получим сумму элементов при всех допустимых значениях индексов суммирования. Слагаемые сгруппируем по-другому, а именно, сначала соберем все слагаемые, у которых первый индекс равен 1, потом, у которых первый индекс равен 2 и т.д. Получим

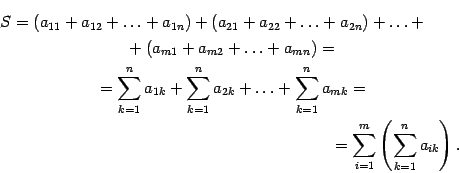
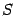
Заменив в этом равенстве в левой части его выражением через знаки суммирования, получим формулу (14.4).

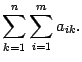
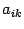
Нужно помнить, что двойная сумма означает сумму элементов для всех допустимых значений индексов суммирования. По этой же причине, если встречается запись, содержащая подряд три или более символов суммирования, то порядок расстановки этих символов можно менять произвольно.

Если границы изменения всех индексов суммирования одинаковы, то можно для суммирования по нескольким индексам использовать запись вида

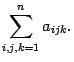
Иногда под символом суммы указывают дополнительные условия, налагаемые на индексы суммирования. Так запись

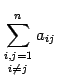
означает, что в сумму не включаются величины , . , то есть с равными индексами.

Иногда в записи суммы не указываются границы изменения индексов, например,

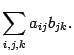
Такая запись используется, когда значения, которые могут принимать индексы, очевидны из предыдущего текста или будут оговорены сразу после окончания формулы.

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Что такое сумма чисел в математике

СУММЫ ВЕЗДЕСУЩИ в математике, поэтому нам потребуются основные приемы обращения с ними. Эта глава знакомит с теми обозначениями и методами, которые помогут освоиться с суммированием.

2.1 ОБОЗНАЧЕНИЯ СУММ

В гл. 1 мы уже сталкивались с суммой первых натуральных чисел, которую старательно выписывали как

Многоточие в таких формулах указывает на то, что пропущенное нужно восполнить по аналогии с соседними членами суммы. Разумеется, мы должны остерегаться сумм типа которые не что иное, как вопиющая бессмыслица.

С другой стороны, включение членов 3 и было излишней

роскошью — достаточно было бы написать Крайне самоуверенные ограничились бы даже записью

Мы будем иметь дело с суммами общего вида

где каждое — определенное каким-то образом число. Такое обозначение имеет то преимущество, что при наличии достаточно богатого воображения можно „представить» себе всю сумму целиком, почти так, как если бы она была выписана полностью.

Каждый элемент такой суммы называется ее членом. Зачастую эти члены определяются косвенно, в виде формул, следуя некоторому легко просматривающемуся правилу, а в ряде случаев приходится записывать суммы в развернутом виде с тем, чтобы стал понятен их смысл. Например, если предполагается, что формула

должна обозначать сумму из а не из членов, то ее следует записать более аккуратно как

Хотя обозначение с использованием широко распространено, оно излишне громоздко и может вызывать разночтения. Используются и другие способы записи суммы, особенно форма записи с явными пределами

которая называется сигма-обозначением, поскольку здесь фигурирует греческая буква (прописная сигма). Это обозначение говорит, что включать в сумму надо именно те члены номер к которых является целым числом, лежащим между нижней и верхней границами 1 и включительно. Это произносится как „сумма по к от 1 до Это — обозначение ввел Жозеф Фурье в 1820 г., и оно вскоре покорило математический мир.

Кстати, величина после знака (в данном случае называется общим членом.

Говорят, что переменный индекс к связан знаком в (2.2), поскольку к в не имеет отношения к тем к, которые появляются за рамками сигма-обозначения. В частности, любая другая буква могла бы заменить к без изменения смысла (2.2). Часто используется буква (возможно потому, что с нее начинается слово «indех»), но мы будем, как правило, суммировать по к, поскольку разумно сохранить i за

Оказывается, что еще более полезным, чем форма записи с явными пределами, является обобщенное сигма-обозначение: мы просто записываем одно или несколько условий под знаком задавая тем самым множество значений индекса, по которым следует проводить суммирование. Например, суммы (2.1) и (2.2) можно записать иначе как

Хотя в этом отвлеченном примере и не видно существенного различия между новым обозначением и обозначением (2.2), обобщенное обозначение позволяет «брать» суммы по множествам значений индекса, не ограниченным последовательными целыми числами. К примеру, сумму квадратов всех нечетных положительных чисел, меньших 100, можно выразить таким образом:

Аналог этой суммы с явными пределами

более громоздок и менее нагляден. Аналогично, сумма обратных всем простым числам между 1 и есть

в случае формы записи с явными пределами потребовалось бы написать

где означает простое число, — количество простых чисел, не превосходящих (Между прочим, эта сумма дает приблизительно среднее число простых делителей „случайного» целого числа, близкого к поскольку около этих целых чисел делятся на . При большом она примерно равна ., где -константа Мертенса [220], означает натуральный логарифм х, а означает

Но самым большим преимуществом обобщенного сигма-обозначения является то, что с ним обращаться гораздо легче, чем с формой записи с явными пределами. Предположим, например, что нам захотелось заменить переменный индекс на . В случае обобщенной формы записи мы имеем

легко сообразить, что происходит, и мы производим подстановку почти без всяких раздумий. А в случае обозначения с явными пределами получаем

в этом случае труднее понять, что стряслось, и больше шансов совершить оплошность.

Тем не менее, форма записи с явными пределами не является совершенно бесполезной. Она имеет округлые, привлекательные формы и быстро пишется, ибо сумма (2.2) состоит из семи символов, в сравнении с восемью, требуемыми для суммы (2.3). Поэтому мы будем зачастую использовать с пределами при формулировке задачи или представлении результата, но предпочтем иметь дело с соотношениями при действиях с суммой, которые требуют преобразования переменной суммирования.

Знак встречается в этой книге более 1000 раз, поэтому надо бы убедиться в том, что мы наверняка знаем, что он означает.

представляет собой сокращенную запись суммы всех членов а, таких, что целое к удовлетворяет заданному условию . (Условие — это некоторое утверждение относительно к, которое может быть либо истинным, либо ложным.) Пока допустим, что лишь для конечного числа к, удовлетворяющих условию в противном случае будет складываться бесконечное число ненулевых членов, и тогда придется несколько исхитриться. Другая крайность: когда ложно для всех целых к, мы получаем «пустую» сумму — пустая сумма по определению равна нулю.

Если знак суммы появляется в тексте, а не в выделенной формуле, то используется слегка измененная форма записи (2.4): мы пишем придавая условию вид нижнего индекса при того чтобы формула не слишком выходила за пределы строки. Аналогично, представляет собой удобный вариант записи (2.2), если мы хотим уместить данное обозначение в одну строку.

Зачастую соблазнительна запись

поскольку при соответствующие члены этой суммы равны нулю — разве не разумнее сложить члена вместо членов? Но не надо поддаваться таким соблазнам: разумность в смысле вычисления и разумность в смысле понимания — это не одно и то же! В дальнейшем мы обнаружим, что как можно более простые верхние и нижние границы индекса суммирования имеют то преимущество, что при простых границах гораздо проще обращаться с суммами. Более того, обозначение типа может даже приводить к опасной двусмысленности, поскольку не совсем ясен его смысл при или (см. упр. 1). Нулевые члены безопасны и часто избавляют от ненужных хлопот.

Обозначения, которые мы обсуждали до сих пор, являются общепринятыми, но сейчас мы собираемся решительно отступить от сложившейся традиции. Кеннет Айверсон в своем языке программирования АПЛ [4, с. 11, см. также 152], внес замечательную идею, которая, как будет видно, существенно упрощает многое из того, что мы собираемся проделать в этой книге. Его идея состоит в том, чтобы просто заключать истинное-или-ложное утверждение в квадратные скобки и считать при этом, что результат равен 1, если данное утверждение истинно, и 0, если данное утверждение ложно. Например,

Нотация Айверсона позволяет выражать суммы без каких бы то ни было ограничений на индекс суммирования, поскольку сумму (2.4) можно переписать в виде

Если ложно, то член равен нулю, так что можно спокойно включать его в состав суммируемых членов. Это упрощает манипулирование с индексом суммирования, ибо нет нужды беспокоиться о граничных условиях.

Необходимо только отметить одну техническую деталь: иногда бывает определено не для всех целых k. Это затруднение можно обойти, допуская, что является „очень сильно нулевым», когда ложно, — оно настолько нулевое, что делает равным нулю, даже когда не определено. Например, если воспользоваться нотацией Айверсона для записи суммы чисел, обратных простым в виде

то при , равном нулю, проблем с делением на нуль не возникает, потому что наше допущение позволяет считать, что [О простое] .

Давайте теперь подытожим то, что обсуждалось до сих пор в отношении сумм. Имеются два заслуживающих внимания способа записи суммы членов: в одном случае используется в другом Запись с многоточием часто подсказывает полезные преобразования (в частности, группировку смежных членов), поскольку, когда вся сумма маячит у нас перед глазами, мы можем уловить упрощающую ее закономерность. Однако обилие добра сродни пороку. Сигма-обозначение компактно, впечатляет родных и близких и зачастую подсказывает преобразования, которые не столь очевидны в случае записи с многоточием. При работе с сигма-обозначением нулевые члены совсем не мешают — напротив, они часто облегчают — операцию.

Значение слова «сумма»

2. Общее количество, совокупность чего-л. Я думаю, что каждый из нас, художников, дорого бы дал, чтобы знать, какую сумму впечатлений зритель выносит, смотря на произведение живописи. Крамской, Письмо В. В. Стасову, 4 мая 1876. — Годовая сумма тепла для субтропиков три тысячи градусов, а в Колхиде она доходит до четырех тысяч пятисот градусов. Паустовский, Колхида.

3. Определенное, то или иное количество денег. Денежная сумма. Подотчетные суммы. □ [Городничий:] Да если спросят, отчего не выстроена церковь при богоугодном заведении, на которую назад тому пять лет была ассигнована сумма, то не позабыть сказать, что началась строиться, но сгорела. Гоголь, Ревизор. Никак нельзя было понять, откуда брались эти непомерные суммы долгов. Тихонов, В беззаботном городе.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

• Сумма (лат. summa — итог, общее количество):

Сумма (математика) — общее количество, результат сложения со знаком

Денежная сумма, сумма оплаты

Сумма (перен., книжн.) — итог, результат какой либо деятельности, например:

Суммарный алфавит, принятый в СССР

Суммарный коэффициент рождаемости

Сумма — жанр научного или дидактического сочинения, например:

СУ’ММА, ы, ж. [латин. summa]. 1. Число, представляющее результат сложения (мат.). Десять и пять дают в сумме пятнадцать. 2. Общее количество чего-н. (книжн.). Сила пролетариата в любой капиталистической стране несравненно больше, чем доля пролетариата в общей сумме населения. Ленин. К сумме разнородных впечатлений неожиданно прибавилось еще одно новое. Лесков. Вся с. человеческих знаний. 3. Какое-н. количество денег. Вы, может быть, думаете, что сумма незначительная? Тургенев. Большая с. Казенные суммы. Неизрасходованные суммы. ◊

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

су́мма

1. матем. результат сложения ◆ Сумма кубов двух чисел равна сумме этих чисел, умноженной на неполный квадрат их разности. А. Н. Барсуков, «Алгебра, учебник для 6-8 классов», 1970 г.

2. фин. определённое количество денег

Фразеологизмы и устойчивые сочетания

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: невысказанный — это что-то нейтральное, положительное или отрицательное?

Ассоциации к слову «сумма&raquo

Синонимы к слову «сумма&raquo

Предложения со словом «сумма&raquo

• Хотя финансовый директор может попросту воспользоваться полным перечнем мер, позволяющих бесплатно получить крупную сумму денег, но существует ряд вопросов, которые следует учитывать, прежде чем сделать это.

Цитаты из русской классики со словом «сумма»

• Из остальных денег ему предстояло погасить некоторые другие векселя Луганского с его бланками и пять тысяч выдать по условию Милашевичу — в остатке наличный гонорар составлял сравнительно небольшую сумму.

Сочетаемость слова «сумма&raquo

Какой бывает «сумма»

Понятия, связанные со словом «сумма»

Мезони́нный креди́т (англ. Mezzanine Loan) — относительно крупный кредит, как правило, необеспеченный (т. е. предоставляемый без залога имущества) или имеющий глубоко субординированную структуру обеспечения (к примеру, залоговое право на имущество третьей очереди, но без права регресса в отношении заёмщика). Срок возврата займа обычно превышает пять лет при погашении основной суммы в конце срока кредита. В рамках типовой оферты заём сопровождается отрывным сертификатом (купоном), дающим право на.

Капитализация процентов — причисление процентов к сумме вклада, позволяет в дальнейшем осуществлять начисление процентов на проценты путем выполнения двойной операции — выплата процентов и пополнение. Начисление процентов на проценты, используемое в некоторых видах банковских вкладов, или при наличии долга проценты, которые включаются в сумму основного долга, и на них также начисляются проценты. То же, что и сложный процент. Проценты по вкладу с капитализацией могут начисляться ежедневно, ежемесячно.

Средневзвешенная стоимость капитала (англ. weighted average cost of capital, WACC) — это средняя процентная ставка по всем источникам финансирования компании. При расчете учитывается удельный вес каждого источника финансирования в общей стоимости.

Эффективная процентная ставка (ЭПС, EIR, Effective Interest Rate) — процентная ставка (ставка дисконтирования), при которой дисконтированная стоимость денежного потока от финансового инструмента (актива, обязательства, инвестиционного проекта и т.д.) равна некоторой оценке текущей стоимости этого инструмента (вложений). Эффективная процентная ставка может определяться за любой временной интервал, но обычно подразумевается годовая эффективная процентная ставка.

Денежный, или банковский, мультипликатор (от лат. multiplicare — множить, приумножать, увеличивать) — экономический коэффициент, равный отношению денежной массы к денежной базе и характеризующий степень роста количества денег за счёт кредитных банковских операций.

Как суммировать числа

В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.

Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.

Количество просмотров этой статьи: 11 630.

Сложение – один из немногих навыков, которые мы изучали в школе, и он действительно пригодился нам в жизни. К счастью, научиться сложению не так уж и трудно. Есть несколько правил сложения, в зависимости от видов чисел, которые вы прибавляете, но wikiHow сделает все за вас. Просто перейдите к первому пункту!

• Например, представим, что в первой кучке было 5 бобов. Во второй – 3 боба. Когда вы смешали кучки и подсчитали все бобы, у вас оказалось 8! Так получилось, потому что 5 + 3 равно 8.

Учите числовые пары. Так как большинство людей считает с помощью десятичных множеств и чисел, делящихся на десять, вы можете использовать более легкий метод – выучить числовые пары, дающие в сумме десять. К примеру: 1+9, 2+8, 3+7, 4+6 и 5+5.

• Предположим, что вам нужно сложить ряд таких чисел, как 2, 16, 9, 3, 5, 18. Вы можете сложить 18 и 2 и получить 20. 4 подходит к 6, так что отнимите 4 от 5, прибавьте к 16, и у вас получится 20. У вас останется единица от 5, которую вы можете прибавить к 9 для того, чтобы получить 10.

• В предыдущем примере после подсчитанных 50 у вас осталось всего 3. Это очень легко подсчитать в уме!

Вторично проверьте результат на пальцах! По возможности вы всегда можете перепроверить ответ с помощью пальцев или другого метода.

• 2, если она сама по себе, должна находиться на месте «единиц».
• В 20 двойка должна находиться на месте «десятых».
• В 200 двойка — на месте «сотых».
• Следовательно, в номере 365 пятерка будет находиться на месте единиц, шестерка – на месте десятых, а 3 – сотых.

• 342
• _16
• __4

• В нашем примере, приведенном выше, сложив 2, 6 и 4, мы получим 12. Запишите последнюю цифру 12 – 2 снизу крайнего правого столбца.

• В этом примере у нас есть число, которое следует вписать в столбец десятых, так что запишите 1 из 12 сверху столбца, расположенного посередине, т.е. над 4 из 342.

• В этом примере мы имеем 1 из 12, плюс 4 от 342 и 1 от 16. В сумме будет 6.

• В данном примере в ответе получилось 362.

• 107.8
• _24.5
• __3.2
• _15.0

• В вышеприведенном примере после 15 не стоял ноль, он был добавлен для того, чтобы было легче различить столбцы.

• Ответ в этом примере будет равен 150.5.

• Вам необходимо уравнять 8 и 4. Как можно превратить 4 в 8, спросите вы? Умножив на 2!
• Умножите на два 3 и 4 из дроби 3/4. Тогда у вас получится 6/8.

Сложите числители. Числитель – это число, стоящее над знаком обыкновенной дроби. Теперь, когда у вас есть 1/8 и 6/8, сложите 1 и 6 для того, чтобы получить 7.

Узнайте ответ. Возьмите полученные числители и запишите их над знаменателем. Знаменатель оставьте без изменений. Это значит, что сумма дробей равна 7/8.

• Для этого вам нужно найти наименьшее число, на которое делятся и числитель, и знаменатель. В данном примере это 3. Разделяем каждое число на 3 для того, чтобы получить сокращенную дробь, в данном случае это 1/2.

Старайтесь оперировать более легкими числами. Если вам пришлось работать всего с несколькими числами, которые не очень увязываются с 10-ми, вы можете прибавить к ним или вычесть определенные числа для того, чтобы вам было легче подсчитать их в уме. К примеру, представим, что вам нужно провести следующее действие: 19 + 30. Было бы гораздо легче прибавить 20 + 30, не так ли? Поэтому прибавьте 1 к 19! И тогда все, что вам будет нужно сделать, – это вычесть ту цифру, которую вы прибавили для того чтобы получить окончательную сумму. Следовательно, 19 + 1 + 30 = 50 и 50 — 1 = 49.

• К примеру, если 7+1+2=10 и 2+3=5, то при сложении 1+2+2+3+7 в сумме вы получите 15.

Прибавляйте их по частям. Разделите на части единицы и десятки для того, чтобы вам было легче работать с цифрами, сложив сначала десятки, а уже затем единицы. Некоторым легче сложить, например, 40+30+10, а затем 2+5+7 вместо 42+35+17.

Занимательная математика: правило Гаусса

Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.

Первая статья из этого цикла посвящена правилу Гаусса.

Немного истории

Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.

Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:

Найти сумму всех натуральных чисел от 1 до 100.

Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.

Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.

Гаусс сгруппировал числа следующим образом:

(1+10) + (2+9) + (3+8) + (4+7) + (5+6)

Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо

Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:

1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100

Находим количество пар в ряде натуральных чисел. В данном случае их 50.

Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.

Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050

Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.

Задачи на использование правила Гаусса

А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.

Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.

В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.

Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.

Задача 1

Найти сумму чисел:

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
• 1 + 2 + 3 + … + 14 + 15 + 16;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.

Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + + (4 + 7) + (5 + 6) = (1 + 10) * 5;
• 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ * 4 + 9 = 45;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050

Задача 2

Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?

С помощью правила Гаусса находим сумму всех весов:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + * 4 + 9 = 45 (г)

Далее смотрим, можно ли этот вес разбить на три равных веса:

Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.

Один из вариантов:

• 9г, 6г
• 8г, 7г
• 5г, 4г, 3г, 2г, 1г

Другие возможные варианты найдите сами с ребенком.

Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).

Задача 3

Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

Значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.

Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.

Задача 4

Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?

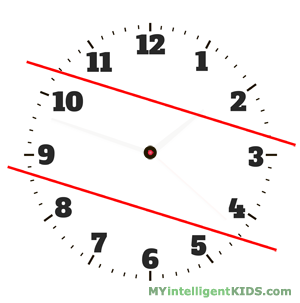
Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.

Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.

Задача 5

Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?

Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:

1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.

Задача 6

Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?

Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:

• первая клетка — 1,
• вторая — 2,
• третья — 3,
• …
• восьмая — 8,
• девятая — 9.

Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.

Задача 7

Вычислить сумму, используя прием Гаусса:

• 31 + 32 + 33 + … + 40;
• 5 + 10 + 15 + 20 + … + 100;
• 91 + 81 + … + 21 + 11 + 1;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
• 1 + 2 + 3 + 4 + 5 + 6;
• 4 + 6 + 8 + 10 + 12 + 14;
• 4 + 6 + 8 + 10 + 12;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.

• 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
• 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
• 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
• 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
• 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
• 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.

Задача 8

Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?

Применяем правило Гаусса, чтобы найти общую массу гирек:

1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)

Вычисляем массу гирек, которые убрали:

Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.

Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.

Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):

1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.

Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.

Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.