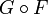Свойства суперпозиций точечно-множественных отображений Текст научной статьи по специальности «Математика»
Рассматриваются суперпозиции точечно-множественных отображений, переводящих каждую точку анализируемой информации в признаковых или сигнальных пространствах в множества с предварительно определенными свойствами. Вводится система суперпозиций, позволяющая продуцировать многозначные отображения с заданными характеристиками.
Похожие темы научных работ по математике , автор научной работы — В. П. Машталир
Комп’ютерне моделювання розподілу поверхневого опору по пластині та в «касеті» для операції «дифузія» в проточному реакторі
Superpositions of point-to-sets maps transferring each point of the analyzable information in features or signal spaces into sets with predefined properties are considered. A system of superpositions permitting to produce multivalued maps with present performances is introduced.
Текст научной работы на тему «Свойства суперпозиций точечно-множественных отображений»
1з зб1льшенням часу осадження р1зниця Miœ поверхневим опором останньо!’ та першо’1′ пластини зменшуеться (рис.8). Це можна пояснити тим, що зпдно з закладеним в модель рiвнянням, поверхневий опiр зменшуеться iз збтьшенням часу проведення процесу.
Таким чином, отримаш результати дозволяють прослщкувати вплив технологiчних параметрiв на вих^ш характеристики напiвпровiдникових пластин по пластин та по довжинi «касети» тд час операци «перша стадiя дифузп з рiдкого джерела» в горизонтальному проточному реакторь
ПЕРЕЛ1 К ПОСИЛАНЬ
1. Корбецький O.P. Модель для анал1зу двовим1рного розпод^у швидкост, тиску та температури в дифузшнш ne4i //Комп’ютерш системи проектування: Теор1я i практика. Biсник Державного унiвeрситeту «Львiвська полiтexнiка». — 1998. — №327. — С. 149 — 157.
2. Корбецький O., Теслюк В. Моделювання руху газу в дифузшнш пeчi з врахуванням теплово!’ конвекцй’ //Тexнiчнi вiстi. -1998. — 1(6), 2(7). — С. 60- 62.
3. Патанкар С.В. Численные методы решения задач теплообмена и динамики жидкости: Пер. с англ. -М.: Энергоатомиздат, 1984. — 150 с.
4. Белов И.А., Кудрявцев H.A. Теплоотдача и сопротивление пакетов труб. — Л.: Энергоатомиздат. Ленингр. Отд-ние, 1987. — 223 с.
5. Писаревский К.Е. Газодинамика диффузионной печи с объемной загрузкой пластин // Электронная техника, Сер. 3, Микроэлектроника. — 1981. — Вып. 6(96). — С. 60 — 66.
6. Korbetsky O., Kotchubey V. Simulation of the diffusant distribution in the diffuse furnace with wafers //Proc. International Workshop on SCCE-II. Vol.1. — Hamburg (Germany). — 1999. -P.160-166.
СВОЙСТВА СУПЕРПОЗИЦИЙ ТОЧЕЧНО-МНОЖЕСТВЕННЫХ
Рассматриваются суперпозиции точечно-множественных отображений, переводящих каждую точку анализируемой информации в признаковых или сигнальных пространствах в множества с предварительно определенными свойствами. Вводится система суперпозиций, позволяющая продуцировать многозначные отображения с заданными характеристиками.
Superpositions of point-to-sets maps transferring each point of the analyzable information in features or signal spaces into sets with predefined properties are considered. A system of superpositions permitting to produce multivalued maps with present performances is introduced.
Сокращение в том или ином смысле неоднозначности интерпретации данных (в частности, редуцирование комбинаторной сложности) является одним из эффективных путей совершенствования информационных технологий, используемых при выработке управленческих решений, в том числе, в интерактивном режиме.
Методы компаративного анализа [1, 2], базирующиеся на метрической иерархической кластеризации признаковых или сигнальных пространств произвольной физической природы, направлены на повышение быстродействия и надежности анализа больших объемов данных. Их суть заключается в прелиминарной обработке эталонной — регистрируемой или гипотетической -количественной и качественной информации о состоянии объекта управления [3, 4]. Эта обработка при анализе текущей обстановки позволяет с существенным сокращением временных затрат находить стратифицированные агрегаты данных, эквивалентные в смысле заданной
меры и величины сходства, которые последовательно уточняют условия принятия решения [1, 5, 6].
Достигаемое снижение комбинаторной емкости наряду с сохранением достоинств (в смысле потенциально высокой надежности) подхода к анализу информации на базе сравнения текущего состояния с эталонным позволяет при заданной вычислительной мощности повышать адекватность условий принятия решений за счет более полного учета различных аспектов функционирования управляемого объекта.
Точечно-множественные (многозначные) отображения, переводящие отдельные элементы в некоторые множества, в концептуальном плане с большой степенью адекватности отражают многие задачи преобразований данных или их признаков и трактовки результатов этой обработки. Проанализируем основные свойства суперпозиций таких отображений. Эти суперпозиции создают предпосылки для формализованного синтеза алгоритмов обработки информации на базе учета свойств отдельных отображений.
Пусть 0 — некоторое множество. Совокупность всех непустых подмножеств множества 0 обозначим через п(0) . Рассмотрим два множества: пусть 01 , 02 — некоторые подмножества конечномерных пространств. Отображение S , которое переводит каждую точку 9′ е 01 в
некоторое подмножество Q множества 02 = ,
является точечно-множественным отображением в = <(9', 9"'):39"^(9', 9")е 0^,(9", 9"')е0=2>,(4)
©2 или отображением 0^ в п(02) :
где 9’е Вот.—!, 9″ е Вот—2 п 1т—^, 9″‘е 1т—2 •
— :01 —> п(02), —(Л) = и —(9′), Предположим, что множества 0^ и 02 конечны, а их
9’е Л е п(01). мощности равны оатй01 = п , еатй02 = т • Тогда
отображение (1) можно естественным образом трактоВ общем случае под прообразом и образом отобра-
вать как матрицу (п X т )
жения — будем понимать соответственно множества
Bom5 = (9′:9’е 0^5(9′) = п(02)>,
Ясно, что любому точечно-множественному отображе-
10 1 . 0 1 0 0 1 . 10
шю 5 соответствует некоторое подмножество 05 пря- состоящую из 0 и 1, элементы а„ которой определяются
мого произведения 01 X 02 , которое назовем опорным соотношениями
05 = ((9′, 9″):9’е BomE, 9″ = 5(9′)>, Г 1,5(9,-‘) = О:9,»еОел(02);
05 е п(01 х02). () 4 10,5(9,.’) = 0:9, ‘iQen(02).
Пусть 51:0.’ —> п(02′) и 5 2:0, » —п(02″) — два Поскольку любой конечный набор (0,> п_ 1 множеств 1 1 , ,=1
многозначных отображения, вообще говоря, с различ- конечной мощности можно с точностью до взаимно
ными прообразами и образами. Определим произведение однозначного соответствия вложить в некоторое под-
51 °52:01′ —п(02″) точечно-множественных отображе- множество IN = ( 1, 2. N> (например, считать, что
ний 51 и 52 следующим равенством
N = ^ card0,) натурального ряда, то имеется воз-
(51 °52)(9′) = и 52(9″), (3) , =1 б б
можность без ограничения общности анализировать
произвольное точечно-множественное отображение 5
Где 9’е 01′, 9’е 01″ . конечных множеств как многозначное отображение
т^ ^ , ^ и , 5:Iw — п(I»Л . Этому отображению будет отвечать квад-
Если множества 02 и 01 имеют различную физи- N N
ческую природу или не пересекаются, наконец, если ратная матрица A5 размерности Nх N и некоторое под-
Bom52 n Im51 = 0 , то ясно, что соотношение (3) те- множество 05 е IN х IN. Множество этих отображений
ряет смысл. Будем устранять данную неопределенность будем обозначать Ф(IN) . Другими словами, если задан суперпозиции отображений сопоставлением результату
произвольный конечный набор многозначных отобра-
пустого множества, которое включим во все системы
подмножеств. Таким образом, нетривиальное (не перево- жений 5,:0, —п(02) , , = 1, п и card0′ < + ^ ,
дящее все значения в пустое множество) многозначное
, , = 1, 2 , то найдется натуральное число N, для которо-
отображение существует тогда и только тогда, когда
го (5,>п= 1 с Ф(^) , причем максимальное значение N
Bom5 1 ф 0 , Im51 n Bom52 ф 0 .
1 1 2 определяется выражением
Остановимся на некоторых свойствах введенной
операции суперпозиции. *max _^ j ‘
Из равенств (2) и (3) очевидным образом следует, что , = 1 п’j = 1 2
опорное множество 0S1 „- е п(01′ х 02″) произведения а минимальное — соотношением
точечно-множественных отображений 51 и 52 либо ,
1 2 Nmin = max card0j •
пустое множество, либо имеет вид , = 1, n,j = 1, 2
Покажем, что если 5^52 е Ф(^) , то ПРИ условии °52)°5з = °(52°5з) .
выполнения операций сложения и умножения элементов
матриц многозначных отображений по правилам П°дчеркнем, что для случая 51; 52, 5з е ф(/^)
справедливость последнего равенства непосредственно Г1 + 1 = 1 + 0 = 0 + 1 = 1 0 + 0 = 0, следует из ассоциативности матричного умножения с
(5) учетом определения операций (5). Прямым следствием данного свойства является возможность исключения из
1 • 1 = 1 • 0 = 0 • 1 = 1, 1 • 1 = 1
, рассмотрения порядка (при наличии соответствующих матрица суперпозиции точечно-множественных отобра- 1 1 1 1
интерпретаций) выполнения произвольного набора
жений задается произведением
точечно-множественных отображений 51, 52, . 5п .
Введем теоретико-множественные операции над точечно-множественными отобр ажениями. Для доказательства введем следующие обозначения: Пересечение многозначных отображений имеет вид: пусть, с одной стороны, А5 °5 = В = (Ь. = . , с
^ «2 . ^ = 51 п 52(01, ®2) = 51 (©1) П 52(02) =
другой, А5 °5 = (9,/»)№ = , . Кроме того, пусть = (Ф:(Йе5, (8′))л(^е 52(9″)),е’е 0150″е 02>,(7)
А=2 = (9,.»)^. = 1 , А = 1 = (9,,’) N. = 1 . Рассмотрим эле- объединение:
мент 9.»‘ матрицы А5 ^ , стоящий на пересечении г-ой — и 5 (0 ©) = 5 (0 ) и 5 (0 ) =
строки и .-го столбца. Очевидно, он равен 0 если и = (Ф:(Ф е 51(е )) у е 52(9 )), 9 е ©1, 9 е ©2>(8) только если принадлежит соответствующему опорному множеству, т.е. (г,.) е 05 °5 , но с учетом (4) имеем,
что для некоторого номера к е ( 1, 2. Щ справед- 51 ^52(01, ©2) 51 (01 )^52(©2)
= :йе51 (9′),(^е 52(9″))л(^й 51 (9′)), ливы включения (г, к) е 0^ и (к,.) е . Тогда 9′ е 0 9″ е 0 > (9)
9,;/ = 1 и 9«..» = 1 , но, принимая во внимание прави-гк к симметрическая разность:
ла (5), окончательно получаем Ь,. = ^ 9^9.» = 1 , 51 /°52(01, 02) = 51 (01 )/°52(02) =
к = 1 = (Ф: (^е51 (9′))л(Фй5 2(9″)),
иначе говоря, 9. «‘ = Ь. , что и требовалось. , (Ф е 52(9»)) л « 51 ^ОХ 9’ е 01,9″е 02>> (10)
Учитывая равенство (6), легко заметить, что опера- ^ __ т ,т
В случаях, когда 5(9) с Ь (Ь — некоторое линейное
ция суперпозиции (з) некоммутативна. Нетрудно убе-
пространство), определим следующие операции
диться, что в то же время эта операция ассоциативна. Действительно, из (з) вытекает, что, с одной стороны,
51 [+]52(01,02) = 51 (01)[+]52(02) = [(51 °52)°5з](9′) = и 5з(9″‘), = и (51(9) +а) — (11)
9″‘е и 52(9″) а е 52(9)
51 [ — ]52(01,02) = 51 (01)[ — ]52(02) =
а с другоЙ, = п (51 (9) — а), (12)
[51 °(52°5з)](9′) = и [ и 5з(9″‘)].
Правые части двух последних равенств совпадают, по- (-5)(9) = -[5(9)] . (14)
скольку для некоторого элемента Ф им принадлежа-
Обратимся далее к более высокому уровню опреде-щего, имеем одну и ту же кванторную интерпретацию: „ , ^
ления операций с многозначными отображениями. Пред-
3^9 «‘, для которого Фе 5з(в»»‘) и 3^9», для которого положим, имеется, вообще говоря, произвольный набор
(базисная система) многозначных отображений N , 9 е 52(9 ) и 9 е 51(9 ) . Тем самым, доказана включающая, в частности, преобразования (7) — (14) и справедливость равенства ряд других точечно-множественных отображений, ассо-
циированных с прикладной ориентацией решаемой зада-
чи. Безусловно, на практике последние играют превалирующую роль, но их конкретизация здесь не только не имеет смысла, но с учетом многообразия потенциально решаемых задач, по всей видимости, и невозможна. Поэтому на множестве всех многозначных отображений введем абстрактную систему Н( К) суперпозиций некоторой базисной системы:
б) если — 1, — 2 е Н(К) и задана операция суперпозиции — 1 °—2 , т.е. — 1 °—2(9) = — 2( — 1 (9)) , тогда
— 1 °—2 е Н(К) (рис. 1, а));
в) если — 2 е Н( К ) ^ — 1 X — 2 е Н(К ), где » X » -декартово произведение отображений, т.е.
— 1 X— 2(91? 92) = — 1 (91 )х— 2(92) (рис. 1, б));
г) если — 2 е Н(К)^ — 1А—2 е Н(К ) , где «А» -диагональное произведение отображений, т.е.
— 1 А— 2(9) = — 1 (9) X —2(9) (рис. 1, в));
Рисунок 1 — К введению системы суперпозиций точечно-множественных отображений
д) если — е Н( К) и определен проектор Рг1 — на г-й компонент отображения, т.е. если —(9) = — 1 (9) X —2(9) X ^—п(9), Рт
е) Е е Н( К), где Е — единичное отображение: Е(9) = 9 , 0е Н(К), где 0 — пустое отображение: 0(9) = 0 , А е Н( К ), где А — постоянное отображение: А(9) = а , а е 0 , ие Н(К), где и — универсальное отображение: и(9) = п(0).
Следует отметить, что приведенное определение композиции точечно-множественных отображений является конструктивным в плане возможности достаточно простого перехода от графической модели последовательности отображений к формульному представлению и наоборот. Так, суперпозиция
«разворачиваемая» слева-направо, с учетом трактовок (см. рис. 1), отображается схемой, показанной на рис.2. С другой стороны, представленная на рис. 3 схема интерпретируется в обратном порядке и соответствует выражению
Рисунок 2 — Пример перехода от формульного представления многозначных отображений к графическому
Рисунок 3 — Пример перехода от графического представления многозначных отображений к формульному
В заключение подчеркнем, что и приведенные выше операции (7) — (14) есть ни что иное, как суперпозиция исходных базисных многозначных отображений. Доста-
точно указать в качестве примера представление объединения и пересечения отображений
— 1 и—2 = (—1 х52) X ( « и » ),
— 1 п—2 = (—1 х52) X ( « п » ).
Таким образом, учитывая отображения (3) и их свойства, соотношения (7) — (14), систему суперпозиций Н( К) и вводя точечно-множественные отображения, ассоциированные с решаемой задачей, можно генерировать последовательности точечно-множественных отображений, направленных на обработку и интерпретацию данных в задачах управления.
1. Машталир В.П. Компаративное распознавание объектов на основе £ -кластеризации множеств эталонов // Радиоэлектроника и информатика. — 1999. — №1 (06). — С. 63-68.
2. Киношенко Е.И., Машталир В.П., Хромушин В.А. Методы синтеза экспертных систем диагностики заболеваний внутренних органов на основе точечно-множественных отображений // Вестник новых медицинских технологий. — 1996. -T.III, №4. — С. 101-107.
3. Mashtalir V.P. Template sets preprocessing for correlation procedures // Proc. The third all-ukranian intern. conf. «Signal/Image Processing and Pattern Recognition». — Kyjiv: UA on IP and SP. — 1996. — P. 63-65.
4. Машталир В.П., Ходарев В.Т. Многозначные отображения в корреляционных системах технического зрения // АСУ и приборы автоматики. — Вып. 96. — Харьков: «Вища школа». -1990. — С. 107-111.
5. Mashtalir V.P., Putyatin E.P. Hierarchical decomposition of reference features for correlation classification // Прац VHAiPT. — 1997. — №2. — С. 36-42.
6. Mashtalir V.P. Template sets preprocessing for correlation procedures // Proc. The third all-ukranian intern. conf. «Signal/Image Processing and Pattern Recognition». — Kyjiv: UA on IP and SP. — 1996. — P. 63-65.
0ПЕРАЦ11 НЕЧ1ТК01 МАТЕМАТИКИ НА П1ДСТАВ1 ГЕНЕТИЧНИХ ТА
Ю. М. Мшаев, О. Ю. Фшмонова, В. В. Давиденко, G. Е. Криксунов, Бенамур Aieo
Рассматривается разработка алгоритмов операций нечеткой математики, реализованных в среде генетических и эволюционных алгоритмов и дальнейшая реализация алгоритмов в среде Matlab — С++. Сфера применения предложенных алгоритмов — идентификация в условиях неопределенности в
виде = *[F] , где , — множества входов и выходов соответственно, представленных в виде нечетких чисел или нечетких переменных, [F] — некоторый оператор.
Розглядаеться розробка алгоритм1в операций неч(ткоЧ математики, реалгзованих в середовищг генетичних та еволю-цшних алгоритмгв та подальша реалгзацгя алгоритмгв в сере-довищ1 Matlab — С++. Сфера застосування запропонованих алгоритмгв — гдентифгкацгя в умовах невизначеностг у виглядг
= *[F] , де , — множини вход1в та виход1в в1дпов1дно, представлених у вигляд1 неч1тких чисел або нечШких змтних, [F] — деякий оператор.
The development of algorithms of operations fuzzy mathematicians, realized in the environment of genetic and evolution algorithms and most further realization of algorithms in the environment Matlab — C++ is considered. The area of using the offered algorithms — an identification in conditions of uncertainty in the manner of = *[F] , where , -ensembles of input and output accordingly, present in the manner of the fuzzy numbers or fuzzy variables, [F] — certain operator.
Широке використання неч1тко! математики i неч1тко! лопки, зумовлене вимогами численних додатюв, проде-монструвало виключно високу ефектившсть цих галузей наукових знань та створило практично нову шформа-цшну технолопю. Нечика лопка (НЛ) та нечика математика (НМа), одержавши початковий iмпульс як складовi частини штучного штелекту, явилися в свою чергу фундаторами нового напрямку в шдустрп знань -soft computing [1], оргашчно включивши в себе НЛ та НМа, нейронш мережi та генетичш алгоритми.
Наявшсть достатньо добре розробленого апарата ней-ронних мереж, генетичних алгоритмiв та еволюцшного програмування дозволяе з нових позицш тдшти до розробки апарату нечико! математики, зробити його менш залежним вщ суб’ективно! оцшки особи, що приймае ршення (ОПР) i дати можлившть тдвищити яюсть ршень, що приймаються, зокрема створити такий алгоритмiчний апарат НМа, який би дозволив викону-вати ршення задач, що зводяться до складних иерацш-них процеив, наприклад, розв’язання систем псевдоль ншних алгебра’1’чних рiвнянь, в яких коефщенти та / або правi частини — нечию числа або неч^ю змшш.
Треба зауважити, що не дивлячись на достатньо вели-ку бiблiографiю, нечика математика (бтьш конкретно -неч^ка арифметика) в сво’й б^ьшоси використовуе
Суперпозиция (математика)
Под свойством суперпозиции или принципом суперпозиции ( лат. Super и positio ;. Dt overlay ) понимается в математике фундаментальное свойство однородных линейных уравнений , ведь все линейные комбинации решений уравнения приводят к дополнительным решениям уравнения. С помощью принципа суперпозиции решения неоднородных линейных уравнений могут быть представлены в виде суммы решений соответствующего однородного уравнения и решения в виде частиц. Принцип суперпозиции часто используется для линейных уравнений, которые трудно решить, таких как линейные дифференциальные уравнения , поскольку исходная проблема сводится к более простым для решения подзадачам. Он имеет широкий спектр приложений, особенно в физике .
Содержание
Основы
Линейные уравнения
Решения однородного и неоднородного линейного вещественного уравнения с неизвестными и Икс 1 > Икс 2 >
Определяющее уравнение в неизвестное , называется линейным , когда он находится в форме Икс
Т ( Икс ) знак равно б
Т ( λ Икс + μ у ) знак равно λ Т ( Икс ) + μ Т ( у )
применяется. Линейное уравнение называется однородным, если правая часть равна нулю , т. Е. Имеет вид
Т ( Икс ) знак равно 0
в противном случае уравнение называется неоднородным. Однородные линейные уравнения имеют хотя бы тривиальное решение . Икс знак равно 0
Скалярное линейное уравнение
с неизвестным однородно и, в частности, удовлетворяется тривиальным решением, в то время как уравнение Икс знак равно ( Икс 1 , Икс 2 ) , x_ )> Икс знак равно ( 0 , 0 )
неоднородна и не выполняется тривиальным решением.
Свойство суперпозиции
Свойство суперпозиции на примере однородного линейного уравнения . Уравнение решается и так же , как и все линейные комбинации этих решений. 2 ⋅ Икс 1 — 3 ⋅ Икс 2 знак равно 0 -3 cdot x_ = 0> ( 3 , 2 ) ( Шестой , 4-й )
Если и являются двумя решениями однородного линейного уравнения, то это уравнение также решает все линейные комбинации двух решений, da Икс ^ >> Икс ¯ >> c Икс ^ + d Икс ¯ > + d >>
Т ( c Икс ^ + d Икс ¯ ) знак равно Т ( c Икс ^ ) + Т ( d Икс ¯ ) знак равно c Т ( Икс ^ ) + d Т ( Икс ¯ ) знак равно 0 + 0 знак равно 0 > + d >) = T (c >) + T (d >) = cT ( >) + dT (>) = 0 + 0 = 0> .
В общем, это утверждение также применимо ко всем линейным комбинациям нескольких решений для образования нового решения.
Однородное линейное уравнение
например, через два решения
Выполняет. Так тоже
Раствор твердых частиц
Принцип суперпозиции в линейном уравнении : решение однородного уравнения (синий), решение частицы (зеленый) и решение неоднородного уравнения (красный) Икс 1 — 2 Икс 2 знак равно 10 -2x_ = 10>
В отличие от однородного линейного уравнения, которое всегда имеет как минимум нуль в качестве решения, неоднородное уравнение не всегда должно быть разрешимым, то есть его множество решений может быть пустым . Если неоднородное уравнение может быть решено, его решения могут быть представлены как сумма решений связанного однородного уравнения и частного решения, то есть любого свободно выбираемого решения неоднородного уравнения: пусть будет конкретным решением неоднородного линейного уравнения и будет общим решением связанной однородной задачи. , то общее решение неоднородного уравнения есть da Икс ¯ >> у у + Икс ¯ >>
Т ( у + Икс ¯ ) знак равно Т ( у ) + Т ( Икс ¯ ) знак равно 0 + б знак равно б >) = T (y) + T (>) = 0 + b = b>
применяется. Этот принцип суперпозиции часто используется для решения неоднородных линейных уравнений, поскольку решить однородное линейное уравнение и найти конкретное решение часто проще, чем решение исходной задачи.
Конкретное решение неоднородного уравнения
Теперь являются решениями соответствующего однородного уравнения у знак равно ( у 1 , у 2 ) , y_ )>
так что все с , то неоднородное уравнение обычно решается у у 1 знак равно 2 у 2 = 2y_ >
Икс знак равно у + Икс ¯ знак равно ( у 1 + Икс ¯ 1 , у 2 + Икс ¯ 2 ) знак равно ( 2 у 2 + 4-й , у 2 — 3 ) знак равно ( 2 т + 4-й , т — 3 ) > = (y_ + > _ , y_ + > _ ) = (2y_ + 4, y_ -3) = (2t + 4, t-3)> с . т ∈ Р. >
Наложение решений
Важным применением принципа суперпозиции является суперпозиция частных решений линейного уравнения для формирования общего решения. Если правая часть неоднородного линейного уравнения может быть представлена в виде суммы , то применяется следующее б б 1 + б 2 + b_ >
и являются и в каждом случае являются решениями индивидуальных проблем Икс 1 > Икс 2 >
тогда общее решение исходной проблемы — это сумма двух отдельных решений, то есть
Такая процедура особенно выгодна, когда отдельные проблемы решить легче, чем исходную. Если соответствующие суммы сходятся, конструкция также может быть обобщена на суперпозицию бесконечного числа индивидуальных решений. Джозеф Фурье использовал такие ряды для решения уравнения теплопроводности и, таким образом, основал анализ Фурье .
Примеры применения
Линейные диофантовы уравнения
Принцип суперпозиции в линейном диофантовом уравнении : решения однородного уравнения (синий), решение частицы (зеленый) и решения неоднородного уравнения (красный) 2 Икс 1 + 3 Икс 2 знак равно 26-е + 3x_ = 26>
В линейных диофантовых уравнениях , неизвестное число вектор для Икс
должны применяться, где и — целые коэффициенты. Затем решения линейных диофантовых уравнений могут быть получены путем объединения решения однородного уравнения с частичным решением, которое можно найти с помощью расширенного алгоритма Евклида . а 1 , . , а п , ldots, a_ > б
Они являются целочисленными решениями линейного диофантова уравнения Икс знак равно ( Икс 1 , Икс 2 ) , x_ )>
2 Икс 1 + 3 Икс 2 знак равно 26-е + 3x_ = 26>
искал. Решения соответствующего однородного уравнения
Частное решение неоднородного уравнения находится здесь
при этом совокупность решений неоднородного уравнения оказывается
Икс знак равно у + Икс ¯ знак равно ( 3 т , — 2 т ) + ( 4-й , Шестой ) знак равно ( 3 т + 4-й , — 2 т + Шестой ) > = (3t, -2t) + (4,6) = (3t + 4, -2t + 6)> С участием т ∈ Z >
Линейные разностные уравнения
Принцип суперпозиции в линейном разностном уравнении : решение однородного уравнения для начального значения (синий), решение частицы для (зеленый) и решение неоднородного уравнения для (красный) Икс п — 2 Икс п — 1 знак равно 3 -2x_ = 3> Икс 0 знак равно 1 = 1> Икс 0 знак равно 0 = 0> Икс 0 знак равно 1 = 1>
должны применяться, где и являются коэффициентами. Решение разностного уравнения зависит от начальных значений . Однородные линейные разностные уравнения с постоянными коэффициентами могут быть решены, например, с помощью соответствующего характеристического уравнения . а 0 ( п ) , . , а k ( п ) (п), ldots, а_ (п)> б ( п ) Икс 0 , . , Икс k — 1 , ldots, x_ >
Линейное разностное уравнение первого порядка с постоянными коэффициентами
Икс п — 2 Икс п — 1 знак равно 3 -2x_ = 3>
результаты для начального значения результат . Чтобы найти явное представление решения в зависимости от начального значения, рассматривается связанное с ним однородное разностное уравнение Икс 0 знак равно c = c> ( 2 c + 3 , 4-й c + 9 , 8-е c + 21-е , 16 c + 45 , . )
чьим решением для начального значения является результат , то есть у 0 знак равно c = c> ( 2 c , 4-й c , 8-е c , 16 c , . )
является. Частное решение неоднородного уравнения является результатом выбора начального значения , которое затем приводит к Икс ¯ 0 знак равно 0 > _ = 0> ( 3 , 9 , 21-е , 45 , . )
применяется. Таким образом, возникает явное решение неоднородной задачи
Икс п знак равно у п + Икс ¯ п знак равно c 2 п + 3 ( 2 п — 1 ) знак равно ( c + 3 ) 2 п — 3 = y_ + > _ = c2 ^ +3 (2 ^ -1) = (c + 3) 2 ^ < n>-3> .
Линейные обыкновенные дифференциальные уравнения
Принцип суперпозиции в линейном обыкновенном дифференциальном уравнении : решения однородного уравнения (синий), решение частицы (зеленый) и решения неоднородного уравнения (красный) для различных начальных условий ж ′ ( Икс ) + Икс ж ( Икс ) знак равно ( 1 + Икс ) е Икс >
В линейных обыкновенных дифференциальных уравнениях неизвестным является функция, для которой ж
а п ( Икс ) ж ( п ) ( Икс ) + ⋯ + а 1 ( Икс ) ж ′ ( Икс ) + а 0 ( Икс ) ж ( Икс ) знак равно г ( Икс ) (x) f ^ (x) + cdots + a_ (x) f ‘(x) + a_ (x) f (x) = g (Икс)>
применяется, где — функции коэффициентов, а другая функция — в правой части. Решение однородного линейного дифференциального уравнения может быть дано через связанную фундаментальную систему, конкретное решение может быть найдено, например, путем изменения констант . а 0 , . , а п , ldots, a_ > г
Ищем решение неоднородного обыкновенного дифференциального уравнения первого порядка
ж ′ ( Икс ) + Икс ж ( Икс ) знак равно ( 1 + Икс ) е Икс >
Общее решение соответствующего однородного уравнения
ЧАС ′ ( Икс ) + Икс ЧАС ( Икс ) знак равно 0
ЧАС ( Икс ) знак равно е — ∫ Икс d Икс знак равно k е — Икс 2 / 2 = ke ^ / 2>>
с постоянной интегрирования . Для нахождения конкретного решения используется подход однородной задачи k ∈ Р. > ж ¯ >>
и пытается найти константу, от которой теперь зависит. Используя правило произведения, для вывода c ( Икс ) Икс ж ¯ >>
ж ¯ ′ ( Икс ) знак равно c ′ ( Икс ) е — Икс 2 / 2 — c ( Икс ) Икс е — Икс 2 / 2 > ‘(x) = c’ (x) e ^ / 2> -c (x) xe ^ / 2>>
и подставив в исходное уравнение
ж ¯ ′ ( Икс ) + Икс ж ¯ ( Икс ) знак равно c ′ ( Икс ) е — Икс 2 / 2 — c ( Икс ) Икс е — Икс 2 / 2 + c ( Икс ) Икс е — Икс 2 / 2 знак равно c ′ ( Икс ) е — Икс 2 / 2 знак равно ( 1 + Икс ) е Икс > ‘(x) + x > (x) = c’ (x) e ^ / 2> -c (x) xe ^ / 2> + c (x) xe ^ / 2> = c ‘(x) e ^ / 2> = (1+ х) е ^ >
и таким образом за счет интеграции
c ( Икс ) знак равно е Икс + Икс 2 / 2 / 2>> ,
где можно установить постоянную интегрирования равной нулю, поскольку интересует только одно специальное решение. В целом решение неоднородной задачи получается как
ж ( Икс ) знак равно ЧАС ( Икс ) + ж ¯ ( Икс ) знак равно k е — Икс 2 / 2 + е Икс + Икс 2 / 2 е — Икс 2 / 2 знак равно k е — Икс 2 / 2 + е Икс > (x) = ke ^ / 2> + e ^ / 2> e ^ / 2> = ke ^ / 2> + e ^ > .
Раствор затем однозначно определяется путем выбора начального условия , например . ж ( 0 ) знак равно k + 1
Линейные уравнения в частных производных
Решение однородного уравнения теплопроводности с начальным условием ЧАС т — ЧАС Икс Икс знак равно 0 -h_ = 0> 2 грех ( π Икс )
Частичное решение неоднородного уравнения теплопроводности с нулевым начальным условием ж т — ж Икс Икс знак равно π 2 грех ( π Икс ) -f_ = pi ^ sin ( pi x)>
Решение неоднородного уравнения теплопроводности с начальным условием ж т — ж Икс Икс знак равно π 2 грех ( π Икс ) -f_ = pi ^ sin ( pi x)> 2 грех ( π Икс )
В случае линейных дифференциальных уравнений в частных производных неизвестная является функцией нескольких переменных, для которых ж
должны применяться, где , и и функции коэффициентов. Однородные, а также неоднородные линейные уравнения в частных производных могут быть решены, например, с использованием фундаментальных решений или метода разделения . Икс знак равно ( Икс 1 , . , Икс м ) , ldots, x_ )> α знак равно ( α 1 , . , α м ) , ldots, альфа _ )> а α ( Икс ) (х)> г ( Икс )
ж т — ж Икс Икс знак равно π 2 грех ( π Икс ) -f_ = pi ^ sin ( pi x)>
с граничными условиями Дирихле и начальным условием . Решение соответствующего однородного уравнения ж ( 0 , т ) знак равно ж ( 1 , т ) знак равно 0 ж ( Икс , 0 ) знак равно 2 грех ( π Икс )
ЧАС т — ЧАС Икс Икс знак равно 0 -h_ = 0>
с теми же начальными и граничными условиями получаем с помощью сепарационного подхода
ЧАС ( Икс , т ) знак равно Ф. ( Икс ) г ( т )
с чем применяется
ЧАС т — ЧАС Икс Икс знак равно Ф. ( Икс ) г ′ ( т ) — Ф. ″ ( Икс ) г ( т ) знак равно 0 -h_ = F (x) G ‘(t) -F’ ‘(x) G (t) = 0>
и, таким образом
Поскольку левая часть уравнения зависит только от, а правая — только от, обе части должны быть равны константе . Так должны для и обыкновенных дифференциальных уравнений Икс т k Ф. г
каково решение для данных начальных условий k знак равно — π 2 >
ЧАС ( Икс , т ) знак равно 2 грех ( π Икс ) е — π 2 т т>>
полученные результаты. Используя тот же подход, можно получить частичное решение неоднородного уравнения с нулевым начальным условием как ж ( Икс , 0 ) знак равно 0
который приносит общее решение через
ж ( Икс , т ) знак равно ЧАС ( Икс , т ) + ж ¯ ( Икс , т ) знак равно 2 грех ( π Икс ) е — π 2 т + грех ( π Икс ) ( 1 — е — π 2 т ) знак равно грех ( π Икс ) ( е — π 2 т + 1 ) > (x, t) = 2 sin ( pi x) e ^ t> + sin ( pi x) (1-e ^ t>) = sin ( pi x) (e ^ t> +1)>
Приложения
литература
- Ганс Вильгельм Альт : Линейный функциональный анализ: введение, ориентированное на приложения . 5-е издание. Springer-Verlag, 2008, ISBN 3-540-34186-2 .
- Бернд Аульбах : Обыкновенные дифференциальные уравнения . 2-е издание. Spectrum Academic Publishing House, 2004, ISBN 3-8274-1492-X .
- Альбрехт Бойтельшпахер : линейная алгебра. Введение в науку о векторах, картах и матрицах . 7-е издание. Vieweg, 2009 г., ISBN 3-528-66508-4 .
- Питер Бундшу : Введение в теорию чисел . 6-е издание. Springer-Verlag, 2010, ISBN 3-540-76490-9 .
- Герд Фишер : линейная алгебра: введение для новых студентов . 17-е издание. Vieweg Verlag, 2009, ISBN 3-8348-0996-9 .
- Юрген Йост : Уравнения с частными производными: Эллиптические (и параболические) уравнения . 1-е издание. Springer-Verlag, 2009, ISBN 3-540-64222-6 .
веб ссылки
- Эрик В. Вайсштейн : принцип суперпозиции . В: MathWorld (английский).
-
Эта страница последний раз была отредактирована 3 февраля 2020 в 17:21.
Текст доступен по лицензии «Creative Commons Attribution / Share Alike» ; Информацию об авторах и статусе лицензии интегрированных медиафайлов (таких как изображения или видео) обычно можно вызвать, щелкнув по ним. На содержание могут распространяться дополнительные условия. Используя этот сайт, вы соглашаетесь с условиями использования и политикой конфиденциальности .
Wikipedia® — зарегистрированная торговая марка Wikimedia Foundation Inc.
Принцип суперпозиции. Функциональная полнота системы логических функций
Элементарные функции позволяют получать сложные функции путем изменения индексов переменных и подстановки других функций вместо переменных исходной функции. Возможность такой подстановки обуславливается тем, что области значений их переменных совпадают. Рассмотренный принцип называют принципом суперпозиции функций.
Функцию fk+1(x), полученную из функций f1(x), f2(x), . fk(x), путем применения (возможно многократного) принципа суперпозиции, будем называть суперпозицией функций f1(x), f2(x), . fk(x). При этом для записи сложных функций, кроме введенных знаков, будем использовать скобки. Например имея элементарные функции
можно, пользуясь принципом суперпозиции, получить следующие функции:
Функция f3(x) получена путем подстановки в функцию f1(x) вместо переменной х2 функции f2(x). Функция f4(x) получена из функции f2(x) путем подстановки вместо переменной х3 логической функции f1(x).
Использование принципа суперпозиции позволяет установить связи между элементарными функциями, т.е. построить логические выражения, позволяющие записать одни элементарные функции через другие.
Рассмотрим связи между некоторыми элементарными функциями.
Из таблицы 2.5 следует, что функция f1(x) на всех наборах принимает значения, противоположные функции f14(x).
Используя принцип суперпозиции, запишем
Приведем без пояснения некоторые широко применяемые соотношения, связывающие элементарные функции:
При использовании принципа суперпозиции возникает вопрос, каким должен быть состав элементарных логических функций, которые позволяют с их помощью построить произвольную логическую функцию, зависящую от конкретного числа переменных.
Система логических функций f1(x), f2(x), . fs(x) называется функционально полной, если любая логическая функция может быть представлена суперпозицией этих функций, взятых в любом конечном числе экземпляров.
Функционально полная система логических функций f1(x), f2(x), . fs(x) называется минимальной, если удаление из нее хотя бы одной функции превращает систему в неполную. При рассмотрении совокупности логических функций f1(x), f2(x), . fs(x) возникает вопрос, как установить, является ли данная совокупность функций полной. Ответ на этот вопрос дает теорема о функциональной полноте (теорема Поста-Яблонского), которая устанавливает необходимые и достаточные условия функциональной полноты произвольной совокупности логических функций [1].
Анализ функций двух переменных по указанным в теореме свойствам показывает, что существует большое число различных функционально полных систем элементарных логических функций. Перечислим некоторые из них:
— функция Шеффера (И-НЕ);
— функция Пирса (ИЛИ-НЕ);
— функция ИЛИ и НЕ;
— функция импликации и константы 0 и т.д.
Приведенные функционально полные системы являются минимальными. Добавление к минимальным функционально полным системам других логических функций позволяет получать совокупности логических функций, обладающие свойством полноты, но неминимальные по числу входящих в них функций. На практике из неминимальных функционально полных систем логических функций широкое распространение получила система, состоящая из функций И, ИЛИ, НЕ.
Особый интерес, с практической точки зрения, представляют функционально полные системы, содержащие функции константы 0 и 1, так как эти функции просто реализуются в цифровых устройствах. К таким системам логических функций относятся следующие совокупности функций:
— равнозначность и дизъюнкция;
— сумма по модулю два и дизъюнкция.
Указанные совокупности функций при наличии констант 0 и 1 позволяют реализовать произвольную логическую функцию любого конечного числа переменных. Логические функции описывают условия функционирования цифровых устройств, т.е. устройств, входные и выходные сигналы которых можно отождествлять с нулевыми и единичными значениями логических переменных или функций. Для построения цифровых устройств, реализующих произвольные логические функции, необходимо располагать совокупностью элементов, которые реализовали бы все функции, входящие в одну из функционально полных систем логических функций. Условимся в дальнейшем элементы, реализующие логические функции, называть логическими элементами. Логическому элементу будем приписывать название логической функции. Например, для краткости вместо “логический элемент, реализующий функцию ИЛИ-НЕ”, будем говорить “логический элемент ИЛИ-НЕ”.
Каждая функция функционально полной системы реализуется определенным типом логического элемента. Совокупность логических элементов, с помощью которых осуществляется техническая реализация функционально полной системы логических функций, называется функционально полной системой логических элементов или базисом.
Задача построения цифрового устройства из логических элементов, реализующих функционально полную систему логических функций, эквивалентна математической задаче представления сложной логической функции более простыми функциями, которые реализованы данными логическими элементами. В связи с существованием большого количества функционально полных систем логических элементов возникает вопрос о том, какие из них представляют наибольший практический интерес для построения функционально полных совокупностей логических элементов.
При выборе функционально полной системы логических функций для ее реализации в виде системы логических элементов прежде всего учитывается возможность достаточно простой технической реализации отдельных логических функций, входящих в систему. Так, например, на практике получили широкое распространение системы логических элементов, реализующие функционально полные системы, содержащие логические функции И-НЕ, ИЛИ-НЕ, которые имеют достаточно простую техническую реализацию. С другой стороны, функционально полные системы, в которые входят логические функции сумма по модулю два, импликация, запрет и другие, не нашли практического применения, так как их реализация более сложная.
При практическом построении цифровых устройств системы логических элементов, реализующие минимальные функционально полные системы, зачастую оказываются менее удобными, чем системы элементов, содержащие большее число различных элементов и реализующие не минимальные функционально полные системы логических функций. Например, к такой системе относятся совокупности логических элементов И, ИЛИ, НЕ или логических элементов И, сумма по модулю два, генератор единицы и др. Это объясняется тем, что такие совокупности элементов позволяют находить более оптимальные по сложности структуры проектируемых цифровых устройств.
С другой стороны, увеличение числа различных логических функций, реализуемых элементами, приводит к увеличению стоимости выпускаемых систем логических элементов. Отсюда следует, что существует оптимальное количество различных элементов, входящих в систему, позволяющее получить цифровые устройства минимальной стоимости. В настоящее время состав функционально полных систем логических элементов, выпускаемых промышленностью, определяется из опыта проектирования цифровых устройств, так как точных методов определения оптимальных совокупностей логических элементов не найдено. При начертании схем цифровых устройств используются условные графические обозначения логических элементов, которые установлены ГОСТом ЕСКД 2.743-82. На рис. 2.1 приведены условные графические обозначения наиболее распространенных логических элементов. Размеры
логических элементов на схеме определяются ГОСТ и варьируются в зависимости от числа входов, выходов элементов и формата чертежа.
Физическая реализация схем логических элементов может быть самой разнообразной. Логические элементы могут быть построены на базе электронных ламп, полупроводниковых приборов, электромагнитных и электромеханических устройств, ферритов и т.д. Наибольшее распространение в настоящее время получили логические элементы, выполненные на основе полупроводниковых цифровых интегральных схем микросхем.
Функциональное программирование
В математике композиция (суперпозиция) функций — это применение одной функции к результату другой. Частным случаем такой операции является применение к выражению одной и той же функции несколько раз.
Функция Nest[func,exps,n] последовательно применяет n раз функцию func к выражению expr . Для того чтобы проследить за процессом получения конечного выражения, используется функция NestList с теми же аргументами. Эта функция генерирует список результатов, полученных при применении функции func к выражению expr на каждой итерации. На рис. 9.11 мы воспользовались функциями Nest и NestList для того, чтобы пять раз применить к выражению 16 неопределённую функцию g (примеры In[1] и In[2] ) и функцию вычисления квадратного корня Sqrt (примеры In[3] и In[4] ). Результаты вычислений в ячейках Out[1] и Out[3] , как и ожидалось, совпадают с последними элементами списков в Out[2] и Out[4] , соответственно.

Функции Fold и FoldList работает с функциями двух аргументов. Заданная в виде Fold[func,var,] функция на первой итерации применяет функцию func к аргументам var и a1 , на второй итерации применяет func к результату предыдущей итерации и аргументу a2 и так далее, до последнего элемента в списке. На рис. 9.12 приведены примеры использования функций Fold и FoldList для неопределённой функции f (примеры In[1] и In[2] ) и функции возведения в степень Power (примеры In[3] – In[6] ).

9.2.2. Композиция нескольких функций
В более широком смысле композиции функций в качестве аргумента функции можно использовать результат выполнения другой функции. В Mathematica последовательное применение к выражению нескольких функций называется вызовом вложенной функции ( nested function call ) (П. Веллин и др. [14, с. 89]). В примере на рис. 9.13 сначала мы применили к числу 2. функцию Log (пример In[1] ), а затем к полученному результату последовательно — функции Sin и Sqrt (примеры In[2] – In[3] ). Однако все указанные операции можно совершить за одно действие. В примере In[4] мы вызываем вложенную функцию Sqrt[Sin[Log[2.]]] : сравнив выходные данные в Out[3] и Out[4] , мы убедимся, что оба подхода применения к аргументу последовательно нескольких функций приводят к одинаковому результату.
Когда мы пользуемся первым подходом, мы можем проследить за процессом вычисления, поскольку помимо конечного результата получаем промежуточные результаты действия каждой функции (в нашем случае это Out[1] и Out[2] ). Для получения промежуточных результатов при использовании второго подхода используется функция Trace . В примере In[5] на рис. 9.13 мы применяем Trace к вложенной функции In[4] .

Композицию функций можно осуществлять менее наглядным, но более традиционным для Mathematica способом — при помощи встроенной функции Composition . Указывается она в следующем виде: Composition[func1,func2. ][arg] , где funci — функции в порядке, обратном порядку их применения к аргументу (или аргументам) arg , т.е., последней применяется функция func1 , предпоследней — func2 и т.д. В примере In[1] на рис. 9.14 при помощи Composition мы осуществляем тот же набор действии, что и на рис. 9.13.
Для получения промежуточных результатов выполнения вложенной функции при данном подходе используется функция ComposeList[,arg] . Однако, у ComposeList порядок функций в аргументе обратный в сравнении с Composition : функция func1 применяется первой — ср. примеры In[1] и In[2] на рис. 9.13. Также обратим внимание на то, что формат вывода результата данных функциями Trace и ComposeList различный: если в первом случае мы имеем вложенный список, содержащий как вычисляемое выражение в явном виде, так и результат вычислений, то во втором — одномерный список с результатами вычислений.
Подробней о композиции функций см. книгу Е. М. Воробьёва [1, с. 134–136].
Научный форум dxdy
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву , правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
суперпозиция отношения
Всем доброго времени суток. Собственно есть задача, которую я должен решить, но я не прошу решить, а только разъяснить мне что же такое эта суперпозиция и с чем ее едят. Откровенно говоря, определение в лекции мне ни сколько не облегчило задачу. Вот что у меня есть:
Суперпозицией отношений ^m,]$» /> называется m-отношение = (rho _1^m,rho _2^m. rho _^m)]$» /> на множествах ,. ]$» /> такое, что = (a_1^i,a_2^i. a_m^i)]$» /> тогда и только тогда, когда найдутся элементы ,b_2^j in . b_^j in
Отношения заданы матрицей.
Вот что я понял: нужно сопоставить каждый ряд отношений , заданых матрицей ( 5 отношений, 5 столбцов в каждой матрице) каждому ряду отношения ]$» /> на предмет выполнимости условия ^i,b_s^j) wedge (b_1^j,b_2^j. b_^j,a_m^i),s = 1,2. n — 1]$» />. Т.е. это ряды матриц где 5-й элемент равен 5-му элементу матрицы ]$» /> и при этом 6-й элемент ]$» /> равен 5-му элементу (в данном конкретном примере)?
любой нормальный человек прочтя
уперпозицией отношений ^m,]$» /> называется m-отношение = (rho _1^m,rho _2^m. rho _^m)]$» /> на множествах ,. ]$» /> такое, что = (a_1^i,a_2^i. a_m^i)]$» />
не будет читать дальше (если это ему не надо почему-то)
напишите попонятней. в случае, допустим , и двухэлементное (тогда матрица 2х2) будет
чтобы можно было хоть что-то увидеть глазами

и множества непонятно откуда взялись:((
— Пт дек 17, 2010 21:26:24 —

и напомните, что такое -отношение, чтоб не гуглить
![$[B]$](https://dxdy-02.korotkov.co.uk/f/9/4/b/94b3ccddd17f19527554b98f8c57c75182.png)
и множества непонятно откуда взялись:((
Это определение из конспекта лекций по дискретной математике. Я его не понимаю и спросить мне не у кого. Хорошо что есть интернет. Вот задача:
Для отношений ,,,,,S]$» /> на множестве З, заданных с помощью матрицы найти суперпозицию ,,,,)]$» />, наличие функциональности в суперпозиции.
= begin> 1&3&1&1&4 \ 2&4&2&2&3 \ 4&1&3&2&7 \ 4&9&4&4&1 end]$» />, = begin> 2&4&4&2&3 \ 1&3&1&1&7 \ 3&2&3&5&2 \ 1&3&1&1&2 \ 4&1&3&2&5 end]$» />, = begin> 4&1&3&2&4 \ 1&3&1&1&5 \ 2&3&4&3&2 \ 3&3&4&1&5 end]$» />, = begin> 1&3&1&1&2 \ 6&8&5&5&2 \ 4&1&3&2&1 end]$» />, = begin> 1&3&1&1&3 \ 3&2&1&4&4 \ 4&1&3&2&9 \ 1&3&1&1&4 end]$» />,> 1&1&2&4&3&6 \ 4&2&5&2&4&8 \ 7&5&4&1&9&7 \ 2&4&3&1&6&7 \ 4&2&5&2&3&9 \ 4&7&5&2&3&5 \ 7&5&4&1&9&8 end]$» />
потому что много букв и среди них мало знакомых

и напомните, что такое -отношение, чтоб не гуглить
— Сб дек 18, 2010 11:07:46 —
Это определение из конспекта лекций по дискретной математике. Я его не понимаю и спросить мне не у кого.
по всей видимости, Вы неудачно законспектировали — я не могу из этих объяснений понять
Давайте наметим такой план
1) что такое «отношение» и как его задать с помощью матрицы
2) что такое m-отношение и как его задать с помощью матрицы
3) что такое суперпозиция отношений — на каком множестве она задается, как его задать с помощью матриц
4) что такое «функциональность в суперпозиции»
Я к сожалению не имею физической возможности посещать лекции, и по этой причине преподаватели идут на встречу, высылая конспекты своих лекций на мой email. Так что конспект составлен именно преподавателем.
1. Под n-арным отношением или n — отношением ]$» /> на множествах ,. ]$» /> понимается закон (характеристическое свойство), выделяющий в декартовом произведении times times . times ]$» /> некоторое подмножество . >^n subseteq times times . times ]$» />, называемое графиком (n-мерным) отношения ]$» />. Если = = . = = A]$» />, то говорят об n-отношении ]$» /> на множестве А с графиком ]$» />.
2.Так как n-отношение ]$» /> можно рассматривать как подмножества декартова произведения times times . times ]$» />, существуют различные способы задания n-отношений, аналогичные способам задания множеств. Так график . >^n]$» /> удобно задавать матрицей, строками которой являются векторы отношения ]$» />.
3. определение суперпозиции детально описано в первом топе. Вот пример (тоже из конспекта лекций):
> 0&1&1 \ 1&0&0 \ 1&1&1 end]$» />, > 0&0&0 \ 0&1&0 \ 1&1&1 \ 1&1&1 end]$» />, > 0&0&1 \ 0&1&1 \ 1&1&0 end]$» />, = begin> 0&0&0&0 \ 1&0&1&1 \ 1&1&0&0 \ 1&1&1&1 end]$» />, = (rho _1^3,rho _2^3,rho _3^3) = begin> 0&1&1 \ 1&1&0 \ 1&1&1 end]$» />
4. Отношение ]$» /> на множествах ,. ]$» /> называется функциональным при отображении его в бинарное отношение ]$» /> на множествах times times . times )]$» /> и ]$» />, если для каждой последовательности элементов ) in times times . times >]$» /> сечение a_i^1,a_i^2. a_i^()]$» /> содержит не более одного элемента ) in ]$» />.Очепятка. Что должно быть на самом деле — могу только догадываться, либо in ]$» />, либо ]$» />. [url]http://ru.math.wikia.com/wiki/Функциональное_отношение[/url] определение простое и понятное. Поскольку суперпозиция отношений тоже является отношением(!?) то и свойствами обладает теми же.
![$[rho _<<A_1></p>
<p>Так график . >^n]$» /> удобно задавать матрицей</p>
<p>Если множества конечны и каждое состоит из элементов — каких размеров будет матрица?</p>
<p><img decoding=](https://dxdy-01.korotkov.co.uk/f/8/2/0/8205cbc3813ef6af9bd1bb683957169182.png)
и оно непонятное: откуда там взялись множества ?
в этом примере матрицы, задающие отношения, состоят из 0 и 1, как и должно быть. В Вашем же примере там натуральные числа, что непонятно
в этом примере матрицы, задающие отношения, состоят из 0 и 1, как и должно быть. В Вашем же примере там натуральные числа, что непонятно

Тут как раз всё в порядке. Матрица строится, как я понял следующим образом, это просто список тех наборов на которых отношение выполнено.

и оно непонятное: откуда там взялись множества ?
Смею предположить, что для отношений ^m,$» /> верно, что
times B_1$» />,
times B_2$» />,
.
^m subseteq A_1 times ldots times A_ times B_$» />,
times A_m$» />.
После того, как мы вкурили на чём определены отношения уже можно осознать, что говорится здесь:
Суперпозицией отношений ^m,]$» /> называется m-отношение
= (rho _1^m,rho _2^m. rho _^m)]$» /> на множествах ,. ]$» /> такое, что = (a_1^i,a_2^i. a_m^i)]$» /> тогда и только тогда, когда найдутся элементы ,b_2^j in . b_^j in
Меня правда смущают верхие индексы у букв и , но на них закроем глаза.
Тогда уже и понятно что делать.

Тут как раз всё в порядке. Матрица строится, как я понял следующим образом, это просто список тех наборов на которых отношение выполнено.
Да и вообще, разве не принято сначала определять всякие штуки на двух объектах, а потом ассоциативностью или как-нибудь ещё доопределять для многих?
Последний раз редактировалось OcbMuHor 18.12.2010, 20:41, всего редактировалось 1 раз.
Одно дело матрица ]$» />, и совсем другое матрица ,. >^i]$» />. Поскольку ,. >^i subseteq times times . times ]$» /> и совсем не обязательна эквивалентность отношения и прямого произведения множеств (на множестве). Например, right>]$» />, = left < < < 1,1 >, < 1,2 >, < 1,3 >, < 2,1 >, < 2,2 >, < 2,3 >, < 3,1 >, < 3,2 >, < 3,3 >> right>]$» />, = left< > right> = left < < < 1,2 >, < 1,3 >, < 2,3 >> right>]$» />, согласно определению топа №6 п.2. = begin> 1&2 \ 1&3 \ 2&3 end]$» />
Что касается множества В, то именно это меня и вводит в заблуждение. Но следуя неумолимой логике можно предположить что на множестве В задано отношение S, а на множестве А — отношения R1,R2,R3,R4,R5. И что множества есть подмножества одного множества, на котором по условию задачи заданы отношения S,R1,R2,R3,R4,R5.
![lt;></p>
<p>,, mapsto , langlerangle$» /></p>
<p>Одно дело матрица ]$» />, и совсем другое матрица ,. >^i]$» />. Поскольку ,. >^i subseteq times times . times ]$» /> и совсем не обязательна эквивалентность отношения и прямого произведения множеств (на множестве). Например, right>]$» />, = left < < < 1,1 >, < 1,2 >, < 1,3 >, < 2,1 >, < 2,2 >, < 2,3 >, < 3,1 >, < 3,2 >, < 3,3 >> right>]$» />, = left< > right> = left < < < 1,2 >, < 1,3 >, < 2,3 >> right>]$» />, согласно определению топа №6 п.2. = begin> 1&2 \ 1&3 \ 2&3 end]$» /><br />Что касается множества В, то именно это меня и вводит в заблуждение. Но следуя неумолимой логике можно предположить что на множестве В задано отношение S, а на множестве А — отношения R1,R2,R3,R4,R5. И что множества есть подмножества одного множества, на котором по условию задачи заданы отношения S,R1,R2,R3,R4,R5.</p>
<p>Для вашего примера выше можете считать, что все и равны $» />. <br />Что вам нужно сделать? для начала нарисовать вот так линии:</p>
<p>= begin <cccc|c>1&3&1&1&4 \ 2&4&2&2&3 \ 4&1&3&2&7 \ 4&9&4&4&1 end]$» />, = begin <cccc|c>2&4&4&2&3 \ 1&3&1&1&7 \ 3&2&3&5&2 \ 1&3&1&1&2 \ 4&1&3&2&5 end]$» />, = begin <cccc|c>4&1&3&2&4 \ 1&3&1&1&5 \ 2&3&4&3&2 \ 3&3&4&1&5 end]$» />, = begin <cccc|c>1&3&1&1&2 \ 6&8&5&5&2 \ 4&1&3&2&1 end]$» />, = begin <cccc|c>1&3&1&1&3 \ 3&2&1&4&4 \ 4&1&3&2&9 \ 1&3&1&1&4 end]$» />, <ccccc|c>1&1&2&4&3&6 \ 4&2&5&2&4&8 \ 7&5&4&1&9&7 \ 2&4&3&1&6&7 \ 4&2&5&2&3&9 \ 4&7&5&2&3&5 \ 7&5&4&1&9&8 end]$» /></p>
<p>Дальше — понять, что можно перебирать не все элементы их ^4$» />, а только те наборы, которые в встречаются слева от линии.<br />Ну и пошли смотреть по строкам:<br />Видим в : , таким образом нужно найти в остальных отношениях строки с такими же первыми четырьмя элеметами:<br />: ,<br />: ,<br />: ,<br />: ,<br />а из пятых элементов составляем строку и ищем в строку с таким началом: <br /> откуда следует, что композиции будет принадлежать элемент<br />.<br />И т. д.</p>
<p>— Вс дек 19, 2010 05:56:25 —</p>
<p>Да и вообще, разве не принято сначала определять всякие штуки на двух объектах, а потом ассоциативностью или как-нибудь ещё доопределять для многих?</p>
<p>Я слабо представляю как такую вещь определить сначала на двух объектах, а потом воспользоваться ассоциативностью. Такое хорошо, когда что-то бинарное есть. И ассоциативное. Тут бинарного ничё нет.<br />(А так вы даже декартово произведение множеств не определите, кстати.)</p>
<h2>2.7. Суперпозиция функций. Замыкание набора функций. Замкнутые классы функций. Полные наборы. Базисы</h2>
<p>Основные понятия. Пусть имеется некоторый набор К (или, как иногда говорят, класс), состоящий из конечного числа булевых функций.</p>
<p>1. Суперпозицией функций из этого набора называются новые функции, полученные с помощью конечного числа применения двух операций:</p>
<p>а) переименование любой переменной, входящей в любую функцию из К (или в любую уже построенную суперпозицию);</p>
<p>б) подстановка любой функции из набора К (или любой построенной ранее суперпозиции) вместо любой переменной в любую функцию из К (или в любую ранее построенную суперпозицию).</p>
<p>Короче говоря, суперпозиция – это любая функция, которую можно получить из данного класса переименованиями переменных и подстановками. Суперпозицию еще иначе называют сложной функцией.</p>
<p>Например , если дана одна функция х | x (штрих Шефера) то ее суперпозициями, в частности, будут следующие функции x| y , x| ( x| y ), x| ( y| z ) и т. д.</p>
<p>2. Замыканием набора функций из К называется множество всех суперпозиций из этого класса.</p>
<p>3. Класс функций К называется замкнутым , если его замыкание совпадает с ним самим.</p>
<p>4. Набор функций называется полным , если его замыкание совпадает со множеством всех логических функций. Иначе говоря, полный набор – это множество таких функций, через которые можно выразить все остальные булевы функции.</p>
<p>5. Неизбыточный полный набор функций называется базисом.</p>
<p>(Слово «неизбыточный» означает что если какую-то функцию удалить из набора, то этот набор перестанет быть полным).</p>
<p>6) Функция называются шефферовской , если она (одна) является базисом.</p>
<p>Примеры . 1. Набор функций ( , , ), т. е. конъюнкция, дизъюнкция и отрицание являются полным набором (так как их суперпозициями являются ДНФ и КНФ, которыми можно представить любую логическую функцию), но он не является базисом, так как это набор избыточен, поскольку с помощъю правил де Моргана можно удалить конъюнкцию или дизъюнкцию, ибо x y x y , x y x y . Наборы же ( , ) и ( , ), очевидно,</p>
<p>2. Так как любую функцию можно представить в виде полинома Жегалкина (п. 6), то ясно что функции конъюнкция, сложение по модулю 2 и константы «0» и «1» являются полным набором, но эти четыре функции также не являются базисом, поскольку 1 + 1 = 0, и поэтому константу «0» можно исключить из полного набора (однако для построения полиномов</p>
<p>Жегалкина константа «0» необходима, поскольку выражение «1 + 1» не является полиномом Жегалкина). Таким образом, базисом является набор функций (1, +, ).</p>
<p>3. Докажем, что функция «штрих Шеффера» х|y = xy (т. е. отрицание конъюнкции, или функция «не и») является базисом, и, следовательно, шефферовской функцией. Действительно, x | x = xx x откуда</p>
<p>( x|y ) | ( x|y ) = x | y xy xy .</p>
<p>Итак, отрицание и конъюнкция являются суперпозициями штриха Шеффера, а так как эти 2 функции образуют базис, то любую логическую функцию можно представить в виде суперпозиции штриха Шеффера. Иными словами, класс функций, состоящий всего из одной этой функции, является полным.</p>
<p>Ясно, что класс, состоящий всего из одной функции, всегда является неизбыточным. Таким образом, штрих Шеффера является базисом, а значит, шефферовской функецией.</p>
<p>4. Аналогично, стрелка Пирса (т. е. отрицание дизъюнкции, «не или»)</p>
<p>шефферовской. Действительно, x y x y , а потому</p>
<p>откуда ( x y ) ( x y ) x y x y x y . Рассуждая как и</p>
<p>выше, убеждаемся, что стрелка Пирса – шефферовская функция.</p>
<p>Среди функций трех или более переменных шефферовских функций очень много (конечно, выражение других булевых функций через шефферовскую функцию большого числа переменных не очень просто, поэтому в технике они используются редко).</p>
<p>Заметим, что вычислительное устройство чаще всего базируется на полном наборе функций (часто на базисах). Если в основе устройства лежат конъюнкция, дизъюнкция и отрицание, то для этих устройств важна проблема минимизации ДНФ, если в основе устройства лежат другие функции, то полезно уметь алгоритмически минимизировать выражения через эти функции.</p>
<p>Пять наиболее важных классов логических функций.</p>
<p>1. Класс Т 0 – это набор всех тех логических функций, которые на нулевом наборе принимают значение 0. Говорят, что класс Т 0 – это класс функций, сохраняющих 0: f T 0 означает, что f (0, 0, … , 0) = 0 (в таблице истинности такой функции первое значение равно нулю).</p>
<p>2. Класс Т 1 – это набор всех логических функций которые на единичном наборе принимают значение 1 (это класс функций, сохраняюших единицу ): f (1, 1, … , 1) = 1 (в таблице истинности такой функции последнее значение равно единице).</p>
<p>Заметим, что число функций от п переменных, принадлежащих клас-</p>
<p>сам Т 0 и Т 1 равно половине числа всех функций, т. е. равно 2 2 n 1 , так как у функции первое значение – либо 0, и она T 0 , либо 1, и тогда она не T 0 , аналогичные рассуждения верны и для Т 1 ; так же выясняется что одновременно входят и в Т 0 , и в Т 1 четверть всех функций, а не входят ни в тот, ни в другой класс тоже четверть и т. д.</p>
<p>3. Класс L – класс линейных функций т. е. функций, для которых по- ли-ном Жегалкина не содержит конъюнкций. Иными словами, функция f ( x 1 , x 2 , … , x п ) является линейной , если ее полином Жегалкина имеет вид:</p>
<p>f ( x 1 , x 2 , … , x п ) = 0 + 1 x 1 + 2 x 2 +…+ п x п .</p>
<p>Заметим, что число линейных функций от п переменных равно 2 п+ 1 , так как каждый из ( п + 1) — го коэффициентов линейной функции может принимать одно из 2 значений .</p>
<p>Лемма ( необходимый признак линейности функции ) . В таблице истин-</p>
<p>ности непостоянной линейной функции содержится одинаковое число нулей и единиц .</p>
<p>Доказательство по индукции по числу переменных. База индукции:</p>
<p>для непостоянных линейных функций от одной переменной х и x = х + 1 это очевидно. Индукционный переход: если для f ( x 1 , x 2 , … , x п ) = x 1 + x 2 +…+ x п утверждение уже доказано, то оно верно и для</p>
<p>F ( x 1 , x 2 , … , x п , x n+ 1 ) = x 1 + x 2 +…+ x п + x n+ 1 .</p>
<p>Действительно, добавление новой переменной удваивает таблицу истинности; в той части таблицы, где новая переменная равна нулю (т. е. в которой к сумме переменных добавляется 0), число нулей и единиц как было, так и осталось одинаковым; в той части таблицы, где х п+ 1 = 1, нули становятся единицами, а единицы нулями, но так как их было одинаковое количество, то такое же соотношение и осталось. Если в линейной функции есть слагаемые с переменными, перед которыми стоит коэффициент 0, то такие переменные являются фиктивными и не влияют на соотношение нулей и единиц в таблице истинности. Индукционный переход совершен, и лемма доказана.</p>
<p>Следствие ( достаточный признак нелинейности функции ) . Если в таб-</p>
<p>лице истинности функции есть и нули и единицы, но их число – разное, то такая функция заведомо нелинейна.</p>
<p>Замечания: 1) разумеется, нелинейная функция может иметь в таблице истинности одинаковое число нулей и единиц; 2) в таблице истинности непостоянной линейной функции от п переменных содержится по 2 п нулей и единиц.</p>
<p>4. Класс М – класс монотонных функций. Опишем класс этих функций более подробно. Пусть имеются 2 набора из п переменных:</p>
<p>1 = ( х 1 , х 2 , … , х п ) и 2 = ( y 1 , y 2 , … , y п ) .</p>
<p>Будем говорить, что набор 1 предшествует (или меньше ) набора 2 (и будем записывать это так: 1 2 ), если для всех i = 1, 2, … , n выполняются неравенства х i y i . Если же среди указанных неравенств есть неравенства противоположного смысла (т. е. если при некотором i x i y j ), то такие наборы называются несравнимыми. Например, при п = 2 наборы (0, 1) и (1, 0) не сравнимы между собой. Функция от п переменных называется монотонной , если для любых двух сравнимых наборов на меньшем наборе она принимает меньшее или равное значение (понятно, что несравнимые наборы – это те, в которых есть некоторые координаты типа (0, 1) в одном наборе и (1, 0) в другом на тех же местах. Заметим также, что в дискретной математике монотонные функции это только как бы « монотонно возрастающие функции», «монотонно убывающие» функций здесь не рассматриваются). Важно помнить, что набор (0, 0, … , 0) сравним с любым другим набором той же длины и предшествует ему, а набор (1, 1, … , 1) тоже сравним с любым другим набором и следует за ним. Поэтому если в верхней строчке таблицы истинности стоит значение функции, равное 1, или в последней строчке стоит значение функции, равное 0, то такая функция заведомо не монотонна. Так как при стандартной записи таблицы истинности для любых двух сравнимых наборов значений аргументов предшествующий набор расположен выше последующего, то если хотя бы для одной пары сравнимых наборов значений аргументов соответствующие значения функции таковы, что ноль расположен ниже единицы, то такая функция также заведомо не монотонна. Например, в нижеследующей таблице функции f 1 , f 2 являются монотонными функциями, а функции f 3 , f 4 – нет:</p>
<p>Легко проверить также, что функция (00010101) является монотонной. Очевидно также, что если в таблице истинности (при естественном порядке набора переменных) вверху стоят нули, а затем единицы, то эта функция точно является монотонной.</p>
<p>5. Класс S – класс самодвойственных функций. Функция п переменных f ( x 1 , x 2 ,…, x п ) называется самодвойственной , если для любых наборов</p>
<p>значений аргументов выполняется равенство: f ( x 1 , x 2 . x n ) f ( x 1 , x 2 . x n ) , т. е. если на противоположных наборах значений аргументов она принимает противоположные значения. Например, функции f 1 , f 2 – являются самодвойственными, а функции f 3 , f 4 – не являются.</p>
<p>Лемма. В таблице истинности противоположные наборы значений аргументов расположены симметрично относительно середины таблицы.</p>
<p>Доказательство. Так как наборы значений аргументов в таблице истинности являются наборами двоичных цифр чисел 0, 1, 2, … , 2 п – 1, то, если в строке с номером k расположен набор k – 1 = ( x 1 , x 2 ,…, x п ) в симмет-</p>
<p>ричной относительно середины строке, т. е. в строке с номером 2 п – k ,</p>
<p>расположен набор 2 п – k = (2 п – 1) – ( k – 1) = (1, 1, … , 1) – ( x 1 , x 2 ,…, x п ) =</p>
<p>= (1 – х 1 , 1 – х 2 , … , 1 – х п ) = ( x 1 , x 2 . x n ), что и требовалось доказать. Следствия: 1) для выяснения, входит ли данная функция в S , надо</p>
<p>сравнить все пары значений функции, расположенных симметрично относительно середины таблицы. Если значения функции во всех парах противоположны (т. е. при сложении в сумме дают единицу), то рассматриваемая функция – самодвойственная; 2) таким образом, чтобы построить самодвойственную функцию, мы можем первую половину ее значений выбрать произвольно, а вторая определяется однозначно условием симметрии. Поэтому всех самодвойственных функций от п переменных существу-</p>
<p>ет столько же, сколько всех функций от ( п – 1) переменных, т. е. 2 2 n 1 . Утверждения: 1) каждый из классов функций Т 0 , Т 1 , L , M , S замкнут. Это утверждение следует непосредственно из определения самих этих</p>
<p>классов, а также из определения замкнутости (например, суперпозиция функции, сохраняющей 0, с функцией, сохраняющей 0, является тоже функцией, сохраняющей 0; суперпозиция линейной функции с линейной функцией является тоже линейной функцией, и т. д.); 2) каждый из классов функций Т 0 , Т 1 , L , M , S не является полным. Действительно, замыкание каждого из этих классов совпадает с ним самим, а не с множеством всех логических функций, покольку существуют функции, не входящие в эти классы (существуют функции, не сохраняющие ноль или единицу, нелинейные, немонотонные, несамодвойственные).</p>
<p>Теорема Поста . Для того чтобы некоторый набор функций К был полным необходимо и достаточно чтобы в него входили функции не принадлежащие каждому из классов T 0 , T 1 , L , M , S.</p>
<p>Заметим, что необходимость этого утверждения очевидна, так как если бы все функции из набора К входили в один из перечисленных классов, то и все суперпозиции, а значит, и замыкание набора входило бы в этот класс, и класс К не мог быть полным .</p>
<p>Достаточность этого утверждения доказывается довольно сложно, и мы не будем его здесь приводить .</p>
<p>Из этой теоремы следует довольно простой способ выяснения полноты некоторого набора функций. Для каждой из этих функций выясняется принадлежность ее к перечисленным выше классам. Результаты заносятся в так называемую таблицу Поста , которая имеет вид (в нашем примере эта таблица составлена для четырех функций, причем знаком «+» мы отмечаем принадлежность функции соответствующему классу, знак «–» означает, что функция в него не входит):</p>
<h2>Функции, суперпозиция функций, обратная функция. Ограниченность и монотонность функций одного вещественного переменного. Единственность предела. Понятие приближенного значения корня уравнений. Метод половинного деления нахождения приближенного корня</h2>
<p><img decoding=](https://dxdy-02.korotkov.co.uk/f/1/b/3/1b35589f240d544d6f8f26b32cf4acda82.png)
Опр.1. Даны .Если каждому элементу поставить по некоторому правилу ставится в соответствие единственный эл-т , то говорят, что на мн-ве X задана функция со значением в мн-ве Y и обозначают .
Х – называется О.О.Ф. и называется значением функции на Эл-те Х и мн-во всех значений функции называется множеством значений функции и обознач. .
Опр.2. Пусть , . Функция назыв. суперпозицией функций и если выполнено и обозначается ,т.е. .
Опр.3.Дана функция . Если , то функция назыв. взаимнооднозначной.
Опр.4. Дана ф. . Пусть ф. взаимнооднозначная, тогда существует существует единственный из О.О.Ф., такой что . Обозначим .Таким образом, на множестве Х задается функция , которая называется обратной функцией .
Замеч.1.Обратные функции существуют только у взаимнооднозначных. Применяется следующая терминология:
1) если О.О.Ф. Х есть N, то функция называется последовательностью. — -член последовательности.
2) тогда называется функцией одного вещественного переменного.
2) Ограниченность и монотонность функций одного вещественного переменного.
Функция называется ограниченной, если множество значений этой функции – ограниченное мн-во или если сущ-ет М>0 такое, что
1) не убывающей(возрастающей) если
2) не возрастающей(убывающей) если
3) если ф. одна из 4 типов, то её наз-ют монотонной.
4) если возрастающая или убывающая, то строго монотонная.
Т1. Пусть строго монотонная, тогда у неё существует обратная и обратная – строго монотонная того же типа.
Док-во: докажем для возрастающей функции. Пусть . Если , то
. Значит ф. взаимнооднознач. (по опр.3) и у неё есть обратная (по опр.4). Докажем, что возрастающая.(от противного).
. Противоречие с тем, что . Значит возрастающая по опр.6.
Замеч.2. Обратная функция существует не только у строгомонотонных.
3) Окрестность точки, предельные изолированные точки, предел функции и последовательность.
Опр.1. Пусть . Множество ===
=- это окрестность точки .
= — проколотая окрестность точки .
Опр.2. Точка называется предельной точкой мн-ва Х если . Точка называется изолированной точкой мн-ва , если и сущ-ет такое что .
Опр.3. Дана ф. ,, — предельная точка Х. Число или точка В называется пределом функции f в точке или при если для любого существует такое, что из выполняется . Это обозначается: или .
Опр. 4. Число или точка b называется пределом последовательности если такое, что выполняется . Обозначается или
4) Единственность предела.
Если существует предел функции в т.а, то этот предел единственный.
Док-во: пусть пределов 2, т.е.
. по опр.3 пар.3 для этого сущ-ет такое что .По опр.3пар.3 для этого же сущ-ет такое, что
-противоречие, значит b=c и предел – единственный.
5) Ограниченность функции имеющ. Предел. Теоремы о стабилизации знака и о определенном переходе в неравенство.
Т2 (об ограниченности функции имеющей предел) Если сущ. , то функция f ограничена в некоторой проколотой окрестности точки а.
Т3 (о стабилизации знака)Если ,тогда f(x)>0 в некоторой точка проколотой окрестности точки а.
Т4 (о предельном переходе к неравенству)
Пусть существует 2 предела
и пусть в некоторой проколотой окрестности точки а,
6) Теорема о пределе сжатой функции.
Пусть и пусть в некоторой проколотой окрестности точки ,
Док-во: возьмём , по опр.3 пар.3 сущ-ет , такое что по опр.3 пар.3 для того же сущ-ет
по усл. сущ-ет , такая что
итак, т.к. мы брали произвольно, то сущ-ет , такое что выполняется нер-во, то по опр.3 пар.3 сущ-ет .
7) Предел суммы разности и частность
Доказательство (приведем для суммы):
Возьмем по опред.3 ( Дана функция , a-предельная точка множества X. Число или точка b называется пределом функции f в точке a, или при x стремящимся к а, если для , такое что выпол. ) дляпо опред.3(приведенному выше)
По определению 3 мы придем ч.т.д.
 Предел произведения
Предел произведения
Лемма1 Пусть f-функция ограничена в некоторой проколотой окрестности точки а. Пусть ,тогда
ПоусловиюВозьмем по по оред.3 ( Дана функция , a-предельная точка множества X. Число или точка b называется пределом функции f в точке a, или при x стремящимся к а, если для , такое что выпол.)