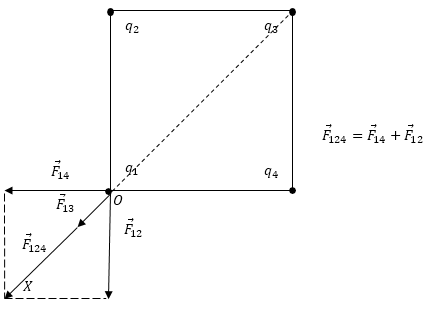
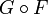Принцип суперпозиции электрических полей
Допустим, что у нас есть три точечных заряда. Эти заряды взаимодействуют. Можно провести эксперимент и измерить силы, которые действуют на каждый заряд. Для того чтобы найти суммарную силу, с которой на один заряд действует второй и третий, необходимо силы, с которыми действуют каждый из них сложить по правилу параллелограмма. Возникает вопрос, равна ли измеряемая сила, которая действует на каждый из зарядов, сумме сил со стороны двух других, если силы рассчитаны по закону Кулона. Исследования показали, что измеряемая сила равна сумме вычисляемых сил в соответствии с законом Кулона со стороны двух зарядов. Такой эмпирический результат выражается в виде утверждений:
- сила взаимодействия двух точечных зарядов не изменяется, если присутствуют другие заряды;
- сила, действующая на точечный заряд со стороны двух точечных зарядов, равна сумме сил, действующих на него со стороны каждого из точечных зарядов при отсутствии другого.
Данное утверждение называется принципом суперпозиции. Этот принцип является одной из основ учения об электричестве. Он так же важен, как и закон Кулона. Его обобщение на случай множества зарядов очевидно. Если имеется несколько источников поля (количество зарядов N), то результирующую силу, действующую на пробный заряд q можно найти как:
где $overrightarrow>$ — сила, с которой действует на заряд q заряд $q_i$ если остальные N-1 заряд отсутствуют.
Принцип суперпозиции (1) позволяет, используя закон взаимодействия между точечными зарядами, вычислить силу взаимодействия между зарядами, находящимися на теле конечных размеров. Для этого необходимо разбить каждый из зарядов на малые заряды dq, которые можно считать точечными, взять из попарно, вычислить силу взаимодействия и провести векторное сложение полученных сил.
Полевая трактовка принципа суперпозиции
Принцип суперпозиции имеет полевую трактовку: напряженность поля двух точечных зарядов равна сумме напряженностей, которые создаются каждым из зарядов, при отсутствии другого.
Готовые работы на аналогичную тему
В общем случае принцип суперпозиции относительно напряженностей можно записать так:
где $
Подтверждено инженерной практикой, что принцип суперпозиции соблюдается вплоть до очень больших напряженностей полей. Очень значительные напряженности имеют поля в атомах и ядрах (порядка $^-^frac$), но и для них использовали принцип суперпозиции в расчетах энергетических уровней атомов и данные расчетов совпали с данными экспериментов с большой точностью. Однако надо отметить, что при очень малых расстояниях (порядка $sim ^м$) и экстремально сильных полях принцип суперпозиции, возможно, не выполняется. Так, к примеру, на поверхности тяжелых ядер напряженности достигают порядка $sim ^frac$ принцип суперпозиции выполняется, но при напряженности $^frac$ возникают квантово — механические нелинейности взаимодействия.
Если заряд распределен непрерывно (нет необходимости учитывать дискретность), то суммарная напряженность поля найдется как:
В уравнении (3) интегрирование проводят по области распределения зарядов. Если заряды распределены по линии ($tau =frac-линейная плотность распределения заряда$), то интегрирование в (3) проводят по линии. Если заряды распределены по поверхности и поверхностная плотность распределения $sigma =frac$, то интегрируют по поверхности. Интегрирование проводят по объему, если имеют дело с объемным распределением заряда: $rho =frac$, где $rho $ — объемная плотность распределения заряда.
Принцип суперпозиции в принципе позволяет определить $overrightarrow$ для любой точки пространства по известному пространственному распределению заряда.
Задание: Одинаковые точечные заряды q находятся в вершинах квадрата со стороной a. Определите, какая сила, действует на каждый заряд со стороны других трех зарядов.
Изобразим силы, действующие на один из зарядов в вершине квадрата (выбор не важен, так как заряды одинаковы) (рис.1). Результирующую силу, действующую на заряд $q_1$, запишем как:
Силы $
Модуль силы $
Направим ось OX как указано на рис. 1, спроектируем уравнение (1.1), подставим полученные модули сил, получим:
Ответ: Сила, действующая на каждый из зарядов в вершинах квадрата равна: $F=fracleft(frac+1>right).$
Задание: Электрический заряд равномерно распределен вдоль тонкой нити в равномерной линейной плотностью $tau $. Найдите выражение для напряженности поля на расстоянии $а$ от конца нити на ее продолжении. Длина нити равна $l$.

Выделим на нити точечный заряд $dq$, запишем для него из закона Кулона выражение для напряженности электростатического поля:
В заданной точке все векторы напряженности направлены одинаково, вдоль оси Х, поэтому, имеем:
Так как заряд по условию задачи равномерно распределен по нити с линейной плотностью $tau $, то можно записать следующее:
Подставим (2.4) в уравнение (2.1), проинтегрируем:
Ответ: Напряженность поля нити в указанной точке вычисляется по формуле: $E=frac.$
Принцип суперпозиции — определение, формула и значение
Большая часть популярных доктрин, открытых на сегодня, описывает довольно своеобразные явления — механические движения, тепловые процессы, электрические явления и так далее. Однако существуют мнения, которые относятся ко всем областям физических явлений. Одним из таких теоретических понятий считается принцип суперпозиции (ПС).
- Общая концепция
- Напряжение электростатического поля
- Введение в волновую суперпозицию
- Конструктивное и деструктивное вмешательство
- Две синусоиды в противоположных направлениях
- Линии электропередач
- Принцип супербора
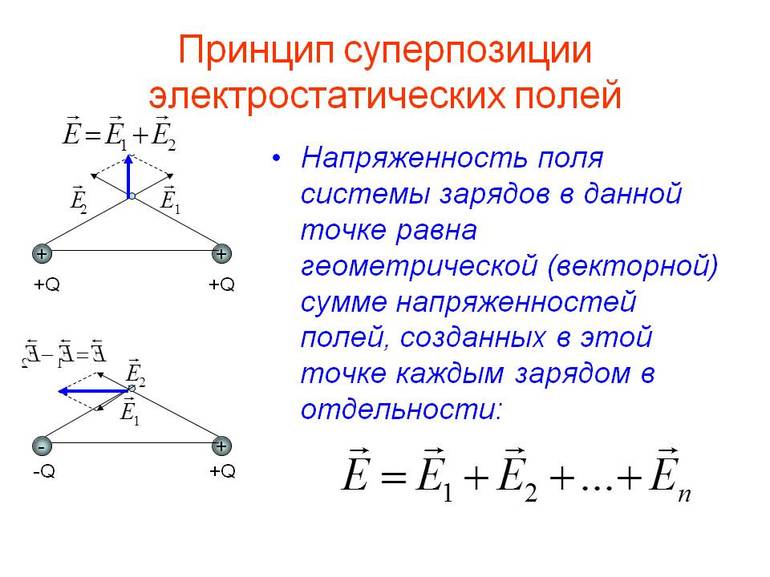
Общая концепция
Можно столкнуться с принципом суперпозиции всякий раз, когда есть больше одного источника электростатического поля. Затем в каждой точке пространства происходит сборка линий, поступающих из каждого источника. Поскольку интенсивность является вектором, в каждой точке добавляют друг к другу векторы любого из источников, то есть учитывают их значения направления и отдачи.
Самый простой способ — добавить параллельные векторы, затем просто вычесть значения, и уравнение становится скалярным. В любом ином случае угол между векторами должен быть принят во внимание. В общем, векторное уравнение суперпозиции полей может быть сохранено через знак суммы. Определяется принцип суперпозиции формулой:
E = ∑ − → E i E → = ∑ E i →
Напряжение электростатического поля
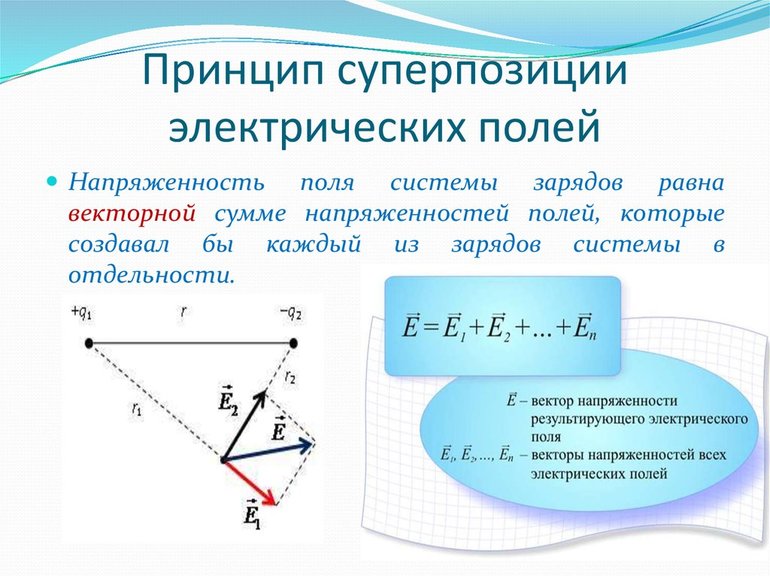
Стоит рассмотреть напряжённость электрического поля, принцип суперпозиции, создаваемый двумя начальными зарядами одновременно в любой точке пространства. Например, есть 2 источника, положительный заряд и отрицательный, примерно одинаковых значений, то есть диполь. Нужно выяснить результирующую напряжённость электростатического поля в 3 точках.
Сначала отмечают вспомогательные линии, которые проходят через каждую из трёх точек и оба источника. Затем по очереди рисуют интенсивность в каждой из точек, основываясь на обеих линиях. Стоит отметить важную информацию о принципе суперпозиции электрических полей: направление и возврат вектора интенсивности будут такими же, как и у линии, действующей на положительный заряд, размещённый в этой точке.
Нужно рассмотреть первый пункт, поскольку пробный заряд всегда +. Интенсивность от источника плюсового будет влево. Он представлен в виде вектора E1 +. Ток от источника отрицания будет отправлен в то же место, поскольку противоположные заряды притягивают друг друга. Он как вектор E1-. Поскольку сила электростатического поля будет вектором, результирующий ток — сумма двухкомпонентных линий. Он в виде E1. Первая точка близка к положительному источнику, потому вектор интенсивности от него больше, чем отрицательный заряд.
Разделяя их, однажды в точке 2 сила, исходящая от нагрузки отрицательного Е2, направляется на источник, а исходящая от нагрузки положительного Е2 + направляется от него. Точка 2 находится на одинаковом расстоянии от обоих полей, поэтому значения линий напряжения E2 + E2 равны. Так как векторы не параллельны, применяют метод параллелограмма для их добавления — рисуют его стороны, что являются векторами интенсивности (ВИ). Сумма — диагональ, исходящая из начала. В результате получают E2.
Точно так же это будет для пункта 3. E3 + от источника, E3 направлена наоборот. Длинная диагональ представляет собой сумму векторов компонентов, то есть результирующей интенсивности в точке E3.
Полученные уравнения являются векторными, поэтому в расчётах следует учитывать не только значение, но также их направление и возврат. Это означает, что для трёх точек только одна с номером 1 может быть легко представлена в скалярной форме. Поскольку векторы E1 + E1 находятся на одной прямой, они параллельны. Их значения должны быть добавлены, потому что их возвраты, то есть стрелки, будут в одном направлении. Следовательно, в этом случае скалярное уравнение выглядит так же, как вектор.
Введение в волновую суперпозицию
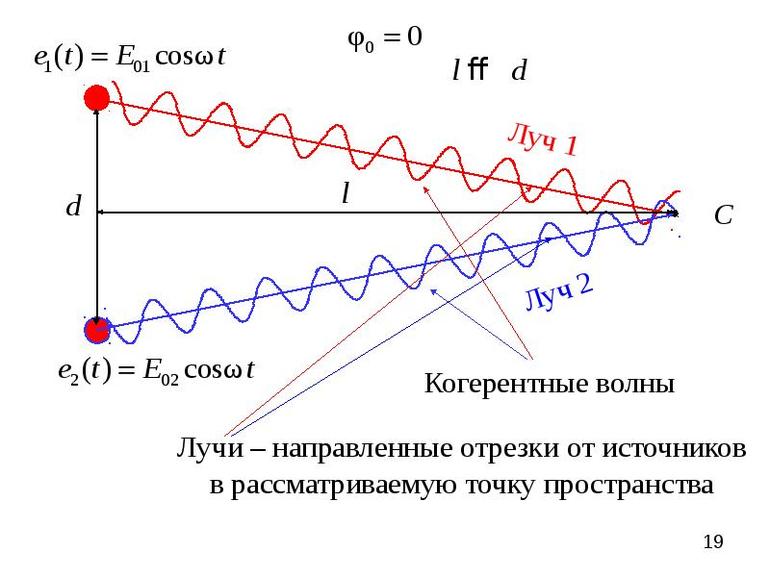
Волны окружают нас, и их присутствие влияет на ряд явлений. Можно представить себе нахождение в лодке и слышимую сирену корабля. В этом случае можно получить звуковую волну непосредственно, а также ту, которая отражается от морской воды. Чтобы понять это, нужно сосредоточиться на базовой концепции суперпозиции, а также на знаниях, связанных с теоремой.
Пример струнной волны для определения суперпозиции на основе теоремы поможет лучше всё понять. В соответствии с этим чистое перемещение любого компонента строки в течение заданного времени равно алгебраическому набору смещений, вызванных каждой волной. Потому такой метод добавления отдельных сигналов для оценки частоты называется принципом суперпозиции.
ПС выражается утверждением, что перекрывающиеся волны алгебраически добавляются для создания результирующей линии. Исходя из этого (f1, f2 …., fn), они не мешают движению друг друга. Следовательно, суперпозиция волн может привести к следующим трем последствиям:
- Всякий раз, когда две волны с одной частотой движутся с похожей скоростью в одном и том же направлении в нужной среде, они перекрывают друг друга и создают эффект, называемый помехой.
- В ситуации, когда 2 линии с равными частотами передвигаются с примерной скоростью в противоположных направлениях, они перекрывают друг друга, создавая стационарность.
- Наконец, когда две волны, имеющие слегка изменяющиеся частоты, движутся с одинаковой скоростью в одном и том же направлении, они перекрывают друг друга: получается биение.
Конструктивное и деструктивное вмешательство
Это когда две волны движутся в определённом или одном и том же направлении. Согласно ПС, последующее смещение можно записать в виде решения:
y (x, t) = y m sin (kx-ωt) + y m sin (kx-ωt+ϕ) = 2 y m cos (ϕ/2) sin (kx-ωt+ϕ/2)
Эта волна имеет развитие амплитуды, которая зависит от фазы (ϕ). Считается, что две линии находятся в фазе (ϕ = 0). Они мешают конструктивно. Кроме того, результирующая часть имеет двойную амплитуду по сравнению с отдельными волнами. С другой стороны, задача, когда две линии имеют противоположную фазу (ϕ = 180). Они оказывают разрушающее воздействие на друг друга.
Две синусоиды в противоположных направлениях
Бегущая волна распространяется из одного места в другое, но стоячая выглядит как неподвижная. Предположим, что две линии (имеющие одинаковые свойства — амплитуду, длину и частоту) передвигаются в противоположных направлениях.
Основываясь на системе суперпозиции, конечная амплитуда может быть записана как формулировка:
y (x, t) = y m sin (kx-ωt) + y m sin (kx+ωt) = 2 y m sin (kx) cos (ωt)
Согласно теореме о суперпозиции, несколько волн не называют бегущими, поскольку зависимость положения и времени делится. В этом случае амплитуда, в зависимости от точки или местоположения, составляет 2ymsin (kx). Она не будет смещаться, но сможет стоять с колебанием вверх и вниз на основе независимого cos (wt).
Линии электропередач
Электрическое поле в пространстве обычно можно создать силовыми линиями. Понятие было введено М. Фарадеем при изучении закона взаимодействия магнетизма. Затем концепцию индукции разработал Джон Максвелл.
Важные особенности магнитной теории заключаются в следующем:

- Линия электропередачи или напряжённости — касательная, в которой каждая из её точек совпадает с направлением силы, действующей на положительный точечный заряд, размещённый в этой точке поля.
- Линии растяжения почти параллельны в пространстве между пластинами. Их плотность одинакова. Это говорит о том, что поле в этой области пространства является однородным.
- В электрополе силовые линии потенциала не замкнуты. Они начинаются на плюсовых зарядах и заканчиваются минусовыми. Они нигде не пересекаются. Плотность силовых линий больше у заряженных тел, где напряжённость поля больше.
Принцип супербора

С точки зрения квантовой механики, этот принцип содержит большое количество особенностей, которые нельзя просто принять. Это связано с тем, что фактически эта отрасль физики имеет дело, прежде всего, с другими состояниями объекта. С точки зрения традиционной механики, они должны быть элементарно взаимоисключающими. Принцип суперпозиции, который на квантовом уровне еще не полностью понят ученым, подразумевает, среди прочего, необходимость суперотбора, то есть главного класса фактора, который оказывает наибольшее влияние на пучок сил в определенный момент.
Подводя итоги, можно сказать следующее: в тот момент, когда поток электростатического поля больше, чем 1 заряд, то в каждой точке пространства поля всех линий собираются, и результирующий ВИ является суммой всех компонентов.
Принцип суперпозиции электрических полей.
Принцип суперпозиции (наложения) полей формулируется так: Если в данной точке пространства различные заряженные частицы создают электрические поля , напряженности которых и т.
Принцип суперпозиции (наложения) полей формулируется так:
Если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых и т. д., то результирующая напряженность поля в этой точке равна: .
Принцип суперпозиции полей справедлив для случая, когда поля, созданные несколькими различными зарядами, не оказывают никакого влияния друг на друга, т. е. ведут себя так, как будто других полей нет. Опыт показывает, что для полей обычных интенсивностей, встречающихся в природе, это имеет место в действительности.
Благодаря принципу суперпозиции для нахождения напряженности поля системы заряженных частиц в любой точке достаточно воспользоваться выражением напряженности поля точечного заряда.


На рисунке ниже показано, как в точке A определяется напряженность поля , созданная двумя точечными зарядами q1 и q2.

Силовые линии электрического поля.
Электрическое поле в пространстве принято представлять силовыми линиями. Понятие о силовых линиях ввел М. Фарадей при исследовании магнетизма. Затем это понятие было развито Дж. Максвеллом в исследованиях по электромагнетизму.
Силовая линия, или линия напряженности электрического поля, — это линия, касательная к которой и каждой ее точке совпадает с направлением силы, действующей на положительный точечный заряд, находящийся в этой точке поля.
На рисунках ниже изображены линии напряженности положительно заряженного шарика (рис. 1); двух разноименно заряженных шариков (рис. 2); двух одноименно заряженных шариков (рис. 3) и двух пластин, заряженных разными по знаку, но одинаковыми по абсолютной величине зарядами (рис. 4).

Линии напряженности на последнем рисунке почти параллельны в пространстве между пластинами, и плотность их одинакова. Это говорит о том, что поле в этой области пространства однородно. Однородным называется электрическое поле, напряженность которого одинакова во всех точках пространства.
В электростатическом поле силовые линии не замкнуты, они всегда начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Они нигде не пересекаются, пересечение силовых линий говорило бы о неопределенности направления напряженности поля в точке пересечения. Плотность силовых линий больше вблизи заряженных тел, где напряженность поля больше.
Поле заряженного шара.

Напряженность поля заряженного проводящего шара на расстоянии от центра шара, превышающем его радиус r ≥ R. определяется по той же формуле, что и поля точечного заряда . Об этом свидетельствует распределение силовых линий (рис. а), аналогичное распределению линий напряженности точечного заряда (рис. б).

Заряд шара распределен равномерно по его поверхности. Внутри проводящего шара напряженность поля равна нулю.
1.2. Закон Кулона. Принцип суперпозиции
Пусть имеются два заряженных макроскопических тела, размеры которых пренебрежимо малы по сравнению с расстоянием между ними. В этом случае каждое тело можно считать материальной точкой или «точечным зарядом».
Французский физик Ш. Кулон (1736–1806) экспериментально установил закон, носящий его имя (закон Кулона) (рис. 1.5):

Рис. 1.5. Ш. Куло́н (1736–1806) — французский инженер и физик
В вакууме сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов, обратно пропорциональна квадрату расстояния между ними и направлена по прямой, соединяющей эти заряды:

На рис. 1.6 показаны электрические силы отталкивания, возникающие между двумя одноименными точечными зарядами.

Рис. 1.6. Электрические силы отталкивания между двумя одноименными точечными зарядами
Напомним, что , где и — радиус-векторы первого и второго зарядов, поэтому силу, действующую на второй заряд в результате его электростатического — «кулоновского» взаимодействия с первым зарядом можно переписать в следующем «развернутом» виде
Отметим следующее, удобное при решении задач, правило: если первым индексом у силы ставить номер того заряда, на который действует эта сила, а вторым – номер того заряда, который создает эту силу, то соблюдение того же порядка индексов в правой части формулы автоматически обеспечивает правильное направление силы — соответствующее знаку произведения зарядов: — отталкивание и — притяжение, при этом коэффициент всегда.
Для измерения сил, действующих между точечными зарядами, был использован созданный Кулоном прибор, называемый крутильными весами (рис. 1.7, 1.8).

Рис. 1.7. Крутильные весы Ш. Кулона (рисунок из работы 1785 г.). Измерялась сила, действующая между заряженными шарами a и b

Рис. 1.8. Крутильные весы Ш. Кулона (точка подвеса)
На тонкой упругой нити подвешено легкое коромысло, на одном конце которого укреплен металлический шарик, а на другом — противовес. Рядом с первым шариком можно расположить другой такой же неподвижный шарик. Стеклянный цилиндр защищает чувствительные части прибора от движения воздуха.
Чтобы установить зависимость силы электростатического взаимодействия от расстояния между зарядами, шарикам сообщают произвольные заряды, прикасаясь к ним третьим заряженным шариком, укрепленным на ручке из диэлектрика. По углу закручивания упругой нити можно измерить силу отталкивания одноименно заряженных шариков, а по шкале прибора — расстояние между ними.
Надо сказать, что Кулон не был первым ученым, установившим закон взаимодействия зарядов, носящий теперь его имя: за 30 лет до него к такому же выводу пришел Б. Франклин. Более того, точность измерений Кулона уступала точности ранее проведенных экспериментов (Г. Кавендиш).
Чтобы ввести количественную меру для определения точности измерений, предположим, что на самом деле сила взаимодействия зарядов обратна не квадрату расстояния между ними, а какой-то другой степени:
Никто из ученых не возьмется утверждать, что d = 0 точно. Правильное заключение должно звучать так: эксперименты показали, что d не превышает.
Результаты некоторых из этих экспериментов приведены в таблице 1.
Таблица 1.
Результаты прямых экспериментов по проверке закона Кулона
Эксперимент
Год
Сам Шарль Кулон проверил закон обратных квадратов с точностью до нескольких процентов. В таблице приведены результаты прямых лабораторных экспериментов. Косвенные данные, основанные на наблюдениях магнитных полей в космическом пространстве, приводят к еще более сильным ограничениям на величину d. Таким образом, закон Кулона можно считать надежно установленным фактом.
В СИ единица силы тока (ампер) является основной, следовательно, единица заряда q оказывается производной. Как мы увидим в дальнейшем, сила тока I определяется как отношение заряда , протекающего через поперечное сечение проводника за время , к этому времени:
Отсюда видно, что сила постоянного тока численно равна заряду, протекающему через поперечное сечение проводника за единицу времени, соответственно этому:
В СИ единицей измерения электрического заряда является кулон (Кл) — электрический заряд, протекающий за 1 секунду через поперечное сечение проводника при постоянной силе тока в 1 A:

Коэффициент пропорциональности в законе Кулона записывается в виде:

При такой форме записи из эксперимента следует значение величины , которую принято называть электрической постоянной. Приближенное численное значение электрической постоянной следующее:
Поскольку чаще всего входит в уравнения в виде комбинации
приведём численное значение самого коэффициента
Как и в случае элементарного заряда, численное значение электрической постоянной определено экспериментально с высокой точностью:
Кулон — слишком большая единица для использования на практике. Например, два заряда в 1 Кл каждый, расположенные в вакууме на расстоянии 100 м друг от друга, отталкиваются с силой
Для сравнения: с такой силой давит на землю тело массой
Это примерно масса грузового железнодорожного вагона, например, с углем.
Принцип суперпозиции полей
Принцип суперпозиции представляет собой утверждение, согласно которому результирующий эффект сложного процесса воздействия представляет собой сумму эффектов, вызываемых каждым воздействием в отдельности, при условии, что последние взаимно не влияют друг на друга (Физический энциклопедический словарь, Москва, «Советская энциклопедия», 1983, стр. 731). Экспериментально установлено, что принцип суперпозиции справедлив для рассматриваемого здесь электромагнитного взаимодействия.
В случае взаимодействия заряженных тел принцип суперпозиции проявляет себя следующим образом: сила, с которой данная система зарядов действует на некоторый точечный заряд, равна векторной сумме сил, с которыми действует на него каждый из зарядов системы.
Поясним это на простом примере. Пусть имеются два заряженных тела, действующие на третье с силами и соответственно. Тогда система из этих двух тел — первого и второго — действует на третье тело с силой
Это правило справедливо для любых заряженных тел, не только для точечных зарядов. Силы взаимодействия двух произвольных систем точечных зарядов вычисляются в Дополнении 1 в конце этой главы.
Отсюда следует, что электрическое поле системы зарядов определяется векторной суммой напряженностей полей, создаваемых отдельными зарядами системы, т. е.

Сложение напряженностей электрических полей по правилу сложения векторов выражает так называемый принцип суперпозиции (независимого наложения) электрических полей. Физический смысл этого свойства заключается в том, что электростатическое поле создается только покоящимися зарядами. Значит, поля различных зарядов «не мешают» друг другу, и поэтому суммарное поле системы зарядов можно подсчитать как векторную сумму полей от каждого из них в отдельности.
Так как элементарный заряд весьма мал, а макроскопические тела содержат очень большое количество элементарных зарядов, то распределение зарядов по таким телам в большинстве случаев можно считать непрерывным. Для того чтобы описать как именно распределен (однородно, неоднородно, где зарядов больше, где их меньше и т. п.) заряд по телу введем плотности заряда следующих трех видов:
· объемная плотность заряда :
где dV — физически бесконечно малый элемент объема;
· поверхностная плотность заряда :
где dS — физически бесконечно малый элемент поверхности;
· линейная плотность заряда :
где — физически бесконечно малый элемент длины линии.
Здесь всюду — заряд рассматриваемого физически бесконечно малого элемента (объема, участка поверхности, отрезка линии). Под физически бесконечно малым участком тела здесь и ниже понимается такой его участок, который, с одной стороны, настолько мал, что в условиях данной задачи, его можно считать материальной точкой, а, с другой стороны, он настолько велик, что дискретностью заряда (см. соотношение ) этого участка можно пренебречь.
Общие выражения для сил взаимодействия систем непрерывно распределенных зарядов приведены в Дополнении 2 в конце главы.
Пример 1. Электрический заряд 50 нКл равномерно распределен по тонкому стержню длиной 15 см. На продолжении оси стержня на расстоянии 10 см от ближайшего его конца находится точечный заряд 100 нКл (рис. 1.9). Определить силу взаимодействия заряженного стержня и точечного заряда.

Рис. 1.9. Взаимодействие заряженного стержня с точечным зарядом
Решение. В этой задаче силу F нельзя определить, написав закон Кулона в форме или (1.3). В самом деле, чему равно расстояние между стержнем и зарядом: r, r + a/2, r + a? Поскольку по условиям задачи мы не имеем права считать, что a r, применение закона Кулона в его исходной формулировке, справедливой только для точечных зарядов невозможно, необходимо использовать стандартный для таких ситуаций приём, который состоит в следующем.
Если известна сила взаимодействия точечных тел (например, закон Кулона) и необходимо найти силу взаимодействия протяженных тел (например, вычислить силу взаимодействия двух заряженных тел конечных размеров), то необходимо разбить эти тела на физически бесконечно малые участки, написать для каждой пары таких «точечных» участков известное для них соотношение и, воспользовавшись принципом суперпозиции, просуммировать (проинтегрировать) по всем парам этих участком.
Всегда полезно, если не сказать — необходимо, прежде чем приступать к конкретизации и выполнению расчета, проанализировать симметрию задачи. С практической точки зрения такой анализ полезен тем, что, как правило, при достаточно высокой симметрии задачи, резко сокращает число величин, которые надо вычислять, поскольку выясняется, что многие из них равны нулю.
Разобьём стержень на бесконечно малые отрезки длиной , расстояние от левого конца такого отрезка до точечного заряда равно .
Равномерность распределения заряда по стержню означает, что линейная плотность заряда постоянна и равна
Следовательно, заряд отрезка равен , откуда, в соответствии с законом Кулона, сила, действующая на точечный заряд q в результате его взаимодействия с точечным зарядом , равна
В результате взаимодействия точечного заряда q со всем стержнем, на него будет действовать сила
Подставляя сюда численные значения, для модуля силы получаем:
Из (1.5) видно, что при , когда стержень можно считать материальной точкой, выражение для силы взаимодействия заряда и стержня, как и должно быть, принимает обычную форму закона Кулона для силы взаимодействия двух точечных зарядов:
Пример 2. Кольцо радиусом несет равномерно распределенный заряд . Какова сила взаимодействия кольца с точечным зарядом q, расположенным на оси кольца на расстоянии от его центра (рис. 1.10).
Решение. По условию, заряд равномерно распределен на кольце радиусом . Разделив на длину окружности, получим линейную плотность заряда на кольце Выделим на кольце элемент длиной . Его заряд равен .

Рис. 1.10. Взаимодействия кольца с точечным зарядом
В точке q этот элемент создает электрическое поле
Нас интересует лишь продольная компонента поля, ибо при суммировании вклада от всех элементов кольца только она отлична от нуля:
Интегрируя по находим электрическое поле на оси кольца на расстоянии от его центра:
Отсюда находим искомую силу взаимодействия кольца с зарядом q:
Обсудим полученный результат. При больших расстояниях до кольца величиной радиуса кольца под знаком радикала можно пренебречь, и мы получаем приближенное выражение
Это не удивительно, так как на больших расстояниях кольцо выглядит точечным зарядом и сила взаимодействия дается обычным законом Кулона. На малых расстояниях ситуация резко меняется. Так, при помещении пробного заряда q в центр кольца сила взаимодействия равна нулю. Это тоже не удивительно: в этом случае заряд q притягивается с равной силой всеми элементами кольца, и действие всех этих сил взаимно компенсируется.
Поскольку при и при электрическое поле равно нулю, где-то при промежуточном значении электрическое поле кольца максимально. Найдем эту точку, дифференцируя выражение для напряженности Е по расстоянию
Приравнивая производную нулю, находим точку где поле максимально. Оно равно в этой точке
Пример 3. Две взаимно перпендикулярные бесконечно длинные нити, несущие равномерно распределенные заряды с линейными плотностями и находятся на расстоянии а друг от друга (рис. 1.11). Как зависит сила взаимодействия между нитями от расстояния а?
Решение. Сначала обсудим решение этой задачи методом анализа размерностей. Сила взаимодействия между нитями может зависеть от плотностей заряда на них, расстояния между нитями и электрической постоянной, то есть искомая формула имеет вид:
где — безразмерная постоянная (число). Заметим, что вследствие симметричного расположения нитей плотности заряда на них могут входить только симметричным же образом, в одинаковых степенях. Размерности входящих сюда величин в СИ известны:

Рис. 1.11. Взаимодействие двух взаимно перпендикулярных бесконечно длинных нитей
По сравнению с механикой здесь появилась новая величина — размерность электрического заряда. Объединяя две предыдущие формулы, получаем уравнение для размерностей:
Приравнивая степени при М и Т в обеих частях этого уравнения, немедленно получаем В левой части нет величины размерности заряда, откуда следует, что или Наконец, приравнивая степени при размерности длины, получаем уравнение откуда следует, что Окончательно имеем:
Таким образом, оказывается, что сила взаимодействия нитей не зависит от расстояния между ними. Напомним, что безразмерную постоянную С методом анализа размерностей определить невозможно. В сущности мы уже получили ответ на вопрос задачи, но приведем также и точное ее решение, которое позволит найти С. На рис. 1.11 справа показан вид сверху на плоскость, содержащую нить точкой А отмечено сечение плоскостью чертежа нити . Напряженность электрического поля, создаваемого нитью в точке, где находится элемент второй нити, равна
На элемент нити действует сила
Нас, однако, интересует лишь компонента этой силы вдоль оси ибо продольная составляющая компенсируется точно такой же силой, действующей на симметричный элемент нити внизу. Выразим все расстояния через угол :
Что такое суперпозиция в физике
2.4. Суперпозиция состояний
Наличие в окружающем нас мире «противоестественных» (с классической точки зрения) состояний, объективность их существования подтверждены физическими экспериментами, и этот факт является прямым следствием одного из самых фундаментальных принципов квантовой механики — принципа суперпозиции состояний. Или лучше сказать наоборот: это неотъемлемое свойство природы нашло свое отражение в основном теоретическом принципе квантовой механики. Сформулировать его можно следующим образом.
Принцип суперпозиции состояний : если система может находиться в различных состояниях, то она способна находиться в состояниях, которые получаются в результате одновременного «наложения» друг на друга двух или более состояний из этого набора.
В квантовой теории есть два качественно различных вида суперпозиции в соответствии с тем, что чистые состояния могут описываться вектором состояния, а смешанные — матрицами плотности. Поэтому и накладываться друг на друга могут либо векторы состояния, либо матрицы плотности. Мы пока будем говорить о суперпозиции чистых состояний, чтобы подчеркнуть это обстоятельство, обычно используют выражения «когерентная суперпозиция», «когерентные состояния».
В классической физике понятие суперпозиции тоже широко используется. Все мы рисовали в школе стрелочки векторов для сил, приложенных к телу, и по правилу параллелограмма (треугольника) находили результирующий вектор силы. Мы пользовались при этом принципом суперпозиции классической физики, суть которого в том, что результирующий эффект от нескольких независимых воздействий представляет собой сумму эффектов, вызываемых каждым воздействием в отдельности. Он справедлив для систем или физических полей, описываемых линейными уравнениями.
Но в классической физике принцип суперпозиции является приближенным, а не универсальным, фундаментальным. Это скорее следствие линейности уравнений движения соответствующих систем и служит достаточно хорошим приближением, когда нелинейные эффекты незначительны.
Иная ситуация — в квантовой механике. В ней принцип суперпозиции является фундаментальным, одним из основных постулатов, определяющих структуру математического аппарата теории. Из него следует, например, что состояния квантовомеханической системы должны изображаться векторами линейного пространства, что операторы физических величин должны быть линейными и т. д.
Но основное отличие не в этом. Давайте вчитаемся еще раз более внимательно в формулировку этого принципа: если система может находиться в различных состояниях, то она может одновременно находиться сразу в двух (и более) состояниях! Например, если в качестве отдельных состояний системы взять пространственные координаты ее центра масс, и наша система способна принимать различные положения в пространстве, то из принципа суперпозиции следует, что она в состоянии находиться одновременно сразу во всех точках пространства — то есть быть полностью «размазанной» во всем пространственно-временном континууме. И это будет вполне естественное состояние с точки зрения квантовой теории! Для практической реализации такого необычного состояния системы нет принципиальных теоретических запретов. Разве это не удивительно? Не противоречит нашим привычным представлениям о реальности? Именно это явное противоречие «здравому смыслу» приводит в отчаяние уже не одно поколение физиков. Положение усугубляется тем, что никаких ограничений в квантовой теории на этот принцип не накладывается — он в равной степени применим и к макроскопическим объектам, и к микрочастицам.
Основное отличие принципа суперпозиции в квантовой теории от его классического аналога в том, что состояния, которые «накладываются» друг на друга в квантовой теории, — это альтернативные, взаимоисключающие состояния, когда одно из них полностью отрицает другое. Если мы находимся где-то в одном месте, значит, в другом месте нас нет — это подсказывает здравый смысл. Но в квантовой теории складываются именно такие взаимоисключающие состояния, и система может находиться в таких состояниях одновременно!
В классической физике, если взять те же силы, они вовсе не противоречат друг другу. Одна может спокойно действовать наряду с другой, и они вполне мирно «уживаются» друг с другом, а при их сложении мы получаем такую же обычную силу, которая не хуже и не лучше других сил. Только если мы сложим две противоположные и одинаковые по модулю силы, их равнодействующая будет равна нулю. Силы тогда взаимно компенсируются, они как бы «уничтожают» друг друга, и на тело вообще никакие силы действовать не будут.
А что получается в квантовой теории? Там все состояния несовместимы друг с другом. Но если мы сложим, например, два таких взаимоисключающих состояния, то уже не сможем сказать, что система при этом «уничтожится». Система при квантовом подходе может «исчезнуть» только в одном случае — если у нее нет вообще никаких состояний, а в случае суперпозиции мы имеем как минимум два. Отсутствие системы как элемента реальности в квантовой теории возможно лишь тогда, когда мы вообще не можем сопоставить с системой никаких состояний. Если такие состояния есть, значит, есть и система. Но вот что она из себя представляет , когда находится в суперпозиции двух взаимоисключающих состояний? Что происходит со спином, когда на состояние « спин-вверх » накладывается состояние « спин-вниз »? Это все равно что человек стоит одновременно «на ногах» и в то же самое время «вверх ногами». Как такое может быть, как это понимать? «Хороший вопрос», который может свести с ума, если подходить к нему с точки зрения наших привычных представлений о реальности.
Хотя и здесь может помочь аналогия с классическими представлениями. Если мы продолжим рассуждать о нашем примере с двумя противоположными силами, то придем к выводу, что ситуация в квантовой теории отдаленно ее напоминает. Итак, мы имеем равнодействующую двух сил, которая равна нулю, — что это означает? Можно сказать, что такой физической величины, как сила, для нашей системы в явном виде практически не существует. Две уравновешивающие силы находятся как бы в скрытом состоянии, они не проявлены, недоступны для восприятия и непосредственного наблюдения за результатами действия каждой из этих сил в отдельности. Лишь когда мы уберем одну из этих сил, то сможем явно убедиться в наличии второй, например, по ускорению, которое приобретет тело под действием оставшейся силы.
Что-то похожее происходит и в квантовой теории. Для простоты мы будем говорить о суперпозиции состояний с равными весами. Когда система пребывает в суперпозиции двух (и более) состояний, то в явном виде они не существуют — система не имеет характерных особенностей ни того, ни другого состояния. Так, если человек может находиться в двух состояниях — «на ногах» и «на голове» — то, когда он пребывает в суперпозиции этих состояний, мы, глядя со стороны, не увидим ни одного из них. На «языке» квантовой теории это означает, что система в этом случае находится в нелокальном состоянии — нет такого локального элемента реальности, который являлся бы «носителем» этих двух состояний. Человека в нашем примере вообще нет в качестве локального объекта, иными словами — «в своем физическом теле», и это вполне логично, поскольку ситуацию, когда мы видим его стоящим одновременно и «на ногах», и «на голове», действительно трудно себе вообразить. Но это не говорит о том, что наша система исчезла, перестала существовать. Так же, как и силы в классическом примере вовсе не исчезают от того, что одна из них уравновешивает другую. Они продолжают существовать, и в их наличии можно убедиться, нарушив равновесие этих сил, то есть каким-то образом воздействовав на систему.
В случае суперпозиции состояний похожая ситуация. Система имеет два различных состояния в качестве потенциально возможных локальных своих проявлений. Это те состояния, которые мы можем явно наблюдать и зафиксировать, но, чтобы их «проявить», нам необходимо с системой каким-то образом « проконтактировать ». Здесь есть два принципиально различных варианта: во-первых, произвести прямое измерение системы, то есть осуществить взаимодействие с измерительным прибором (окружением). В этом случае мы просто разрушаем суперпозицию состояний и «проявляем» одно из потенциальных состояний системы в его локальном, привычном для нас материальном облике. Этот физический процесс, как нам уже известно, называется декогеренцией. Второй вариант: «проявлять» то или иное локальное состояние при помощи так называемых унитарных (обратимых) операций. В этом случае сохраняется возможность снова перевести систему в суперпозиционное состояние. В этом заключается принципиальное отличие от первого варианта, где такая возможность утрачивается. Точнее, реализовать ее можно было только в том случае, если бы мы умели управлять состоянием всей объединенной системы, в состав которой вошла наша исходная система при взаимодействии. Такие унитарные операции сейчас применяются для манипулирования кубитами в квантовом компьютинге .
Необычную особенность квантовой суперпозиции — нелокальность и непроявленный потенциальный характер такого состояния, можно пояснить еще следующим образом. В отличие от классической суперпозиции, в квантовом случае мы никогда не получим промежуточное значение между состояниями, участвующими в суперпозиции. Например, классическая суперпозиция двух цветов, черного и белого, дает в результате серый цвет, но квантовая суперпозиция никакой серый цвет дать не в состоянии, никакого цвета вообще не будет — лишь при декогеренции, при взаимодействии (измерении) можно получить один из цветов — либо черный, либо белый.
Столь необычные состояния объектов, которые находятся в нелокальной суперпозиции, будоражат умы физиков уже многие десятилетия. Что будет, если мы совместим несовместимое? Что будет, если «наложим» друг на друга добро и зло, жизнь и смерть? В последнем случае часто вспоминают «кота Шредингера», которого физики приводят в качестве примера, поясняющего всю необычность состояний, существующих в окружающем мире, если не ограничиваться привычными рамками классической реальности. Такие состояния имеют место, когда мы готовы выйти за пределы предметного мира и хотим «заглянуть» в реальность более высокого уровня, более широкую, содержащую весь материальный мир в качестве своей составной части.
При квантовой суперпозиции живого и мертвого кота он не может находиться в некоем промежуточном полуживом (полумертвом) состоянии, как это могло иметь место в классическом варианте. Он именно одновременно и жив, и мертв, находится сразу в двух этих состояниях. Но вся парадоксальность такой ситуации в квантовой теории легко снимается, поскольку в этом случае кота просто нет в качестве локального объекта нашего материального мира. Можно сказать как угодно — что кот находится в потустороннем мире, в информационной сфере, в квантовом домене совокупной реальности и т. п. Но самое главное, что как обычного кота, которого можно погладить, — его просто нет. В своем физическом теле, в привычном облике кота, то есть в качестве локального объекта нашего материального мира он просто не существует. Он находится в состоянии более общего типа, а локальное состояние — только один из частных случаев, один из возможных вариантов бытия нашего кота. Он может проявиться из нелокальной суперпозиции в процессе декогеренции. Лишь тогда мы можем увидеть его, и уже не в каком-то парадоксальном сочетании жизни и смерти, а только в одном из этих состояний. Но такое объяснение квантовой теории, этот вывод, этот результат не всех устраивает. Ведь если система может находиться в таких «противоестественных» состояниях, то придется признать наличие более глубокой и всеобъемлющей реальности. Весь привычный для нас мир материи (вещества и физических полей) оказывается тогда лишь незначительной частью совокупной квантовой реальности. По сути, признание этого факта означает крушение основы мировоззрения большинства из нас. Поэтому многие не готовы принять эти выводы квантовой теории.
Но, может быть, принцип суперпозиции — это выдумка физиков-теоретиков? Возможно, это лишь математические манипуляции, которые не имеют под собой никакой реальной физики? Конечно же, нет, этот принцип не был «взят с потолка», уместно сказать, что он был выстрадан при становлении квантовой механики. Только с помощью этого принципа удавалось объяснить многие физические эксперименты, которые не укладывались в рамки классического описания. Это сама реальность при более пристальном взгляде на нее «подсказывала» тот способ, который позволял адекватно ее описывать, сама природа помогала найти тот теоретический метод, благодаря которому получались правильные количественные значения величин и удавалось точно предсказывать результаты физических экспериментов.
Стоило «копнуть» законы природы чуть глубже, как оказалось, что окружающий нас мир — лишь часть чего-то более емкого, всеобъемлющего. Квантовая теория раздвинула границы реальности, показав, что материальный мир и классические состояния — это далеко не все, что нас окружает. Принцип суперпозиции существенно расширил сферу состояний и оставил на долю классического мира только незначительную часть в пределах совокупной квантовой реальности.
Сама природа подсказала, что когерентные суперпозиционные состояния — вовсе не абстракция, а неотъемлемый элемент окружающей реальности. Собственно говоря, для объяснения физических процессов и явлений они и были введены. Но понадобилось достаточно много времени, прежде чем пришло понимание, почему в одних случаях суперпозиционные состояния имеют место, а в других нет, по каким законам они «живут», какие процессы нелокальную суперпозицию разрушают, а какие восстанавливают. И основная роль в том, что понимание этих процессов стало возможно, опять-таки принадлежит самой природе, поскольку ответы на эти вопросы исследователи стали получать в результате интенсивной практической работы над реальными физическими системами, позволяющими использовать когерентную суперпозицию в качестве рабочего ресурса для квантового компьютера и других технических устройств. Во многом благодаря непосредственной работе с когерентными состояниями, манипуляции ими в физических лабораториях, покров таинственности с нелокальных состояний стал спадать — они начали раскрывать свои поразительные свойства, удивительные особенности и небывалые, по сравнению с классическими состояниями, возможности.
Когерентные состояния очень чувствительны к внешним воздействиям. Они возможны для чистых состояний, то есть для замкнутых (изолированных) систем, либо для псевдочистых состояний (квазизамкнутых систем) в промежутках времени, которые меньше периода декогеренции. Может возникнуть вопрос: что толку в этих состояниях, если когерентная суперпозиция не наблюдаема, если любые попытки измерения (наблюдения) такую суперпозицию разрушают, приводят к декогеренции? Да, суперпозиция не наблюдаема, это нелокальное состояние. Наблюдать в виде локальных форм можно только результат декогеренции этого состояния. И, тем не менее, когерентные состояния научились использовать на практике. Когерентность по отдельным степеням свободы системы можно сохранять на временах, меньших времени декогеренции окружением, ее можно восстанавливать, поддерживать, ею можно манипулировать. При этом, как уже говорилось, когерентность не нарушают унитарные преобразования системы, и их сейчас широко используют для управления когерентными состояниями, например, в квантовом компьютинге .
Такие состояния обладают необычными свойствами. Наличие нелокальных корреляций между подсистемами (кубитами) обеспечивает согласованное их поведение, когда все кубиты ведут себя как единое целое, мгновенно реагируя на любые изменения состояния хотя бы одного из них. Все это оправдывает затраченные усилия, поскольку ресурс квантового компьютера в этом случае возрастает экспоненциально по сравнению с обычным . Квантовый компьютер все вычисления выполняет как бы в «потустороннем мире», за пределами материального мира локальных форм — там, где когерентная суперпозиция не нарушена. А результаты этих вычислений мы уже можем увидеть в привычной дискретной форме, «проявив» его при помощи процесса декогеренции.
Если говорить о теоретическом описании суперпозиционных состояний, о математическом формализме, то представление состояния в виде результата суперпозиции некоторого числа других состояний — это математическая процедура, которая всегда возможна и не имеет отношения к физике. Она аналогична разложению волны на компоненты Фурье. Имеет ли такое разложение физический смысл, будет ли оно полезно, зависит от конкретной задачи, от конкретных физических условий и тех величин, которые нас интересуют.
Вместе с тем, расширение класса состояний, изучение физики когерентных суперпозиционных состояний определяют некоторые специфические особенности в структуре математического аппарата квантовой теории. Как я пытался показать выше, принцип суперпозиции состояний — это что-то вроде операции суммирования. Суперпозиция означает, что состояния можно каким-то образом складывать, получая при этом новые состояния системы. Поэтому состояния необходимо связать с какими-либо математическими объектами, которые допускают сложение, и получаются математические объекты того же типа. Из наиболее простых математических структур, удовлетворяющих этим условиям, нам известны векторы, которые и сопоставляются различным состояниям системы. Такие векторы называются в квантовой теории векторами состояния — к их рассмотрению мы сейчас и перейдем.
Принцип суперпозиции
Принцип суперпозиции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
- результат воздействия на частицу нескольких внешних сил есть сумма результатов воздействия каждой из сил.
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что электростатический потенциал, создаваемый в данной точке системой зарядов, есть сумма потенциалов отдельных зарядов.
Принцип суперпозиции может принимать и иные формулировки, которые, подчеркнём, полностью эквивалентны приведённой выше:
- Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя;
- Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.
- Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.
Именно Принцип суперпозиции в электродинамике
Рис.1 Иллюстрация принципа суперпозиции в электростатике
Принцип суперпозиции является следствием, прямо вытекающим из рассматриваемой теории, а вовсе не постулатом, вносимым в теорию априори. Так, например, в электростатике принцип суперпозиции есть следствие того факта, что уравнения Максвелла в вакууме линейны. Именно из этого следует, что потенциальную энергию электростатического взаимодействия системы зарядов можно легко сосчитать, вычислив потенциальную энергию каждой пары зарядов.
Другим следствием линейности уравнений Максвелла является тот факт, что света не рассеиваются и вообще никак не взаимодействуют друг с другом. Этот закон можно условно назвать принципом суперпозиции в оптике.
Подчеркнём, что электродинамический принцип суперпозиции не есть незыблемый закон Природы, а является всего лишь следствием линейности уравнений Максвелла, т. е. уравнений классической электродинамики. Поэтому, когда мы выходим за пределы применимости классической электродинамики, вполне стоит ожидать нарушение принципа суперпозиции.
Примеры нарушения электродинамического принципа суперпозиции
Если рассматривается электродинамика не в вакууме, а в какой-либо среде, то принцип суперпозиции может нарушаться. Так, например, если намагниченность среды нелинейно зависят от приложенного поля, это приводит к нелинейным поправкам в уравнениях Максвелла. Прямым следствием этого является нарушение принципа суперпозиции в такой квантовой электродинамике фотон может на некоторое время превратиться в электрон-позитронную пару , которая уже может взаимодействовать с другими фотонами. Эффективно это приводит к тому, что фотоны могут взаимодействовать друг с другом. Такого типа процессы ( Отсутствие принципа суперпозиции в нелинейных теориях
Тот факт, что уравнения классической электродинамики линейны, является скорее исключением, чем правилом. Многие фундаментальные теории современной физики являются нелинейными. Например, квантовая хромодинамика — фундаментальная теория сильных взаимодействий — является разновидностью теории Янга — Миллса, которая нелинейна по построению. Это приводит к сильнейшему нарушению принципа суперпозиции даже в классических (неквантованных) решениях уравнений Янга — Миллса.
Другим известным примером нелинейной теории является общая теория относительности. В ней также не выполняется принцип суперпозиции. Например, Солнце притягивает не только Землю и Луну, но также и само взаимодействие между Землёй и Луной. Впрочем, в слабых гравитационных полях эффекты нелинейности слабы, и для повседневных задач приближённый принцип суперпозиции выполняется с высокой точностью.
Рис.2 Нарушение принципа суперпозиции во взаимодействиях атомов
Наконец, принцип суперпозиции не выполняется, когда речь идёт о взаимодействии атомов и раздела Википедии на русском языке. Оригинальная статья находится по адресу: Принцип суперпозиции. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
Принцип суперпозиции полей

Одним из важнейших принципов, существующих в электростатике, является принцип суперпозиции полей. Кратко рассмотрим суть этого принципа, выведем его математическую формулу.
Действие силового поля
Силовое поле – это особая форма материи, действие которого заключается в силовом влиянии на носители заряда. То есть, если у тела есть некоторый электрический заряд, и оно находится в силовом электрическом поле, то со стороны этого поля на тело будет действовать определенная сила, тем большая, чем больше напряженность поля.
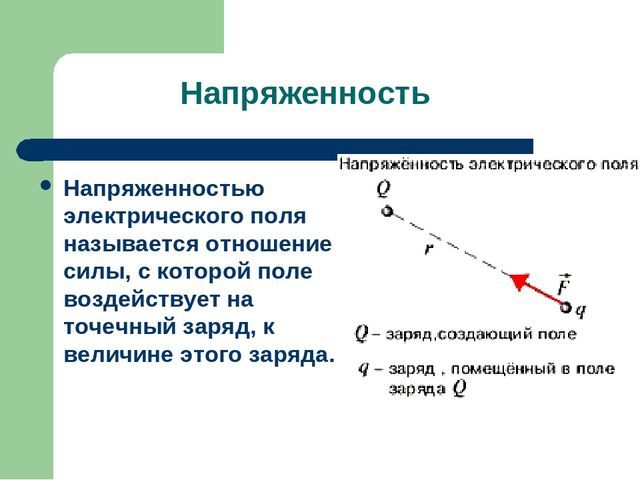
Рис. 1. Напряженность электрического поля.
Природа поля не обязательно должна быть электрической. Действие гравитационного силового поля заключается в силовом воздействии на тела, имеющие массу (носители «гравитационного заряда»).
Даже силы трения можно представить в виде поля сил трения, поскольку трение также оказывает на движущиеся соприкасающиеся тела силовое действие.
Сложение действия полей
Что произойдет с зарядом, на который действует несколько полей ?
Опыт показывает, что сила, действующая на заряд со стороны поля, не зависит от других сил, тоже действующих на заряд. При этом их источником могут являться другие поля. Фактически, несколько полей будут действовать на заряд независимо, каждое будет создавать силу, точно такую же, как если бы это поле в точке было бы единственным.
Таким образом, если заряд помещен одновременно в несколько электрических полей, он испытывает одновременное действие нескольких сил. А если на материальную точку действует несколько сил, то результатом их действия будет одна равнодействующая сила, которая находится векторным сложением исходных сил:
Сила, действующая на заряд, равна произведению напряженности поля на величину заряда:
Поскольку заряд в рассматриваемой ситуации один и тот же, то:
Принцип суперпозиции
Выражение в скобках представляет собой векторную сумму напряженностей всех полей, действующих на заряд. Получается, что результат действия на заряд нескольких полей эквивалентен действию одного поля, напряженность которого равна векторной сумме напряженностей всех полей, действующих на заряд. Иначе можно сказать, что результирующее поле, существующее в точке, является векторной суммой всех полей, его составляющих. В этом и состоит принцип суперпозиции (наложения) полей.
Если в данной точке пространства электрическое поле создано несколькими зарядами, и напряженность поля каждого по отдельности равна $overrightarrow_,overrightarrow_,…$, то результирующая напряженность этого поля равна векторной сумме напряженностей составляющих его полей.
То есть, формула принципа суперпозиции полей записывается следующим образом:
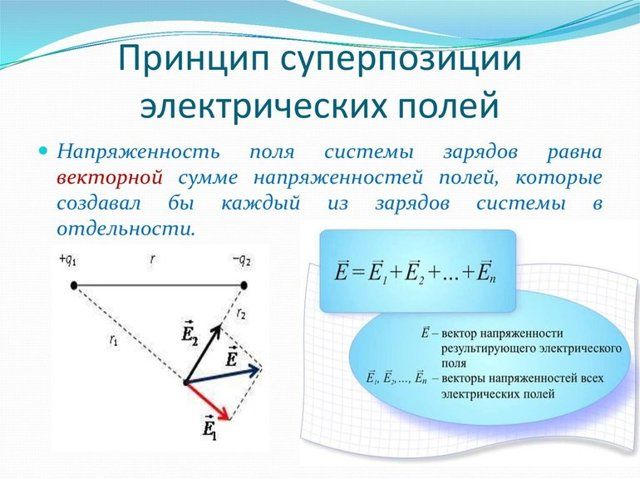
Рис. 2. Принцип суперпозиции электрических полей.
Отметим, что потенциал результирующего поля не обязательно равен сумме потенциалов исходных полей. Это происходит потому, что потенциал – скалярная величина, не учитывающая направление.
Принцип суперпозиции полей позволяет не только находить напряженность поля, создаваемые несколькими зарядами. Гораздо чаще возникает ситуация, когда заряд распределен по телу неравномерно. В этом случае тело можно разбить на множество элементарных тел, каждое из которых имеет свой заряд, отличный от прочих. А потом поле в любой точке пространства вычисляется, как векторная сумма полей всех элементарных зарядов. При уменьшении размера элементарного тела до нуля сумма заменяется интегралом по объему. Данный способ используется при определении картины картину сложных электрических полей, например, при проектировании электровакуумных приборов.
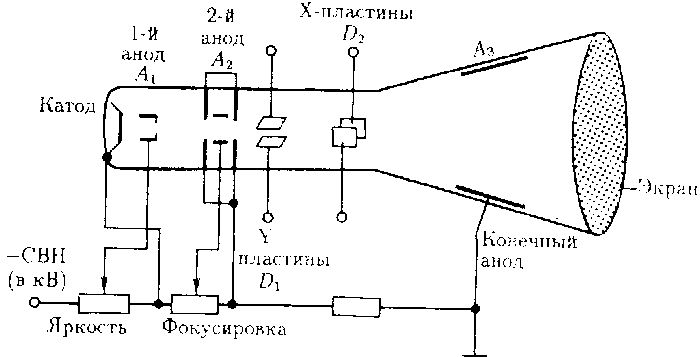
Рис. 3. Устройство электронно-лучевой трубки.
Принцип суперпозиции вовсе не так очевиден и универсален, как кажется на первый взгляд. Он действует лишь для линейных полей. Если поле нелинейно – принцип суперпозиции не работает. Примером нелинейного поля является поле сил трения. Если на тело действует несколько внешних сил, то, пока оно не сдвинется, сила трения равна векторной сумме отдельных составляющих. Но, как только тело сдвинулось, сила трения останется неизменной по модулю, даже если мы будем увеличивать количество действующих на тело сил.
Что мы узнали?
Принцип суперпозиции полей заключается в том, что результирующая напряженность поля, состоящего из нескольких исходных полей равна векторной сумме их напряженностей. Принцип суперпозиции выполняется для всех линейных полей, к числу которых относится и электрическое.