Задача оптимизации

Экономические задачи на оптимальный выбор

Что выгоднее: купить упаковку чипсов весом 210 граммов за 150 рублей или упаковку весом 90 граммов за 70 рублей? Сегодня мы узнаем, что удачные покупки — это не только товары по скидке или два по цене одного. Заодно разберем одну из важных тем в экономике.

Оптимизация

С задачами на оптимальный выбор мы сталкиваемся чаще, чем может показаться на первый взгляд. Когда в магазине пытаемся немного сэкономить деньги, когда ищем лучшую модель гаджета по соотношению цена–качество. При любой покупке нам хочется получить выгоду, и задачи на оптимизацию как раз про это.

Вернемся к чипсам. Может показаться, что купить маленькую пачку чипсов выгоднее: она дешевле. Но что если посмотреть на стоимость одного грамма?
Для маленькой пачки получим (frac approx 0,78) рублей за грамм.
А для большой пачки: (frac approx 0,71) рублей за грамм.
Получается, что в большой пачке один грамм чипсов стоит немного дешевле, чем в маленькой. То есть выгоднее купить большую пачку.

В чем заключаются задачи на оптимизацию? Решим пример, который поможет лучше почувствовать всю суть задач на оптимизацию.

Пример 1. Среди прямоугольников с периметром p найти прямоугольник с наибольшей площадью.

Решение. Вспомним, что площадь прямоугольника вычисляется по формуле S = xy, где x, y – его стороны.

Периметр находится по формуле p = 2x + 2y.

Теперь подставим полученное значение в формулу площади:
(S = frac

* x = frac = −x^2 + frac

* x)

Заметим: у нас получилось уравнение параболы, ветви которой направлены вниз. Условно изобразим ее.

Представим, что вместо параболы мы сложили слитки золота. Если мы возьмем золото только из нижнего ряда, то получим всего 4 слитка. Если все, что ниже второго, то уже 4 + 3 = 7. Чтобы получить максимум золота, нам нужно собрать все слитки от самого верхнего ряда.

Тогда, чтобы получить наибольшую площадь, нам нужно взять значение х в верхней точке параболы, то есть в ее вершине.

Найдем вершину параболы по формуле:

Вспомним, что (y = frac

= frac

− x), следовательно, (y = frac

− frac

= frac

Получаем, что (x = y = frac

), а значит, наибольшая площадь будет достигаться, если прямоугольник будет квадратом.

Ответ: квадрат со стороной (frac

Подходы к оптимизации

Для каждой задачи или загадки нужен свой подход, идея. Какие идеи заложены в задачи по оптимизации?

Необходимо понять, от каких величин зависит искомая переменная, чтобы найти ее максимальное или минимальное значение.

Необходимо сократить количество неизвестных переменных в полученной зависимости.

Исследовать полученную зависимость и найти наибольшее или наименьшее значение.

Решим несколько задач, чтобы понять на практике все идеи.

Пример 2. Вика владеет двумя цветочными магазинами в городах Е. и П. В магазинах продают одинаковую продукцию, однако магазин в городе П. использует более современные технологии. Работники магазина в городе Е. трудятся t 2 часов в неделю и за эту неделю производят 3t единиц продукции. Работники магазина в городе П. трудятся t 2 часов в неделю и за эту неделю производят 6t единиц продукции.

За каждый час работы Вика платит сотрудникам 500 рублей. Но перед сотрудниками стоит важная задача: еженедельно они должны производить 300 единиц продукции. Какую наименьшую сумму может выплачивать Вика сотрудникам?

Решение. Переведем задачу с языка математики.

Например, в магазине в городе Е. работает два флориста. Первый работает по 8 часов в день с понедельника по пятницу, а второй по 10 часов в день с понедельника по субботу. Всего они еженедельно будут работать 8 * 5 + 10 * 6 = 100 часов.

По условию эти 100 часов будут равны t 2 . Мы можем найти (t = sqrt = 10). Сколько единиц продукции будут производить эти флористы? Из задачи следует, что это 3t = 3 * 10 = 30.

А сколько заработают за эту неделю флористы? Вместе их зарплата составит 500 * 100 = 50000 рублей.

Так можно проследить зависимость одной переменной от другой.

Перейдем к решению задачи.

Шаг 1. У нас есть два магазина, в которых работает неизвестное количество сотрудников неизвестное количество времени. Что делать, если мы чего-то не знаем? Вводить переменную.

Введем переменную на время работы сотрудников. В этом случае нам неважно, сколько их и как долго работает каждый. Мы берем все их часы суммарно.

Пусть в городе Е. сотрудники работают x 2 часов в неделю, а в городе П. сотрудники работают y 2 часов в неделю.

Для удобства составим небольшую таблицу.

Город	Е.	П.
Время работы сотрудников	x 2	y 2
Количество произведенной продукции
Сумма зарплаты

Следующую строку, которую необходимо заполнить — это количество произведенной продукции. По условию в городе Е. за x 2 часов произведут 3x единиц товара, а в городе П. за y 2 часов произведут 6y единиц товара.

Город	Е.	П.
Время работы сотрудников	x 2	y 2
Количество произведенной продукции	3x	6y
Сумма зарплаты

А какую зарплату Вика должна выплатить сотрудникам? Для этого необходимо количество часов умножить на ставку за час.

Город	Е.	П.
Время работы сотрудников	x 2	y 2
Количество произведенной продукции	3x	6y
Сумма зарплаты	500x 2	500y 2

Шаг 2. Пусть S — сумма, которую Вика выплачивает сотрудникам. Получаем уравнение:

Также следует вспомнить о целях, которые поставила Вика: еженедельно должно производиться 300 единиц товара, следовательно, 3x + 6y = 300. Выразим из этого уравнения y:

Шаг 3. Теперь можно подставить значение у в первое уравнение:

S = 500(x 2 + (50 − 0,5x) 2 = 500(x 2 + (2500 − 50x + 0,25x 2 )) = 500(1,25x 2 − 50x + 2500)

Получаем, что S = 625x 2 − 25000x + 1250000.

Шаг 4. Заметим, что это парабола с ветвями вверх. Изобразим ее условный график.

Наименьшее значение достигается в вершине параболы. Найдем ее.

6. Вычислим значение у: y = 50 − 0,5x = 50 − 0,5 * 20 = 50 − 10 = 40.

7. Вика должна выплачивать еженедельно: S = 500(20 2 + 40 2 ) = 500(400 + 1600) = 500 * 2000 = 1000000 рублей.

Ответ: 1000000 рублей.

Ну что ж, кажется, Вике стоит пересмотреть свою бизнес-модель.

Возможности функции наиболее полно раскрываются именно в задачах на оптимизацию. В них функция перестает быть абстрактными переменными и становится реально существующими вещами.

Алгоритм решения задач на оптимизацию

Итак, перед нами уже складывается алгоритм решения задач на оптимизацию. Распишем его чуть подробнее.

Шаг 1. Выделить значение, которое необходимо найти, и выразить его с помощью переменной.

Шаг 2. Выразить неизвестные значения через другую переменную. Составить уравнение.

Шаг 3. Составить функцию y = f(x) — это математическая модель.

Чтобы закрепить алгоритм в памяти, обратимся к следующему примеру.

Пример 3. Городские власти собрали команду художников из 44 человек, которые должны расписать два объекта в городе. Если на первом объекте работает t художников, то власти должны выплатить им 5t 2 тысяч рублей. Если на втором объекте работает t художников, то власти должны выплатить им t 2 тысяч рублей. Как нужно распределить художников по объектам, чтобы власти города выплатили им наименьшую сумму? Сколько тысяч рублей власти города должны будут заплатить в этом случае?

Решение
Шаг 1. Мы не знаем, сколько человек работает на каждом объекте — то есть получаем неизвестные переменные.

Мы можем выразить количество художников на каждом объекте через х и у. Тогда x + y = 44. Можно ли сократить количество переменных?

Решим небольшую задачу. Перед котом разложили 5 игрушек, некоторыми из которых он поиграл. Сколько игрушек остались нетронутыми?

Если кот поиграл х игрушками, то нетронутыми останутся 5−x игрушек. Например, при x=3 получим, что нетронутыми останутся 2 игрушки.

Применим аналогичные рассуждения к задаче. Было 44 художника, из них х отправились работать на первый объект. Сколько художников отправится работать на второй объект? 44 − x.

Шаг 2. Найдем, какую зарплату необходимо будет выплатить художникам на каждом объекте.

Поскольку на первом объекте работает х человек, по условию им необходимо выплатить 5x 2 тысяч рублей.

Поскольку на втором объекте работает 44 − x человек, им необходимо выплатить (44 − x) 2 = 1936 − 88x + x 2 .

В сумме власти города должны будут выплатить 5x 2 + 1936 − 88x + x 2 = 6x 2 − 88x + 1936 тысяч рублей.

Шаг 3. Это парабола с ветвями вверх, ее наименьшее значение достигается в вершине.

Шаг 4. В этом моменте необходимо задуматься: может ли х принимать нецелые значения? По условию нет, поскольку за х мы взяли количество человек.

Ситуация, когда один и тот же человек на треть находится на одном объекте, а другая его часть на другом, невозможна ни с биологической, ни с физической точки зрения. Значит, х — целое число.

Как быть в этом случае? Рассмотрим параболу, начертив ее условный график.

Заметим, что чем дальше будет располагаться значение х от вершины параболы, тем больше будет сумма выплат. Нам необходимо найти сумму выплат в ближайших от вершины целых значениях х.

Есть ещё и шаг 5. Поскольку вершина лежит в точке (7frac), получаем два случая: x = 7, x = 8.

При x = 7 власти выплатят художникам 6 * 7 2 − 88 * 7 + 1936 = 294 − 616 + 1936 = 1614 тысяч рублей.

При x = 8 власти выплатят художникам 6 * 8 2 − 88 * 8 + 1936 = 384 − 704 + 1936 = 1616 тысяч рублей.

Наименьшая возможная сумма выплат художникам — это 1614 тысяч рублей.

Ответ: 1614.

Фактчек

В задачах на оптимизацию необходимо найти наилучшее решение для заданной ситуации: наименьшую сумму выплат, наибольшую производительность и так далее.
Чтобы решить задачи на оптимизацию, необходимо следовать алгоритму и идеям, которые в них заложены.
Идея 1: необходимо понять, от каких величин зависит искомая переменная, чтобы найти ее максимальное или минимальное значение.
Идея 2: необходимо сократить количество неизвестных переменных в полученной зависимости.
Идея 3: исследовать полученную зависимость и найти наибольшее или наименьшее значение.
В задачах на оптимизацию очень часто встречается функция, которая задает ситуацию из условия. Для ее исследования можно прибегнуть к графикам или производной.

Проверь себя

Задание 1.
Что выгоднее купить: большую или маленькую порцию картошки фри? В большой порции 150 грамм, а стоит она 80 рублей. В маленькой порции 70 грамм, а стоит она 60 рублей.

Большую порцию.
Маленькую порцию.
Порции одинаковы по выгоде.
Невозможно определить.

Задание 2.
Дана парабола с ветвями, направленными вверх. В какой точке достигается ее наименьшее значение?

При x=0.
При y=0.
В вершине параболы.
Невозможно определить.

Задание 3.
Выплаты зарплаты работникам в фирме Огонек считается по формуле x 2 − 24x + 1000, где х — количество отработанных часов. Какую наименьшую зарплату может выплатить фирма?

Задание 4.
В зависимости от условий, на поле может вырасти − 2a 2 + 60a + 300 килограмм урожая, где a — скорость роста культур. Какое наибольшее количество килограмм может вырасти на поле?

Ответы: 1. – 2 2. – 3 3. – 3 4. – 2

2. Ограничения в виде неравенств g (х) > О.
3. Ограничения в виде равенств h_k(x) = 0.
4. Область допустимых значений хе D с R».

Задача оптимизации в общем виде:

ограничения I рода h_k(x) = 0, k = 1, К ;

ограничения II рода g_y(x) S 0, j = 1, J;

хе D с R».

Классификация задач оптимизации

В зависимости от вида целевой функции и соотношения ограничений выделяют различные задачи оптимизации, классификация которых приведена на рис. 1.3.

Существует несколько признаков классификации. Основные критерии следующие:

1. По типу параметров задачи оптимизации. Различают непрерывные задачи оптимизации (continues optimization), дискретные (discrete) и целочисленные (integer optimization).

Классификация задач оптимизации

Рис. 1.3. Классификация задач оптимизации

2. По критерию размерности допустимого множества параметров D. Задачи оптимизации по этому критерию делятся на задачи одномерной и многомерной оптимизации.
3. По критерию наличия или отсутствия ограничений на допустимое множество D. Различают задачи условной (constrained) и безусловной (unconstrained) оптимизации. Этот признак классификации имеет место как для одномерных, так и для многомерных задач оптимизации.
4. По характеру ограничений. Различают детерминированную оптимизацию и стохастическую. Если множество допустимых значений включает случайные компоненты, то имеет место стохастическое программирование. При этом стохастическая оптимизация может относиться и к дискретной задаче.
5. По виду целевой функции и виду ограничений. Различают линейное и нелинейное программирование.

Задача линейного программирования содержит линейную целевую функцию, ограничения в задаче также линейны.

При нарушении линейности целевой функции или ограничений имеет место нелинейная задача оптимизации. Классификация задач нелинейного программирования в основном определена видом целевой функции и приведена на рис. 1.4.

Ниже представлены постановки основных задач оптимизации в соответствии с рис. 1.3.

Задача одномерной безусловной оптимизации

Ограничения отсутствуют, К = J = 0, D = R’, т. е. задача без ограничений с одномерным вектором. Вид f(x) произвольный.

Задача многомерной безусловной оптимизации

Ограничений нет, K = J = О, D = R», хе[-оо,оо]./(х) — любого вида.

Задача условной многомерной оптимизации

Задача линейного программирования

Целевая функция — линейна, ограничения тоже линейны.

Наиболее известные классические задачи линейного программирования: транспортная задача, задача о диете и другие.

целочисленного программирования

В задачах целочисленного программирования компоненты вектора принимают только целые значения. Известны классические задачи целочисленного программирования: задача о коммивояжере, раскраски графов, теории расписания.

Задача нелинейного программирования

Особо развито выпуклое и квадратичное программирование. Приведенная классификация сделана по виду нелинейности целевой функции, при этом предполагалось, что ограничения ф<х) — линейны.

Рис. 1.4. Классификация задач нелинейного программирования

Оптимизация. Классические задачи оптимизации

Оптимизация — это выбор наилучшего варианта из множества возможных. Если критерий выбора известен и вариантов немного, то решение может быть найдено путем перебора и сравнения всех вариантов. Однако часто бывает так, что число возможных вариантов настолько велико, что полный перебор практически невозможен. В таких случаях приходится формулировать задачу на языке математики и применять специальные методы поиска оптимального решения, т.е. методы оптимизации.

Все задачи оптимизации делятся на два больших класса:

1) задачи математического программирования и 2) задачи оптимального управления. Первые называют еще статическими задачами, а вторые динамическими. Если говорить кратко, то различие между этими классами задач состоит в том, что в задаче математического программирования необходимо найти оптимальное число (в общем случае вектор), а в задаче оптимального управления — оптимальную функцию. С формально-математической точки зрения, это различие существенное, но в прикладном плане оно зачастую оказывается весьма условным.

Далее мы будем рассматривать задачи математического программирования. Во-первых, потому, что именно к ним сводится большинство реальных задач планирования и управления в экономике; а во-вторых, потому, что многие задачи оптимального управления могут быть сформулированы при условии, что временная характеристика дискретна, и сведены таким образом к задачам математического программирования.

Задачи математического программирования: классификация моделей и методов

В общем случае задача математического программирования состоит в нахождении вектора х = [х₁,х₂. х_п) т , при котором достигается наибольшее или наименьшее значение непрерывной скалярной функции / (х), при условии, что х е М , где М — допустимая область, представляющая собой некоторое подмножество «-мерного евклидова пространства R n .

Математическая форма записи этой задачи (для определенности сформулируем ее как задачу максимизации) такова:

Функцию f(x) называют целевой, а условия, описывающие множество М, — системой ограничений. В зависимости от вида этой функции и свойств допустимой области М задача математического программирования относится к тому или иному классу. Существуют различные принципы классификации задач математического программирования.

Наиболее важный классификационный признак — выпуклость. По этому признаку все задачи математического программирования разделяются на выпуклые и невыпуклые.

Определение 1.1. Задача математического программирования называется выпуклой, если состоит в максимизации (минимизации) выпуклой вверх (вниз) целевой функции на выпуклом множестве, в противном случае задача является невыпуклой.

Выпуклые задачи занимают особое место среди прочих задач математического программирования. Чтобы решить задачу (1.1), нужно найти все точки локальных максимумов, а затем, сравнив значения целевой функции в них, определить точку глобального максимума. В общем случае это очень сложная задача, поскольку локальных максимумов может быть много и поиск каждого из них может быть трудоемок. Однако если задача является выпуклой, то ситуация существенно упрощается.

Теорема 1.1, В выпуклой задаче математического программирования локальный экстремум одновременно является и глобальным. Выпуклая задача математического программирования может иметь только один строгий экстремум.

Если задача (1.1) выпуклая, то, найдя точку локального экстремума, мы можем быть уверены, что нашли решение или, по крайней мере, одно из решений.

Другой способ классификации задач математического программирования основан на способах задания ограничений задачи, т.е. множествам. Возможны следующие варианты:

1) ограничений может не быть вообще;
2) они могут быть заданы системой уравнений;
3) для задания ограничений могут использоваться неравенства.

Определение 1.2. Если f(x) представляет собой действительную непрерывно дифференцируемую функцию и ограничения на переменные не накладываются (т.е. М = R»), то задача (1.1) называется классической задачей на экстремум (безусловный экстремум).

В основе решения задач такого вида лежит теория дифференциального исчисления, в частности теория экстремумов, и опирающиеся на нее методы.

Определение 1.3. Если /(х) представляет собой действительную непрерывно дифференцируемую функцию, а множество М задано системой уравнений

bj — действительные числа, то задача (1.1) называется классической

задачей на условный (относительный) экстремум.

Эти задачи сводятся к задачам безусловной оптимизации с помощью метода множителей Лагранжа. Поэтому для их решения и анализа используется тот же аппарат, что и для задач на безусловный экстремум.

Нужно заметить, что авторы некоторых учебников и монографий не относят классические задачи на экстремум к задачам математического программирования, аргументируя это тем, что теория и методы их решения появились задолго до появления самого термина «математическое программирование». Если придерживаться такой трактовки, то задачами математического программирования следует считать только такие задачи (1.1), в системе ограничений которых содержатся неравенства. Задачи с ограничениями-неравенствами, в свою очередь, принято делить на два класса — нелинейные и линейные.

Определение 1.4. Задача вида

Универсального и эффективного метода решения задач нелинейного программирования (даже выпуклых, не говоря уже о невыпуклых) не существует. Класс задач нелинейного программирования сам по себе довольно обширен. В нем выделяют отдельные категории задач, имеющих ту или иную специфику, позволяющую строить более эффективные, чем в общем случае, алгоритмы. В качестве примера можно привести сепарабельные, квадратичные, дробно-линейные задачи.

Определение 1.5. Если целевая функция задачи нелинейного программирования представима в виде

то задача называется задачей сепарабельного программирования.

Определение 1.6. Если целевая функция f(x) задачи нелинейного программирования представляет собой полином второй степени, а система ограничений линейна, то задача называется задачей квадратичного программирования.

Определение 1.7. Если целевая функция f(x) задачи нелинейного программирования представляет собой дробно-линейную функцию, а система ограничений линейна, то задача называется задачей дробно-линейного программирования.

Определение 1.8. Если f(x) представляет собой линейную функцию, а множество М задается с помощью системы линейных уравнений и неравенств, то задача (1.1) называется задачей линейного программирования.

Линейное программирование принято рассматривать как самостоятельный раздел математического программирования ввиду той особой роли, которую оно играет в экономической теории и практике.

Линейное программирование имеет развитую теорию. Существует много эффективных методов решения задач линейного программирования. Кроме того, существуют приемы, позволяющие расширить область применения методов решения задач линейного программирования. Некоторые задачи математического программирования, формально не относящиеся к линейным, могут быть преобразованы и решены методами, используемыми для решения линейных задач. Это относится, например, к задачам дробнолинейного программирования.

Важную роль в теории и практике математического программирования играют также задачи целочисленного (дискретного) программирования.

Определение 1.9. Если на переменные задачи (1.1) накладывается условие целочисленности, то она называется задачей целочисленного программирования.

В экономике большое число задач носит целочисленный характер. Это связано с физической неделимостью многих объектов расчета. Но интерес к целочисленному программированию обусловлен еще и тем, что многие нелинейные невыпуклые задачи могут быть сведены к задачам линейного программирования с дополнительным требованием целочисленности. Теория целочисленного программирования используется также для разработки методов решения комбинаторных задач, например для составления расписаний.

Перейдем к рассмотрению методов решения задач математического программирования. Методы, которые применяют для решения задач математического программирования, не менее разнообразны, чем модели. Как правило, метод решения определенного класса задач имеет несколько модификаций. Например, для решения задач линейного программирования используют симплекс- метод. Кроме простого симплекс-метода, существуют еще симплекс-метод с обратной матрицей, двойственный симплексметод, метод последовательного сокращения невязок и ряд других модификаций.

Вместе с тем между моделями и методами нет взаимно однозначного соответствия. Одна и та же задача может решаться разными методами, и один и тот же метод может быть использован для решения задач, относящихся к разным категориям.

Несмотря на разнообразие, все методы решения задач математического программирования имеют некоторые общие черты. Во-первых, практически все они являются численными. То есть представляют собой алгоритмы, ориентированные на компьютерную реализацию. Во-вторых, любой алгоритм, как бы он ни был сложен или оригинален, представляет собой реализацию одного из трех основных принципов:

— последовательное приближение;
— последовательный анализ вариантов;
— случайный поиск.

Большинство методов решения задач математического программирования основаны на принципе последовательного приближения: в некоторой точке пространства переменных определяется допустимое направление возрастания (или убывания — в зависимости от постановки задачи) целевой функции и делается шаг в этом направлении. Затем анализируется результат, т.е. проверяется, не является ли новая точка искомым решением. Если нет, то вся процедура повторяется вновь. По этому принципу построены, например, градиентные методы, а также один из наиболее часто применяемых и эффективных методов математического программирования -— симплексный метод. Как правило, методы этой группы очень эффективны. Недостаток этих методов состоит в том, что они могут найти только локальный экстремум. Если задача невыпуклая (многоэкстремальная), то мы не будем иметь гарантию, что найденное таким способом решение действительно оптимально.

Другую группу составляют методы последовательного анализа вариантов. Сюда относятся такие известные методы, как динамическое программирование, метод ветвей и границ. Содержанием этих методов является построение правил отбраковки подмножеств допустимых вариантов, среди которых не может содержаться оптимального решения. Сама эта процедура, как правило, существенно учитывает специфику задачи. Поэтому здесь трудно разработать стандартные алгоритмы, которые могли бы применяться для решения широкого круга прикладных задач. Но зато эти методы могут быть использованы для решения невыпуклых и комбинаторных задач.

Еще один возможный принцип, лежащий в основе методов решения задач математического программирования, — случайный поиск: формируется некоторый случайный вариант решения (для этого используются компьютерные программы, генерирующие псевдослучайные числа) и вычисляется соответствующее значение целевой функции. Новый вариант сравнивается с лучшим, из ранее достигнутых. Если сравнение в пользу нового варианта, то он запоминается вместо того, который был раньше, и процедура повторяется. Эффективность метода определяется скоростью, с которой компьютер генерирует и оценивает варианты. А это обычно происходит очень быстро. Кроме того, сама процедура генерирования вариантов может быть не совсем случайной, а лишь носить элемент случайности. Но, разумеется, гарантии нахождения оптимума нет. Поэтому эти методы применяют лишь тогда, когда нет более надежных и эффективных; а также в тех нередких на практике случаях, когда нужно найти не обязательно оптимальный, а хотя бы достаточно хороший результат.

Задачи оптимизации и методы их решения

Методы оптимизации относятся к разделу прикладной математики – математическое программирование. Математическое программирование — раздел прикладной математики, изучающий способы оптимизации – совершенствование и повышение эффективности организации, планирования и управления в различных системах на основе вычислительных методов. Таким образом, в основе математического программирования лежит математический аппарат решения задач оптимизации.

Можно указать некоторые приложения математического программирования в исследовании операций:

оптимизация технико-экономических систем

автоматика (распознавание систем, фильтрация, управление технологическими процессами, роботы)

техника (управление размерами, оптимизация информационных систем, компьютерных сетей)

математическая экономика (решение макроэкономических задач, оптимизация моделей предпринимательства)

теория принятия решений и игр

Постановка любой задачи оптимизации начинается с определения набора независимых переменных, определении области допустимых значений для этих переменных (ограниченные задачи). Обычно оптимизируется скалярная мера качества, которая зависит от переменных (целевая функция). Решение оптимизационной задачи – это приемлемый набор значений переменных, которому отвечает оптимальное решение целевой функции. Под оптимальным решением понимают максимальность или минимальность целевой функции.

Общая постановка задач оптимизации

Найти ,

где – векторный аргумент, по которому ведется оптимизация,– область допустимых значений,– целевая функция.

где — оптимальное значение целевой функции,- значение аргумента, при котором определяется.

Постановка задачи минимизации или максимизации не нарушает общности:

– определяется функциями ограничения:

где — ограничения неравенства, а- ограничения равенства.

Классификация разделов математического программирования

По виду решаемой задачи можно выделить следующие разделы математического программирования:

Линейное программирование (ЛП) – раздел математического программирования, изучающий задачу поиска минимальной (максимальной) линейной функции при линейных ограничениях в виде равенств или неравенств.

Нелинейное программирование – раздел математического программирования, изучающий методы решения и характер экстремума в задачах оптимизации с нелинейной целевой функцией и (или) нелинейными ограничениями.

Стохастическое программирование — раздел математического программирования, изучающий модели выбора оптимальных решений в ситуациях, характеризуемых случайными величинами.

Существуют также методы, которые при решении задач оптимизации учитывают специфику этих задач. Такие методы превосходят по эффективности общие алгоритмы и их выделяют в отдельный класс методов для решения задач специальной структуры.

Разделы математического программирования

Можно выделить следующие разделы:

Целочисленное программирование — решает задачи оптимизации, в которых на значения переменных наложено требование целочисленности.

Квадратичное программирование — решает задачи оптимизации с квадратичной целевой функцией и линейными ограничениями.

Геометрическое программирование – решает задачи оптимизации, в которых целевая функция и ограничения представляют собой обобщенные многочлены с положительными коэффициентами.

Сепарабельное программирование — решает задачи оптимизации с сепарабельной целевой функцией и сепарабельными ограничениями.

Дробно-линейное программирование — решает задачи оптимизации с дробно-линейной целевой функцией и линейными ограничениями.

Оптимизация: что это, назначение и способы оптимизации

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Мы часто слышим выражения такого плана: «Нужно оптимизировать схему работы городского транспорта», «Необходимо оптимизировать затраты» и т.п.

Что же это такое – «оптимизация», для чего она нужна, и каковы способы оптимизации? Рассмотрим эти вопросы в данной статье.

Оптимизация

Оптимизация — это максимум пользы при минимуме затрат

Допустим, есть задача: оптимизировать поставки сезонных овощей в сеть супермаркетов. Что это значит? Это значит, что нужно сделать следующее:

Найти надежных поставщиков, занимающихся скупкой излишков выращенных овощей у местного населения.
Выйти на крупных фермеров местного и соседнего региона.
Заключить договоры на поставки продукции.
Наладить регулярную и оперативную доставку.

Данный алгоритм описывает меры, которые нужно предпринять, чтобы сезонные овощи всегда были на прилавках магазинов.

Вывод: оптимизация – это ряд действий, которые нужно выполнить для того, чтобы достичь максимально благоприятного результата при минимальных затратах.

Определение

В переводе с латинского слово «оптимизация» обозначает «наилучший». Оптимизировать (найти наилучший вариант функционирования из всех имеющихся) можно любой процесс, любое действие и любую цель. Оптимизация возможна в различных сферах деятельности человека.

Математика – точная наука, поэтому термин «оптимизация» в этой области имеет конкретную лаконичную формулировку:

Формулировка

Сайты, размещенные в интернете, также можно оптимизировать.

Это необходимо для того, чтобы контент, размещенный на этих интернет-ресурсах, «увидели» бы как можно больше поисковых систем и прочитало максимальное количество пользователей сети. Подробней о методах продвижения сайтов можно узнать, пройдя по этой ссылке: Что такое SEO-оптимизация.

Далее в статье мы немного подробней остановимся на процессах оптимизации в сфере экономики.

Оптимизация бизнеса

Предприниматель, открывая свой бизнес, делает это с целью получения материальной выгоды, т.е. прибыли. Он ставит перед собой 2 задачи: сначала выйти на окупаемость («выжить»), а затем – развить свое детище.

И если «выжить» еще как-то можно с помощью стартового капитала, упорства и работоспособности предпринимателя, то расширить бизнес невозможно без грамотного управления и выполнения комплекса специальных мер – то есть, без оптимизации бизнеса.

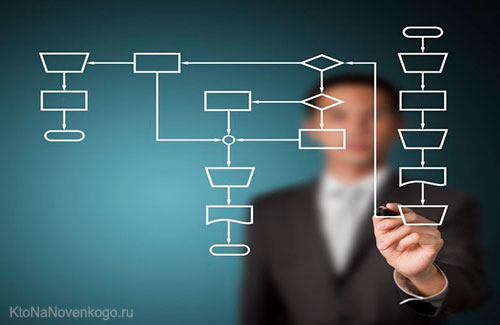
Схема

Рассмотрим схематичный алгоритм (что это?) оптимизации бизнес-процесса:

анализ существующего положения дел (от структуры бизнеса до количественных показателей его эффективности);
разработка мер оптимизации, например:
1. смена поставщика сырья (товара),
2. привлечение для постоянной или разовой работы высококвалифицированных специалистов,
3. отказ от убыточных направлений бизнеса и т.д.;
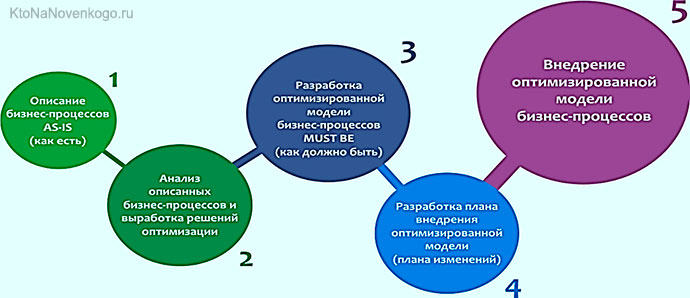
Умение взглянуть трезвым взглядом на свой бизнес и принять решение о его оптимизации – это один из талантов успешных бизнесменов.

Оптимизация производства

Главная цель любого производства – это получение дохода. Чем выше прибыль при минимизированных затратах, тем выше ликвидность (эффективность) кампании. Достичь этой цели возможно, проведя оптимизацию производства.

Это значит, что необходимо выполнить «настройку» производственного процесса таким образом, чтобы затраты на производство были минимально возможными (без потери качества), а прибыль – максимальной при имеющихся входных данных.

Рассмотрим методы, которые могут помочь провести оптимизацию:
1. четкий учет затрат на всех этапах производственного процесса;
2. минимизация себестоимости продукции (затрат на сырье, зарплату персонала, оплату коммунальных расходов, амортизацию средств производства); (в том числе – автоматизация и механизация этапов производственного процесса);
3. переобучение кадров в соответствии с внедряемыми инновационными технологиями и проведенной модернизацией;
4. уменьшение объема отходов;
5. рационализация использования рабочего времени сотрудников;
6. вариативность ценовой политики; (о том, что это такое, можно прочитать в другой статье нашего блога);
7. оптимизация персонала (подробней об этом – в следующем подразделе статьи).
Важно: осуществление оптимизации производства возможно только с помощью комплексного подхода.

Так, модернизация средств производства не принесет должного эффекта без переобучения персонала и наличия рынка сбыта продукции. Это касается и других методов оптимизации.

Оптимизация персонала

Задачи какого-либо производственного или иного процесса решаются людьми, которые его обслуживают, т.е. персоналом.

Определение равновесного состояния, при котором выполнение поставленных задач обеспечивается определенным количеством сотрудников, называется оптимизацией персонала.

Задача кадровых работников или сотрудников высшего звена заключается в определении минимального количества работников определенной квалификации для обеспечения максимальной эффективности производственного (или иного рабочего) процесса.

При этом оптимизация может осуществляться несколькими методами:
1. сокращением малоэффективных штатных должностей и (или) неэффективных сотрудников, не оказывающих положительного влияния на образование прибыли предприятия;
2. повышением квалификации работников;
3. совмещением функций в служебных обязанностях конкретных сотрудников.
Данные методы могут применяться как по отдельности, так и в комплексе. Выбор метода зависит от конкретной ситуации, сложившейся в кампании.

В этой статье затронуты лишь некоторые сферы, в которых оптимизация является важным аспектом для достижения нужного результата. Читайте наш блог, и вы будете знать больше других.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (3)

В процессе оптимизации важно сохранять баланс. Так как стремление снизить затраты любыми способами часто сказывается на качестве конечной услуги или товара. А это приведет к потере клиентов, и прибыль снизится, хотя задача была иная.

Что такое «оптимизация» — мы видим на примере отечественного образования. И на примере медицины также. Руководители рассудили рационально, например так: «Зачем в деревне школа, когда родители могут отвозить детей на своей машине в городскую школу»?

А что, верно. Ведь у каждого взрослого человека, проживающего в сельской местности, есть личный автотранспорт. А дороги сейчас в любую глушь идеальные, в отличие от советского периода. Вот это живой пример оптимизации.

Серега: есть такое дело. К сожалению, еще не все либералы из 90-х ушли на пенсию. Многие до сих пор «оптимизируют» и не выковыряешь. Есть и молодые выпускники ВШЭ, у которых мозги не в ту сторону повернули.

Сейчас власти начинают осознавать перекосы. Исправят быстро, я уверен. С дорогами то получается, а ведь никто не верил. Вот бы еще и с дураками так же быстро разобраться.
Похожие записи: