Суммарная погрешность

Погрешность измерений

Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.

По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.

(1.2), где X — результат измерения; Х₀ — истинное значение этой величины.

Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением

(1.3), где Х_д — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.

Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:

(1.4)

По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные .

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

первые — погрешностью градуировки шкалы или ее небольшим сдвигом;
вторые — старением элементов средства измерения.

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений.

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:

(1.5), где X_н – номинальное значение меры; Х_д – действительное значение меры

Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:

(1.6), где X_п – показания прибора; Х_д – действительное значение измеряемой величины.

Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному

(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

(1.7)

Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

(1.8)

Предел допускаемой погрешности средств измерений – наибольшая без учета знака погрешность средства измерений, при которой оно может быть признано и допущено к применению. Данное определение применяют к основной и дополнительной погрешности, а также к вариации показаний. Поскольку свойства средств измерений зависят от внешних условий, их погрешности также зависят от этих условий, поэтому погрешности средств измерений принято делить на основные и дополнительные .

Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.

Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Погрешности средств измерений подразделяются также на статические и динамические .

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений.

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Большая Энциклопедия Нефти и Газа

При расчете суммарной погрешности результатов измерений следует учитывать требования и условия, указанные в паспорте и руководствах по эксплуатации средств измерений. Если эти результаты вышли за пределы нормативного допуска, то измерения необходимо повторить. [2]

Определение численной величины суммарной погрешности результата измерения для приборов какого-либо типа требует большого количества весьма точных измерений, проводимых на большом числе приборов данного типа, в различных температурных условиях при применении установочных мер различных классов. [3]

В самом общем виде суммарная погрешность результата измерений складывается из случайной и систематической состав: ляющих. Источниками погрешностей результатов хроматографи-ческих измерений являются факторы, которые можно разбить на три группы: 1) поддающиеся количественной оценке; 2) не поддающиеся количественной оценке; 3) неизвестные. [4]

Для обыкновенных и технических измерений указывают только суммарную погрешность результата измерения . При этом, если эта погрешность найдена без вероятностного суммирования составляющих, то в записи погрешности отсутствует доверительная вероятность. Вообще, если при записи погрешности результата измерения не указана доверительная вероятность, то это следует считать свидетельством того, что границы погрешности оценены невероятностным путем. Это замечание не относится, конечно, к тем случаям, когда из приведенного расчета погрешностей и сопровождающего расчет описания видно то значение вероятности ( доверительной вероятности), которое было принято при вычислении. [5]

Требуемая точность измерения непосредственно определяется допускаемым значением ба суммарной погрешности результата измерений . Из этого значения должна быть выделена часть бЕ, определяющая допускаемые значения случайной и систематической составляющей погрешности регистрации результатов измерений. Остальная часть 6j, определит значение бЕп, используемое в дальнейшем анализе для выбора первичного преобразователя. [6]

В таких условиях вклад погрешностей собственно измерительных устройств в суммарную погрешность результата измерений становится все меньше и меньше. Например, для такого распространенного в настоящее время вида измерений, как измерение массы движущихся объектов, погрешность применяемых средств измерений составляет лишь 5 — 6 % от суммарной погрешности результата взвешивания. Остальную часть составляют методические погрешности ( которые не могут быть отражены в нормативной документации на приборы), погрешности, вносимые работой вспомогательных устройств, и субъективные ошибки операторов, обусловленные динамикой процесса измерений. [7]

Наиболее полной характеристикой точности выполняемых по данной методике измерений является суммарная погрешность результата измерений . Она нормируется пределами допускаемого значения суммарной погрешности результата измерения. Эти пределы устанавливают симметричный интервал, соответствующий истинному значению суммарной погрешности результата измерения. [8]

При использовании современных сложных методов измерений погрешности средств измерений далеко не определяют суммарную погрешность результатов измерений , поскольку большое значение приобретают погрешности метода измерений, ошибки операторов, неизменность условий проведения измерений и др. Поэтому важно обеспечить не только единообразие средств измерений, но и единство измерений и его достоверность, характеризующую доверие к результатам измерений. [9]

Правильность выбора средств по точности определяется достижением равенства между фактической ( гарантированной) суммарной погрешностью результата измерений параметра Д2ф и допускаемым ( требуемым) значением суммарной погрешности ДЕтр при условии, что фактические значения ограничительных технических характеристик средств измерений будут выше или равны требуемым значениям этих характеристик. [10]

Если в / S ( Х) лежит в диапазоне от 0 8 до 8, то при определении суммарной погрешности результата измерения необходимо учитывать как неисключенные систематические, так и случайные погрешности. [11]

Следует заметить, что термин погрешность метода измерения является не совсем удачным, вызывая представление о неправильности метода измерения, тогда как в действительности под этим термином подразумевается суммарная погрешность результата измерения . [12]

Наиболее полной характеристикой точности выполняемых по данной методике измерений является суммарная погрешность результата измерений. Она нормируется пределами допускаемого значения суммарной погрешности результата измерения . Эти пределы устанавливают симметричный интервал, соответствующий истинному значению суммарной погрешности результата измерения. [13]

В некоторых случаях погрешность показаний прибора не может быть отделена от погрешностей, свойственных какому-либо конкретному методу измерения. В этих случаях поверка приборов производится специально с целью выявления суммарной погрешности результата измерения , свойственной данному методу. [14]

Контроль за работами по обеспечению единства измерений в стране возложен на Госстандарт СССР — государственных инспекторов, которым в соответствии с положением О государственном надзоре за стандартами и средствами измерений в СССР, утвержденным Постановлением Совета Министров СССР от 28 сентября 1983 г., предоставлено право запрещать использование результатов измерений, погрешности которых не оценены с необходимой точностью. В методических требованиях и правилах ГСИ содержится положение, что погрешность измерений в реальных условиях вызывается рядом причин. Так, в суммарную погрешность результата измерений входят и погрешности метода, и погрешности, вызванные влиянием различных внешних факторов и субъективные ошибки операторов, и погрешности обработки результатов измерений, т.е. комплекс всех погрешностей измерительного процесса. При этом для многих современных измерительных процессов характерен малый удельный вес погрешности показаний прибора в суммарной погрешности результата измерения, в суммарной погрешности измерительного процесса. Например, результаты метрологического анализа процесса измерения диаметров отверстий индикаторными нутромерами показали, что погрешность собственно средств измерений составляет лишь 13 5 % суммарной погрешности результата измерения диаметра отверстия. [15]

Объединение погрешностей (интервалов) потребуется, если условия измерений отличаются от условий передачи единицы, и имеется информация о других источниках неопределенности, представленной, как правило, совокупностью нормированных погрешностей.

Объединение погрешностей основано на предположении, что разность между измеренным и истинным значением величины могла бы принимать случайные значения величины, равномерно распределенной в пределах нормированного или оцененного интервала по каждому влияющему фактору. Оценка СКО при этом максимально завышена и является «оценкой сверху«. Дисперсии складываются, находим оценку СКО объединенной погрешности. В соответствии с предельной теоремой объединенный закон распределения нескольких случайных величин стремится к нормальному закону.

Суммирование составляющих погрешности не требуется при выполнении значительной части технических измерений, когда общие погрешности определены симметричными пределами допускаемой погрешности (при Р=1) или представлены классом точности и известны до выполнения измерений.

Задача суммирования (объединения) составляющих погрешности может возникнуть как до, так и после выполнения прямых или косвенных измерений какого-либо параметра. Эта задача весьма сложная, ее решение на уровне классической теории измерений пока находится в стадии осмысления и разработки.

При суммировании иногда придерживаются принципа «оценки сверху». Это означает, что оцененная суммарная погрешность (интервал) принимается «чуть» больше расчетной в надежде на то, что вероятность попадания истинного значения измеряемой величины в этот интервал может оказаться «чуть» выше принятой вероятности.

Обычное арифметическое суммирование погрешностей дает слишком завышенные погрешности с вероятностью 1. Результат измерений с такими погрешностями считается грубым и имеет заниженную ценность. Тем не менее, существует устойчивая рекомендация: две составляющие систематической погрешности суммировать арифметически.

В основу суммирования составляющих погрешности в современной метрологии положены принципы, заимствованные из теории вероятностей и математической статистики. При суммировании любых составляющих погрешности действует правило: общая дисперсия нескольких независимых случайных величин равна сумме дисперсий каждой из них.

Существует общая рекомендация по несущественности отдельных составляющих погрешности — отличие дисперсий не менее чем в 10 раз, или различие оценок СКО более чем в 3 раза.

Суммирование случайных погрешностей.

В обычных прямых многократных измерениях выявляют одну случайную составляющую, которую почти всегда объединяют с общей систематической погрешностью. В редком случае, когда случайная составляющая погрешности больше суммарной систематической погрешности в 8 и более раз, то систематические погрешности можно считать несущественными.

В случае измерений, в процессе которых поправки определены экспериментально и их случайные составляющие погрешности существенны, то оценку СКО суммарной случайной составляющей погрешности измерений величины В определяют по следующей формуле:

где _i — оценка СКО i-той случайной составляющей погрешности; n — число случайных составляющих погрешности.

При представлении результата измерений могут быть использованы одна или две или три сигмы, оцененные по формуле (16).

Суммирование систематических погрешностей

Основные принципы и методы суммирования погрешностей прямых измерений, применяемые в российских документах, были впервые регламентированы ГОСТ 8.207-76 «ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Общие положения».

При прямых однократных измерениях все составляющие систематической погрешности обычно считаются существенными, а случайная погрешность считаются пренебрежимо малой, если она в 8 раз меньше наименьшей систематической составляющей. Обычно рассматривают следующие составляющие систематической погрешности: погрешность переданной и хранимой единицы величины; погрешности, обусловленные отличием рабочих условий измерений от условий, принятых за нормальные условия. Каждая составляющая погрешности может быть выражена пределами допускаемой основной и дополнительной погрешности или оценками погрешности (с вероятностью 0,95).

Принято также считать, что поправки, если бы они были определены для каждой систематической составляющей погрешности, были бы распределенными по равномерному закону в пределах соответствующего интервала.

Суммарную погрешность измерения Д_Р вычисляют по формуле

где Д_i— i-тая систематическая составляющая погрешности; k_Р — коэффициент, определяемый принятой доверительной вероятностью;

m -количество составляющих систематической погрешности.

Коэффициент k_Р при разной доверительной вероятности Р для разного количества составляющих m выбирают в соответствии с табл. 3.

Таблица 3 Коэффициент k_Р при разной вероятности Р

Доверительная вероятность Р

Количество составляющих погрешности

Доверительную вероятность для вычисления суммарной систематической погрешности рекомендуют принимать той же, что при вычислении случайной погрешности измерения, обычно Р=0,95.

Рекомендации ISO основаны на суммировании дисперсий составляющих погрешности и использовании предельной теоремы для оценки доверительного интервала.

Если руководствоваться «оценкой сверху» и считать, что вероятный разброс показаний СИ от каждого систематического эффекта мог бы быть распределенным равномерно и (или) по закону Симпсона, то суммарную погрешность измерения Д_Р вычисляют по формуле:

где k_Р — коэффициент охвата, определяемый принятой доверительной вероятностью Р (обычно k_0,95=2 при Р=0,95 и k_0,997=3 при Р=0,997);

Д_i — интервал для i-ой систематической составляющей погрешности при равномерном распределении измеренных значений;

m -количество составляющих систематической погрешности, распределенных равномерно;

Д_j — интервал для j-ой систематической составляющей погрешности при распределении измеренных значений по закону Симпсона;

q -количество составляющих систематической погрешности, распределенных по закону Симпсона.

Суммирование систематических и случайных погрешностей

Далее анализу подвергаются систематические погрешности, которые имеются всегда. В российских документах они обычно выражены нормированными пределами допускаемой погрешности средств измерений, указанными в паспорте СИ. Иногда в нормированном пределе содержится доля собственной случайной погрешности СИ, которая перейдет в разброс измеренных значений, и оставшаяся доля систематической погрешности будет меньше предельной. Если известны погрешности СИ, указанные, например, в сертификате о его калибровке, то они должны быть приведены к доверительной вероятности оцененной случайной погрешности.

При прямых многократных измерениях все систематические составляющие погрешности считаются существенными и случайная составляющая погрешности меньше суммарной оценки систематической погрешности менее чем в 8 раз. Суммарная оценка систематической погрешности и оценка случайной погрешности должны быть приведены к одной и той же вероятности. Суммарную оценку погрешности измерения находят путем построения композиции распределений показаний, изменяющихся от случайных и систематических эффектов.

Общая суммарная оценка погрешности при ответственных измерениях, например, в научных исследованиях, вычисляется по следующей формуле [19]:

где t_P — коэффициент Стьюдента при n?30; k — коэффициент, использованный при оценивании суммарной систематической погрешности; Д_i — предел допускаемой i-той составляющей систематической погрешности; у — оценка СКО случайной погрешности среднего измеренного значения, вычисленная по формуле:

где X_i — i-е измеренное значение величины; — среднее измеренное значение величины; n — общее количество измеренных значений.

Рекомендация ISO суммирования систематических и случайных составляющих погрешности основана на суммировании дисперсий составляющих погрешности и использовании предельной теоремы для оценки доверительного интервала.

Суммарную погрешность измерения Д_Р вычисляют по формуле:

где k_Р — коэффициент охвата, определяемый принятой доверительной вероятностью Р (k_0,95=2 или k_0,997=3) и остальные обозначения как в формулах (16) и (18).

В обоснованных случаях иногда пользуются трапецеидальным законом распределения при добавлении систематической погрешности.

Однако при проведении обычных лабораторных измерений часто пользуются совсем упрощенным способом оценки суммарной погрешности многократных измерений — обычным арифметическим суммированием, всегда обеспечивающим «оценку сверху«.

Суммирование составляющих погрешности при косвенных измерениях.

При выполнении косвенных измерений аргументами функции являются результаты прямых (или других косвенных измерений) со своими измеренными значениями и погрешностями.

Пусть требуется получить результат измерений величины , связанной с результатами измерений других величин ;…; … , где погрешности представлены с доверительной вероятностью 0,99 или 1, некоторой зависимостью, называемой «моделью измерений» [35]:

Необходимо найти отдельно и отдельно , чтобы объединить их в один результат измерений.

Оценку погрешности косвенного измерения найдем по формуле:

Наиболее простым способом объединения погрешностей косвенных измерений с использованием функций, в которых аргументы суммируются или перемножаются или делятся, является следующий способ.

Пусть необходимо найти погрешность Д_Z измеренной величины Z, определяемой через результаты измеренных прямыми методами величин и , где погрешности представлены с доверительной вероятностью 0,99 или 1, как следующие функции:

Тогда погрешность косвенных измерений для этих трех функций определяется по одной и той же формуле:

Если аргументы функции находятся в какой-либо степени, то слагаемые в формуле (24) множатся на соответствующий показатель степени.

Если аргументов более двух, в формулу (24) добавятся соответствующие слагаемые для новых составляющих погрешности, умноженные на соответствующий показатель степени.

Для случая, когда функция представлена разностью величин , погрешность, вычисленная по формуле (24) может оказаться существенно заниженной. Для такой и более сложных функциональных зависимостей целесообразно выполнить математическое моделирование косвенных измерений, чтобы убедиться в обоснованности полученной оценки погрешности. Для этого необходимо получить разброс измеренных значений косвенно измеряемой величины с перебором хотя бы крайних значений интервала для истинных значений каждого аргумента. Ширина данного разброса является оценкой погрешности косвенного измерения. Обычно такой интервал слишком завышен, так как вероятность того, что истинное значение измеренных аргументов окажется одновременно в крайних положениях соответствующего доверительного интервала, чрезвычайно мала. Поэтому доверительная вероятность для оценок погрешности косвенного измерения по формулам (23) и (24) приближается к 1, даже если доверительная вероятность для оценок погрешности аргументов была принята 0,95 и выше.

Суммарная погрешность и достоверность измерений

Задача объединения составляющих погрешности может возникнуть как до, так и после выполнения прямых или косвенных измерений какого-либо параметра. Ее решение на уровне классической теории измерений пока находится в стадии осмысления и разработки.

Суммирование составляющих погрешности не требуется при выполнении значительной части технических измерений, когда общие погрешности представлены допускаемой погрешностью (при Р = 1) или классом точности.

Объединение нормированных погрешностей основано на предположении, что разность между измеренным и истинным значением величины могла бы принимать случайные значения величины, равномерно распределенной в пределах нормированного интервала по каждому влияющему фактору. В соответствии с предельной теоремой объединенный закон распределения нескольких случайных величин стремится к нормальному закону.

При суммировании придерживаются принципа «оценки сверху». Предполагается, что оцененная суммарная погрешность (интервал) принимается «чуть» больше расчетной в надежде на то, что вероятность попадания истинного значения измеряемой величины в этот интервал может оказаться «чуть» выше принятой вероятности.

В основу суммирования составляющих погрешности в современной метрологии положены принципы, заимствованные из теории вероятностей и математической статистики. При суммировании любых составляющих погрешности действует правило: общая дисперсия нескольких независимых случайных величин равна сумме дисперсий каждой из них.

Обычное арифметическое суммирование погрешностей дает слишком завышенную погрешность измерений с вероятностью 1. Результат измерений с такими погрешностями считается грубым и имеет заниженную ценность. Тем не менее, существует устойчивая рекомендация:две составляющие систематической погрешности суммировать арифметически.

Суммирование случайных погрешностей.

В случае измерений, в процессе которых поправки определены экспериментально и их случайные составляющие погрешности оказались существенными и выраженными своими оценками СКО, то оценку СКО суммарной случайной составляющей погрешности измерений величины В определяют по следующей формуле:

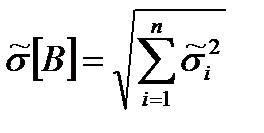
, (16)

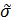
где _i – оценка СКО i-той случайной составляющей погрешности;

n – число случайных составляющих погрешности.

Суммирование систематических погрешностей.

Суммарную погрешность измерения Δ_Р вычисляют по формуле:

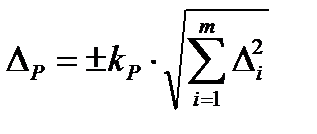
, (17)

где Δ_i – i-тая систематическая составляющая погрешности;

k_Р – коэффициент, определяемый принятой доверительной вероятностью;

m – количество составляющих систематической погрешности.

Коэффициент k_Рпри разной доверительной вероятности Р для разного количества составляющих m выбирают в соответствии с таблице 3.

Таблица 3 – Коэффициент k_Рпри разной вероятности Р

вероятность Р

Количество составляющих погрешности

Рекомендации ISO основаны на суммировании дисперсий составляющих погрешности и использовании предельной теоремы теории вероятностей для оценки доверительного интервала.

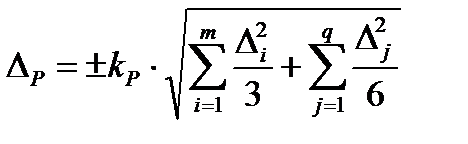
, (18)

где k_Р – коэффициент охвата, определяемый принятой доверительной вероятностью Р (обычно k_0,95 = 2 при Р = 0,95 и k_0,997 = 3 при Р = 0,997);

Δ_i – интервал для i-ой систематической составляющей погрешности при равномерном распределении измеренных значений;

m – количество составляющих систематической погрешности, распределенных равномерно;

Δ_j – интервал для j-ой систематической составляющей погрешности при распределении измеренных значений по закону Симпсона;

q – количество составляющих систематической погрешности, распределенных по закону Симпсона.

Суммирование систематических и случайных погрешностей.

Далее анализу подвергаются систематические погрешности, которые имеются всегда. В российских документах они обычно выражены нормированной допускаемой погрешностью средств измерений, указанными в паспорте СИ. Иногда в нормированной погрешности содержится доля собственной случайной погрешности СИ, которая перейдет в будущий разброс измеренных значений, и оставшаяся доля систематической погрешности будет меньше нормированной. Если известны погрешности СИ, указанные, например, в сертификате о его калибровке, то они должны быть приведены к доверительной вероятности оцененной случайной погрешности.

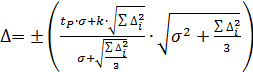
, (19)

где t_P – коэффициент Стьюдента при n≤30;

k – коэффициент, использованный при оценивании суммарной систематической погрешности;

Δ_i – допускаемая i-тая составляющая систематическая погрешность;

σ – оценка СКО случайной погрешности среднего измеренного значения, вычисленная по формуле:

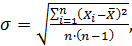
(20)

где X_i – i-е измеренное значение величины;

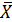
– среднее измеренное значение величины;

n – общее количество измеренных значений.

Суммарную погрешность измерения Δ_Р вычисляют по формуле:

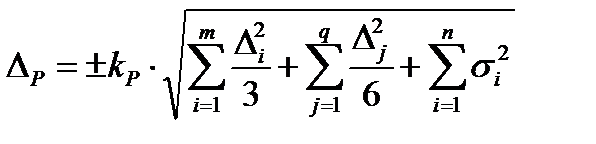
. (21)

где k_Р – коэффициент охвата, определяемый принятой доверительной вероятностью Р (k_0,95 = 2 или k_0,997 = 3) и остальные обозначения как в формулах
(16) и (18).

В обоснованных случаях иногда пользуются трапецеидальным законом распределения при добавлении систематической погрешности, обусловленной ее дополнительным источником.

Однако при проведении обычных лабораторных измерений часто пользуются совсем упрощенным способом оценки суммарной погрешности многократных измерений – обычным арифметическим суммированием, всегда обеспечивающим «оценку сверху».

Суммирование составляющих погрешности при выполнении косвенных
измерений.

При выполнении косвенных измерений аргументами функции являются результаты прямых (или других косвенных) измерений со своими измеренными значениями и погрешностями.

Пусть требуется получить результат измерений величины , связанной с результатами измерений других величин ;…; … , где погрешности представлены с доверительной вероятностью от 0,99 до 1, некоторой зависимостью, называемой «моделью измерений» [35]:

. (22)

Необходимо найти отдельно и отдельно , чтобы объединить их в один результат измерений.

Оценку погрешности косвенного измерения найдем по формуле:

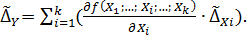
(23)

Пусть необходимо найти погрешность Δ_Z измеренной величины Z, определяемой через результаты измеренных прямыми методами величин и , где погрешности представлены с доверительной вероятностью 0,99 или 1, как следующие функции:

; , ; .

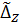
Тогда погрешность косвенных измерений для этих функций определяется по одной и той же формуле:

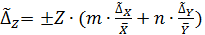
, (24)

Если аргументы функции находятся в какой-либо степени, то слагаемые в формуле (24) множатся на показатель степени.

Для более сложных функциональных зависимостей целесообразно выполнить математическое моделирование косвенных измерений, чтобы убедиться в обоснованности полученной оценки погрешности. Для этого необходимо получить разброс измеренных значений косвенно измеряемой величины с перебором хотя бы крайних значений интервала для истинных значений каждого аргумента. Ширина данного разброса является оценкой погрешности косвенного измерения. Обычно такой интервал слишком завышен, так как вероятность того, что истинное значение измеренных аргументов окажется одновременно в крайних положениях соответствующего доверительного интервала, чрезвычайно мала. Поэтому доверительная вероятность для оценок погрешности косвенного измерения по формулам (23) и (24) приближается к 1, даже если доверительная вероятность для оценок погрешности аргументов была принята 0,95 и выше.

Доверительная вероятность служит показателем достоверности измерений.

5.6 Представление погрешности в результате измерений.
Правила округления

Рекомендации по формам представления результатов измерений даны в МИ 1317-2004 и в правилах ПМГ 96-2009.

Поскольку измеренное значение (показание прибора) это всегда случайная величина, то результат измерений должен быть представлен всей совокупностью возможных значений измеряемой величины. Поэтому полная информация об измеряемой величине может быть представлена только интервалом на числовой оси с указанием функции распределения плотности вероятности.

При представлении результата воспроизведения единицы величины первичным государственным эталоном принято разделять оценки погрешности на систематические и случайные составляющие (например, оценка СКО случайной погрешности, систематическая погрешность при заданной доверительной вероятности и стабильность за установленный интервал времени). Такой же подход целесообразно использовать при представлении сведений о любых эталонах единиц величин разных разрядов. В особо ответственных случаях (при установлении физических констант, при определении постоянных коэффициентов (функций) влияния, при дальнейшем использовании результатов измерений в других измерениях) также целесообразно указывать и систематические и случайные погрешности.

В таблице 4 приведено сопоставление различных вариантов представления погрешности и показателей неопределенности в результатах измерений.

Таблица 4 – Сопоставление вариантов представления показателей
неопределенности измерений в терминах погрешности и неопределенности

Показатели точности (неопределенности) измерений	Представление результата измерений в терминах погрешности	Представление результата измерений в терминах неопределенности
Суммарная погрешность при заданной вероятности (расширенная суммарная неопределенность)
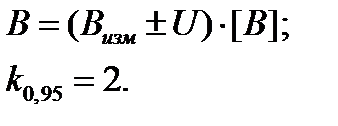Оценка среднего квадратического отклонения систематической погрешности (суммарная стандартная неопределенность по типу В)	В=(В_изм±σ_с)·[B]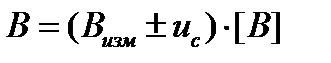
Стандартное отклонение случайной погрешности (стандартная неопределенность по типу А)
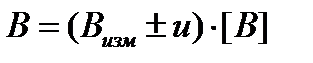Оценка среднего квадра-тического отклонения суммарной погрешности; (суммарная стандартная неопределенность)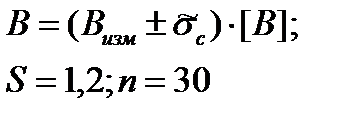
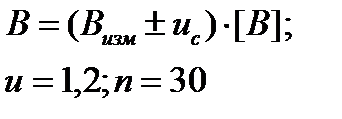Нормированная погрешность или целевая неопределенность	В=(В_изм±Δ_Р=1)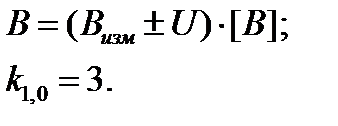

Правила округления.

При представлении результата измерений должно быть разумное сочетание значащих цифр в измеренном значении величины и в погрешности измерений.

Нормированную допускаемую погрешность (вероятность всегда 1) выражают числом, содержащим одну значащую цифру, если она от 3 до 8, или двумя значащими цифрами, первая из которых 1 или 2. Использование одной цифры 9 не рекомендуется (округляют до 10). В случае нормированной допускаемой погрешности числовое значение погрешности не требует изменения (округления).

Оцененную погрешность при любой выбранной вероятности выражают числом, содержащим одну значащую цифру, если она после округления от 5 до 9, или двумя значащими цифрами, первая из которых от 1 до 4. В таком случае числовое значение погрешности округляют в большую сторону (увеличивают на 1), если отбрасываемая цифра равна или более 5, и в меньшую сторону (оставляют без изменения), если она менее 5. Для высокоточных измерений погрешность выражают двумя любыми значащими цифрами.

После округления оцененной погрешности реальное значение вероятности будет отличаться от ранее выбранного значения. При округлении погрешности в большую сторону выбранную вероятность можно оставить без изменения, а при округлении в меньшую сторону декларируемую вероятность рекомендуется уменьшить.

Округление погрешности производится лишь при представлении окончательного результата. Все предварительные вычисления производят с тремя излишними значащими цифрами.

Измеренное значение округляют до той же цифры, которой заканчивается округленное значение оцененной абсолютной погрешности или значение допускаемой погрешности. Излишние цифры в целых числах заменяют нулями, а в десятичных дробях отбрасывают.

Дата добавления: 2018-06-01 ; просмотров: 1961 ; Мы поможем в написании вашей работы!

Что такое суммарная погрешность результатов измерения

Всероссийский научно-исследовательский институт
оптико-физических измерений

ПОИСК И НАВИГАЦИЯ

Погрешности измерений

Погрешность результата измерения (англ. error of a measurement) – отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Примечания:

Истинное значение величины неизвестно, его применяют только в теоретических исследованиях.
На практике используют действительное значение величины x_Д ,в результате чего погрешность измерения Dx_ИЗМ определяют по формуле: Dx_ИЗМ = x_ИЗМ —x_Д , где x_ИЗМ – измеренное значение величины.
Синонимом термина погрешность измерения является термин ошибка измерения, применять который не рекомендуется как менее удачный.

Систематическая погрешность измерения (англ. systematic error) – составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.
Примечание. В зависимости от характера измерения систематические погрешности подразделяют на постоянные, прогрессивные, периодические и погрешности, изменяющиеся по сложному закону.
Постоянные погрешности — погрешности, которые длительное время сохраняют свое значение, например в течение времени выполнения всего ряда измерений. Они встречаются наиболее часто.
Прогрессивные погрешности — непрерывно возрастающие или убывающие погрешности. К ним относятся, например, погрешности вследствие износа измерительных наконечников, контактирующих с деталью при контроле ее прибором активного контроля.
Периодические погрешности — погрешности, значение которых является периодической функцией времени или перемещения указателя измерительного прибора.
Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей.

Инструментальная погрешность измерения (англ. instrumental error) – составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений.

Погрешность метода измерений (англ. error of method) – составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений.
Примечания:

Вследствие упрощений, принятых в уравнениях для измерений, нередко возникают существенные погрешности, для компенсации действия которых следует вводить поправки. Погрешность метода иногда называют теоретической погрешностью.
Иногда погрешность метода может проявляться как случайная.

Погрешность (измерения) из-за изменений условий измерения – составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.
Примечание. Этот термин применяют в случае неучтенного или недостаточно учтенного действия той или иной влияющей величины (температуры, атмосферного давления, влажности воздуха, напряженности магнитного поля, вибрации и др.); неправильной установки средств измерений, нарушения правил их взаимного расположения и др.

Субъективная погрешность измерения – составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора.
Примечания:

Встречаются операторы, которые систематически опаздывают (или опережают) снимать отсчеты показаний средств измерений.
Иногда субъективную погрешность называют личной погрешностью или личной разностью.

Неисключенная систематическая погрешность – составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости.
Примечания:

1. Иногда этот вид погрешности называют неисключенный (ые) остаток (остатки) систематической погрешности.
2. Неисключенная систематическая погрешность характеризуется ее границами. Границы неисключенной систематической погрешности θ при числе слагаемых N≤3 вычисляют по формуле:

Случайная погрешность измерения (англ. random error) – составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.

Абсолютная погрешность измерения (англ. absolute error of a measurement) – погрешность измерения, выраженная в единицах измеряемой величины.

Абсолютное значение погрешности (англ. absolute value of an error) – значение погрешности без учета ее знака (модуль погрешности).
Примечание. Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности.

Относительная погрешность измерения (англ. relative error) – погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.
Примечание. Относительную погрешность в долях или процентах находят из отношений:

Рассеяние результатов в ряду измерений (англ. dispersion) – несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей.
Примечания:

Количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей.
Оценками рассеяния результатов в ряду измерений могут быть: — размах, — среднее квадратическое отклонение (экспериментальное среднее квадратическое отклонение), — доверительные границы погрешности (доверительная граница). (в ред. Изменения N 2, введенного Приказом Росстандарта от 04.08.2010 N 203-ст)

Размах результатов измерений (англ. ) – оценка R_n рассеяния результатов единичных измерений физической n величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле:

где x_max и x_min — наибольшее и наименьшее значения физической величины в данном ряду измерений.
Примечание. Рассеяние обычно обусловлено проявлением случайных причин при измерении и носит вероятностный характер.

Среднее квадратическое отклонение результатов единичных измерений в ряду измерений (англ. experimental (sample) standard deviation) – характеристика S рассеяния результатов измерений в ряду равноточных измерений одной и той же физической величины, вычисляемая по формуле:

где: x_i — результат i-го единичного измерения; x ̅ — среднее арифметическое значение n единичных результатов измерений величины.
Примечание — СКО S является оценкой стандартного отклонения сигма — параметра распределения результатов измерений и одновременно оценкой стандартного отклонения распределения случайной погрешности этих результатов. (п. 9.14 в ред. Изменения N 2, введенного Приказом Росстандарта от 04.08.2010 N 203-ст)

Среднее квадратическое отклонение среднего арифметического значения результатов измерений (англ. experimental (sample) standard deviation) – характеристика S_x рассеяния среднего арифметического значения результатов равноточных измерений одной и той же величины, вычисляемая по формуле:

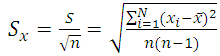
formula9-15

Доверительные границы погрешности результата измерений – наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.

Поправка (англ. correction) – значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности.
Примечание. Знак поправки противоположен знаку погрешности. Поправку, прибавляемую к номинальному значению меры, называют поправкой к значению меры; поправку, вводимую в показание измерительного прибора, называют поправкой к показанию прибора.

Поправочный множитель (англ. correction factor) – числовой коэффициент, на который умножают неисправленный результат измерения с целью исключения влияния систематической погрешности.
Примечание. Поправочный множитель используют в случаях, когда систематическая погрешность пропорциональна значению величины.

Точность результата измерений (англ. accuracy of measurement) – одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения.
Примечание. Считают, что чем меньше погрешность измерения, тем больше его точность.

Неопределенность измерений (англ. uncertainty of measurement) – параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине.

Погрешность метода поверки – погрешность применяемого метода передачи размера единицы при поверке.

Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешность воспроизведения единицы физической величины – погрешность результата измерений, выполняемых при воспроизведении единицы физической величины.
Примечание. Погрешность воспроизведения единицы при помощи государственных эталонов обычно указывают в виде ее составляющих: неисключенной систематической погрешности; случайной погрешности; нестабильности за год.

Погрешность передачи размера единицы физической величины – погрешность результата измерений, выполняемых при передаче размера единицы.
Примечание. В погрешность передачи размера единицы входят как неисключенные систематические, так и случайные погрешности метода и средств измерений.

Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения.

Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения.

Промах – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.
Примечание. Иногда вместо термина промах применяют термин грубая погрешность измерений.

Предельная погрешность измерения в ряду измерений – максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи.

Погрешность результата однократного измерения – погрешность одного измерения (не входящего в ряд измерений), оцениваемая на основании известных погрешностей средства и метода измерений в данных условиях (измерений).
Пример. При однократном измерении микрометром какого-либо размера детали получено значение величины, равное 12,55 мм. При этом еще до измерения известно, что погрешность микрометра в данном диапазоне составляет +/- 0,01 мм, и погрешность метода (непосредственной оценки) в данном случае принята равной нулю. Следовательно, погрешность полученного результата будет равна +/- 0,01 мм в данных условиях измерений.

Суммарное среднее квадратическое отклонение среднего арифметического значения результатов измерений – характеристика S_∑ рассеяния среднего арифметического результатов измерений, обусловленная влиянием случайных и неисключенных систематических погрешностей и вычисляемая по формуле:

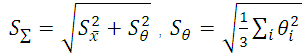
formula9-30

где: — СКО неисключенных систематических погрешностей при равномерном распределении каждой из них.

Суммарные погрешности

Суммарная погрешность средства измерения А равняется арифметической сумме систематической и случайной погрешностей и характеризует наибольшую статическую погрешность средства измерения в исследуемой точке шкалы (ГОСТ 8.009—84 [13]; ГОСТ 8.508—84 [17]).

Отметим, что в разных точках шкалы измерительного устройства

величины А (как и Д_с и А) могут быть различны, поэтому для характеристики устройства в целом рассматривают наибольшую суммарную погрешность Д_т. В этом случае говорят, что погрешность СИ не превосходит величины Д_т.

Аналогично могут быть рассмотрены максимальная систематическая погрешность Д_ст и максимальная случайная погрешность А», как наибольшие погрешности из полученных в различных точках шкалы средства измерений.

Суммарная погрешность, подсчитанная по формуле (4.12), является абсолютной и имеет ту же размерность, что и измеряемая величина.

Кроме абсолютных значений подсчитываются относительная 6 и приведенная у суммарные погрешности:

где x_N — нормирующее значение.

Относительная и приведенная суммарные погрешности обычно выражаются в процентах, но могут выражаться и в виде относительных величин.

Для иллюстрации изложенного (см. рис. 4.2) наряду с другими величинами отложена величина суммарной погрешности.

Поскольку в состав суммарной погрешности входит случайная погрешность, то суммарная погрешность также является случайной величиной. Оценим доверительную вероятность Р, с которой найдена абсолютная суммарная погрешность Д, если доверительная вероятность оценки абсолютной случайной погрешности составляет Р (аналогично могут быть рассмотрены доверительные вероятности относительных и приведенных погрешностей).

Напомним, что систематическая погрешность Д_с — это погрешность, которая остается постоянной при повторных измерениях одной и той же величины. Другими словами, Д_с, по определению, есть постоянная величина и в силу этого имеет доверительную вероятность, равную единице.

Воспользуемся теоремой умножения вероятностей, которая гласит: если сложное событие С состоит из ряда независимых исходов простых событий A_v А₂, . А_п и его осуществление означает одновременное появление всех исходов, то вероятность такого сложного события равна произведению вероятностей исходов (см. работу [34, с. 46]), т.е.

где знак П соответствует логической операции «и».

Независимость исходов при этом означает, что осуществление одного из них не влияет на вероятность осуществления остальных.

В нашем случае выражение (4.15) принимает вид

где Р(Д_с) — доверительная вероятность систематической погрешности (/ > (Д_С) = 1); /’(Л) — доверительная вероятность случайной погрешности; Р (Д) — доверительная вероятность суммарной погрешности.

Таким образом, в рассмотренном случае доверительная вероятность суммарной погрешности численно равна доверительной вероятности случайной погрешности.

Другими словами, с доверительной вероятностью Р абсолютная суммарная погрешность исследованного средства измерения не превосходит величины А.

Соотношения (4.12), (4.13) и (4.14) позволяют оценить значения абсолютной, относительной и приведенной суммарных погрешностей средств измерений.

Полученные значения абсолютной суммарной погрешности А (или относительной 8, или приведенной у суммарных погрешностей) позволяют присвоить исследованному средству измерений тот или иной класс точности (см. подраздел 3.4). Присвоенный класс точности должен соответствовать требованиям ГОСТ 8.401—80 [15].

Отметим, что для решения поставленной задачи по определению численного значения класса точности полученные значения А, или 8, или у округляются до ближайшего большего значения стандартного ряда и являются классом точности данного средства измерений. Например, для СИ, имеющего 8 = ±1,2%, класс точности (L5); для СИ, имеющего у = ±3,2%, класс точности 4,0 и т.д.

Присвоенный класс точности заносится в техническую документацию на СИ. Кроме того, класс точности наносится на шкалы, щитки или корпуса средств измерений в соответствии с требованиями ГОСТ 8.401-80 [15].

Суммирование составляющих погрешности измерения

При суммировании погрешностей применяются три основных способа.

1. Способ арифметического суммирования погрешностей.

Суммарная погрешность вычисляется по формуле

где бу; — суммарная относительная погрешность;

bk — к-я суммируемая относительная погрешность; т — количество суммируемых погрешностей.

Суммирование по данному способу приводит к завышенному по сравнению с действительным значению суммарной погрешности, которое тем больше, чем больше число суммируемых погрешностей т. Поэтому на практике способ применяется при условии т 1 (К = 1,1 при Р = 0,95 и К= 1,4 при Р = 0,99):

Рекомендуется применять этот способ при т> 3.

3. Способ моментов.

Суммарная погрешность вычисляется по одной из формул для оценки погрешности косвенного измерения, когда установлен вид зависимости и вычислены или известны погрешности прямых измерений аргументов.

Данный способ позволяет получить более точное по сравнению с указанными выше способами значение суммарной погрешности:

Если —у «1, то полученное выражение можно упростить, восполь- зовавшись разложением в степенной ряд:

Суммирование систематической и случайной составляющих погрешности производится при определении границ погрешности результата измерения.

В зависимости от соотношения суммарной неисключённой систематической и случайной составляющих погрешности установлено три способа определения границ погрешности результата измерения.

1. Если отношение суммарной неисключённой систематической погрешности к оценке среднего квадратического отклонения результата измерения меньше 0,8, т. е.

то неисключёнными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата измерения равна (доверительной погрешности):

где t — коэффициент Стьюдента или Лапласа, который в зависимости от доверительной вероятности Р и числа результатов наблюдений п находят по таблицам.

то случайной составляющей погрешности по сравнению с систематической пренебрегают и принимают, что

Примечание: погрешность, возникающая из-за пренебрежения одной из составляющих погрешности результата измерения при выполнении указанных неравенств, не превышает 15 %.

3. Если неравенства не выполняются, т. е.

то границу погрешности результата измерения находят путём построения композиции распределений случайных и неисключённых систематических погрешностей, рассматриваемых как случайные величины.

Границу погрешности результата измерения вычисляют по формуле (без учета знака)

где К — коэффициент, зависящий от соотношения случайной и неисклю- ченной систематической погрешностей;

с — оценка суммарного СКО результата измерения.

Коэффициент К вычисляют по эмпирической формуле:

Оценку суммарного СКО результата измерения вычисляют по формуле:

Раздельное представление границ систематической погрешности и СКО результата измерения целесообразно в тех случаях, когда полученный результат используется как промежуточный при нахождении других данных или когда он подвергается анализу или сопоставлению с другими результатами.

Суммарная погрешность по формулам (2.120)—(2.122) представляется в случае, если результат измерения является окончательным и требуется лишь оценить границы зоны той неопределенности, с которой он установлен.