Что такое суммарная скорость

Закон сложения скоростей

В классической механике применяют термин, который звучит, как абсолютная скорость точки. Данная величина является суммой двух векторов: относительная и переносная скорости точки. В подобном равенстве выражена теорема сложения скоростей. Общепринятым положением является равенство скорости движения какого-либо объекта в рамках неподвижной системы отсчета и векторной суммы скорости аналогичного физического тела в условиях относительно подвижной системы отсчета. Данными координатами определяется непосредственное нахождение тела.

Классический закон сложения скоростей определяет, что скорость тела относительно неподвижной системы отсчета представляет собой геометрическую сумму двух скоростей, включая скорость тела относительно подвижной системы отсчета и скорость подвижной системы отсчета относительно неподвижной.

Классический вид, формула расчета

Релятивистским законом сложения скоростей являются соотношения, справедливые для частицы, перемещающейся параллельно относительной скорости систем отсчета:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Соотношение теории имеет следующий вид:

Преобразование координат и времени

Закон сложения скоростей вытекает из физических процессов. Представленное выше соотношение получено в результате преобразований координат и времени. Можно представить частицу, которая в определенное время (t^) зафиксирована в точке с координатами: (x^) , (y^) , (z^) .

Спустя какой-то небольшой промежуток времени (Delta t^) частица переместилась в точку:

В системе отсчета (K^) .

Таким образом, при движении частицы происходят два события. Можно записать следующую формулу:

где ( Delta v^_) представляет собой х компоненту скорости частицы в системе (K^.)

Такие же равенства можно вычислить относительно других компонент. Аналогично координатам преобразуются разности координат и промежутки времени (Delta x) , (Delta y) , (Delta z) . (Delta t) .

Уравнения будут иметь следующий вид:

(Delta x=Delta x^+VDelta t^)

Исходя из составленных формул можно сделать вывод о том, что компоненты скорости той же частицы в системе (К) будут записаны следующим образом:

Уравнение представляет собой закон сложения скоростей. Данную закономерность можно привести в векторный вид:

Координаты в системе (К) и системе (K^) будут параллельны.

Алгоритм решения задач

Существуют правила, которые являются основой механической физики. Исходя из данных соотношений, можно рассмотреть примеры сложения скоростей. Простейшими объектами для объяснения физических законов являются, к примеру, человек и любой перемещающийся в пространстве объект, с которым он прямо или косвенно взаимодействует.

Пример

Можно представить, что человек совершает прямолинейное движение вдоль коридора пассажирского поезда со скоростью пять километров в час. При этом равномерная скорость состава составляет 100 километров в час. Скорость человека, относительно пространства, которое его окружает, будет равна 105 километрам в час. Следует учитывать одинаковое направление перемещения человека и поезда.

В случае, когда направления движения человека и транспорта противоположны, данный принцип также справедлив. Тогда человек будет двигаться относительно окружающего пространства со скоростью 95 километров в час.

При рассмотрении объектов, скорости которых равны, можно сделать вывод, что относительно друг друга они неподвижны. Во время вращения скорость рассматриваемого тела представляет собой совокупность скоростей перемещения тела относительно движущейся поверхности другого объекта.

Решение задач на сложение скоростей выполняется в несколько этапов:

1. Следует начать с выбора тела отсчета, которое связано с неподвижной системой координат.
2. Далее необходимо определить тело отсчета, которое совершает движение по отношению к первому телу, и связать его с подвижной системой координат.
3. Изучение движения тела в двух координатных системах.
4. Запись закона сложения скоростей, относительно конкретных условий задачи.

Задача 1

На примере рассмотрено равномерное движение двух поездов друг за другом. Первый поезд перемещается со скоростью 80 км/ч, а второй — 60 км/ч. Требуется рассчитать, какова скорость второго поезда относительно первого.

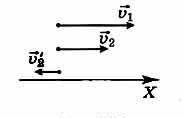
Решение

Следует обозначить скорость первого транспортного средства по отношению к земле с помощью (vec>.)

Тогда скорость второго поезда составит (vec>.)

Исходя из закона сложения скоростей:

где (vec^>) является искомой скоростью второго поезда по отношению к первому.

Такой метод сложения скоростей наглядно представлен на рисунке. Схематично скорость второго поезда по отношению к первому направлена противоположно направлению перемещения поездов, и можно наблюдать удаление второго поезда от первого. Проекция скорости (vec^>) на ось ОХ будет записана таким образом:

Ответ: скорость второго поезда относительно первого составит -20 км/ч

Задача 2

Река течет со скоростью (v = 1,5) м/с. Требуется определить модуль скорости (v_) по отношению к воде. Необходимо учитывать, что в случае движения катера перпендикулярно относительно берега, его скорость составляет (v_=2) м/с.

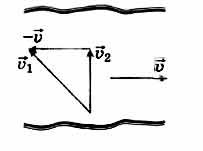
Решение

Исходя из закона сложения скоростей:

Формула для расчета скорости катера относительно реки:

Векторное сложение скоростей представлено на рисунке. На схеме получаем треугольник скоростей с прямым углом, поэтому:

Ответ: модуль скорости (v_) по отношению к воде составляет (2,5) м/с.

Задача 3

Скорость движения самолета относительно воздуха составляет 300 км/ч. Объект движется в северном направлении. При возникновении северо-западного ветра, скорость которого 100 км/ч по отношению к земле, самолет должен сохранить исходное направление. Требуется рассчитать угол, под которым летчик удерживает направление самолета для продолжения пути на север, а также скорость самолета относительно земли.

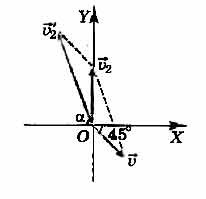
Решение

Необходимо связать неподвижную систему отсчета с землей, а подвижную — с воздухом. Скорость самолета по отношению к земле можно рассчитать, как сумму скорости самолета относительно воздуха и скорость ветра относительно земли. В таком случае, исходя из закона сложения скоростей:

Рисунок демонстрирует направление этих скоростей. Направление скоростей выполнено таким образом, чтобы проекции скорости самолёта относительно ветра и скорости ветра на оси ОХ равнялись по модулю и были направлены противоположно:

Если рассматривать проекцию на ось ОУ, то уравнение примет такой вид:

В таком случае, искомая скорость самолета составит:

Данное равенство позволит определить угол α:

Подставив числовые характеристики, получим:

Найти (sin alpha) можно таким образом:

Скорость самолета относительно земли составит:

Ответ: угол, под которым летчик удерживает направление самолета для продолжения пути на север, равен (76^) ; скорость самолета относительно земли примерно равна 220 км/ч.

Кинематика точки и твердого тела. Часть 2

Как выглядят законы различных видов движения? Как найти скорость движения и другие характеристики? Все эти вопросы будут обсуждаться в этой статье.

План урока:

Закон сложения скоростей

Как уже упоминалось в предыдущем уроке, скорость тела зависит от выбранной наблюдателем системы отсчета. Разберем следующий пример: в безветренную погоду пчела летит со скоростью относительно земли. Это будет собственная скорость пчелы. Затем погода меняется и начинает дуть ветер, перпендикулярный скорости пчелы. Скорость ветра обозначена (см. рисунок 1).

Рисунок 1 – Первоначальная скорость пчелы и ветра

Естественно, что ветер начнет сдувать пчелу с первоначального курса. Собственная скорость не изменяется, так как это характеристика самой пчелы, но ее скорость относительно земли (по модулю и направлению) изменится и станет (см. рисунок 2):

Рисунок 2 – Изменившаяся скорость пчелы

Систему отсчета, связанную с землей, можно считать неподвижной. Если же рассматривать движение пчелы относительно воздуха, можно говорить о движущейся со скоростью v₂ системе отсчета.

Рисунок 3 – Векторы скорости и перемещений при движении пчелы при ветре

Мгновенная скорость, направление мгновенной скорости

Средняя скорость. Средняя путевая скорость

Так как в реальной жизни тела редко движутся с постоянной скорость, но необходимо как-то описывать их движение и скорость, ввели понятие мгновенной скорости.

Мгновенная скорость – это скорость тела в выбранный конкретный момент времени.

Если по определению скорости разделить перемещение на суммарное время пути, можно получить средняя скорость:

Фактически, это та же формула, которая используется при расчетах для прямолинейного равномерного движения.

То есть средняя скорость движения – это такая скорость, с которой тело должно было бы двигаться, если бы оно перемещалось из начальной точки в конечную равномерно и прямолинейно. Из выражения для вычисления средней скорости можно увидеть, что средняя скорость сонаправлена вектору перемещения.

Касательно же мгновенной скорости, чтобы ее найти, необходимо разделить общее время Δt на одинаковые отрезки Δt₁, Δt₂,…Δt_n, и найти средние скорости за эти отрезки времени:

А куда направлена мгновенная скорость? Из рисунка 5 видно, что при уменьшении отрезков времени Δt_b направление вектора перемещения ему соответствующее постепенно приближается к направлению касательной к траектории. Значит, мгновенная скорость направлена по касательной к линии траектории.

Еще одна важная характеристика, использующаяся в кинематике – средняя путевая скорость. Из названия вытекает, что средняя путевая скорость – это отношение пути (S), пройденного телом, к отрезку времени (t), за которое оно этот путь прошло:

Именно о путевой скорости идет речь, когда говорят, что автомобиль ехал из одного города в другой со скоростью 70 км/ч, например.

Ускорение. Касательное ускорение. Центростремительное ускорение

Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.

Единицы измерения ускорения:

Рисунок 6 – Тело перемещается из точки 1 в точку 2 (в верхнем правом углу дана иллюстрация к разности векторов)

Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить на маленькие отрезки времени и рассматривать ускорение на каждом из них.

Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).

Рисунок 7 – Полное, касательно и центростремительное ускорение тела, движущегося из точки 1 в точку 2

Равноускоренное движение

Прямолинейное равноускоренное движение. Определение скорости при равноускоренном движении. Уравнения движения при равноускоренном движении

Когда движение тела происходит с постоянным по модулю и направлению ускорением, такой тип движения называют равноускоренным. Для него справедливо выражение:

Частный случай равноускоренного движения – прямолинейное равноускоренное движение. Как следует из названия, это движение вдоль прямой линии с постоянным ускорением.

При условии, что ускорение сонаправлено начальной скорости, формула для вычисления скорости при прямолинейном равноускоренном движении записывается в скалярном виде:

Если же ускорение противонаправлено начальной скорости, это выражение станет таким:

Рассмотрим график зависимости скорости от времени при равноускоренном движении (см. рисунок 8). Считаем, что тело совершает движение вдоль оси ОХ, а все величины – начальная скорость (v_ox) , ускорение (a_x) – взяты в проекции на эту ось.

Рисунок 8 – График зависимости скорости от времени при прямолинейном равноускоренном движении

Как известно из предыдущего курса физики, путь, который прошло тело, можно найти как площадь фигуры под графиком зависимости скорости движения от времени. Общую площадь под графиком можно найти как сумму площадей прямоугольника ABCD и треугольника ADE.

Свободное падение

Движение тела, брошенного вертикально вверх. Движение тела, брошенного под углом к горизонту. Криволинейное равноускоренное движение

Примерами движения с постоянным ускорением может служить свободное падение, движение брошенного вертикально вверх тела, движение тела, брошенного под углом к горизонту. Поговорим об этих видах движения подробнее.

• Свободное падение

Представим, что какое-то небольшое, но тяжелое тело подняли на высоту h, а затем отпустили (см. рисунок 9).

Рисунок 9 – Свободное падение тела

Тело начнет падать. Принимаем допущение, что на это тело воздействует одна только сила тяжести (силой сопротивления воздуха и силой ветра пренебрегаем). Тогда тело будет двигаться вертикально вниз, а его ускорение будет равняться ускорению свободного падения:

• Движение тела, брошенного вертикально вверх

Представим, что тело подкинули вертикально наверх с начальной скоростью v₀ (см. рисунок 10).

Рисунок 10 – Тело бросили вертикально вверх

Очевидно, что тело сначала будет лететь вверх, постепенно замедляясь, пока его скорость не уменьшится до нуля. Затем тело полетит вниз, постепенно ускоряясь. Получается, что максимальной своей скорости тело будет достигать два раза – у земли, и эта скорость будет равно начальной скорости v₀ (вообще нужно было бы писать v_oy, но так как рассматривается движение вдоль только одной оси OY, опустим индекс y).

Отсюда можно найти полное время полета:

• Движение тела, брошенного под углом к горизонту

Данный тип движения чуть сложнее, чем предыдущие два, так как придется рассматривать движение сразу вдоль двух осей OX и OY (см. рисунок 11). Этот тип движения относится к криволинейному равноускоренному движению. Будем считать, что тело подбросили с начальной скоростью под углом α к горизонту.

Рисунок 11 – Тело брошено под углом к горизонту

Уравнения движения в общем виде по двум осям выглядят так:

Еще время полета можно посчитать, учитывая что в двух моментах – в начале полета и в конце. Значит можно посчитать:

Равномерное движение точки по окружности

Центростремительное ускорение

Представим себе равномерное движение по окружности: во время этого типа движения скорость не меняется по модулю, однако меняется по направлению (см. рисунок 12).

Рисунок 12 – Изменение направления скорости при равномерном движении по окружности

За изменение направления скорости отвечает центростремительное ускорение ( Оно, так же как и скорость, постоянно по модулю, но меняется по направлению – в любой точке окружности оно направлено к ее центру. Центростремительное ускорение можно найти по формуле:

Как рассчитывается скорость при лобовом столкновении автомобилей?

Несомненно, любое ДТП – это крайне неприятное происшествие, которое нередко заканчивается трагедией. Однако, как бы ни хотелось сторонам побыстрее все забыть, в любом случае, необходимо определить виновника и оценить причиненный ущерб. Помочь в выполнении такой задачи может правильная классификация вида ДТП и воссоздание общей картины событий, частью которой является скорость движения обоих автомобилей.

Расчет скорости, и как происходит лобовое столкновениеРаспространенные причины лобовых столкновений автомобилейКак избежать лобового столкновенияЧто делать, если столкновения не избежать

Расчет скорости, и как происходит лобовое столкновение

Многие автолюбители считают, что при столкновении двух машин лоб в лоб их скорости суммируются, и конечный результат окажется таким же, как при столкновении одного автомобиля на суммарной скорости об бетонную стену.

То есть предположим, что два транспортных средства перед столкновением двигались со скоростью 65 км/ч каждое, но будет ли это означать, что один такой автомобиль, врезавшийся на скорости 130 км/ч в бетонную стену, получит такие же повреждения, как и машины в предыдущем варианте? Складываются ли скорости при лобовом столкновении? Давайте попытаемся разобраться в этом вопросе.

При столкновении транспортных средств все происходит буквально за считанные секунды, в течение которых каждый из автомобилей деформируется, либо полностью разрушается. Основными факторами, влияющими на силу разрушений, выступает конструкция машин и их скорость, а по линии удара действует ударный импульс. Направленность этой линии в процессе столкновения зависит от направления и скорости перемещения двух тел. Если транспортные средства передвигались на разных скоростях, то и линия удара пройдет под меньшим углом по отношению к оси машины, движущейся с большей скоростью.

В то же время, рассматривая столкновение транспортного средства с каким-либо препятствием, в этом процессе можно выделить два последующих этапа: момент соприкосновения (считается до момента максимального сближения) и момент перемещения транспортного средства, который длится до самого разъединения автомобилей. Первый этап характеризуется частичным переходом кинетической энергии движения в потенциальную тепловую энергию, энергию упругой деформации и т.д. С началом второго этапа, полученная потенциальная энергия деформации снова трансформируется в кинетическую энергию транспортного средства. Если же речь идет о неупругих телах, то удар закончится уже на первом этапе.

Даже если предположить, что машина двигалась с небольшой скоростью, ее кинетическая энергия будет достаточно большой, а удар в неподвижную стену с большой массой приведет к поглощению всей его энергии. Прочная и жесткая стена почти не деформируется.

Конечно, нельзя сказать, что удар о каменную стену будет полностью идентичным столкновению двух одинаковых легковых машин. К примеру, если одно транспортное средство движется быстрее другого, то суммарная энергия, выделяемая при столкновении, будет меньше аналогичного показателя в предыдущем случае. Более легкий автомобиль или транспортное средство, передвигающееся с меньшей скоростью, получит больше энергии, чем та, которую они имели до момента столкновения. То есть, выясняя, суммируется ли скорость при лобовом столкновении, необходимо понимать, что прибавить необходимо не этот показатель, а импульсы – сочетание скоростей и масс.

Энергия тратится на деформацию (сопровождается выделением тепла) и упругую деформацию с изменением импульса (скорости по модулю направления). Баланс данных деформаций определяется начальными условиями ДТП, а конечный результат исходит из баланса происходящих деформаций. Таким образом, происходит гашение импульсов.

Распространенные причины лобовых столкновений автомобилей

Если вас интересует, как можно избежать лобового столкновения, тогда нелишним будет знать о возможных причинах, которые приводят к подобной неприятности. Так, в большинстве случаев столкновение транспортных средств является результатом обгона с выездом на полосу встречного движения, объезда разных препятствий (в том числе и других припаркованных автомобилей), пересечения перекрестков (в особенности кольцевых), а также следствием опережения с перемещением в крайнюю левую полосу и перестроения.

Также нельзя не вспомнить и о превышении скоростного режима, что также является частой причиной создания аварийных ситуаций на дорогах. Такое поведение особенно опасно, если автомобилист не владеет основными навыками вождения, вследствие чего машина может опрокинуться (особенно актуально для условий гололеда).

Обратите внимание! Согласно информации, предоставляемой ГИБДД, большая часть лобовых столкновений происходит именно в зимний период, когда поверхность дороги покрывается ледовой коркой, а водители оказываются неподготовленными к подобным погодным условиям.

Нередко первопричиной ДТП также становится излишняя самоуверенность водителей. Решившись обогнать движущееся впереди транспортное средство, далеко не все автомобилисты правильно оценивают скорость автомобиля, едущего по встречной полосе, и попутных транспортных средств. Кроме того, из поля их зрения исчезают различные оптические эффекты, возникающие в результате ограниченной видимости и плохих дорожных условий.

Частой причиной лобовых столкновений автомобилей можно назвать и усталость водителя, который просто засыпает за рулем и несознательно направляет свое транспортное средство на полосу встречного движения. Такое нередко случается с водителями габаритных фур, а понять, что человек спит за рулем, можно, исходя из динамики разгона машины на встречной полосе и траектории ее движения.

Интересно знать! Зарубежное издание «Форбс» называет основной причиной лобовых аварий пьянство водителей. Не секрет, что даже небольшое количество алкоголя в крови человека заметно снижает его реакцию на все происходящее, из-за чего в той же Америке происходит половина всех аварий на дорогах.

Что касается отечественных автолюбителей, то можно с уверенностью сказать, что это далеко не единственное основание для роста аварийных ситуаций на дорогах. Водитель может потерять контроль над управлением автомобиля и вследствие заноса, блокировки руля или выезда на плохой участок дороги.

Как избежать лобового столкновения

Так как же уйти от лобового столкновения на трассе, если на вас несется неуправляемый автомобиль? Главное – это постараться избежать удара лоб в лоб, поскольку в таком случае повреждения автомобиля и травмы пассажиров часто оказываются более значительными, чем при других вариантах столкновений (например, при ударе по касательной). Поэтому, первое, что нужно сделать в непредвиденной ситуации – это сбросить скорость и постараться затормозить и только после этого начинать действовать рулем.

Однако, если вы видите, что лобовое столкновение все равно неминуемо, лучше направить авто в сторону от дороги. В любом случае, въезд в кустарник, кювет или сугроб будет менее опасным, чем встреча с встречным транспортом (конечно, больших деревьев, столбов или стен также лучше избегать).

Важно! При лобовом ударе подушки безопасности не срабатывают, поэтому единственное, что может спасти водителя и пассажиров – это ремень безопасности.

Кроме того, как только вы заметили, что встречное авто выехало из своей полосы движения и оказалось практически рядом с вашей машиной, лобовому удару лучше предпочесть касательное столкновение с попутным транспортным средством. Этот совет актуален и для ситуаций, когда на дороге появляется неожиданное препятствие (например, крупное животное), и у вас нет возможности уйти от встречи с ним.

Достаточно большое количество тяжелых или даже смертельных травм появляются вследствие ударов в боковые части транспортного средства. В том случае, когда вы не сразу заметили приближающийся сбоку автомобиль, а остановка собственного транспортного средства точно приведет к столкновению, постараться уйти от него можно и с помощью увеличения скорости. Нужно понимать, что попытка предотвращения лобового столкновения с одним автомобилем всегда может закончиться встречей с другим.

Знаете ли Вы? Согласно официальной статистике ГИБДД России, за первое полугодие 2016 года (с января по июнь) в ДТП погибло больше 8 000 человек, а причиной 34,3 тыс. аварий стало низкое качество дорожного покрытия. В сравнении с прошлым годом, рост подобных ДТП составил 7,8%.

Что делать, если столкновения не избежать

Из-за растерянности многие водители не успевают вовремя среагировать на появившуюся опасность, и часто предпринимать какие-либо действия для ухода от столкновения с летящим на вас автомобилем уже поздно.

Что же делать при лобовом столкновении? На самом деле вариантов у вас немного, и помимо уже описанных действий, основным из которых является попытка ухода от удара лоб в лоб, все, что вам остается, – это предупредить остальных участников дорожного движения об аварийной ситуации. Вполне вероятно, что звуковой или световой сигнал подействует и на водителя встречного транспортного средства, выводя его из ступора. Так, раздающийся в такие моменты громкий сигнал действует как раздражитель, способный привести в чувство растерявшегося или усталого человека.

Однако, если несущийся на вас водитель потерял контроль над своим транспортным средством, то таким образом вы только сможете предупредить остальных водителей о неизбежной аварии, хотя и это уже немало.

Хорошо, если в критической ситуации вы оказались пристегнуты ремнем безопасности, но если это не так, постарайтесь быстро лечь набок, перебравшись на пассажирское сиденье – это избавит вас от опасных травм от летящих предметов. Пристегнутому водителю также необходимо закрыть руками лицо, что поможет защитить глаза и лицо от осколков разбитого стекла, а также быстро убрать ноги с педалей (так вы убережете себя от серьезных переломов стоп и голеней).

Как бы там ни было, но в любой ситуации стоит сохранять спокойствие и не поддаваться панике. Только так вы сможете сориентироваться и сделать все возможное, чтобы максимально снизить возможность получения повреждений.

Обратите внимание! Разговор по мобильному телефону в процессе управления транспортным средством увеличивает риск аварийной ситуации в четыре раза, а если водитель еще и сообщения додумался набирать, то вероятность получения повреждений при лобовом столкновении увеличивается в целых шесть раз. Скорость реакции водителя в такой ситуации снижается на 9% и 30% соответственно.

Лобовое столкновение

Среди автомобилистов не первый год бытует мнение, что лобовое столкновение машин является особенно опасным из-за того, что при ударе их скорость суммируется – именно из-за этого выжить в такой аварии и не получить серьезных увечий крайне тяжело. Но так ли это на самом деле? Постараемся разобраться с данным вопросом, рассматривая его с точки зрения обычной физики из школьного курса.

Кратко самое интересное

Машины получат больше повреждений при лобовом ударе?

Нет, повреждения будут такими же, как при ударе любой из них о неподвижное препятствие.

Почему это происходит?

Хотя суммарная скорость будет выше, но её приходится делить пополам, вычисляя количество кинетической энергии – общая масса автомобилей также возросла вдвое.

Можно ли уменьшить силу удара?

Это достигается благодаря деформации автомобиля – большинство современных повреждаются довольно легко, эффективно гася удар.

Складываются ли скорости при лобовом столкновении автомобилей?

Казалось бы, все довольно логично – если два одинаковых автомобиля едут со скоростью 50 километров в час и столкнутся лоб в лоб, причем столкновение будет четко выверенным – без малейших углов отклонения – то и скорость движения обоих нужно складывать – получится 100 км/ч. Однако на практике этого не происходит. Специально для наглядности ведущие программы «Разрушители легенд» устроили эксперимент, в ходе которого доказали, что автомобиль, сталкиваясь с неподвижной преградой, получает точно такие же разрушения, как при ударе о другую машину, движущуюся навстречу. Почему? Постараемся разобраться.

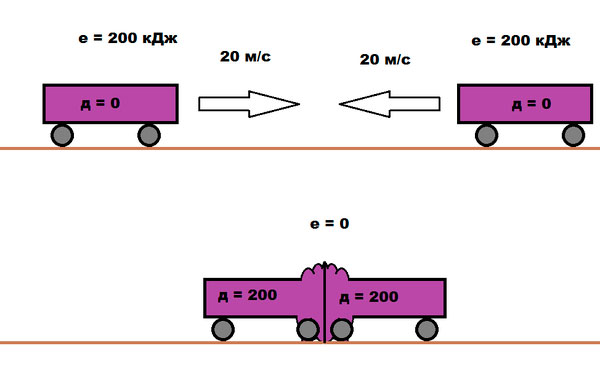
Самое простое объяснение – двойная деформация. Она крайне важна, так как во многом удар по машине и пассажирам зависит от ускорения – в данном случае отрицательном, ведь скорость падает с 50 километров до нуля. При этом автомобиль проходит считанные десятки сантиметров – именно столько, сколько позволяет деформированная передняя часть. То есть, при ударе об стену автомобиль деформируется, грубо говоря, на 50 сантиметров. Именно за это расстояние гасится скорость до полного нуля.

Что же изменится, если вместо стены взять другой автомобиль? По сути – ничего! Да, каждая из машин двигалась со скоростью 50 км/ч. Они врезались друг в друга лоб в лоб. Скорость каждой упала до нуля. Но ведь деформировались они одинаково – каждая на 50 сантиметров! То есть, кинетическая энергия поглощается уже не одним автомобилем, а двумя. Благодаря этому скорость гасится точно так же, как в первом примере. И импульс практически не изменится. Также не стоит забывать, что повреждения люди получают вовсе не из-за деформации автомобиля, а именно из-за резкого отрицательного ускорения.

Вполне очевидно, что суммировать следует вовсе не скорость двух автомобилей, а ту энергию, которой они обладают. Она находится по простой формуле – скорость умноженная на массу. То есть, скорость тоже влияет на количество повреждений. Но и масса имеет не меньшее значение. И хотя энергия при лобовом ударе складывается, но два автомобиля, едущих со скоростью в 50 км/ч получат вовсе не такие повреждения, как один, врезавшийся в неподвижную стену на скорости 100 км/ч.

Так что, суммировать скорости при лобовом столкновении однозначно не нужно – это выдает элементарное незнание школьного курса физики и в первую очередь третьего закона Ньютона – сила действия равна силе противодействия, но они имеют противоположное направление.

Что будет, если врезаться в неподвижную машину?

Ещё один интересный вопрос, вытекающий из первого. С одной стороны – по логике, если машина не двигалась, то есть, скорость была равна нулю, то и особых повреждений она получить не должна, когда в неё врежется другая. Практика же показывает совершенно обратное.

Дело в том, что в момент столкновения движущаяся машина передает часть импульса неподвижной. То есть, ускорение резко увеличивается, что и приводит к серьезным повреждениям автомобиля и травмам пассажиров.

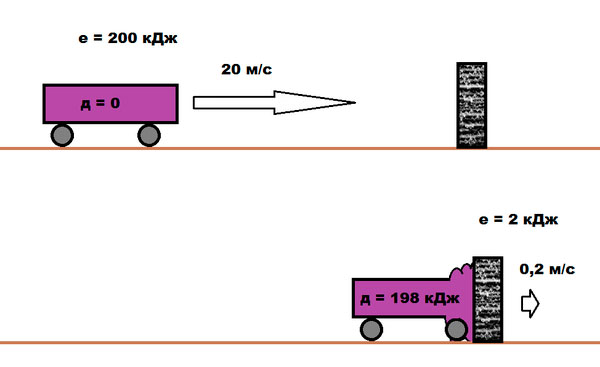
С другой стороны, для водителя и пассажиров движущейся машины это куда предпочтительнее, чем удар о неподвижную стену. Ведь последняя останется не деформированной и устоит на месте. То есть, весь импульс придется на движущуюся машину, а значит и повреждения будут куда более серьезными. При ударе же о неподвижную машину деформируются уже обе, что снижает повреждения первой. К тому же, часть энергии удара уходит на то, чтобы сдвинуть неподвижную машину, а значит, количество кинетической энергии уменьшается.

Отдельно стоит отметить, что одна машина воздействует на другую с силой, вычисляемой по формуле F=m*a – второй закон Ньютона. То есть, масса крайне важна. Именно из-за этого шансы на выживание у пассажиров легкового автомобиля, столкнувшегося с фурой или грузовиком, довольно низки. Даже если грузовик едет довольно медленно – около 20-30 км/ч, а легковой автомобиль мчится около 100 км/ч, повреждения последнего будут ужасающими. И здесь играет роль уже не скорость грузового автомобиля, а его большая масса и практически полное отсутствие деформации. Это в сумме и приводит к тому, что в легковой автомобиле при такой аварии пассажиры выживают довольно редко.

Что сделать, чтобы снизить опасность?

Пожалуй, самый простой способ обеспечить высокую выживаемость пассажиров и водителя – увеличить деформационную способность автомобиля. Да-да, именно поэтому многие современные машины смотрятся настолько хлипкими по сравнению со старыми, выпущенными 40-60 лет назад. Скорость возрастает, поэтому приходится пожертвовать прочностью, чтобы хоть как-то снизить риск серьезных травм и смерти. Причем, чем длиннее передняя часть (по крайней мере, это актуально при лобовом столкновении), тем безопаснее пройдет удар для людей, сидящих внутри.

Для примера рассмотрим две машины – у одной передняя часть (сминаемая) имеет длину в 50 сантиметров, а у другой – 150. Пренебрежем погрешностями и допустим, что передняя часть сминается полностью. То есть, пассажиры первой машины сбросят скорость с 50 км/ч до нуля за 0,5 метра, а второй – за 1,5 метра. Разумеется, ускорение здесь будет совершенно разным. А значит и перегрузки сильно отличатся – риск получить травмы резко снижается.

Сложное движение точки. Теорема Кориолиса

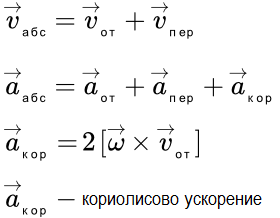
Определение сложного (составного) движения точки. Определение абсолютного, относительного и переносного движения, скорости и ускорения. Доказательство теоремы о сложении скоростей и теоремы Кориолиса о сложении ускорений. Кориолисово (поворотное) ускорение.

Здесь мы покажем, что при сложном движении, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где – кориолисово ускорение.

Пример применения изложенной ниже теории приводится на странице “Сложное движение точки. Пример решения задачи”.

Сложное (составное) движение точки

Часто встречаются случаи, когда точка совершает известное движение относительно некоторого твердого тела. А это тело, в свою очередь, движется относительно неподвижной системы координат. Причем движение точки относительно тела и закон движения тела относительно неподвижной системы координат известны или заданы. Требуется найти кинематические величины (скорость и ускорение) точки относительно неподвижной системы координат.

Такое движение точки называется сложным или составным.

Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.

Далее, для ясности изложения, будем считать, что подвижная система координат жестко связана с некоторым твердым телом. Мы будем рассматривать движение точки относительно тела (относительное движение) и движение тела относительно неподвижной системы координат (переносное движение).

Относительное движение точки при сложном движении – это движение точки относительно тела (подвижной системы координат) считая, что тело покоится.

Переносное движение точки при сложном движении – это движение точки, жестко связанной телом, вызванное движением тела.

Абсолютное движение точки при сложном движении – это движение точки относительно неподвижной системы координат, вызванное движением тела и движением точки относительно тела.

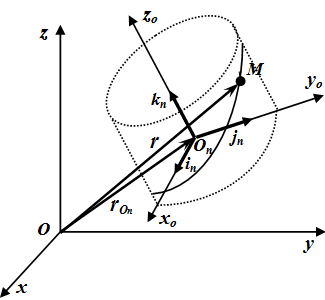
Пусть Oxyz – неподвижная система координат, O_n x_o y_o z_o – подвижная система координат, жестко связанная с телом. Пусть – единичные векторы (орты), направленные вдоль осей x_o , y_o , z_o подвижной системы координат. Тогда радиус-вектор точки M в неподвижной системе определяется по формуле:
(1) ,
где – радиус-вектор точки O_n – начала подвижной системы координат, связанной с телом.

Относительная скорость и ускорение

При относительном движении изменяются координаты x_o , y_o , z_o точки относительно тела. А векторы являются постоянными, не зависящими от времени. Дифференцируя (1) по времени, считая постоянными, получаем формулы для относительной скорости и ускорения:
(2) ;
(3) .

Относительная скорость точки при сложном движении – это скорость точки при неподвижном положении тела (подвижной системы координат), вызванная движением точки относительно тела.

Относительное ускорение точки при сложном движении – это ускорение точки при неподвижном положении тела, вызванное движением точки относительно тела.

Переносная скорость и ускорение

При переносном движении изменяются векторы , определяющие положение тела. Относительные координаты точки x_o , y_o , z_o являются постоянными. Дифференцируя (1) по времени, считая x_o , y_o , z_o постоянными, получаем формулы для переносной скорости и ускорения:
(4) ;
(5) .

Переносная скорость точки при сложном движении – это скорость точки, жестко связанной с телом, вызванная движением тела.

Переносное ускорение точки при сложном движении – это ускорение точки, жестко связанной с телом, вызванное движением тела.

Производные по времени от – это скорость и ускорение начала подвижной системы координат O_n : ; .

Найдем формулы для производных по времени от векторов . Для этого возьмем две произвольные точки твердого тела A и B . Их скорости связаны соотношением:

(см. страницу “Скорость и ускорение точек твердого тела”). Рассмотрим вектор , проведенный из точки A в точку B . Тогда
.
Дифференцируем по времени и применяем предыдущую формулу:
.
Итак, мы нашли формулу для производной по времени от вектора, соединяющего две точки тела:
.
Поскольку векторы жестко связаны с телом, то их производные по времени определяются по этой формуле:
(6) , , .

Подставляем в (4):

.
Таким образом, выражение (4) приводит к формуле для скорости точек твердого тела.

Выполняя подобные преобразования над формулой (5), получим формулу для ускорения точек твердого тела:
,
где – угловое ускорение тела.

Абсолютная скорость и ускорение

При абсолютном движении изменяются как векторы , определяющие положение тела, так и относительные координаты точки x_o , y_o , z_o .

Абсолютная скорость точки при сложном движении – это скорость точки в неподвижной системе координат.

Абсолютное ускорение точки при сложном движении – это ускорение точки в неподвижной системе координат.

Теорема о сложении скоростей

При составном движении абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.

Доказательство

Дифференцируем (1) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (2) и (4).
(1) ;
(7)
.

Теорема Кориолиса о сложении ускорений

При составном движении абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где
– кориолисово ускорение.

Доказательство

Дифференцируем (7) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (3) и (5).
(7) .

.

Что такое суммарная скорость

Разговоры на общие автомобильные темы всех участников форумов

• Перейти на страницу:

Сообщения: 322 Зарегистрирован: 20 май 2008, 00:00 Награды: 1

Рейтинг: 11 537

Репутация: +11

Сложение скоростей при ДТП. Да или нет? Тема №2

Сообщение sergey987 » 14 фев 2015, 23:31

air007 писал(а): Закон физики, сила действия равна силе проитводействия. Соотвественно не будет 80+80, будет просто 80 и как в стену (грубо гря) Тут еще деформация металла смягчила удар

Да. А вот если 0+80 (т.е. одна машина стоит), то будет 40 как в стену.

Сообщения: 42 Зарегистрирован: 15 янв 2010, 00:00 Награды: 1

Рейтинг: 48

Репутация: 0

Сообщение wer82 » 18 фев 2015, 13:38

Сообщения: 157 Зарегистрирован: 08 фев 2011, 00:00 Награды: 1

Рейтинг: 407

Репутация: 0

Сообщение max72rus82 » 18 фев 2015, 14:19

Господа, я с вас удивляюсь. Обсуждаем физику, а до сих пор в топике не было ни одной формулы, одни пространные рассуждения. Физика — точная наука, любое утверждение нужно подтверждать формулами. Основной закон, который нужно применять при рассмотрении этой ситуации — закон сохранения энергии. Для удобства будем измерять все величины в метрической системе.
Итак, едут друг другу навстречу 2 автомобиля каждый весом в 1500 кг со скоростью 72 км/час, т.е. 20 метров в секунду (м/c) Затем они сталкиваются друг с другом точно лоб в лоб, после чего останавливаются. Вся энергия удара была поглощена корпусами автомобилей. Сколько было этой энергии? Считаем по формуле кинетической энергии, т.е. mv-квадрат пополам mv*v/2 Итак, каждый автомобиль принёс с собой в точку столкновения энергию 1500*20*20=600 000 Джоулей (Дж). Эта энергия распределилась между ними равномерно, т.к. у них равные массы. Итак, каждый автомобиль был вынужден поглотить своим корпусом 600 кДж. Другой случай. Автомобиль врезается в абсолютно неупругую бетонную стену с той же скоростью 20 м/c. Сколько энергии будет вынужден поглотить его корпус? Да ровно столько же, т.е. кинетическую энергию mv-квадрат пополам, а именно 600 кДж. Вывод — при столкновении двух одинаковых автомобилей на равной скорости удар будет равноценен удару в абсолютно неупругую бетонную стену. Скорости не складываются

Другое дело, что столкновение на скорости 72 км/час с бетонной стеной — это на самом деле очень много, такие случаи в практике бывают очень редко. Посчитаем, насколько это опасно для человека. Здесь можно применить другую формулу — расчет предельного ускорения. Примем, что после столкновения автомобиль движется равнозамедленно, и капот у него сминается ровно на 1 метр. Формула расчета пути при равнозамедленном движении выглядит так S=v*v/2a Если S (путь) у нас равен 1 метр, то ускорение будет, как нетрудно посчитать, 200 метров на секунду в квадрате, а это более чем 20*g, т.е. 20-кратная перегрузка. Понятно, что такую перегрузку не выдержит ни один космонавт. Выводы — столкновение с бетонной стеной скорости 72 км/час смертельно, и столкновение со встречным автомобилем на такой скорости также смертельно. Но такие прямые лобовые столкновения бывают нечасто. Если автомобили стукаются немножко вскользь, то картина уже совсем другая. Тут действует формула S=(v*v)-(v0*v0)/2a , т.е. кинетическая энергия меньше на скорость «отскока» от точки столкновения.

Из этих формул вытекает ещё один вывод — с увеличением скорости кинетическая энергия растёт квадратично, а не линейно. Если в предыдущей задачке предположить, что автомобиль двигался со скоростью 36, а не 72 км/час, то перегрузка будет не двадцать «же», а всего лишь пять «же», а это уже вполне переносимая перегрузка для человека.

Ещё очень важное значение, как уже было отмечено некоторыми форумчанами, имеет величина сминаемого пространства. Если в условиях предыдущей задачки предположить, что сминаемое пространство не 1 метр, а полметра, то и перегрузки будут вдвое сильнее. Именно поэтому столкновение в рамных прочных автомобилях зачастую опаснее, чем в деформируемых.

Сообщения: 686 Зарегистрирован: 28 сен 2014, 00:00

Рейтинг: 3 686

Репутация: +8

Сообщение Peshik70 » 18 фев 2015, 14:37

Ну и осталось для полноты картины рассмотреть столкновение с неподвижным автомобилем такой же массы. В отличие от удара в бетонную стенку и от удара во встречный автомобиль энергия удара поделится пополам между этими двумя автомобилями (в идеальных условиях, конечно). Соответственно, на каждый авто придётся в два раза меньше поглощённой энергии, чем при первых двух случаях. Поэтому таки лобовое столкновение опаснее, чем удар в неподвижное авто.

Краш-тесты, суммарная скорость при столкновении

вот прям не ожидал от нормального журнала этого бреда про 120 км/ч. Когда они выпустили анонс статьи в инстаграмме им там тоже много комментариев прилетело, что никакими 120 км/ч там даже не пахнет. Но авторевю зачем то стоит на своём.
Очень уважительно отношусь к журналу, но тут прям не понятно что. Глупость, желание словить хайп или что то ещё.

Jettaвод

Moderator

Песня о встречном

PavelRM

Профессиональный советчик

Пока не смотрел, но в заголовке явно указано, что это суммарная скорость 120. Я так понял там машина ехала 60 и барьер 60. Так что всё правильно.

Беляш

Профессиональный советчик

это правильно для броского заголовка. По сути это тоже самое, что рапид врезается в неподвижное препятствие на скорости 60 км/ч. То есть если так смотреть в тесте ничего не изменилось.
Это не значит, что АР плохие — наоборот они молодцы, что активно двигают вопрос безопасности.

OldCoder

Мастер-советчик

Не соглашусь с Вами. «Телега» тоже имеет энергию, которая куда-то должна деться. Так что говорят про удвоенную энергию они все правильно. Но есть и существенное отличие от «реальной жизни» — в большинстве случаев встречный автомобиль тоже деформируется, поглощая энергию удара, а вот «телега», насколько я могу судить по видео, как-то не очень. То есть получился вариант, как будто Поло прилетает примерно на 100-110 км/ч в неподвижное препятствие.
Так что задумка в целом неплохая, но никакой революционности или «правды жизни» в ней не вижу.

Nikonist

Профессиональный советчик

В статье написано что и почему и как распредкляются энергии. Там не так всё просто в первую очередь из-за деформируемого баръера. Заголовок тоже считаю неудачным, хотели хайпануть, но в результате теперь их самих потопят и никто разбираться не будет.

Nikonist

Профессиональный советчик

Так-то всё так, только даже 2 автомобиля одинаковой массы движущиеся на скорости 60 км/ч обладают вдвое меньшей энергией, чем один автомобиль такой же массы на 120 км/ч. Поэтому и последствия будут разные. Всё эти релятивистские сложения скоростей в заголовке это всё же неправильно

Nikonist

Профессиональный советчик

По сути это тоже самое, что рапид врезается в неподвижное препятствие на скорости 60 км/ч. То есть если так смотреть в тесте ничего не изменилось.

Нет, там будут разные энергии, как раз из-за тележки с деформируемым баръером. Доберусь до компа выложу выдержку из статьи, возможно станет понятнее, хотя Ютубу это не помогло

Nikonist

Профессиональный советчик

Сохранение энергии​

Помните, как высчитывается кинетическая энергия? Правильно, по формуле Е = 0,5mV2. То есть зависимость от массы — прямо пропорциональная, но от скорости уже квадратичная. Кинетическая энергия машины массой 1400 кг, которая едет со скоростью 50 км/ч, — 135 килоджоулей. Если автомобиль врезается в жесткий барьер, как было при наших ранних краш-тестах, то около 32 кДж уйдет в энергию отскока и тепло при трении, а кузов автомобиля при деформации должен будет поглотить оставшиеся 103 кДж.
Теперь разгоняем автомобиль до 64 км/ч — и направляем в деформируемый барьер. Кинетическая энергия машины возрастает до 231 кДж. Но алюминиевые соты поглощают 90 кДж, а потери на отскок и трение увеличиваются до 36 кДж. То есть на саму машину остается 105 кДж — всего на 2 кДж больше, чем при 50 км/ч и абсолютно жесткой стенке.
А теперь посчитаем расклад при нашем новом ударе. Суммарная кинетическая энергия Polo и 1400-килограммового барьера аж 389 кДж! Вычитаем 90 кДж, которые берет на себя деформируемый барьер, и еще 62 кДж на отскок и трение. Получается, что силовой структуре кузова Polo нужно поглотить оставшиеся 237 кДж. В 2,3 раза больше, чем при старом краш-тесте на 64 км/ч!
Вот почему сам удар был скоротечнее и намного жестче: пиковое замедление левого порога Polo вместо привычных 30—35g составило 64g. Если переводить это в привычные понятия, то такое испытание с тележкой на суммарных 120 км/ч эквивалентно удару о деформируемый барьер на 78—80 км/ч!
Так что Volkswagen Polo у нас стойкий солдатик. Не оловянный, а стальной. А если немецкие инженеры повысят пороговую нагрузку ограничителей ремней и сделают клапаны подушки безопасности более тугими? Да, нагрузки на грудь водителя возрастут, но голова точно окажется в большей безопасности. И Polo сможет пройти и наш новый краш-тест, верно?

Увы, все гораздо сложнее.
С этого года комитет Euro NCAP использует новый фронтальный краш-тест с точно такой же встречной тележкой массой 1400 кг, какую применили мы. Но, во-первых, степень перекрытия не 30%, а 50%. Во-вторых, прикрепленный к ней деформируемый барьер объемнее и поглощает не 90, а 120 кДж энергии. А главное — и тележка, и испытуемый автомобиль разгоняют всего лишь до 50 км/ч, то есть суммарная скорость составляет 100 км/ч. В итоге на долю машины приходится 112 кДж — всего на 9 кДж больше, чем при старом, «одиночном» ударе на 64 км/ч.

Admin

Administrator

Сообщения 2,992 Реакции 2,970 Адрес Россия, Москва Авто VW Touran 1.6 MPI BSE 2008, VW Tiguan 2.0 TDI DBGC 2018

Не соглашусь с Вами. «Телега» тоже имеет энергию, которая куда-то должна деться. Так что говорят про удвоенную энергию они все правильно. Но есть и существенное отличие от «реальной жизни» — в большинстве случаев встречный автомобиль тоже деформируется, поглощая энергию удара, а вот «телега», насколько я могу судить по видео, как-то не очень. То есть получился вариант, как будто Поло прилетает примерно на 100-110 км/ч в неподвижное препятствие.
Так что задумка в целом неплохая, но никакой революционности или «правды жизни» в ней не вижу.

Не так! Третий закон Ньютона.
Энергия столкновения переходит в массу деленную на 2.

Был целый выпуск передачи «Разрушителей легенд» на канале Дискавери посвященный этому вопросу.
Одинаковые машины, сравнивают столкновения:
1. 80км/ч в стену
2. 160км/ч в стену
3. лобовое 80км/ч + 80км/ч.
если кратко: разницы нет между 80км/ч в стену и лобовое столкновение 80км/ч + 80км/ч.

Очень показательное видео:

Беляш

Профессиональный советчик

телега тут имеет такую же массу как автомобиль. Такую же скорость как автомобиль. Значит их скорости нужно сложить и поделить на два. То есть скорость столкновения получается 60 км/ч в неподвижную тележку. Зачем АР цепляется за свои 120 км/ч вообще не понимаю.
При чем видно, что они понимают в чем подвох но всё равно продолжают стоять на своём. Такое чувство, что какой то большой начальник посчитал что будет 120 км/ч и сказал написать это в заголовок. Они и пишут. А дальше начинается натягивание совы на глобус, так как в комментариях им указали, что их 120 км/ч это бред.

Nikonist

Профессиональный советчик

Это верно только в частном случае (как у разрушителей), а в реальности (разные по весу и жесткости авто) всё будет иначе.

Возьмём для примера разрушителей и посчитаем что и как у них было.
Имеем 3 абсолютно одинаковых авто, допустим по 1,5 т весом. Сначала одно авто разгоняем до 50 миль/ч (примерно 80 км/ч или 22 м/с) и впечатываем его в стену.
Авто 1.5 т весом на 80 км/ч обладает энергией 373 кДж. Поскольку деформируемого барьера нет (жесткая стена) вся энергия раскладывается на две части, к примеру 70 кДж (точная цифра неизвестна) тратится на отскок и тепло, соответственно оставшиеся 303 кДж энергии идёт на деформацию автомобиля. Запомним эту цифру.
Теперь оставшиеся 2 автомобиля впечатываем лоб в лоб на 80 км/ч. Каждый обладает энергией 373 кДж, суммарная энергия движущихся навстречу автомобилей 786 кДж, при встрече 140 кДж тратится на отскок и тепло, оставшиеся 606 кДж тратятся м/у автомобилями на деформацию. Поскольку автомобили абсолютно одинаковые, энергия на деформацию тратится поровну, т.е. имеем те же 303 кДж.
Т.е. в данном случае (абсолютно одинаковые авто) разрушители полностью правы!

Теперь рассмотрим тест Авторевю.

Есть автомобиль VW Поло имеющий с манекенами и аппаратурой массу 1332 кг.
Есть жесткая тележка массой 1400 кг с закрепленным на ней деформируемым барьером, про который известно что он при ударе поглотит 90 кДж энергии.
Разгоняем автомобиль и тележку до 60 км/ч и впечатываем лоб в лоб.
WV Polo на 60 км/ч обладает энергией 185 кДж, тележка 194 кДж.
Таким образом при их встрече высвобождается 379 кДж суммарной энергии. Тележка поглощает только 90 кДж энергии (после смятия деформируемого барьера тележка фактически превращается в недеформируемое препятствие, как например стена — вы же не считаете энергию деформации стены, т.к. деформация стены отсутствует). Еще по словам АР 62 кДж тратится на отскок и трение (откуда они взяли эту цифру не уточнили, но наверняка не с потолка). Итого от общих 379 кДж энергии отнимаем 90 и 62 кДж, получаем 227 кДж. Именно столько энергии остается на деформацию Поло. И этот удар по энергии аналогичен удару о неподвижное препятствие с таким же деформируемым барьером на скорости примерно 82 км/ч. Т.е. удар на тесте действительно намного жестче.
Т.е. в данном случае Авторевю тоже правы!

Кто не понял просто перечитайте еще раз, во встречных ударах не всё так просто.

PS А в комментариях к ролику на Ютубе и к их статье на сайте просто подавляющее количество это мягко говоря дебилоиды.
Хотя АР тоже «молодцы», такой хайповый заголовок был не нужен, можно было и иначе обозвать, да и объяснение простыми словами с энергиями и т.п. нужно было засунуть в описание видео, и всё.

Беляш

Профессиональный советчик

Масса тележки и автомобиля одинаковые (разница мала, можно считать одинаковая). То есть имеем столкновение поло с неподвижной тележкой на скорости 60 км/ч. Вся разница энергий образовалась только от изменений площади перекрытия.
Больше ни от чего. Не стоит называть комментаторов дебилам когда сами не разобрались в вопросе.

Nikonist

Профессиональный советчик

Да что вы говорите? Ну ладно, пусть будет по-вашему, пусть аналогичная тележка закреплена намертво и никуда после удара не откатится, посчитаем?

Энергия у тележки 0, т.к. она стоит на месте. Энергия VW Polo на 60 км/ч 185 кДж. При впечатывании Polo в закрепленную неподвижно тележку часть накопленной Поло энергии забирает на себя деформируемый барьер тележки (90 кДж), еще часть энергии, ну пусть будет 30 кДж уходит на отскок и трение. Итого из 185 кДж энергии на деформацию Поло остается всего 65 кДж. Напомню что в случае летящей в лоб тележки на деформацию Поло оставалось 227 кДж.
Т.е. вы ошиблись всего в 3,5 раза, такая мелочь, правда?

Я же специально выше в сообщении написал — «Кто не понял просто перечитайте еще раз, во встречных ударах не всё так просто.»
Перечитаете, глядишь и сами разберётесь, и других голословно обвинять не будете

Nikonist

Профессиональный советчик

Что-то все молчат.
А ведь наверняка многое непонятно, может кто и обиду затаил.
Давайте еще раз попробуем разобраться на нескольких примерах.

Как известно удары подразделяются на абсолютно упругие (тела отскакивают друг от друга, пример бильярдные шары), абсолютно неупругие (тела после удара как бы слипаются друг с другом, пример пластилиновые шары, пуля застрявшая в ящике с песком) и нечто среднее (большинство реальных ударов).

Для простоты допустим что во всех наших примерах удары будут абсолютно неупругими, т.е. автомобиль будет втыкаться в другое препятствие и не отскакивать. Всякие деформируемые барьеры и т.п. рассматривать пока не будем вообще. Поэтому условимся что деформируется у нас только автомобиль, тележка / стена выполнены из толстенного твердого сплава и не деформируется абсолютно.
Будем смотреть только на энергии при ударе.

Абсолютно неупругий удар характеризуется тем, что часть механической энергии «теряется» — переходит в деформацию, тепло, и т.п.

1. Пусть у нас есть автомобиль массой 1400 кг движущийся со скоростью 60 км/ч (16,67 м/с). Данный автомобиль врезается в неподвижную стену (либо насмерть приваренную к стене тележку).
Вся энергия движущегося на этой скорости автомобиля Е равна mv2/2, т.е. в нашем случае 194 кДж. Во время удара вся накопленная автомобилем энергия поглощается самим автомобилем, т.к. стена неподвижна и деформации не подвергается. То есть автомобиль при ударе должен поглотить 194 кДж

2. Пусть теперь такой же автомобиль массой 1400 кг на скорости 60 км/ч врезается в аналогичный автомобиль свободно стоящий на дороге (без тормозов). Т.е. после соударения автомобили «слипаются» и продолжают двигаться уже вместе в сторону движения первого автомобиля.
По закону сохранения импульса m 1 V 1 +m 2 V 2 = (m 1 +m 2 )V общая , где m 1 и m 2 массы автомобилей (у нас они одинаковые), V 1 и V 2 начальные скорости автомобилей (у нас V 2 =0) , Vобщая — результирующая скорость автомобилей после удара. Поскольку m 2 V 2 =0, то V общая = m 1 V 1 / (m 1 +m 2 ), и в нашем случае получаем 8,33 м/с, т.е. после удара оба автомобиля будут двигаться вместе со скоростью 30 км/ч.
По закону сохранения энергии Е начальная = Е конечная + Q (деформации, теплоты и т.п.) , где Е начальная — общая начальная кинетическая энергия движения автомобилей, Е конечная — общая конечная кинетическая энергия двух врезавшихся автомобилей движущихся вместе после удара, Q (деформации, теплоты и т.п.) — энергия потерянная в результате удара на деформацию, нагрев и т.д.
Е начальная = m 1 V 1 ²/2 + m 2 V 2 ²/2. Т.к. в нашем случае V 2 =0, то Е начальная = 194 кДж, т.е. та же самая что и в первом примере, что логично.
Е конечная = (m 1 +m 2 )V общая ²/2, в нашем случае Е конечная = 97 кДж, таким образом энергия Q пошедшая на деформацию и теплоту составляет 194 — 97 = 97 кДж, т.е. каждый автомобиль должен поглотить всего по 48,5 кДж, что в 4 раза меньше чем в первом примере

3. Пусть теперь навстречу первому авто массой 1400 кг и едущему со скоростью 60 км/ч движется аналогичный автомобиль на такой же скорости.
По закону сохранения импульса m 1 V 1 — m 2 V 2 = (m 1 +m 2 )V общая , расшифровка обозначений такая же как и во втором примере. Движение встречное, импульс величина векторная, поэтому импульсы вычитаются друг из друга. Т.к. в нашем случае m 1 V 1 = m 2 V 2 , то их разность равна нулю, иными словами после удара два слипшихся автомобиля никуда не двигаются, их общая скорость 0 км/ч. Т.е. вся их кинетическая энергия пошла на деформацию и теплоту.
Е начальная = m 1 V 1 ²/2 + m 2 V 2 ²/2 = 388 кДж (это суммарная энергия 2-х движущихся навстречу автомобилей), Е конечная = 0, Q (деформации, теплоты и т.п.) = 388 кДж, или по 194 кДж на каждый автомобиль.
Это то же самое значение что и в первом примере — т.е. лобовой удар идентичных автомобилей движущихся на одинаковой скорости аналогичен удару в стену.

4. Пусть теперь навстречу первому авто массой 1400 кг и едущему со скоростью 60 км/ч на той же скорости движется металлическая тележка такой же массы. Мы условились что тележка выполнена из твердого сплава, никаких деформируемых барьеров на ней не закреплено, это просто жёсткая недеформируемая тележка.
Импульсы и суммарная энергия аналогичны 3 примеру, т.е. нужно куда-то рассеять 388 кДж кинетической энергии автомобиля и тележки. И вроде всё как в 3-м примере, но выплывает одно большое но. Разделить эту энергию поровну мы уже не можем, тележка не деформируется и поглотить энергию не может. В итоге все 388 кДж достаются автомобилю, это именно он вынужден деформироваться и поглощать всю энергию (представьте встречное столкновение пластилинового и стального шара одной массы, всю энергию будет вынужден поглощать шарик из пластилина).

Так что разница м/у столкновением со стеной и с тележкой действительно есть. Тем более масса тележки постоянна, плюс на ней стоит деформируемый барьер поглощающий известное количество энергии. А вот массы испытуемых автомобилей будут разными, и больше всего «не повезет» в столкновении с тележкой относительно легким автомобилям, вынуждая производителей улучшать пассивную безопасность прежде всего на них.

PS Это всё разумеется исключительно моё ИМХО, может где и накосячил с расчётами.

PPS EuroNCAP с 2020 года тоже использует тележки, правда деформируемый барьер там поглощает 120 кДж, перекрытие составляет 50%, а скорость автомобиля и тележки по 50 км/ч, у Авторевю в первом тесте условия были намного жёстче: