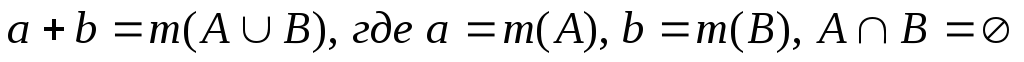Что такое сумма разность произведение частное в математике правило

Что такое произведение и частное в математике?

Разность — результат вычитания; произведение — результат умножения; сумма — результат сложения; частное — результат деления.

Что такое произведение и частное математика?

Умножение. Умножить некоторое число (множимое) на целое число (множитель) — значит повторить множимое слагаемым столько раз, сколько указывает множитель. Результат называется произведением. . Данное произведение получает название делимого, данный сомножитель — делителя, искомый сомножитель — частного.

Что такое частное чисел в математике?

Число, на которое делят делимое, называется делитель. Результат деления – частное. Числа, которые соединены знаком деления, тоже называются частное.

Что такое частное это плюс или минус?

Определение частного чисел Частное чисел — это результат деления одного числа на другое. . При этом число a будет делимым, а число b — делителем.

Что такое сумма и разность?

Разность – результат вычитания. Слагаемое – число, которое складывают. Сумма – результат сложения.

Что такое частное разность и произведение?

Разность — результат вычитания; произведение — результат умножения; сумма — результат сложения; частное — результат деления.

Как называются числа при умножении?

Так же, как и при сложении и вычитании, числа при умножении тоже имеют свое название. Первое число при умножении называется первый множитель. Второе число при умножении называется второй множитель. Результат умножения называют произведение.

Что нужно сделать чтобы найти неизвестный делитель?

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Что такое множитель по математике?

Компоненты умножения называются множители. Первый множитель показывает, какое число прибавляют, второй множитель показывает – сколько раз прибавляют это число. Результат умножения называется произведение.

Что значит отношение в математике?

, а иногда выражаемое арифметически как безразмерное отношение (результат деления) двух чисел, непосредственно отображающее, сколько раз первое число содержит второе (не обязательно целое). Проще говоря, соотношение показывает для каждого количества чего-то одного сколько есть чего-то другого.

Что такое разность это деление или минус?

Разность — это отнять. Результат вычитания называется разность. При чтении это будет звучать так: «уменьшаемое минус вычитаемое равно разность». Сумма — это сложить.

Что такое Что такое разность?

Разность r чисел a и b — это результат вычитания числа b из числа a . В случае если вычитаются большие числа или десятичные дроби, то используют способ вычитания в столбик.

Что означает множитель?

МНОЖИТЕЛЬ — МНОЖИТЕЛЬ, множителя, муж. (мат.). В действии умножения число, которое показывает, сколько раз нужно повторить слагаемым какое нибудь другое число (множимое), чтобы получить произведение.

Как определить разность?

Разность получается путем вычитания одного числа (вычитаемого) из другого (уменьшаемого). То есть, чтобы определить разность, нужно просто вычесть из большего числа меньшее. Например, числа 15 и 10.

Как найти уменьшаемое вычитаемое разность?

Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое. Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность. Названия компонентов при умножении: множитель, множитель, произведение.

Что такое сумма слагаемых?

Слагаемые — это два числа, которые прибавляются друг к другу. В результате чего получается их сумма. . Здесь, например число 2 — первое слагаемое (или «левое» слагаемое), а число 1 — второе (или «правое» слагаемое). Число три — их сумма.

Порядок действий в математике

В каждом доме есть свой порядок: сначала моем руки, затем едим обед, сначала все уроки — а потом гулять. Так вот, в математике тоже есть последовательность действий, которую важно соблюдать.

О чем эта статья:

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

Операции отношения:

больше или равно (≥);

меньше или равно (≤);

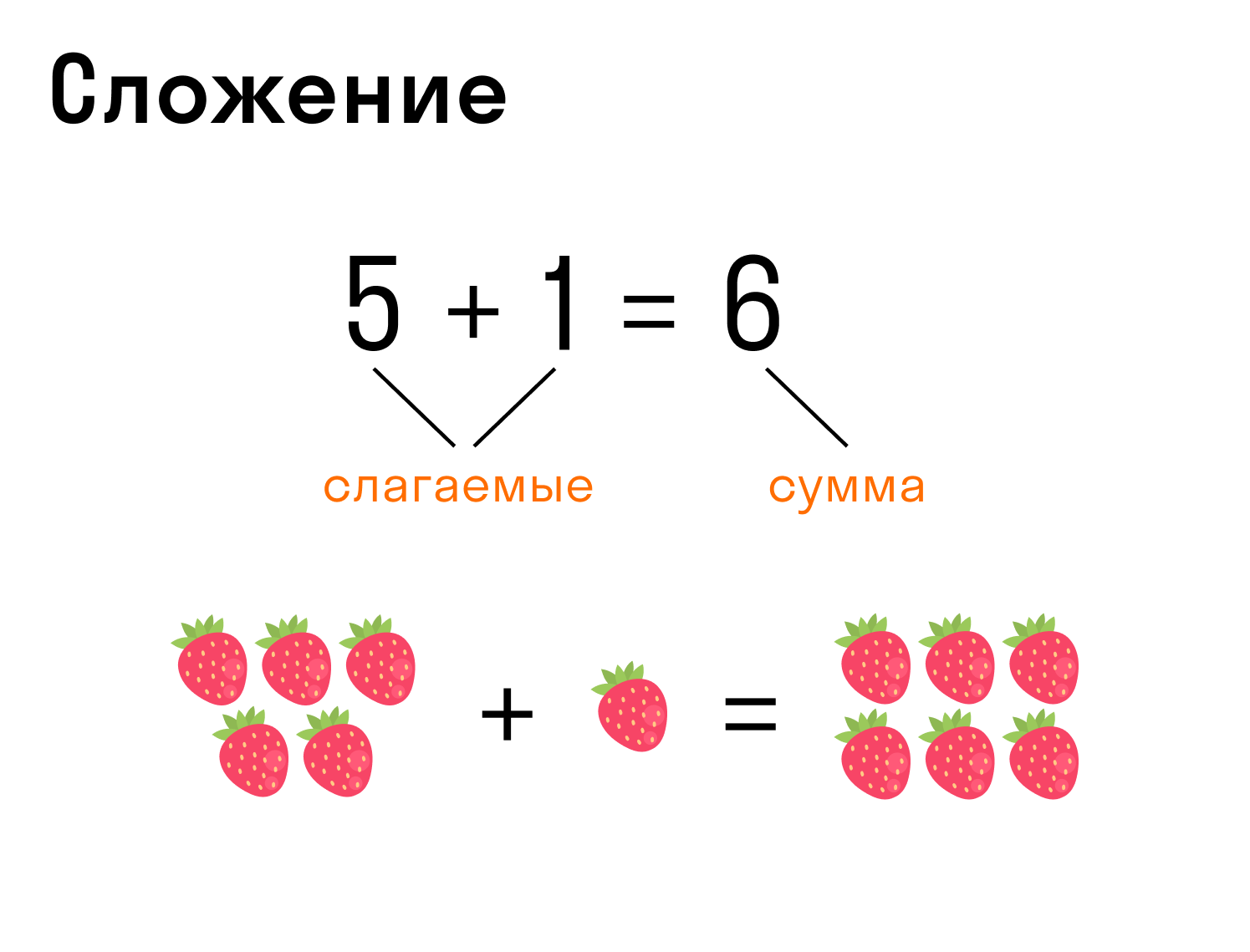
Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

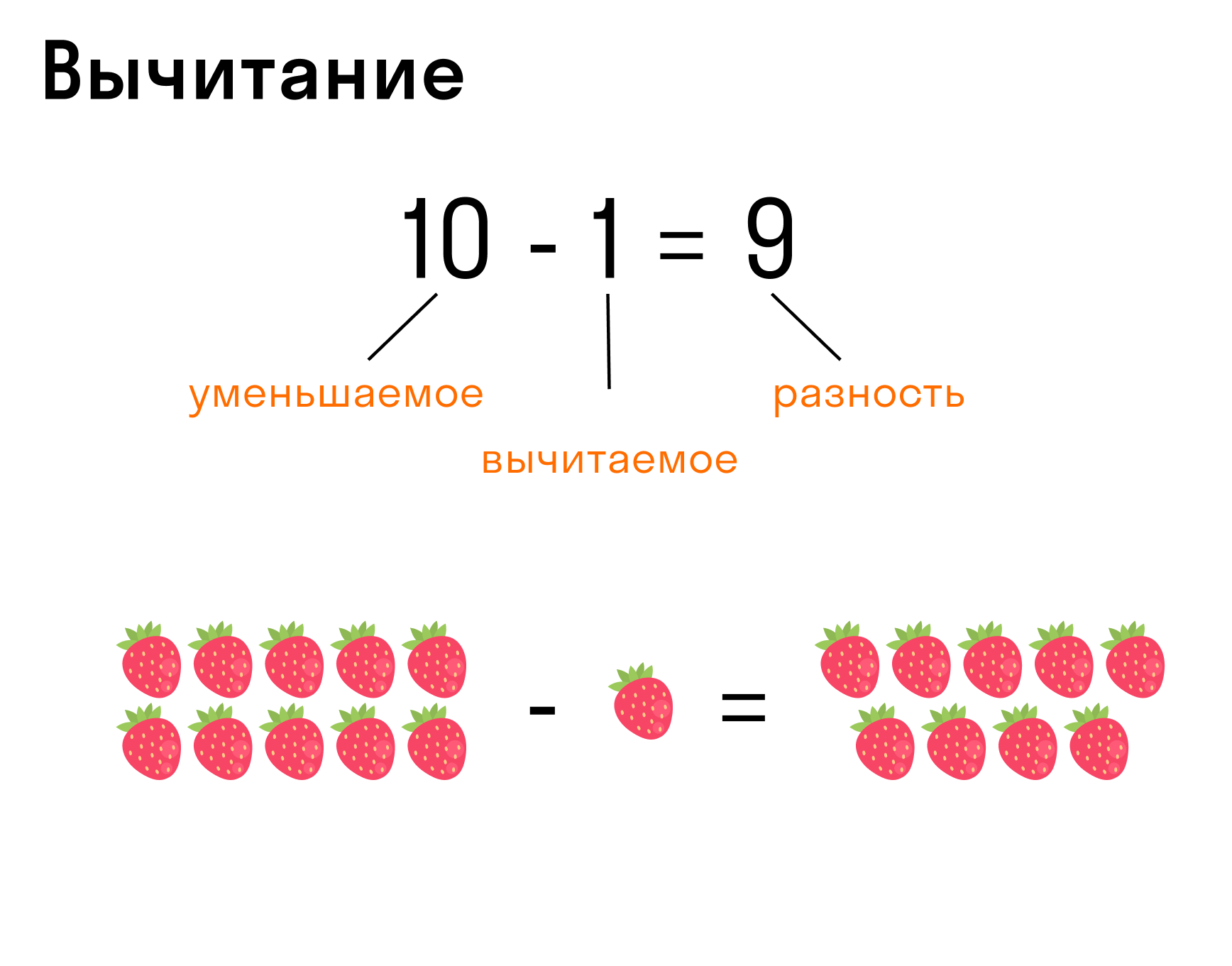
Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

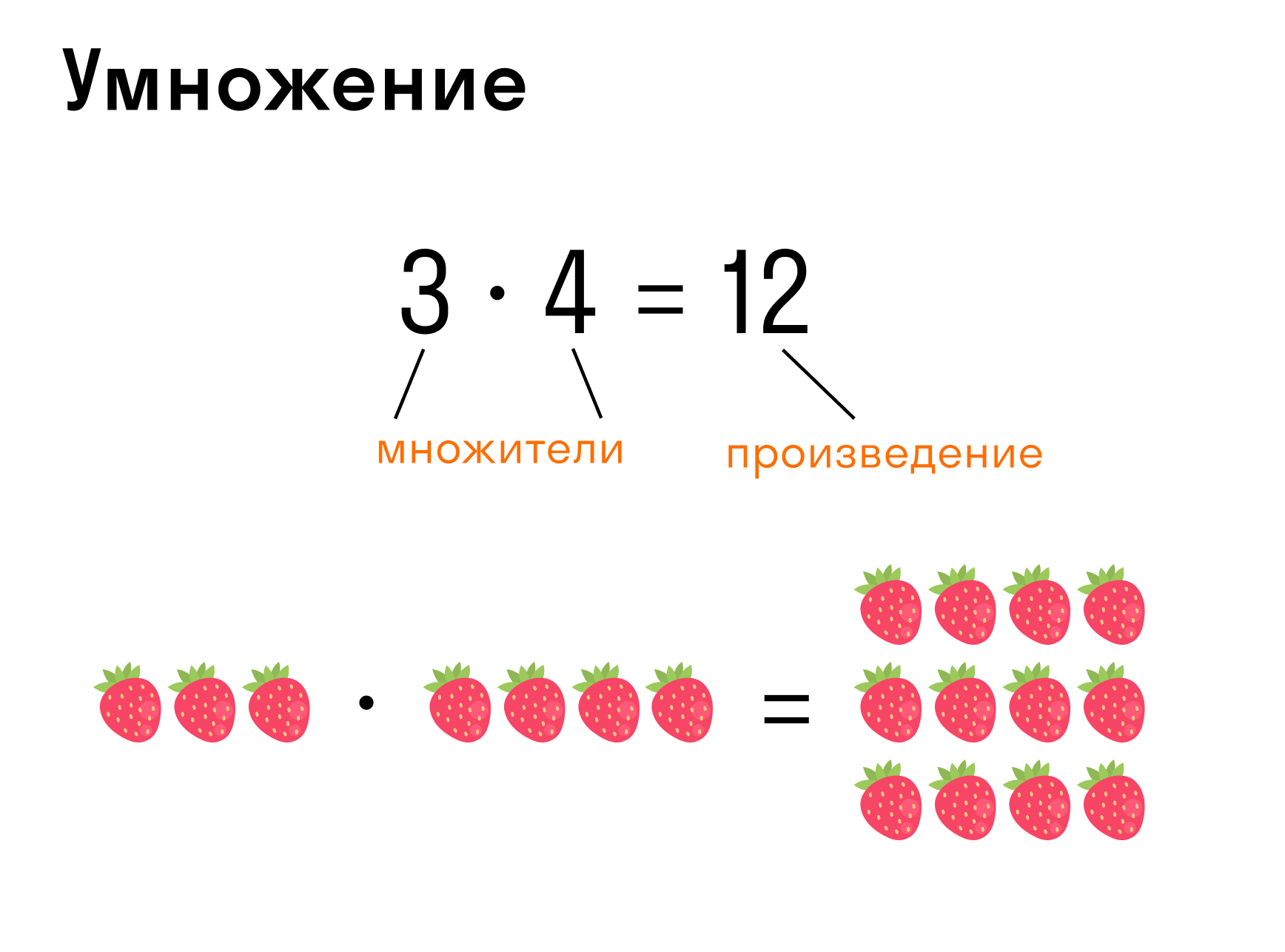
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.

3 × 4 = 3 + 3 + 3 + 3, то есть число 3 сложили 4 раза само с собой.

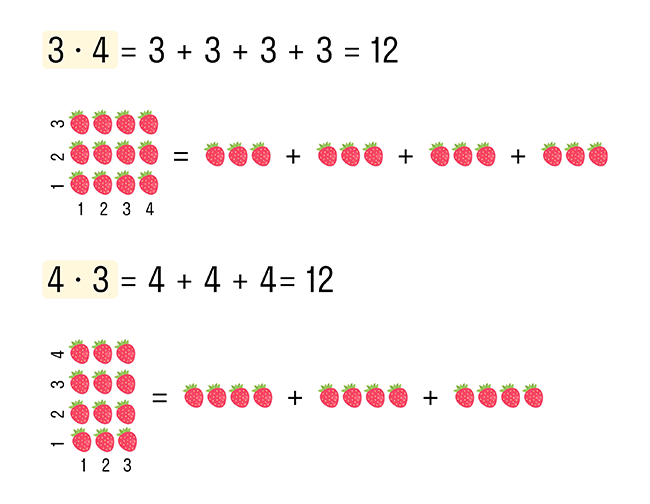
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 × 2 = 5 + 5 = 10 и 2 × 5 = 2 + 2 + 2 + 2 + 2 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

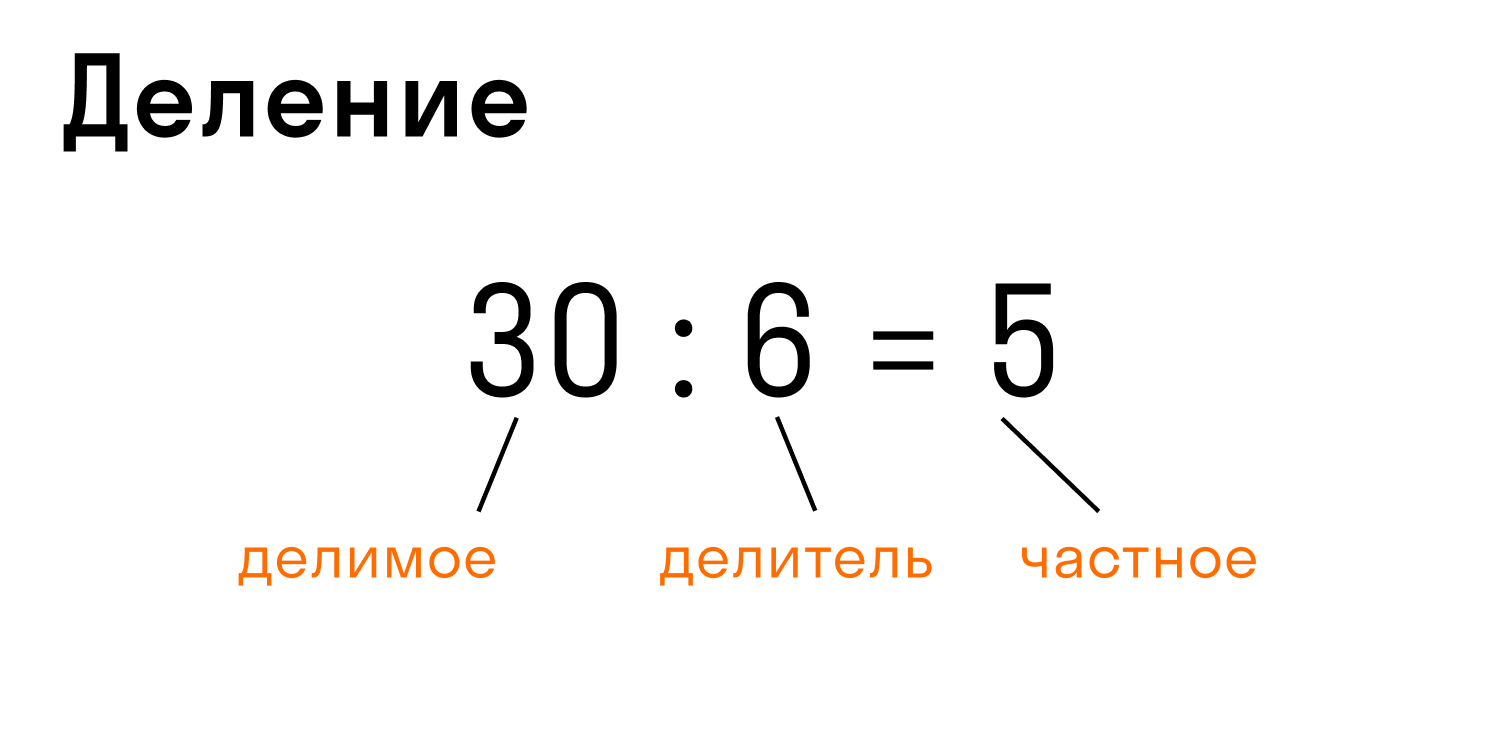
В этом случае произведение делителя 6 и частного 5 в качестве проверки дает делимое 30.

Сложение и вычитание, умножение и деление попарно представляют обратные друг другу действия. А теперь давайте узнаем порядок выполнения арифметических действий.

Порядок вычисления простых выражений

Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:

действия выполняются по порядку слева направо

сначала выполняется умножение и деление, а затем — сложение и вычитание.

Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.

Что первое, умножение или деление? — По порядку слева направо.

Сначала умножение или сложение? — Умножаем, потом складываем.

Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Рассмотрим порядок арифметических действий в примерах.

Пример 1. Выполнить вычисление: 11 − 2 + 5.

В нашем выражении нет умножения, деления и скобок, поэтому выполняем все действия слева направо. Сначала вычтем два из одиннадцати:

Затем прибавим к результату пять и в итоге получим четырнадцать:

Вот запись всего решения: 11 − 2 + 5 = 9 + 5 = 14.

Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 × 7 : 5?

Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Сначала выполняем деление десяти на два:

Теперь результат умножаем на семь:

И получившееся в число делим на пять:

Запись всего решения выглядит так: 10 : 2 × 7 : 5 = 5 × 7 : 5 = 35 : 5 = 7.

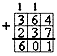
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.

Например, в такой последовательности можно решить пример по действиям:

Действия первой и второй ступени

В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.

Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.

С этими терминами правило определения порядка выполнения действий звучит так:

Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 − 2 × 3) × (12 − 4) : 2.

Как правильно решить пример:

Сначала определим порядок действий. Выражение содержит скобки, поэтому сначала будем выполнять действия в выражениях, которые заключены в эти скобки.

Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание.

Итак, мы определили первые три действия:

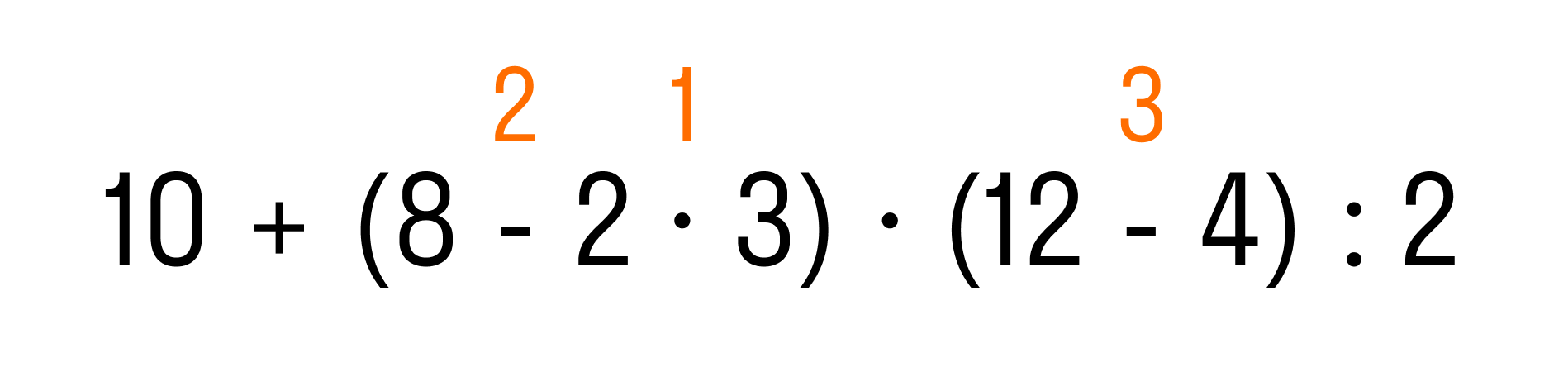
Когда выполнены все действия в скобках, по правилу дальше мы должны выполнить умножение и деление, и в последнюю очередь — сложение. Теперь мы знаем, в каком порядке решать пример:

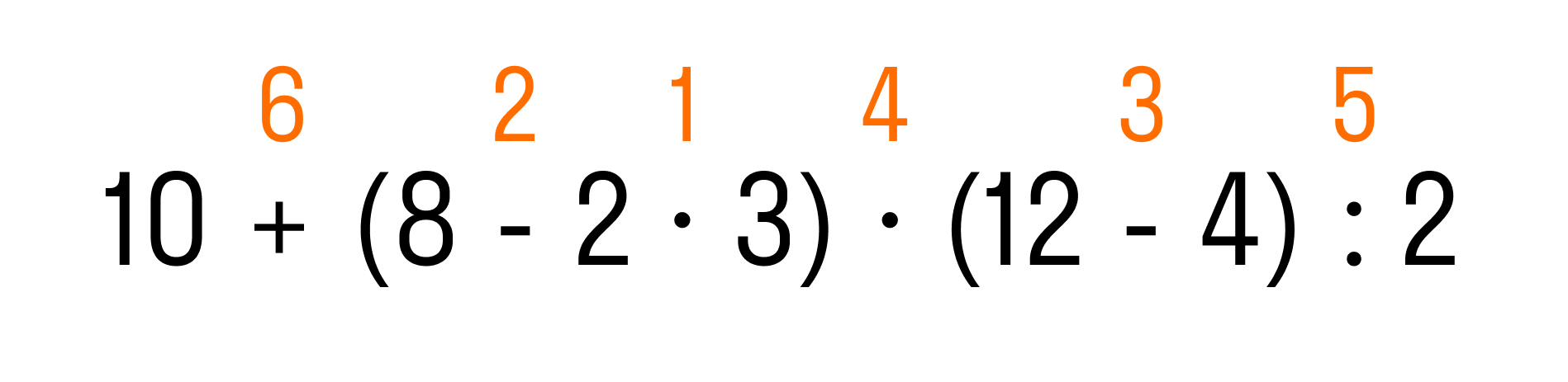
Осталось решить пример по действиям:

1. 2 × 3 = 6
2. 8 − 6 = 2
3. 12 − 4 = 8
4. 2 × 8 = 16
5. 16 : 2 = 8
6. 10 + 8 = 18

На этом все действия выполнены.

Ответ: 10 + (7 − 2 × 3) × (12 − 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 × (2 + 3)).

Для начала определим порядок действий

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 × (2 + 3). Но это выражение также содержит скобки, поэтому начнем сначала с действий в них:

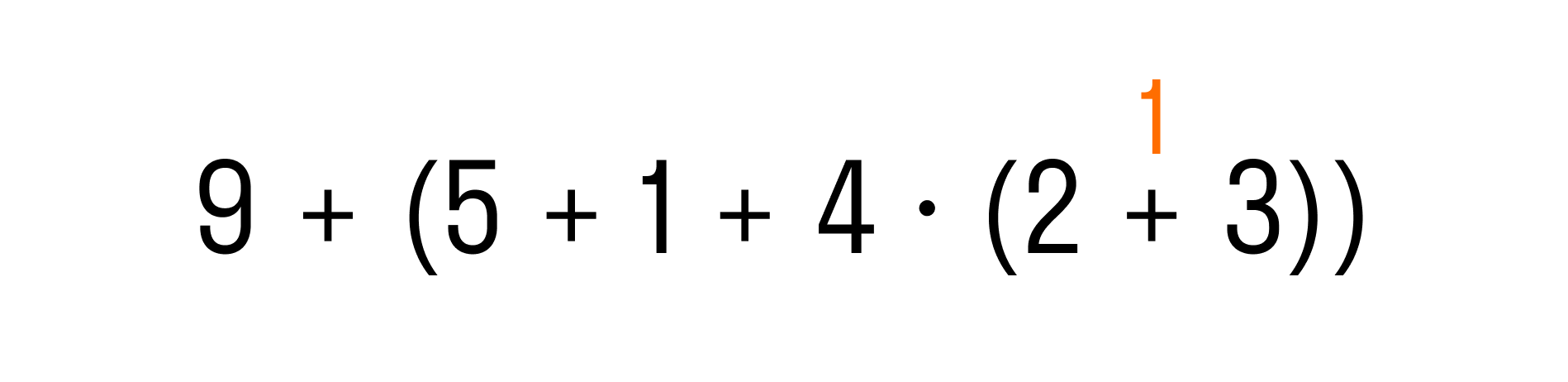
Теперь перейдем к выражению во внешних скобках. Первым действием по правилу будет умножение, а затем слева направо — две операции сложения:

Что такое произведение сумма частное?

Разность — результат вычитания; произведение — результат умножения; сумма — результат сложения; частное — результат деления.

Что такое произведение и частное?

Разберёмся с определениями суммы, разности, произведения и частного целых чисел. . Произведением называется результат умножения целых чисел. Числа, которые участвуют в умножении, называются множителями. Частное — это результат, который получается при делении одного числа на другое.

Что такое сумма и что такое разность?

Разность – результат вычитания. Слагаемое – число, которое складывают. Сумма – результат сложения.

Что такое произведение суммы в математике?

Произведение суммы и разности двух выражений можно найти как произведение многочленов. . -ab и +ab — противоположные слагаемые, поэтому их сумма равна нулю. Вывод: Произведение суммы и разности двух выражений равно разности квадратов этих выражений.

Что означает произведение и разность?

Произведение — это умножение одного числа на другое. Частное — результат деления чисел, произведение — результат умножения чисел, сумма — результат сложения чисел, разность — результат вычетания. . Разность — это результат вычитания.

Что такое делимое и делитель и частное?

Число, которое делят, называется делимое. Число, на которое делят делимое, называется делитель. Результат деления – частное. Числа, которые соединены знаком деления, тоже называются частное.

Что означает вычитание?

Вычитание — арифметическое действие, обратное сложению. Вычесть одно число (вычитаемое) из другого (уменьшаемого) значит найти такое третье (называемое разностью между уменьшаемым и вычитаемым), которое, будучи сложено с вычитаемым, даст сумму, равную… …

Что такое сумма частное разность?

Разность — результат вычитания; произведение — результат умножения; сумма — результат сложения; частное — результат деления.

Что такое разность в примерах?

Разность получается путем вычитания одного числа (вычитаемого) из другого (уменьшаемого). То есть, чтобы определить разность, нужно просто вычесть из большего числа меньшее. Например, числа 15 и 10.

Что такое сумма чисел 2 класс?

Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых). . Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.

Как умножить сумму на разность?

Доказательство формул сокращенного умножения

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a 2 — b 2 .

Как найти произведение разности?

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Как умножить сумму на другую сумму?

Умножить число на сумму можно двумя способами: 1) Чтобы умножить число на сумму, можно сначала выполнить сложение, а затем умножить число на полученный результат. 4 · (3 + 5) = 4 · 8 = 32. 2) Для умножения числа на сумму, можно умножить данное число на каждое слагаемое отдельно и полученные результаты сложить.

В каком действии разность?

Вычитание — действие, обратное сложению. Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Что такое разность каким знаком обозначается?

Теория множеств и теория чисел

Символ TeX (Команда TeX)	Символ (Юникод)	Название
		Произношение
(setminus)		«разность … и …», «минус», «… без …»
(to)	→	Функция (отображение)
		«из … в …»,

Что такое произведение чисел в четвертом классе?

Произведение чисел это результат умножения этих чисел. Краткая запись суммы одинаковых слагаемых. Результат умножения называется произведением, а умножаемые числа – множителями.

Что такое сумма, разность, произведение, частное в математике?

В каких ещё значениях, не связанных с математикой, употребляются эти слова?

Я математик по образованию, специальность: учитель математики. Проработала всю жизнь преподавателем математики в педвузе.

Необходимо оговориться. Речь в дальнейшем пойдет о сумме, разности, произведении, частном чисел.

Ответы на данные вопросы хотя и простые, но вызывают затруднения у учащихся. Чтобы можно было более подробно рассмотреть эту обобщающую тему, предлагаю вашему вниманию полезный материал по ней. Заметка называется «Математика для блондинок».

Мне понравилась методика изучения.

Задается провокационный вопрос:

Разность — это поделить или умножить?

Пытаются заинтересовать (ни одна предложенная версия не является верной!)))

Разность — это отнять. Результат вычитания называется разность.

Сумма — это сложить. Результат сложения называется сумма.

Произведение — это умножить. Результат умножения называется произведение.

Частное — это деление. Результат деления называется частное.

Таким простым языком объясняются верные понятия суммы, разности, произедения и частного в математике. Немного упрощенно записаны лишь словосочетания: разность — это отнять, сумма — прибавить, произведение — умножить, частное — разделить. Если быть точными, так не утверждают.

Итак, результат сложения чисел (слагаемых) — это их сумма, результат вычитания чисел (уменьшаемого и вычитаемого) — это разность, результат умножения чисел (сомножителей) — это произведение, а результат деления чисел (делимого на делитель), причем делитель не должен быть равен нулю, иначе деление нельзя выполнить, есть частное этих чисел.

О других значениях данных слов не задумываюсь, математика затмевает все.)))

Это такие математические понятия.

Сумма — это результат сложения. Числа, которые складывают, называют первое слагаемое и второе слагаемое. Обозначается таким знаком: +.

Разность — это результат вычитания. Числа, которые вычитают, называют уменьшаемое (то, которое больше) и вычитаемое (то, которое меньше). Обозначается таким знаком: -.

Произведение — это результат умножения. Числа, которые умножают, называются первым множителем и вторым множителем. Обозначается таким знаком: *.

Частное — это результат деления. Числа, которые делят, называются делимое (то, которое больше), делитель (то, которое меньше). Обозначается таим знаком: :.

Эти все понятия проходят в начальной школе.

В математике есть четыре простые операции, которые можно применить к двум числам и получить такие результаты:

сумма — это результат сложения чисел,

разность — это результат вычетания от одного числа другого,

произведение — это результат умножения чисел,

частное — это уже результат деления чисел.

I. Математические понятия СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ взаимосвязаны с математическими терминами СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ, ДЕЛЕНИЕ.

Все определения даются здесь на множестве натуральных чисел.

Каждой паре чисел ставится в соответствие число, называемое их СУММОЙ.

Сумма состоит из стольких единиц, сколько их содержится в числах (слагаемых) из данной пары.

СУММА есть результат сложения чисел-слагаемых.

Вычитание — это операция, обратная сложению. Она состоит в нахождении одного из слагаемых по сумме и другому слагаемому. Данная сумма называется уменьшаемым, данное слагаемое — вычитаемым, а искомое слагаемое — РАЗНОСТЬЮ.

РАЗНОСТЬ — это число, являющееся результатом вычитания, остаток вычитания.

Каждой паре чисел можно поставить в соответствие число, которое состоит из стольких единиц, сколько их содержится в первом числе из пары, взятых столько раз, сколько единиц содержится во втором числе из пары. Это соответствующее таким образом паре чисел (они называются сомножителями) число называется ПРОИЗВЕДЕНИЕМ.

ПРОИЗВЕДЕНИЕ — это результат умножения.

Деление есть операция, обратная умножению.

Деление — это нахождение одного из сомножителей по произведению и другому сомножителю. Данное произведение называется делимым, данный сомножитель — делителем, а искомый сомножитель — это ЧАСТНОЕ, то есть число, полученное от деления одного числа на другое.

II. ДРУГИЕ ЗНАЧЕНИЯ СЛОВ СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ.

Все используемые в качестве математических понятий слова могут иметь и другие лексические значения.

СУММА в переносном значении означает совокупность, общее количество чего-либо.

Например. Профессионализм педагога заключается в сумме знаний, умений и навыков, передаваемых им своим ученикам. Отсутствие нужной суммы денег заставило отказаться от покупки.

РАЗНОСТЬ имеет значения разницы, несходства, отличия в чем-либо.

Например. Разность интересов намного хуже разницы в возрасте. Дружба может начаться с представления об общности взглядов , а вражда — с разности взглядов.

ПРОИЗВЕДЕНИЕ означает что-либо произведенное в процессе труда, создание чего-нибудь, продукт труда, творчества, искусства и т.п.

Например. Высокое художественное произведение заставляет человека думать над своей жизнью. На конкурсе юных пианистов мальчик играл произведение П.И. Чайковского. Эта шкатулка — настоящее произведение искусства.

ЧАСТНОЕ — это что-то личное, персональное, принадлежащее только одному человеку, это его собственность, его и только его достояние. И будь то самоличные мысли, будь то имущество или что-нибудь другое, но оно принадлежит только ему, частному лицу.

Например. Подруга подарила мне записную книжку с надписью «Частное». Хорошо ли противопоставлять частное общественному?

Слова Сумма, Разность, Произведение и Частное очень знакомо ученикам школ и других учебных заведений веди с этими определениям им приходиться на каждом уроке математики.

1) Сумма

Суммой является результат, полученный после сложения (+) двух или более чисел.

Суммой так же является итоговая стоимость товара (сумма к оплате), общая совокупность знаний, впечатлений и много чего.

2) Разность

В математике означает результат вычитания числе (-).

Слово разность так же может употребляться в качестве слова разницы чего-либо. Например, разность мнений, разность взглядов, разность показателей и т.д.

3) Произведение

Произведением является результат, полученный после умножения чисел (*).

Кроме математики это слово еще употребляется в качестве обозначения результата творческого процесса (произведение искусства), в качестве глагола от «производить».

4) Честное

Этим словом обозначают результат деления двух чисел (:).

Слово «частное» мы так же можем услышать при обозначении принадлежности чего либо одному собственнику (частное лицо, частная собственность, частное дело).

Все эти четыре термина употребляются преимущественно в математике.

Сумма — это когда происходит складывание двух чисел;

Разность- это вычитание одного числа из другого;

Частное — это деление одного числа на другое;

Произведение — это умножение одного числа на другое.

Сумма — это результат сложения, причем слово может относиться не только к цифрам.

Разность — это то, что получается после вычитания чисел.

Произведение — то что получается после умножения, слово имеет и другое значение.

Частное — это то, что получается после деления.

По сути, все четыре слова в вопросе, а именно сумма, разность, произведение и частное, отражаю четыре основные математические действия, которые являются азами. Именно с обучения данным действиям начинается увлекательный путь в мир математики. Таким образом,

Суммой в математике назовем число, которое получим в результате прибавления одного числа к другом. Разность это число противоположное сложению, это когда отнимают от большего числа меньшее. Произведением назовем число, которое получится в результате умножения одного числа на другое. Разность это противомоложное произведению число. Получаем разность так: делим одно число на другое.

Частное — результат деления чисел, произведение — результат умножения чисел, сумма — результат сложения чисел, разность — результат вычетания. Это элементарные математические действия, которые можно проводить с числами.

Сумма, разность, произведение, частное — это результат математических действий, с которых мы все начинали свое знакомства с математикой. В жизни эти слова мы тоже используем, но значение вкладываем в них больше математическое, хоть складывать можем и не числа. Произведение еще может быть и художественным. Это совсем другое значение слова, которое мы применяем в жизни.

Хорошие книги не всегда было легко купить. Помню даже что наша семья заказывала их в другом городе у родственников. Хотя наш город областной и гораздо более крупный. Но там был к ним «доступ». Уж не знаю каким путём. В основном различные собрания сочинений зарубежных авторов, но и не только. Были времена советские, люди макулатуру сдавали. И за это получали что-то типа талончиков. На которые уже в свою очередь можно было купить книги. Причин в общем много. Вот ещё одна из них: Тогда не было такого ЗАСИЛЬЯ информации : Телевизор: каналов не счесть а не три-четыре, где сельский час, человек и закон. в смысле не так много интересных передач. Сейчас каналов Сотни. Любая тематика и любая информация. Интернет-то же самое-море инфы на любой вкус. Где ещё ты сам можешь не только внимать но и творить, пусть это будут даже посты на каком-нибудь сайте.

Конкурентов у книги много. Голова у человека забита инфой до предела и даже больше.

Раньше любая какая то новая информация-будь то книга, это интересно, увлекательно, у других нет. Сейчас же-Всё наоборот. Куда бежать от этой всей инфы? Нужной, а больше ненужной. Не у всех хватает ума, воли, времени или чего-то там ещё. Чтобы отрешиться от теле, да и где-то интернет «жвачки». Ограничить к ним доступ до.. нужной нормы. И лучше полежать, почитать хорошую книгу. А ненужную инфу-на помойку. То есть-мимо себя. Толку от неё нет, только мозг устаёт и заси. забивается в смысле.

Как надо фильтровать то что мы едим, с кем общаемся, чем занимаемся. так надо и беречь своё время. И умело потреблять информацию познавательную, развлекательную. Какую нужно, сколько нужно. В общем Сказать легко-сделать непросто, такой вывод.

Немножко человек стал более «тупой» как говорил М.Задорнов. Не в смысле глупый. А в смысле более ленивый и «раб комфорта». Книгу надо взять, листать страницы, думать.

А не у всех есть на это силы, желание и время. Поэтому смарфон, зомобящик и комп-наши «друзья».

Нужно видеть все предложение, чтобы определить нужно ли это словосочетание выделять запятыми. В большинстве случаев оно запятыми не выделяется. Это словосочетание не выступает в роли вводных слов, потому как можно это словосочетание заменить на аналогичное ему «чаще всего». Например:

1) В большинстве своем они живут в рамках. ==> Чаще всего они живут в рамках.

Даже если мы это предложение немного видоизменим, все равно запятые не нужны вокруг этого словосочетания

2) Они в большинстве своем живут в рамках. — не выступает это словосочетание как уточнение, даже при большом желании.

Можно даже опустить слово «своем» и все равно запятые будут не нужны:

3) Они в большинстве живут в рамках.

А вот если «в большинстве своем» заменить на «в основном», то запятая уже будет нужна, как пример:

4) В основном, они живут в рамках. (в данном случае имеет значение вводной конструкции со значением ‘как правило’ (т.е., отсутствует грамматическая связь с членами предложения).

Давайте решать предложенную вами задачу по действиям.

1) 3/4 : 3/5 = 5/4 (метра) — длина второго полотенца

2) 5/4 + 3/4 = 2 (метра) — суммарная длина первых двух полотенец

3) 2 * 5/12 = 10/12 = 5/6 (метра) — длина третьего полотенца

4) 5/6 : 5/4 = 4/6 = 2/3 — такую часть составляет длина третьего полотенца от длины второго полотенца

Ответ: Длина третьего полотенца составляет 2/3 части от длины второго полотенца.

В любой сказке нге обходится без волшебных предметов, которые помолгают главным героям исполнить свое предназначение, данное судьбое в этот кратковременный период времени о котором идет повествование. Кроме неодушевленных предметов в сказках упоминаются и одушевленные волшебные помошники, которых высшие силы направляют главному герою в подмогу. В частности в этой сказке о молдодильных яблоках и живой воде, за которыми отправляются в путешествие, исполняя сыновий долг, три сына ослепшего и одряхлевшего царя, такие персонажи-помощники и предметы есть. Помошниками в этой сказке оказываются сестры Яги, в количестве трех лиц, покоренные харизмой Ивана младшего сына, а также богатырский говорящий конь и птица Нагай. Что касается предметов, это если можно к ним этот термин применить и были эти самые яблоки и вода живая.

Существительное мужского рода Кустарник следует отнести ко второму склонению и выделить в его составе нулевое окончание, что мы можем подтвердить склонением этого слова по падежам: Кустарник-Кустарника-Кустарнику-Кустарником-Кустарнике. Для нахождения корня подбираем однокоренные слова: Кустарник-Кустарничек-Кустарниковый-Куститься-Кустик-Кустище-Полукустарник-Куста­рь-Кустарничать-Куст. Корнем существительного оказывается морфема КУСТ-. Далее выделим суффикс -АР- от слова Кустарь, и суффикс существительного -НИК.

Получаем: КУСТ-АР-НИК_ (корень-суффикс-суффикс-нулевое окончание), основа слова КУСТАРНИК.

Замены в выражениях

Любое число в выражении может быть заменено таким же числом, но записанным в другой форме. Возьмём для примера следующее выражение, которое уже вычислено:

Давайте заменим число 15 на само себя, но запишем его в другом виде:

(10 + 5) + 3 = 18

Видно, что мы заменили число 15 на выражение в скобках (10 + 5). Но главное выражение 15 + 3 = 18 не пострадало от этого, потому что 15 и (10 + 5) это одно и то же. Ведь 10 + 5 = 15.

Давайте заменим число 18 на само себя, но запишем его в другом виде:

(10 + 5) + 3 = 3 × 6

Теперь заменим последнюю шестёрку на неё же саму, но опять же запишем её в другом виде:

(10 + 5) + 3 = 3 × 2 × 3

Теперь сравним два выражения: первое, которое у нас было и новое, которое мы видоизменили:

(10 + 5) + 3 = 3 × 2 × 3

На первый взгляд покажется, что это два разных выражения. И так подумает любой, кто увидит эти два выражения в первый раз. Но мы знаем, что это одно и то же выражение. Вся разница в том, что мы видоизменили некоторые его параметры.

Изменять внешний вид этого выражения можно хоть до бесконечности. Главное, чтобы не нарушалось равенство. Значок равенства (=) должен оправдывать своё положение. Помните второй урок? Знак равенства ставится между числами или выражениями только тогда, когда они равны между собой.

Подобные операции, где одно число или выражение заменяется на само себя, но записанное в другом виде, называют преобразованием или представлением.

Представление в виде суммы

Любое число или выражение можно представить в виде суммы. Например, число 10 можно представить в виде суммы 5+5 или 7+3 или 8+2. Как угодно, лишь бы соблюдалось равенство между числом и представленной суммой. Выглядеть это может следующим образом:

В книгах можно встретить задания следующего содержания: представьте в виде суммы и далее приводятся числа или выражения, которые нужно представить в виде суммы. Это как раз тот случай, когда надо включать свои творческие способности и решить какие числа (или выражения) использовать, чтобы выполнить задание.

Представление в виде разности

С прошлых уроков известно, что разность это результат, который получается в результате вычитания одного числа из другого. Но разностью также называется выражение, которое соединено знаком вычитания (−). Например следующие выражения являются разностями:

Любое число можно представить в виде разности. Например, число 50 можно представить в виде разности 90−40 или 80−30 или 60−10. Как угодно, лишь бы соблюдалось равенство между числом 50 и представленной разностью. Выглядеть это может следующим образом:

Представление в виде произведения

С прошлых уроков известно, что произведение это результат, который получается в результате умножения одного числа на другое. Но произведением также называется выражение, которое соединено знаком умножения (×). Например следующие выражения являются произведениями:

Любое число можно представить в виде произведения. Например, число 30 можно представить в виде произведения 5×6 или 10×3 или 15×2. Как угодно, лишь бы соблюдалось равенство между числом 30 и представленным произведением. Выглядеть это может следующим образом:

Представление в виде частного

С прошлых уроков известно, что частное это результат, который получается в результате деления одного числа на другое. Но частным также называется выражение, которое соединено знаком деления (÷). Например, следующие выражения являются частными:

Любое число можно представить в виде частного. Например, число 5 можно представить в виде частного 15÷3 или 25÷5 или 30÷6. Как угодно, лишь бы соблюдалось равенство между числом 5 и представленным частным. Выглядеть это может следующим образом:

На этом данный урок завершён. Для закрепления материала, попробуйте выполнить следующие задания:

Задание 1. Представьте в виде суммы следующие числа: 20, 30, 45, 50. Можете представить любыми числами. Например, первое число 20 можно представить как 15 + 5.

Задание 2. Представьте в виде разности следующие числа: 10, 15, 12, 5 Можете представить любыми числами. Например, первое число можно представить как 15 − 5.

Задание 3. Представьте в виде произведения следующие числа: 30, 40, 72.

Задание 4. Представьте в виде частного следующие числа: 7, 5, 9, 3

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

45 thoughts on “Замены в выражениях”

в 4 шаге где нужно решить задание нету скрытых ответах, я не знаю как себя проверить.

Что такое разность чисел и как ее найти

К слову «разность» можно подобрать однокоренные слова, такие как, различный, разный. То есть, разность имеет значение того, что между объектами имеются какие-либо отличия, что они не одинаковые. В математике данный термин является часто используемым. Изучение разности чисел начинается с первого класса. Это основной, базовый процесс, который должен знать каждый.

По мимо математики, без определения разности не обходится ни одна точная наука. Разность определяется и в быту, ежедневно. Например, при походе в магазин, необходимо из числа, которое является номиналом купюры, вычесть стоимость продукта. То, что останется (сдача), будет называться разностью. Таким образом, разность чисел — это результат математического действия, вычитания.

Виды математических действий и их результаты

• Вычитание (результат — разность).
• Сложение (результат — сумма).
• Деление (частное).
• Умножение (произведение).

Данные действия являются основополагающими в вычислительных процессах. Они не взаимозаменяемы. Это индивидуальные виды вычислений, которые не следует путать.

Общее понимание разности чисел

Как найти разность чисел

Чтобы найти разность чисел, необходимо выполнить процесс вычитания. А именно, из уменьшаемого вычесть (или отнять) вычитаемое. В результате получится разность.

В данном случае, разность равна 5. Уменьшаемое 7, его мы уменьшаем, делаем меньше. Вычитаемое 2, это число мы вычитаем (отнимаем).

Данную процедуру можно записать и в буквенном выражении.

В — разность; С — уменьшаемое; А — вычитаемое.

Общее понимание разности чисел

В младших классах ученикам объясняют то, чтобы найти разность чисел, нужно из большего числа вычесть меньшее. Это наиболее часто встречающееся правило. Но, при более глубоком изучении математики становится ясно, что и из меньшего числа можно вычесть большее. Тогда получится результат со знаком «-«.

Пример: 5 — 7 = — 2,

Но дело в том, что разность показывает:

— чем отличаются числа,

— на сколько они отличаются,

— на сколько одно число больше другого,

— на сколько одно число меньше другого,

— отличаются ли числа, или они равны.

Следовательно, разность не может выражаться со знаком «-«. Иначе, она не будет иметь логического смысла. Поэтому, в ситуациях, когда из меньшего вычитается большее, берется модуль разности, то есть число без минуса «-«. Знак «модуля» в математике обозначается двумя вертикальными линиями, между которыми пишется число. Модуль всегда положительный.

Общее понимание разности чисел

Математика включает себя бесконечное количество различных чисел, не только целых, но и дробных. Разность дробей находится аналогичным способом.

Пример: 1 — 1/4 = 3/4,

Разность 3/4, уменьшаемое 1, вычитаемое 1/4.

То же самое можно проводить с процентами, буквенными и числовыми выражениями в скобках.

Как проверить, верно ли найдена разность

В математических вычислениях большую роль играет проверка. Когда решен пример по поиску разности, чтобы проверить его правильность, нужно совершить обратное действие.

Пример: 8 — 5 = 3, (разность 3),

Чтобы совершить проверку, сделаем известное уменьшаемое неизвестным. Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.

Тогда получим: 5 + 3 = 8 (получилось 8, как и было, следовательно, пример решен верно).

Общее понимание разности чисел

Второй способ проверки: 8 — 3 = 5 (тоже верно). Чтобы найти вычитаемое, из уменьшаемого отнимают разность.

То есть, чтобы уметь проверять правильность решения, важно знать не только, как найти разность, но и как вычисляются уменьшаемое и вычитаемое.

Бывают примеры, когда разность равна нулю (0). Это означает, что уменьшаемое и вычитаемое равны между собой. Нет между ними разности, различия.

Сложные примеры с разностью

В математике помимо стандартного нахождения разности существует множество усложненных вычислений, которые можно решать не в одно действие.

Пример: Из уменьшаемого 40 нужно отнять два вычитаемых 10 и 15.

Данный пример можно вычислить одним действием или двумя.

Решение в одно действие: 40 — 10 — 15 = 15,

Решение в два действия:

Сначала находим сумму: 10 + 15 = 25,

Главное, чтобы ответы совпали в обоих способах.

Общее понимание разности чисел

Также, может вызвать затруднение пример: Утройте разность. В данном случае нужно будет найти разность чисел и умножить ее на 3.

Навык нахождения разности бесспорно важен. Но не более и не менее, чем навыки нахождения суммы, произведения, частного. В математике все взаимосвязано и без одних знаний невозможно получить другие. Не зря говорят, что математика является «царицей наук», и ее азы используются повсеместно.

Поэтому, для достижения успеха в математике одной лишь школьной программы будет не достаточно. Для достижения максимальных результатов в изучении этого предмета мы рекомендуем начать посещать курсы по математике для школьников в Москве. Обучение на этих курсах проходит по запатентованной методологии в малых группах. Это увеличивает эффективность занятий в несколько раз.

Что такое частное в математике?

Математика – уникальная наука, которая привлекает точностью и последовательностью. Каждый, кто начал изучать эту важную дисциплину, должен разобраться, что такое частное в математике.

Деление

В математике есть четыре простейших операции:

• Сложение
• Вычитание
• Деление
• Умножение

Если мы говорим о частном, то нас будет интересовать такая операция, как деление.

Деление всегда обратно умножению. Это математическая величина, которую мы получим, разделив одно число на другое. Есть ряд символов, которые обозначают его:

• Двоеточие (:)
• Косая черта (/)
• Обелюс (тире между двумя точками ÷)

В учебных пособиях для учеников 1 – 5 классов есть простое и точное определение этого понятия. Деление – это операция, в результате которой мы получаем число, которое при умножении на делитель дает делимое. Число, о котором говорится в первой части определения, и есть частное.

Частное рассказывает, во сколько раз одно число больше другого.

Наглядные примеры

Чтобы лучше понять, что такое частное чисел в математике, следует обратиться к примерам. Они помогут разложить знания по полочкам в вашей голове. Решение примеров – это лучший тренажер для усвоения новых знаний. Приступим к их решению.

Итак, частное получается, если делимое поделить на делитель. При помощи символов эту операцию можно записать следующим образом:

a:b=c

Запишем простой пример из математики:

80:2=40

80 – делимое (оно делится)

2 – это делитель (на него разделяют)

Восемьдесят больше, чем сорок, в два раза.

Другой пример выглядит так:

120:2=60

Сто двадцать больше, чем шестьдесят, в два раза.

Проверка

Если вы провели операцию деления и сомневаетесь в результате, на помощь придет проверка. Для этого умножьте делитель на частное. Если в результате вы получили делимое, то пример решен верно:

Если после знака равно вы увидели знакомое вам делимое, то можете поставить себе твердую пятерку. Вы научились находить частное чисел и делать проверку. Это очень важно, чтобы в дальнейшем освоить более сложные понятия в алгебре и геометрии.

Частное – это основа математики. Если ученик не смог понять его суть, то двигаться дальше просто бессмысленно. Обратитесь к учителю, если это понятие так и осталось для вас туманным. Педагог разъяснит все ошибки и укажет на подводные камни.

Полное и неполное частное

В результате проведения математических подсчетов частное может быть двух видов:

• Полное. В результате деления мы получаем целое число:

100:2=50

50 – полное частное

• Неполное. Если в результате мы получаем остаток:

51:2=25 (остаток 1)

25 – неполное частное

1 – остаток от деления

Если вы откроете учебник математики, то увидите, что частное в задачах обозначают при помощи различных символов (переменных). Для этого используют латинские буквы:

30:6=x

Чтобы найти частное, следует делимое разделить на делитель:

Ответ 5 – это частное в данном примере.

Абстрактные определения и туманные рассуждения плохо усваиваются мозгом школьника. Поэтому всегда держите под рукой задачник со списком упражнений по математике. Он поможет понять различные математические категории на практике. Конкретные цифры, записанные в тетради, станут главными помощниками.