Что такое сумма коэффициентов полученного многочлена первой степени

Что такое сумма коэффициентов полученного многочлена первой степени

Многочленом с одной переменной называется выражение вида

`P(x) = a_n x^n + a_(n-1) x^(n-1) +a_(n-2) x^(n-2) + . + a_2 x^2 + a_1 x + a_0 (a_n != 0)`. (8)

Числа `a_0`, `a_1`, `. `, `a_n` — это коэффициенты многочлена; `a_n` называют старшим коэффициентом, `a_0` — свободным членом.

Степенью многочлена называют наибольшую степень переменной, входящую в многочлен.

Например, степень многочлена `P = x^4 — x^3 — x^2 + 2x + 1` равна `4`; степень многочлена `25 + x^5 — 3x` равна `5`; степень многочлена `17` равна `0`, т. к. переменная в это выражение не входит; наконец, выражение `3x^2 + x +5+ 2/x` многочленом не является, поэтому о его степени говорить бессмысленно. Многочлен `P(x) = 0` называют нулевым многочленом. Степень нулевого многочлена не определена.

Два многочлена называются равными, если равны все их коэффициенты. Многочлен равен нулю, если все его коэффициенты равны нулю.

Число `a` называется корнем многочлена `F(x)`, если `F(alpha) = 0`.

Приведём основные сведения о многочленах.

Для любых двух многочленов `F(x)` и `G(x)` существует единственная пара многочленов `P(x)` (частное) и `Q(x)` (остаток) такая, что `F(x) = G(x) * P(x) + Q(x)`, причём степень остатка `Q(x)` меньше степени делителя `G(x)`, или `Q(x)` есть нулевой многочлен. Покажем, как на практике находят частное и остаток от деления многочленов.

Разделите с остатком многочлен `F(x) = 18x^5 + 27x^4 -37x^3 — 14x + 20`

на многочлен `G(x) = 2x^2 + 3x -5`.

Процедура деления многочленов очень похожа на деление целых чисел. Если степень делимого не меньше степени делителя, то делаем следующее: делим старший член многочлена `F(x)` на старший член многочлена `G(x)`, получившийся результат записываем в частное. Умножаем результат на весь делитель `G(x)` и вычитаем полученное из исходного многочлена `F(x)`. После этих действий член со старшей степенью `x` сокращается. Если в результате вычитания у оставшегося многочлена степень не меньше, чем степень делителя, то можно сделать ещё один шаг деления и т. д.

Деление закончится тогда, когда степень делимого будет меньше степени делителя. В случае, когда в делимом отсутствуют некоторые степени переменных, для удобства записи лучше оставить пустые места для соответствующих членов (хотя это не обязательно).

Вернёмся к нашему примеру. Первый член частного равен `(18x^5)/(2x^2) = 9x^3`. При умножении на делитель `2x^2 +3x-5` получаем `18x^5 + 27x^4 — 45x^3`. После вычитания из исходного многочлена от него остаётся `8x^3 -14x +20`. Степень многочлена, оставшегося после вычитания, равна `3`. Это больше степени делителя, поэтому можно сделать следующий шаг деления. Делим `8x^3` на `2x^2` и получаем `4x`, умножаем `4x` на `2x^2 +3x-5`, получаем `8x^3 +12x^2 -20`; вычитаем этот многочлен из `8x^3 -14x +20` и т. д.

Частное равно `9x^3 +4x -6`; остаток равен `24x-10`.

Таким образом, `18x^5 + 27x^4 — 37x^3 -14x + 20 = (2x^2 + 3x — 5)(9x^3 + 4x — 6) + (24x — 10)`.

Теорема 2. (Теорема Безу и следствия из неё).

1) Теорема Безу. Остаток от деления многочлена `F(x)` на многочлен `(x-alpha)` равен `F(alpha)`.

2) Число `alpha` является корнем многочлена `F(x)` тогда и только тогда, когда многочлен `F(x)` делится на многочлен `(x-alpha)`.

3) Если `alpha` и `beta` — различные корни многочлена `F(x)`, то он делится на многочлен `(x- alpha)(x- beta)`.

4) Многочлен степени `n` не может иметь более `n` корней.

1) Разделим с остатком многочлен `F(x)` на многочлен `(x-alpha)`. Тогда остаток либо равен нулю, либо является многочленом нулевой степени (т. к. степень остатка меньше степени делителя, а степень делителя равна `1`). Поэтому можно записать, что

`F(x) = (x-alpha) G(x) +C` (9)

Через `G(x)` здесь обозначено частное от деления, вид которого нас не интересует.

Равенство (9) верно при всех значениях `x`. Подставим в него `x=alpha`.

Тогда `F(alpha) = (alpha — alpha)G(alpha) + C`, или `F(alpha) = C`.

Подставим `C=F(alpha)` в (9) и получим

`F(x) = (x — alpha) G (x) + F(alpha)`. (10)

Первая часть доказана.

2) Из (10) следует, что `F(x)` делится на `(x — alpha)` тогда и только тогда, когда `F(alpha) = 0`, т. е. тогда и только тогда, когда `alpha` есть корень многочлена `F(x)`.

3) `alpha` — корень `F(x) => F(x)` делится на `(x- alpha) => F(x) = (x- alpha) G(x)`. Подставим в последнее равенство (которое верно для всех значений переменной `x`) `x= beta`. Тогда `F(beta) = (beta — alpha) G(beta)`.

`F(beta) = 0` (т. к. `beta` -корень `F(x)`), поэтому `(beta — alpha)G(beta) = 0 =>G(beta) = 0` (т. к. `beta != alpha`); отсюда `G(x)` делится на `(x- beta)`, т. е. `G(x) = H(x) * (x- beta)`. Подведём итог: `F(x) = (x- alpha) G(x) = (x -alpha)(x- beta) H(x)`, т. е. `F(x)` делится на `(x- alpha)(x- beta)`.

4) Теперь становится понятным, что многочлен степени `n` не может иметь больше, чем `n` корней.

Остатки от деления многочлена `F(x)` на многочлены `(x-3)` и `(x+5)` равны `2` и `(-9)` соответственно. Найдите остаток от деления многочлена `F(x)` на многочлен `x^2 + 2x -15`.

Заметим, что `x^2 + 2x -15 = (x-3)(x+5)`.

По теореме Безу `F(3) = 2`; `F(-5) =-9`.

Поделим `F(x)` с остатком на `x^2 + 2x -15`:

`F(x) = (x^2 + 2x — 15)G(x) + r(x)`.

Степень остатка не превосходит степени делителя, поэтому остаток – это либо многочлен первой степени, либо нулевой степени, либо равен нулю. В любом случае, остаток представим в виде `r(x) = ax +b` (если `a!= 0`, то получим многочлен первой степени; если `a=0`, `b!=0`, то будет многочлен нулевой степени; если `a=b=0`, то получим нулевой многочлен). Итак,

`F(x) = (x^2 + 2x-15)G(x) + ax+b`. (11)

Подставим в равенство (11) `x=3` и `x=-5`:

`F(3) = 0 * G(3) + 3a + b`; `F(-5)=0 * G(-5) -5a+b`, откуда $$ left3a+b=2,\ -5a+b=-9.endright.$$

Решая эту систему, нахоим, что `a=(11)/8`, `b=- (17)/8`.

Пусть $$ sqrt[3]>+sqrt[3]>=x$$. Возведём обе части этого равенства в куб и преобразуем:

Число `x=4` является корнем этого уравнения. Докажем, что других корней нет (и тем самым будет доказана справедливость равенства (12)). Поскольку `x=4` является корнем, многочлен `x^3 — 3x-52` делится на `x-4` без остатка. Выполняя деление, получаем:

У квадратного трёхчлена `x^2 +4x+13` отрицательный дискриминант, поэтому уравнение (13) имеет ровно один корень `x=4`.

При каких `a` и `b` многочлен `F(x)=x^4 +ax^3 — 2x^2 +19x+b` делится на многочлен `x^2 -3x+2`?

1-й способ. Выполним деление с остатком:

Приравниваем коэффициенты остатка к нулю

2-й способ. `x^2 -3x+2=(x-1)(x-2)`.

Многочлен делится на `(x-1)(x-2)` тогда и только тогда, когда `x=1` и `x=2` являются корнями многочлена. То есть,

Многочлен, его стандартный вид, степень и коэффициенты членов

После изучения одночленов переходим к многочленам. Данная статья расскажет о всех необходимых сведениях, необходимых для выполнения действий над ними. Мы определим многочлен с сопутствующими определениями члена многочлена, то есть свободный и подобный, рассмотрим многочлен стандартного вида, введем степень и научимся ее находить, поработаем с его коэффициентами.

Многочлен и его члены – определения и примеры

Определение многочлена было дано еще в 7 классе после изучения одночленов. Рассмотрим его полное определение.

Многочленом считается сумма одночленов, причем сам одночлен – это частный случай многочлена.

Из определения следует, что примеры многочленов могут быть различными: 5 , 0 , − 1 , x , 5 · a · b 3 , x 2 · 0 , 6 · x · ( − 2 ) · y 12 , — 2 13 · x · y 2 · 3 2 3 · x · x 3 · y · z и так далее. Из определения имеем, что 1 + x , a 2 + b 2 и выражение x 2 — 2 · x · y + 2 5 · x 2 + y 2 + 5 , 2 · y · x являются многочленами.

Рассмотрим еще определения.

Членами многочлена называются его составляющие одночлены.

Рассмотрим такой пример, где имеем многочлен 3 · x 4 − 2 · x · y + 3 − y 3 , состоящий из 4 членов: 3 · x 4 , − 2 · x · y , 3 и − y 3 . Такой одночлен можно считать многочленом, который состоит из одного члена.

Многочлены, которые имеют в своем составе 2 , 3 трехчлена имеют соответственное название – двучлен и трехчлен.

Отсюда следует, что выражение вида x + y – является двучленом, а выражение 2 · x 3 · q − q · x · x + 7 · b – трехчленом.

По школьной программе работали с линейным двучленом вида a · x + b , где а и b являются некоторыми числами, а х – переменной. Рассмотрим примеры линейных двучленов вида: x + 1 , x · 7 , 2 − 4 с примерами квадратных трехчленов x 2 + 3 · x − 5 и 2 5 · x 2 — 3 x + 11 .

Для преобразования и решения необходимо находить и приводить подобные слагаемые. Например, многочлен вида 1 + 5 · x − 3 + y + 2 · x имеет подобные слагаемые 1 и — 3 , 5 х и 2 х . Их подразделяют в особую группу под названием подобных членов многочлена.

Подобные члены многочлена – это подобные слагаемые, находящиеся в многочлене.

В примере, приведенном выше, имеем, что 1 и — 3 , 5 х и 2 х являются подобными членами многочлена или подобными слагаемыми. Для того, что бы упростить выражение, применяют нахождение и приведение подобных слагаемых.

Многочлен стандартного вида

У всех одночленов и многочленов имеются свои определенные названия.

Многочленом стандартного вида называют многочлен, у которого каждый входящий в него член имеет одночлен стандартного вида и не содержит подобных членов.

Из определения видно, что возможно приведение многочленов стандартного вида, например, 3 · x 2 − x · y + 1 и __formula__, причем запись в стандартном виде. Выражения 5 + 3 · x 2 − x 2 + 2 · x · z и 5 + 3 · x 2 − x 2 + 2 · x · z многочленами стандартного вида не является, так как первый из них имеет подобные слагаемые в виде 3 · x 2 и − x 2 , а второй содержит одночлен вида x · y 3 · x · z 2 , отличающийся от стандартного многочлена.

Если того требуют обстоятельства, иногда многочлен приводится к стандартному виду. Многочленом стандартного вида считается и понятие свободного члена многочлена.

Свободным членом многочлена является многочлен стандартного вида, не имеющий буквенной части.

Иначе говоря, когда запись многочлена в стандартном виде имеет число, его называют свободным членом. Тогда число 5 является свободным членом многочлена x 2 · z + 5 , а многочлен 7 · a + 4 · a · b + b 3 свободного члена не имеет.

Степень многочлена – как ее найти?

Определение самой степени многочлена базируется на определении многочлена стандартного вида и на степенях одночленов, которые являются его составляющими.

Степенью многочлена стандартного вида называют наибольшую из степеней, входящих в его запись.

Рассмотрим на примере. Степень многочлена 5 · x 3 − 4 равняется 3 , потому как одночлены, входящие в его состав, имеют степени 3 и 0 , а большее из них 3 соответственно. Определение степени из многочлена 4 · x 2 · y 3 − 5 · x 4 · y + 6 · x равняется наибольшему из чисел, то есть 2 + 3 = 5 , 4 + 1 = 5 и 1 , значит 5 .

Следует выяснить, каким образом находится сама степень.

Степень многочлена произвольного числа — это степень соответствующего ему многочлена в стандартном виде.

Когда многочлен записан не в стандартном виде, но нужно найти его степень, необходимо приведение к стандартному, после чего находить искомую степень.

Найти степень многочлена 3 · a 12 − 2 · a · b · c · a · c · b + y 2 · z 2 − 2 · a 12 − a 12 .

Для начала представим многочлен в стандартном виде. Получим выражение вида:

3 · a 12 − 2 · a · b · c · a · c · b + y 2 · z 2 − 2 · a 12 − a 12 = = ( 3 · a 12 − 2 · a 12 − a 12 ) − 2 · ( a · a ) · ( b · b ) · ( c · c ) + y 2 · z 2 = = − 2 · a 2 · b 2 · c 2 + y 2 · z 2

При получении многочлена стандартного вида получаем, что отчетливо выделяются два из них − 2 · a 2 · b 2 · c 2 и y 2 · z 2 . Для нахождения степеней посчитаем и получим, что 2 + 2 + 2 = 6 и 2 + 2 = 4 . Видно, что наибольшая из них равняется 6 . Из определения следует, что именно 6 является степенью многочлена − 2 · a 2 · b 2 · c 2 + y 2 · z 2 , следовательно и исходного значения.

Коэффициенты членов многочлена

Когда все члены многочлена являются одночленами стандартного вида, то в таком случаем они имеют название коэффициентов членов многочлена. Иначе говоря, их можно называть коэффициентами многочлена.

При рассмотрении примера видно, что многочлен вида 2 · x − 0 , 5 · x · y + 3 · x + 7 имеет в своем составе 4 многочлена: 2 · x , − 0 , 5 · x · y , 3 · x и 7 с соответствующими их коэффициентами 2 , − 0 , 5 , 3 и 7 . Значит, 2 , − 0 , 5 , 3 и 7 считаются коэффициентами членов заданного многочлена вида 2 · x − 0 , 5 · x · y + 3 · x + 7 . При преобразовании важно обращать внимание на коэффициенты, стоящие перед переменными.

Многочлен стандартного вида

Стоило только разобраться с одночленами, как неугомонная алгебра принесла нам новое испытание. Многочлены — кто они такие, стоит ли их опасаться и что предпринимать при встрече с ними лицом к лицу в 7 классе.

О чем эта статья:

Определение многочлена

Многочлен — это сумма одночленов. Получается, что многочлен — не что иное, как несколько одночленов, собранных «под одной крышей».

Одночлен — это произведение, состоящее из числового множителя и одной или нескольких переменных, каждая из которых взята в неотрицательной степени.

Рассмотрим примеры многочленов:

Если многочлен состоит из двух одночленов, его называют двучленом:

• 10x − 3x 2
• 10x — одночлен
• −3x 2 — одночлен

Многочлен — это сумма одночленов, поэтому знак «минус» относится к числовому коэффициенту одночлена. Именно поэтому мы записываем −3x 2 , а не просто 3x 2 .

Этот же многочлен можно записать вот так:

• 10x – 3x 2 = 10x − 3x 2 = 10x + (−3x 2 ).

Это значит, что каждый одночлен важно рассматривать вместе со знаком, который перед ним стоит.

Многочлен вида 10x − 3x 2 + 7 называется трехчленом.

Линейный двучлен — это многочлен первой степени: ax + b. a и b здесь — некоторые числа, x — переменная.

Если разделить многочлен с переменной x на линейный двучлен x − b (где b — некоторое положительное или отрицательное число) — остаток будет только многочленом нулевой степени. То есть некоторым числом N, которое можно определить без поиска частного.

Если многочлен содержит обычное число — это число является свободным членом многочлена.

• Например, в многочлене 6a + 2b − x + 2 число 2 — свободный член.

Свободный член многочлена не имеет буквенной части. Кроме того, любое числовое выражение — это многочлен. Например, вот такие числовые выражения — тоже многочлены:

• 16 + 13
• (7 − 2) ∙ 9
• (25 + 25) : 5

Такие выражения состоят из свободных членов.

Коэффициенты многочлена

Коэффициенты членов многочлена — это числа, которые указаны перед переменными множителями. Если перед переменной нет числа, то коэффициент этого члена = 1.

Иными словами — коэффициенты членов многочлена — это члены многочлена, представленные в виде стандартных одночленов.

Например:

Дан многочлен 2x + 5x − 18y

Все одночлены имеют стандартный вид. 2, 5 и 18 — коэффициенты членов данного многочлена.

Многочлен стандартного вида

Недостаточно просто знать, что такое многочлен и что такое одночлен. Это целая алгебраическая экосистема, где у всего есть названия, определения и особенности.

Давайте разберемся, что такое многочлен стандартного вида. Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов.

Получается, что всякий многочлен можно привести к стандартному виду. Таким образом можно получить многочлен, работать с которым гораздо проще и приятнее.

К стандартному виду многочлен приводится очень просто. Нужно лишь привести в нем подобные слагаемые.

Подобные слагаемые — это подобные члены многочлена. Приведение подобных слагаемых в многочлене — приведение его подобных членов. Тут же возникает резонный вопрос: Что такое подобные члены многочлена? Это члены с одинаковой буквенной частью.

Давайте разберем на примере, как «нестандартный» многочлен приводится к стандартному виду.

Дан красавец многочлен: 3x + 5xy 2 + x − xy 2

Приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

• 3x и x — подобные слагаемые.
• 5xy 2 и −xy 2 — подобные слагаемые.

Получаем многочлен вот такого вида: 3x + 5xy 2 + x − xy 2 = 4x + 4xy 2 .

Как видите, в получившемся многочлене нет подобных членов. Такой многочлен — это многочлен стандартного вида.

Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.

Степень многочлена

Многочлен может иметь степень — имеет на это полное право.

Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов.

Из определения можно сделать вывод, что степень многочлена возможно определить только после приведения его к стандартному виду.

1. Приводим многочлен к стандартному виду.
2. Выбираем одночлен с наибольшей степенью.

Рассмотрим на примере:

Дан многочлен 6x + 4xy 2 + x + xy 2

Сначала приводим многочлен к стандартному виду — для этого приводим подобные слагаемые:

• 6x и x — подобные слагаемые
• 4xy 2 и xy 2 — подобные слагаемые

Получаем многочлен стандартного вида 6x + 4xy 2 + x + xy 2 = 7x + 5xy 2 .

• Степень первого одночлена (7x) — 1.
• Степень второго одночлена (5xy 2 ) — 3.
• Наибольшая из двух степеней — 3.

Отсюда делаем вывод, что многочлен 7x + 5xy 2 — многочлен третьей степени.

Кроме того, можно сделать вывод, что и исходный многочлен 6x + 4xy 2 + x + xy 2 — многочлен третьей степени, поскольку оба многочлена равны друг другу.

В некоторых случаях необходимо сначала привести к стандартному виду одночлены многочлена, а затем уже и сам многочлен.

Пример:

Дан многочлен 6xx 2 + 5xx 2 − 3xx 3 − 3x 2 x

Приведем его к стандартному виду: 6xx 3 + 5xx 2 − 3xx 3 − 3x 2 x = 6x 4 + 5x 3 − 3x 4 − 3x 3

Получившийся многочлен без труда приводим к стандартному виду. Приводим подобные слагаемые:

• 5x 3 и −3x 3 — подобные слагаемые.
• 6x 4 и −3x 4 — подобные слагаемые.
• 6x 4 + 3x 3 − 3x 4 − 3x 3 = 3x 4 − 2x 3
• 6xx 3 + 5xx 2 − 3xx 3 − 3x 2 x — многочлен четвертой степени.

Практика

Кажется, со стандартным видом многочлена все понятно. Чтобы без труда приводить любой многочлен к стандартному виду, нужно потренироваться, ведь в 7 классе только и разговоров, что о многочленах. Давайте разберем несколько примеров. Попробуйте решить их самостоятельно, сверяясь с ответами.

Задание раз. Приведите многочлен к стандартному виду и определите его степень: 4x + 6xy 2 + x − xy 2 .

Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

• 4x и x — подобные слагаемые.
• 6xy 2 и −xy 2 — подобные слагаемые.

Получаем многочлен стандартного вида: 4x + 6xy 2 + x − xy 2 = 5x + 5xy 2 .

Ответ: стандартный вид многочлена 5x + 5xy 2 . Данный многочлен — многочлен второй степени.

Задание два. Приведите многочлен к стандартному виду: 2x 2 y 3 − xy 3 − x 4 − x 2 y 3 + xy 3 + 2x 4 .

Как решаем: сначала необходимо привести все одночлены к стандартному виду: 2x 2 y 3 − xy 3 − x 4 − x 2 y 3 + xy 3 + 2x 4 = (−x 4 + 2x 4 ) + (2x 2 y 3 − x 2 y 3 ) + (− xy 3 + xy 3 ) = x 4 + x 2 y 3 + 0 = x 4 + x 2 y 3 .

Многочлен приведен к стандартному виду.

Ответ: x 4 + x 2 y 3

Задание три. Приведите многочлен к стандартному виду и определите его степень: 8x + 8xy 2 − x + xy 2 .

Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

• 8x и −x — подобные слагаемые.
• 8xy 2 и xy 2 — подобные слагаемые.

Получаем многочлен стандартного вида: 8x + 8xy 2 − x + xy 2 = 7x + 9xy 2 .

Ответ: стандартный вид многочлена 7x + 9xy 2 , данный многочлен — многочлен третьей степени.

Разобраться в многочленах не так-то просто. В этой теме немало нюансов и подводных камней. Чтобы не запутаться в множестве похожих одно на другое определений, побольше практикуйтесь. Чтобы перейти на следующую ступень и начать выполнение арифметических действий с многочленами, важно научиться приводить многочлен к стандартному виду.

Многочлены

Говорят, что степень многочлена равна $n$, если его наибольший ненулевой коэффициент стоит у $x^n$.

Многочлены, подобно скалярам, можно складывать, вычитать и умножать, получая другие многочлены. Многочлены также можно делить, но результат не всегда получается многочленом. В этом смысле множество многочленов является кольцом, подобно кольцу остатков по модулю.

#Представление многочленов и чисел

Программно представлять многочлен проще всего через vector или обычный статический массив, содержащий его коэффициенты по порядку. Помимо непосредственно многочленов, удобно представлять в таком виде и длинные числа, притворившись, что $x$ равно $10$ или основанию любой другой системы счисления:

$$ begin A(x) &= a_0 + a_1cdot x + a_2 cdot x^2 + dots + a_n cdot x^n \ &= a_0 + a_1cdot 10 + a_2 cdot 10^2 + dots + a_n cdot 10^n end $$

При операциях с длинными числами (например, при умножении), можно проводить соответствующую операцию с многочленами, а затем производить каррирование результата: проходить от нижних разрядов получившегося многочлена к верхним и «сдвигать» переполнившиеся разряды:

Из соображений производительности следует выбирать настолько большое основание, насколько вмещается в используемый тип данных (например, $10^9$ или $2^$ для int ).

#Коэффициенты разложений

Коэффициенты при $a^x b^y$, получаемые при возведении бинома $(a+b)$ в $n$-ную степень, называются биномиальными коэффициентами:

$$ (a + b)^n = sum_^n C_n^k cdot a^k cdot b^ $$ Их удобно считать по следующей формуле: $$ C_n^k = binom = frac <(n - k)! k!>$$ В более общем случае определяют полиномиальный коэффициент, равный количеству раз, которое элемент $a_1^ a_2^ ldots a_k^$ появится при раскрытии скобки $(a_1+a_2+ldots+a_k)^n$: $$ P(x_1, x_2, ldots, x_k) = frac $$

Биномиальные коэффициенты применяются в комбинаторике и в отрыве от многочленов. В задачах по программированию их подсчет часто требуется проводить по модулю, для чего нужно уметь искать обратные к факториалам.

#Умножение многочленов

При умножении двух многочленов степени $n$ и $m$ получается многочлен степени $(n+m)$. Прямая формула для произведения многочленов имеет вид

$$ left(sum_^n a_i x^iright)cdotleft(sum_^m b_j x^jright)=sum_^x^ksum_a_i b_j $$

Её наивный подсчёт требует $O(n^2)$ операций, но далее в этой главе мы разберем несколько более эффективных алгоритмов — самый быстрый из которых работает всего за $O(n log n)$.

Этот факт позволяет сводить много комбинаторных задач к произведению многочленов и использованию уже известных алгоритмов для его подсчета. Разберем несколько примеров таких задач.

#2-рюкзак

Даны два массива $a$ и $b$ размера $n$ и $m$. Требуется найти число различных возможных сумм $(a_i + b_j)$.

$n, m, a_i, b_i le 10^5$.

Рассмотрим многочлены $A(x)$ и $B(x)$, в которых коэффициент при $k$-той степени равен числу равных $k$ элементов в соответствующем массиве.

Рассмотрим произведение $C = A cdot B$. В получившемся многочлене коэффициент $c_t$ при $x^t$ будет равен

$$ c_t cdot x^t = sum_ a_p cdot b_q cdot x^ $$

что в свою очередь равно количеству способов набрать сумму ровно $t$.

Значит, мы можем перемножить эти два многочлена за $O(n log n)$ и просто подсчитать число ненулевых коэффициентов результата.

#Мульти-рюкзак

Задача «Вор в магазине» является небольшой модификацией предыдущей:

Имеется $n$ типов предметов различных целых стоимостей $a_i$. Требуется найти количество различный сумм стоимостей наборов из ровно $k$ предметов (возможно, с повторениями).

$n, k, a_i le 1000$

Опять же, рассмотрим многочлен, в котором коэффициент при $i$-той степени равен единице, если существует предмет со стоимостью $i$, и нулю в противном случае.

Если $k=2$, наша задача свелась к предыдущей: нужно домножить многочлен на самого себя и посмотреть на число ненулевых коэффициентов. В общем же случае нам нужно возвести многочлен в степень $k$ и также посчитать ненулевые коэффициенты результата.

Если возводить многочлен в $k$-ную степень наивно, то асимптотика такого решения будет $O(n k^2 log (nk))$: нужно $O(k)$ раз перемножать два многочлена, больший из которых имеет длину $O(nk)$.

Воспользуемся бинарным возведением в степень: умножение многочленов ведь ассоциативно. В данном случае асимптотика будет не более $O(nk log (nk) log k)$: нужно $O(log k)$ раз умножать два многочлена порядка $O(nk)$. Но на самом деле, так как на каждой итерации размер многочлена будет увеличиваться в два раза, в асимптотике учтется только последнее (самое большое) умножение, и поэтому в действительности время работы составит $O(nk log (nk))$.

#Свёртки

Свёрткой (англ. convolution) называется операция применения некоторой «оконной» функции ко всем отрезкам фиксированной длины исходной функции.

Свёртка «площадь функции на единичном отрезке»

В дискретном случае свертке соответствует сумме вида

$$ (f * g)(x)= f(1) cdot g(x-1) + f(2) cdot g(x-2) + dots + f(k) cdot g(x — k) $$ В ещё более узком смысле, свертка это результат перемножения многочленов: $$ (A cdot B)_k = a_0 cdot b_k + a_1 cdot b_ + ldots + a_k cdot b_0 $$

то есть $k$-тый коэффициент результата равен применению какой-то оконной функции, заданной коэффициентами $B(x)$, к коэффициентам $A(x)$. Значит, подобные функции можно быстро считать через матричное умножение.

Например, так можно (неэффективно) искать битовую подстроку $t$ в строке $s$: запишем символы $s$ как коэффициенты многочлена $A(x)$ и символы $t$ в обратном порядке как коэффициенты многочлена $B(x)$ и перемножим. В позициях многочлена-результата, где коэффициенты равны $|t|$, строка $t$ входит в $s$.

Также с помощью этого трюка можно решать и другие задачи, например выполнять «fuzzy searching»: коэффициенты, равные $(|t|-d)$, соответствуют вхождениям с ровно $d$ ошибками.

Многочлен — виды, определение с примерами решения

Многочлен – это сумма одночленов, причем сам одночлен — это частный случай многочлена.

Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена

Многочлены от одной переменной и действия над ними

Определение многочленов от одной переменной и их тождественное равенство

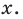
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной

По определению одночлена числа и буквы (в нашем случае одна буква — ) в нем связаны только двумя действиями — умножением и возведением в натуральную степень. Если в этом одночлене произведение всех чисел записать перед буквой, а произведение всех степеней буквы записать как целую неотрицательную степень этой буквы (то есть записать одночлен в стандартном виде), то получим выражение вида , где — некоторое число. Поэтому одночлен от одной переменной — это выражение вида где — некоторое число, — целое неотрицательное число. Если то показатель степени переменной называется степенью одночлена. Например, — одночлен шестой степени, — одночлен второй степени. Если одночлен является числом, не равным нулю, то его степень считается равной нулю. Для одночлена, заданного числом 0, понятие степени не определяется (поскольку ).

По определению многочлен от одной переменной — это сумма одночленов от одной переменной . Поэтому

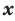
многочленом от одной переменной : называется выражение вида

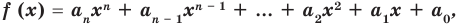
(1)

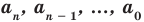
где коэффициенты — некоторые числа.

Если , то этот многочлен называют многочленом степени от переменной . При этом член называют старшим членом многочлена , число — коэффициентом при старшем члене, а член — свободным членом. Например, — многочлен третьей степени, у которого свободный член равен 1, а коэффициент при старшем члене равен 5.

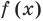
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена записывают так:

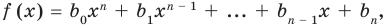
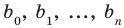
где — некоторые числа.

Теорема 1. Одночлены где и где , тождественно равны тогда и только тогда, когда и Одночлен тождественно равен нулю тогда и только тогда, когда

Поскольку равенство одночленов

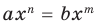
(2)

выполняется при всех значениях (по условию эти одночлены тождественно равны), то, подставляя в это равенство , получаем, что Сокращая обе части равенства (2) на (где по условию), получаем При из этого равенства имеем: Поскольку 2 то равенство возможно только тогда, когда Таким образом, из тождественного равенства получаем, что и Если известно, что для всех то при получаем Поэтому одночлен тождественно равен нулю при (тогда ).

Далее любой одночлен вида будем заменять на 0.

Теорема 2. Если многочлен тождественно равен нулю (то есть принимает нулевые значения при всех значениях ), то все его коэффициенты равны нулю.

Значком обозначено тождественное равенство многочленов.

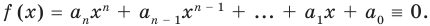
Для доказательства используем метод математической индукции. Пусть

При имеем поэтому То есть в этом случае утверждение теоремы выполняется.

Предположим, что при это утверждение также выполняется: если многочлен то

Докажем, что данное утверждение выполняется и при Пусть (3)

Поскольку равенство (3) выполняется при всех значениях , то, подставляя в это равенство получаем, что Тогда равенство (3) обращается в следующее равенство: Вынесем в левой части этого равенства за скобки и получим

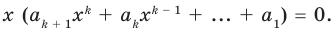
(4)

Равенство (4) должно выполняться при всех значениях . Для того чтобы оно выполнялось при должно выполняться тождество

В левой части этого тождества стоит многочлен со степенями переменной от до Тогда по предположению индукции все его коэффициенты равны нулю: Но мы также доказали, что поэтому наше утверждение выполняется и при Таким образом, утверждение теоремы справедливо для любого целого неотрицательного то есть для всех многочленов.

Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают или просто (поскольку ).

Теорема 3. Если два многочлена и тождественно равны, то они совпадают (то есть их степени одинаковы и коэффициенты при одинаковых степенях равны).

Пусть многочлен , а многочлен Рассмотрим многочлен Поскольку многочлены и по условию тождественно равны, то многочлен тождественно равен 0. Таким образом, все его коэффициенты равны нулю.

Но Тогда Отсюда Как видим, если допустить, что у какого-то из двух данных многочленов степень выше, чем у второго многочлена (например, больше ), то коэффициенты разности будут равны нулю. Поэтому начиная с (-го номера все коэффициенты также будут равны нулю. То есть действительно многочлены и

имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.

Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.

Пример:

Докажите, что выражение

является полным квадратом.

Решение:

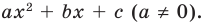
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида Получаем тождество:

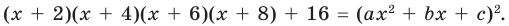
(5)

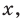
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях получаем систему равенств. Этот этап решения удобно оформлять в следующем виде:

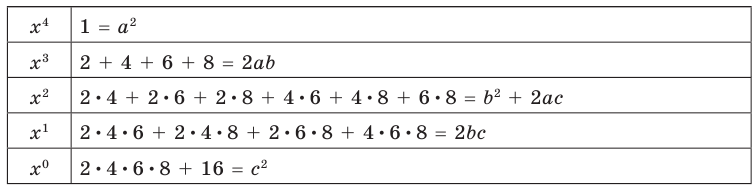
Из первого равенства получаем или

При из второго равенства имеем а из третьего — Как видим, при этих значениях и последние два равенства также выполняются. Следовательно, тождество (5) выполняется при (аналогично можно также получить ). Таким образом,

Действия над многочленами. Деление многочлена на многочлен с остатком

Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.

Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.

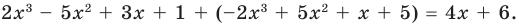
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, При сложении многочленов разных степеней всегда получаем многочлен, степень которого равна большей степени слагаемого.

Например, Деление многочлена на многочлен определяется аналогично делению целых чисел. Напомним, что целое число делится на целое число если существует такое целое число что

Определение: Многочлен делится на многочлен (где — не нулевой многочлен), если существует такой многочлен что

Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что

многочлен делится на многочлен (где — не нулевой многочлен) с остатком, если существует такая пара многочленов и что причем степень остатка меньше степени делителя (в этом случае многочлен называют неполным частным.)

Например, поскольку то при делении многочлена на многочлен получаем неполное частное : и остаток 2.

Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.

Пример №1

Разделим многочлен на многочлен

Решение:

Докажем, что полученный результат действительно является результатом деления на с остатком.

Если обозначить результат выполнения первого шага алгоритма через второго шага — через третьего — через то операцию деления, выполненную выше, можно записать в виде системы равенств:

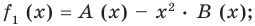
(1)

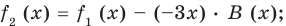
(2)

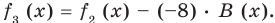
(3)

Сложим почленно равенства (1), (2), (3) и получим

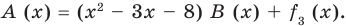
(4)

Учитывая, что степень многочлена меньше степени делителя обозначим (остаток), а (неполное частное). Тогда из равенства (4) имеем: то есть

а это и означает, что мы разделили на с остатком.

Очевидно, что приведенное обоснование можно провести для любой пары многочленов и в случае их деления столбиком. Поэтому описанный выше алгоритм позволяет для любых делимого и делителя (где — не нулевой многочлен) найти неполное частное и остаток

Отметим, что в случае, когда степень делимого меньше степени делителя , считают, что неполное частное а остаток

Теорема Безу. Корни многочлена. Формулы Виета

Рассмотрим деление многочлена на двучлен Поскольку степень делителя равна 1, то степень остатка, который мы получим, должна быть меньше 1, то есть в этом случае остатком будет некоторое число R. Таким образом, если разделить многочлен на двучлен , то получим

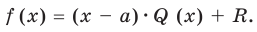
Это равенство выполняется тождественно, то есть при любом значении При имеем Полученный результат называют теоремой Безу.

Теорема 1 (теорема Безу). Остаток от деления многочлена на двучлен равен (то есть значению многочлена при ).

Пример №2

Докажите, что делится на без остатка.

Решение:

► Подставив в вместо значение 1, получаем: . Таким образом, остаток от деления на равен 0, то есть делится на без остатка.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Степень полинома: как определить, примеры и упражнения

Видео: Степень полинома: как определить, примеры и упражнения

Содержание:

В степень полинома в а переменная задается членом с наибольшим показателем, и если многочлен имеет две или более переменных, то степень определяется суммой показателей каждого члена, причем большая сумма является степенью полинома.

Давайте посмотрим, как определить степень многочлена на практике.

Предположим, что многочлен P (x) = -5x + 8x 3 + 7 — 4x 2 . Этот многочлен является одной переменной, в данном случае это переменная Икс. Этот многочлен состоит из нескольких членов, а именно:

-5x; 8x 3 ; 7; — 4x 2

Давайте выберем из четырех членов тот, у которого показатель больше, это член:

А теперь какой показатель? Ответ: 3. Следовательно, P (x) — многочлен степени 3.

Если рассматриваемый многочлен имеет более одной переменной, то степень может быть:

-По отношению к переменной

Абсолютная степень находится, как объяснено в начале: добавление показателей каждого члена и выбор наибольшего.

Вместо этого степень полинома по отношению к одной из переменных или букв является наибольшим значением показателя степени, которое имеет указанная буква. Суть станет яснее с примерами и решенными упражнениями в следующих разделах.

Примеры степени полинома

Многочлены могут быть классифицированы по степени: первая степень, вторая степень, третья степень и так далее. В примере на рисунке 1 энергия является одночленом первой степени массы.

Также важно отметить, что количество членов, которые имеет многочлен, равно класс плюс 1. Так:

-Полиномы первой степени имеют 2 члена:₁х + а_или

-У полинома второй степени есть 3 члена:₂Икс 2 + а₁х + а_или

-Полином третьей степени состоит из 4 членов:₃Икс 3 + а₂Икс 2 + а₁х + а_или

И так далее. Внимательный читатель заметит, что многочлены в предыдущих примерах записаны в виде уменьшение, то есть помещая термин на первое место Высокий класс.

В следующей таблице показаны различные полиномы, как от одной, так и от нескольких переменных, и их соответствующие абсолютные градусы:

Таблица 1. Примеры многочленов и их степеней.

Полиномиальный	Степень
3x 4 + 5x 3 -2x + 3	4
7x 3 -2x 2 + 3x-6	3
6	0
х-1	1
Икс 5 -bx 4 + abx 3 +ab 3 Икс 2	6
3x 3 Y 5 + 5x 2 Y 4 — 7xy 2 + 6	8

Последние два полинома имеют более одной переменной. Из них термин с наивысшей абсолютной степенью был выделен жирным шрифтом, чтобы читатель мог быстро проверить степень. Важно помнить, что если переменная не имеет записанного показателя степени, подразумевается, что указанный показатель равен 1.

Например, в избранном термине ab 3 Икс 2 есть три переменные, а именно: к, б Y Икс. В этот срок к повышается до 1, то есть:

Таким образом ab 3 Икс 2 = а 1 б 3 Икс 2

Поскольку показатель b равен 3, а показатель x равен 2, немедленно следует, что степень этого члена равна:

Y — это абсолютная степень многочлена, поскольку ни один другой член не имеет более высокой степени.

Порядок работы с многочленами

При работе с многочленами важно обращать внимание на его степень, так как в первую очередь и перед выполнением какой-либо операции удобно выполнить следующие шаги, в которых степень предоставляет очень важную информацию:

-Закажите полином предпочтения в порядке убывания. Таким образом, термин с самой высокой степенью находится слева, а член с самой низкой степенью — справа.

-Уменьшить подобные термины, процедура, которая состоит в алгебраическом сложении всех терминов одной и той же переменной и степени, найденных в выражении.

-Если это точно, полиномы дополняются, вставляя члены с коэффициентом 0, если отсутствуют члены с показателем степени.

Упорядочить, уменьшить и дополнить многочлен

Учитывая многочлен P (x) = 6x 2 — 5x 4 — 2х + 3х + 7 + 2х 5 — 3x 3 + х 7 -12 предлагается расположить его в порядке убывания, сократить аналогичные термины, если они есть, и дополнить отсутствующие термины, если необходимо.

Первое, что нужно искать, — это член с наибольшим показателем, который представляет собой степень многочлена, который оказывается равным:

Следовательно, P (x) имеет степень 7. Затем полином упорядочивается, начиная с этого члена слева:

Р (х) = х 7 + 2x 5 — 5x 4 — 3x 3 + 6x 2 — 2х + 3х + 7-12

Теперь подобные термины уменьшены, а именно: — 2x и 3x с одной стороны. А 7 и -12 с другой. Чтобы уменьшить их, коэффициенты складываются алгебраически, а переменная остается неизменной (если переменная не появляется рядом с коэффициентом, помните, что x 0 = 1):

Замените эти результаты на P (x):

Р (х) = х 7 + 2x 5 — 5x 4 — 3x 3 + 6x 2 + х -5

И, наконец, проверяется полином на предмет отсутствия какой-либо экспоненты, и действительно, отсутствует член с показателем 6, поэтому он завершается такими нулями:

Р (х) = х 7 + 0x 6 + 2x 5 — 5x 4 — 3x 3 + 6x 2 + х — 5

Теперь можно заметить, что в полиноме осталось 8 членов, поскольку, как было сказано ранее, количество членов равно степени +1.

Важность степени полинома при сложении и вычитании

С полиномами вы можете выполнять операции сложения и вычитания, в которых добавляются или вычитаются только одинаковые члены, которые имеют одинаковую переменную и одинаковую степень. Если одинаковых терминов нет, просто указывается сложение или вычитание.

После того, как было выполнено сложение или вычитание, последнее является суммой противоположных величин, степень полученного многочлена всегда равна или меньше степени многочлена при добавлении наивысшей степени.

Решенные упражнения

— Упражнение решено 1

Найдите следующую сумму и определите ее абсолютную степень:

к 3 — 8ax 2 + х 3 + 5а 2 х — 6ax 2 — Икс 3 + 3а 3 — 5 место 2 х — х 3 + а 3 + 14ax 2 — Икс 3

Решение

Это многочлен с двумя переменными, поэтому его удобно сократить:

к 3 — 8ax 2 + х 3 + 5а 2 х — 6ax 2 — Икс 3 + 3а 3 — 5 место 2 х — х 3 + а 3 + 14ax 2 — Икс 3 =

= а 3 + 3а 3 + а 3 — 8ax 2 — 6ax 2 + 14ax 2 + 5а 2 x — 5 место 2 х + х 3 — Икс 3 — Икс 3 — Икс 3 =

Оба члена имеют степень 3 по каждой переменной. Следовательно, абсолютная степень полинома равна 3.

— Упражнение выполнено 2

Выразите площадь следующей плоской геометрической фигуры в виде многочлена (рисунок 2 слева). Какова степень полученного многочлена?

Решение

Поскольку это площадь, результирующий многочлен должен иметь степень 2 от переменной x. Чтобы определить подходящее выражение для площади, фигура разбивается на известные области:

Площадь прямоугольника и треугольника соответственно: основание x высота Y основание x высота / 2

К₁ = х. 3x = 3x 2 ; К₂ = 5. х = 5х; К₃ = 5. (2x / 2) = 5x

Заметка: основание треугольника 3x — x = 2x, а его высота 5.

Теперь три полученных выражения складываются, и мы получаем площадь фигуры как функцию от Икс:

11. Многочлены. Действия над многочленами

(2.3)

Где

Называется Многочленом n-й степени от одной переменной Х, записанным в стандартном виде.

Числа Называются Коэффициентами дан­ного многочлена, – Старшим коэффициентом, – Свободным членом.

Если необходимо указать степень многочлена то пишут

Если то называется Приведенным многочленом.

Если кроме рассмотреть случай то многочлен вида называется Многочленом нулевой степени, он есть число.

Каждое слагаемое вида многочлена (2.3) называется Одночленом.

Два многочлена, заданные в виде (2.3), называются Равными, если равны все их коэффициенты при соответствующих степенях переменной Х.

Для всякого многочлена и многочлена определены следующие операции:

1) Умножение Многочленов на число

2) Сложение Многочленов:

3) Умножение Многочленов производят по следующему правилу: каждый член одного многочлена умножают на каждый член второго многочлена, полученные результаты складывают и приводят подобные;

4) деление Многочленов (при условии, что степень делителя меньше или равна степени делимого) выполняется по правилу «деления углом».

Результат деления записывается в виде:

или (2.4)

Где – частное (многочлен); – остаток (степень остатка меньше степени делителя).

Многочлен делится Нацело на если или

Если где то результат деления многочлена на согласно формуле (2.4), можно записать в виде равенства

(2.5)

Где R0 – число.

И остаток R0 в равенстве (2.5) можно вычислить по Схеме Горнера:

(2.6)

При вычислении коэффициентов (2.6) используют таблицу:

Верхняя строка заполняется коэффициентами заданного многочлена (2.3), нижняя – числами, которые вычисляют по формулам (2.6).

Число называется Корнем многочлена если

Число называется Корнем кратности K многочлена если

и

Теорема 1 (Безу). Число х0 является корнем многочлена тогда и только тогда, когда делится нацело на

Теорема 2. Число является остатком от деления многочлена на тогда и только тогда, когда

Теорема 3. Пусть – приведенный многочлен с целыми коэффициентами. Если он имеет целые корни, то они содержатся среди целых делителей свободного члена.

Представление многочлена в виде произведения двух или нескольких многочленов (если это возможно) называется Разложением на множители.

Общий вид разложения на множители:

Где А, A1; …; АM; B1; …; Bm; C1; …; Cm R (const);

Х1; Х2; …; Хk – корни многочлена

Квадратные трехчлены не имеют действительных корней.

Основные методы разложения:

1) вынесение общего множителя за скобки;

2) метод группировки:

— с предварительными преобразованиями слагаемых;

3) использование формул сокращенного умножения;

4) использование формул разложения квадратного трехчлена на множители

5) выделение полного квадрата и сведение к разности квадратов;

6) введение новой переменной;

7) поиск корней многочлена среди делителей свободного члена, использование теоремы Безу.

Многочлен может зависеть не только от одной переменной, но и от двух трех и т. д. Данные многочлены называются Многочленами от нескольких переменных. Тогда их Одночленом называют выражение, представляющее собой произведение чисел и переменных в некоторых степенях. Степенью Одночлена называют сумму показателей степеней всех входящих в него переменных. Старшая степень многочлена нескольких переменных определяется старшей степенью его одночлена.

Многочлен от двух переменных называется Симметрическим, если при замене переменных X На У и У на X Выражение не меняется.

Над многочленами от нескольких переменных можно выполнять действия, аналогичные действиям над многочленами от одной переменной. Для разложения данных многочленов на множители применяются те же методы, что и для Многочленов от одной переменной.

Пример 1. Представить многочлен в стандартном виде, определить его степень:

1) 2)

Решение. 1) Раскроем скобки и приведем подобные:

Данный многочлен является многочленом 2-й степени относительно Х.

2) Умножим многочлен на одночлен

Приведем подобные и получаем многочлен

Который является многочленом 5-й степени от двух переменных Х, У (наибольшее суммарное значение показателей имеем в первом одночлене: 2 + 3 = 5).

Пример 2. Найти частное и остаток от деления многочлена на многочлен Результат деления записать в виде равенства.

Решение. Воспользуемся правилом «деления углом»:

– частное (целая часть);

– остаток (многочлен 1-й степени).

Пример 3. Проверить, делится ли многочлен нацело на Если нет, то найти значение остатка (не выполняя деления).

Решение. У данного многочлена свободный член есть число Поскольку число 5 не является делителем числа –3, то – не является корнем многочлена (см. теорему 3). Значит, согласно теореме 1, не разделится нацело на

Остаток находим по теореме 2.

Пример 4. Разложить многочлен на множители:

1) 2)

3) 4)

5) 6)

7)

Решение. 1) Используем метод вынесения общего множителя за скобки:

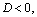
Поскольку у квадратного трехчлена то получен ответ.

2) Воспользуемся методом группировки:

Для дальнейшего разложения выделим полный квадрат и сведем к разности квадратов:

Поскольку дискриминанты квадратных трехчленов отрицательны, окончательно получаем разложение

3) Вначале преобразуем данное выражение, а затем используем метод группировки и формулу разности квадратов:

Вычисляем корни полученного квадратного трехчлена:

Поэтому

4) Вынесем общий множитель за скобки и воспользуемся формулой разности кубов:

Получили искомое разложение.

5) Для многочлена запишем целые делители свободного члена: (см. теорему 3). Подставим данные значения вместо убеждаемся, что является корнем, так как

Разделим заданный многочлен на

Получаем

Для многочлена выполним аналогичные действия.

Проверкой делителей свободного члена находим корень 2.

Тогда

Квадратный трехчлен разлагаем на множители, используя формулы корней. Окончательно получаем:

6) Для многочлена найдем целый корень среди делителей свободного члена Это число –1. Для дальнейшего разложения воспользуемся схемой Горнера:

Х3 Х2 Х1 Х0

Х2 Х1 Х0

Таким образом, Квадратный трехчлен имеет корни и а потому окончательно получаем:

7) Для разложения многочлена воспользуемся методом введения новой переменной. Пусть Тогда имеем Корни этого многочлена – числа 4 и –2. Поэтому Возвращаясь к старой переменной, имеем

Пример 5. Найти A И B из заданного равенства и доказать, что A + B = 0:

Решение. Приведем правую часть заданного равенства к общему знаменателю:

или

Поскольку знаменатели дробей равны, приравняем числители и сгруппируем в правой части коэффициенты при Х. Многочлен в правой части запишем в стандартном виде: