Принцип работы сумматора
Сумматоры — это комбинационные устройства, предназначенные для сложения чисел. Сумматорами называют логические устройства, выполняющие арифметические суммирование кодов двоичного числа. Символическое изображение одноразрядного двоичного сумматора показано на рис.10.29. Сумматор имеет три входа, где — слагаемые одинакового разряда, – слагаемое переноса; на выходе формируется – сумма cлагаемых и – слагаемое переноса в старший разряд.
Функционирование однозарядного сумматора показано в таблице, приведённой на рис.10.30. В этом случае при сложении слагаемых используется перевод десятичных чисел в двоичные числа.
Pиc.10.29. Символическое изображение одноразрядного двоичного сумматора
При сложении слагаемых или 0+1+0 получается десятичное число 1. Такому числу соответствует двоичное число 01, при этом Аналогично, 1+1+0 = 2, которому соответствует двоичное число 10, при этом . При сложении чисел 1+1+1 = 3, которому соответствует двоичное число 11, при этом и так далее.
Сумматоры могут быть последовательного и параллельного действия. В сумматорах последовательного действия коды двоичных чисел вводятся в последовательной форме слагаемое за слагаемым, начиная с младшего разряда.
На рис.10.31 изображена схема сумматора последовательного действия, предназначенного для суммирования четырёхразрядных двоичных чисел. Сумматор построен на трёх регистрах сдвига, D-триггере и на одноразрядном сумматоре.
Рис.10.30. Таблица функционирования одноразрядного сумматора
Рис.10.31. Схема сумматора последовательного действия
Функционирование сумматора приведено в таблице рис.10.32, где слагаемое pi для первого разряда всегда равно нулю.
Рис.10.32. Таблица функционирования сумматора
Для ускорения операции сложения используются сумматоры параллельного действия, которые состоят из нескольких однозарядных сумматоров. В таких сумматорах слагаемые поступают одновременно на соответствующие входы однозарядных сумматоров, при этом каждый из однозарядных сумматоров формирует на своих выходах суммы соответствующих разрядов и слагаемые переноса, передаваемых на входы старших разрядов. Схема четырёхразрядного сумматора параллельного действия приведена на рис.10.33.
Рис.10.33. Схема четырёхразрядного сумматора параллельного действия
- 5 Компенсационный резистор в схеме сумматора
- 6 Симуляция работы сумматора на ОУ в Proteus
- 6.1 Симуляция инвертирующего сумматора
- 6.2 Симуляция неинвертирующего сумматора
- 7 АЧХ и ФЧХ сумматора
- 8 Сравнение неинвертирующих сумматоров
- 9 Плюсы и минусы инвертирующего и неинвертирующего сумматора
- 10 Применение аналогового сумматора
Что такое сумматор
В общем смысле слова, сумматор – это какое-либо устройство, которое что-либо суммирует и выдает на выходе сумму этих воздействий. Сумматор можно представить в виде какого-либо неизвестного нам ящика, на который поступает входные воздействия и на выходе такого ящика выдается их сумма.
В электронике сумматоры делятся на две группы:
- сумматоры аналоговых сигналов
- сумматоры цифровых сигналов
В этой статье мы будем разбирать аналоговые сумматоры.
Аналоговый сумматор
Многие помнят осциллограмму постоянного напряжения.
Если, допустим, цена нашего квадратика 1 В, то на данной картинке мы видим постоянное напряжение амплитудой в 1 В. Суммировать постоянное напряжение – одно удовольствие. Для этого достаточно сложить амплитуды этих сигналов в любой момент времени.
На рисунке ниже мы видим два сигнала A и B и сумму этих сигналов: A+B. Если сигнал A = 2 В, сигнал B = 1 В, то сумма этих сигналов составит 3 В.
Все то же самое касается и сигналов с отрицательной полярностью.
При сложении сигналов с равной амплитудой, но разной полярности, в сумме получаем 0. То есть эти два сигнала взаимно себя скомпенсировали: 1 +(-1)=0. Все становится намного веселее, если мы начинаем складывать сигналы, которые меняются во времени, то есть переменные сигналы. Они могут быть как периодические, так и непериодические.
Рассмотрим самый простой пример. Есть два синусоидальных сигнала с одинаковыми амплитудами, частотами и фазами. Подадим их на сумматор. Что получится в итоге?
Получим синусоиду с амплитудой в два раза больше. Как вообще она получилась? Вычисления производятся довольно просто. Каждая точка синусоиды A+B – это сложение точек в одинаковый момент времени синусоид А и B. Для наглядности взяли 3 точки: t1 , t2 и t3 .
В момент времени t1 у нас амплитуда сигнала А была равна 1 В, амплитуда сигнала В тоже 1 В.
В сумме их результат в момент времени t1 будет равен 2 В, что мы и видим на сигнале A+B
В момент времени t2 амплитуда сигнала A была 0 В, амплитуда сигнала В тоже 0 В. Как нетрудно догадаться, 0+0=0, что мы и видим на сигнале A+B в момент времени t2 .
Ну а в момент времени t3 амплитуда сигнала А = -1 В, амплитуда сигнала В = -1 В, в результате их сумма -1+(-1) = – 2 В, что мы как раз и видим на синусоиде А+B в момент времени t3 . Отсюда вывод: для сложения сигналов надо суммировать амплитуды сигналов в одинаковые моменты времени.
Если сместить фазу одного из сигналов на 180 градусов, относительно другого, а амплитуды и частоты сигналов оставить без изменения, то чему будет равняться их сумма? Сместим второй сигнал на 180 градусов и суммируем их амплитуды в каждый момент времени. Сумма будет равняться нулю, что и видно на рисунке ниже.
Сложение двух сигналов в Proteus
Если надо сложить в теории два каких-нибудь два сложных сигнала с разными фазами, амплитудами, частотами, то проще всего прибегнуть к различным симуляторам.
Один из них – это Proteus. С помощью него можно сложить два любых сигнала и посмотреть их сумму.
Для этого надо выбрать синусоидальный генератор.
Затем виртуальный осциллограф.
Задать параметры генератору.
Теперь можно сложить два синусоидальных сигнала с одинаковыми амплитудами, фазами и частотами.
Прописать амплитуду и частоту каждого сигнала и нажать «пуск».
Нажать правой кнопкой мыши на виртуальный осциллограф и нажать Digital Oscilloscope.
Сумматор
Двоичный сумматор может быть определён тремя способами:
1. табличным, в виде таблицы истинности,
2. аналитическим, в виде формулы (СДНФ),
3. графическим, в виде логической схемы.
Так как формулы и схемы могут преобразовываться, то, одной таблице истинности двоичного сумматора могут соответствовать множества различных формул и схем. Поэтому, табличный способ определения двоичного сумматора является основным.


| x0=A | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| x1=B | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | ||
| x2=Pi-1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | Название действия (функции) | Номер функции |
| Si | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | Бит суммы по модулю 2 | F3,150 |
| Pi | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | Бит переноса | F3,232 |

Принципиальная схема одноразрядного сумматора в несимметричной троичной системе счисления в трёхбитной одноединичной системе троичных логических элементов

Принципиальная схема троичного одноразрядного сумматора в двухбитной системе троичных логических элементов
Принципиальная схема троичного полного одноразрядного сумматора, работающего в троичной симметричной системе счисления Фибоначчи в трёхбитной одноединичной системе троичных логических элементов

Принципиальная схема троичного полного сумматора в троичной симметричной системе счисления Фибоначчи в двухбитной системе троичных логических элементов
См. также
Примечания
- ↑ 12 Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5
- ↑Считающие часы Вильгельма Шиккарда
- ↑Троичный бинарный (двухоперандный) сумматор по модулю 3 (четвертьсумматор) в троичной несимметричной системе счисления и в троичной симметричной системе счисления с соответствием (0,1,-1)=(0,1,2) в трёхбитной одноединичной системе троичных логических элементов
- ↑Троичный бинарный сумматор по модулю 3 (четвертьсумматор) в троичной несимметричной системе счисления в трёхбитной одноединичной системе троичных логических элементов
- ↑А.С.Куликов. Двоичные сумматоры. Быстрый двоичный сумматор
- ↑Троичный тринарный сумматор в троичной несимметричной системе счисления в трёхбитной системе троичных логических элементов
- ↑http://andserkul.narod2.ru/troichnie_summatori/ А.С.Куликов. Троичные сумматоры
- ↑Троичный тринарный сумматор-вычитатель в троичной симметричной системе счисления Фибоначчи в трёхбитной системе троичных логических элементов [неавторитетный источник?]
- ↑Троичный тринарный сумматор-вычитатель в троичной симметричной системе счисления Фибоначчи в двухбитной системе троичных логических элементов [неавторитетный источник?]
- ↑Компьютеры Фибоначчи. Троичное зеркально-симметричное сложение и вычитание
Литература
- Угрюмов Е. П. Элементы и узлы ЭЦВМ. М.: Высшая школа, 1976. — 232 с.
- Угрюмов Е. П. Цифровая схемотехника. — СПб.: БХВ-Петербург, 2001. — 528 с.
- Жан М. Рабаи, Ананта Чандракасан, Боривож Николич. 11. Проектирование арифметических блоков: Сумматор // Цифровые интегральные схемы. Методология проектирования = Digital Integrated Circuits. — 2-е изд. — М .: Вильямс, 2007. — С. 912. — ISBN 0-13-090996-3
Ссылки
- Сумматор — статья из Большой советской энциклопедии Яндекс.Словари: Сумматор
- Аналоговые системы
- Компьютерная арифметика
- Электроника
- Математическая логика
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Сумматор» в других словарях:
Сумматор — в нейронных сетях блок, суммирующий сигналы, поступающие от нейронов через синапсы. В общем случае сумматор может преобразовывать сигналы и передавать их нейронам или сумматорам тоже через синапсы. См. также: Нейронные сети Финансовый словарь… … Финансовый словарь
сумматор — регистр, накопитель, тотализатор, суммирующее устройство; интегросумматор Словарь русских синонимов. сумматор сущ., кол во синонимов: 1 • интегросумматор (1) … Словарь синонимов
СУММАТОР — узел арифметического устройства ЭВМ, осуществляющий операцию суммирования чисел. Выполняется на логических элементах, интегральных схемах … Большой Энциклопедический словарь
СУММАТОР — (1) аналоговый устройство аналоговых вычислительных (см.) для преобразования информационных сигналов различных физ. процессов в суммы нескольких физ. величин. В зависимости от физ. природы входных и выходных величин суммирующие устройства делятся … Большая политехническая энциклопедия
сумматор — 3.1.28 сумматор: Элемент кабельной распределительной сети, обеспечивающий сложение энергии радиосигналов (оптических сигналов) на общей нагрузке. Источник … Словарь-справочник терминов нормативно-технической документации
СУММАТОР — а; м. Основной узел арифметического устройства цифровой вычислительной машины или отдельный прибор, выполняющий операцию сложения двух чисел. Стрелка сумматора. * * * СУММАТОР СУММАТОР, узел арифметического устройства ЭВМ, осуществляющий операцию … Энциклопедический словарь
сумматор — (лат. summa сумма) один из элементов цифровой вычислительной машины, выполняющий суммирование. Новый словарь иностранных слов. by EdwART, , 2009. сумматор а, м. ( … Словарь иностранных слов русского языка
сумматор — sudėtuvas statusas T sritis automatika atitikmenys: angl. adder; combining unit; summation instrument; summator; summer vok. Addiereinrichtung, f; Addierer, m; Addierwerk, n; Summator, m; Summierer, m; Summierungseinrichtung, f rus. сумматор, m;… … Automatikos terminų žodynas
Сумматор акустоэлектронный — 24 Источник: ГОСТ 28170 89: Изделия акустоэлектронные. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
сумматор комбинационного типа — kombinacinis sudėtuvas statusas T sritis automatika atitikmenys: angl. coincidence type adder vok. Kombinationsaddierglied, n rus. комбинационный сумматор, m; сумматор комбинационного типа, m pranc. additionneur de combinaison, m … Automatikos terminų žodynas
Сумматоры
Сумматор представляет собой комбинационное цифровое устройство (КЦУ), предназначенное в основном для суммирования двоичных чисел. Кроме того, с помощью сумматора могут выполняться вычитание, умножение, деление, преобразование чисел в дополнительный код и некоторые другие операции. Обычно сумматор состоит только из логических элементов, а результат операции направляется затем для записи в регистр.
Классификация сумматоров может быть проведена по трем основным признакам:
числу входов (полусумматоры, одноразрядные и многоразрядные сумматоры). Многоразрядные сумматоры, в свою очередь, подразделяются на последовательные и параллельные; последние по способу организации межразрядных переносов подразделяются на сумматоры с последовательным и параллельным переносом и с групповой структурой;
способу тактирования (синхронные и асинхронные сумматоры);
системе счисления (двоичные, двоично-десятичные и др.).
Полусумматорами (рис. 4.8, 4.9) называют КЦУ с двумя входами (а, b)и двумя выходами, на одном из которых вырабатывается сигнал суммы (выход S),а на другом – сигнал переноса (выход Р).Табл. 4.5 является таблицей истинности полусумматора.
| Рис. 4.8. Условное обозначение полусумматора | Рис. 4.9. Схема полусумматора на логических элементах |
Таблица истинности полусумматора
| а | b | S | P |
Одноразрядным сумматором (рис. 4.10, 4.11) называют КЦУ с тремя входами и двумя выходами. Кроме двух входов для чисел он имеет третий вход, на который подается сигнал переноса из предыдущего разряда. Одноразрядный сумматор является основным элементом многоразрядных сумматоров. Он выполняет арифметическое сложение одноразрядных двоичных чисел ai и bi и перенос Pi—1 из предыдущего разряда с образованием на выходе суммы Si и переноса Pi в старший разряд (табл. 4.6).
Аналогичным способом могут быть построены логические схемы вычитателей. Как сумматоры, так и вычитатели предназначены для выполнения основных арифметических операций – сложения и вычитания. Имея на входе дополнительные средства для изменения знака второго аргумента, сумматор может прибавлять к первому слагаемому второе с измененным знаком,
т.е. вычитать, а вычитатель – вычитать из уменьшаемого вычитаемое с измененным знаком, т.е. прибавлять. Таким образом, в арифметико-логических устройствах (АЛУ) в большинстве случаев используется только один из двух рассматриваемых узлов, традиционно – именно сумматор, хотя по всем показателям вычитатель подобен сумматору.
| Рис. 4.10. Условное обозначение одноразрядного сумматора | Рис. 4.11. Схема одноразрядного сумматора на логических элементах |
Таблица истинности одноразрядного сумматора
| аi | bi | Pi-1 | Si | Pi |
Операции сложения и вычитания бывают последовательными и параллельными. В данном случае под последовательностью понимается поочередное, разряд за разрядом, сложение (или вычитание) на одноразрядной схеме с задержкой переносов (или займов) для использования их как третьих аргументов в следующем такте, т. е. в разряде.
При параллельных сложениях (или вычитаниях) используются столько одноразрядных сумматоров (или вычитателей), сколько разрядов в исходных числах (точнее – сколько разрядов в самом большом из них числе). Эти одноразрядные сумматоры взаимодействуют между собой по цепям переносов (или займов). Очевидно, что полный параллелизм при этом не достигается, так как переносы и займы распространяются с некоторой, хотя и небольшой, задержкой от младших разрядов к старшим. Имеется в виду схемное распространение займа в отличие от логического, направленного в противоположную сторону. Проблема сокращения времени распространения переносов (или займов) по разрядам – одна из главных при проектировании АЛУ.
Отметим некоторые особенности логики работы сумматоров и вычитателей:
сумма равна 1, если единичные значения принимает нечетное число аргументов;
выходной перенос равен 1, если единичные значения принимают больше двух аргументов;
разность равна 1, если при отсутствии входного займа из 1 вычитается 0 или из 0 вычитается 1; она также равна 1, если аргументы равны при наличии входного займа;
выходной заем равен 1, если из 0 вычитается 1, а также если аргументы равны при наличии входного займа.
В структуре АЛУ часто присутствует накопительный блок, состоящий из комбинационного сумматора (или вычитателя) и регистра результата. Подобный блок необходим при реализации последовательного алгоритма вычислений, когда вновь поступающий аргумент прибавляется к ранее накопленному результату или из него вычитается, а новый результат вычислений заменяет исходный.
Функцию накопительного блока, сочетающего функции сумматора (или вычитателя) и регистра, может выполнять набор Т-триггеров, работающих в режиме инверсии состояния, т.е. сложения по модулю 2. Такой сумматор на основе T-триггеров называют накопительным.Он уже является не комбинационным устройством, а конечным автоматом, поскольку обладает памятью.
Операции сложения (или вычитания) с учетом переноса (или займа) выполняются всегда над тремя аргументами, поэтому накопительный сумматор (или вычитатель) должен содержать управляющие коммутационные схемы, чтобы разнести сложение (или вычитание) на два такта. В этом состоит главный его недостаток. В остальном накопительный сумматор (или вычита-
тель) – самый простой и экономичный. Помимо несложных коммутационных схем он содержит дополнительно только цепи переноса (или займа).
Булевы функции, описывающие работу одноразрядного двоичного сумматора (по табл. 4.6), можно записать в следующем виде:
Используя различные варианты преобразования этих функций, можно реализовать большое число структур одноразрядных двоичных сумматоров (например по схеме, показанной
на рис. 4.12).
Рис. 4.12. Схема одноразрядного двоичного сумматора
Для обработки многоразрядных чисел объединяется соответствующее число одноразрядных сумматоров. При этом отдельные разряды обрабатываемых чисел А и В подаются на входы ai и bi. На вход Pi подается перенос из предыдущего, более младшего разряда. Формируемый в данном разряде перенос Pi+1 передается в следующий, более старший разряд. Такая организация процесса формирования переноса, называемая последовательным переносом, снижает быстродействие многоразрядного сумматора, так как получение результата в старшем разряде сумматора обеспечивается только после завершения распространения переноса по всем разрядам. Поэтому иногда организуется параллельный перенос.
Исследование и сравнение полусумматора и сумматора
Основной элементарной операцией, которую можно выполнять с числами в цифровых устройствах — это арифметическое сложение двух одноразрядных двоичных чисел. АЛУ — Арифметико-логическое устройство процессора, будет обязательно содержать в составе своём такие элементы как сумматоры. Такие схемы позволят, к примеру, складывать двоичные числа. Но помимо сложения они обладают есть еще множеством функций.
Ключевые слова
Текст научной работы
Основной элементарной операцией, которую можно выполнять с числами в цифровых устройствах — это арифметическое сложение двух одноразрядных двоичных чисел.
АЛУ — Арифметико-логическое устройство процессора, как правило, в составе своем обязательно содержит такие элементы, как сумматоры. Такие схемы позволят, к примеру, складывать двоичные числа. Но помимо сложения они обладают есть еще множеством функций.
Арифметико-логическое устройство — это специальное комбинационное устройство в интегральном исполнении, при помощи которого можно выполнить некоторый спектр операций для обработки не одноразрядных данных, притом действие, которое выполняется в текущий момент времени, можно будет определить сочетанием сигналов на управляющих входах.
Блок арифметико-логического устройства — это основной элемент процессоров и микропроцессоров, использующийся в совокупности с регистрами и иными блоками управления.
Микросхемы арифметико-логического устройства разнообразных серий по своему функционалу похожи, в том числе и по назначению выводов.
Сумматоры относят к важным компонентам устройств цифровой обработки сигналов. Суммирование, вычитание, умножение — эти некоторые арифметические функции используют сумматор как строительный блок. Помимо этого, сумматор также зачастую может являться как основной элемент, ограничивающий быстродействие схемы. Таким образом, создание быстродействующей схемы сумматора — это одна из важных задач — к разработке и оптимизации сумматора нужно отнестись с должным вниманием. Данную оптимизацию разрешается выполнить как на уровне логических элементов, так и на уровне схемы. Чаще всего, на этапе оптимизации на уровне логики разработчики стремятся так записать булевы уравнения, чтобы схема получилась наиболее быстрой или с минимальным размером. С другой стороны, на этапе оптимизации на уровне схемы размеры транзисторов и топология схемы подбираются так, дабы получить максимальное быстродействие.
Процесс сложения будет происходить следующим образом. Предположим, нам нужно произвести сложение чисел из двоичной системы исчисления 1001 и 0011. Для начала, необходимо сложить числа младших разрядов (последние цифры): 1+1=10. Получается, что младшем разряде будет 0, а 1 — это перенос в противоположный разряд, т.е. в старший. Затем: 0 + 1 + 1(от переноса) = 10, т.е. в текущем разряде опять же записывается 0, а 1 перейдет в противоположный младшему разряд. На следующем этапе уже получается: 0 + 0 + 1(от переноса) = 1. Как итог, сумма будет равняться 1100.
Полусумматор
Теперь, не будем обращать внимание на перенос из предыдущего разряда, а будем рассматривать только то, как будет сформировываться сумма данного разряда. При условии, что нам были предоставлены два 0 и две 1, то получится, что сумма данного разряда равняется 0. Но, если же одним из двух слагаемых будет единица, то сумма равняется уже 1. Для получения таких результатов необходимо использовать вентиля «ИСКЛЮЧАЮЩЕГО ИЛИ».
Для того, чтобы перенести 1 в следующий разряд, нужно чтобы два слагаемых равнялись 1. Данная операция реализуется при помощи вентиля «И».
С помощью приведенной ниже схемы, которая именуется полусумматором, можно реализовать сложение в рамках одного разряда (не учитывая возможной пришедшей 1 из противоположного разряда). Полусумматор располагает двумя входами (для слагаемых) и двумя выходами (для суммы и переноса). На схеме, изображенной ниже, продемонстрирован полусумматор, состоящий из вентилей «ИСКЛЮЧАЮЩЕЕ ИЛИ» и «И».

Рисунок 1. Схема полусумматора.
Сумматор
Сумматор, в отличие от полусумматора, располагает тремя выходами, а не двумя, т.к. у него есть возможность учитывать перенос из прошлого разряда. Но, как минус, придется немного усложнить схему, дабы учесть перенос. Как итог, можно сказать, что она состоит из двух полусумматоров.

Рисунок 2. Схема сумматора.
Для примера разберем один из случаев. Необходимо сложить 0 и 1, а также 1 из переноса. Сперва найдем совокупность текущего разряда. Как можно заключить по левой схеме «ИСКЛЮЧАЮЩЕЕ ИЛИ», в которую будут входить a и b, на выходе получаем 1. В последующее «ИСКЛЮЧАЮЩЕЕ ИЛИ» уже входят две единицы. Следовательно, окончательный ответ будет равен 0.
Дальше рассмотрим, что будет происходить с процессом переноса. Сперва, в первый вентиль «И» приходят 0 и 1 (a и b). Как итог — 0. Во следующий вентиль (правее) приходят две 1, которые дают единицу. Проход сквозь вентиль «ИЛИ» нуля от первого «И» и единицы от второго «И» как итог дает нам 1.
Работу схемы можно проверить простым сложением 0+1+1= 10. Получается, что 0 будет оставаться в текущем разряде, а единица перейдет в противоположный. Из этого следует, что логическая схема работает правильно.
Для того, чтобы дать описание работы такой схемы с учетом всех возможных вариантов на входе, можно воспользоваться следующей таблицей истинности.
Сумматоры. Полусумматоры и полные сумматоры. Параллельный сумматор с параллельным переносом. Сумматор-вычитатель

Комбинационный сумматор – это цифровое устройство, предназначенное для арифметического сложения чисел, представленных в виде двоичных кодов.
Обычно сумматор представляет собой комбинацию одноразрядных сумматоров. При сложении двух чисел в каждом разряде производится сложение трех цифр: цифры первого слагаемого Ai, цифры второго слагаемого Bi и цифры переноса из младшего разряда Pi-1. В результате суммирования на выходных шинах получается сумма S i и перенос в старший разряд P i.
Сумматоры с поразрядным переносом выпускаются в виде микросхем на 2 и 4 разряда. Например, К561ИМ1 – сумматор на 4 разряда. Для увеличения разрядности до 8 необходимо взять две микросхемы и соединить их последовательно по цепи переноса.
Сумматор с поразрядным последовательным переносом наиболее прост с точки зрения схемной реализации, однако имеет низкое быстродействие. Время выполнения операции зависит от разрядности так как включает в себя затраты времени на вычисление во всех более младших разрядах и выполнение в них переносов.
Для повышения быстродействия используются сумматоры с параллельным переносом.
По числу входов различают: полусумматоры, полные сумматоры.
Полусумматор
Полусумматор (Half Summator) складывает два числа самого младшего разряда A, B без учета переноса. Результат сложения S и перенос в старший разряд P (рис.1) значения, которых представлены в таблице истинности (табл.1).
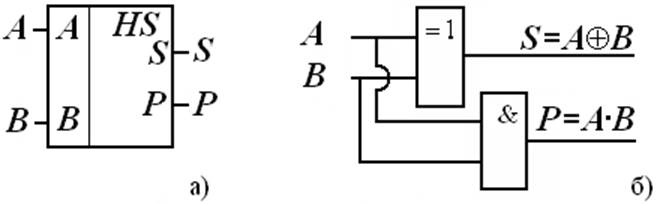
Рис. 1 Обозначение одноразрядного полусумматора, (а),
и его функциональная схема, (б).
Таблица истинности полусумматора Таблица 1
Из таблицы 1 следует, что, если A = 1 и B = 1, то происходит переполнение разряда S = 0 и вырабатывается сигнал переноса в старший разряд P = 1.
Вывод: максимальное значение результата сложения на полусумматоре с учетом переноса равно: A0 + B0 = 12+12 = 102 = 210, где P0 = 1, S0 = 0.
Аналитические выражения выходных сигналов:
Полный сумматор
Одноразрядный полный сумматор (Summator) имеет три входа: для разряда слагаемого An, разряда слагаемого Bn и входного сигнала переноса из младшего разряда Pn-1.
Результат сложения Sn и перенос в старший разряд Pn (рис. 3.2) значения, которых представлены в таблице истинности (табл. 2).
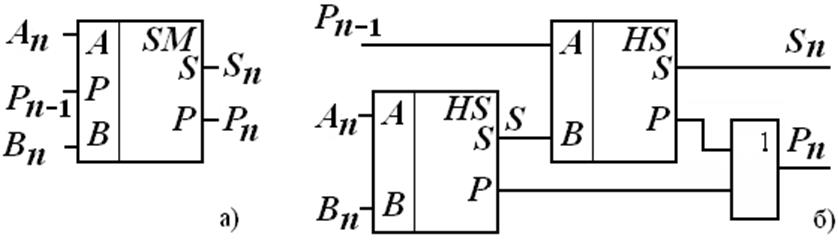
Рис. 2 Обозначение одноразрядного полного сумматора, (а),
и его функциональная схема на полусумматорах, (б).
Вместо элемента 2ИЛИ можно использовать третий полусумматор, у которого S = P n.
Таблица истинности одноразрядного полного сумматора Таблица 2
B n
P n –1
S n
P n
Вывод: сложение в двоичной системе производится с учетом переноса из младшего разряда аналогично «сложению в столбик» в десятичной системе. При этом максимальное значение результата сложения в одном разряде с учетом переносов равно: An + Bn + Pn—1 = 12+12+12 = 112 = 310, где Pn = 1, Sn = 1.
Как видно из карт Карно, функция результата не минимизируется, а функция переноса упрощается (табл. 3), что сделано также в аналитическом виде и реализовано на логических элементах (рис. 3).
Из таблицы истинности следуют выражения для сигналов:
Карта Карно для Sn Карта Карно для Pn Таблица 3
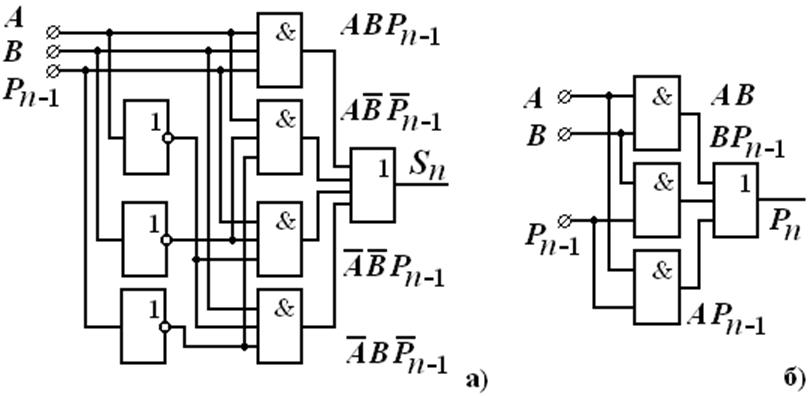
Рис. 3 Принципиальная схема одноразрядного полного сумматора
на элементах И, ИЛИ, НЕ: получение суммы (а), и переноса, (б).
Параллельный многоразрядный сумматор состоит из n одноразрядных сумматоров (рис. 4). Входные сигналы подаются на одноразрядные сумматоры одновременно. Если появляются сигналы переноса, то они поступают в старший разряд.
Вывод: пока не состоится сложение в младшем разряде и не определится значение переноса не может быть определена сумма в разряде более старшем.
Максимальное значение результата сложения с учетом переносов: Pn, Sn = 112 = 310.
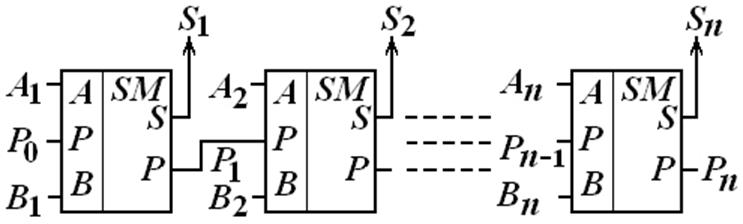
Рис. 4 Параллельный многоразрядный сумматор
При использовании обратного кода перенос из самого старшего разряда подается на вход переноса самого младшего разряда. В остальных случаях на вход самого младшего разряда подается логический ноль.
Сумматоры с поразрядным переносом выпускаются в виде микросхем на 2 и 4 разряда. Например, К561ИМ1 – сумматор на 4 разряда. Для увеличения разрядности до 8 необходимо взять две микросхемы и соединить их последовательно по цепи переноса.
Сумматор с поразрядным последовательным переносом наиболее прост с точки зрения схемной реализации.
Быстродействие данного сумматора ограничено временем, за которое сигнал переноса последовательно распространяется через все разряды сумматора.
Этот недостаток отсутствует у параллельных сумматоров с параллельным переносом.
Параллельный сумматор с параллельным переносом
В данных устройствах сигнал переноса формируется с одновременным (параллельным) учетом всех переносов в младших разрядах, по отношению к рассматриваемому разряду.
Для построения сумматора с параллельным переносом используются две вспомогательные функции.
Функция генерации (порождения переноса) – принимает единичное значение, если перенос на выходе данного разряда появляется независимо от наличия или отсутствия входного переноса:
Функция прозрачности (транзита переноса) – принимает единичное значение, если перенос на выходе данного разряда появляется только при наличии входного переноса. Это следует из выражения (3.1):
Тогда перенос на выходе младшего разряда:
что, с учетом выражений для дополнительных функций, соответствует зависимости для определения переноса одноразрядного сумматора (1).
Сумматоры
Построение двоичных сумматоров обычно начинается с сумматора по модулю 2. В таблице 1 приведена таблица истинности этого сумматора. Ее можно получить исходя из правил суммирования в двоичной арифметике.
| X | Y | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
В соответствии с таблицы истинности получим схему сумматора по модулю 2 (рис. 1).
Рис. 1 — Принципиальная схема, реализующая таблицу истинности сумматора по модулю 2.
Сумматор по модулю 2 (для двоичной арифметики его схема совпадает со схемой исключающего «ИЛИ») изображается на схемах как показано на рисунке 3.
Рис. 2 — Условное графическое обозначение сумматора по модулю 2
Сумматор по модулю 2 выполняет суммирование без учета переноса. В полном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена в таблице 2.
| X | Y | Сумма | Перенос |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
В соответствии с принципами построения произвольной таблицы истинности получим схему полусумматора. Эта схема приведена на рисунке 5.
Рис. 3 — Принципиальная схема, реализующая таблицу истинности полусумматора.
Полусумматор изображается на схемах как показано на рисунке 6.
Рис. 4 — Условное графическое обозначение полусумматора
Схема полусумматора формирует перенос в следующий разряд, но не может учитывать перенос из предыдущего разряда, поэтому она и называется полусумматором. Таблицу истинности полного двоичного одноразрядного сумматора можно получить из правил суммирования двоичных чисел. Она приведена в таблице 3. В обозначении входов использовано следующее правило: в качестве входов использованы одноразрядные числа A и B; перенос обозначен буквой P; для обозначения входа переноса используется буква I (сокращение от английского слова input – вход); для обозначения выхода переноса используется буква O (сокращение от английского слова output – выход).
| PI | A | B | S | PO |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
В соответствии с принципами построения принципиальной схемы по произвольной таблице истинности получим схему полного двоичного одноразрядного сумматора (рис. 5). Ее можно минимизировать, но это несколько усложняет принципы построения сумматоров.
Рис. 5 — Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора.
Полный двоичный одноразрядный сумматор изображается на схемах как показано на рисунке 9.
Рис. 6 — Условное графическое обозначение полного двоичного одноразрядного сумматора
Для того чтобы получить многоразрядный сумматор, достаточно соединить входы и выходы переносов соответствующих двоичных разрядов. Схема соединения одноразрядных сумматоров для реализации четырехразрядного сумматора приведена на рисунке 7.
Рис. 7 — Принципиальная схема многоразрядного двоичного сумматора.
Одноразрядные сумматоры практически никогда не использовались, так как почти сразу же были выпущены микросхемы многоразрядных сумматоров. Полный двоичный четырехразрядный сумматор изображается на схемах как показано на рисунке 8.
Рис. 8 — Изображение полного двоичного многоразрядного сумматора на схемах.
Естественно, в приведенной на рисунке 7 схеме рассматриваются только принципы работы двоичных сумматоров. В реальных схемах никогда не допускают последовательного распространения переноса через все разряды многоразрядного сумматора. Для увеличения скорости работы двоичного сумматора применяется отдельная схема формирования переносов для каждого двоичного разряда. Таблицу истинности для такой схемы легко получить из алгоритма суммирования двоичных чисел, а затем применить хорошо известные нам принципы построения цифровой схемы по произвольной таблице истинности.
Что такое сумматор и полусумматор

Чипинфо Сумматоры: определения, классификация, уравнения, структуры и применение
Распродажа
Электронные компоненты со склада по низким ценам, подробнее >>>
Содержание ChipNews
О журнале ChipNews
Литература
Новости электроники
Популярные материалы
Комментарии
люди куплю транзистар кт 827А 0688759652
как молоды мы были и как быстро пробежали годы кулотино самое счастливое мое время
Светодиод — это диод который излучает свет. А если диод имеет ИК излучение, то это ИК диод, а не «ИК светодиод» и «Светодиод инфракрасный», как указано на сайте.
Подскажите 2т963а-2 гарантийный срок
Сумматоры: определения, классификация, уравнения, структуры и применение
Основной элементарной операцией, выполняемой над кодами чисел в цифровых устройствах, является арифметическое сложение.
Сумматор логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учет знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры.
Сумматоры классифицируют по различным признакам.
- двоичные;
- двоично-десятичные (в общем случае двоично-кодированные);
- десятичные;
- прочие (например, амплитудные).
- одноразрядные,
- многоразрядные.
- четвертьсумматоры (элементы «сумма по модулю 2»; элементы «исключающее ИЛИ»), характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма;
- полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноименные разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом перенос в следующий (более старший разряд);
- полные одноразрядные двоичные сумматоры, характеризующиеся наличием трех входов, на которые подаются одноименные разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом перенос в следующий (более старший разряд).
- последовательные, в которых обработка чисел ведется поочередно, разряд за разрядом на одном и том же оборудовании;
- параллельные, в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется свое оборудование.
Параллельный сумматор в простейшем случае представляет собой n одноразрядных сумматоров, последовательно (от младших разрядов к старшим) соединенных цепями переноса. Однако такая схема сумматора характеризуется сравнительно невысоким быстродействием, так как формирование сигналов суммы и переноса в каждом i-ом разряде производится лишь после того, как поступит сигнал переноса с (i-1)-го разряда.Таким образом, быстродействие сумматора определяется временем распространения сигнала по цепи переноса. Уменьшение этого времени основная задача при построении параллельных сумматоров.
Для уменьшения времени распространения сигнала переноса применяют: конструктивные решения, когда используют в цепи переноса наиболее быстродействующие элементы; тщательно выполняют монтаж без длинных проводников и паразитных емкостных составляющих нагрузки и (наиболее часто) структурные методы ускорения прохождения сигнала переноса.
- с последовательным переносом;
- с параллельным переносом;
- с групповой структурой;
- со специальной организацией цепей переноса.
- сумматоры со сквозным переносом, в которых между входом и выходом переноса одноразрядного сумматора оказывается наименьшее число логических уровней [1];
- сумматоры с двухпроводной передачей сигналов переноса [1, 2];
- сумматоры с условным переносом (вариант сумматора с групповой структурой, позволяющий уменьшить время суммирования в 2 раза при увеличении оборудования в 1,5 раза) [3];
- асинхронные сумматоры, вырабатывающие признак завершения операции суммирования, при этом среднее время суммирования уменьшается, поскольку оно существенно меньше максимального.
Сумматоры, которые имеют постоянное время, отводимое для суммирования, независимое от значений слагаемых, называют синхронными.
- комбинационный, выполняющий микрооперацию «S = A плюс B», в котором результат выдается по мере его образования (это комбинационная схема в общепринятом смысле слова);
- сумматор с сохранением результата «S = A плюс B»;
- накапливающий, выполняющий микрооперацию «S = S плюс B».
Последние две структуры строятся либо на счетных триггерах (сейчас практически не используются), либо по структуре «комбинационный сумматор регистр хранения» (сейчас наиболее употребляемая схема).
- разрядность;
- статические параметры: Uвх, Uвх, Iвх и так далее, то есть обычные параметры интегральных схем;
- динамические параметры. Сумматоры характеризуются четырьмя задержками распространения:
- от подачи входного переноса до установления всех выходов суммы при постоянном уровне на всех входах слагаемых;
- от одновременной подачи всех слагаемых до установления всех выходов суммы при постоянном уровне на входе переноса;
- от подачи входного переноса до установления выходного переноса при постоянном уровне на входах слагаемых;
- от подачи всех слагаемых до установления выходного переноса при постоянном уровне на входах слагаемых.
Четвертьсумматор
Простейшим двоичным суммирующим элементом является четвертьсумматор. Происхождение названия этого элемента следует из того, что он имеет в два раза меньше выходов и в два раза меньше строк в таблице истинности по сравнению с полным двоичным одноразрядным сумматором. Наиболее известны для данной схемы названия: элемент «сумма по модулю 2» и элемент «исключающее ИЛИ». Схема (рис. 1) имеет два входа а и b для двух слагаемых и один выход S для суммы. Работу ее отражает таблица истинности 1 (табл. 1), а соответствующее уравнение имеет вид
Рис. 1
Таблица 1
Данный элемент выпускается в виде интегральных схем (ИС) типа ЛП5 (серии 133, 155, 530, 531, 533, 555, 1531, 1533); ЛП12 (555); ЛП107 (100, 500, 1500); ЛП2 (561, 564); ЛП14 (1561) и т. п.
Реализуем четвертьсумматор в базисах И-НЕ, ИЛИ-НЕ и с использованием только одного инвертора, для чего преобразуем уравнение (1):
Схемы, полученные по уравнениям (2)(4), приведены на рис. 2.
Рис. 2
Полусумматор
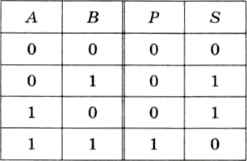
Полусумматор (рис. 3) имеет два входа a и b для двух слагаемых и два выхода: S сумма, P перенос. Обозначением полусумматора служат буквы HS (half sum полусумма). Работу его отражает таблица истинности 2 (табл. 2), а соответствующие уравнения имеют вид:
Рис. 3
Таблица 2
Из уравнений (5) следует, что для реализации полусумматора требуется один элемент «исключающее ИЛИ» и один двухвходовый вентиль И (рис. 3б).
Полный одноразрядный двоичный сумматор
Он (рис. 4) имеет три входа: a, b для двух слагаемых и p для переноса из предыдущего (более младшего) разряда и два выхода: S сумма, P перенос в следующий (более старший) разряд. Обозначением полного двоичного сумматора служат буквы SM. Работу его отражает таблица истинности 3 (табл. 3).
Рис. 4
Таблица 3
Отметим два момента. Первый: в табл. 2 и 3 выходные сигналы P и S не случайно расположены именно в такой последовательности. Это подчеркивает, что PS рассматривается как двухразрядное двоичное число, например, 1 + 1 = 210 = 102 , то есть P = 1, а S = 0 или 1 + 1 + 1 = 310 = 112, то есть P = 1, а S = 1. Второй: выходные сигналы P и S полного двоичного сумматора относятся к классу самодвойственных функций алгебры логики. Самодвойственными называют функции, инвертирующие свое значение при инвертировании всех переменных, от которых они зависят. Обратите внимание, что P и S для четвертьсумматора и полусумматора не являются самодвойственными функциями! Преимущества, вытекающие из этого свойства полного двоичного сумматора, будут рассмотрены при анализе возможностей ИС типа 155ИМ1.
Уравнения, описывающие работу полного двоичного сумматора, представленные в совершенной дизъюнктивной нормальной форме (СДНФ), имеют вид:
Уравнение для переноса может быть минимизировано:
P = ab + ap + bp. (7)
При практическом проектированиии сумматора уравнения (6) и (7) могут быть преобразованы к виду, удобному для реализации на заданных логических элементах с некоторыми ограничениями (по числу логических входов и др.) и удовлетворяющему предъявляемым к сумматору требованиям по быстродействию.
Например, преобразуем уравнения (6) следующим образом:
Из выражений (8) следует, что полный двоичный сумматор может быть реализован на двух полусумматорах и одном двухвходовом элементе ИЛИ. Соответствующая схема приведена на рис. 5.
Рис. 5
Из выражения (8) для S также следует:
S = a Е b Е p. (9)
Примечание. Так как операция Е в выражении (9) коммутативна (переменные можно менять местами), то следует, что три входа полного двоичного сумматора абсолютно равноправны и на любой из них можно подавать любую входную переменную. Это полезно помнить, разводя печатные платы, на которых установлены ИС сумматоров.
К настоящему времени разработано большое число схем сумматоров. Доказано (нашим отечественным ученым Вайнштейном), что при использовании только одного инвертора нельзя реализовать полный двоичный сумматор со сложностью Pкв < 16, а при двух инверторах Pкв < 14, где Pкв вес по Квайну, используемый как оценка сложности любых комбинационных схем. Pкв это общее число всех входов всех логических элементов схемы без учета инверторов.
Рис. 6
Покажем, используя два метода, как была получена рациональная (с использованием только одного инвертора) схема полного двоичного сумматора, явившаяся основой схем ИС сумматоров типа 7480, 155ИМ1 и др.
Первый метод основан на использовании значения выходного переноса P как вспомогательной переменной при определении выходной суммы S (табл. 4). В табл. 4 при наборах переменных, являющихся нереальными (например, единичное значение переноса при нулевых значениях всех входных переменных), поставлены безразличные значения (крестик) для функции S, которые можно доопределять произвольным образом.
Таблица 4
| ╧ наб. | a | b | p | P | S |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | x |
| 2 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | x |
| 4 | 0 | 1 | 0 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 | x |
| 6 | 0 | 1 | 1 | 0 | x |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | x |
| 10 | 1 | 0 | 1 | 0 | x |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | x |
| 13 | 1 | 1 | 0 | 1 | 0 |
| 14 | 1 | 1 | 1 | 0 | x |
| 15 | 1 | 1 | 1 | 1 | 1 |
Из карты Карно для функции S (рис. 6) следует:
S = abp + Pa + Pb + Pp = = abp + P(a + b + p). (10)
Второй метод основан на применении диаграмм Венна. На рис. 7а показана диаграмма Венна для трех переменных а, b, p; области, ограниченные окружностями, соответствуют переменным а, b, p, а области, обозначенные цифрами от 0 до 7 соответствующим конъюнкциям (например, 5 = abp). Область, заштрихованная на рис. 7б, очевидно, соответствует функции P = ab + ap + bp. Функция S представлена заштрихованной областью на рис. 7в. Ее можно представить суммой произведения функции a + b + p (рис. 7г) на функцию ab + ap + bp (рис. 7д) и функции abp (рис. 7е). Очевидно, что в этом случае получается выражение для S, аналогичное уравнению (10).
Рис. 7
Схема сумматора, реализованного по уравнениям (7) и (10), приведена на рис. 8а. В данной схеме используются многовходовые логические элементы И и ИЛИ. Если использовать только двухвходовые элементы, то получаются схемы, приведенные на рис. 8б,в.