Глава 12 Двоичный сумматор
Сложение — простейшая арифметическая операция. Если мы хотим создать компьютер (а именно в этом заключается цель этой книги), сначала нужно найти способ создания устройства, складывающего два числа. По сути, компьютеры выполняют только операцию сложения. Если нам удастся сконструировать механизм, умеющий складывать, мы окажемся способны создать устройство, использующее операцию сложения для того, чтобы вычитать, умножать, делить, рассчитывать платежи по ипотеке, отправлять ракеты на Марс, играть в шахматы и вносить путаницу в наши телефонные счета.
Сумматор, который мы построим, будет большим, нескладным, медленным и шумным по сравнению с современными калькуляторами и компьютерами. Самое интересное заключается в том, что мы соберем эту машину из простых электрических устройств, о которых говорили в предыдущих главах, — переключателей, лампочек, проводов, батарейки и реле, объединенных в различные логические вентили. Этот сумматор будет состоять исключительно из деталей, которые уже были изобретены 120 лет назад. Особенно хорошо то, что нам не нужно ничего собирать в своей гостиной; вместо этого мы можем конструировать на бумаге и в уме.
Эта машина будет работать исключительно с двоичными числами, в ней будут отсутствовать некоторые современные функции. Вы не сможете использовать клавиатуру для ввода чисел, подлежащих сложению; вместо этого будет ряд переключателей. Роль дисплея для отображения результатов в этом сумматоре исполнит ряд лампочек.
Однако машина сумеет сложить два числа, и она сделает это фактически как компьютер.
Сложение двоичных чисел похоже на сложение десятичных. Если хотите сложить два десятичных числа, например 245 и 673, вы разбиваете задачу на более простые этапы. На каждом этапе складываете две десятичные цифры. В данном примере начинаете со сложения 5 и 3. Эта задача решается быстрее, если вы знаете таблицу сложения.
Большая разница между сложением десятичных и двоичных чисел заключается в том, что в случае с двоичными числами используется более простая таблица.
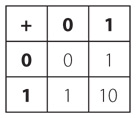
Если вы выросли среди дельфинов, вероятно, вы в школе учили эту таблицу, громко произнося:
0 плюс 0 равно 0,
0 плюс 1 равно 1,
1 плюс 0 равно 1,
1 плюс 1 равно 0, 1 в уме.
Вы можете добавить в эту таблицу нули так, чтобы каждый результат представлял 2-битное значение.

Таким образом, результатом сложения пары двоичных чисел являются два бита, которые называются разрядом суммы и разрядом переноса (1 плюс 1 равно 0, 1 в уме). Теперь мы можем разделить таблицу сложения двоичных чисел на две таблицы. Первая — для разряда суммы.

Вторая — для разряда переноса.
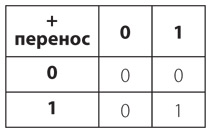
Сложение двоичных чисел удобно рассматривать так, поскольку наш сумматор выполняет операции суммирования и переноса отдельно. Для создания двоичного сумматора потребуется сконструировать схему, выполняющую эти операции. Работа исключительно в двоичной системе счисления значительно упрощает задачу, поскольку все части схемы — переключатели, лампочки и провода — могут представлять двоичные цифры.
Как и при сложении десятичных чисел, мы складываем двоичные числа столбец за столбцом, начиная с крайнего правого.

Обратите внимание: при сложении значений в третьем столбце справа 1 переносится в следующий столбец. Это происходит снова в шестом, седьмом и восьмом столбцах справа.
Какого размера двоичные числа мы хотим сложить? Поскольку мы создаем сумматор прямо в уме, то можем сделать так, чтобы он складывал очень длинные числа. Однако давайте будем благоразумными и ограничимся двоичными числами длиной до восьми бит, то есть будем складывать двоичные числа в диапазоне от 0000 0000 до 1111 1111 (десятичные от 0 до 255). Сумма двух 8-битных чисел может достигать двоичного значения 1 1111 1110 (десятичного значения 510).
Пульт управления нашим двоичным сумматором может выглядеть так.

На этом пульте есть два ряда по восемь переключателей. Этот набор переключателей — устройство ввода, которое мы будем использовать для ввода двух 8-битных значений. В этом устройстве выключенный переключатель (положение вниз) соответствует значению 0, а включенный (положение вверх) — 1, как в случае с настенными переключателями в вашем доме. Устройство вывода в нижней части пульта — ряд из девяти лампочек, которые отобразят результат сложения. Негорящая лампочка соответствует значению 0, горящая — 1. Нам требуется девять лампочек, поскольку сумма двух 8-битных чисел может быть 9-битным числом.
В остальном сумматор будет состоять из логических вентилей, соединенных различными способами. Переключатели будут активировать реле в логических вентилях, которые, в свою очередь, будут зажигать нужные лампочки. Например, если мы хотим сложить числа 0110 0101 и 1011 0110 (из предыдущего примера), включаем соответствующие переключатели.
Загоревшиеся лампочки показывают результат: 1 0001 1011. По крайней мере, мы на это надеемся. Мы ведь еще не собрали устройство!
В предыдущей главе я упомянул, что в этой книге буду использовать множество реле. Для 8-битного сумматора, который мы создаем, требуется не менее 144 реле — по восемнадцать для каждой из восьми пар битов, которые складываем. Если бы я показал готовую схему, вы бы наверняка испугались. Никому не под силу разобраться в схеме, состоящей из ста сорока четырех хитро соединенных реле. Вместо этого мы будем решать такую задачу поэтапно, используя логические вентили.
Возможно, вы сразу заметили связь между логическими вентилями и сложением двоичных чисел, когда увидели таблицу для разряда переноса, который возникает в результате сложения двух однобитных чисел.
Вероятно, вы узнали в ней результат работы вентиля И.
Таким образом, вентиль И вычисляет значение разряда переноса при сложении двух двоичных цифр.
Ага! Мы определенно делаем успехи. Наш следующий шаг, похоже, заключается в том, чтобы убедить некоторые реле вести себя так:
Это вторая часть задачи при сложении пары двоичных цифр. Вычислить значение разряда суммы оказывается не так просто, как значение разряда переноса, но мы справимся и с этой сложностью.
Первое, что нужно понять, — это то, что результат работы вентиля ИЛИ близок к тому, что нам нужно, за исключением значения в правом нижнем углу.
Результат работы вентиля И-НЕ также близок к тому, что нам требуется, за исключением значения в верхнем левом углу:
Итак, давайте подключим вентили ИЛИ и И-НЕ к одним и тем же входам.

В следующей таблице представлены выходные сигналы вентилей ИЛИ и И-НЕ и их сравнение с тем, что мы хотим получить от сумматора.

Заметьте, что мы хотим получить значение 1, только если выходные сигналы обоих вентилей ИЛИ и И-НЕ равны 1. Это говорит о том, что эти два выходных сигнала могут являться входными сигналами для вентиля И.

Обратите внимание: во всей этой схеме по-прежнему есть только два входа и один выход. Два входа относятся к обоим вентилям ИЛИ и И-НЕ. Выходные сигналы вентилей ИЛИ и И-НЕ подаются на вход вентиля И, и это дает именно тот результат, к которому мы стремимся.

На самом деле у этой схемы есть название: вентиль исключающее ИЛИ (Искл-ИЛИ, оно же — сложение по модулю 2). Она называется так потому, что выход равен 1, если вход A равен 1 или вход B равен 1, но не оба одновременно. Вместо того чтобы рисовать вентили ИЛИ, И-НЕ и И, мы можем использовать обозначение, которым инженеры-электрики показывают вентиль Искл-ИЛИ.
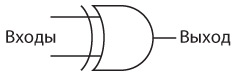
Это обозначение очень похоже на обозначение вентиля ИЛИ, но имеет дополнительную кривую линию со стороны входа.
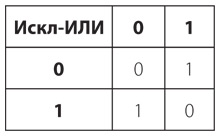
Вентиль Искл-ИЛИ — это последний логический элемент, который будет подробно описан в этой книге. Иногда в электротехнике используется шестой вентиль, называющийся вентилем совпадения или эквивалентности, поскольку выход равен 1 только при одинаковых сигналах на входе. Вентиль совпадения на выходе действует противоположно вентилю Искл-ИЛИ, поэтому его обозначение аналогично обозначению вентиля Искл-ИЛИ, но дополнено кружком со стороны выхода[17].
Давайте повторим все, что уже знаем. При сложении двух двоичных чисел получается бит суммы и бит переноса.

Для получения этих результатов можно использовать следующие два вентиля.
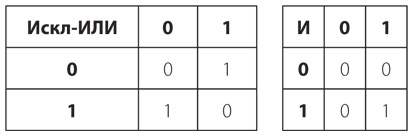
Разряд суммы двух двоичных чисел задается выходом вентиля Искл-ИЛИ, а разряд переноса — выходом вентиля И, поэтому можно комбинировать вентили И и Искл-ИЛИ для сложения двух двоичных цифр A и B.

Вместо многократного перерисовывания вентилей И и Искл-ИЛИ можно просто нарисовать схему, подобную следующей.
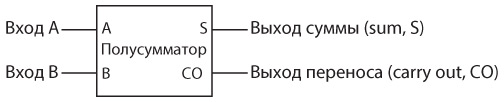
Существует причина, по которой эта схема называется полусумматором. Разумеется, она складывает две двоичные цифры и выдает бит суммы и бит переноса. Однако длина подавляющего большинства двоичных чисел превышает один бит. То, что полусумматор не может сделать, так это прибавить возможный бит переноса, получившийся в результате предыдущей операции сложения. Представьте, что складываем два двоичных числа.
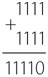
Мы можем использовать полусумматор только для сложения цифр в правом крайнем столбце: 1 плюс 1 равно 0, 1 переносится. В случае со вторым столбцом справа нам, по сути, нужно сложить три двоичные цифры из-за переноса. И это касается всех остальных столбцов. Каждая последующая операция сложения двух двоичных цифр может включать бит переноса из предыдущего столбца.
Для сложения трех двоичных цифр понадобятся два полусумматора и вентиль ИЛИ, соединенные следующим образом.
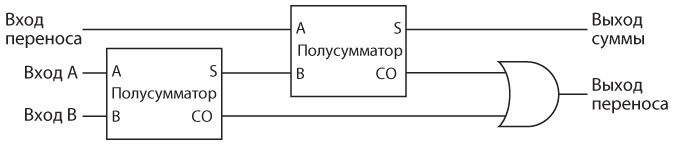
Чтобы разобраться в этой схеме, начнем со входов A и B первого полусумматора слева. Результат — бит суммы и бит переноса. Эта сумма должна быть добавлена к переносу из предыдущего столбца, поэтому они являются входами для второго полусумматора. Сумма, полученная от второго полусумматора, — окончательная. Два переноса из полусумматоров — входы для вентиля ИЛИ. Может показаться, что здесь нужен второй полусумматор, и такая схема, безусловно, сработала бы. Однако если вы проанализируете все возможности, то обнаружите, что оба переноса из двух полусумматоров никогда не равны 1. Вентиля ИЛИ достаточно для их сложения, поскольку он действует так же, как вентиль Искл-ИЛИ, если оба входных сигнала одновременно не равны 1.
Вместо многократного перерисовывания этой схемы можем просто назвать ее полным сумматором.
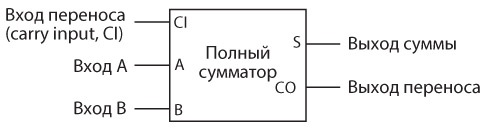
В следующей таблице представлены все возможные комбинации входов для полного сумматора и результирующие выходы.
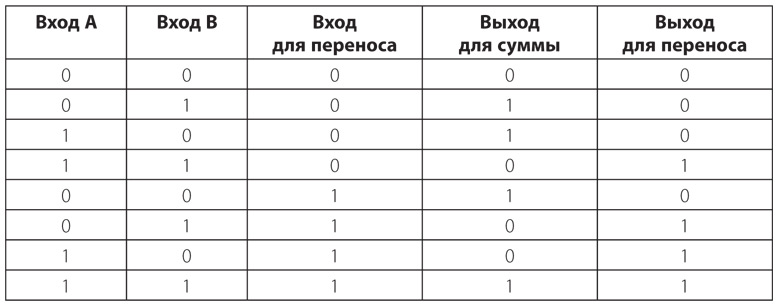
В начале этой главы я сказал, что для создания сумматора потребуются 144 реле. Вот как я это понял: для каждого вентиля И, ИЛИ и И-НЕ требуются по два реле. Таким образом, вентиль Искл-ИЛИ состоит из шести реле. Полусумматор — это вентиль Искл-ИЛИ и вентиль И, поэтому для его создания необходимы восемь реле. Каждый полный сумматор — два полусумматора и вентиль ИЛИ, то есть 18 реле. Нам нужны восемь полных сумматоров для создания 8-битной машины, или 144 реле.
Вспомните наш исходный пульт управления с переключателями и лампочками.
Теперь мы можем начать присоединять переключатели и лампочки к полному сумматору.
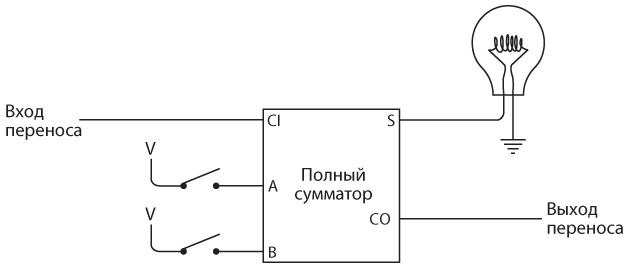
Сначала подключим два крайних правых переключателя и крайнюю правую лампочку к полному сумматору.

Когда вы начинаете складывать два двоичных числа, первый столбец цифр отличается от остальных тем, что не может содержать бит переноса из предыдущего столбца. В первом столбце нет бита переноса, поэтому вход для переноса полного сумматора соединяется с землей, то есть его значением является 0 бит. Разумеется, в результате сложения первой пары двоичных цифр может получиться бит переноса. Этот выход переноса — вход для следующего столбца.
Для следующих двух цифр и лампочки вы используете полный сумматор, подключенный так.
Выход переноса, полученный от первого полного сумматора, является входом для второго полного сумматора. Каждый последующий столбец цифр складывается по той же схеме. Каждый разряд переноса из одного столбца подается на вход для переноса следующего столбца.
Наконец, восьмая и последняя пара переключателей подключена к последнему полному сумматору.
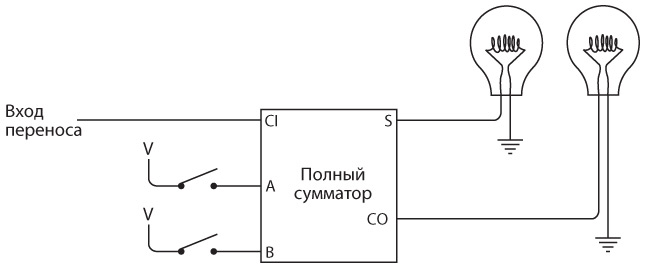
Здесь последний выход для переноса подключен к девятой лампочке.
Вот еще один способ изобразить схему из восьми полных сумматоров (full adder, FA), в которой каждый выход для переноса (CO) подключен к следующему входу для переноса (CI).

Представим единое обозначение 8-битного сумматора, входы обозначим буквами от A0 до A7 и от B0 до B7, выходы — буквами от S0 до S7 (от sum — «сумма»).

Это распространенный способ обозначения отдельных битов многобитного числа. Биты A0, B0 и S0 являются младшими, а биты A7, B7 и S7 — старшими. Например, вот как с помощью этих букв с индексами можно было бы представить двоичное число 0110 1001.

Индексы начинаются с 0 и увеличиваются по мере перехода ко все более значимым цифрам, поскольку они соответствуют показателю степени двойки.

Если вы умножите каждую степень двойки на цифру, расположенную под ней, и сложите результаты, получите десятичный эквивалент числа 0110 1001, который равен 64 + 32 + 8 + 1, или 105.
По-другому 8-битный сумматор можно изобразить так.

Восьмерки внутри стрелок указывают на то, что каждая из них — это группа из восьми отдельных сигналов. Индексы символов A7 … A0, B7 … B0 и S7 … S0 также обозначают восьмиразрядность числа.
Как только соберете один 8-битный сумматор, вы сможете создать второй. Их легко расположить каскадом, чтобы сложить два 16-битных числа.
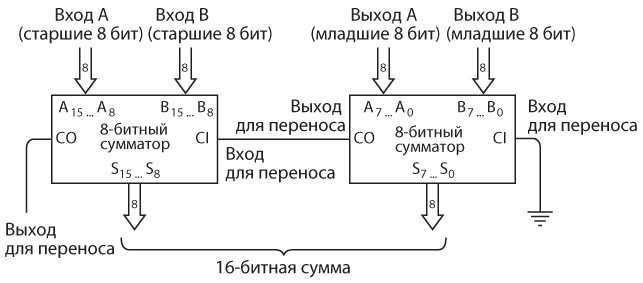
Выход для переноса правого сумматора связан со входом для переноса левого. Левый сумматор в качестве входных значений принимает самые старшие восемь цифр двух слагаемых и в качестве выходного значения выдает самые старшие восемь цифр.
Теперь вы можете спросить: «Неужели компьютеры действительно складывают числа именно так?»
В принципе да. Но не совсем.
Во-первых, сумматоры могут быть быстрее тех, которые мы описали. Если вы посмотрите на то, как работает эта схема, то поймете, что выход переноса от младшей пары цифр необходим для сложения со следующей парой, выход переноса от второй пары цифр — для сложения с третьей парой и т. д. Общая скорость сумматора равна количеству битов, умноженному на скорость одного полного сумматора. Это называется сквозным переносом. Быстрые сумматоры используют дополнительные схемы ускоренного переноса.
Во-вторых (и это самое главное), компьютерам больше не нужно реле! Однако первые цифровые компьютеры, созданные в начале 1930-х годов, использовали реле, позднее — вакуумные лампы. Современные компьютеры создаются на основе транзисторов. Транзисторы в основном функционируют так же, как и реле, однако (как мы увидим далее) они намного быстрее, компактнее, тише, дешевле и потребляют гораздо меньше энергии. Для построения 8-битного сумматора по-прежнему требуются 144 транзистора (или больше, если вы хотите заменить сквозной перенос схемой ускоренного переноса), однако при этом размер схемы микроскопический.
Что такое сумматор и полусумматор.

Полусумма́тор — комбинационная логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). . Существуют сумматоры и полусумматоры работающие не в двоичной логике. Отличается от полного сумматора тем, что не имеет входа переноса из предыдущего разряда.

Відповідь:
Полусумматор — комбинационная логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). . Существуют сумматоры и полусумматоры работающие не в двоичной логике. Отличается от полного сумматора тем, что не имеет входа переноса из предыдущего разряда.
Новые вопросы в Информатика
Даю 100 балов. Ошибка на пайтоне. Не работает insert в tkinter. Код: from tkinter import * root = Tk() #функция добавления чисел def add_digit(digit): … n.insert(1.0, digit) #текстовое поле n = Entry(root, width=35).grid(column=0, row=0, columnspan=3) #кнопки 1-0 but1 = Button(root, width=5, height=3, text=’1′, bg=’lightgrey’, fg=’black’, bd=5, padx=10, command=lambda : add_digit(1)).grid(column=0,row=1, stick=’wens’) but2 = Button(root, width=5, height=3, text=’2′, bg=’lightgrey’, fg=’black’, bd=5, padx=10, command=lambda : add_digit(2)).grid(column=1,row=1, stick=’wens’) but3 = Button(root, width=5, height=3, text=’3′, bg=’lightgrey’, fg=’black’, bd=5, padx=10, command=lambda : add_digit(3)).grid(column=2,row=1, stick=’wens’) but4 = Button(root, width=5, height=3, text=’4′, bg=’lightgrey’, fg=’black’, bd=5, padx=10, command=lambda : add_digit(4)).grid(column=0,row=2, stick=’wens’) but5 = Button(root, width=5, height=3, text=’5′, bg=’lightgrey’, fg=’black’, bd=5, padx=10, command=lambda : add_digit(5)).grid(column=1,row=2, stick=’wens’) but6 = Button(root, width=5, height=3, text=’6′, bg=’lightgrey’, fg=’black’, bd=5, padx=10, command=lambda : add_digit(6)).grid(column=2,row=2, stick=’wens’) but7 = Button(root, width=5, height=3, text=’7′, bg=’lightgrey’, fg=’black’, bd=5, padx=10, command=lambda : add_digit(7)).grid(column=0,row=3, stick=’wens’) but8 = Button(root, width=5, height=3, text=’8′, bg=’lightgrey’, fg=’black’, bd=5, padx=10, command=lambda : add_digit(8)).grid(column=1,row=3, stick=’wens’) but9 = Button(root, width=5, height=3, text=’9′, bg=’lightgrey’, fg=’black’, bd=5, padx=10, command=lambda : add_digit(9)).grid(column=2,row=3, stick=’wens’) but0 = Button(root, width=5, height=3, text=’0′, bg=’lightgrey’, fg=’black’, bd=5, padx=10, command=lambda : add_digit(0)).grid(column=1,row=4, stick=’wens’) #кнопки + — but_pl = Button(root, width=7, height=5, text=’+’, bg=’grey’, fg=’black’, bd=5, padx=10).grid(column=3, row=2) but_mi = Button(root, width=7, height=5, text=’-‘, bg=’grey’, fg=’black’, bd=5, padx=10).grid(column=3, row=3) #настройка столбцов root.grid_columnconfigure(0, minsize=60) root.grid_columnconfigure(1, minsize=60) root.grid_columnconfigure(2, minsize=60) #настройка строки root.grid_rowconfigure(1, minsize=60) root.grid_rowconfigure(2, minsize=60) root.grid_rowconfigure(3, minsize=60) root.grid_rowconfigure(4, minsize=60) root.mainloop()
Оберіть результат виконання програми в Thonny: print (‘Мова програмування Python’) 1Мова програмування Python 2Python 3’Мова програмування Python’ 4Py … thon Мова програмування
Встановіть відповідність між повідомленнями про помилку які з’являються в клітинках та причинами їх появи А. Відсутні дані для обчислень Б. Спроба под … ілити на нуль В. У формулі для математичних обчислень міститься посилання на клітинку, вмістом якої є текст #DIV/0! #VALUE! #N/A
Ви маєте вихідний код розмітки, який не можна змінювати. Стилізуйте елементи згідно їх вмісту. Пофарбуйте мене в рожевий колір (color:pink). Даний ел … емент має залишитись неоформленим. Пофарбуйте мене в сірий колір (color:grey). Даний елемент має залишитись неоформленим. Пофарбуйте мене в червоний колір (color:red). Даний елемент має залишитись неоформленим. Пофарбуйте мене в зелений колір (color:green). Пофарбуйте мене в жовтий колір (color:yellow). Пофарбуйте мене в рожевий колір (color:pink). Даний елемент має залишитись неоформленим. Пофарбуйте мене в сірий колір (color:grey). Даний елемент має залишитись неоформленим. Пофарбуйте мене в червоний колір (color:red). Даний елемент має залишитись неоформленим. Пофарбуйте мене в зелений колір (color:green). Пофарбуйте мене в жовтий колір (color:yellow).
Пожалуйста, срочно! (Программирование по Python) Решите задачу с пошаговым объяснением. Напишите программу, которая принимает имя файла и выводит … его расширение. Если расширение у файла определить невозможно, выбросите исключение.
Пожалуйста, срочно. (Программирование по Python) Решите задачу при помощи метода S.split(symbols) 1.Вы принимаете от пользователя последовательность … чисел, разделённых запятой. Составьте список и кортеж с этими числами.
Напиши программу, анализирующую успеваемость по набору оценок Программа запрашивает ввод набора оценок через пробел. Затем происходит анализ успеваемо … сти. Стабильной успеваемостью считается ситуация, в которой каждая оценка больше или равна предыдущей. Программа должна производить: 1. Ввод набора оценок с помощью input(), формирование списка оценок и вывод его на экран. 2. Вывод результата анализа: «Стабильная успеваемость!» или «Стабильной успеваемости нет». Программа должна работать в точности вот так Введите оценки через пробел: 3 4 4 5 5 5 Анализ набора[3, 4, 4, 5, 5, 5] Стабильная успеваемость!
В классе учатся `28` человек. Назовём человека скромным, если у него в классе не более трёх друзей. Оказалось, что у каждого в классе скромными оказал … ись не менее трёх друзей. Найдите все возможные варианты количества скромных людей в классе. В качестве ответа укажите сумму найденных значений.
Полный одноразрядный сумматор.
Связь между двоичной арифметикой и алгеброй логики позволяет реализовать логические схемы основных элементов процессора и памяти компьютера.
Сумматор — это устройство, предназначенное для сложения двоичных чисел.
Рассмотрим сначала более простое устройство – полусумматор.
Построим таблицу истинности для устройства реализующего арифметическую операцию сложения. Операция «+» бинарная, поэтому полусумматор должен иметь два входа (A и B). В результате сложения двух одноразрядных двоичных чисел может получиться двухразрядное число (с переносом в следующий разряд). Значит, устройство должно иметь два выхода (P — перенос в следующий разряд, S — результат, остающийся в текущем разряде).
| A | B | P | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
По данной таблице истинности построим СДНФ (см. алгоритм построения СДНФ):
- Для переноса в старший разряд: P = A ∧ B
- Для текущего разряда: S = ¬ A ∧ B ∨ A ∧ ¬ B
Преобразуем логическую формулу для S:
(¬ A • B) + (A • ¬ B) = (¬ A • A) + ( ¬ A • B) + (A • ¬ B) + (¬ B • B) =
= ¬ A • (A + B) + ¬ B • (A + B) = (A + B) • ¬ (A • B)
С учетом формулы для переноса имеем:
S = (A + B) • ¬ (A • B) = (A + B) • ¬ P
Таким образом, полусумматор можно построить, используя четыре простейших логических элемента: два конъюнктора, дизъюнктор и инвертор (см. рис.1, слева показано условное обозначение полусумматора):
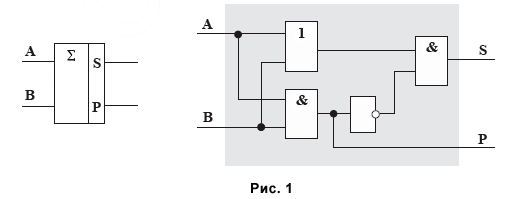
Итак, получено устройство, реализующее суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.
Для реализации полного одноразрядного сумматора необходимо учесть перенос из младшего разряда (P0). Поэтому сумматор должен иметь три входа. Построим таблицу истинности для устройства с учетом третьего входа:
| A | B | P0 | P | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Построим СДНФ для выхода P (перенос в старший разряд):
P =(¬ A ∧ B ∧ P0) ∨ (A ∧ ¬ B ∧ P0) ∨ (A ∧ B ∧ ¬ P0) ∨ (A ∧ B ∧ P0)
Преобразуем:
1) (A ∧ B ∧ ¬ P0) ∨ (A ∧ B ∧ P0) = (A ∧ B) ∧ (¬ P0 ∨ P0) = A ∧ B
Имеем, P = (¬ A ∧ B ∧ P0) ∨ (A ∧ ¬ B ∧ P0) ∨ (A ∧ B)
2) (¬ A ∧ B ∧ P0) ∨ (A ∧ B) = B ∧(¬ A ∧ P0 ∨ A) = B ∧ (¬ A ∨ A ) ∧ (P0 ∨ A) =
= B ∧ (P0 ∨ A) = (B ∧ P0) ∨ (A ∧ B)
Имеем, P = (A ∧ ¬ B ∧ P0) ∨ (B ∧ P0) ∨ (A ∧ B)
3) (A ∧ B) ∨ (A ∧ ¬ B ∧ P0) = A ∧ (B ∨ ¬ B ∧ P0) = A ∧ (B ∨ ¬ B)(B ∨ P0) =
= A ∧ (B ∨ P0) = (A ∧ B) ∨ (A ∧ P0)
Таким образом, для переноса в старший разряд получили:
P = A ∧ B ∨ A ∧ P0 ∨ B ∧ P0
Проанализируем таблицу истинности для выхода S. Значение S отлично от нуля в том случае, если единица поступает ровно на один вход (при этом на двух других входах фиксируется ноль), или на все три входа сразу, т. е.:
S = ¬ (A ∧ B ∨ A ∧ P0 ∨ B ∧ P0) ∧ (A ∨ B ∨ P0) ∨ (A ∧ B ∧ P0)
С учетом формулы для переноса в старший разряд, имеем:
S = ¬ P ∧ (A ∨ B ∨ P0) ∨ (A ∧ B ∧ P0)
Таким образом, одноразрядный двоичный сумматор можно реализовать с помощью следующей схемы (см. рис. 2, слева показано условное обозначение сумматора), которая соответствует полученным логическим формулам (1) и (2).
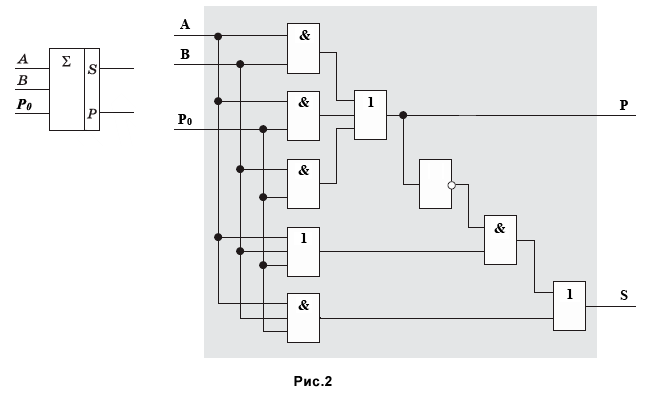
Заметим, что логические функции P и S можно выразить с помощью других формул. В таком случае для одноразрядного двоичного сумматора потребуется другая логическая схема.
Сумматоры
Сумматор — это узел ЭВМ, предназначенный для сложения кодов двоичных чисел. Сумматоры делятся на последовательные (накапливающие) и параллельные (комбинационные). Накапливающие сумматоры имеют низкое быстродействие, поэтому они рассматриваться не будут. В комбинационных сумматорах слагаемые поступают на входы одновременно, а на выходе получается код суммы. После снятия слагаемых результат пропадает. Эти устройства не обладают памятью и строятся на логических элементах.
Составим таблицу истинности устройства для сложения двух одноразрядных чисел а и Ь:
Здесь р — перенос в старший разряд; s — значение суммы. Устройство, реализующее эту таблицу истинности, называют двоичным полусумматором. Его можно синтезировать по ФАЛ для каждого из выходов:

Составим схему на произвольных элементах (рис. 3.14).

Рис. 3.14. Схемная реализация и условное обозначение полусумматора
При сложении многоразрядных чисел необходимо складывать три двоичные цифры в каждом разряде: два слагаемых и единицу переноса из предыдущего разряда Р_х. Наличие этой единицы переноса несколько меняет таблицу сложения двоичных чисел:
ФАЛ для цени суммы:

Карта Карно для функции переноса представлена на рис. 3.15.

Рис. 3.15. Карта Карно для цепи переноса
Уравнение для St не минимизируется. Устройство, реализующее эти ФАЛ, называется сумматором (полным сумматором). Он имеет три входа и два выхода. Цена сумматора по уравнениям составляет Ц = 25. Путем совместной минимизации уравнений Sj и Pj удается снизить цену до 20, и в таком виде выпускаются микросхемы сумматоров. Например, К155ИМ1 — полный одноразрядный сумматор (рис. 3.16).

Рис. 3.16. Полный сумматор
Для сложения многоразрядных чисел сумматор составляют из одноразрядных. Пусть требуется сложить два четырехразрядных двоичных числа: Aw В:

Составим схему сумматора (рис. 3.17).

Рис. 3.17. Многоразрядный сумматор
Получился многоразрядный сумматор с последовательным переносом. Такие сумматоры выпускают в виде отдельных микросхем. Например, ИМС К155 ИМЗ — четырехразрядный сумматор с последовательным переносом. Время сложения чисел определяется временем распространения переноса и равно 55 нс (для четырех разрядов). С ростом числа разрядов быстродействие сумматора уменьшается, так как цепь переноса последовательная.
Вспомним формулу переноса:

Найдем эти переносы:

Видно, что имея только слагаемые, можно формировать перенос в любом разряде, не дожидаясь его появления в предыдущем разряде, причем с помощью только двухуровневой схемы (один слой конъюнкторов и один дизъюнктор). Такая схема называется схемой ускоренного переноса (параллельного переноса). Она может быть встроена в сумматор (сумматор с параллельным переносом) или выпускаться отдельно. Например, ИМС К155 ИМ6 четырехразрядпый сумматор с параллельным переносом. Время сложения чисел равно 27 нс.
При большом числе разрядов сложность схемы ускоренного переноса сильно возрастает. Поэтому сумматор разбивают на группы по четыре или восемь разрядов. Внутри группы выполняют параллельный перенос, а между группами — параллельный или последовательный. Такие сумматоры называют сумматорами с групповым переносом.
Многоразрядный сумматор условно обозначают так, как показано на рис. 3.18.

Рис. 3.18. Условное обозначение многоразрядного сумматора
С помощью сумматоров можно не только складывать, но и вычитать двоичные числа. При использовании дополнительных кодов операцию вычитания двух положительных чисел заменяют операцией суммирования положительного и отрицательного чисел, при этом получение дополнительного кода числа является элементарной операцией. Для этого необходимо проипвертировать число и прибавить к нему в младший разряд единицу.
Схема вычитателя числа А из числа В приведена на рис. 3.19, а схема вычитателя числа В из числа А — на рис. 3.20.

Рис. 3.19. Схема вычитателя числа А из числа В

Puc. 3.20. Схема вычитателя числа В из числа А
Схема инкремент/декремент. Возьмем три полусумматора и соединим их следующим образом (рис. 3.21).

Рис. 3.21. Схема инкремент/декремент
Подавая на управляющий вход Z ноль или единицу, проанализируем состояние выхода при различных входных сигналах:
Сумматоры
Параллельные многоразрядные сумматоры
Последовательный многоразрядный сумматор
Повышение быстродействия параллельных сумматоров
Принцип построения БУП (блок ускоренного переноса)
Сумматором – называется комбинационное логическое устройство, предназначенное для выполнения операции арифметического сложения чисел в двоичном коде.
Для начала получим ФАЛ, описывающие операции арифметического сложения.
Таблица истинности для сложения одноразрядных двоичных кодов.
S реализовать через ИЛИ нельзя, т.к. существует отличие в четвертой строке.
Результат сложения не может быть представлен двоичным кодом, разрядность которого равна разряду.
Данный вид сумматора называют неполным или полусумматором.
Полусумматор – комбинационное логическое устройство предназначенное для сложения двоичных одноразрядных чисел и не имеющие входа или выхода переноса.
Полный сумматор – комбинационное логическое устройство для сложения чисел в двоичном коде, где есть вход переноса в младший разряд и выход переноса в старший разряд.
Таблица истинности для полного одноразрядного сумматора.
В случае использования двух разрядных чисел:
Функции «=1» и «≥2» можно реализовать в разных базисах И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.
≥2 функция мажоритарности, т.е. в импликанте 2 или больше единиц.
Многоразрядные сумматоры по принципу действия могут быть :
— параллельные
— последовательные
Параллельные многоразрядные сумматоры
Параллельно подаются разряды слагаемых, но перенос получается последовательно.
Для исключения получения ложного результата на выходе схемы установлены логические элементы «И». Сигнал Z должен появляться на их входах не ранее, чем после последовательной передачи сигнала Р по всем разрядам сумматора.
Типовая структурная схема:
К 155 ИМ3 Построен на одноразрядных сумматорах.
УГО SM
Последовательный многоразрядный сумматор
Используют один одноразрядный сумматор, который последовательно разряд за разрядом, начиная с младшего, выполняет операцию сложения в соответствующих разрядах. Снижается быстродействие устройства, применяется калькулятор, где низкие требования к быстродействию.
Строится на основе одноразрядного сумматора + необходимое тактирование и устройства для записи входной и выходной информации (регистр).
Регистры не входят в состав сумматора.
Каждый тактовый импульс обеспечивает подачу более старшего разряда слагаемых на входы одноразрядного сумматора из регистров и запись в регистр на выходе значений сумма всех разрядов последовательно.
Повышение быстродействия параллельных сумматоров
Трудность в достижении быстродействия связана с тем, что процесс распространения переносов носит последовательный характер. Следовательно задержка в распространении переносов увеличивается при получении последнего переноса.
Пути понижения задержки распространения переноса:
1.При построении схем одноразрядных сумматоров стремятся к уменьшению числа логических элементов в цепи между входом, на который поступает сигнал переноса рi и выходом, на котором формируется передаваемый в следующий разряд сигнал переноса рi+1.
По таблице истинности можно составить функцию переноса в разных базисах:
И-НЕ СДНФ
ИЛИ-НЕ СКНФ => aibi + (ai + bi)pi = abVapVbp
И-ИЛИ-НЕ
СКНФ
2.В цепях от рi к рi+1 прим. логический элемент с повышенным быстродействием.
3.В цепях от рi к рi+1 сигналы с выхода каждого логического элемента должен поступать на возможно меньшее число других логических элементов, т.к. присоединение дополнительных логических элементов приводит к повышению задержки распространения сигнала следует понижение быстродействия.
4. Пример устройства формирования переноса в параллельной форме (блок ускоренного переноса)
Переносы из БУП поступают на все разрядные сумматоры одновременно. БУП встроен. БУП встроен в ИМС сумматора.
При этом разрядные сумматоры не содержат цепей формирования переносов. Они формируют только ?Si и величины xi и yi для получения которой переносы не требуются.
Величины xi и yi необходимы для формирования переносов в БУП.
Они определяют следующие ситуации:
yi = 1 : в i-том разряде перенос рi+1 в следующий (i+1) разряд надо формировать не зависимо от поступления рi переноса в данный разряд из предыдущего.
xi = 1: : в i-том разряде перенос рi+1 должен формироваться только при условии поступления рi из предыдущего разряда.
Принцип построения БУП
Перенос p2 должен формироваться при условии y1 = 1 или при условии x1 = 1 и
p1 = 1, т.е.
Аналогично выражения для переносов можно построить и в другие разряды
Можете самостоятельно убедится в справедливости:
Имея эти выражения можно строить схемы
Величины xi и yi формируются одновременно, следовательно одновременно формируются рi -переносы. После поступления рi из БУП в разрядных сумматорах формируются суммы Si по выражениям:
Вернутся к содержанию.
Одноразрядные сумматор и полусумматор
Одноразрядные сумматор и полусумматор предназначены для сложения двоичных разрядов.
Полусумматор представляет собой комбинационную схему, имеющую два входа и два выхода. Условное графическое обозначение полусумматора приведено на рис. 2.10, а, где А и В – слагаемые двоичные цифры, каждая из которых может принимать значение 0 или 1; S и P – выводы, на которых появляется результат сложения. Вывод S предназначен для выдачи суммы слагаемых А и В, а вывод Р – для выдачи переноса в следующий (i+1)—й разряд. Полусумматор функционирует в соответствии с таблицей истинности (табл. 2.5).
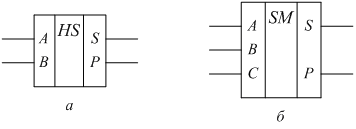
Рис. 2.10. Условное графическое обозначение полусумматора HS (а) и сумматора SM (б)
Таблица 2.5 Таблица 2.6
| А | В | С | P | S |
| А | В | P | S |
В соответствии с табл. 2.5 функции выходов S и P имеют вид
или .
Полный одноразрядный двоичный сумматор предназначен для построения многоразрядных сумматоров и имеет три входа и, следовательно, предназначен для сложения трёх двоичных цифр. Условное графическое обозначение полного одноразрядного двоичного сумматора приведено на рис. 2.10, б, а таблица истинности, в соответствии с которой функционирует сумматор, – в табл. 2.6. А и В – двоичные разряды чисел; С – входной перенос в данный разряд из предыдущего разряда. Это разделение входов сумматора условно, так как все три входа (А, В и С) имеют одинаковый вес. На выходе S появляется разряд суммы, а на выходе Р – разряд переноса в следующий разряд.
Функциональная схема полного одноразрядного двоичного сумматора строится на основе функций суммы S и переноса Р, составляемых по таблице истинности (табл. 2.6):
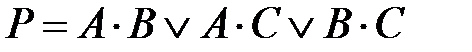
;
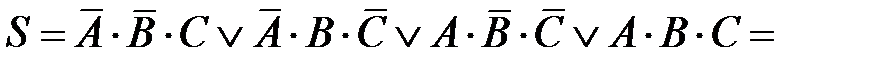
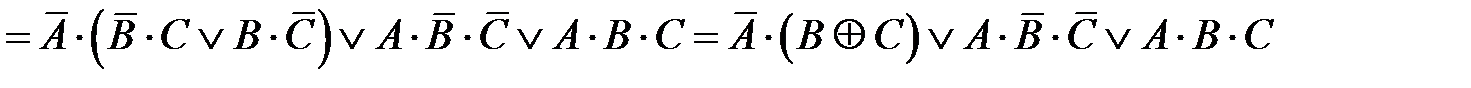
Наиболее удачные схемы одноразрядных сумматоров, содержащих наименьшее количество элементов и наименьшее количество входов у элементов, получены эмпирическим путём. Одна из таких функциональных схем приведена на рис. 2.11.
Логические уравнения для значений суммы и переноса в этой схеме следующие:
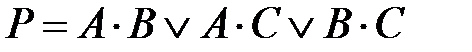
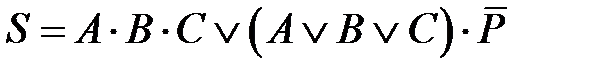
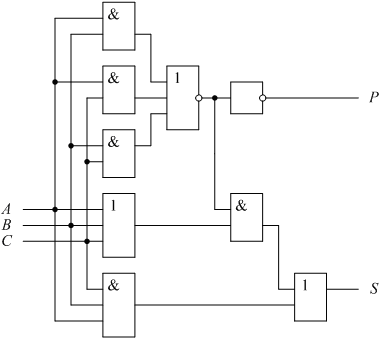
| Рис. 2.11. Функциональная схема одноразрядного суматора на элементах И, ИЛИ, ИЛИ НЕ, НЕ |
Как видно из рис. 2.11, схема состоит из 9 логических элементов. Общее число входов – 20. В данной схеме ни один логический элемент не нагружается на входы двух других элементов.
Если для реализации сумматора использовать соотношения
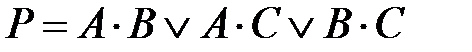
,
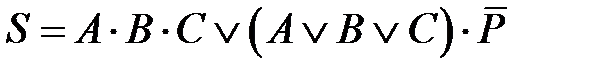
,
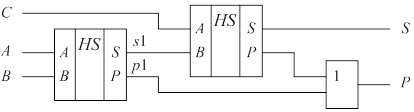
| Рис. 2.12. Функциональная схема одноразрядного сумматора,состоящего из двух полусумматоров и схемы «2ИЛИ» |
то у девяти используемых логических элементов общее число входов будет равно 19.
Функциональная схема полного двоичного одноразрядного сумматора, состоящая из двух совершенно одинаковых частей (полусумматоров и схемы 2ИЛИ, объединяющей сигналы с этих частей), представлена на рис. 2.12. Полусумматор HS1 суммирует две цифры слагаемых без учёта переносов из младшего разряда. При этом вырабатывается промежуточный сигнал переноса р1 и промежуточная сумма чисел s1. Полусумматор HS2 производит суммирование промежуточной суммы s1 и сигнала переноса С из младшего разряда.
Если в полусумматоре HS1 сигнал переноса не возник, то он может возникнуть в полусумматоре HS2при условии поступления на вход сумматора сигнала переноса из младшего разряда и значения «1» одного из слагаемых. Если же сигнал переноса появился в полусумматоре HS1, то сигнал переноса р1 из полусумматора HS2 не появится. Общий сигнал переноса сумматора равен логической сумме переносов обоих полусумматоров. Сигнал суммы S вырабатывается на выходе полусумматора HS2.
Если реализовать схему, изображённую на рис. 5.10, на логических элементах И, ИЛИ, НЕ, то общее число элементов будет равно 9. Общее число входов такой схемы равно 16. Таким образом, схема полного одноразрядного двоичного сумматора, состоящего из двух полусумматоров, является наиболее экономичной.
Арифметические устройства
Двоичный сумматор(SM — SuМ — сумма) — это комбинационное цифровое устройство, предназначенное для арифметического сложения чисел, представленных в виде двоичных кодов. Сумматоры используются в операциях суммирования и вычитания чисел, а также составляют основу умножения и деления чисел.
По принципу обработки разрядов чисел различают последовательные и параллельные сумматоры. В последовательных сумматорах сложение чисел осуществляется поразрядно (последовательно), в параллельных – все разряды обрабатываются одновременно.
По числу выводов различают полусумматоры, одноразрядные сумматоры и многоразрядные сумматоры.
Полусумматор (HS — HalfSum — полусумма), — это устройство, производящее сложение двух одноразрядных двоичных чисел:
Сложение двух одноразрядных двоичных чисел можно отразить таблицей сложения (таблицей истинности), в которой А и В — значения входных чисел, S — значение результата суммирования и Р — значение переноса в старший разряд (рис. 1,а). Работа устройства, реализующего эту таблицу истинности (полусумматора), описывается уравнениями: S = A B (исключающее ИЛИ), P=A·B (И) и имеет логическую структуру, изображенную на рис. 1,б.

| A | B | P | S |
Поскольку полусумматор имеет только два входа, он может использоваться для суммирования лишь в младшем разряде.
Полный сумматор.При суммировании двух многоразрядных чисел для каждого разряда (кроме младшего) необходимо использовать устройство, имеющее дополнительный вход переноса. Такое устройство называют полным сумматором.
Полный одноразрядный сумматор суммирует три одноразрядных двоичных числа: два слагаемых Ai, Bi и перенос, поступивший из младшего разряда Pi-1. Полный одноразрядный сумматор можно построить из двух полусумматоров HS и логического элемента ИЛИ (рис. 2). Один полусумматор используется для сложения i-го разряда двоичных чисел, а второй полусумматор складывает результат первого полусумматора с переносом из (i-1) разряда.

а
| Входы | Выходы | |||
| Ai | Bi | Pi-1 | Si | Pi |
Для сложения двух многоразрядных двоичных чисел используют многоразрядные сумматоры, представляющие собой в простейшем виде последовательное соединение одноразрядных сумматоров (рис. 3,а). Сигнал переноса последовательно передается с выхода предыдущего разряда сумматора на вход переноса следующего разряда. Рассмотренный сумматор называется параллельным сумматором.

В виде интегральных микросхем выпускаются одноразрядные, двухразрядные и четырехразрядные двоичные сумматоры. В корпусе микросхемы К155ИМ3 четыре полных одноразрядных сумматора объединены в схему четырехразрядного сумматора (рис. 3,б). С целью наращивания разрядности суммируемых чисел микросхемы соединяют последовательно, для чего выход переноса Р непосредственно соединяют со входом переноса Р0 микросхем, принадлежащим более высоким разрядам. У микросхемы, суммирующей младшие разряды чисел, вход переноса Р0 следует соединять с общим проводом.
Вычитание двух чисел. Рассмотренные сумматоры можно использовать для вычитания двоичных чисел. В этом случае операция вычитания заменяется сложением уменьшаемого А с вычитаемым В (Впр=В4В3В2В1), представленным в дополнительном коде. Дополнительный код Вдоп образуется из обратного (инверсного) кода ( ) добавлением к нему единицы (Вдоп=Вобр+1).
Очевидно, для четырехразрядных чисел, записанных в этих кодах, справедливы равенства
Следовательно, операцию вычитания можно представить в виде
Следует отметить, что если А > В, то ответ формируется в прямом коде, при этом образуется 1 переноса в более старший разряд, при А < В ответ формируется в обратном коде и 1 переноса в более старший разряд не образуется.
На рисунке 4 представлена схема вычитателя на базе сумматора. Наличие или отсутствие логической 1 на выходе переноса Р, используют для распознавания знака результата, образуя циклический перенос, т. е. соединяя выход переноса Р со входом переноса Р0. Когда сигнал переноса соответствует логической 1, то на выходах S4S3S2S1 формируется результат в прямом коде, при нулевом значении сигнала переноса результат формируется в обратном коде, который несложно преобразовать в прямой.

Цифровой компаратор. Цифровые компараторы выполняют сравнение двух двоичных чисел. Они могут определять равенство двух двоичных чисел А и В с одинаковым количеством разрядов либо вид неравенства А>В или А
Цифровой компаратор можно построить на сумматоре, подавая на один суммирующий вход прямой код числа А, на другой — инверсный код числа В (рис. 5). Легко убедиться, что при А=Вна выходах S4S3S2S1 формируются логические единицы, подключив к ним элемент И, получим 1 на его выходе. При A>Bединица формируется на выходе переноса Р. Для определения неравенства А

Контрольные вопросы.
1. Что называется полусумматором?
2. Опишите принцип действия полусумматора.
3. Что называется полным одноразрядным сумматором?
4. Опишите принцип действия полного одноразрядного сумматора.
5. Опишите структуру и принцип действия многоразрядного сумматора.
6. Как с помощь сумматора осуществляется операция вычитания?
7. Как с помощь сумматора осуществляется сравнение двух двоичных чисел?
Лабораторная работа №6.Изучение четырехразрядного параллельного сумматора
Цель работы.Изучение устройства и принципа действия четырехразрядного параллельного сумматора.
1. Провести исследование работы четырехразрядного параллельного сумматора. В процессе исследования провести сложение двоичных чисел указанных преподавателем. Полученные результаты занести в таблицу 1. Провести проверку путем перевода слагаемых и суммы в десятичную систему.
| А(2) | В(2) | S(16) | S(2) | А(10)+В(10)=S(10) |
| P (HL1) | HG1 |
2. Провести вычитание двоичных чисел указанных преподавателем, заменив его сложением прямого кода уменьшаемого с дополнительным кодом вычитаемого. Полученные результаты занести в таблицу 2. Провести проверку путем перевода уменьшаемого, вычитаемого и разности в десятичную систему.
| А(2) | В(2) | Bобр | Вдоп | S(16) | S(2) | А(10)+В(10)=S(10) |
| P (HL1) | HG1 |
3. Провести сравнение двоичных чисел указанных преподавателем. Полученные результаты занести в таблицу 3. Провести проверку путем перевода двоичных чисел в десятичную систему.
| А(2) | В(2) | Bобр | P (HL1) | HG1 | >, | А(10) ? В(10) |
| А … В | ||||||
| А … В | ||||||
| А … В | ||||||
| А … В | ||||||
| А … В | ||||||
| А … В | ||||||
| А … В |
Указания по выполнению лабораторной работы.
Работа выполняется на универсальном стенде с использованием платы П3 и технологической карты III-3.

Рис. 6. Схема к карте III-3.
Карта III-3 (рис. 6) предназначена для исследования работы сумматора двух четырехразрядных двоичных чисел на микросхеме К155ИМ3 (D2). Для задания двух четырехразрядных слагаемых используются тумблеры SA4 – SA1 (слагаемое А) и регистр D1 (слагаемое В). Ввод слагаемого В в регистр может осуществляться как в параллельном коде с тумблеров SA4 – SA1 (тумблер SA5 должен находиться в верхнем положении), так и в последовательном с кнопки SB2 (SA5 — в нижнем положении) (см. л.р. №3). Импульс записи задается кнопкой SB2.
Индикация слагаемых осуществляется индикаторами HL2 – HL5 и HL6 – HL9. Сумма в четырех первых разрядах дешифруется в блоке индикации и высвечивается в виде шестнадцатеричного числа на семисегментном индикаторе HG1. Сигнал переноса P в старший (пятый) разряд подается на индикатор HL1. Таким образом, сигнал переноса P также является 0 или 1 в старшем (втором) разряде шестнадцатеричного числа суммы, а число на индикаторе HG1 – числом в младшем (первом) разряде.
Замену вычитания двоичных чисел сложением на стенде можно проводить двумя способами.
1-й способ. Записать в регистр дополнительный код вычитаемого, тумблерами SA4 – SA1 набрать прямой код уменьшаемого. Индикатор HG1 покажет результат вычитания в виде шестнадцатеричного числа. Сигнал на выходе переноса Р (индикатор HL1) не учитывается.
2-й способ. Записать в регистр обратный код вычитаемого, тумблерами SA4 – SA1 набрать прямой код уменьшаемого. Недостающая 1 прибавляется сигналом на входе переноса Р0 путем нажатия кнопки. Сигнал на вход переноса Р0 подается через инвертор D2.3 (при отпущенной кнопке SB3 Р0=0, при нажатой Р0=1).
Для сравнения двух двоичных чисел в регистр записать обратный код числа В и тумблерами SA4 – SA1 набрать прямой код числа А. При А=В индикатор HG1 покажет шестнадцатеричное число F (S=11112). При А>В загорится индикатор HL1 (Р=1). Во всех остальных случаях А
Техническое описание стенда универсального ОАВТ
Стенд предназначен для выполнения лабораторных работ по электронике.
На передней (наклонной) панели стенда установлены разъем X1, тумблеры (SA1 – SA5) и кнопки (SB1 – SB3) ввода информации и задания режимов работы, исследуемых устройств, а так же светодиодный дисплей. Разъем X1 предназначен для подключения сменных плат с исследуемыми устройствами.

Переключатели SA1 – SA4, SB2 и SB3 предназначены для подачи логических сигналов с уровнями «0» (соответствующий вывод замкнут на общий провод) или «1» (вывод – на +5В). Тумблер SA5 подключается всеми своими выводами к разъему и поэтому может использоваться в качестве переключателя «двух сигналов в одну линию» или, наоборот, «одного сигнала на два направления». Кнопка SB1 подключена к схеме защиты от «дребезга» на триггере. С помощью этой кнопки формируется одиночный импульс с крутыми фронтами, необходимый для нормальной работы исследуемых триггеров, регистров и счетчиков. При нажатии SB1 на соответствующем контакте разъема X1 появляется логический 0, а при отпускании – логическая 1. Этот блок на схемах обозначается как формирователь одиночного импульса (F ).
Светодиодный дисплей служит для индикации режимов работы, а также входной и выходной информации исследуемых устройств. Дисплей состоит из девяти светодиодов HL1 – HL9, позволяющих индицировать в 9 разрядах уровни логической «1» (светодиод светится) и логического «0» (не светится), и семисегментного индикатора HG1 для индикации числа в десятичном или шестнадцатеричном кодах.