Что такое суммарный спин

Спин электрона

Спин электрона (и других микрочастиц) — это квантовая величина, у которой нет классического аналога. Это внутреннее свойство электрона, которое можно уподобить заряду или массе. Понятие спина было предложено американскими физиками Д. Уленбеком и С. Гаудсмитом для того, чтобы объяснить существование тонкой структуры спектральных линий. Ученые предположили, что электрон имеет собственный механический момент импульса, который не связан с движением электронам в пространстве который был назван спином.

Если считать, что электрон имеет спин (собственный механический момент импульса ($>_s$)), то значит должен иметь собственный магнитный момент ($>_$). В соответствии с общими выводами квантовой физики спин квантуется как:

где $s$ — спиновое квантовое число. Проводя аналогию с механическим моментом импульса, проекция спина ($L_$) квантуется таким образом, что число ориентаций вектора $>_s$ равно $2s+1.$ В опытах Штерна и Герлаха ученые наблюдали две ориентации, то $2s+1=2$, следовательно, $s=frac$.

При этом проекция спина на направление внешнего магнитного поля определена формулой:

где $m_s=pm frac$-магнитное спиновое квантовое число.

Получилось, что экспериментальные данные привели к необходимости введения дополнительной внутренней степени свободы. Для полного описания состояния электрона в атоме необходимы: главное, орбитальное, магнитное и спиновое квантовые числа.

Позднее Дирак показал, что наличие спина следует из полученного им релятивистского волнового уравнения.

Атомы первой валентной группы периодической системы имеют валентный электрон, находящийся в состоянии с $l=0$. При этом момент импульса всего атома равен спину валентного электрона. Поэтому когда обнаружили для подобных атомов, пространственное квантование момента импульса атома в магнитном поле это стало доказательством существования спина только двух ориентаций во внешнем поле.

Готовые работы на аналогичную тему

Спиновое квантовое число, отличаясь от других квантовых чисел, является дробным. Количественную величину спина электрона можно найти в соответствии с формулой (1):

Для электрона имеем:

Иногда говорят, что спин электрона ориентирован по направлению или против направления напряженности магнитного поля. Такое высказывание является неточным. Так как при этом на самом деле имеется в виду направление его составляющей $L_.$

Из опытов Штерна и Герлаха получено, что $p_$ (проекция собственного магнитного момента электрона) равна:

где $_B$ — магнетон Бора.

Найдем отношение проекций $L_$ и $p_$, применяя формулы (4) и (5), имеем:

Выражение (6) называют спиновым гиромагнитным отношением. Оно в два раза превышает орбитальное гиромагнитное отношение. В векторной записи гиромагнитное отношение записывают как:

Опыты Эйнштейна и де Гааза определили спиновое гиромагнитное отношение для ферромагнетиков. Это дало возможность определить спиновую природу магнитных свойств ферромагнетиков и получить теорию ферромагнетизма.

Задание: Найдите численные значения: 1) собственного механического момента импульса (спина) электрона, 2) проекции спина электрона на направление внешнего магнитного поля.

Решение:

В качестве основания для решения задачи используем выражение:

где $s=frac$. Зная величину $hbar =1,05cdot ^Джcdot с$, проведем вычисления:

В качестве основы для решения задачи используем формулу:

где $m_s=pm frac$-магнитное спиновое квантовое число. Следовательно, можно провести вычисления:

Ответ: $L_s=9,09cdot ^cdot , L_=pm 5,25cdot ^Джcdot с.$

Задание: Каков спиновый магнитный момент электрона ($p_$) и его проекция ($p_$) на направление внешнего поля?

Решение:

Спиновый магнитный момент электрона может быть определен из гиромагнитного соотношения как:

Собственный механический момента импульса (спина) электрона можно найти как:

Подставим выражение для спина электрона в формулу (2.1), имеем:

Используем известные для электрона величины:

поведем вычисление магнитного момента:

Из опытов Штерна и Герлаха получено, что $p_$ (проекция собственного магнитного момента электрона) равна:

Вычислим $p_$ для электрона:

Ответ: $p_=1,6cdot ^Acdot м^2, p_=9,27cdot ^Acdot м^2.$

Что такое спин в физике: момент импульса, бозоны, фермионы

Итак, полностью абстрагируемся и забываем любые классические определения. Ибо спин – это понятие, присущее исключительно квантовому миру. Попробуем разобраться в том, что это такое.

Больше полезной информации для учащихся – у нас в телеграм.

Спин и момент импульса

Спин (от английского spin – вращаться) – собственный момент импульса элементарной частицы.

Теперь вспомним, что такое момент импульса в классической механике.

Момент импульса – это физическая величина, характеризующая вращательное движение, точнее, количество вращательного движения.

В классической механике момент импульса определяется как векторное произведение импульса частицы на ее радиус вектор:

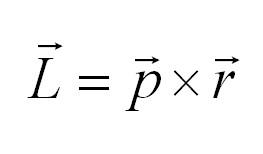
По аналогии с классической механикой спин характеризует вращение частиц. Их представляют в виде волчков, вращающихся вокруг оси. Если частица имеет заряд, то, вращаясь, она создает магнитный момент и явлеятся своего рода магнитом.

Однако данное вращение нельзя трактовать классически. Все частицы помимо спина обладают внешним или орбитальным моментом импульса, характеризующим вращение частицы относительно какой-то точки. Например, когда частица движется по круговой траектории (электрон вокруг ядра).

Спин же является собственным моментом импульса, то есть характеризует внутреннее вращательное состояние частицы вне зависимости от внешнего орбитального момента импульса. При этом спин не зависит от внешних перемещений частицы.

Представить, что же там вращается внутри частицы, невозможно. Однако факт остается фактом – для заряженных частиц с разнонаправленными спинами траектории движения в магнитном поле будут различны.

Спиновое квантовое число

Для характеристики спина в квантовой физике введено спиновое квантовое число.

Спиновое квантовое число – одно из квантовых чисел, присущих частицам. Часто спиновое квантовое число называют просто спином. Однако следует понимать, что спин частицы (в понимании собственного момента импульса) и спиновое квантовое число – это не одно и то же. Спиновое число обозначается буквой J и принимает ряд дискретных значений, а само значение спина пропорционально приведенной постоянной Планка:

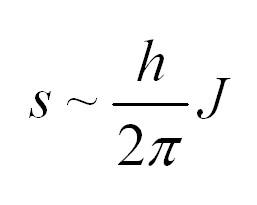
Бозоны и фермионы

Разным частицам присущи разные спиновые числа. Так, главное отличие состоит в том, что одни обладают целым спином, а другие – полуцелым. Частицы обладающие целым спином называются бозонами, а полуцелым – фермионами.

Бозоны подчиняются статистике Бозе-Эйнштейна, а фермионы – Ферми-Дирака. В ансамбле частиц, состоящем из бозонов, любое их количество может находиться в одинаковом состоянии. С фермионами все наоборот – наличие двух тождественных фермионов в одной системе частиц невозможно.

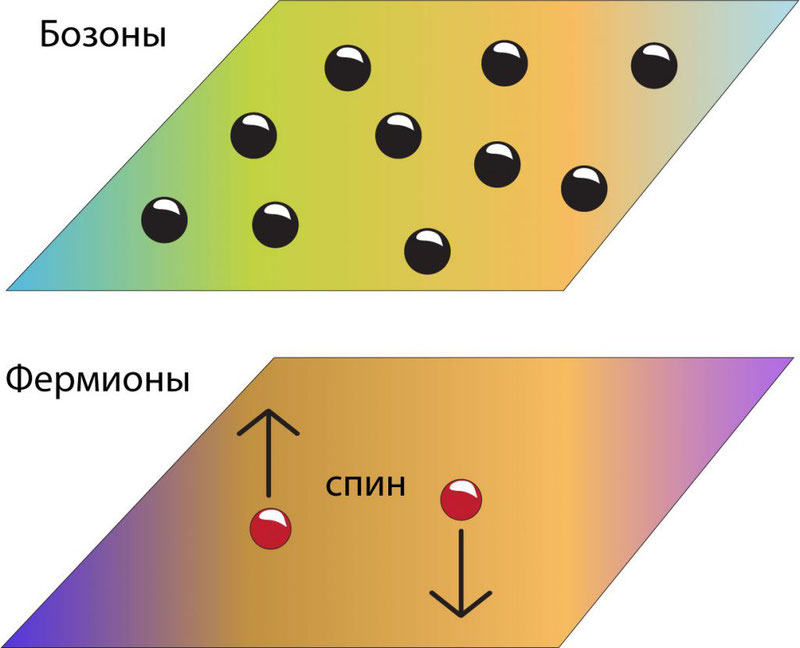
Бозоны: фотон, глюон, бозон Хиггса. Подробнее о бозоне Хиггса — в отдельной статье.

Фермионы: электрон, лептон, кварк

Попробуем представить, чем отличаются частицы с разными спиновыми числами на примерах из макромира. Если спин объекта равен нулю, то его можно представить в виде точки. Со всех сторон, как ни вращай этот объект, он будет одинаков. При спине равном 1 поворот объекта на 360 градусов возвращает его в состояние, идентичное первоначальному состоянию.

Например, карандаш, заточенный с одной стороны. Спин равный 2 можно представить в виде карандаша, заточенного с двух сторон — при повороте такого карандаша на 180 градусов мы не заметим никаких изменений. А вот полуцелый спин равный 1/2 представляется объектом, для возвращения которого в первоначальное состояние нужно соверщить оборот в 720 градусов. Примером может служить точка, движущаяся по листу Мебиуса.

Итак, спин — квантовая характеристика элементарных частиц, которая служит для описания их внутреннего вращения, момент импульса частицы, не зависящий от ее внешних перемещений.

Надеемся, что вы осилите эту теорию быстро и сможете при случае применить знания на практике. Ну а если задачка по квантовой механике оказалось непосильно сложной или не можете не забывайте о студенческом сервисе, специалисты которого готовы прийти на выручку. Учитывая, что сам Ричард Фейнман сказал, что «в полной мере квантовую физику не понимает никто», обратиться за помощью к опытным специалистам – вполне естественно!

Спин электрона — определение, классификация и примеры значений

Спин электрона (от англ. «вращение») относится к физическому свойству субатомных частиц, в соответствии с которым каждая элементарная частица имеет собственный момент импульса фиксированной величины.

Это внутреннее свойство, такое как масса или электрический заряд. Когда говорят о спине, вместо буквы l пишется буква s.

В 1920 году химики пришли к выводу, что с известными квантовыми числами (масса, электрический заряд) было невозможно полностью описать электроны в атоме. В химии электроны играют ведущую роль.

Что такое спин в физике

Около 1925 г. три исследователя Ральф Крониг, Гаудсмит и Уленбек начали с идеи, что электрон, который вращается вокруг атомного ядра, похож на Землю, двигающуюся вокруг Солнца.

Как Земля имеет вращательное движение, так и электрон, связанный с атомом, вращается сам по себе.

Полный угловой момент Земли представляет собой векторную сумму ее орбитального углового момента и ее углового момента вращения. Но в случае электрона нельзя рассчитать его угловой момент вращения так, как рассчитывают момент Земли, основываясь на массе, радиусе и угловой скорости.

Электрон является держателем отрицательного электрического заряда. Вращение создает магнитное поле, которое называется спином.

Спин обеспечивает меру собственного момента импульса каждой частицы. Он необходим, чтобы определить тип частицы.

Добавив спин в качестве четвертого числа, можно было дать более полное объяснение характеристик спектров атомов, обладающих одним электроном. Можно представить электрон как крутящийся мяч, а спин как связанный с этим вращением момент. Но в этом случае скорость движения получится выше скорости света.

Существование спина подтверждается многими экспериментальными результатами. До сих пор неизвестно, из чего складывается спин протона. Нельзя провести измерение относительно оси Х и оси У одновременно.

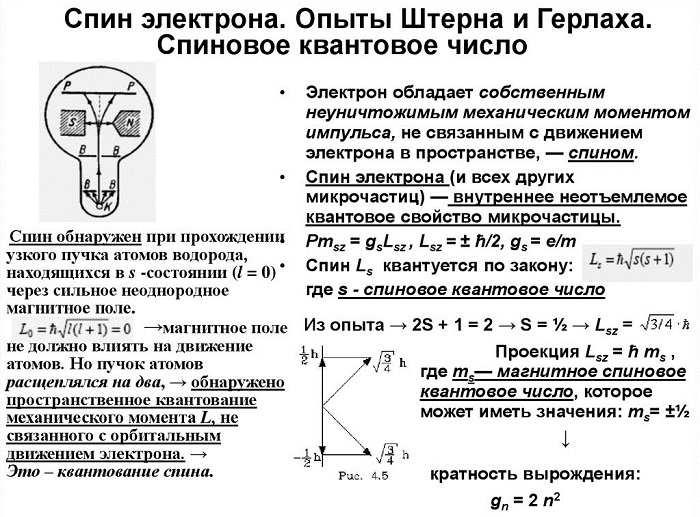
Вскоре концепция была распространена на все субатомные частицы, включая протоны, нейтроны и античастицы. Свойства большинства парамагнитных и ферромагнитных веществ определяет обусловленный спином электрона магнитный момент.

Техника и наука нашли широкое применение определенных свойств, связанных с этим физическим свойством. Правило Хунда говорит, что суммарный спин должен быть максимальным (при распределении электронов в пределах энергетического уровня).

Классификация элементарных частиц по спину

Какое значение может принимать спиновое квантовое число?

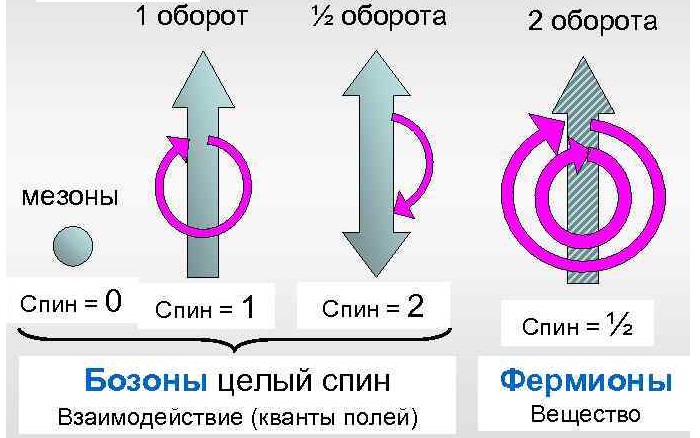
Принципы квантовой механики указывают, что значения спина в нормальных условиях ограничены целым или полуцелым числом, кратным постоянной Планка.

Фермионы (электроны, кварки, нейтрино) имеют полуцелые значения (½, 3/2).

Бозоны (фотоны, глюоны, бозоны) имеют спины 0, 1, 2. У фотона спин — 1.

Некоторые экзотические частицы, такие как пион, имеют значение 0.

1/2 — это спин одиночного электрона. Такая система называется дублет.

Магнитный спиновый момент существует для незаряженных частиц, таких как фотон. Ферромагнетизм возникает из-за выравнивания спинов (иногда и от орбитальных магнитных моментов).

В настоящее время микроэлектроника находит применение для определенных свойств или эффектов, связанных с природой вращения, таких как магнитосопротивление или гигантское магнитосопротивление, которое используется в жестких дисках.

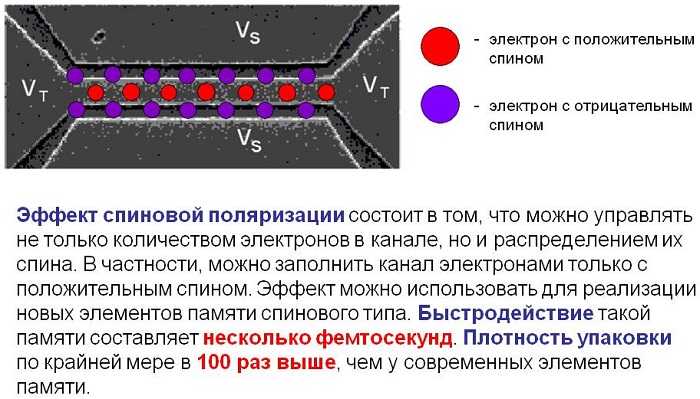
Также рассматривается возможность использования этих свойств для будущих компьютеров, в которых спин изолированной системы может служить квантовым битом (кубитом). Сейчас ученые пытаются контролировать спин, используя сверхкороткие импульсы лазера.

Квантовое число характеризует собственный момент движения электрона, одно из состояний микрофизической системы (например, атома, молекулы и т. д.), возможных согласно квантовой теории. Обычно это целое или полуцелое число (n или n + 1/2).

Для четкого описания системы необходимо предоставить полный набор чисел (измеренных одновременно). Открытие трудно переоценить. Без него нельзя было бы построить квантовые вычислители, а многие свойства атомов и материалов так и остались бы загадкой.

Что такое суммарный спин

Спин (от англ. spin — вертеть[-ся], вращение) — собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы.

Спин измеряется в единицах ħ (приведённой постоянной Планка, или постоянной Дирака) и равен где J — характерное для каждого сорта частиц целое (в том числе нулевое) или полуцелое положительное число — так называемое спиновое квантовое число, которое обычно называют просто спином (одно из квантовых чисел).

В связи с этим говорят о целом или полуцелом спине частицы.

Существование спина в системе тождественных взаимодействующих частиц является причиной нового квантовомеханического явления, не имеющего аналогии в классической механике: обменного взаимодействия.

Содержание

Свойства спина

Любая частица может обладать двумя видами углового момента: орбитальным угловым моментом и спином.

В отличие от орбитального углового момента, который порождается движением частицы в пространстве, спин не связан с движением в пространстве. Спин — это внутренняя, исключительно квантовая характеристика, которую нельзя объяснить в рамках релятивистской механики. Если представлять частицу (например, электрон) как вращающийся шарик, а спин как момент, связанный с этим вращением, то оказывается, что поперечная скорость движения оболочки частицы должна быть выше скорости света, что недопустимо с позиции релятивизма.

Будучи одним из проявлений углового момента, спин в квантовой механике описывается векторным оператором спина >,» width=»» height=»» /> алгебра компонент которого полностью совпадает с алгеброй операторов орбитального углового момента >.» width=»» height=»» /> Однако, в отличие от орбитального углового момента, оператор спина не выражается через классические переменные, иными словами, это только квантовая величина. Следствием этого является тот факт, что спин (и его проекции на какую-либо ось) может принимать не только целые, но и полуцелые значения (в единицах постоянной Дирака ħ ).

Примеры

Ниже указаны спины некоторых микрочастиц.

спин	общее название частиц	примеры
0	скалярные частицы	π -мезоны, K-мезоны, хиггсовский бозон, атомы и ядра 4 He, чётно-чётные ядра, парапозитроний
1/2	спинорные частицы	электрон, кварки, мюон, тау-лептон, нейтрино, протон, нейтрон, атомы и ядра 3 He
1	векторные частицы	фотон, глюон, W- и Z-бозоны, векторные мезоны, ортопозитроний
3/2	спин-векторные частицы	Δ-изобары
2	тензорные частицы	гравитон, тензорные мезоны

На июль 2004 года, максимальным спином среди известных элементарных частиц обладает барионный резонанс Δ(2950) со спином 15/2. Спин ядер может превышать 20

История

В 1921 году опыт Штерна — Герлаха подтвердил наличие у атомов спина и факт пространственного квантования направления их магнитных моментов.

В 1924 году, ещё до точной формулировки квантовой механики, Вольфганг Паули вводит новую, двухкомпонентную внутреннюю степень свободы для описания валентного электрона в щелочных металлах. В 1927 году он же модифицирует недавно открытое уравнение Шрёдингера для учёта спиновой переменной. Модифицированное таким образом уравнение носит сейчас название уравнение Паули. При таком описании у электрона появляется новая спиновая часть волновой функции, которая описывается спинором — «вектором» в абстрактном (то есть не связанном прямо с обычным) двумерном спиновом пространстве.

В 1928 году Поль Дирак строит релятивистскую теорию спина и вводит уже четырёхкомпонентную величину — биспинор.

Математически теория спина оказалась очень прозрачной, и в дальнейшем по аналогии с ней была построена теория изоспина.

Спин и магнитный момент

Несмотря на то, что спин не связан с реальным вращением частицы, он тем не менее порождает определённый магнитный момент, а значит, приводит к дополнительному (по сравнению с классической электродинамикой) взаимодействию с магнитным полем. Отношение величины магнитного момента к величине спина называется гиромагнитным отношением, и, в отличие от орбитального углового момента, оно не равно магнетону ():

Что еще за спин?

Если вы думаете, что экспрессия была лишней, вы ошибаетесь. Спин — одна из тех странных вещей в квантовой механике, пытаясь понять которые, вы думаете, что интуиция и личный жизненный опыт вам помогут. Но это не так. Напротив, ваша интуиция более вероятно упадет на колени перед вами. Попробуйте не доверять ей.

Начнем с того, что у всех частиц есть фундаментальный спин. Спин — «ось» от английского spin. Так же, как электрический заряд или масса, спин помогает определить тип частицы.

Некоторые частицы, вроде электронов, позитронов и кварков (протоны и нейтроны состоят из кварков, также фундаментальных частиц Стандартной модели), обладают спином ½. Они известны как «фермионы». Другие, фотоны, глюоны, а также W- и Z-частицы, обладают спином 1. Они известны как «бозоны». Очевидно, фермионы и бозоны ведут себя по-разному.

Если все это время вы согласно кивали, тонкий голосок у вас в голове, наверное, говорил что-то типа «полспина чего?». Стоит отметить, к внутреннему голосу по-хорошему нужно прислушиваться, поэтому давайте поговорим о том, как работает спин электрона.

Это как маленький гироскоп, но не совсем.

Почему электроны? Потому что если вы поймете, что такое спин электрона, все остальное будет простым. Попробуйте представить, что электрон — это маленький гироскоп. Он вращается и вертится без остановки. Вне зависимости от того, что вы делаете с ним, вы не можете замедлить или ускорить вращение электрона; вы просто можете изменить его положение.

Что бы вы ни делали, у электрона всегда будет спин ½. Но ½ чего? Числа, известного как «приведенная постоянная Планка». Это очень маленькое число. Очень.

Вот вам первый странный факт. Обычно вы можете замедлить вращающееся тело. Супермен смог остановить вращение Земли, например.

С другой стороны, мы имеем дело с маленьким вращающимся гироскопом. Угловой момент — это одна из тех постоянных величин, которые сводят с ума физиков. При изменении направления спина электрона, угловой момент передается куда угодно — от орбиты до другого электрона.

Поскольку у электрона есть заряд, и поскольку он «вращается по оси», он создает небольшое магнитное поле. Так работает любой электромагнит. Мы можем обнаружить магнитное поле электрона или отклонить отдельные электроны, используя другие магниты, чтобы выяснить, в каком направлении вращается электрон. Но…

Магнитное поле работает совсем не так.

Возьмите маленький заряженный шарик и закрутите его вокруг оси. Вы создадите магнит. Вне зависимости от того, насколько велик или мал шар, оказывается, что магнитное поле будет точно предсказано кратным угловым моментом. Есть куча констант, связанных с зарядом и массой шарика, но не с размером.

Проблема в том, что если представить электрон таким же образом, описанная выше процедура не прокатит вообще. Магнитное поле будет в два раза больше. Точнее, в 2,0023193044 раза. Это число измерено с безумным уровнем точности и вычислено теоретически. В игру вступает эта чертова «квантовая теория поля», потому что мы можем сделать несколько точных предсказаний.

Странный факт номер два: вы не можете, не имеете права думать об электроне, как о маленькой микроскопической заряженной сфере. Просто получатся неправильные цифры.

Хотя у электронов есть фиксированный спин, вы можете предположить, что компоненты спина в определенном направлении могут принимать любое старое значение, которое нам нравится. Подумайте об этом в следующем примере. Допустим, у меня была метровая палка (длиной в 1 метр), одним концом воткнутая в землю под углом. Вы можете измерить высоту от верхнего конца до земли, и в зависимости от угла, получите значение между 0 и 1 метром.

Вы знаете, что Земля вращается, но если вы когда-нибудь видели глобус, вы в курсе, что он наклонен где-то под углом 23 с половиной градуса по отношению к плоскости орбиты. Другими словами, если вы измерите «ось» (или спин) Земли сверху донизу, вы получите меньше, чем полную длину оси. Ось представляется немного расшатанной из стороны в сторону.

С электронами такое не работает. Если вы создали небольшое магнитное поле, чтобы различить их, вы выясните, что отдельный электрон в 100 % случаев вертится вверх и в 100 % случаев вертится вниз, в зависимости от случая, и никогда — между. Что более странно, не имеет значения, как вы будете настраивать свою измерительную аппаратуру, вы всегда придете к одному и тому же начальному результату: либо одна сторона, либо другая, третьего не дано.

И здесь у нас рождается третий странный факт. Предположим, вы измеряете электрон и выясняете, что он обладает верхним спином. После вы пытаетесь измерить спин слева-направо. Здравый смысл подскажет вам, что число будет равно нулю, так как вы знаете, что электрон вертится снизу вверх, а не слева направо. Но как мы отмечали выше, здравый смысл вам не поможет. Выясняется, что: а) в половине случаев, когда вы измеряете электрон, он будет «слева», в половине — «справа», и б) право и лево определяется абсолютной случайностью. Правда. Ничто во вселенной не сможет сказать вам, какую сторону выберет электрон. Такого рода случайность сильно огорчала Эйнштейна (вспомните его высказывание о том, что Бог не играет в кости).

Вам нужно дважды повернуть электрон, чтобы он выглядел, «как прежде»

В прошлом мы часто говорили о волновой функции частиц. Квадрат волновой функции подскажет вам вероятность нахождения частицы в определенном месте в определенное время. Что примечательно в электроне (и во всех частицах со спином ½), так это то, что если вы повернете всю вселенную на 360 градусов, у волновой функции появится знак минуса в начале.

Это четвертый странный факт. Вам нужно дважды повернуть электрон вокруг оси, и он будет выглядеть так же, как и в начале.

Казалось бы, ничего странного. В конце концов, чего переживать о волновой функции, если знак минуса ничего не делает. -2 в квадрате = 2 в квадрате.

Тот же эффект возникнет, если вы представите, будто подменяете один электрон другим. Ничего не меняется, только появляется знак минус перед всей волновой функцией. Кажется незначительным, пока вы не поймете, что…

Знак минус — это то, что делает вас возможным.

Представьте два электрона со спинами в одном направлении, один и другой — наверх (эксперты также должны понять, что у двух электронов один и тот же импульс). Теперь поменяем их местами. Для нас ничего не изменилось, но в квантовой механике вся вселенная погрузилась в хаос. Волновая функция вроде бы не изменилась, поскольку никаких существенных отличий одного электрона от другого нет, но так или иначе, мы ставим знак минус в начале.

Еще раз: ничего не меняется, но умножается на -1. Единственное число, с которым это работает, это 0. Другими словами, нулевая волновая функция равна нулевой вероятности, или отсутствию шансов вообще.

Другой способ сказать это: электроны (и все фермионы: кварки, позитроны, нейтрино и т.д.) не могут находиться в одном и том же месте с одним и тем же спином. Это знаменитый «запрет Паули». Он предсказывает, что электроны в атомах не могут быть в одном и том же состоянии, но вместе этого занимают разные орбитали. Если бы все было не так, электроны занимали бы самые низкие уровни, и элементы вели бы себя скучновато, как водород. Скучно и не способствует зарождению жизни.

Бозоны, другой тип частиц, не работают по этому принципу. Поменяйте местами два бозона, и ничего не изменится. Поверните бозон единожды, и все вернется в нормальное русло. У них спин равен одному, что означает только то, что они ведут себя точно так, как вы ожидаете. Но таковы лишь бозоны, обнаруженные на сегодняшний день. У бозона Хиггса (если он существует) спин 0, у гравитона (если он существует) спин 2, но мы пока можем о них не говорить. Бозоны могут находиться в одном месте и обладать одним и тем же спином. Вот почему мы можем получить конденсат Бозе-Эйнштейна, который представляет собой кучу бозонов в одном состоянии.

«Фишка» не в том, что спин — странная штука, хотя с этим никто не спорит. «Фишка» в том, что спин лежит в центре куда более серьезных и фундаментальных вещей, в основе их работы, чем вы можете подозревать.

Научная электронная библиотека

,

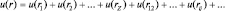
где rij – расстояние между электронами в атоме. Если взаимодействие между электронами было бы сильнее, чем у электронов с ядром, то атомная система не смогла бы существовать из-за отталкивания электронов.

Поэтому, пренебрегая величинами u(rij), можно ввести задачу к анализу движения электрона в эффективном поле ядра (заряд которого уменьшен на величину заряда электронов, не включая исходного, как правило, внешнего, наиболее удаленного от ядра).

В этом случае удается решить уравнение Шредингера и получить приближенный ответ, аналогичный решению для одного электрона в водородоподобном атоме (ионе). Зная характер движения электрона в различных состояниях, можно рассчитать и то воздействие, которое окажет электрон на атомный «остов», т.е. узнать, как этот «остов» деформируется.

Повторяя решение многократно, в принципе, возможно проанализировать поведение электрона все с большей и большей точностью. Однако, начиная с какого-то момента эти поправки к энергии электрона станут соизмеримыми с энергией взаимодействия отдельных электронов и дальнейшая процедура расчета значительно усложняется, более сложными будут задачи о состоянии электронов в молекулах – многоядерных системах. Здесь мало помогает даже такое «одноэлектронное» приближение. Тем не менее, для качественного анализа можно считать электроны независимыми и сверять расчеты с экспериментальными исследованиями, открывая новые свойства атомов эмпирически.

Одной из важнейших проблем, не разрешенных классической физикой, оставалось объяснение магнитных свойств вещества, поэтому обсуждение поведения атомов в магнитном поле с соответствующей экспериментальной проверкой оказалось актуальным, полезным для различных технологий. Считая, что в некоторых состояниях электронная плотность атома имеет в среднем вид «кольца», можно анализировать взаимодействие атома c внешним полем, как взаимодействие кругового тока (где Т – период «обращения» электрона) с магнитным полем, характеризующимся вектором магнитной индукции (рис. 16).

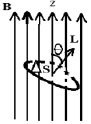
Рис. 16. Атом в магнитном поле

Из электродинамики известна величина энергии взаимодействия кругового тока с внешним магнитным полем, поток вектора которого через площадку ΔS равен ΔΦ: , но IΔS есть величина магнитного момента кругового тока, а поэтому . Гиромагнитное отношение для кругового тока нам известно:

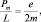
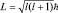
а .

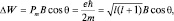
но поэтому , или, обозначая (магнетон Бора), имеем: .

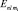
Так как, например, при l = 1, ml = –1, 0, +1, к энергетическому уровню добавляется (или вычитается) энергия ΔW и он «расщепится» на три подуровня (рис. 17). В соответствующем спектре атома, помещенного в магнитное поле, должны появиться дополнительные «спектральные» линии. Этот эффект впервые наблюдал Зееман и поэтому носит название «нормального эффекта Зеемана». Кстати, становится ясным наименование квантового числа ml, названного магнитным орбитальным квантовым числом, так как именно оно характеризует энергию взаимодействия «орбитального» движения электрона в атоме с внешним магнитным полем. Без внешнего поля этот уровень трижды «вырожден», так как ΔW = 0. Но в сложных атомах вырождение снимается и без внешнего поля, о причине которого легко догадаться, так как всегда имеются поля, создаваемы другими электронами.

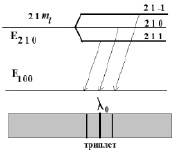
Рис. 17. «Расщепление» спектральных линий (эффект Зеемана)

Из факта взаимодействия атома с магнитным полем следует сразу несколько выводов. Если наблюдается взаимодействие электрона с внешними по отношению к нему полями, то энергетические уровни смещаются. Это приводит к тому, что в спектре сложного атома длины волн при переходах с уровней En10 и En00 оказываются различными. Дополнительное воздействие внутри атома на внешний (как правило) электрон оказывают остальные электроны. Справедливо и обратное утверждение: если в спектре наблюдается эффект «расщепления» линий («тонкая структура» спектральных линий»), то это означает, что у электрона появилось какое-то дополнительное взаимодействие с внешними полями и дополнительно «движение», кроме орбитального.

По своему строению ближе всего к водородоподобным атомам относятся щелочные металлы, у которых внешний электрон «легко» отщепляется с образованием иона. Это означает, что один электрон у металла находится далеко от ядра, а поэтому весь атом можно представить как электрон плюс положительный остаток – «остов», имеющий заряд q = e+. Этот внешний электрон занимает в атоме «энергетические ступеньки», расположенные аналогично уровням в водородоподобном атоме. При «переходах» между уровнями атомы излучают в видимом (оптическом) диапазоне длин волн» а поэтому такой внешний электрон часто называют «оптическим». Уравнение Шредингера в этом случае по форме не отличается от его записи для водородоподобных атомов, однако потенциальная энергия взаимодействия валентного оптического электрона с остовом атома щелочного металла должна быть представлена в виде разложения на составляющие его взаимодействия с точечным зарядом, диполем, квадруполем и т.д., как это делается в электродинамике при расчетах полей сложно распределенных зарядов. Математически такой подход соответствует разложению функции u(r) в ряд (1.9.1):

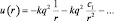
(1.9.1)

На больших расстояниях взаимодействие ослабевает, поэтому можно ограничиться двумя первыми слагаемыми в (1.9.1). Тогда:

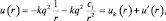
где величина uk(r) – аналогична записи потенциальной энергии взаимодействия, в атоме водорода, а U′(r) характеризует дополнительное взаимодействие электрона с атомным остовом щелочного металла.

При решении уравнения Шредингера методом Фурье изменится лишь запись «радиального» уравнения в системе (8.3), которое примет вид (1.9.2):

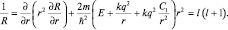
(1.9.2)

Преобразуем это уравнение следующим образом:

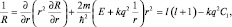
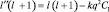
которое формально аналогично основному уравнению, если ввести обозначение . Считая величину, l′ как и l положительной и решая квадратное уравнение относительно, l′ имеем:

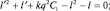
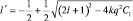
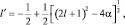
Из разложения (a + b)n в биномиальный ряд, полагая a = (2l + 1)2 и b = –4α, а также ограничиваясь первыми членами ряда, получим:

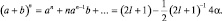
Тогда . Энергия n-го состояния электрона щелочного металла запишется как , где n′ = nr + l′ + 1. Тогда

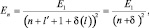
(1.9.3)

если иметь в виду, что n = nr + l + 1.

Поправка δ объясняет смещение спектральных линий соответствующих уровней щелочного металла по сравнению с атомом водорода.

При помещении атома щелочного металла во внешнее магнитное поле каждый подуровень расщепляется на мультиплеты в соответствии с эффектом Зеемана. Но кроме этого, в спектре щелочных металлов было замечено такое двойное («дублетное») расщепление линий, которое не могло быть описано с помощью магнитного орбитального квантового числа, так как, во-первых, величина расщепления, т.е. расходимость линий в спектре была меньше, чем у триплетов и мультиплетов, а во-вторых, средней линии при этом не наблюдалось. Эти отличия позволяли предположить, что причина не кроется в «орбитальном» движении электрона, а может быть связана с дополнительным «собственным» движением, аналогичным (в планетарной модели) вращению планет вокруг собственной оси. Именно такую мысль впервые высказали Уленбек и Гаудсмит, назвав величину механического момента собственного движения спином («спин» – веретено»). Также как все характеристики движения в атоме кантованы, эта величина должна быть квантована и, чтобы достичь согласия с экспериментом, добавочная энергия взаимодействия с магнитным полем должна всегда принимать всего два значения. Соответствующее квантовое число также принимает два значения в отличие от ml, количество значений которых может быть только нечетным.

Сравним энергии: ΔW = μБBml и ΔWсоб = μБBms, где величина ms, принимающая эти 2 возможных значения по аналогии с ml, была названа магнитным спиновым квантовым числом. Вдвое меньшая расходимость линий в спектре «подсказывает», что . Если обозначить собственный механический момент электрона , а его проекцию на ось Oz как Sz, то по аналогии с орбитальным моментом , следует записать: если Lz = mlħ, то

если , то , где есть спиновое квантовое число.

Таким образом, электрон обладает не только массой и зарядом, но и собственным механическим моментом. Законы электродинамики и механики требуют, чтобы у заряженной частицы, обладающей механическим моментом, был магнитный момент. Для «орбитального» движения гиромагнитное отношение позволяет записать что , а в случае «собственного» движения , так как существует эксперименты (опыты Эйнштейна – де Гааэа и Барнета) с магнитными материалами, приводящие именно к данному результату. Тогда или .

Проекция магнитного момента , а и тогда . Аналогично рассуждая, имеем:

; .

.

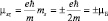
Если у свободного электрона ось совместить со спином, то его магнитной характеристикой явится величина магнетона Бора, которая равна:

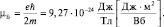
Эта величина, конечно, мала, но учитывая количество электронов в веществе и ограниченные возможности в ориентации («по полю или против поля») следует признать, что магнитные свойства многих веществ могут определяться в основном собственными магнитными моментами электронов.

Возникает необходимость прямой проверки наличия у электрона собственного магнитного и механического моментов. На том пути у экспериментатора возникает ряд трудностей. Первая трудность: как «приготовить» электроны; вторая – каким должно бить магнитное поле?; третья – как «отделить электроны с от электронов , т.е. ориентированных по «полю» или «против поля»?

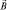
Допустим, что мы приготовили пучок электронов в электроннолучевой трубке и поместили этот пучок во внешнее магнитное поле. Тогда модельно, можно предсказать результат взаимодействия» рассматривая пучок электронов как направленно движущиеся «магнитные стрелки» (механическая аналогия). В поле с индукцией эти стрелки ориентируются по двум направлениям.

Если поле однородно, то силы и , действующие на электроны, одинаковы по величине и направлены в различные стороны, компенсируя друг друга. На экране все электроны попадут в одну и ту же точку, т.е. разделения пучка не произойдет. Если же сделать поле неоднородным, то и станут различными и эта разница будет тем более значительной, чем крупнее размер «магнитной стрелки». Другими словами, размеры объекта должны быть соизмеримы с неоднородностям магнитного поля. Размеры электрона настолько малы, что практически не удается провести задуманный эксперимент и необходимо в качестве «магнитной стрелки» избрать более крупную систему – атом. При этом состояние атома должно быть таким, чтобы его магнитные свойства определялись магнитным моментом только одного электрона. Может ли это быть достигнуто в многоэлектрон- ной системе?

Чтобы ответить на этот вопрос, рассмотрим атомы с точки зрения совокупности векторов-моментов как орбитальных, так и собственных. Рассмотрим понятие о «векторной модели» атома.

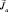
Уже в механике системы точек формулировалась теорема о том, что момент импульса системы равен сумме моментов импульса составляющих его частей (точек) Обозначая полный механический момент атома , мы должны, следовательно, записать:

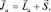
(1.9.5)

где , , а – суммарный механический момент орбитального движения электронов (Z – порядковый номер элемента); а – суммарный механический момент собственного движения тех же электронов. Отличие от механической системы заключится в том, что теперь каждая из стих величин квантована:

(1.9.6)

где индекс «a» говорит о том, что мы имеем дело с атомом. Можно ввести и величину полного момента импульса по отношению к отдельному электрону. Тогда

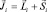
где ; ; (1.9.7)

где j – квантовое число полного момента электрона. В конечном счете, результат сложения зависит от положения всех и в пространстве, что определяется квантованием проекций или квантовыми числами ml и ms. Понятно, что вектор имеет смысл ориентировать относительно поля , но как быть с остальными векторами? И здесь важным оказывается факт взаимодействия. Действительно, почему вектор момента ориентируется во внешнем поле? По-видимому, потому, что с ним связан магнитный момент , и это приводит к ориентации и механического момента вместе с магнитным, т.е. атом также следует изобразить в виде «магнитной стрелки», только более крупной, чем электрон. А вот спиновый момент может ориентироваться и относительно и относительно и в зависимости от того, какое поле сильнее. В этом случае можно говорить, например, «спин – орбитальном взаимодействии». В эту схему начинают «включаться» электростатические взаимодействия.

Для атомов легких элементов наибольшее взаимодействие – это спин – орбитальное, а для тяжелых – существенно взаимодействие спинового и орбитального с полным моментом атома. Таким образом «формируется» состояние атома. Так, например, если символ состояния обозначается , то это означает, что La = 1, (число 2 = Sa + 1 именуют кратностью состояния), , так как Ja = La + Sa. Исторически эти обозначения называют символами термов. Буквами S, P, D, F и т.д. обозначают состояния соответственно для 0, 1, 2, 3 и т.д. Такие же буквы характеризуют и отдельный электрон. Если орбитальное квантовое число l = 1, 2, 3, . то соответствующие буквы s, p, d, f обозначают эти состояния. Для электронов в состоянии с главным квантовым числом n = 1, 2, 3, 4, . приняты обозначения латинскими заглавными буквами К, L, М, N, O, . В этом случае говорят, что электроны находятся на К-слое, L-слое, М-слое и т.д., а затем на 1s-оболочке, 2р-оболочке и т.п.

Рассмотрим поведение веществ во внешнем магнитном поле и магнитные свойства вещества.

1. Если , магнитный момент , то вещество, состоящее из таких атомов «равнодушно» ко внешнему полю, т.е. оно является диамагнетиком. Правда, внешнее поле «деформируем» орбитальное движение электронов и «наводит», индуцирует в атоме дополнительные движения, на которые расходуется энергия внешнего поля. Поэтому диамагнитный эффект ослабления магнитного поля наблюдается для всех веществ. Если внешнее поле переменное во времени , то диамагнетизм можно описать качественно в рамках явлений электромагнитной индукции классической электродинамики. Возникают эффекты «выталкивания» диамагнетика из поля в моменты «включения» поля и «втягивании» в момент «выключения».

2. Если , то во внешнем поле происходит ориентация , и поля атомов складываются с внешнем полем, усиливая его. Тепловое движение «мешает» такой ориентации, поэтому, во-первых, результирующее поле пропорционально внешнему полю, а во-вторых, при отключении внешнего поля вещество «само размагничивается».

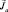
3. Наконец, для понимания «магнетизма» необходимо упомянуть о «спиновом» магнетизме или, точнее, о ферромагнетизме. Для ферромагнетиков , в основном обеспечивается спиновыми составляющими, которые в монокристаллических блоках («доменах») ориентированы параллельно. Вещество («магнитная руда»), составленное из доменов, может быть модельно представлено (рис. 18). На рис. 18а домены не ориентированы, а на рис. 18б – ориентированы по внешнему полю.

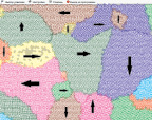
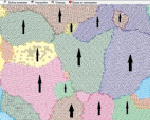
Рис. 18. Доменная структура ферромагнетиков

В отсутствии внешнего поля отдельные домены могут иметь различные направления суммарного магнитного момента, входящих в него атомов. При наличии внешнего поля происходит резкий поворот магнитных моментов «по полю В0» («скачки Баркгаузена»), что приводит к значительному усилению поля за счет магнитного поля доменов. Трение между доменами мешает их разориентации (при выключении поля) тепловым движением, поэтому для ферромагнетиков наблюдается явление остаточного магнетизма, что может быть использовано для практически; (радиотехника, электротехника, приборостроение, автоматика и т.п.).

Доказательством существования спина явились опыты Штерна и Герлаха. Для выявления существования спинового момента атомы могут быть представлены магнитными стрелками. Расчет, проведенный для атомов серебра, показал, что суммарный момент при учете всех электронов равен нулю, кроме внешнего электрона, у которого спин не равен нулю (не скомпенсирован). Поэтому магнитные свойства атомов серебра полностью определяются только спином, (а значит собственным магнитным моментом внешнего электрона), если таковой действительно существует. При наличии спинового момента его вектор ориентирован либо по полю, либо против поля. Создав неоднородное магнитное поле, Штерн и Герлах обнаружили на экране две полоски осажденных атомов серебра, пропущенных через внешнее магнитное поле, доказав тем самым не только существование магнитного момента у электронов, но и его квантованность с квантовым числом, принимающим два и только два возможных значения. Попытка трактовать образование спина как результат собственного механического вращения электрона тем не менее окончилась неудачей: чтобы магнитный момент электрона был равен магнетону Бора необходимо, чтобы скорость движения отдельных частей самого электрона была больше с – скорости света в вакууме.