Прямая и обратная пропорциональные зависимости
план-конспект урока по алгебре (6 класс) по теме
Тема: Прямая и обратная пропорциональные зависимости.
Тип урока: изучение нового материала с применением информационных технологий
- закрепить основные понятия: пропорция, основное свойство пропорции;
- сформировать умение решать задачи с помощью пропорции, логически мыслить при определении зависимости в соответствии с условием задачи;
- развивать грамотную математическую речь; память, внимание, делать выводы, основанные на рассуждениях;
- прививать интерес к математике; воспитывать любовь к природе.
Методы обучения: коммуникативный, дифференцированный, исследовательско-поисковый.
Формы организации урока: фронтальный опрос, индивидуальная работа, самопроверка.
Оборудование: м/м проектор, экран, компьютер, монитор, презентация.
Все слайды меняются по клику мышки
Вспомнить основные понятия: пропорция, основное свойство пропорции (фронтальный опрос)
Устное обсуждение способов решения задач нового вида (поиск решения)
В ходе устного осуждения определить, как изменяются зависимые между собой величины.
Проверь себя – тестовая работа
Теоретический тест позволяет скорректировать дальнейшую подачу материала
Взаимопроверка с использованием м/м проектора
Работа в парах сменного состава
Решение задач по теме урока (исследование решения задач нового вида на пропорциональную зависимость)
Работа с учебником, индивидуальная работа – дифференцированный подход
Прямая пропорциональная зависимость
Обратная пропорциональная зависимость
Обратная пропорциональная зависимость
п.22, № 805; 811; 812
Релаксация, подведение итогов
Урок математики в 6 классе.
Тема: Прямая и обратная пропорциональные зависимости.
Цели: сформировать у учащихся понятия прямой и обратной пропорциональной зависимости.
- закрепить основные понятия: пропорция, основное свойство пропорции;
- сформировать у учащихся понятия прямой и обратной пропорциональной зависимости;
- сформировать умение решать задачи с помощью пропорции;
- логически мыслить при определении зависимости в соответствии с условием задачи;
- развивать грамотную математическую речь; память, внимание, делать выводы, основанные на рассуждениях;
- содействовать развитию познавательного интереса, творческих способностей, умению сравнивать, анализировать;
- прививать интерес к математике;
- развивать навыки устойчивого внимания.
Оборудование: компьютер, мультимедийный проектор.
Тип урока: « Изучение и первичное закрепление новых знаний»
Структура и ход урока.
- Организационный этап.
- приветствие;
- готовность учащихся к уроку.
Сегодня мы с вами познакомимся с новыми понятиями: прямая и обратная пропорциональные зависимости, и будем учиться решать задачи, опираясь на новые знания.
- Актуализация опорных знаний и умений учащихся.
- Что такое пропорция?
- Сформулируйте основное свойство пропорции.
- Какие перестановки членов пропорции снова приводят к верным пропорциям?
- Составьте три новые верные пропорции из пропорции: 5_15=4:12
- Какие перестановки членов пропорции снова приводят к верным пропорциям?
- Составьте три новые верные пропорции из пропорции:
а) 135 : __ = 90 : 2
б) 18 : 3 = __ : __
Постановка перед учащимися учебной проблемы
А помогут ли нам полученные знания в решении практических задач?
- Формирование новых знаний.
Устное обсуждение (поиск решения) (слайд 4)
- За 2 кг овощей заплатили 10 рублей. Сколько стоят 8 кг овощей?
- Во сколько раз купили больше овощей?
- Если больше купили, то меньше или больше должны заплатить?
Вывод: если количество товара увеличивается в несколько раз, то и увеличивается стоимость покупки во столько же раз.
В ходе устного осуждения учащиеся определяют, как изменяются зависимые между собой величины в данной задаче.
Определение: две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
- Два трактора вспахали поле за 6 дней. За сколько дней вспашут это поле 4 трактора, если будут работать с той же производительностью?
- Если количество тракторов будет больше, то чтобы вспахать то же самое поле потребуется больше или меньше дней?
- Во сколько раз увеличилось количество тракторов? Во сколько раз меньше дней потребуется, чтобы выполнить ту же работу?
В ходе устного осуждения учащиеся определяют, как в этой задаче изменяются зависимые между собой величины.
Определение: две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз
Тестовая работа — проверь себя .
Теоретический тест позволяет скорректировать дальнейшую подачу материала.
«Да» и «нет» не говорите, знаком их изобразите:
- Зависимость между количеством товара и стоимостью покупки является прямой пропорциональностью.
- Рост ребенка и его возраст прямо пропорциональны.
- При постоянной ширине прямоугольника его длина и площадь прямо пропорциональны.
- Скорость автомобиля и время его движения обратно пропорциональны.
- Скорость автомобиля и его пройденный путь обратно пропорциональны.
- Две величины называются обратно пропорциональными, если при увеличении одной из них в два раза другая в два раза уменьшается.
- Грузоподъемность машин и их количество прямо пропорциональны.
- Периметр квадрата и длина его стороны прямо пропорциональны.
Проверим ответы: взаимопроверка с использованием м/м проектора (слайд 9)
Поставь себе оценку: (слайд 10)
8 правильных ответов – «5»
7-6 правильных ответов – «4»
5-4 правильных ответов – «3»
5. Формирование умений и навыков.
Решение задач уровня обязательной подготовки: (слайд 11; 12)
6. Этап первичной проверки.
Учащиеся выполняют самостоятельную работу по вариантам с взаимопроверкой в парах.
1 вариант — № 785;
2 вариант — № 836;
Проверяем решение: 1 вариант – слайд 14; 2 вариант – слайд 17)
7. Постановка домашнего задания:
- изучить п.22, № 805; 811; 812
- составить текст двух задач на прямую и обратную пропорциональные зависимости (решение на следующем уроке выполнит сосед по парте)
8. Подведение итогов урока. Рефлексия.
- Какие величины называются прямо пропорциональными? Приведите примеры прямо пропорциональных величин.
- Какие величины называют обратно пропорциональными? Приведите примеры обратно пропорциональных величин.
- Приведите примеры величин, у которых зависимость не является ни прямо, ни обратно пропорциональной.
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Прямая и обратная пропорциональные зависимости Кириллина Г.А. МАОУ ДСОШ №4 с УИОП г.Домодедово
Актуализация знаний Что такое пропорция? Сформулируйте основное свойство пропорции. Какие перестановки членов пропорции снова приводят к верным пропорциям? Составьте три новые верные пропорции из пропорции: 5 : 15 = 4 : 12
Найдите пропущенные числа Какое из этих заданий имеет единственное решение, а какое – много решений? Почему? а) 1 3 5 : __ = 9 0 : 2 б) 1 8 : 3 = __ : __
Устное обсуждение (поиск решения) 1 . За 2 кг овощей заплатили 10 рублей. Сколько стоят 8 кг овощей? 2 . Два трактора вспахали поле за 6 дней. За сколько дней вспашут это поле 4 трактора, если будут работать с той же производительностью?
«Да» и «нет» не говорите, знаком их изобразите. « да » знаком « + », « нет » знаком « — ».
1.Зависимость между количеством товара и стоимостью покупки является прямой пропорциональностью. 2. Рост ребенка и его возраст прямо пропорциональны. 3.При постоянной ширине прямоугольника его длина и площадь прямо пропорциональны.
4. Скорость автомобиля и время его движения обратно пропорциональны. 5. Скорость автомобиля и его пройденный путь обратно пропорциональны. 6. Две величины называются обратно пропорциональными, если при увеличении одной из них в два раза другая в два раза уменьшается.
7. Грузоподъемность машин и их количество прямо пропорциональны. 8. Периметр квадрата и длина его стороны прямо пропорциональны. ?
Поставь себе оценку: 8 правильных ответов – « 5 » 7-6 правильных ответов – « 4 » 5-4 правильных ответов – « 3 »
№ 784 Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?
Решение. Масса семени (кг) Масса масла (кг) 21 5,1 7 х Определим зависимость и составим пропорцию: 21_7=5,1:х х=7*5,1:21 х=1,7 Ответ: 1,7кг масла
№ 785 Для строительства стадиона 5 бульдозеров расчистили площадку за 210 минут. За какое время 7 бульдозеров расчистили бы эту площадку?
Решение. К-во бульдозеров Время.(мин) 5 210 7 х Определим зависимость и составим пропорцию: 7_5=210:х х=210*5:7 х= 150( мин). Ответ: 150 мин.
№ 836 Некоторое расстояние ласточка пролетела за 0,5ч со скоростью 50 км/ч. За сколько минут пролетит то же расстояние стриж, если будет лететь со скоростью 100 км/ч?
Решение. Скорость (км/час) Время (час) ласточка 50 0,5 стриж 100 х Определим зависимость и составим пропорцию: 100_50=0,5:х х=50*0,5:100 х=0,25 Ответ: 0,25 час.=15 минут
? Проверь себя: Какие величины называются прямо пропорциональными? Приведите примеры прямо пропорциональных величин. Какие величины называют обратно пропорциональными? Приведите примеры обратно пропорциональных величин. Приведите примеры величин, у которых зависимость не является ни прямо, ни обратно пропорциональной.
Домашнее задание. п. 22 № 805; 811; 812. Составить текст двух задач на прямую и обратную пропорциональные зависимости (решение на следующем уроке выполнит сосед по парте)
По теме: методические разработки, презентации и конспекты
Прямая и обратная пропорциональные зависимости.
Цель урока: — познакомить с прямой и обратной пропорциональными .

Урок математики в 6-м классе по теме «Прямая и обратная пропорциональные зависимости» ( конспект+увлекательная презентация).
Урок +презентация. Физкультминутка.
Конспект урока по теме «Прямая и обратная пропорциональная зависимости»
Урок обобщения и закрепления материала по теме «Прямая и обратная пропорциональная зависимости». На уроке показана практическая значимость пропорций в жизни человека. В конспекте используются ЭОР.

Прямая и обратная пропорциональные зависимости. Решение задач
Прямая и обратная пропорциональные зависимости. Решение задач. Слайдовая презентация.

Прямая и обратная пропорциональные зависимости
Урок обобщения материала, можно использовать для подготовки к контрольной работе.

«Прямая и обратная пропорциональные зависимости» 6 класс
Прямая и обратная пропорциональные зависимости.

Урок математики в 6 классе по теме: «Прямая и обратная пропорциональные зависимости»
Тема урока: Прямая и обратная пропорциональные зависимости.Тип урока: Урок объяснение новой темы.Цель урока: ввести новые понятия по теме «Прямая и обратная пропорциональные зависимос.
Прямая и обратная пропорциональные зависимости

В этом уроке мы закрепим представления о пропорциях. Введем понятия прямо пропорциональных и обратно пропорциональных величин. Научимся составлять пропорции при решении задач на прямую и обратную пропорциональные зависимости.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока «Прямая и обратная пропорциональные зависимости»
Сегодня на уроке мы продолжим работать с пропорциями, а точнее познакомимся с прямой и обратной пропорциональными зависимостями.
Задача
Сколько нужно сахара, чтобы сварить варенье из 5 кг черешни, если по рецепту на 2 кг ягод нужно 3 кг сахара?

Из решения видно, что во сколько раз больше имеется черешни, во столько раз больше понадобится сахара.
Эту же задачу можно решить и при помощи пропорции. Запишем кратко условие задачи в виде таблицы, обозначив за неизвестную нам массу сахара буквой х. Смотрите, у нас есть столбик, где мы будем записывать массу ягод, и столбик, где мы укажем соответствующую массу сахара на массу ягод. Итак, по условию задачи известно, что по рецепту на 2 кг ягод нужно 3 кг сахара. Нам нужно узнать, сколько кг сахара потребуется на 5 кг ягод.

Такая зависимость между массой ягод и массой сахара условно обозначается в таблице одинаково направленными стрелками. Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то и вторая тоже возрастает (стрелка тоже вверх).

Задача
Велосипедист, двигаясь с постоянной скоростью, проехал 10 км за 20 минут. Какой путь проедет велосипедист за 50 минут?
Решение: для наглядности запишем кратко условие задачи в виде таблицы.

Понятно, что путь увеличится во столько раз, во сколько раз увеличится время. Ставим стрелки в одном направлении.

Такие величины, как масса ягод для варенья и масса сахара, время и пройденный за это время при постоянной скорости путь, и т.д. называют прямо пропорциональными величинами.
Определение
Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Задача
Автомобиль ехал 3 часа со скоростью 60 км/ч. За какое время он продет это же расстояние, если будет ехать со скоростью 90 км/ч?

Из решения видно, что во сколько раз скорость автомобиля больше, во столько раз меньше времени тратится на этот же путь.
Эту же задачу решим при помощи пропорции. Запишем в таблицу кратко условие задачи. За х обозначим неизвестное нам время.

Понятно, что чем больше скорость автомобиля, тем меньше времени ему понадобится на преодоление этого же пути. Такая зависимость между скоростью и временем, затраченным на пройденный путь, условно обозначается в таблице противоположно направленными стрелками. Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то вторая убывает (стрелка вниз). Составим пропорцию. Т.к. стрелки направлены в разные стороны, то второе отношение перевернём.

Задача
5 рабочих выполнили заказ за 132 часа. За какое время этот же заказ смогут выполнить 12 рабочих?

Понятно, что чем больше будет задействовано рабочих, тем быстрее выполнится заказ. Значит, ставим стрелки в противоположном направлении. Составим пропорцию:

Такие величины, как скорость автомобиля и время, за которое он проедет определённый путь, число работников и время, за которое они выполняют заказ, и т.д. называют обратно пропорциональными величинами.
Определение
Две величины называются обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
Не всякие две величины являются прямо пропорциональными или обратно пропорциональными.
Например, возраст человека и размер его обуви не связаны пропорциональной зависимостью. Зависимость между величинами есть. Размер обуви с возрастом увеличивается, но не во столько же раз.

Возраст дерева и его высота не связаны пропорциональной зависимостью. В этом случае зависимость между величинами есть. Действительно, высота дерева с возрастом увеличивается, но не во столько же раз.
Прямая и обратная пропорциональность
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.
Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.
Прямая пропорциональность
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.
Изобразим на рисунке расстояние, пройденное автомобилем за 1 час
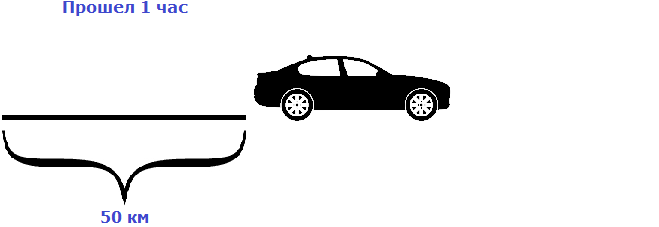
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км
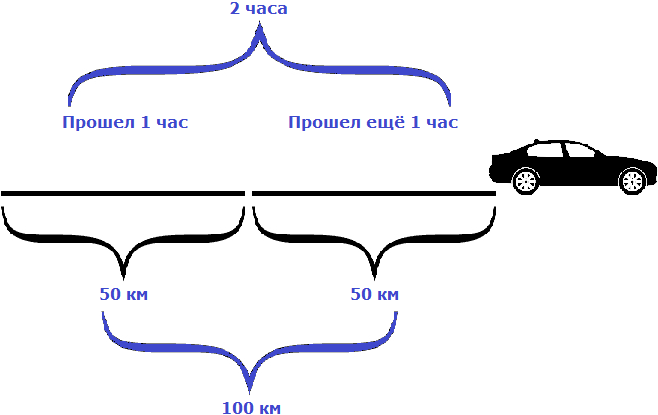
Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.
Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.
Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.
Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.
Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.
В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.
Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50
Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.
Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения и составляют пропорцию:
Это отношение можно прочитать следующим образом:
Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.
Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.
Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.
Запишем чему равно отношение тридцати рублей к одному килограмму
Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:
Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.
Обратная пропорциональность
Рассмотрим следующий пример. Расстояние между двумя городами 80 км. Мотоциклист выехал из первого города, и со скоростью 20 км/ч доехал до второго города за 4 часа.
Если скорость мотоциклиста составила 20 км/ч это значит, что каждый час он проезжал расстояние равное двадцати километрам. Изобразим на рисунке расстояние, пройденное мотоциклистом, и время его движения:
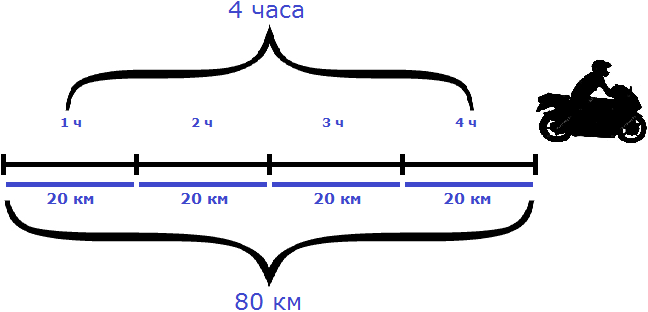
На обратном пути скорость мотоциклиста была 40 км/ч, и на тот же путь он затратил 2 часа.
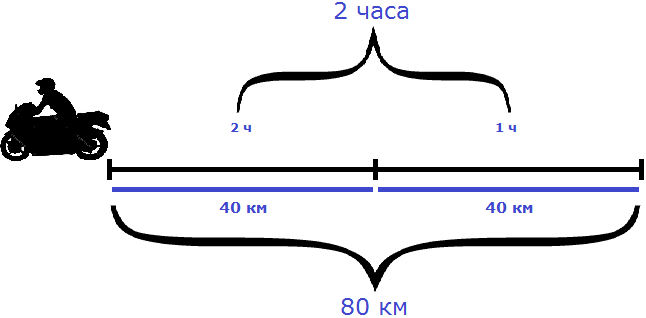
Легко заметить, что при изменении скорости, время движения изменилось во столько же раз. Причем изменилось в обратную сторону — то есть скорость увеличилась, а время наоборот уменьшилось.
Такие величины, как скорость и время называют обратно пропорциональными. А взаимосвязь между такими величинами называют обратной пропорциональностью.
Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая увеличивается во столько же раз.
К примеру, если на обратном пути скорость мотоциклиста составила бы 10 км/ч, то те же 80 км он преодолел бы за 8 часов:
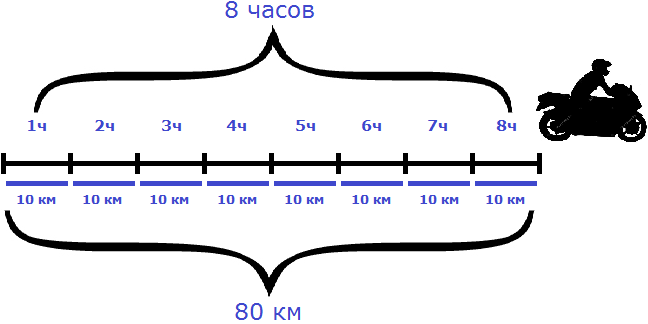
Как видно из примера, уменьшение скорости привело к увеличению времени движения во столько же раз.
Особенность обратно пропорциональных величин заключается в том, что их произведение всегда постоянно. То есть при изменении значений обратно пропорциональных величин, их произведение остается неизменным.
В рассмотренном примере расстояние между городами было равно 80 км. При изменении скорости и времени движения мотоциклиста, это расстояние всегда оставалось неизменным
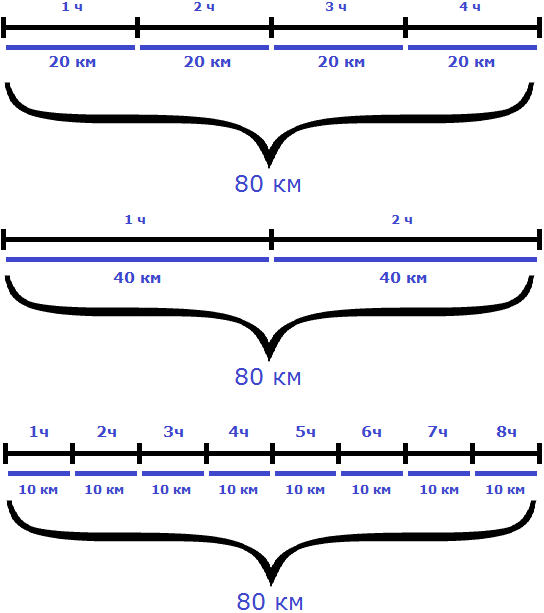
Мотоциклист мог проехать это расстояние со скоростью 20 км/ч за 4 часа, и со скоростью 40 км/ч за 2 часа, и со скоростью 10 км/ч за 8 часов. Во всех случаях произведение скорости и времени было равно 80 км
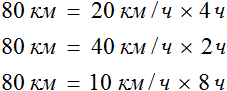
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Прямая и обратная пропорциональные зависимости
1) — периметр квадрата, — его сторона.
= 4.
Если = 1 см, то = 41 = 4 (см).
Если = 2 см, то = 42 = 8 (см).
Если = 4 см, то = 44 = 16 (см).
Получаем, что каждый раз, увеличивая сторону квадрата в 2 раза, его периметр также будет увеличиваться в 2 раза. Аналогично, если сторону квадрата будем уменьшать в какое-то число раз, то и периметр квадрата будет уменьшаться в это же число раз. Следовательно, величины и прямо пропорциональны. Можно сказать еще и так: «величина прямо пропорциональна величине » или «зависимость между величинами и является прямой пропорциональностью«.
2) При движении с постоянной скоростью, пройденный путь и время движения прямо пропорциональны, т.к. пройденный путь равен произведению скорости и времени движения.
Пусть скорость движения пешехода 8 км/ч.
Если = 1 ч, то = 81 = 8 (км).
Если = 3 ч, то = 83 = 24 (км).
Если = 9 ч, то = 89 = 72 (км).
Получаем, что каждый раз, увеличивая время в пути в 3 раза, путь также будет увеличиваться в 3 раза, а это и говорит о том, что зависимость между величинами и является прямой пропорциональностью, при условии движения с постоянной скоростью.
Свойство прямо пропорциональных величин:
| Если две величины прямо пропорциональны, то отношение соответствующих значений этих величин равно одному и тому же, постоянному для данных величин, числу. |
В рассмотренных выше примерах для величин и это число равно 4, т.к. : = 4 : 1 = 8 : 2 = 16 : 4 = 4, а для величин и это число равно 8, т.к. : = 8 : 1 = 24 : 3 = 72 : 9 = 8.
Обратная пропорциональная зависимость
| Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз. |
Примеры:
1) Если расстояние является постоянной величиной, то скорость и время движения обратно пропорциональны, т.к. время движения равно частному от деления расстояния на скорость движения.
Пусть расстояние равно 80 км.
Если = 10 км/ч, то = 80 : 10 = 8 (ч).
Если = 20 км/ч, то = 80 : 20 = 4 (ч).
Если = 40 км/ч, то = 80 : 40 = 2 (ч).
Получаем, что каждый раз, увеличивая скорость движения в 2 раза, время движения будет уменьшаться в 2 раза, а это и говорит о том, что зависимость между величинами и является обратной пропорциональностью, при том условии, что расстояние нужно проехать одинаковое.
2) и — стороны прямоугольника, а его площадь 36 см 2 .
Если = 3 см, то = 36 : 3 = 12 (см).
Если = 6 см, то = 36 : 6 = 6 (см).
Получаем, что величины и обратно пропорциональны, т.к. увеличивая (уменьшая) одну сторону прямоугольника в 2 раза, чтобы его площадь не изменилась, вторую сторону нужно уменьшить (увеличить) в 2 раза.
Свойство обратно пропорциональных величин:
| Если две величины обратно пропорциональны, то произведение соответствующих значений этих величин равно одному и тому же для данных величин числу. |
В рассмотренных выше примерах для величин и это число равно 80, т.к. = 108 = 204 = 402 = 80, а для величин и это число равно 12, т.к. = 312 = 66 = 36.
Не всякие величины являются прямо пропорциональными или обратно пропорциональными. Например, размер обуви человека увеличивается при увеличении его возраста, но эти величины не являются пропорциональными, т.к. при удвоении возраста размер обуви человека не удваивается.
Пусть нам дана задача:
Украшение состоит из белого и желтого золота массой 192 г. При этом масса белого золота относится к массе желтого золота как 5 : 7. Надо найти массу белого и желтого золота, из которых сделано украшение.
Мы можем считать, что все украшение состоит из 5 + 7 = 12 частей одинаковой массы. По условию масса украшения равна 192 г, а значит, масса одной части украшения равна 192 : 12 = 16 г.
Белое золото соответствует 5 частям, то есть имеет массу 5 16 = 80 г, а желтое золото соответствует 7 частям, то есть имеет массу 7 16 = 112 г.
Итак мы получили, что украшение состоит из 80 г белого золота и 112 г желтого золота.
То есть мы число 192 (масса украшения) представить в виде суммы двух слагаемых — 80 и 112, отношение которых равно 5 : 7.
В этом случае говорят, что число 192 разделили в отношении 5 : 7, или по-другому, число 192 представили в виде суммы двух слагаемых, пропорциональных числам 5 и 7.
Тема урока: «Прямая и обратная пропорциональные зависимости». 6-й класс
Назад Вперёд
Загрузить презентацию (261 кБ)
Учебный предмет: математика; 6 класс (учебник «Математика 6» Н.Я.Виленкин и др.)
Тема: Прямая и обратная пропорциональные зависимости.
Тип урока: изучение нового материала с применением информационных технологий
- Образовательные:
- закрепить основные понятия: пропорция, основное свойство пропорции;
- сформировать у учащихся понятия прямой и обратной пропорциональной зависимости;
- сформировать умение решать задачи с помощью пропорции;
- логически мыслить при определении зависимости в соответствии с условием задачи;
- развивать грамотную математическую речь; память, внимание, делать выводы, основанные на рассуждениях;
- содействовать развитию познавательного интереса, творческих способностей, умению сравнивать, анализировать;
- прививать интерес к математике;
- развивать навыки устойчивого внимания.
Методы обучения: коммуникативный, дифференцированный, исследовательско-поисковый.
Формы организации урока: фронтальный опрос, индивидуальная работа, самопроверка.
Оборудование: м/м проектор, экран, компьютер, монитор, презентация.
1. Организационный этап
Проверка готовности учащихся к уроку.
– Сегодня мы с вами познакомимся с новыми понятиями: прямая и обратная пропорциональные зависимости, и будем учиться решать задачи, опираясь на новые знания.
- Что такое пропорция?
- Сформулируйте основное свойство пропорции.
- Какие перестановки членов пропорции снова приводят к верным пропорциям?
- Составьте три новые верные пропорции из пропорции: 5 : 15 = 4 : 12
- Какие перестановки членов этой пропорции снова приводят к верным пропорциям?
- Составьте три новые верные пропорции из пропорции: (слайд 3)
а) 135 : __ = 90 : 2
б) 18 : 3 = __ : __– Какое из этих заданий имеет единственное решение, а какое – много решений? Почему?
Постановка перед учащимися учебной проблемы
– А помогут ли нам полученные знания в решении практических задач?
3. Формирование новых знаний
Устное обсуждение (поиск решения) (слайд 4)
- Во сколько раз купили больше овощей?
- Если больше купили, то меньше или больше должны заплатить?
Вывод: если количество товара увеличивается в несколько раз, то и увеличивается стоимость покупки во столько же раз.
В ходе устного осуждения учащиеся определяют, как изменяются зависимые между собой величины в данной задаче.
Определение: две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
- Если количество тракторов будет больше, то чтобы вспахать то же самое поле потребуется больше или меньше дней?
- Во сколько раз увеличилось количество тракторов? Во сколько раз меньше дней потребуется, чтобы выполнить ту же работу?
В ходе устного осуждения учащиеся определяют, как в этой задаче изменяются зависимые между собой величины.
Определение: две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз
Тестовая работа – проверь себя
Теоретический тест позволяет скорректировать дальнейшую подачу материала (слайды 6; 7;

«Да» и «нет» не говорите, знаком их изобразите: (слайд 5)
- Зависимость между количеством товара и стоимостью покупки является прямой пропорциональностью.
- Рост ребенка и его возраст прямо пропорциональны.
- При постоянной ширине прямоугольника его длина и площадь прямо пропорциональны.
- Скорость автомобиля и время его движения обратно пропорциональны.
- Скорость автомобиля и его пройденный путь обратно пропорциональны.
- Две величины называются обратно пропорциональными, если при увеличении одной из них в два раза другая в два раза уменьшается.
- Грузоподъемность машин и их количество прямо пропорциональны.
- Периметр квадрата и длина его стороны прямо пропорциональны.
Проверим ответы: взаимопроверка с использованием м/м проектора (слайд 9): + – + + – + – +
Поставь себе оценку: (слайд 10)
8 правильных ответов – «5»
7-6 правильных ответов – «4»
5-4 правильных ответов – «3»4. Физкультминутка
5. Формирование умений и навыков
Решение задач уровня обязательной подготовки (слайды 11; 12)
6. Этап первичной проверки
Учащиеся выполняют самостоятельную работу по вариантам с взаимопроверкой в парах.
Прямая и обратная пропорциональность — формулы, свойства и графики функций
Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.
Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.
Прямая пропорциональность
Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.
Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.
Функция прямой пропорциональности и ее график

Эта зависимость описывается следующей формулой:
Здесь k и называется коэффициентом пропорциональности.

Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.
Пример построения
Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).
Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k < 0 (справа).
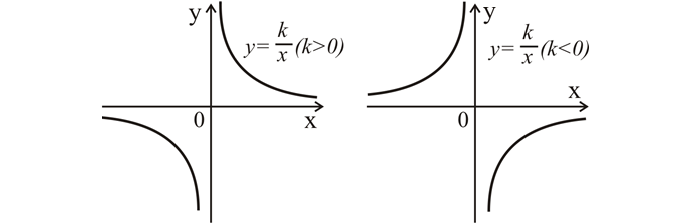
Свойства функции прямой пропорциональности

Основные свойства следующие:
область определения, значений составляют все действительные числа;
возрастает при всех значениях x, если k > 0;
если коэффициент со знаком «-», т. е. если k < 0, то убывает;
если k > 0, то прямая располагается в 1 — 3 координатных четвертях и образует острый угол с осью Х, если k < 0, то прямая находится во 2 - 4 четвертях и образует тупой угол с осью Х.
Обратная пропорциональность
Рост одного параметра ведет к уменьшению другого в такое же количество раз, и наоборот, при уменьшении одной величины другая увеличивается во столько же. Это значит, что они обратно пропорциональны друг другу.

Пример: трое рабочих выполнят порученную им работу за 2 часа, а 6 человек такое же задание осилят за 1 час. То есть двукратное увеличение числа работников привело к уменьшению затраченного времени вдвое. Конечно, если прочие факторы неизменны (производительность труда, условия работы).
Функция обратной пропорциональности и ее график
Функция задается формулой:
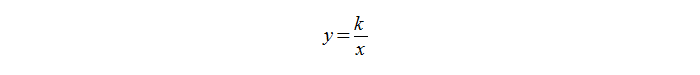
где k – любое действительное число, кроме 0.
График данной зависимости — это гипербола, ее ветви находятся в 1 и 3 четвертях системы координат при k > 0, или во 2 и 4, если коэффициент меньше 0. Ветви гиперболы симметричны относительно точки (0; 0).
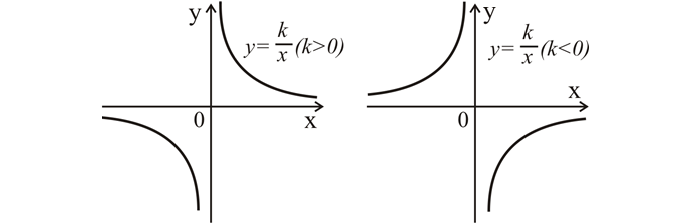
Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:
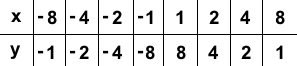
Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
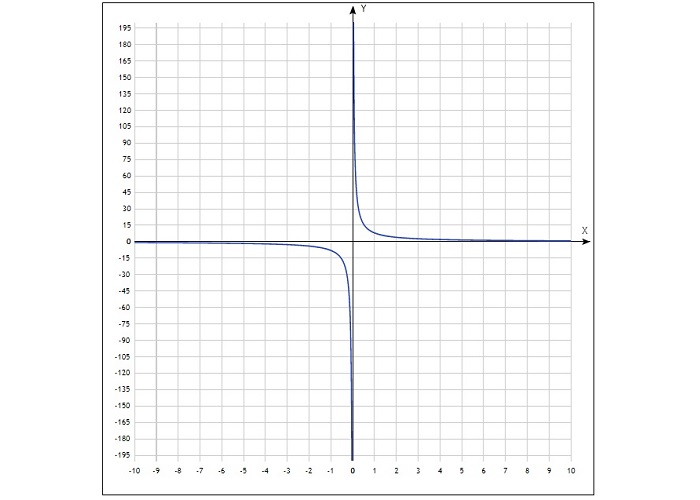
Свойства функции обратной пропорциональности

области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;
если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;
оси координат 0х и 0у — это асимптоты по отношению к ветвям гиперболы, которые приближаются к ним, но не достигают их.
К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.
Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.
Урок математики в 6 классе по теме «Прямая и обратная пропорциональные зависимости»
Разработала
учитель математики
МОУ «Михайловской СОШ имени
Героя Советского Союза В.Ф. Нестерова»
Клеймёнова Д.М.1. Дидактическая :
способствовать формированию и закреплению умений и навыков решения задач с помощью пропорций;
научить выделять в условиях задач две величины и устанавливать вид зависимости между ними;
записывать краткую запись и составлять пропорцию;
закреплять навыки и умения решать уравнения, имеющие вид пропорции.
2. Развивающая :
развивать память, внимание, продолжить развитие математической речи учащихся;
способствовать развитию творческой деятельности учащихся и интереса к предмету математика.
3. Воспитательная :
воспитывать аккуратность, формировать интерес к математике;
воспитывать умение внимательно выслушивать мнение других, воспитание уверенности в себе, воспитание культуры общения.
Оборудование: ТСО необходимые для презентации: компьютер и проектор, листочки для записи ответов, карточки для проведения этапа рефлексии (по три каждому), указка.
Тип урока: урок применения знаний.
Формы организации урока: фронтальная, коллективная, индивидуальная работа.
Структура урока:
Организационный момент, приветствие, пожелания.
Проверка изученного материала.
Сообщение темы урока.
Этап обобщения и систематизации знаний.
Повторение изученного материала.
Этап контроля и самоконтроля знаний и способов действий.
Этап подведения итогов урока.
Организационный момент. (слайд 3)
(Приветствие, фиксация отсутствующих, проверка подготовленности учащихся к учебному процессу, раздача листочков и карточек для проведения рефлексии, проверка подготовленности классного помещения к занятию, организация внимания школьника).Учитель читает: (слайд №3 )
Математика – основа и царица всех наук,
И тебе с ней подружиться я советую, мой друг.
Ее мудрые законы если будешь выполнять,
Свои знанья приумножишь,
Станешь ты их применять.
Сможешь по морю ты плавать,
Сможешь в космосе летать.
Дом построить людям сможешь:
Будет он сто лет стоять.
Не ленись, трудись, старайся,
Познавая соль наук.
Все доказывать пытайся,
Но не покладая рук.2. Проверка изученного материала.
(выявляет проблемы в знаниях и способах деятельности учащихся и определяет причины их возникновения, устраняет в ходе проверки обнаруженные пробелы.)
Устный опрос: (слайд №4 )
Что называется отношением двух чисел?
Как найти дробь от числа?
Что такое пропорция?
Какие величины называются прямо пропорциональными?
Что показывает отношение двух чисел?
Как найти число по его дроби?
Основное свойство пропорции.
Какие величины называются обратно пропорциональными?
Закончите фразу: (слайд 5). (Дети сначала выполняют задание самостоятельно, записывая на листочках только буквы, соответствующие правильному ответу. Затем поднимают руку. После этого учитель вслух читает вопрос, а уч-ся отвечают).
Прямой пропорциональной зависимостью называется такая зависимость величин, при которой…
Обратной пропорциональной зависимостью называется такая зависимость величин, при которой…
Чтобы найти неизвестный крайний член пропорции …
Средний член пропорции равен …
Пропорция верна, если…
С) … при увеличении одной величины в несколько раз, другая уменьшается во столько же раз.
Х) …произведение крайних членов равно произведению средних членов пропорции.
А) …при увеличении одной величины в несколько раз, другая увеличивается на столько же.
П) …нужно произведение средних членов пропорции разделить на известный крайний член.
У) …при увеличении одной величины в несколько раз, другая увеличивается во столько же раз.
Е) …отношению произведения крайних членов к известному среднему.
Ответ: УСПЕХ. (слайд 6 )
Графический диктант (слайды 7-10).
«Да» и «нет» не говорите,
А значком изобразите.
«Да» значком «+», нет значком «-».
(Учащиеся, работают самостоятельно. Ответы записывают на листочках. Самопроверка, используя слайд № . По-окончании урока учитель просматривает листочки)
Если площадь прямоугольника постоянная величина, то его длина и ширина – обратно пропорциональные величины.
Рост ребенка и его возраст прямо пропорциональны.
При постоянной ширине прямоугольника его длина и площадь прямо пропорциональны.
Скорость автомобиля и время его движения обратно пропорциональны.
Скорость автомобиля и его пройденный путь обратно пропорциональны.
Выручка кассы кинотеатра прямо пропорциональна количеству проданных билетов, проданных по одной и той же цене.
Грузоподъемность машин и их количество обратно пропорциональны.
Периметр квадрата и длина его стороны прямо пропорциональны.
При постоянной цене стоимость товара и его масса – обратно пропорциональные величины.
Ответ: + — + + — + + — — (Слайд №10 )
Получи оценку.(слайд №11)
8 -9 правильных ответов – «5»
6-7 правильных ответов – «4»
4-5 правильных ответов – «3»
Устный счёт : ( слайды 12-13)
Ну-ка, в сторону карандаши!
Ни бумажек, ни ручек, ни мела!
Устный счёт! Мы творим это дело
Только силой ума и души!
Задание: Найди неизвестный член пропорции:


Ответы: 1) 39; 24; 3; 24; 21.
Сообщение темы урока. слайд №14 (Обеспечивает мотивацию учения школьников.)
Тема нашего урока «Прямая и обратная пропорциональные зависимости».
На предыдущих уроках мы рассматривали прямую и обратную пропорциональную зависимость величин. Сегодня на уроке мы будем решать разные задачи с помощью пропорции, устанавливая вид связи между данными. Повторим основное свойство пропорций. А следующий урок, завершающий по данной теме, т.е. урок – контрольная работа.
Демонстрируется слайд № 15
Этап обобщения и систематизации знаний.
Составить пропорции для решения задач: (работают в тетрадях)
а) Велосипедист за 3ч проезжает 75км. За сколько времени проедет велосипедист 125км с той же скоростью?
б) 8 одинаковых труб заполняют бассейн за 25 минуты. За сколько минут заполнят бассейн 10 таких труб?
в) Бригада из 8 рабочих выполняет задание за 15 дней. Сколько рабочих сможет выполнить это задание за 10 дней, работая с той же производительностью?
г) Из 5,6 кг помидоров получают 2 л томатного соуса. Сколько литров соуса можно получить из 54 кг помидоров?
Проверить ответы. ( Слайд № 16 )( самооценка: поставить + или – карандашом в тетради; проанализировать ошибки)
Ответы: а) 3:х=75:125 в) 8 : х=10 : 15
б) 8 :10= Х :2 5 г) 5,6 :54=2 : Х
2) Физкультминутка. (слайд № 17-22)
Из-за парт мы быстро встали
И на месте зашагали.
А потом мы улыбнулись,
Сели – встали, сели – встали
За минутку сил набрались.
Плечи ваши распрямите,
Вправо, влево повернитесь
И за парту вновь садитесь.
3) Решите задачу (слайд № 23)
№ 788 (стр. 130, учебник Виленкина) (после разбора самостоятельно)
Весной при проведении работ по озеленению города на улице посадили липы. Принялось 95% вех посаженных лип. Сколько посадили лип, если принялось 57 лип?
О каких двух величинах говорится в задаче? (о количестве лип и их процентах)
Какая зависимость между этими величинами? (прямо пропорциональная)
Составьте краткую запись, пропорцию и решите задачу.

х

100
; ; х=60.
Ответ: 60 лип посадили.
4) Решите задачу: (слайд №24-25 )(после разбора решить самостоятельно; взаимопроверка, затем решение отображается на экране слайд № 23)
Для отопления здания школы заготовлено угля на 180 дней при норме расхода 0,6т угля в день. На сколько дней хватит этого запаса, если его расходовать ежедневно по 0,5т?
Краткая запись:

0,6

180
Составим пропорцию:
; ; дней
5) №793 (стр. 131) (поле разбора самостоятельно; самоконтроль.
В железной руде на 7 частей железа приходится 3 части примесей. Сколько тонн примесей в руде, которая содержит 73,5т железа?
Решение: (слайд №27)

7

73,5
; ;
Ответ: 31,5 кг примесей.
6) Подведение итогов итого этапа. (слайд №28)
Итак, сформулируем алгоритм решения задач с помощью пропорций.
Алгоритм решения задач на прямую
и обратную пропорциональные зависимости:
Неизвестное число обозначается буквой х.
Условие записывается в виде таблицы.
Устанавливается вид зависимости между величинами.
Прямо пропорциональная зависимость обозначается одинаково направленными стрелками, а обратно пропорциональная зависимость — противоположно направленными стрелками.
Находится её неизвестный член.
5. Повторение изученного материала. (слайд №29)
№ 763 (и) (стр. 125) (с комментированием у доски)

6. Этап контроля и самоконтроля знаний и способов действий.
(слайд №30-32)Самостоятельная работа (10 – 15 мин)(Взаимопроверка: по готовым слайдам учащиеся друг у друга проверяют самостоятельную работу, выставляя при этом + или -. Учитель в конце урока собирает тетради для просмотра).
Решите задачи, составляя пропорции.
№ 1. На путь от одного поселка до другого со скоростью 12,5 км/ч велосипедист затратил 0,7 ч. С какой скоростью он должен был ехать, чтобы преодолеть этот путь за 0,5 ч?
Краткая запись:

12,5

0,7
Составим пропорцию:
; ; км/ч
№ 2. Из 5 кг свежих слив получается 1,5 кг чернослив. Сколько чернослива получится их 17,5 кг свежих слив?
Краткая запись:

5

1,5
Составим пропорцию:
; ; кг
№ 3. Автомобиль проехал 500 км, истратив 35л бензина. Сколько литров бензина потребуется, чтобы проехать 420 км?
Краткая запись:

500

35
Составим пропорцию:
; ; л
№ 4 . За 2 ч поймали 12 карасей. Сколько карасей поймают за 3 ч?
Ответ: ответа не существует т.к. эти величины ни прямо пропорциональны, ни обратно пропорциональны.
№ 5 Шесть маляров могут выполнить некоторую работу за 18 дней. Сколько еще маляров надо пригласить, чтобы работа была выполнена за 12 дней?
Краткая запись:

6

18
Составим пропорцию:
; ; маляров выполнят работу за 12 дней.
1) 9 -6=3 маляра нужно ещё пригласить.
Дополнительная (слайд №33)
№ 6. Горнорудному предприятию требуется закупить на определённую сумму денег 5 новых машин по цене 12 тыс. руб. за одну. Сколько таких машин сможет купить предприятие, если цена за одну машину станет15 тыс. рублей?
Краткая запись:
Количество машин (шт.)

5

12
Составим пропорцию:
; ; машины.
Подведение результатов сам работы . Слайд №31-32
Этап подведения итогов урока
Что мы узнали на уроке? (Понятия прямой и обратной пропорциональной зависимости двух величин)
Приведите примеры прямо пропорциональных величин.
Приведите примеры обратно пропорциональных величин.
Приведите примеры величин, у которых зависимость не является ни прямо, ни обратно пропорциональной.
Рефле к сия (слайд 34) .(Учащиеся поднимают карточку, соответствующую их состоянию)
Оцените свою работу на урок е .
Удовлетворены ли вы результатом своей работы?
Да Нет Не знаю .
Задание на дом (слайд 35)
Спасибо за урок слайд №36
Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд Математика, 6. « Мнемозина», 2009.
А.С. Чесноков, К.И. Нешков Дидактические материалы по математике 6 класс.
И. Я. Депман, Н. Я. Виленкин За страницами учебника математики: Книга для учащихся 5-6 классов. М., 1998.






