Арифметические устройства. сумматоры и субтракторы
Основной элементарной операцией, выполняемой над кодами чисел в цифровых устройствах, является арифметическое сложение.
Сумматор – электронная логическая схема, выполняющая арифметическое сложение кодов двух чисел. Этот узел лежит в основе арифметико-логического устройства ЭВМ (АЛУ).
Полусумматор. Простейшего устройства, являющегося звеном сумматора. Это устройство реализует сложение двух одноразрядных двоичных чисел А и В. В результате получается двухразрядное двоичное число. Его младшую цифру обозначим S(от лат. Summa), а старшую, которая будет перенесена в старший разряд, – Co (от англ. Carry out – выходной перенос).
| Слагаемые | Перенос | Сумма | |
| A | B | Co | S |
Полусумматор имеет два входа (слагаемые) и два выхода – сумму в данном разряде и перенос в следующий разряд. Из таблицы видно, что перенос формируется ЛФ AND (И): Co = AB.
Для составления ЛФ для S можно обратиться к логическому конвертеру, но здесь результат очевиден – функция Исключающее ИЛИ (XOR – от eXclusive OR). Исключающее ИЛИ осуществляет математическую операцию сложение двух бит по модулю 2. Математики обозначают эту операцию знаком «псевдоплюс».
Рис. 1. Схема полусумматора на ЛЭ XOR и AND
В программе EWB имеется специальный инструментарий для выделения функциональных блоков из больших схем. Его можно использовать для создания дополнительной библиотеки цифровых узлов.
Проведем построение субблока полусумматора по схеме рис. 1. Путем растяжения выделенных частей, придадим схеме такой вид, чтобы внутрь выделяющей рамки входил только полусумматор. Это и будет субблок (подсхема). Проводники, пересекающие контур субблока, образуют его выводы, поэтому их число и расположение надо контролировать.
После выделения субблока, пока его элементы имеют активный красный цвет, входим в меню Circuit (цепь) и выбираем Create Subcircuit. В появившемся меню Subcircuit впечатываем в строке Name название, например НА (Half-Adder), и выбираем Сору from Circuit. На рабочем поле появится дополнительное окно с развернутой схемой субблока (рис. 2).
Рис 2. Создание субблока полусумматора
Эту подсхему можно отредактировать стандартными приемами. Можно добавить выводы, вытянув провод из нужной точки до края внутреннего поля окна (возникнет дополнительная контактная площадка). Если контактную площадку вытянуть за пределы окна, то соответствующий вывод будет удален. После редактирования и проверки правильности подсхемы это окно можно закрыть.
Для выбора схемного изображения субблока в свернутом виде, надо нажать в ряду выбора компонентов на иконку Favorites (Избранные). В результате получим иконку с изображением субблоков и возможность дальнейшего выбора Choose SUB. Выбрав в последнем окне Accept (согласиться), получим искомое схемное изображение субблока в свернутом виде. К внутреннему содержанию субблока можно вернуться двойным щелчком по его схемному изображению.
Библиотеку раздела Favorites можно докомплектовать уже существующими и часто используемыми компонентами, нажав на соответствующую иконку ПКМи выбрав опцию Add to favorites (Добавить к избранным). Создание такой специализированной пользовательской панели для конкретной схемы иногда бывает удобно. Для использования полученного субблока в новом окне, необходимо скопировать схемное изображение субблока в свернутом виде в буфер обмена.
Открыв новое окно (New) и нажав на иконку Favorites, увидим, что внутри нет никаких элементов. После команды Past на экране возникнет схемное изображение субблока, а в открытом окне – Favorites иконка для его выбора.
В цифровом наборе Digital программы EWB существует специальный библиотечный компонент полусумматор (англ. – Half-Adder). Он эквивалентен созданному нами субблоку, но имеет иное графическое оформление. Данный схемный компонент располагается в основной библиотеке, что удобнее.
Пример создания субблока приведен по двум соображениям:
- показать технику создания новых субблоков;
- раскрыть возможное содержание библиотечного полусумматора.
В отличие от вновь созданных субблоков готовые библиотечные компоненты не раскрывают своих схем и не дают возможности их редактировать (в большинстве компонентов редактируются только их параметры).
Схемы, в которых использован вновь созданный и стандартный полусумматоры показаны на рис. 3 и 4.
Рис. 3. Схема включения разработанного полусумматора
Рис. 4. Схема включения библиотечного полусумматора
Данная схема называется полусумматором, так как реализует суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.
Полный одноразрядный сумматор. При сложении старших разрядов многоразрядных двоичных слов необходимо в схеме учесть перенос из предыдущего (младшего) разряда. Такое устройство является полным сумматором. Оно должно иметь три входа: А и В – одноименные разряды двух складываемых чисел, Сi – входной перенос из предыдущего (младшего) разряда (от англ. Carry in – входной перенос) и два выхода: S – сумма в данном разряде и Co – перенос в следующий (старший) разряд.
Таблица истинности для одноразрядного сумматора:
| Входы | Выходы | |||
| A –первоеслагаемое | B– второе слагаемое | Ci– перенос | S– сумма | Co –перенос |
Сумматор удобно представить в виде двух полусумматоров, из которых первый суммирует разряды А и В, а второй к результату прибавляет бит переноса Ci (рис. 5).
Рис. 5. Схема сумматора на двух полусумматорах
В цифровом наборе Digital программы EWB существует специальный библиотечный компонент полный сумматор (англ. – Full-Adder) (рис. 6).
Рис. 6. Схема включения библиотечного сумматора
Многоразрядный сумматор – устройство, предназначенное для сложения двух многоразрядных кодов, формирующее на выходе код суммы и сигнал переноса в случае, если результат сложения не может быть представлен кодом, разрядность которого совпадает с разрядностью кодов слагаемых.
Многоразрядные сумматоры подразделяются на:
- последовательные – операция сложения выполняется последовательно разряд за разрядом, начиная с младшего;
- параллельные – все разряды входных кодов суммируются одновременно.
- комбинационные сумматоры – не имеют собственной памяти;
- накапливающие сумматоры – снабжены собственной внутренней памятью, в которой аккумулируются результаты выполненной операции (каждое слагаемое прибавляется к уже имеющемуся в устройстве значению).
Параллельный сумматор с последовательным переносом – строится как цепочка полных одноразрядных сумматоров, соединенных последовательно по цепям переноса. На каждый разряд ставится одноразрядный сумматор, причем выход (перенос) сумматора младшего разряда подключен ко входу сумматора старшего разряда. Для суммирования младших разрядов чисел полусумматора уже достаточно, так как в этом случае отсутствует сигнал входного переноса.
На рис. 7 представлена схема суммирования двух трехразрядных двоичных чисел А + B = S. В поразрядной записи операция имеет следующие обозначения:
(а3 а2 а1)+(b3 b2 b1)=(s4 s3 s2 s1)
Рис. 7. Схема суммирования трехразрядных чисел
В соответствии с изложенным, соберем схему 3-разрядного параллельного сумматора с последовательным переносом (рис. 10).
Рис. 10. Схема 3-разрядного параллельного сумматора
с последовательным переносом
Субтракторы (вычитатели) выполняют операции, противоположные тем, которые выполняют сумматоры.
| Операнды | Заем | Разность | |
| A | B | Bo | D |
Полувычитатель имеет два входа (уменьшаемое и вычитаемое) и два выхода – разность в данном разряде и заем из старшего разряда.
Рис. 11. Общая схема полувычитателя
Рис. 12. Схема полувычитателя на ЛЭ XOR, NOT и AND
Полный вычитатель (рис. 13) имеет входы a, b, Bi и выходы D, Bo. По аналогии с полным сумматором полный вычитатель можно собрать из двух полувычитателейи логического элемента ИЛИ (рис. 14).
Рис. 13. Общая схема полного вычитателя
Таблица истинности для одноразрядного вычитателя:
| Входы | Выходы | |||
| A –уменьшаемое | B– вычитаемое | Bi– перенос | D– разность | Bo –перенос |
Рис. 14. Схема полного вычитателя на двух полувычитателях
В соответствии с изложенным, соберем схему 3-разрядного параллельного вычитателя с последовательным переносом (рис. 15).
Рис. 15. Схема 3-разрядного параллельного вычитателя
с последовательным переносом
Статьи к прочтению:
Сумматоры, принцип действия
Похожие статьи:
АЛУ – одна из основных функциональных частей процессора, осуществляющая непосредственное преобразование информации. Все операции, выполняемые в АЛУ,…
Лабораторная работа №3 МНОГОРАЗРЯДНЫЕ ДВОИЧНЫЕ СУММАТОРЫ. СЛОЖЕНИЕ ЧИСЕЛ С ФИКСИРОВАННОЙ ЗАПЯТОЙ В ОБРАТНОМ И ДОПОЛНИТЕЛЬНОМ КОДАХ Цель работы. Изучение…
Уроки 27 — 30
Предикаты и кванторы. Логические элементы компьютера. Логические задачи
§23. Предикаты и кванторы. §24. Логические элементы компьютера. §25. Логические задачи
Как следует из названия, сумматор предназначен для сложения (суммирования) двоичных чисел. Сначала рассмотрим более простой элемент, который называют полусумматором. Он выполняет сложение двух битов с учетом того, что в результате может получиться двухразрядное число (с переносом в следующий разряд).
Обозначим через А и В входы полусумматора, а через Р и S — выходы (перенос в следующий разряд и бит, остающийся в текущем разряде). Таблица истинности этого устройства показана на рис. 3.30.
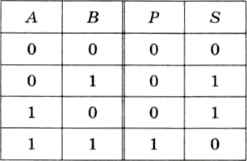
Рис. 3.30
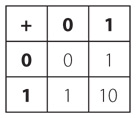
Легко увидеть, что столбец Р — это результат применения операции «И» ко входам А и В, а столбец S — результат операции «исключающее ИЛИ»:
Р = А • В, S = A ⊗ B = А • B + A • B .
Формулу для S можно также записать в таком виде:
S = А • B + A • B = (A + B) • ( А + B ) = (A + B)( A • B ) = (A + B) • P ,
что позволяет построить полусумматор, используя всего четыре простейших элемента (рис. 3.31).
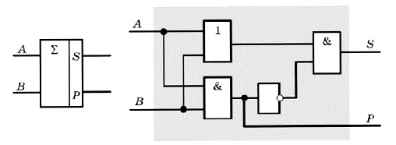
Рис. 3.31
Слева показано условное обозначение полусумматора, греческая буква ∑ здесь (и в математике) обозначает сумму.
Полный одноразрядный сумматор учитывает также и третий бит С — перенос из предыдущего разряда. Сумматор имеет три входа и два выхода. Таблица истинности и обозначение сумматора показаны на рис. 3.32, 3.33.
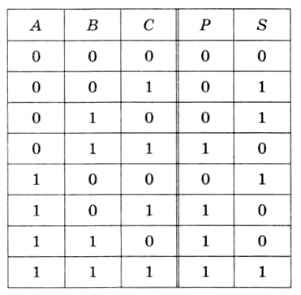
Рис. 3.32
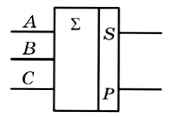
Рис. 3.33
Логические функции для выходов сумматора вы можете найти самостоятельно.
Сумматор можно построить с помощью двух полусумматоров и одного элемента «ИЛИ» (рис. 3.34).
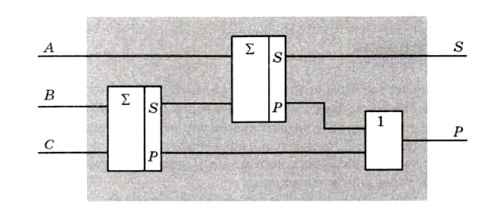
Рис. 3.34
Сначала складываются биты В и С, а затем к результату добавляется бит А. Перенос на выходе сумматора появляется тогда, когда любое из двух промежуточных сложений даёт перенос.
Для сложения многоразрядных чисел сумматоры объединяют в цепочку. При этом выход Р одного сумматора (перенос в следующий разряд) соединяется с входом С следующего. На рисунке 3.35 показано, как складываются два трёхразрядных числа: X =1102 и Y = 0112. Сумма Z — 10012 состоит из четырёх битов, поэтому на выходе последнего сумматора бит переноса будет равен 1.
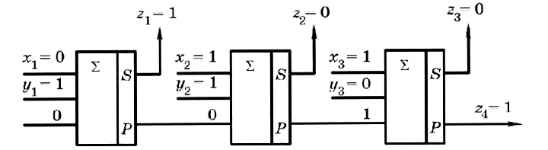
Рис. 3.35
Сложение начинается с самого младшего разряда. На вход первого сумматора подаются младшие биты исходных чисел, х1 и y1 а на третий вход — ноль (нет переноса из предыдущего разряда). Выход S первого сумматора — это младший бит результата, z1 а его выход Р (перенос) передаётся на вход второго сумматора и т. д. Выход Р последнего из сумматоров представляет собой дополнительный разряд суммы, т. е. z4.
Сумматор играет важную роль не только при сложении чисел, но при выполнении других арифметических действий. Фактически он является основой арифметического устройства современного компьютера.

Следующая страница Вопросы и задания

Cкачать материалы урока
Счетные схемы ЭВМ. Счетчики и сумматоры
Аннотация: Рассматривается принцип действия счётных схем как основы построения арифметических устройств.
Счетными схемами, лежащими в основе построения арифметических устройств ЭВМ, являются счетчики и сумматоры. Любые, даже самые сложные, вычислительные схемы представляют собой комбинацию счетчиков различных разновидностей и сумматоров, реализующих вычисления, как правило, в дополнительном коде (подробно кодирование информации в двоичном коде и соответствующая арифметика представлены в «Заключение» ).
Двоичные счетчики
Счетчиком называют функциональный узел, предназначенный для счета сигналов [1, c. 252].
По мере поступления входных сигналов счетчик последовательно перебирает свои состояния в определенном для данной схемы порядке. В частности, двоичные счетчики, рассматриваемые в настоящем пособии, перебирают последовательность двоичных кодов. В том случае, если последовательность выдается с возрастанием кода, счетчик называется суммирующим, если код уменьшается с приходом каждого счетного сигнала, то счетчик называется вычитающим. Если в счетчике предусмотрено переключение из суммирующего режима в вычитающий и обратно, он называется реверсивным. Количество схем счетчиков огромно [1, 2, 3]. Их изучение является отдельной, обширной темой, и задачей данного курса не является.
Простейший синхронный суммирующий счетчик можно построить на счетных, или Т -триггерах (от англ . toggle — кувыркаться). Счетным Т -триггером называют так называемый JK — триггер , который работает в счетном режиме, когда на J- и K -входы постоянно подана логическая 1. JK — триггер представляет собой соединение двух однотактных D -триггеров-защелок (рис. 9.1.а), на С -входы которых поступают противоположные уровни сигналов.
При подаче и на выходе нижнего элемента И будет постоянный логический 0, поскольку =0″ />. А состояние верхнего элемента И будет определяться состоянием выхода » /> всей схемы. Если в предыдущий момент времени , а =1″ /> то на выходе элемента И-ИЛИ будет логическая . При она записывается в первый D — триггер , а при отрицательном фронте на — во второй D — триггер и выдается на выход всей схемы: формируется передний фронт импульса . При на инверсном выходе схемы =0″ />. Этот сигнал переведет при первый D — триггер в нулевое состояние, а при — второй D — триггер и выход всей схемы переводится в нулевое состояние схемы (формируется задний фронт импульса ) так, как показано на рис. 9.1,б.
Рис. 9.1. JK-триггер: а — функциональная схема; б — временная диаграмма работы; в — УГО JK-триггера; г — УГО счетного Т-триггера

Таким образом, в счетном режиме частота входных сигналов уменьшается в два раза. Факт переключения триггера в противоположное состояние при прохождении заднего фронта сигнала отображается на УГО динамическим входом в виде треугольника (рис. 9.1,в и г). Все ранее рассмотренные управляющие сигналы были статическими.
При последовательном соединении нескольких счетных Т-триггеров получаем схему простейшего синхронного счетчика (рис. 9.2,а). При этом выход самого последнего триггера будет являться самым старшим разрядом двоичного кода на выходе счетчика, выход самого первого триггера — младшим разрядом в соответствии с временной диаграммой, представленной на рис. 66,б. Данной схеме соответствует УГО на рис. 9.2.б. Как правило, у счетчиков предусматриваются вход для принудительного сброса в нулевое состояние (когда все триггеры схемы сброшены в ) и выход переноса , устанавливаемый в 1 в том случае, когда прошла вся последовательность импульсов (рис. 9.2,в). Для схемы 3-разрядного счетчика, представленной на рис. 9.2, это коды от 000_ до 111_.
увеличить изображение
Рис. 9.2. Суммирующий двоичный счетчик: а — функциональная схема; б — временная диаграмма работы; в — УГО
Выход переноса может быть использован для последовательного соединения нескольких счетчиков с целью повышения разрядности подсчитываемого числа. Такие схемы называются схемами с последовательным переносом. Существуют также и более сложные схемы с параллельным переносом [1, c. 257-262].
Сумматоры
Сумматором называют функциональный узел, выполняющий сложение одно- или многоразрядных двоичных чисел в соответствии с правилами двоичного сложения.
Подробно вопросы двоичной арифметики освещены в «Заключение» . Правила двоичного сложения можно представить в виде таблицы истинности будущей логической схемы (табл. 9.1) двоичного сумматора и построить эту схему по принципам, изложенным в лекции 3.
Входной перенос из младшего по (отношению к текущему) разряда 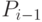 Текущий разряд первого слагаемого Текущий разряд первого слагаемого 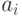 Текущий разряд второго слагаемого Текущий разряд второго слагаемого 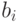 Текущий разряд суммы Текущий разряд суммы  Выходной перенос из текущего разряда суммы Выходной перенос из текущего разряда суммы 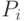 0 0
| 0 | 0 | 0 | 0 |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |

Данная схема построена исходя из тождества
Тождество вытекает из правил де Моргана

; .
Условное обозначение полусумматора.
Одноразрядным сумматором называется устройство для сложения двух одноразрядных кодов, имеющее три входа и два выхода и формирующее из сигналов входных слагаемых и сигнала переноса из младших разрядов величины суммы и переноса в старший разряд .
Таблица истинности одноразрядного сумматора показана ниже. Таблица записана для i-ых разрядов складываемых чисел. ФАЛ, описывающие работу одноразрядного сумматора, и соответствующие таблице истинности будут следующими
Функционирование одноразрядного сумматора определяется ФАЛ (4) и (5). Одноразрядный сумматор строится на двух полусумматорах.
Многоразрядным сумматором называется устройство, предназначенное для сложения двух многоразрядных кодов, формирующее на выходе код суммы и сигнал переноса. Многоразрядные сумматоры подразделяются на последовательные и параллельные.
В последовательных сумматорах операция сложения выполняется последовательно разряд за разрядом, начиная с младшего. В параллельных все разряды входных кодов суммируются одновременно.
Различают комбинационные сумматоры — устройства, не имеющие собственной памяти, и накапливающие сумматоры, снабженные собственной внутренней памятью, в которой аккумулируются результаты выполненной операции.
В АЛУ широко используют многоразрядные параллельные сумматоры.
Структурная схема комбинационного параллельного сумматора с последовательным переносом показана ниже.
4-х разрядный сумматор выполнен с использованием трёх одноразрядных сумматоров и одного полусумматора. Разряды кодов слагаемых подаются на входы сумматоров, выходы суммы которых присоединяются к логическим элементам И.
Логические элементы И используются, как ключи, на вторые входы которых подаётся сигнал Z, определяющий момент считывания результата. Выход сигнала переноса сумматора нулевого разряда подается на вход переноса сумматора первого разряда и т.д.
Реальные схемы многоразрядных сумматоров строятся только с применением одноразрядных сумматоров, что позволяет, используя их последовательное включение, увеличить разрядность кодов слагаемых.
Время выполнения операции сложения в данной схеме определяется последовательным переносом сигнала p из разряда в разряд. Сигнал Z для считывания результата подается не ранее, чем после передачи сигнала переноса по всем разрядам сумматора.
Таким образом, скорость суммирования параллельных сумматоров ограничивается только использованием последовательного принципа передачи сигнала переноса. Увеличение разрядности слагаемых ещё больше ухудшает положение. Для повышения скорости вычислений используют сумматоры с параллельным переносом.
Суть построения сумматоров с параллельным переносом состоит в отказе от использования при суммировании i-х разрядов слагаемых сигнала переноса, сформированного при суммировании предыдущих (i-1)-х разрядов. В каждом разряде, как сигнал суммы, так и сигнал переноса непосредственно формируются из входных переменных. Устройство, формирующее сигналы переноса из значений входных кодов, называют блоком ускоренного переноса (БУП) или схемой ускоренного переноса (СУП). Поясним возможность реализации такого решения.
Ранее было показано, что логическое выражение для образования сигнала переноса в данном разряде имеет следующий вид:
Преобразуем это выражение.
Здесь применена теорема упрощения ;
Теорема поглощения А+АВ=А
Также другие тождества: ; ; ; AA=A; A+1=1; A*0=0;
Вводятся следующие понятия
— функция переноса;
— функция передачи переноса.
Тогда запись (6) преобразуется к виду
Из полученного выражения следует, что возникновение переноса в данном i-том разряде возможно в случаях:
1) если равны единицы значения суммируемых разрядов();
2) если перенос не вырабатывается в данном разряде, а проходит через него из предыдущего разряда (=1).
Покажем способ формирования переноса в i–ом разряде параллельного сумматора.
Выполняя аналогичные действия вплоть до нулевого разряда, находят логическое выражение (ФАЛ), описывающее закон формирования сигнала переноса в произвольном разряде
где p — сигнал переноса, переданный на вход схемы при последовательном соединении нескольких однотипных устройств.
Для реализации переноса в каждом разряде требуется иметь i+1 схем И с числом входов от 1 до i+1 и одну схему ИЛИ с i+1 входами. Так как общее число схем для выработки одновременного переноса равно ,то при больших i построение сумматоров с цепями параллельного переноса практически невозможно. Обычно в этом случае ограничиваются четырьмя разрядами (i£ 4). При необходимости разработки сумматоров с большей разрядностью применяют устройства с групповой структурой.
Сумматоры с цепным переносом реализуют внутри выделенных групп параллельный перенос, а между группами используется последовательный перенос.
5.1.2 Операции АЛУ.
Рассмотрим работу АЛУ на примере схемы показанной ниже. Принципиальная схема одного разряда АЛУ выполнена в базисе логических элементов ИЛИ-НЕ. На входы АЛБ поступает входная информация А В (значения -го разряда слагаемых ) из буферных регистров. Арифметико-логический блок состоит из трёх ступеней:
1-ступень логических операций и формирования полусумм;
2-ступень генерации переносов;
3-ступень формирования полных сумм.
На входы S-S подаются коды выполняемой операции. Код S-S формируется в устройстве управления и входит в состав микрокоманд. Перечень выполняемых операций в зависимости от значений кодов S-S приведен в таблице 1.
Сумматоры
Сумматор — это узел ЭВМ, предназначенный для сложения кодов двоичных чисел. Сумматоры делятся на последовательные (накапливающие) и параллельные (комбинационные). Накапливающие сумматоры имеют низкое быстродействие, поэтому они рассматриваться не будут. В комбинационных сумматорах слагаемые поступают на входы одновременно, а на выходе получается код суммы. После снятия слагаемых результат пропадает. Эти устройства не обладают памятью и строятся на логических элементах.
Составим таблицу истинности устройства для сложения двух одноразрядных чисел а и Ь:
Здесь р — перенос в старший разряд; s — значение суммы. Устройство, реализующее эту таблицу истинности, называют двоичным полусумматором. Его можно синтезировать по ФАЛ для каждого из выходов:

Составим схему на произвольных элементах (рис. 3.14).

Рис. 3.14. Схемная реализация и условное обозначение полусумматора
При сложении многоразрядных чисел необходимо складывать три двоичные цифры в каждом разряде: два слагаемых и единицу переноса из предыдущего разряда Р_х. Наличие этой единицы переноса несколько меняет таблицу сложения двоичных чисел:
ФАЛ для цени суммы:

Карта Карно для функции переноса представлена на рис. 3.15.

Рис. 3.15. Карта Карно для цепи переноса
Уравнение для St не минимизируется. Устройство, реализующее эти ФАЛ, называется сумматором (полным сумматором). Он имеет три входа и два выхода. Цена сумматора по уравнениям составляет Ц = 25. Путем совместной минимизации уравнений Sj и Pj удается снизить цену до 20, и в таком виде выпускаются микросхемы сумматоров. Например, К155ИМ1 — полный одноразрядный сумматор (рис. 3.16).

Рис. 3.16. Полный сумматор
Для сложения многоразрядных чисел сумматор составляют из одноразрядных. Пусть требуется сложить два четырехразрядных двоичных числа: Aw В:

Составим схему сумматора (рис. 3.17).

Рис. 3.17. Многоразрядный сумматор
Получился многоразрядный сумматор с последовательным переносом. Такие сумматоры выпускают в виде отдельных микросхем. Например, ИМС К155 ИМЗ — четырехразрядный сумматор с последовательным переносом. Время сложения чисел определяется временем распространения переноса и равно 55 нс (для четырех разрядов). С ростом числа разрядов быстродействие сумматора уменьшается, так как цепь переноса последовательная.
Вспомним формулу переноса:

Найдем эти переносы:

Видно, что имея только слагаемые, можно формировать перенос в любом разряде, не дожидаясь его появления в предыдущем разряде, причем с помощью только двухуровневой схемы (один слой конъюнкторов и один дизъюнктор). Такая схема называется схемой ускоренного переноса (параллельного переноса). Она может быть встроена в сумматор (сумматор с параллельным переносом) или выпускаться отдельно. Например, ИМС К155 ИМ6 четырехразрядпый сумматор с параллельным переносом. Время сложения чисел равно 27 нс.
При большом числе разрядов сложность схемы ускоренного переноса сильно возрастает. Поэтому сумматор разбивают на группы по четыре или восемь разрядов. Внутри группы выполняют параллельный перенос, а между группами — параллельный или последовательный. Такие сумматоры называют сумматорами с групповым переносом.
Многоразрядный сумматор условно обозначают так, как показано на рис. 3.18.

Рис. 3.18. Условное обозначение многоразрядного сумматора
С помощью сумматоров можно не только складывать, но и вычитать двоичные числа. При использовании дополнительных кодов операцию вычитания двух положительных чисел заменяют операцией суммирования положительного и отрицательного чисел, при этом получение дополнительного кода числа является элементарной операцией. Для этого необходимо проипвертировать число и прибавить к нему в младший разряд единицу.
Схема вычитателя числа А из числа В приведена на рис. 3.19, а схема вычитателя числа В из числа А — на рис. 3.20.

Рис. 3.19. Схема вычитателя числа А из числа В

Puc. 3.20. Схема вычитателя числа В из числа А
Схема инкремент/декремент. Возьмем три полусумматора и соединим их следующим образом (рис. 3.21).

Рис. 3.21. Схема инкремент/декремент
Подавая на управляющий вход Z ноль или единицу, проанализируем состояние выхода при различных входных сигналах:
Цифровые арифметические схемы
В этой главе давайте поговорим об основных арифметических схемах, таких как двоичный сумматор и двоичный вычитатель. Эти схемы могут работать с двоичными значениями 0 и 1.
Двоичный сумматор
Самая основная арифметическая операция – сложение. Схема, которая выполняет сложение двух двоичных чисел, называется двоичным сумматором . Во-первых, давайте реализуем сумматор, который выполняет сложение двух битов.
Полумесяц
Половина сумматора представляет собой комбинационную схему, которая выполняет сложение двух двоичных чисел A и B, состоящих из одного бита . Он выдает две выходные суммы, S & carry, C.
Таблица истинности Half сумматора показана ниже.
| входные | Выходы | ||
|---|---|---|---|
| В | С | S | |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Когда мы добавляем два бита, результирующая сумма может иметь значения в диапазоне от 0 до 2 в десятичном виде. Мы можем представить десятичные цифры 0 и 1 одним битом в двоичном виде. Но мы не можем представить десятичную цифру 2 с одним битом в двоичном виде. Итак, нам требуется два бита для представления его в двоичном виде.
Пусть, sum, S – младший значащий бит и перенос, C – старший значащий бит полученной суммы. Для первых трех комбинаций входов, carry, C равен нулю, а значение S будет равно нулю или единице в зависимости от количества единиц, присутствующих на входах. Но, для последней комбинации входных данных, carry, C равен единице, а sum равен нулю, поскольку результирующая сумма равна двум.
Из таблицы Truth мы можем напрямую записать логические функции для каждого вывода как
S = A o p l u s B
Мы можем реализовать вышеуказанные функции с 2-входным вентилем Ex-OR и 2-входным вентилем AND. Принципиальная электрическая схема полумесяца показана на следующем рисунке.
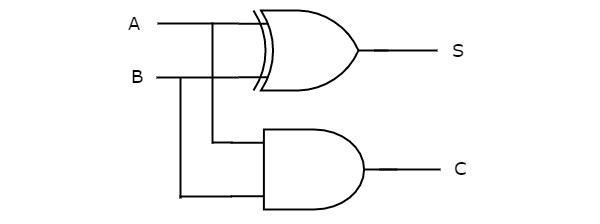
В приведенной выше схеме два входных логических элемента ИЛИ-И и два входных И логических элемента И дают сумму, S и перенос, C соответственно. Следовательно, Half-сумматор выполняет сложение двух битов.
Полный сумматор
Полный сумматор представляет собой комбинационную схему, которая выполняет сложение трех битов A, B и C в . Где A & B – два параллельных значащих бита, а C in – бит переноса, который генерируется из предыдущего этапа. Этот полный сумматор также выдает две выходные суммы, S & carry, C out , которые аналогичны полумесяцу.
Таблица истинности полного сумматора показана ниже.
| входные | Выходы | |||
|---|---|---|---|---|
| В | С в | C out | S | |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Когда мы добавляем три бита, результирующая сумма может иметь значения в диапазоне от 0 до 3 в десятичном виде. Мы можем представить десятичные цифры 0 и 1 одним битом в двоичном виде. Но мы не можем представлять десятичные цифры 2 и 3 одним битом в двоичном виде. Итак, нам требуется два бита для представления этих двух десятичных цифр в двоичном виде.
Пусть, sum, S – младший значащий бит и перенос, C out – старший значащий бит из результирующей суммы. Легко заполнить значения выходов для всех комбинаций входов в таблице истинности. Просто посчитайте количество единиц на входах и запишите эквивалентное двоичное число на выходах. Если C in равен нулю, то полная таблица истинности сумматора такая же, как в таблице истинной половины сумматора.
Мы получим следующие логические функции для каждого вывода после упрощения.
S = A o p l u s B o p l u s C i n
c o u t = A B + l e f t ( A o p l u s B r i g h t ) c i n
Сумма S равна единице, когда на входах присутствует нечетное число единиц. Мы знаем, что вентиль Ex-OR производит вывод, который является нечетной функцией. Таким образом, мы можем использовать либо два входа Ex-OR с 2 входами, либо один вентиль Ex-OR с 3 входами, чтобы получить сумму S. Мы можем реализовать перенос C , используя два вентиля И с двумя входами И и один вентиль ИЛИ. Принципиальная электрическая схема полного сумматора показана на следующем рисунке.
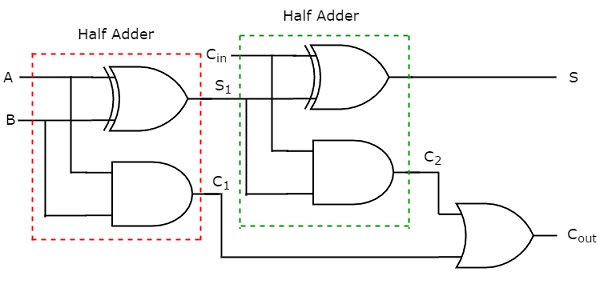
Этот сумматор называется полным сумматором, потому что для реализации одного полного сумматора нам нужны два полумесяца и один вентиль ИЛИ. Если C in равно нулю, то Полное сумматор становится Полумесяным. Мы можем легко проверить это из приведенной схемы или из булевых функций выходов полного сумматора.
4-битный двоичный сумматор
4-разрядный двоичный сумматор выполняет сложение двух 4-разрядных чисел . Пусть 4-битные двоичные числа, A = A 3 A 2 A 1 A 0 и B = B 3 B 2 B 1 B 0 . Мы можем реализовать 4-битный двоичный сумматор одним из следующих двух способов.
Для суммирования двух старших значащих битов используйте один половинный сумматор и три полных сумматора.
Используйте четыре полных сумматора для однородности. Поскольку начальный перенос C in равен нулю, полный сумматор, который используется для добавления младших значащих битов, становится половинным сумматором.
Для суммирования двух старших значащих битов используйте один половинный сумматор и три полных сумматора.
Используйте четыре полных сумматора для однородности. Поскольку начальный перенос C in равен нулю, полный сумматор, который используется для добавления младших значащих битов, становится половинным сумматором.
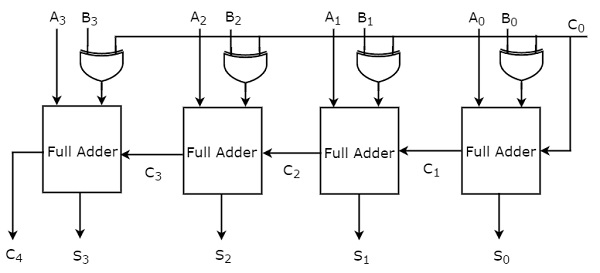
Пока мы рассматривали второй подход. Блок-схема 4-битного двоичного сумматора показана на следующем рисунке.
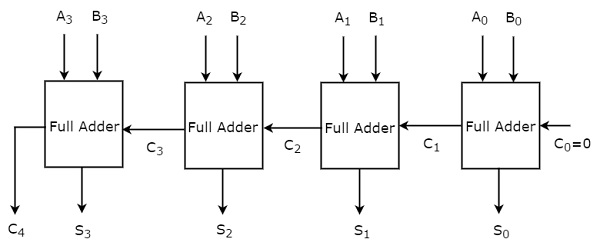
Здесь 4 полных сумматора расположены каскадом. Каждый полный сумматор получает соответствующие биты двух параллельных входов A и B. Выходной сигнал переноса одного полного сумматора будет входом переноса последующего полного сумматора более высокого порядка. Этот 4-битный двоичный сумматор производит результирующую сумму, имеющую не более 5 бит. Итак, проводить последний этап Полный сумматор будет MSB.
Таким образом, мы можем реализовать любой двоичный сумматор более высокого порядка, просто каскадируя необходимое количество полных сумматоров. Этот двоичный сумматор также называется сумматором с волновым переносом (двоичным), потому что перенос распространяется (колебания) от одного этапа к следующему этапу.
Бинарный вычитатель
Схема, которая выполняет вычитание двух двоичных чисел, известна как двоичный вычитатель . Мы можем реализовать двоичный вычитатель следующими двумя способами.
- Каскад Полные вычитатели
- Метод дополнения 2
В первом методе мы получим n-битный двоичный вычитатель путем каскадного вычитания ‘n’ полных вычитателей. Итак, сначала вы можете реализовать Half-вычитатель и Full-вычитатель, аналогично Half-сумматору и полному сумматору. Затем вы можете реализовать n-битный двоичный вычитатель, каскадируя ‘n’ полных вычитателей. Итак, у нас будут две отдельные схемы для двоичного сложения и вычитания двух двоичных чисел.
Во втором методе мы можем использовать один и тот же двоичный сумматор для вычитания двух двоичных чисел, просто выполнив некоторые изменения во втором входе. Итак, внутренне двоичная операция сложения имеет место, но на выходе получается вычитание.
Мы знаем, что вычитание двух двоичных чисел A & B может быть записано как,
A B = A + l e f t ( 2 ′ s :: c o m p m e n t o f B r i g h t )
R i g h t a r r o w A B = A + l e f t ( 1 ′ s : к о м п л и м е н т o f B r i g h t ) + 1
4-разрядный двоичный вычитатель
4-разрядный двоичный вычитатель производит вычитание двух 4-разрядных чисел . Пусть 4-битные двоичные числа, A = A 3 A 2 A 1 A 0 и B = B 3 B 2 B 1 B 0 . Внутренне работа 4-разрядного двоичного вычитателя аналогична работе 4-разрядного двоичного сумматора. Если нормальные биты двоичного числа A, дополненные биты двоичного числа B и начального переноса (заимствования), C в качестве единицы применяются к 4-разрядному двоичному сумматору, то он становится 4-разрядным двоичным вычитающим веществом. Блок-схема 4-разрядного двоичного вычитателя показана на следующем рисунке.
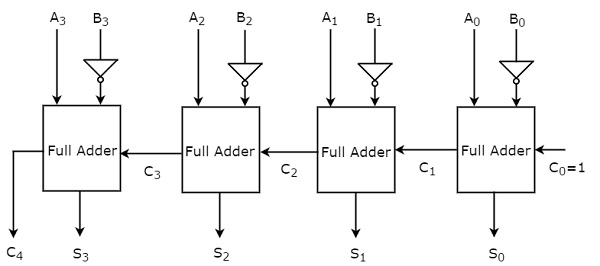
Этот 4-разрядный двоичный вычитатель выдает выходной сигнал, имеющий не более 5 бит. Если двоичное число A больше двоичного числа B, то значение MSB на выходе равно нулю, а оставшиеся биты содержат величину AB. Если двоичное число A меньше двоичного числа B, то MSB выходного значения равно единице. Итак, возьмите 2-е дополнение вывода, чтобы получить величину AB.
Таким образом, мы можем реализовать любой двоичный вычитатель более высокого порядка, просто каскадируя необходимое количество полных сумматоров с необходимыми модификациями.
Двоичный сумматор / вычитатель
Схема, которую можно использовать для сложения или вычитания двух двоичных чисел в любое время, называется двоичным сумматором / вычитателем . И двоичный сумматор, и двоичный вычитатель содержат набор полных сумматоров, которые каскадируются. Входные биты двоичного числа A непосредственно применяются как в двоичном сумматоре, так и в двоичном вычитателе.
Есть два различия в входах полных сумматоров, которые присутствуют в двоичном сумматоре и двоичном вычитателе.
Входные биты двоичного числа B непосредственно применяются к полным сумматорам в двоичном сумматоре, тогда как дополненные биты двоичного числа B применяются к полным сумматорам в двоичном вычитателе.
Первоначальный перенос, C 0 = 0, применяется в 4-разрядном двоичном сумматоре, тогда как начальный перенос (C 0) 1 применяется в 4-разрядном двоичном вычитателе.
Входные биты двоичного числа B непосредственно применяются к полным сумматорам в двоичном сумматоре, тогда как дополненные биты двоичного числа B применяются к полным сумматорам в двоичном вычитателе.
Первоначальный перенос, C 0 = 0, применяется в 4-разрядном двоичном сумматоре, тогда как начальный перенос (C 0) 1 применяется в 4-разрядном двоичном вычитателе.
Мы знаем, что вентиль Ex-OR с 2 входами производит выход, который совпадает с выходом первого входа, когда другой вход равен нулю. Точно так же это производит вывод, который является дополнением первого ввода, когда другой ввод – один.
Поэтому мы можем применить входные биты двоичного числа B к 2-входным вентилям Ex-OR. Другим входом для всех этих ворот Ex-OR является C 0 . Таким образом, исходя из значения C 0 , вентили Ex-OR создают либо нормальные, либо дополненные биты двоичного числа B.
4-разрядный двоичный сумматор / вычитатель
4-разрядный двоичный сумматор / вычитатель производит либо сложение, либо вычитание двух 4-разрядных чисел на основе значения начального переноса или заимствования, ? 0 . Пусть 4-битные двоичные числа, A = A 3 A 2 A 1 A 0 и B = B 3 B 2 B 1 B 0 . Работа 4-разрядного двоичного сумматора / вычитателя аналогична работе 4-разрядного двоичного сумматора и 4-разрядного двоичного сумматора.
Примените обычные биты двоичных чисел A и B и начальный перенос или заимствование, C 0 от внешнего к 4-битному двоичному сумматору. Блок-схема 4-битного двоичного сумматора / вычитателя показана на следующем рисунке.
Если начальный перенос, ? 0 равен нулю, то каждый полный сумматор получает нормальные биты двоичных чисел A & B. Таким образом, 4-разрядный двоичный сумматор / вычитатель выдает выход, который является сложением двух двоичных чисел A & B.
Если начальный заем равен 0 , то каждый полный сумматор получает нормальные биты двоичного числа A и дополненные биты двоичного числа B. Таким образом, 4-битный двоичный сумматор / вычитатель выдает результат, который является вычитанием двух двоичных номера A и B.
Следовательно, с помощью дополнительных шлюзов Ex-OR одна и та же схема может использоваться как для сложения, так и для вычитания двух двоичных чисел.
Сумматор (электроника)
Сумматор является цифровой схемой , которая выполняет сложение чисел. Во многих компьютерах и других типах процессоров сумматоры используются в арифметико-логических устройствах или АЛУ . Они также используются в других частях процессора, где они используются для вычисления адресов , индексов таблиц, операторов увеличения и уменьшения и подобных операций.
Хотя сумматоры могут быть построены для многих представлений чисел , таких как десятичное двоичное кодирование или избыточное число , наиболее распространенные сумматоры работают с двоичными числами . В случаях, когда дополнение до двух или до единиц используется для представления отрицательных чисел , легко преобразовать сумматор в сумматор-вычитатель . Другие представления чисел со знаком требуют большей логики в отношении базового сумматора.
СОДЕРЖАНИЕ
Двоичные сумматоры [ править ]
Полусумматор [ править ]
Половина сумматор добавляет две отдельные двоичные цифры A и B . Он имеет два выхода: сумма ( S ) и перенос ( C ). Сигнал переноса представляет собой переход к следующей цифре многозначного сложения. Значение суммы составляет 2 С + С . Простая конструкция полусумматора, изображенная справа, включает в себя ворота XOR для S и и ворота для C . Булева логика для суммы (в данном случае S ) будет A′B + AB ′, тогда как для переноса ( C ) будет AB . С добавлением логического элемента ИЛИ для объединения их выходов переноса два полусумматора могут быть объединены в полный сумматор. [1] Полусумматор складывает два входных бита и генерирует перенос и сумму, которые являются двумя выходами полусумматора. Входные переменные полусумматора называются дополнительными и дополнительными битами. Выходные переменные — это сумма и перенос. Таблица истинности для полусумматора:
| Входы | Выходы | ||
|---|---|---|---|
| А | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |

Полный сумматор [ править ]
Полный сумматор в действии. Полный сумматор дает количество единиц на входе в двоичном представлении.
Схематический символ для 1-битного полного сумматора с C in и C out, нарисованными на сторонах блока, чтобы подчеркнуть их использование в многобитном сумматоре
Полный сумматор добавляет двоичные числа и счета для значений , переносимых в, так и снаружи. Один-бит полный сумматор добавляет три один-битных чисел, часто пишется как A , B и C в ; A и B — это операнды, а C in — это бит, перенесенный из предыдущего менее значимого этапа. [2] Полный сумматор обычно является компонентом каскада сумматоров, которые складывают 8, 16, 32 и т. Д. Двоичные числа. Схема выдает двухбитный выходной сигнал. Выходной перенос и сумма обычно представлены сигналами C out и S , где сумма равна 2 C out. + S .
Полный сумматор может быть реализован множеством различных способов, например, с помощью специальной схемы на уровне транзистора или составлен из других вентилей. Один пример реализации: S = A ⊕ B ⊕ C in и C out = ( A ⋅ B ) + ( C in ⋅ ( A ⊕ B )) .
В этой реализации последний логический элемент ИЛИ перед выходом переноса может быть заменен логическим элементом исключающее ИЛИ без изменения результирующей логики. Использование только двух типов вентилей удобно, если схема реализуется с использованием простых микросхем интегральной схемы, которые содержат только один тип вентилей на микросхему.
Полный сумматор также может быть построен из двух полусумматоров, подключив A и B ко входу одного полусумматора, затем взяв его суммарный выход S в качестве одного из входов для второго полусумматора и C в качестве другого входа, и наконец, выходы переноса двух полусумматоров подключаются к логическому элементу ИЛИ. Суммарный выход второго полусумматора — это конечный суммарный выход ( S ) полного сумматора, а выход логического элемента ИЛИ — это конечный выход переноса ( C out ). Критический путь полного сумматора проходит через оба логических элемента XOR и заканчивается на суммирующем бите s. . Предполагая, что вентиль XOR занимает 1 задержку для завершения, задержка, вызванная критическим путем полного сумматора, равна
Критический путь переноса проходит через один вентиль XOR в сумматоре и через 2 логических элемента (AND и OR) в блоке переноса, и поэтому, если логическим элементам AND или OR требуется 1 задержка для завершения, задержка составляет
Таблица истинности для полного сумматора:
| Входы | Выходы | |||
|---|---|---|---|---|
| А | B | C в | C из | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Сумматоры, поддерживающие несколько битов [ править ]
Сумматор с переносом пульсации [ править ]
Можно создать логическую схему, используя несколько полных сумматоров для добавления N- битных чисел. Каждый полный сумматор вводит C in , который является C из предыдущего сумматора. Этот вид сумматора называется сумматором с пульсационным переносом (RCA), поскольку каждый бит переноса «пульсирует» до следующего полного сумматора. Обратите внимание, что первый (и только первый) полный сумматор может быть заменен полусумматором (при условии, что C in = 0).
Компоновка сумматора с волновым переносом проста, что позволяет сократить время разработки; однако сумматор с переносом пульсаций работает относительно медленно, поскольку каждый полный сумматор должен ждать, пока бит переноса будет вычислен из предыдущего полного сумматора. Задержка затвора может быть легко вычислен путем проверки полной суммирующей схемы. Каждый полный сумматор требует трех уровней логики. В 32-битном сумматоре с переносом пульсации имеется 32 полных сумматора, поэтому задержка критического пути (наихудший случай) равна 3 (от входа до переноса в первом сумматоре) + 31 × 2 (для распространения переноса в последних сумматорах) = 65 задержки выхода на посадку. [3] Общее уравнение для задержки наихудшего случая для n -битного сумматора пульсации переноса, учитывающее как сумму, так и биты переноса, выглядит следующим образом:
Т CRA ( п ) знак равно Т HA + ( п — 1 ) ⋅ Т c + Т s знак равно Т FA + ( п — 1 ) ⋅ Т c знак равно 3 D + ( п — 1 ) ⋅ 2 D знак равно ( 2 п + 1 ) ⋅ D . >(n)=T_>+(n-1)cdot T_>+T_>=T_>+(n-1)cdot T_=3D+(n-1)cdot 2D=(2n+1)cdot D.>
Конструкция с чередующимися полярностями переноса и оптимизированными вентилями И-ИЛИ-Инвертировать может работать примерно в два раза быстрее. [4]
Сумматор с упреждением [ править ]
Чтобы сократить время вычислений, инженеры разработали более быстрые способы сложения двух двоичных чисел с помощью сумматоров с упреждающим переносом (CLA). Они работают, создавая два сигнала ( P и G ) для каждой битовой позиции в зависимости от того, распространяется ли перенос из менее значимой битовой позиции (по крайней мере, один вход равен 1), генерируемых в этой битовой позиции (оба входа равны 1 ) или убит в этой битовой позиции (оба входа равны 0). В большинстве случаев P — это просто выход суммы полусумматора, а G — выход переноса того же сумматора. После того, как сгенерированы P и G, создаются переносы для каждой битовой позиции. Некоторые передовые архитектуры с упреждающим просмотром — это Манчестерская цепь переноса , сумматор Брента – Кунга (BKA) [5] и сумматор Когге – Стоуна (KSA). [6] [7]
Некоторые другие архитектуры многобитового сумматора разбивают сумматор на блоки. Можно изменять длину этих блоков в зависимости от задержки распространения схем для оптимизации времени вычислений. Эти блочные сумматоры включают сумматор пропуска переноса (или обхода переноса), который будет определять значения P и G для каждого блока, а не каждого бита, и сумматор выбора переноса, который предварительно генерирует сумму и значения переноса для любого возможного переноса. введите (0 или 1) в блок, используя мультиплексоры для выбора соответствующего результата, когда известен бит переноса.
Комбинируя несколько сумматоров с опережающим переносом, можно создавать сумматоры еще большего размера. Это можно использовать на нескольких уровнях для создания еще более крупных сумматоров. Например, следующий сумматор представляет собой 64-битный сумматор, который использует четыре 16-битных CLA с двумя уровнями блоков опережающего переноса .
Другие конструкции сумматор включают кэрри-выберите гадюка , условная сумма сумматор , кэрри-пропуском сумматор и кэрри-полный сумматор.
Сумматоры Carry-save [ править ]
Если схема сложения должна вычислять сумму трех или более чисел, может быть полезно не распространять результат переноса. Вместо этого используются трехвходовые сумматоры, генерирующие два результата: сумму и перенос. Сумма и перенос могут подаваться на два входа последующего сумматора с 3 числами, не дожидаясь распространения сигнала переноса. Однако после всех этапов сложения необходимо использовать обычный сумматор (например, волновой перенос или опережающий просмотр) для объединения окончательной суммы и результатов переноса.
3: 2 компрессора [ править ]
Полный сумматор можно рассматривать как компрессор с потерями 3: 2 : он суммирует три однобитовых входа и возвращает результат как одно двухбитное число; то есть он отображает 8 входных значений на 4 выходных значения. Таким образом, например, двоичный вход 101 дает результат 1 + 0 + 1 = 10 (десятичное число 2). Выполнение представляет собой один бит результата, а сумма представляет собой нулевой бит. Точно так же полусумматор можно использовать как компрессор с потерями 2: 2 , сжимая четыре возможных входа в три возможных выхода.
Такие компрессоры можно использовать для ускорения суммирования трех или более слагаемых. Если слагаемых ровно три, макет называется сумматором с сохранением переноса . Если слагаемых четыре или более, необходимо более одного уровня компрессоров, и существуют различные возможные конструкции для контура: наиболее распространенными являются деревья Дадды и Уоллеса . Этот вид схемы чаще всего используется в умножителях , поэтому эти схемы также известны как умножители Дадды и Уоллеса.