Что такое сумма ряда

Сумма ряда

Пуская задано числовую последовательность $a_1, a_2,dots _n,dots ,$ тогда выражение:

$a_1+ a_2+dots _n+dots =sumlimits^_$называется числовым рядом.

Введем понятия частичных сумм ряда: $S_1= a_1, S_2=a_1+a_2, S_3=a_1+a_2+a_3,dots ,S_n=a_1+a_2+a_3+dots + a_n, dots .$ Эти частичные суммы образуют некоторую числовую последовательность $left(S_nright).$

Если последовательность частичных сумм $S_n$ ряда при неограниченном возрастании $n$, стремится к некоторому числу $S$, то есть:

$_ S_n= >S,$то этот ряд называется сходящимся, а число $S$ — его суммой.

В этом случае записывают:

В противоположном случае ряд называют расходящимся. Если

$_ S_n= >infty ,$то говорят, что расходящийся ряд имеет бесконечную сумму.

Последовательность $left right>$ называется ограниченной сверху, если существует такое число М, $Min $R, что $a_n

Последовательность $left right>$ называется ограниченной, если она ограничена как снизу, так и сверху, т.е. существует такое число М $ > 0$.

($Min $R), что $forall n:, , , left|a_ right|le M$.

Число а называется пределом последовательности $left right>$,если для любого сколь угодно малого положительного числа $varepsilon $найдётся такой номер $n_ in $N, зависящий от $varepsilon $, что для всех натуральных чисел $nge n_ $ выполняется неравенство $left|a_ -aright|

Готовые работы на аналогичную тему

Тогда $a=mathoplimits_ a_ , $означает, что $forall >0, , , exists n<>_ =n_ ()in $N такое, что для всех $nge n_ ,, , nin $N: $left|a_ -aright|

Приведём некоторые свойства сходящихся последовательностей.

• Если последовательность имеет предел, то он единственен.
• Если последовательность имеет конечный предел, то эта последовательность ограничена.
• Если последовательность возрастает (убывает) и ограничена сверху (снизу), то она имеет конечный предел.
• Если последовательность возрастает (убывает) и не ограничена сверху (снизу), то она имеет бесконечный предел + $infty$ (- $infty$).

Основные свойства сходящихся рядов

Ряды (1) и (2) одновременно сходятся или расходятся, причем если ряд (1) сходится до $S$, то ряд (2) сходится к

[R_n=S-left(a_1+ a_2+dots _nright).]

Присоединение или откидывание конечного числа первых членов не влияет на сходимость или расходимость ряда.

Остаток ряда $R_nto 0,$ если $nto infty $.

Действительно, если в равенстве $R_n= S-S_n$ перейти в пределу при $nto infty $, то

Если ряд (1) сходится и его сумма $S$, то ряд

$sumlimits^__n>,$где $c=const$, также сходится и его сумма равняется $cS.$

Сходящиеся ряды можно пожно почленно суммировати и отнимать, тоесть если ряды:

$sumlimits^_ sumlimits^_$сходятся и имеют соответствующие суммы A, B, то сходятся также и ряды

$sumlimits^_<<(a>_npm b_n)> $и суммы суммы их равняются $A pm B$.

Решение. Подсчитаем $S_ $:

Найти сумму ряда $sum limits _^left(sqrt -2sqrt +sqrt right) $.

Пользуясь определением суммы ряда и раскрывая неопределённость вида $left(infty -infty right)$, при вычислении предела, получим:

Исследовать на сходимость ряд

и найти его сумму.

Решение. Обозначим $frac =a_ $ общий член ряда. Тогда частичная сумма ряда $S_ =a_ +a_ +. +a_ =frac +frac +, . , +frac $. Так как $frac =frac -frac $, то $S_ =left(1-frac right)+left(frac -frac right)+ldots +left(frac -frac right)=1-frac $. Тогда $mathoplimits_ S_ =mathoplimits_ left(1-frac right)=1, ,

Исследовать на сходимость ряд

и найти его сумму.

Решение. Обозначим $frac +4n-3> =a_ $ общий член ряда. Тогда,частичная сумма ряда $S_ =frac +frac +, . , +frac +4n-3> $. Так как

Сумма ряда

Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится [1] . Элементы ряда представляют собой комплексные числа (в частности, вещественные).

Содержание

Определение

Пусть ^infty a_i=a_1+a_2+ldots» width=»» height=»» /> — числовой ряд. Число называется n-ой частичной суммой ряда ^infty a_i» width=»» height=»» />.

Сумма (числового) ряда — это предел частичных сумм , если он существует и конечен. Таким образом, если существует число sum_^a_i» width=»» height=»» />, то в этом случае пишут ^a_i=S» width=»» height=»» />. Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.

Сходимость числовых рядов

Свойство 1. Если ряд

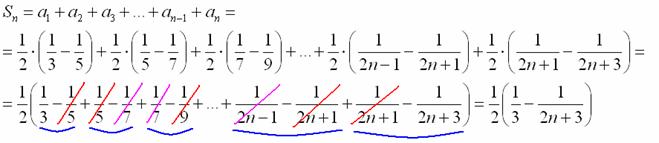
Почти все слагаемые частичной суммы благополучно взаимоуничтожаются:

Прямо такие пометки и делаем карандашом в тетради. Чертовски удобно.

Осталось вычислить элементарный предел и узнать сумму ряда:

Ответ:

Аналогичный ряд для самостоятельного решения:

Вычислить сумму ряда

Примерный образец чистового оформления решения в конце урока.

Очевидно, что нахождение суммы ряда – это само по себе доказательство его сходимости (помимо признаков сравнения, Даламбера, Коши и др.), о чём, в частности, намекает формулировка следующего задания:

Найти сумму ряда или установить его расходимость

По внешнему виду общего члена можно сразу сказать, как ведёт себя этот товарищ. Без комплексов. С помощью предельного признака сравнения легко выяснить (причём даже устно), что данный ряд будет сходиться вместе с рядом . Но перед нами редкий случай, когда без особых хлопот рассчитывается ещё и сумма.

Решение: разложим знаменатель дроби в произведение. Для этого нужно решить квадратное уравнение:

Множители лучше расположить в порядке возрастания: .

Выполним промежуточную проверку:

Таким образом, общий член ряда:

Коэффициенты получились целые и это радует:

На всякий случай выполним ещё одну промежуточную проверку:

Поэтапные проверки – королевы зачётов

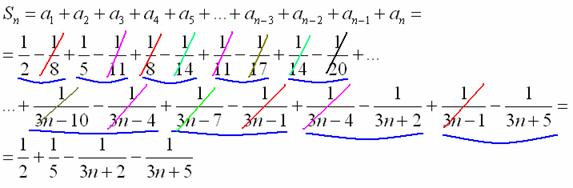
Составим энную частичную сумму и уничтожим всё, что можно уничтожить:

Как видите, в этот раз противоположные числа не расположены рядышком. Поэтому на практике всегда лучше перестраховаться и записать побольше членов ряда – чтобы наверняка понять, какие слагаемые исчезнут, а какие – нет. По той же причине крайне желательно выполнять пометки карандашом.

Опыт показывает, что чаще всего студенты испытывают затруднения с хвостом суммы. В этой связи ещё раз повторим принцип, по которому записаны члены . Отчего ж не повторить?

В общий член ряда :
– ВМЕСТО «эн» подставляем : ;
– ВМЕСТО «эн» подставляем : ;
– ВМЕСТО «эн» подставляем : .

На завершающем этапе находим сумму ряда:

Ответ:

Изящный ряд для самостоятельного решения:

Найти сумму ряда или установить его расходимость

Решение и ответ в конце урока.

Вероятно, на этом рубеже у многих посетителей возникла уверенность в своих навыках и желание раствориться на просторах Интернета. Рекомендую немного задержаться, поскольку ниже по течению среди, казалось бы, такого однообразия приветливо моргают глазами большие крокодилы.

Усложняем задание и набиваем руку:

Вычислить сумму ряда

Решение: со знаменателем тут никаких проблем:

Множители, как я уже отмечал, целесообразно расположить в порядке возрастания.

Здесь на последних шагах проведено почленное сложение двух уравнений системы.

Что и требовалось проверить.

Запишем частичную сумму «эн» членов ряда, при этом обращаем внимание на тот факт, что «счётчик» ряда «начинает работать» с номера . Как и в предыдущих примерах, надёжнее растянуть кобру на приличную длину:

Однако если мы запишем в одну-две строчки, то всё равно будет довольно трудно сориентироваться в слагаемых (их таки 3 в каждом члене). И здесь нам на помощь придёт… геометрия. Заставим плясать змею под свою дудочку:

Да, прямо так и пишем в тетради один член под другим и прямо так их вычёркиваем. Кстати, собственное изобретение. Как понимаете, не от самого лёгкого задания в этой жизни =)

В результате зачистки получаем:

И, наконец, сумма ряда:

Ответ:

Вычислить сумму ряда

Это пример для самостоятельного решения.

Рассматриваемая задача, конечно, не радует нас разнообразием – на практике встречается либо бесконечно убывающая геометрическая прогрессия, либо ряд с дробно-рациональным общим членом и разложимым многочленом в знаменателе (к слову, далеко не каждый такой многочлен даёт возможность найти сумму ряда). Но, тем не менее, иногда попадаются необычные экземпляры, и по сложившейся доброй традиции я завершаю урок какой-нибудь любопытной задачей:

Вычислить сумму ряда, если она существует

Решение: формулировка уже интригует. Интересен тот факт, что все члены данного ряда отрицательны. Почему? На интервале логарифм меньше нуля, а за счёт аргумента при любом натуральном «эн» (начиная с ) мы каждый раз и попадаем в этот интервал.

Таким образом, если ряд сходится, то будет отрицательна и его сумма. Только вот есть мааааленькая проблемка – найти это значение, если оно существует =)

Алгоритм такой же, главное, догадаться, с какой стороны подступиться к решению. Предыдущий опыт подсказывает, что нужно попытаться представить общий член ряда в виде суммы двух или бОльшего количества слагаемых. Из этих соображений преобразуем выражение в скобках и используем свойства логарифма:

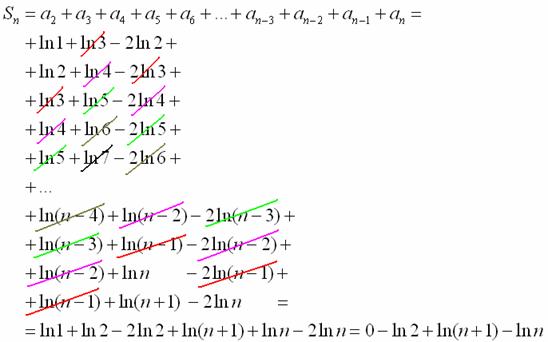
Ну что же, выглядит вполне перспективно, давайте разберёмся с частичной суммой ряда:

В целях устранения неопределённости вновь используем свойство логарифма:

Получено конечное число, а значит, ряд сходится. Как и ожидалось, сумма получилась отрицательной.

Ответ:

Поздравляю со знаменательным событием! Коль скоро вы читаете эти строки, то сегодня на вашу долю выпал редкий и счастливый случай – когда в частичной сумме ряда удалось массово ликвидировать слагаемые. Удалось же? =)

Не каждый день бывает! Но то ли ещё будет

Решения и ответы:

Пример 2: Решение:

Дважды используем формулу для нахождения суммы бесконечно убывающей геометрической прогрессии: .
Для первого ряда: , для второго ряда: .

Ответ: сумма ряда

Пример 4: Решение: Методом неопределенных коэффициентов разложим общий член ряда в сумму дробей:

Таким образом:

Найдём частичную сумму ряда:

Вычислим сумму ряда:

Ответ:

Пример 6: Решение: разложим знаменатель общего члена в произведение и методом неопределённых коэффициентов получим сумму дробей:

Таким образом:
Составим частичную сумму и проведём упрощения:

Вычислим сумму ряда:

Ответ:

Пример 8: Решение: представим общий член ряда в виде:

Методом неопределённых коэффициентов разложим его в сумму дробей:

Таким образом:
Запишем частичную сумму:

Вычислим сумму ряда:

Ответ:

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Zaochnik.com – профессиональная помощь студентам,

cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys

© Copyright mathprofi.ru, Александр Емелин, 2010-2022. Копирование материалов сайта запрещено

Нахождение суммы числового ряда. Первая часть.

В теме про основные понятия числовых рядов было указано определение суммы ряда. Вот оно:

Если существует конечный предел $S=lim_S_n$, то его называют суммой ряда $sumlimits_^u_n$ и сам ряд именуют сходящимся. Если же $lim_S_n=infty$ или $lim_S_n$ не существует, то ряд называют расходящимся.

Если понятие «частичная сумма» вызывает вопросы, то советую посмотреть раздел про частичную сумму ряда, обратив внимание на пример №4. В этом примере подробно раскрывается суть частичной суммы и остатка.

В данной теме нас будет интересовать вопрос нахождения сумм числовых рядов по определению. Определение суммы ряда опирается на значение $lim_S_n$, поэтому для нахождения суммы нам нужно выполнить два шага:

1. Составить n-ю частичную сумму $S_n$;
2. Найти $lim_S_n$ (если он существует).

Если конечный $lim_S_n$ существует, то его значение и будет суммой рассматриваемого ряда, а сам ряд будет именоваться сходящимся. Если же $lim_S_n=infty$ или $lim_S_n$ не существует, то ряд будет расходиться. Есть несколько стандартных приёмов, которые применяются для нахождения суммы числовых рядов. Например, для нахождения суммы ряда, общий член которого имеет вид рациональной дроби $u_n=frac$, вполне подходит такой алгоритм:

1. Разложить дробь $frac$ на элементарные дроби (процедура разложения описана тут).
2. Записать выражение для частичной суммы $S_n$, используя результаты предыдущего пункта.
3. Перегруппировать слагаемые в выражении для $S_n$, приведя их к удобному для сокращения виду.
4. Используя результат предыдущего пункта, найти $lim_S_n$.

Для нахождения суммы ряда нередко удобно использовать и такое свойство:

Пусть общий член ряда $sumlimits_^u_n$ можно представить в виде $u_n=b_-b_n$. Если существует конечный предел $lim_b_n=b$, то ряд $sumlimits_^u_n$ сходится. При этом частичная сумма ряда равна $S_=b_-b_1$, а сумма ряда $S=b-b_1$.

Доказательство этого свойства может быть интересно не всем читателям, поэтому я скрою его под примечание.

Запишем частичную сумму ряда $sumlimits_^u_n$. Так как $u_n=b_-b_n$, то будем иметь:

Как видите, выражения под знаком сумм одинаковы. Сделаем одинаковыми и пределы суммирования. Прибавляя и вычитая $b_1$, для первой суммы получим:

Аналогично, прибавляя и вычитая $b_$ для второй суммы получим:

Вернёмся к сумме $S_n$:

Так как $lim_b_n=b$, то и $lim_b_=b$. Тогда $lim_S_n$ будет таким:

Во всех изложенных ниже примерах члены рядов будем обозначать буквами $u_1$ (первый член ряда), $u_2$ (второй член ряда) и так далее. Запись $u_n$ будет обозначать общий член ряда.

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=(-1)^$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов числового ряда:

Вопрос в следующем: чему равна эта сумма? Если в частичных суммах мы станем брать чётное количество слагаемых, они попарно сократятся:

Итак, частичная сумма, содержащая чётное количество слагаемых, равна 0. Т.е. если $n$ – чётное число, то $S_n=0$. Фразу «n – чётное число» можно записать так: $n=2k$, $kin N$. В самом деле, подставляя вместо $k$ значения 1, 2, 3, 4 будем получать $n=2cdot 1=2$, $n=2cdot 2=4$, $n=2cdot 3=6$, $n=2cdot 4=8$ и так далее. Итак, $S_=0$.

Если мы станем брать нечётное количество слагаемых (1, 3, 5 и т.д.), то сумма станет равна 1:

Таким образом, если $n$ – нечётное число, то $S_n=1$. Фразу «n – нечётное число» можно записать так: $n=2k-1$, $kin N$. В самом деле, подставляя вместо $k$ значения 1, 2, 3, 4 будем получать $n=2cdot 1-1=1$, $n=2cdot 2-1=3$, $n=2cdot 3-1=5$, $n=2cdot 4-1=7$ и так далее. Итак, $S_=1$.

Формально равенство $S_=1$ можно доказать с помощью формулы $S_=S_+u_$. Так как $S_=0$, то $S_+u_=0$, т.е. $S_=-u_$. Так как $u_=(-1)^=left((-1)^2right)^kcdot (-1)^1=-1$, то $S_=-(-1)=1$.

Возникает вопрос: как быть с пределом $lim_S_n$? Ведь если $n$ – чётное число, т.е. $n=2k$, то:

С другой стороны, если $n$ – нечётное число, то:

Что мы получили? А получили мы следующее: последовательность частичных сумм $$ имеет две подпоследовательности: $\>$ и $\>$, пределы которых различны. Следовательно, последовательность $$ не имеет предела. Вывод: ряд не имеет суммы, т.е. расходится.

Здесь стоит обратить внимание вот на что: следует различать случаи, когда предел равен бесконечности (см. следующий пример №2), и когда предела попросту не существует. Хотя и в том и в другом случаях ряд будет расходиться.

Ответ: ряд расходится.

Найти сумму ряда $sumlimits_^(3n+1)$.

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=3n+1$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов заданного числового ряда:

Эту сумму можно записать в более коротком виде. Дело в том, что последовательность 4, 7, 10, 13 и т.д. есть арифметическая прогрессия, первый член которой равен 4, а разность равна 3. Сумма первых n членов этой прогрессии такова:

Так как $lim_S_n=+infty$, то ряд расходится.

Если немного выйти за рамки данной темы, то стоит отметить, что расходимость этого ряда легко доказывается с помощью необходимого признака сходимости.

Ответ: ряд расходится.

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов заданного числового ряда:

Почему я пишу именно $frac$, а не $frac$, будет ясно из дальнейшего повествования. Однако запись частичной суммы ни на йоту не приблизила нас к цели. Нам ведь нужно найти $lim_S_n$, но если мы просто запишем:

то эта запись, совершенно верная по форме, ничего нам не даст по сути. Чтобы найти предел, выражение частичной суммы предварительно нужно упростить.

Для этого есть стандартное преобразование, состоящее в разложении дроби $frac$, которая представляет общий член ряда, на элементарные дроби. Вопросу разложения рациональных дробей на элементарные посвящена отдельная тема (см., например, пример №3 на этой странице). Раскладывая дробь $frac$ на элементарные дроби, будем иметь:

Приравниваем числители дробей в левой и правой частях полученного равенства:

Чтобы найти значения $A$ и $B$ есть два пути. Можно раскрыть скобки и перегруппировать слагаемые, а можно просто подставить вместо $n$ некие подходящие значения. Сугубо для разнообразия в этом примере пойдём первым путём, а следующем – будем подставлять частные значения $n$. Раскрывая скобки и перегруппировывая слагаемые, получим:

В левой части равенства перед $n$ стоит ноль. Если угодно, левую часть равенства для наглядности можно представить как $0cdot n+ 2$. Так как в левой части равенства перед $n$ стоит ноль, а в правой части равества перед $n$ стоит $2A+2B$, то имеем первое уравнение: $2A+2B=0$. Сразу разделим обе части этого уравнения на 2, получив после этого $A+B=0$.

Так как в левой части равенства свободный член равен 2, а в правой части равенства свободный член равен $3A+B$, то $3A+B=2$. Итак, имеем систему:

Можно решать эту систему методом Крамера, методом Гаусса или с помощью обратной матрицы. Однако проще всего банально выразить из первого уравнения $A=-B$ и подставить во второе:

Так как $B=-1$, то $A=-B=1$. Подставляя найденные значения $A=1$ и $B=-1$ в формулу $frac=frac+frac$, будем иметь:

Итак, $u_n=frac-frac$. Используем полученное разложение для того, чтобы упростить формулу частичной суммы ряда. Покажу сначала решение стандартным путём, принятым в большинстве решебников и методичек.

Первый способ упрощения формулы для частичной суммы.

Мы получили разложение общего члена ряда на две дроби: $u_n=frac-frac$. Чтобы этот результат был более наглядным, я распишу несколько первых членов ряда по этой формуле:

Давайте распишем частичную сумму, учитывая полученное разложение каждого элемента:

Как видите, все слагаемые этой суммы сокращаются, – кроме первого и последнего:

Итак, $S_n=frac-frac$. Этот способ упрощения формулы для частичной суммы имеет простую суть: разложить общий член ряда на элементарные дроби, а потом сократить слагаемые.

Однако можно ли считать вышеуказанные рассуждения строгим доказательством? Полагаю, что в общем случае нет, и поясню почему. Дело в том, что мы должны «увидеть» (как любят писать некоторые авторы – «легко увидеть»), что слагаемые сокращаются. А если мы «увидим» не все слагаемые, которые останутся после сокращения? Где гарантии, что мы сократим именно то, что нужно? Нет гарантий. Понятно, что в случае рассматриваемой конкретной задачи всё тривиально и очевидно, но далеко не все частичные суммы рядов имеют такую простую структуру.

Формулу $S_n=frac-frac$ можно принять в качестве гипотезы, которую ещё нужно доказать. Доказательство удобнее всего проводить методом математической индукции. Так как доказательством заинтересуются не все читатели, то я его скрыл под примечание.

Доказательство будем проводить методом математической индукции. На первом шаге нужно проверить, выполнено ли доказываемое равенство $S_n=frac-frac$ при $n=1$. Мы знаем, что $S_1=u_1=frac$, но даст ли выражение $frac-frac$ значение $frac$, если подставить в него $n=1$? Проверим:

Итак, при $n=1$ равенство $S_n=frac-frac$ выполнено. На этом первый шаг метода математической индукции закончен.

Предположим, что при $n=k$ равенство выполнено, т.е. $S_k=frac-frac$. Докажем, что это же равенство будет выполнено при $n=k+1$. Для этого рассмотрим $S_$:

Так как $u_n=frac-frac$, то $u_=frac-frac=frac-frac$. Согласно сделанному выше предположению $S_k=frac-frac$, поэтому формула $S_=S_k+u_$ примет вид:

Вывод: формула $S_n=frac-frac$ верна при $n=k+1$. Следовательно, согласно методу математической индукции, формула $S_n=frac-frac$ верна при любом $nin N$. Равенство доказано.

В стандартном курсе высшей математики обычно довольствуются «вычёркиванием» сокращающихся слагаемых, не требуя никаких доказательств. Итак, мы получили выражение для n-й частичной суммы: $S_n=frac-frac$. Найдём значение $lim_S_n$:

Вывод: заданный ряд сходится и сумма его $S=frac$.

Второй способ упрощения формулы для частичной суммы.

Этот способ основан на свойстве, записанном в начале страницы. По сути, он схож с предыдущим, – разница лишь в применении уже готовой теоремы, доказанной нами ранее. Вернёмся к записи общего члена ряда:

Обозначим $b_n=frac$, тогда $b_=frac=frac$. Таким образом, $u_=b_-b_$. При этом $lim_b_n=0$. Согласно упомянутому свойству, ряд $sumlimits_^u_n$ сходится. При этом его сумма равна $S=0-b_1=frac$. Если есть необходимость, можно записать и частичную сумму ряда:

Третий способ упрощения формулы для частичной суммы.

Честно говоря, я сам предпочитаю большей частью именно этот способ Давайте запишем частичную сумму в сокращённом варианте:

Мы получили ранее, что $u_k=frac-frac$, поэтому:

Сумма $S_n$ содержит конечное количество слагаемых, поэтому мы можем переставлять их так, как нам заблагорассудится. Я хочу сначала сложить все слагаемые вида $frac$, а уж затем переходить к слагаемым вида $frac$. Это означает, что частичную сумму мы представим в таком виде:

Конечно, развёрнутая запись крайне неудобна, поэтому представленное выше равенство оформим более компактно:

Теперь преобразуем выражения $frac$ и $frac$ к одному виду. Приведём, например, дробь $frac$ к виду $frac$. Выражение в знаменателе дроби $frac$ я представлю в таком виде:

И сумму $sumlimits_^frac$ теперь можно записать так:

Если равенство $sumlimits_^frac=sumlimits_^frac$ не вызывает вопросов, то пойдём далее. Если же вопросы есть, то прошу развернуть примечание.

Как мы получили преобразованную сумму? показатьскрыть

У нас был ряд $sumlimits_^frac=sumlimits_^frac$. Давайте вместо $k+1$ введём новую переменную, – например, $t$. Итак, $t=k+1$.

Как изменялась старая переменная $k$? А изменялась она от 1 до $n$. Давайте выясним, как же будет изменяться новая переменная $t$. Если $k=1$, то $t=1+1=2$. Если же $k=n$, то $t=n+1$. Итак, выражение $sumlimits_^frac$ теперь стало таким: $sumlimits_^frac$.

У нас есть сумма $sumlimits_^frac$. Вопрос: а не всё ли равно, какую букву использовать в этой сумме? Банально записывая букву $k$ вместо $t$, получим следующее:

Вот так и получается равенство $sumlimits_^frac=sumlimits_^frac$.

Таким образом, частичную сумму можно представить в следующем виде:

Заметьте, что суммы $sumlimits_^frac$ и $sumlimits_^frac$ отличаются лишь пределами суммирования. Сделаем эти пределы одинаковыми. Начнём с первой суммы.

Сделаем так, чтобы верхний предел суммирования стал равен $n+1$. Если $k=n+1$, то $frac=frac$. Прибавляя и вычитая из первой суммы $frac$, получим:

Для второй суммы $sumlimits_^frac$ сделаем так, чтобы нижний предел суммирования был равен 1. Если $k=1$, то $frac=frac$. Прибавляя и вычитая $frac$, получим:

С учётом полученных результатов, выражение для $S_n$ примет такой вид:

Если пропустить все пояснения, то процесс нахождения сокращённой формулы для n-й частичной суммы примет такой вид:

Напомню, что мы приводили дробь $frac$ к виду $frac$. Разумеется, можно поступить и наоборот, т.е. представить дробь $frac$ в виде $frac$. Конечное выражение для частичной суммы не изменится. Процесс нахождения частичной суммы в этом случае я скрою под примечание.

Как найти $S_n$, если приводить к виду иной дроби? показатьскрыть

Заданный ряд сходится и сумма его $S=frac$.

Продолжение темы нахождения суммы ряда будет рассмотрено во второй и третьей частях.

Числовые ряды, их суммы, сходимость, примеры

Первое знакомство с числовыми рядами у наших читателей состоялось в средней школе при изучении арифметической прогрессии и геометрической прогрессии . Из этих уроков Вы узнали, что для задания этих последовательностей необходимо определить закон нахождения каждого члена последовательности, обычно записываемый в виде формулы.

Если u 1 , u 2 , u 3 , . u n , . — бесконечная последовательность чисел, то формально записанное выражение

называется бесконечным числовым рядом (или просто числовым рядом). Многоточие в конце (иногда шутят, что в нём-то и заключена суть ряда) указывает, что выражение (1) не имеет последнего слагаемого, за каждым слагаемым всегда стоит следующее. Таким образом, числовой ряд есть «бесконечная» сумма чисел.

Короче (с символом «сигма») числовой ряд (1) можно записать в виде

где индексы внизу и вверху символа суммы означают, что нужно взять сумму чисел u n , когда n принимает целочисленные значения от 1 до ∞.

Числа u 1 , u 2 , u 3 , . u n , . называются членами числового ряда, а член ряда, стоящий на n-м месте от начала, — его общим членом.

Примерами числовых рядов могут служить:

Задать числовой ряд – это значит указать правило, закон образования его членов, по которому можно найти любой его член ( ещё раз вспомните школьные уроки об арифметической и геометрической прогрессиях ). Чаще всего числовой ряд задаётся формулой общего члена как функция от натурального числа n. Например, если , то тем самым определён следующий числовой ряд:

если то получим числовой ряд

Если в дальнейшем будем говорить, что дан числовой ряд, то будем подразумевать, что задан его общий член.

Пример 1. Записать первые пять членов числового ряда, если дана формула его общего члена:

Решение. Подставляем в формулу вместо n последовательно числа 1, 2, 3, 4, 5. Получаем:

Пример 2. Записать формулу общего члена числового ряда, если даны пять его первых членов:

Решение. Ищем закономерность образования членов ряда. Нетрудно заметить, что знаменатель является числом 3 в некоторой степени. Для первого члена ряда степень равна нулю, то есть 1 — 1, для второго члена степень равна 1, то есть 2 — 1, для пятого — 4, то есть 5 — 1. Следовательно, степень числа три равна n — 1. В свою очередь, в числителе число всегда на 2 меньше 3n. Следовательно, формула общего члена ряда:

Решить задачи на числовые ряды самостоятельно, а затем посмотреть решения

Пример 3. Записать первые 3 члена ряда и .

Пример 4. Определить общий член ряда

Сумма числового ряда

При сложении конечного числа слагаемых всегда получается определённый числовой результат, вычислить же сумму бесконечного числа слагаемых не может ни человек, ни компьюьтер, поскольку процесс сложения членов числового ряда (по самому определению) никогда не кончается.

Это означает, что выражение (1) является формальным, ведь сумма бесконечного числа слагаемых не определена. Но тем не менее в этом выражении поставлен знак суммирования и подразумевается, что члены ряда как-то складываются. Сумма любого конечного числа слагаемых будет найдена, если их складывать последовательно по одному. Это приводит к мысли поставить в соответствие числовому ряду некоторое число и назвать его суммой числового ряда. С этой целью вводят понятие частичной суммы ряда.

Приближенные суммы числового ряда (1)

называются частичными суммами числового ряда.

Сумма n первых членов числового ряда называется n-й частичной суммой:

Частичные суммы числового ряда имеют конечное число слагаемых, это «обычные» суммы, их можно найти, подсчитать. Для числового ряда получаем бесконечную последовательность его частичных сумм.

Понятие сходимости числовых рядов

Если значения частичных сумм при неограниченном возрастании n, то есть, при стремятся к некоторому числу S, то есть имеет предел

то числовой ряд называется сходящимся.

Это число S называется суммой числового ряда. В этом смысле можно записать такое равенство:

Пример сходящегося числового ряда:

Не для всякого числового ряда последовательность его частичных сумм стремится к определённому пределу. Например, для ряда

частичные суммы принимают попеременно значения 1 и 0:

Если предел последовательность частичных сумм ряда не существует, то числовой ряд называется расходящимся. Расходящийся ряд суммы не имеет.

Пример 5. Определить частичную сумму числового ряда

разложив общий член ряда на элементарные дроби с помощью метода неопределённых коэффициентов, и найти сумму ряда.

Решение. Разложим общий члена ряда на элементарные дроби:

Так как дроби равны и знаменатели равны, числители также должны быть равны:

Это равенство в силе для всех n:

Частичная сумма ряда:

Пример 6. Исследовать сходимость числового ряда (2) .

Решение. Составим частичные суммы ряда:

Представим их в виде

Нетрудно заметить закономерность в образовании частичных сумм: каждая представляет разность между единицей и дробью, числитель которой 1, а знаменатель n-й частичной суммы равен n + 1, т.е.

Найдём предел последовательности частичных сумм:

Следовательно, числовой ряд (2) сходится, его последовательность равна 1.

Исследуем сходимость числового ряда (3):

который называется геометрическим, так как его члены представляют собой члены геометрической прогрессии, первый член которой равен a, а знаменатель q.

Рассмотрим частичную сумму этого ряда:

Она равна сумме членов геометрической прогрессии, если

Найдём предел последовательности частичных сумм геометрического ряда. Следует различать четыре возможности:

1. Если то , поэтому

2. Если то не существует, значит и последовательность частичных сумм не имеет предела.

3. Если q =1, то получается ряд a + a + a +. + . . Его n-я частичная сумма

в зависимости от знака a.

4. Если q = — 1, то получается ряд

Его частичные суммы попеременно равны a и 0:

и т.д. Но такая последовательность не имеет предела.

Мы выяснили, что геометрический ряд (3) сходится, если знаменатель меньше единицы:

причём его сумма равна

и расходится, если равен или больше единицы:

Пример 7. Исследовать сходимость числовых рядов:

Решение. Это геометрические ряды. Для ряда (*)

для ряда (***) q = 4/3; для ряда (****) q = — 1. Следовательно, первые два ряда сходятся, а последние два расходятся.

Пример 8. Опредедить, сходится ли числовой ряд

В случае положительного ответа найти его сумму.

Решение. Данный ряд является геометрическим рядом с первым членом и . Так как , ряд сходится. Сумму ряда найдём по формуле суммы геометрического ряда .

Установить сходимость ряда самостоятельно, а затем посмотреть решение

Пример 9. Установить, сходится ли ряд

Свойства сходящихся числовых рядов

Пусть дан ряд с общим членом . Тогда ряд с общим членом , то есть ряд

называют произведением ряда (1) на число c. Сходимость ряда (1) гарантирует сходимость и его произведения на число c. Это устанавливается следующей теоремой.

Теорема 1. Если ряд (1) сходится и имеет сумму, равную S, то его произведение на число c также сходится и имеет сумму, равную S:

Следовательно, общий множитель членов сходящихся рядов можно выносить за скобки, имея при этом в виду выполнение равенства (12).

Пусть даны два ряда с общими членами и :

Тогда ряд с общим членом

называют суммой этих рядов:

Теорема 2. Сумма двух сходящихся рядов есть сходящийся ряд, причём его сумма равна

где S ‘ и S » — суммы слагаемых рядов:

Это означает, что сходящиеся ряды можно почленно складывать, а с учётом теоремы 1 и вычитать, имея при этом в виду для суммы рядов выполнение равенства (16), а для разности рядов – равенства

Определение. Разность суммы S и частичной суммы S n сходящегося числового ряда разывается остатком ряда и обозначается R n :

Для сходящегося ряда

то есть предел остатка сходящегося ряда при равен нулю.

Теорема 3. Если ряд сходится, то сходится и любой его остаток, и, наоборот, если сходится какой-либо остаток ряда, то и сам ряд также сходится.

Это означает, что на сходимость ряда не влияет любое конечное число его первых членов. В ряде можно отбрасывать или прибавлять к нему любое конечное число членов. От этого сходимость (или расходимость) ряда не нарушается, но меняется его сумма.

Если сходимость ряда установлена на основании определения сходимости, то одновременно будет найдена и его сумма. Так мы поступили при исследовании сходимости рядов (2) и (3). Однако таким способом решить вопрос о сходимости ряда часто бывает весьма трудно. Поэтому используют другой способ, который даёт возможность лишь установить факт сходимости (расходимости) ряда, так как сумму сходящегося ряда можно всегда найти с любой степенью точности, подсчитав сумму достаточно большого числа его первых членов.

Пример 10. Найти сумму числового ряда

Решение. Из теорем 1 и 2 о свойствах сходящихся рядов следует:

если ряды и сходятся и и , то для любых действительных чисел α и β ряд также сходится и .

Приступим к признакам сходимости рядов.

Необходимый признак сходимости числового ряда

Теорема. Если ряд сходится, то предел его общего члена при

Следствие. Если предел общего члена ряда при

не равен нулю, то ряд расходится.

Пример 11. Используя необходимый признак сходимости, исследовать сходимость числового ряда

Решение. Общий член ряда

Найдём его предел при

Следовательно, данный ряд расходится.

Пример 12. Используя необходимый признак сходимости, исследовать сходимость числового ряда

Решение. Найдём предел общего члена ряда при

Так как (предел общего члена не равен нулю), данный ряд расходится.

Установить сходимость ряда самостоятельно, а затем посмотреть решение

Пример 13. Используя необходимый признак сходимости, установить, сходится ли ряд

Пример 14. Установить, сходится ли ряд

Пример 15. Записать первые пять членов числового ряда

и установить, сходится ли этот ряд.

Решение. Пять первых членов данного числового ряда:

Найдём предел общего члена ряда при

Так как (предел общего члена равен нулю), данный ряд сходится.

Мы выяснили, что если числовой ряд сходится, то предел его общего члена равен нулю, а значит, выполняется условие (17).

Однако выполнение условия (17) не гарантирует сходимости числового ряда, оно не является достаточным для этого. Есть расходящиеся ряды, пределы общих членов которых при

Примером такого ряда служит ряд (4):

который называется гармоническим. Последовательность его частичных сумм

монотонно возрастает, поскольку члены ряда положительны. Покажем, что она возрастает неограниченно. Для этого члены гармонического ряда, начиная с третьего, объединим в группы:

В первую включим два члена (3-й и 4-й), во вторую

члена (с 5-го по 8-й), в третью

членов (с 9-го по 16-й) и т.д, каждый раз увеличивая вдвое число членов в группе. Таких групп, очевидно, бесконечное множество. Если заменить члены ряда в каждой группе их последними членами, то сумма членов этой группы уменьшится и тогда справедливы неравенства

Сумма членов каждой группы больше 1/2, а сумма членов, включённых в достаточно большое число групп, как угодно велика. Следовательно, последовательность частичных сумм гармонического ряда неограниченно возрастает, а ряд расходится, хотя его общий член

стремится к нулю.

Заметим, что частичные суммы гармонического ряда возрастают хотя и ограниченно, но медленно.

Исследование сходимости ряда обычно начинают с проверки выполнения условия (17), чтобы сразу выделить расходящиеся ряды, для которых это условие не выполняется. Однако выполнение этого условия говорит лишь о том, что ряд может сходиться. Сходится он или расходится, должно показать дополнительное исследование с помощью достаточных признаков, рассмотрение которых дано в последующих урока раздела «Ряды».

Что такое сумма ряда

РЯДЫ. Многие задачи в математике приводят к формулам, содержащим бесконечные суммы, например,

Такие суммы называются бесконечными рядами, а их слагаемые – членами ряда. (Многоточие означает, что число слагаемых бесконечно.) Решения сложных математических задач редко удается представить в точном виде посредством формул. Однако в большинстве случаев эти решения можно записать в виде рядов. После того, как такое решение найдено, методы теории рядов позволяют оценить, сколько членов ряда необходимо взять для конкретных вычислений или как записать ответ в наиболее удобном виде. Наряду с числовыми рядами мы можем рассматривать т.н. функциональные ряды, слагаемыми которых являются функции. Многие функции можно представить с помощью функциональных рядов. Изучение числовых и функциональных рядов является важной частью математического анализа.

В примерах (1) и (2) сравнительно легко догадаться, по какому закону образуются последовательные члены. Закон образования членов ряда может быть гораздо менее очевидным. Например, для ряда (3) он станет ясен, если этот ряд записать в следующем виде:

Сходящиеся ряды.

Поскольку сложение бесконечного числа членов ряда физически невозможно, необходимо определить, что именно следует понимать под суммой бесконечного ряда. Можно представить себе, что указанные операции сложения и вычитания выполняются последовательно, одна за другой, например, на компьютере. Если возникающие при этом суммы (частичные суммы) все ближе и ближе подходят к некоторому числу, то это число разумно назвать суммой бесконечного ряда. Таким образом, сумму бесконечного ряда можно определить как предел последовательности частичных сумм. При этом такой ряд называется сходящимся.

Найти сумму ряда (3) нетрудно, если заметить, что преобразованный ряд (4) можно записать в виде

Последовательные частичные суммы ряда (5) равны

и т.д.; можно заметить, что частичные суммы стремятся к 1. Таким образом, этот ряд сходится и его сумма равна 1.

В качестве примера бесконечных рядов можно рассматривать бесконечные десятичные дроби. Так, 0,353535. – это бесконечная периодическая десятичная дробь, являющаяся компактным способом записи ряда

Закон образования последовательных членов здесь понятен. Аналогично, 3,14159265. означает

но закон образования последующих членов ряда здесь неочевиден: цифры образуют десятичное разложение числа p, и трудно сразу сказать, какова, например, 100 000-я цифра, хотя теоретически эту цифру можно вычислить.

Расходящиеся ряды.

О бесконечном ряде, который не сходится, говорят, что он расходится (такой ряд называют расходящимся). Например, ряд

расходится, так как его частичные суммы равны 1/2, 1, 1 1 /₂, 2. Эти суммы не стремятся ни к какому числу как к пределу, поскольку, взяв достаточно много членов ряда, мы можем сделать частичную сумму сколь угодно большой. Ряд

также расходится, но по другой причине: частичные суммы этого ряда попеременно обращаются то в 1, то в 0 и не стремятся к пределу.

Суммирование.

Найти сумму сходящегося ряда (с заданной точностью), последовательно суммируя его члены, хотя теоретически и возможно, но практически трудно осуществимо. Например, ряд

сходится, и сумма его с точностью до десяти знаков после запятой равна 1,6449340668, но для того, чтобы вычислить ее с этой точностью, потребовалось бы взять ок. 20 млрд. членов. Такие ряды обычно суммируют, первоначально преобразуя их с помощью различных приемов. При этом используют алгебраические или вычислительные методы; например, можно показать, что сумма ряда (8) равна p 2 /6.

Обозначения.

Работая с бесконечными рядами, полезно иметь удобные обозначения. Например, конечную сумму ряда (8) можно записать как

Такая запись указывает на то, что n последовательно полагается равным 1, 2, 3, 4 и 5, а результаты складываются:

Аналогично, ряд (4) можно записать в виде

где символ Ґ указывает на то, что мы имеем дело с бесконечным рядом, а не с конечной его частью. Символ S (сигма) называют знаком суммирования.

Бесконечная геометрическая прогрессия.

Мы смогли просуммировать ряд (4), так как существовала простая формула для его частичных сумм. Аналогично, можно найти сумму ряда (2), или в общем виде,

если r принимает значения между –1 и 1. В этом случае сумма ряда (9) равна 1/(1 – r); при других значениях r ряд (9) расходится.

Можно рассматривать периодические десятичные дроби вроде 0,353535. как иной способ записи бесконечной геометрической прогрессии

Это выражение можно записать также в виде

где в скобках стоит ряд (9) с r = 0,01; следовательно, сумма ряда (10) равна

Тем же способом можно представить в виде обычной дроби любую периодическую десятичную дробь.

Признаки сходимости.

В общем случае простой формулы для частичных сумм бесконечного ряда не существует, так что для установления сходимости или расходимости ряда прибегают к специальным методам. Например, если все члены ряда положительны, то можно показать, что ряд сходится, если каждый его член не превосходит соответствующего члена другого ряда, о котором известно, что он сходится. В принятых обозначения это можно записать следующим образом: если a_n і 0 и сходится, то сходится, если 0 Ј b_n Ј a_n. Например, так как ряд (4) сходится и

то можно сделать вывод, что ряд (8) тоже сходится. Сравнение представляет собой основной метод, позволяющий устанавливать сходимость многих рядов, сопоставляя их с простейшими сходящимися рядами. Иногда используют более специальные признаки сходимости (их можно найти в литературе по теории рядов.) Приведем еще несколько примеров сходящихся рядов с положительными членами:

Сравнение можно использовать и для установления расходимости ряда. Если ряд расходится, то и ряд также расходится, если 0 Ј b_n Ј a_n.

Примерами расходящихся рядов могут служить ряды

и, в частности, т.к. гармонический ряд

В расходимости этого ряда можно убедиться, сосчитав следующие частичные суммы:

и т.д. Таким образом, частичные суммы, которые оканчиваются членами 1/4, 1/8, 1/16, 1/32, ј , превосходят частичные суммы расходящегося ряда (6), и поэтому ряд (14) должен расходиться.

Абсолютная и условная сходимости.

К таким рядам, как

метод сравнения неприменим, поскольку члены этого ряда имеют разные знаки. Если бы все члены ряда (15) были положительными, то мы получили бы ряд (3), о котором известно, что он сходится. Можно показать, что отсюда следует также сходимость ряда (15). Когда изменением знаков отрицательных членов ряда на противоположные его можно превратить в сходящийся, говорят, что исходный ряд сходится абсолютно.

Знакопеременный гармонический ряд (1) не является абсолютно сходящимся, т.к. ряд (14), состоящий из тех же, но только положительных членов, не сходится. Однако с помощью специальных признаков сходимости для знакопеременных рядов можно показать, что ряд (1) в действительности сходится. Сходящийся ряд, который не сходится абсолютно, называется условно сходящимся.

Операции с рядами.

Исходя из определения сходящегося ряда, легко показать, что его сходимость не нарушится от вычеркивания или приписывания к нему конечного числа членов, а также от умножения или деления всех членов ряда на одно и то же число (разумеется, деление на 0 исключается). При любой перестановке членов абсолютно сходящегося ряда его сходимость не нарушается, а сумма не меняется. Например, так как сумма ряда (2) равна 1, сумма ряда

также равна 1, поскольку этот ряд получается из ряда (2) перестановкой соседних членов (1-го члена со 2-м и т.д.). Можно как угодно изменять порядок следования членов абсолютно сходящегося ряда, лишь бы в новом ряду присутствовали все члены исходного. С другой стороны, перестановка членов условно сходящегося ряда может изменить его сумму и даже сделать его расходящимся. Более того, члены условно сходящегося ряда всегда можно переставить так, что он будет сходиться к любой заранее заданной сумме.

Два сходящихся ряда Sa_n и Sb_n можно почленно складывать (или вычитать), так что сумма нового ряда (который также сходится) складывается из сумм исходных рядов, в наших обозначениях

При дополнительных условиях, например, если оба ряда абсолютно сходятся, их можно умножать друг на друга, как это делается для конечных сумм, причем получающийся двойной ряд (см. ниже) будет сходиться к произведению сумм исходных рядов.

Суммируемость.

Несмотря на то, что принятое нами определение сходимости бесконечного ряда кажется естественным, оно не является единственно возможным. Сумму бесконечного ряда можно определить и другими способами. Рассмотрим, например, ряд (7), который может быть записан компактно в виде

Как мы уже говорили, его частичные суммы попеременно принимают значения 1 и 0, и поэтому ряд не сходится. Но если мы образуем поочередно попарные средние его частичных сумм (текущее среднее), т.е. вычислим сначала среднее значение первой и второй частичных сумм, затем среднее второй и третьей, третьей и четвертой и т.д., то каждое такое среднее будет равно 1/2, и поэтому предел попарных средних также окажется равным 1/2. В этом случае говорят, что ряд суммируем указанным методом и его сумма равна 1/2. Было предложено много методов суммирования, позволяющих приписывать суммы довольно обширным классам расходящихся рядов и тем самым использовать некоторые расходящиеся ряды в вычислениях. Для большинства целей способ суммирования полезен, однако, только в том случае, если применительно к сходящемуся ряду он дает его конечную сумму.

Ряды с комплексными членами.

До сих пор мы молчаливо предполагали, что имеем дело лишь с действительными числами, но все определения и теоремы применимы и к рядам с комплексными числами (за исключением того, что суммы, которые могут быть получены при перестановке членов условно сходящихся рядов, не могут принимать произвольные значения).

Функциональные ряды.

Как мы уже отмечали, членами бесконечного ряда могут быть не только числа, но и функции, например,

Суммой такого ряда также является функция, значение которой в каждой точке получается как предел вычисленных в этой точке частичных сумм. На рис. 1 показаны графики нескольких частичных сумм и суммы ряда (при x, изменяющемся от 0 до 1); s_n(x) означает сумму первых n членов. Сумма ряда представляет собой функцию, равную 1 при 0 Ј x 0 (за исключением тех случаев, когда r – неотрицательное целое число; в последнем случае ряд обрывается после конечного числа членов). Формула (17) называется биномиальным разложением для произвольной степени.

Ряды Дирихле.

Рядами Дирихле называются функциональные ряды вида S (1/a_n x ), где числа a_n неограниченно возрастают; примером ряда Дирихле может служить дзета-функция Римана

Ряды Дирихле часто используются в теории чисел.

Тригонометрические ряды.

Так называются функциональные ряды, содержащие тригонометрические функции; тригонометрические ряды специального вида, используемые в гармоническом анализе, называются рядами Фурье. Примером ряда Фурье может служить ряд

суммой которого является «прямоугольная волна» (рис. 2). На рис. 3 представлены несколько первых частичных сумм и показано, как они аппроксимируют сумму ряда.

Асимптотические ряды.

расходится при всех значения x (кроме нуля). Иначе говоря, если мы выберем какое-то значение x и начнем последовательно суммировать члены ряда, то частичные суммы не будут стремится к пределу. Однако бывает, что в этом случае существует весьма сложная функция f(x), обладающая следующим свойством: если мы возьмем конкретную частичную сумму ряда (18), например сумму первых трех его членов, то разность между f(x) и этой частичной суммой, вычисленной при некотором значении x, будет мала при всех значениях x вблизи 0. Иначе говоря, хотя мы не может добиться хорошей аппроксимации функции f(x) в какой-либо конкретной точке x, далекой от нуля, взяв даже очень много членов ряда, но при x, близком к 0, всего лишь несколько его членов дают весьма хорошее ее приближение. Такие ряды называются асимптотическими. В численных расчетах асимптотические ряды обычно полезнее, чем сходящиеся, поскольку они с помощью небольшого числа членов обеспечивают достаточно хорошее приближение. Асимптотические ряды широко используются в теории вероятностей и математической физике.

Двойные ряды.

Иногда приходится суммировать двумерные массивы чисел

Мы можем просуммировать по строкам, а затем сложить построчные суммы. Вообще говоря, у нас нет особых оснований отдавать предпочтение строкам перед столбцами, но если суммирование сначала проводить по столбцам, то результат может оказаться другим. Например, рассмотрим двойной ряд

Здесь каждая строка сходится к сумме, равной 0, и сумма построчных сумм поэтому также равна нулю. С другой стороны, сумма членов первого столбца равна 1, а всех остальных столбцов равна 0, поэтому сумма сумм по столбцам равна 1. Единственными «удобными» сходящимися двойными рядами являются абсолютно сходящиеся двойные ряды: их можно суммировать по строкам или столбцам, равно как и любым другим способом, и сумма всегда получается одной и той же. Какого-либо естественного определения условной сходимости двойных рядов не существует.

Маркушевич А.И. Ряды. Элементарный очерк. М., 1957
Зигмунд А. Тригонометрические ряды, тт. 1–2. М., 1965
Мандельбройт С. Ряды Дирихле. Принципы и методы. М., 1973
Кудрявцев Л.Д. Курс математического анализа, тт. 1–2. М., 1981
Эдвардс Р. Ряды Фурье в современном изложении, тт. 1–2. М., 1985

Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?