Что такое сумма отрезков

Сканирующая прямая

Метод сканирующей прямой (англ. scanline) заключается в сортировке точек на координатной прямой либо каких-то абстрактных «событий» по какому-то признаку и последующему проходу по ним.

Он часто используется для решения задач на структуры данных, когда все запросы известны заранее, а также в геометрии для нахождения объединений фигур.

#Точка, покрытая наибольшим количеством отрезков

Задача. Дан набор из $n$ отрезков на прямой, заданных координатами начал и концов $[l_i, r_i]$. Требуется найти любую точку на прямой, покрытую наибольшим количеством отрезков.

Рассмотрим функцию $f(x)$, равную числу отрезков, покрывающих точку $x$. Понятно, что каждую точку этой функции мы проверить не можем.

Назовем интересными те точки, в которых происходит смена количества отрезков, которыми она покрыта. Так как смена ответа может происходить только в интересной точке, то максимум достигается также в какой-то из интересных точек. Отсюда сразу следует решение за $O(n^2)$: просто перебрать все интересные точки (это будут концы заданных отрезков) и проверить для каждой по отдельности ответ.

Это решение можно улучшить. Отсортируем интересные точки по возрастанию координаты и пройдем по ним слева направо, поддерживая количество отрезков cnt , которые покрывают данную точку. Если в данной точке начинается отрезок, то надо увеличить cnt на единицу, а если заканчивается, то уменьшить. После этого пробуем обновить ответ на задачу текущим значением cnt .

Как такое писать: нужно представить интересные точки в виде структур с полями «координата» и «тип» (начало / конец) и отсортировать со своим компаратором. Удобно начало отрезка обозначать +1, а конец -1, чтобы просто прибавлять к cnt это значение и не разбивать на случаи.

Единственный нюанс — если координаты двух точек совпали, чтобы получить правильный ответ, сначала надо рассмотреть все начала отрезков, а только потом концы (чтобы при обновлении ответа в этой координате учлись и правые, и левые граничные отрезки).

Такое решение работает за $O(n log n)$ на сортировку. Если координаты небольшие, то от логарифма можно избавиться, если создать vector событий для каждой различной координаты и просто итерироваться по всем целочисленным координатам и событиям в них. Также всегда хорошей идеей будет сжать координаты.

Рассмотрим теперь несколько смежных задач.

#Длина объединения отрезков

Задача. Дан набор из $n$ отрезков на прямой, заданных координатами начал и концов $[l_i, r_i]$. Требуется найти суммарную длину их объединения.

Как и в прошлой задаче, отсортируем все интересные точки и при проходе будем поддерживать число отрезков, покрывающих текущую точку. Если оно больше 0, то отрезок, который мы прошли с прошлой рассмотренной точки, принадлежит объединению, и его длину нужно прибавить к ответу:

Время работы $O(n log n)$.

#Скольким отрезкам принадлежит точка

Пусть теперь надо для $q$ точек (не обязательно являющихся концами отрезков) ответить на вопрос: скольким отрезкам принадлежит данная точка?

Воспользуемся следующим приемом: сразу считаем все запросы и сохраним их, чтобы потом ответить на все сразу. Добавим точки запросов как события с новым типом 0, который будет означать, что в этой точке надо ответить на запрос, и отдельным полем для номера запроса.

Теперь аналогично отсортируем точки интереса и пройдем по ним слева направо, поддерживая cnt и отвечая на запросы, когда их встретим.

#Количество пересекающихся отрезков

Задача. Дан набор из $n$ отрезков на прямой, заданных координатами начал и концов $[l_i, r_i]$. Требуется для каждого отрезка сказать, с каким количеством отрезков он пересекается (в частности, он может иметь одну общую точку или быть вложенным).

Вместо того, чтобы для каждого отрезка считать количество отрезков, с которыми он пересекается, посчитаем количество отрезков, с которыми он не пересекается, и вычтем это число из $(n-1)$.

1. Какой-то отрезок закончился в координате $r_i$.
2. Какой-то отрезок с таким-то индексом начался в координате $l_j$.

Теперь нам достаточно пройтись по этим событиям слева направо, поддерживая количество встреченных событий первого типа и вычитая его из ячейки ответа для событий второго типа.

Аналогично пройдемся справа налево, находя отрезки, лежащие строго справа. Итоговое время работы будет $O(n log n)$ на сортировку.

#Сумма на прямоугольнике

Перейдем к двумерному сканлайну.

Задача. Даны $n$ точек на плоскости. Требуется ответить на $m$ запросов количества точек на прямоугольнике.

Во-первых, сожмем все координаты (и точек, и запросов): будем считать, что они все порядка $O(n + m)$.

Теперь разобьём каждый запрос на два запроса суммы на префиксах: сумма на прямоугольнике $[x_1, x_2] times [y_1, y_2]$ равна сумме на прямоугольнике $[0, x_2] times [y_1, y_2]$ минус сумме на прямоугольнике $[0, x_1] times [y_1, y_2]$.

Создадим дерево отрезков для суммы и массив ans для ответов на запросы. Теперь будем проходиться в порядке увеличения по всем интересным $x$ — координатам точек и правых границ префиксных запросов — и обрабатывать события трёх типов:

1. Если мы встретили точку, то добавляем единицу к ячейке $y$ в дереве отрезков.
2. Если мы встретили «левый» запрос префиксной суммы, то посчитаем через дерево отрезков сумму на отрезке $[y_1, y_2]$ и вычтем его из ячейки ответа.
3. Если мы встретили «правый» запрос, то аналогично прибавим сумму на $[y_1, y_2]$ к ячейке ответа.

Таким образом, мы решим задачу в оффлайн за $O(n log n)$: сжатие координат / сортировка плюс $O(n)$ запросов к дереву отрезков (или любой другой структуре для динамической суммы).

Сумма на прямоугольнике как вспомогательная подзадача также часто используется в задачах на инверсии в перестановках и запросы на поддеревьях.

#Площадь объединения прямоугольников

Задача. Дано $n$ прямоугольников, требуется найти площадь их объединения.

Вдохновляясь предыдущим подходом, можно создать два типа событий:

1. прямоугольник с $y$-координатами от $y_1$ до $y_2$ начинается в точке $x_1$;
2. прямоугольник с $y$-координатами от $y_1$ до $y_2$ заканчивается в точке $x_2$;

и затем как-то пройтись по этим событиям в порядке увеличения $x$ и посчитать общую площадь подобно тому, как мы делали с одномерными отрезками.

Если обобщать подход напрямую, то нам нужно завести массив размера $Y$ (максимальной $y$-координаты) и для каждой $y$-параллели поддерживать число прямоугольников, которые её покрывают, и каждый раз, когда $x$-координата события меняется, добавлять к ответу разницу $x$-координат старого и нового события, помноженную на число ненулевых элементов в массиве (точек на вертикальной сканирующей прямой, которые покрываются хотя бы одним прямоугольником).

Но это в худшем случае работает за $O(nY)$, что достаточно долго. Чтобы получить более приятную асимптотику, заменим массив деревом отрезков, в узлах которого будет храниться минимум и число элементов с таким минимумом (изначально минимум 0 и таких элементов на всём массиве $Y$).

Чтобы обновить ответ, нужно помножить разницу $x$-координат соседних событий на число ненулевых элементов, которое можно найти, вычтя из $Y$ количество минимумов-нулей на всём дереве. Одномерная задача пересчета этой информации при прибавлениях на отрезке остается упражнением читателю.

Такой алгоритм работает за $O(n log n)$, если аккуратно сжать координаты, и за $O(n log Y)$, если этого не делать. Этот метод также обобщается на задачу нахождения площадей и других геометрических фигур.

Сумма и разность длин отрезков

Назовите фигуры, изображенные на экране (точка, отрезок, ломаная, треугольник, квадрат, четырёхугольник)

Что такое отрезок?

Отрезок – это часть прямой, у которой есть начало и конец.

Как обозначают начало и конец отрезка?

Начало и конец отрезка обозначают заглавными буквами латинского алфавита.

3. Этап усвоения новых знаний

Вспомните, при каком действии мы находим сумму?

Сумму находим сложением.

Какой знак при этом ставим?

Сложение обозначает знак (+)

При каком действии мы находим разность?

Разность находим при вычитании.

Какой знак при этом ставим?

Вычитание обозначает знак (-)

Начертите два отрезка длиной 3 см и 6 см.

Как найти сумму этих отрезков?

Измерить длину первого отрезка при помощи циркуля.

Отложить длину первого отрезка на луче, обозначив его начало и конец.

Измерить при помощи циркуля второй отрезок.

Отложить длину второго отрезка на луче от конца отрезка, полученный отрезок является суммой.

Запомните, конец одного отрезка является началом другого; суммой отрезков является отрезок.

Чтобы найти сумму длин двух отрезков, нужно сложить длины этих отрезков.

Как найти разность этих же отрезков?

Чтобы найти разность отрезков, необходимо:

Измерить длину первого отрезка при помощи циркуля

Отложить длину первого отрезка на луче, выделить его “дугой”.

Измерить длину второго отрезка при помощи циркуля.

Отложить длину второго отрезка на луче, выделить его “дугой” другого цвета.

Измерить длину оставшейся части отрезка – это будет разностью отрезков.

Запомните, что при вычитании отрезков оба отрезка нужно построить на луче от его начала.

Чтобы найти разность длин двух отрезков, нужно из длины большего отрезка вычесть длину меньшего отрезка.

4. Этап закрепления новых знаний

Задание 1

Сколько отрезков на этом рисунке?

Найдите длину самого большого отрезка. 4 см+3 см=7 см

Задание 2

Начертите отрезок 9 см. Отметьте на нём точку так, чтобы получился отрезок длиной 2 см. Узнайте длину второго отрезка. 9 cм-2 cм=7 cм

Задание 3

Начертите путь божьей коровки: вверх 2 см, вправо 5 см. вниз 2 см, влево 5 см.

Какая фигура получилась?

Правильно, получился четырёхугольник. Как найти, сколько сантиметров проползла божья коровка?

Надо сложить длины всех сторон.

2 см+5 см+2 м+5 см=14 см

Логические задания

Задание

Нарисуйте такую же фигуру произвольных размеров. Узнайте, на сколько меньшая сторона в четырёхугольнике короче большей. Используйте при этом циркуль.

5. Этап подведения итогов

Что нового вы узнали о сумме и разности?

Мы узнали, что бывает сумма и разность длин отрезков.

Чем выражена разность отрезков?

Она выражена отрезком.

Чем выражена сумма отрезков?

Она выражена отрезком.

Чем отличается построение отрезков на луче при их сложении от построения отрезков при их вычитании?

При сложении конец первого отрезка является началом второго отрезка, а при вычитании – оба отрезка имеют общее начало.

Сумма и разность отрезков

Плюс и Минус получили задание от царицы Математики научиться находить сумму и разность отрезков. Они решили это задание выполнять вместе. Дружно работая, они справились с заданием и теперь знают, как строить отрезки при помощи линейки или при помощи линейки и циркуля. И конечно, друзья научились находить сумму и разность отрезков.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока «Сумма и разность отрезков»

— Буду делать та-а-к, потом вот та-ак, а потом вот так.

— Привет, Плюс! Я хотел пригласить тебя погулять. Но, как видно, ты опять чем-то занят.

— О, минус! Привет! Да вот получил очередное задание от царицы Математики — научиться складывать отрезки, то есть находить сумму отрезков.

— Ой, вот здорово! Мне она тоже дала похожее задание, только находить не сумму, а разность отрезков. Давай разберемся вместе, а потом пойдем гулять.

— Хорошо. Вместе — веселее. Ну, вот посмотри. Надо нарисовать отрезок. Ставлю точку, кладу линейку, и от точки провожу прямую линию.

Получился луч, то есть прямая, у которой есть начало — наша точка, но нет конца.

— Стоп-стоп, Плюс. Как это нет конца. Ты же остановился и перестал ее рисовать.

— Да, остановился. Но, её можно тянуть бесконечно, но не будем. Нам хватит и того, что нарисовали.

— Дальше я могу отложить на этом луче отрезок двумя способами. Например, мне нужен отрезок длиной 6 сантиметров. Я могу приложить линейку к лучу так, чтобы отметка ноль на линейке совпала с точкой, которую мы поставили. Это обязательно! А сама линейка должна лежать точно под прямой, близко-близко. И напротив нужной отметки, на прямой, ставим еще одну точку.

Расстояние между двумя точками и будет отрезком длиной 6 сантиметров. А теперь от этой второй точки я построю еще один отрезок длиной, например, 5 сантиметров.

— А почему от второй точки? Почему не от первой?

— Потому что, если надо найти сумму отрезков, конец первого отрезка как раз и будет началом второго отрезка. Не перебивай меня, пожалуйста. Итак, я продолжаю.

Опять прикладываю линейку к прямой, но теперь так, чтобы отметка ноль оказалась строго напротив второй точки. А там, где на линейке стоит пятерка, на прямой ставлю еще одну точку.

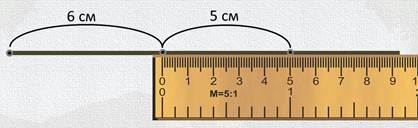
Вот появился и еще один отрезок. Если сложить их вместе, получится третий, более длинный отрезок. А теперь найдем сумму первых двух отрезков, то есть длину полученного третьего отрезка. Получаем:

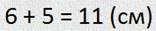
— Так это и есть нахождение суммы двух отрезков?

— Да. Чтобы найти сумму двух отрезков, надо к длине первого отрезка прибавить длину второго отрезка.

— А ты что-то там говорил про второй способ построения отрезков.

— Да, можно построить отрезки и с помощью циркуля. Главное, чтобы циркуль был хороший, не разболтанный.

— Что значит, циркуль разболтанный?

— Это когда ножки циркуля плохо закреплены и легко сдвигаются и раздвигаются. Измерения таким циркулем будут неточные.

Ну так вот. Допустим, нам надо нарисовать отрезки длиной 8 и 4 сантиметра. Начинаем точно так же, как и в первый раз. Ставим точку. От точки под линейку проводим луч.

А теперь возьмем циркуль, установим его ножки так, чтобы иголочка циркуля встала на линейке на отметку ноль, а грифель на отметку 8

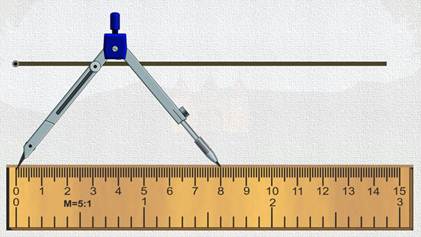
Теперь переносим циркуль на прямую так, чтобы иголочка встала на точку начала луча, а грифель сделает на луче еще одну точку. Вот и получится отрезок, длина которого 8 сантиметров.

Опять ставим циркуль на линейку, устанавливаем ножки так, чтобы иголочка стояла на нулевой отметке, а грифель на отметке 4. Переносим циркуль на луч, но теперь его иголочка стоит на второй точке, а грифель ставит новую точку на прямой.

Получился отрезок длиной 4 сантиметра

— А теперь будешь находить сумму двух отрезков?

— Да. Складываю длины первого и второго отрезков. Получаем:

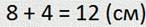
В результате сложения двух маленьких отрезков получился третий, больший, длина которого равна сумме длин двух меньших отрезков.

— Ну, Плюсик, ты своё задание закончил?

— Да. Теперь давай разбираться с твоим заданием. Тебе надо найти разность двух отрезков?

— Да, разность двух отрезков… Как же мне это задание выполнить? А, кажется, я догадался!

Я возьму два отрезка, которые ты складывал. Первый длиной 6 сантиметров, а второй — 5 сантиметров. Построю на луче отрезок в 6 сантиметров, а потом из той же точки начала луча построю второй отрезок длиной 5 сантиметров.

А вот видна разница между длинами отрезков. Эта разница и будет разностью длин отрезков. А найдем мы ее так:

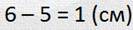
— А теперь найди разность второй пары отрезков.

— Легко! Опять отмеряю от начала луча 8 сантиметров, потом от той же точки начала луча отмеряю 4 сантиметра. И вот она, разность двух отрезков.

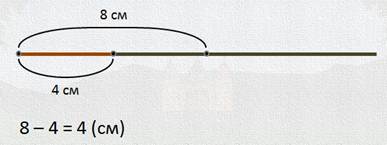
— Ух ты! Классно! Ты так быстро справился с заданием!

— Это потому, что рядом был ты, мой друг.

— Действительно, вместе любое дело легче делать. Недаром говорят: «Совместная работа, как песня весёлая». А ты заметил, что когда я находил сумму двух отрезков, то первый отрезок начинал строить от начала луча, а второй — от конца первого отрезка. И при этом выполнял действие сложение.

— Конечно, заметил. А когда я находил разность двух отрезов, то оба отрезка строил от начала луча. И выполнял вычитание.

Сумма длин отрезков

Цель способствовать формированию знаний об измерении и складывание отрезков.

Тип урока: закрепление

1. Научиться сравнивать и складывать отрезки, закрепить знание и умение считать в от 10 до 20 в порядке возрастания, измерять отрезок, решение задач.
2. Развивать память, произвольное внимание, логическое мышление, способствовать расширению кругозора у учащихся.
3. Воспитывать умение работать в коллективе, в парах.

Оборудование: части дома, картинка Строитель, таблица «Компоненты сложения»

Прозвенел долгожданный наш звонок

Сегодня на уроке мы будем строителями.

И будем строить дом.

С чего мы начнем строить дом? (С фундамента)

Что является фундаментом математики?(число)

Открыли тетради четыре клеточки вниз от работы записали

Каллиграфическая минутка

Показали свою готовность!Ручку на лоток

б) Устный счет

Строитель нам принес кирпичи,но нужно уметь посчитать кирпичи.

Значит необходимо посчитать работаю в парах в порядке возрастания от 10 до 20

Не забываем та пара, которая справилась, показывают свою готовность кирпичи

3.Сообщение темы урока

Просмотр содержимого документа
«Сумма длин отрезков»

Тема: Сумма длин отрезков

Цель способствовать формированию знаний об измерении и складывание отрезков.

Тип урока: закрепление

Научиться сравнивать и складывать отрезки, закрепить знание и умение считать в от 10 до 20 в порядке возрастания, измерять отрезок, решение задач.

Развивать память, произвольное внимание, логическое мышление, способствовать расширению кругозора у учащихся.

Воспитывать умение работать в коллективе, в парах.

Оборудование: части дома, картинка Строитель, таблица «Компоненты сложения»

Прозвенел долгожданный наш звонок

Актуализация знаний у учащихся

а)Минутка чистописание

Сегодня на уроке мы будем строителями.

И будем строить дом.

С чего мы начнем строить дом? (С фундамента)

Что является фундаментом математики?(число)

Открыли тетради четыре клеточки вниз от работы записали

Каллиграфическая минутка

Показали свою готовность!Ручку на лоток

б) Устный счет

Строитель нам принес кирпичи ,но нужно уметь посчитать кирпичи.

Значит необходимо посчитать работаю в парах в порядке возрастания от 10 до 20

Не забываем та пара, которая справилась , показывают свою готовность кирпичи

3.Сообщение темы урока

Начерти отрезок 6 см и 2 см, докажи ,что у тебя получились отрезки.Сможем ли мы узнать длину обоих отрезков не пользуясь линейкой. — Мы умеем складывать числа. А сегодня на уроке мы будем учиться складывать и отрезки. И узнаем что такое “сумма отрезков”

Что такое отрезок?

Что значит сумма?

Какой знак используем при сложении?

Можем ли мы узнать длину обоих отрезков не измеряя с помощью линейки.

4Работа по выполнению действий с отрезками

Чего не хватает у нашего дома?(окон и двери)

А)Сложение окно

— Какие знания вы использовали , чтоб решить данные выражение?

— Что такое сумма длин отрезко?

Б)Сравни дверь

2 см+1 см*10 см +2 см

-Расскажите подробно как вы выполняли задание на сравнение?

5 Закрепление

Задача. Крыша

Прибежали к нам зайчата , чтоб помочь построить дом. И записка в месте с ними. Решите задачу и взаимообратную задачу. «Было 6 зайчат ,потом 2 убежали на обед. Сколько зайчат осталось?»

— Задачи говорится о ?

-Сколько Было зайчат?

-Убежали сколько зайчат?

-Осталось нам известно сколько зайчат?

-Какие главные слова мы выберим для записи условия задачи?

— Что вас заинтересовало на уроке?

-Что значит сумма длин отрезков, как вы понимаете?

-Что вы можете сказать о своей выполненной работе?

Встали те ребята у кого получилось построить дом , получают оценку отлично. У тех у кого не хватило одной части дома и им еще нужно постараться ,они получают 4.

Измерение отрезков

Штангенциркуль, линейка, рулетка. Все эти предметы являют собой измерительные инструменты, позволяющие проводить измерение отрезков. Почему людям так важно измерять — вопрос экзистенциальный. И тем не менее у него есть вполне конкретный геометрический ответ. В данном уроке мы постараемся обстоятельно изложить содержание этого ответа. Как пользоваться линейкой тоже, кстати, обсудим.

Интересно углубиться? Нюансы измерения физических тел можно найти вот здесь в разделе физики у нас на сайте. В данном уроке мы будем разбирать только ту информацию, которая непосредственно связана с геометрией.

Предмет измерений

Прежде чем что-либо измерять, необходимо в принципе определиться с тем, что такое мера. Измерять можно популяцию нелетающих попугаев, напряжение в электрической цепи, погодные условия на Южном полюсе, количество сахара в лимонадах.

Иными словами, измерить можно все что угодно. Значит, один из первостепенных критериев определения меры — предмет измерений. Непосредственно тот объект, который будет поддаваться оценке.

Отрезок как предмет измерений

Прямая и луч бесконечны, и измерить их не представляется возможным. Из простых линейных (одномерных) фигур геометрии в качестве предмета измерения может выступать только отрезок. Вспомним, что отрезок отличается от луча тем, что имеет не только точку начала, но и точку конца. Расстояние, заключенное между этими точками, называется длиной. Аксиома о том, чему равна длина отрезка, гласит следующее:

$A_6$. Каждый отрезок имеет определенную длину, большую нуля.

Примечание. Измерение отрезков было бы неосуществимо, если бы в геометрии существовала логическая дыра «нулевой отрезок». Раз отрезок обладает началом и концом, между ними по определению что-то должно быть заключено. Некоторая величина.

И пусть даже она очень-очень маленькая, ее всегда можно выразить числом. В противном случае отрезок бы имел свойства точки, а это, как мы уже давно выяснили, разные фигуры.

Единица измерения

Выбрав предмет измерений, то есть ответив на вопрос «что?», мы должны далее выразить его количественным образом — ответить на следующий логический вопрос, сколько есть этого «что».

Расшифруем: чтобы определить, чему равна длина отрезка, требуется обозначить единицу измерения и ее эталон. Сравнивая отрезок с эталоном, мы будем получать величину, выраженную в выбранных единицах измерения.

Справка: об эталонах

Эталон — это образец, воспроизводящий единицу измерения с наибольшей точностью. Созданием и хранением исторических эталонов занимается Международное бюро мер и весов, штаб-квартира которого расположена в пригороде Парижа.

Современная система величин включает в себя семь основных единиц измерения — длины, массы, времени, количества вещества, силы света, температуры и силы тока. Вкупе эти величины составляют Международную систему единиц (СИ). Подробное ее изучение вас ждет в курсе физики.

Цилиндр из платино-иридиевого сплава — до 2018 года эталон килограмма. Его сместил более точный подход к измерению массы, основанный на расчете энергии по постоянной Планка.

Зачем в измерениях эталоны? Все просто: это инициатива стандартизации знаний о физическом мире. Можно ведь не просто измерить все что угодно, но еще и представить результаты измерений в каких угодно величинах.

Вообразите себе то же измерение отрезков в спичечных коробках. Людям было бы крайне сложно договориться, у кого самый подходящий для измерений коробок. Стандарты в виде эталонов по своей сути позволяют именно это — договариваться.

Метрическая система

За единицу измерения длины в СИ принят метр. Эталон метра — это длина пути, который проходит свет в вакууме за интервал времени $frac$ долю секунды, где $c$ — скорость света, равная $299 792 458~м/с$.

К 1982 году, когда погрешность в измерении скорости света достигла минимума, был утвержден окончательный эталон метра на основе $frac$ секунды. До этого в течение почти двух столетий за эталон метра принималась $frac$ Парижского меридиана. Переход к использованию скорости света в определении метра обусловлен воспроизводимостью и точностью.

Исторический эталон метра. Перед вами — мраморная доска на стене здания по улице Вожирар напротив Люксембургского дворца. После перехода Европы на метрическую систему такие «напоминалки» развешивали по всему Парижу.

Представьте, как вдруг в палатах мер и весов всего мира по некоторым странным обстоятельствам исчезают оригинал и копии эталона метра. Пришлось бы перемеривать меридиан Земли. Но что, если еще к тому же Земля сожмется в размерах?

Точность — вежливость королей, а скорость света остается постоянной. Эксперимент с вакуумом легко воспроизвести в лабораторных условиях, чтобы, в случае чего, восстановить значение метра.

Измерение отрезков в метрической системе

Метр — это примерно полтора шага. Для предметов, нас окружающих, это большая единица измерения. В геометрии часто приходится проводить как раз именно измерение небольших отрезков.

Вспомним пресловутый спичечный коробок. Измерять в метрах, чему равна длина отрезка столь малого, было бы неоправданно сложно. Для удобства расчетов и измерений в науке принят принцип кратных и дольных единиц.

Приведем наиболее для нас необходимые:

Величина	Название	Краткое обозначение
$10^$ (=$frac$ м)	дециметр	дм
$10^$ (=$frac$ м)	сантиметр	см
$10^$ (=$frac$ м)	миллиметр	мм

Принцип прост: добавляя приставку «деци», «санти» или «милли», вы уменьшаете метр на $10^$, $10^$ или $10^$ единиц соответственно. Дольные единицы также можно переводить меж собой.

📕 Задача. Даны следующие длины отрезков: $AB=12~см$, $DC=9~мм$, $JK=7~дм$. Приведите длины всех отрезков к метрам. Отдельно выразите длину отрезка $JK$ в миллиметрах.

Измерение отрезков мы не проводим. Мы пока только приводим значения к стандарту. Выразим для начала длины отрезков $AB,~DC,~JK$ в метрах.

1. Перевод в метры. По таблице имеем, что $1~см=1~м*frac$. Значит, чтобы выразить длину отрезка $AB$ в метрах, нам достаточно разделить указанное значение в сантиметрах на $100$. Аналогично для отрезков $DC$ и $JK$, только деление будем проводить на $1000$ и $10$ соответственно. Считаем:

2. Перевод в миллиметры. Отрезок $JK$ равен $7~дм$. Чтобы получить значение в миллиметрах, величину нужно умножить на $100$. Имеем: $$JK=7*100=700~мм$$

Трудности с переводом величин? Вам сюда!

Если сложно переводить величины

Для этого просто нужно немного попрактиковаться. Однако если вам совсем сложно рассчитать, чему равна длина отрезка в той или иной единице, предлагаем в помощь небольшие хитрости.

Составьте «уравнение». Распишем пример для дециметра: $1~дм=frac*1~м$. Смотрите на данное равенство как на уравнение, где можно умножать обе части. Если бы нам понадобилось вычислить, сколько метров в $10$ дециметрах, мы могли бы просто умножить обе части «уравнения» на $10$:

Какая математическая операция происходит в итоге? Деление $10$ на $10$. В одном метре десять дециметров.

Обратное «уравнение». Если переводить нужно не в метры, а из метров, равенство можно «развернуть» в обратную сторону. По таблице мы получали равенства таким образом, чтобы дольные единицы были выражены как цельные, а метр как их часть. Сделаем наоборот. На примере миллиметра: $$1~мм*textcolor>=frac*1~м*textcolor>$$

Из чего получаем «уравнение-перевертыш»: $1~м=1000~мм$. Чтобы найти, сколько миллиметров, например, в $20$ метрах, умножаем обе части на $20$:$$1~м*textcolor=1000~мм*textcolor$$

«Уравнение» между дольными единицами. Если измерение отрезков требует перевода между дольными единицами («дециметр-сантиметр» и т. п.), обычно по таблице СИ «ходят» вверх-вниз и делят значения долей. Звучит запутанно, согласны. Вы до этого обязательно додумаетесь сами со временем, а пока гармонии ради покажем прием с «уравнениями» и для этого случая. Скажем, измерение отрезков провели в миллиметрах, а записать требуется в сантиметрах.

Пользуемся обратными уравнениями:

$1~м=1000~мм$ и $1~м=100~см$.

Как видим, оба равенства содержат часть «$1~м$», и мы можем их уравнять: $1000~мм=100~см$. Сокращаем и получаем следующее: $1~см=10~мм$. Однако это еще не все. Значение нам задано в миллиметрах, а не в сантиметрах. Что дано — приводим к единице, а уже после умножаем. Пусть нужно перевести $54~мм$. Имеем:

Ну, не совсем-то это все уравнения, — в них нет переменных. Мы их так обозвали, чтобы у вас возникли положительные ассоциации с операцией умножения обеих частей для сохранения тождественности.

Измерение отрезков: измерительные инструменты

После того, как были заданы предметные и количественные характеристики, нам остается лишь определить на основе эталона измерительные инструменты, которые бы фиксировали, чему равна длина отрезка. Подытоживая, можно сказать, что составляющие всякого измерения — это неизменно:

• предмет измерения;
• единица измерения;
• измерительные инструменты.

Сумма длин частей

Измерительные инструменты длины многообразны: и для сверхточных измерений найдется, и для подсчетов со средней погрешностью. Школьный курс геометрии обходится обычной линейкой с сантиметровой шкалой.

Устройство инструментов, позволяющих измерить длины отрезков, нехитрое и напрямую связано с аксиомой о сумме длин частей отрезка:

$A_7$. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Рассмотрим линейку как единую систему отрезков. На нулевой отметке расположим точку $A$, конец линейки обозначим точкой $O$. Каждую сантиметровую отметку инструмента — $1$, $2$, $3$ … $14$ — также обозначим отдельными точками. По аксиоме о сумме длин частей про длину отрезка $AO$ можно заключить:

Уменьшение погрешности миллиметровой шкалой

Чтобы измерить длины отрезков точнее, на шкалу сантиметровой линейки наносят еще одну шкалу ближайшей дольной единицы — миллиметровую. Сантиметр состоит из десяти миллиметров, и все деления миллиметра — $1$, $2$ … $9$ — можно представлять в виде дополнительной точки. Измерительные инструменты становятся точнее за счет того, что внутри каждого сантиметрового отрезка содержится десять миллиметровых.

Как пользоваться линейкой, чтобы измерить длины отрезков

Разберем, как пользоваться линейкой, чтобы измерить длины отрезков. Измерим длину отрезка $AB$. Для этого начало отрезка совместим с нулевой отметкой. Линейка должна при этом располагаться строго параллельно отрезку. Точка конца отрезка будет указывать на значение длины отрезка. В нашем примере длина отрезка $AB$ равняется $9$ сантиметрам и $5$ миллиметрам:$$AB=9,5~см$$

Отрезок $AB$ состоит из $9$ сантиметровых отрезков и $5$ миллиметровых. Длина отрезка выражается в единицах измерения согласно цене деления основной шкалы. В нашем случае — в сантиметрах. Миллиметры указываются как дольная часть сантиметра.

Отрезки и углы

7. На плоскости помещается множество точек и прямых. Принимают, что можно на плоскости строить точки и прямые ; на практике для построения прямой употребляется линейка.

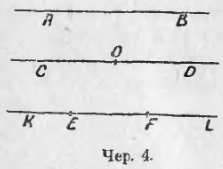
Прямая тянется без конца в обе стороны. На чер. 4 построена прямая AB; воображением можно продолжить ее без конца в обе стороны. Если построить какую-либо точку, напр., точку O, на прямой CD (чер. 4), то прямая разделится на 2 части: одна часть тянется от точки O вправо без конца, а другая – от точки O влево без конца. Каждая из этих частей называется лучом . Здесь имеем 2 луча: луч OD и луч OC.

Мы можем через каждую точку построить бесчисленное множество лучей.

Если возьмем на прямой 2 точки, напр., на прямой KL (чер. 4) точки E и F, то часть прямой линии между этими точками называется отрезком . На чертеже имеем отрезок EF.

8. Сравнить 2 данных отрезка AB и CD (чер. 5).

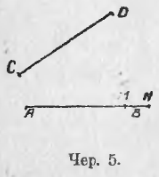
Перенесем отрезок CD так, чтобы точка C попала в A, и вращаем его около точки A до тех пор, пока отрезок CD не пойдет по отрезку AB. Когда этого достигнем, заметим, куда попадет точка D: если она попадет в B, то наши отрезки равны ; если D попадет куда-либо между точками A и B (напр., в M), то отрезок CD считается меньше отрезка AB, и если точка D попадет за точку B (напр., в N), то отрезок CD больше отрезка AB.

«Сравнить» два отрезка понимаем в смысле установить, равны ли они или один больше другого.

9. Найти сумму двух данных отрезков.

Взяты два отрезка AB и CD (чер. 6); надо сложить эти отрезки.

Для этого переносим отрезок CD так, чтобы точка C попала в B, и затем вращаем его около B до тех пор, пока он не пойдет по продолжению отрезка AB. Отметим, куда попадет точка D; если она попадет в K, то отрезок BK = CD и AK = AB + BK или AK = AB + CD.

Всякий отрезок можно разбить промежуточными точками на сумму нескольких слагаемых; напр.:

AB = AC + CD + DE + EF + FB (чер. 7)

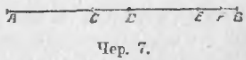
Для нас ясно, что сумма отрезков не изменяется от перестановки слагаемых .

10. Найти разность двух отрезков.

Даны два отрезка AB и CD (чер. 8); надо из большего отрезка AB вычесть меньший CD.

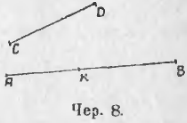
Переносим отрезок CD так, чтобы точка D попала в точку B, и станем вращать его около B до тех пор, пока он не пойдет по направлению BA; отметим, когда этого достигнем, куда попадет точка C. Если C попадет в K, то KB = CD и AK = AB – KB или AK = AB – CD.

Можно данный отрезок умножить на 2, на 3, на 4 и т. д., т. е. повторить его слагаемым 2, 3 и т. д. раз.

Из пп. 8-10 нам важно усвоить, что 1) к отрезкам, как и к числам, приложимы понятия: «равно», «больше» и «меньше»; 2) понятия о «сумме и разности двух отрезков» имеют вполне определенный смысл.

На практике для построения отрезка, равного данному, пользуются циркулем .

11. Упражнения. 1. Назвать слагаемые отрезки и их сумму в каждом из следующих изображений; записать (чер. A).

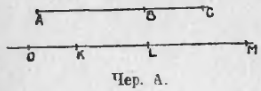
2. На тех же чертежах указать, какой отрезок можно считать разностью двух других отрезков; записать.

3. Данный отрезок разбить на 2, на 3, на 4 слагаемых; записать.

4. Данный отрезок представить, как разность двух других отрезков.

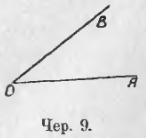
12. Мы можем построить фигуру, состоящую из двух лучей, исходящих из одной точки , – такая фигура называется углом . На чер. 9 изображен угол, состоящий из лучей OA и OB, исходящих из точки O. Эта точка называется вершиною угла, а каждый луч называется его стороною . Слово «угол» заменяется знаком ∠. Угол называется тремя буквами, из которых одна ставится при вершине, а две другие где-либо на сторонах угла, – буква при вершине ставится в середине названия угла. На чер. 9 имеем ∠AOB или ∠BOA; иногда угол называют одной буквою, поставленной при его вершине, говоря ∠O. Стороны угла (лучи) надо считать идущими без конца.

Особенный случай угла представится тогда, когда его стороны составляют одну прямую линию; такой особенный угол называют выпрямленным или развернутым углом (на чер. 12 изображены выпрямленные углы AOB и A₁O₁B₁).

Каждый угол делит плоскость на 2 части, на две области . Одну из этих частей называют внутреннею областью угла и говорят, что она лежит внутри угла, а другую называют внешнею областью угла и говорят, что она лежит вне угла. Какую именно из этих двух частей называть внешнею областью, а какую внутреннею, – дело условия. Следует всякий раз отмечать как-либо внутреннюю, напр., область. Мы будем отмечать внутреннюю область угла кривыми линиями, начерченными на внутренней области между сторонами угла; на чер. 10 отмечены внутренние области углов ABC, DEF и выпрямленного ∠KLM.

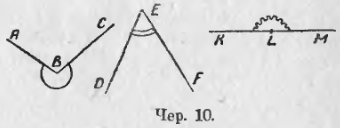
Полезно вырезать углы из листа тонкого картона: кусок картона является грубым изображением части плоскости; начертив на нем два луча, исходящих из одной точки, и разрезав этот кусок по сторонам начерченного угла, мы разделим кусок картона на 2 части; возьмем одну из этих частей, про которую хотим считать, что она лежит внутри угла, а другую удалим, – тогда будем иметь модель угла вместе с его внутреннею областью. Для правильного толкования этой модели надо иметь в виду, что кусок картона есть изображение лишь части плоскости, а сама плоскость тянется без конца.

13. Сравнить два данных угла ∠ABC и ∠DEF (чер. 11).

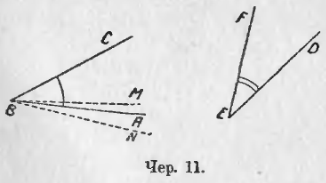
«Сравнить» два угла значит установить, равны ли эти углы, или один больше другого. Для этого мы станем накладывать один угол на другой так, чтобы их внутренние области пошли друг по другу: если при этом окажется, что можно достигнуть того, чтобы вершины и стороны наших углов совместились, то мы говорим, что эти углы равны; если же вершины и по одной стороне у наших углов совпадут, а другие стороны не совпадут, то углы не равны, и меньшим мы читает тот, внутренняя область которого уложится на внутренней области другого.

Упражнение. Вырезать из бумаги модели углов вместе с их внутренними областями и, накладывая эти модели друг на друга, установить возможность случаев, описанных выше; вырезав модель одного угла, вырезать затем модель угла ему равного и модели углов ему не равных (большего или меньшего).

Обратимся к углам ABC и DEF (чер. 11); внутренняя область каждого из них на чертеже отмечена. Переносим ∠DEF так, чтобы его вершина E попала в точку B и его сторона EF пошла бы по стороне BC, – тогда внутренние области углов расположатся одна по другой. Если сторона ED пойдет при этом по стороне BA, то ∠DEF = ∠ABC; если сторона ED пойдет внутри ∠ABC, напр., по лучу BM, то ∠DEF < ∠ABC (здесь внутренняя область угла DEF уляжется на внутренней области ∠ABC, и еще останется незанятой область ABM); если сторона ED пойдет вне ∠ABC, напр., по лучу BN, то ∠DEF >∠ABC.

Полезно повторить те же рассуждения для углов ABC и DEF (с отмеченными внутренними областями), данных на чер. 11 bis.

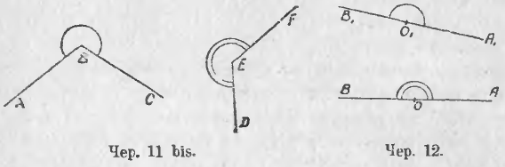
Применим изложенный способ сравнения двух углов к двум выпрямленным углам. Пусть имеем 2 выпрямленных угла ∠AOB и ∠A1O1B1 (чер. 12), внутренние области которых на чертеже отмечены. Наложив один из этих углов на другой так, чтобы вершина O₁ одного попала в вершину O другого и чтобы сторона O₁A₁ одного пошла по стороне OA другого, мы придем к заключению, что и другие стороны этих углов O₁B₁ и OB совпадают, так как линии A₁O₁B₁ и AOB суть прямые, положение которых определяется двумя точками. (Говорят иногда: «OB есть продолжение OA» вместо того, чтобы говорить, что линия AOB есть прямая). Поэтому приходим к заключению:

Все выпрямленные углы равны между собою.

14. Выпрямленный ∠AOB (чер. 12) делит плоскость на 2 области, на внутреннюю и внешнюю. Если перегнуть плоскость по прямой AOB, то обе эти части придут в совпадение. Поэтому можно принять, что внутренняя и внешняя области у выпрямленного угла равны между собою.

Если имеем какой-либо невыпрямленный угол, напр., ∠DEF (чер. 11 или чер. 11 bis), то, продолжив одну его сторону, напр., сторону DE (на чертежах продолжений не начерчено), мы увидим, что о нашем угле можно установить, что он или меньше выпрямленного (чер. 11), или больше его (чер. 11 bis); зависит это от того, какую из двух частей плоскости принять за внутреннюю область угла. Обычно выбирают внутреннюю область угла так, чтобы этот угол оказался меньше выпрямленного, причем условимся в таком случае не отмечать внутренней области угла. Иногда происхождение угла укажет, что за внутреннюю область надо счесть ту часть плоскости, что угол окажется больше выпрямленного. Эти случаи в дальнейшем будут иногда иметь место, и тогда мы уже должны отмечать внутреннюю область угла.

15. Найти сумму двух углов : ∠AOB и ∠PNM (чер. 13), или сложить ∠AOB и ∠PNM.

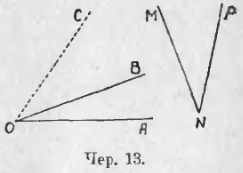
Здесь на чертеже не отмечены внутренние области углов; согласно замечанию предыдущего п., это значит, что их надо выбрать так, чтобы каждый угол был меньше выпрямленного, и мы ясно видим эти области.

Перенесем ∠PNM так, чтобы его вершина N совпала вершиною O угла AOB, и вращением около точки O достигнем того, чтобы сторона NP пошла по стороне OB; тогда внутренние области наших углов окажутся приложенными друг к другу, – это обстоятельство является существенным для сложения углов. Отметим затем, как пойдет сторона NM: пусть, напр., она пойдет по лучу OC. Тогда получим новый ∠AOС, который принимается за сумму двух данных углов. Мы можем написать:

1) ∠BOC = ∠PNM, 2) ∠AOC = ∠AOB + ∠BOC
и 3) (на основании 1) ∠AOC = ∠AOB + ∠PNM.

Так же можно складывать несколько углов; можно разбивать данный угол на несколько слагаемых. На чер. 14 имеем:

∠AOE = ∠AOB + ∠BOC + ∠COD + ∠DOE.

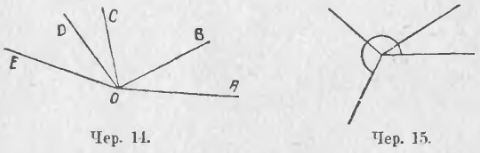
Легко построить два или несколько приложенных друг к другу углов, чтобы сумма их оказалась равна выпрямленному углу. Возможно, что сумма нескольких углов окажется больше выпрямленного угла (чер. 15), внутреннюю область этой суммы следует отметить.

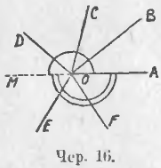
Возможен еще особый случай сложения углов, когда внутренние области слагаемых углов покрывают собою, когда их приложат друг друга, всю плоскость. На чер. 16 имеем такие углы: ∠AOB, ∠BOC, ∠COD, ∠DOE, ∠EOF и ∠FOA. В этом случае, построив луч OM, являющийся продолжением луча OA, видим, что сумма наших углов состоит из двух выпрямленных углов: 1) выпрямленный ∠AOM, внутренняя область которого отмечена одною кривою линиею, и 2) выпрямленный ∠AOM, внутренняя область которого отмечена двойною кривою линиею. Здесь мы имеем:

∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOF + ∠FOA = 2 выпрямленным углам.

Говорят: Сумма всех последовательных углов, окружающих точку, равна двум выпрямленным углам .

Если имеются слагаемые углы еще, кроме построенных на чер. 16, то их придется прикладывать к прежним опять по первому выпрямленному углу, и тогда сумма получается больше двух выпрямленных углов, равная трем выпрямленным углам, больше трех выпрямленных углов и т. д.

16. Найти разность двух углов : ∠AOB и ∠MNP (чер. 17), или вычесть ∠MNP из ∠AOB, полагая, что ∠MNP < ∠AOB.

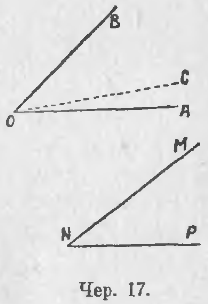
Перенесем ∠MNP так, чтобы его вершина N попала в вершину O угла AOB; вращением около точки O достигнем затем, чтобы сторона NM пошла по стороне OB, причем внутренние области этих углов расположатся одна на другой. Пусть сторона NP пойдет по лучу OC; тогда получим новый ∠AOC, о котором знаем, что ∠AOC + ∠COB = ∠AOB, откуда, согласно определению вычитания, как действия обратного сложению, получим:

∠AOC = ∠AOB – ∠COB,
но ∠COB = ∠MNP; поэтому
∠AOC = ∠AOB – ∠MNP.

Из пп. 13-16 мы должны усвоить мысль, что к углам, как и к отрезкам, приложимы понятия: больше, меньше, равно , и что понятия о сумме и разности двух углов имеют определенный смысл.

17. Упражнения. 1. Построить два приложенных друг к другу угла, назвать их буквами, указать их сумму и записать сложение этих углов.

2. На том же чертеже указать, что один из углов есть разность двух других; записать его.

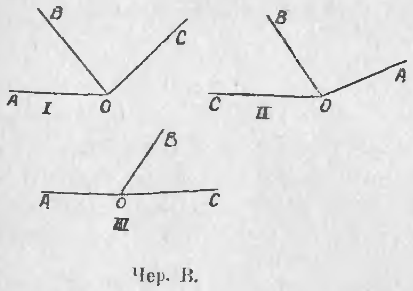
3. На следующих чертежах (см. чер. B) ∠AOB выразить разностью двух других углов.

4. Данный угол разбить на 2, на 3, на 4 слагаемых; всякий раз записывать это; сделать то же самое с выпрямленным углом.

5. Данный угол представить в виде разности между выпрямленным и каким-либо другим углом. Какое построение необходимо для этого?

6. Производить сложение и вычитание углов, пользуясь моделями углов, вырезанными из бумаги.

18. В дальнейшем мы часто будем нумеровать углы, чтобы, называя их нумерами, сократить письмо. Нумера углов будем писать внутри каждого угла около вершины.

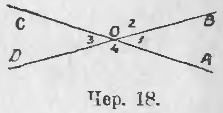
Построим ∠AOB (чер. 18) и будем называть его ∠1. Дополним этот угол до выпрямленного. Задача имеет два решения: построим луч OC, служащий продолжением луча OA; тогда получим ∠BOC или ∠2, удовлетворяющий требованию, так как видим, что

∠1 + ∠2 = выпрямленному углу.

Здесь мы имеем пример сложения двух углов, когда сумма равна выпрямленному углу, – такие углы называют смежными: ∠1 и ∠2 суть смежные углы. Чтобы 2 угла можно было назвать именем «смежные», надо, чтобы 1) они были приложены друг к другу и 2) чтобы их сумма равнялась выпрямленному углу, или, что то же самое, чтобы эти углы имели общую вершину (у углов 1 и 2 общая вершина O), одну общую сторону (у наших углов общая сторона OB) и чтобы две другие стороны являлись продолжением одна другой (OC есть продолжение OA).

Второе решение нашей задачи получится, если продолжить сторону OB, – пусть OD есть продолжение OB; тогда получим еще ∠AOD или ∠4, смежный с ∠1. Назовем еще полученный угол COD через ∠3.

Исследуем 2 полученных решения нашей задачи, т. е. ∠2 и ∠4. Мы видим особенность расположения ∠2 и ∠4: у них общая вершина O, стороны одного из них являются продолжениями сторон другого, а именно OC есть продолжение OA и обратно, и OB есть продолжение OD и обратно, – такие два угла называются вертикальными.

Затем мы знаем, что и ∠2 и ∠4 дополняют каждый в отдельности ∠1 до выпрямленного; отсюда заключаем, что

Вот более подробное изложение последнего соображения. Согласно построению, мы имеем:

1) ∠1 + ∠2 = выпрямленному углу;
2) ∠1 + ∠4 = выпрямленному углу.

Мы видим, что оба сложения ведут к одинаковой сумме (все выпрямленные углы ведь равны между собою), и, кроме того, одно слагаемое (а именно ∠1) в обоих сложениях одно и то же; отсюда заключаем, что и другие слагаемые должны быть равны между собою, т. е. ∠2 = ∠4.

Если построить две пересекающихся прямых линии, то получим две пары вертикальных углов. На чер. 18 имеем прямые AC и BD, одна пара вертикальных углов есть ∠2 и ∠4, а другая ∠1 и ∠3. Все предыдущее применимо к каждой паре вертикальных углов; напр., для пары ∠1 и ∠3 имеем, что каждый из них дополняет ∠2 до выпрямленного, следовательно, ∠1 = ∠3. Поэтому имеем теорему:
Вертикальные углы равны между собою.

Упражнение. Построить через точку три прямых и указать полученные вертикальные углы; записать их равенство.

Дерево отрезков: просто и быстро

Накануне очередного запуска курса «Алгоритмы для разработчиков» мы провели открытый урок. На нём поговорили об известной идее дерева отрезков, обсудили, как его строить, обновлять и быстро O(log n) вычислять сумму чисел любого отрезка данного массива. Алгоритм очень простой и экономный: нужно O(n) памяти. Для закрепления материала решили олимпиадную задачу.

Вебинар провёл опытный программист и преподаватель, а также руководитель курса «Алгоритмы для разработчиков» Евгений Волосатов.

Присказка

Дерево отрезков — это структура данных, которая позволяет алгоритмически просто и логарифмически быстро находить сумму элементов массива на заданном отрезке.

К примеру, представьте, что надо найти сумму следующих чисел:

При этом нам нужно не просто вычислить сумму чисел указанной последовательности (сумму элементов определённого массива), а максимально быстро найти сумму любой последовательности из этих чисел. То есть мы можем задать какой-нибудь интервал (отрезок) и максимально быстро дать ответ, чему равна сумма чисел из этого интервала:

Что значит быстро? Это значит быстрее, чем, если бы мы просто суммировали числа. Ведь чисел может быть и миллионы, и миллиарды…

Именно желание быстро находить сумму последовательных элементов и стало мотивацией нашего вебинара. Причём, речь идёт не только о сумме, но и о других задачах, например, вычислении любой ассоциативной функции. Таким образом, мы говорим об операциях, выполнение которых не зависит от порядка вычисления.

Возвратимся к нашему ряду:

Очевидно, что если мы хотим находить результат быстро, нужно посчитать некоторые суммы заранее. Первое, что приходит на ум, складывать попарно:

Теперь, если нужно найти сумму чисел, мы можем сделать это практически моментально. Например, чтобы найти сумму упомянутого выше отрезка, достаточно будет 13 прибавить к 9. Всё элементарно: для нахождения суммы четырёх чисел мы сложили только два.

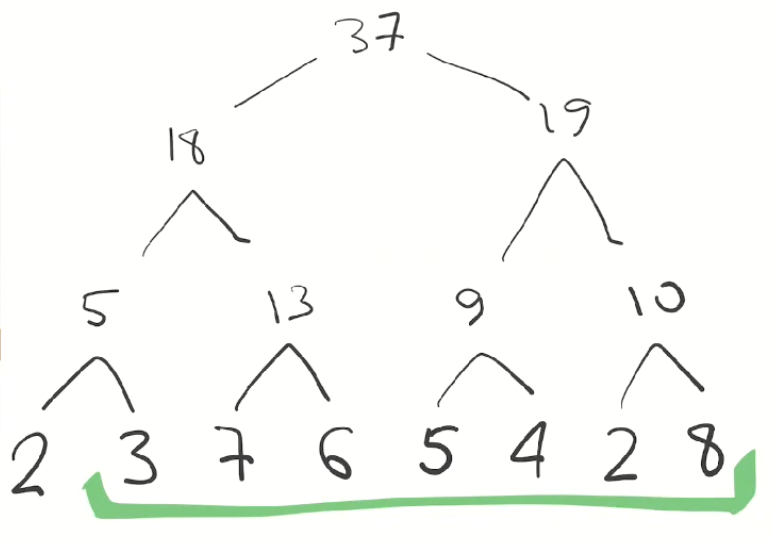
Чтобы найти сумму этого отрезка, нам нужно сложить элементы, которые, так или иначе, покрывают наш отрезок:

Разумеется, 3 + 13 + 19 = 35. Обратите внимание, чтобы найти сумму семи чисел, мы сложили только три. Если бы отрезок состоял из тысячи элементов, достаточно было бы сложить в среднем 10 элементов, так как мы имеем логарифмическую сложность с логарифмом по основанию 2. И это быстро!

Полное двоичное дерево

Полное двоичное дерево — это дерево, у каждого элемента которого есть ровно два дочерних элемента.

Для работы с полным двоичным деревом можно и нужно использовать такую структуру данных, как массив. Нумеровать этот массив удобно с единицы. Пронумеруем каждый элемент двоичного дерева натуральными числами от 1 до 2 n -1:

Вся красота подхода в том, что очень легко вычислять номер детей и родителей.
Формула вычисления «левого ребёнка»: i*2, «правого»: i*2+1.

Например, вычислим номера детей у пятого элемента:

А как от «ребёнка» подняться к «родителю»? Используем целочисленное деление i / 2

Ок, а как определить, левый ребёнок или правый? Ответ следующий: у левых детей чётные номера, у правых — нечётные.

Запомним эти моменты.

Возвратившись к нашему примеру бинарного дерева, зададимся вопросом, как нам его построить? Смотрите, у нас вначале есть массив чисел:

Для него нужно построить двоичное дерево. Сколько потребуется памяти для хранения двоичного дерева, внизу которого находятся эти элементы?

Ответ на этот вопрос — 2n, если n является степенью двойки.

Идём дальше, ведь перед нами возникают ещё два вопроса:

1. с какого элемента необходимо разместить исходные числа в массиве полного двоичного дерева?
2. с какого элемента и в какую сторону мы начнём заполнять наше дерево предварительно рассчитанными суммами?

Ответить на первый вопрос достаточно просто: у нас 8 элементов, всего в массиве будет 16 элементов, значит, первый элемент будет под номером 16 — 8 = 8. И начинать строить мы будем слева-направо и снизу-вверх, начиная с 7 элемента, складывая значения у детей, вот так:

Далее необходимо определить, как именно находить сумму нужного отрезка. Вернёмся к нашему первому примеру, пронумеруем элементы и зададим отрезок, причём обозначим первый элемент в отрезке, который нужно сложить, буквой L, а последний — R:

Теперь необходимо ввести ещё одно понятие, чтобы был ясен алгоритм действий. Речь идёт о понятии фундаментальных элементов и соответствующих им фундаментальных отрезков. Фундаментальный элемент — это какой угодно элемент из всего массива, и ему соответствует фундаментальный отрезок, то есть те элементы из начального массива, которые являются его непосредственными детьми/внуками. Для фундаментального элемента с номером 4 “5” фундаментальный отрезок будет с 8 по 9 элемент: [“2”; “3”]:

Что касается фундаментального элемента с номером 10 — “7” (мы обозначили его L), он совпадает со своим фундаментальным отрезком. Можно ли расширить этот фундаментальный отрезок, не выходя за пределы L-R? В нашем случае можно. Правило для левой границы такое: если это левый ребёнок, то фундаментальный отрезок можно расширить, новый фундаментальный элемент будет являться родителем текущего. То есть мы можем в программе писать следующее:

Теперь перейдём к правому элементу R. Он является фундаментальным элементом и левым ребёнком, поэтому расширить область мы уже не можем (выйдем за пределы отрезка). Значит, можем добавить этот элемент к ответу:

Далее нужно, чтобы левый элемент двигался к правому, а правый — к левому. Для левого элемента с индексом L = 10 следующий индекс равен 5, т. к. он пойдёт к родителю. Но пойдёт сначала вправо, а потом вверх:

Итак, значение L перешло на уровень выше и немного правее. Как же будет уменьшаться R? С помощью формулы (R – 1) / 2.

Вот такой алгоритм. Что касается следующих значений переменных L и R, то далее они будут перемещаться следующим образом:

Если же в дереве будет не 8 элементов, а неудобное число, скажем 12, нам придётся дополнить дерево (двоичное дерево должно быть полным) до 16-ти.
Формула для вычисления количества элементов (берётся целая часть логарифма):

Теперь вычислим ассоциативную функцию нахождения минимума. Вот наше дерево и отрезок:

Как думаете, сколько раз в нашей функции будет задействован элемент № 5 — один или два? Разумеется, один, но каким образом это проверяется в алгоритме? На самом деле, этот элемент является либо левым, либо правым сыном, а значит, выполнится действие либо для L, либо для R.

+

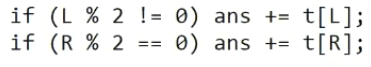
Теперь рассмотрим операцию изменения. Допустим, изменился какой-нибудь элемент, например, вместо 7 пришёл 0. Чтобы наше дерево отрезков осталось в рабочем состоянии, необходимо обновить всех родителей, причём нужно идти до самого верха.

Решение олимпиадной задачи

Одно из требований к таким задачам — всё должно работать быстро. Итак, имеем следующее условие:

Будем решать её, используя знания о дереве отрезков. В результате получим следующий код на C#:

Отправляем на проверку, видим, что решение принято и является полным, а значит, наш алгоритм работает.

На этом всё, если хотите подробностей, смотрите видео целиком. Также можете на досуге почитать следующие авторские статьи нашего преподавателя Евгения Волосатова на Хабре: