Числовые и Буквенные выражения

Контрольные вопросы:

1. Определение суммы двух целых неотрицательных чисел. Операция сложения.

2. Существование и единственность суммы.

3. Законы сложения.

4. Произведение двух целых неотрицательных чисел. Операция умножения.

5. Существование и единственность произведения.

6. Законы умножения.

7. Определение произведения двух целых неотрицательных чисел.

8. Связь с начальным курсом математики

Литература: (2) гл. II, 12 пп 54-56; (3) гл. III, §§ 13, 15; (4) гл. II, 10-15; (5) гл. II, 5 пп 38-43; (6) гл. VIII, с. 240-249.

Сумма целых неотрицательных чисел существование и единственность суммы

Определение: Суммой целых неотрицательных чисел a и b называется целое неотрицательное число a + b, равное числу элементов в объединении непересекающихся множеств А и В, таких, что m(A) = a, m(B) = b

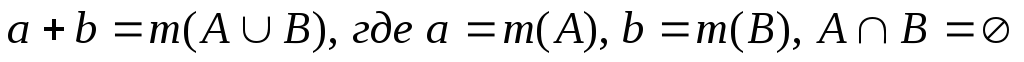
a + b – сумма, a и b – слагаемые.

Теорема: сумма любых двух целых неотрицательных чисел существует и она единственна.

Существование: пусть a и b – целые неотрицательные числа, тогда a=m(A), b=m(B), где А и В – множества любой природы и АВ=Ø. Так как А ≠Ø и В≠Ø, то АВ≠Ø и является конечным множеством =>с Z₀, что с = m(AB). Тогда по определению суммы целых неотрицательных чисел с и есть сумма чисел a и b.

II Единственность: покажем, что сумма a+b единственна и не зависит от выбора представителей в классах эквивалентности.

Пусть числа a и b кроме множеств А и В определяют множества А₁ и B₁, и пусть с₁= m (A₁B₁). Покажем, что с = с₁(а это будет тогда, когда АВ~A₁B₁).

Дано: A ~ A₁, B ~ B₁, A₁ B₁=A B = Ø.

Доказать: A B ~ A₁ B₁.

Для того, чтобы показать, что А В ~ , нужно показать, что между ними существует хотя бы одно взаимно однозначное соответствие. Построим его.

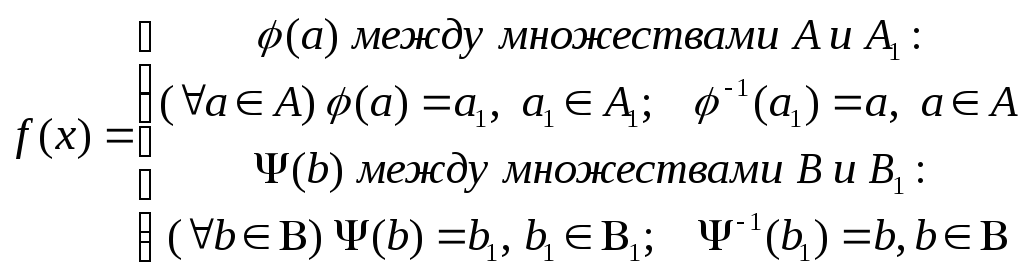
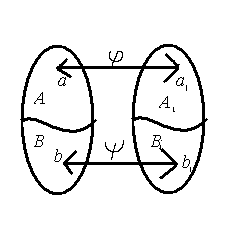
Т.о. будет взаимно однозначно поставлен элемент из множестваА₁В₁ =>.

Операция отыскания суммы называется сложением.

Основные законы сложения целых неотрицательных чисел

1. Коммутативный закон: (а,b  Z₀◦) [a + b = b + a]

Пусть, а = m (A), b = m (B), A B = Ø.

Так как на множестве всех множеств справедлив коммутативный закон операции объединения: АВ =ВA, а равные множества имеют равные численности, то m (AB) = т(BA).

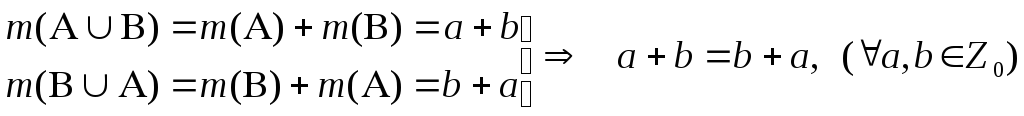
Тогда:

2. Ассоциативный закон: (а,b, c Î Z₀) [(a + b) + c = a + (b + c)]

Доказательство опирается на свойство ассоциативности объединения множеств:

(A B)C = A(BC) => m ((AB)C) = m (A(BC))

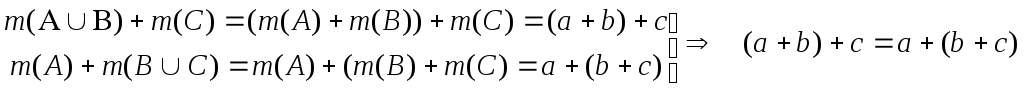
Пусть даны К конечных множеств, причем никакие два из них не имеют общих элементов: тогда, если а₁= m (A₁), a₂= m (A₂)… a_k = m (A_k), то a₁+ a₂ + …+ a_k = m (A₁ A₂ … A_k).

Произведение целых натуральных чисел

Определение: Произведением целых неотрицательных чисел a и b называется целое неотрицательное число a * b, удовлетворяющее следующим условиям:

1) a * b = a + a +…+ a, при b > 1,

2) a * 1 = a, при b = 1,

3) a * 0 = 0, при b = 0.

Действие нахождения произведения чисел a и b называется умножением, а числа а и b – множителями.

Дадим теретико-множественное обоснование этого определения.

Пусть А_i ∩Аj= Ø и m (A_j) = m (Aj) = a.

Если множеств будет «b», а каждое из них содержит по «а» элементов, то множество A₁A₂…A_b будет содержать а * b элементов, т.к. m (A₁A₂…A_b) = m (A₁) + m (A₂) +…+ m (A_b) = a + a +…+ a = a * b.

Существование и единственность произведения целых неотрицательных чисел при таком подходе вытекает из существования и единственности суммы любого конечного числа слагаемых. Существование и единственность произведений а * 1 и а * 0 принимается по определению.

Именно с таким подходом к определению произведения целых неотрицательных чисел знакомятся учащиеся в начальной школе.

Однако для вывода законов умножения и правил, связывающих умножение с другими действиями, удобен другой подход.

Определение: Произведением целых неотрицательных чисел а и b называется целое неотрицательное число а * b, равное числу элементов в декартовом произведении множеств А и В, таких, что m (A) = a, m (B) = b.

a * b = m (A B), a = m (A),где b = m (B) .

1. Если b = 1, то m (B) = 1 => B = ₁>, пусть A = ₁, x₂,…x_a>, т.е. m (A) = a

A B = <(x ₁y₁), (x ₂y₁). (x _a y₁)> и тогда очевидно, что m (A B) = a. A так как m (A B) = m (A) * m (B) (правило произведения), то a * 1 = a.

2. Если b = 0, то m (B) = 0 => B = Ø, тогда A B = Ø => m (AB) =0= m (A) * m (B).Откуда получаем: a * 0 = 0.

Теорема: Произведение любых двух целых неотрицательных чисел существует и оно единственно.

Так как по определению a * b = m (A B), то для доказательства достаточно показать существование такого декартового произведения множеств. Но для любых конечных множеств множество (АВ) существует, значит существует и целое неотрицательное число m (A B), которое принимается за произведение чисел a и b, где a = m (A), b = m (B).

Пусть A ~ A₁ и B ~ B₁ и m (A) = m (A₁) = a, m (B) = m (B₁) = b. Найдем A B и A₁ B₁ .

Пусть a * b = m (A B)и a * b = m (A₁ B₁).

Чтобы показать единственность произведения, достаточно показать, что А * В ~ А₁ * В₁_. А для этого нужно показать, что между этими множествами существует взаимно однозначное соответствие.

Так как A ~ A₁, то существует взаимно однозначное соответствие , при котором

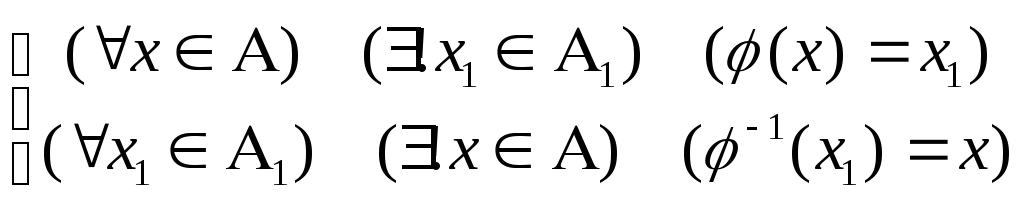
Так как В ~ B₁, то существует взаимно однозначное соответствие при котором

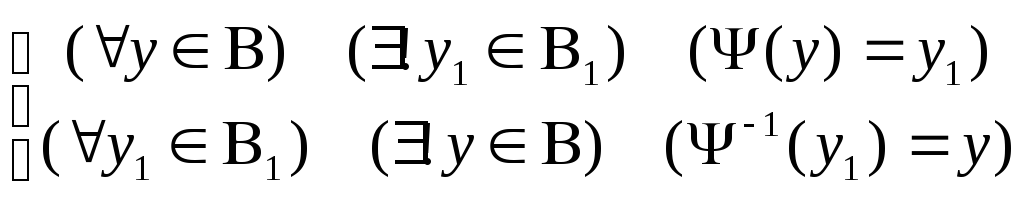
Тогда зададим соответствие f (x, y) таким образом, что

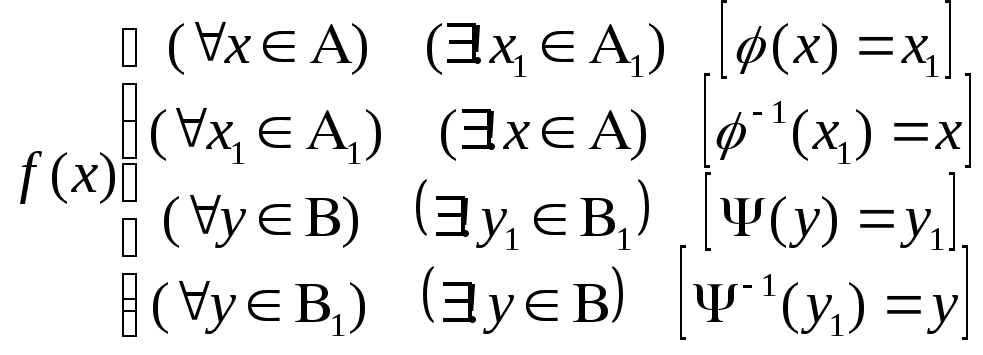
, т.е.

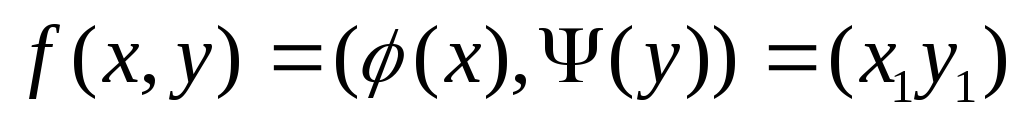
Очевидно, что f является взаимно однозначным соответствием, т.к. любой паре (x,y) ставится в соответствие единственная пара (x_1, y₁) и наоборот.

Основные законы действия умножения

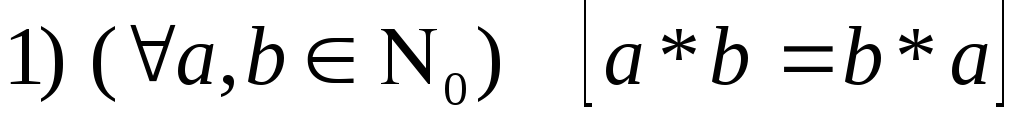
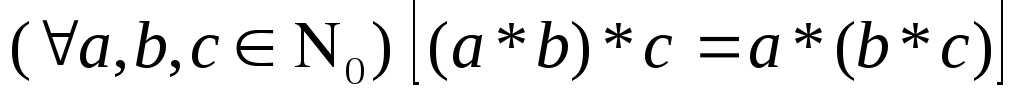
2)

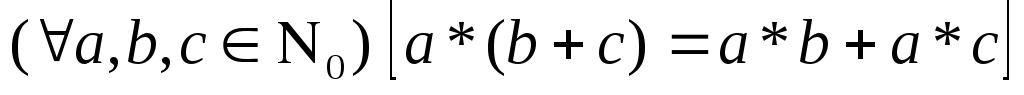
3)

4)

Доказательство этих законов предлагается провести самостоятельно.

Лекция № 29. ОПЕРАЦИИ НАД ЦЕЛЫМИ НЕОТРИЦАТЕЛЬНЫМИ ЧИСЛАМИ (КОЛИЧЕСТВЕННАЯ ТЕОРИЯ).

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Числовые и буквенные выражения

Строго говоря, математика состоит из выражений. В этой статье разберем, что такое числовые и буквенные выражения и научимся выполнять различные арифметические действия.

О чем эта статья:

Числовые выражения: что это

Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.

Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.

Например:

Это простые числовые выражения.

Более сложные числовые выражения состоят из нескольких чисел и знаков арифметических действий:

Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.

Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.

11 — значение числового выражения 5 + 6.

48 — значение числового выражения 6 * 8.

При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:

Сначала выполняется действие, записанное в скобках.

Затем выполняются действия деления и умножения слева направо.

В последнюю очередь выполняются действия сложения и вычитания слева направо.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Пример 1. Найдите значение числового выражения: 3 * (2 + — 4

Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)

(6 + 7) * (13 + 2) = 195

Часто бывает нужно сравнить два числовых выражения.

Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.

Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2

Сначала находим значение первого выражения:

Затем находим значение второго выражения:

Сравниваем получившиеся результаты:

Пример 2. Сравните следующие числовые выражения:
5 * (12 — 2) — 7 и (115 + 9) — (7 — 3)

Находим значение первого выражения, соблюдая порядок выполнения арифметических действий:

5 * (12 — 2) — 7 = 43

Затем находим значение:

Сравниваем полученные результаты:

Буквенные выражения

Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.

В буквенном выражение есть цифры, знаки арифметических действия и буквы.

Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.

Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.

У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:

Сначала следует прочитать его полностью.

Затем оно записывается.

Третьим шагом идет подстановка значения неизвестного в выражение.

А затем производится вычисление, согласно очередности выполнения арифметических действий.

Пример 1. Найдите значение выражения при x = 4: 5 + x.

Читаем: найдите сумму числа 5 и x.

Подставляем вместо неизвестного x число 4.

Вычисляем: 5 + 4 = 9.

Пример 2. Найдите значение выражения: (4 + a) * (2 + x) при а = 2 и х = 5.

Читаем: найдите произведение суммы числа 4 и а и суммы числа 2 и x.

Подставляем вместо неизвестного a число 2.

Вычисляем 4 + 2 = 6.

Подставляем вместо неизвестного x число 5.

Вычисляем 2 + 5 = 7.

Находим произведение 6 * 7 = 42.

Записываем результат: (4 + 2) * (2 + 5) = 42.

Выражения с переменными

Переменная — буквенное обозначение элемента, который может принимать любое числовое значение.

Например, в выражении x + a — 8

Если вместо переменных подставить числа, то буквенное выражение x + a — 8 станет числовым выражением. Вот так:

подставляем вместо переменной x число 5, а вместо переменной a — число 10, получаем 5 + 10 — 8.

Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.

После подстановки значения переменных находим значение x + a — 8 = 5 + 10 — 8 = 7.

Часто можно встретить буквенные выражения, записанные следующим образом:

Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.

5x — это произведение числа 5 и переменной x.

4a — это произведение числа 4 и переменной a.

Числа 4 и 5 называют коэффициентами.

Коэффициент показывает, во сколько раз будет увеличена переменная.

Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.

Умножение, сложение, вычитание и деление целых чисел: основные свойства

Умножение, сложение, вычитание и деление — основные операции с целыми числами. Результаты этих операций с любыми целыми числами обладают рядом характеристик. Иначе говоря, операции умножения, сложения, вычитания и деления целых чисел обладают свойствами. Данная статья посвящена рассмотрению основных свойств умножения, сложения, вычитания и деления целых чисел.

Сложение целых чисел. Основные свойства

Все свойства сложения натуральных чисел оказываются справедливы и для целых чисел. Ведь множество целых чисел ℤ включает в себя множество натуральных чисел ℕ . Приведем ниже основные свойства сложения.

Коммутативное свойство сложения

Переместительное (коммутативное свойство) или переместительный закон.

От перемены мест слагаемых сумма не меняется.

Согласно этому свойству, справедливо равенство:

35 + 251 = 251 + 35

Свойство коммутативности работает вне зависимости от знака.

— 528 + 3700 = 3700 + — 528

Ассоциативное свойство сложения

Сочетательное (ассоциативное свойство) или сочетательный закон.

Сложение целого числа с суммой двух целых чисел эквивалентно сложению суммы двух первых чисел с третьим.

a + b + c = a + b + c

Примечание: данное свойство применимо и для большего количества слагаемых.

Вот несколько примеров. Согласно свойству ассоциативности справедливы равенства:

64 + 81 + ( — 49 ) = 64 + 81 + ( — 49 ) = 64 + 81 + ( — 49 );

( 128 + ( — 75 ) ) + 96 = 128 + ( ( — 75 ) + 96 ).

Свойства сложения, связанные с числом 0

1. Число нуль — нейтральный по сложению элемент.

Прибавление нуля к любому целому числу не меняет этого числа.

2. Сумма любого целого числа и противоположного ему числа равна нулю.

Умножение целых чисел. Основные свойства

Как и в случае со сложением, все свойства умножения натуральных чисел переносятся на целые числа.

Для умножения также действуют переместительный и сочетательный (коммутативный и ассоциативный) законы.

Переместительное свойство умножения

От перемены мест множителей произведение не меняется.

Приведем пример. Очевидно, что произведение целых чисел 2 · 3 эквивалентно произведению 3 · 2 .

Сочетательное свойство умножения

Сочетательное свойство для умножения эквивалентно сочетательному свойству сложения. В буквенном виже оно записывается следующим образом:

a · ( b · c ) = ( a · b ) · c

a , b , c — произвольные целые числа.

Примечание: данное свойство применимо и для большего количества множителей.

В соответствии с этим свойством можно говорить о справедливости следующих равенств:

— 12 · 3 · 8 = — 12 · 3 · 8 ;

119 · ( ( — 251 ) · 36 ) = ( 119 · ( — 251 ) ) · 36 .

Умножение числа на нуль

Результатом умножения любого целого числа на нуль является число нуль.

Справедливо и обратное: произведение двух целых чисел a и b равно нулю, если хотя бы один из множителей равен нулю.

a · b = 0 если a = 0 или b = 0 .

Умножение числа на единицу

Умножение любого целого числа на единицу дает в результате это число. Иными словами, умножение на единицу не изменяет умножаемое число.

Произведение целого числа a на сумму двух чисел b и c равно сумме произведений a · b и a · c .

a · ( b + c ) = a · b + a · c

Данное свойство часто используется при упрощении выражений, одновременно содержащих как операции сложения, так и умножения.

В совокупности с ассоциативным свойством и распределительным законом можно легко расписать произведение целого числа на сумму из более чем трех слагаемых, а также произведение сумм.

Вычитание целых чисел. Основные свойства

Вычитание — действие, обратное сложению. Число c является разностью двух чисел a и b тогда, когда сумма b + c равна a . Можно сказать, что разность чисел a и b — это сумма чисел a и — b . Свойства вычитания являются следствием свойств сложения и умножения.

Основные свойства вычитания

Вычитание чисел не обладает переместительным свойством за исключением случая, когда a = b . a — b ≠ b — a .

Разность целых чисел, равных друг другу: a — a = 0 .

Вычитание суммы двух чисел из другого числа: a — ( b + c ) = a — b — c .

Вычитание целого числа из суммы: a + b — c = a — c + b = a + ( b — c ) .

Распределительное свойство умножения относительно вычитания: a · ( b — c ) = a · b — a · c .

Деление целых чисел. Основные свойства

Деление — операция, обратная умножению. Число c называется частным от деления чисел a и b , когда произведение b · c равно a . Запишем основные свойства деления целых чисел.

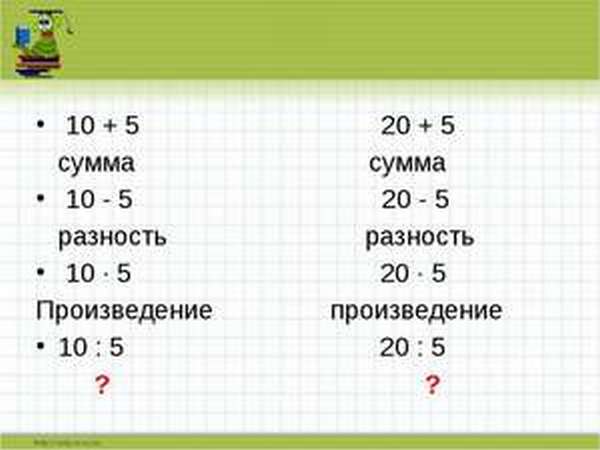
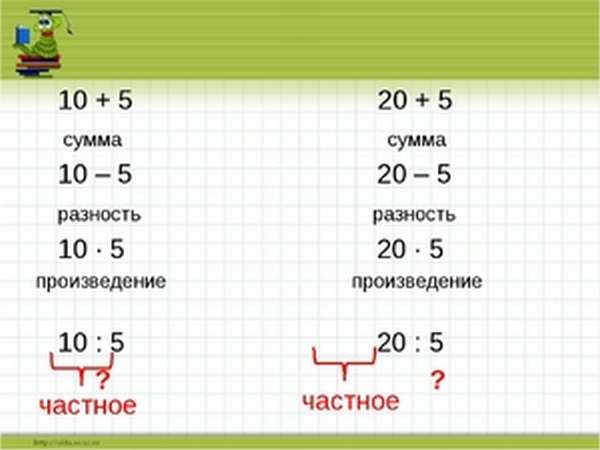
Сумма разность произведение и частное что это

Разность — результат вычитания; произведение — результат умножения; сумма — результат сложения; частное — результат деления.

Что такое разность, произведение, сумма, частное?

Что такое «закон стороны» и как им пользоваться?
Что такое «закон стороны» и как им пользоваться? Александр Казакевич, 22 декабря 2007 «Я была такая страшненькая… пока ты не махнул мне рукой» Известно, что человек может общаться с другими людьми как при помощи слов, так и при помощи жестов. В середине прошлого столетия ученые пришли к неожиданному для многих, в том числе и для самих себя, выводу: ока.

Что такое МЛМ?
Сегодня в мире свыше 5000 МЛМ-компаний, а сама индустрия МЛМ существует больше 50 лет. В Россию сетевой маркетинг пришел уже более 20 лет назад. А началось все в конце 80-х годов. Когда в России появилась всем известная компания Гербалайф. У того большинства, кто был на презентации этой компании, впечатление от презентации сложилось негативное. 90-е годы б.

Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.

Арифметические действия с числами

Разность в математике

Как найти разницу величин

Математические действия с разностью чисел

Простые примеры

Более сложные примеры

Математика для блондинок

Арифметические действия с числами

Основными арифметическими действиями в математике являются:

Каждый результат этих действий также имеет своё название:

сумма — результат, получившийся при сложении чисел,

разность — результат, получившийся при вычитании чисел,

произведение — результат умножения чисел,

частное — результат деления.

Это интересно: что такое модуль числа?

Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:

сумма — прибавить,

разность — отнять,

произведение — умножить,

частное — разделить.

Разность в математике

Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:

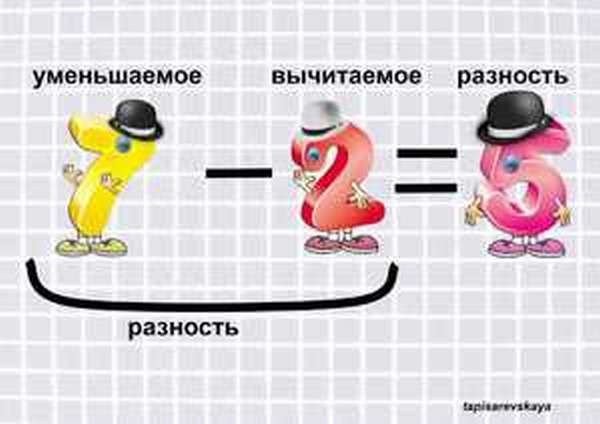
Разность чисел означает, насколько одно из них больше другого.

Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.

Это вычитание одного числа из другого.

Это цифра, составляющая остаток при минусовании двух величин.

Это величина, являющаяся результатом вычитания двух значений.

Разность показывает количественное различие между двумя цифрами.

Это результат одного из четырёх арифметических действий, которым является вычитание.

Это то, что получится, если из уменьшаемого отнять вычитаемое.

И все эти определения являются верными.

Как найти разницу величин

Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:

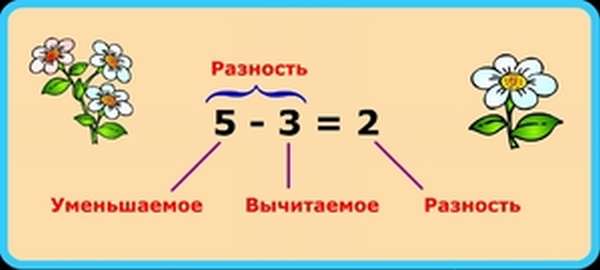
Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.

Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:

Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.

Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?

Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).

Вычитаемое — это математическое число, которое вычитают из уменьшаемого.

Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:

Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.

Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

Математические действия с разностью чисел

Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.

Простые примеры

Пример 1. Найти разницу двух величин.

20 — уменьшаемое значение,

Решение: 20 — 15 = 5

Ответ: 5 — разница величин.

Пример 2. Найти уменьшаемое.

32 — вычитаемое значение.

Решение: 32 + 48 = 80

Пример 3. Найти вычитаемое значение.

17 — уменьшаемая величина.

Решение: 17 — 7 = 10

Ответ: вычитаемое значение 10.

Более сложные примеры

На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.

Пример 4. Найти разницу трёх значений.

Даны целые значения: 56, 12, 4.

56 — уменьшаемое значение,

12 и 4 — вычитаемые значения.

Решение можно выполнить двумя способами.

1 способ (последовательное отнимание вычитаемых значений):

1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым),

2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):

1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым),

Ответ: 40 — разница трёх значений.

Пример 5. Найти разницу рациональных дробных чисел.

Даны дроби с одинаковыми знаменателями, где

4/5 — уменьшаемая дробь,

Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.

Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5

Пример 6. Утроить разницу чисел.

А как выполнить такой пример, когда требуется удвоить или утроить разницу?

Вновь прибегнем к правилам:

Удвоенное число — это величина, умноженная на два.

Утроенное число — это величина, умноженная на три.

Удвоенная разность — это разница величин, умноженная на два.

Утроенная разность — это разница величин, умноженная на три.

7 — уменьшаемая величина,

5 — вычитаемая величина.

2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.

Пример 7. Найти разницу величин 7 и 18.

7 — уменьшаемая величина,

Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?

И опять есть применяемое для конкретного случая правило:

Если вычитаемое больше уменьшаемого, разница окажется отрицательной.

Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.

Математика для блондинок

Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.

В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.

И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:

сумму — сложением слагаемых,

произведение — умножением множителей,

частное — делением делимого на делитель.

что такое разность и сумма

Автор Ваня Ромашин задал вопрос в разделе Образование за рубежом

что такое разность,произведение,сумма,частное, и получил лучший ответ

Ответ от Ирина Робертовна Махракова[гуру]
Разность – результат вычитания; произведение – результат умножения; сумма – результат сложения; частное – результат деления.

* 666 — сумма всех чисел на рулетке.
* 666 — сумма квадратов первых семи простых
подробнее.

Что такое сумма разность произведение и частное?

Разность — результат вычитания; произведение — результат умножения; сумма — результат сложения; частное — результат деления.

Что такое произведение и частное?

Произведением называется результат умножения целых чисел. Числа, которые участвуют в умножении, называются множителями. Частное — это результат, который получается при делении одного числа на другое. Число, которое делят, называется делимым, а число, на которое делят, называется делителем.

Что такое сумма разница?

Сумма — результат сложения. Разность чисел — это результат вычитания.

Что такое произведение и частное математика?

Умножение. Умножить некоторое число (множимое) на целое число (множитель) — значит повторить множимое слагаемым столько раз, сколько указывает множитель. Результат называется произведением. . Данное произведение получает название делимого, данный сомножитель — делителя, искомый сомножитель — частного.

Что означает разность?

Разность чисел и — это результат вычитания числа из числа .

Что такое произведение и частное чисел?

Произведение — это результат умножения чисел. . Частное — это результат деления чисел.

Что такое делимое и делитель и частное?

Число, которое делят, называется делимое. Число, на которое делят делимое, называется делитель. Результат деления – частное. Числа, которые соединены знаком деления, тоже называются частное.

Что такое сумма чисел 2 класс?

Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых). . Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.

Что такое сумма частное разность?

Разность — результат вычитания; произведение — результат умножения; сумма — результат сложения; частное — результат деления.

Что такое разность это минус или деление?

Разность — это отнять. Результат вычитания называется разность. При чтении это будет звучать так: «уменьшаемое минус вычитаемое равно разность«.

Что такое делитель и произведение?

Деление — есть нахождение одного из сомножителей по произведению и другому сомножителю. Данное произведение получает название делимого, данный сомножитель — делителя, искомый сомножитель — частного. Произведение делителя 5 и частного 7 дает делимое 35 (проверка деления).

Что означает произведение по математике?

Произведение — в математике: результат операции умножения. Произведение — теоретико-категорное обобщение декартового произведения множеств.

Что такое уменьшаемое вычитаемое и разность?

Числа при вычитании называются уменьшаемое, вычитаемое, разность. Уменьшаемое – число, из которого вычитают. Вычитаемое – число, которое вычитают. Разность – результат вычитания.

Что такое разность в примерах?

Разность получается путем вычитания одного числа (вычитаемого) из другого (уменьшаемого). То есть, чтобы определить разность, нужно просто вычесть из большего числа меньшее. Например, числа 15 и 10.

Что значит найти разность арифметической прогрессии?

Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии и обозначается d.

Что такое разность Википедия?

Ра́зность — многозначный термин: результат вычитания. Разность (минералогия) (например, «среднезернистые разности» или «мелоподобные разности»)

Как найти разность чисел в математике

Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.

Арифметические действия с числами

Разность в математике

Как найти разницу величин

Математические действия с разностью чисел

Простые примеры

Более сложные примеры

Математика для блондинок

Арифметические действия с числами

Основными арифметическими действиями в математике являются:

сложение,

вычитание,

умножение,

деление.

Каждый результат этих действий также имеет своё название:

сумма — результат, получившийся при сложении чисел,

разность — результат, получившийся при вычитании чисел,

произведение — результат умножения чисел,

частное — результат деления.

Это интересно: что такое модуль числа?

Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:

сумма — прибавить,

разность — отнять,

произведение — умножить,

частное — разделить.

Разность в математике

Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:

Разность чисел означает, насколько одно из них больше другого.

Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.

Это вычитание одного числа из другого.

Это цифра, составляющая остаток при минусовании двух величин.

Это величина, являющаяся результатом вычитания двух значений.

Разность показывает количественное различие между двумя цифрами.

Это результат одного из четырёх арифметических действий, которым является вычитание.

Это то, что получится, если из уменьшаемого отнять вычитаемое.

И все эти определения являются верными.

Как найти разницу величин

Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:

Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.

Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:

Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.

Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?

Читайте также: Атмосферный фронт: что это такое, основные признаки и разновидности, особенности в центральной России

Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).

Вычитаемое — это математическое число, которое вычитают из уменьшаемого.

Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:

Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.

Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

Математические действия с разностью чисел

Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.

Простые примеры

Пример 1. Найти разницу двух величин.

20 — уменьшаемое значение,

Решение: 20 — 15 = 5

Ответ: 5 — разница величин.

Пример 2. Найти уменьшаемое.

32 — вычитаемое значение.

Решение: 32 + 48 = 80

Пример 3. Найти вычитаемое значение.

17 — уменьшаемая величина.

Решение: 17 — 7 = 10

Ответ: вычитаемое значение 10.

Более сложные примеры

На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.

Пример 4. Найти разницу трёх значений.

Даны целые значения: 56, 12, 4.

56 — уменьшаемое значение,

12 и 4 — вычитаемые значения.

Решение можно выполнить двумя способами.

1 способ (последовательное отнимание вычитаемых значений):

1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым),

2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):

1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым),

Ответ: 40 — разница трёх значений.

Пример 5. Найти разницу рациональных дробных чисел.

Даны дроби с одинаковыми знаменателями, где

4/5 — уменьшаемая дробь,

Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.

Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5

Пример 6. Утроить разницу чисел.

А как выполнить такой пример, когда требуется удвоить или утроить разницу?

Вновь прибегнем к правилам:

Удвоенное число — это величина, умноженная на два.

Утроенное число — это величина, умноженная на три.

Удвоенная разность — это разница величин, умноженная на два.

Утроенная разность — это разница величин, умноженная на три.

7 — уменьшаемая величина,

5 — вычитаемая величина.

2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.

Пример 7. Найти разницу величин 7 и 18.

7 — уменьшаемая величина,

Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?

И опять есть применяемое для конкретного случая правило:

Если вычитаемое больше уменьшаемого, разница окажется отрицательной.

Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.

Математика для блондинок

Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста. Расскажу, где снять крутую шлюху в Крыму. Вот сайт с проститутками: https://sexanketa-krym.com/ Очень крутые путаны.. Настоятельно советую присмотреться к данному ресурсу и заняться сексом, тем более это не дорого.

В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.

И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:

Как найти разность чисел в математике

Основными арифметическими действиями в математике являются:

сложение;

вычитание;

умножение;

деление.

Каждый результат этих действий также имеет своё название:

сумма — результат, получившийся при сложении чисел;

разность — результат, получившийся при вычитании чисел;

произведение — результат умножения чисел;

частное — результат деления.

Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:

сумма — прибавить;

разность — отнять;

произведение — умножить;

частное — разделить.

Разность в математике

Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:

Разность чисел означает, насколько одно из них больше другого.

Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.

Это вычитание одного числа из другого.

Это цифра, составляющая остаток при минусовании двух величин.

Это величина, являющаяся результатом вычитания двух значений.

Разность показывает количественное различие между двумя цифрами.

Это результат одного из четырёх арифметических действий, которым является вычитание.

Это то, что получится, если из уменьшаемого отнять вычитаемое.

И все эти определения являются верными.

Как найти разницу величин

Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:

Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.

Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:

Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.

Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?

Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).

Вычитаемое — это математическое число, которое вычитают из уменьшаемого.

Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:

Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.

Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

Что такое сумма, разность, произведение, частное в математике?

I. Математические понятия СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ взаимосвязаны с математическими терминами СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ, ДЕЛЕНИЕ.

Все определения даются здесь на множестве натуральных чисел.

Каждой паре чисел ставится в соответствие число, называемое их СУММОЙ.

Сумма состоит из стольких единиц, сколько их содержится в числах (слагаемых) из данной пары.

СУММА есть результат сложения чисел-слагаемых.

Вычитание — это операция, обратная сложению. Она состоит в нахождении одного из слагаемых по сумме и другому слагаемому. Данная сумма называется уменьшаемым, данное слагаемое — вычитаемым, а искомое слагаемое — РАЗНОСТЬЮ.

РАЗНОСТЬ — это число, являющееся результатом вычитания, остаток вычитания.

ПРОИЗВЕДЕНИЕ — это результат умножения.

Деление есть операция, обратная умножению.

Деление — это нахождение одного из сомножителей по произведению и другому сомножителю. Данное произведение называется делимым, данный сомножитель — делителем, а искомый сомножитель — это ЧАСТНОЕ, то есть число, полученное от деления одного числа на другое.

II. ДРУГИЕ ЗНАЧЕНИЯ СЛОВ СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ.

Все используемые в качестве математических понятий слова могут иметь и другие лексические значения.

СУММА в переносном значении означает совокупность, общее количество чего-либо.

Например. Профессионализм педагога заключается в сумме знаний, умений и навыков, передаваемых им своим ученикам. Отсутствие нужной суммы денег заставило отказаться от покупки.

РАЗНОСТЬ имеет значения разницы, несходства, отличия в чем-либо.

ПРОИЗВЕДЕНИЕ означает что-либо произведенное в процессе труда, создание чего-нибудь, продукт труда, творчества, искусства и т.п.

Например. Высокое художественное произведение заставляет человека думать над своей жизнью. На конкурсе юных пианистов мальчик играл произведение П.И. Чайковского. Эта шкатулка — настоящее произведение искусства.

ЧАСТНОЕ — это что-то личное, персональное, принадлежащее только одному человеку, это его собственность, его и только его достояние. И будь то самоличные мысли, будь то имущество или что-нибудь другое, но оно принадлежит только ему, частному лицу.

Например. Подруга подарила мне записную книжку с надписью «Частное». Хорошо ли противопоставлять частное общественному?

Как найти уменьшаемое и вычитаемое число?

Как в математике найти разницу чисел мы уже разобрались. Это довольно просто. Но сможем ли мы найти уменьшаемое и вычитаемое число, если одно число неизвестно? Конечно можем, так как нам будут известны два других числа. Например, как мы можем найти уменьшаемое число? Если мы знаем значение разницы и вычитаемого, то сумма этих двух чисел равняется уменьшаемому:

Y – 10 = 18, где Y – число уменьшаемое

Значит, Y = 18 + 10

18 + 10 = 28

Y = 28

Вычитаемое находится так же просто. Если мы знаем разницу и уменьшаемое, значит вычитаемое мы получим, отняв от уменьшаемого числа разность:

28 – B = 10, где B – число вычитаемое

Значит, B = 28 – 10

28 – 10 = 18

B = 18

Натуральные числа

Математические действия с разностью чисел

Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.

Простые примеры

Пример 1. Найти разницу двух величин.

20 — уменьшаемое значение,

Решение: 20 — 15 = 5

Ответ: 5 — разница величин.

Пример 2. Найти уменьшаемое.

32 — вычитаемое значение.

Решение: 32 + 48 = 80

Пример 3. Найти вычитаемое значение.

17 — уменьшаемая величина.

Решение: 17 — 7 = 10

Ответ: вычитаемое значение 10.

Более сложные примеры

На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.

Пример 4. Найти разницу трёх значений.

Даны целые значения: 56, 12, 4.

56 — уменьшаемое значение,

12 и 4 — вычитаемые значения.

Решение можно выполнить двумя способами.

1 способ (последовательное отнимание вычитаемых значений):

1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым),

2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):

1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым),

Ответ: 40 — разница трёх значений.

Пример 5. Найти разницу рациональных дробных чисел.

Даны дроби с одинаковыми знаменателями, где

4/5 — уменьшаемая дробь,

Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.

Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5

Пример 6. Утроить разницу чисел.

А как выполнить такой пример, когда требуется удвоить или утроить разницу?

Вновь прибегнем к правилам:

Удвоенное число — это величина, умноженная на два.

Утроенное число — это величина, умноженная на три.

Удвоенная разность — это разница величин, умноженная на два.

Утроенная разность — это разница величин, умноженная на три.

7 — уменьшаемая величина,

5 — вычитаемая величина.

2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.

Пример 7. Найти разницу величин 7 и 18.

7 — уменьшаемая величина,

Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?

И опять есть применяемое для конкретного случая правило:

Если вычитаемое больше уменьшаемого, разница окажется отрицательной.

Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Похожие записи:
Что такое сумма чисел и разность чисел в математике…
Что такое сумма разность произведение частное в…
Что такое сумма квадратов чисел
Что такое сумма разность уменьшаемое вычитаемое разность
Что такое сумма событий
$Что такое сумма чисел и разность 1 класс$
Что такое сумма чисел и разность 1 класс