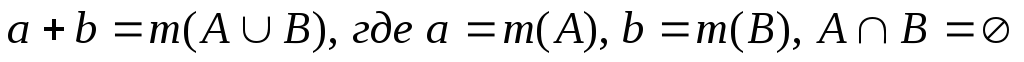Что такое сумма чисел и разность 1 класс

Отсюда следует, что это правило применимо не к любой сумме натуральных чисел , а только к той, в которой хотя бы одно из слагаемых больше, чем вычитаемое .

Как меняется разность при изменении вычитаемого или уменьшаемого

Изменение разности при изменении вычитаемого и уменьшаемого является следствием описанных в уроке изменений суммы чисел с изменением ее слагаемых.

Если уменьшаемое увеличить на некоторое количество единиц, то и разность увеличится на такое же количество единиц.

Если уменьшаемое уменьшить на некоторое количество единиц, то и разность уменьшится на такое же количество единиц.

Если вычитаемое увеличить на некоторое количество единиц, то разность уменьшится на такое же количество единиц.

Если вычитаемое уменьшить на некоторое количество единиц, то разность увеличится на такое же количество единиц.

Если сразу оба числа, и уменьшаемое, и вычитаемое, увеличить или уменьшить на одно и то же количество единиц, то разность не изменится.

Правила вычитания разности

Если нужно вычесть из числа разность других чисел, можно воспользоваться одним из двух способов:
1. Прибавить к данному числу вычитаемое, и из получившейся суммы вычесть уменьшаемое;
2. Вычесть из данного числа уменьшаемое, а потом результат этого действия сложить с вычитаемым.

Это свойство выводится из предыдущих, рассмотренных нами.

Рассмотрим на примере 22 -( 17 — 3 ).

Для начала вычислим обычным способом: сперва узнаем разность в скобках (это будет 17-3= 14 ), а потом вычтем 14 из 22 . Получится 22-14=8 .

22 -( 17 — 3 ) = 8

Теперь вернемся к исходному примеру и отнимем от 22 не разность 17-3 , то есть, не 17 без 3 единиц, а все число 17 .

22 — 17 = 5

Но мы ведь отняли больше, чем нужно было , поэтому нам нужно вернуть лишне взятые 3 единицы обратно, а именно, прибавить их к полученному результату.

5+ 3 = 8

Попробуем решить другим путем : увеличим и уменьшаемое (данное число), и вычитаемое (разность в скобках) на одно и то же число 3 . Получим:

22 +3-( 17 +3- 3 )

Так как 22+3=25 , а 3-3=0 , то в итоге получается:

25- 17 +0 = 8

Как видите, оба способа показали верный результат.

Вычитание однозначного числа

Вы сможете без каких-либо трудностей совершать вычитание любых чисел , если сперва хорошо натренируете себя вычитать однозначные числа в уме из однозначных и двухзначных.

А поскольку вычитание – это действие обратное сложению, тогда необходимо просто выучить на память все суммы однозначных чисел . Пользуясь ими, мы легко сможем получить необходимые вам разности.

Например, нам нужно найти разность чисел 17 и 8 . Для этого нам необходимо вспомнить, какое число при сложении с числом 8 дает сумму 17 ? Это число 9 , потому что 8+9=17 . Значит, если от 17 отнять 8 , мы получим: 17-8=9 .

Хорошо натренировавшись в нахождении разности чисел из суммы однозначных чисел, можно переходить к более сложным случаям вычитания . Подробно эти приемы рассмотрены в разделе рубрики «Устный счет».

Вычитание в столбик многозначных чисел

Так же, как и сложение, разность многозначных чисел удобно находить, используя вычитание в столбик .

Вычитание в столбик – это способ нахождения разности чисел при помощи их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим), и последующего вычисления.

Давайте найдем разность чисел 52063-4825 .

Запишем их друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел , т.е. единицы под единицами, десятки под десятками и т.д. После этого, под вторым слагаемым проводим горизонтальную черту, а между слагаемыми ставим знак действия, т.е. минус. У нас получилась такая запись:

Вычитание в столбик выполняется подобным способом, как и при сложении , только теперь мы отнимаем единицы от единиц, десятки от десятков и так далее.

Переходим к десяткам . У уменьшаемого в разряде десятков мы уже забрали 1 десяток , о чем нам напоминает поставленная точка . Поэтому, мы отнимаем 2 десятка вычитаемого не от 6 , а от 5 десятков , потому что 6-1=5 .

5>2 , значит, действие вычитания возможно : 5-2=3 . Пишем цифру 3 под чертой в разряде десятков , и переходим к сотням.

Сотен в уменьшаемом у нас нет , поэтому мы смотрим, сколько в числе содержится тысяч ? Их тоже 0 . Смотрим следующий разряд . Здесь у нас 5 десятков тысяч. Из них мы берем 1 десяток тысяч (ставим точку над цифрой 5 в уменьшаемом), что составляет 10 тысяч единиц. Из них (из взятых в десятках тысячах ) мы занимаем 1 тысячу для того, чтобы закончить вычитание в разряде сотен (ставим точку над цифрой 0 в разряде тысяч уменьшаемого).

1 тысяча единиц – это 10 сотен. Кроме этих занятых, больше в уменьшаемом сотен нет. В вычитаемом 8 сотен, поэтому находим разность сотен уменьшаемого и вычитаемого : 10-8=2 . Пишем результат под чертой в разряде сотен.

В разряде тысяч уменьшаемого у нас осталось 9 тысяч единиц (потому что 1 тысячу мы отдали для разряда сотен в качестве 10 сотен). Отнимаем от нее 4 тысячи вычитаемого, получаем: 9-4=5 , которые записываем под чертой в разряде тысяч.

Десятков тысяч в уменьшаемом осталось 5-1=4 (помните, мы для разряда сотен занимали?), в вычитаемом их нет совсем , то есть, 0 . Поэтому мы просто сносим цифру 4 в результат под черту в разряд десятков тысяч.

После нахождения разности чисел способом вычитания в столбик записываем ответ в строчном примере:

50063-4825 = 45238.

Как проверить действия сложение и вычитание?

После того, как вы закончили арифметическое действие, нужно проверить правильность ответа , то есть, удостовериться, что вычисление было сделано без ошибок .

Проверить сложение можно двумя способами: обратным сложением и вычитанием.

Обратное сложение означает, что мы меняем слагаемые местами, и складываем их еще раз. Если результат будет такой же, как и после первого сложения, значит, вычисление было верным.

Например, в уроке сложение чисел мы находили сумму: 5728+803 = 6531 . Проверим правильность результата способом обратного сложения :

Как видите, сложив слагаемые в другом порядке, мы получили тот же самый результат, а значит, вычисление было правильным .

Проверка сложения вычитанием – это способ, при котором нужно из суммы, которую получили после выполнения действия сложение, отнять одно из слагаемых. Если результат этого вычитания будет равен второму слагаемому (или сумме остальных слагаемых, если их больше двух), значит сложение было выполнено верно.

Проверим эту же сумму вычитанием : отнимем от результата 6531 слагаемое 5728 .

И этот способ проверки показал правильность нашего решения.

Проверить вычитание также возможно и сложением, и другим вычитанием.

Проверка вычитания сложением основана на взаимосвязи вычитания и сложения. Зная, что уменьшаемое – это сумма, а остаток и вычитаемое – это слагаемые, мы можем сложить между собой вычитаемое и остаток, и, если получим в результате уменьшаемое, значит, мы правильно сделали действие.

Вот так выглядит проверка вычитания сложением на примере вычисленной на этом уроке разницы 50063-4825 = 45238 :

Проверка вычитания вычитанием также основывается на взаимосвязи вычитания и сложения, а также на переместительном законе сложения. Так как уменьшаемое – это сумма двух слагаемых: вычитаемого и остатка, и сумма не зависит от порядка сложения слагаемых, то очевидно, что мы можем отнять от уменьшаемого остаток . Если результат этого действия будет равен вычитаемому , значит наша первая разность вычислена верно.

Урок математики в 1 классе «Прибавление и вычитание 1. Сумма и разность.»

На данном уроке дети учатся прибавлять и вычитать 1. Знакомятся с понятиями сумма и разность.

Содержимое разработки

Тема «Прибавление и вычитание числа 1. Сумма и разность».

Тип урока: решение учебной задачи.

Задачи: способствовать формированию умений называть одно предыдущее (последующее) число, выполнять движения по шкале влево или вправо от данного числа на 1 единицу; создать условия для знакомства с новыми понятиями «сумма» и «разность».

Планируемые результаты

Предметные: познакомятся с понятиями «сумма» и «разность»; научатся: выполнять прибавление 1 к 10, вычитание 1 из 10; использовать приемы вычислений: название одного, двух, трех чисел, следующих за данным числом (предшествующих данному числу); указывать разряд «десяток».

Метапредметные: Познавательные : общеучебные – овладение понятиями «сумма» и «разность», разряд «десяток»; прибавление 1 к 10, вычитание 1 из 10; овладение приемами вычислений: название одного, двух, трех чисел, следующих за данным числом (предшествующих данному числу); логические – построение рассуждения в форме связи простых суждений.

Регулятивные: планировать свои действия в соответствии с поставленной задачей и условиями ее реализации.

Коммуникативные: формулировать собственное мнение и позицию.

Личностные: расширяют познавательные интересы, учебные мотивы.

— Добрый день уважаемые дети. К нам сегодня на урок пришли гости, давайте с ними поздороваемся (дети выполняют поклон головой).

Прозвенел звонок для нас.
Все зашли спокойно в класс.
Встали все у парт красиво,
Поздоровались учтиво.
Тихо сели, спинки прямо.
Вижу, класс наш хоть куда.
Мы начнём урок, друзья.
Будем отвечать активно,
Хорошо себя вести,
Чтобы гости дорогие.
Захотели вновь прийти!

— А теперь начнем.

Быть должны всегда в порядке:
Ручки, книжки и тетрадки.
А девиз у нас такой:
«Все, что надо, — под рукой!»

Актуализация опорных знаний

— Ребята давайте немного посчитаем. К доске идут 3 ребенка и их задача? (вставить нужный знак и цифру)

Устный счет (индивидуальная работа)

— Пока дети работают, мы с вами тоже будем трудиться. Внимательно слушайте вопросы и отвечайте быстро.

1. Сосчитать до 10 через 1 начиная с 1. (1,3,5,7,9)

2. Начать с другого числа (2,4,6,8,10)

3. спуститься вниз через 1 (10,8,6,4,2,0)

4. с 9 ступеньки спуститься через 1. (9,7,5,3,1)

— Совсем скоро мы с вами начнем работать с числами от 1 до 20. Может быть кто – то из вас умеет считать?

— Кто может посчитать от 20 до 1.

— Теперь работаем с веерами.

5. Покажите число, которое стоит перед числом 5.

6. Покажите число, которое стоит слева от 7.

7. Покажите число, которое стоит между 3 и 5.

8. Покажите соседей числа 1.

— Молодцы. Внимательно послушайте задачу. На двух тарелках было всего 10 яблок. Когда с одной тарелки переложили на другую 2 яблока, на обеих тарелках их стало поровну. Сколько яблок было на каждой тарелке? (10= 3+7). Докажите.

— Давайте проверим работу наших ребят, которые работали у доски. ( дети отвечают и доказывают) Молодцы.

3. Открытие нового знания, способа действия.

Работа по учебнику

— откроем учебники на стр 31 задание 1. ( учащиеся выполняют задания, отвечают на вопросы, высказывают свое мнение)

— Какое число будет завтра и какое было вчера, если сегодня 8 марта? (вчера 7 марта, завтра – 9 марта)

— что мы предполагаем, называя «завтра»; что мы имеем в виду, называя «вчера», если сегодня – 10 апреля? ( вчера — 9 апреля, завтра — 11 апреля.)

— если сегодня – 6 мая? ( вчера — 5 мая, завтра – 7 мая)

— Если сегодня – 15 июня? (вчера – 14 июня, завтра 15 июня).

Стр 31 Задание 2.

— Назовите числа, следующие при счете за данными числами. (называют числа)

— Следующее задание 3.

— Назовите числа, предыдущие при счете данным числам. (называют числа).

— Молодцы. Следующее задание 4.

— Как можно прибавлять и вычитать число 1. Сделайте вывод. ( Чтобы к числу прибавить 1, можно назвать следующее за ним при счете число. Чтобы из числа вычесть 1, можно назвать предыдущее при счете ему число.)

4. Физминутка

Руки? НА МЕСТЕ
Ноги? НА МЕСТЕ
Локти? У КРАЯ
Спина? ПРЯМАЯ.

Следующее задание 5. Выполните сложение и вычитание. Назовите результат. (выполняют вычисления).

— Молодцы. Задание 6. Прочитайте математические записи. Число, которое получается при сложении, называют словом «сумма». Число, которое получается при вычитании, называют словом «разность».

Работа в тетради стр 23 № 1,2,3 (слайд)

— Задание 7, 8 . Назовите Сумму чисел. Назовите разность чисел. ( дети отвечают)

Работа в тетради стр 24 №4

5. Включение нового в активное использование в сочетании с раннее изученным, освоенным.

— задание 11. Прочитайте задачу. Что известно? Что требуется узнать? (10+4=14)

Слагаемые. Сумма. Уменьшаемое. Вычитаемое. Разность

— Сегодня мы узнаем, как называются числа при сложении и вычитании. Будем решать примеры и отвечать на сказочные вопросы.

— Расставьте данные числа в порядке возрастания, чтобы узнать, в мир сказок какого писателя мы отправимся.

— А.С. Пушкин – великий русский писатель, произведения которого интересны и любимы и взрослыми, и детьми. Наш урок математики будет посвящён сказкам А. С. Пушкина, которые он написал, заложив в основу народные сказки, рассказанные ему любимой няней.

2. Устный счёт

— Сколько стихотворных сказок было написано Александром Сергеевичем?
— Правильно, пять.

— Из какой сказки эти строки?

Белка там живёт ручная,
Да затейница какая!
Белка песенки поёт
Да орешки всё грызёт.

— Попробуйте справиться со следующим заданием и «расщёлкать» цепочку примеров, как белка – золотые орешки.

5 – 1 ○ -2 ○ +3 ○ -2 ○ +2 ○ -1 □

1 + 2 ○ -2 ○ +3 ○ +2 ○ -3 ○ +1 □

– Помогите закончить следующие строчки:

Ветер по морю гуляет
И кораблик подгоняет;
Он бежит себе в волнах
На раздутых парусах.
По морю, по океану
В царство славного … Салтана.

— Молодцы! Вы должны отправить кораблики к нужному берегу.

— Царица и её сын Гвидон плыли по морю в бочке 3 дня и 3 три ночи. Сколько дней и ночей царица и её сын находились в бочке?
— Правильно, шесть. Три плюс три будет – шесть.

Я круглое и гладкое.
Но не румяное и не сладкое.
Глядят в меня,
А видят себя. (Зеркало)

— Кто из героев сказок А. С. Пушкина очень часто смотрел в зеркало?
— Правильно, царица из сказки «Сказка о мёртвой царевне и семи богатырях».

— До обеда царица смотрелась в зеркало 5 раз, а после обеда – 2раза. Сколько раз посмотрела царица в зеркало за весь день?
— Правильно, семь раз. Потому что к пяти прибавить два будет – семь.

— В лесу жили в домике 7 богатырей и одна царевна. Сколько всего человек жило в домике?
— Совершенно верно, восемь. К семи прибавить один будет – восемь.

4)

— Из каких фигур состоит иллюстрация к сказке А. С. Пушкина «Сказка о рыбаке и рыбке»?

— Домик состоит: из синего большого квадрата и жёлтого маленького квадрата, из красного большого треугольника и зелёного маленького треугольника.
Дерево состоит из зелёного овала и коричневого четырёхугольника.
Солнышко – это жёлтый круг. Пенёк – коричневый квадрат.

Физкультминутка для глаз

Глазки видят всё вокруг,
Обведу я ими круг.
Глазкам видеть всё дано:
Где окно и где крыльцо.
Обведу я снова круг,
Посмотрю на мир вокруг.

Актуализация знаний 2

3. Формирование знаний

— Сколько кораблей с белыми парусами? Шесть.
— Сколько кораблей с красными парусами? Два.
— Сколько всего кораблей? Восемь.
— Правильно.

— Число 6 – это первое слагаемое; число 2 – это второе слагаемое; число 8 – сумма.

— Запись чисел «шесть плюс два» читается: «Сумма чисел шесть и два».

Таким образом, числа, которые складываются, называются слагаемыми, а результат сложения – их суммой.

Два «слагаемые» в ряд
Друг за дружкою стоят.
Вслед за ними знак «равно» —
Он известен нам давно.
Что в итоге получаем,
Словом «суммой» называем.

— Назовите второе слагаемое. Два.

— Найдите сумму чисел четыре и один. Сумма чисел четыре и один равна пяти.

— Назовите каждое число в этой записи математическим «именем».
— Слагаемое, слагаемое, сумма.

— Сколько рыбок поймал старик? Шесть.
— Сколько рыбок кот пытается съесть? Две.
— Правильно. Шесть минус два равно – четыре.

— В математике число шесть в таких равенствах называют уменьшаемым, число два – вычитаемым, четыре – разностью.

— Запись чисел «шесть минус два» читается: «Разность чисел шесть и два». Значит, число, которое уменьшают, называется уменьшаемым, а число, которое вычитают, называется вычитаемым. Результат является разностью.

Хоть я у всех всё отнимаю,
Но это вовсе не беда.
Я роль свою ведь выполняю,
А это, верьте, не со зла.
Поэтому вы знать должны
что компоненты все важны.
Уменьшаемое, вычитаемое, разность.

— Назовите уменьшаемое. Восемь.

— Найдите разность чисел шесть и один. Разность чисел шесть и один равна пяти.

— Назовите числа в примере их математическим «именем».

Физкультминутка

Дунул ветер – полетели.
Мы летели, мы летели
И на землю тихо сели.
Ветер снова набежал
И листочки все поднял.
Закружились, полетели
И на землю тихо сели.

Актуализация знаний 3

4. Закрепление знаний

Вдруг шатёр
Распахнулся… и девица,
Шамаханская царица,
Вся сияя, как заря,
Тихо встретила царя.

— Из какой сказки эти строки?
— Правильно, «Золотой петушок».

1)
— У Васи было три книги. Ему подарили ещё 2 книги. Сколько книг стало у Васи? Правильно, пять. Запишите этот пример. Назовите первое слагаемое –три; второе слагаемое – два; сумму – пять.

2)

-Назовите первое и второе слагаемое и запишите, сколько получится в сумме.

— Первое слагаемое – четыре, второе слагаемое два, сумма – шесть.
— Первое слагаемое – пять, второе слагаемое – три, сумма – восемь.
— Первое слагаемое – три, второе слагаемое – четыре, сумма – семь.

— Уменьшаемое равно девяти, вычитаемое – двум. Запиши разность этих чисел и вычисли её.

— Уменьшаемое равно четырём, вычитаемое – двум. Запиши разность и вычисли.
4 — 2 = 2

— Запиши разность чисел пять и два и найди её значение.
5 — 2 = 3

3)
— В море плавало восемь золотых рыбок. Одна из них уплыла. Сколько рыбок осталось?
— Верно, семь.
От восьми отнять один, будет семь.

— На ветке сидело четыре синички. К ним прилетело ещё две. Сколько птиц стало?
— Правильно, восемь. К четырём прибавить два, получится шесть.

— На полянке сидело девять зайчиков. Двое из них побежали в лес. Сколько зайчиков осталось на полянке?
— Правильно, семь. От девяти отнять два, равно семь.

Пять лодок у причала,
Волна их весело качала.
Три лодки взяли рыбаки,
Чтоб переплыть простор реки.
А сколько лодок у причала
Волна по-прежнему качала?

— Верно, две.
— От пяти отнять три равно – два.

4) Самостоятельная работа

Быстрое обучение детей счету примеров в пределах 10 и 20

Обучение будущего школьника счету в пределах 10 – это первый шаг к устному счету. Важно, чтобы ребенок запомнил процессы всех вычислений, как делают это старшие. Второй этап состоит из осваивания основных методов вычисления. Преимуществом здесь уже становится не произвольное получение из воспоминаний готовых ответов, а осознание и заучивание способов сложения и вычитания в цифрах. Как научить ребенка считать примеры в пределах 10, какие игровые приемы можно использовать для лучшего усвоения?

Учимся решать примеры до 10

Для того чтобы выучиться верно и мгновенно считать, нужно постоянно решать примеры. Для высчитывания и запоминания на начальных этапах следует сделать акцент на мышлении ребенка на основе наглядных образов. Здесь возникает проблема: дети часто не воспринимают математические понятия. Решением станут практические действия с жизненными примерами.

Учителя используют три основных метода для обучения счету:

1. На принципе знания числового состава
2. Запоминать наизусть таблицы действий, включая деление и умножение.
3. Использовать спец.приемы для получения результата.

Рассмотрим все методики по порядку.

Примеры на вычитание с картинками

Принцип знания состава

Подготовка должна начинаться с изучения азов математики. Рассказывая ребенку, нужно объяснять, что каждое число это группа с заданным количеством элементов.

Состав числа для запоминания

Важно! Мало сосчитать до пяти. Убедитесь, что вы предлагаете показать пять пальцев, положить на стол пять конфет или изобразить на листке пять кругов.

Необходимо связать число и сказочных героев или другие знакомые для ученика предметы:

1. Одна репка.
2. Две стороны у монетки.
3. Три медведя.
4. Четыре стороны света.
5. Пять пальцев на ручке малыша.

Ребенка важно приучать к картинке, соединенной со всеми элементами. Необходимо играть в математическое домино. Для этого нужно взять десять кубиков с размером ребра 1,5-2 см, стоящих в коробке. Подойдут и детали конструктора Лего. Если нет подходящих предметов, то можно распечатать другие пособия.

Исходя из знания состава, ребенок может решить, складывать ему или вычитать. Например, чтобы ответить, сколько будет «шесть плюс три», он должен знать, что 6 и 3 равняются 9. А «семь минус два» получится пять, потому что 7 это 2 и 5.

Пособие для изучения состава

Запоминания таблиц наизусть

Есть большое количество приемов приучить ребенка сразу запомнить таблицы. Почти половина примеров на сложение и вычитание бессознательно заучиваются детьми по окончании ознакомления с законом перемещения.

Можно брать стихи, подпевки. Самым популярным образцом служит строка песни «Дважды два четыре, это всем известно в целом мире». Отличную информацию находят, познакомившись с методикой Николая Зайцева, программой «Песнезнайка».

Для закрепления знания табличных данных, можно предложить детям работать с:

• раскрасками;
• компьютерными играми по математике;
• мультимедийными презентациями.

Умение прибавлять в тестах со звездочкой поможет потом учить сложный материал.

Использование вычислительных приемов

Наивысший уровень результата устного счета – это способность нахождения самого быстрого и удобного метода для подсчета итога. Так, например, одним из легких способов обучить школьника считать на занятиях является техника присчитывания и «перепрыгивания». Дети быстро усваивают, что при добавлении 1 получается последующее значение, а при уменьшении на 1 получается предыдущее. После этого можно узнать о лучшем напарнике числа 2 – кузнечике, который умеет перескочить цифру и вызвать результат сложения или вычитания 2.

Как объяснить связь сложения и вычитания

Для лучшего восприятия следует научить малыша составу. Методика заключается в трех шагах:

1. На привычных предметах усвоить, что одно из слагаемых может меняться в сторону уменьшения, другое возрасти при одинаковой сумме. Удачным пособием станут упаковки для яиц (по 10); боксы для печенья (по 6,8 или 12), календарные дни (по 7).
2. Следует проследить, чтобы ребенок сделал записи в тетради по возможным комбинациям числительных.
3. Вместе с учеником подготовить карточки с надписями: 6 + 3 = 9; 4 + 5 = 9; 2 + 7 = 9; 1 + 8 = 9. Лучше распределить каждый пример на отдельную карточку.

Теперь нужно приложить усилия к запоминанию. Ребенок должен наизусть, не считая, запомнить все возможные комбинации слагаемых, дающих одну сумму. Не нужны длинные занятия. Успех придет быстрее, когда урок на запоминание будет быстрым, как перерыв между лепкой или рисованием.

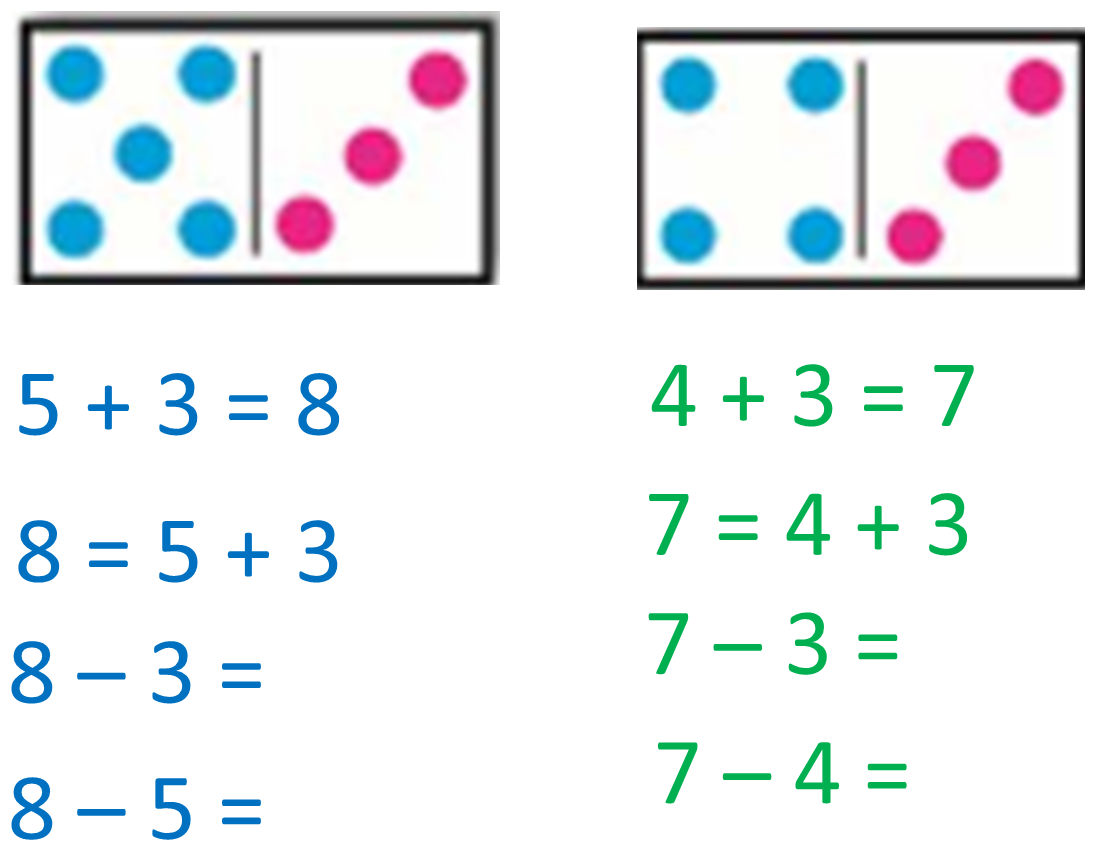
Связь между сложением и вычитанием

Если ребенок все запомнил и не пытается «посчитать», можно приступать к следующему шагу. При замене знакомых карточек новыми, малыш должен писать сразу ответы. Приступаем к самому сложному – вычитать, используя знание составляющих. Вначале необходимо повторить карточки с действиями. Потом нужно спросить у ребенка, что будет с результатом, если убрать одно из слагаемых.

Данная цепочка поможет оценить связь сложения с вычитанием методом запоминания. Ученик должен понять, что вспомнить знакомое сочетание легче, чем считать в уме. В дальнейшем принцип поможет легче освоить решение линейных уравнений.

Когда можно решать примеры в пределах 20

При полном усвоении навыков счета до 10 рекомендуют приступить к действиям на втором десятке. Здесь необходимо только понимание, без подсказки и списывания у соседа. Как научить считать и разъяснять примеры ребенку в пределах 20? Следует придерживаться пошаговой методики:

1. Выучить порядковый счет второго десятка, очередность каждого элемента числового ряда. Для облегчения запоминания используют одинаковые предметы – карточки, кубики. Нанести числа только на первые десять единиц. Разложить их рядами, первый десяток с подписями, под ним второй, «слепой».
2. Запоминать по схеме 14 – к слову четыре добавляется «– надцать», и так с каждым новым термином. Ребенок должен усвоить смысл названия порядковых чисел от 11 до двадцати.
3. Приступить к понятию первый десяток, потом добавлять элементы второго ряда и проговаривать действия. «Десять плюс четыре получится четырнадцать». Должны прозвучать так все данные в интервале второго десятка.
4. Отработать действия со сложением без перехода. По типу 10 + 6 = 16; 16 – 6 = 10. Когда этот этап освоен, выполняют действия повышенной сложности.

Пазлы для счета до 20

Примеры с переходом через десяток требуют развивать навыки устного счета. Знание состава числа при равной сумме облегчают запоминание алгоритма расчета по действиям на сложение и вычитание в пределах 100.

Как научить решать примеры в уме?

Для облегчения устного счета эффективны упражнения для ежедневной тренировки. К шести годам детвора может самостоятельно сосчитать количество конфет, кубиков или мячиков. Им не нужно использовать свои пальчики. Родителям необходимо вовремя подсказать, направить малыша для формирования навыков решения примеров в уме. Ребенок должен освоить:

• простейший счет;
• сумму и разность;
• различие между «большим» или «меньшим» значением.

Визуальное восприятие счета – решение в столбик поможет быстрее научиться считать устно. Педагоги начального обучения рекомендуют начинать с простого. Сосчитать количество фруктов, от ребенка нужно услышать итоговый ответ, без проговаривания последовательных цифр числового ряда.

Несколько уроков, и малыш поймет, что можно сразу называть сумму. Для усложнения спрашивают, а если добавить еще три груши, сколько всего будет фруктов. «Добавки» не должно быть перед глазами. Юному счетоводу придется представить в уме и дать правильный ответ.

Прибавляем в уме

Следует устно повторять примеры на состав, учитывая все возможные двузначные пары. Для облегчения задачи можно применить карточки, затем полностью отказаться от них, перейдя целиком на устный счет. Все задания легче выполнять в течение дня, чтобы освоить быстрее счет:

• Во время прогулки повторить с ребенком список планируемых покупок. После расчета у кассы малыш должен перечислить все товары. Если список не полный, малыш должен правильно назвать продукты или предметы для дальнейшего шопинга.
• Номерные знаки на машинах послужат разминкой для сложения или вычитания на улице. Различные сочетания цифр помогают быстрее научиться считать. Если впереди машина с трехзначным номером, можно сложить все составляющие. Затем отнимать из самого большого значения наименьшее.
• В учебных материалах опубликованы задачки для дошкольников. Они сопровождаются рисунками, четверостишьями, чтобы добавить игровую изюминку к «сухой» математике.

Важно! Каждый ребенок имеет особенности развития, одному будет легче усвоить материал, другой может схватывать на лету. Нужно грамотно направлять и помогать изучать азы математики.

Дети тренируются в устном счете

Интересные способы научить прибавлять и отнимать

Ребенок должен запомнить многие числовые комбинации. Чтобы помочь лучше понять этот материал, рекомендуется предложить ему следующие задачи:

• Рассортировать данное количество объектов в три тарелки, создав разные комбинации (варианты разные: повесить игрушки на две елки, расставить цветы в двух вазах, разместить гномов в двух домах);
• дополнить число до желаемого;
• заполнить ячейки, в которых записан состав с присвоенным номером;
• дорисовать домино.

Поможет усвоить устный счет игра в интервал между значениями. Мама говорит, что загадала определенное число в промежутке от 5 до 18. Ребенок должен угадать, если он ошибается, взрослый определяет место в ряду, регулируя поиски словами «больше», «меньше», «добавь один», «отними два».

Ребенку будет сложно понять на уроках математику в первом классе, если он не усвоил технику счета. Терпение, игровые методы, непринужденность и регулярность упражнений это необходимые условия для успешного обучения. Даже одна десятая материала, усвоенного ребенком самостоятельно, поможет освоить школьную программу.

Урок математики по теме «Связь сложения и вычитания», 1-й класс

Д. Долгожданный дан звонок,
Начинается урок.

У. На наш урок пришел гость. Отгадаем загадку и узнаем, кто он.

Взойдет Егор на бугор –
Выше леса, выше гор,
С бугра спускается –
За травой скрывается.

Д. Это солнце, потому что всходит оно утром высоко, а вечером скрывается. (Слайд 1)

У. На своих лучиках Солнышко принесло нам задания для урока. Прочитаем задания. (Слайд2)

Д. Реши задачи в стихах, назови тему урока, чему должны научиться, физминутка,

выполни практическую работу и сделай вывод, реши примеры, проверь себя, реши задачи, подведи итог.

У. Готовы, дети, выполнить задания, которые шлет нам солнышко?

II. Устный счет

У. Первый лучик солнца прислал нам задание. Прочитайте его.

Д. Реши задачи в стихах.

1. Три яблока было у Коли,
Пять дали товарищи в школе.
Яблок сколько всего
Стало, друзья у него?

2. Шла лисица
Вдоль тропинки
И несла грибы
В корзинке.
Пять опят
И пять лисичек
Для лисят
И для лисичек.
Сколько грибов несла лиса?

3. У Антона росла одна липа,
А Филипп посадил семь лип.
Сколько всего лип посадили
Антон и Филипп?

На доске записывается решение каждой задачи.

У. Чем похожи данные равенства?

Д. В равенствах выполняется действие сложение.

У. Какое равенство лишнее и почему?

Д. Лишнее 1+7=8, потому что в-первых двух прибавляем 5.

Д. Лишнее 5+5=10, потому что в других двух получается одинаковый ответ 8.

У. Вспомните, как называются числа при сложении?

Д. Числа при сложении называются первое слагаемое, второе слагаемое, сумма.

У. Прочитать данные равенства, используя слова первое слагаемое, второе слагаемое, сумма.

Дети читают примеры.

У. Молодцы! Вы выполнили первое задание Солнышка. Приступаем к выполнению второго задания. Прочитать его.

Д. Назови тему урока.

У. Прочитать числа.

У. Расположить их в порядке увеличения.

У. Какое число лишнее и почему?

Д. Лишнее число 10, потому что каждое новое число увеличивается на 3. 3+3=6, 6+3=9, а 9+1=10.

Д. Лишнее число 10, потому что в его записи использовали две цифры, а в остальных одну.

На доске запись

У. Используя числа 3, 6, 9 и знаки “+”, “-”, “=”, составить равенства.

Дети составляют равенства и записывают на доске

У. Что общего в равенствах?

Д. В равенствах мы использовали числа 3,6,9.

У. Чем отличаются?

Д. Равенства отличаются знаками.

Д. Составлены разные равенства.

У. Существует ли связь между равенствами на сложение и вычитание? Какая?

Д. Из суммы 9 вычитаем первое слагаемое 3, получаем второе слагаемое 6.

Д. Из суммы 9 вычитаем второе слагаемое 6, получаем первое слагаемое 3.

У. Сформулируйте тему урока.

Д. Связь сложения и вычитания. (Слайд 3)

У. Выполнили второе задание Солнышка. Прочитать третье задание.

Д. Чему должны научиться? (Слайд 3)

У. Сформулируйте цели урока.

Д. Мы должны: познакомиться с взаимосвязью между сложением и вычитанием, вывести правило.

У. Верно. Но еще мы должны учиться считать примеры, т.е формировать вычислительный навык, развивать математическую речь, умение сравнивать и воспитывать трудолюбие.(Слайд 4)

У. Молодцы! Вы выполнили три задания Солнышка. Приступаем к выполнению четвертого задания. Прочитать его.

Д. Физминутка. (Слайд 5)

Солнце глянуло в кроватку…
Раз, два, три, четыре, пять.
Все мы делаем зарядку,
Надо нам присесть и встать.
Руки вытянуть пошире,
Раз, два, три, четыре, пять.
Наклониться – три, четыре,
И на месте поскакать.
На носок, потом на пятку.
Все мы делаем зарядку.

III. Изучение нового материала

1. Практическая работа.

У. Вы выполнили четвертое задание Солнышка. Прочитать пятое задание. (Слайд 6)

Д. Выполни практическую работу и сделай вывод.

У. Положить на парту 5 кругов красного цвета и 2 круга синего цвета.

У. Сколько кругов красного цвета?

У. Сколько кругов синего цвета?

У. Сколько всего кругов?

У. Как это записать?

У. А теперь убрать 5 кругов красного цвета.

Сколько кругов было?

У. Сколько осталось?

У. Как получили 2?

У. Положите круги обратно.

Сколько всего кругов?

У. Уберите 2 синих круга. Сколько кругов осталось?

У. Как получили 5?

На доске получился столбик примеров.

Д. Числа в равенствах одинаковые и равенства между собой взаимосвязаны.

У. Прочитать данные равенства, используя слова первое слагаемое, второе слагаемое, сумма.

У. Прочитайте второе равенство, используя названия чисел из первого равенства.

Д. Из суммы 7 вычесть первое слагаемое 5 получили второе слагаемое 2.

Д. Из суммы 7 вычесть второе слагаемое 2 получили первое слагаемое 5.

У. Какое правило можно сформулировать?

Д. Если из суммы вычесть одно слагаемое, то получится другое слагаемое.

У. Молодцы! Вы выполнили пятое задание Солнышка. Прочитать шестое задание. (Слайд 7)

2. Работа по учебнику. Страница 24

У. Прочитайте равенства.

У. Объясните, как они образовались.

Дети по рисунку учебника объясняют.

У. Сейчас мы научимся читать равенства по-другому, используя слова первое слагаемое, второе слагаемое, сумма.

Прочитайте первое равенство, используя названия чисел.

Дети читают равенство.

У. Как получили второе равенство? Как получили третье равенство?

У. Прочитайте первое равенство, используя названия чисел.

Дети читают равенство.

У. Как получили второе равенство? Как получили третье равенство

У. Закончить предложения.

У. Молодцы! Вы выполнили шестое задание Солнышка. Прочитать седьмое задание.

У. Как можно себя проверить.

Д. Нужно решить примеры.

У. Заданий будет три. Выберите то, которое вы сможете выполнить.

Группа 1

Решить, используя правило.

Группа 2

Используя равенство, составить еще три равенства, связанных между собой.

Группа 3

Составить равенства, связанные между собой, используя числа и знака: 8, 2, 10, -, +, =.

После выполнения работа проверяется.

У. Молодцы! Вы выполнили седьмое задание Солнышка. Прочитать восьмое задание.

IV. Повторение пройденного материала

У. Страница учебника 24, №4.

Прочитать задачу 1.
О чем задача?
Назовите условие задачи.
Назовите вопрос задачи.
Решение задачи.
Ответ задачи.

Вторая задача решается самостоятельно и проверяется.

У. Молодцы! Вы выполнили восьмое задание Солнышка. Прочитать девятое задание.

V. Итог

У. Чему учились на уроке? Для чего нам необходимо знать это правило?

Вы достигли поставленных целей в начале урока?

Какое настроение. Дорисуйте свое солнышко.

У. Народная мудрость говорит: Мир освещается солнцем, а человек знанием.

Объясните ее смысл. (Слайд

У. На каждом уроке вы узнаете новое. Сегодня вы выучили правило. Повторите его хором.

Примеры на сложение и вычитание

Примеры на сложение и вычитание — простейшие операции, с которых начинается знакомство детей с математикой. Чтобы щелкать арифметические задачи как орешки, нужно практиковаться как можно чаще. Предлагаем вашему вниманию примеры, которые помогут ребенку «набить руку» — от совсем легких к более сложным.

Примеры на сложение и вычитание для дошкольников

Данные примеры в одно и два действия могут осилить дошкольники. Важно, чтобы ребенок запомнил правило: от перемены мест слагаемых сумма не меняется.

Сложение и вычитание до 5

Сложение и вычитание до 10

Вставь пропущенные знаки

От ребенка требуется понять, какой знак («+» или «–») должен стоять на месте пустой клетки, чтобы получилось верное равенство. Если ответ не кажется очевидным сразу, малыш решает в уме два примера, подставив как плюс, так и минус.

Эти задания подойдут для дошкольников, освоивших устный счет в пределах 10.

Что нужно сделать с цифрами 3 и 4, чтобы получить 7? Очевидно, сложить (если вычесть 4 из 3, получится отрицательное число, а это понятие ребенку-дошкольнику и ученику первых классов пока не известно).

А что нужно сделать с 9 и 4, чтобы вышло 5? Не сложить: 9 + 4 = 13. Зато 9 — 4 = 5.

По тому же принципу решаются остальные примеры.

Примеры на сложение и вычитание для 1 класса

Если складывать и вычитать числа до 10 умеет большинство дошколят, то примеры на сложение и вычитание в пределах 20, с переходом через разряд, предлагают уже ученикам первого класса. Переход через разряд происходит, когда в одном равенстве смешиваются однозначные и двузначные числа: например, при сложении двух цифр мы получаем двузначное число (5 + 7 = 12), при вычитании из двузначного числа — однозначное.

Вот несколько упражнений:

Сложение и вычитание в пределах 20

Подставь пропущенное число

Это, по сути, завуалированные уравнения в одно действие. Для их решения ребенок должен уметь оперировать двузначными числами, знать такие понятия, как слагаемые, уменьшаемое, вычитаемое, разность и сумма, и понимать принципы решения уравнений со сложением и вычитанием.

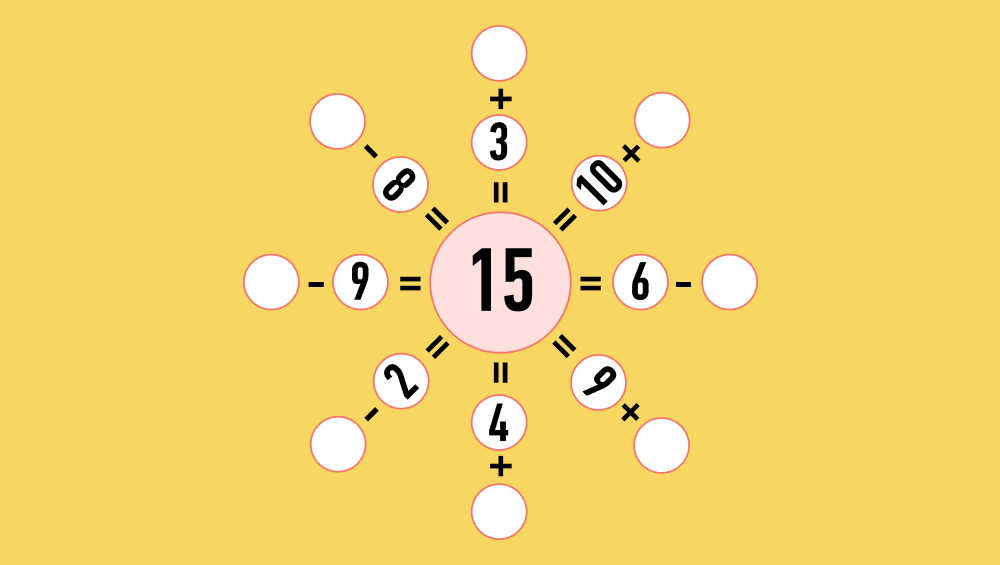
В центре — число 15, которое должно получиться в результате всех предложенных равенств. Число, от которого нужно отнять 8, чтобы получить 15, получаем, прибавив 8 к 15. Уменьшаемое равно 23.

3 + х (пропущенное число в равенстве) = 15. Отнимаем от суммы одно слагаемое, чтобы получить второе: 15 — 3 = 12.

Подставьте числа, чтобы получились верные равенства

Здесь от ребенка также требуется уметь складывать и вычитать в пределах 20. Придется последовательно решить в уме несколько примеров, чтобы найти верную комбинацию чисел.

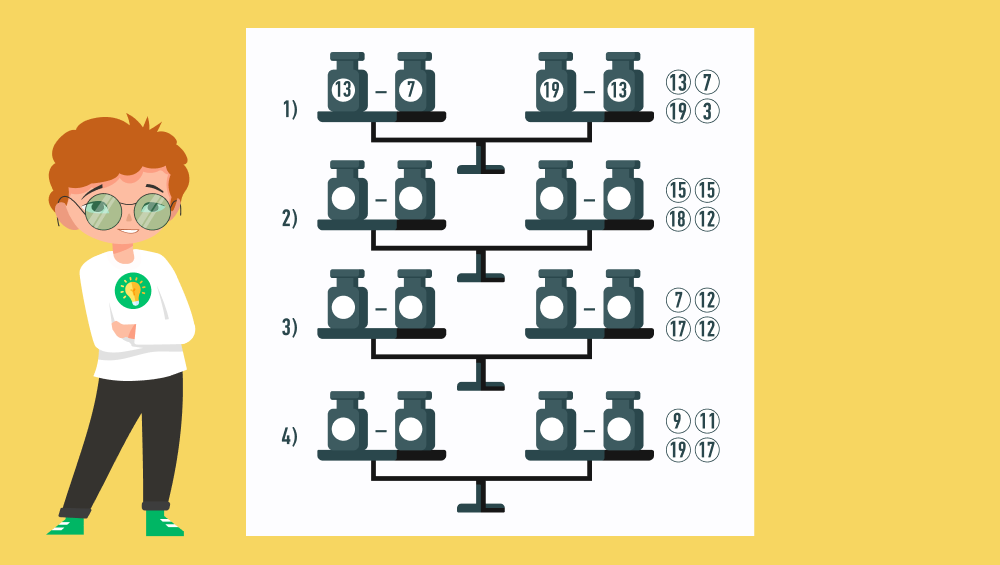
Итак, нам даны четыре числа: 12, 18 и 15 (дважды). С их помощью, выполняя вычитание, нужно получить два одинаковых числа — слева и справа. Наблюдательный ученик быстро заметит, что 18 — 15 = 15 — 12 (= 3). В данном случае уменьшаемые и вычитаемые располагаются друг от друга крест-накрест.

Что нужно сделать с числами 7, 17 и 12 (дважды), чтобы получить верное неравенство? Опять же путем нехитрой подстановки вычисляем: 17 — 12 = 12 — 7 = 5.

По той же схеме решаем последний пример: 19 — 11 = 17 — 9 = 8.

Задачи на сложение и вычитание до 20

Чтобы ребенок не заскучал за примерами, можно «упаковать» их в занимательные математические игры или задачи с интересными условиями. Представляем три примера заданий на сложение и вычитание в пределах 20:

1. Мама приготовила 16 пирожков с мясом на всю семью и накрыла на стол. Невоспитанный, но ловкий котенок Степа сумел утащить два пирожка. Сколько пирожков осталось на столе?
2. У Маши было 16 книг. В день ее рождения родственники преподнесли ей еще 2. Так совпало, что еще 1 книгу подарили ей одноклассники. Сколько книг оказалось у Маши?
3. В январе было 10 праздничных дней и еще 6 выходных, когда Коля не ходил в школу. Из всех своих свободных январских дней мальчик провел 5 у бабушки, 1 — в большом семейном кругу и еще 1 — в гостях у друга, в остальные был с родителями. Сколько свободных дней за месяц мальчик провел с мамой и папой?

Примеры на сложение и вычитание для 2 класса

Эти задания — уже для второклассников, которые полностью освоили сложение и вычитание двузначных чисел, умеют выполнять арифметические операции как в уме, так и в столбик.

Сложение двузначных чисел

Вычитание двузначных чисел

Задачи на сложение и вычитание в пределах 100

1. Оля весит 30 килограммов, а ее маленькая сестра — всего 12. На сколько килограммов старшая сестра тяжелее младшей?
2. Между третьим и вторым этажом Мишиного дома — 11 ступенек, столько же — между вторым и первым. А на первом этаже всего 4 ступеньки до выхода из подъезда. Сколько ступенек приходится преодолеть Мише по пути на улицу, если он живет на третьем этаже?
3. У Анны Сергеевны 28 дней оплачиваемого отпуска в год. Весной она уже брала отпуск на 10 дней. Летом семья предложила ей уехать на две недели на море. Хватит ли Анне Сергеевне отпуска, чтобы отправиться на морской курорт? Останется ли у нее еще несколько дней отпуска?

Примеры на сложение и вычитание для 3 класса

С такими примерами легко справятся ученики третьего класса. Многие из примеров на трехзначные числа уже сложно решить в уме — у ребенка должен сформироваться навык арифметического подсчета в столбик. Впрочем, если он способен справляться со сложением и вычитанием длинных чисел в уме, это большой плюс.

Сложение трехзначных чисел

Вычитание трехзначных чисел

Задачи на сложение и вычитание в пределах 1000

1. Ира пришла в продуктовый магазин. Она решила купить плавленый сыр за 200 рублей, масло за 120 рублей и хлеб за 53 рубля. Сколько денег потратит Ира?
2. За три предновогодних дня в супермаркете раскупили 745 килограммов мандаринов. В первый день купили 143 килограмма, во второй — еще 211. Сколько килограммов мандаринов купили в последний предновогодний день?
3. В юности Денис любил покупать журналы. Его любимый журнал об автомобилях стоил 187 рублей, однако с тех пор он подорожал на 83 рубля. А журнал о звездах стоил 94 рубля, теперь же — на 43 рубля дороже. Сколько денег придется заплатить Денису сейчас, если он решит по старой памяти купить оба журнала?

Примеры на сложение и вычитание для 4 класса

Ученику четвертого класса уже вполне по силам примеры и задачи, требующие сложения и вычитания чисел в пределах 10 000. Упражнения для практики:

Сложение до 10 000

Вычитание до 10 000

Задачи на сложение и вычитание в пределах 10 000

1. Платье в бутике стоило 2000 рублей, но в честь праздника на него сделали скидку. Теперь оно подешевело на 238 рублей. Сколько теперь стоит платье?
2. Прабабушка Светы — долгожительница. Она родилась в далеком 1916 году. Сколько ей лет, если сейчас 2020-й?
3. Семья из двух человек съездила в тур выходного дня за 5800 рублей. В эту сумму входили транспортные расходы, расходы на питание и экскурсии. Транспортные расходы семьи составили 2200 рублей, на питание ушло еще 1700. Сколько денег ушло на экскурсии?

Математика — это не только решение примеров и уравнений, но и развитие логического мышления, умения работать с информацией, анализировать, отделять главное от второстепенного, выстраивать причинно-следственные связи и принимать верные решения. Умназия предлагает большое количество математических задач на логику и смекалку в сюжетном игровом формате с приятной озвучкой и красочными иллюстрациями:

Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате

П. 7 Вычитание натуральных чисел и их свойства

Мы можем не только собирать в группы различные предметы, то есть, складывать их, но и забирать из существующей группы определенное их количество.

Например, в кошельке было 1850 рублей. В магазине было потрачено 780 рублей. Чтобы узнать, сколько осталось денег, можно вытащить кошелек и пересчитать их. Но можно поступить по-другому: из той суммы, которая была в кошельке, отнять ту сумму, что была потрачена в магазине. Разница этих чисел , то есть, на сколько единиц изначальная сумма денег больше той суммы, которую потратили, и будет остатком денег.

Компоненты вычитания:

Про действие вычитание также говорят, что нужно из одного числа вычесть другое , или одно число уменьшить на другое .

Совершая вычитание натуральных чисел, вы должны помнить, что из одного натурального числа можно вычесть только равное ему или меньшее натуральное число. Действительно, мы никак не можем отобрать единиц предметов больше, чем их есть в наличии.

Поэтому, уменьшаемое натуральное число всегда больше или равное вычитаемому. Другими словами, мы всегда вычитаем из большего меньшее или из равного равное .

Связь вычитания и сложения

Действие вычитание непосредственно связано с действием сложение .

Действительно, когда мы ищем сумму, мы складываем все единицы, из которых состоят числа, вместе. То есть, получаем число, которое складывается из разных чисел.

А когда мы ищем разность, мы из одного числа (уменьшаемое) отнимаем некоторое количество единиц (вычитаемое), которые входят в его состав , и получаем другое количество единиц . То есть, получаем число ( разность ), которое также составляло уменьшаемое , пока от него не отняли вычитаемое . Поэтому разность и имеет второе название – остаток – то, что осталось от числа, после вычитания его части.

Из этого мы можем сделать вывод, что, если сложить обратно обе части одного числа (разность и вычитаемое), то мы получим уменьшаемое .

Уменьшаемое – это сумма вычитаемого и разности . То есть, разность и вычитаемое – это слагаемые .

Когда мы складываем числа, слагаемые нам известны , и нужно вычислить их сумму . А когда мы вычитаем , нам даются сумма (уменьшаемое) и одно из слагаемых (вычитаемое) этой суммы, а второе слагаемое (разность) нам нужно вычислить .

Рассмотрим это на примере. Мы нашли разность 8-5=3 . Это означает, что мы разложили одно данное нам число 8 на два: 5 (данное нам уменьшаемое ) и 3 (найденная нами разность ). Но мы знаем, что состав числа – это слагаемые , которые в сумме дают нам это самое число . Поэтому, найденную нами разность чисел мы можем превратить в сумму чисел , сложив остаток с вычитаемым: 3+5=8 .

Свойства разности натуральных

чисел

Свойства разности натуральных чисел состоят из:

• Правила вычитания суммы из числа и числа из суммы;
• Зависимость разности от изменения уменьшаемого или вычитаемого.
• Правило вычитания разности из числа;

Рассмотрим каждый пункт подробнее.

Правила вычитания суммы из числа и числа из суммы

Как вычесть сумму из числа

Действительно, так как сумма – это объединение всех слагаемых , то очевидно, что, отнимая последовательно каждое слагаемое , каждое ее составляющее число, мы в конце концов отнимем всю сумму .

Рассмотрим это на примере из урока сложение чисел.

325 +( 12 + 64 + 5 ) = 325 +81 = 406

Я запишу это в виде разности:

406 -( 12 + 64 + 5 ) = 325

и покажу, что результат будет равен первому слагаемому:

406 — 12 = 394;
394- 64 = 330;
330- 5 = 325 .

Как видите, все верно.

Как вычесть число из суммы

Действительно, вы знаете, что, если уменьшить одно из слагаемых на какое-то число, то и сумма уменьшится на это же самое число. Следовательно, если нам нужно сумму чисел уменьшить на какое-то число, то для этого достаточно уменьшить на это число одно из слагаемых суммы.

Для рассмотрения я возьму тот же пример, только сумму расчленю на слагаемые, а слагаемое в скобках заменю суммой:

325 +81 = ( 191 + 65 + 150 )

Превращаю выражение в разность:

( 191 + 65 + 150 )-81 = 325

и покажу, что результат также будет равен первому слагаемому:

191 -81 = 110;
110+ 65 = 175;
175+ 150 = 325
или
150 -81 = 69;
69+ 191 = 260;
260+ 65 = 325 .

Я недаром написал в правиле, что нужно отнимать от подходящего слагаемого суммы , потому что, если оно будет меньше вычитаемого , то оно нам не подходит. Так, в нашем примере 65 .