Что такое зависимость между числами

Что такое зависимость между числами

Follow Us:

Send Us Your Feedback / Suggestion

For further assistance, please Contact Us

Обнаружен блокировщик рекламы

Поскольку мы изо всех сил пытались сделать для вас онлайн-расчеты, мы обращаемся к вам с просьбой предоставить нам разрешение, отключив Adblocker для этого домена.

Or

Disable your Adblocker and refresh your web page 😊

ДОБАВИТЬ ЭТОТ КАЛЬКУЛЯТОР НА ВАШ ВЕБ-САЙТ:

Добавьте калькулятор соотношений на свой сайт, чтобы упростить использование этого калькулятора напрямую. Создайте учетную запись для этого виджета без проблем, поскольку он на 100% бесплатный, простой в использовании и вы можете добавить его на несколько онлайн-платформ.

Загрузите приложение «Калькулятор коэффициентов» для мобильного телефона, чтобы вы могли рассчитать свои значения в своих руках.

Онлайн-калькулятор соотношений поможет вам определить одинаковые коэффициенты, указав три из четырех частей двух соотношений. Кроме того, этот калькулятор соотношений лучше всего подходит для нахождения пятой и шестой частей из трех соотношений, давая любые четыре части. Наш решатель соотношений выполняет следующие семь операций как с двумя, так и с тремя отношениями.

• Найдите эквивалент отношения
• Сделайте соотношение больше
• Сделайте соотношение меньше
• Упростить соотношение
• Упростите соотношение до формы “1: n: m”
• Упростите соотношение до формы “n: 1: m”
• Упростите соотношение до формы “n: m: 1”

Прежде чем мы собираемся использовать этот калькулятор соотношений, мы должны знать основное определение, формулу соотношения и то, как найти соотношение вручную. Продолжайте читать, чтобы получить краткие сведения о том, как делать соотношения.

Кроме того, вы можете попробовать наш онлайн-калькулятор пропорций, который поможет вам легко решить проблему пропорций разными методами.

Что такое коэффициент?

Его можно определить как «сравнение двух конкретных чисел, очень часто представленных в виде дробей». Просто он показывает, сколько одной части отношения содержится в другой части. Наш искатель соотношений разработан для вычисления этого контраста и определения взаимосвязи между числами.

как посчитать соотношение чисел (шаг за шагом):

Отношение состоит из двух частей: числитель и знаменатель, как и дробь. Если у нас есть два отношения, и мы хотим вычислить соотношение для недостающего значения в соотношении, просто выполните следующие действия:

• Запишите отношения в виде дроби и вставьте любую переменную (x или y) в пропущенное значение
• Установите дроби равными друг другу
• Используя перекрестное умножение, сгенерируйте уравнение
• Найдите недостающую переменную
• Наконец, попробуйте калькулятор соотношений, чтобы проверить свой ответ.

Вы можете воспользоваться нашим онлайн-калькулятором дробей, чтобы сложить, вычесть, умножить или разделить две или три дроби. Здесь у нас есть ручной пример, чтобы прояснить понимание:

Пример:

У нас есть 6 кусочков пиццы, из которых съедаются 2. Теперь мы хотим знать, сколько кусочков можно съесть из 54 кусочков пиццы?

Решение:

Шаг 1:

Запишите соотношение в виде дроби как:

Съеденный ломтик / всего ломтик = 2/6

Съеденный ломтик / всего ломтик = x / 54

Шаг 2:

Приравняйте дроби друг к другу:

Шаг 3:

Мы рекомендуем вам использовать наш калькулятор соотношений, если вы собираетесь решать комплексные отношения больших чисел.

Как использовать онлайн-калькулятор соотношений:

Наш калькулятор – точный инструмент для упрощения и поиска неизвестного значения в соотношении. Вам просто нужно придерживаться следующих пунктов для расчета соотношений:

Входы:

• Прежде всего, нажмите вкладку, чтобы выбрать, сколько соотношений вы хотите выполнить
• вычисления. Это может быть A: B или A: B: C
• Затем выберите метод расчета из раскрывающегося списка этого калькулятора.
• Затем введите в поля в соответствии с выбранными входными параметрами.
• Как только вы закончите, нажмите кнопку расчета

Выходы:

• Отсутствующие значения
• Упрощение соотношения
• Визуальное представление отношения (круговая диаграмма)

Заметка:

Этот калькулятор соотношений не даст вам значений, которые вам не нужны; он даст вам результат в соответствии с входными параметрами.

Что такое золотое сечение?

Когда две величины имеют то же отношение, что и отношение их суммы к большей из двух величин, то это соотношение называется золотым сечением. Например, если величины выражены в x и y, то золотое сечение между x и y равно (x + y) / x = x / y.

Конечное примечание:

К счастью, вы узнали о том, как рассчитать соотношение соотношения вручную и с помощью калькулятора. Соотношение используется везде, от приготовления пищи до строительства дома. Это очень полезно для образования K-12 и во многих других областях науки, таких как механика, бизнес и бухгалтеры, еда и многие другие. Когда дело доходит до решения отношений для комплексных чисел, просто используйте онлайн-калькулятор соотношений, который поможет вам найти недостающее значение в соотношении и выполнить упрощение отношения по вашему желанию.

Калькулятор соотношения

Вы можете использовать этот инструмент для получения наиболее упрощенного соотношения или для сравнения двух одинаковых соотношений.

Соотношение

Соотношение в математике — это термин, который используется для сравнения двух или более чисел. Он используется, чтобы указать, насколько велика или мала величина по сравнению с другой. В отношении две величины сравниваются с помощью деления. Здесь делимое называется «антецедентом», а делитель — «консеквентом». Например, в группе из 30 человек 17 из них предпочитают ходить по утрам, а 13 — ездить на велосипеде. Чтобы представить эту информацию в виде соотношения, запишем его как 17:13. Здесь символ ‘:’ читается как «есть к». Таким образом, отношение людей, предпочитающих ходить пешком, к людям, предпочитающим езду на велосипеде, читается как «17 к 13».

Что такое соотношение?

Соотношение определяется как сравнение двух величин в одних и тех же единицах измерения, которое показывает, сколько одного количества присутствует в другом количестве. Коэффициенты можно разделить на два типа. Одно из них — соотношение части к части, а другое — соотношение части к целому. Соотношение частей к частям показывает, как связаны две различные сущности или группы. Например, соотношение мальчиков и девочек в классе составляет 12: 15, тогда как соотношение частей к целому обозначает соотношение между определенной группой и целым. Например, из каждых 10 человек 5 любят читать книги. Таким образом, соотношение части к целому составляет 5: 10, что означает, что каждые 5 человек из 10 любят читать книги.

Формула соотношения

Мы используем формулу соотношения при сравнении соотношения между двумя числами или величинами. Общая форма представления соотношения между двумя величинами, скажем, «a» и «b», — это a: b, которое читается как «a равно b».

Форма дроби, представляющая это соотношение, — a/b. Чтобы еще больше упростить соотношение, мы следуем той же процедуре, которую используем для упрощения дроби. a:b = a/b. Давайте разберемся в этом на примере.

Пример. В классе из 50 учеников 23 девочки, а остальные мальчики. Найдите соотношение количества мальчиков к количеству девочек.

Общее количество студентов = 50; Количество девушек = 23.

Общее количество мальчиков = Общее количество учеников — Общее количество девочек
= 50 — 23
= 27

Таким образом, желаемое соотношение (Количество мальчиков: Количество девочек) равно 27:23.

Расчет коэффициентов

Для того чтобы рассчитать соотношение двух величин, мы можем использовать следующие шаги. Давайте разберемся в этом на примере. Например, если для приготовления пышных блинов необходимо 15 стаканов муки и 20 стаканов сахара, давайте рассчитаем соотношение муки и сахара, используемых в рецепте.

• Шаг 1: Найдите величины обоих сценариев, для которых мы определяем соотношение. В данном случае это 15 и 20.
• Шаг 2: Запишите его в форме дроби a /b. Итак, мы записываем это как 15/20.
• Шаг 3: По возможности еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 15/20 может быть упрощено до 3/4.
• Шаг 4: Поэтому соотношение муки к сахару можно выразить как 3:4.

Используйте бесплатный онлайн-калькулятор коэффициентов, чтобы проверить свои ответы при расчете коэффициентов.

Как упростить соотношения?

Соотношение выражает, сколько требуется одного количества по сравнению с другим количеством. Два термина в соотношении могут быть упрощены и выражены в их низшей форме. Соотношения, выраженные в их наименьших выражениях, легко понять и могут быть упрощены так же, как мы упрощаем дроби. Чтобы упростить соотношение, мы используем следующие шаги. Давайте разберемся в этом на примере. Например, давайте упростим соотношение 18:10.

• Шаг 1: Запишите заданное соотношение a:b в виде дроби a/b. Записав соотношение в виде дроби, мы получим 18/10.
• Шаг 2: Найдите наибольший общий коэффициент ‘a’ и ‘b’. В этом случае GCF из 10 и 18 равен 2.
• Шаг 3: Разделите числитель и знаменатель дроби на GCF, чтобы получить упрощенную дробь. Здесь, разделив числитель и знаменатель на 2, мы получаем, (18÷2)/(10÷2) = 9/5.
• Шаг 4: Представьте эту дробь в форме соотношения, чтобы получить результат. Таким образом, упрощенное соотношение составляет 9:5.

Используйте бесплатный онлайн-калькулятор коэффициентов упрощения, чтобы проверить свои ответы.

Советы и рекомендации по соотношению:

• В случае, если оба числа «a» и «b» равны в соотношении a: b, то a: b = 1.
• Если a > b в соотношении a : b, то a : b > 1.
• Если a < b в соотношении a : b, то a : b < 1.
• Перед их сравнением необходимо убедиться в том, что единицы измерения двух величин одинаковы.

Эквивалентные Соотношения

Эквивалентные соотношения аналогичны эквивалентным дробям. Если предшествующий (первый член) и последующий (второй член) данного соотношения умножаются или делятся на одно и то же число, отличное от нуля, это дает эквивалентное соотношение. Например, когда антецедент и следствие соотношения 1:3 умножаются на 3, мы получаем, (1 × 3) : (3 × 3) или 3: 9. Здесь 1:3 и 3:9 являются эквивалентными соотношениями. Аналогично, когда оба члена соотношения 20:10 делятся на 10, это дает 2:1. Здесь 20:10 и 2:1 являются эквивалентными соотношениями. Бесконечное число эквивалентных соотношений любого заданного соотношения может быть найдено путем умножения предшествующего и последующего на положительное целое число.

Таблица коэффициентов

Таблица коэффициентов — это список, содержащий эквивалентные коэффициенты любого заданного соотношения в структурированном виде. В следующей таблице соотношений приведено соотношение между соотношением 1:4 и четырьмя его эквивалентными соотношениями. Эквивалентные соотношения связаны друг с другом умножением числа. Эквивалентные соотношения получаются путем умножения или деления двух членов соотношения на одно и то же число. В примере, показанном на рисунке, давайте возьмем соотношение 1:4 и найдем четыре эквивалентных соотношения, умножив оба члена соотношения на 2, 3, 6 и 9. В результате мы получаем 2:8, 3:12, 6:24, и 9:36.

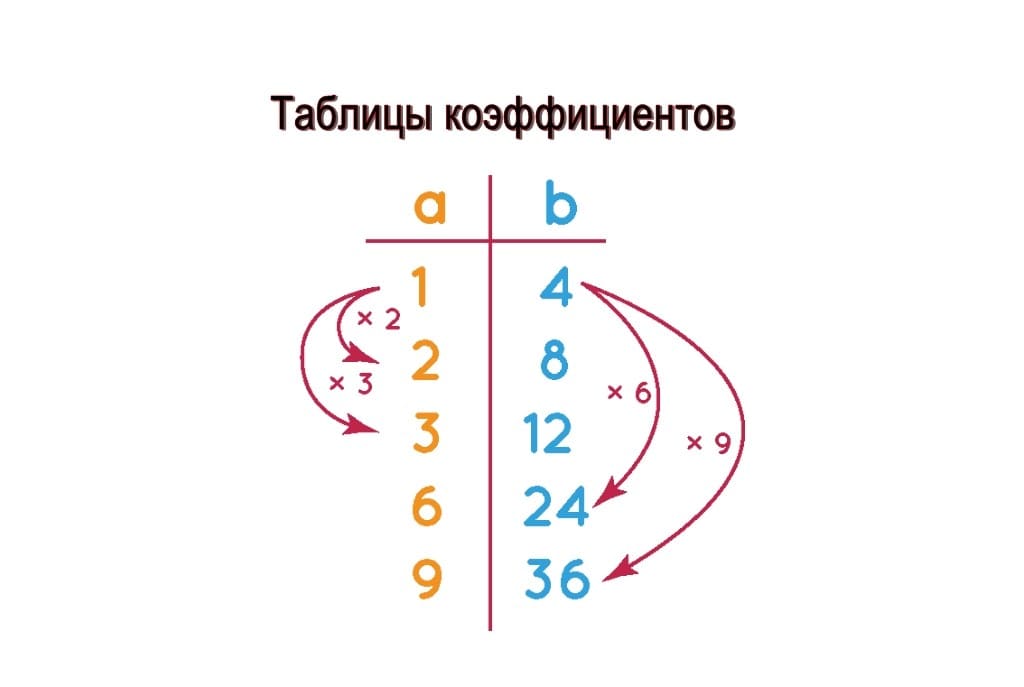
Используйте бесплатный онлайн-калькулятор эквивалентных коэффициентов, чтобы проверить свои ответы.

Примеры соотношения

Пример 1. В школьном зале 49 мальчиков и 28 девочек. Выразите соотношение числа мальчиков к числу девочек.

Решение:

Учитывая, что количество мальчиков = 49, а количество девочек = 28. GCF 49 и 28 равен 7. Теперь, для упрощения, разделите два термина на их GCF, который равен 7. Это означает, (49 ÷ 7)/(28 ÷ 7) = 7/4. Следовательно, соотношение числа мальчиков к числу девочек = 7:4.

Пример 2: В музыкальном классе 30 учеников. 10 из них были взрослыми, а остальные — детьми. Каково соотношение числа детей к общему числу учащихся в музыкальном классе?

Решение:

Учитывая, что общее количество учащихся в музыкальном классе = 30, а общее количество взрослых = 10. Следовательно, количество детей, посещавших музыкальный класс = 30 -10, что равно 20. Отношение общего числа детей к общему числу учащихся в музыкальном классе = 20: 30, что в упрощенном виде дает 2:3.

Пример 3: Упростите заданное соотношение, 87:75.

Чтобы упростить данное соотношение, мы сначала найдем GCF 87 и 75, что равно 3. Затем мы разделим каждый член на 3. Это означает, (87 ÷ 3)/(75 ÷ 3) = 29/25. Таким образом, соотношение 87:75 в простейшей форме равно 29:25.

Как ваш ребенок может овладеть математическими понятиями?
Математическое мастерство приходит с практикой и пониманием того, «Почему» стоит за «Что». Почувствуйте разницу в математике.

Узнать ещё

Как решать IQ задачи? Многие IQ задачи подчинены общим закономерностям. Уже само по себе прохождение iq теста раз за разом ведет к улучшению результата. Решая iq-задачи, вы вырабатываете iq навыки и умение правильно распределять время.

Существуют несколько основных типов задач. Попробуем их систематизировать. В большинстве задач на iq надо найти зависимость чисел, даже если это задание на связь букв. Зависимость между числами может быть подчинена не одной, а нескольким закономерностям.

Найти пропущенное число:

1) 2 6 10 … 18

(Ответ: 14. Сначала нужно определить закономерность получения каждого последующего числа. Это — прибавление к предыдущему 4. При прохождении iq теста вы либо вписываете ответ 14 в поле для ответа, либо выбираете его из нескольких предложенных вариантов).

2) 2 6 18 54 …

(Ответ: 162. Каждое последующее число получаем, умножая предыдущее на 3).

Заменить вопрос числом:

2 3 6 15 42 ?

(Ответ: 123. Здесь зависимость чисел может быть получена двумя способами. Первый: число умножаем на 3, из результата вычитаем 3: 2 x3 — 3 = 3; 3х3-3=6 и т. д. Второй: последовательно прибавляем степени тройки: 2 + 3^0=3; 3+3^1=6 и т.д.).

Определить закономерность и найти число:

2 3 8 27 112 ?

Найти недостающее число:

1) 17; 13; 11; ?; 5; 3; 2

2) 81; 49; 25; ?; 1

Как научить ребенка решать iq задачи? Для начала предложите ему поискать решение самостоятельно. Если найти зависимость между числами ему не удается, обсудите, какая числовая закономерность была использована в каждом конкретном случае. Постарайтесь не просто рассказывать ребенку решение, но, задавая наводящие вопросы, подводите его к самостоятельным выводам. Теперь попросите ребенка придумать для вас подобные задания. Отнеситесь к их разгадке со всей серьезностью. Расскажите ему, что зависимость чисел в каждом тесте может быть самая разная и надо пробовать использовать различные подходы, чтобы найти верное решение.

Регулярная IQ-тренировка — один из действенных способов развития логического мышления.

13 комментариев на «Найти зависимость чисел в задачах IQ»

Неужели вообще можно самому до такого додуматься? Первые три — это нормальные примеры. Но остальные можно решить только в результате случайной догадки. Особенно, если дается 30 минут и нет калькулятора, как можно в уме умножить все эти числа, догадаться что к ним нужно прибавить или отнять, и нигде не ошибиться в расчетах? Это не тест на интеллект, а тест на математические способности. Почему то в тестах на интеллект таких математических задач очень много.

Как правило, в тестах IQ задания следуют в порядке возрастания уровня сложности. Таким образом, есть и простые примеры, решение которых не вызывает особых затруднений, и более сложные. Логические цепочки зашифрованы не только в математических примерах, но и в рисунках, в словах, в буквах, так что каждый, кто проходит тест, имеет возможность проявить те или свои способности. Видеть различного рода закономерности можно научиться. Важнее, на мой взгляд, научиться получать удовольствие не только от результата, но и и от самого процесса обучения 🙂

Эти задачи имеют к «математическим способностям» очень опосредованное отношение. Скорее, это задачки на быстроту устного счета — очень полезный навык для советских продавцов без калькуляторов, и не более того. Современная математика — это тензоры, категории, функторы, дифференциальные формы, топология, алгебраическая геометрия, теория групп, не говоря уж о примитивном математическом анализе. И чем меньше в математике арифметических манипуляций с числами, тем более «высшей» и «настоящей» она считается. Я вот, к примеру, с легкостью могу вычислить в уме интеграл Пуассона. Но вот корячиться без калькулятора над тем, какую арифметическую пакость подсунул мне составитель задачки, да еще и на время (понятное дело, что без лимита времени любую такую задачку можно решить!) — это просто унизительная и дилетантская профанация понятия «математические способности». В подобных арифметических ребусах никакой «красоты» нет. (Хотя, может быть, для продавцов или любителей сканвордов, которые не знают из математики ничего, кроме арифметики — возможно, и есть.) Красота есть в римановой геометрии, в теории групп, в теоремах комплексного анализа, если уж на то пошло. И кстати говоря, в задачах типа «продолжить ряд» правильным ответом может быть взято заведомо любое число. Всегда существует такая закономерность (интерполяционный многочлен Лагранжа, если что) которая дает сколько угодно любых наперед заданных чисел данного ряда плюс любое к нему приписанное число. Так что с точки зрения строгой математики, подобные задачи вообще бессмысленны.

Умение видеть связь между числами — полезная тренировка для развития логического мышления. Разумеется, закономерностей между числами можно найти много.
Замечательно, что Вы любите и понимаете математику. Возможно, у Вас врождённые математические способности. Или (и) Вас учили по классическому образцу, от простого — к сложному.
Когда я просматриваю некоторые современные школьные учебники, по ассоциации представляется картинка: пришел маленький мальчик в спортзал в 1-й раз, а ему сразу предлагают поднять штангу весом 100 кг.
Тренировка нужна и важна в любом деле.

Спасибо. Теперь я понял что требуется в таких тестах, а то даже задачи не понимал:)

Спасибо! Я тоже к 37 годам, благодаря вам поняла, что от меня требуется в этих «ребусах»!
Последний пример 81;49;25;х;1 я решила по другому. Я сначала ряд сделала не по убывающей, а по возрастающей.
49+(8*4)=81
25+(8*3)=49
х+(8*2)=25 отсюда х=9
1+(8*1)=9
Так тоже можно решать?

Nadin, Вы нашли свое решение, и оно тоже верное. Разгадывать числовые «ребусы» интересно, правда?

Я бы не был столь оптимистичен — результат теста рассматривает машина, а значит ваш результат не будет засчитан.

Уважаемый Nadin, у вас оригинальный подход, но решение неверно, в результате последнего действия результат должен равняться «1»

у меня опыт работы 10 лет в трудовой.
сейчас меняю работу. и скоро будет тест на iq.

получается весь мой опыт работы будет коту под хвост, если я не пройду это тестирование?

п.с. с цифрами я могу. А вот связку алфавитов и их порядковые номера (в русском и латинском алфавитах) мне вообще не понять. Кому это надо?

Тест на IQ — всего лишь тест на IQ. Если кадровик толковый, он это понимает. Но лучше все же подготовиться.
К тому же, задания на буквы — это тоже, по большей части, задания на числа.

IQ тест мне напомнил старый анекдот —
Кадровик кандидату «На свои года что-то вы не очень подвижны».
Кандидат кадровику «А вам кто нужен — бухгалтер или обезьяна?»

Что нужно знать об отношении двух чисел в математике за 6 класс

Отношение чисел является частным данных чисел.

Запись отношения принято обозначать с помощью арифметического действия деления. Также допускается представление отношения в виде обыкновенной дроби:

Здесь записано отношение чисел a и b. Число а может называться предыдущим членом, b играет роль последующего члена.

Запись отношения пары чисел таких, как 75 и 25, имеет вид:

75 : 25 = 75 25 = 3

С помощью объяснения отношения можно выразить следующее:

• во сколько раз первое число больше по сравнению со вторым;
• какую часть первое число составляет от второго числа.

При решении задач на уроках по математике в шестом классе на тему «Отношение чисел» можно часто встретить примеры с процентами. Поэтому важно ознакомиться с особенностью понятия процентного соотношения и записать его в конспект.

Вычислить процентное отношение пары чисел можно путем деления одного числа на второе, а полученный результат следует умножить на 100.

Даны два числа: 52 и 400. Требуется определить, сколько процентов составляет первое число от второго числа. Воспользуемся правилом вычисления процентного соотношения и запишем:

52 : 400 · 100 % = 13 %

Подобные отношения можно найти в заданиях, где по условию определены некие величины, и требуется вычислить их процентное соотношение. Знание определенных правил вычисления поможет значительно упростить решение. Среди вопросов могут быть такие:

• на сколько процентов была перевыполнена работа;
• на сколько процентов готов результат;
• указать повышение или снижение цены товара в процентах

и другие вопросы, в которых присутствует понятие «процент».

Свойства отношения чисел

В том случае, когда имеется пара чисел или значений одинаковой величины, обозначенных как a и b, справедливы следующие соотношения:

• отношение a к b является результатом частного a и b;
• когда a>b, отношение a:b говорит о том, во сколько раз число a больше по сравнению с b;
• когда aa является некой частью от b;
• процентное отношение a к b представляет собой отношение a:b, которое умножили на 100%.

Ключевое свойство частного: частное сохраняется без изменений в том случае, когда делимое и делитель умножают или делят на одинаковое число.

Основное свойство частного позволяет вывести главное свойство отношения.

Основное свойство отношения: при умножении или делении членов какого-то отношения на одинаковое число, которое не равно нулю, данное отношение сохранится без изменений.

Примеры решения задач с пояснениями

Месячный план производства равен 1200 изделий. В результате предприятие произвело 2300 изделий. Требуется определить процент превышения плана.

Данную задачу можно решить двумя способами. Рассмотрим их по отдельности.

Способ 1. Запишем, что 1200 изделий являются планом, то есть составляют 100 %. Определим, количество изделий, изготовленных больше плана:

Вычислим разницу между фактом и планом в процентах:

1100 от 1200 ⇒ 1100 : 1200 · 100 % = 91 , 7 % .

Попробуем выполнить вычисления другим методом.

Способ 2. Сначала найдем разницу между планом и фактом в процентах:

2300 от 1200 ⇒ 2300 : 1200 · 100 % = 191 , 7 % .

Далее определим процент перевыполнения плана:

191 , 7 % — 100 % = 91 , 7 % .

Поставлена задача вспахать землю на участке поля площадью 500 га. В течение первого дня было обработано 150 га почвы. Требуется вычислить, сколько процентов удалось вспахать от общего запланированного объема.

Найдем отношение обработанной земли к общей площади поля и запишем результат в процентном выражении:

150 : 500 · 100 % = 150 500 · 100 % = 3 10 · 100 % = 0 , 3 · 100 % = 30 % .

Производительность мастера составила 45 деталей, а по плану требовалось изготовить 36 деталей. Нужно найти процент фактически проделанной работы от планируемого объема.

Здесь вычислим отношения чисел и запишем результат в процентном выражении:

45 : 36 · 100 % = 1 , 25 · 100 % = 125 %

Задания для самостоятельной работы

Должность председателя желали занять два претендента. Явка на голосовании составила 120 человек. Распределение голосов соответствует пропорции 3:5. Требуется определить количество голосов, которые получил победитель.

Отношение количества хвойных деревьев к лиственным в лесу можно выразить как 1:4. Нужно вычислить процент лиственных деревьев.

Сельскохозяйственные растения высаживают на площади 24 Га. Зерновые культуры и овощные распределены в соответствии с отношением 5:3. Необходимо вычислить площадь в Га, которую занимают овощные культуры.

Найти зависимость между числами

Пожалуйста, используйте IE6/7/8 с плагином MathPlayer, Firefox с установленными математическими шрифтами или Opera 9.5 и выше.

Объявления		Последний пост
	Запущен новый раздел «Задачки и головоломки»	29.08.2019 00:42
	Актуарий в PPF Life Insurance (Junior)	25.03.2021 21:35
	Разделу «Задачки и головоломки» исполнилось два года	21.08.2021 01:51

Есть исходные числа, 5 штук, на их основании формируется шестое число. Других переменных, кроме 5 чисел — нет, но могут быть константы.

Действия между 5 числами не известны, алгоритм не доступен. Действия могут быть любого характера, не только математические, а, например, по-битный сдвиг, что-то еще хитрее и т.п.

Примеров 5 и результирующим чисел имеем больше кол-во. Т.е. алгоритм может их выдавать до бесконечности.

Можно ли без реверс-инжиниринга программного кода определить алгоритм, зависимости?

Хотя бы в теории хочу понять, возможно ли решение этой задачи?

Если задача решается и для этого не потребуются «нереальные» ресурсы, то я готов премировать исполнителя хотя бы теоретической части.

То есть у вас есть программа, которая по 5 числам вычисляет шестое и вы хотите
угадать алгоритм.

Допустим, у вас есть гипотеза, а числа имеют тип int, который принимает $2^$ значений.
Значит надо проверить $2^$ случаев.

Если вам платят за поиск а не за результат, то лучше работы не придумаешь.

Задача формулируется при задании базового множества функций (алгоритмов), условий композиции и меры сложности. Нейронные сети — частный случай.
Не берусь решать (занят) но посмотреть интересно. Пришлите на mail около 1000 наборов (шестерок чисел).
Вопросы: Значения функции формируются детерминировано, случайно или в условиях игры? Меняется ли неизвестная функция?

———————————
PS Сменю nickname на yog-urt. Причины: 1 — техническая, 2 — ассоциации (например, поручик Ржевский и лебеди на пруду), 3 — другое.

Если уж мы говорим об обратном инженеринге, то проще дизассеблировать программу, чем ломать голову. Как правило, это не так сложно, как кажется на первый взгляд.

При таких общих условиях найти алгоритм невозможно в принципе. Причём, независимо от количества испытаний (примеров) и быстродействия компьютера, используемого нами для поиска исходного алгоритма. Вот набросок доказательства.

Допустим, что мы провели $n$ испытаний и потом каким-то способом отыскали алгоритм, который, принимая на входе любую из испытанных нами пятёрок чисел, даёт правильный ответ на выходе. Назовём этот алгоритм $A_0$ . Для любой пятёрки $$ он даёт на выходе число $A_0(p_1,p_2,p_3,p_4,p_5)$ . Теперь мы пребываем в уверенности, что для любой наперёд заданной пятёрки чисел мы сможем, используя этот алгоритм, предсказать результат испытания. Покажем, что это невозможно.

Пусть $p_0$ — наибольшее из чисел, входящих в пятёрки чисел в наших первых $n$ испытаниях. Рассмотрим теперь следующий алгоритм $A_1$ : если на вход $A_1$ подаётся пятёрка $$ , то выдать в качестве ответа число $A_0(p_0+1,p_0+1,p_0+1,p_0+1,p_0+1)+1$ ; в противном случае использовать для нахождения ответа просто алгоритм $A_0$ . Алгоритм $A_1$ , хотя и выглядит несколько искусственно, но является алгоритмом в самом настоящем смысле этого слова. Результаты работы $A_0$ и $A_1$ одинаковы для всех пятёрок чисел в наших первых $n$ испытаниях, и в нашем распоряжении нет никаких способов определить, какой же из алгоритмов использовался в реальности в этих испытаниях. Но при этом существует ситуация ( $$ на входе), в которой эти алгоритмы дают разный ответ.

P.S. Премиальные за доказательство неразрешимости задачи готов принять

Редактировалось 1 раз(а). Последний 20.09.2012 15:05.

сыроватое доказательство. не доказано, что для набора $[p_0+1,p_0+1,p_0+1,p_0+1,p_0+1]$ алгоритмы будут давать разный результат — первый-то алгоритм не проверялся на данном наборе. потом, среди n наборов не обязательно присутствует набор $[p_0,p_0,p_0,p_0,p_0]$ .
приведу свой вариант невозможности определения алгоритма:
пусть неизвестный алгоритм программы имеет вид:
$f(a,b,c,d,e)=left\end$
вероятность, что в тестируемое число наборов попадет набор $[a_0,b_0,c_0,d_0,e_0]$ пренебрежимо мала. следовательно мы сделаем вывод, что искомым алгоритмом является $f^*$ , а не $f$ , что формально неверно. с другой стороны, нет никаких оснований считать, что алгоритм имеет другой вид.
гоните мое бабло

Редактировалось 1 раз(а). Последний 20.09.2012 16:31.

Пример (и контрпример) Дмитрия правильный и очевидный, но…
В условии задачи алгоритм существует и доказывать его несуществование – пустая затея, также как и невозможность его «найти».
В литературе известны различные варианты постановок и решений подобных задач – просто нужно подобрать подходящий для автора. Чтобы поставить корректную задачу (вписать в известный вариант), нужно хотя бы посмотреть, какие же там числа, узнать требования к точности аппроксимирующей функции, ограничена ли сложность искомого алгоритма и т. п. Обычно практические задачи укладываются в математические – нужно желание понять автора. Может быть ,увидим что-то интересное?

Цитата
zklb (Дмитрий)
не доказано, что для набора $[p_0+1,p_0+1,p_0+1,p_0+1,p_0+1]$ алгоритмы будут давать разный результат — первый-то алгоритм не проверялся на данном наборе.

Напоминаю, что алгоритм $A_1$ при подаче на вход пятёрки $$ по определению выдаёт ответ $A_0(p_0+1,p_0+1,p_0+1,p_0+1,p_0+1)+1$ , т.е. он использует алгоритм $A_0$ для вычисления $A_0(p_0+1,p_0+1,p_0+1,p_0+1,p_0+1)$ , к этому числу прибавляет единицу и то, что получилось, выдаёт в качестве ответа. Так что $A_0(p_0+1,p_0+1,p_0+1,p_0+1,p_0+1)$ и $A_1(p_0+1,p_0+1,p_0+1,p_0+1,p_0+1)$ всегда различаются на единицу и проверка этого обстоятельства каким-либо испытанием не требуется.

Цитата
zklb (Дмитрий)
потом, среди n наборов не обязательно присутствует набор $[p_0,p_0,p_0,p_0,p_0]$ .

Цитата
yog-urt
В условии задачи алгоритм существует и доказывать его несуществование – пустая затея, также как и невозможность его «найти».

1) Никто и не пытался доказать несуществование алгоритма — доказывалась невозможность его найти.
2) Из того, что алгоритм существует, вовсе не следует, что существует способ его найти с использованием имеющейся информации. Причём, как видно из приведённых выше рассуждений, даже если мы случайно правильно угадаем этот алгоритм и будем проводить успешные испытания до скончания времён, то и тогда не сможем быть уверенными, что правильно его угадали. Потому что для любого конечного числа проведённых испытаний можно подобрать по меньшей мере два (что и делается в доказательстве; на самом деле их не два, а бесконечное число) алгоритма, дающих одинаковые (и правильные) результаты для всех уже проведённых испытаний, но разные результаты для некоторых других, ещё не испытанных данных. Так что после проведения любого конечного числа испытаний у нас просто нет никакого способа отличить правильный алгоритм от неправильного.

Редактировалось 1 раз(а). Последний 21.09.2012 02:46.

Цитата
yog-urt
Чтобы поставить корректную задачу (вписать в известный вариант), нужно хотя бы посмотреть, какие же там числа, узнать требования к точности аппроксимирующей функции, ограничена ли сложность искомого алгоритма и т. п.

У вас уже есть алгоритм, который работает как надо. Тогда,
1) Запускаем его $n$ раз с различными 5 числами (генерируются случайные 5 чисел с нужными свойствами и они передаются алгоритму). $n$ очень большое число. Чем оно больше, тем лучше.
2) На основе полученных $n$ испытаний, осуществляем аппроксимацию (интерполяцию или экстраполяцию или обе в зависимости от требований). Существуют и другие методы аппроксимации все зависит только от требований.

Полученная после аппроксимации функция будет описывать зависимость пятёрок, описанной исходным алгоритмом.

Цитата
zklb (Дмитрий)
сыроватое доказательство. не доказано, что для набора $[p_0+1,p_0+1,p_0+1,p_0+1,p_0+1]$ алгоритмы будут давать разный результат — первый-то алгоритм не проверялся на данном наборе. потом, среди n наборов не обязательно присутствует набор $[p_0,p_0,p_0,p_0,p_0]$ .
приведу свой вариант невозможности определения алгоритма:
пусть неизвестный алгоритм программы имеет вид:
$f(a,b,c,d,e)=left\end$
вероятность, что в тестируемое число наборов попадет набор $[a_0,b_0,c_0,d_0,e_0]$ пренебрежимо мала. следовательно мы сделаем вывод, что искомым алгоритмом является $f^*$ , а не $f$ , что формально неверно. с другой стороны, нет никаких оснований считать, что алгоритм имеет другой вид.
гоните мое бабло

открещиваюсь от бабла) корил коллегу за сыроватость доказательства, а оказалось зря, да и у самого-то недочет. для успокоения отмечу, что необходимо выполнение условия $f^*(a_0,b_0,c_0,d_0,e_0)nepi$ , иначе разницы между $f^*$ и $f$ фактически не будет.

Все рассуждения относительно некорректности задачи в «постановке» автора очевидны и оговорены. Я не стал бы еще раз останавливаться на этих вопросах, если бы не один момент, связанный с использованием термина «найти» и «невозможно найти в принципе!» (jinma) Далее этот термин незаметно подменяется на «не существует способа найти».
И все-таки, если понятие «невозможно найти» используется в смысле «не существует алгоритма, определяющего искомую функцию
1. гарантировано за конечное число шагов (jinma);
2. с вероятностью не менее P за фиксированное число шагов (Дмитрий);
3. за ограниченное практическими возможностями число шагов» (sphinx-pinastri);
4. аналогично,
то все tip-top.
Но обратите внимание, что при «маленьком» уточнении исходной задачи ответы на вопрос о существовании алгоритма (и, более того, способа) при различных его определениях (в соответствии с пп 1-3) могут быть различными. Что тогда понимать под «можно найти»? С учетом этого правильнее говорить о существовании (несуществовании) того или иного алгоритма, определяющего в конкретной задаче искомую конструкцию, а не о возможности (невозможности) ее найти. Тем более, что вопрос о возможности «найти» не обязательно увязан с алгоритмическим характером поиска? Нельзя же из умозаключения «не будет уверенности, что мы его нашли», делать вывод о том, что он не найден, и, более того, что его нельзя найти и считать это доказательством «невозможности найти в принципе».
Однажды я задал своему приятелю задачку: «Найди, — говорю, — функцию: $ R^ to R$ по следующим наборам значений в нескольких точках». Он, едва взглянув на эти значения, сразу сказал: «Наверняка, это корень кубический из произведения арктангенсов этих чисел». Я был ошеломлен, поскольку это был правильный ответ. Потом он пояснил, что учел пределы моей фантазии по придумыванию функций.
Вы «нашли» область определения функции $y=1/sin(x^e)$ ? А мы нашли число $pi$ ? Нашел ли Кантор множество Кантора? А Уайлс нашел доказательство теоремы Ферма?
Я нашел число $sqrt 2$ . Это такое положительное число, которое при умножении само на себя дает 2! (! — не факториал, хотя, какая разница).
При отсутствии аксиоматики, определяющей понятие «найти» и отделяющей его от понятия «существует», не имеет смысла доказывать что-то относительно «найти» в отрыве от «существует».
Подобные задачи на форуме не редкость (найти алгоритм шифрования, датчика псевдослучайных чисел, предлагались алгоритмы сжатия безызбыточных данных,…). Написал, чтобы из-за неточного использования терминов не затевались дискуссии относительно очевидных и одинаково понимаемых вещей.
А задача – никакая, на нее даже смотреть не хочется.

—————————————
PS Ссылка по пп 1-3 на авторов постов не критика, а наоборот. Как раз там нормальные подходы к доказательству несуществования соответствующих алгоритмов.

Какая бы ни была задача, обсуждение уже получилось интересным.

Сначала по поводу «найти». Я подразумевал, что когда мы что-то «находим», мы всё-таки знаем, что именно «нашли». А иначе какой вообще смысл говорить «я нашёл»? Например, кто-то говорит: «Я нашёл снежного человека»; и тут же добавляет: «Но я совсем не уверен, что нашёл именно снежного человека». Или «Я нашёл доказательство теоремы Ферма, но не знаю, доказывает ли оно теорему Ферма и вообще является ли доказательством». В этих примерах, на мой взгляд, налицо несколько странное (по крайней мере, с точки зрения математики) употребление слова «нашёл». И если его употреблять в этом смысле, то доказать неразрешимость поставленной plr задачи действительно не получится. Потому что решение можно просто «угадать». Более того, тогда можно сказать что алгоритм в задаче можно «найти», не увидев вообще ни одного примера работы алгоритма. Лично мне подобное словоупотребление не представляется продуктивным (и, как мне кажется, вряд ли оно подразумевалось автором задачи).

Теперь по поводу «невозможно найти решение». Можно интерпретировать это как «не существует алгоритма, позволяющего найти решение». Но, честно говоря, я под этой фразой подразумевал более сильное утверждение, действительно не связанное с алгоритмическим характером поиска. А именно, что даже если мы и «найдём» какое-то «решение», то не сможем узнать, правильное ли оно. А более сильным это утверждение является потому, что из него следует несуществование алгоритма, позволяющего найти решение (если бы такой алгоритм существовал, мы смогли бы его использовать для нахождения решения и доказательства его верности).

Редактировалось 1 раз(а). Последний 23.09.2012 03:20.

Цитата
plr
Есть исходные числа, 5 штук, на их основании формируется шестое число. Других переменных, кроме 5 чисел — нет, но могут быть константы.

Действия между 5 числами не известны, алгоритм не доступен. Действия могут быть любого характера, не только математические, а, например, по-битный сдвиг, что-то еще хитрее и т.п.

Примеров 5 и результирующим чисел имеем больше кол-во. Т.е. алгоритм может их выдавать до бесконечности.

Можно ли без реверс-инжиниринга программного кода определить алгоритм, зависимости?

Хотя бы в теории хочу понять, возможно ли решение этой задачи?

Если задача решается и для этого не потребуются «нереальные» ресурсы, то я готов премировать исполнителя хотя бы теоретической части.

Цитата
plr
Найти зависимость между числами
Есть исходные числа, 5 штук, на их основании формируется шестое число. Других переменных, кроме 5 чисел — нет, но могут быть константы.

Уважаемый plr !
Вы имеете закодированное сообщение из 5 цифр и хотите его расшифровать не имея ключа. Так вот, в недрах секретных служб всех государств существует целая наука (назовём её условно) «теория передачи секретных сообщений» основной опорой которой является постулат – по одному сообщению, не имея ключа расшифровать сообщение невозможно и в то же время утверждается что с увеличением количества перехваченных сообщений вероятность расшифровки возрастает почти катастрофически. Оставлю в покое секретные службы и приведу конкретный пример из жизни. Во время археологических раскопок археологи находили таблички и изделия с изображением отдельных иероглифов и долго не могли их расшифровать. Однако, когда нашли в одном месте МНОГО предметов с изображениями (надписями) в одном и том же месте , то это позволило после анализа восстановить письменность и прочитать надписи. К сожалению я уже забыл кто, где и когда это сделал.
Успехов Вам! Любарцев В.В.

Отношения

Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.

Частное двух чисел и , отличных от нуля, называют отношением чисел и , или отношением числа к числу .

Где и — члены отношения; число — предыдущий член отношения; — последующий член отношения.

14 : 7 — отношение числа 14 к числу 7;

6 : 25 — отношение числа 6 к числу 25;

— отношение числа к числу ;

1,15 : 0,36 — отношение числа 1,15 к числу 0,36.

Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .

Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и .

Основное свойство отношения:

Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Запишем отношение числа 3 к числу 10 и найдем его значение:

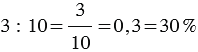
То есть отношение двух чисел можно выразить в процентах.

Процентное отношение двух чисел — это их отношение, выраженное в процентах.

Процентное отношение показывает, сколько процентов одно число составляет от другого.

Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.

Пример:

Сколько процентов составляет число 5 от числа 10?

5 10 2 1 · 100 % = 1 2 · 100 % = 100 2 % = 50 % .

Ответ: 50% составляет число 5 от числа 10.

Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.

Например:

Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.

Отношение длины прямоугольника к его ширине равно 12 : 100 = .

Отношение ширины прямоугольника к его длине равно 100 : 12 = .

Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.

На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.

Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).

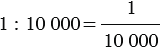
Пусть на карте задан масштаб , то есть карта сделана в масштабе одна десятитысячная.

Найдем, какой длине на местности соответствует отрезок 5 см на карте.

Для решения обозначим через длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:

5 : = 1 : 10 000;

Решаем данное уравнение:

= 510 000;

= 50 000;

50 000 см = 500 м = 0,5 км.

Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.

Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.

Для решения обозначим через длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:

: 9,5 = 1 : 10 000;

Решаем данное уравнение:

= 9,5 : 10 000;

= 0,00095;

0,00095 км = 0,95 м = 95 см.

Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.

Статистическая зависимость. Корреляция и регрессия. Элементы дисперсионного анализа.

Как известно, случайные величины X и Y могут быть либо зависимыми, либо независимыми. Существуют следующие формы зависимости – функциональная и статистическая. В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y=f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.

Однако, если X и Y случайные величины, то между ними может существовать зависимость иного рода, называемая статистической. Дело в том, что на формирование значений случайных величин X и Y оказывают влияние различные факторы. Под воздействием этих факторов и формируются конкретные значения X и Y. Допустим, что на Х и У влияют одни те же факторы, например Z1, Z2, Z3, тогда X и Y находятся в полном соответствии друг с другом и связаны функционально. Предположим теперь, что на X воздействуют факторы Z1, Z2, Z3, а на только Y и Z1, Z2. Обе величины и X и Y являются случайными, но так как имеются общие факторы Z1 и Z2, оказывающие влияние и на X и на Y, то значения X и Y обязательно будут взаимосвязаны. И связь это уже не будет функциональной: фактор Z3, влияющий лишь на одну из случайных величин, разрушает прямую (функциональную) зависимость между значениями X и Y, принимаемыми в одном и том же испытании. Связь носит вероятностный случайный характер, в численном выражении меняясь, от испытания к испытанию, но эта связь определенно присутствует и называется статистической. При этом каждому значению X может соответствовать не одно значение Y, как при функциональной зависимости, а целое множество значений.

ОПРЕДЕЛЕНИЕ. Зависимость случайных величин называют статистической, если изменения одной из них приводит к изменению закона распределения другой.

ОПРЕДЕЛЕНИЕ. Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные коррреляционной зависимостью, оказываются коррелированными.

Именно корреляционные зависимости наиболее часто встречаются в природе в силу взаимовлияния и тесного переплетения огромного множества самых различных факторов, определяющих значения изучаемых показателей.

Корреляционную зависимость Y от X можно описать с помощью уравнения вида:

где yx — условное среднее величины Y, соответствующее значению x величины X, а f(x) некоторая функция. Уравнение (1) называется выборочным уравнением регрессии Y на X. Функцию f(x) называют выборочной регрессией Y на X, а ее график – выборочной линией регрессии Y на X.

Совершенно аналогично выборочным уравнением регрессии X на Y является уравнение: xy=φ(y)

В зависимости от вида уравнения регрессии и формы соответствующей линии регрессии определяют форму корреляционнной зависимости между рассматриваемыми величинами – линейной, квадратической, показательной, экспоненциальной.

Важнейшим является вопрос выбора вида функции регрессии f(x) [или φ(y)], например линейная или нелинейная (показательная, логарифимическая и т.д.)

На практике вид функции регрессии можно определить, построив на координатной плоскости множество точек, соответствующих всем имеющимся парам наблюдений (x;y).

Рис. 1. Линейная регрессия значима. Модель Y=a+bX.

Рис. 2. Линейная регрессия незначима. Модель Y=

Рис. 3. Линейная регрессия значима. Нелинейная модель (y=ax2+bx+c)

Например, на рис.1. видна тенденция роста значений Y с ростом X, при этом средние значения Y располагается визуально на прямой. Имеет смысл использовать линейную модель (вид зависимости Y от X принято называть моделью) зависимости Y от X. На рис.2. средние значения Y не зависят от x, следовательно линейная регрессия незначима (функция регрессии постоянна и равна ). На рис. 3. прослеживается тенденция нелинейности модели.В частности, если изменение одной из величин изменяет среднее значение другой, то такая статистическая зависимость называется корреляционной.

Сущность дисперсионного анализа состоит в проверке гипотезы о тождественности выборочных дисперсий одной и той же генеральной дисперсии.

Дисперсия характеризует важные конструкторские и технологические показатели как:

рассеивание точек попадания при стрельбе и др.

И еще дисперсионный анализ одновременно решает проблему проверки гипотезы о равенстве средних значений выборок.

Задача сравнения дисперсий сводится к проверке исходной гипотезы (нулевой гипотезы ) о принадлежности двух выборок одной и той же генеральной совокупности.

Для проверки гипотезы о равенстве дисперсий нужно иметь независимую функцию, вычислимую по данным эксперимента.

Такой функцией является функция Фишера (распределение Фишера, F -распределение), определяемая так:

Где U и V случайные величины, имеющие распределение ;

k₁ и k₂ соответствующие степени свободы случайных величин U и V соответственно, , ;

N₁ и N₂ — количество испытаний (объемы выборок).

является мерой сравнения дисперсий потому, что дисперсии, являясь суммой квадратов ошибок, имеют распределение .

Распределение хи-квадрат определяется следующим образом:

Где v — число степеней свободы, e- число Эйлера (2,71…), Г — гамма-функция.

График плотности F -распределения показан на рис. 5.2.

Итак, случайная величина

где и — несмещенные оценки дисперсий, полученных из независимых выборок, взятых из нормальных совокупностей, имеет распределение Фишера ( F -распределение).

Рис. 5.2. График плотности F -распределения

Величина F — случайна, поэтому судить однозначно по ее величине о подтверждении или опровержении гипотезы об однородности исследуемых выборок нельзя.

Поэтому вводится q уровень значимости, численно равный вероятности неприемлемых отклонений от принятой гипотезы. Области неприемлемых значений F показаны на рис. 5.2 штриховкой. Граничные точки допустимых значений F определяются точками F₁ и F₂, соответствующих вероятностям q/2.

Если вычисленное по данным эксперимента значение F попадает в область между точками F₁ и F₂:

то принятая гипотеза не опровергается.

Заметим, что случайная величина

также имеет F -распределение со степенями свободы и соответственно. Следовательно, вероятность попадания числа F в левую критическую область равна:

Отсюда следует, что левая критическая точка F -распределения соответствует правой критической точке F* -распределения. Т. е. правые точки распределений F и F* определяют левую и правую точки F₁ и F₂. Поэтому в таблицах представлены только правые F₂ критические точки F -распределения.

В таблицах значения F₂ приведены в зависимости от q/2, числа степеней свободы и .

Обычно при вычислении F в числитель отношения ставят значение большей дисперсии.

Итак, при принятая гипотеза не опровергается, при — не подтверждается.

Чем меньше уровень значимости q, тем меньше вероятность забраковать проверяемую гипотезу, когда она верна, т. е. совершить ошибку первого рода.

Но с уменьшением уровня значимости (увеличения F₂) расширяется область допустимых ошибок, что приводит к увеличению вероятности принятия неверного решения, т. е. совершения ошибки второго рода.

В заключение изложенного отметим, что как бы ни был велик объем статистического материала и критерий Фишера (впрочем, как и любой другой) не может дать абсолютно достоверный ответ о справедливости или несправедливости проверяемой гипотезы, так как мы оперируем случайными числами.

То есть, опровержение гипотезы ни в коем случае не означает категорического, логического опровержения гипотезы при F>F₂, равно как и подтверждение гипотезы при не означает категорического доказательства ее справедливости. Не исключено, что в том и в другом случае решение может оказаться ошибочным.

Суждение о подтверждении или отклонении выдвинутой гипотезы высказывается с определенной степенью достоверности.