Что такое задача обратная данной

Урок «Обратные задачи»

Педагогические задачи: познакомить с обратными задачами; показать связь данных и искомого чисел в таких задачах; закреплять знание таблицы сложения и вычитания в пределах 20, умение решать выражения вида: 30 + 5, 35 – 5, 35 – 30; развивать внимание, наблюдательность, логическое мышление.

Планируемые образовательные результаты:

Личностные: имеют мотивацию к учебной деятельности; принимают и осваивают социальную роль обучающегося; стремятся к развитию внимания, памяти, логического мышления, смекалки; проявляют самостоятельность, личную ответственность.

Предметные: имеют представление об обратных задачах; знают, как составить задачи, обратные данной; устную и письменную нумерацию чисел в пределах 100; что такое отрезок; умеют: составлять задачи, обратные данной, решать задачи и выражения изученных видов, чертить отрезки заданной длины.

Метапредметные (критерии сформированности/оценки компонентов УУД): регулятивные: формулируют учебную задачу урока на основе того, что уже известно и усвоено, и того, что ещё неизвестно; прогнозируют и контролируют собственную деятельность и деятельность партнёра, при необходимости вносят корректировки; осознают качество и уровень усвоения; способны к мобилизации волевых усилий; познавательные: выделяют и формулируют познавательную цель, выделяют необходимую информацию, структурируют знания; создают алгоритм деятельности; анализируют объекты, сравнивают их; строят логическую цепочку рассуждений, устанавливают причинно-следственные связи; коммуникативные: умеют слушать, слышать и понимать партнёров по речевому высказыванию; уважают в общении и сотрудничестве всех участников образовательного процесса, при возникновении спорных ситуаций не создают конфликтов.

м етоды и формы обучения: частично-поисковый; индивидуальная, фронтальная, групповая.

Основные понятия и термины: сравнить, отрезок, точка, сантиметр, сложить, вычесть, задача, обратная задача.

с ценарий урока

I. Каллиграфическая минутка.

В руки в ручки мы берём,

Числа мы писать начнём…

Учитель предлагает ученикам рассмотреть числа, записанные на доске:

6 7 6 7 6 7 6 7 … 13 13 13 13 …

– Как связаны между собой записанные вами числа?

II. Устный счёт.

Устно мы теперь считаем,

Навык счёта развиваем.

– Найдите значение суммы чисел 3 и 4.

– Значение этой суммы вычтите из числа 17.

– Найдите значение суммы чисел 6 и 4.

– Значение этой суммы вычтите из числа 30.

– Из суммы чисел 70 и 8 вычтите число 8.

– Из суммы чисел 60 и 5 вычтите число 60.

– Разность чисел 10 и 8 прибавьте к числу 20.

– Разность чисел 9 и 3 прибавьте к числу 90.

– Маше 8 лет. Мама на 20 лет старше Маши, а папа на 1 год старше мамы. Сколько лет маме? Сколько лет папе?

При выполнении заданий учащиеся пользуются сигнальными карточками .

– А теперь выполните задания на смекалку – задачи 5, 6 (с. 26, 27) .

Задача 5 (с. 26). ( У Юры – пудель. У Димы – овчарка. У Алёши – такса.)

Задача 6 (с. 27). (Синих карандашей – 6.)

III. Сообщение темы и целей учебной деятельности.

– А теперь будьте внимательны. Я зачитаю вам слова-понятия, а вы должны назвать общее слово, которое их объединяет: условие, вопрос, данные числа, искомое число. (Задача.)

– Что вы знаете о задаче? Какие виды задач знаете?

– Сегодня вы узнаете новое о задачах. Вам самостоятельно предстоит сделать открытие.

IV. Открытие новых знаний.

– Прочитайте задачу 1(1) (с. 26) и выберите схему, которая соответствует данной задаче. Опираясь на условие и ответ решённой задачи, составьте две другие задачи, которые соответствуют схемам.

(1-я задача. У Веры было 10 рублей. На эти деньги она купила блокнот, который стоил 6 рублей, и карандаш. Сколько стоил карандаш?

2-я задача. У Веры было 10 рублей. На эти деньги она купила карандаш, который стоил 4 рубля, и блокнот. Сколько стоил блокнот?)

– Теперь сравните решения всех задач. Установите связь между ними.

Решение : 1) 6 + 4 = 10;

– Такие задачи называются обратными .

Руки ставим все вразлёт, Руки в стороны держите,

Появился самолёт. Друг на друга посмотрите,

Мах крылом туда-сюда, Раз и два, раз и два.

Делай раз и делай два. Опустите руки вниз,

Раз и два, раз и два. И на место все садитесь!

Для закрепления нового материала учащимся предлагается составить задачу по данным числам (или по данной схеме), а затем составить задачи, обратные данной.

– Разберите задачу 2 (с. 26) . Выделите условие и вопрос, назовите данные и искомое числа. Составьте краткую запись или схему. Решите задачу самостоятельно. Сформулируйте и запишите ответ.

– Составьте две задачи, обратные данной.

V. Работа с геометрическим материалом.

– Рассмотрите чертёж, данный в задании 1 (с. 27) .

– Сколько отрезков изображено на чертеже? (Три.)

– Можно ли, не измеряя самый большой отрезок, узнать его длину?

– Каким образом? (Сложить длины двух других отрезков.)

– Какова длина большого отрезка? Проверьте это измерением. Вы были правы?

– Начертите отрезок длиной 10 сантиметров.

– Поставьте на нём точку так, чтобы получился отрезок длиной 4 сантиметра.

– Какова длина другого вновь полученного отрезка?

– Можно ли это узнать, не производя измерений? Как?

– Проверьте ваше предположение, измерив отрезок. Вы были правы?

VI. Решение выражений.

– Самостоятельно (по вариантам: вариант I – 1-й столбик; вариант II – 2-й столбик) решите выражения из задания 4 (с. 27) . Затем устно решите 3-й столбик данного номера.

Задачи, обратные данной. 2-й класс

Назад Вперёд

Авторы учебника: «Математика» Моро М.И, Бантова М.И. и другие (1 часть); тетради: «Математика» Моро М.И., Волкова С.И. (1 часть).

Класс: 2.

УМК: «Школа России».

Тип урока: комбинированный.

Форма урока:урок-путешествие (с использованием ИКТ).

Цель урока: знакомство детей с новым математическим понятием: «обратные задачи», установление связи между прямой и обратной задачей.

Предметные результаты:

• Уметь узнавать и составлять обратные задачи.
• Уметь использовать в речи термин «обратная» задача.
• Знать структуру задачи.
• Уметь решать задачи в одно действие.
• Уметь выделять её части и анализировать содержание текстовой задачи.
• Уметь составлять краткую запись или схематический рисунок.
• Уметь выполнять вычисления изученных видов.

Метапредметные результаты:

• Личностных УУД: Способность к самооценке на основе критерия успешности учебной деятельности; позитивному отношению к уроку математики, учебно-познавательный интерес к учебному материалу.
• Регулятивных УУД: Уметь учащимися принимать и сохранять учебную задачу, планировать своё действие в соответствии с поставленной задачей; оценивать правильность выполнения действия на уровне адекватной оценки; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; овладение умениями проговаривать последовательность действий на уроке, умение формулировать цель урока с помощью учителя.
• Познавательные УУД: Уметь осуществлять логические операции; описывать математические объекты; ориентироваться в своей системе знаний, строить небольшие математические высказывания.
• УУД Коммуникативные: Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; учиться работать в паре, формулировать собственное мнение и позицию.

Методы и формы работы: совместная с учителем учебно-познавательная деятельность, работа в парах, математическая игра, учебный (проблемный) диалог,самостоятельная работа,наблюдение за математическими объектами (моделирование (сравнение, анализ)).

Оборудование:

• Для учителя: ПК, мультимедиа проектор, экран, презентация, выполненная в PowerPoint, рабочая тетрадь, учебник, математические «Ёлочки» и «Грибочки» для работы у доски, указка.
• Для учащихся: «Светофорчик», учебник, рабочая тетрадь, ручка, цветные карандаши, индивидуальный раздаточный материал (математические «Ёлочки», схемы для заполнения (составление кратких записей к задачам)).

Последовательность и продолжительность этапов урока

• Организационный момент – 2 мин.
• Актуализация опорных знаний – 5 мин.
• Самоопределение к деятельности (постановка темы и цели урока) – 8 мин.
• Гимнастика для глаз – 2 мин.
• Работа по теме урока (первичное закрепление знаний) – 9 мин.
• Физкультминутка – 2 мин.
• Работа над пройденным материалом – 7 мин.
• Домашние задание – 2 мин.
• Рефлексия учебной деятельности – 3 мин.

Ход урока

I. Организационный момент.

– Сегодня я приглашаю вас в увлекательное путешествие по математическому лесу. Наше путешествие будет идти под девизом, который написан на слайде. Прочитаем его. (Слайд 2)

Чтоб водить корабли.
Чтобы лётчиком стать
Надо прежде всего
Математику знать.
И на свете нет профессии,
Вы смекайте-ка
Где бы нам не пригодилась
Математика.

– Это девиз нашего урока. Как вы его понимаете? (Чтобы стать хорошим летчиком капитаном, надо хорошо учиться. Преодолевать трудности, стараться самим добывать знания.)

– С каким настроением вы пришли на урок – покажите при помощи сигналов на «Светофорчике». (Слайд 3)

– Откройте тетрадь и зафиксируйте место и время нашей встречи.

– Ну, что вперед за знаниями.

II. Актуализация опорных знаний.

Первая наша остановка «Соображай-ка»

1. Индивидуальная работа у доски (на местах работа в парах)

Закрепление знаний состава числа.

– Посмотрите, какие чудесные математические ёлочки. Как вы думаете, какое задание я вам хочу предложить?

– У вас на столах есть карточки с математическими ёлочками. (Приложение 1)

– Каждая пара веточек даёт в сумме число на макушке, числа на веточках могут быть однозначные и двузначные.

(У доски 3 ученика – вписывают числа в круги. (Приложение 5) Самостоятельная работа на местах в парах.)

– Кто согласен, покажите зелёный сигнал «Светофора», а кто не согласен – красный.

– С какой целью выполняли это задание? (повторили состав числа, способы получения чисел 7, 11, 15).

2. Устный счёт (Слайд 4)

– На поляне растут математические грибы. Эти грибочки необычные они волшебные. Посмотрите, какие числа записаны на шляпках грибов, поставьте их в порядке убывания (уменьшения) и вы узнаете, какое слово спряталось на грибочках. (Приложение 2) Ответ: 55, 50, 45, 35, 25, 15.

– Что вы знаете о задаче? Назовите основные части задачи (условие, вопрос, решение, ответ). (Слайд 5)

– Как вы думаете, зачем мы выполняли это задание? (повторили порядок чисел при счёте (в натуральном ряду, вспомнили части задачи)).

Учитель закрепляет на доске карточку со словом «задачи».

III. Гимнастика для глаз.

Остановка «Глазково»

– Ребята сейчас мы попадём на лесную игровую полянку, где вам нужно глазками следить за движениями предметов. (Слайд 6)

IV. Самоопределение к деятельности (постановка темы и цели урока).

– Посмотрите, сегодня к нам на урок снова пришел Учёный Математик. (Слайд 7)

– Как вы думаете, зачем он к нам пришёл? Что-то он не весёлый. Может быть что-нибудь случилось? (У Математика в руках листочек с буквами).

– Оказывается, Математик так спешил к нам, что пока бежал у него по листочку все буквы рассыпались. Поможем Математику расшифровать слово? Поставьте буквы в порядке возрастания их высоты и узнаете слово.
— Какое слово получилось? (Обратные). (Приложение 3)

– Итак, чем мы будем сегодня заниматься на уроке? (Решать обратные задачи). (Слайд

– А обратные задачи, это какие?

– Попробуёте сформулировать проблему, которую необходимо разрешить на уроке? (Узнать о том, что такое обратные задачи и проверить наши предположения по этой проблеме).

– Вот сегодня мы будем исследователями, понаблюдаем и разрешим данную проблему.

Остановка «Задачкино» (Слайд 9)

Задачи на слайдах (схемы краткой записи для заполнения учащимися (Приложение 4)).

– Прочитайте тексты. Это одна и та же задача? В чём сходство? О чем говориться в задаче? (О кленовых и дубовых листочках, сколько упало листочков на землю). В чём отличие?

1. На землю с деревьев упало 5 дубовых и 6 кленовых листочков. Сколько всего на земле листочков?
2. В лесу листопад. На землю с деревьев упало 11 листочков. Кленовых было 6. Сколько на земле дубовых листочков?
3. В лесу листопад. На землю с деревьев упало 11 листочков. Из них было 5 дубовых. Сколько на земле кленовых листочков?

– Прочитайте первую задачу. О чем говориться в задаче? (Дубовых – 5 л., кленовых – 6 л., не знаем сколько всего на земле листочков).

– Впишите самостоятельно на карточках данные, которые известны и неизвестны в задаче.

– Решите задачу №1.

Эталон для взаимопроверки и взаимоконтроля. (Слайд 10)

– Прочитайте вторую задачу. О чем говориться в задаче? (О кленовых и дубовых листочках, сколько упало листочков на землю).

– Чем задача похожа на предыдущую и чем отличается от неё? (В обеих задачах речь идёт о кленовых и дубовых листочках, и в той, и другой

задаче на земле 6 кленовых листочков В первой задаче известно, что упало

5 дубовых листочков и нужно узнать, сколько всего упало на землю листочков с двух деревьев, во второй задаче известна общее количество листочков и нужно узнать, сколько на земле дубовых листочков.)

– Запишите кратко условие.

– Решите задачу №2.

Эталон для взаимопроверки и взаимоконтроля. (Слайд 10)

– Что вы можете сказать о решениях этих задач?

– Прочитайте третью задачу. Как изменилось ее условие? (Известно, сколько всего упало кленовых и дубовых листочков, и на земле кленовых листочков. Не знаем, сколько дубовых.)

– Что надо узнать? Запишите задачу кратко.

– Решите задачу №3.

Эталон для взаимопроверки и взаимоконтроля. (Слайд 10)

– Внимательно посмотрите на условия этих трех задач. Что вы о них можете сказать? (Они похожи.)

– Что одинаково? (Данные, числа.) — Чем отличаются?

– Внимательно посмотрите на решения задач. Что одинаково? (Числа.) — Чем отличаются? (Действиями:1) +; 2) -; 3) -.)

– Как назовем вторую и третью задачи? (Обратные первой.)

– Конечно, это обратные задачи.

– В какой форме мы записали задачи? (в форме краткой записи).

– А можно их оформить в виде схематического рисунка (Слайд 11)

– Кто может поделиться с Математиком о том, как понял, что такое обратная задача? (Задачи, в которых объект (число) и результат меняются местами (известное становится не известным, а неизвестное известным), называются обратными первой).

– Какую цель ставили? (узнать, что такое обратные задачи)

– Какой получили результат? (мы выяснили, что такое обратная задача и решили их).

– Что ещё нового мы узнали? В каком виде можно оформить кратко задачу? (схематический рисунок).

– Проверили мы наши предположения? Математик говорит, что вы молодцы.

V. Работа по теме урока

– Откройте учебник на стр. 26, № 2. (Слайд 12)

Остановка «Речная»

– Откройте тетрадь и запишите номер задания № 2.

– Прочитайте задачу. Запишите кратко.

– Решение и ответ задачи запишите самостоятельно.

– Составьте обратные задачи (устно). (Коллективное составление с комментированием).

1 вариант: решает задачу с вопросом: Сколько поймал лещей?

2 вариант: решает задачу с вопросом Сколько поймал окуней?

Самостоятельная работа. Фронтальная проверка.

Эталон для взаимопроверки и взаимоконтроля. (Слайд 13)

– Кому было легко решать задачи, покажите зелёный сигнал «Светофора».

– Кто затруднялся при работе с этим заданием, покажите жёлтый сигнал.

– С какой целью выполняли это упражнение из учебника? (закрепили умение решать задачи, учились устно составлять и решать обратные задачи).

VI. Остановка «Отдыхайкино»

Учитель показывает танцевальные движения. (Слайд 14)

1. Движения ногами (сгибание и разгибание колен), руки на пояс.
2. Подняться на носочки и поднимать медленно руки вверх.
3. Круговые движения тазом (вправо, влево).
4. Повторить 1 танцевальное движение.
5. Хлопки руками.
6. Повторить 1 танцевальное движение.

VII. Работа над пройденным материалом

Остановка «Узнайкино» (Слайд 15)

– Откройте тетрадь с печатной основой с. 34 №19.

– Прочитайте задание. Раскрасьте кружки с номерами обратных задач.

Докажите, что вы их верно нашли.

– Зачем мы выполняли это задание? Чему учились? (узнавать обратные задачи, уметь отличить обратную от данной (прямой) задачи).

VIII. Домашнее задание

1. Учебник: стр. 26, № 3.
2. Р. т.: стр. 34 № 18, № 19 (решить задачи).(Слайд 16)

IX. Рефлексия учебной деятельности

– Вспомните девиз нашего путешествия.

Чтоб водить корабли.
Чтобы лётчиком стать
Надо прежде всего
Математику знать.
И на свете нет профессии,
Вы смекайте-ка
Где бы нам не пригодилась
Математика.

– Мы сегодня с вами хорошо поработали, и я считаю, что из вас должны получиться хорошие и летчики и капитаны и вы сможете для себя выбрать любую другую нужную профессию. Математические знания важны для всех сфер деятельности.

– Посмотрите, как смотрит на нас Математик. Он улыбается. Почему? (Доволен тем, как мы поработали на уроке исследователями). (Слайд 17)

– Что нового вы узнали на уроке? Чему научились?

– Какие задачи называются обратными?

– Кто испытывал трудности при работе?

– Какие? Что нужно сделать, чтобы их устранить?

– Оцените свою работу на уроке при помощи «Светофорчика». (Слайд 18)

– Молодцы! Спасибо за работу на уроке. Наш помощник Учёный Математик благодарит вас и вручает «медальки» за работу на уроке в виде цветных кленовых и дубовых листочков: зелёный – активно работал на уроке, жёлтый – хорошо работал, красный – работал на уроке, но нужна ещё помощь.

Урок математики «Обратные задачи», 2 класс. Школа России. Конспект

Учитель. Посмотрите на доску. Что скажете? (Два личика: грустное и весёлое.)
— В улыбке участвует 18 лицевых мышц, а для неудовольствия приходится напрягать на 25 мышц больше. Какое значение имеет для человека хорошее настроение и улыбка? Давайте улыбнёмся, и я уверена, что в результате нашей совместной деятельности на уроке у всех останется хорошее настроение.

— Какое количество мышц мы используем для выражения своего плохого настроения? (18 + 25 = 43.)
1. Индивидуальная работа (связь между сложением и вычитанием).
— Что можете сказать? (Это действие первой ступени, сумма. Дети называют компоненты при сложении.)
— Можете назвать ещё действие первой ступени? (Вычитание.)
— Как называются числа при сложении? (Слагаемые.)
— Какое действие можно считать обратным действию сложения? (Вычитание.)
— Запишите к этому выражению равенство с обратным действием, когда известно значение суммы и первое слагаемое, а затем наоборот.
Учащиеся выполняют задание.
43 — 18 = 25
43 — 25 = 18
Самопроверка:
— Какое действие является обратным сложению? (Вычитание.)
2. Работа в парах (связь между умножением и делением).
— Вы вспомнили о действиях первой ступени, а какие действия вы знаете ещё? (Действия второй ступени.)
— Какое задание можно предложить? (Учащиеся предлагают варианты заданий, где в записи используются действия второй ступени.)
— Составьте и запишите на листах выражения второй ступени, используя числа 9 и 5.
Учащиеся выполняют задание.
(Записывают 9 х 5, 5 х 9, могут ещё записать 9 : 5 или 5 : 9.)
— Почему никто из вас не записал выражение вида 9 : 5 или 5 : 9? (Ответы учащихся.)
— Возникла проблема. Можем мы с уверенностью ответить на поставленный вопрос? (Нет.)
— Почему? (Нам надо ещё многому научиться.)
— Эти выражения я оставлю, к ним мы ещё вернёмся на следующих уроках и обязательно ответим на этот вопрос.
— Какое действие является обратным действию умножения? (Деление.)
— Запишите к этому выражению равенства с обратным действием.
Учащиеся выполняют задание.
45 : 9 = 5
45 : 5 = 9
Самопроверка:
— Что повторили? (Ответы учащихся.)
Вывод: вычитание является обратным действием сложения.
Деление является обратным действием умножения.
— С какой целью повторили? (Ответы учащихся.)
— Где ещё используются числовые выражения? (В решении задач.)
— Что вы знаете о задачах? (Они бывают простые и составные.)
— Цель урока — провести исследование двух задач: выявить сходства, отличия, дать название этим задачам.

На доске представлена запись задач.
Задачи:
• В эту зиму из 81 дня, прожитых волжанами, 20 дней являются холодными. Сколько дней тёплых было за этот период?
• В эту зиму из прожитых волжанами дней 20 являются холодными, а 61 тёплыми. Сколько дней за этот период прожито волжанами?
— Прочтите. Что скажете? В чём сходство? В чём различие? Какая связь между задачами? (В задачах говорится об одних и тех же предметах, но известное и неизвестное меняется.)
— Как вы думаете, в связи с этим задачи будут иметь одинаковые решения?
Учащиеся выдвигают гипотезу.
— О чём говорится в задачах? Какие главные слова можно выделить?
— Давайте решим задачи.
Учащиеся записывают решения.

— Сравните решения задач. Есть ли между ними связь? От чего она зависит?
Вывод: решение второй задачи является проверкой решения первой задачи.
— Какую цель ставили? (Дать название данным задачам.)
— Как можно назвать эти задачи? Какие есть предположения? Обратите внимание на знаки в решении. Объясните свой выбор. (Обратные задачи.)
— Проверим.
Появляется слайд «Обратные задачи».
— Какую цель ставили? (Дать название задачам.)
— Какой получили результат? (Мы выявили название.)
Физкультминутка
— 1-й ряд приседает тогда, когда в частном получается результат, равный 3; 2-й ряд приседает тогда, когда в частном получается результат, равный 4; 3-й ряд приседает тогда, когда в частном получается результат, равный 5.

— Где пригодится вам умение считать устно, зачем надо учить таблицу умножения и соответствующие случаи деления?
— Возвращаемся к нашей теме. Кто с уверенностью может сказать, что он всё понял и научился решать такие задачи?

1. Работа в парах «Поиск обратных задач».
Учитель выдаёт каждой паре учащихся конверт, содержащий в себе несколько задач. Учащиеся находят среди них обратные.
Задание: обведите номера обратных задач, докажите свой выбор.
1. В классе 26 учеников, 17 из них мальчики. Сколько девочек в классе?
2. В классе 17 мальчиков, а девочек на 8 меньше. Сколько девочек в классе?
3. В классе 17 мальчиков и 9 девочек. Сколько всего детей в классе?
4. В классе 35 учеников, 17 из них мальчики. Сколько девочек в классе?
Появляется ответ на слайде: 1,3.
— Докажите, что эти задачи обратные.
На слайде — задача под номером 4.
— А почему эта задача не является обратной, ведь в условии есть сходство с номерами 1 и 3? (В условиях разные числовые данные.)
— Давайте вернёмся к первым задачам о погоде. Откуда я взяла число 81?
81 = 31 + 31 + 19
(В декабре и январе по 31 дню, а в феврале прожили 19 дней на сегодняшний момент.)
— Что записано? (Выражение.) Что можете сказать? (Есть одинаковые слагаемые, их можно заменить умножением.)
Появляется запись на слайде:
31 + 31 + 19 = 81
31 х 2 + 19 = 81
— Что скажете о действиях разных ступеней?
— Пока вы были на перемене, я наблюдала за одним мальчиком. Он торопился из столовой на урок и перешагивал по две ступеньки, поднимаясь вверх, при этом считая. Он считал: «Один, два, три, четыре», а дальше оставалась одна ступенька. Сколько всего он насчитал ступенек?
Учащиеся предполагают.
2 2 2 2 1 = 9
— Что заметили? (Можно заменить одинаковые слагаемые умножением.)
2 х 4+1 = 9
— Почему результат не поменялся? (Знаем правило выполнения действий.)
— А если какой-нибудь ученик забыл правило, то что делать? (Воспользоваться источником информации — учебником.)
2. Самостоятельная работа (по выбору учащихся).
1-й уровень: 80 — 20 + 7 = .
2-й уровень: 70 — 2 — 5 = .
3-й уровень: 48 — 12 : 2 • 3 = .
Проверка по образцу.
— Кто какой уровень выбрал и почему?
1-й уровень : 80 — 20 + 7 = 67.
2-й уровень: 70 — 2 — 5 = 60.
3-й уровень: 48 — 12 : 2 — 3 = 30.
Самооценка (кто не допустил ошибок, ставит на полях «+»).
— Где можно было допустить ошибку? (В выборе действия, в вычислении.)
— Что следует посоветовать своим товарищам? (Дома выучить таблицу умножения и правило.)

— Какую цель ставили? (Провести исследование двух задач, выявить сходства, различия, дать определение этим задачам.)
— Какого достигли результата? Что помогло достижению успеха? (Вера в свои силы, хорошее настроение, взаимопомощь.)
— Чья работа на уроке вам понравилась? Нарисуйте на полях настроение, оставшееся после урока (кружок с улыбкой или кружок с дугой вверх).
Домашнее задание (но выбору учащихся).
1. Составить и решить задачу по выражению: 17 + 10.
2. Составить и решить задачу, обратную данной, по выражению: 12 + 14.

Задачи, обратные данной

Минус получил задание от царицы Математики составить обратные задачи. Он никак не мог понять, как задачи могут быть обратными. И тут ему на помощь пришёл Плюс, который объяснил Минусу, что значит «обратные задачи» и научил его составлять задачи, обратные данной.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока «Задачи, обратные данной»

— Вот незадача… Точнее, задача…

— Минус, к тебе можно зайти?

— Здравствуй, Минус. Ты чем это так расстроен?

— Понимаешь, наша царица-Математика задала мне задачу. А получилась прямо какая-то незадача. Я не понимаю, что мне делать. Может быть, ты мне поможешь разобраться?

— Конечно! Все, что в моих силах. Ну рассказывай!

— Вот прочитай задачу.

— На болото царевны-лягушки прилетело 8 стрел. Из них 5 стрел прилетели из тридевятого царства, а остальные — из тридесятого государства. Сколько стрел прилетело из тридесятого государства?

Ну и что же здесь трудного? Совсем простенькая задача!

— Задачка-то простенькая. Но царица-Математика приказала мне составить к этой задаче какие-то обратные. Я понимаю, что можно куда-нибудь пойти, а потом вернуться обратно. Или кому-нибудь что-то подарить, а потом потребовать эту вещь обратно. Но вот что такое обратные задачи…

— Ну, Минус, я от тебя такого не ожидал. Ничего себе — сначала подарить, а потом потребовать подарок обратно. То, что ты кому-то подарил, тебе уже не принадлежит. Это не твоя вещь, так что обратно ты требовать ее не имеешь право.

— Да ладно, я это знаю. Я просто неудачно пошутил. Давай все-таки поговорим про задачи, обратные данной.

— Для того, чтобы ты понял, что такое задачи, обратные данной, надо составить краткое условие к задаче. О чем говорится в задаче.

— О том, что на болото царевны-лягушки прилетели стрелы.

— Значит, задача про стрелы. Давай еще раз прочитаем задачу, найдем в ней числа и выделим главные, опорные слова, которые помогут составить краткое условие. Читай первое предложение.

— На болото царевны-лягушки прилетело восемь стрел.

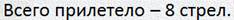
— Из них 5 стрел прилетело из тридевятого царства. Но это тоже прилетело.

— Да…надо подумать. А-а, восемь — это всего прилетело, а пять — из тридевятого царства.

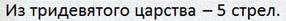
— А остальные — из тридесятого государства. Остальные — это неизвестно сколько.

Читаю дальше: сколько стрел прилетело из тридесятого государства?

— Нам надо узнать, сколько стрел прилетело из тридесятого государства. Получается вот такая запись.

Ну, теперь давай решим эту задачу.

— Задачка-то простая, для первоклашек. Нам надо узнать ту часть всех стрел, которые прилетели из тридесятого государства. Это мы будем находить, конечно, с моим любимым знаком — минусом.

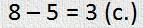
Ну вот, задача решена. А где же обратные задачи?

— А теперь давай посмотрим еще раз на краткое условие задачи. В ней было известно, сколько всего стрел прилетело и сколько прилетело из тридевятого царства. А узнать надо было, сколько прилетело из тридесятого государства. Теперь мы и это знаем.

А вот чтобы составить задачи, обратные данной, надо изменить условие задачи так, чтобы то, что в первой задаче было известным, в обратной задаче, наоборот, становилось неизвестным. А то, что было неизвестным, становилось известным.

Давай составим новую задачу, в которой неизвестным будет второе число — количество стрел, которые прилетели из тридевятого царства:

Задача: На болото царевны-лягушки прилетело 8 стрел. Из них 3 стрелы прилетели из тридесятого государства, а остальные — из тридевятого царства. Сколько стрел прилетело из тридевятого царства?

— Ну, и эту задачку решить очень легко. Опять известно, сколько всего стрел, и известна та часть стрел, которую прислали из тридесятого государства. А узнать надо ту часть стрел, которая прилетела из тридевятого царства. Часть, как обычно, находим вычитанием. Я, Минус, на посту. Получили:

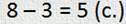
Отлично! Спасибо, Плюсик! Ты, как всегда, меня выручаешь!

— Не спиши, Минус! Ведь мы составили только одну задачу, обратную данной. Но в задаче есть еще одно число, которое ни разу пока не было неизвестным.

— Ну да, не было неизвестным общее количество стрел.

— На болото царевны-лягушки прилетело несколько стрел. Из них 5 стрел прилетело из тридевятого царства, 3 стрелы — из тридесятого государства. Сколько всего стрел прилетело царевне-лягушке?

В этой задаче известна часть стрел, прилетевшая из тридевятого царства. И та часть стрел, которая прилетела из тридесятого государства. Надо узнать, сколько всего стрел прилетело.

Э-э, да мне в этой задаче делать нечего. Твоя очередь, Плюс.

— Конечно, эта задача решается со знаком плюс, ведь известны части, а надо узнать целое, т.е., сколько всего. Получаем:

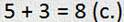
— Ничего себе! Была одна задача, а стало три!

— Ну, Минус, ты понял, что такое обратная задача?

— Кажется понял. В задачах, обратных данной, каждое число по очереди становится неизвестным.

— А сейчас без моей помощи попробуй составить такие обратные задачи. Вот тебе задача. Слушай:

Петя играл в боулинг. 7 раз он сбивал кегли, а 3 раза промахнулся. Сколько всего раз бросал шар Петя?

— Так, составляю краткое условие:

А можно слово всего я напишу не снизу, а объединю две строчки фигурной скобкой?

— Конечно, так даже понятнее будет.

— Ой-ёй-ёй, Плюс, здесь нужен ты, ведь надо узнать, сколько всего.

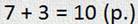
— Теперь составляю обратные задачи.

В первой задаче неизвестным будет число удачных бросков, когда Петя сбивал кегли, а остальные числа будут известны.

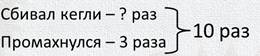
Вот в этой задаче уже нужен я, Минус, так как надо узнать только часть брошенных шаров. Получаем:

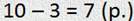
А еще одна задача нужна?

— Да, конечно. В задаче три данных, значит и задач должно быть три — одна прямая и две обратных.

— Так-так. Еще неизвестным не было количество промахов. Изменяю краткое условие:

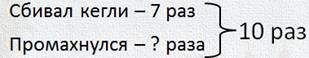
И опять здесь надо узнать часть бросков, поэтому задачу надо решать вычитанием. Получим:

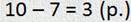
— Молодец, Минус! Так как мы составляем обратные задачи?

— В задачах, обратных данной, по очереди каждое данное становится неизвестным. А еще я заметил, что обратные задачи являются проверкой первой задачи.

— Абсолютно верно. И не забудь, обычно задач столько, сколько данных в задаче, включая неизвестное.

— Теперь я все понял. Пойду доложу царице-Математике о том, что ее задание выполнено. Спасибо, Плюсик! Пока.

Задачи, обратные данной

Цель урока: знакомство детей с новым математическим понятием: «обратные задачи», установление связи между прямой и обратной задачей.

Просмотр содержимого документа
«Задачи, обратные данной»

УМК: «Школа России».

Тема: «Задачи, обратные данной».

Цель урока: знакомство детей с новым математическим понятием: «обратные задачи», установление связи между прямой и обратной задачей.

· Уметь узнавать и составлять обратные задачи.
· Уметь использовать в речи термин «обратная» задача.
· Знать структуру задачи.
· Уметь решать задачи в одно действие.
· Уметь выделять её части и анализировать содержание текстовой задачи.
· Уметь составлять краткую запись или схематический рисунок.
· Уметь выполнять вычисления изученных видов.

Личностных УУД:
— Способность к самооценке на основе критерия успешности учебной деятельности; позитивному отношению к уроку математики, учебно-познавательный интерес к учебному материалу.
Регулятивных УУД:
— Уметь учащимися принимать и сохранять учебную задачу, планировать своё действие в соответствии с поставленной задачей; оценивать правильность выполнения действия на уровне адекватной оценки; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; овладение умениями проговаривать последовательность действий на уроке, умение формулировать цель урока с помощью учителя.
Познавательные УУД:
— Уметь осуществлять логические операции; описывать математические объекты; ориентироваться в своей системе знаний, строить небольшие математические высказывания.
УУД Коммуникативные:
— Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; учиться работать в паре, формулировать собственное мнение и позицию.

Методы и формы работы: совместная с учителем учебно-познавательная деятельность, работа в парах, математическая игра, учебный (проблемный) диалог, самостоятельная работа, наблюдение за математическими объектами (моделирование (сравнение, анализ)).

Организационный момент.

— Сегодня я приглашаю вас в увлекательное путешествие по математическому лесу. Наше путешествие будет идти под девизом, который написан на слайде. Прочитаем его.

Чтоб водить корабли.
Чтобы лётчиком стать
Надо прежде всего
Математику знать.
И на свете нет профессии,
Вы смекайте – ка
Где бы нам не пригодилась
Математика.

— Это девиз нашего урока. Как вы его понимаете? (Чтобы стать хорошим летчиком, капитаном, надо хорошо учиться. Преодолевать трудности, стараться самим добывать знания.)
— С каким настроением вы пришли на урок – покажите при помощи сигналов на «Светофорчике».

—Итак, вперед, за знаниями!

II. Каллиграфическая минутка.

В руки в ручки мы берём,

Числа мы писать начнём…

Учитель предлагает ученикам рассмотреть числа, записанные на доске:

6 7 6 7 6 7 6 7… 13 13 13 13…

– Как связаны между собой записанные вами числа?

III. Устный счёт.

Устно мы теперь считаем,

Навык счёта развиваем.

– Найдите значение суммы чисел 3 и 4.

– Значение этой суммы вычтите из числа 17.

– Найдите значение суммы чисел 6 и 4.

– Значение этой суммы вычтите из числа 30.

– Из суммы чисел 70 и 8 вычтите число 8.

– Из суммы чисел 60 и 5 вычтите число 60.

– Разность чисел 10 и 8 прибавьте к числу 20.

– Разность чисел 9 и 3 прибавьте к числу 90.

– Маше 8 лет. Мама на 20 лет старше Маши, а папа на 1 год старше мамы. Сколько лет маме? Сколько лет папе?

При выполнении заданий учащиеся пользуются сигнальными карточками.

– А теперь выполните задания на смекалку – задачи 5, 6 (с. 26, 27).

Задача 5 (с. 26). (У Юры – пудель. У Димы – овчарка. У Алёши – такса.)

Задача 6 (с. 27). (Синих карандашей – 6.)

IV. Гимнастика для глаз.

V. Самоопределение к деятельности (постановка темы и цели урока).

– А теперь будьте внимательны. Я зачитаю вам слова-понятия, а вы должны назвать общее слово, которое их объединяет: условие, вопрос, данные числа, искомое число. (Задача.)

– Что вы знаете о задаче? Какие виды задач знаете?

– Сегодня вы узнаете новое о задачах. Вам самостоятельно предстоит сделать открытие.

— Посмотрите, сегодня к нам на урок снова пришел Учёный Математик.
— Как вы думаете, зачем он к нам пришёл? Что-то он не весёлый. Может быть, что-нибудь случилось? (У Математика в руках листочек с буквами).
— Оказывается, Математик так спешил к нам, что пока бежал у него по листочку все буквы рассыпались. Поможем Математику расшифровать слово? Поставьте буквы в порядке возрастания их высоты и узнаете слово.
— Какое слово получилось? (Обратные).

— Итак, над какой темой мы будем сегодня работать на уроке? (Решать обратные задачи).
— А обратные задачи, это какие?
— Попробуйте сформулировать проблему, которую необходимо разрешить на уроке? (Узнать о том, какие задачи называются обратными и проверить наши предположения по этой проблеме).
— Вот сегодня мы будем исследователями, понаблюдаем и разрешим данную проблему.
– Прочитайте задачу 1(1) (с. 26) и выберите схему, которая соответствует данной задаче. Опираясь на условие и ответ решённой задачи, составьте две другие задачи, которые соответствуют схемам.

(1-я задача. У Веры было 10 рублей. На эти деньги она купила блокнот, который стоил 6 рублей, и карандаш. Сколько стоил карандаш?

2-я задача. У Веры было 10 рублей. На эти деньги она купила карандаш, который стоил 4 рубля, и блокнот. Сколько стоил блокнот?)

– Теперь сравните решения всех задач. Установите связь между ними.

Решение: 1) 6 + 4 = 10;

– Такие задачи называются обратными.

— Что вы можете сказать о решениях этих задач?
— Внимательно посмотрите на условия этих трех задач. Что вы о них можете сказать? (Они похожи.)
— Что одинаково? (Данные, числа.) — Чем отличаются?
— Внимательно посмотрите на решения задач. Что одинаково? (Числа.) — Чем отличаются? (Действиями:1) +; 2) -; 3) -.)
— Как назовем вторую и третью задачи? (Обратные первой.)
— Конечно, это обратные задачи.
— В какой форме мы записали задачи? (в форме краткой записи и
в виде схематического рисунка)
— Кто может поделиться с Математиком о том, как понял, что такое обратная задача? (Задачи, в которых объект (число) и результат меняются местами (известное становится не известным, а неизвестное известным), называются обратными первой).
— Какую цель ставили? (узнать, что такое обратные задачи)
— Какой получили результат? (мы выяснили, что такое обратная задача и решили их).
— Что ещё нового мы узнали? В каком виде можно оформить кратко задачу? (схематический рисунок).
— Проверили мы наши предположения? Математик говорит, что вы молодцы.

Для закрепления нового материала учащимся предлагается составить задачу по данным числам (или по данной схеме), а затем составить задачи, обратные данной.

– Разберите задачу 2 (с. 26). Выделите условие и вопрос, назовите данные и искомое числа. Составьте краткую запись или схему. Решите задачу самостоятельно. Сформулируйте и запишите ответ.

– Составьте две задачи, обратные данной.

— Кому было легко решать задачи, покажите зелёный сигнал «Светофора».
— Кто затруднялся при работе с этим заданием, покажите жёлтый сигнал.
— С какой целью выполняли это упражнение из учебника? (закрепили умение решать задачи, учились устно составлять и решать обратные задачи).
VI.Физкультминутка.

Руки ставим все вразлёт, Руки в стороны держите,

Появился самолёт. Друг на друга посмотрите,

Мах крылом туда-сюда, Раз и два, раз и два.

Делай раз и делай два. Опустите руки вниз,

Раз и два, раз и два. И на место все садитесь!

VII. Работа с геометрическим материалом.

– Рассмотрите чертёж, данный в задании 1 (с. 27).

– Сколько отрезков изображено на чертеже? (Три.)

– Можно ли, не измеряя самый большой отрезок, узнать его длину?

– Каким образом? (Сложить длины двух других отрезков.)

– Какова длина большого отрезка? Проверьте это измерением. Вы были правы?

– Начертите отрезок длиной 10 сантиметров.

– Поставьте на нём точку так, чтобы получился отрезок длиной 4 сантиметра.

– Какова длина другого вновь полученного отрезка?

– Можно ли это узнать, не производя измерений? Как?

– Проверьте ваше предположение, измерив отрезок. Вы были правы?

VI. Решение выражений.

– Самостоятельно (по вариантам: вариант I – 1-й столбик; вариант II – 2-й столбик) решите выражения из задания 4 (с. 27). Затем устно решите 3-й столбик данного номера.

VII. Домашнее задание.

1. Учебник: стр. 26, № 3, №4.

VIII . Рефлексия учебной деятельности.

— Вспомните девиз нашего урока.

Чтоб водить корабли.
Чтобы лётчиком стать
Надо прежде всего
Математику знать.
И на свете нет профессии,
Вы смекайте – ка
Где бы нам не пригодилась

— Мы сегодня с вами хорошо поработали, и я считаю, что из вас должны получиться хорошие и летчики и капитаны и вы сможете для себя выбрать любую другую нужную профессию. Математические знания важны для всех сфер деятельности.
— Посмотрите, как смотрит на нас Математик. Он улыбается. Почему? (Доволен тем, как мы поработали на уроке исследователями).
— Что нового вы узнали на уроке? Чему научились?
— Какие задачи называются обратными?
— Кто испытывал трудности при работе?
— Какие? Что нужно сделать, чтобы их устранить?
— Оцените свою работу на уроке при помощи «Светофорчика».

Задачи, обратные данной

Приготовьте свои ушки и глазки,
Чтобы они могли всё видеть,
Слышать и запоминать.

Громко прозвенел звонок –
Начинается урок.

2. Этап подготовки учащихся к активному сознательному усвоению знаний

1. Целеполагание

Сегодня на уроке мы узнаем, что такое обратные задачи.

2. Устный счёт

Задание 1

Решите примеры. Дополните столбики одним своим примером. Запишите только ответы.

12 — 6 = 6 — У 5 + 7 = 12 — А 80 — 10 = 70 — О
13 — 6 = 7 — З 6 + 7 = 13 — Й 70 — 20 = 50 — Н
14 — 6 = 8 — Н 7 + 7 = 14 — К 60 — 30 = 30 — И

6, 7, 8, 9, 12, 13, 14, 15, 70, 50, 30, 10.

Расположите числа в порядке возрастания, чтобы узнать название города, по которому мы будем путешествовать сегодня на уроке.

6, 7, 8, 12, 13, 14, 30, 50, 70.
У З Н А Й К И Н О

Какое получилось слово?

В этом городе живут забавные человечки, которые очень любознательны и хотят все знать.

Задание 2

Чтобы попасть в город УЗНАЙКИНО нужно ответить на вопросы:

Назовите однозначные числа.
Назовите двузначные числа.
Назовите самое маленькое двузначное число.
Назовите самое маленькое однозначное число.
Назовите числа предшествующие числам: 6, 12, 30, 50, 70. 5, 11, 29, 49, 69.
Назовите числа, следующие за числами: 10, 15, 30, 50, 70. 11, 16, 31, 51, 71.
Назовите числа, которые находятся между числами 15 и 30. 16-29

А вот и наш помощник. Зовут его Путейка, потому что он очень любит путешествовать. Путейка познакомит вас с городом, расскажет интересные истории, проверит ваши знания.

Какой предмет помогал героям сказок находить нужное место?
Правильно, клубок ниток помогал героям сказок находить нужное место. Какой прибор помогает современным путешественникам?
Верно, компас помогает современным путешественникам. Что вы знаете о компасе? Компас – это устройство, облегчающее ориентирование на местности. Когда не было компаса, то люди ориентировались по солнцу, луне и звёздам, по местным признакам. А потом изобрели прибор, на котором изобразили четыре стороны света: Север, Юг, Запад, Восток. В центре компаса находится вращающаяся стрелка, 2 половины которой раскрашены в синий и красный цвет. Красная стрелка показывает на Юг, синяя – на Север.

Задание 3

Мы попали на улицу Сравнительную. Поставьте нужный знак, чтобы продолжить путешествие по улице.

1 дес… 10 1 дес = 10
1 р. …1 к. 1 р. > 1 к.
23… 32 23 4 дм
78 …75 78 > 75

Задание 4

Продолжим наш путь на общественном транспорте. Для этого нужно купить билет.

Сколько нужно получить сдачи с 10 рублей, если билет стоит 5 рублей? 5
Если билет стоит 6 рублей? 4
Если билет стоит 8 рублей? 2

Задание 5

Помогите Путейке сосчитать общественный транспорт, который находится на станции.
На станции находилось 5 автобусов, а троллейбусов на 6 больше. Сколько всего автобусов и троллейбусов на станции?
Решите задачу.

1) 5 + 6 = 11 (тр.)
2) 11 + 5 = 16 (м.)

3. Этап усвоения новых знаний

Мы прибыли на станцию «Задачкино». На этой станции мы узнаем, как решаются задачи, в которых число и результат меняются местами.

1. В апреле было 14 пасмурных дней и 16 ясных дней. Сколько дней в апреле?
2. В апреле 30 дней. Из них 14 дней были пасмурными. Сколько ясных дней было в апреле?
3. В апреле 30 дней. Ясными были 16 дней. Сколько пасмурных дней было в апреле?

Это одна и та же задача?
Нет, разные задачи.

Какая связь между задачами?
Говорится про одно и то же, но известное и неизвестное меняются.

Как вы думаете, эти задачи будут иметь одинаковое решение?
Давайте решим эти задачи.

Прочитайте 1 задачу.
Что известно? Пасмурных дней было 14. Ясных дней было 16.
Что спрашивается в задаче?
Каким действием решим задачу?

Прочитаем 2 задачу.
В чем сходство и в чем отличие этой задачи от предыдущей?
Что известно? В апреле 30 дней. Пасмурных дней было 14.
Что нужно узнать? Сколько ясных дней было в апреле.
Как решим эту задачу?

Прочитайте 3 задачу.
Как изменилось ее условие?
Какая будет краткая запись?

П. – ? дн.
Яс. – 16 дн. (общая скобка, 30 дн.)

Что нужно узнать?
Как решается эта задача?

Внимательно посмотрите на условия этих трех задач. Что вы о них можете сказать?
Они похожи. Что в этих задачах одинаково?
Данные, числа одинаковы. Чем задачи отличаются?
Ставятся вопросы разные. Что было известно, стало неизвестно и наоборот.
Сравните решения задач. Что одинаково?
Числа.
Чем отличаются?
Действиями. Другими словами, действия обратные.
Как назовем вторую и третью задачи по отношению к первой?
Задачи, обратные первой. Значит, что такое обратная задача?

Задачи, в которых объект (число) и результат меняются местами (известное становится не известным, а неизвестное известным), называются обратными первой.

Вместе с человечком мы добрались до остановки «Отдыхайкино».

4. Этап закрепления новых знаний

Мы добрались до улицы Решайкино. Как вы думаете, чем занимаются жители города на этой улице?
Правильно, они решают задачи. Давайте поможем им решить задачи.

Задание 1

1. В классе 20 учеников. 7 из них мальчики. Сколько девочек в классе?
2. В классе 7 мальчиков, а девочек на 6 больше. Сколько девочек в классе?
3. В классе 7 мальчиков и 13 девочек. Сколько всего детей в классе?

Найдите среди этих задач обратные.

Конечно № 1 и 3 – это обратные задачи. Объясните, почему вы так считаете?

Молодцы ребята, вы справились с заданием и попали на улицу Составляйкино.
Как думаете, чем занимаются жители города Узнайкино на этой улице?
Правильно, с забавными человечками мы будем составлять задачи обратные данной.

Задание 2

Прочитайте задачу.
В одном доме проживает 8 человечков, а в другом доме — 9. Сколько всего человечков проживает в двух домах?
Составим чертёж к задаче. Что известно в задаче?
Что спрашивается в задаче?
Как решается эта задача?

Ответ: 17 человечков.

Составим задачи, обратные данной. Не забывайте, что, решив исходную задачу, надо взять её ответ и включить его в новую задачу, не меняя сюжета, а одно из известных сделать искомым.

Задание 3

В двух домах проживает 17 человечков. В одном доме проживает 8 человечков. Сколько человечков проживает во втором?Составьте чертёж задачи.
Решите задачу.

Ответ: 9 человечков.

Составьте ещё одну задачу.
В двух домах проживает 17 человечков. В одном доме проживает 9 человечков. Сколько проживает в первом доме?
Составьте чертёж задачи.
Решите задачу.

Ответ: 8 человечков.

Чем отличаются схемы обратных задач от схемы данной задачи?

А если нет компаса и не светит солнце, можно ли как-то ещё сориентироваться на местности?
Как могут помочь знания о том, с какой стороны у деревьев растёт мох?
C какой стороны дерева муравьи строят муравейники?

В незнакомой такой обители
неприметно для нас живёт
Очень рыженький, очень маленький,
Муравьиный такой народ.
Озабоченный, сосредоточенный,
И у каждого ноша своя.
Ну, скажите, а вы разве видели
Безработного муравья? Р. Дерикот

Задание 4

Жители города Узнайкино говорят: «Трудолюбив, словно муравей».
Что значит эта поговорка?

Народ города предлагает вам потрудиться самостоятельно.

Самостоятельная работа

Задание 1

Человечек поймал 6 окуней и 8 лещей. Сколько всего рыб он поймал?
— Нарисовать схематический чертёж и решить задачу.

Проверьте себя и оцените свои успехи.

Задание 2

Решите задачи, обратные данной, используя чертежи.

14 — 6 = 8 (л.) 14 — 8 = 6 (ок.)

Ответ: 8 лещей. Ответ: 6 окуней.

Проверьте себя и оцените свои успехи.

5. Этап подведения итогов

Вот и подошло наше путешествие к концу.
С какими задачами мы познакомились сегодня на уроке?
Какие задачи называются обратными?

Еще раз запомните! Задачи, в которых объект (число) и результат меняются местами (известное становится не известным, а неизвестное известным), называются обратными первой.

Обратная задача

Обратная задача — тип задач, часто возникающий во многих разделах науки, когда значения параметров модели должны быть получены из наблюдаемых данных.

Обратные задачи являются некорректно поставленными задачами. Из трёх условий корректно поставленной задачи (существование решения, единственность решения и его устойчивость) в обратных задачах наиболее часто нарушается последнее. В функциональном анализе обратная задача представляется в виде отображения между метрическими пространствами. Обратные задачи обычно формулируются в бесконечномерных пространствах, но ограничение на конечность измерений и целесообразность вычисления конечного числа неизвестных параметров приводят к изменению задачи в дискретной форме. В этом случае используют метод регуляризации для того, чтобы избежать переобучения.

Содержание

Линейная обратная задача

Линейная обратная задача может быть описана в следующем виде:

,

где — линейный оператор, описывающий явные отношения между данными и параметрами модели, и представляющий собой физическую систему. В случае дискретной линейной обратной задачи, описывающей линейную систему, и являются векторами, что позволяет использовать следующее представление задачи:

,

где является матрицей.

Примеры

Примером линейной обратной задачи служит интегральное уравнение Фредгольма первого порядка.

Для существенно гладкого определённый выше оператор является компактным на таких банаховых пространствах, как Пространства . Даже если отображение является взаимно однозначным, обратная функция не будет непрерывной. Таким образом, даже маленькие ошибки в данных будут сильно увеличены в решении . В этом отношении обратная задача по определению из измеренных данных будет являться некорректной.

Для получения численного решения необходимо аппроксимировать интеграл с помощью численного интегрирования и дискретных данных. Результирующая система линейных уравнений будет некорректно поставленной задачей.

Преобразование Радона также является примером линейной обратной задачи.

Нелинейная обратная задача

В нелинейных обратных задачах ставятся более сложные отношения между данными и моделью, которые описываются уравнением:

Здесь представляет собой нелинейный оператор, который не может быть приведён к виду линейного отображения, переводящего в данные. Линейные обратные задачи были полностью решены с теоретической точки зрения в конце XIX века, из нелинейных до 1970 года был решён только один класс задач — задача обратного рассеяния. Существенный вклад внесла российская математическая школа (Крейн, Гельфанд, Левитан).

Ссылки

Международные научные журналы

• Вычислительная математика
• Функциональный анализ

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Обратная задача» в других словарях:

Обратная задача — [dual prob­lem] см. Двойственная задача … Экономико-математический словарь

обратная задача — Задача определения физических свойств возмущающего тела путем наблюдения создаваемых им эффектов полей и потенциалов; нахождение модели по наблюдённым данным. Противоположна прямой задаче, в которой по известной модели вычисляют создаваемый ею… … Справочник технического переводчика

Обратная задача — при рассмотрении процессов восстановление ситуации для меньших времен; обратная задача в смысле восстановления ситуации в прошлом не всегда разрешима, даже если есть решение прямой задачи; иногда понятие применяется достаточно условно,… … Мир Лема — словарь и путеводитель

обратная задача — atvirkštinis uždavinys statusas T sritis fizika atitikmenys: angl. inverse problem vok. inverse Aufgabe, f; Umkehrproblem, n rus. обратная задача, f pranc. problème inverse, m … Fizikos terminų žodynas

обратная задача гравиразведки — Определение пространственного распределения источников поля силы тяжести по распределению в пространстве измеренных значений силы тяжести или значений вторых производных потенциала силы тяжести. [ГОСТ Р 52334 2005] обратная задача гравиразведки… … Справочник технического переводчика

обратная задача сейсморазведки — Определение параметров сейсмогеологического разреза на основе интерпретации сейсморазведочных данных [ГОСТ 16821 91] Тематики сейсморазведка … Справочник технического переводчика

обратная задача теплового НК — Определение конфигурации тела и дефектов по экспериментально регистрируемым изменениям температуры во времени и пространстве. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное… … Справочник технического переводчика

обратная задача теплопроводности — (для расчёта температуры и плотности теплового потока по экспериментальным замерам внутри тела) [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN inverse heat conduction problem … Справочник технического переводчика

обратная задача магниторазведки — Определение модели геологической среды по наблюдениям магнитного поля. [ГОСТ 24284 80, статья 135] Источник: ГОСТ Р 53795 2010: Изучение недр геологическое. Термины и определения … Словарь-справочник терминов нормативно-технической документации

обратная задача сейсморазведки — en seismic stratigraphy Источник: ГОСТ Р 53795 2010: Изучение недр геологическое. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации