Что такое зависимая переменная и независимая переменная в алгебре

Независимая переменная

Первое, с чем необходимо определиться при планировании эксперимента, — это сколько будет уровней независимой переменной и каковы они будут. Уровни независимой переменной — это ее конкретные значения. Они могут быть заданы в любой измерительной шкале, т.e. могут быть как количественными, так и качественными.

Независимая переменная обязательно имеет как минимум два уровня, которые отражают особенности се воздействия на зависимую переменную. Иначе она просто перестает быть переменной. В примере с решением задач у независимой переменной два качественных уровня, заданных в шкале наименований: 1 — душное помещение; 2 — проветренное помещение. Если исследователь желает проследить более топкие, количественные соотношения между тем, насколько воздух в помещении насыщен кислородом, и уровнем интеллектуальной активности испытуемых, он может выразить свою независимую переменную в более сильной шкале, определяя, например, различные значения содержания кислорода на 1 м 3 воздуха.

Если исследователь обнаруживает разницу в успешности решения задач в душном и проветриваемом помещении, то у него есть некоторые основания полагать, что духота влияет на качество решения задач. Во всяком случае выполняются первые два условия каузального вывода. Иначе говоря, изменение зависимой переменной в соответствии с изменением независимой переменной позволяет говорить о влиянии независимой переменной на зависимую.

Экспериментальные планы с независимой переменной, имеющей два уровня, называют одноуровневыми — вероятно, потому, что один из уровней независимой переменной отражает нормальное, обычное состояние дел, которое характеризуется отсутствием воздействия (в нашем примере этому состоянию соответствует проветриваемое помещение). Воздействие на испытуемых, приводящее к ухудшению решения задач, оказывает другой уровень независимой переменной, отражающий ненормальное состояние дел (в нашем примере — душное помещение).

У независимой переменной может быть больше двух уровней. Экспериментальные планы, в которых у независимой переменной больше двух уровней, называют многоуровневыми. Например, если нас интересует, влияет ли то, с кем ребенок гуляет на детской площадке, на то, в какие игры предпочитает играть ребенок, то в этом случае исследователь управляет одной независимой переменной с четырьмя уровнями: 1 — гуляет один, 2-е няней, 3 — с родителями, 4-е друзьями. И если, к примеру, ребенок, гуляющий с няней, гораздо дольше предпочитает играть в догонялки (а не в другие игры), то исследователь имеет основания считать, что этот фактор определяет интересы ребенка в предпочтении данной игры.

Отметим, что, если задача экспериментатора состоит в том, чтобы не просто отметить влияние одной переменной на другую, а выяснить еще и характер такой связи, он обязан использовать именно многоуровневые независимые переменные. В противном случае характер связи не будет установлен. Так, например, исследователь, изучающий психофизические зависимости между различными концентрациями пахучего вещества и соответствующими ощущениями, должен взять несколько таких концентраций, чтобы понять, описывается ли искомая зависимость логарифмическим или степенным законом. Одноуровневый план не предоставит ему такой возможности.

При планировании эксперимента исследователь должен четко определиться с тем, сколько уровней имеет независимая переменная и как именно, согласно его гипотезе, они влияют на зависимую переменную. После этого перед ним встанет вопрос о том, как наиболее надежно отличить разные уровни переменной друг от друга. Чем лучше разные уровни независимой переменной разведены, т.е. чем яснее зафиксированы их различия, тем нагляднее будет их влияние на зависимую переменную. Если же уровни независимой переменной с трудом можно отличить друг от друга, то и их влияние на зависимую переменную будет менее заметным. В этом случае исследователь рискует пропустить результат, важный для подтверждения гипотезы, пройти мимо своего открытия.

Кроме того, исследователь должен определиться с тем, сколько независимых переменных он задействует в своем исследовании. Если независимая переменная одна, говорят об однофакторных экспериментальных планах. В зависимости от количества уровней независимой переменной однофакторные планы могут быть либо одноуровневыми, либо многоуровневыми.

Если исследователь задействует две и более независимых переменных, которые все вместе влияют на одну и ту же зависимую переменную, такие планы называют многофакторными. Многофакторные планы могут включать в себя либо одноуровневые, либо многоуровневые независимые переменные. Например, исследователь проверяет гипотезу о том, что примерно одинаковая успешность мальчиков и девочек в выполнении теста интеллекта сопряжена с тем, что мальчики существенно лучше решают арифметические задания, а девочки — анаграммы. Это будет пример многофакторного плана, в котором первая переменная (пол) имеет два уровня (мальчики и девочки), а вторая переменная (тин задачи) гоже имеет два уровня (арифметические задания и анаграммы).

Если же исследователя интересует, как меняется качество решения задач у людей с разным режимом дня («совы» и «жаворонки»), то он будет строить эксперимент с одной одноуровневой и одной многоуровневой переменными: первая переменная (режим дня) имеет два уровня («совы» и «жаворонки»), вторая переменная (время дня) имеет четыре уровня (утро, день, вечер и ночь). При этом зависимой переменной в обоих случаях будет качество решения задач.

Таким образом, независимая переменная играет ключевую роль в планировании экспериментального исследования, и еще до того, как приступать к практическим действиям, исследователь должен четко представлять, сколько в его исследовании будет независимых переменных, какие именно, сколько уровней будет у каждой и как эти уровни он будет фиксировать в исследовании.

Понятие переменной в эксперименте. Зависимая, независимая, антецедентная и промежуточная переменные

Переменнаяможет быть определена как эмпирически наблюдаемое свойство некоторого явления, которое может принимать более одного значения. Например, такие переменные, как пол и национальность, могут принимать ограниченное число значений, и могут быть «измерены» лишь качественно, путем приписывания им таких характеристик, как “мужской” или “англичанин”. Другие переменные, как, например, возраст и годовой доход, могут иметь гораздо более широкий спектр значений; их можно измерять количественно путем подсчета.

Переменные занимают центральное место в процессе исследования по двум причинам. Во-первых, предоставляя более четкие эмпирические определения, они помогают установить, за чем следует наблюдать, чтобы проверить нашу теорию. Во-вторых, зная, какова роль переменных в рамках гипотез, мы можем организовать наше наблюдение. Переменные, которые рассматриваются как меняющие свое значение в ответ на изменение значения других переменных, называются зависимыми переменными. Их значение зависит от значения других переменных. Переменные, которые воздействуют на значение других переменных, меняя свои собственные значения, называются независимыми переменными.

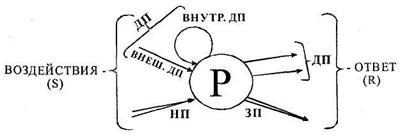
Будет ли переменная зависимой или независимой, определяется отношением, утверждаемым гипотезой, содержащей данную переменную. Одна и та же переменная может быть зависимой в одном исследовании и независимой в другом. Например, некий исследователь, наблюдая за лоббистской борьбой заинтересованных групп, мог бы сделать вывод, что, чем больше в государстве организованных групп, связанных определенными интересами, тем выше будет уровень правительственных расходов на программы по социальному обеспечению. В этом случае число групп является независимой переменной (НП), а уровень расходов – зависимой переменной (ЗП). Другой исследователь мог бы прийти к выводу, что группы, связанные определенными интересами, возникают в результате осознания людьми возможности получения от правительства определенных благ, и утверждать, что, чем больше средств правительство тратит на социальное обеспечение, тем больше будет число организованных групп, имеющих свои интересы. Здесь правительственные расходы – независимая переменная, а количество групп – зависимая. Различие между двумя точками зрения на возникающие в этих случаях отношения изображены на.

. Промежуточные переменные осуществляют связь между независимыми и зависимыми переменными. В этом случае заинтересованные группы не могли бы воздействовать на уровень правительственных ассигнований, если бы они Не занялись парламентской деятельностью, чтобы получить фонды, предназначенные для этой цели. Если бы организациям было запрещено действовать в кулуарах законодательных органов, появление организаций, представляющих заинтересованные группы, не связывалось бы с уровнем правительственных ассигнований.

Промежуточные переменные регулируют взаимосвязи между другими переменными. Это означает, что значение, принимаемое промежуточными переменными, может воздействовать на силу и направление отношений между другими переменными. Поскольку промежуточные переменные определяют отношения между другими переменными, знание роли, которую они играют, будет оказывать влияние на наши ожидания, касса

Последний тип переменной, существенный в этой связи, – это антецедентная переменная. В то время как промежуточные переменные занимают место между независимой и зависимой переменными, антецедентные переменные вступают в действие до независимой переменной. Проводившиеся в США исследования поведения на выборах показали, что люди, глубоко осознающие партийную принадлежность, с большей вероятностью принимают участие в голосовании, чем те, у кого такого осознания нет. Мы могли бы сделать из этого вывод, что осознание партийной принадлежности способствует участию в голосовании. Однако что заставляет одних глубоко чувствовать партийную принадлежность, а других нет? Вероятно, важную роль в формировании у человека чувства партийной принадлежности играет глубина чувства партийной принадлежности, свойственного его родителям. Таким образом, партийная принадлежность родителей является антецедентной переменной в каузальной цепи, обусловливающей вероятность голосования.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Переменная (математика) — Variable (mathematics)

Для переменных в информатике см. Переменная (информатика). Для использования в других целях см. Переменная (значения).

В математика, а Переменная это символ, который функционирует как заполнитель для переменного выражения или количество, и часто используется для представления произвольного элемента набор. В добавление к числа, переменные обычно используются для представления векторов, матрицы и функции. [1] [2]

Изготовление алгебраические вычисления с переменными, как если бы они были явными числами, позволяет решить ряд задач за одно вычисление. Типичным примером является квадратичная формула, что позволяет решать все квадратное уровненеие —Просто подставляя числовые значения коэффициентов данного уравнения вместо переменных, которые их представляют.

В математическая логика, а Переменная является либо символом, представляющим неуказанный срок теории (т.е. метапеременная ), или основной объект теории, которым манипулируют, не обращаясь к его возможной интуитивной интерпретации.

Содержание

Этимология

«Переменная» происходит от латинского слова, вариабилис, с «вари (нас)«» означает «различные» и «-ābilis«’означает« -способный », что означает« способный к изменению ». [3]

Генезис и эволюция концепции

В 7 веке Брахмагупта использовали разные цвета для представления неизвестных в алгебраических уравнениях в Брахмаспхунасиддханта. Один из разделов этой книги называется «Уравнения нескольких цветов». [4]

В конце 16 века Франсуа Виет представил идею представления известных и неизвестных чисел буквами, которые в настоящее время называются переменными, и идею вычисления с ними, как если бы они были числами, чтобы получить результат простой заменой. Соглашение Виэта заключалось в использовании согласных для известных значений и гласных для неизвестных. [5]

В 1637 г. Рене Декарт «изобрел соглашение о представлении неизвестных в уравнениях Икс, у, и z, и знает а, б, и c«. [6] Вопреки соглашению Виэта, слово Декарта все еще широко используется.

Начиная с 1660-х годов, Исаак Ньютон и Готфрид Вильгельм Лейбниц независимо разработал исчисление бесконечно малых, который по сути состоит из изучения того, как бесконечно малый вариация переменное количество вызывает соответствующее изменение другой величины, которая является функция первой переменной. Почти столетие спустя Леонард Эйлер исправил терминологию исчисления бесконечно малых и ввел обозначение у = ж(Икс) для функции ж , это Переменная Икс и его ценность у . До конца 19 века слово Переменная относился почти исключительно к аргументы и значения функций.

Во второй половине 19-го века выяснилось, что основы исчисления бесконечно малых не были достаточно формализованы, чтобы иметь дело с очевидными парадоксами, такими как нигде дифференцируемый непрерывная функция. Чтобы решить эту проблему, Карл Вейерштрасс представил новый формализм, состоящий в замене интуитивного понятия предел по формальному определению. Старое понятие предела было «когда Переменная Икс меняется и имеет тенденцию к а , тогда ж(Икс) стремится к L «, без какого-либо точного определения» имеет тенденцию «. Вейерштрасс заменил это предложение формулой

в котором ни одна из пяти переменных не считается изменяющейся.

Эта статическая формулировка привела к современному понятию переменной, которое представляет собой просто символ, представляющий математический объект который либо неизвестен, либо может быть заменен любым элементом данного набор (например, набор действительные числа ).

Конкретные виды переменных

Обычно переменные играют разные роли в одной и той же математической формуле, и для их различения были введены имена или квалификаторы. Например, генерал кубическое уравнение

интерпретируется как имеющий пять переменных: четыре, а, б, c, d , которым приняты числа и пятая переменная, Икс, понимается как неизвестный номер. Чтобы их различать, переменная Икс называется неизвестно, а остальные переменные называются параметры или же коэффициенты, а иногда константы, хотя последняя терминология неверна для уравнения и должна быть зарезервирована для функция определяется левой частью этого уравнения.

В контексте функций термин Переменная обычно относится к аргументам функций. Обычно это имеет место в таких предложениях, как «функция действительной переменной «, » Икс — переменная функции ж: Икс ↦ ж(Икс) «, » ж является функцией переменной Икс «(означает, что на аргумент функции ссылается переменная Икс ).

В том же контексте переменные, не зависящие от Икс определять постоянные функции и поэтому называются постоянный. Например, постоянная интеграции — произвольная постоянная функция, добавляемая к определенному первообразный для получения других первообразных. Потому что сильные отношения между многочлены и полиномиальная функция, термин «константа» часто используется для обозначения коэффициентов многочлена, которые являются постоянными функциями неопределенных.

Это использование «константы» как сокращения «постоянной функции» следует отличать от обычного значения этого слова в математике. А постоянный, или же математическая константа является хорошо и однозначно определенным числом или другим математическим объектом, например, числами 0, 1, π и элемент идентичности из группа.

Другие конкретные имена переменных:

• An неизвестный переменная в уравнение который должен быть решен.
• An неопределенный — это символ, обычно называемый переменной, который появляется в многочлен или формальный степенной ряд. Формально неопределенное — это не переменная, а постоянный в кольцо многочленов или кольцо формальный степенной ряд. Однако из-за сильной связи между полиномами или степенными рядами и функции которые они определяют, многие авторы рассматривают индетерминанты как особый вид переменных.
• А параметр — величина (обычно число), которая является частью входных данных проблемы и остается постоянной в течение всего решения этой проблемы. Например, в механика масса и размер твердого тела равны параметры для изучения его движения. В Информатика, параметр имеет другое значение и обозначает аргумент функции.
• Свободные переменные и связанные переменные
• А случайная переменная это своего рода переменная, которая используется в теория вероятности и его приложения.

Все эти наименования переменных имеют семантический природа, и способ вычисления с ними (синтаксис ) одинаково для всех.

Зависимые и независимые переменные

В исчисление и его применение к физика и другие науки, довольно часто рассматривать переменную, например у , возможные значения которой зависят от значения другой переменной, скажем Икс . С математической точки зрения зависимый Переменная у представляет собой значение функция из Икс . Для упрощения формул часто бывает полезно использовать один и тот же символ для зависимой переменной. у и отображение функций Икс на у . Например, состояние физической системы зависит от измеримых величин, таких как давление, то температура, пространственное положение, . и все эти величины изменяются по мере развития системы, то есть они являются функцией времени. В формулах, описывающих систему, эти величины представлены переменными, которые зависят от времени и, таким образом, рассматриваются неявно как функции времени.

Следовательно, в формуле a зависимая переменная — это переменная, которая неявно является функцией другой (или нескольких других) переменных. An независимая переменная переменная, которая не зависит. [7]

Свойство переменной быть зависимой или независимой часто зависит от точки зрения и не является внутренним. Например, в обозначениях ж(Икс, у, z) , все три переменные могут быть независимыми, а запись представляет собой функцию трех переменных. С другой стороны, если у и z зависит от Икс (находятся зависимые переменные), то обозначение представляет функцию единственного независимая переменная Икс . [8]

Примеры

Если определить функцию ж от действительные числа к действительным числам

тогда Икс переменная, обозначающая аргумент определяемой функции, которое может быть любым действительным числом. В личности

переменная я является суммирующей переменной, которая по очереди обозначает каждое из целых чисел 1, 2, . п (его еще называют индекс потому что его изменение распространяется на дискретный набор значений), а п является параметром (в формуле не изменяется).

В теории многочлены, полином степени 2 обычно обозначается как топор 2 + bx + c, куда а, б и c называются коэффициенты (они считаются фиксированными, т. е. параметры рассматриваемой задачи), а Икс называется переменной. При изучении этого полинома на предмет его полиномиальная функция это Икс обозначает аргумент функции. При изучении полинома как объекта в себе Икс считается неопределенным и часто пишется с заглавной буквы, чтобы указать этот статус.

Обозначение

В математике переменные обычно обозначаются одной буквой. Однако за этой буквой часто следует нижний индекс, как в Икс₂ , и этот индекс может быть числом, другой переменной ( Икс_я ), слово или сокращение слова ( Икс_в и Икс_из ), и даже математическое выражение. Под влиянием Информатика, в чистой математике можно встретить имена переменных, состоящие из нескольких букв и цифр.

Вслед за французским философом и математиком 17 века, Рене Декарт, буквы в начале алфавита, например а, б, c обычно используются для известных значений и параметров, а буквы в конце алфавита, например Икс, у, z, и т обычно используются для неизвестных и переменных функций. [9] В печатном виде математика, нормой является установка переменных и констант в курсив. [10]

Например, общая квадратичная функция условно записывается как:

куда а, б и c являются параметрами (также называемыми константами, потому что они постоянные функции ), пока Икс — переменная функции. Более явный способ обозначить эту функцию —

что делает статус функции-аргумента Икс ясный, и тем самым неявно постоянный статус а, б и c. С c встречается в члене, который является постоянной функцией Икс, это называется постоянный срок. [11] : 18

Конкретные области и приложения математики обычно имеют определенные соглашения об именах для переменных. Переменным с похожими ролями или значениями часто присваиваются последовательные буквы. Например, три оси в 3D координатное пространство условно называются Икс, у, и z. В физике названия переменных во многом определяются физическое количество они описывают, но существуют различные соглашения об именах. вероятность и статистика использовать Икс, Y, Z для имен случайные переменные, сохраняя Икс, у, z для переменных, представляющих соответствующие фактические значения.

Есть много других способов обозначения. Обычно переменные, играющие схожую роль, представлены последовательными буквами или одной и той же буквой с разными нижний индекс. Ниже приведены некоторые из наиболее распространенных вариантов использования.

1. Какую переменную называют независимой? Какую переменную называют зависимой? 2. Какую зависимость называют функциональной?
3. Как иначе называется независимая переменная? Как иначе
зависимая переменная?
4. Что называют значениями функции? Что называют областью определения
функции?
5. Какими способами может быть задана функция?
6. Что называют графиком функции?
7. Как построить график любой функции? Что для этого необходимо сделать?
8. Что показывает график функции? Что можно найти с его помощью?
9. Какую функцию называют прямой пропорциональностью,
10. Что такое коэффициент прямой пропорциональности?
11. Что представляет собой график прямой пропорциональности?
12. Что необходимо знать и сделать, чтобы построить график функции у = kx ?
13. В каких четвертях будет расположен график прямой пропорциональности, если k > 0 ?
14. В каких четвертях будет расположен график прямой пропорциональности,
если к < 0 ?
15. Какую функцию называют линейной?
16. Что является графиком линейной функции?
17. Какой вид принимает линейная функция, если b = 0 ? Что будет являться графиком?
18. Какой вид принимает линейная функция, если к = 0 ? Что будет являться
графиком?
19. Какой вид принимает линейная функция, если b = 0 и k = 0 2 Что будет являться графиком?
20. Что такое угловой коэффициент прямой?
21. Каким будет угол наклона прямой, если k > 0
21. Каким будет угол наклона прямой, если k > 0?
22. Каким будет угол наклона прямой, если zeta < 0 ?
23. В каком случае графики двух линейных функций пересекаются?
24. В каком случае графики двух линейных функций будут параллельны?
25. В какой точке график линейной функции пересекает ось у?
26. Как изменится график линейной функции, если в области определения будут не все числа?

1. Какую переменную называют независимой? Какую переменную называют зависимой?

х — независимая переменная

у — зависимая переменная

2. Какую зависимость называют функциональной?

Функцией или функциональной зависимостью переменной у от переменной х называется такая зависимость, при которой каждому значению х ставится в соответствие единственное значение у

3. Как иначе называется независимая переменная? Как иначе

4. Что называют значениями функции? Что называют областью определения

Область определения функции — это множество всех значений аргумента

Значение y, соответствующее заданному значению x, называют значением функции.

5. Какими способами может быть задана функция?

1) аналитический; 2) графический; 3) табличный; 4) словесным описанием.

6. Что называют графиком функции?

Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

7. Как построить график любой функции? Что для этого необходимо сделать?

График любой функции можно построить прямыми вычислениями значения функции y=f(x) и методом дифференциального исчисления.

• При прямом вычислении значений функции y=f(x) необходимо задать интервал [a;b] вычислений и шаг h. Получается таблица, по которой можно построить график.

• Построение графика функции методом дифференциального исчисления предполагает схематичное построение, используя свойства функции.

8. Что показывает график функции? Что можно найти с его помощью?

График функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо х.

9. Какую функцию называют прямой пропорциональностью?

Прямой пропорциональностью называется функция, которую можно задать формулой у=кх, где х – независимая переменная, а к – некоторое число, неравное нулю

10. Что такое коэффициент прямой пропорциональности?

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

11. Что представляет собой график прямой пропорциональности?

График функции прямой пропорциональности – это прямая, которая пересекает точку начала координат.

12. Что необходимо знать и сделать, чтобы построить график функции у = kx ?

Зная, что график функции y = kx – прямая, можно его построить, не составляя подробной таблицы. Достаточно знать две точки прямой. Одна из них начало координат, а вторая выбирается произвольно, например, точка B (2; 4). Через эти две точки проводится прямая.

13. В каких четвертях будет расположен график прямой пропорциональности, если k > 0 ?

14. В каких четвертях будет расположен график прямой пропорциональности,

15. Какую функцию называют линейной?

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

16. Что является графиком линейной функции?

17,18,19. Какой вид принимает линейная функция, если b = 0 ? Что будет являться графиком?

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

20. Угловой коэффициент отвечает за угол наклона прямой.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k < 0.

При k > 0: функция принимает отрицательные значения на промежутке (-∞, -b/k) и положительные значения на промежутке (-b/k, +∞)

Зависимые и независимые переменные — Dependent and independent variables

Зависимые и независимые переменные — это переменные в математическом моделировании , статистическом моделировании и экспериментальных науках . Зависимые переменные получили это название, потому что в эксперименте их значения изучаются в предположении или требовании, чтобы они зависели в соответствии с каким-либо законом или правилом (например, математической функцией ) от значений других переменных. Независимые переменные, в свою очередь, не рассматриваются как зависящие от какой-либо другой переменной в рамках рассматриваемого эксперимента. В этом смысле некоторые общие независимые переменные — это время , пространство , плотность , масса , скорость потока жидкости и предыдущие значения некоторого наблюдаемого значения, представляющего интерес (например, численность населения) для прогнозирования будущих значений (зависимая переменная).

Из двух всегда зависимая переменная, вариация которой изучается путем изменения входных данных, также известных как регрессоры в статистическом контексте. В эксперименте любую переменную, которой манипулирует экспериментатор, можно назвать независимой переменной. Модели и эксперименты проверяют влияние независимых переменных на зависимые. Иногда, даже если их влияние не представляет прямого интереса, независимые переменные могут быть включены по другим причинам, например, чтобы учесть их потенциальный смешивающий эффект.

В одной переменной исчислении , А функции , как правило , в виде графика с горизонтальной осью , представляющей независимую переменную и вертикальную ось , представляющую зависимую переменную. В этой функции y — зависимая переменная, а x — независимая переменная.

СОДЕРЖАНИЕ

Математика

В математике функция — это правило для получения входных данных (в простейшем случае числа или набора чисел) и предоставления выходных данных (которые также могут быть числами). Символ, обозначающий произвольный ввод, называется независимой переменной , а символ, обозначающий произвольный вывод, называется зависимой переменной . Самый распространенный символ для ввода — x , а наиболее распространенный символ для вывода — y ; сама функция обычно записывается y = f ( x ) .

Возможно иметь несколько независимых переменных или несколько зависимых переменных. Например, в исчислении с несколькими переменными часто встречаются функции вида z = f ( x , y ) , где z — зависимая переменная, а x и y — независимые переменные. Функции с несколькими выходами часто называют векторными функциями .

Моделирование

При математическом моделировании зависимая переменная изучается, чтобы увидеть, изменяется ли она при изменении независимых переменных и насколько сильно. В простой стохастической линейной модели y _i = a + b x _i + e _i член y _i — это i- е значение зависимой переменной, а x _i — i- е значение независимой переменной. Термин e _i известен как «ошибка» и содержит изменчивость зависимой переменной, не объясняемую независимой переменной.

С несколькими независимыми переменными модель имеет вид y _i = a + b x _{i , 1} + b x _{i , 2} + . + b x _{i, n} + e _i , где n — количество независимых переменных.

Линейная регрессия модель сейчас обсуждается. Чтобы использовать линейную регрессию, создается диаграмма рассеяния данных с X в качестве независимой переменной и Y в качестве зависимой переменной. Это также называется двумерным набором данных, ( x ₁ , y ₁ ) ( x ₂ , y ₂ ) . ( x _i , y _i ) . Модель простой линейной регрессии принимает вид Y _i = a + B x _i + U _i , для i = 1, 2, . n . В этом случае U _i , . U _n — независимые случайные величины. Это происходит, когда измерения не влияют друг на друга. Посредством распространения независимости независимость U _i подразумевает независимость от Y _i , даже если каждый Y _i имеет различное математическое ожидание. Каждый U _i имеет математическое ожидание 0 и дисперсию σ 2 .

Ожидание Y _i Доказательства:

E [ Y я ] знак равно E [ α + β Икс я + U я ] знак равно α + β Икс я + E [ U я ] знак равно α + β Икс я . ] = E [ alpha + beta x_ + U_ ] = alpha + beta x_ + E [U_ ] = alpha + beta x_ .>

Линия наилучшего соответствия для двумерного набора данных принимает форму y = α + βx и называется линией регрессии. α и β соответствуют точке пересечения и наклону соответственно.

Моделирование

При моделировании зависимая переменная изменяется в ответ на изменения независимых переменных.

Статистика

В эксперименте переменная, которой манипулирует экспериментатор, — это то, что, как было доказано, работает, и называется независимой переменной. Зависимая переменная — это событие, которое, как ожидается, изменится при манипулировании независимой переменной.

В инструментах интеллектуального анализа данных (для многомерной статистики и машинного обучения ) зависимой переменной назначается роль как целевая переменная (или в некоторых инструментах какатрибут метки), в то время как независимой переменной может быть назначена рольобычной переменной. Известные значения целевой переменной предоставляются для набора обучающих данных и наборатестовых данных, но должны быть спрогнозированы для других данных. Целевая переменная используется валгоритмахконтролируемого обучения, но не в неконтролируемом обучении.

Синонимы статистики

В зависимости от контекста, независимая переменная иногда называется «предикторная переменная», регрессор , ковариата , «управляемая переменная», «объясняющая переменная», переменная воздействия (см. Теорию надежности ), « фактор риска » (см. Медицинскую статистику ) ». особенность »(в машинном обучении и распознавании образов ) или« входная переменная ». В эконометрике термин «управляющая переменная» обычно используется вместо «ковариата».

«Объясняющая переменная» Некоторые авторы предпочитают «независимую переменную», когда величины, рассматриваемые как независимые переменные, не могут быть статистически независимыми или не поддающимися независимому манипулированию исследователем. Если независимая переменная упоминается как «объясняющая переменная», тогда термин «ответная переменная» некоторые авторы отдают предпочтение зависимой переменной.

В сообществе экономистов независимые переменные также называют экзогенными .

В зависимости от контекста, зависимая переменная иногда называется «ответная переменная», «регрессионная переменная», «критерий», «прогнозируемая переменная», «измеряемая переменная», «объясненная переменная», «экспериментальная переменная», «отвечающая переменная», «конечная переменная», «выходная переменная», «цель» или «метка». В экономике эндогенные переменные обычно ссылаются на цель.

«Объясненная переменная» Некоторые авторы предпочитают «зависимую переменную», когда величины, рассматриваемые как «зависимые переменные», могут не быть статистически зависимыми. Если зависимая переменная упоминается как «объясненная переменная», тогда термин «прогнозирующая переменная» некоторые авторы предпочитают использовать независимую переменную.

Переменные также могут упоминаться по их форме: непрерывная или категориальная , которая, в свою очередь, может быть, среди прочего, бинарной / дихотомической, номинально категориальной и порядковой категорией.

Примером может служить анализ тенденций изменения уровня моря, проведенный Вудвортом (1987) . Здесь зависимой переменной (и переменной, представляющей наибольший интерес) был годовой средний уровень моря в данном месте, для которого был доступен ряд годовых значений. Первичной независимой переменной было время. Использовалась ковариата, состоящая из годовых значений среднегодового атмосферного давления на уровне моря. Результаты показали, что включение ковариаты позволило получить более точные оценки тенденции в зависимости от времени по сравнению с анализами, в которых ковариата не использовалась.

Прочие переменные

Можно подумать, что переменная изменяет зависимые или независимые переменные, но на самом деле она не может быть в центре внимания эксперимента. Так что переменная будет оставаться постоянной или отслеживаться, чтобы попытаться минимизировать ее влияние на эксперимент. Такие переменные могут быть обозначены как «управляемая переменная», « управляющая переменная » или «фиксированная переменная».

Посторонние переменные, если они включены в регрессионный анализ в качестве независимых переменных, могут помочь исследователю с точной оценкой параметров ответа, прогнозом и степенью соответствия , но не представляют существенного интереса для исследуемой гипотезы . Например, в исследовании, посвященном изучению влияния послесреднего образования на заработок в течение всей жизни, некоторыми посторонними переменными могут быть пол, этническая принадлежность, социальный класс, генетика, интеллект, возраст и т. Д. Переменная является посторонней только тогда, когда можно предположить (или показать), что она влияет на зависимую переменную . Если он включен в регрессию, он может улучшить соответствие модели . Если он исключен из регрессии и если он имеет ненулевую ковариацию с одной или несколькими интересующими независимыми переменными, его исключение приведет к смещению результата регрессии из-за влияния этой независимой переменной, представляющей интерес. Этот эффект называется искажением или смещением пропущенной переменной ; в этих ситуациях необходимы изменения конструкции и / или контроль переменных статистических данных.

Посторонние переменные часто делятся на три типа:

1. Субъектные переменные, представляющие собой характеристики изучаемых людей, которые могут повлиять на их действия. Эти переменные включают возраст, пол, состояние здоровья, настроение, происхождение и т. Д.
2. Блокирующие переменные или экспериментальные переменные — это характеристики людей, проводящих эксперимент, которые могут влиять на поведение человека. Пол, наличие расовой дискриминации, язык или другие факторы могут считаться такими переменными.
3. Ситуационные переменные — это характеристики среды, в которой проводилось исследование или исследование, которые отрицательно влияют на результат эксперимента. Включены температура воздуха, уровень активности, освещение и время суток.

При моделировании изменчивость, не охватываемая независимой переменной, обозначается и известна как « остаточный », «побочный эффект», « ошибка », «необъяснимая доля», «остаточная переменная», «нарушение» или «допуск». «. е я >

Зависимые и независимые переменные

Основой анализа связи между двумя переменными является подготовка двумерных таблиц (cross-tabulation), представляющая собой взаимное пересечение двух рядов распределений.

Переменные для рядов распределения определяются гипотезами исследователя. Одна переменная рассматривается как фактор (причина), влияющая на исследуемое явление другая — как показатель этого явления.

Один и тот же признак (представленный в инструментарии вопросом анкеты) в процессе анализа может выступать и в качестве показателя и в качестве фактора.

Например, одна гипотеза может быть сформулирована так: «Уровень образования влияет на удовлетворенность работой: чем выше уровень образования, тем выше уровень удовлетворенности работой». Другая гипотеза, требующая проверки, может быть следующей: «Удовлетворенность работой влияет на общую удовлетворенность человека жизнью: чем выше удовлетворенность работой, тем выше удовлетворенность жизнью».

В первом случае удовлетворенность работой выступает в качестве показателя, а во втором — в качестве фактора. Когда признак в процессе статистической проверки гипотезы рассматривается в качестве фактора, он называется независимой переменной (подлежащим); когда признак рассматривается в качестве показателя, в статистическом анализе он называется зависимой неременной (сказуемым).

Содержательный смысл таблицы, построенной на основе результатов кросс-табуляции, заключается в следующем. По признаку, рассматриваемому в качестве независимой переменной, исследователь разбивает всю совокупность опрошенных на отдельные группы (подгруппы).

Наряду с общим результатом одномерного распределения по изучаемому показателю, исследователь параллельно получает результаты распределения мнений отдельных подгрупп населения, и эти результаты сравнивает между собой. Чем больше различие в характере ответов у этих групп, тем о большей связи между двумя переменными можно говорить.

Обращаясь к приведенному выше примеру, можно сказать, что, проверяя первую гипотезу, исследователь всю совокупность разбивает на группы с различным уровнем образования (здесь, напомним, проверять гипотезу будет тем легче, чем более произведенная группировка соответствует выдвинутой гипотезе: если речь идет об уровне образования, то полученные группы должны различаться между собой именно по уровню образования); проверяя же вторую гипотезу, исследователь разбивает всю совокупность на группы людей, различающихся между собой по уровню удовлетворенности работой.

Построенная двумерная таблица позволяет «на глаз» увидеть, различаются ли ответы у разных групп населения. В таком виде обычно и рассматривает результаты исследования заинтересованный потребитель информации. Но результаты, оцениваемые «на глаз», часто, могут вводить в заблуждение.

Поэтому основной задачей исследователя-аналитика, представляющего результаты опроса в виде двумерных распределений является статистическая экспертиза — оценка и отбор качественной информации. Просмотрев и статистически оценив сотни (а то и тысячи) двумерных таблиц, он должен для широкой аудитории (и для своего дальнейшего анализа) отобрать только те, которые соответствуют статистическим критериям качества информации.

Другими словами, исследователь, прежде чем публиковать результаты двумерного анализа, должен осуществить статистическую экспертизу, позволяющую либо «пропустить» результаты исследования для широкого обнародования (в том случае, если полученные данные статистически обоснованы), либо «отбраковать» таблицы (в тех случаях, когда видимые «на глаз» различия статистически недостоверны в силу тех или иных причин, и могут привести к неверным выводам).

Если исследователь не удовлетворен результатами статистической про-верки (другими словами, интуиция подсказывает ему, что гипотеза была верной), он может в дальнейших исследованиях проверять ее, совершенствуя инструментарий и организацию сбора информации. Но он не должен представлять для широкой аудитории данные, не соответствующие статистическим критериям.

Прежде чем рассмотреть особенности использования статистических показателей для последовательного осуществления шагов объяснительного анализа, рассмотрим двумерную таблицу, с точки зрения описания и интерпретации кросс-табуляции полученных данных.

ЗАВИСИМАЯ ПЕРЕМЕННАЯ И НЕЗАВИСИМАЯ ПЕРЕМЕННАЯ, ОТНОШЕНИЯ МЕЖДУ НИМИ

Независимая переменная. Исследователь должен стремиться оперировать в эксперименте только независимой переменной. Эксперимент, где это условие соблюдается, называют чистым экспериментом. Но чаще всего в ходе эксперимента, варьируя одну переменную, экспериментатор изменяет вместе с тем ряд других. Это изменение может быть вызвано действием экспериментатора и обусловлено связью двух переменных. Например, в эксперименте по выработке простого двигательного навыка он наказывает испытуемого за неудачи электрическим током. Размер наказания может выступать в качестве независимой переменной, а скорость выработки навыка — зависимой переменной. Наказание не только закрепляет у испытуемого соответствующие реакции, но и порождает у него ситуативную тревогу, которая влияет на результаты — увеличивает число ошибок и уменьшает скорость выработки навыка.

Центральная проблема при проведении экспериментального исследования — выделение независимой переменной и ее изоляция от других переменных. В качестве независимых переменных в психологическом эксперименте могут выступать:

·особенности ситуации (внешние условия);

·управляемые особенности (состояния) испытуемого.

Последние часто называют «переменными организма». Иногда выделяют четвертый вид переменных — константные характеристики испытуемого (интеллект, пол, возраст и т. д.), но, на мой взгляд, они относятся к дополнительным переменным, поскольку на них нельзя воздействовать, а можно лишь учесть их уровень при формировании экспериментальных и контрольных групп.

Характеристика задания — то, чем может манипулировать экспериментатор более или менее свободно. По традиции, идущей от бихевиоризма, считается, что экспериментатор варьирует только характеристики стимулов (stimulus variables), но в его распоряжении гораздо больше возможностей. Экспериментатор может варьировать стимулы или материал задания, изменять тип ответа испытуемого (вербальный или невербальный ответ), менять шкалу оценивания и т.д. Он может варьировать инструкцию, меняя цели, которых должен достичь испытуемый в ходе выполнения задания. Экспериментатор может варьировать средства, которые имеет испытуемый для решения задачи, и ставить перед ним препятствия. Он может изменять систему поощрений и наказаний в ходе выполнения задания и т.д.

К особенностям ситуации следует отнести те переменные, которые непосредственно не входят в структуру экспериментального задания, выполняемого испытуемым. Это может быть температура в помещении, обстановка, наличие внешнего наблюдателя и т.д.

Эксперименты по выявлению эффекта социальной фасилитации (усиления) проводились по следующей схеме: испытуемому давалась какая-либо сенсомоторная или интеллектуальная задача. Он сначала выполнял ее в одиночку, а затем в присутствии другого человека или нескольких людей (последовательность, разумеется, менялась в разных группах). Оценивалось изменение продуктивности испытуемых. В этом случае задача испытуемого оставалась неизменной, изменялись лишь внешние условия эксперимента.

Что может варьировать экспериментатор?

Во-первых, это физические параметры ситуации: расположение аппаратуры, внешний вид помещения, освещенность, звуки и шумы, температура, размещение мебели, окраска стен, время проведения эксперимента (время суток, длительность и т.д.). То есть все физические параметры ситуации, не являющиеся стимулами.

Во-вторых, это социально психологические параметры: изоляция — работа в присутствии экспериментатора, работа в одиночку — работа с группой и т.д.

В-третьих, это особенности общения и взаимодействия испытуемого (испытуемых) и экспериментатора.

Судя по публикациям в научных журналах, за последние годы резко возросло количество экспериментальных исследований, в которых применяется варьирование внешних условий.

К «организменным переменным», или неуправляемым характеристикам испытуемых, относятся физические, биологические, психологические, социально-психологические и социальные признаки. Традиционно их относят к «переменным», хотя большинство из них является неизменным или относительно неизменным на протяжении жизни. Влияние дифференциально-психологических, демографических и прочих константных параметров на поведение индивида изучают в корреляционных исследованиях. Однако авторы большинства учебников по теории психологического метода, например М. Мэтлин, относят эти параметры к числу независимых переменных эксперимента.

Как правило, в современном экспериментальном исследовании дифференциально-психологические особенности индивидов, такие как интеллект, пол, возраст, социальное положение (статус) и т.д., учитываются в качестве дополнительных переменных, которые контролируются экспериментатором в общепсихологическом эксперименте. Но эти переменные могут превращаться во «вторую основную переменную» в дифференциально-психологическом исследовании, и тогда используется факторный план.

Зависимая переменная. Психологи имеют дело с поведением испытуемого, поэтому в качестве зависимой переменной выбираются параметры вербального и невербального поведения. К ним относятся: число ошибок, которое совершила крыса, пробегая лабиринт; время, которое затратил испытуемый при решении задачи, изменения мимики его лица при просмотре эротического фильма; время двигательной реакции на звуковой сигнал и т.д.

Выбор поведенческого параметра определяется исходной экспериментальной гипотезой. Исследователь должен ее максимально конкретизировать, т.е. добиться того, чтобы зависимая переменная была операционализирована — поддавалась регистрации в ходе эксперимента.

Параметры поведения условно можно разделить на формально-динамические и содержательные. Формально-динамические (или пространственно-временные) параметры достаточно легко поддаются аппаратурной регистрации. Приведем примеры этих параметров.

1. Точность. Наиболее часто регистрируемый параметр. Поскольку большинство заданий, предъявляемых испытуемому в психологических экспериментах, являются задачами на достижения, то точность или противоположный параметр — ошибочность действий — будет главным регистрируемым параметром поведения.

2. Латентность. Психические процессы протекают скрытно от внешнего наблюдателя. Время от момента предъявления сигнала до выбора ответа называется латентным временем. В некоторых случаях латентное время является важнейшей характеристикой процесса, например при решении мыслительных задач.

3. Длительность, или скорость, исполнения. Является характеристикой исполнительного действия. Время между выбором действия и окончанием его выполнения называют скоростью действия (в отличие от латентного времени).

4. Темп, или частота действий. Важнейшая характеристика, особенно при исследовании простейших форм поведения.

5. Продуктивность. Отношение числа ошибок или качества выполнения действий ко времени выполнения. Служит важнейшей характеристикой при исследовании научения, познавательных процессов, процессов принятия решения и т. д. Содержательные параметры поведения предполагают категоризацию формы поведения либо в терминах обыденного языка, либо в терминах той теории, предположения которой проверяются в данном эксперименте.

Распознавание различных форм поведения — дело специально обученных экспертов или наблюдателей. Требуется немалый опыт, чтобы характеризовать один поступок как проявление покорности, а другой — как проявление подобострастия.

Проблема фиксации качественных особенностей поведения решается посредством: а) обучения наблюдателей и разработки карт наблюдения; б) измерения формально-динамических характеристик поведения с помощью тестов.

Зависимая переменная должна быть валидной и надежной. Надежность переменной проявляется в устойчивости ее регистрируемости при изменении условий эксперимента в течение времени. Валидность зависимой переменной определена только в конкретных условиях эксперимента и применительно к определенной гипотезе.

Можно выделить три типа зависимых переменных: 1) одновременную; 2) многомерную; 3) фундаментальную. В первом случае регистрируется лишь один параметр, и именно он считается проявлением зависимой переменной (между ними существует функциональная линейная связь), как, например, при изучении времени простой сенсомоторной реакции. Во втором случае зависимая переменная многомерна. Например, уровень интеллектуальной продуктивности проявляется во времени решения задачи, его качестве, трудности решенной задачи. Эти параметры могут фиксироваться независимо. В третьем случае, когда известно отношение между отдельными параметрами многомерной зависимой переменной, параметры рассматриваются в качестве аргументов, а сама зависимая переменная — в качестве функции. Например, фундаментальное измерение уровня агрессии F(a) рассматривается как функция отдельных ее проявлений (а) мимики, пантомимики, брани, рукоприкладства и др.

Существует еще одно важное свойство зависимой переменной, а именно — сензитивность (чувствительность) зависимой переменной к изменениям независимой. Суть в том, что манипуляция независимой переменной влияет на изменение зависимой. Если же мы манипулируем независимой переменной, а зависимая не изменяется, то зависимая переменная несензитивна по отношению к независимой. Два варианта проявления несензитивности зависимой переменной получили названия «эффект потолка» и «эффект пола». Первый случай встречается тогда, когда предъявляемая задача так проста, что уровень ее выполнения много выше всех уровней независимой переменной. Второй эффект, напротив, возникает тогда, когда задание настолько сложно, что уровень его выполнения оказывается ниже всех уровней независимой переменной.

Итак, как и прочие компоненты психологического исследования, зависимая переменная должна быть валидна, надежна, обладать чувствительностью к изменению уровня независимой переменной.

Существуют два основных приема фиксации изменений зависимой переменной. Первый применяется наиболее часто в экспериментах с участием одного испытуемого. Изменение зависимой переменной регистрируется во время эксперимента вслед за изменением уровня независимой переменной. Примером является фиксация результатов в экспериментах по научению. Кривая научения представляет собой классический вариант тренда — изменения успешности выполнения заданий в зависимости от числа проб (времени проведения эксперимента). Для обработки таких данных применяется статистический аппарат анализа трендов. Второй прием фиксации изменения уровня независимой переменной называются отсроченным измерением. Между воздействием и эффектом проходит определенный промежуток времени, его длительность устанавливается по времени отдаленности следствия от причины. Например, прием дозы алкоголя увеличивает время сенсомоторной реакции не сразу, а по прошествии определенного времени. То же самое можно сказать о влиянии заучивания конкретного количества иностранных слов на успешность перевода текста на редкий язык: эффект проявляется не сразу (если проявляется).

Отношения между переменными. В основе построения современной экспериментальной психологии лежит формула К. Левина — поведение есть функция личности и ситуации:

Необихевиористы ставят в формулу вместо Р (личность) О (организм), что более точно, если считать испытуемыми не только людей, но и животных, а личность редуцировать к организму.

Как бы то ни было, большинство специалистов по теории психологического эксперимента, в частности МакГиган, считают, что в психологии существуют два типа законов: 1) «стимул—ответ»; 2) «организм—поведение».

Первый тип законов обнаруживается в ходе экспериментального исследования, когда стимул (задача, ситуация) — это независимая переменная, а зависимая переменная — ответ испытуемого.

Второй тип законов является продуктом метода систематического наблюдения и измерения, поскольку свойствами организма управлять с помощью психологических средств нельзя.

Существуют ли «пересечения»? Разумеется. Ведь в психологическом эксперименте зачастую учитывается влияние так называемых дополнительных переменных, большинство из которых является дифференциально-психологическими характеристиками. Следовательно, есть смысл добавить в список и «системные» законы, описывающие влияние ситуации на поведение личности, обладающей определенными свойствами. Но в психофизиологических и психофармакологических экспериментах можно воздействовать на состояние организма, а в ходе формирующего эксперимента — целенаправленно и необратимо изменять те или иные свойства личности.

В классическом психологическом поведенческом эксперименте устанавливается функциональная зависимость вида

где R — ответ, a S — ситуация (стимул, задача). Переменная S систематически варьируется, а детерминируемые ею изменения ответа испытуемого фиксируются. В ходе изучения проявляются условия, при которых испытуемый ведет себя тем или иным образом. Результат фиксируется в форме линейной или нелинейной зависимости.

Другой тип зависимостей символизируется как зависимость поведения от личностных свойств или состояний организма испытуемого:

R = f (О) или R = f(P).

Исследуется зависимость поведения испытуемого от того или иного состояния организма (болезни, усталости, уровня активации, фрустрации потребностей и т.д.) или от личностных свойств (тревожности, мотивации и т.д.). Исследования проводятся с участием групп людей, различающихся по данному признаку: свойству или актуальному состоянию.

Естественно, эти две строгие зависимости являются простейшими формами отношений между переменными. Возможны более сложные зависимости, устанавливаемые в конкретном эксперименте, в частности, факторные планы позволяют выявить зависимости вида R = f (S₁, S₂), когда ответ испытуемого зависит от двух варьируемых параметров ситуации, а поведение является функцией состояния организма и среды.

Остановимся на формуле Левина. В общей форме она выражает идеал экспериментальной психологии возможность предсказать поведение конкретной личности в определенной ситуации. Переменная «личность», которая входит в состав этой формулы, вряд ли может рассматриваться лишь как «дополнительная». Традиция необихевиоризма предлагает использовать термин «промежуточная» переменная. В последнее время за такими «переменными» — свойствами и состояниями личности — закрепился термин «переменная-модератор», т.е. посредник.

Рассмотрим основные возможные варианты отношений между зависимыми переменными. Существует, как минимум, шесть видов связи переменных. Первый, он же простейший, — отсутствие зависимости. Графически он выражается в форме прямой, параллельной оси абсцисс на графике, где по оси абсцисс (X) отложены уровни независимой переменной. Зависимая переменная не чувствительна к изменению независимой (см. рис. 4.8).

Монотонно возрастающая зависимость наблюдается тогда, когда увеличению значений независимой переменной соответствует изменение зависимой переменной (см. рис. 4.9).

Монотонно убывающая зависимость наблюдается, если увеличению значений независимой переменной соответствует уменьшение уровня независимой переменной (см. рис. 4.10).

Нелинейная зависимость U-образного типа обнаруживается в большинстве экспериментов, в которых выявляются особенности психической регуляции поведения: (см. рис. 4.11).

Инвертированная U-образная зависимость получается в многочисленных экспериментальных и корреляционных исследованиях как в психологии личности, мотивации, так и в социальной психологии (см. рис. 4.12).

Последний вариант зависимости обнаруживается не так часто, как предыдущие, — сложная квазипериодическая зависимость уровня зависимой переменной от уровня независимой (см. рис. 4.13).

При выборе способа описания работает «принцип экономии». Любое простое описание лучше, чем комплексное, даже если они одинаково успешны. Поэтому аргументы, распространенные в отечественных научных дискуссиях типа «Все гораздо сложнее на самом деле, чем представляет автор» по меньшей мере бессмысленны. Тем более что никто не знает, как «на самом деле».

Так называемое «комплексное описание», «многомерное описание» есть зачастую просто попытка уйти от решения научной проблемы, способ маскировки личной некомпетентности, которую хотят скрыть за путаницей корреляционных связей и сложносоставными формулами, где все всему равняется.