Вопрос 1-1. Понятие «задача» в начальном курсе математики. Функции задач. Классификация задач.
Любое математическое задание можно рассмотреть как задачу, выделив в нем условие, т.е. ту часть, где содержатся сведения об известных и неизвестных значениях величин, об отношениях между ними, и требование, т.е. указание на то, что нужно найти.
Для выполнения каждого требования применяется определенный метод или способ действия, в зависимости от которого выделяют различные виды математических задач: на построение, доказательство, преобразование, комбинаторные задачи, арифметические и т.д.
В начальном курсе математики понятие «задача» используется тогда, когда речь идет об арифметических задачах. Они формулируются в виде текста, в котором находят отражение количественные отношения между реальными объектами. Поэтому их называют «текстовыми», «сюжетными», «вычислительными».
Под задачей будем понимать сформулированный словами вопрос, ответ на который может быть получен только с помощью выбора арифметического действия.
Функции задач.Активизация познавательной деятельности учащихся привела к необходимости решения проблемы по определению функций задач в обучении, их роли и места в этом процессе.
Под функцией решения задачи мы понимаем проектируемые учителем изменения в деятельности и психике учащихся, которые должны произойти в результате решения задач. Конечно, в результате решения каждой задачи происходит не одно какое-либо определенное изменение (например, приобретение умение решать задачи данного вида, развитие мышления, воображения и т.п.), а разные изменения в знаниях, умениях, способностях.
В методике обучения решению задач выделяют четыре основных функции: обучающая, воспитывающая, развивающая и контролирующая.
Обучающая функция задач направлена на формирование у учащихся системы математических знаний, умений и навыков в процессе их усвоения, среди которых можно выделить следующие:
а) задачи вводятся для подготовки к введению новых понятий; для ознакомления с новыми понятиями, свойствами, связями, для показа области применения и расширения формируемых математических знаний и умений;
б) для формирования вычислительных навыков;
в) для обучения общим методам и приемам решения задач на разных этапах обучения, развития у учащихся общих умений решения любых математических задач;
г) для контроля и оценки знаний, умений, навыков учащихся.
Развивающая функция задач направлена на формирование таких приемов мышления, как анализ, синтез, обобщение, абстрагирование и др.; на развитие познавательных способностей.
Воспитывающая функция задач направлена на воспитание у учащихся интереса к предмету, воли, приучает систематическому умственному труду, самоконтролю, формирует моральные качества личности.
Решение задач формирует у учащихся такие общеучебные умения, как умение планировать свою деятельность, внимательно воспринимать учебную информацию, мотивировать каждый шаг деятельности, рационально оформлять результаты своих действий и пр.
Контролирующая функция задач направлена на определение уровня усвоения учащимися учебного материала, способности их к самостоятельному изучению материала, уровня развития и сформированности познавательных интересов школьников.
Функции задач в обучении взаимосвязаны, но в каждом конкретном случае выделяется и реализуется ведущая функция задачи.
Классификация задач. Центральным звеном в умении решать задачи является усвоение связей между данными и искомыми. От того, как хорошо усвоены эти связи, зависит умение решать задачи. Учитывая это, в начальных классах ведется работа под группами задач, решение которых основывается на одних и тех же связях между данными и искомыми, а отличаются они конкретным содержанием и числовыми данными. Группы таких задач называются группами одного вида.
Все задачи можно разделить на две группы: простые и составные.
Простой называется задача, для решения которой необходимо установить одну связь между числовыми данными и искомым.
Составной называется задача, для решения которой устанавливается две или более связей.
Составные задачи делятся на составные нетиповые задачи и составные типовые.
Процесс решения простых задач является одновременно процессом формирования математических понятий. В связи с этим, в зависимости от тех понятий, которые рассматриваются в курсе математики начальных классов, простые задачи делятся на три группы.
Первая группа включает простые задачи, раскрывающие конкретный смысл арифметических действий: конкретный смысл действия сложения, вычитания, умножения, деления (деление на равные части и деление по содержанию).
Вторая группа – простые задачи, при решении которых раскрывается взаимосвязь между результатами и компонентами арифметических действий. Это простые задачи на нахождение неизвестного компонента (нахождение неизвестного слагаемого, уменьшаемого, вычитаемого, множителя, делимого, делителя.)
Третья группа – простые задачи, раскрывающие новый смысл арифметических действий. Это задачи на увеличение и уменьшение числа на несколько единиц (прямая и косвенная форма); задачи на увеличение числа в несколько раз (прямая и косвенная форма); на уменьшение числа в несколько раз (прямая и косвенная форма); на разностное сравнение; на кратное сравнение.
Для составных нетиповых задач нет такого единого основания классификации, которое позволило бы разделить их на группы, т.к. составные задачи включают различные сочетания тех или иных видов простых задач (их более 100).
К составным типовым относятся задачи на пропорциональную зависимость величин. Выделяют 3 группы таких задач: задачи на нахождение четвертого пропорционального (6 видов); на пропорциональное деление (4 вида); на нахождение неизвестного по двум разностям (2 вида).
В задачах на нахождение 4-го пропорционального даны три величины, связанные прямо или обратно пропорциональной зависимостью, из них 2 переменные и одна постоянная; при этом даны 2 значения одной переменной величины и одно из соответствующих значений другой переменной, а второе значение этой величины является искомым.
Например, задача 1.
Из 2 м полотна получается 3 наволочки. Сколько таких наволочек получится из 42 м полотна?
Задачи на пропорциональное деление включают 3 величины, из них одна постоянная и 2 переменные, даны два или более значений одной переменной и сумма соответствующих значений другой переменной, слагаемые этой суммы являются искомыми.
Например, задача 2.
Для ремонта школы привезли 475 штук красных кирпичей и 425 штук белых кирпичей, одинаковых по массе. Масса всех кирпичей 3 600 кг. Найди массу красных и белых кирпичей в отдельности.
Задачи на нахождение неизвестных по двум разностям включают три величины: 2 переменные и 1 постоянную, причем даны два значения одной переменной и разность соответствующих значений другой переменной, а сами значения этой переменной являются искомыми.
Например, задача 3.
В одну столовую привезли 5 одинаковых ящиков фруктов, в другую – 2 таких же ящика. В первую столовую привезли на 24 кг больше, чем во вторую. Сколько килограммов фруктов привезли в каждую столовую?
Методико-математическая характеристика основных понятий исследования
С термином «задача» люди постоянно сталкиваются в повседневной жизни как на бытовом, так и на профессиональном уровне. Каждому из нас приходится решать те или иные проблемы, которые зачастую мы называем задачами. Проблема решения и чисто математических задач, и задач, возникающих перед человеком в процессе его производственной или бытовой деятельности, изучается издавна, однако до настоящего времени нет общепринятой трактовки самого понятия «задача». В широком смысле слова под задачей понимается некоторая ситуация, требующая исследования и разрешения человеком.
Отдельно стоят математические задачи, решение которых достигается специальными математическими средствами и методами. Среди них выделяют задачи научные, решение которых способствует развитию математики и ее приложений, и задачи учебные, которые служат для формирования необходимых математических знаний, умений и навыков.
Учебные математические задачи различаются по характеру их объектов. В одних задачах все объекты математические (числа, геометрические фигуры, функции и т.п.), в других объектами являются реальные предметы (люди, животные, автотранспортные и механические средства, сплавы, жидкости и т.д.) или их свойства и характеристики (количество, возраст, скорость, производительность, длина, масса и т.п.). Задачи, все объекты которых математические (доказательства теорем, вычислительные упражнения, установление признаков изучаемого математического понятия и т.д.), часто называют математическими заданиями.
Любое математическое задание можно рассматривать как задачу, выделив в нём условие, т.е. ту часть, где содержатся сведения об известных и неизвестных значениях величин, об отношениях между ними, и требование — все неизвестные величины или отношения между ними, которые надо найти.
Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми.
Текстовой задачей будем называть [6, 3] описание некоторой ситуации (явления, процесса) на естественном и (или) математическом языке с требованием либо дать количественную характеристику какого-то компонента этой ситуации (определить числовое значение некоторой величины по известным числовым значениям других величин и зависимостям между ними), либо установить наличие или отсутствие некоторого отношения между ее компонентами или определить вид этого отношения, либо найти последовательность требуемых действий.
Придерживаясь современной терминологии, можно сказать, что текстовая задача представляет собой словесную модель ситуации, явления, события, процесса и т.п. Как в любой модели, в текстовой задаче описывается не все событие или явление, а лишь его количественные и функциональные характеристики.
Основная особенность текстовых задач состоит в том, что в них не указывается прямо, какое именно действие (или действия) должно быть выполнено для получения ответа на требование задачи.
В каждой задаче можно выделить:
· числовые значения величин, которые называются данными, или известными (их должно быть не меньше двух);
· некоторую систему функциональных зависимостей в неявной форме, взаимно связывающих искомое с данными и данные между собой;
· требование, которое надо выполнить, или вопрос, на который надо найти ответ.
Числовые значения величин и существующие между ними закономерности, т.е. количественные и качественные характеристики объектов задачи и отношений между ними, называют условиями (или условием) задачи.
Требования могут быть сформулированы как в вопросительной, так и в повествовательной форме. Величину, значения которой требуется найти, называют искомой величиной, а числовые значения искомых величин — искомыми, или неизвестными.
Текстовые задачи имеют и другие названия: практические, аналитические, арифметические и др.
Л.М. Фридман называет такие задачи сюжетными. И понимает под этим словом задачи, в которых описан некоторый жизненный сюжет (явление, событие, процесс), с целью нахождения определённых колличественных характеристик или значений. Сюжетные задачи — это наиболее древний вид школьных задач. Они всегда широко использовались и будут использоваться в обучении математике. Ещё задолго до нашей эры в Древнем Египте, Вавилоне, Китае, Индии были известны и многие методы их решения. Однако со временем цели и функции решения сюжетных задач существенно изменялись и видоизменяются до сих пор.
Если примерно до XIX в. цели решения этих задач были чисто практические: научить решать задачи, которые часто встречаются в жизненной практике, то затем эти цели значительно расширились и, кроме практических целей, они начинают использоваться как важное общеобразовательное и методическое средство.

Л.М. Фридман так описывает происхождение понятия «задача» [16, 63]: проблемная ситуация образуется из следующих компонентов: действующего субъекта С, цели его деятельности — объекта О, на который направлена деятельность субъекта С, и преграды (затруднения) П.
Однако указанное условие возникновения проблемной ситуации (наличие преграды на пути осуществления цели деятельности) является лишь необходимым, но недостаточным для того, чтобы субъект действительно «вошел» в проблемную ситуацию. Надо чтобы он осознал, заметил эту преграду и чтобы захотел устранить (преодолеть) ее. Следовательно, проблемная ситуация — это не просто затруднение, преграда на пути деятельности субъекта, а осознанное им затруднение, способ устранения которого он желает найти. Только в этом случае у субъекта возникает активная мыслительная деятельность. Он пытается «децентрироваться» от ситуации: до сих пор субъект был центром этой ситуации, а теперь хочет выйти за ее пределы, чтобы взглянуть на нее со стороны. Для этого он как бы «раздваивается»: наряду с физическим субъектом, находящимся в проблемной ситуации, возникает «мыслящий» субъект М, который рассматривает и анализирует возникшую ситуацию как бы со стороны, выявляет все ее составные части, связи и отношения между ними, характер и особенности преграды. Результат этого анализа М выражает на каком-то языке (обычно на естественном).
Тем самым возникает описание проблемной ситуации, т.е. ее знаковая модель — это и есть задача. Итак, генезис задачи можно рассматривать как моделирование проблемной ситуации, в какую попадает субъект в процессе своей деятельности, а саму задачу — как знаковую модель проблемной ситуации.
Известный русский методист В.А. Евтушевский так охарактеризовал функции сюжетных задач в обучении начальной математике: «Задачи, предлагаемые в классе, заключают в себе живой материал для упражнения мышления ученика, для вывода математических правил и для упражнения в приложении этих правил в решении частных практических вопросов» .
Итак, понятие «задача» имеет несколько определений, которые представлены выше, а так же дана общая характеристика текстовой (сюжетной) задачи.
Текстовые задачи в школьном курсе математики
5. Арифметический способ решения задач, его роль в обучении, воспитании, развитии.
“Пока мы будем учить детей на русском языке — не только великом и могучем, но и достаточно трудном, пока мы хотим учить их сравнивать, выбирать наиболее простой путь достижения поставленной цели, пока мы не отказались от воспитания гибкости и критичности мышления, пока мы стараемся увязывать обучение математики с жизнью, нам будет трудно обойтись без текстовых задач — традиционного для отечественной методики средства обучения математике.” (Шевкин А.В.) [7]
В психологии, дидактике известны попытки дать определение задачи. Например, одно из них: “Задача – объект мыслительной деятельности, содержащий требование некоторого практического преобразования или ответа на теоретический вопрос посредством поиска условий, позволяющих раскрыть связи (отношения) между известными и неизвестными элементами” (Л.Л.Гурова.) [2]
В традиционном российском школьном обучении математике текстовые задачи всегда занимали особое место. Они являются важным средством обучения математике. С их помощью учащиеся получают опыт работы с величинами, постигают взаимосвязи между ними, получают опыт применения математики к решению практических задач. Решение задач является наиболее эффективной формой развития математической деятельности.
При обучении математике задачи имеют образовательное, развивающее, воспитательное значение.
Они развивают логическое и алгоритмическое мышление учащихся, вырабатывают практические навыки применения математики. При обучении теоретическим знаниям задачи способствуют мотивации введения понятий, выявлению их существенных свойств, усвоению математической символики и терминологии, раскрывают взаимосвязи одного понятия с другими.
Воспитательное воздействие оказывает общий подход к решению задач: система задач, место, методы и формы ее решения, стиль общения учителя и учащихся, учащихся между собой при решении задач. Решение задач позволяет учащимся воспитывать в себе настойчивость, трудолюбие, активность, самостоятельность, формирует познавательный интерес, помогает вырабатывать и отстаивать свою точку зрения.
Развивающие функции задач заключаются в том, что в деятельности решения задач вырабатываются умения применять теоретические знания на практике, выделять общие способы решения, переносить их на новые задачи, развиваются логическое и творческое мышление, внимание, память, воображение.
Использование исторических задач и разнообразных старинных (арифметических) способов их решения не только обогащает опыт мыслительной деятельности учащихся, но и позволяет им осваивать важный культурно-исторический пласт истории человечества, связанный с поиском решения задач. Это важный внутренний (связанный с предметом), а не внешний (связанный с отметками, поощрениями и т.п.) стимул к поиску решений задач и изучению математики.
С изменением роли и места задач в обучении обновляются и видоизменяются и сами задачи. Раньше они формулировались с помощью слов “найти”, “построить”, “вычислить”, “доказать”, в современной школе чаще используются слова “обосновать”, “выбрать из различных способов решения наиболее рациональный”, “исследовать”, “спрогнозировать различные способы решения” и т.д.
- задачи на движение;
- задачи на работу;
- задачи на проценты;
- задачи на смеси, сплавы и концентрацию;
- задачи, в которых неизвестные – целые числа;
- задачи, для решения которых нужно находить наибольшее или наименьшее значение;
- задачи, решение которых требует рассмотрения нескольких вариантов;
- задачи, процесс решения которых приводит к системе уравнений, содержащей уравнений меньше, чем неизвестных;
- задачи, для решения которых необходимо использовать неравенства.
Задачи на проценты являются традиционными для школы; обучение их решению всегда рассматривалось как необходимое условие подготовки учащихся к жизни. Действительно, это одно из математических понятий, которое часто встречается в повседневной жизни.
К текстовым задачам на проценты относятся задачи, в которых речь идет о вкладах в банк под тем или иным процентом, о прибыли, о выполнении плана, об изменении цены на товар; задачи, в которых происходит преобразование исходного вещества (при сушке, при выпаривании) и т. д. Задачи этого типа очень часто входят составной частью в решение других типовых задач.
Не будучи подготовленными к пониманию, вряд ли учащиеся смогут осмысленно трактовать такие сообщения, как “Банк начисляет120 процентов годовых”, “В выборах приняли участие 56,3 процента избирателей” и т. д., тем более отвечать на подобные вопросы: “Какой капитал, отданный в рост под 6 %, принесет в 6 лет 8 850 руб. процентных денег?”, “Какой будет заработная плата после повышения ее на 35 %, если до повышения она составляла 7 500 руб.?”, “Как изменятся расходы на оплату электроэнергии, если потребление возрастает на 15 %, а стоимость одного кВт / ч увеличится на 20 %?” и т.д. Заметим, что задачи на проценты сегодня становятся еще более актуальны, так как сфера практического приложения процентных расчетов расширяется (повышение цен; объявления коммерческих банков, привлекающих деньги населения на различных условиях; сведения о повышении процента банковского кредита; сведения о доходах по акциям различных предприятий и фондов и т.д.).
Процесс решения задачи можно разделить на 4 основных этапа: осмысление условия задачи (анализ условия), поиск и составление плана решения, осуществление плана решения, изучение (исследование) найденного решения.
Осмысление условия задачи (1 этап).
1) Умение анализировать требование задачи.
Под анализом требования задачи понимается выяснение возможных путей ответа на вопрос задачи.
2) Умение анализировать условие задачи.
Под анализом условия задачи можно понимать выявление такой информации, которая непосредственно не задана условием, но присуща ему.
Составление плана решения задачи (2-й этап).
Составление плана решения задачи, пожалуй, является главным шагом на пути ее решения. Правильно составленный план решения задачи почти гарантирует правильное ее решение. Составляя план решения задачи, всегда следует задавать себе (или решающему задачу ученику) вопрос: «Все ли данные задачи использованы?» Выявление неучтенных данных задачи облегчает составление плана ее решения.
Осуществление плана решения задачи (3-й этап).
План указывает лишь общий контур решения задачи. При реализации плана решающий задачу рассматривает все детали, которые вписываются в этот контур. Эти детали надо рассматривать тщательно и терпеливо. Но при этом ученику (решающему задачу) полезно следовать некоторым советам:
1) Проверяйте каждый свой шаг, убеждайтесь, что он совершён правильно. Иными словами, нужно доказывать правильность каждого шага ссылками на соответствующие, известные ранее математические факты, предложения.
2) Обратить внимание учащихся на необходимость выбора такого способа оформления решения, чтобы зафиксировать решение в краткой и ясной форме.
Изучение найденного решения задачи (4-й этап).
Заключительный этап является необходимой и существенной частью решения задачи. Основным содержанием его должно быть осмысление выполненного решения, формулирование и решение (если это окажется возможным) других задач, явно связанных с решенной, и извлечение из всей проделанной работы выводов о том, как находятся и выполняются решения.
Таким образом, после оформления решения необходимо выявление идей (главной мысли), положенных в основу решения. Решение задачи несколькими способами является одним из путей проверки правильности полученного результата; важно сопоставление найденных решений, выделение более рациональных и поучительных. Это путь воспитания гибкости математического мышления и находчивости.
Даже очень хорошие ученики, получив ответ и тщательно изложив ход решения, считают задачу решенной. А ведь получение результата не означает еще, что задача решена правильно. Тем более не означает, что для решения выбран лучший, наиболее удачный, изящный, если можно так выразиться, вариант. По В. М. Брадису, задачу можно считать решенной, если найденное решение: 1) безошибочно, 2) обоснованно, 3) имеет исчерпывающий характер. [1]
Итак, два совета: «Проверьте результат», «Проверьте ход решения». Проверка результата может производиться различными способами.
Проверяя правильность хода решения, мы тем самым убеждаемся и в правильности результата.
Второй способ проверки результата заключается в получении того же результата применением другого метода решения задачи, поэтому полезно всегда задавать решающему вопрос: «Нельзя ли тот же результат получить иначе?» К тому же получение различных вариантов решения одной и той же задачи имеет важное обучающее значение.
Изложенные выше советы для решения задач позволяют решать многие задачи, но, разумеется, не могут служить рецептом для решения любой задачи. Эти советы, многие из которых сформулировал Д. Пойа[6], правильно ориентируют решающего задачи на поиск решения, сокращают время решения многих задач, повышают вероятность отыскания верного и рационального способа решения задач. Единого же рецепта для решения любых задач попросту не существует.
Общие умения по решению задач:
• умение проводить анализ условия задачи;
• умение применять изученную теорию (определение, правило) на практике;
• умение выделять основную идею в решении отдельной задачи, находить общее в решении нескольких задач и переносить эту идею, это общее на новую задачу;
• умения по самооценке своей деятельности, самоконтролю.
Обучение краткой записи условия задачи — это и есть обучение анализу условия. Краткая запись — это модель текста задачи, материализованная форма проведения действия анализа условия. Начинать поиск решения задачи можно лишь тогда, когда ее условие полностью понято. На ранее перечисленных этапах решения задачи самоконтроль проявляет себя как естественная неотрывная составляющая поисковой деятельности, которая может и не осознаваться учеником. Последнему этапу решения задачи — проверке и исследованию полученного решения присвоен особый статус этапа, на котором осуществляется самоконтроль.
В методике преподавания математике выделены различные формы самоконтроля, проводимые после завершения этапа реализации намеченного плана. Вот примеры таких форм.
1. Проверка совпадения размерности ответа с требованием задачи. Например, при нахождении пути значение скорости (км/ч) умножается на значение времени (ч). Умножение наименований должно дать наименование длины (км).
2. Проверка ответа по здравому смыслу. Например, скорость пешехода не может быть равной 15 км/ч, количество рабочих не может быть дробным и т.д. (Предложить детям задать вопрос “Может ли такое быть?”)
3. Проверка с помощью грубой прикидки. При этом данные грубо округляются, и выясняется порядок возможного результата.
В школьном курсе математики используются два способа решения текстовых задач: арифметический и алгебраический (с помощью составления уравнения или системы уравнений).
Я рассмотрела арифметический способ решения задач. Его использование развивает смекалку и сообразительность, умение ставить вопросы, отвечать на них, то есть развивает естественный язык, готовит школьников к дальнейшему обучению.
Арифметический способ решения текстовых задач позволяет развивать умение анализировать задачные ситуации, строить план решения с учетом взаимосвязей между известными и неизвестными величинами (с учетом типа задач), истолковывать результат каждого действия в рамках условия задачи, проверять правильность решения с помощью составления и решения обратной задачи, то есть формировать и развивать общеучебные умения.
Арифметический способ решения текстовых задач приучает детей к первым абстракциям, позволяют воспитывать логическую культуру, могут способствовать созданию благоприятного эмоционального фона обучения, развитию у школьников эстетического чувства применительно к решению задачи (красивое решение!) и изучению математики, вызывая интерес сначала к процессу поиска решения задачи, а потом и к изучаемому предмету.
При подготовке к ЕГЭ мои ученики решают задачи на движение, работу, производительность труда, процентный прирост, процентное содержание и др. Имея богатый опыт решения текстовых задач не только с помощью составления уравнений, но и арифметическим способом они выбирают наиболее рациональный способ решения задачи. Кроме того, вовлекая их в создание разнообразных математических моделей решения, достигается одна из основных целей обучения математике: воспитание гармонично развитой личности.
Значение слова задача
вопрос, требующий разрешения, то, что задано для решения, разрешения. Неразрешимая задача для философа.
Математический вопрос, для разрешения которого требуется путем вычислений найти какие-н. величины (мат.). Арифметическая, алгебраическая задача. Задачи на правило процентов.
цель; то, что необходимо осуществить, чего необходимо достигнуть; поручение, как заданная кому-н. цель. Вслед за задачами военными встает задача хозяйственная. Ленин. Задача построения фундамента социалистической экономики выполнена. Задача построить внеклассовое социалистическое общество — основная политическая задача второй пятилетки. Ставить себе, перед собой задачу. Иметь что-н. своей задачей. Задача сводится к чему-н., к тому, чтобы. (см. сводиться). Задай лишь мне задачу: без дела, знаешь, от тебя не должен отлучиться я. Пушкин.
Удача, успех, счастье; противоп. незадача (обл.). Во всем-то ему задача, что дивится народ даже. Л. Толстой.
Толковый словарь русского языка. С.И.Ожегов, Н.Ю.Шведова.
То, что требует исполнения, разрешения. Поставить задачу. Выполнить задачу. Боевая з. (поставленная командиром для достижения определенной цели в бою).
Упражнение, к-рое выполняется посредством умозаключения, вычисления. Арифметическая, алгебраическая з. Шахматная з.
Сложный вопрос, проблема, требующие исследования и разрешения. Научная з.
О чем-н. трудновыполнимом, сложном (разг.). Нужно успеть в разные места. 3.!
Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
Цель, к которой стремятся, которую хотят достичь.
Обстоятельства, затруднения, которые надо преодолеть.
Поручение, задание (обычно трудно выполнимые, сложные).
Вопрос (обычно математического характера), требующий нахождения решения по известным данным с соблюдением определенных условий.
Энциклопедический словарь, 1998 г.
Имена, названия, словосочетания и фразы содержащие «задача»:
Большая Советская Энциклопедия
поставленная цель, которую стремятся достигнуть.
Вопрос, требующий решения на основании определённых знаний и размышления (математическая З., шахматная З., логическая З., письменная З.), проблема.
Один из методов обучения и проверки знаний и практических навыков учащихся, применяемых во всех типах общеобразовательных и специальных учебных заведений.
Имена, названия, словосочетания и фразы содержащие «задача»:
Википедия
Зада́ча:
- Задача — проблемная ситуация с явно заданной целью .
- Задача — шахматная позиция с условием, которое необходимо выполнить в заданное число ходов.
Зада́ча — проблемная ситуация с явно заданной целью , которую необходимо достичь; в более узком смысле задачей также называют саму эту цель, данную в рамках проблемной ситуации, то есть то, что требуется сделать. В первом значении задачей можно назвать, например, ситуацию, когда нужно достать предмет, находящийся очень высоко; второе значение слышно в указании: «Ваша задача — достать этот предмет». Несколько более жёсткое понимание «задачи» предполагает явными и определёнными не только цель, но и условия задачи, которая в этом случае определяется как осознанная проблемная ситуация с выделенными условиями . Ещё более узкое определение называет задачей ситуацию с известным начальным состоянием системы и конечным состоянием системы, причём алгоритм достижения конечного состояния от начального известен (в отличие от проблемы , в случае которой алгоритм достижения конечного состояния системы не известен).
В более широком смысле под задачей также понимается то, что нужно выполнить — всякое задание, поручение, дело, — даже при отсутствии каких бы то ни было затруднений или препятствий в выполнении. В учебной и т. п. практике «задача», напротив, принимает более узкий смысл и обозначает упражнение, требующее нахождения решения по известным данным с помощью определённых действий при соблюдении определённых правил совершения этих действий (логическая задача, математическая задача, шахматная задача ).
В отличие от функции , которая может осуществляться постоянно, задача может быть решена.
Решение задачи обычно требует определённых знаний и размышления . Отсюда — понятие «озадачить»: это значит либо «заставить задуматься», либо «поручить выполнение задачи» .
Имена, названия, словосочетания и фразы содержащие «задача»:
Примеры употребления слова задача в литературе.
Задачи, продиктованные его вечной человеческой природой, — самосохранением, жаждой победы и торжества, жаждой обладания, чувственной любовью — определяют авантюрный сюжет.
Задачи, продиктованные его вечной человеческой природой — самосохранением, жаждой победы и торжества, жаждой обладания, чувственной любовью, — определяют авантюрный сюжет.
Вполне справедливо считалось, что пусть Ливия и была фурией, если бы не ее неустанная деятельность, Август ни за что не смог бы выполнить взятую им на себя колоссальную задачу: вернуть Риму мир и безопасность, отнятые долгими и бедственными гражданскими войнами, в которых сам он, спору нет, сыграл такую роковую роль.
Пока мы с вами выжидали летную погоду, обстановка на фронте изменилась, задачу по десантированию авиадесанта с нас сняли.
Партия поставила перед нами эту задачу — создать советский мощный авиамотор, самый мощный мотор в мире.
Быстродействующие электронные счетные машины позволяют с колоссальной скоростью и большой точностью решать самые разнообразные задачи, например, в области внутриатомных процессов, реактивной техники, радиолокации, авиастроения, строительной механики и других отраслях.
В арсенале высотных средств имеется автовышка, но коротка для данной задачи.
К сожалению, мы впоследствии сильно облегчили им задачу, когда фронт у Дюнабурга передвинулся, а автодорога была оставлена.
Тем более актуальной задачей становится, следовательно, автоматизация познавательных методов хотя бы на библиографическо-издательском уровне.
САПР с системой подготовки производства и выполнен ряд работ по автоматизации планово-производственных задач, возникающих при освоении новых изделий.
Короче говоря, задача морали заключается в формировании покорных личностей, которые, несмотря на нищету и унижение, должны соответствовать требованиям авторитарного строя.
Пленум ЦК КПСС указал, что для выполнения Продовольственной программы работникам агропромышленного комплекса нужно изо дня в день наращивать усилия, трудиться так, чтобы огромные средства, направляемые на решение этой задачи, давали отдачу уже сегодня и еще большую — завтра.
С тысяча семьсот сорок девятого по тысяча семьсот пятьдесят восьмой год этой задаче посвятил себя Адамсон, побывавший в Горэ.
С целью решения поставленной задачи вычислялся адаптационный потенциал сердечно-сосудистой системы каждого лицеиста по методике ,разработанной П.
Снятие или уменьшение аффективно-тревожной напряженности в общении представляет необходимое условие для решения основной задачи групповой психотерапии — обучения, в которое входят обучение навыкам адаптивного поведения, коррекция неблагоприятных черт характера и достижение более адекватной социализации.
Источник: библиотека Максима Мошкова
Транслитерация: zadacha
Задом наперед читается как: ачадаз
Задача состоит из 6 букв
Что такое задача в математике 5 класс определение
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.
Сравнение натуральных чисел
Число 0 меньше любого натурального числа.
Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.
Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр
Свойства сложения
Формула пути
S = V · t , г д е S — п р о й д е н н ы й п у т ь , V — с к о р о с т ь д в и ж е н и я , t — в р е м я , з а к о т о р о е п р о й д е н п у т ь S
= 50км, = 2ч, = 25км/ч
, 25км/ч = 50км : 2ч
, 2ч = 50км : 25км/ч
Корень уравнения
Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.
Что значит «Решить уравнение»
Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.
Правила решения уравнений
- Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
- Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
- Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
- Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
- Чтобы найти неизвестное делимое, надо делитель умножить на частное.
- Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Отрезок, прямая, луч
Отрезок
Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)
Свойство длины отрезка
Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки
Два отрезка называют равными, если они совмещаются при наложении.
Свойство прямой
Через две точки проходит только одна прямая.
Измерить отрезок
Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
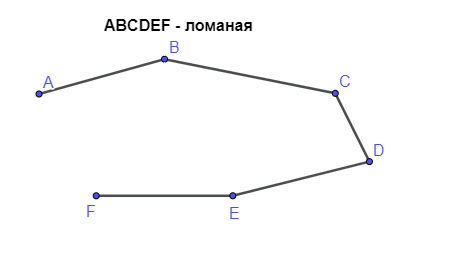
Ломаная
Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом
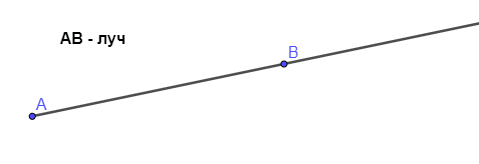
Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
Угол, биссектриса угла
Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы
Два угла называют равными, если они совмещаются при наложении.
Свойство величины угла
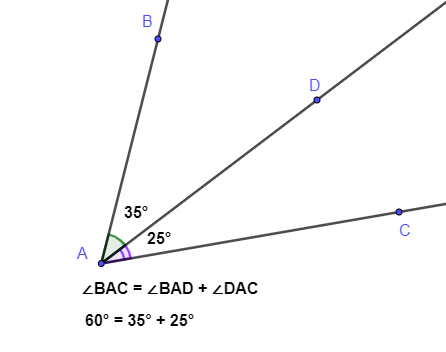
Если между сторонами угла ∠ провести луч , то градусная мера ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.
Биссектриса угла
Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой
Развернутый угол
Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.
Прямой угол
Угол, градусная мера которого равна 90°, называют прямым.
Острый угол
Угол, градусная мера которого меньше 90°, называют острым.
Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
Многоугольники. Равные фигуры
Равные многоугольники
Два многоугольники называют равными, если они совмещаются при наложении.
Равные фигуры
Две фигуры называют равными, если они совмещаются при наложении.
Треугольники: остроугольный, прямоугольный, тупоугольный
Остроугольный треугольник
Если все углы треугольника острые, то его называют остроугольным треугольником.
Прямоугольный треугольник
Если один из углов треугольника прямой, то его называют прямоугольным треугольником.
Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.
Треугольники: равнобедренный, равносторонний, разносторонний
Равнобедренный треугольник
Если две стороны треугольника равны, то его называют равнобедренным треугольником.
Равносторонний треугольник
Если три стороны треугольника равны, то его называют равносторонним треугольником.
Периметр равностороннего треугольника
Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле
Разносторонний треугольник
Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр
Прямоугольник
Если в четырехугольнике все углы прямые, то его называют прямоугольником.
Свойство прямоугольника
Противоположные стороны прямоугольника равны.
Периметр прямоугольника
Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле
Квадрат
Прямоугольник, у которого все стороны равны, называют квадратом.
Периметр квадрата
Если сторона квадрата равна , то его периметр вычисляют по формуле .

Умножение. Свойства умножения
Умножение
- Произведением числа на натуральное число , которое не равно 1, называют сумму, состоящую из слагаемых, каждый из которых равен . В равенства числа и называют множителями, а число и запись — произведением.
- Если один из двух множителей равен 1, то произведение равно второму множителю.
- Если один из множителей равен нулю, то произведение равно нулю.
- Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Свойства умножения
- Переместительный закон умножения:
- Сочетательный закон умножения:
- Распределительное свойство умножения относительно сложения:
- Распределительное свойство умножения относительно вычитания:
Деление. Деление с остатком
Деление
Для натуральных чисел равенство является правильным, если является правильным равенство
В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.
На ноль делить нельзя.
Для любого натурального числа правильными являются равенства:
Деление с остатком
, где — делимое, — делитель, — неполное частное, — остаток, .
Если остаток равен нулю, то говорят, что число делится нацело на число .
Площадь. Площадь квадрата, прямоугольника
Свойства площади фигуры
Равные фигуры имеют равные площади;
Площадь фигуры равна сумме площадей фигур, из которых она состоит.
Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.
Площадь квадрата

где — площадь квадрата, — длина его стороны.
Объем. Объем прямоугольного параллелепипеда, куба
Свойства объема фигуры
Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.
Объем прямоугольного параллелепипеда
где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;
, где — площадь поверхности прямоугольного параллелепипеда.
где — площадь основания параллелепипеда, — его высота.
Объем куба
где — объем куба, — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей
Правильная дробь
Дробь, числитель которой меньше знаменателя, называют правильной
Неправильная дробь
Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.
Сравнение дробей
- Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.
- Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.
- Все правильные дроби меньше единицы, а неправильные — больше или равны единице.
- Любая неправильная дробь больше любой правильной дроби.
Сложение и вычитание дробей с одинаковыми знаменателями
- Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
- Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Сложение и вычитание смешанных чисел
- Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
- Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Преобразование неправильной дроби в смешанное число
Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно
- числитель разделить на знаменатель;
- полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.
Преобразование смешанного числа в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь нужно
- целую часть числа умножить на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- эту сумму записать как числитель неправильной дроби;
- в его знаменателе записать знаменатель дробной части смешанного числа.
Десятичные дроби: свойства, сравнение, округление
Свойства десятичной дроби
Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.
Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.
Сравнение десятичных дробей
Из двух десятичных дробей больше та, у которой целая часть больше.
Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо
- с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
- после чего сравнить полученные дроби поразрядно.
С р а в н и т ь 5 , 03 и 5 , 0375 . 5 , 03 ⏟ 2 = 5 , 0300 ⏟ 4 и 5 , 0375 ⏟ 4 ; 5 , 03 0 0 < 5 , 03 7 5 .
Округление десятичных дробей
Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо
- все следующие за этим разрядом цифры отбросить.
- если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4 , то последнюю из цифр, которые оставляют, не меняют ;
- если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9 , то последнюю из цифр, которые оставляют, увеличивают на единицу.
О к р у г л и т ь 5 , 248 и 3 , 952 : а ) д о д е с я т ы х : 5 , 2 4 8 ≈ 5 , 2 ; 3 , 9 5 2 ≈ 4 , 0 ; б ) д о с о т ы х : 5 , 2 4 8 ≈ 5 , 25 ; 3 , 9 5 2 ≈ 3 , 95 .
Десятичные дроби: сложение, вычитание
Сложение десятичных дробей
Чтобы найти сумму двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
- сложить полученные числа так, как складывают натуральные числа;
- поставить в полученной сумме запятую под запятыми.
Вычитание десятичных дробей
Чтобы найти разность двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
- выполнить вычитание так, как вычитают натуральные числа;
- поставить в полученной разности запятую под запятыми.
Десятичные дроби: умножение, деление
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
- перемножить их как натуральные числа, не обращая внимания на запятые;
- в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
У м н о ж и т ь 1 , 5 и 2 , 25 . 2 × 2 , 25 1 1 , 5 + 1125 225 · 3 3 , 375 — количество цифр после запятой
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.
У м н о ж и т ь 1 , 235 н а 10 , 100 , 1000 . а ) н а 10 : 1 , 235 × 1 0 ⏟ 1 = 12 , 35 б ) н а 100 : 1 , 235 × 1 00 ⏟ 2 = 123 , 5 в ) н а 1000 : 1 , 235 × 1 000 ⏟ 3 = 1235 , 0 = 1235
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.
У м н о ж и т ь 512 , 3 н а 0 , 1 , 0 , 01 и 0 , 001 . а ) н а 0 , 1 : 512 , 3 × 0 , 1 ⏟ 1 = 51 , 23 б ) н а 0 , 01 : 512 , 3 × 0 , 01 ⏟ 2 = 5 , 123 в ) н а 0 , 001 : 512 , 3 × 0 , 001 ⏟ 3 = 0 , 5123
Деление десятичных дробей
Чтобы разделить десятичную дробь на десятичную, надо:
- перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
- выполнить деление на натуральное число.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.
Р а з д е л и т ь 25 , 5 н а 10 , 100 , 1000 . а ) н а 10 : 25 , 5 : 1 0 ⏟ 1 = 2 , 55 ; б ) н а 100 : 25 , 5 : 1 00 ⏟ 2 = 0 , 255 ; в ) н а 1000 : 25 , 5 : 1 000 ⏟ 3 = 0 , 0255 ;
Среднее арифметическое
Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.
Найти среднее арифметическое чисел 15, 25 и 20.
15 + 25 + 20 ⏞ с у м м а ч и с е л 3 ⏟ к о л и ч е с т в о ч и с е л = 60 3 = 20
Примечание:
Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.
V с р е д н я я = S о б щ t о б щ .
1) 200 + 120 = 320(км) -весь путь;
2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;
3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;
4) 4 + 4 = 8(ч) — все время;
5) 320 : 8 = 40(км/ч) — средняя скорость.
Процент
Процентом называют сотую часть величины или числа 1%=
Н а й т и 4 % о т ч и с л а 20 . 20 : 100 = 0 , 2 ( 0 , 2 — э т о 1 % о т ч и с л а 20 ) ; 0 , 2 × 4 = 0 , 8 ( 0 , 8 — и с к о м о е ч и с л о ) . И л и 4 % = 4 100 = 0 , 04 ; 0 , 04 × 20 = 0 , 8 .
Основные правила математики с примерами. 5 класс: 31 комментарий
Пожалуйста, ребята! Удачи в новом учебном году!
Спасибо большущее. Я закончила 4 класс, но из-за санкций у нас ВПР перенесли. Я всё забыла и вот всё опять вспомнила. Всё что важно пишу в блокнот. Советую) потому что перед контрольными можно всё повторить! Ещё раз спасибки ☺️
Спасибо, все очень понятно!
Спасибо большое!
Я всё хорошо запомнила и написала все к.р.
спасибо огромное мне понятней чем в учебнике по математике я в 5 классе…..мне просто тесты здавать надо
КАК РЕШАТЬ ЗАДАЧИ
Рассмотрим план действий, который поможет понять как решать задачи.
- 1. Внимательно прочитай задачу.
- 2. Сделай краткую запись условия или чертёж.
- 3. Объясни, что означает каждое число.
- 4. Повтори вопрос задачи. Подумай, можно ли сразу на него ответить. Каких данных для решения тебе не хватает? Как их найти?
- 5. Составь план решения задачи.
- 6. Реши задачу.
- 7. Проверь решение. Запиши ответ.
А ТЕПЕРЬ БОЛЕЕ ПОДРОБНЕЕ:

Определите, к какому типу относится задача. Это арифметическая задача? Действия с дробями? Решение квадратных уравнений? Прежде чем приступить к решению, выясните, к какой области математики относится задача. Примеры и виды Залач. показаны ниже) Это важно, поскольку значительно упростит поиск способа решения.
Внимательно прочитайте условие задачи. Даже если задача кажется простой, внимательно изучите ее условие. Не следует приступать к решению задачи, лишь бегло ознакомившись с ее условием. Если задача сложна, вам, возможно, понадобится несколько раз перечитать ее условие, чтобы полностью понять его. Не жалейте времени на это и не приступайте к дальнейшим действиям до тех пор, пока не узнаете точно, что дано в условии и что необходимо найти.
Изложите условие задачи. Для лучшего понимания задачи полезно изложить ее условие своими словами. Можно просто пересказать условие, либо записать его в том случае, если вам неудобно говорить вслух (например, на экзамене). Сравните собственное изложение задачи с ее первоначальным условием, выяснив тем самым, правильно ли вы поняли задание.
Изобразите задачу графически. Если вы считаете, что это поможет, представьте задачу графически — возможно, так легче будет определить дальнейшие действия. Необязательно создавать подробную схему, достаточно набросать условие задачи в общих чертах, указав численные значения. При создании схемы справляйтесь с условием задачи, по окончании сравните готовое изображение с условием еще раз. Задайте самому себе вопрос: «Верно ли мой рисунок отображает задачу?» Если да, можно приступить к решению задачи. Если же ответ отрицателен, перечитайте условие еще раз.
- Постройте диаграмму Венна. Эта диаграмма изображает соотношения между величинами, фигурирующими в задаче. Диаграмма Венна особенно полезна при решении арифметических задач.
- Постройте график либо диаграмму.
- Расположите приведенные в условии величины вдоль прямой линии.
- Чтобы представить более сложные объекты, используйте простые геометрические фигуры.
Изучите структуру задачи. Внимательно прочитав условие, вы, возможно, вспомните похожие задачи, решенные вами ранее. Можно построить таблицу с внесенными в нее данными, которая поможет вам определить характер задачи. Отметьте выявленные характерные черты задачи — они помогут вам при ее решении. Не исключено даже, что вы вспомните схожие задачи и сразу получите ответ.
Изучите сделанные пометки. Еще раз проверьте свои записи, убедившись, что вы не ошиблись в числах и прочих данных. Не приступайте к составлению плана решения до тех пор, пока не будете уверены в том, что обладаете всей необходимой информацией и полностью понимаете задачу. Если вы не до конца поняли задачу, изучите схожие примеры в учебнике или в интернете. Ознакомление с похожими задачами, решенными другими людьми, поможет вам понять, что требуется сделать для решения задачи, которую решаете вы.
Составление плана решения

Выясните, какие формулы понадобятся для решения задачи. Если задача достаточно сложна, может потребоваться несколько формул. Ознакомьтесь с необходимым для решения материалом в учебнике.
Выпишите то, что может потребоваться при решения задачи. Составьте последовательный список шагов, которые необходимо сделать, чтобы получить ответ. Это поможет вам правильно организовать свою работу и сосредоточиться на решении задачи. Правильно составленный план поможет также примерно оценить ответ заранее, прежде чем вы решите задачу.
Потренируйтесь на более легкой задаче. Если есть более простая задача, похожая на ту, которую необходимо решить, попробуйте свои силы сначала на ней. Предварительный разбор простой задачи, в которой используются те же приемы и формулы, облегчит решение более сложного задания.
Сделайте обоснованное предположение о том, каким должен быть ответ. Прежде чем приступать к непосредственному решению задачи, попытайтесь оценить ответ. Определите величины и другие факторы, влияющие на оценку. Проверьте свои рассуждения, не упустили ли вы чего-либо из виду.
Решение задачи
Придерживайтесь составленного плана. Выполняйте этапы последовательно в том порядке, в котором вы наметили их ранее. Чтобы избежать ошибок, перепроверяйте результат, полученный на каждом этапе.
Сравнивайте полученные результаты с предварительно сделанными оценками. По завершении каждого этапа полезно сравнить его результат со сделанными ранее оценками; сопоставьте также конечный ответ с его предварительной оценкой. Задайте себе вопрос: «Близки ли мои предположения к полученным результатам?» Если ответ отрицателен, подумайте, почему. Проверьте полученные результаты, просмотрев все шаги решения еще раз
Попробуйте другую схему решения. Если составленный вами план не сработал, вернитесь к этапу планирования и разработайте новый план. Не расстраивайтесь в случае неудачной попытки, учеба не обходится без ошибок — наоборот, вы научитесь на своих ошибках и сможете избежать их в дальнейшем. Выявите сделанные ошибки и продолжайте работу. Не зацикливайтесь на ошибках и не огорчайтесь из-за них.
Проанализируйте задачу. Получив правильный ответ, вернитесь к началу и просмотрите решение еще раз. Анализ задачи и ее решения поможет вам в следующий раз, когда вы столкнетесь с подобной задачей. Также вы лучше усвоите использованные методы и приемы, которые обязательно пригодятся вам в дальнейшем
Советы
- Если вы безуспешно испробовали целый ряд вариантов и не в состоянии продвинуться дальше в решении задачи, обратитесь за помощью к учителю или репетитору. Он выявит допущенные вами ошибки и поможет их исправить.
- Продолжайте использовать диаграммы и арифметические действия. Регулярно просматривайте заметки, сделанные на занятиях. Для облегчения понимания записывайте используемые методы своими словами и применяйте их по мере необходимости.
Какие бывают математические задачи:
ПРОСТЫЕ И СОСТАВНЫЕ ЗАДАЧИ
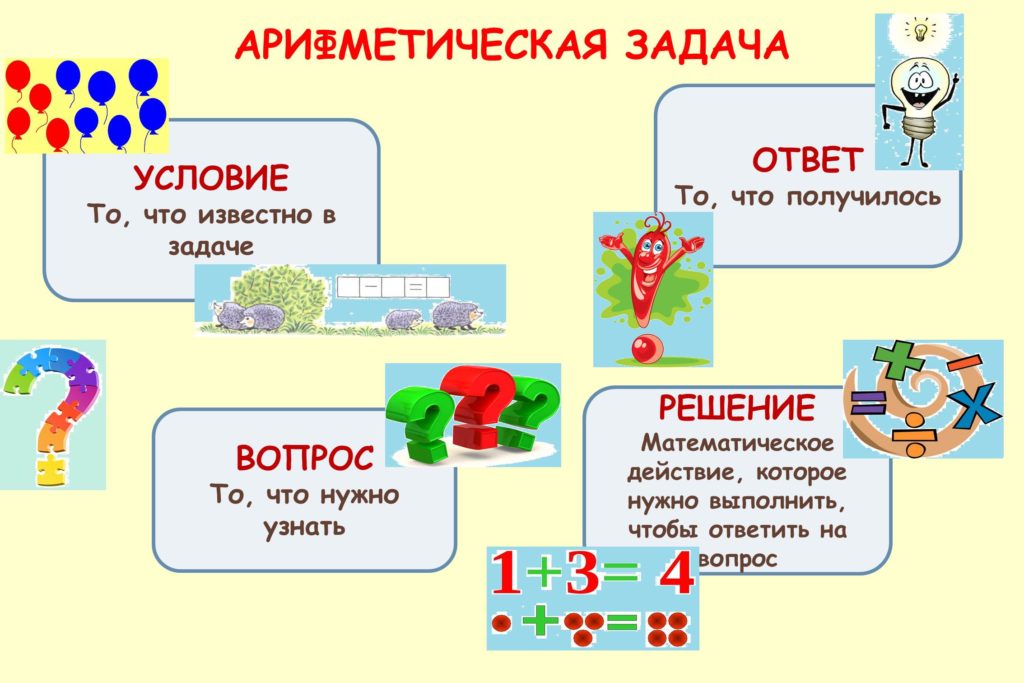
Простые Математические Задачи состоят из 5 частей:
- Условие
- Вопрос
- Краткая Запись
- Решение Ответ

Обязательно в задаче нужно выявлять ОПОРНЫЕ СЛОВА, ОПОРНЫЕ СЛОВА — это основа краткой записи, их нужно уметь находить для определения главного в задаче.
В вазе 3 белых и 2 розовых гвоздики.
Сколько всего гвоздик в вазе?
В указанной задаче:
Первое опорное слово- белые, которое в 1 классе сокращаем 1 буквой Б., но начиная со 2 класса -Бел.
Второе опорное слово — розовые, которое в первом классе, сокращаем словом Р, но начиная со 2 класса- Роз.
Третье опороное слово всегда содержится в вопросе.
В данной задаче третье опорное слово — всего, которое в краткой записи заменяется фигурной скобкой с вопросом посередине

Ответ: 5 гвоздик всего в вазе.


Простые задачи решаются одним действием.
Составные задачи решаются двумя и более действиями, разными способами.
У Иры 3 куклы, что в 2 раза меньше, чем у Светы. Сколько кукол у обеих девочек?
• по действиям с пояснениями
1) 3 • 2 = б (к.) — у Светы
2) 3 + 6 = 9 (к.) — у обеих девочек
• по действиям с вопросами
1. Сколько кукол у Светы? 3-2 = б(к.)
2. Сколько кукол у обеих девочек? 3 + 6 = 9 (к.)
Ответ: у обеих девочек 9 кукол.
ЗАДАЧИ НА НАХОЖДЕНИЕ СУММЫ
a + b = c
первое второе сумма
слагаемое слагаемое
Чтобы найти сумму, надо сложить слагаемые
У балалайки 3 струны, а у контрабаса — 4. Сколько всего струн у этих музыкальных инструментов?
Решение: 3 + 4 = 7 (с.) Ответ: у этих музыкальных инструментов 7 струн.
У Кати 3 книги, что на 2 книги меньше, чем у Иры. Сколько всего книг у девочек?
Решение: 1)3 + 2 = 5 (к.)-у Иры 2) 3 + 5 = 8 (к.) — всего Ответ: всего у девочек 8 книг.
а — b = с
уменьшаемое вычитаемое разность
Чтобы найти разность, надо из уменьшаемого вычесть вычитаемое
У кошки родилось 6 котят. Четырёх котят отдали. Сколько котят осталось?
Решение: 6-4 = 2 (к.) Ответ: осталось 2 котёнка.
У Маши было 4 конфеты. Бабушка дала ей ещё 8 конфет. После обеда девочка съела 3 конфеты. Сколько конфет осталось у Маши?
1) 4 + 8 = 12 (к.) — было у Маши до обеда
2) 12 — 3 = 9 (к.) — осталось после обеда Ответ: у Маши осталось 9 конфет.
ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО УМЕНЬШАЕМОГО
а — b = с
уменьшаемое вычитаемое разность
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое
Когда Вася решил 15 примеров, ему осталось решить ещё 11 при меров. Сколько всего примеров нужно решить Васе?
Решение: 15+ 11 = 26 (п.) Ответ: Васе нужно решить 26 примеров.
Мама решила связать новый шарф. Каждый день в течение неде ли она вязала по 20 см. Какой длины должен получиться шарф, если ей осталось связать ещё 10 см?
1. 20 • 7 = 140 (см) — мама связала за неделю
2. 140 + 10 = 150 (см) — длина шарфа Ответ: шарф должен получиться длиной 150 см.
ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО ВЫЧИТАЕМОГО И СЛАГАЕМОГО
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое
В журнале 45 страниц, а в книге 155 страниц. На сколько страниц в книге больше, чем журнале?
Решение: 155-45 = 110 (стр.) Ответ: в книге на 110 страниц больше.
Катя собрала 12 больших ромашек и 7 маленьких. Несколько ромашек она подарила бабушке, и у девочки осталось 10. Сколько ромашек Катя подарила бабушке?
1. 12 + 7 = 19 (ром.) — собрала Катя
2. 19 — 10 = 9 (ром.) — подарила бабушке Ответ: 9 ромашек Катя подарила бабушке.
ЗАДАЧИ НА УВЕЛИЧЕНИЕ И УИЕНЬШЕНИЕ ЧИСЛА НА НЕСКОЛЬКО ЕДИНИЦ
Увеличить на… значит прибавить к числу несколько единиц
5 увеличить на 2 = 5 + 2
Уменьшить на значит вычесть из числа несколько единиц
5 уменьшить на 2 = 5 — 2
Новорождённый котёнок весит 100 г, а трёхнедельный — на 200 г больше. Сколько весит трёхнедельный котёнок?
Решение: 100 + 200 = 300 (г) Ответ: трёхнедельный котёнок весит 300 г.
Петя купил 15 шоколадок, а Юра на 3 шоколадки меньше. Сколько шоколадок купил Юра?
Решение: 15-3 = 12 (ш.) Ответ: Юра купил 12 шоколадок
ЗАДАЧИ НА НАХОЖДЕНИЕ ПРОИЗВЕДЕНИЯ
a • b = С
первый множитель второй множитель произведение
Чтобы найти произведение, надо перемножить множители
У котёнка 4 лапы. Сколько лап у пятерых котят?
Решение: 4 • 5 = 20 (л.) Ответ: у пятерых котят 20 лап.
С первого куста смородины собрали 3 кг ягод, со второго — 4 кг, а с третьего — в 2 раза больше, чем с первого и со второго вместе. Сколько килограммов смородины собрали с третьего куста?
1. 3 + 4 = 7 (кг) — собрали с двух кустов
2. 7 • 2 = 14 (кг) —собрали с третьего куста Ответ: с третьего куста собрали 14 кг смородины.
ЗАДАЧИ НА НАХОЖДЕНИЕ ЧАСТНОГО
a : b = c
делимое делитель частное
Чтобы найти частное, надо делимое разделить на делитель
У мамы было 10 мандаринов. Она раздала двум дочкам мандарины поровну. Сколько мандаринов получила каждая девочка?
Решение: 10 : 2 = 5 (м.) Ответ: каждая девочка получила 5 мандаринов.
Бабушка сварила варенье: 9 литров малинового и б литров клубничного. Всё варенье она разлила в трёхлитровые банки. Сколько банок с вареньем получилось?
1. 9 + б = 15 (л) — всего варенья сварила бабушка
2. 15 : 3 = 5 (б) — всего банок Ответ: получилось 5 банок с вареньем.
Задачи на нахождение неизвестного делимого
а : b = c
делимое делитель частное
Чтобы найти делимое, надо частное умножить на делитель
За 2 дня учительнице надо проверить тетради учеников. Она со бирается проверять по 14 тетрадей вдень. Сколько всего тетрадей надо проверить?
Решение: 14 • 2 = 28 (т.) Ответ: всего надо проверить 28 тетрадей.
Переводчик в течение недели переводил по 6 страниц в день. Ему осталось перевести ещё 4 страницы. Сколько всего страниц он перевёл?
1. 6 * 7 = 42 (стр.) — перевёл за неделю
2. 42 + 4 = 46 (стр.) — всего
Ответ: 46 страниц перевёл переводчик.
ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО ДЕЛИТЕЛЯ И МНОЖИТЕЛЯ
Чтобы найти неизвестный делитель, надо делимое разделить на частное
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель
Витя собирает марки. Папа подарил ему 20 марок, а дедушка — 15 марок. Все марки Витя разложил в альбом, на 5 страниц поровну. Сколько марок на каждой странице?
1. 20 + 15 = 35 (м.) — всего у Вити
2. 35 : 5 = 7 (м.) — на каждой странице Ответ: на каждой странице по 7 марок.
ЗАДАЧИ НА УВЕЛИЧЕНИЕ ЧИСЛА В НЕСКОЛЬКО РАЗ И МЕНЬШЕНИЕ
Увеличить в… раз значит умножить число
3 увеличить в 2 раза =3-2
Уменьшить в… раз значит разделить число
6 уменьшить в 2 раза = 6:2
Маме 30 лет, а бабушка — в 2 раза старше. Сколько лет бабушке?
Решение: 30 • 2 = 60 (л.) Ответ: бабушке 60 лет.
Масса белого медведя 900 кг, а масса медведицы — в 3 раза меньше. Какова масса медведицы?
Решение: 900 : 3 = 300 (кг) Ответ: масса медведицы 300 кг.
ЗАДАЧИ НА РАЗНОСТНОЕ СРАВНЕНИЕ
Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее
* На сколько 10 больше, чем 5? 10 — 5 = 5; 10 больше, чем 5, на 5
* На сколько 10 меньше, чем 15? 15 — 10 = 5; 10 меньше, чем 15, на 5
В классе 15 мальчиков и 12 девочек. 22 человека посещают школу, а остальные болеют. На сколько меньше болеющих учеников, чем посещающих школу?
1. 15 + 12 = 27 (чел.) — учатся в классе
2. 27 — 22 = 5 (чел.) — болеют
3. 22 — 5 = 17 (чел.) — на сколько меньше Ответ: болеющих учеников на 17 меньше, чем посещающих школу.
Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее
• Во сколько раз 10 больше, чем 5? 10 : 5 = 2; 10 больше, чем 5, в 2 раза
• Во сколько раз 5 меньше, чем 15? 15 : 5 = 3; 5 меньше, чем 15, в 3 раза
Машинка стоит 90 рублей, а шоколадка — в 3 раза дешевле. Сколько стоят машинка и шоколадка вместе?
1. 90 : 3 = 30 (руб.) — стоит шоколадка
2. 90 + 30 = 120 (руб.) — стоят вместе Ответ: машинка и шоколадка стоят 120 рублей.
ЗАДАЧИ НА ДЕЛЕНИЕ ПО СОДЕРЖАНИЮ
Фрукты разложили на тарелки, по 4 штуки на каждую. Сколько по надобилось тарелок?
Понадобилось 2 тарелки
Бабушка раздала внукам 15 яблок, по 5 штук каждому. Сколько Внуков у бабушки?
Решение: 15 : 5 = 3 (внуков) Ответ: у бабушки 3 внука.
ЗАДАЧИ НА ДЕЛЕНИЕ НА РАВНЫЕ ЧАСТИ
Детям раздали конфеты поровну. Сколько детей получило конфеты?
Двое детей получили конфеты
Для подготовки школьного спектакля учительница разделила 30 учеников на 5 групп. Сколько учеников в каждой группе?
Урок 26 Бесплатно Формулы
Сегодня на уроке мы выясним, что называют формулой и где её применяют.

Разберем правила решения и оформления задач, решаемых с помощью формул.
Рассмотрим примеры таких задач и научимся работать с формулами: выражать неизвестные величины через известные.
Формулы
Математический язык- это формальный, искусственно созданный язык, который состоит из математических знаков, символов, терминов, выражений.
В отличие от естественных языков, этот язык более точный, логичный и краткий.
При переходе с разговорного языка на математический многие утверждения, правила, законы становятся яснее и прозрачнее.
Математика, физика, химия и многие другие науки используют язык математики, который в условной форме позволяет представить информацию наглядно и лаконично, не искажая ее при этом.
Естественными языками легче всего выражать качественные характеристики посредством красноречивых предложений.
Математический язык- это в большей степени количественный язык.
Одним из базовых элементов математического языка являются формулы.
У меня есть дополнительная информация к этой части урока!

Давайте разберёмся, что означает слово «Формула».

Значение слова «формула» (от латинского formula- образ, вид) в толковом словаре Ушакова означает — выраженный условными знаками ряд математических величин в их функциональных зависимостях.
В толковом словаре русского языка Ожегова есть еще одно интересное толкование этого слова: формула- комбинация математических знаков, выражающая какое-нибудь утверждение
Обобщая все выше написанное, можно сказать, что формула- это правило (высказывание), записанное на математическом языке с помощью осмысленной комбинации знаков и символов.
Формулы представляют собой некоторые суждения, которые понятны любому человеку, любой национальности, и неважно каким разговорным языком человек владеет.
В формулу входят переменные. Она устанавливает взаимосвязь между величинами, входящими в нее.
Любые правила, записанные с помощью букв, будут являться примерами формул.

Вам уже известны некоторые математические формулы.
Приведем несколько примеров.
Правило нахождения периметра треугольника: РАВС = a + b + c— формула.
Правило нахождения периметра прямоугольника: Р = 2(a + b)— формула.
Правило деления с остатком: a = b ∙ c + r, r b— формула.
Любая буквенная запись арифметических операций и их свойств является формулой.
Формулам находят различное применение:
- С помощью формул можно описать различные процессы, происходящие в природе.
Формула подобно универсальной заготовке позволяет описывать различные процессы, действия, состояния, явления и т.д.
- Формула может являться некоторым логическим утверждением- тождеством.
С помощью формулы-тождества довольно сложные выражения можно преобразовывать и записывать в удобном, компактном виде, т.е. такие формулы-тождества позволяют упрощать вычисления, решать различного рода задачи.
- Из формулы по известным нам математическим правилам и законам можно выразить одну величину через другие.
Порой решение задач подразумевает определение одной величины при знании остальных величин, которые входят в данную формулу, для этого применяют некоторые математические правила и свойства.
Таким образом, формулу можно упрощать и работать с ней, как с уравнением.
Например, пусть х неизвестная величина, а и b— известные величины, тогда можно выразить:

- Совершая различные математические преобразования, из первоначальной формулы методом подстановки можно вывести вторичную.
Происходит это так: некоторая неизвестная величина выражается из одной формулы и подставляется в другую (однако необходимо, чтобы выбранные формулы были совместимы, т.е. соответствовали одному явлению, процессу и т.д.).
Если сразу вывести величину затруднительно, то можно выражать ее по действиям.
Формула является результатом многолетней работы огромного количества ученых.
Современному человеку необходимо лишь отыскать во всем множестве известных формул ту, которая подойдет в конкретной ситуации.
Пройти тест и получить оценку можно после входа или регистрации
Решение задач с помощью формул
Нам часто приходится сталкиваться с решением различных задач.

Решить задачу — это значит через логически верную последовательность математических положений, действий и операций с объектами, величинами, числами выполнить требования задачи, т.е. найти верный ответ.
Существуют различные способы и методы решения задач.
Рассмотрим один из них: решение задач с помощью формул.
Процесс решения задач данным способом можно разделить на несколько основных этапов.
Данная последовательность действий не даст ответа на конкретную задачу, но сделает решение ее более понятным и быстрым и позволит решить даже самые непростые задачи.
Рассмотрим общие правила решения задач с помощью формул.
1. Внимательно прочитать, осмыслить и изучить условие задачи.
Следует установить то, что необходимо найти и что известно.
В задачах в основном содержится только существенная информация, т.е. те данные, которые могут быть использованы при их решении.
2. Для лучшего понимания задачи можно ее условия изобразить графически при помощи рисунка, схемы, чертежа и т.д.
С помощью иллюстрации легче понимать и воспринимать информацию.
3. Определить характерные черты задачи.
Следует понять, какого рода задача, чтобы выбрать верный путь ее решения.
Необходимо определить, какими величинами можно описать происходящие процессы, явления, действия, а также важно выяснить, из какой темы будут взяты формулы (если задача сложная, то могут понадобиться несколько формул).
4. Составить план решения задачи.
5. Выразить неизвестную величину через известные величины, т.е. вывести расчетную формулу.
6. Подставить известные числовые значения и произвести вычисления.
7. Оценить размерность (соответствие единиц измерения) величины, полученной в ответе, проверить найденный ответ на наличие вычислительных ошибок.
8. Записать ответ.
Чтобы верно и быстро решить задачу, важно не только действовать четко по определенному алгоритму, но и грамотно записывать и оформлять решение этой задачи.
Задачи, решаемые с помощью формул, удобно делить на два блока: «Дано» и «Решение».
В «Дано» обычно с помощью букв или символов записывают заданные величины и величины, которые требуется определить; т.е. кратко обозначают условие задачи.
Можно использовать любые буквы для обозначения заданных и искомых величин, но тогда необходимо делать краткое описание того, какую величину обозначает та или иная буква, выбранная вами.
Однако чаще всего буквенные обозначения величин, если они не указаны в условиях задачи, выбираются в соответствии с принятыми в науке символами.
Многие величины уже имеют специальные обозначения.
Например, периметр принято обозначать буквой Р, длину и ширину буквами a и b, пройденный путь — S, скорость буквой V, время — t и т.д.
Каждая величина имеет единицу измерения.
Сразу в «Дано» переводят единицы измерения в единую систему, так как одна и та же величина должна быть выражена единой единицей измерения.
Иногда в задачах одноименные величины могут быть выражены разными числовыми мерами.
Например, расстояние может быть выражено в одной и той же задаче километрами, метрами и сантиметрами, или время может быть представлено в одном условии задачи в часах, в другом условии этой же задачи в минутах.
В таком случае необходимо выполнить перевод из разных единиц измерения в одну общую, которая будет фигурировать при числовых подсчетах.
У меня есть дополнительная информация к этой части урока!

Чаще всего выбор единиц измерения диктуется установленными международными нормами.
Наиболее широко используемой системой единиц в мире является единая интернациональная система. Называется она сокращенно «Система СИ».
Система СИ принята как основная система единиц в большинстве стран мира.
Страны, которые используют традиционные единицы, ввели коэффициенты и поправки, чтобы связать свои единицы измерения с системой СИ.
СИ создана на основе метрической системы, которая была создана французскими учеными. (с метрической системой мы немного познакомились, рассматривая тему «Отрезок. Длина отрезка.»).
Система СИ определяет семь основных единиц и производные единицы, а также набор приставок.
Системой СИ установлены стандартные сокращенные обозначения единиц.