Что такое задача механики

Что такое задача механики

Основная задача, которую решает классическая механика, может быть сформулирована так: в начальный момент известны положения и скорости всех точек, образующих некоторую систему; заданы силы, действующие на все материальные точки этой системы; требуется определить движение точек системы для всех .

Говоря, что «силы заданы», иногда имеют в виду, что они заданы как функции времени, т. е. что заранее известно, как меняются во времени производные для всех точек;

чаще, однако, при этом имеют в виду, что для каждой точки зависит также от положения всех материальных точек в рассматриваемой системе отсчета или от их скорости относительно нее; тогда слова «силы заданы» означают, что силы заранее известны как функции не только времени, но и координат и скоростей точек системы.

Как уже указывалось в предыдущих параграфах, сила — результат сложных физических процессов, обусловливающих взаимодействие материальных объектов. Механика не изучает физическую природу этих взаимодействий. Поэтому силы как функции положений и скоростей материальных точек или тел в каждой конкретной механической задаче считаются известными — их определяют в иных дисциплинах.

В тех случаях, когда физическая природа взаимодействий не изучена, сила как функция координат и скоростей точек может быть все же определена в результате творческих обобщений результатов экспериментальных наблюдений. В исследованиях такого рода могут быть использованы методы механики — типичным примером служит открытие Ньютоном закона всемирного тяготения, однако основная задача механики как науки начинается только после того, как такая предварительная и, вообще говоря, выходящая за рамки механики работа проделана и сила задана как функция времени, координат точек системы и их скоростей.

Рассмотрим систему, состоящую из N материальных точек, и выделим в ней точку. Все силы, действующие на эту точку в результате внутренних и внешних взаимодействий, можно заменить одной силой — их равнодействующей (см. § 4); в силу сказанного выше известна как функция t, координат всех точек системы и их скоростей:

Тогда в соответствии со вторым законом Ньютона в некоторой инерциальной системе отсчета имеют место N равенств

где — радиус-вектор, пров ценный из начала координат к точке.

Проектируя эти равенства на оси координат, получаем

где — проекции указанных выше равнодействующих на оси х, у, z соответственно. Уравнения (28) образуют систему дифференциальных уравнений порядка , так как каждая точка вносит в эту систему три уравнения второго порядка. Эти дифференциальные уравнения называют иногда основными уравнениями динамики системы материальных точек.

Если известны положения и скорости всех точек системы в начальный момент

то решение основной задачи механики сводится к интегрированию основных уравнений динамики (28) при заданной системе начальных данных (29).

В тех случаях, когда речь идет о численном решении задачи, она, разумеется, может быть приближенно доведена до конца, например обычными методами приближенного интегрирования дифференциальных уравнений. Если же, однако, речь идет о нахождении общего решения, т. е. об умении записать решение дифференциальных уравнений (28) в замкнутой форме, то задачу такого рода можно решить лишь для отдельных частных случаев функциональных зависимостей, выражающих силы. Теория дифференциальных уравнений гарантирует лишь то, что это решение существует и является единственным (при нестеснительных для механики ограничениях, наложенных на функции, выражающие силы) и что движение полностью определяется заданными начальными данными (29).

Поэтому все дальнейшее построение механики, ее цели и методы связаны с обходом или преодолением затруднений, обусловленных тем, что основные дифференциальные уравнения динамики систем не могут быть проинтегрированы в общем виде. Методы, которые используются в механике, чтобы преодолеть указанные трудности, могут быть кратко описаны так.

1° Механика тщательно собирает и изучает все те случаи, когда функциональные зависимости, выражающие силы, таковы, что дифференциальные уравнения (28) могут быть сведены к квадратурам и поэтому движения могут быть непосредственно изучены. Так, например, обстоит дело в таком важном случае, как движение материальной точки в поле тяготения какого-либо иного материального объекта. Однако уже в так называемой задаче трех тел, когда рассматривается система из трех материальных точек, движущихся под действием взаимного тяготения, дифференциальные уравнения вида (28) не решаются в общем виде и исследование движения становится значительно сложнее.

2° В тех случаях, когда нельзя найти решение системы дифференциальных уравнений (28) в замкнутой форме, разрабатываются методы, позволяющие значительно упростить эти уравнения для последующего исследования, в частности понизить их порядок. Так, например, при изучении движения абсолютно твердого материального тела, состоящего из бесконечного количества точек, заполняющих некоторый объем, система дифференциальных уравнений вида (28) должна была бы состоять из бесконечного числа уравнений. Однако в механике установлены приемы, позволяющие полностью описать движение всех точек твердого тела с помощью только шести дифференциальных уравнений не выше второго порядка каждое.

3° В тех случаях, когда интегралы уравнений (28) не могут быть найдены даже при предельном упрощении этих уравнений методами механики, изучаются общие свойства решений этих уравнений без их непосредственного нахождения. Так, например, для случая, когда движение происходит в потенциальных полях, механика определяет многие общие свойства движений без того, чтобы доводить до конца задачу об определении самих движений.

4° Наконец, — и, по-видимому, этот прием является наиболее важным и чаще всего употребляемым — вводятся специально выбранные функции от координат точек и их скоростей и изучается зависимость этих функций от времени. В качестве таких функций используются, в частности, введенные выше меры движения — кинетическая энергия Т и количество движения Q системы. Во многих случаях оказывается, что для описания изменения этих функций во времени можно составить дифференциальные уравнения значительно более простые, чем основные дифференциальные уравнения динамики, так что изменение этих функций во времени исследуется гораздо проще. Так, например, можно установить условия, когда количество движения системы Q заведомо не меняется во время движения. В этом случае можно сразу выписать три равенства типа «заданная функция от координат и скоростей точек равна постоянной». Каждый раз, когда удается найти функции от координат точек и их скоростей, которые не изменяются во время движения системы, эти функции называются первыми интегралами дифференциальных уравнений движения.

В механике указываются приемы нахождения таких первых интегралов, которые не только позволяют упростить уравнения движения, но и зачастую дают возможность довести решение задачи до конца. В качестве примера можно указать рассматриваемую ниже задачу о движении материальной точки в поле центральной силы.

Эти четыре основных приема используются механикой для вывода ее обших законов и для изучения некоторых часто встречающихся типов движения или важных классов динамических систем. Предполагается, что не только выполнены все исходные постулаты, о которых шла речь в § 2 этой главы, но что выполняются следующие дополнительные условия.

1° Рассмотрение ведется в инерциальной системе отсчета.

2° Рассматривается движение постоянной по составу системы материальных объектов, т. е. считается, что на протяжении всего движения система состоит из одних и тех же материальных объектов.

3° В пространстве «нет преград», т. е. ничто не препятствует ни одному из рассматриваемых материальных объектов (точек или тел) находиться в любом месте в любой момент времени.

Эти три условия выполняются далеко не всегда, и механика изучает методы, с помощью которых законы, полученные для систем, удовлетворяющих этим условиям, могут быть использованы и в тех случаях, когда какое-либо из этих условий не выполняется. Как мы уже видели выше, предположение о том, что время не зависит от пространства и материи и что пространство является евклидовым, однородным и изотропным, сделало невозможным рассматривать причины такого важнейшего явления материального мира, как взаимодействие материи, и заставило в рамках этой простой модели искать для описания взаимодействия «обходные пути» —ввести понятие о дальнодействии. Тот же прием используется в механике, если условия 1° — 3° не выполнены: помимо сил, возникающих при выполнении условий 1° — 3°, в этих случаях вводятся дополнительные силы, которые подбираются так, чтобы скомпенсировать нарушение условий 1° — 3° и распространить законы механики на случай, когда не все эти условия выполняются. Так, например, поступают в механике для того, чтобы распространить ее законы на случай, когда изучается движение относительно неинерциальных систем отсчета. Аналогичным образом изучается движение системы, материальный состав которой меняется во время движения. Этот же прием используется иногда и для исследования движений в тех случаях, когда в пространстве существуют ограничения, наложенные на координаты и (или) скорости материальных точек или тел, и требуется учесть эти ограничения.

Таким образом, методы механики позволяют не только сформулировать ряд общих теорем и законов, действующих в условиях, когда выполняются предположения 1° — 3°, но и — за счет введения дополнительных сил — использовать эти законы в условиях, когда предположения 1° — 3° не выполняются.

В любом случае, однако, предполагаются выполненными исходные предположения, сформулированные в § 2. Отход от этих предположений невозможен в пределах классической механики и приводит к построению иных систем механики. Такая ситуация возникает, например, при отказе от описанных выше представлений о пространстве и времени и от принципа относительности Галилея. Именно отказ от этих исходных представлений о времени и пространстве и предположение о том, что уравнения и законы механики должны быть инвариантны (или ковариантны) по отношению не к преобразованиям Галилея, а к иным преобразованиям — преобразованиям Лоренца, привели к появлению релятивистской механики. С этими исходными представлениями связаны ограничения, в пределах которых законы классической механики могут применяться при изучении движения объектов реального мира.

Кинематика — основные определения и формулы

Все очень просто. В этом разделе мы «дадим имена самым важным вещам».

Тебе в детстве сказали, что вот это стул и на нем сидят, а вот это стол, на нем едят? Сказали. И после этого ты сидишь на стуле, а ешь за столом. Ну чаще всего 🙂

Так и здесь. Все, о чем мы будем говорить на этом уроке, нужно, чтобы мы говорили на одном языке.

И чтобы на экзамене ты не перепутал, например, траекторию, путь и перемещение.

Кинематика — основные определения и формулы

• Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
• Основная задача механики — указать положение тела в пространстве в любой момент времени, не только в настоящем, но и в будущем.
• Кинематика — это раздел механики, который изучает движение тела, не рассматривая причину этого движения.
• Движение — изменение положения тела в пространстве с течением времени.
• Тело отсчета – тело, относительно которого рассматривается движение.
• Такое движение, при котором все точки тела движутся одинаково, называется поступательным движением.
• Поступательное движение — это движение, при котором любая прямая, соединяющая две любых точки тела, остается параллельна своему начальному положению в любой момент времени.
• Вращательное движение — это такое движение тела, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
• Даже самое сложное движение можно описать комбинацией поступательного и вращательного!
• Материальная точка — тело, размерами которого В ДАННОЙ ЗАДАЧЕ можно пренебречь.
• Координаты — это числа, с помощью которых задается положение материальной точки в пространстве.
• Система координат – способ определения положения тела в пространстве с помощью чисел.
• Система отсчёта — это совокупность неподвижных относительно друг друга тел (тело отсчёта) в связанной с ними системе координат, и отсчитывающих время часов (прибор), по отношению к которой рассматривается движение каких-либо тел.
• Перемещение — вектор, проведенный из начального положения тела в конечное.
• Траектория — линия, по которой движется тело.
• Путь — длина траектории.

Основные определения кинематики

Что ты вспоминаешь при слове «движение»?

Слова учителя физкультуры: «Движение – это жизнь, ребята»? Движение за права человека? Или ту задачку по математике, где пришлось складывать скорости?

Все это означает какие-то изменения. Экологическое движение меняет мир, очищая его. Спорт меняет наше тело. А мы в свою очередь можем изменить свое положение в пространстве, сходив погулять.

Все это и есть движение. Но это понятие очень широкое. Давайте сузим его и определим, а что такое механическое движение?

Что такое механическое движение?

Мы говорили, что движение – это всегда какое-то изменение. Но что меняется при механическом движении?

Ты можешь сказать: «Меняется положение тела». Хорошо, это действительно так.

Но давай представим, что мы сидим в купе поезда, который мчится из Москвы во Владивосток.

Движемся мы или нет? А движется ли поезд?

Кажется, очень легко дать ответы на эти вопросы, потому что и мы вместе с поездом движемся. Но если ты посмотришь на соседей по купе, а они посмотрят на тебя, то никаких изменений (никакого движения) вы не увидите.

Дело в том, что все зависит от точки отсчета.

Так, например, если за точку отсчета взять поезд, то ни мы ни наши соседи по купе относительно поезда двигаться не будем. И поезд не будет двигаться относительно нас.

А вот люди, стоящие на перроне, относительно поезда движутся. И поезд движется относительно них.

Значит для того, чтобы сказать движется тело или нет, нам нужно определить точку отсчета.

Точка отсчета – тело, относительно которого мы рассматриваем движение.

Что еще нам нужно?

Любое движение происходит с течением времени. Если бы не было времени, ничего бы не менялось и не было бы никакого движения.

Значит для того, чтобы было механическое движение, нам нужно чтобы изменялось время.

Механическое движение – это изменение положения тела в пространстве относительно других тел с течением времени.

В чем состоит основная задача механики?

Ты абсолютно прав, движение бывает очень разным!

Основная задача механики – указать положение тела в пространстве в любой момент времени, не только в настоящем, но и в будущем.

То есть уметь предсказывать его!

Если мы хотим знать почему тело движется, мы обращаемся к разделу механики, который называется динамикой. Но пока, чтобы не усложнять все сразу, мы не будем интересоваться причинами движения тела…

Если нам не интересна причина движения тела, мы обращаемся к разделу механики, который называется кинематикой.

Что такое кинематика?

Кинематика – это раздел механики, который изучает движение тела, не рассматривая причину этого движения.

Она просто описывает движение тела, но не объясняет его.

Движение – изменение положения тела в пространстве с течением времени.

Но тело состоит из множества точек. Неужели придется описывать движение каждой из них? Будет, наверное, трудно…

Вовсе нет! Есть два способа облегчить себе эту задачу.

Первый способ. Если все точки тела движутся одинаково, почему бы не рассмотреть движение лишь одной из них?

Такое движение, при котором все точки тела движутся одинаково, называется поступательным движением.

Что такое поступательное движение?

Соединим прямой любые две точки тела. Когда тело движется поступательно, эта прямая будет параллельна каждому своему положению в любой момент времени. Наверное, это трудно представить, но вот тебе рисунок:

Видишь, прямая a параллельна прямой b, и они обе параллельны прямой c.

Записывается это так: (aparallel bparallel c)

И, соответственно, еще одно определение поступательного движения:

Поступательное движение – то, при котором любая прямая, соединяющая две любых точки тела, остается параллельна своему начальному положению в любой момент времени.

Слово «любая» здесь важно. Потому что если в теле найдется хотя бы одна прямая, соединяющая две любых его точки, которая не будет параллельна самой себе при движении, то такое движение не будет считаться поступательным.

Хорошо, с поступательным движением разобрались. А есть ли еще какое-нибудь движение? Что если наш треугольник, перевернуть, сделать из него юлу и раскрутить ее? Будет ли в этом случае тело двигаться поступательно?

Нет. Потому что, например, грань юлы не будет параллельна самой себе во время движения. Тогда какое это движение?

Это вращательное движение.

Что такое вращательное движение?

Что общего у колеса и нашей планеты? Точки этих тел вращаются вокруг прямой по разным окружностям.

И эта прямая называется осью вращения. А такое движение называется вращательным.

Вращательное движение – это такое движение тела, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

И, кстати, ось вращения не обязательно должна проходить через центр тела. Например, когда вы крутите ключи от машины вокруг пальца, ось вращения проходит через кольцо, на котором висят ключи, а не через центр ключей.

И вот что интересно…

Даже самое сложное движение можно описать комбинацией поступательного и вращательного!

Вернемся к тому моменту, когда мы сидели в купе движущегося поезда. Представь, что в твоих руках чашка с чаем и ты размешиваешь в нем кубик сахара. Он будет вращаться вокруг своей оси (вращательное движение) и при этом двигаться вместе с поездом относительно деревьев за окнами (поступательное движение).

Что такое материальная точка и зачем она нужна?

Земля, вращаясь вокруг Солнца, к тому же вращается вокруг своей оси. И все их точки движутся по-разному. Что в этом случае делать? Чтобы ответить на этот вопрос, нужно понять, действительно ли нам это важно.

Если по реке плывут лодка с парусами и яхта, будем ли мы описывать движение всех их точек?

Нам не важны их размеры и формы и движение всех точек этих тел. Но нам важно, например, время, за которое они преодолеют определенное расстояние.

Парусник и яхта – тела, размерами которых в данной задаче можно пренебречь.

Такие тела называются материальными точками.

Следует помнить, что пренебречь их размерами и формой можно не всегда. Так, например, если в задаче необходимо выяснить, смогут ли они пройти через узкое место в реке, их размеры имеют огромное значение!

Решая задачи по кинематике, будем считать тела материальными точками, если условия задачи не требуют другого.

Материальной точкой называется тело, размерами которого В ДАННОЙ ЗАДАЧЕ можно пренебречь.

С этого момента для того чтобы решить основную задачу механики, определить тело в пространстве в любой момент времени мы будем оперировать не всем телом, а ТОЧКОЙ!

Если задача не требует другого – важная оговорка!

Мы можем рассмотреть движение точки в любой момент времени, спрогнозировать положение в будущем и так далее.

Но что для этого необходимо?

Прежде всего понять, что положение тела можно задать числами. И вы наверняка знаете, как они называются…

Координаты тела и положение тела на прямой, плоскости и в пространстве

Как думаете, что связывает дороги, шахматы и спрятанные сокровища?

Координаты.

Координаты — это числа, с помощью которых задается положение материальной точки в пространстве.

Сколько чисел нам нужно, чтобы задать координаты материальной точки? Одно? Два? Три? Давайте разберемся.

Допустим мы заблудились в лесу, долго блуждали и в конце концов вышли на дорогу, где стоит столбик с цифрой «25». Как мы вызовем помощь? Мы позвоним и скажем: «Я нахожусь на 25 километре такого-то шоссе!»

Шоссе – это прямая (ну почти). Значит, чтобы задать координаты на прямой нам достаточно одного числа.

А сколько чисел нам нужно чтобы понять где находится шахматная фигура?

Позиция фигуры в шахматах задается двумя числами, например, Е6 («Е» можно заменить числом). Так мы определяем координаты на плоскости.

На уроке географии, когда мы только начинаем учиться работать с картой, мы определяем координаты географических объектов и нам тоже требуются два числа: широта и долгота.

А вот если мы захотим найти клад, нам потребуются три числа, одно из которых – глубина. Нам важно, насколько глубоко копать.

Так мы определяем положение тела в трехмерном пространстве. Мы с вами живем в таком трехмерном пространстве. У нас трехмерная система координат.

Система координат – это способ определять положение тела в пространстве с помощью чисел.

Давай подытожим. Вырисовывается некоторая система, которая позволяет нам определить положение тела.

Система отсчета или три вещи, необходимые для определения движения

Время

Можем ли мы двигаться вне времени? Движение вне времени невозможно. И значит, его нужно его как-то измерить. У нас должны быть часы или что-то в этом роде для измерения времени.

Тело отсчета

Можем ли мы двигаться сами по себе? Нет. Мы всегда движемся относительно чего-то. И, соответственно, нам нужно что-то, относительно чего мы начнем отсчет движения.

И это что-то называется телом отсчета.

Система координат

Когда мы решаем задачу по механике мы должны определиться в какой системе координат мы будем определять положение точки с помощью чисел.

Система отчета

Таким образом, для определения движения нам нужны три вещи:

• прибор для измерения времени;
• тело отсчета;
• система координат.

В совокупности они образуют систему отсчета.

Система отсчёта — это совокупность неподвижных относительно друг друга тел (тело отсчёта) в связанной с ними системе координат, и отсчитывающих время часов (прибор), по отношению к которой рассматривается движение каких-либо тел.

Для одной и той же ситуации можно выбрать множество разных систем отсчета. В зависимости от этого мы либо упрощаем, либо усложняем себе задачу.

Во времена Коперника люди считали, что Солнце движется вокруг Земли. Ведь Земля относительно нас неподвижна, верно? А солнце восходит и заходит. Поэтому нам кажется, что солнце движется вокруг нас.

Но Коперник немного подумал (ну как немного :)) и поменял систему отсчета! Гипотеза Коперника о том, что это мы вращаемся вокруг Солнца, объяснила множество вещей.

Перемещение. Траектория. Путь.

Перейдем еще ближе к задачам. Пусть некоторая материальная точка двигалась из пункта А в пункт В.

Давай нарисуем это. А чтобы было понятно куда двигалась эта материальная точка, давай обозначим направление движения стрелкой!

Но что есть стрелка?

Это ведь направленный отрезок, то есть вектор. Иными словами, движение – это всегда вектор! Об этом нужно всегда помнить. Нам все время нужно указывать, куда направлено движение.

Этот вектор связывает начальное и конечное положение точки и называется перемещением тела. На рисунке перемещение обозначено как (vec).

Перемещением называется вектор, проведенный из начального положения тела в конечное.

Как много идеально прямых дорог между городами ты видел в своей жизни? Могу поспорить, что ни одной. Если тело оказалось из пункта А в пункте В, оно вовсе не обязательно двигалось по прямой. Тело могло двигаться по кривой или ломаной линии.

Линия, по которой движется тело – это траектория.

А длина траектории – это путь.

• Вектор AB (vec) (черная стрелка на рисунке) — это перемещение тела. Чаще всего обозначается как (vec);
• Кривая AB (красная линия на рисунке) – это траектория тела;
• Длина траектории (длина кривой AB) — это путь. Путь часто обозначают буквой (L).

Перемещение – это всегда вектор, а путь – это всегда число! Запомните это.

Путь всегда больше или равен модулю вектора перемещения:

Почему мы говорим «модулю вектора перемещения», а не просто «вектору перемещения»? Потому что мы не можем сравнивать белое и горячее. Мы не можем сравнить вектор (перемещение) с числом (путь).

Но мы можем сравнить число с числом. Для этого мы «делаем» из вектора число, заключив его под знак модуля. Это число есть длина вектора. А длина вектора — его модуль.

Подробнее об этом вы сможете узнать в Большой теории по векторам .

Самый короткий путь совпадает с перемещением, то есть это прямая. В этом случае они равны.

А может ли перемещение быть равно нулю?

Попробуем это представить…

Но это вовсе не значит, что мы будем бежать на месте!

Мы можем выбежать на улицу, пробежать через парк, но как только вернемся домой, наше перемещение станет равным нулю, ведь мы оказались в том же месте, откуда и начинали движение. Путь, однако, нулю не равен.

Таким образом, мы разобрали основные понятия кинематики. Успешное решение задач напрямую зависит от понимания того, с чем мы работаем и что пытаемся найти. Поэтому давайте еще раз выпишем все определения.

Что такое механика? Предмет, задачи, разделы

Окружающих мир состоит из материальных объектов, которые взаимодействуют между собой различными способами. Задачей естественных наук, в частности физики, является установление характера этих взаимодействий. Один из прикладных разделов физики называется механика. В статье речь пойдет о том, что такое механика, каков предмет и задачи данной науки, какие существуют отрасли механики.

Механика — это.

Слово «механика» переводится с греческого как «искусство построения машин». Механика — это наука о движении объектов материального мира и их взаимодействии. Иными словами, любое материальное тело занимает какое-либо место в пространстве. Его перемещение называется механическим движением. Это движение, а также то, как тела при нем взаимодействуют друг с другом, и изучает механика.

Спектр исследований этой науки очень широк. Он включает изучение движения небесных тел, перемещения летательных аппаратов, машин, динамики жидкостей и газов.

Предмет и задачи

Понять, что такое механика, поможет изучение ее предмета и задач.

Главной задачей является описание механического перемещения объектов — выведение уравнения движения. Это делается с помощью системы координат, угла поворота, скорости и других категорий. Иначе говоря, выведенный закон движения позволяет высчитать положение тела в момент времени.

Предмет механики — это решение задач и вопросов, связанных с исследованием движения или равновесия тел и их взаимодействий при этом.

Разделы механики

Поскольку исследования механики касаются многих сфер науки, в ней выделяют несколько разделов:

• классическая (механика Ньютона) — изучает движения материальных дел;
• релятивистская (механика Эйнштейна) — базируется на постулатах теории относительности;
• квантовая — исследует движение элементарных частиц.

Классическая механика

Механика Ньютона включает следующие направления: кинематику, динамику и статику.

Кинематика исследует механическое движение тел без учета причин, его вызывающих. Иначе говоря, этот раздел исследует положение тела в пространстве по истечении определенного времени. В основном, законы и исследования кинематики применяются в расчетах движений механизмов и машин.

В области исследования динамической механики находится перемещение материальных объектов в результате воздействия, примененного к ним. Иными словами, эта наука объясняет, почему тело, к которому приложили силу, оказалось в той или иной точке пространства.

Статическая механика изучает равновесие тел под воздействием, приложенным к ним. Она делится на равновесную и неравновесную.

Разделы классической механики изучаются обычно в средней школе. Кроме них, существует еще несколько направлений этой науки:

• механика сплошных сред;
• статистическая;
• теоретическая;
• вычислительная и др.

Механика релятивистская

Что такое механика Эйнштейна? Если тела движутся с очень высокой скоростью, например, близкой к скорости света, то физические законы для них становятся иными. Время и пространство изменяют свои свойства по отношению к таким телам. Вопросы этих искажений и изучает релятивистская механика.

Слово «релятивистский» означает «относительный». Поэтому постулаты эйнштейновский теории относительности играют здесь важную роль.

В классической механике существует три измерения: длина, ширина и высота. Релятивистская добавляет еще одно измерение — время. Таким образом, пространство считается четырехмерным, и перемещение тел и их характеристики будут зависеть не только от направления движения, но и от скорости.

Эйнштейн считал, что для движущихся наблюдателей время течет медленнее, чем для находящихся в состоянии покоя. Чем выше скорость — тем медленнее время. При достижении скорости света время совсем остановилось бы.

Квантовая механика

Эта наука является составляющей квантовой физики. Обе они исследуют законы мира элементарных частиц — нуклонов, электронов, кварков и т. д.

Классическая механика, описывающая явления макромира, не способна объяснить движения, происходящие на уровне элементарных частиц. Эти задачи взяла на себя квантовая механика. Эта наука является достаточно молодой, и в ее области еще много неисследованного.

Слово «квант» означает любую неделимую единицу чего-либо.

• фотон — частица электромагнитного излучения;
• глюон — частица векторного поля;
• гравитон — квант гравитационного взаимодействия;
• фонон — квант колебаний кристаллов.

Итак, что такое механика? Данный раздел физики изучает материальные тела, их перемещения в пространстве, законы перемещений и взаимодействие движущихся тел между собой. Самые обширные ее разделы это классическая, релятивистская и квантовая.

Механика

Механика является одним из разделов физики. Под механикой обычно понимают классическую механику. Механика – наука, изучающая движение тел и происходящие при этом взаимодействия между ними.

В частности, каждое тело в любой момент времени занимает определенное положение в пространстве относительно других тел. Если со временем тело меняет положение в пространстве, то говорят, что тело движется, совершает механическое движение.

Механическим движением называется изменение взаимного положения тел в пространстве с течением времени.

Основная задача механики – определение положения тела в любой момент времени. Для этого нужно уметь кратко и точно указать, как движется тело, как при том или ином движении изменяется его положение с течением времени. Другими словами – найти математическое описание движения, т. е. установить сязи между величинами, характеризую­щими механическое движение.

При изучении движения материальных тел используют такие понятия, как:

– тело, размерами которого в данных условиях движения можно пренебречь. Это понятие используется при поступательном движении, или когда в изучаемом движении можно пренебречь вращением тела вокруг его центра масс,
• абсолютно твердое тело – тело, расстояние между двумя любыми точками которого не меняется. Понятие применяется, когда можно пренебречь деформацией тела.
• сплошная изменимая среда – понятие применимо, когда можно пренебречь молекулярной структурой тела. Используется при изучении движения жидкостей, газов, деформируемых твердых тел.

Классическая механика основана на принципе относительности Галилея и законах Ньютона. Поэтому, ее еще называют – механикой Ньютона.

Механика изучает движение материальных тел, взаимодействия между материальными телами, общие законы изменения положений тел со временем, а также причины вызывающие эти изменения.

Общие законы механики подразумевают, что они справедливы при изучении движения и взаимодействия любых материальных тел (кроме элементарных частиц) от микроскопических размеров до объектов астрономических.

Механика включает в себя следующие разделы:

(изучает геометрическое свойство движения тел без причин, вызвавших это движение), (изучает движение тел с учетом причин вызвавших это движение), (изучает равновесие тел под действием сил).

Следует отметить, что это не все разделы, которые входят в механику, но это основные разделы, которые изучает школьная программа. Кроме разделов указанных выше существует еще ряд разделов как имеющих самостоятельное значение, так и тесно связанных между собой и с указанными разделами.

• механика сплошных сред (включает в себя гидродинамику, аэродинамику, газовую динамику, теорию упругости, теорию пластичности);
• квантовая механика;
• механика машин и механизмов;
• теория колебаний;
• механика переменной масс;
• теория удара;
• и др.

Появление дополнительных разделов связано как с выходом за границы применимости классической механики (квантовая механика), так и с детальным изучением явлений происходящих при взаимодействии тел (например, теория упругости, теория удара).

Но, несмотря на это, классическая механика не теряет своего значения. Она является достаточной для описания в широком диапазоне наблюдаемых явлений без необходимости обращаться к специальным теориям. С другой стороны она проста для понимания и создает базу для других теорий.

Механика имеет большое значение для многих разделов астрономии, особенно для небесной механики (где изучаются движения планет, звезд и т. д.).

Особое значение механика имеет для техники. В гидродинамике, аэродинамике, динамике машин и механизмов, теории движения наземных, воздушных и транспортных средст используют уравнения и методы теоретической механики.

Основные формулы механики в физике с пояснениями

Физика — одна из самых важных наук на Земле, которая описывает практически все известные человеку процессы и явления. В данной статье мы подробнее остановимся на ее большом разделе, который называется «механикой».

Что изучает механика в физике

Механика — это одна из физических наук, которая изучает движение тел и их взаимодействие друг с другом во время движения. Этот раздел физики описывает движение как искусственно созданных летательных аппаратов, так и физических небесных объектов; атмосферные и подводные течения; движение жидкостей и газов в природе; перемещение среды в электромагнитных полях; движение крови по сосудам и т.д.

Движение в механике — это изменение во времени и пространстве положения тел (или их частей) относительно друг друга.

Науку механику в зависимости от свойств пространства, времени и материи, на которых основывается каждая механическая теория, подразделяют на следующие виды:

• классическую (раздел физической науки, основанный на открытиях Ньютона и Галилея);
• релятивистскую (раздел физической науки, который описывает процессы механического движения, происходящие при скоростях, сопоставимых со скоростью света);
• квантовую (наука о физических явлениях и процессах, действия которых можно сравнить с постоянной Планка).

Основные направления, формулы и пояснения

В механике выделяют следующие основные разделы:

• кинематику (науку, которая описывает количественные характеристики движения: время, расстояние, скорость);
• статику (науку о телах, находящихся в равновесии при воздействии на них внешних сил);
• динамику (науку о движении тел при воздействии на них внешних сил).

Механика изучает движения материальных тел, при этом все материальные объекты делятся на 3 вида:

1. Материальная точка (это материальное тело, чьи размеры можно не учитывать).
2. Твердое тело (тело, в котором расстояние между любыми его точками неизменно).
3. Сплошная среда (газ, жидкость и другие вещества, подверженные деформации).

По предмету изучения механику подразделяют на:

• теоретическую (наука об общих законах движения, которая изучает и описывает движение материальных точек и твердых тел);
• механику сплошных сред (наука, которая изучает движение тел, непрерывно заполняющих пространство и представляющих собой сплошную среду);
• прикладную (наука, которая описывает принцип работы технических механизмов).

Рассмотрим детальнее основные разделы механики. И начнем с кинематики.

Кинематика

Раздел кинематики отвечает на вопросы о том, как именно происходит механическое движение тела.

Механическое движение

Механическое движение — это перемещение тела с течением времени и относительно других объектов в пространстве.

Для расчета этих изменений понадобится система отсчета, которая состоит из:

• объекта, относительно которого будет происходить отсчет движения;
• системы координат, в которой находится объект отсчета;
• часов (для измерения времени).

В системе отсчета метр является единицей длины, а секунда — единицей времени.

Другими важными определениями в кинематике являются:

1. Материальная точка — это объект, размеры которого можно не учитывать в расчетах.
2. Траектория движения тела (линия, по которой движется объект).
3. Путь, пройденный телом (определенный участок траектории, пройденный объектом за определенное время).

Существует 2 вида движения согласно траектории:

• прямое;
• криволинейное.

Поступательное и вращательное движение твердого тела

В кинематике выделяют два вида движения:

• поступательное;
• вращательное.

Поступательное движение — это движение твердого тела, при котором все его точки проходят одну и ту же траекторию и в любой момент времени обладают одинаковыми по направлению и величине векторами скорости и ускорения, синхронно меняющихся для любой точки объекта.

Вращательное движение — это вид механического движения, при котором материальное тело проходит траекторию окружности. При этом все точки тела описывают окружности, которые находятся в параллельных плоскостях. Центры всех окружностей находятся на одной прямой, которая перпендикулярна к плоскостям окружностей (называется осью вращения).

Кинематические уравнения движения

Определение местоположения материальной точки в пространстве можно осуществить двумя способами:

• учитывая зависимость координат от времени;
• учитывая зависимость от времени радиус-вектора.

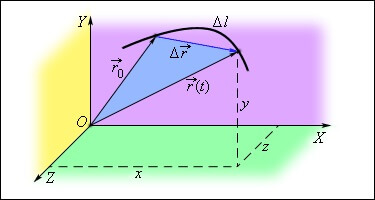
Эту зависимости можно представить в виде кинематических уравнений движения:

(vec r=vec rleft(tright))

Нулевой вектор на данной иллюстрации — это радиус-вектор положения точки в начальный момент времени.

Кинематические характеристики (скорость, ускорение)

Основными кинематическими характеристиками являются:

Скорость ((vec v)) — это векторная величина, которая характеризует направление и быстроту движения.

Среднюю скорость можно вычислить по формуле:

где (Deltavec r ) — перемещение, (Delta t) — время, за которое это перемещение произошло.

Символом (∆) обозначается разность однотипных величин или совсем маленьких интервалов.

Мгновенная скорость может быть вычислена тогда, когда (Delta trightarrow0) и вектор перемещения совпадает с путем перемещения:

Ускорение тела (a) является величиной, равной отношению изменения скорости движения тела к длительности промежутка времени, за которое это изменение скорости произошло. Оно рассчитывается по формуле:

Мгновенным ускорение будет являться тогда, когда среднее ускорение за промежуток ∆t → 0, м/с²:

Динамика, законы Ньютона

Динамика — это раздел механики, который изучает причины изменения движения тел. Классическая механика видит причины этих изменений в воздействии на объекты различных сил. Расскажем подробно, какими параметрами и характеристиками оперирует раздел динамики.

Динамические характеристики поступательного движения

Основными характеристиками в динамике являются:

1. Сила ( (vec F) ) — это векторная величина, которая характеризует воздействие тел друг на друга, из-за чего с ними происходят определенные изменения: они приобретают ускорение или подлежат деформации. Сила, как любой вектор, имеет модуль, направление и точку приложения.
2. Масса ( (m) ) — это физическая величина, характеризующая гравитационные и инерционные свойства объекта.
3. Импульс ( (vec p) ) — это векторная величина, которая рассчитывается по формуле: (vec p=mtimesvec v)

где (m) — масса тела, а (vec v) — его скорость.

Импульс иллюстрирует, как механическое движение может передаваться от одного материального тела к другому.

• Импульс силы ( (vec Fdt) ) — векторная величина, которая по направлению совпадает с направлением силы и численно равняется произведению силы и времени ее воздействия на тело.

Виды сил

В динамике выделяют несколько видов сил, которые могут воздействовать на объект:

1. сила притяжения;
2. сила упругости;
3. силы трения.

Закон всемирного тяготения, открытый Ньютоном, гласит, что сила ( (F) ) гравитационного притяжения между двумя телами массами ((m_1 и m_2)) , которые находятся на расстоянии ( (r) ) друг от друга, пропорциональна обеим массам, обратно пропорциональна расстоянию в квадрате и действует вдоль прямой линии, соединяющей тела.

Сила притяжения определяется по формуле:

где (G) — гравитационная постоянная, которая равна (6,67times10^ Н*м²/кг²)

Сила упругости — это сила, возникающая при упругой деформации тела.

Рассчитывается она по формуле:

где (x) — величина деформации, (k) — коэффициент упругости, а знак — говорит о том, что направление силы упругости всегда противоположно тому направлению, куда смещается тело.

Силы трения возникают при движении касающихся друг друга объектов или их частей. Они бывают:

• сухого трения (сила скольжения, сила покоя);
• вязкого трения (характерно для перемещающихся слоев жидкости или газа).

Сила сухого трения определяется по формуле:

где (N) — сила нормального давления, а (k) — коэффициент сухого трения.

Сила вязкого трения зависит от скорости движения тела ( (v) ) и рассчитывается по формуле:

(α) — коэффициент вязкого трения.

Разобрав основные динамические характеристики, можем переходить к основам динамики — законам Исаака Ньютона.

Первый закон Ньютона

Законы Ньютона, опубликованные им в 1687 году, лежат в основе механики. Они помогают описать движение тел с небольшими скоростями по сравнению со скоростью света.

Первый закон Ньютона предполагает существование таких систем отсчета, в которых материальные тела находятся в покое или движутся равномерно и по прямой, при условии, что на них нет воздействия каких-либо сил или действие этих сил скомпенсировано. Такие системы принято называть инерциальными. Все остальные законы Ньютона действительны именно для таких систем.

Первый закон Ньютона также часто называют законом инерции.

Инерция — это сохранение материальным объектом скорости и направления своего движения, при условии, что на него нет воздействия других тел и сил.

Второй закон Ньютона

Второй закон Ньютона иллюстрирует зависимость ускорения тела от его массы и силы, воздействующей на него. Причем чем больше сила, которая действует на объект, тем больше ускорение, которое тело приобретает.

Формулируется он в виде следующей формулы:

где (vec F) — это векторная сила, воздействующая на объект;

(vec a) — векторное ускорение тела;

Читается так: ускорение, с которым движется объект, прямо пропорционально действующей на тело силе и обратно пропорционально массе тела.

Третий закон Ньютона

Третий закон великого английского ученого предполагает, что при воздействии одного тела на другое с определенной силой, второе тело действует на первое с такой же силой. Их часто называют силами действия и противодействия.

Математически закон выражается так:

где (vec F_1) — это сила действия, а (vec F_2) — сила противодействия.

Формулируется так: объекты действуют друг на друга с силами, противоположными по направлению и равными по модулю.

Закон сохранения импульса

Закон сохранения импульса — это следствие из законов Ньютона: при движении тел в инерциальной системе без внешнего воздействия импульс сохраняется во времени, а при воздействии внешних сил на тело, скорость изменения импульса определяется суммой приложенных сил.

Математически это выражается так:

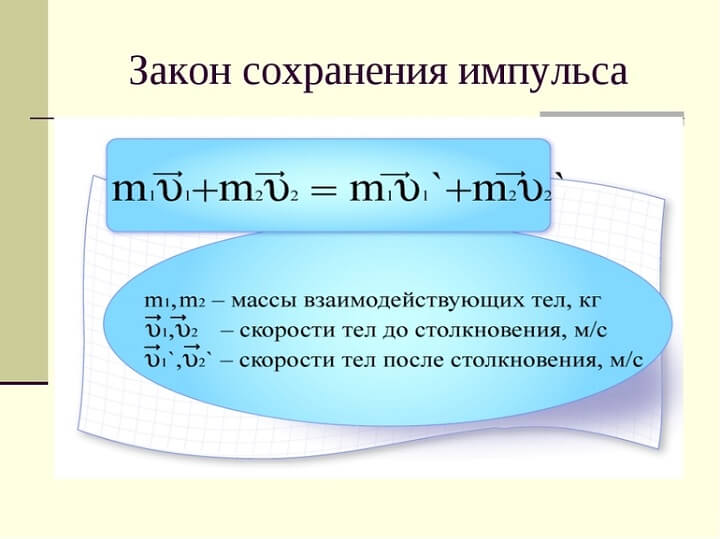
Точнее закон сохранения импульса можно сформулировать таким образом: векторная сумма импульсов всех тел, находящихся в системе, — величина постоянная, если внешнее воздействие на систему отсутствует или же их векторная сумма равна нулю.

Закон сохранения момента импульса

Закон сохранения момента импульса звучит так: момент импульса тел в замкнутой системе (в которой отсутствует воздействие внешних сил) относительно любой неподвижной точки не изменяется со временем.

Основное уравнение динамики вращательного движения

Работа и механическая энергия

Энергия — это способность физических объектов совершать определенную работу, поэтому количественно работа и энергия измеряются в одних и тех же единицах — джоулях (Дж).

Механическая работа будет численно равна изменениям механической энергии. Работа в механике бывает постоянной и переменной силы.

Работа постоянной и переменной силы

Сила, воздействующая на тело, когда перемещает его на определенное расстояние, совершает работу. В том случае, когда сила постоянна по величине и направлению, а движение прямолинейно, можно говорить о работе постоянной силы.

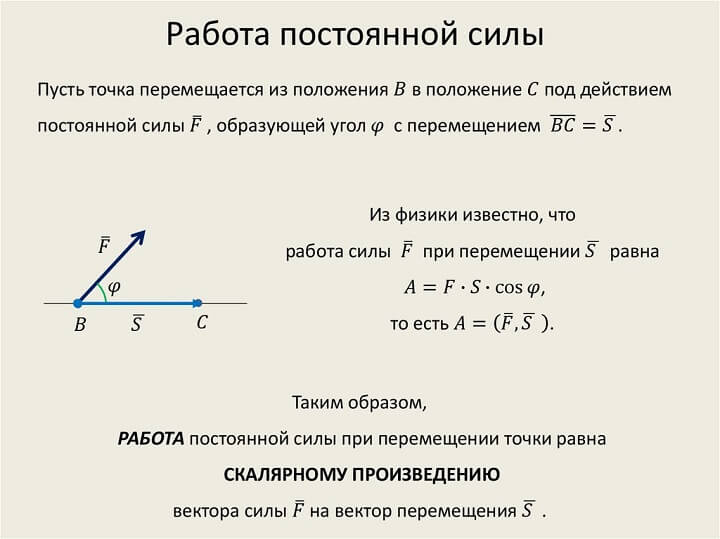
Если траектория движения объекта не прямолинейна, а сила, действующая на тело, не является постоянной, нужно говорить о работе переменной силы. Чтобы ее рассчитать, необходимо весь путь разбить на прямолинейные отрезки. Полная работа будет в таком случае равна сумме работ на всех прямолинейных участках.

Энергия

Энергия — это скалярная величина, которая является количественной мерой различных форм движения материи. Энергия, которая является мерой механического движения и механического взаимодействия тел с другими объектами и между собой, называется механической.

Изменение механической энергии системы ( (Delta W) ) определяется работой ( (A) ), которую совершают внешние силы, воздействующие на систему:

Механическая энергия бывает двух видов:

• кинетической;
• потенциальной.

Кинетическая

Кинетическая энергия — это скалярная функция, которая является количественной мерой движения материальных тел, рассматриваемых в конкретной механической системе. Кинетическая энергия зависит только от массы ( (m) ) и модуля скорости материальной точки ( (v) ).

Рассчитывается кинетическая энергия ( (E) ) по формуле:

Измеряется в джоулях.

Потенциальная

Потенциальная энергия — это физическая величина, которая обозначает энергию взаимодействия тел или их частей между собой. Потенциальная энергия зависит только от расстояния, на котором находятся объекты. Имеет числовое значение, но не имеет вектора направления.

Потенциальной энергией обладают следующие виды тел:

• объекты, находящиеся на какой-либо высоте от поверхности земли;
• упруго деформированные тела (пружина);
• сжатые газы.

Потенциальная энергия тела, поднятого над землей ( (E) ), рассчитывается по формуле:

(E=mtimes gtimes h)

где (m) — масса тела, (h) — высота над землей, (g) — ускорение свободного падения на нашей планете.

Потенциальная энергия упруго деформированного тела ( (E) ) определяется по формуле:

где (x) — удлинение, (k) — жесткость.

Потенциальная энергия измеряется в джоулях.

Закон сохранения механической энергии

Закон сохранения энергии в механике известен всем со школы.

Энергия не исчезает и не возникает снова, она только переходит из одного вида энергии в другой или передается от одного объекта к другому.

Разобраться в такой сложной науке, как физика, довольно трудно. Не у всех есть время и желание вникать в процессы физических явлений. Но без паники! Подтянуть оценки по сложному предмету поможет образовательный сервис Феникс.Хелп. Обращайтесь в любое время!

Предмет и задачи механики. Физические величины и их измерения. Системы единиц.

Механика представляет из себя учение о простейшей форме движения тел при перемещении их или их частей друг относительно друга. Внутренние свойства материи в данном случае не учитываются. Разделы: кинематика (изучает движение тел без рассмотрения причин этого движения); динамика (изучает причины движения в виде сил и параметры движения этими силами вызванные); статика (изучает взаимодействие тел без видимого движения); аэродинамика ( изучает взаимодействие твердых тел с газообразной средой при движении внутри этой среды); гидродинамика (изучает движение жидкости относительно твердых тел в жидкости и других плотных средах). Предметом механики является движение. Основной задачей механики является описание механического движения тел, то есть установление закона (уравнения) движения тела на основе характеристик, описывают (координаты, перемещение, длина пройденного пути, угол поворота, скорость, ускорение и т.п.).

Основная задача механики — предсказывать будущее положение тел.

Физи́ческая величина́ — физическое свойство материального объекта, физического явления, процесса, которое может быть охарактеризовано количественно.

Величина	Единица
Наименование	Символ размерности	Наименование	Обозначение
русское	русское	международное
Длина	L	метр	м	m
Масса	M	килограмм [К 3]	кг	kg
Время	T	секунда	с	s
Сила электрического тока	I	ампер	А	A
Термодинамическая температура	Θ	кельвин	К	K
Количество вещества	N	моль	моль	mol
Сила света	J	кандела	кд	cd

Системы отсчета. Системы координат. Векторные и координатные методы описания.

1.Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и прибора для измерения времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел.

Материальная точка – тело, размерами и формой которого можно пренебречь.

2.Система координат — комплекс определений, реализующий способ определять положение точки или тела с помощью чисел или других символов.

Совокупность чисел, определяющих положение конкретной точки, к примеру, называется координатами этой точки.

3. Наиболее используемая система координат— прямоугольная система координат (декартова система координат).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае.

Векторная величина характеризуется как минимум 2 параметрами: собственная величина и направление. К ним же относят и производные величины ( скорость, ускорение и тд). Механические величины не обладающие называются скалярными (путь, время, масса и тд). Они могут быть преобразованы с помощью арифметических и алгебраических функций в производные физические величины, тогда как векторные величины напрямую не могут быть преобразованы этими математическими функциями.

Описание движения материальной точки в векторной и координатной форме. Вектор перемещения.

Движение точки по окружности. Векторы угловой скорости и углового ускорения.

Рассматривается для абсолютно упругих тел, те можно утверждать что все точки такого т ела движутся по окружности , центр коих лежит на оси вращения, а угловая скорость этих точек одинакова во всех частях тела.

Угловая скорость –векторная величина W, характеризующая быстроту вращения твердого тела и направленная по правилу правого винта.

W=limdФ/dtприdtà0, где Ф- угол поворота,t-время. Единица измерения (рад/с). Вращение с постоянной угловой скоростью называетсяравномерным. Если вращение является равномерным, тоW=Ф/t, где Ф- конечный угол поворота за времяt.

Угловое ускорение — векторная величина Е, Характеризующая быстроту изменения угловой скорости твердого тела. E=limdW/dt при dtà0, где W-угловая скорость, t-время. Единица измерения(рад/с).

Равномерное вращение можно характеризовать периодом обращения T, под которым понимают время, за которое тело делает один оборот.dt=T,dФ=2П, тоW=2П/Т откуда Т=2П/W,v=W/2П =>W=2Пv

Изменение длины

Если в одной системе отсчета покоящаяся линейка имеет длину l, то в системе отсчета, в которой линейка движется со скоростью u вдоль своей оси, ее длина

Этот эффект называется релятивистским сокращением продольных размеров тела. Поперечные размеры тела не изменяются при переходе в другие инерциальные системы отсчета.

4. Сложение скоростей: Если в одной системе отсчета тело имеет скорость v= (v_x, v_y, v_z), то его скорость v‘ = (v’_x, v’_y, v’_z) в другой системе отсчета равна

Пусть система движется относительно системы со скоростью ; аналогично, система движется относительно со скоростью он говорит о том, какую относительную скорость систем и будет регистрировать наблюдатель в

Система материальных точек.

В механике рассматривается движение и равновесие материальных точек.

Несколько материальных точек образуют собою одну систему, если нельзя рассматривать движение какой-либо из них независимо от рассмотрения движения каких-либо из остальных.

Импульс системы.

Будем предполагать, что на систему из N материальных точек действуют внешние силы и что силы взаимодействия между точками системы подчиняются третьему закону Ньютона. Силы взаимодействия между точками системы называют внутренними.

Тогда определим полный импульс системы точек как сумму:

Моме́нти́мпульса (кинетический момент, угловой момент, орбитальныймомент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Момент импульса > материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:

Закон Стокса

В 1851Джордж Стокс получил выражение для силы трения (также называемой силой лобового сопротивления), действующей на сферические объекты с очень маленькими числами Рейнольдса (например, очень маленькие частицы) в непрерывной вязкой жидкости, решая уравнение Навье — Стокса:F=6пrnV где r- радиус сферического объекта n – (ню) вязкость жидкости V-скорость частицы. Если частицы падают в вязкой жидкости под действием собственного веса, то установившаяся скорость достигается, когда эта сила трения совместно с силой Архимеда точно уравновешиваются силой гравитации. Результирующая скорость равна: V=(2r^2g(pч-pж)/9npч – плотность частиц, pж – плотность жидкости, r-радиус частицы, n-(ню)вязкость жидкости.

Гармонический осциллятор

Гармони́ческийосцилля́тор (в классической механике) — система, которая при смещении изположенияравновесияиспытывает действие возвращающейсилыF, пропорциональной смещению x (согласнозакону Гука):

где k — коэффициент жёсткости системы.

3.1) Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания).

Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

3.2) Если имеется ещё и сила трения(затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором.

4) Энергия колебаний4.1)При механическихколебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическаяэнергия тела W: (Скорость тела v=ds/dt)

Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы: где U — потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.

Сравнивая формулы для кинетический и потенциальной энергии механического маятника можно сделать следующие выводы:

1.Полная механическая энергия тела не изменяется при колебаниях:
2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.
3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на p (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная — минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.

Гармоническая волна

Гармонической волной называется линейная монохроматическая волна, распространяющаяся в бесконечной динамической системе. В распределённых системах общий вид волны описывается выражением, являющимся аналитическим решением линейного волнового уравнения

где – некоторая постоянная амплитуда волнового процесса, определяемая параметрами системы, частотой колебаний и амплитудой возмущающей силы; – круговая частота волнового процесса, – период гармонической волны, – частота; – волновое число, – длина волны, – скорость распространения волны; – начальная фаза волнового процесса, определяемая в гармонической волне закономерностью воздействия внешнего возмущения.

· продольные волны (волны сжатия) — частицы среды колеблются параллельно (по) направлению распространения волны (как, например, в случае распространения звука);

· поперечные волны (волны сдвига) — частицы среды колеблются перпендикулярно направлению распространения волны (электромагнитные волны, волны на поверхностях разделения сред);

Амплитудой звуковой волны называется половина разницы между самым высоким и самым низким значением плотности. На графике амплитуде будет соответствовать разница между самой высокой (или низкой) точкой волны и горизонтальной осью графика.

Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярнаявеличина, размерность которой совпадает с размерностью определяемой физической величины.

Фаза волны — понятие, полностью аналогичное и по сути совпадающее с понятием фаза колебания. Аргумент функции или , описывающей волну, причем обычно линейно зависящий от времени и координат, но иногда и произвольно от них зависящий.

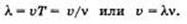
Скорость, с которой распространяется возмущение в упругой среде, называют скоростью волны* Она определяется упругими свойствами среды. Расстояние, на которое распространяется волна за время, равное периоду колебаний в ней (Г), называется длиной волны l (ламбда).

Предмет и задачи механики. Физические величины и их измерения. Системы единиц.

Механика представляет из себя учение о простейшей форме движения тел при перемещении их или их частей друг относительно друга. Внутренние свойства материи в данном случае не учитываются. Разделы: кинематика (изучает движение тел без рассмотрения причин этого движения); динамика (изучает причины движения в виде сил и параметры движения этими силами вызванные); статика (изучает взаимодействие тел без видимого движения); аэродинамика ( изучает взаимодействие твердых тел с газообразной средой при движении внутри этой среды); гидродинамика (изучает движение жидкости относительно твердых тел в жидкости и других плотных средах). Предметом механики является движение. Основной задачей механики является описание механического движения тел, то есть установление закона (уравнения) движения тела на основе характеристик, описывают (координаты, перемещение, длина пройденного пути, угол поворота, скорость, ускорение и т.п.).

Основная задача механики — предсказывать будущее положение тел.

Физи́ческая величина́ — физическое свойство материального объекта, физического явления, процесса, которое может быть охарактеризовано количественно.

Величина	Единица
Наименование	Символ размерности	Наименование	Обозначение
русское	русское	международное
Длина	L	метр	м	m
Масса	M	килограмм [К 3]	кг	kg
Время	T	секунда	с	s
Сила электрического тока	I	ампер	А	A
Термодинамическая температура	Θ	кельвин	К	K
Количество вещества	N	моль	моль	mol
Сила света	J	кандела	кд	cd

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

© cyberpedia.su 2017-2020 — Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.