Что такое задача для дошкольников как объяснить

Как научить ребенка решать задачи

В подготовительной группе детского сада идёт серьёзная подготовка к школе. Некоторые занятия приближены к школьным урокам, хотя и проходят в игре. Помимо того, что идёт активная подготовка к обучению грамоте, при которой малыши знакомятся с буквами и звуками родного языка, дети получают элементарные математические представления: ориентируются в размерах, знакомятся с массой, объёмом, учатся считать, узнают состав числа. Кроме всего этого очень важно научить малыша решать арифметические задачи. Умение решать задачи по математике значительно облегчит жизнь ребёнка в первом классе школы. Естественно, что речь идёт о простейших задачах в одно действие на сложение и вычитание. Летом перед школой ребёнок может и не посещать дошкольное учреждение, а устранять некоторые пробелы к школе нужно. Можно конечно заниматься с репетитором, а можно самостоятельно поупражнять ребёнка в решении задач, тем более ничего сложного в этом нет.

Как же научить ребёнка решать задачи?

Во-первых, необходимо мотивировать ребёнка на желание решать арифметические задачи. Объяснить ему, для чего нужно уметь их решать.Мотив — это величайший двигатель действия. Если у дошкольника не наблюдается ни малейшего интереса к решению арифметических задач, то первоначально можно просто поиграть с ним в школу и это будет игровой мотив. Некоторые дети с радостью решают задачи просто потому, что им нравится это делать.

Во-вторых, самое важное – научить выделять части задачи:

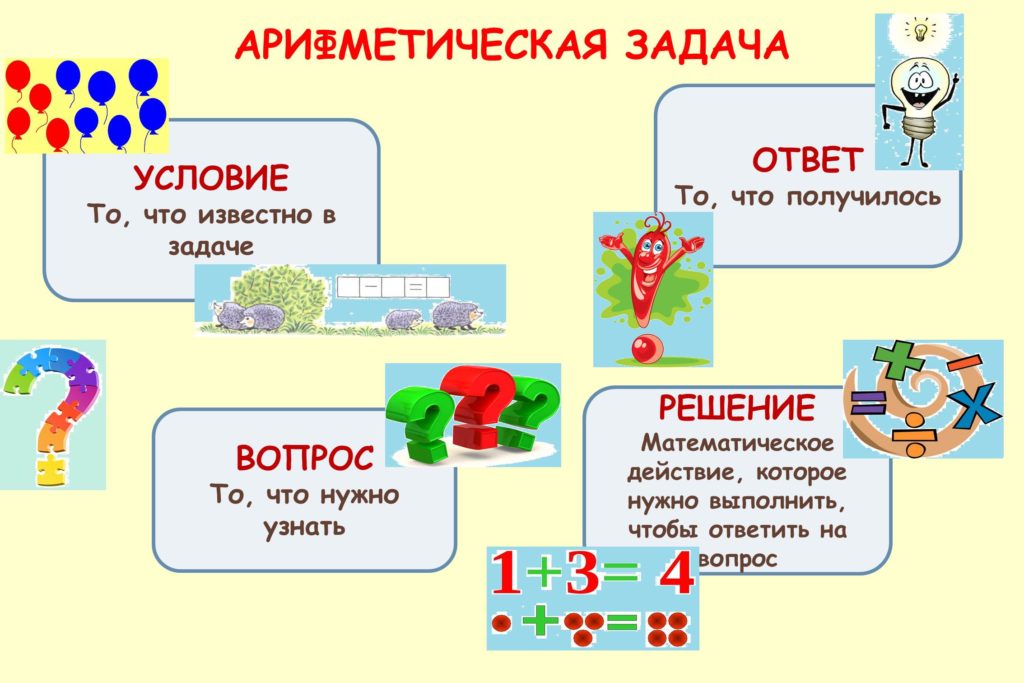
Очень важно, чтобы ребёнок ориентировался в первую очередь в этих частях. Конкретно понимал, что дано в задаче и, что нужно узнать. Соответственно, понимая вопрос, малыш легко определит действие, которое необходимо совершить (вычитание или сложение).

Разъяснить состав задачи возможно с помощью наглядного материала. Наглядность может быть разнообразная:Очень хороший способ – инсценировать задачу. Опять же с помощью игры. Это может быть сюжетно-ролевая игра «Магазин», когда предлагается условие, что поступило, например три коробки с мороженым «Пломбир» и одна коробка с мороженым «Эскимо», вопрос: сколько всего коробок мороженого привезли в магазин? Здесь нужно задавать вопросы типа: Что нам известно? А что необходимо узнать? Разъяснить по ходу задачи, что то, что известно – это условие задачи, а то, что нужно найти – это её вопрос. Так, например, можно делить конфеты или яблоки, приглашать кукол в гости (пришло 4 девочки и 2 мальчика) и т.д. Для выделения частей задачи можно использовать счётные палочки разных цветов.

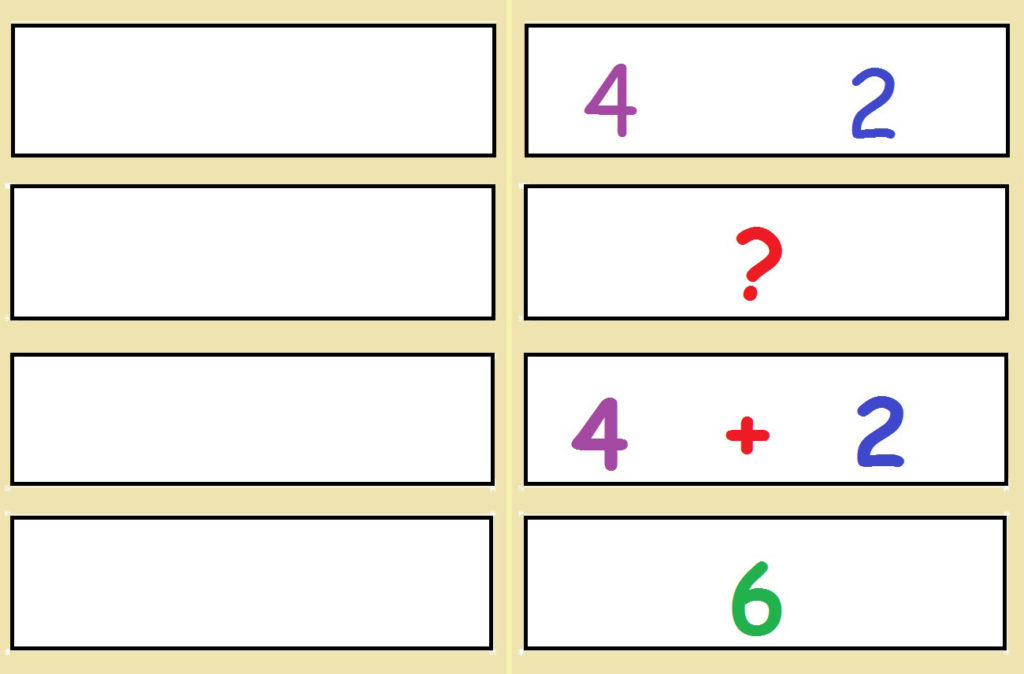
Очень наглядно составные части задачи демонстрируют карточки, обозначающие состав задачи.Даётся 4 пустые карточки, которые постепенно заполняются. На первой карточке пишется то, что известно в задаче. На второй – вопрос, на третьей – выбранное действие, и на четвёртой – ответ. Всё проговаривается словами.

Ещё один способ наглядно продемонстрировать состав задачи – рисование условия и выделение вопрос. Нужно попросить ребёнка нарисовать, например, ёжика в одном краю, а в другом яблоки. Очень хорошо использовать с этой целью доску для школьных мелков или магнитную доску, на которые легко можно как наносить предметы, так и убирать их. Например, такая история: ёжик нашёл 3 зелёных яблока (ребёнок изображает ёжика и яблоки), а затем ещё одно красное (подрисовывает ещё яблоко). Сколько яблок стало у ёжика? На вычитаниеаналогично. Ёжик нашёл 4 яблока (ребёнок изображает ёжика и яблоки), встретил белку и угостил её одним яблоком (одно яблоко стирает с доски). Сколько яблок осталось у ёжика?

После того, как ребёнок поймёт, как разделить задачу на составные части необходимо упражнять его в выделении этих частей, чтобы дошкольник самостоятельно, без помощи взрослого выделял каждую часть задачи и проговаривал её. На помощь так же придёт наглядный материал.

В-третьих, необходимо научит ребёнка проводить анализ задачи. Нужно ещё раз проговорить, как получился ответ, что для этого было сделано, и почему было выбрано именно то математическое действие, а не другое. Главное преподносите ребёнку информацию с лёгкостью, ненавязчиво и ни в коем случае не заставляйте его решать задачи, играйте с ним, введите соревновательный элемент, ведь ребёнок не воспринимает родителей как педагогов.

Как научить детей решать задачи по математике: советы именитых педагогов и простых мам

Научить детей решать задачи по математике — дело учителя, но и родители не должны оставаться в стороне, если их чадо «тормозит» в этом вопросе. Одним учебником математики сыт не будешь. Ведь если научить ребенка самостоятельно решать задачи в 1-3 классах, дальше он будет щелкать как семечки не только задачи по математике, но и по физике, химии, геометрии и др. И самое главное — этот навык пригодится ребенку в жизни!

vogazeta.ru

В статье Как научить ребенка математике мы подробно писали, из каких 4 частей состоит любая задача и что нужно сделать в первую очередь, чтобы ребенок понял, чего от него хотят и как ответить на вопрос задачи. Уяснив алгоритм решения задач, ребенок сможет самостоятельно решить практически любую задачу, даже несмотря на то, что они все кажутся такими разными.

Основные типы задач по математике: краткий конспект

Небольшой ликбез, т.к. далеко не все родители учились в педагогических ВУЗах и владеют методикой преподавания. Пробежимся по теории, чтобы понимать, кто, кому и чего «должен». Зная ключевые моменты, вам будет проще помочь ребенку в решении задач, которые вызывают у него сложности, вы сможете определить, где пробелы в знаниях и что нужно «подтянуть» в каждом конкретном случае.

iqsha.ru

Рассмотрим самые распространенные виды задач в начальных классах.

1. Простые задачи на сложение и вычитание

К этой группе относятся несколько задач, но для всех есть общие рекомендации:

• Решаются в одно действие.
• Иногда удобно составить уравнение.
• На их примере ребенок должен научится выполнять краткую запись.
• Если краткого условия недостаточно, нарисовать рисунок. Если не помог рисунок, показываем на конкретных предметах и производим действия с ними.
• Четко усвоить, что «+» — это прибавить, увеличить, а «-» — уменьшить, отнять, вычесть.
• Хорошо запомнить компоненты арифметических действий:

слагаемое + слагаемое = сумма
уменьшаемое — вычитаемое = разность

• Понять разницу между словами «стало» и «осталось». Четко понимать, что значит «на … меньше», «на … больше».

• Важно понять и запомнить: чтобы узнать, НА СКОЛЬКО одно число больше или меньше другого, нужно из большего числа вычесть меньшее.

• Важно понять и запомнить: чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

• Важно понять и запомнить: чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.

• Важно понять и запомнить: чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.

Задачи с косвенным вопросом

Это самые коварные задачи из этой группы. Внимательно прочитайте условие — и поймете почему.

На стоянке у первого подъезда 7 машин. Это на 2 машины больше, чем на стоянке у второго подъезда. сколько машин на стоянке у второго подъезда.

2. Составные задачи на сложение и вычитание

Эти задачи решаются двумя и более действиями.

Есть несколько способов решения:

• по действиям с пояснениями;
• по действиям с вопросами;
• выражением.

В решении таких задач главное:

• найти главное и сделать краткую запись;
• разложить эту задачу на несколько простых и составить план решения;
• помнить главное: по двум данным находим третье.

3. Задачи на понимание смысла действий умножения и деления

• Важно запомнить названия компонентов действий и понять их смысл:

1-й множитель х 2-й множитель = произведение
делимое : делитель =частное

• Ребенок должен понимать, что 1-й множитель показывает, КАКОЕ число повторяется а 2-й множитель показывает — СКОЛЬКО РАЗ оно повторяется.

Это очень важно для правильной записи в задачах, иначе получится бессмыслица.

Советы о том, как научить ребенка осознанно относиться к умножению и делению, вы найдете в нашей статье Как научить детей быстро считать: математика до школы. Если возникли проблемы с решением задач на умножение — сдайте чуть-чуть назад, закрепите осознание этого арифметического действия.

4. Простые задачи на умножение и деление

• Очень важно понять и запомнить разницу «в «, «на».

«Во сколько раз» или «на сколько»? Предлог «на» — это сложение или вычитание, а «в» — умножение или деление.

• Важно понять и запомнить: чтобы узнать, во сколько раз одно число больше или меньше другого, нужно большее число разделить на меньшее.

5. Составные задачи на все 4 арифметические действия

6. Задачи на цену, количество, стоимость

7. Задачи на движение

Это отдельная обширная тема, вернемся к ней позже.

Типичные ошибки в решении задач

Ошибка №1. Ребенок невнимательно прочитал условие задачи.

Часто бывает так, что ошибки возникают от невнимательности. Так часто бывает в задачах с косвенным вопросом. Ребенок смотрит на цифры, вроде все логично, но… не верно.

Например: «У Маши 8 конфет, это на 2 меньше, чем у Кати. Сколько конфет у Кати».

Ребенок видит «на 2 меньше» и делает «логичный» вывод, что надо отнять. Отнять можно от бОльшего числа, т.е. сразу напрашивается решение 8-2=6. И ответ: 6 конфет у Кати. А ответ-то не тот! Если внимательно почитать условие, то станет понятно, что у Кати конфет больше чем у Маши. И вовсе тут не отнимать надо.

Как исправить ошибку. Сразу разберитесь с условием, поможет краткая запись.

Ошибка №2. Ребенок допустил ошибку в решении.

Когда в задаче несколько неизвестных, решение затрудняется, требуется выполнить не одно действие, а придумать целую цепочку рассуждений.

Как исправить ошибку. Для начала определим, каких данных нам не хватает. Решаем по действиям. Находим нужные числа (помним правило: по двум неизвестным находим третье), подставляем их и отвечаем на вопрос задачи.

Ошибка №3. Неправильная запись ответа.

Часто ребенок пишет не то пояснение.

Как исправить ошибку. Нужно внимательно прочитать вопрос задачи. Уяснить раз и навсегда, что ответ начинается с числа, а дальше пишем, что требовалось найти (переписываем формулировку вопроса задачи).

Творческий подход в решении задач

www.craftykidsathome.com

• Учите ребенка рассуждать.
• Придумывайте задачи с лишними или недостающими данными.

Пусть ребенок сам вычеркнет лишнее, те данные, которые не влияют на решение.

• Дайте условие, а ребенок пусть сам придумает ответ.
• Пусть ребенок сам составит обратную задачу.
• Придумать несколько задач на одно решение.
• Придумать, как решить задачу другим способом и объяснить его.

На школу надейся, а сам не плошай

Заглянем в педагогику и «расшифруем» мысли умных и заслуженных, исходя из сегодняшних реалий.

В далеком 1867 году К. Ушинский сказал: «У хороших преподавателей дело выходит так, что арифметическая задача есть вместе занимательный рассказ, урок сельского хозяйства или домашней экономии, или историческая или статистическая тема и упражнение в языке».

• Ученика нужно поставить в такие условия, чтобы он оказался в эпицентре событий, т.е., решая задачу, видел ее применение в жизни.

Не всегда задачи в школьном учебнике «вдохновляют» современных школьников. Многим не ясно условие по одной простой причине: ребенок не имеет представления о том, что говорится. Например, задача про надои и бидоны с молоком, а городской «деть» и корову-то в глаза не видел, не то, что тонны молока в бидонах. Или в задаче использованы такие значения, которые в жизни нереальны — это затрудняет восприятие, т.к. ребенок все воспринимает буквально.

Задача родителей — помочь ребенку ПОНЯТЬ условие. Любым способом: хоть рисуй, хоть танцуй.

• К решению задач нужно подходить творчески.

Интерес заставляет ребенка быть активным, а активность в свою очередь усиливает внимание.

В каждодневной жизни нам то и дело приходится решать задачи. Привлекайте ребенка, задавайте вопросы, просите совета. Например, тема ремонта. Вычислить метраж комнаты; просчитать нужное количество краски, зная расход на метр квадратный; купить линолеум, зная длину и ширину комнаты; просчитать, какой метраж выгоднее, если есть напольное покрытие шириной 2, 5 метра и 3 метра, чтобы меньше остатков было и по цене вышло выгоднее. Купить ткань на пошив постельного белья, зная размеры матраса. Примеров масса! И это работает гораздо эффективнее, чем «бездушная» задача в учебнике, которая совершенно не привязана к жизни и не вызывает эмоциональный отклик.

• При решении жизненных задач у ребенка помимо всего прочего развивается наблюдательность, речь, появляется рабочее настроение, развиваются творческие способности и самостоятельность.

Через некоторое время вы заметите, что ребенок различными способами комбинирует информацию, с легкостью составляет задачи сам, находя идеи в окружающем мире, а не высасывая из пальца.

• Когда ребенка просят составить собственную задачу, нужно следить и за содержанием, и за решением. Задача должна быть осмысленной и целесообразной.

Например, нельзя допускать таких «ляпов», как «Я съел 13 желтых груш и 20 зеленых яблок. Сколько фруктов я съел?» Задача теряет смысл, если она оторвана от жизни.

• От задачи надо идти к примеру, а не наоборот.

Дети мыслят не абстрактно, а конкретными образами. Пример 12-6 ни о чем не говорит, а вот ситуация, когда из 12 человек 6 уже купили билеты на футбольный матч — это совсем другое дело. Тут ребенок не задумываясь ответит, что оставшиеся шестеро очень рискуют, нужно поторопиться, иначе билетов может не хватить и придется сидеть у телевизора, вместо того, чтобы активно скандировать на трибунах в поддержку любимой команды.

Лебединцев в своей книге «Введение в современную методику математики» писал: «То влияние, которое может оказывать обучение счислению и вообще математике на умственное развитие детей, находится в прямой зависимости от материала, которым мы пользуемся при обучении; если в учебном материале будут преобладать отвлеченные упражнения в действиях и хитроумные задачи с условиями, лишенными внутренней связи и, по существу, далекими от жизни, то, упражняя учащихся на таком материале, мы, может быть, и выработаем у них формальные навыки в вычислениях и, пожалуй, изощрим их ум для разгадывания разных ребусов и головоломок, но отнюдь не сделаем их более способными к правильному мышлению в жизни или какой-либо области знания…».

Французский педагог Жан Мосе тоже был уверен, что «заставлять ребенка начинать с отвлеченного правила и затем предлагать ему задачи — это значит идти наперекор ходу развития человеческого ума…».

Практические советы по решению задач от реальных мам

fb.ru

Что нам Ушинский, Лебединцев и Мосе, спросим у тех, кто «из нашей песочницы». Как они помогают своим детям решать задачи по математике, что «работает», какие приемы на практике доказали свою эффективность и помогли повысить успеваемость.

Татьяна, мама учеников 4 кл. и 6 кл.

«Я знаю, что особую сложность у детей вызывают задачи на скорость, поэтому начала готовить своих мальчишек к этому уже с 1 класса. Когда ехали к бабушке в Пинск, говорили о скорости, засекали время, считали сколько мы проехали км, смотрели на знаки и вычисляли сколько нам останется времени, если мы будем ехать с такой же скоростью и сколько, если папа будет ехать с другой. В общем, я очень удивлялась, когда мои пацаны на скорость задачи решали как орехи. Я поняла, что в моем детстве не хватало практического представления того, о чем говорилось в задачах».

Ольга, мама ученика 1 кл. и ученицы 4 кл.

«С задачами старшая плохо дружит)) Почти всегда приходит за помощью. Стараюсь выработать алгоритм решения, но частенько упираюсь в «лень подумать». Если совсем «затык», рисуем схемы. На дополнительные задачи совсем нет времени, а сама по своей воле заниматься ими дочь точно не будет)) Иногда встречаются задачи с некорректно поставленным вопросом, тут приходится помогать с формулировкой ответа.

Младшего усадить за математику очень сложно. В те редкие моменты, когда дело доходит до задач, он их решает в уме и выдает ответ устно).»

Вероника, мама учеников 2 кл. и 4 кл.

«Младший задачи решает без проблем, но ненавидит чертить схемы к ним и писать пояснения. Старший ходит на факультатив по математике, дома домашку сам делает».

Катерина, мама ученика 2 кл. и ученицы 5 кл.

«Сын отлично справляется сам. Он такие схемы рисует, что я иногда в шоке)). Если за помощью обращается дочь, стараюсь упростить условие задачи до понятных образов, а потом она сама догадывается, как сложную модель решить».

Татьяна, мама ученицы 5 кл.

«Чаще всего прибегаем к рисованию. Прямо вот как по условию… садимся и рисуем, как есть. Так сказать, наглядность помогает. Велосипедист выехал… значит рисуем человечка на велосипеде, город из которого он выехал и тд)))) Если катер плывет по течению, рисуем море, волны)))))) С пояснениями никогда исправлений со стороны учителя не было, да и у нас, собственно, тоже вопросов не возникало. Смотри по условию, что спрашивают — и пиши ответы возле каждого действия».

Наталья, мама ученика 5 кл.

«Приходилось объяснять дроби на примере сломанных карандашей, порванных в клочья бумажек. В гостях в тот момент был друг-проектировщик, он именно так решил наглядно пояснить сыну задачу. Я обычно прибегаю к помощи рисования. В задачах на скорость/время/расстояние рисовали целые истории: кто куда и на чем поехал, кого встретил по дороге и в какой момент. Порой решение задач превращалось в мультфильм, одного черновика обычно мало. Несколько раз решали задачи всей семьей: мама отдельно от папы, потом сравнивали результаты и каждый объяснял ребенку свой «самый рациональный и простой» способ. Как правило, у мужчин своя логика)), мое решение обычно отличается от папиного».

Уважаемые читатели! Делитесь в комментариях своими находками и сложностями в решении задач по математике с детьми. будем разы разобраться вместе и помочь советами и полезными статьями на интересующие вас темы.

Предлагаем Вашему вниманию программы развивающих занятий с собаками- терапевтами в зависимости от возраста ребёнка и Ваших пожеланий:

Как научить ребенка решать задачи?

Сколько мемов и шуток ходит в интернете, сколько фотографий перечеркнутых на первый взгляд правильных решений!

Сколько родителей и детей вспоминают всех дальних родственников, кто может «помочь» решить задачку в третьем классе.

Так ли ужасна программа и как научить ребенка решать задачи?

Начнем со справки.

Решение задач — это важнейшее средство формирования математических знаний, умений, навыков учащихся и одна из основных форм изучения математики, а также средство математического развития ребенка.
В начальных классах ведется работа над группами задач, решение которых основывается на одних и тех же связях между данными и искомым, а отличаются они конкретным содержанием и числовыми данными. Группы таких задач называются задачами одного вида.

С методической точки зрения для полноценной работы над задачей ученик должен:
— уметь хорошо читать и понимать смысл прочитанного;
— уметь анализировать текст задачи, выявлять его структуру и взаимоотношения между данными и искомыми;
— уметь правильно выбирать и выполнять арифметические действия;
— уметь записывать решение задач с помощью соответствующей математической символики;
— умение составлять задачи.

Начальный курс математики ставит основной целью научить младших школьников решать задачи арифметическим методом, который сводится к выбору арифметического действия или действий, моделирующих связи между данными и искомыми величинами.

Виды задач:
• Простые;
• Текстовые;
• Составные;
• Обратные.

Всего в начальной школе ученики изучают 38 типов задач.

Но как научить ребенка ориентироваться в этом многообразии и научиться «видеть задачу»?

Вначале детей нужно научить определять, что перед ним она. Задача.

Для того, чтобы это сделать, используйте скулхак «Лупа». Упражнение простое — поиграйте с ребенком в игру «угадай, где задача.»

«Маше 10 лет, а у Миши есть 100 рублей.

Это задача? Нет? А почему?

Маше 10 лет, Миша на два года старше. Сколько у них денег?

А это задача? Снова нет? А почему? Ведь есть условие, вопрос.

Да, правильно, по этим условиям нельзя найти решение!

Маше 10 лет, Мише 12 лет. Во сколько раз папа старше Маши?

Задача? А почему? Чего не хватает?

Жили-были два крокозябры. У одного было 32 зуба, а у другого на 25 зубов больше. На сколько зубов у второго крокозябры больше?

А это как раз задача.

Потому что есть условие, вопрос, возможно решение и будет ответ.

Данная тренировка очень важна, и в некоторых учебниках приводят небольшое количество «незадач», над которыми «весельчаки» смеются.

Цель таких упражнений дать понять детям, что задача является таковой, если есть:

1. Условие
2. Вопрос
3. Решение
4. Ответ

Во всех остальных случах — нет.

Если быть внимательным, то можно увидеть, что из пяти предложенных текстов, есть лишь два поля для решения.

То есть смысл упраженения — разглядеть задачи, найти их и решить.

Очень важный навык для маленьких учеников!

Итак, скулхак № 1 по решению задач: Прежде чем учить ребенка решать задачи, научите его их видеть.

В следующих статьях мы раскроем другие важные аспекты решения задач по математике в начальной школе

12 февраля с 12:00 по мск мы проводим однодневный онлайн-тренин «38 типов задач начальной школы за 1 день!»

• Научитесь решать все 38 типов задач начальной школы
• Узнаете как научить ребенка понимать текст задачи
• Узнаете как научить ребенка оформлять краткую запись
• Узнаете как научить ребенка определить, как решать задачу
• Сможете объяснить разницу между 2*9 и 9*2 в задаче
• Получите простой Алгоритм-инструкцию «Как решать задачи»
• Узнаете типы задач 1 класса и способы простого объяснения
• Узнаете типы задач 2 класса и способы простого объяснения
• Узнаете типы задач 3 класса и способы простого объяснения
• Узнаете типы задач 4 класса и способы простого объяснения
• Узнаете Формулу «треугольник» для решения задач на движение, цену, количество и стоимость.

Вам понравилась статья? Сохраните себе на стену, чтобы не потерять

Похожее

Автор

Рената Кирилина

Эксперт №1 по эффективному обучению детей в школе, мама троих детей, прошла путь от учителя до директора школы Посмотреть все записи автора Рената Кирилина

«Ты просто не хочешь думать!». Почему ребёнок не может решить задачу и 5 способов ему помочь

Вечер, за окном уже темно, все собираются спать. Все, кроме школьника, который пытается решить задачу по математике. И не может. Почему? В блоге проекта «Математические тропинки» Александр Маркеллов и Екатерина Бредихина рассказывают, как помочь ребенку понимать условия задач и искать решение.

Иногда родители сталкиваются с проблемой: ребёнок сидит перед задачей и не может её решить. Что можно сделать в такой ситуации?

• Сказать: «Ну ты и балбес, это же элементарно! Просто думать не хочешь!»;
• Долго объяснять, потом решить самому и дать переписать;
• Открыть ГДЗ и дать ребёнку списать;
• Попытаться понять, в чем именно у ребёнка трудность и помочь эту трудность преодолеть.

Думаю, понятно, что плохого в первых трёх вариантах. Они могут решить проблему с вашими эмоциями или с конкретной задачей, но не помогут наладить отношения и, главное, — не научат ребёнка решать задачи самому. Скорее всего, самооценка ребёнка упадет, а в следующий раз, когда он увидит подобную задачу, у него возникнут такие же трудности.

Важное замечание: иногда нам, взрослым, то, что мы уже умеем делать, кажется элементарным, но это всего лишь иллюзия. При обучении ребёнок встречает множество трудностей, которые ему нужно преодолевать: понимать концепции, запоминать приёмы. Если вы попробуете освоить новую область, вы точно так же будете в затруднительном положении, и вам будут непонятны многие вещи. Это нормальный процесс обучения, поэтому важно признать за ребёнком право испытывать трудности.

Решение задачи — это сложный процесс, состоящий из разных этапов. В этой статье попробую показать, что это за этапы, чтобы вы могли понять, на каком из них могут возникнуть сложности у ребёнка.

Возьмем для примера такую задачу для учеников третьего класса: «Ваня, Витя и Арсений пошли собирать грибы. Всего они собрали 48 грибов. Ваня собрал на 6 грибов больше, чем Арсений. А Арсений собрал на 12 грибов меньше, чем Витя. Сколько грибов собрал каждый из ребят?».

Задачу можно решить с помощью уравнения, но в третьем классе такую задачу нужно решить по действиям. С помощью уравнения дети учатся решать задачи в пятом классе.

На мой взгляд, процесс решения задачи состоит из 5 этапов:

1. Прочитать условие задачи;
2. Понять концепцию задачи и нарисовать схему;
3. Решить задачу по действиям;
4. Записать решение;
5. Проверить верность решения.

В чём заключается метод? Наша задача — понять, на каком именно этапе ребёнок испытывает сложность. Мы будем помогать ребёнку с каждым этапом по очереди. Если ребёнок после этого благополучно решает задачу, значит, сложность была именно в этом этапе, и его нужно тренировать отдельно.

1. Прочитать условие

Ребёнок прочитал задачу, отлично! Но как понять, разобрался ли он, о чём там речь, или нет? Чтобы это проверить, а также помочь разобраться, что там происходит, задайте ребёнку вопросы по условию. В нашей задаче это могут быть такие вопросы:

• Что надо узнать в задаче?
• Сколько детей собирали грибы?
• Ребята собрали одинаковое количество?
• Кто собрал меньше всех?
• На сколько грибов Ваня собрал больше, чем Арсений?
• На сколько грибов Витя собрал больше, чем Арсений?
• Что получится, если у Вани и у Вити забрать 6 и 12 грибов?
• Чего не хватает, чтобы ответить на вопрос из задачи?

Если после этих вопросов ребёнок решает задачу, значит, проблема была именно на этом этапе.

Как тренировать?

Сначала давать задачи в одно действие, потом — в два действия. Просить самого задавать вопросы к задачам. Давать задачи с избыточным условием — лишней информацией, которая не нужна для решения. Это помогает фокусироваться на главном и отбрасывать ненужное. Таких задач много в учебнике «Сопрунова, Посицельская, Посицельский: Математика и информатика.»

2. Понять концепцию задачи и нарисовать схему

Этот этап самый сложный, так как требует понимания концепций. Но и его можно успешно тренировать. Если ребёнок сам не может нарисовать схему, можно предложить ему разные схемы на выбор:

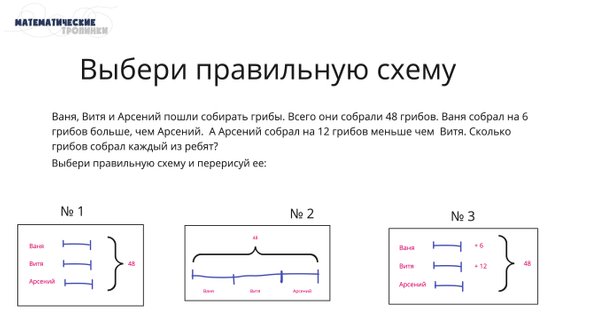
Первая схема просто не соответствует условию задачи: у ребят было разное количество грибов. Вторая схема верная, но она не приближает нас к решению задачи. А вот третья схема очень точно отображает условие и позволяет с ней работать.

Как тренировать?

Уровень 1. Соедини условие и схему.

Мы столкнулись с проблемой: если у задачи есть вопрос, у ребёнка срабатывает рефлекс и он сразу бросается её решать. А нам это пока что не надо. Поэтому там, где это нам не нужно, мы убрали вопрос в задаче.

Уровень 2. Нарисуй схему к условиям.

Как ещё тренировать?

Можно делать такие задания:

• Придумай задачу по схеме;
• Исправь схему по описанию/исправь описание по схеме.

3. Решить по задачу по действиям

Вот как выглядит решение задачи:

У каждого типа задачи разная методология решения, которую нужно изучать, решая сначала более простые задачи. В методологию решения этой задачи мы сейчас не будем погружаться, потому что это очень узкая тема. Но остается вопрос: как тренироваться, если у ребёнка сложность на этом этапе?

Отличный способ — решать задачи именно по схеме.

4. Записать решение

Это сложный вопрос: школьная действительность такова, что почти вся проверка знаний — это письменные экзамены (контрольные, экзамены для поступления, олимпиады). Ребёнку важно уметь записывать свои мысли так, чтобы его было легко понять. Иногда в школах уделяют этому чрезмерное внимание. Важно понять, какие требования у вашего учителя и стараться их придерживаться. На мой взгляд, если ребёнок дошел до этого этапа — это здорово. Ведь он освоил навык решения задачи. Дальше уже дело техники.

5. Проверить верность решения

Важный этап, о котором не стоит забывать. Нужно посмотреть на ответ и прикинуть, похоже ли это на правду? Не получилось ли так, что пешеход у нас идет со скоростью 1000 км в час? А потом подставить ответ в условия и проверить, всё ли сходится? Хороший вопрос для ребенка, чтобы он тренировался проверять задачу: «Где обычно ошибаются другие дети?» Или «Покажи опасное место в задаче, где можно легко ошибиться». Это заостряет внимание на сложных местах в задаче.

Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.

Как научить ребенка решать задачи по математике легко

Математика — один из основных предметов школьной программы и важная наука, помогающая развивать множество навыков. Как помочь ребенку полюбить этот предмет и что делать родителям, если у школьника возникли сложности с решением задач, разбираемся в статье.

Материал подготовлен при помощи экспертов: организатора Matemaris school, автора курсов по многоклеточной математике и развитию осознанности в обучении Марис Сегинёвой, а также психолога Ингрид Мазенцевой.

Для чего нужна математика

По разным причинам, детям в начальной школе кажется, что математика — это только арифметика: похожие один на другой примеры и однотипные задачи. Интерес к этому предмету быстро угасает, потому что за всем этим ребенок не видит смысла. Обычное «надо научиться считать» работает не всегда. А зачем же еще нужна математика?

Для изучения мира

В начальных классах необходимость изучения математики проще всего объяснить, обратив внимание ребенка на то, что она окружает нас повсюду. Начать можно с простого: от счета ступенек до подсчета лапок у паучков, номеров маршрутных такси и автобусов и сдачи в магазине. Рассказывайте, что математика помогает вам готовить и планировать покупку самоката. С помощью математики строят мосты, ракеты и даже создают любимые игры ребенка на телефоне. Детям часто сложно соотнести примеры в учебнике и реальную жизнь. Кажется, что между ними нет никакой связи. Помогите доказать, что это не так.

Детям непросто соотнести примеры в учебнике и реальную жизнь, помогите им увидеть связь. Фото: Julija Sulkovska/shutterstock.com

Можно пойти дальше и рассказать ребенку, например, про числа Фибоначчи: это последовательность чисел, в которой каждое число, начиная с третьего, равно сумме предыдущих. В природе многое имеет строение, в основе которого лежит последовательность Фибоначчи — раковина улитки или наше ухо, и такую же закономерность мы обнаружим на срезе кочана капусты. И это все — математика! Удивительно? Конечно!

Для развития интеллекта

Математика — это не только красота и способ познавать мир, но и понятные правила. Умение искать последовательные и логичные решения помогает также размышлять над любой возникающей проблемой: если есть условие, значит, есть и решение, которое поможет прийти к ответу. Математика помогает рассуждать, искать взаимосвязи, формулировать свои мысли. Эти знания понадобятся детям в будущем: выбрать оптимальные условия в банке, разобраться, сколько рулонов обоев купить, чтобы сделать ремонт, или понять, сколько будет стоить йогурт со скидкой 20%.

Для формирования воображения

Да, математика — наука точная. Но чтобы решать задачи, нужны не только логика и умение считать. Не менее важно развитое воображение. Иначе как вы посчитаете, кто из пассажиров быстрее добежит до поезда, не представив и пассажиров, и поезд?

Организатор Matemaris school, автор курсов по многоклеточной математике и развитию осознанности в обучении

Если откроете философский словарь, увидите, что математика — это философская наука. Если вы делите мир на естественные науки и гуманитарные, вы должны понимать, что естественные науки изучают природу. Их всего шесть: химия, физика, биология, география, геология и астрономия. Математика к ним не относится. Математика — это выдумка и абстракция. Математик Давид Гильберт говорил про своего друга: «Он стал поэтом. Ему не хватило воображения, чтобы заниматься математикой». И это правда так — чтобы заниматься абстрактной математикой, надо иметь развитое воображение.

Чтобы заниматься абстрактной математикой, надо иметь развитое воображение. Фото: Volodymyr TVERDOKHLIB/shutterstock.com

Для достижения целей

Чтобы найти правильный ответ в математической задаче, ребенку понадобятся внимательность, настойчивость, ответственность, точность и аккуратность. Решить неправильно и начать решать снова, пока не получится найти тот самый, правильный, вариант. Не расстраиваться, если что-то идет не так, уметь откладывать и возвращаться к задаче, пока не достигнешь цели, — важнейший навык не только для школьника, который делает домашнюю работу, но и для взрослых.

Для тренировки памяти

Математика учит запоминать правила и формулы — без них решить задачи не получится. Но не только этот факт помогает развивать память: оказывается, когда ребенок решает математические задачи, он постоянно возвращается к своему прошлому опыту, «доставая» из памяти решения тех задач, над которыми работал на прошлых уроках. Это как компьютер, который обучается на основе загруженных в него данных.

Почему дети сталкиваются со сложностями при изучении математики

Когда у ребенка возникают сложности с математикой, многие взрослые сразу решают, что у школьника просто нет математических способностей. По мнению же педагогов, школьная программа до 6-го класса доступна всем и от способностей никак не зависит — считать могут научиться все.

Организатор Matemaris school, автор курсов по многоклеточной математике и развитию осознанности в обучении

Ко мне приводили «девочку-нематематика»: родители утверждали, что она любит рисовать, поэтому, скорее всего, она гуманитарий. Я ответила, что тоже люблю рисовать и это вообще ничего не значит. Мы начали заниматься, и в 7-8 классе она уже выигрывала олимпиады. Я ей просто не рассказывала, что она нематематик. Не надо вешать ярлыки.

Научить решать примеры можно всех: нужен определенный подход, ведь каждый ребенок осваивает программу в своем темпе. Фото: Lena Ogurtsova/shutterstock.com

Конечно, каждый ребенок осваивает программу в своем темпе. Одному нужно решить пару примеров — и он уже готов к следующей теме, другому и 20 примеров будет мало. Этих детей надо учить по-разному: давать разное время на решение задачи, по-разному эти задачи формулировать. Но научить решать можно всех. Более того, ученые уже неоднократно доказали, что разделения на гуманитариев и технарей не существует. А постоянное напоминание ребенку о том, как сложна математика, может привести к математической тревожности.

Математическая тревожность — это эмоциональное напряжение, вызванное необходимостью решать обычные арифметические задачи. Возникновение этого напряжения никак не зависит от интеллектуальных способностей человека и/или ребенка. Вызвано оно чаще всего влиянием окружающей среды. Бороться с тревожностью можно несколькими способами, методы будут зависеть от причины: где-то помогут дыхательные упражнения, где-то репетитор по самому предмету, а где-то — специалист, который будет работать именно с состоянием человека, то есть психолог или психиатр.

Как же не допустить развития математической тревожности у ребенка и помочь ему увидеть красоту математики? Разбираемся, как решать математические задачки вместе с детьми с удовольствием.

Как решать задачи, чтобы было интересно

Итак, мы выяснили, что любого ребенка можно заинтересовать математикой и научить считать. Разобрались, как мотивировать и объяснять школьнику цели и задачи предмета. Теперь переходим к практике — решаем задачи.

Осваиваем навык счета

Первый класс начинается с изучения цифр и состава числа. Это один из важнейших периодов познания математики, а потому важно, чтобы ребенок эти темы хорошо понял. Для освоения навыка устного счета и понятия состава числа может подойти все что угодно: и счетные палочки, и игрушки, и яблоки. Старайтесь как можно чаще делать примеры наглядными.

Когда ребенок только учится считать, старайтесь как можно чаще делать примеры наглядными. Фото: Chekyravaa/shutterstock.com

Организатор Matemaris school, автор курсов по многоклеточной математике и развитию осознанности в обучении

Детям очень важно при освоении счета что-то держать. Да, пальцы тоже подойдут! Все мы когда-то считали на пальцах, этого не надо бояться, это тоже этап развития, от которого ребенок рано или поздно уйдет. Как ему помочь? Здесь важен ежедневный счет: каждый день по 5 минут решать примеры — это точно даст результат. Есть еще один лайфхак — счет египетскими цифрами. В каждом учебнике первого класса показывают римские цифры, но египетские — гораздо проще. Там семь палочек — это 7. Пишем еще две палочки — уже 9. Здесь можно затронуть и историю математики: рассказать детям о Древнем Египте, береге Нила, пирамидах. Это же так увлекательно! Потом объясняем, что после десяти есть еще один значок — арочка. А если три арочки? Это же уже 30. Для детей это очень понятная схема.

Используем игровой формат

Ведущая деятельность у детей в начальной школе еще не сменилась окончательно, не перешла от игровой к познавательной. А потому так важно играть, находить интересные решения, головоломки, увлекательные задачки. Сегодня делать это очень просто — есть и приложения, и настольные игры, и книги, которые помогают увлечь ребенка математикой, и олимпиадные задачи. Начать можно с самых простых (есть даже олимпиады для дошкольников) — чтобы ребенок понял, что ему это по силам и он справляется. Постепенно задачи можно усложнять. Главное — внимательно следить за интересом ребенка и подбирать такие форматы, которые будут не слишком простыми, но и не отобьют желание найти верный ответ.

Не ругаем за плохой результат

Ругать за то, что у ребенка возникают сложности с предметом, — прямой путь к математической тревожности. Что важно делать родителям, если у ребенка не получилось решить задачу? Надо поддержать и предложить помощь: «Давай разберемся, что не получилось».

Всегда старайтесь видеть прогресс своего ребенка, замечать любое движение вперед. Фото: Nina Buday/shutterstock.com

Советы родителям, если у ребенка возникли сложности с математикой

Но что же делать родителям, если ребенок приходит из школы и говорит, что математика ему не нравится? Здесь может быть две причины: либо ребенку тяжело, либо слишком легко и ему скучно. Если ребенку сложно:

1. Вернитесь к счету на пальцах, палочках, египетских числах, яблочках — подойдет любой наглядный материал.
2. Придумывайте свои задачи. Если вы их придумываете сами, задачи становятся близкими к реальной жизни — и это очень важно. Пускай ребенок сочиняет задачи сам: умение сформулировать условие, понять структуру задачи ценно. Задачки можно записывать — это также тренировка письма, которая тоже для детей в начальной школе важна.
3. Найдите «задачи на разрезание» — можно найти текстовые и в картинках.
4. Уделяйте внимание математике на каникулах — порешайте нестандартные задачки, найдите олимпиадные — те, что попроще.

Если ребенку слишком сложно дается математика, поддержите его и будьте на его стороне.

Организатор Matemaris school, автор курсов по многоклеточной математике и развитию осознанности в обучении

Тем, кому наскучило, я бы тоже посоветовала нестандартные задачи и олимпиады, только посложнее. Этим детям важно понимать смысл математики. Просто щелкать задачки — мало. Задавайте вопросы «зачем?» и «почему?» Важно показать, что математика — это не только арифметика. Что еще можно делать? Усложнять обычные задачи: скучно считать однозначные? А давай двузначные! Скучно умножать на 3? А давай на 23 умножим!

Родители должны быть сами заинтересованы в математике, иначе увлечь ребенка предметом не получится. Фото: Halfpoint/shutterstock.com

И самый главный совет — родители должны быть сами заинтересованы в математике. Увлечь ребенка предметом, не видя в нем смысла и красоты, не получится. Если вы сами не захотите разобраться и восхититься красотой математической задачи, ребенок быстро это заметит и сам вряд ли проявит желание заниматься математикой.

Итак, математика в начальных классах — предмет, доступный всем детям. Математика помогает:

• изучать мир
• мыслить логически
• развивать воображение
• достигать целей
• развивать память

Если у ребенка возникают сложности с математикой в школе, это не значит, что у него нет склонностей к этому предмету и он гуманитарий. Более того, постоянное напоминание о том, что у ребенка сложности, может привести к появлению математической тревожности. Вместо навешивания ярлыков родителям лучше обратить свое внимание и ребенка на способы сделать математику интереснее и проще:

• разобраться с составом числа
• использовать игровой подход
• не ругать за плохой результат

Если же у ребенка уже возникли проблемы с предметом, важно найти причину. Если ему слишком сложно, стоит вернуться на пару шагов назад — к устному счету и задачам попроще. Если слишком просто — идите вперед и поддерживайте интерес ребенка к предмету. И самое главное — интересуйтесь сами. Тогда и у ребенка не возникнет никаких проблем с математикой ни сейчас, ни в будущем.

Представленье – мать ученья, или Как научить ребенка решать задачи, которые его решать не учили

А знаете ли вы, что если с самого раннего возраста играть с детьми в математические игры, то в школе у них не будет проблем ни с арифметикой, ни с алгеброй, ни с геометрией? Математик и педагог Марк Беденко, автор многочисленных учебных пособий, убежден: ребенок может решить любую математическую задачу, если он ее себе хорошо представляет.

Когда не рано начинать

Было время, когда я считал, что с трехлетними малышами нельзя заниматься математикой – наукой, требующей работы с абстракциями. А ребенок трех лет мыслит конкретно – какие у него абстракции могут быть? Но опыт математика Александра Звонкина говорит о том, что всё возможно. Будучи выпускником мехмата, а не учителем, он не знал того, что трехлетки не должны знать математику, что им «еще рано». Он просто начал с ними заниматься. Конечно, малыши не будут выводить формулы и доказывать теоремы. Но даже двухлетний ребенок способен представлять какие-то математические объекты.

Метод Звонкина: проверено на себе

Я не сразу поверил Звонкину, но когда моей дочери исполнилось 11 месяцев, и она стала хоть что-то понимать из того, о чем я ей говорю, я попробовал с ней заниматься математикой. Мы играли в игры, которые Звонкин рекомендует. Я не знал, дает ли это какой-то результат: ее словарный запас был ограничен одним-единственным словом. Но когда ей исполнилось полтора года, и мы с ней начали общаться достаточно активно, выяснилось, что она представляет очень многие вещи. Если исчезали какие-то объекты, она представляла, что с ними случилось. Если какие-то похожие объекты требовалось соединить, она их находила и соединяла. Если из двух объектов надо было составить один, составляла. Для нее не представляли трудности задачи, где надо было мысленно что-то повернуть, растянуть, сжать – все то, что называется геометрическими преобразованиями. И я убедился, что Звонкин абсолютно прав! Ребенок может не знать, что перед ним треугольник, и при этом благополучно с ним работать. Сейчас моей дочери 13 лет, она весьма продвинута в программировании, стабильно побеждает на математических олимпиадах и очень любит решать разнообразные задачи.

Алгоритм на каждый случай не напишешь

В образовательный стандарт записана такая формулировка: «Ребенок должен применять свои знания в ситуациях, с которыми он может столкнуться в своей деятельности». По сути верно. Но это слишком уж широко! Мало ли какая деятельность может быть у ребенка? Мы живем в открытой системе, невозможно перебрать все задачи, с которыми может столкнуться ребенок в жизни. Если заузить проблему и вести речь только о математике, то и здесь мы часто сталкиваемся с задачами «со звездочкой», которые нельзя «расколоть» при помощи заранее известного алгоритма. Однако нестандартность подобных задач бывает разной.

Строим логические цепочки

Иногда для решения задачи нужно пройти запутанным логическим путем и не сбиться. Умение выстраивать длинную логическую цепь необходимо любому математику. Однако психологи полагают, что в раннем возрасте ребенок не может этого делать. Он не доверяет самому себе, знает, что где-то внимание убежит, он проколется и сделает глупость. Конечно, тянуть логические цепочки можно научить, но, во-первых, не всех маленьких детей, а во-вторых, – все равно это не очень легко ложится на детскую природу.

Хитрые свойства

Есть задачи, которые предполагают использование каких-то хитрых математических свойств, о которых ребенок не знает. Совершенствоваться в решении таких задач необходимо детям, которые, готовятся стать, например, математиками, поступать в Физтех и т.д. На развитие мышления в целом такие задачи значительного влияния не оказывают.

Представь, чтобы решить

Наконец, достаточно большой блок задач требует представить некий объект, который ребенка не учили представлять. Например, что получится, если мы возьмем резиновое колечко и три раза перекрутим? Или как разрезать круглый торт тремя прямыми на семь частей? Задача не очень сложная, если представляешь, как выглядит торт, что такое нож и как они в пространстве взаимодействуют. А если не представляешь, то решить ее невозможно.

Даже «Кенгуру» знает

Из этих трех типов задач для меня самые важные – последние. Потому что если построена развитая система математических представлений, то учить ребенка намного легче. Две другие имеют, по крайней мере в младшей школе, подчиненное значение, хотя на олимпиадах встречаются задачи всех трех типов. Но если мы возьмем, например, тестовую олимпиаду «Кенгуру», то в ней предлагаются задания несложные с точки зрения математических конструкций, но зато требующие представлять самые разные вещи. Тот факт, что по массовости «Кенгуру» превосходит все другие математические олимпиады вместе взятые, – показатель того, что и детям подобные задачи нравятся.

Чему не учат в школе

Разумеется, развитием математических представлений в школе занимаются, но обычно задачи такого типа имеют подчиненное значение.

Школьные учителя в большинстве своем считают, что любая наука – это сложная, логически организованная система. И вот он на уроке начинает строить эту пирамиду знаний, от простого к сложному, настраивать третий этаж, четвертый – и вдруг оказывается, что у вас есть только четвертый этаж, а все остальные уже развалились.

Логическая цепь в детской голове превысила возможности элемента, и все посыпалось. Стройная система превратилась в разобранные пазлы: где-то соединены куски, где-то перепутались, а где-то вообще потерялись. И определить, какие именно кирпичи выпали, ребенок не может. Да и учитель тоже. В этой ситуации мы вынуждены заниматься сизифовым трудом: латать здесь, добавлять там. Все время мы занимаемся закреплением, повторением.

Повторенье мать ученья – слышал каждый. Но педагоги забывают, что повторенье – это мать скуки, если ребенок с первого раза не понял, что от него требуется.

Заучить повторением можно, а вот понять со второго раза – труднее, чем с первого. Ребенок-то ведь уверен, что он все сделал для понимания. И он ставит шлагбаум, защиту и не пускает знания в себя. А то, что он какие-то глубинные вещи просто не представил – ну и ладно. Он не знает, что это надо было делать.

Математика и жизнь

Есть люди, которые в детстве не усвоили сложные проценты, а теперь они искренне не понимают, почему приходится отдавать столько денег за банковские кредиты. А все идет из школьного: «я не понимаю сложных процентов, поэтому я ничего не понимаю». Сколько взрослых прокололось на том, что они неправильно интерпретировали какие-то вероятностные процессы. Тридцать людей съели это лекарство – и им помогло, значит, надо брать, мне тоже поможет! А как насчет того, чтобы посмотреть, сколько людей съели и им не помогло? Об этом информация есть или нет?

Девочки и математика

Конечно, все это сугубо индивидуально. То, что с легкостью представляет один ученик, может совершенно не представлять его сосед по парте. Если один ребенок представляет в деталях процесс сцепления вагончиков и перецепления их в другом порядке, то другой может этого совершенно не представлять, и задачи такого типа будут вызывать у него огромные затруднения. Если один ребенок прекрасно отслеживает, что произойдет с объектом при повороте, то другой понимает это со скрипом. Более того – и его мама тоже не понимает. У подросших девочек вообще очень часто встречаются проблемы с пространственными представлениями, и там, где шестилетняя ученица играючи все представляет, шестнадцатилетняя красотка – уже через раз. Есть объекты, на которых чаще сыплются мальчики, есть и такие, на которых сыплются все подряд.

Представьте себе, представьте себе!

Я абсолютно убежден: если система математических представлений создается вовремя, в тот момент, когда ребенок готов ее принять, то всех этих позднейших «не понимаю» можно легко избежать. Система эта быть достаточно «развесистой», чтобы подхватить детей, которые предлагаемый им объект не представляют, и дать им для анализа другой объект, который, как говорят математики, изоморфен первому, то есть его математическое поведение то же самое, но ребенок лучше его представляет. В этом случае математическое понятие, которое прячется за этим объектом, он тоже поймет. Кто-то лучше решает задачи про конфеты, а другой – про машинки или деньги. И если удается построить систему, позволяющую всем детям представлять все, чему их учат, – это открывает такие безграничные возможности для учителя, что просто дух захватывает!

Где буксуют олимпиадники

Стандарты, которые требуют понимания математических представлений, появились недавно, а свои пособия, посвященные этой теме, я начал выпускать несколько лет назад. Конечно же, не потому, что я предвидел эти стандарты. Просто я изучал анализ результатов международных тестирований и отчетливо видел, на чем прокалываются российские школьники. Поэтому я и занялся этой темой. Для развития всех этих разнообразных сюжетов с математическими представлениями необходим определенный инструментарий. У меня есть несколько серий пособий, которые это реализуют. Если ребенок понимает многие математические действия и явления, то он может применить свои знания.

Геометрия – царица математики

Мы знаем, что любое геометрическое преобразование – это сдвиг, поворот, отражение или деформация. Если ты умеешь сдвигать, поворачивать, отражать и деформировать объект, то для тебя невозможно придумать такую задачу, какой бы «кучерявой» она не была, чтобы не свелась к одному из этих четырех действий. Конечно, ребенок может ошибиться, принять поворот в одну сторону за поворот в другую сторону или обнаружить отражение там, где его нет – бывает! Но это совсем другая ситуация, чем та, когда ты не знаешь, с какой стороны браться за эту задачу.

Я говорю про геометрию не потому, что только в ней есть такие задачи – просто это наиболее наглядно, пространственные проще изложить. Как раз гораздо более сложные вещи в арифметике. Еще хуже дело обстоит с временными представлениями. Что было раньше? Что потом? Поведение числового ряда вызывают такие же трудности. Но если ребенок будет хорошо представлять все эти процессы, уйдут и проблемы.

Ошибки – это не страшно

Бывает, что ребенок щелкает одни задачки и прокалывается на других. Ничего! Мы подставим ему костылик, поможем, разберем. Нам тоже не всегда удается слета сообразить какие-то вещи. Невозможно проявлять смекалку во всех случаях. Главное – чтоб интегрально набегало. Ведь если ребенок умеет представлять очень много всякого математического, то его легко учить чему угодно. И даже можно и не учить вовсе, потому что он способен до всего дойти самостоятельно.

Как научить ребенка решать задачи ? ‍♀️

Если ребенка научить решать задачи по математике с 1 по 4 класс, то дальше ему будет не сложно постигать другие точные предметы и не только в школе. Ведь практически в любой сфере жизни нужны навыки измерений, определений, расчетов, и сделать это без знания математики крайне сложно. Начиная с первых уроков арифметики, следует донести эту мысль малышам, чтобы они понимали — задача не живет только на страницах учебника, она входит в повседневную жизнь и влияет на нее.

Способов, как правильно научить ребенка решать и понимать задачи по математике, существует несколько, элементы каждого из них можно применять не только во 2 и 3 классе, но даже в старшем возрасте. Формировать такие навыки необходимо, они во многом повлияют на дальнейшие успехи в учебе.

Как научить решать задачи по математике ребенка 1-4 классов

Поскольку знакомство с математикой начинается в начальной школе, то и приобретение навыка справляться с такими головоломками происходит в данный период.

Важно понимать, что научившись справляться с математическими заданиями в начальной школе, ребенок сможет успешно овладеть химией, физикой, астрономией и другими предметами в старших классах. Родители просто обязаны помочь своему чаду с математикой в первых классах, поскольку данный вид занятий напрямую связан с четким логическим мышлением, способностью анализировать, делать выводы.

Кроме этого, задания на счет тренируют память, внимание, развивают способность рассуждать, положительно сказываются на когнитивных способностях в целом.

Общий алгоритм обучения

Следует придерживаться такой последовательности шагов, чтобы научить детей правильно выполнять математические задания:

1. Внимательное чтение условий и разложение заданий на этапы: условие, вопрос, решение, ответ.
2. Составление плана для выяснения неизвестного. Для маленьких хорошо применять рисунки — схемы на данном этапе, приводить примеры из личного опыта, которые аналогичны условию задачи, для лучшего ее восприятия.

Также уместно использование простеньких сценариев, которые позволяют детям «быть внутри задания».

Распространенные ошибки в решении задач

Главные ошибки в процессе поиска ответа следующие:

• беглое чтение условия задачи, которое не позволяет определить, какой именно ответ нужен;
• неправильное понимание последовательности действий, особенно при поиске нескольких неизвестных;
• некорректный ответ может быть формальным, когда перепутаны единицы измерения или же неправильно вычисленным.

Важно научить малыша самостоятельно исправлять и находить ошибки, перепроверять задачу, а не просто откладывать ее в сторону, если что-то не получилось.

Особенности решения задач в 1 классе

На начальном этапе используются так называемые «текстовые» задания, которые знакомят малышей в 1 классе с арифметикой и проблематикой поиска неизвестных данных. Для таких заданий характерно:

• описание простых сюжетов в задании, которые понятны и знакомы ребенку;
• решение таких головоломок помогает осознать важность математических знаний;
• формирование ключевых умений: выделение условия и вопроса, установление зависимости между понятиями и данными, построение логической цепочки решения, проверка результата.

Для того, чтобы научить первоклашек таким понятиям как «условие», «ответ», «неизвестное» следует использовать такие методы:

• дополнительные, наводящие вопросы по условиям;
• составление схем — рисунков условий;
• перевод текста в схематическую модель;
• объяснение значений фраз в условии задания;
• выбор варианта решения, исходя из схемы;
• обозначение в схеме известных и неизвестных разными способами.

Успешное получение навыков в решении простых задач поможет освоить математическую дисциплину в последующих этапах обучения.

В математике второго года обучения также основными остаются текстовые задачи, которые требуют найти неизвестное при наличии двух известных чисел. Если ребенок не понимает, как следует работать с задачами по математике во 2 классе, то не следует паниковать и критиковать его. Еще вполне можно наверстать то, что упущено. Рекомендовано пройтись по основам данной проблемы и разобраться с ней:

• убеждаемся, что малыш усвоил знаки «+», «—», «=» и понимает, как они действуют;
• учим составлять краткую запись условий;

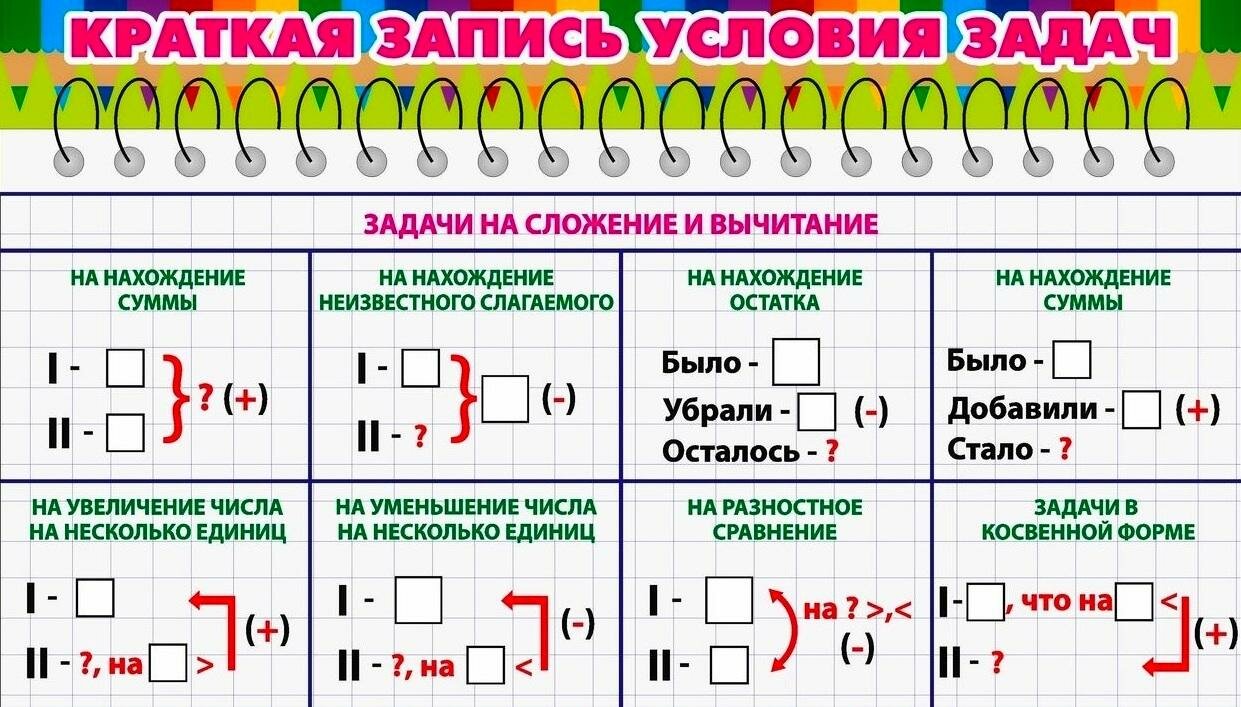
Пример краткой записи условий

При последовательной работе и выполнении подобных заданий, дети начинают запоминать их и понимают причинно-следственные связи между действиями и результатами, что в конечном итоге и требуется для работы с арифметикой.

Специфика обучению решения математических задач в 3 классе

Важной возрастной особенностью третьеклассника является активное развитие мыслительных процессов, что позволяет усваивать большие объемы информации и понимать сложные действия. Особенностями обучения решению арифметических заданий на данном этапе можно назвать следующие:

• изменения поставленных вопросов в заданиях, которые требуют отличать простые и сложные головоломки и самостоятельно выбирать пути их решения;
• поиск нескольких путей решения, демонстрация понимания различных действий, единиц измерения, необходимых для нахождения ответа;

Образец решения задачи

Важно также учить детей самостоятельно придумывать математические задачи, чтобы развивать их логическое мышление и способность формулировать задания.

Как просто решать задачи в 4 классе

В это период очень важно закрепить навыки работы с задачами разной степени сложности, чтобы применять их в дальнейшем. В 4 классе следует развивать не только автоматизацию процесса решения математических заданий, но и стимулировать интерес к ним разными способами:

• изменение условий, предполагающее нахождение нескольких способов решения;
• модификация числовых данных и единиц измерения;
• использование кратких схем и чертежей вместо текстовых условий;
• обнаружение ошибок в уже решенной задаче;
• замена цифр на буквы.

Только используя различные альтернативные варианты обучения можно подвести ребенка к простому алгоритму, применяемому к любой задаче:

1. Ознакомление с условием.
2. Определение неизвестных и способы их поиска.
3. Анализ и вычисление.
4. Ответ на главный вопрос.
5. Проверка корректности найденного числового значения.
6. Оформление задания письменно.

Если учителю и родителям удалось привести ученика к данному алгоритму работы с математическими головоломками, то он сможет успешно решать простые и сложные задачи.

Доказано, что школьный курс математики способен освоить любой школьник, у которого нормально развита логика и работают мыслительные процессы. Зачастую родители предпочитают считать, что если ребенку трудно дается математика, то у него просто гуманитарный склад ума и эта дисциплина ему не нужна.

Такая точка зрения в корне неверна, поскольку именно математика развивает логическое и критичное мышление, без которых ни один гуманитарий не может быть успешным.

Скорее всего, трудности связаны с психологическими проблемами. Для обучения детей, у которых есть проблемы с арифметикой в начальной школе, можно применять такие приемы:

• акцентировать внимание на смысле фраз, а не числах;
• учить малыша отличать главную и второстепенную информацию;
• использовать рисование схем, моделей решения;
• применять цветовую гамму для создания контраста известных и неизвестных величин;
• описывать вместо условий задания ситуации, знакомые ребенку в его жизненном опыте;
• привлекать внимание к возможности применить знание математических действий и правил в реальной жизни;
• использовать образы и условных героев-помощников.

Как научить ребенка решать логические задачи по математике

Такая разновидность заданий дает возможность развивать логику детей и позволяет им обретать навыки нестандартного мышления. Постановка логических задач часто предполагает изобретение особого способа их решения, но все же существуют некоторые разработанные методы их решения, которым и следует обучить школьников:

• метод рассуждений;
• таблицы истинности;
• метод блок — схем;
• средства алгебры высказываний;
• графический метод;
• математический бильярд.

При использовании рассуждений важно разделить условие задания на маленькие фрагменты и сделать последовательные выводы из каждого из них, таким образом ребенок приходит к ответу. Данный вариант решения можно также применять, начиная с конца условия, что тоже приводит к решению, но другим путем.

Применение таблиц истины дает возможность разделить все данные в тексте задачи на истинные и ложные, сравнить их наглядным образом и сделать соответствующие умозаключения о варианте ответа.