Что такое сумматор в электронике

Сумматор (электроника) — Adder (electronics)

An сумматор это цифровая схема который выполняет добавление чисел. во многих компьютеры и другие виды процессоры сумматоры используются в арифметико-логические устройства или же ALU. Они также используются в других частях процессора, где используются для расчета адреса, индексы таблицы, операторы увеличения и уменьшения и аналогичные операции.

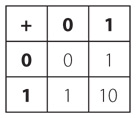
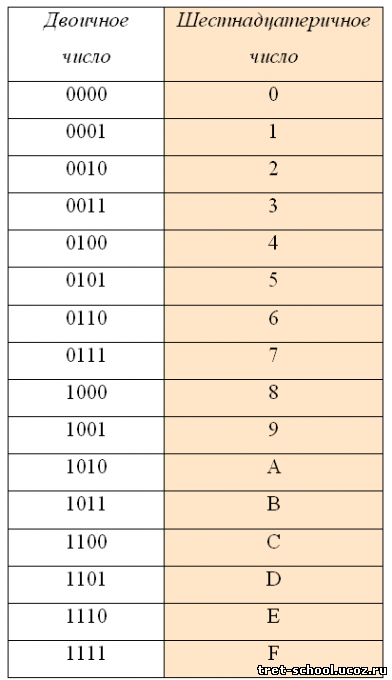
Хотя сумматоры можно построить для многих числовые представления, Такие как двоично-десятичный или же превышение-3, самые распространенные сумматоры работают на двоичные числа.В случаях, когда два дополнения или же дополнение используется для представления отрицательные числа, легко превратить сумматор в сумматор – вычитатель.Другой представление числа со знаком требуется больше логики в отношении базового сумматора.

Содержание

Двоичные сумматоры

Полусумматор

В полусумматор добавляет две одиночные двоичные цифры А и B. Имеет два выхода, сумма (S) и нести (C). Сигнал переноса представляет собой переполнение в следующую цифру многозначного сложения. Стоимость суммы составляет 2C + S . Самая простая конструкция полусумматора, изображенная справа, включает в себя Ворота XOR за S и И ворота за C. Логическая логика для суммы (в данном случае S) будет A’B + AB ′ тогда как для переноски (C) будет AB. С добавлением ИЛИ ворота для объединения их выходов переноса два полусумматора могут быть объединены в полный сумматор. [1] Полусумматор складывает два входных бита и генерирует перенос и сумму, которые являются двумя выходами полусумматора. Вход переменные полусумматора называются дополнительным и дополнительным битами. Выходные переменные — это сумма и перенос. В таблица истинности для полусумматора:

Входы		Выходы
А	B	C	S
0	0	0	0
1	0	0	1
0	1	0	1
1	1	1	0

Полный сумматор

Полный сумматор в действии. Полный сумматор дает количество единиц на входе в двоичном представлении.

Схематическое изображение 1-битного полного сумматора с C_в и C_из нарисованы по сторонам блока, чтобы подчеркнуть их использование в многобитовом сумматоре

А полный сумматор складывает двоичные числа и учитывает как входящие, так и исходящие значения. Однобитовый полный сумматор складывает три однобитовых числа, часто записываемых как А, B, и C_в; А и B операнды, и C_в немного перенесен из предыдущего менее значимого этапа. [2] Полный сумматор обычно является компонентом каскада сумматоров, которые складывают 8, 16, 32 и т. Д. Двоичные числа. Схема выдает двухбитный выходной сигнал. Выходной перенос и сумма обычно представлены сигналами C_из и S, где сумма равна 2C_из + S .

Полный сумматор может быть реализован разными способами, например, с помощью специального транзистор -уровневый контур или состоящий из других ворот. Один пример реализации с S = А ⊕ B ⊕ C_в и C_из = (А ⋅ B) + (C_в ⋅ (А ⊕ B)) .

В этой реализации последний ИЛИ ворота до того, как выносной вывод может быть заменен Ворота XOR без изменения итоговой логики. Использование только двух типов вентилей удобно, если схема реализуется с использованием простых Интегральная схема чипы, которые содержат только один тип ворот на чип.

Полный сумматор можно также построить из двух полусумматоров, подключив А и B на вход одного полусумматора, затем взяв его сумму-выход S как один из входов второго полусумматора и C_в в качестве другого входа, и, наконец, выходы переноса от двух полусумматоров подключаются к логическому элементу ИЛИ. Выходная сумма второй полусумматора является окончательным выходом суммы (S) полного сумматора, а выход логического элемента ИЛИ является окончательным выходом переноса (C_из). Критический путь полного сумматора проходит через оба логических элемента XOR и заканчивается на суммирующем бите. s. Предполагая, что вентиль XOR требует 1 задержки для завершения, задержка, вызванная критическим путем полного сумматора, равна

Критический путь переноса проходит через один вентиль XOR в сумматоре и через 2 логических элемента (AND и OR) в блоке переноса, и поэтому, если логическим элементам AND или OR требуется 1 задержка для завершения, задержка составляет

В таблица истинности для полного сумматора:

Входы			Выходы
А	B	Cв	Cиз	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

Сумматоры, поддерживающие несколько битов

Сумматор с пульсацией

Можно создать логическую схему, используя несколько полных сумматоров для добавления N-битовые числа. Каждый полный сумматор вводит C_в, какой C_из предыдущего сумматора. Такой сумматор называется сумматор с волновым переносом (RCA), поскольку каждый бит переноса «перетекает» на следующий полный сумматор. Обратите внимание, что первый (и только первый) полный сумматор можно заменить полусумматором (при условии, что C_в = 0).

Компоновка сумматора с волновым переносом проста, что позволяет сократить время разработки; однако сумматор с переносом пульсаций работает относительно медленно, поскольку каждый полный сумматор должен ждать, пока бит переноса будет вычислен из предыдущего полного сумматора. В задержка ворот можно легко вычислить, проверив полную схему сумматора. Каждый полный сумматор требует трех уровней логики. В 32-битном сумматоре с переносом пульсации имеется 32 полных сумматора, поэтому задержка критического пути (наихудший случай) равна 3 (от входа до переноса в первом сумматоре) + 31 × 2 (для распространения переноса в последних сумматорах) = 65 задержки выхода на посадку. [3] Общее уравнение для задержки наихудшего случая для п-битовый сумматор пульсации переноса, учитывающий как сумму, так и биты переноса,

Конструкция с чередующимися полярностями переноса и оптимизированная И-ИЛИ-Инвертировать ворота могут быть примерно в два раза быстрее. [4]

Сумматор с упреждением

Чтобы сократить время вычислений, инженеры разработали более быстрые способы сложения двух двоичных чисел с помощью сумматоры с упреждением (CLA). Они работают, создавая два сигнала (п и грамм) для каждой битовой позиции, в зависимости от того, распространяется ли перенос из менее значимой битовой позиции (по крайней мере, один вход равен 1), генерируется в этой битовой позиции (оба входа равны 1) или уничтожается в этой битовой позиции (оба входы равны 0). В большинстве случаев, п это просто сумма вывода полусумматора и грамм — выход переноса того же сумматора. После п и грамм генерируются, создаются переносы для каждой битовой позиции. Некоторые передовые архитектуры с упреждающим просмотром — это Манчестерская цепочка для переноски, Гадюка Брента-Кунга (BKA), [5] и Когге – Стоун гадюка (KSA). [6] [7]

Некоторые другие архитектуры многобитового сумматора разбивают сумматор на блоки. Можно изменять длину этих блоков в зависимости от Задержка распространения схем для оптимизации времени вычислений. Эти блочные сумматоры включают сумматор с пропуском переноса (или обходом переноса) что определит п и грамм значения для каждого блока, а не для каждого бита, и переносной сумматор который предварительно генерирует сумму и значения переноса для любого возможного ввода переноса (0 или 1) в блок, используя мультиплексоры для выбора соответствующего результата когда бит переноса известен.

Комбинируя несколько сумматоров с опережающим переносом, можно создавать сумматоры еще большего размера. Это можно использовать на нескольких уровнях для создания еще более крупных сумматоров. Например, следующий сумматор представляет собой 64-битный сумматор, который использует четыре 16-битных CLA с двумя уровнями опережающие транспортные единицы.

Другие конструкции сумматора включают переносной сумматор, сумматор условной суммы, сумматор, и полный сумматор.

Сумматоры Carry-save

Если схема сложения должна вычислять сумму трех или более чисел, может быть полезно не распространять результат переноса. Вместо этого используются трехвходовые сумматоры, дающие два результата: сумму и перенос. Сумма и перенос могут подаваться на два входа последующего сумматора с 3 числами, не дожидаясь распространения сигнала переноса. Однако после всех этапов сложения для объединения итоговой суммы и результатов переноса необходимо использовать обычный сумматор (например, волновой перенос или опережающий просмотр).

3: 2 компрессора

Полный сумматор можно рассматривать как 3: 2 компрессор с потерями: он суммирует три однобитовых ввода и возвращает результат как одно двухбитное число; то есть он отображает 8 входных значений на 4 выходных значения. Таким образом, например, двоичный вход 101 приводит к выходу 1 + 0 + 1 = 10 (десятичное число 2). Выполнение представляет собой один бит результата, а сумма представляет собой нулевой бит. Точно так же полусумматор можно использовать как 2: 2 компрессор с потерями, сжимая четыре возможных входа в три возможных выхода.

Такие компрессоры можно использовать для ускорения суммирования трех или более слагаемых. Если слагаемых ровно три, макет известен как переносной сумматор. Если слагаемых четыре или более, необходимо более одного уровня компрессоров, и существуют различные возможные конструкции для контура: наиболее распространенными являются Дадда и Деревья Уоллеса. Этот вид схемы чаще всего используется в множители, поэтому эти схемы также известны как множители Дадды и Уоллеса.

Основы цифровой техники

Здесь и по названию понятно что сумматор это устройство выполняющее функцию арифметического сложения. Конечно-же все здесь происходит в двоичном коде.

Если вдруг кто не в курсе, то в двоичном коде тоже все складывается и вычитается и даже своя собственная алгебра существует! Правда об этом уже разговор отдельный и по этому поводу есть отдельные статьи:
Логические числа, представление логических чисел
Алгебра логических элементов

Ну да, ладно, отвлеклись.
Одноразрядный цифровой сумматор имеет три входа: два входа слагаемых и вход переноса (от предыдущего сумматора). При этом правила сложения чуток усложняются. Одноразрядный сумматор обозначается так:

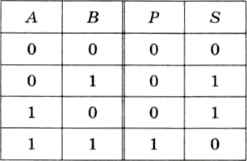
Сумматор имеет входы А и В — слагаемые, С — вход переноса, S — выход суммы, Р — выход переноса. Табличка истинности:

Входы			Выходы
Слагаемые		Вход переноса	Сумма	Выход переноса
А	B	C	S	P
0	0	0	0	0
0	1	0	1	0
1	0	0	1	0
1	1	0	0	1
0	0	1	1	0
0	1	1	0	1
1	0	1	0	1
1	1	1	1	1

На выходе S представляется сумма сложения трех переменных — А, В, С. При переполнении сумматора, т. е. когда в результате сложения формируется единица в старшем разряде выходного числа, на выходе переноса Р формируется уровень лог. 1, который подается на вход переноса С следующего сумматора. В принципе, старшим разрядом суммы является выход переноса Р. В целом работу сумматора полностью иллюстрирует таблица. Из таких одноразрядных сумматоров составляются многоразрядные сумматоры (обычно 4-х разрядные), которые бывают последовательного и параллельного действия. Сумматоры последовательного действия обладают более низким быстродействием.

Вычитатель

Со сложением двоичных чисел все понятно. Как же осуществить на микросхемах-сумматорах операции вычитания двоичных чисел? Допустим необходимо выполнить вычитание: 11 — 5 = 6. В двоичных эквивалентах произведем операцию сложения числа 1011 (число 11) и обратный код числа 5, равный 1010 (прямой код 0101). Итак:

Если отбросить единицу в старшем (пятом) разряде, то получится код 0101, который соответствует числу 5. Но это не число 6. Значит к результату необходимо прибавить единицу. Кстати, операция увеличения какого-либо числа на единицу называется инкрементом , уменьшения на единицу — декрементом . На рисунке показана схема четырехразрядного вычитателя:

Инверторы микросхемы DD1 формируют обратный код числа В. Число А поступает на входы А1-А4 сумматора DD2, обратный код числа В — на входы В1-В4 сумматора. На вход переноса Р0 подан уровень лог. 1, что обеспечивает прибавление к результату сложения единицы (т. е. инкремент результата). На выходах S1-S4 сумматора в итоге получается разность между числами А и В.

Десятичный сумматор

Чаще приходится суммировать десятичные числа. Ниже на рисунке приведена схема сумматора двоично-десятичных чисел на основе двоичных сумматоров.

Операцию сложения выполняет сумматор DD1. При сумме большей или равной десяти на выходе микросхемы DD2, которая является схемой сравнения входов, формируется сигнал переноса Р10. На второй вход (Y1-Y4) микросхемы DD2 подается двоичный эквивалент числа 9 (1001). Сумматор DD3 осуществляет десятичную коррекцию результата суммирования. При отсутствии сигнала переноса на выходе микросхемы DD3 повторяется код числа, который был на выходе DD1, поскольку на входы В поданы лог. 0. При наличии сигнала переноса Р10=1 на входах В2-В3 устанавливаются лог. 1, что соответствует коду числа 6. Допустим есть числа А=8 и В=4. На выходе сумматора DD1 появляется код числа 12 (8+4=12). На выходе DD2 формируется сигнал переноса, сумматор DD3 выполняет операцию 12+6=18. Числу 18 соответствует код 10010. На выходах S сумматора DD3 устанавливается код 0010 (собственный перенос микросхемы DD3 не учитывается). Поскольку на выходе Р10 число 10, на выходах сумматора число 2 (0010), то в результате получается число 12.

Сумматор-накопитель

Интересными свойствами обладает сумматор-накопитель, показанный на рисунке

На рисунке показан простейший сумматор-накопитель. На один вход сумматора подается число К, а на второй — число с выхода регистра. В начале работы регистр обнуляется (сброс). Если на входы В сумматора DD1 подать некоторое число К, то при подаче импульса на вход С регистра (такт) в него запишется число К (в начальный момент на выходе регистра лог.0). Это же число К попадет на входы А сумматора и по следующему такту в регистр запишется уже число 2К, которое опять попадет на входы А сумматора. На выходе сумматора появится число 3К и по следующему такту запишется в регистр и т. д. То есть, в сумматоре-накопителе постепенно нарастает число. Когда в сумматоре-накопителе накопленное число превышает его объем, равный 2 n-1 , на выходе переноса появляется сигнал лог. 1, а на выходах S число nK-2 n .

Применение таких сумматоров весьма разнообразно. Если вместо регистра установить ОЗУ (это делается в многоканальных системах), тогда такой узел становится важнейшей частью микропроцессора. Посмотрим на эти свойства сумматора-накопителя. Поскольку сигнал переноса сумматора появляется через W=2 n /K тактовых импульсов, то такой сумматор является обратным преобразователем входного числа К в число W. Это число можно подсчитать на счетчике. Ну а если выразить частоту появления имульсов переноса через число К, получится вот это:

Это значит, что получается преобразователь кода числа К в частоту импульсов. Такой преобразователь можно использовать в электронных музыкальных инструментах (ЭМИ), всяких звонках и т. п.

Цифровая электроника

Сумматоры – это класс КЦУ, выполняющих операцию арифметического сложения двух двоичных n-разрядных чисел. Сумматоры бывают полными и неполными. Неполный сумматор или полусумматор — это комбинационное устройство с двумя входами и двумя выходами, выполняющее операцию сложения двух одноразрядных чисел в соответствии с таблицей истинности, где А и В – входные одноразрядные числа, S_п/см. – выход суммы, а P_п/см. – выход переноса в старший разряд:

Записанные по таблице истинности ФАЛ для переменных S_п/см. и P_п/см. имеют вид

Первое уравнение для S_п/см. обозначает операцию Исключающее ИЛИ (Сложение по модулю два), а второе — для P_п/см. – операцию логической конъюнкции. Поскольку во всех сериях микросхем имеются элементы Исключающее ИЛИ, то структурную схему полусумматора удобно синтезировать на основе именно этого элемента и элемента И ( рис. 4.6,а ). Условное графическое обозначение полусумматора приведено на рис. 4.6,б .

Рис. 4.6.Структурная схема и УГО полусумматора.

Полный одноразрядный сумматор выполняет операцию арифметического сложения двух одноразрядных чисел A и B с учетом переноса из младшего разряда Р_-1. Он имеет три входа и два выхода. Работа полного одноразрядного сумматора задается таблицей истинности:

Записав СДНФ для переменных S и P и выполнив ряд тождественных преобразований можно получить следующие ФАЛ для полного сумматора:

Выражение есть ни что иное, как значение выхода переноса полусумматора над величинами S_п/см. и Р_-1. Учитывая этот факт и анализируя полученные логические уравнения, можно сделать заключение о возможности реализации полного сумматора на основе двух полусумматоров и одного элемента ИЛИ. Структура полного одноразрядного сумматора представлена на рис. 4.7,а , а его УГО – на рис. 4.7,б .

Рис. 4.7. Схема и УГО полного одноразрядного сумматора.

Из таблицы истинности полного одноразрядного сумматора очевидно, что на выходе суммы S формируется единица, а на выходе переноса Р – нуль при наличии единицы на одном из входах A, B или Р_-1. При наличии единиц на любых двух из трех входов полного сумматора, на выходе S будет нуль, а на выходе P – единица. При наличии на всех трех входах логических единиц, на обоих выходах сумматора присутствуют единицы. При нулях на всех трех входах выходы также принимают нулевые состояния. Структура, реализующая описанное правило и положенная в основу микросхем сумматоров 155 и 555 серий, приведена на рис. 4.8 .

Рис. 4.8.Структурная схема одноразрядного полного сумматора, положенная в основу микросхем ТТЛ-типа.

При суммировании многоразрядных двоичных чисел с помощью одноразрядных сумматоров их необходимо соединить в последовательные структуры. Выходы переноса Р микросхем младших разрядов подключаются к входам переноса Р_-1 микросхем старших разрядов. Отдельные разряды слагаемых подаются на входы А и В микросхем соответствующих разрядов, а с их выходов S снимаются разряды результата суммирования. Выход переноса P микросхемы самого старшего разряда является выходом переноса результата суммирования всего n-разрядного числа.

Такой способ наращивания разрядности сумматоров путем последовательного объединения нескольких полных сумматоров меньшей разрядности достаточно прост в схемной реализации, но при этом имеет существенный недостаток – низкое быстродействие. Распространение переноса в таких структурах осуществляется последовательно от микросхемы к микросхеме. Этого недостатка лишены сумматоры с параллельным переносом. Выражение для переноса в старший разряд одноразрядного полного сумматора можно преобразовать к следующему виду

Введем обозначения и , где g_i – функция переноса, h_i – функция передачи переноса. Тогда

В общем случае можно записать

где — перенос в самый младший разряд из предыдущего сумматора, если таковой предусмотрен в структуре цифрового устройства. В противном случае =0. Таким образом, сигнал p_i можно получить одновременно с появлением всех разрядов а_i и в_i на входах сумматора, не дожидаясь формирования переноса в отдельных разрядах полных одноразрядных сумматоров. В случае четырехразрядных чисел А и В можно записать

Для построения четырехразрядного сумматора с параллельным переносом необходимо полученные ФАЛ для p_i каждого разряда реализовать в каком-либо базисе, например И-НЕ. Далее выходные сигналы p_i с каждой части такой комбинационной схемы должны быть поданы на соответствующие входы Р_-1 полных одноразрядных сумматоров. Пример такой структуры приведен на рис. 4.9 .

Из рисунка видно, что даже для четырехразрядного сумматора требуется достаточно сложная комбинационная схема формирования переноса. Поэтому схемы сумматоров с параллельным переносом реализуют обычно для сложения чисел с разрядностью не более четырех бит.

При необходимости реализации быстродействующих сумматоров для сложения двоичных чисел большей разрядности используют два подхода. Первый заключается в использовании полных сумматоров с параллельным переносом в качестве базовых элементов и объединении их в общую последовательную структуру. Сумматоры, реализованные по такой структуре, называются сумматорами с цепным переносом. Подобная структура не может обладать максимальным быстродействием, но при этом является простой в схемотехнической реализации.

Рис. 4.9. Схема четырехразрядного сумматора с параллельным переносом.

Второй подход также основан на использовании набора сумматоров с параллельным переносом. Но их объединение в общую структуру основано на принципе параллельной передачи переноса. В этом случае требуется дополнительная комбинационная схема, реализующая параллельный перенос между параллельными сумматорами. Сумматоры с такой структурой называются параллельно-параллельными. Они имеют максимальное быстродействие, но их реализация требует дополнительных аппаратных затрат.

Сумматоры и цифровые компараторы: принцип работы, схемы

Что такое сумматоры?

Сумматоры — это комбинационные устройства, предназначенные для сложения чисел. Рассмотрим сложение двух одноразрядных двоичных чисел, для чего составим таблицу сложения (таблицу истинности), в которой отразим значения входных чисел А и В, значение результата суммирования S и значение переноса в старший разряд P (см. рис. 3.48).

Цифровые сумматоры

Работа устройства, реализующего таблицу истинность (рис. 3.48), описывается следующими уравнениями

Очевидно, что по отношении: к столбцу S реализуется логическая функция «исключающее ИЛИ», т. е. S = А + В.

Устройство, реализующее таблицу (рис. 3.48), называют полусумматором, и оно имеет логическую структуру, изображенную на рис. 3.49.

Поскольку полусумматор имеет только два входа, он может использоваться для суммирования лишь в младшем разряде.

При суммировании двух многоразрядных чисел для каждого разряда (кроме младшего) необходимо использовать устройство, имеющее дополнительный вход переноса. Такое устройство (рис. 3.50) называют полным сумматором и его можно представить как объединение двух полусумматоров (Р_вх — дополнительный вход переноса).

Цифровые компараторы

Цифровые компараторы выполняют сравнение двух чисел, заданных в двоичном коде. Они могут определять равенство двух двоичных чисел A и B с одинаковым количеством разрядов либо вид неравенства A> B или A < B. Цифровые компараторы имеют три выхода.

Схема одноразрядного компаратора представляет собой структуру логического элемента «исключающее ИЛИ-НЕ» (рис. 3.51).

Из анализа схемы следует, что если A= B, то F = 1, в противном случае, т. е. при А ≠ В, F = 0. Если А > В, т. е. А = 1, В = 0, то С = 1, а если А < В, т. е. А = 0, В = 1, то D = l.

Если попарно равны между собой все разряды двух n-разрядных двоичных чисел, то равны и эти два числа А и В. Применяя цифровой компаратор для каждого разряда, например, четырехзначных чисел, и определяя значения F1, F2, F3, F4 логических переменных на выходах компараторов, факт равенства А = В установим в случае, когда F = F1 · F2 · F3 · F4 = 1. Если же F = 0, то А ≠ В.

Неравенство А > В обеспечивается (для четырехразрядного числа) в четырех случаях: или А₄ > В₄, или А₄ = В₄ и А₃ > В₃, или А₄ = В₄, А₃ = В₃ и А₂ > В₂, или А₄ = В₄, А₃ = В₃, А₂ = В₂ и A₁ > В₁ (где А₄ и В₄ — старшие разряды чисел А и В). Очевидно, что если поменять местами А₁ и B₁, то будет выполняться неравенство А < В.

Цифровые компараторы выпускают, как правило, в виде самостоятельных микросхем. Так, микросхема К564ИП2 (рис. 3.52) является четырехразрядным компаратором, в котором каждый из одноразрядных компараторов аналогичен рассмотренной ранее схеме. Данная микросхема имеет расширяющие входы А < В, А = В, А >В, что позволяет наращивать разрядность обоих чисел. Для этого компараторы соединяют каскадно или параллельно (пирамидально).

Рассмотрим каскадное соединение компараторов К564ИП2 для сравнения двух восьмиразрядных чисел (рис. 3.53). При этом соединении выходы А = В и А В микросхемы младших разрядов подают соответственно потенциалы U0 и U1 (U0 соответствует логическому 0, a U1 — «1»). В последующих микросхемах на входах А > В поддерживают потенциал логической единицы U1.

Сумматоры.

Для суммирования сигналов обычно применяют схему инвертированного усиления (рис. 2.5, а). Источники входных напряжений м_1вх, и_2вх, и_3вх, подключаемые к инвертирующему входу усилителя через резисторы R_lBX, R_2bx, ^Звх’ подсоединены к общей точке усилителя. Прямой (неинвертирующий) вход усилителя также соединен с общей точкой схемы. Выход усилителя соединен с инвертирующим входом резистором R_oc, образующим отрицательную обратную связь усилителя. Цепи источников питания усилителя на схеме не показаны.

В зависимости от полярности входных напряжений они будут суммироваться (и_1вх, и_2вх) или вычитаться (—м_3вх):

Рис. 2.5. Схемы суммирования сигналов: а — сумматор; б — элемент сравнения

Если сопротивления резисторов входных цепей одинаковы, то суммирование входных напряжений производится с одинаковыми коэффициентами усиления:

Элемент сравнения реализован схемой разностного усиления напряжений (рис. 2.5, б). Входные сигналы от двух независимых источников поданы на прямой и инвертирующий входы усилителя. Источники входного напряжения подключены к общей точке усилителя. Выход усилителя соединен с инвертирующим входом резистором R_oc, образующим отрицательную обратную связь усилителя. Цепи источников питания усилителя на схеме также не показаны.

Выходное напряжение усилителя равно разности напряжений по прямому и инвертирующему входам, умноженных на коэффициенты усиления по соответствующим входам:

Резисторы R, R₃, подключенные к неивертирующему входу по схеме делителя напряжения, предназначены для уравнивания коэффициентов усиления усилителя по прямому и инвертирующему входам.

Если принять R_lBX = R_2bx, R _oc = R₃, то реализуется усиление разности напряжений по входам с одинаковыми коэффициентами усиления

Функциональные преобразователи предназначены для воспроизведения нелинейных зависимостей (t/_BX), используемых в системах автоматического управления для формирования сигналов с заданными нелинейными функциями регулирования.

В САУ электропод- вижного состава используют нелинейные зависимости характеристик намагничивания, а также ограничений тяговых характеристик электродвигателей по условиям коммутации и сцепления. Для воспроизведения таких зависимостей обычно применяют кусочно-линейные функ- Рис. 2.6. Схема функционального преобразователя ции, которые достаточно просто можно реализовать на основе схем операционных усилителей с резисторно-диодными обратными связями.

В качестве примера рассмотрена схема воспроизведения характеристики намагничивания тягового электродвигателя, применяемая в блоке автоматического управления реостатным торможением электровозов ВЛ80С (рис. 2.6).

Рис. 2.7. Характеристика намагничивания

Схема воспроизводит характеристику намагничивания тремя линейными отрезками (рис. 2.7) посредством операционного усилителя DA1 (см. рис. 2.6) с инвертированным усилением. На интервале изменения входного напряжения от 0 до t/_lBX диоды VD1, VD2 заперты положительным опорным напряжением U_Qn, поэтому характеристика намагничивания воспроизводится линейным отрезком, идущим из начала координат.

Коэффициент наклона отрезка определяется отношением сопротивлений резисторов обратной связи R_,, и входной цепи R_HV

Диоды VD1, VD2 в обратной связи усилителя DA1 отпираются последовательно при достижении выходного напряжения (— U_Bblx) величины, при которой напряжение смещения, создаваемое опорным напряжением U_on на катодах диодов через резисторы R_lon, К»2оп’ становится отрицательным. При этом параллельно основному резистору обратной связи R_oc подключаются дополнительно резисторы R_loc, R20C’ которые изменяют коэффициент усиления и соответственно коэффициенты наклона линейных отрезков характеристики:

Величина сопротивлений резисторов обратных связей R_loc, R20C’ подключаемых через диоды VD1, VD2, определяется коэффициентами наклона К, К, К₂ линейных отрезков воспроизводимой характеристики по следующим формулам:

Сопротивления резисторов цепей смещения определяются величинами выходного напряжения (—?/_1вых, — U_2bux), при которых происходит отпирание диодов VD1, VD2 и изменение наклона линейных отрезков характеристики

При воспроизведении более сложных нелинейных зависимостей в ряде случаев применяют параллельное включение двух и более операционных усилителей с использованием разделительных диодов. Для реализации нелинейных логарифмических зависимостей включают в обратную связь операционных усилителей транзисторные усилители. Известны также типовые схемы функциональных преобразователей, таких как квадраторы, экспоненциальные, синусные и др.

Как работают сумматоры и какова его роль в цифровой электронике

Сумматоры — это комбинированные цифровые устройства, осуществляющие арифметическое (в противоположность логическому) сложение и вычитание чисел. Они облодают самостоятельными значениями и являются ядром схем при построение арифметико-логических устройств, реализующих несколько различных операций, являющихся частью всех процессоров.

Основными техническими параметрами сумматоров являются: аппаратная сложность и быстродействие и поэтому имеется огромное множество вариантов сумматоров, которые имеют разветвлённую и обширную классификацию. Выделяя главные моменты, остановимся лишь на некоторых из них.

1) одноразрядный сумматор
2) сумматор для последовательных операндов
3) для параллельных операндов с последовательным переносом
4) для параллельных операндов с параллельным переносом
5) с последовательным распространением переноса по це-почке замкнутых ключей
6) групповой структуры с цепным переносом
7) групповой структуры с параллельным межгрупповым переносом
с условным переносом
9) накапливающий сумматор

Кроме сумматоров можно реализовать вычитатели, но это почти никогда не используется, поскольку вычитание осуществляется методом сложения с использованием дополнительных или обратных кодов.

Полный вариант лекции «Сумматоры» из курса цифровой электроники в формате Word

Он имеет три входа (2 слагаемых и перенос из предыдущего разряда) и 2 выхода (суммы и переноса в следующий разряд). Схема одноразрядного сумматора представлена на рисунке ниже:

Используется для последовательных операндов содержит в своем внутреннем составе один одно-разрядный сумматор, обрабатывающий в порядке очереди разряд за разрядом, начиная с младшего. Сложив младшие разряды, одноразрядный сумматор вырабатывает общую сумму младшего разряда результата и перенос, который запоминается, но только на один такт. В следующем такте складываются вновь поступившие разряды слагаемых с переносом из младшего разряда и т. п.

Сумматор для параллельных операндов с последовательным переносомвыглядит как цепочка одноразрядных, включенных последовательно по цепям переноса. Для схемы с одноразрядными сумматорами, вырабатывающими инверсии суммы и переноса, такая цепочка показана на рисунке ниже, так как функции суммы и переноса самодвойственны. Там, где в разряд сумматора должны поступать инверсные аргументы, в их линиях находятся инверторы, а там, где вырабатывается инверсная сумма, инвертор имеется в выходной цепи. Учтите, что инверторы не входят в цепи переноса передачи — они при этом не тормозят работу сумматора в целом.

Параллельный сумматор с параллельным переносом разработан специально для получения наилучшего быстродействия. Концепция к решению этой многоходовки требует некоторых пояснений. Дело в том, что рассматриваемые сумматоры представляют из себя комбинационные схемы, и вырабатываемые ими функции могут быть описаны в нормальных формах, например, в ДНФ, что приводит к двухъярусной реализации при наличии парафазных аргументов и к трёхъярусной при однофазных. Т.е, предельное быстродействие оценивается несколькими элементарными задержками. Однако реальные схемы таких пределов не способны достичь, т. к. построение сумматоров многоразрядных слов на основе нормальных форм дало на выходе громоздкие схемы. Реальные схемы облодают модульнуой структурой, т. е. состоят из подсхем (разрядных схем), что сильно упрощает их, но не даёт максимального быстродействия.

Сумматор с передачей сигнала переноса по цепочке замкнутых ключей. Среди компромиссных вариантов существующих сумматоров, занимающих промежуточное положение между последовательным и параллельным переносами, имеется оригинальный вариант, который в первом математическом приближении оценивается как обладающий простотой сумматора с последовательным переносом при быстродействии, почти как у сумматора с параллельным переносом.

Предложенный метод предусматривает разделение задачи вычисления сигналов переноса в две операции. В первой части для всех разрядов (параллельно во времени) задаются условия вычисления переносов, а во второй части идет простая передача информации по образованной части цепи.

Сумматор с условным переносом — давно известная структура, которая чуть раньше не нашла широкого использования, но сейчас возродилась в новейших СБИС программируемой логики. Эта структура улучшает быстродействие при последовательном переносе. В СБИС, начиная с семейства микросборок FLEX 8000 фирмы Altera, была реализована цепь последовательных переносов с очень низкими задержками (около 1 нс на разряд, чуть позже задержка переноса была уменьшена до 0,2 нс на разряд). Это возродило уже изрядно упавший интерес к структурам с последовательным переносом и к методам улучшения их быстродействия.

Накапливающий сумматор обычно представляет собою сочетание комбинационного сумматора и регистра

Схемы усреднителя и сумматора

Если мы возьмем три одинаковых резистора и подключим один конец каждого из них к общей точке, а затем подадим три входных напряжения (по одному на каждый из свободных концов резисторов), напряжение, наблюдаемое в общей точке, будет равно среднему арифметическому этих трех напряжений.

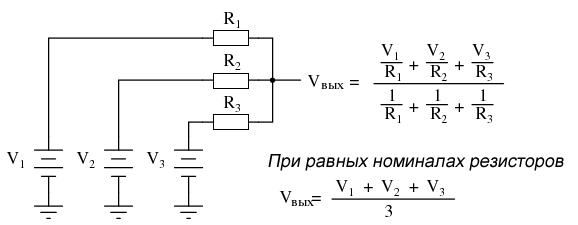
Схема «пассивного усреднителя»

Эта схема действительно не что иное, как практическое применение теоремы Миллмана:

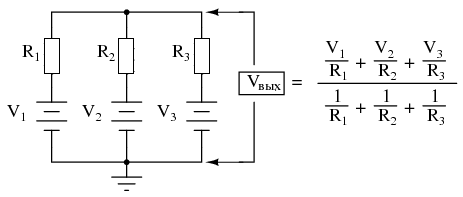
Теорема Миллмана

Эта схема широко известна как пассивный усреднитель, поскольку она создает среднее напряжение без усилительных компонентов. Пассивный просто означает, что эта схема без усиления. Большое уравнение справа от схемы усреднителя исходит из теоремы Миллмана, в которой описывается напряжение, создаваемое несколькими источниками напряжения, соединенными друг с другом через отдельные сопротивления. Поскольку три резистора в схеме усреднителя равны друг другу, мы можем упростить формулу Миллмана, записав R₁, R₂ и R₃ просто как R (одно, одинаковое сопротивление вместо трех отдельных сопротивлений):

Если мы возьмем пассивный усреднитель и используем его для подключения трех входных напряжений к схеме усилителя на операционном усилителе с коэффициентом усиления 3, мы сможем превратить эту функцию усреднения в функцию сложения. Результат называется схемой неинвертирующего сумматора:

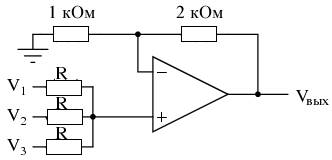
Схема неинвертирующего сумматора на операционном усилителе

С делителем напряжения, состоящим из комбинации 2кОм/1кОм, схема неинвертирующего усилителя будет иметь коэффициент усиления по напряжению 3. Принимая напряжение от пассивного усреднителя, которое представляет собой сумму V₁, V₂ и V₃, деленную на 3, и умножая это среднее арифметическое на 3, мы приходим к выходному напряжению, равному сумме V₁, V₂ и V₃:

[V_ = V_1 + V_2 + V_3 ]

То же самое можно сделать и с инвертирующим усилителем на операционном усилителе, используя пассивный усреднитель в качестве части схемы делителя обратной связи. Результат называется схемой инвертирующего сумматора:

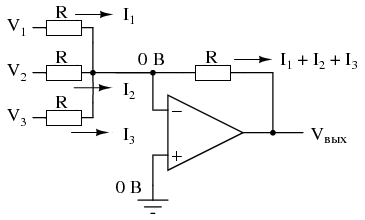
Схема инвертирующего сумматора на операционном усилителе

Теперь, когда правые стороны трех усредняющих резисторов соединены с точкой виртуальной земли инвертирующего входа операционного усилителя, теорема Миллмана больше не применяется так, как раньше. Напряжение на виртуальной земле теперь удерживается отрицательной обратной связью ОУ на 0 вольт, тогда как раньше оно свободно доходило до среднего значения V₁, V₂ и V₃. Однако, при всех значениях резисторов, равных друг другу, токи через каждый из трех резисторов будут пропорциональны их соответствующим входным напряжениям. Поскольку эти три тока будут складываться в узле виртуальной земли, алгебраическая сумма этих токов через резистор обратной связи будет создавать напряжение на V_вых, равное V₁ + V₂ + V₃, за исключением обратной полярности. Изменение полярности – это то, что делает эту схему инвертирующим сумматором.

[V_ = -(V_1 + V_2 + V_3 )]

Схемы сумматоров весьма полезны дя аналогового компьютерного проектирования, так же как и схемы умножителя и делителя. Опять же, чрезвычайно высокий дифференциальный коэффициент усиления операционного усилителя позволяет нам строить эти полезные схемы с минимальным количеством компонентов.