Что такое задача коммивояжера

Задача коммивояжера

Наверное только ленивый не слышал о задаче коммивояжера. Но в чем ее суть и почему об этой задаче так часто говорят в теории алгоритмов? А суть в том, что нужно обойти все пункты по кратчайшему маршруту, при этом, не заходя ни в один из пунктов дважды. Казалось бы, что особенного в этой задаче? Давайте предположим, что у нас всего три точки 1,2 и 3. Какие у нас есть маршруты? Очевидно, шесть маршрутов:

1. Сначала 1, потом 2, потом 3.
2. Сначала 1, потом 3, потом 2.
3. Сначала 2, потом 1, потом 3.
4. Сначала 2, потом 3, потом 1.
5. Сначала 3, потом 1, потом 2.
6. Сначала 3, потом 2, потом 1.

То есть, мы три раза берем по два, так как точек у нас три, а потом мы еще двумя разными способами обходим две оставшиеся точки. А если точек будет 4? Тогда мы четыре раза выберем каждую из точек и используем все комбинации из трех оставшихся точек, коих 6. То есть, тут будет 6*4. Таким образом, можно продолжить формулу дальше и увидеть, что количество всех вариантов – факториал от количества пунктов, которые надо обойти.

Если у нас немного точек, то мы сможем перебрать все варианты. Но в реальной жизни объектом может быть гораздо больше. А с увеличением количества пунктов количество вариантов резко возрастает. Например, факториал от 10 это 3 628 800. А 20!=2 432 902 008 176 640 000. Это порядка десяти в восемнадцатой степени. Тактовая частота современных процессоров порядка нескольких гигагерц (десять в степени девять). Даже если мы будем на каждый вариант тратить один такт процессорного времени (что уже невозможно, на самом деле на одну итерацию придется потратить очень много тактов), то это уже займет порядка миллиарда секунд. Это примерно тридцать лет. А если точек будет еще больше, например 30, или даже 40, то на перебор всех вариантов не хватит времени существования Вселенной.

Для иллюстрации этой проблемы (ее еще называют проблемой «комбинаторного взрыва») я разработал программу, производящую такой перебор (полный текст вы можете скачать с гитхаба):

Уже при 11 элементах алгоритм полного перебора падает в исключение «переполнение стека». Ясно, что это не метод решения. Как же тогда быть? Как вариант, можно использовать жадный алгоритм. В чем его суть? Сначала берем первую попавшуюся точку. Затем ищем ближайшую к ней. Проводим в нее ребро, и ищем следующую ближайшую точку. И так пока не обойдем все точки. Разумеется, никто не гарантирует, что это будет самый короткий путь. Но он будет достаточно коротким. Вот например, как сработает алгоритм для 11 случайных точек:

А как программа справиться с большим количеством точек? Например, 30?

Согласитесь, вполне даже неплохо справляется, несмотря на то, что жадные алгоритмы – наиболее простая идя решения задачи коммивояжера. Какие есть еще способы? В частности, другие наиболее простые методы это:

• Случайный перебор.
• Метод минимального остовного дерева.
• Метод имитации отжига.

С первым методом все понятно. Мы просто берем и составляем случайный путь. Можно сделать так несколько раз и выбрать наиболее удачный вариант. Метод остовного дерева состоит в том, что мы формулируем задачу в терминах теории графов, и сводим данную задачу к задаче нахождения так называемого минимального остовного дерева. Под остовным деревом в теории графов подразумевается некий подграф данного графа с тем же числом вершин, что и у исходного. Говоря простыми словами, у нас есть граф, и мы удаляем из него ребра, до тех пор, пока этот граф еще связан и в нем не будет никаких циклов. То есть, останется оставное дерево.

Другой метод – это метод имитации отжига. Он похож на случайный перебор. Разница в том, что в методе имитации отжига мы берем начальный вариант (который тоже может быть получен случайно). Затем мы случайным образом меняем этот первоначальный вариант. С определенной вероятность мы замещаем текущую комбинацию новой. Причем, вероятность замещения для случая, когда мы получаем лучший вариант, должна быть больше. Затем мы уменьшаем вероятность замещения или шаг изменения – в зависимости от того, какую модификацию алгоритма мы реализовали. Общая идея состоит в том, что мы как бы эмулируем процесс отжига металла. Сначала у нас температура «высокая» и изменения очень сильно «скачут». Но потом система «остывает» и изменения замедляются.

Еще для решения задачи коммивояжера можно применить разные эвристические алгоритмы, например, муравьиный алгоритм, генетический алгоритм, методы динамического программирования.

Задача коммивояжера

Задача коммивояжёра (коммивояжёр — бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и т. п.) и соответствующие матрицы расстояний, стоимости и т. п. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется среди гамильтоновых циклов.

Существует несколько частных случаев общей постановки задачи, в частности геометрическая задача коммивояжёра (также называемая планарной или евклидовой, когда матрица расстояний отражает расстояния между точками на плоскости), треугольная задача коммивояжёра (когда на матрице стоимостей выполняется неравенство треугольника), симметричная и асимметричная задачи коммивояжёра. Также существует обобщение задачи, так называемая обобщённая задача коммивояжёра.

Общая постановка задачи, впрочем как и большинство её частных случаев, относится к классу NP-сложных задач.

Содержание

Методы решения

Простейшие

• полный лексический перебор
• случайный перебор
• метод включения ближайшего города
• метод самого дешёвого включения

Все эффективные (сокращающие полный перебор) методы решения задачи коммивояжёра — методы эвристические. В большинстве эвристических методов находится не самый эффективный маршрут, а приближённое решение. Зачастую востребованы так называемые any-time алгоритмы, то есть постепенно улучшающие некоторое текущее приближенное решение.

Задача коммивояжёра есть NP-полная задача. Часто на ней проводят обкатку новых подходов к эвристическому сокращению полного перебора.

На практике применяются различные модификации более эффективных методов: метод ветвей и границ и метод генетических алгоритмов, а также алгоритм муравьиной колонии.

Метод ветвей и границ

Для решения задачи коммивояжёра предложен в 1963 году группой авторов (Дж. Литл, К. Мурти, Д. Суини, К.Кэрол). [1]

Литература

• Ананий В. ЛевитинГлава 3. Метод грубой силы: Задача коммивояжера // Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Algorithms. — М.: «Вильямс», 2006. — С. 159-160. — ISBN 0-201-74395-7
• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд ШтайнАлгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1

Примечания

1. ↑ Костевич Л.С. Математическое программирование: Информ. технологии оптимальных решений: Учеб. пособие / Л.С. Костевич. — Мн.: Новое знание, 2003. ил., стр. 150, ISBN 985-6516-83-8

См. также

Ссылки

Упаковка в контейнеры: двумерная упаковка • линейная упаковка • упаковка по весу • упаковка по стоимости

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Задача коммивояжера» в других словарях:

задача коммивояжера — Задача поиска кратчайшего пути для обхода заданного количества пунктов (городов). Это трудноразрешимая проблема. [http://www.rfcmd.ru/glossword/1.8/index.php?a=index&d=4826] Тематики защита информации EN traveling salesman problem … Справочник технического переводчика

Задача о коммивояжере — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

Задача о коммивояжёре — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

Задача коммивояжёра — Оптимальный маршрут коммивояжёра через 15 крупнейших городов Германии. Указанный маршрут является самым коротким из всех возможных 43 589 145 600. Задача коммивояжёра (англ. Travelling salesman problem, TSP) (коммивояжёр&#16 … Википедия

задача о коммивояжере — задача о бродячем торговце Вид задачи математического программирования, состоит в отыскании наилучшего маршрута для коммивояжера (бродячего торговца), который должен объехать все порученные ему города и вернуться назад за кратчайший срок или с… … Справочник технического переводчика

Задача о коммивояжере, о бродячем торговце — [travelling salesman problem] вид задачи математического программирования, состоит в отыскании наилучшего маршрута для коммивояжера (бродячего торговца), который должен объехать все порученные ему города и вернуться назад за кратчайший срок или с … Экономико-математический словарь

Задача О Коммивояжере — задача математического программирования по определению оптимального маршрута движения коммивояжера, цель которого состоит в том, чтобы посетить все объкты, записанные в задании, за кратчайший срок и с наименьшими затратами. В теории графов З.о к … Словарь бизнес-терминов

Коммивояжёра задача — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

ЗАДАЧА О КОММИВОЯЖЕРЕ — вид задачи математического программирования; состоит в отыскании наилучшего маршрута для коммивояжера, который должен объехать все порученные ему города и вернуться назад за кратчайший срок или с наименьшими затратами на проезд. На языке теории… … Большой экономический словарь

ЗАДАЧА О КОММИВОЯЖЕРЕ — (TRAVELING SALESMAN PROBLEM) вид задачи программирования матем., состоит в отыскании наилучшего маршрута для коммивояжера, который должен объехать все порученные ему города и вернуться назад за кратчайший срок или с наименьшими затратами на… … Глоссарий терминов по грузоперевозкам, логистике, таможенному оформлению

Что такое «задача коммивояжёра»

Благодаря ей у нас есть навигаторы и системы принятия решений.

В 19-м и 20-м веке по городам ездили коммивояжёры (сейчас их называют «торговые представители»). Они ходили по домам и предлагали людям купить разные товары. Тактика была такой: коммивояжёр приезжал в город, обходил большинство домов и отправлялся в следующий город. Города были небольшими, поэтому обойти всё было вполне реально.

Чем больше городов посетит коммивояжёр, тем больше домов он сможет обойти и больше заработать с продаж. Самая большая проблема, которая всегда стояла перед коммивояжёрами, звучала так:

как быстрее всего объехать все города в этом районе?

В 19-м веке все добирались из города в город на лошадях и повозках, поэтому время полностью зависело от расстояния между городами. С другой стороны, коммивояжёру нужно было вернуться домой после поездок, поэтому классическая задача коммивояжёра звучит так:

как найти самый короткий маршрут между городами, чтобы побыть в каждом хотя бы по одному разу и вернуться домой.

Кажется, что задача очень простая и современные компьютеры могут быстро её решить, но это не так. Если городов будет больше 66, то компьютеру понадобится несколько миллиардов лет, чтобы найти правильный ответ. Давайте выясним, почему это так.

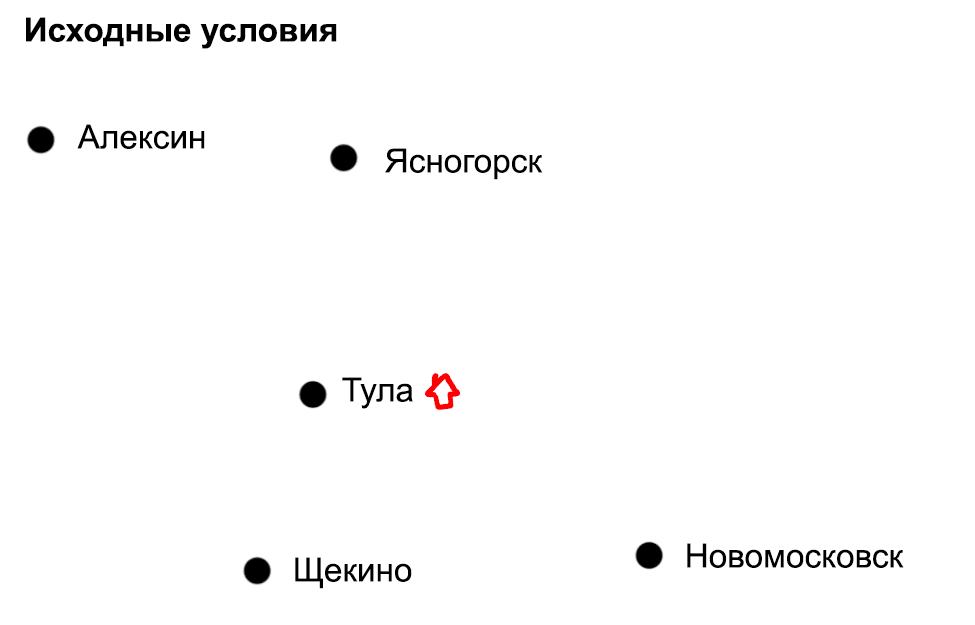
Что такого особенного в этой задаче?

На самом деле это задача не про расстояния, а про поиск оптимального решения по выбранному параметру в сложной системе. Дело в том, что расстояние — это только одна характеристика маршрута. А могут быть и другие:

Время в пути. Время не обязательно напрямую зависит от расстояния. Например, в Санкт-Петербурге можно пойти ночью самым коротким путём и застрять на разводке мостов. По расстоянию это будет километр, а по времени — три часа.

Количество и частота. У нас могут быть лимиты на посещения: не более или не менее определённого количества городов. В классической задаче — нужно побыть в каждом городе не менее одного раза. Также могут быть ограничения вроде «не более одного раза» или «побывать в каждом городе дважды».

Направление движения. Не по всем дорогам можно проехать в обе стороны — есть направления с односторонним движением. Это значит, например, что из одной точки до другой не получится доехать напрямую. Значит, придётся выбирать другой маршрут.

Зависимости. Например, вам нужно по пути отвезти документы в одно учреждение, но перед этим забрать их в другом. Если не выполнить этот порядок, поездка теряет смысл, потому что не выполнено важное условие.

Всё сразу. Может оказаться так, что нам нужно построить такой маршрут:

• посетить все города центрального региона России самым коротким путём;
• в каждом городе посмотреть три главных достопримечательности;
• потратив минимум денег на дорогу и проживание;
• побывать в каждом городе не больше одного раза;
• и успеть всё это за 5 дней.

Всё и сразу не получится

Возьмём для примера маршрут по городам России. В нём 5 условий:

1. Все города региона.
2. Каждый город проезжать не более одного раза.
3. Общая длина маршрута должна быть минимальной.
4. Общая сумма потраченных денег на дорогу и проживание должна быть минимальной.
5. Общая длительность поездки не должна превышать 5 дней.

Скорее всего, ни нам, ни компьютеру не получится построить такой маршрут, чтобы выполнить все условия сразу. Это окажется физически невозможно.

Чтобы такого не было, заранее выбирают одно или два критичных условия, а остальное как получится. Например, нам важно уложиться в 5 дней. Вторым важным параметром, допустим, выберем просто посещение каждого города. Вот что у нас получится в итоге:

1. ⚠️ Все города региона.
2. ⚠️ Общая длительность поездки не должна превышать 5 дней.
3. Каждый город можно проезжать сколько угодно раз.
4. Общая длина маршрута — как получится.
5. Хотелось бы, чтобы общая сумма потраченных денег на дорогу и проживание должна быть минимальной, но на всякий случай возьмём с собой денег с запасом.

Теперь нам гораздо проще построить такой маршрут, потому что есть главные критерии, а остальным можно пожертвовать.

Почему это сложно для компьютера

Возьмём простой случай: у нас есть города и таблица расстояний между ними. Задача — найти самый короткий маршрут посещения всех городов ровно по одному разу, без возвращения в первый город.

1. Если у нас в таблице 4 города, то вариантов первого выбора у нас тоже 4.
2. Когда мы выбрали первый город, то у нас есть 3 варианта, в какой город поехать вторым.
3. Во втором городе у нас вариантов следующего города осталось 2 — третий либо четвёртый.
4. В третьем городе у нас остаётся всего один вариант, куда поехать для завершения маршрута.

Так как в города мы можем поехать в любой последовательности, то всего у нас получается 4 × 3 × 2 × 1 = 24 варианта маршрута. Это называется факториал числа, когда нам нужно последовательно перемножить все числа от 1 до этого числа.

Когда у нас 24 варианта и всего один параметр — минимальный маршрут, — компьютер легко с этим справится простым перебором. Но если таких городов будет уже 15, у нас появится почти полтора миллиарда комбинаций маршрутов. Это уже сложнее, но за час-полтора мощный компьютер справится и с этим. И это только с одним параметром!

Если мы к 15 добавим ещё два города, то получим уже 355 миллиардов комбинаций. Такой объём вычислений потребует гораздо больше времени.Теоретический предел для компьютера — 66 городов. Если городов 67, то число возможных комбинаций маршрутов будет равно 36×10 93 — это больше предела Бремерманна. Для справки, в России 173 города.

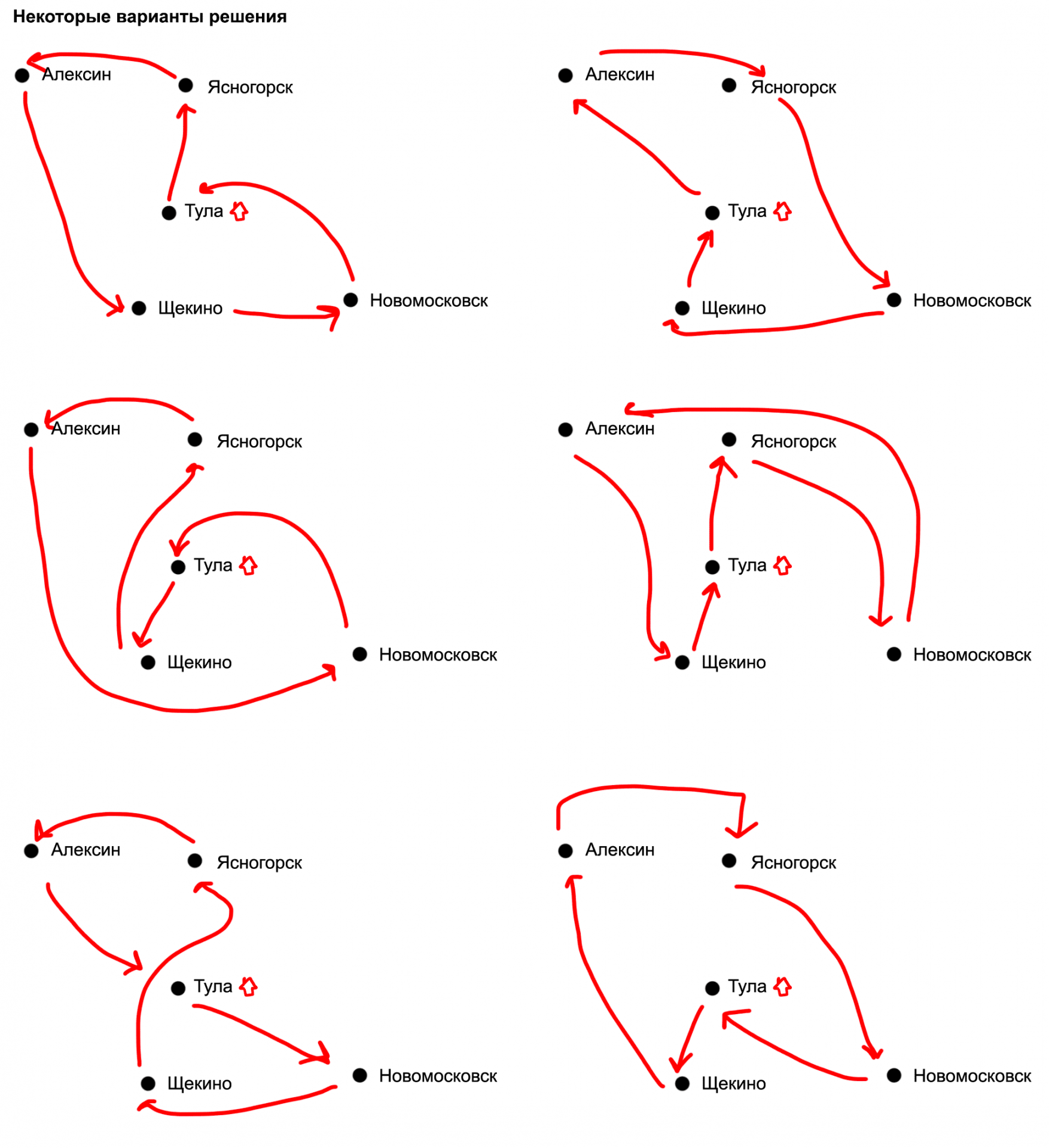
Что за предел Бремерманна

Представьте компьютер размером с нашу Землю на современных транзисторных процессорах. В нём миллиарды миллиардов транзисторов, и все они работают на максимально возможной частоте. Такой компьютер может обработать 10 75 операций в секунду. Если такой компьютер будет работать столько, сколько существует Земля, то за всё это время он сможет обработать 10 93 бит информации. А при 67 городах наше число маршрутов получается в 36 раз больше, поэтому компьютер никогда не сможет рассчитать нужный нам маршрут.

И что тогда делать?

Если нам нужен самый короткий идеальный маршрут, то мы сможем его найти только для небольшого числа городов. Но если можно отойти от идеала и сделать маршрут чуть длиннее, то с этим компьютер уже может справиться.

Дело в том, что когда мы добавляем допустимую погрешность в решение, компьютеру становится намного проще найти ответ. В этом случае задача сводится к тому, чтобы подобрать любой маршрут, который укладывается в рамки допустимой погрешности. Для этого используют специальные алгоритмы, которые позволяют за приемлемое время найти маршрут с погрешностью 1% от минимальной длины.

Где применяется

На алгоритмах решения задачи коммивояжёра построены все современные навигаторы в машинах и телефонах. Ведь ровно это алгоритм и делает: ищет самый короткий маршрут между двумя точками, а в качестве промежуточных «городов» у него перекрёстки.

Но это не единственное применение этого алгоритма, ещё он используется:

• для организации логистики и перевозок в крупных компаниях, чтобы строить оптимальные маршруты по времени, объёму груза и топливу;
• в системах принятия решений, когда на входе есть много параметров и нужно найти оптимальную цепочку действий;
• на производстве при организации конвейера, чтобы сократить время простоя и сделать сборку деталей максимально эффективной;
• при составлении туристических маршрутов;
• в экономике для анализа эффективности финансовых инструментов.

Что дальше

В следующих статьях начнём решать эту задачу разными способами и смотреть, какие алгоритмы с ней справляются лучше всего.

Задача коммивояжера

Задача коммивояжёра — это задача комбинаторной оптимизации, направленная на поиск наиболее оптимального маршрута, который хотя бы по одному разу проходил через определенные города с последующим возвратом в исходный город.

Общие сведения о задаче коммивояжера

Логистика имеет тесные связи с математикой и другими точными науками, поскольку по большей части вопросов пытается найти оптимальные значения действий экономических субъектов и результатов их хозяйственной деятельности. Одним из примеров подобного поиска в логистике является задача коммивояжера.

Задача коммивояжера представляет собой одну из самых известных задач комбинаторной оптимизации. Суть этой задачи сводится к поиску самого выгодного маршрута, который хотя бы единожды проходил через указанные города и в конце путешествия возвращался в исходный город.

При формулировки конкретной задачи из категории задачи коммивояжера важно указать критерий, по которому будут определять самый выгодный маршрут. В большинстве случаев используют один из следующих критериев:

• Кратчайший маршрут (т.е. тот маршрут, который требует преодоления наименьшего расстояния);
• Быстрейший маршрут (т.е. тот маршрут, на преодоление которого требуется затратить наименьшее время);
• Самый дешевый маршрут (т.е. тот маршрут, на преодоление которого требуется затратить наименьший объем финансовых средств);
• Совокупный (интегральный) критерий и т.д.

Помимо этого, в условиях задачи указываются соответствующие матрицы расстояний, стоимости и тому подобного. Обычно указанию подлежит однократное прохождение маршрута через каждый город. В этом случае выбор осуществляется среди гамильтоновых циклов (т.е. замкнутого пути, простого цикла, в который входят все вершины графа).

Рассматриваемая нами задача была названа в честь профессии коммивояжера — посредника между продавцом товара и покупателем, который действовал, как правило, по поручению фирмы, занимался сбытом товара, т.е. разъезжал и предлагал покупателям товары по образцам и каталогам.

Готовые работы на аналогичную тему

На данный момент существует несколько частных случаев общей постановки задачи коммивояжера. Например, часто решают, так называемую геометрическую (планетарную, евклидовую) задачу коммивояжера. Она соответствует ситуации, когда матрица расстояний отражает расстояния между точками на плоскости.

Еще отдельно рассматривают и решают метрическую задачу коммивояжера. Согласно ее условиям, на матрице стоимостей выполняется неравенство треугольника. Еще существуют симметричная, асимметричная и обобщенная задачи коммивояжёра.

Оптимизационная постановка задачи коммивояжёра относится к классу NP-трудных задач. Кроме того, она считается трансвычислительной задачей, поскольку уже при сравнительно малом числе городов (больше 65) ее решение не может быть найдено через перебор вариантов никакими компьютерными программами за время, меньшее нескольких миллиардов лет.

История задачи коммивояжера

Определенную связь с задачей коммивояжёра имеет задача о поиске гамильтонового цикла. В данную категорию входят задача о ходе коня, которая известна науке с XVIII века, и задача икосиан (XIX век). Последняя представляет собой математическую головоломку, в которой надо пройти по графу с 20 вершинами, побывав в каждой из них только один раз.

В 1832 г. была опубликована книга с советами старого курьера, в которой рассказывалось о задаче, похожей на задачу коммивояжера, однако инструменты математики для её решения не использовали. Первые упоминания задачи коммивояжера в качестве математической задачи на оптимизацию принадлежат австрийско-американскому математику Карлу Менгеру-младшему, который сформулировал её на математическом коллоквиуме в 1930 году.

В 1950-60-е гг. задача коммивояжёра привлекла внимание американских и европейских ученых. Большой вклад в изучение и решение задачи принадлежит Дж. Данцигу, Д. Р. Фалкерсону и С. Джонсону, которые в 1954 году сформулировали задачу в виде задачи дискретной оптимизации и для её решения использовали метод отсечений.

В итоге ученые смогли построить путь коммивояжёра для одной частной постановки задачи с 49 городами и обосновать его оптимальность. В 1960-70-е гг. задача изучалась многими учеными как в теоретической плоскости, так и для практического использования ее результатов в сферах экономики, информатики, биологии и химии.

Методы решения задачи коммивояжера

Все эффективные методы решения задачи коммивояжёра, которые сокращают полный перебор, являются эвристическими методами. Большая их часть позволяет найти не самый эффективный маршрут, а только приближённое решение. Кроме того, большое распространение получили, так называемые, any-time-алгоритмы, которые постепенно улучшают некоторое текущее приближенное решение.

Для достаточно больших задач оптимальные или приблизительные решения позволяют находить методы дискретной оптимизации, в частности, ветвей и границ. Применение этого метода впервые было предложено в 1963 г. группой авторов (К. Кэрол, Д. Суини, К. Мурти, Дж. Литл).

Однако метода ветвей и границ для быстрого поиска маршрутов обычно недостаточно. Поэтому для поиска маршрутов приемлемой длины возможно комбинированное применение точных методов с эвристическими.

В 1987 году для решения задачи коммивояжёра использовали метод эластичной сети, который базируется на использовании механизмов установления упорядоченных нейронных связей. Каждый из маршрутов рассматривался как отображение окружности на плоскость. Соседние точки на окружности должны отображаться в точки, по возможности ближайшие.

Также стоит указать, что математики предлагали для решения задачи коммивояжера использование, так называемых, муравьиного алгоритма, генетического алгоритма, алгоритма динамического программирования.

Задача коммивояжера

Задача коммивояжера (Travelling salesman problem, сокращённо TSP) является одной из самых известных задач комбинаторной оптимизации, состоящей в поиске оптимального объекта в конечном множестве объектов. Попросту говоря, заключается эта задача в том, что нужно найти наиболее выгодный маршрут, проходящий через конкретные города хотя бы один раз, а затем возвращающийся в исходный город.

Краткая историческая справка

Доподлинно неизвестно, когда задача коммивояжера была поставлена в первый раз. Но в 1832 году появилась книга «Коммивояжёр — как он должен вести себя и что должен делать для того, чтобы доставлять товар и иметь успех в своих делах — советы старого курьера», и в ней описывалась данная проблема.

Одним из ранних вариантов задачи можно назвать задачу Icosian Game, разработанную ирландским математиком Уильямом Гамильтоном в 19 столетии. В ней нужно было найти маршруты на графе с двадцатью узлами. А первые данные о подобной задаче в качестве математической датируются 1930 годом.

Тогда австрийский экономист Карл Менгер на математическом коллоквиуме сказал, что проблемой посыльного называется задача определения кратчайшего пути между конечным множеством мест с известным расстоянием между ними. Некоторое время спустя появилась и известная нам вариация задачи – задача странствующего торговца (коммивояжера). Ее предложил американский математик Хасслер Уитни.

Коротко о значении задачи

Условия задачи говорят о критерии выгодности маршрута (с точки зрения расстояния, дешевизны и других составляющих). Маршрут должен проходить только один раз через каждый город, а после – возвращаться в начальную точку.

На первый взгляд может показаться, что найти оптимальный маршрут очень просто, но в действительности это нелегкая задача. К тому же есть разные вариации задачи, например, геометрическая, метрическая, симметричная, асимметричная или обобщенная задача.

С учетом разных свойств задачи уже во второй половине 20 века изучать ее стали не столько с практическим уклоном, сколько с теоретическим – она послужила моделью для разработки новейших алгоритмов оптимизации. На ее примере были разработаны метод ветвей и границ, метод отсечений, всевозможные эвристические алгоритмы и другие.

Начиная с 1960 года, задачу коммивояжера начали изучать программисты, экономисты, химики, биологи и представители других наук. А все по той простой причине, что к ее решению сводятся и решения огромного количества практических задач в разных областях науки и жизни.

В современном мире задача коммивояжера помогает оптимизировать работу транспортных отделов и отделов логистики, упрощает работу почтовых и курьерских служб, повышает эффективность мониторинга объектов, например, станций сотовых операторов и нефтяных вышек.

Способность решить эту задачу позволяет оптимизировать и многие производственные процессы, находить оптимальные стратегии ведения хозяйства, экономить ресурсы.

Чем задача коммивояжера полезна для развития мышления

Ритм современной жизни кардинально меняет отношение людей ко времени. Сегодня люди становятся все более нетерпеливыми, не любят ждать, ищут новые возможности оптимизировать свое время и находить наиболее эффективные решения задач и проблем. Естественно, здесь же встает и вопрос о более оптимальном использовании других ресурсов, в том числе и интеллектуальных, и физических, и финансовых.

Именно поэтому решение задачи коммивояжера несет практическую пользу. Оно не просто настраивает сознание и интеллект человека на определенный – более эффективный с практической точки зрения лад, но и развивает абстрактное, логическое, пространственное и другие виды мышления, которыми мы все активно пользуемся в каждодневной жизни.

Безусловно, решить эту задачу может попытаться каждый, но без специальных знаний и навыков не стоит ждать каких-то серьезных продвижений (не зря же ее решением занимаются целые научные сообщества!). Однако потренироваться вполне можно.

Для этого у вас есть прекрасная возможность пройти нашу бесплатную онлайн-программу «Нейробика», некоторые задания из которой включают в себя элементы задачи коммивояжера. Всего же в ней представлено более 20 интересных заданий, направленных на развитие мышления. Попробуйте – думаем, что вам понравится этот курс.

Понравилась статья? Присоединяйтесь к нашим сообществам в соцсетях или каналу в Telegram и не пропускайте выход новых полезных материалов:
Telegram Вконтакте Facebook

Глава 45. Задача коммивояжёра

Может быть, алгоритм, основанный на полном переборе вариантов, не является самым эффективным (в смысле быстродействия) для решения задачи коммивояжёра? Увы, доказано, что не существует алгоритма решения, имеющего степенную сложность (то есть требующего порядка n a операций для некоторого a ) — любой алгоритм будет хуже. Всё это делает задачу коммивояжёра безнадёжной для ЭВМ с последовательным выполнением операций, если n хоть сколько-нибудь велико.

В таком случае следует отказаться от попыток отыскать точное решение задачи коммивояжёра и сосредоточиться на поиске приближённого — пускай не оптимального, но хотя бы близкого к нему. В виду большой практической важности задачи полезными будут и приближённые решения.

Заметим, что интеллект человека, не вооружённый вычислительной техникой, способен отыскивать такие приближённые решения задач, требующих огромного перебора вариантов в поисках оптимального. Вспомним хотя бы шахматы. Человек может весьма успешно соперничать в этой игре с вычислительной машиной либо вовсе не прибегая к перебору, либо сводя его к минимуму. Человек руководствуется при этом интуицией и набором эвристик (находок) — правил, которые обычно помогают в решении задач, хотя эффективность таких правил и не имеет достаточного обоснования. В качестве подобной универсальной эвристики можно упомянуть категорический императив Канта: «поступай с другими так, как тебе хотелось бы, чтобы поступали с тобой». Другой, более приземлённый пример даёт золотое правило валютного спекулянта: «когда все продают доллары, ты покупай, а когда все покупают — продавай».

Задачи комбинаторной оптимизации

Переборные задачи, нацеленные на поиск оптимального варианта, называют задачами комбинаторной оптимизации.

Задача коммивояжёра может быть поставлена как задача оптимизации. В качестве множества X достаточно взять S n (множество перестановок n -элементного множества), а в качестве целевой функции U ⁡ x — длину замкнутой ломаной, проходящей через n заданных точек в порядке, заданной перестановкой x ∈ X .

Метод градиентного спуска

Для множеств X , для которых определено отношение близости, годятся и другие методы. Среди них — метод градиентного спуска.

Суть метода градиентного спуска отражена в его названии и заключается в следующем. Строится последовательность x 0 x 1 x 2 x 3 … ⊂ X , в которой начальный элемент x 0 выбирается произвольно (возможно, случайным образом), а каждый последующий является одним из соседей предыдущего, причём именно тем из соседей, для которого значение функции U будет наименьшим. Построение последовательности завершается тогда, когда последовательность значений целевой функции U ⁡ x 0 U ⁡ x 1 U ⁡ x 2 U ⁡ x 3 … перестанет быть монотонно убывающей.

Имеется вероятностная версия метода градиентного спуска. На каждом шаге для элемента множества X выбирается случайный сосед. Если значение целевой функции в случайной соседней точке уменьшилось, она добавляется в последовательность, и мы переходим к следующему шагу. Если же нет, то снова выбирается случайный сосед. Алгоритм останавливается, если достаточно долго не пополняется последовательность (не происходит переход к следующему шагу): вероятно, алгоритм в этом случае привёл в точку локального минимума.

Метод имитации отжига

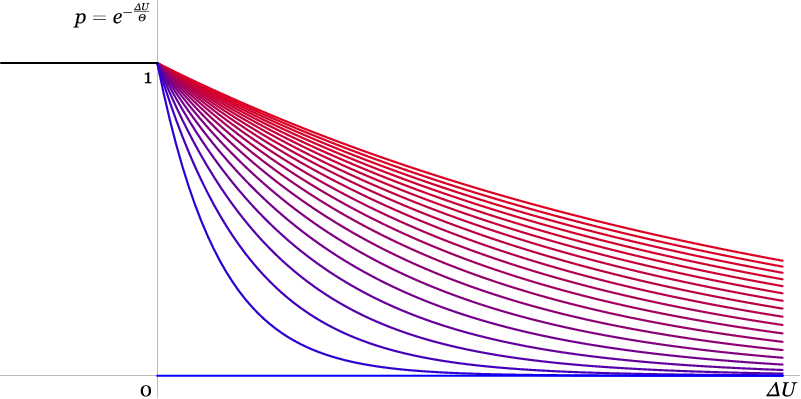
Метод имитации отжига является модификацией вероятностного метода градиентного спуска. Отличие заключается в поведении алгоритма, когда U ⁡ x ⩽ U ⁡ x ˜ , где x — очередной элемент последовательности, а x ˜ — его сосед, выбранный наугад. Вероятностный метод градиентного спуска отвергал такого соседа безусловно, а метод имитации отжига допускает добавление такого «плохого» соседа в последовательность, правда, с некоторой вероятностью p , зависящей от того, насколько плохой сосед ухудшил целевую функцию. Возьмём разность ∆ U = U ⁡ x ˜ − U ⁡ x (она неотрицательна, если сосед «плохой») и положим p = e − ∆ U Θ . Здесь e — некоторое число, большее единицы (какое именно, не принципиально, но обычно берут e ≈ 2,718281828459045… — основание натуральных логарифмов), а Θ — некоторое положительное число, называемое температурой.

На рисунке 45.1. «Вероятность мутации для метода имитации отжига» показаны зависимости вероятности мутации от величины ∆ U при различных значениях температуры Θ . Высоким температурам соответствуют графики, чей цвет ближе к красному, низким — к синему. Как и положено, значение вероятности заключено в отрезке 0 1 . При отрицательных ∆ U вероятность равна 1 , что соответствует случаю «хорошей» мутации.

Приложение на рисунке 45.2 позволяет понаблюдать за процессами, присходящими при поиске оптимального решения задачи коммивояжёра методом имитации отжига.

Постановка задачи коммивояжера и алгоритмы решения

Задача коммивояжера — задача математического программирования по определению оптимального маршрута движения коммивояжера, цель которого состоит в том, чтобы посетить все объекты, записанные в задании, за кратчайший срок и с наименьшими затратами. В теории графов — это поиск пути, связывающего два или более узла, с использованием критерия оптимальности.

Задача коммивояжера является типичной задачей оптимизации, которая широко применяется при разработке программного обеспечения. Задача о коммивояжере является упрощенной моделью для многих других задач дискретной оптимизации, а также часто является подзадачей. В своей области (оптимизации дискретных задач) она служит своеобразным катализатором, стимулирующим разработку наиболее эффективных методов, алгоритмов и способов их машинной реализации.

Задача коммивояжера формулируется очень просто: на плоскости (в пространстве) расположены N городов, заданы расстояния между каждой парой городов. Требуется найти маршрут минимальной длины с посещением каждого города ровно один раз и с возвращением в исходную точку.

В задаче коммивояжера целевой функцией, которую надо минимизировать, является стоимость обхода.

Особенностью задачи о коммивояжере является необходимость дополнительно учитывать расстояния от города до города, которые предполагаются известными. Эти «расстояния» можно заменить на количество затраченного времени, стоимость проезда или предполагать другие произвольные значения. В общем случае мы даже не предполагаем, что стоимость проезда из I в J обязательно совпадает со стоимостью обратного проезда из I в J. Данная задача соединяет в себе простоту условия и сложность решения, обусловленную большими размерами поискового пространства.

На графах задача формулируется следующим образом: требуется найти гамильтонов цикл наименьшей стоимости во взвешенном полном графе. Т.е. выйдя из стартовой вершины, посетить каждую вершину графа ровно один раз и вернуться в начальную по кратчайшему пути.

Методы решения задачи коммивояжера

Задачи коммивояжера решаются посредством различных методов, выведенных в результате теоретических исследований. Все эффективные методы (сокращающие полный перебор) — методы эвристические. В большинстве эвристических методов находится не самый эффективный маршрут, а приближённое решение. Зачастую востребованы так называемые any-time алгоритмы, то есть постепенно улучшающие некоторое текущее приближенное решение.

Выделяют следующие группы методов решения задач коммивояжера, которые относят к простейшим:

а) Полный перебор.

Полный перебор (или метод «грубой силы») — метод решения задачи путем перебора всех возможных вариантов. Сложность полного перебора зависит от количества всех возможных решений задачи. Если пространство решений очень велико, то полный перебор может не дать результатов в течение нескольких лет или даже столетий.

б) Случайный перебор.

Обычно выбор решения можно представить последовательностью выборов. Если делать эти выборы с помощью какого-либо случайного механизма, то решение находится очень быстро, так что можно находить решение многократно и запоминать «рекорд», т. е. наилучшее из встретившихся решений. Этот наивный подход существенно улучшается, когда удается учесть в случайном механизме перспективность тех или иных выборов, т. е. комбинировать случайный поиск с эвристическим методом и методом локального поиска. Такие методы применяются, например, при составлении расписаний для Аэрофлота.

в) Жадные алгоритмы (метод ближайшего соседа, метод включения ближайшего города, метод самого дешевого включения).

Жадный алгоритм — алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. «Жадным» этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность. При решении задачи коммивояжера жадный алгоритм превратится в стратегию «иди в ближайший (в который еще не входил) город». Жадный алгоритм, очевидно, бессилен в этой задаче. Рассмотрим для примера сеть (рисунок 9), представляющую узкий ромб. Коммивояжер стартует из города 1. Алгоритм «иди в ближайший город» выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.