Алгоритм и его свойства. Примеры алгоритмов

АЛГОРИТМ

АЛГОРИТМ – система правил, сформулированная на понятном исполнителю языке, которая определяет процесс перехода от допустимых исходных данных к некоторому результату и обладает свойствами массовости, конечности, определенности, детерминированности.

Слово «алгоритм» происходит от имени великого среднеазиатского ученого 8–9 вв. Аль-Хорезми (Хорезм – историческая область на территории современного Узбекистана). Из математических работ Аль-Хорезми до нас дошли только две – алгебраическая (от названия этой книги родилось слово алгебра) и арифметическая. Вторая книга долгое время считалась потерянной, но в 1857 в библиотеке Кембриджского университета был найден ее перевод на латинский язык. В ней описаны четыре правила арифметических действий, практически те же, что используются и сейчас. Первые строки этой книги были переведены так: «Сказал Алгоритми. Воздадим должную хвалу Богу, нашему вождю и защитнику». Так имя Аль-Хорезми перешло в Алгоритми, откуда и появилось слово алгоритм. Термин алгоритм употреблялся для обозначения четырех арифметических операций, именно в таком значении он и вошел в некоторые европейские языки. Например, в авторитетном словаре английского языка Webster’s New World Dictionary, изданном в 1957, слово алгоритм снабжено пометкой «устаревшее» и объясняется как выполнение арифметических действий с помощью арабских цифр.

Слово «алгоритм» вновь стало употребительным с появлением электронных вычислительных машин для обозначения совокупности действий, составляющих некоторый процесс. Здесь подразумевается не только процесс решения некоторой математической задачи, но и кулинарный рецепт и инструкция по использованию стиральной машины, и многие другие последовательные правила, не имеющие отношения к математике, – все эти правила являются алгоритмами. Слово «алгоритм» в наши дни известно каждому, оно настолько уверенно шагнуло в разговорную речь, что сейчас нередко на страницах газет, в выступлениях политиков встречаются выражения «алгоритм поведения», «алгоритм успеха» и т.д.

Проблема определения понятия «алгоритм».

На протяжении многих веков понятие алгоритма связывалось с числами и относительно простыми действиями над ними, да и сама математика была, по большей части, наукой о вычислениях, наукой прикладной. Чаще всего алгоритмы представлялись в виде математических формул. Порядок элементарных шагов алгоритма задавался расстановкой скобок, а сами шаги заключались в выполнении арифметических операций и операций отношения (проверки равенства, неравенства и т.д.). Часто вычисления были громоздкими, а вычисления вручную – трудоемкими, но суть самого вычислительного процесса оставалась очевидной. У математиков не возникала потребность в осознании и строгом определении понятия алгоритма, в его обобщении. Но с развитием математики появлялись новые объекты, которыми приходилось оперировать: векторы, графы, матрицы, множества и др. Как определить для них однозначность или как установить конечность алгоритма, какие шаги считать элементарными? В 1920-х задача точного определения понятия алгоритма стала одной из центральных проблем математики. В то время существовало две точки зрения на математические проблемы:

Все проблемы алгоритмически разрешимы, но для некоторых алгоритм еще не найден, поскольку еще не развиты соответствующие разделы математики.

Есть проблемы, для которых алгоритм вообще не может существовать.

Идея о существовании алгоритмически неразрешимых проблем оказалась верной, но для того, чтобы ее обосновать, необходимо было дать точное определение алгоритма. Попытки выработать такое определение привели к возникновению теории алгоритмов, в которую вошли труды многих известных математиков – К.Гедель, К.Черч, С.Клини, А.Тьюринг, Э.Пост, А.Марков, А.Колмогоров и многие другие.

Точное определение понятия алгоритма дало возможность доказать алгоритмическую неразрешимость многих математических проблем.

Появление первых проектов вычислительных машин стимулировало исследование возможностей практического применения алгоритмов, использование которых, ввиду их трудоемкости, было ранее недоступно. Дальнейший процесс развития вычислительной техники определил развитие теоретических и прикладных аспектов изучения алгоритмов.

Понятие «алгоритма».

В повседневной жизни каждый человек сталкивается с необходимостью решения задач самой разной сложности. Некоторые из них трудны и требуют длительных размышлений для поиска решений (а иногда его так и не удается найти), другие же, напротив, столь просты и привычны, что решаются автоматически. При этом выполнение даже самой простой задачи осуществляется в несколько последовательных этапов (шагов). В виде последовательности шагов можно описать процесс решения многих задач, известных из школьного курса математики: приведение дробей к общему знаменателю, решение системы линейных уравнений путем последовательного исключения неизвестных, построение треугольника по трем сторонам с помощью циркуля и линейки и т.д. Такая последовательность шагов в решении задачи называется алгоритмом. Каждое отдельное действие – это шаг алгоритма. Последовательность шагов алгоритма строго фиксирована, т.е. шаги должны быть упорядоченными. Правда, существуют параллельные алгоритмы, для которых это требование не соблюдается.

Понятие алгоритма близко к другим понятиям, таким, как метод (метод Гаусса решения систем линейных уравнений), способ (способ построения треугольника по трем сторонам с помощью циркуля и линейки). Можно сформулировать основные особенности именно алгоритмов.

Наличие исходных данных и некоторого результата.

Алгоритм – это точно определенная инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных чисел делимое может быть любым, а делитель не может быть равен нулю.

Массовость, т.е. возможность применять многократно один и тот же алгоритм. Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так алгоритм сложения применим к любой паре натуральных чисел.

Детерминированность.

При применении алгоритма к одним и тем же исходным данным должен получаться всегда один и тот же результат, поэтому, например, процесс преобразования информации, в котором участвует бросание монеты, не является детерминированным и не может быть назван алгоритмом.

Результативность.

Выполнение алгоритма должно обязательно приводить к его завершению. В то же время можно привести примеры формально бесконечных алгоритмов, широко применяемых на практике. Например, алгоритм работы системы сбора метеорологических данных состоит в непрерывном повторении последовательности действий («измерить температуру воздуха», «определить атмосферное давление»), выполняемых с определенной частотой (через минуту, час) во все время существования данной системы.

Определенность.

На каждом шаге алгоритма у исполнителя должно быть достаточно информации, чтобы его выполнить. Кроме того, исполнителю нужно четко знать, каким образом он выполняется. Шаги инструкции должны быть достаточно простыми, элементарными, а исполнитель должен однозначно понимать смысл каждого шага последовательности действий, составляющих алгоритм (при вычислении площади прямоугольника любому исполнителю нужно уметь умножать и трактовать знак «x» именно как умножение). Поэтому вопрос о выборе формы представления алгоритма очень важен. Фактически речь идет о том, на каком языке записан алгоритм.

Формы представления алгоритмов.

Для записи алгоритмов необходим некоторый язык, при этом очень важно, какой именно язык выбран. Записывать алгоритмы на русском языке (или любом другом естественном языке) громоздко и неудобно.

Например, описание алгоритма Евклида нахождения НОД (наибольшего общего делителя) двух целых положительных чисел может быть представлено в виде трех шагов. Шаг 1: Разделить m на n. Пусть p – остаток от деления.

Шаг 2: Если p равно нулю, то n и есть исходный НОД.

Шаг 3: Если p не равно нулю, то сделаем m равным n, а n равным p. Вернуться к шагу 1.

Приведенная здесь запись алгоритма нахождения НОД очень упрощенная. Запись, данная Евклидом, представляет собой страницу текста, причем последовательность действий существенно сложней.

Одним из распространенных способов записи алгоритмов является запись на языке блок-схем. Запись представляет собой набор элементов (блоков), соединенных стрелками. Каждый элемент – это «шаг» алгоритма. Элементы блок-схемы делятся на два вида. Элементы, содержащие инструкцию выполнения какого-либо действия, обозначают прямоугольниками, а элементы, содержащие проверку условия – ромбами. Из прямоугольников всегда выходит только одна стрелка (входить может несколько), а из ромбов – две (одна из них помечается словом «да», другая – словом «нет», они показывают, соответственно, выполнено или нет проверяемое условие).

На рисунке представлена блок-схема алгоритма нахождения НОД:

Построение блок-схем из элементов всего лишь нескольких типов дает возможность преобразовать их в компьютерные программы и позволяет формализовать этот процесс.

Формализация понятия алгоритмов. Теория алгоритмов.

Приведенное определение алгоритма нельзя считать представленным в привычном математическом смысле. Математические определения фигур, чисел, уравнений, неравенств и многих других объектов очень четки. Каждый математически определенный объект можно сравнить с другим объектом, соответствующим тому же определению. Например, прямоугольник можно сравнить с другим прямоугольником по площади или по длине периметра. Возможность сравнения математически определенных объектов – важный момент математического изучения этих объектов. Данное определение алгоритма не позволяет сравнивать какие-либо две таким образом определенные инструкции. Можно, например, сравнить два алгоритма решения системы уравнений и выбрать более подходящий в данном случае, но невозможно сравнить алгоритм перехода через улицу с алгоритмом извлечения квадратного корня. С этой целью нужно формализовать понятие алгоритма, т.е. отвлечься от существа решаемой данным алгоритмом задачи, и выделить свойства различных алгоритмов, привлекая к рассмотрению только его форму записи. Задача нахождения единообразной формы записи алгоритмов, решающих различные задачи, является одной из основных задач теории алгоритмов. В теории алгоритмов предполагается, что каждый шаг алгоритма таков, что его может выполнить достаточно простое устройство (машина), Желательно, чтобы это устройство было универсальным, т.е. чтобы на нем можно было выполнять любой алгоритм. Механизм работы машины должен быть максимально простым по логической структуре, но настолько точным, чтобы эта структура могла служить предметом математического исследования. Впервые это было сделано американским математиком Эмилем Постом в 1936 (машина Поста) еще до создания современных вычислительных машин и (практически одновременно) английским математиком Аланом Тьюрингом (машина Тьюринга).

История конечных автоматов: машина Поста и машина Тьюринга.

Машина Поста – абстрактная вычислительная машина, предложенная Постом (Emil L.Post), которая отличается от машины Тьюринга большей простотой. Обе машины «эквивалентны» и были созданы для уточнения понятия «алгоритм».

В 1935 американский математик Пост опубликовал в «Журнале символической логики» статью Финитные комбинаторные процессы, формулировка 1. В этой статье и появившейся одновременно в Трудах Лондонского математического общества статье английского математика Тьюринга О вычислимых числах с приложением к проблеме решения были даны первые уточнения понятия «алгоритм». Важность идей Поста состоит в том, что был предложен простейший способ преобразования информации, именно он построил алгоритмическую систему (алгоритмическая система Поста). Пост доказал, что его система обладает алгоритмической полнотой. В 1967 профессор В.Успенский пересказал эти статьи с новых позиций. Он ввел термин «машина Поста». Машина Поста – абстрактная машина, которая работает по алгоритмам, разработанным человеком, она решает следующую проблему: если для решения задачи можно построить машину Поста, то она алгоритмически разрешима. В 1970 машина Поста была разработана в металле в Симферопольском университете. Машина Тьюринга была построена в металле в 1973 в Малой Крымской Академии Наук.

Абстрактная машина Поста представляет собой бесконечную ленту, разделенную на одинаковые клетки, каждая из которых может быть либо пустой, либо заполненной меткой «V». У машины есть головка, которая может перемещаться вдоль ленты на одну клетку вправо или влево, наносить в клетку ленты метку, если этой метки там ранее не было, стирать метку, если она была, либо проверять наличие в клетке метки. Информация о заполненных метками клетках ленты характеризует состояние ленты, которое может меняться в процессе работы машины. В каждый момент времени головка находится над одной из клеток ленты и, как говорят, обозревает ее. Информация о местоположения головки вместе с состоянием ленты характеризует состояние машины Поста. Работа машины Поста заключается в том, что головка передвигается вдоль ленты (на одну клетку за один шаг) влево или вправо, наносит или стирает метки, а также распознает, есть ли метка в клетке в соответствии с заданной программой, состоящей из отдельных команд.

Машина Тьюринга состоит из счетной ленты (разделенной на ячейки и ограниченной слева, но не справа), читающей и пишущей головки, лентопротяжного механизма и операционного исполнительного устройства, которое может находиться в одном из дискретных состояний q0, q1, …, qs , принадлежащих некоторой конечной совокупности (алфавиту внутренних состояний), при этом q0 называется начальным состоянием. Читающая и пишущая головка может читать буквы рабочего алфавита A = a0, a1, …, at >, стирать их и печатать. Каждая ячейка ленты в каждый момент времени занята буквой из множества А. Чаще всего встречается буква а0 – «пробел». Головка находится в каждый момент времени над некоторой ячейкой ленты – текущей рабочей ячейкой. Лентопротяжный механизм может перемещать ленту так, что головка оказывается над соседней ячейкой ленты, при этом возможна ситуация выхода за левый край ленты, которая является аварийной (недопустимой), или машинного останова, когда машина выполняет предписание об остановке.

Современный взгляд на алгоритмизацию.

Теория алгоритмов строит и изучает конкретные модели алгоритмов. С развитием вычислительной техники и теории программирования возрастает необходимость построения новых экономичных алгоритмов, изменяются способы их построения, способы записи алгоритмов на языке, понятном исполнителю. Особый тип исполнителя алгоритмов – компьютер, поэтому необходимо создавать специальные средства, позволяющие, с одной стороны, разработчику в удобном виде записывать алгоритмы, а с другой – дающие компьютеру возможность понимать написанное. Такими средствами являются языки программирования или алгоритмические языки.

Алгоритм и его свойства. Примеры алгоритмов

Цель занятия: познакомить учащихся с понятием алгоритма, исполнителями алгоритмов, примерами алгоритмов в жизни, алгоритмическим способом решения задач, закрепить полученные знания с помощью электронного теста, развивать навыки самоконтроля.

Ход урока

Организационный момент.
Подготовка к изучению нового материала. (ознакомление с планом и целью занятия) .
Изучение нового материала. (просмотр электронного урока с использованием мультимедиа проектора) . Слайды + текст лекции.
По ходу урока учащиеся конспектируют определения и отвечают на вопросы.
Закрепление темы занятия (работа уч-ся на компьютере) . Электронный тест с последующей самопроверкой. Решение алгоритмических задач.
Подведение итогов. Выставление оценок с учетом процентного выполнения теста.
Задание на дом. (выучить определения, привести примеры алгоритмов из жизненной практики.)

Изучение нового материала.

Один из важнейших этапов решения задач на ЭВМ – составление алгоритма. О том, что такое алгоритмы, какими общими свойствами они обладают и как исполняются, мы и поговорим на этом уроке.

В 1983 году отмечалось 1200-летие со дня рождения одного из величайших ученых Средней Азии и средневекового Востока Мухамада ибн Мусы аль-Хорезми. Он написал ряд трактатов по арифметике и алгебре, в том числе книгу «Арифметика индусскими цифрами» – о счете с помощью десяти цифр и правилах арифметических действий с числами.

Имя ученого аль-Хорезми превратилось в понятие algorithmi, первоначально обозначавшее десятичную систему исчисления и правила арифметических действий в этой системе. Отсюда и возник современный научный термин «алгоритм».

Каждый из нас ежедневно использует различные алгоритмы: инструкции, правила, рецепты и т.п. Обычно мы это делаем не задумываясь. Например, открывая дверь ключом, никто не размышляет над тем, в какой последовательности выполнять действия. Однако чтобы научить кого-нибудь открывать дверь, придется четко указать и сами действия, и порядок их выполнения. То же потребуется и при указании маршрута поездки.

Сравним эти алгоритмы. На первый взгляд, между ними нет ничего общего. Одно дело – открывать дверь, другое – ехать в гости. Но если приглядеться внимательно, можно заметить существенное сходство между ними. Прежде всего, это строгий порядок выполнения действий.

Мы можем теперь сказать, что алгоритм – это организованная последовательность действий. Данную формулировку, конечно, нельзя считать определением алгоритма. Например, мы не объяснили, что означают слова «организованная» и «действия». Скажем сразу: абсолютно строгого определения алгоритма не существует. Алгоритм – это одно из тех основных понятий (категорий) математики, которые не обладают формальным определением в терминах более простых понятий, а абстрагируются непосредственно из опыта.

На слайде еще одно задание. Выполните его, используя для записи ответа любой текстовый редактор или бумагу и карандаш.

Сравните свой ответ с правильным.

Налить в чайник воду.
Зажечь спичку.
Открыть кран газовой горелки.
Поднести спичку к горелке.
Поставить чайник на плиту.
Ждать, пока вода закипит.
Выключить газ.

Рассмотренные нами алгоритмы составлены для исполнения человеком. Но человек далеко не единственный возможный исполнитель алгоритмов. Все живые существа и даже отдельные клетки исполняют различные алгоритмы. Способны на это и созданные человеком устройства – роботы-манипуляторы и станки с программным управлением. Но прежде чем составлять алгоритм решения задачи, нужно узнать, какие действия предполагаемый исполнитель способен выполнить.

Поясним сказанное на примере. Допустим, нужно решить квадратное уравнение.

Десятикласснику требуется минимум инструкций, потому что он уже знает способ решения.

Восьмикласснику понадобятся намного более сложные инструкции, потому что он этого еще не проходил.

Теперь мы можем уточнить понятие алгоритма: это организованная последовательность действий, допустимых для некоторого исполнителя.

Первое. Требуется исполнитель.
Второе. Процесс должен быть разбит на этапы, понятные исполнителю.
Третье. Должно быть определено начальное состояние текста и его требуемое конечное состояние.

Теория алгоритмов имеет большое практическое значение. Алгоритмический тип деятельности важен не только как одна из эффективных форм труда человека. Через алгоритмизацию, через расчленение сложных действий на всё более простые, на действия, выполнение которых доступно машинам, пролегает путь к автоматизации различных процессов.

Далее под алгоритмом будет пониматься конечная последовательность указаний, адресованных исполнителю, четко и однозначно задающая процесс решения задач какого-либо типа во всех деталях и позволяющая получить за конечное число шагов результат, однозначно определяемый исходными данными.

Такое свойство алгоритма, как однозначность результата при заданных исходных данных, называется определенностью (детерминированностью) .

Заметим, что большинство алгоритмов могут выполняться при достаточно разнообразных наборах исходных данных, то есть использоваться для решения не какой-либо одной задачи, а целого класса подобных задач. Это свойство алгоритма называется массовостью.

С алгоритмами человек встречается на каждом шагу.

Пример 1. Дан угол. Необходимо провести биссектрису. (Есть способ, как, пользуясь линейкой и циркулем, можно решить эту задачу.)

Пример 2. Даны два целых числа. Необходимо найти их разность. (Имеется правило, в котором ясно изложен весь порядок действий с цифрами данных чисел.)

В приведенных примерах речь идет о том, как сложную работу представить в виде последовательности простых действий. Вычитание многоразрядных чисел сводится к действиям с цифрами. При делении угла пополам выполняются несложные построения линейкой и циркулем.

Однако высказанные соображения следует дополнить. Ведь правила вычитания формулируются для любых многоразрядных чисел, а не для каких-то конкретных двух. Инструкция проведения биссектрисы тоже такова, что, пользуясь ею, можно разделить пополам любой угол. То есть каждому алгоритму присуща массовость – пригодность для решения не какой-либо одной, а целого класса задач.

Такое свойство алгоритма, как однозначность результата при заданных исходных данных, называется определенностью (детерминированностью) .На этом занятии мы познакомились с такими важнейшими понятиями, как алгоритм, исполнитель, система команд исполнителя, узнали основные свойства алгоритма.

Алгоритмические задачи

№1. Старик должен переправить на лодке через реку волка, козу и капусту. Лодка может выдержать только старика и одного “пассажира”. В каком порядке старик перевезет пассажиров? Не забудь, что волк может съесть козу, а коза – капусту. Найди 2 варианта решения.

Алгоритм решения задачи:

1 вариант	2 вариант
1) __________________________	1) _________________________
2) _________________________	2) _________________________
3) __________________________	3) _________________________

№2 Два мальчика и двое взрослых должны переправиться на другую сторону реки на плоту, который выдерживает либо двух мальчиков, либо одного мальчика и одного взрослого. Как осуществить переправу? Найди несколько способов решения этой задачи.

Алгоритм решения задачи:

1 способ	2 способ	3 способ
1 шаг
2 шаг
3 шаг
4 шаг
5 шаг

Обозначения: 1м- один мальчик, 2м – два мальчика, 1в – один взрослый.

1. Практикум по решению задач

Злоумышленник поменял местами действия в алгоритме вычисления среднего арифметического из квадратного корня трёх чисел:

Присвоить а значение (а 2 +в 2 +с 2 ) /3.

Сообщить “Среднее арифметическое квадратов равно”

Восстановите правильный порядок действий.

2. Исправьте следующий алгоритм решения уравнения (х-2) (х+2) =0:

Присвоить х значение +-2.

Сообщить “Корни уравнения равны”.

Сообщить первое значение х.

Сообщить второе значение х.

3. Автомобиль проехал три участка пути разной длины с разными скоростями. Составьте алгоритм нахождения средней скорости автомобиля.

4. Проснувшись утром, школьник почувствовал недомогание. Находившийся рядом злоумышленник тут же составил для него следующий алгоритм:

Если температура выше 37 0 , то:

Несмотря на недомогание, школьник исправил этот алгоритм, добавив всего две строки. Какие строки добавил школьник?

5. Запишите в виде алгоритмов правила определения знака:

А) произведения двух действительных чисел;

Б) суммы двух действительных чисел.

6. В записи алгоритма вычисления значения выражения (х 2 — 5х+5) / (х 6 — 4х 2 +3)

ввести х
если х 6 — 4х 2 + 3=0, то:
сообщить “При таком х значение выражения не определено”.
иначе:
присвоить у значение (х 2 — 5х +5) /(х 6 — 4х 2 +3) .
конец ветвления.
сообщить у.

Верните действие на свое место.

1.Которые из документов являются алгоритмами?

а) Правило правописания приставок, оканчивающихся на з,с(да)

б) Программа телепередач

в) Кулинарный рецепт приготовления блюда

г) Инструкция по сборке проданного в разобранном виде шкафа

2. В каких случаях правильно заканчивается предложение: Алгоритм – это

а) конечная последовательность действий, приводящая к искомому результату при любых допустимых исходных данных

б) указание на выполнение действий

в) конечный набор понятных некоторому исполнителю команд, выполнение которых приводит к однозначному решению поставленной задачи

г) программа в машинных кодах

3. Расчлененность алгоритма на отдельные элементарные действия – это

4. Которые из документов являются алгоритмами?

А) Каталог книг в библиотеке

Б) Порядок набора международного телефонного номера

В) Рецепт приготовления клея

Г) Настенный календарь на текущий год

Подведение итогов. Выставление оценок с учетом процентного выполнения теста.

Задание на дом. (выучить определения, привести примеры алгоритмов из жизненной практики.)

Алгоритм

Алгори́тм — набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное число действий. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Это связано с тем, что работа каких-то инструкций алгоритма может быть зависима от других инструкций или результатов их работы. Таким образом, некоторые инструкции должны выполняться строго после завершения работы инструкций, от которых они зависят. Независимые инструкции или инструкции, ставшие независимыми из-за завершения работы инструкций, от которых они зависят, могут выполняться в произвольном порядке, параллельно или одновременно, если это позволяют используемые процессор и операционная система.

Ранее часто писали «алгорифм», сейчас такое написание используется редко, но, тем не менее, имеет место (например, Нормальный алгорифм Маркова).

Часто в качестве исполнителя выступает некоторый механизм (компьютер, токарный станок, швейная машина), но понятие алгоритма необязательно относится к компьютерным программам, так, например, чётко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек.

Понятие алгоритма относится к первоначальным, основным, базисным понятиям математики. Вычислительные процессы алгоритмического характера (арифметические действия над целыми числами, нахождение наибольшего общего делителя двух чисел и т. д.) известны человечеству с глубокой древности. Однако, в явном виде понятие алгоритма сформировалось лишь в начале XX века.

Частичная формализация понятия алгоритма началась с попыток решения проблемы разрешения (нем. Entscheidungsproblem ), которую сформулировал Давид Гильберт в 1928 году. Следующие этапы формализации были необходимы для определения эффективных вычислений [1] или «эффективного метода» [2] ; среди таких формализаций — рекурсивные функции Геделя — Эрбрана — Клини 1930, 1934 и 1935 гг., λ-исчисление Алонзо Чёрча 1936 г., «Формулировка 1» Эмиля Поста 1936 года и машина Тьюринга. В методологии алгоритм является базисным понятием и получает качественно новое понятие как оптимальности по мере приближения к прогнозируемому абсолюту. В современном мире алгоритм в формализованном выражении составляет основу образования на примерах, по подобию. На основе сходства алгоритмов различных сфер деятельности была сформирована концепция (теория) экспертных систем.

Содержание

История термина

Страница из «Алгебры» аль-Хорезми — хорезмского математика, от имени которого происходит слово алгоритм.

Современное формальное определение алгоритма было дано в 30—50-е годы XX века в работах Тьюринга, Поста, Чёрча (тезис Чёрча — Тьюринга), Н. Винера, А. А. Маркова.

Само слово «алгоритм» происходит от имени хорезмского учёного Абу Абдуллах Мухаммеда ибн Муса аль-Хорезми (алгоритм — аль-Хорезми). Около 825 года он написал сочинение, в котором впервые дал описание придуманной в Индии позиционной десятичной системы счисления. К сожалению, персидский оригинал книги не сохранился. Аль-Хорезми сформулировал правила вычислений в новой системе и, вероятно, впервые использовал цифру 0 для обозначения пропущенной позиции в записи числа (её индийское название арабы перевели как as-sifr или просто sifr, отсюда такие слова, как «цифра» и «шифр»). Приблизительно в это же время индийские цифры начали применять и другие арабские учёные. В первой половине XII века книга аль-Хорезми в латинском переводе проникла в Европу. Переводчик, имя которого до нас не дошло, дал ей название Algoritmi de numero Indorum («Алгоритмы о счёте индийском»). По-арабски же книга именовалась Китаб аль-джебр валь-мукабала («Книга о сложении и вычитании»). Из оригинального названия книги происходит слово Алгебра (алгебра — аль-джебр — восполнение).

Таким образом, мы видим, что латинизированное имя среднеазиатского учёного было вынесено в заглавие книги, и сегодня считается, что слово «алгоритм» попало в европейские языки именно благодаря этому сочинению. Однако вопрос о его смысле длительное время вызывал ожесточённые споры. На протяжении многих веков происхождению слова давались самые разные объяснения.

Одни выводили algorism из греческих algiros (больной) и arithmos (число). Из такого объяснения не очень ясно, почему числа именно «больные». Или же лингвистам больными казались люди, имеющие несчастье заниматься вычислениями? Своё объяснение предлагал и энциклопедический словарь Брокгауза и Ефрона. В нём алгорифм (кстати, до революции использовалось написание алгориѳм, через фиту) производится «от арабского слова Аль-Горетм, то есть корень». Разумеется, эти объяснения вряд ли можно счесть убедительными.

Упомянутый выше перевод сочинения аль-Хорезми стал первой ласточкой, и в течение нескольких следующих столетий появилось множество других трудов, посвящённых всё тому же вопросу — обучению искусству счёта с помощью цифр. И все они в названии имели слово algoritmi или algorismi.

Про аль-Хорезми позднейшие авторы ничего не знали, но поскольку первый перевод книги начинается словами: «Dixit algorizmi: …» («Аль-Хорезми говорил: …»), всё ещё связывали это слово с именем конкретного человека. Очень распространённой была версия о греческом происхождении книги. В англо-норманнской рукописи XIII века, написанной в стихах, читаем:

Алгоризм был придуман в Греции. Это часть арифметики. Придуман он был мастером по имени Алгоризм, который дал ему своё имя. И поскольку его звали Алгоризм, Он назвал свою книгу «Алгоризм».

Около 1250 года английский астроном и математик Иоанн Сакробоско написал труд по арифметике Algorismus vulgaris, на столетия ставший основным учебником по вычислениям в десятичной позиционной системе счисления во многих европейских университетах. Во введении Сакробоско назвал автором науки о счёте мудреца по имени Алгус (Algus). А в популярной средневековой поэме «Роман о Розе» (1275—1280) Жана де Мена «греческий философ Алгус» ставится в один ряд с Платоном, Аристотелем, Евклидом и Птолемеем! Встречался также вариант написания имени Аргус (Argus). И хотя, согласно древнегреческой мифологии, корабль «Арго» был построен Ясоном, именно этому Арго приписывалось строительство корабля.

«Мастер Алгус» (или Аргус) стал в средневековой литературе олицетворением счётного искусства. И в уже упоминавшейся «Романе о розе», и в известной итальянской поэме «Цветок», написанной Дуранте, имеются фрагменты, в которых говорится, что даже «mestre Argus» не сумеет подсчитать, сколько раз ссорятся и мирятся влюблённые. Английский поэт Джефри Чосер в поэме «Книга герцогини» (1369 г.) пишет, что даже «славный счётчик Аргус» (noble countour Argu) не сможет счесть чудовищ, явившихся в кошмарных видениях герою.

Впрочем, греческая версия была не единственной. Мифический АлГор (Algor) именовался то королём Кастилии (Rex quodam Castelliae), то индийским королём, то арабским мудрецом (philosophus Algus nomine Arabicus), то египетским божеством. Соответственно АлГорРитм — это ритм (порядок) бога Гора (АлГора).

Однако со временем такие объяснения всё менее занимали математиков, и слово algorism (или algorismus), неизменно присутствовавшее в названиях математических сочинений, обрело значение способа выполнения арифметических действий посредством арабских цифр, то есть на бумаге, без использования абака. Именно в таком значении оно вошло во многие европейские языки. Например, с пометкой «устар.» оно присутствует в представительном словаре английского языка Webster’s New World Dictionary, изданном в 1957 г.

Алгоритм — это искусство счёта с помощью цифр, но поначалу слово «цифра» относилось только к нулю. Знаменитый французский трувер Готье де Куанси (Gautier de Coincy, 1177—1236) в одном из стихотворений использовал слова algorismus-cipher (которые означали цифру 0) как метафору для характеристики абсолютно никчёмного человека. Очевидно, понимание такого образа требовало соответствующей подготовки слушателей, а это означает, что новая система счисления уже была им достаточно хорошо известна.

Многие века абак был фактически единственным средством для практичных вычислений, им пользовались и купцы, и менялы, и учёные. Достоинства вычислений на счётной доске разъяснял в своих сочинениях такой выдающийся мыслитель, как Герберт Аврилакский (938—1003), ставший в 999 г. папой римским под именем Сильвестра II. Новое с огромным трудом пробивало себе дорогу, и в историю математики вошло упорное противостояние лагерей алгорисмиков и абацистов (иногда называемых гербекистами), которые пропагандировали использование для вычислений абака вместо арабских цифр. Интересно, что известный французский математик Николя Шюке (Nicolas Chuquet, 1445—1488) в реестр налогоплательщиков города Лиона был вписан как алгорисмик (algoriste). Но прошло не одно столетие, прежде чем новый способ счёта окончательно утвердился, столько времени потребовалось, чтобы выработать общепризнанные обозначения, усовершенствовать и приспособить к записи на бумаге методы вычислений. В Западной Европе учителей арифметики вплоть до XVII века продолжали называть «магистрами абака», как, например, математика Никколо Тарталью (1500—1557).

Итак, сочинения по искусству счёта назывались Алгоритмами. Из многих сотен можно выделить и такие необычные, как написанный в стихах трактат Carmen de Algorismo (латинское carmen и означает стихи) Александра де Вилла Деи (Alexander de Villa Dei, ум. 1240) или учебник венского астронома и математика Георга Пурбаха (Georg Peurbach, 1423—1461) Opus algorismi jocundissimi («Веселейшее сочинение по алгоритму»).

Постепенно значение слова расширялось. Учёные начинали применять его не только к сугубо вычислительным, но и к другим математическим процедурам. Например, около 1360 г. французский философ Николай Орем (Nicolaus Oresme, 1323/25-1382) написал математический трактат Algorismus proportionum («Вычисление пропорций»), в котором впервые использовал степени с дробными показателями и фактически вплотную подошёл к идее логарифмов. Когда же на смену абаку пришёл так называемый счёт на линиях, многочисленные руководства по нему стали называть Algorithmus linealis, то есть правила счёта на линиях.

Можно обратить внимание на то, что первоначальная форма algorismi спустя какое-то время потеряла последнюю букву, и слово приобрело более удобное для европейского произношения вид algorism. Позднее и оно, в свою очередь, подверглось искажению, скорее всего, связанному со словом arithmetic.

В 1684 году Готфрид Лейбниц в сочинении Nova Methodvs pro maximis et minimis, itemque tangentibus… впервые использовал слово «алгоритм» (Algorithmo) в ещё более широком смысле: как систематический способ решения проблем дифференциального исчисления.

В XVIII веке в одном из германских математических словарей, Vollstandiges mathematisches Lexicon (изданном в Лейпциге в 1747 г.), термин algorithmus всё ещё объясняется как понятие о четырёх арифметических операциях. Но такое значение не было единственным, ведь терминология математической науки в те времена ещё только формировалась. В частности, выражение algorithmus infinitesimalis применялось к способам выполнения действий с бесконечно малыми величинами. Пользовался словом алгоритм и Леонард Эйлер, одна из работ которого так и называется — «Использование нового алгоритма для решения проблемы Пелля» (De usu novi algorithmi in problemate Pelliano solvendo). Мы видим, что понимание Эйлером алгоритма как синонима способа решения задачи уже очень близко к современному.

Однако потребовалось ещё почти два столетия, чтобы все старинные значения слова вышли из употребления. Этот процесс можно проследить на примере проникновения слова «алгоритм» в русский язык.

Историки датируют 1691 годом один из списков древнерусского учебника арифметики, известного как «Счётная мудрость». Это сочинение известно во многих вариантах (самые ранние из них почти на сто лет старше) и восходит к ещё более древним рукописям XVI в. По ним можно проследить, как знание арабских цифр и правил действий с ними постепенно распространялось на Руси. Полное название этого учебника — «Сия книга, глаголемая по еллински и по гречески арифметика, а по немецки алгоризма, а по русски цифирная счётная мудрость».

Таким образом, слово «алгоритм» понималось первыми русскими математиками так же, как и в Западной Европе. Однако его не было ни в знаменитом словаре В. И. Даля, ни спустя сто лет в «Толковом словаре русского языка» под редакцией Д. Н. Ушакова (1935 г.). Зато слово «алгорифм» можно найти и в популярном дореволюционном Энциклопедическом словаре братьев Гранат, и в первом издании Большой советской энциклопедии (БСЭ), изданном в 1926 г. И там, и там оно трактуется одинаково: как правило, по которому выполняется то или иное из четырёх арифметических действий в десятичной системе счисления. Однако к началу XX в. для математиков слово «алгоритм» уже означало любой арифметический или алгебраический процесс, выполняемый по строго определённым правилам, и это объяснение также даётся в следующих изданиях БСЭ.

Алгоритмы становились предметом всё более пристального внимания учёных, и постепенно это понятие заняло одно из центральных мест в современной математике. Что же касается людей, от математики далёких, то к началу сороковых годов это слово они могли услышать разве что во время учёбы в школе, в сочетании «алгоритм Евклида». Несмотря на это, алгоритм всё ещё воспринимался как термин сугубо специальный, что подтверждается отсутствием соответствующих статей в менее объёмных изданиях. В частности, его нет даже в десятитомной Малой советской энциклопедии (1957 г.), не говоря уже об однотомных энциклопедических словарях. Но зато спустя десять лет, в третьем издании Большой советской энциклопедии (1969 г.) алгоритм уже характеризуется как одна из основных категорий математики, «не обладающих формальным определением в терминах более простых понятий, и абстрагируемых непосредственно из опыта». Как мы видим, отличие даже от трактовки первым изданием БСЭ разительное! За сорок лет алгоритм превратился в одно из ключевых понятий математики, и признанием этого стало включение слова уже не в энциклопедии, а в словари. Например, оно присутствует в академическом «Словаре русского языка» (1981 г.) именно как термин из области математики.

Одновременно с развитием понятия алгоритма постепенно происходила и его экспансия из чистой математики в другие сферы. И начало ей положило появление компьютеров, благодаря которому слово «алгоритм» вошло в 1985 г. во все школьные учебники информатики и обрело новую жизнь. Вообще можно сказать, что его сегодняшняя известность напрямую связана со степенью распространения компьютеров. Например, в третьем томе «Детской энциклопедии» (1959 г.) о вычислительных машинах говорится немало, но они ещё не стали чем-то привычным и воспринимаются скорее как некий атрибут светлого, но достаточно далёкого будущего. Соответственно и алгоритмы ни разу не упоминаются на её страницах. Но уже в начале 70-х гг. прошлого столетия, когда компьютеры перестали быть экзотической диковинкой, слово «алгоритм» стремительно входит в обиход. Это чутко фиксируют энциклопедические издания. В «Энциклопедии кибернетики» (1974 г.) в статье «Алгоритм» он уже связывается с реализацией на вычислительных машинах, а в «Советской военной энциклопедии» (1976 г.) даже появляется отдельная статья «Алгоритм решения задачи на ЭВМ». За последние полтора-два десятилетия компьютер стал неотъемлемым атрибутом нашей жизни, компьютерная лексика становится всё более привычной. Слово «алгоритм» в наши дни известно, вероятно, каждому. Оно уверенно шагнуло даже в разговорную речь, и сегодня мы нередко встречаем в газетах и слышим в выступлениях политиков выражения вроде «алгоритм поведения», «алгоритм успеха» или даже «алгоритм предательства». Академик Н. Н. Моисеев назвал свою книгу «Алгоритмы развития», а известный врач Н. М. Амосов — «Алгоритм здоровья» и «Алгоритмы разума». А это означает, что слово живёт, обогащаясь всё новыми значениями и смысловыми оттенками.

Определения алгоритма

Формальное определение

Разнообразные теоретические проблемы математики и ускорение развития физики и техники поставили на повестку дня точное определение понятия алгоритма.

Первые попытки уточнения понятия алгоритма и его исследования осуществляли в первой половине XX века Алан Тьюринг, Эмиль Пост, Жак Эрбран, Курт Гедель, А. А. Марков, Алонзо Чёрч. Было разработано несколько определений понятия алгоритма, но впоследствии было выяснено, что все они определяют одно и то же понятие (см. Тезис Чёрча — Тьюринга) [3]

Алгоритм

Понятие алгоритма, являющееся фундаментальным понятием математики и информатики, возникло задолго до появления вычислительных машин. Первоначально под словом алгоритм понимали способ выполнения арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи. Само же слово алгоритм появилось в Средние века, когда европейцы познакомились со способами выполнения арифметических действий, описанными узбекским математиком Мухаммедом бен Муса аль-Хорезми. Слово алгоритм — европеизированное произношение слов аль-Хорезми.

В своем нынешнем смысле слово алгоритм часто ассоциировалось с алгоритмом Евклида, который представляет собой процесс нахождения наибольшего общего делителя (НОД) двух чисел.

Приведем современное описание алгоритма Евклида с использованием блок-схемы (см. “Способы записи алгоритмов”):

Стрелка “ ”, используемая при описании данного алгоритма, обозначает операцию замещения или присваивания (см. “Операторы языка программирования”). Разумеется, в книге Евклида “Начала” этот алгоритм сформулирован не совсем так (а записан совсем не так). В данном случае мы продемонстрировали современную формулировку этого алгоритма и одну из распространенных наглядных форм записи алгоритмов.

Любой алгоритм существует не сам по себе, а предназначен для определенного исполнителя (см. “Исполнители алгоритмов”). Алгоритм описывается в командах исполнителя, который этот алгоритм будет выполнять. Объекты, над которыми исполнитель может совершать действия, образуют так называемую среду исполнителя, а множество команд, которые исполнитель может выполнять, — систему команд исполнителя (СКИ).

Таким образом, алгоритм можно рассматривать как последовательность команд управления работой исполнителя (предписание исполнителю на выполнение последовательности действий).

Свойства алгоритма

Значение слова алгоритм очень схоже со значением слов рецепт, инструкция. Однако любой алгоритм в отличие от рецепта или способа обязательно обладает следующими свойствами.

1. Выполнение алгоритма разбивается на последовательность законченных действий-шагов. Только выполнив одно действие (команду), можно приступать к исполнению следующего. Это свойство алгоритма называется дискретностью. Произвести каждое отдельное действие исполнителю предписывает специальное указание в записи алгоритма (команда).

2. Понятность — алгоритм не должен содержать предписаний, смысл которых может восприниматься исполнителем неоднозначно, т.е. запись алгоритма должна быть настолько четкой и полной, чтобы у исполнителя не возникало потребности в принятии каких-либо самостоятельных решений. Алгоритм всегда рассчитан на выполнение “не размышляющего” исполнителя. Алгоритм составляется из команд, входящих в СКИ.

Рассмотрим известный пример “бытового” алгоритма — алгоритм перехода улицы: “Посмотри налево. Если машин нет, дойди до середины улицы. Если есть, подожди, пока они проедут, и т.д.”. Представьте себе ситуацию: машина слева есть, но она не едет — у нее меняют колесо. Если вы думаете, что исполнитель алгоритма должен ждать, то вы поняли этот алгоритм. Если же вы решили, что улицу переходить можно, считая алгоритм подправленным ввиду непредвиденных (по вашему мнению!) обстоятельств, то вы не усвоили понятие алгоритма.

3. Детерминированность (определенность и однозначность). Каждая команда алгоритма определяет однозначное действие исполнителя, и должно быть однозначно определено, какая команда выполняется следующей. То есть если алгоритм многократно применяется к одному и тому же набору исходных данных, то на выходе он получает каждый раз один и тот же результат.

4. Результативность — исполнение алгоритма должно закончиться за конечное число шагов, и при этом должен быть получен результат решения задачи. В качестве одного из возможных результатов может быть и установление того факта, что задача решений не имеет.

Свойство результативности содержит в себе свойство конечности — завершение работы алгоритма за конечное число шагов.

5. Массовость — алгоритм пригоден для решения любой задачи из некоторого класса задач, т.е. алгоритм правильно работает на некотором множестве исходных данных, которое называется областью применимости алгоритма.

Свойство массовости определяет скорее качество алгоритма, а не относится к обязательным свойствам (как дискретность, понятность и пр.). Существуют алгоритмы, область применимости которых ограничивается единственным набором входных данных или даже отсутствием таковых (например, получение фиксированного числа верных цифр числа p). Правильнее говорить о том, что алгоритм должен быть применим к любым данным из своей области определения, и слово массовость не всегда подходит для описания такого свойства.

Понятие алгоритма

Обобщив вышесказанное, сформулируем следующее понятие алгоритма.

Алгоритм — понятное и точное предписание исполнителю на выполнение конечной последовательности действий, приводящей от исходных данных к искомому результату.

Приведенное определение не является определением в математическом смысле слова, т.е. это не формальное определение (формальное определение алгоритма см. в статье “Теория алгоритмов”).

Отметим, что для каждого исполнителя набор допустимых действий (СКИ) всегда ограничен — не может существовать исполнителя, для которого любое действие является допустимым. Перефразированное рассуждение И.Канта обосновывает сформулированное утверждение следующим образом: “Если бы такой исполнитель существовал, то среди его допустимых действий было бы создание такого камня, который он не может поднять. Но это противоречит допустимости действия «Поднять любой камень»”.

Интересно, что существуют задачи, которые человек, вообще говоря, умеет решать, не зная при этом алгоритм ее решения. Например, перед человеком лежат фотографии кошек и собак. Задача состоит в том, чтобы определить, кошка или собака изображена на конкретной фотографии. Человек решает эту задачу, но написать алгоритм решения этой задачи пока чрезвычайно сложно.

С другой стороны, существуют задачи, для которых вообще невозможно построить процедуру решения. Причем данный факт можно строго доказать. Об этом вы можете прочитать в статье “Алгоритмически неразрешимые проблемы”.

Методические рекомендации

Данная тема традиционно изучается в базовом курсе информатики основной школы. Содержание статьи “Алгоритм” может рассматриваться в качестве базового минимума информации по этой теме для учеников 8–9-х классов. В пропедевтическом курсе информатики (5–7-е классы) более актуальным является составление конкретных алгоритмов с использованием различных форм их записи, в том числе и для учебных исполнителей (см. “Исполнители алгоритмов”).

Каждый из нас ежедневно решает задачи различной сложности: как быстрее добраться в школу или на работу в условиях нехватки времени; в каком порядке выполнять дела, намеченные на текущий день, и т.д. Некоторые задачи настолько сложны, что требуют длительных размышлений для нахождения решения (иногда решение так и не удается найти), другие задачи мы решаем автоматически, так как выполняем их ежедневно на протяжении многих лет (почистить утром зубы; позвонить другу по телефону). В большинстве случаев решение каждой задачи можно подразделить на простые этапы.

Пример. Задача “Звонок другу по телефону” подразделяется на следующие этапы (шаги):

1. Поднять телефонную трубку.

2. Если услышал гудок, то набрать номер друга, иначе конец решения задачи с отрицательным результатом (телефон неисправен).

3. Определить тип гудков: “вызов” или “занято”. Если “вызов”, перейти к шагу 4, если “занято”, перейти к шагу 6.

4. Дождаться 6 вызывающих гудков (конкретное число гудков в алгоритме для разных людей может быть различным).

5. Если за это время абонент не поднял трубку, то конец решения задачи с отрицательным результатом (абонент не отвечает). Иначе начать разговор (задача решена успешно).

6. Положить телефонную трубку; конец решения задачи с отрицательным результатом (абонент занят).

Последовательность шагов, приведенная в примере 1, является алгоритмом решения задачи “Звонок другу по телефону”. Исполнитель этого алгоритма — человек. Объекты алгоритма — телефон и телефонные сигналы.

При разборе алгоритма “Звонок другу по телефону” следует обратить внимание на п. 4 (“дождаться 6 вызывающих гудков”): без указания конкретного числа гудков нарушается сразу несколько свойств алгоритма (дискретность, определенность и результативность). Естественно, вместо числа 6 в алгоритме может стоять любое другое разумное число.

Для решения любой задачи надо знать, что дано и что следует получить, т.е. у задачи есть исходные данные (некие объекты) и искомые результаты. Для получения результатов необходимо знать способ решения задачи, то есть располагать алгоритмом, в котором указано, какие действия и в каком порядке следует выполнить, чтобы решить задачу (получить искомые результаты). Далее следует разобрать свойства алгоритма на примере решения какой-либо бытовой проблемы. Составление алгоритмов для решения бытовых проблем только на первый взгляд кажется простым, мы очень многие действия делаем автоматически, и их формализация требует от учащихся учета многих деталей и факторов.

При изложении теоретического материала необходимо обратить внимание на то, почему приведенное определение алгоритма не является строгим математическим определением, а является только описанием понятия алгоритм, раскрывающим его сущность. Оно не является формальным потому, что в нем используются такие не уточняемые понятия, как “система правил”, “исходные данные”, и т.д.

В рамках изучения этой темы желательно также обсудить вопрос, является ли способ переправки Волка, Козы и Капусты через реку алгоритмом (эта задача рассматривается во многих учебниках информатики как пример задачи на построение алгоритмов)? Иногда ученики сначала склоняются к мнению, что решение упомянутой задачи алгоритмом не является, т.к. не обладает свойством массовости. Но способ решения частной задачи — это тоже алгоритм (см. замечания о массовости в тексте статьи).

Стоит отметить, что областью применимости данного конкретного алгоритма являются все наборы объектов, которые характеризуются теми же взаимоотношениями, что и Волк, Коза и Капуста. Например, Удав, Кролик и Морковка.

Иногда вызывает споры и свойство конечности алгоритма. В качестве контрпримеров приводятся алгоритмы работы операционной системы и атомной электростанции. Не углубляясь в спор, заметим, что здесь делается попытка представить алгоритм, в котором в качестве исходного объекта рассматривается компьютер, обладающий непрерывными свойствами (бесконечная бесперебойная работа вне зависимости от действий пользователя и проблем с “железом”). Алгоритмы же работают по определению только с дискретными объектами (см. статью “Теория алгоритмов”). Кроме того, свойство конечности существенно при доказательстве ряда фундаментальных утверждений в теории алгоритмов (см., например, “Алгоритмически неразрешимые проблемы”), поэтому опускать его даже в рамках базового курса информатики не следует.

Важным при изучении данной темы является и понятие исполнителя. Причем оказывается, что гораздо проще построить алгоритм для программно-управляемого автомата (в том числе компьютера), чем для человека. Подробнее об этом рассказано в статье “Исполнители алгоритмов”. Для управления автоматом или компьютером можно придумать формальный язык описания алгоритмов. Такие языки называются “Языки программирования”, а сам алгоритм, записанный на таком языке, — программой.

При изучении данной темы полезным оказывается построение алгоритмов, известных ученикам из курса математики, но записываемых в математике менее формально. Например, алгоритм решения квадратного уравнения (в информатике более полезно решать обобщенно-квадратное уравнение, в котором коэффициент при x2 может быть равен 0), алгоритм решения задач на построение (здесь особое внимание следует уделять детерминированности алгоритма) и т.п.

В курсе информатики средней школы к понятию алгоритма можно вернуться в контексте изучения темы “Моделирование”. Ведь алгоритм можно рассматривать как информационную модель деятельности исполнителя.

В профильном курсе информатики углубление данной темы происходит в результате знакомства с основами “Теории алгоритмов”, в рамках которой в первую очередь дается уже формальное определение алгоритма.

Алгоритмы

Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.

Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.

При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.

В процессе разработки алгоритма решения задачи можно выделить следующие этапы:

Этап 1 . Математическое описание решения задачи.
Этап 2 . Определение входных и выходных данных.
Этап 3 . Разработка алгоритма решения задачи.

Базовые алгоритмические конструкции

В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:

следование (линейный алгоритм);
ветвление (разветвляющийся алгоритм);
цикл-пока (циклический алгоритм).

Линейные алгоритмы

Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.

alt

Пример

ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.

На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:

Этап 1. Математическое описание решения задачи.

Математическим решением задачи является известная формула:

где с-длина гипотенузы, a, b – длины катетов.

Этап 2. Определение входных и выходных данных.

Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.

Этап 3. Разработка алгоритма решения задачи.

На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма.

Блок-схема

Разветвляющиеся алгоритмы

Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.

Алгоритм ветвления

Пример

ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.

Этап 1. Математическое описание решения задачи.

Из курса математики известно, если x > y, то наибольшее число x, если x < y, то наибольшее число y, если x = y, то число x равно числу y.

Этап 2. Определение входных и выходных данных.

Входными данными являются значения чисел x и y. Выходным данными являются:

наибольшее число
любое из чисел, если числа равны

Для решения задачи нам необходимо знать значения x и y.

Этап 3. Разработка алгоритма решения задачи.

Начало алгоритма.
Ввод значений x и y.
Сравниваем x и y. Если x = y, то переход к шагу 4, иначе к шагу 5.
Вывод информации: числа x и y равны. Переход к шагу 8.
Сравниваем x и y. Если x > y, то переход к шагу 6, иначе к шагу 7.
Вывод информации: число x больше y. Переход к шагу 8.
Вывод информации: число y больше x. Переход к шагу 8.
Конец алгоритма.

блок-схема

В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма

В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:

первая: это элементы 1, 2, 3, 4, 8.
вторая: это элементы 1, 2, 3, 5, 6, 8
третья: это элементы 1, 2, 3, 5, 7, 8.

Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.

Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.

Циклические алгоритмы

Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.

Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.

При разработке алгоритма циклической структуры выделяют следующие понятия:

параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
начальное и конечное значения параметров цикла;
шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.

Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.

В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:

начальные значения цикла;
конечные значения цикла;
шаг цикла.

В тело цикла входят:

многократно повторяющиеся действия для вычисления искомых величин;
подготовка следующего значения параметра цикла;
подготовка других значений, необходимых для повторного выполнения действий в теле цикла.

В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.

Пример

ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.

Этап 1. Математическое описание решения задачи.

Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:

где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.

Этап 2. Определение входных и выходных данных.

Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.

Выходные данные – значение суммы членов последовательности натуральных чисел.

Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.

Подготовка цикла заключается в задании начального и конечного значений параметра цикла.

начальное значение параметра цикла равно 1,
конечное значение параметра цикла равно n,
шаг цикла равен 1.

Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.

Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:

Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.

Этап 3. Разработка алгоритма решения задачи.

Введем обозначения: S – сумма последовательности, i – значение натурального числа.

Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.

В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма. Номера элементов соответствуют номерам шагов словесного описания алгоритма.

Информатика

Алгоритм — это система точных и понятных предписаний о содержании и последовательности выполнения конечного числа действий, необходимых для решения любой задачи данного типа.

Примеры: правила сложения, умножения, решения алгебраических уравнений и т.п.

1.Универсальность (массовость) — применимость алгоритма к различным наборам исходных данных.

2.Дискретность — процесс решения задачи по алгоритму разбит на отдельные действия.

3.Конечность — каждое из действий и весь алгоритм в целом обязательно завершаются.

4.Результативность — по завершении выполнения алгоритма обязательно получается конечный результат.

5.Выполнимость (эффективность) — результата алгоритма достигается за конечное число шагов.

6.Детерминированность (определенность) — алгоритм не должен содержать предписаний, смысл которых может восприниматься неоднозначно. Т.е. одно и то же предписание после исполнения должно давать один и тот же результат.

7.Последовательность – порядок исполнения команд должен быть понятен исполнителю и не должен допускать неоднозначности.

1. вычислительные алгоритмы , работающие со сравнительно простыми видами данных, такими как числа и матрицы, хотя сам процесс вычисления может быть долгим и сложным;

2. информационные алгоритмы , представляющие собой набор сравнительно простых процедур, работающих с большими объемами информации (алгоритмы баз данных);

3. управляющие алгоритмы , генерирующие различные управляющие воздействия на основе данных, полученных от внешних процессов, которыми алгоритмы управляют.

По типу передачи управления алгоритмы бывают: основные (главные выполняемые программы) и вспомогательные (подпрограммы).

Для задания алгоритма необходимо описать следующие его элементы:

1.набор объектов, составляющих совокупность возможных исходных данных, промежуточных и конечных результатов;

3.правило непосредственной переработки информации (описание последовательности действий);

5.правило извлечения результатов.

Способы описания алгоритмов.

Символьный, когда алгоритм описывается с помощью специального набора символов (специального языка).

Словесная форма записи алгоритмов обычно используется для алгоритмов, ориентированных на исполнителя-человека. Команды такого алгоритма выполняются в естественной последовательности, если не оговорено противного.

Графическая запись с помощью блок-схем осуществляется рисованием последовательности геометрических фигур, каждая из которых подразумевает выполнение определенного действия алгоритма. Порядок выполнения действий указывается стрелками. Графическая запись алгоритма имеет ряд преимуществ: каждая операция вычислительного процесса изображается отдельной геометрической фигурой и графическое изображение алгоритма наглядно показывает разветвления путей решения задачи в зависимости от различных условий, повторение отдельных этапов вычислительного процесса и другие детали.

Правила создания блок – схем:

1.Линии, соединяющие блоки и указывающие последовательность связей между ними, должны проводится параллельно линиям рамки.

2.Стрелка в конце линии может не ставиться, если линия направлена слева направо или сверху вниз.

3.В блок может входить несколько линий, то есть блок может являться преемником любого числа блоков.

4.Из блока (кроме логического) может выходить только одна линия.

5.Логический блок может иметь в качестве продолжения один из двух блоков, и из него выходят две линии.

6.Если на схеме имеет место слияние линий, то место пересечения выделяется точкой. В случае, когда одна линия подходит к другой и слияние их явно выражено, точку можно не ставить.

7.Схему алгоритма следует выполнять как единое целое, однако в случае необходимости допускается обрывать линии, соединяющие блоки.

В линейном алгоритме операции выполняются последовательно, в порядке их записи. Каждая операция является самостоятельной, независимой от каких-либо условий. На схеме блоки, отображающие эти операции, располагаются в линейной последовательности.

В алгоритме с ветвлением предусмотрено несколько направлений (ветвей). Каждое отдельное направление алгоритма обработки данных является отдельной ветвью вычислений. Направление ветвления выбирается логической проверкой, в результате которой возможны два ответа:

1.«да» — условие выполнено.

2.«нет» — условие не выполнено.

Циклические алгоритмы содержат цикл – это многократно повторяемый участок алгоритма.Различают циклы с предусловием и постусловием.Также циклы бывают детерминированные и итерационные.Цикл называется детерминированным, если число повторений тела цикла заранее известно или определено. Цикл называется итерационным, если число повторений тела цикла заранее неизвестно, а зависит от значений параметров (некоторых переменных), участвующих в вычислениях.

Понятие алгоритма. Свойства алгоритмов. Формы описания и виды алгоритмов

Алгоритм — точное предписание исполнителю совеpшить определенную последовательность действий для достижения поставленной цели за конечное число шагов.

Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi – латинского написания имени Мухаммеда аль-Хорезми (787 – 850) выдающегося математика средневекового Востока. В своей книге «Об индийском счете» он сформулировал правила записи натуральных чисел с помощью арабских цифр и правила действий над ними столбиком. В дальнейшем алгоритмом стали называть точное предписание, определяющее последовательность действий, обеспечивающую получение требуемого результата из исходных данных.

Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством. Создание алгоритма, пусть даже самого простого, — процесс творческий. Он доступен исключительно живым существам, а долгое время считалось, что только человеку. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами.

Данное выше определение алгоритма нельзя считать строгим – не вполне ясно, что такое «точное предписание» или «последовательность действий, обеспечивающая получение требуемого результата».

Поэтому обычно формулируют несколько общих свойств алгоритмов, позволяющих отличать алгоритмы от других инструкций.

Такими свойствами являются:

• Дискретность (прерывность, раздельность) – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.

• Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.

• Результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов.

• Массовость – алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.

На основании этих свойств иногда дается определение алгоритма, например: “Алгоритм – это последовательность математических, логических или вместе взятых операций, отличающихся детерменированностью, массовостью, направленностью и приводящая к решению всех задач данного класса за конечное число шагов”.

Такая трактовка понятия “алгоритм” является неполной и неточной.

Во-первых, неверно связывать алгоритм с решением какой-либо задачи. Алгоритм вообще может не решать никакой задачи.

Во-вторых, понятие “массовость” относится не к алгоритмам как к таковым, а к математическим методам в целом. Решение поставленных практикой задач математическими методами основано на абстрагировании – мы выделяем ряд существенных признаков, характерных для некоторого круга явлений, и строим на основании этих признаков математическую модель, отбрасывая несущественные признаки каждого конкретного явления. В этом смысле любая математическая модель обладает свойством массовости. Если в рамках построенной модели мы решаем задачу и решение представляем в виде алгоритма, то решение будет “массовым” благодаря природе математических методов, а не благодаря “массовости” алгоритма.

Различают следующие виды алгоритмов:

линейный – список команд (указаний), выполняемых последовательно друг за другом;

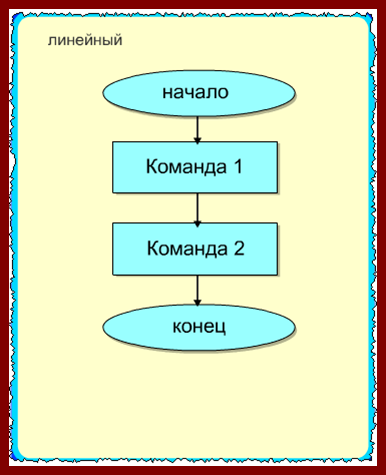
разветвляющийся – алгоритм, содержащий хотя бы одну проверку условия, в результате которой обеспечивается переход на один из возможных вариантов решения;

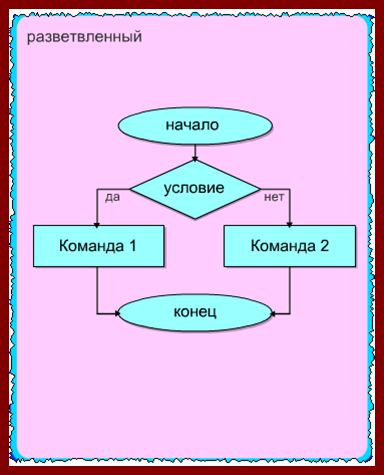
циклический – алгоритм, предусматривающий многократное повторение одной и той же последовательности действий. Количество повторений обусловливается исходными данными или условием задачи.