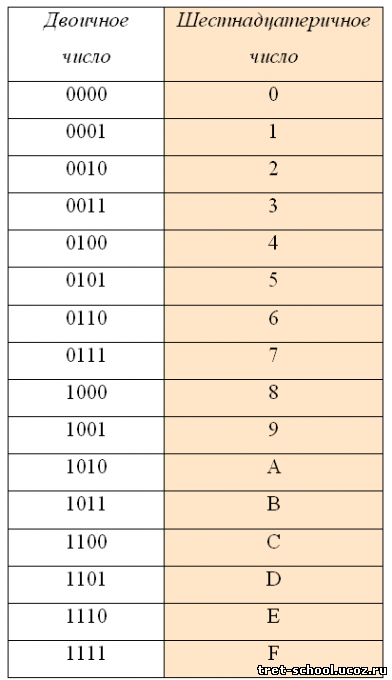
Особенности точного введения репетитором по математике понятия иррационального числа
Можно проверить, и доказать, что для перевода обыкновенной дроби в десятичный код (код конца соответствующего ей отрезка) можно использовать обычное деление в столбик. А в этом случае получается периодическая дробь. Например, 3/7=0,428571428571428571428571. или коротко 0,(428571). Все обыкновенные дроби имеют периодические коды.
Однако, можно организовать последовательность выбора отрезков, что в дясятичном коде не будет повторяться никакой одинаковый набор цифр, например 5,5050050005000050000050000005.
Все эти отрезки, вложенные друг в друга, будут иметь по теореме Кантора единственную общую точку. Она не может изображать обыкновенную дробь, и поэтому для ее координаты нет никакой иной привычной и знакомой записи, кроме этого кода. Мы вынуждены мириться с тем, что нужно вводить новые числа, как-то их называть, обозначать более или менее удобно и вводить действия с ними.
Cложение иррациональных чисел.

Числа назовем иррациональными, а действия будем выполнять так, чтобы их результаты означали бы тоже самое, что и в случае с рациональными. Почему? К отрезку с длиной 5,5050050005000050000050000005 можно «положить» рядом отрезок длиной 2 см? Да. Получится новый отрезок, длину которого надо научиться как то измерять.
Рациональной длины у него нет (это очень легко доказывается). Раньше мы находили длину этого отрезка сложением. Не будем разрушать сложившийся образ и назовем суммой чисел 5,5050050005000050000050000005. и 2 именно длину их «склейки».
Умножение иррациональных чисел.

Что показывает произведение двух рациональных чисел? Площадь прямоугольника, построенного на этих сторонах. Не будем разрушать и это представление о результате умножения и назовем произведением иррациональных чисел -площадь прямоугольника, построенного на таких отрезках.
На самом деле, в высшей математике, а именно в такой ее дисциплине, как «основания математики» понятие «площадь» вводится более точно, более тонко и очень сложно. Необходимость измерять площади любых фигур так, чтобы их зрительное сравнение (если одна фигура внутри другой — значит ее площадь меньше площади первой) соответствовало числовому, заставляет определить площадь прямоугольника с иррациональными сторонами так, чтобы сохранялось отношение порядка. Для этого вводятся понятия супремум и инфинум множества, отдельно изучаются и уже после них вводится точное определение квадрируемости фигуры, в частности площади прямоугольника: рассмотрим множество всех прямоугольников с рациональными сторонами, расположенных внутри заданного прямоугольника и множество те, которые его в себя содержат. Их площади определяются произведением рациональных чисел. Супремум «вписанных» площадей и инфинум «описанных» существуют, совпадают (это доказывается) и такое число называется площадью прямоугольника.
Это определение называют предельным. Площадь прямоугольника с иррациональными сторонами это некоторое число, расположенное на числовой прямой. Для фигур с кривыми границами есть очень близкое по «духу» определение через вписанные и описанные многоугольники.
Далее через супремум и инфинум четко доказывается свойства умножения. Самое важное из них — распределительный закон.
а(в+с)=ав+ас
Площадь (супремум) прямоугольника с иррациональным сторонами (а, в+с) равна сумме площадей (сумме супремумов) двух других прямоугольников со сторонами (а, в) и (а,с).
Следствием распределительного закона для иррациональных чисел являются сохранение правил раскрытия скобок, приведения подобных слагаемых и формул сокращенного умножения. Поэтому удается аккуратно и строго доказать теорему Пифагора, а чрез нее можно получить целый букет чисел (сторон прямоугольников) квадраты которых (результаты их умножения на себя) равны двум, трем, пяти и так далее. Поэтому существуют числа :
Вот так. Конечно, школьнику этого не объяснишь. Тем более, не объяснить, почему существует такое число:

Для этого вводится деление иррациональных чисел и средствами геометрии через него и через подобие доказывается, что по заданному прямоугольнику даже с иррациональными сторонами можно построить квадрат с той же площадью (для этого надо научиться через окружность, построенную на диаметре а+в, получать сторону будущего квадрата — отрезок длины «корень из ав»). Тогда рассматривая, например, прямоугольник со сторонами «корень из 2» и «единица», можно будет сказать, что существует отрезок (то есть число) у которого квадрат равен уже «корню из трех, умноженному на единицу»,то есть существует корень из корня из двух.
Это все сложнейшие вопросы основания математики. Естественно, что примерно 95 процентов репетиторов по математике сами в этом не разбираются, а если и разбираются, то не смогут донести и десятой части всей этой кухни даже до очень сильного ученика.
Я обычно обрываю объяснения на распределительном законе умножения иррациональных чисел, говорю, что теорема Пифагора верна и получаю корни из двух, из трех и пяти через нее. Этого вполне достаточно. Среднему и, тем более слабому ученику хватит объяснения существования корня из двух через рисунки квадратов.
Колпаков А.Н. Репетитор по математике.
Pages: 1 2

Обо мне

Я Колпаков Александр Николаевич, репетитор по математике. Опыт преподавания 18 лет. Автор статей и методик индивидуального обучения. Высшее педагог.образование (диплом МПГУ). За плечами непрерывная практика проведения частных уроков (со 2-го курса МПГУ). Мои ученики — победители школьных, районных и городских олимпиад. Ученики последних 5 лет — студенты престижных вузов: МГУ, ВШЭ, ФА, МФТИ, РЭА и др. Обсудить вопросы и записаться на занятия можно по телефонам 8(916) 081-68-55 моб. и 8(495) 756-93-95 дом. или написав на адрес alex36@mail.ru
Ограниченные множества. Супремум и инфимум | матан #002
Определение. Множество $Xsubsetmathbb$ называется ограниченным сверху, если существует число $b$ такое, что $$forall,xin X to xle b.$$ При этом говорят, что число $b$ ограничивает множество $X$ сверху.
Определение. Множество $Xsubsetmathbb$ называется ограниченным снизу, если существует число $a$ такое, что $$forall,xin X to xge a.$$ При этом говорят, что число $a$ ограничивает множество $X$ снизу.
Определение. Множество $Xsubsetmathbb$ называется ограниченным, если оно ограничено и сверху и снизу.
Определение. Множество $Xsubsetmathbb$ называется неограниченным сверху, если оно не является ограниченным сверху.
Определение. Множество $Xsubsetmathbb$ называется неограниченным снизу, если оно не является ограниченным снизу.
Определение. Множество $Xsubsetmathbb$ называется неограниченным, если оно не является ограниченным.
Определение. Верхней гранью непустого множества $Xsubsetmathbb$ называется число $b$, удовлетворяющее условиям:
- $forall,xin X to xle b$;
- $forall,b’ b’$
($forall,varepsilon>0 to exists,xin X: x > b — varepsilon$).
Определение. Нижней гранью непустого множества $Xsubsetmathbb$ называется число $a$, удовлетворяющее условиям:
- $forall,xin X to xge a$;
- $forall,a’> a to exists,xin X: x < a'$
($forall,varepsilon>0 to exists,xin X: x < a + varepsilon$).
Верхняя и нижняя грани множества $X$ обозначаются символами $sup X$, $inf X$ соответственно.
Теорема (единственности). Числовое множество не может иметь больше одной верхней грани.
Доказательство. Допуская противное, предположим, что каждое из чисел $b$ и $b’$ ($bne b’$) является верхней гранью множества $X$. Пусть, для определённости, $b’ < b$. Но тогда $b'$ не является верхней гранью множества $X$.
Получили противоречие.Теорема доказана.
Замечание. Заметим, что в условиях теоремы не предполагается существование верхней грани. Теорема утверждает, что если верхняя грань существует, то она единственна. Значительно более глубокой является теорема о существовании верхней грани.
Теорема (о существовании верхней грани). Всякое непустое ограниченное сверху числовое множество имеет верхнюю грань.
Доказательство. Пусть $A$ — непустое ограниченное сверху множество. Рассмотрим непустое множество $B$, элементами которого являются все числа $b$, ограничивающие множество $A$ сверху. Тогда $$ forall,ain A, forall,bin B to ale b. $$ Из аксиомы непрерывности следует, что для некоторого $cinmathbb$ $$ forall,ain A, forall,bin B to ale cle b. $$ Покажем, что $exists,sup A = c$.
Первое условие из определения верхней грани выполнено для $c$ в силу того, что $$ forall,ain A to ale c.$$ Покажем, что выполняется и второе.
Следовательно, $c=sup A$, и теорема доказана.
Определение. Расширенным множеством действительных чисел $overline
В множестве $overline
Рассматривая множество $Xsubsetmathbb$ как подмножество расширенного множества действительных чисел ($Xsubsetoverline
Тогда получим, что для непустого неограниченного сверху числовогомножества $X$ $$sup X = +infty.$$
Учитывая предыдущую теорему, получаем, что всякое непустое числовое множество имеет в расширенном множестве действительных чисел $overline
Замечание. Все изложенные выше утверждения очевидным образом переносятся на понятие нижней грани.
Точные грани числовых множеств
Множество X вещественных чисел (X ⊂ (mathbb)) называется ограниченным сверху, если существует вещественное число C такое, что все элементы множества X не превосходят C, то есть
$$
exists C in mathbb: forall x in X rightarrow x leq C.label
$$
Всякое вещественное число C, обладающее свойством eqref, называется верхней гранью числового множества X.
Аналогично, множество X ⊂ (mathbb) называется ограниченным снизу, если
$$
exists C’inmathbb: forall x in X rightarrow x geq C’.label
$$
Всякое вещественное число С ‘ , удовлетворяющее условию eqref, называют нижней гранью числового множества X.
Если числовое множество множество ограничено как сверху, так и снизу, его называют ограниченным, то есть X — ограниченное множество>(Leftrightarrowleft exists Cinmathbb: forall xin X rightarrow C’ leq x leq Cright>).
По условию (B=left: forall x in X rightarrow x geqslant Cright>). Поэтому
$$
rceil B=left: exists x_C in X rightarrow x_C < Cright>.nonumber
$$
Определение точной верхней и нижней грани.
Пусть числовое множество X ограничено сверху, тогда выполняется условие eqref, а число C является верхней гранью множества X. Очевидно, что любое число, большее C, также является верхней гранью множества X. Таким образом, ограниченное сверху множество имеет бесконечно много верхних граней, среди которых особую роль имеет наименьшая. Речь идет о числе M, которое обладает следующими свойствами:
- M — верхняя грань множества X;
- любое число M’ меньшее M, не является верхней гранью множества X.
Это число M будем в дальнейшем называть точной верхней гранью множества X. Исходя из вышесказанного, сформулируем определение точной верхней грани множества.
Число M называется точной верхней гранью числового множества X, если выполняются следующие условия:
- $$forall x in X rightarrow x leq Mlabel$$
- $$forallalpha < M exists x_alphain X: x_alpha >alphalabel$$
Точная верхняя грань числового множества X обозначается sup X («супремум»). Таким образом,
$$
left Leftrightarrow left wedge left alpharight>.nonumber
$$
Число M = sup X, вообще говоря, может как принадлежать, так и не принадлежать множеству X. Например, если X — множество чисел x таких, что 1 ≤ x sup X = 2 ∉ X. Если X1 — объединение множеств X и числа 3, то sup X1=3 ∈ X1.
Из определения точной верхней грани множества следует, что если у числового множества X есть точная верхняя грань M, то она единственна.
Число m называется точной нижней гранью числового множества X, если выполняются следующие условия:
- $$forall x in X rightarrow x geqslant mnonumber$$
- $$forallbeta > m exists x_betain X: x_beta < mnonumber$$
Точная нижняя грань множества X обозначается inf X («инфимум»). Таким образом,
$$left=left wedge left m exists x_betain X: x_beta < betaright>nonumber$$
Существование точной верхней (нижней) грани.
Если непустое множество вещественных чисел X ограничено сверху, то существует sup X; если непустое множество X ограничено снизу, то существует inf X.
Докажем существование верхней точной грани. По условию множество X не пусто, то есть содержит хотя бы один элемент. Возможны два случая:
- множество X содержит хотя бы одно неотрицательное число;
- все элементы множества X отрицательны.
Первый случай. Предположим, что все элементы множества X неотрицательны. По условию множество X ограничено сверху, а значит выполняется условие eqref. Пусть C=c0,c1c2…cn…; тогда c0 — неотрицательное целое число, причем C < c0+1, где c0+1 = n0 ∈ (mathbb). Следовательно, $$forall xin X rightarrow x < C < n_0.label$$
Если x=a0,a1a2…=a0,n> — произвольный элемент множества X, то из eqref следует, что 0 ≤ a0 < n0. Рассмотрим множество E целых частей элемента множества X. Так как E — конечное непустое множество целых неотрицательных чисел, то в этом множестве есть наибольший элемент (
Множество X0 состоит из всех тех элементов множества X, у которых целая часть равна (
Пусть E1 — множество первых десятичных знаков элементов множества X0. Так как множество E1 конечно (его элементы могут быть числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и непусто, то существует (
Пусть (X_1=left
Продолжая эти рассуждения, построим последовательность Xk> непустых множеств и последовательность десятичных знаков (
Рассмотрим десятичную дробь (overline x=
$$forall xin X rightarrow x leq overline x,label$$
Возьмем произвольное число x ∈ X и пусть x = a0,an>. Чтобы проверить выполнение условия eqref, рассмотрим три произвольных случая:
$$xnotin X_k при k=0,1,2,…,label$$
$$xin X_k при k=0,1,2,…,label$$
$$exists m: xin X_, xnotin X_label$$
Из eqref следует, что (a_0 <
Проверим условие eqref. Если x’ < 0, то eqrefимеет место при любом (widetilde xin X), т.к. все элементы множества X неотрицательны.
Пусть (0 leq x’ leq overline x) и (x’=a’_0,left\). Тогда либо (a’_0 <
Во втором случае условию eqref удовлетворяет произвольный элемент (widetilde xin X_m), так как
Итак, условия eqref и eqref выполняются, то есть x = sup X. То есть мы доказали предположение, что существует точная верхняя грань при предположении, что все элементы множества X неотрицательны.
Если множество X содержит хотя бы один неотрицательный элемент x0 ≥ 0, то множество (left\) состоит из неотрицательных чисел, причем (sup X=sup widetilde X). Поэтому непустое ограниченное сверху числовое множество X имеет точную верхнюю грань.
Второй случай. Если все элементы множества X отрицательны, то произвольный элемент x ∈ X записываются в виде
Пусть (a_0^ast) — наименьшее из чисел a0 в записи eqref для всех x ∈ X, (a_1^ast) — наименьший из первых десятичных знаков тех элементов множества X, у которых (a_0=a_0^ast); (a_2^ast) — наименьший из вторых десятичных знаков тех элементов множества X, у которых (a_0=a_0^ast, a_1=a_1^ast) и т.д. Указанным способом определяется число (x^ast=-a_0^ast,a_1^ast…a_n^ast…=-a_0^ast,left\). По аналогии с первым случаем доказывается, что число x * является точной верхней гранью множества.
Если X и Y — непустые множества вещественных чисел такие, что для любого x ∈ X и любого y ∈ Y справедливо неравенство $$x leq y,label$$ то существуют sup X и inf Y, причем $$forall xin X и forall yin Y rightarrow x leq sup X leq inf Y leq y.label$$
Доказательство
Так как X — непустое множество, ограниченное сверху любым элементом множества Y в силу eqref, то по теореме 1 существует sup Y. Аналогично из ограниченности непустого множества Y снизу любым элементом множества X следует существование inf Y. По определению точных граней $$forall xin X rightarrow x leq sup X, forall yin Y rightarrow inf Y leq y.label$$ Из eqref следует, что для доказательства утверждения eqref достаточно показать, что $$sup X leq inf Y.label$$Из неравенства eqref следует, что каждое число y ∈ Y является верхней гранью множества X. Точная верхняя грань множества X, то есть число sup X, есть наименьшая из всех верхних граней множества X. Следовательно, для любого y ∈ Y выполняется неравенство $$sup X leq y.label$$
Из неравенства eqref следует, что sup X есть нижняя грань множества Y. Точная нижняя грань множества Y, то есть число inf Y, есть наибольшая из всех нижних граней множества Y. Значит, sup X ≤ inf Y.
Пусть ξ — любое вещественное число такое, что $$sup X leq xi leq inf Ylabel$$ Тогда из eqref и eqref следует неравенство $$x leq xi leq y,label$$ которое справедливо для любого x ∈ X и любого y ∈ Y. Про число ξ говорят, что оно отделяет множество X от множества Y. Поэтому теорему 2 часто называют теоремой об отделимости числовых множеств.
Научный форум dxdy
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву , правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Супремум и инфимум
| Последний раз редактировалось PAV 31.10.2011, 22:03, всего редактировалось 3 раз(а). |
| убрал звездочки как знаки умножения |
Помогите пожалуйста разобраться с нахождением супремума и инфимума, в теории всё понятно, но на практике не знаю как применить.
Нужно найти верхний предел, нижний предел у x_n$» /> а также

Инфи м ум, с буквой «м».
Ответьте последовательно на вопросы:
Как ведет себя второе слагаемое в зависимости от ?
Третье слагаемое?
Сумма?
Извините, опечатался)
Я так понял, нужно подставить и вместо ?
Нет-нет, тут сразу три непонятности: почему , если в условии ? зачем умножать на ? почему это надо подставлять вместо ?
Я имел в виду, что надо просто исследовать, чему равен в зависимости от . И так как сразу это сделать трудно, то для начала рассмотрим отдельные слагаемые, а потом найдём сумму. Я исследую первое и второе слагаемое, а Вы в этом же духе третье, OK?
Первое слагаемое: оно равно для любого .
Второе слагаемое, $» />. Как известно, в четной степени равно , а в нечетной . Но в показателе стоит , а прибавление меняет четность. Поэтому $» /> равно , когда нечетно, и , когда четно. Да еще множитель . Всё слагаемое при нечетных равно , а при четных .
Да, я именно это и имел в виду, только немного другим способом, как нас учили
У меня получилось тоже самое. Верхний предел получился , а нижний . Это так?
Нет, например, уже при получаем + 3 (-1)^frac 2 = 1 + 2 (-1)^2 + 3 (-1)^0 = 1+2+3=6$» />.
Поэтому Вы все-таки не спешите, а расскажите мне про третье слагаемое.
Последний раз редактировалось brilliant 11.02.2011, 18:57, всего редактировалось 1 раз.

Похоже я понял. Третье слагаемое всегда будет четным, при любых значениях . Т.е. в конечном итоге получается:

И выходит, что верхний предел , нижний . Так?

А при ? Математика, ох, хитрая штука.
— Пт фев 11, 2011 18:04:51 —
Третье слагаемое в зависимости от . Только третье слагаемое. Без него у Вас нет шансов угадать.
Можете даже пока на не умножать.
Составьте табличку хотя бы для от до .

Действительно, что-то я уже совсем запутался. У третьего слагаемого четность меняется через каждые 2 . Т.е. он два раза четный, два раза нечетный.

Третье слагаемое всегда будет четным, при любых значениях .
Извините за вмешательство, но у меня третье слагаемое получается всегда 3 или -3. Я уже примерно до 120 проверил.
А 3 и -3 — числа НЕчётные. Это я точно помню.
Я имел в виду не четность/нечетность, а положительность/отрицательность
Верхний , нижний в конченом итоге у меня получилось.

У третьего слагаемого четность меняется через каждые 2 . Т.е. он два раза четный, два раза нечетный.
Да. Согласитесь, что как-то угадать это было бы сложно. И тем более предсказать, какая будет сумма этого со вторым слагаемым, у которого период иной.
А ответ — да, такой.
Спасибо за помощь. А что здесь будет и , те же значения?
Да, те же. Но важно понимать, что в других случаях это может быть и не так.
Например, такая последовательность: дальше только чередуются и . Супремум, инфимум, верхний предел, нижний предел — всё ясно?
И второе. Вы знаете, что супремум и инфимум не обязательно достигаются, то есть не обязательно есть элементы последовательности, равные супремуму или инфимуму. Пример: Здесь супремум , но ни один элемент не равен .
Инфимум и супремум — Infimum and supremum
Множество действительных чисел (полые и заполненные кружки), подмножество из (закрашенных кружков), а нижняя грань Заметим , что для конечных, полностью упорядоченные множества инфимум и минимальное равны. п S п S .
Набор действительных чисел (синие круги), набор верхних границ (красный ромб и круги) и наименьшая такая верхняя граница, то есть верхняя грань (красный ромб). А А А
В математике , то нижняя грань (сокращенно инф ; множественном инфимумы ) из подмножества в виде частично упорядоченного множества является наибольшим элементом в том , что меньше или равна ко всем элементам , если такой элемент существует. Следовательно, термин наибольшая нижняя граница (сокращенно GLB ) также широко используется. S п п S ,
Супремумом (сокращенно SUP ; множественном супремумами ) подмножества частично упорядоченного множества является наименьшим элементом в том , что больше или равны ко всем элементам , если такой элемент существует. Следовательно, супремум также называется наименьшей верхней границей (или LUB ). S п п S ,
Инфимум в точном смысле двойственен понятию супремума. Инфима и верхняя граница действительных чисел — частные частные случаи, которые важны в анализе , и особенно в интеграции Лебега . Однако общие определения остаются в силе и в более абстрактном контексте теории порядка, где рассматриваются произвольные частично упорядоченные множества.
Понятия infimum и supremum аналогичны понятиям минимума и максимума , но более полезны при анализе, поскольку они лучше характеризуют специальные множества, которые могут не иметь минимума или максимума . Например, набор положительных действительных чисел (не включая ) не имеет минимума, потому что любой заданный элемент можно просто разделить пополам, что приведет к меньшему числу, которое все еще находится в. Однако существует ровно одна точная нижняя грань положительного числа. вещественные числа: которое меньше всех положительных действительных чисел и больше любого другого действительного числа, которое может использоваться в качестве нижней границы. р + ^ > 0 р + ^ > р + . ^ .> 0 ,
СОДЕРЖАНИЕ
Формальное определение
Нижняя граница подмножества частично упорядоченного множества является элементом из таким образом, что S ( п , ≤ ) а п
Нижняя грань для называется точной гранью (или точной нижней границей , или совпадением ), если а S S
Аналогичным образом , верхняя граница подмножества частично упорядоченное множество является элементом из таким образом, что S ( п , ≤ ) б п
Верхняя граница из называется супремумом (или минимум верхней границы или присоединиться к ) из если б S S
Существование и уникальность
Инфима и супрема не обязательно существуют. Существование инфимума подмножества из не может потерпеть неудачу , если уже не нижняя границы вообще, или , если множество нижних границ не содержит наибольший элемент. Однако, если точная нижняя грань или супремум существует, она уникальна. S п S
Следовательно, частично упорядоченные множества, для которых, как известно, существуют определенные инфимы, становятся особенно интересными. Например, решетка — это частично упорядоченное множество, в котором все непустые конечные подмножества имеют как верхнюю, так и нижнюю границу, а полная решетка — это частично упорядоченное множество, в котором все подмножества имеют как верхнюю, так и нижнюю границу. Более подробную информацию о различных классах частично упорядоченных множеств, возникающих из таких соображений, можно найти в статье о свойствах полноты .
Если супремум подмножества существует, он уникален. Если содержит наибольший элемент, то этот элемент является супремумом; в противном случае супремум не принадлежит (или не существует). Точно так же, если нижняя грань существует, она уникальна. Если содержит наименьший элемент, то этот элемент является точной нижней гранью; в противном случае нижняя грань не принадлежит (или не существует). S S S S S
Отношение к максимальным и минимальным элементам
Инфимумом подмножество частично упорядоченного множества предполагая , что она существует, не обязательно принадлежат Если это произойдет, это минимальное или наименьший элемент из Аналогично, если верхняя грань принадлежит к нему является максимальное или наибольший элемент из S п , S . S . S S , S .
Например, рассмотрим набор отрицательных действительных чисел (исключая ноль). В этом наборе нет наибольшего элемента, поскольку для каждого элемента набора существует другой, более крупный элемент. Например, для любого отрицательного действительного числа существует другое отрицательное действительное число, которое больше. С другой стороны, каждое действительное число, большее или равное нулю, безусловно, является верхней границей этого множества. Следовательно, это наименьшая верхняя граница отрицательных вещественных чисел, поэтому супремум равен 0. Это множество имеет супремум, но не имеет наибольшего элемента. Икс , Икс 2 , >,> 0
Однако определение максимальных и минимальных элементов является более общим. В частности, в наборе может быть много максимальных и минимальных элементов, в то время как инфима и верхняя граница уникальны.
В то время как максимумы и минимумы должны быть членами рассматриваемого подмножества, нижняя грань и верхняя грань подмножества не обязательно должны быть членами этого подмножества.
Минимальные верхние границы
Наконец, частично упорядоченное множество может иметь множество минимальных верхних границ без точной верхней границы. Минимальные верхние границы — это те верхние границы, для которых не существует строго меньшего элемента, который также является верхней границей. Это не означает, что каждая минимальная верхняя граница меньше, чем все другие верхние границы, это просто не больше. Различие между «минимальным» и «минимальным» возможно только в том случае, если данный заказ не является полным . В полностью упорядоченном наборе, как и в реальных числах, концепции те же.
В качестве примера, пусть будет набором всех конечных подмножеств натуральных чисел и рассмотрим частично упорядоченный набор, полученный путем взятия всех наборов вместе с набором целых чисел и набором положительных действительных чисел, упорядоченных по включению подмножества, как указано выше. Тогда очевидно, что оба и больше всех конечных наборов натуральных чисел. Тем не менее, ни одно из них не меньше и не обратное: оба набора являются минимальными верхними границами, но ни одно из них не является супремумом. S S Z > р + , ^ ,> Z > р + ^ > р + ^ > Z >
Свойство с наименьшей верхней границей
Свойство наименьшей верхней границы является примером вышеупомянутых свойств полноты, которые типичны для набора действительных чисел. Это свойство иногда называют дедекиндовской полнотой .
Если упорядоченный набор имеет свойство, заключающееся в том, что каждое непустое подмножество, имеющее верхнюю границу, также имеет наименьшую верхнюю границу, то говорят, что оно имеет свойство наименьшей верхней границы. Как отмечалось выше, набор всех действительных чисел имеет свойство наименьшей верхней границы. Точно так же набор целых чисел имеет свойство наименьшей верхней границы; если есть непустое подмножество и существует некоторое число такое , что каждый элемент из меньше или равно , то есть не менее верхняя граница для целого числа , что верхняя граница для и меньше или равна любой другой верхней границы для упорядоченная комплект также имеет наименее верхнюю границу собственности, а пустое подмножество имеет также верхнюю грань: минимум всего набора. S S S р > Z > S Z > п s S п , ты S , S S .
Примером набора, в котором отсутствует свойство наименьшей верхней границы, является набор рациональных чисел. Пусть будет набор всех рациональных чисел таких, что Then имеет верхнюю границу ( например, или ), но не имеет наименьшей верхней границы в : Если мы предполагаем, что это наименьшая верхняя граница, противоречие немедленно выводится, потому что между любыми двумя действительными числами и (включая и ) существует некоторое рациональное число, которое само должно быть наименьшей верхней границей (если ) или членом большего чем (если ). Другой пример — гиперреалы ; не существует точной верхней границы множества положительных бесконечно малых. Q , ,> S q q 2 < 2. S 1000 , 6 Q > п ∈ Q > Икс у 2 >> п п , п > 2 >> S п п < S >>
Имеется соответствующее свойство наибольшей нижней границы ; упорядоченный набор обладает свойством наибольшей нижней границы тогда и только тогда, когда он также обладает свойством наименьшей верхней границы; наименьшая верхняя граница набора нижних границ набора является наибольшей нижней границей, а наибольшая нижняя граница набора верхних границ набора является наименьшей верхней границей набора.
Если в частично упорядоченном множестве каждое ограниченное подмножество имеет супремум, это относится и для любого множества в пространстве функций , содержащее все функции из , чтобы , где , если и только если для всех Например, он применяется для вещественных функций, и, так как они могут рассматривать частные случаи функций, для вещественных чисел и последовательностей действительных чисел. п Икс , Икс п , ж ≤ грамм ж ( Икс ) ≤ грамм ( Икс ) Икс ∈ Икс . п
Свойство наименьшей верхней границы является индикатором супремы.
Инфима и супрема действительных чисел
В анализе , инфимумы и супремумы подмножеств этих действительных чисел особенно важны. Например, отрицательные действительные числа не имеют наибольшего элемента, а их верхняя грань равна (что не является отрицательным действительным числом). Полнота действительных чисел влечет (и эквивалентно) , что любое ограниченное непустое подмножество действительных чисел имеет инфимум и супремум. Если не ограничена снизу, часто формально пишет Если есть пустые , одна запись S 0 S S инф S знак равно — ∞ . S = — infty.> S инф S знак равно + ∞ . S = + infty.>
Характеристики
Следующие формулы зависят от обозначения, которое удобно обобщает арифметические операции над множествами: Пусть множества и скаляр определяют А , B ⊆ р , ,> р ∈ р . .>
В тех случаях, когда существуют нижняя и верхняя границы множеств и , выполняются следующие тождества: А B
- п знак равно инф А если и только есть Минорант, и для каждого есть с п ϵ > 0 0> а ϵ ∈ А in A> а ϵ < п + ϵ .
- п знак равно Как дела А если и только это Мажорантный и если для каждого существует с п ϵ > 0 0> а ϵ ∈ А in A> а ϵ > п — ϵ > p- epsilon>
- Если и тогда и А ⊆ B инф А ≥ инф B Как дела А ≤ Как дела B .
- Если тогда и р > 0 0> инф ( р ⋅ А ) знак равно р ( инф А ) Как дела ( р ⋅ А ) знак равно р ( Как дела А ) .
- Если тогда и р ≤ 0 инф ( р ⋅ А ) знак равно р ( Как дела А ) Как дела ( р ⋅ А ) знак равно р ( инф А ) .
- инф ( А + B ) знак равно ( инф А ) + ( инф B ) а также Как дела ( А + B ) знак равно ( Как дела А ) + ( Как дела B ) .
- Если и — непустые множества положительных действительных чисел, то аналогично для супремумов А B инф ( А ⋅ B ) знак равно ( инф А ) ⋅ ( инф B ) Как дела ( А ⋅ B ) знак равно ( Как дела А ) ⋅ ( Как дела B ) .
- Если не пусто, и если тогда, где это уравнение также выполняется, когда используется определение . В качестве альтернативы это равенство может быть записано как Более того, тогда и только тогда, когда где если тогда S ⊆ ( 0 , ∞ ) 1 S знак равно < 1 s : s ∈ S >, >: = left >: s in S right >,> 1 Как дела S знак равно инф 1 S S>> = inf _ <>>> Как дела S знак равно ∞ S = infty> 1 ∞ знак равно 0 >: = 0> 1 Как дела s ∈ S s знак равно инф s ∈ S 1 s . s>> = inf _ >.> инф S знак равно 0 S = 0> Как дела 1 S знак равно ∞ , > = infty,> инф S > 0 , S> 0,> 1 инф S знак равно Как дела 1 S . S>> = sup _ <>>.>
Двойственность
Для подмножеств действительных чисел имеет место другой вид двойственности: где инф S знак равно — Как дела ( — S ) , — S знак равно < - s : s ∈ S >. .>
Примеры
Инфима
- Инфимумом множества чисел является число является нижней границей, но не самая большая нижняя граница, и , следовательно , не инфимумом. < 2 , 3 , 4 >> 2. 1
- В более общем смысле, если набор имеет наименьший элемент, то наименьший элемент является точной нижней гранью для набора. В этом случае его еще называют минимумом набора.
- инф < 1 , 2 , 3 , … >знак равно 1. = 1.>
- инф < Икс ∈ р : 0 < Икс < 1 >знак равно 0. : 0 = 0.>
- инф < Икс ∈ Q : Икс 3 >2 > знак равно 2 3 . : x ^ > 2 right > = < sqrt [] >.>
- инф < ( - 1 ) п + 1 п : п знак равно 1 , 2 , 3 , … >знак равно — 1. + >: n = 1,2,3, ldots right > = — 1.>
- Если — убывающая последовательность с пределом, то ( Икс п ) п знак равно 1 ∞ < displaystyle left (x_ right) _ ^ > Икс , инф Икс п знак равно Икс . < displaystyle inf x_ = x.>
Супрема
В последнем примере, супремумом множества рациональных чисел является иррациональным , что означает , что рациональные являются неполными .
Одно из основных свойств супремума:
Супремум подмножества из которых является набором мощности некоторого множества, является верхней гранью по отношению к (подмножеству) подмножеств из является объединением элементов S ( п , ⊆ ) , п ⊆ S п S .
Общая топология
Для начала рассмотрим топологию пространства в одной координате, затем расширим знания для многомерного пространства.
Интервалы
Интервал в одноостной системе координат, то есть в такой, в которой присутствует только координата x — это участок прямой, заключённый между точками a и b. Если интервал включает точки a и b, то интервал называется закрытым, если точки a и b не включены, то такой участок называется открытым интервалом.
Также интервал может быть ограничен только с одной стороны:
Мажоранта и миноранта
a будет являться мажорантой множества A, если a ≥ x для любого x ∈ A
a будет являться минорантой множества A, если a ≤ x для любого x ∈ A
Множество называется закрытым, если у множества есть мажоранта и миноранта.Максимум и минимум
Максимумом множества A называется точка, которая удовлетворяет условию = x, x ∈ A>
Минмум множества A: =Супремум и инфимум
Супремум — это наименьшая из всех мажорант, инфимум — это наибольшая из всех минорант.
Пример
Пусть точка x0 ∈ R n и r > 0.
Обозначим открытый шар с центром в точке x0 и радиусом r:
Br(x0) := 0||Выберем в качестве подмножества R n множество А: A ⊂ R n . Точка x0, которая принадлежит R n может быть охарактеризована так:
Точка x0 является внутренней точкой множества, если можно выбрать такое значение r0, что существует открытая сфера Br(x0) ⊂ A, при r0 > 0
Предельной точкой называется такая точка x0, что для любого r0 выполняется условие Br(x0) ∩ A ≠ ∅ (Br — открытая сфера с центром в точке x0 и любым радиусом, пересечение Br со множеством A не является пустым множеством)
Граничная точка множества: для любого r > 0 выполняются условия Br(x0) ∩ A ≠ ∅ и Br(x0) ∩ (R n A) ≠ ∅
Множество внутренних точек множества А обозначается A° и называется внутренностью множества.
Множество предельных точек множества А обозначается A .
Множество граничных точек множества А называется границей множества и обозначается ∂A.
Открытое множество
Множество А является открытым множеством, если все его точки являются внутренними, то есть для любой x0 существует такое значение r0 > 0, что Br(x0) ⊂ A.
Примеры
- Открытый интервал является открытым множеством R
- Открытая сфера является открытым множеством R n
- Пустое множество ∅ и всё пространство R n — открытые множества
Свойства
- Объединение неограниченного количества открытых множеств является открытым множеством
- Пересечение открытых множеств является открытым множеством
- Множество A ⊂ R n является открытым только если A = A°, частный случай — множество внутренних точек всегда является открытым множеством
- Для множества A ⊂ R n множество внутренних точек это пересечение всех открытых множеств содержащихся в A
Закрытое множество
Множество A ⊂ R n называется закрытым если дополнение R n A — это открытое множество
Примеры
- Закрытые интервалы являются закрытыми множествами
- Дополнение открытой сферы является закрытым множеством ⊂ R n
- Пустое множество ∅ и всё пространство R n являются закрытым множеством (и открытым одновременно)
Свойства
- Объединение неограниченного количества закрытых множеств является закрытым множеством
- Пересечение закрытых множеств является закрытым множеством
- Множество A ⊂ R n является закрытым тогда и только тогда, когда A = A , частный случай — множество предельных точек всегда является закрытым множеством
Ограниченое множество
Множество A ⊂ R n является ограниченым если существуют r > 0 и точка x0 такие, что A ⊂ Br(x0). Например, открытая сфера — это ограниченное множество, плоскость не является ограниченным множеством.
Компактное множество
Множество называется компактным, если оно закрыто и ограничено. Например, закрытый интервал является компактным множеством.
Супремум и инфимум числовых множеств.
Выше было описано правило, устанавливающее признак равенства двух вещественных чисел. Опишем теперь правило, позволяющее установить, какое из двух вещественных чисел больше.
Пусть оба вещественных числа имеют знак +.

Найдем первую по порядку цифру в этих числах, которые не равны друг другу. Пусть это будет цифра с номером n, т.е.

(заметим,что символами математики это записывается так: ). Тогда, если , то считаем, что a>b, а если , то a
Если вещественные числа а и b разных знаков, то большим считается число, имеющее знак +.
Пусть оба числа имеют знак –. Назовем модулем вещественного числа это же число, но со знаком +.

Это правило будет необходимо нам ниже.
Определение. Множество, элементами которого являются вещественные числа, называется числовым множеством.
Числовые множества мы будем обозначать , где под х будут пониматься вещественные числа.
Для того, чтобы все дальнейшие определения и теоремы записывались в принятой математической форме, введем специальные значки, которые носят название кванторов. Их два:
Знакназывается “квантор общности” и читается “для каждого” ( есть перевернутая буква А из английского выражения “for All”).
Знак называется “квантором существования” и читается “существует” ( есть перевернутая буква Е из английского слова “Exist”). Вариантом этого квантора является знак!, который читается “существует единственный” или “существует один и только один”.
А теперь перейдем к определениям.
Определение 1. Числовое множество называется ограниченным сверху, если (читается: существует такое , что для любого выполнено условие x меньше либо равно M) .Число М называется верхней гранью числового множества .
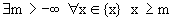
Определение 2. Числовое множество называется ограниченным снизу, если . Число m называется нижней гранью числового множества .
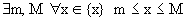
Определение 3. Числовое множество называется ограниченным, если .
Очевидно,что если, скажем, существует одна верхняя грань, то их бесконечно много: если, например, М – верхняя грань числового множества ,то М+1, М+2, М+3 и т.д. – также верхние грани для .
Определение 4. Наименьшая из верхних граней называется точной верхней гранью или супремумом числового множества (обозначение sup).
Наибольшая из нижних граней называется точной нижней гранью или инфимумом числового множества (обозначение inf).
Эти понятия столь важны, что опишем их в других терминах.
Sup определяется двумя свойствами:

Первое свойство означает, что sup – верхняя грань, т.е. все элементы не превосходят sup.

Второе свойство означает, что любая попытка уменьшить эту верхнюю грань приводит к появлению элемента из , который окажется больше .
Говоря образно, sup это планка, перепрыгнуть которую нельзя, но любая попытка опустить эту планку хоть чуть-чуть приводит к тому, что кто-то ее преодолевает.
Аналогично, inf определяется двумя свойствами:

Заметим, что сами sup и inf могут как принадлежать, так и не принадлежать множеству x.
Теперь мы в состоянии доказать важнейшую теорему этого раздела и одну из важнейших теорем всего мат. анализа.
Теорема о существовании супремума и инфимума.
Если числовое множество не пусто и ограничено сверху, то у него существуетsup.
Если числовое множество не пусто и ограничено снизу, то у него существуетinf.
Мы докажем эту теорему только для sup при одном дополнительном предположении – в множестве имеются положительные числа. Доказательство разбивается на три части.
Процедура построения sup .

Пусть М – верхняя грань для , т.е. . Проделаем следующее построение:
а) Выбросим из множества все отрицательные числа.
б) У оставшихся чисел выпишем те цифры , которые стоят перед запятой. Множество этих цифр конечно, т.к. этих цифр не более чем [M] (целая часть М). Обратите внимание, что именно в этом месте используется ограничение теоремы – существование верхней грани. Если бы верхней грани не существовало, то множество было бы бесконечным.
В силу конечности множества из этих цифр до запятой можно выбрать самую большую -–ведь их же конечное число. Обозначим самую большую из этих цифр через .
в) Выбросим из все те числа, у которых цифра до запятой меньше. У оставшихся чисел выпишем первую цифру после запятой. Этих цифр не более 10. Выберем из них самую большую и обозначим ее через .
г) Выбросим из все те числа, у которых первая цифра после запятой меньше . У оставшихся чисел выпишем вторую цифру после запятой. Этих цифр не более 10. Выберем из них самую большую и обозначим ее через .
д) Выбросим из все те числа, у которых…
Повторяя эту операцию до бесконечности мы построим число

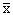
Покажем,что и естьsup.
Проверим первое свойство sup .
Возьмем любое . Если х имеет знак –, то ясно, что .
Пусть х имеет знак +. Тогда

Сравним . Вспомним, что было самым большим из . Поэтому может быть всего два варианта: либо , либо . В первом случае и дальнейшая проверка ни к чему.
Если же , то сравним . Опять-таки по построению возможны два варианта: либо и тогда и дальнейшая проверка ни к чему, либо .
Если , то сравним. Опять-таки по построению возможны два варианта: либо и тогда и дальнейшая проверка ни к чему, либо .
Продолжая этот процесс и дальше, получим, что возможны два следующих варианта.
а) Найдется какое-то n, для которого . Тогда .
б) Для всех n . Тогда . Поэтому всегда и первое свойство супремума выполнено.
Проверка второго свойства супремума.
Заметим,что второе свойство можно записать так: . Возьмем положительное :

.

Так как , то найдется такое n,что

но вспомним процедуру построения. На n-м шаге после выбрасывания во множестве оставались лишь те числа, для которых . Любое из этих чисел будет больше x’ (т.к. ), но естественно, меньше или равно . Поэтому любое из этих чисел удовлетворяет второму свойству супремума.

Подумайте сами, что надо изменить в процедуре построения, если во множестве есть только отрицательные числа.