Что такое суперпозиция функций
В научной среде широко известна шутка на эту тему «нелинейность» сравнивается с «не-слоном» — все создания, кроме «слонов», являются «не-слонами». Сходство заключается в том, что большинство систем и явлений в окружающем нас мире нелинейны, за малым исключением. Вопреки этому, в школе нас учат «линейному» мышлению, что очень плохо, с точки зрения нашей готовности к восприятию всепроникающей нелинейности Вселенной, будь то ее физические, биологические, психологические или социальные аспекты. Нелинейность концентрирует в себе одну из основных сложностей познания окружающего мира поскольку следствия, в общей своей массе, не пропорциональны причинам, две причины, при взаимодействии, не аддитивны, то есть следствия являются более сложными, чем простая суперпозиция, функциями причин. То есть, результат, получающийся в результате присутствия и воздействия двух причин, действующих одновременно, не является суммой результатов, полученных в присутствии каждой из причин в отдельности, при отсутствии другой причины. [c.168]
Сложная функция. Пусть функция у = f(u) есть функция от переменной и, определенной на множестве U с областью значений У, а переменная и в свою очередь является функцией и = д(х] от переменной ж, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция у = f(g(x называется сложной функцией (или композицией функций, суперпозицией функций, функцией от функции). [c.37]
Сложная функция. Функция, заданная в виде у =f(g(x)), называется сложной функцией х или суперпозицией функций g и / Сложную функцию часто записывают в виде у = Ди), где и = g(x). при этом аргумент х называют независимой переменной, а и — промежуточным аргументом. [c.26]
Определение 9. Ее in на некотором промежутке X определена функция г-ф(лг) с множеством значений Z и на множестве Z определена функция у =/(z), то функция у Л (f(x)), где у(у) — неубывающая выпуклая функция одного переменного, /(х) — выпуклая функция, является выпуклой функцией. [c.93]
Пример 3.28. Вернемся к примеру 3.27. На рис. 3.24 показан в виде штрих-пунктирной кривой результат суперпозиции двух функций принадлежности, соответствующих тем квантификаторам, которые имеются в этом примере. С помощью уровня отсечки со значением 0,7 получены нечеткие интервалы на оси абсцисс. Теперь мы можем сказать, что диспетчер должен ожидать изменения плана [c.144]
Другой способ определения функции F, отличный от способа суперпозиции, состоит в том, что при применении какого-либо квантификатора к другому квантификатору происходит некое монотонное преобразование исходной функции принадлежности, сводящееся к растяжению и сдвигу максимума функции в ту или другую сторону. [c.145]
Пример 3.29. На рис. 3.25 показаны два результата, полученные с помощью суперпозиции и сдвига с растяжением, для случая, когда ХА и X соответствуют квантификатору часто. Разница состоит, по-видимому, в том, что суперпозиция вычленяет в функции принадлежности часто те значения, которые часто встречаются. В случае же сдвига и растяжения мы можем интерпретировать результат как появление нового квантификатора со значением часто-часто, который можно при желании аппроксимировать, например, значением очень часто. [c.145]
Покажите, что суперпозиция строго возрастающей функции и функции полезности, представляющей некоторое отношение предпочтения >, также является функцией полезности, представляющей это отношение предпочтения. Какие из нижеприведенных функций могут выступать в качестве такого преобразования [c.38]
Первое из соотношений (2) представляет собой не что иное, как запись правила, согласно которому каждой функции F(x), принадлежащей семейству монотонно неубывающих абсолютно непрерывных функций, ставится в соответствие одна и только одна непрерывная функция w(j ). Это правило линейно, т.е. для него верен принцип суперпозиции [c.240]
Доказательство. Если отображение F непрерывно, функция М0 непрерывна как суперпозиция непрерывных функций. Чтобы доказать вторую часть утверждения, рассмотрим функцию [c.59]
Сложные е функции (суперпозиции) [c.92]
Метод функциональных преобразований предполагает также использование эвристического подхода. Например, использование логарифмических преобразований в качестве операторов В и С приводит к информационным критериям построения идентифицируемых моделей и использованию мощного инструмента теории информации [6]. Пусть оператор В представляет собой суперпозицию операторов умножения на функцию ,(.) и сдвига на функцию К0(), оператор С — оператор [c.107]
Здесь будут в общих чертах приведены результаты решения ряда вариационных задач (1)—(3). Они решались методом последовательной линеаризации ( 19—21) еще в 1962—1963 гг., когда технология метода только начинала складываться и проходила проверку. Поэтому мы остановимся лишь на некоторых деталях. Прежде всего заметим, что функции С и С2 были заданы достаточно сложными выражениями, являющимися суперпозицией вспомогательных функций, в том числе и заданных таблично. Поэтому при решении сопряженной системы ф=—fx
Пусть теперь (ДА и (д — произвольные функции, соответствующие каким-то значениям квантификаторов частоты. На рис. 3.23 показаны две одногорбые кривые, отвечающие этим функциям. Результат их суперпозиции — двугорбая кривая, показанная штриховой линией. Каков ее смысл Если, например, (ДА есть редко, а (д — часто, [c.143]
Преимущество такого способа определения F состоит в том, что при монотонных преобразованиях вид функции принадлежности меняется не кардинально. Ее унимодальность или монотонность сохраняется, и переход от нового вида функции к словесной оценке, соответствующей некоторому квантификатору, происходит куда проще, чем от многогорбых функций, возникающих в результате операции суперпозиции. [c.145]
Исследуем теперь зависимость р от нормы амортизации12. Из формулы (4.11) вытекает, что эта зависимость представима в виде суперпозиции двух функций. Первая есть р = р (А), где А = %Ао + Д.%А — взвешенная сумма интегральных дисконтированных амортизации. [c.35]
Пусть / Ж—>Ж — монотонно возрастающая функция, а и Х—>Ж — некоторая квазивогнутая функция, заданная на выпуклом множестве X, тогда их суперпозиция также будет квазивогнутой функцией. [c.45]
Соотношение (2.15) — это OWA-оператор Ягера, причем, поскольку функции принадлежности (2.16) имеют трапециевидную форму, то и линейная суперпозиция (2.15) является трапециевидным нечетким числом (что легко доказывается при использовании сегментного правила вычислений [35]). И можно свести операции с функциями принадлежности к операциям с их вершинами. Если обозначить трапециевидное число (2.16) как (аь а2, аз, а4), где а соответствуют абсциссам вершин трапеции, то выполняется [c.39]
«Учебник по дискретной математике. Суперпозиция функций. Замыкание набора функции.Замкнутые классы функций. Полные наборы. Базисы»
Пусть имеется некоторый набор K, состоящий из конечного числа булевых функций. Суперпозицией функций из этого набора называются новые функции, полученные с помощью конечного числа применения двух операций;
можно переименовать любую переменную, входящую в функцию из K;
вместо любой переменной можно поставить функцию из набора K или уже образованную ранее суперпозицию.
Суперпозицию еще иначе называют сложной функцией.
Пример 7.1. Если дана одна функция х|y (штрих Шеффера), то ее суперпозициями, в частности, будут следующие функции x|x, x|(x|y), x|(y|z) и т. д.
Замыканием набора функций из K называется множество всех суперпозиций. Класс функций K называется замкнутым, если его замыкание совпадает с ним самим.
Набор функций называется полным, если его замыкание совпадает со всеми логическими функциями. Иначе говоря, полный набор – это множество таких функций, через которые можно выразить все остальные булевы функции.
Неизбыточный полный набор функций называется базисом (“неизбыточный” означает, что если какую-то функцию удалить из набора, то этот набор перестанет быть полным).
Пример 7.2. Конъюнкция, дизъюнкция и отрицание являются полным набором (в этом убедились в разд. 5), но не являются базисом, так как это набор избыточен, поскольку с помощью правил де Моргана можно удалить конъюнкцию или дизъюнкцию. Любую функцию можно представить в виде полинома Жегалкина (разд. 6). Ясно, что функции конъюнкция, сложение по модулю 2 и константы 0 и 1 являются полным набором, но эти четыре функции также не являются базисом, поскольку 1+1=0, и поэтому константу 0 можно исключить из полного набора (для построения полиномов Жегалкина константа 0 необходима, поскольку выражение “1+1” не является полиномом Жегалкина).
Легко видеть, что одним из способов проверки полноты какого-то набора К является проверка того, что через функции из этого набора выражаются функции другого полного набора (можно проверить, что через функции из К можно выразить конъюнкцию и отрицание или дизъюнкцию и отрицание.
Существуют такие функции, что одна такая функция сама является базисом (здесь достаточно проверить только полноту, неизбыточность очевидна). Такие функции называются шефферовскими функциями. Это название связано с тем, что штрих Шеффера является базисом. Напомним, что штрих Шеффера определяется следующей таблицей истинности:
Так как очевидно , т. е. отрицание является суперпозицией штриха Шеффера, а дизъюнкция тогда , штрих Шеффера сам является базисом. Аналогично, стрелка Пирса является шефферовской функцией (студенты могут проверить это сами). Для функций 3-х или более переменных шефферовских функций очень много (конечно, выражение других булевых функций через шефферовскую функцию большого числа переменных сложно, поэтому в технике они редко используются).
Заметим, что вычислительное устройство чаще всего базируется на полном наборе функций (часто на базисах). Если в основе устройства лежат конъюнкция, дизъюнкция и отрицание, то для этих устройств важна проблема минимизации ДНФ; если в основе устройства лежат другие функции, то полезно уметь алгоритмически минимизировать выражения через эти функции.
Перейдем теперь к выяснению полноты конкретных наборов функций. Для этого перечислим 5 важнейших классов функций:
- Т0 – это набор всех тех логических функций, которые на нулевом наборе принимают значение 0 (Т0 – это класс функций, сохраняющих 0);
- Т1 – это набор всех логических функций, которые на единичном наборе принимают значение 1 (Т1 – это класс функций, сохраняющих единицу) (заметим, что число функций от п переменных принадлежащих классам Т0 и Т1 равно 2 2n-1 );
- L – класс линейных функций т. е. функций, для которых полином Жегалкина содержит только первые степени переменных;
- М – класс монотонных функций. Опишем класс этих функций более подробно. Пусть имеются 2 набора из п переменных: s1 = (x1, x2. xn)
s 1 = ( х1 , х2 , … , хп ) и s 2 = ( y1 , y2,… , yп) . Будем говорить, что набор s 1 меньше набора s 2 (s 1 £ s 2 ), если все хi £ yi. Очевидно, что не все наборы из п переменных сравнимы между собой (например, при п = 2 наборы (0,1) и (1,0) не сравнимы между собой). Функция от п переменных называется монотонной , если на меньшем наборе она принимает меньшее или равное значение. Разумеется, эти неравенства должны проверяться только на сравнимых наборах. Понятно, что несравнимые наборы – это те, в которых есть некоторые координаты типа (0,1) в одном наборе и (1,0) в другом на соответствующих местах (в дискретной математике монотонные функции это только как бы “монотонно возрастающие функции”, “монотонно убывающие” функции здесь не рассматриваются).
Пример. В нижеследующей таблице функции f1, f2 являются монотонными функциями, а функции f3, f4 – нет.
Композиция отображений
Компози́ция фу́нкций (суперпози́ция фу́нкций) в математике — это применение одной функции к результату другой.
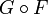
Композиция функций F и G обычно обозначается .
Содержание
Определение
Пусть и две функции. Тогда их композицией называется функция , определённая равенством:
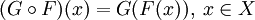
.
Связанные определения
- Термин «сложная функция» может быть применим к композиции двух функций, тем не менее он чаще употребляется в ситуации когда на вход функции нескольких переменных подаётся набор функций от одной или нескольких исходных переменных. Например функция G вида G(x,y) = F(u(x,y),v(x,y))
Свойства композиции
Дополнительные свойства
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Композиция отображений» в других словарях:
Функция (математика) — У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения … Википедия
ХОПФА ИНВАРИАНТ — инвариант гомотопич. класса отображений топологич. пространств. Впервые был определенX. Хопфом ([1], [2]) для отображений сфер Пусть непрерывное отображение. Переходя, если нужно, к гомотопному отображению, можно считать это отображение… … Математическая энциклопедия
МЕРОМОРФНОЕ ОТОБРАЖЕНИЕ — комплексных пространств обобщение понятия мероморфной функции. Пусть Xи Y комплексные пространства, А открытое подмножество в X такое, что нигде не плотное аналитич. одмпожество, и пусть дано аналитич. отображение Отображение f наз. мероморфным… … Математическая энциклопедия
ПОЧТИКОЛЬЦО — одно из обобщений понятия ассоциативного кольца. П. это кольцоид над группой, т. е. универсальная алгебра, в к рой имеется ассоциативная операция умножения и операция сложения; относительно сложения П. должно быть группой (не обязательно… … Математическая энциклопедия
НОРМИРОВАНИЕ — логарифмическое нормирование, оценка поля, отображение поля Кв где Г линейно упорядоченная абелева группа, а присоединяемый элемент считается больше любого элемента из группы и для любого . При этом Н. должно удовлетворять следующим условиям:… … Математическая энциклопедия
ОПЕРАТОР — отображение одного множества на другое, каждое из к рых наделено нек рой структурой (алгебраич. операциями, топологией, отношением порядка). Общее определение О. совпадает с определением отображения или функции: пусть Xи Y два множества;… … Математическая энциклопедия
Топология — (от греч. tоpos место и …логия (См. . Логия) часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных… … Большая советская энциклопедия
НЕПРЕРЫВНОЕ ОТОБРАЖЕНИЕ — отображение топологич. пространства Xв топологич. пространство У такое, что для всякой точки и для всякой окрестности ее образа f(x0) существует такая окрестность точки х 0 , что Это определение является перефразировкой окрестност ного… … Математическая энциклопедия
Непрерывное отображение — или непрерывная функция в математике это отображение из одного пространства в другое, при котором близкие точки области определения переходят в близкие точки области значений. Наиболее общее определение формулируется для отображений… … Википедия
ГОМОЛОГИИ ТЕОРИЯ — топологических пространств часть алгебраич. топологии, осуществляющая связь между топологич. н алгебраич. понятиями: приводя в соответствие каждому пространству определенную последовательность групп, а непрерывному отображению пространств… … Математическая энциклопедия
Что такое суперпозиция функций
Действие (или, иначе, операция) суперпозиции функций имеет ряд интересных свойств и много важных применений. Напомним определение и простейшие свойства суперпозиции для функций действительной переменной (функций, области определения и множества значений которых являются подмножествами множества действительных чисел).
Пусть — произвольные функции действительной переменной. Суперпозицией этих функций (именно в том порядке, в котором они записаны) называется такая функция , что:
а) область определения образована теми числами до из области определения функции для которых принадлежит области определения функции
б) значение функции в какой угодно точке из области ее определения связано со значениями равенством
Таким образом, чтобы найти значение функции в точке нужно найти а затем Число и есть значение функции в точке
Если функция и в точке принимает значение , то это будем изображать так:
Читается такая схема одним из следующих способов: «функция и в точке принимает значение «функция и точке ставит в соответствие точку «точка «о является образом точки под действием функции . Для суперпозиции функций такая схема будет иметь вид
(если функция ) точке ставит в соответствие точку а функция точке — точку , то функция точке ставит в соответствие точку
Пример. Пусть . Чтобы найти значение суперпозиции этих функций в некоторой точке нужно возвести в квадрат,
и найти значение в точке
Объединяя эти две схемы, получаем
Таким образом, функция каждой точке ставит в соответствие можно задать формулой
Рассмотрим теперь суперпозицию функций , т. е. суперпозицию тех же самых функций, но в обратном порядке. Получим
Это означает, что суперпозиция функций есть функция
Таким образом, суперпозиция функций зависит от порядка, в котором записаны функции.
Будем обозначать суперпозицию функций , т. е.
Особую роль относительно операции суперпозиции играет функция которую будем обозначать Схема этой функции такая:
для каждого числа .
Очевидно, для любой функции выполняются равенства
или, в виде схемы,
Дадим отдельное обозначение и для функции , а именно
Мы будем рассматривать множества функций, имеющих следующее свойство:
Если функции принадлежат заданному множеству функций, то и суперпозиция этих функций также принадлежит этому множеству.
О таком множестве говорят, что оно замкнуто относительно операции суперпозиции функций, или, иначе, что суперпозиция является внутренней операцией для такого множества.
Найдем, например, суперпозицию двух линейных функций. Пусть Для произвольного числа имеем
а следовательно, . Отсюда суперпозиция двух заданных линейных функций снова есть линейная функция.
Легко доказать, что это верно и в общем случае: если , то , т. е. снова функция линейная. При этом коэффициенты этой функции выражаются через коэффициенты помощью равенств
Следовательно, множество всех линейных функций вместе с каждыми двумя функциями содержит и их суперпозицию, т. е. суперпозиция является внутренней операцией для множества всех линейных функций.
Результат суперпозиции для линейных функций также зависит, вообще говоря, от порядкаих записи. Например, если , то есть функция , причем — это функция .
Следовательно, , т. е. для данных функций
Другим примером множества функций, замкнутого относительно суперпозиции, является множество всех многочленов вида
с целыми коэффициентами. Действительно, пусть
— два таких многочлена. Тогда суперпозицией , как легко убедиться, является такое выражение:
Это есть многочлен степени , который имеет вид
где коэффициенты выражаются определенным образом через коэффициенты
Общее правило для нахождения чисел по известным коэффициентам довольно громоздкое, но в каждом конкретном случае коэффициенты удается вычислить без особых трудностей. Например, пусть
В рассмотренных примерах множества функций, замкнутые относительно суперпозиции, были бесконечны. Однако это условие не является необходимым для замкнутости. Для множества, которое состоит лишь из двух функций которые мы обозначили суперпозиция также будет внутренней операцией.
т. е. условие замкнутости выполняется.
Даже из приведенных примеров видно, что множества, для которых суперпозиция является внутренней операцией, могут быть очень разными. Далее мы рассмотрим строение таких множеств для функций, определенных на конечных множествах.
Упражнения
1. Найти суперпозиции где (-соответственно функции;
2. Будут ли замкнуты относительно суперпозиции такие множества функций:
а) множество всех функций вида , где а — произвольное действительное число;
б) множество всех функций вида а, где а — произвольное рациональное число;
в) множество функций каждая из которых рассматривается на множестве всех действительных чисел без нуля;
Формулы и суперпозиции булевых функций
Табличный способ задания булевой функции не является эффективным. Им практически нельзя воспользоваться при большом числе переменных. Помимо этого способа существует способ представления булевых функций в виде формул. Этот способ аналогичен аналитическому способу задания функций действительного переменного.
Как известно, в математическом анализе мы исходили из определенного множества элементарных функций и строили из них сложные функции, записывая их в виде формул, например: и т.п. Аналогично обстоит дело для булевых функций, но только вместо элементарных функций математического анализа мы используем элементарные булевы функции — главным образом, те функции от одной и от двух переменных, которые мы определили ранее.
Но в отличие от математического анализа в теории булевых функций ставится задача представления любой булевой функции такой формулой, которая содержала бы строго определенное конечное множество элементарных булевых функций. Эти функции назовем пока условно «базисными функциями». Множества таких базисных функций могут быть разными, но, так или иначе, мы хотим иметь нечто вроде функционального базиса (или множества таких базисов), через элементы которого можно было бы выразить любую булеву функцию. Аналогичная задача не может быть решена для функций действительного переменого. Для булевых же функций задача оказывается разрешимой, и это обусловлено прежде всего тем, что булева функция является конечной функцией.
Чтобы математически точно сформулировать и решить поставленную выше задачу, нам необходимо уточнить понятие формулы. В анализе, поскольку там не возникала задача подобного рода, мы могли ограничиться интуитивной идеей формулы как некоего способа представления функции. В теории булевых функций мы хотим доказывать утверждения вида «любая булева функция может быть представлена формулой над заданным множеством базисных функций есть функция от переменных, а булевы функции — произвольные (и не обязательно различные) функции от одного и того же числа переменных, которое обозначим называемую суперпозицией функций так, что для любого
Таким образом, суперпозиция есть не что иное, как композиция булевых операторов , где булев оператор задается семейством координатных функций .
Для суперпозиции используется также обозначение . Предположение о том, что все функции , — функции от одного и того же числа переменных, не ограничивает общности, поскольку, как было показано ранее, любое конечное множество булевых функции всегда можно рассматривать как множество функций от одного и того же числа переменных.
Замечание 6.4. Обратим внимание на то, что в общем случае «уравнивание» числа переменных функций , связано с добавлением фиктивных переменных, а его, как известно, можно осуществлять разными способами. Поэтому суперпозиция , вообще говоря, определена однозначно лишь с точностью до равенства булевых функций согласно определению 6.2.
Пусть дано некоторое множество булевых функций — формулы над множеством — функция из переменных, то выражение есть формула над множеством Замечание 6.5. 1. Строго говоря, в формуле фигурирует не сама булева функция из множества . Но мы, чтобы не усложнять терминологию, будем отождествлять обозначения базисных функций, т.е. функции из заданного множества .
Пример 6.6. а. Пусть . Это множество, состоящее из функций дизъюнкции, конъюнкции и отрицания, называют стандартным базисом. Формулами над стандартным базисом будет любое переменное: и т.д. Далее, из переменных как формул и функции или . Эти формулы, однако, естественно записывать несколько иначе. Поскольку каждая булева функция от двух переменных (каковы, в частности, дизъюнкция и конъюнкция) является одновременно бинарной операцией на множестве , то формулы с такими функциями обычно записывают в «инфиксной форме», т.е. как и т.п. Аналогично для отрицания используют запись , а не .
Кроме того, в формулах над стандартным базисом, во-первых, опускают скобки, используя ассоциативность булевых операций пишут ; во-вторых, опускают, как правило, внешние скобки, записывая формулу, аналогичную последней, просто как ; в-третьих, используют соглашение о «старшинстве» (или о приоритете) операций, полагая, что самый высокий приоритет имеет операция отрицания (т.е. она всегда выполняется перед конъюнкцией и дизъюнкцией), затем идет конъюнкция и после нее — дизъюнкция.
С учетом сказанного формула может быть переписана так:
Согласно определению формулы, можно представить процесс построения формулы (6.6) следующим образом. Из переменных и функции , затем из нее и функции отрицания получаем формулу , т.е. формулу . Далее из переменных и функции строим формулу , а из нее, переменного — формулу , которую записываем как . И наконец, из формул и функции , т.е. формулу (6.6).
Описанный процесс можно наглядно изобразить в виде ориентированного дерева (рис. 6.3). Листья этого дерева помечены переменными или константами формулы, а каждый узел, не являющийся листом, — одной из функций из множества
б. Рассмотрим множество булевых функций , которое называют базисом Жегалкина. При записи формул над базисом Жегалкина используют те же принципы, что и при записи формул над стандартным базисом. Приоритет операции конъюнкции считается выше приоритета операции сложения по модулю 2. Так как последняя ассоциативна, то при записи формул с этой операцией соответствующим образом опускают скобки. Так, формулами над базисом Жегалкина будут:
Процесс построения первых двух формул изображен в виде деревьев на рис. 6.4.
в. Пусть множество базисных функций не равна булевой функции . Поэтому при записи формул над множеством следует заботиться о расстановке скобок. Примеры формул над множеством
Внешние скобки мы опускаем и в этом случае. Дерево, показывающее процесс построения первой из записанных выше формул, изображено на рис. 6.5.
Мы будем использовать запись , указывая тем самым, что формула , и только их. Множество переменных формулы .
Нам понадобится также понятие подформулы.
Из определения и рассмотренных примеров следует, что процесс построения формулы есть процесс определения некоторой сложной булевой функции, т.е. суперпозиции. Формула «собирается» из «элементарных формул», т.е. переменных и базисных функций, так, что на каждом шаге из уже полученных формул строится новая, более сложная формула. Естественно назвать эти «промежуточные» формулы подформулами рассматриваемой формулы. Так, в примере б.б.а формулы (и, конечно, переменные и базисные функции) — это подформулы формулы (6.6).
Строго понятие подформулы может быть введено следующим образом. Пусть или , где — функция из переменных, а , суть формулы над 1) все формулы ;
2) для каждого все подформулы формулы .
В дереве, изображающем процесс построения формулы, каждое поддерево, все листья которого являются также и листьями всего дерева, определяет некоторую подформулу.
Каждому набору значений переменных, входящих в заданную формулу, можно определенным образом сопоставить значение этой формулы. Вычисление этого значения в точности соответствует процессу построения формулы из подформул (в конечном счете из переменных и базисных функций).
Пример 6.7. Полагая в формуле (6.6) , получим значение формулы (6.6), равное
Таким образом, по каждому набору значений переменных формулы можно по определенному алгоритму вычислить значение формулы. Это значит, что каждая формула определяет (или представляет) некоторую булеву функцию. Введем понятие функции, представляемой формулой над множеством представляет проектирующую функцию над множеством , a — функция из переменных , то формула представляет суперпозицию функций ;
4) других булевых функций, представляемых формулами над множеством , где , а каждая из функций есть либо элемент и называть замыканием множества представляется формулой , то будем писать , или, короче, .
Определение 6.3. Множество булевых функций 1) замкнутым, если любая формула над , и полно, если всякая булева функция есть некоторая суперпозиция над .
Замечание 6.6. Можно заметить, что определение формулы и суперпозиции над заданным множеством булевых функций похоже на определение Ω-замыкания множества в алгебрах. Эти определения, равно как и основанные на них определения замкнутости и полноты множеств булевых функций, могут быть переведены полностью на алгебраический язык. Тогда замкнутое множество булевых функций, согласно определению 6.3, окажется не чем иным, как замкнутым подмножеством некоторой алгебры булевых функций, а полное множество булевых функций — системой образующих этой алгебры. Однако при попытке чисто алгебраической интерпретации определения 6.3 возникают некоторые технические трудности, обсуждение которых выходит за рамки этого курса.
Пример 6.8. Для каждой из определенных в 6.1 функций от двух переменных мы можем записать следующие формулы над стандартным базисом:
Если мы пополним стандартный базис функцией (импликацией), то формула для эквивалентности примет вид
Тот факт, что одна и та же функция (в данном случае эквивалентность) может быть представлена по крайней мере двумя разными формулами над одним и тем же множеством, а именно над , показывает, что соответствие между формулами над фиксированным множеством и представляемыми ими функциями не является взаимно однозначным. Эта ситуация до некоторой степени аналогична разложению по базису векторов конечномерного линейного пространства. Формула, представляющая некоторую булеву функцию, выражает «разложение» этой функции по фиксированному «функциональному базису». Одна и та же функция может иметь несколько таких разложений. В отличие от линейной алгебры в этом случае возникает ситуация, когда возможны различные разложения заданной функции по одному и тому же базису. Например, формулы и над стандартным базисом представляют одну и ту же функцию.
Назовем эквивалентными формулы, которые представляют равные функции. Эквивалентным (или тождественным) преобразованием формулы ) называют выражение
где формулы и должно содержать все существенные переменные функций /(#1. жп) и g(yi. ym), представляемых формулами
Пример 6.9. В тождествах пересечение множеств переменных в левых и правых частях пусто, причем во втором тождестве правая часть вообще не содержит переменных. В тождестве указанное пересечение равно .
Все записанные в примере 6.8 выражения являются тождествами над множеством , причем во всех этих тождествах множества переменных в левой и правой частях тождества совпадают. Такого же рода тождества — аксиомы булевой алгебры* (кроме тождеств и ) и вытекающие из них тождества (подобные, например, законам де Моргана).
*Поскольку все переменные, фигурирующие в этих тождествах, есть булевы переменные, то речь здесь идет об аксиомах булевой алгебры применительно к частному случаю — двухэлементной булевой алгебре
Правила тождественных преобразований булевых функций
Без доказательства сформулируем следующие правила тождественных преобразований.
Теорема 6.1. 1. Если в тождестве (6.7) некоторые переменные заменить произвольными формулами (над множеством и булевыми функциями любому сложному высказыванию, составленному из некоторых «простых» высказываний с использованием указанных выше логических связок, однозначно сопоставляется формула над множеством , т.е. каждому простому высказыванию сопоставляется булево переменное (так что разным высказываниям сопоставляются и разные переменные), а связки заменяются соответствующими функциями из множества . Тогда, например, высказыванию (читается: «если , то , и если , то «) будет сопоставлена формула .
Таким образом, с логической точки зрения формула над множеством есть высказывание. Поскольку мы имеем возможность вычислять значения формул и проводить их эквивалентные преобразования (используя, в частности, аксиомы булевой алгебры), мы получаем алгебраический аппарат для упрощения сложных высказываний (путем эквивалентных преобразований) и вычисления их истинностных значений.
Но тогда возникают вопросы: как практически построить для любой наперед заданной булевой функции представляющую ее формулу над фиксированным множеством базисных функций Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Суперпозиция функций
Суперпозицией функций f1, …, fm называется функция f, полученная с помощью подстановок этих функций друг в друга и переименования переменных.
Пусть имеются два отображения и , причем непустое множество. Тогда супер позицией или композицией функций и называется функция , определенная равенством для всякого .
Областью определения суперпозиции является множество .
Функция называется внешней, а -внутренней функцией для суперпозиции .
Функции, представленные в виде композиции «более простых», называются сложными функциями.
Примерами использования суперпозиции являются: решение системы уравнений методом подстановки; нахождение производной от функции; нахождение значения алгебраического выражения с помощью подстановки в него значения заданных переменных.
Рекурсивные функции
Рекурсией называется такой способ задания функции, при котором значения определяемой функции для произвольных значений аргументов выражаются известным образом через значения определяемой функции для меньших значений аргументов.
Примитивно рекурсивная функция
Определение понятия примитивно рекурсивной функции является индуктивным. Оно состоит из указания класса базовых примитивно рекурсивных функций и двух операторов (суперпозиции и примитивной рекурсии), позволяющих строить новые примитивно рекурсивные функции на основе уже имеющихся.
К числу базовых примитивно рекурсивных функций относятся функции следующих трёх видов:
Нулевая функция— функция без аргументов, всегда возвращающая0.
Функция следованияодного переменного, сопоставляющая любому натуральному числунепосредственно следующее за ним натуральное число .
Функции , где , от n переменных, сопоставляющие любому упорядоченному набору натуральных чисел число из этого набора.
Операторы подстановки и примитивной рекурсии определяются следующим образом:
Оператор суперпозиции (иногда—оператор подстановки). Пусть — функция от m переменных, а — упорядоченный набор функций отпеременных каждая. Тогда результатом суперпозиции функцийв функцию называется функцияотпеременных, сопоставляющая любому упорядоченному набору натуральных чисел число .
Оператор примитивной рекурсии. Пусть — функция от n переменных, а — функция от переменных. Тогда результатом применения оператора примитивной рекурсии к паре функций и называется функция от переменной вида ;
В данном определении переменнуюможно понимать как счётчик итераций, — как исходную функцию в начале итерационного процесса, выдающего некую последовательность функцийпеременных, начинающуюся с , и — как оператор, принимающий на входпеременных , номер шага итерации , функцию на данном шаге итерации, и возвращающий функцию на следующем шаге итерации.
Множество примитивно рекурсивных функций — это минимальное множество, содержащее все базовые функции и замкнутое относительно указанных операторов подстановки и примитивной рекурсии.
В терминах императивного программирования — примитивно рекурсивные функции соответствуют программным блокам, в которых используется только арифметические операции, а также условный оператор и оператор арифметического цикла (оператор цикла, в котором число итераций известно на момент начала цикла). Если же программист начинает использовать оператор цикла while, в котором число итераций заранее неизвестно и, в принципе, может быть бесконечным, то он переходит в класс частично рекурсивных функций.
Укажем на ряд широко известных арифметических функций, являющихся примитивно рекурсивными.
Функция сложения двух натуральных чисел () может быть рассмотрена в качестве примитивно рекурсивной функции двух переменных, получаемой в результате применения оператора примитивной рекурсии к функциям и , вторая из которых получается подстановкой основной функции в основную функцию :
Умножение двух натуральных чисел может быть рассмотрено в качестве примитивно рекурсивной функции двух переменных, получаемой в результате применения оператора примитивной рекурсии к функциям и , вторая из которых получается подстановкой основных функций и в функцию сложения:
Симметрическая разность(абсолютная величина разности) двух натуральных чисел () может быть рассмотрена в качестве примитивно рекурсивной функции двух переменных, получаемой в результате применения следующих подстановок и примитивных рекурсий:
Суперпозиция функций (сложная функция).

(g(x))=e 2x , g((x))=.
Определение
Пусть идве функции. Тогда их композицией называется функция, определённая равенством:

.
Свойства композиции

.
Если F = idX — тождественное отображение на X, то есть

,

.
Если G = idY — тождественное отображение на Y, то есть

,

.
Рассмотрим пространство всех биекций множества X на себя и обозначим его . То есть если, то— биекция. Тогда композиция функций изявляетсябинарной операцией, а —группой. idX является нейтральным элементом этой группы. Обратным к элементу является—обратная функция.
Группа , вообще говоря, некоммутативна, то есть .
Дополнительные свойства
Композиция непрерывных функций непрерывна. Пусть —топологические пространства. Пусть идве функции,. Тогда.
Композиция дифференцируемых функций дифференцируема. Пусть . Тогда, и

.
Счетные и несчетные множества.
Два конечных множества состоят из равного числа элементов, если между этими множествами можно установить взаимно однозначное соответствие. Число элементов конечного множества – мощность множества.
Для бесконечного множества можно установить взаимно однозначное соответствие между всем множеством и его частью.
Самым простым из бесконечных множеств является множество N.
Определение. Множества А и В называются эквивалентными (АВ), если между ними можно установить взаимно однозначное соответствие.
Если эквивалентны два конечных множества, то они состоят из одного и того же числа элементов.
Если же эквивалентные между собой множества А и В произвольны , то говорят, что А и В имеют одинаковую мощность. (мощность = эквивалентность).
Для конечных множеств понятие мощности совпадает с понятием числа элементов множества.
Определение. Множество называется счетным, если можно установить взаимно однозначное соответствие между ним и множеством натуральных чисел. (Т.е. счетное множество – бесконечное, эквивалентное множеству N).
(Т.е. все элементы счетного множества можно занумеровать).
Свойства отношения равномощности.
1) АА- рефлексивность.
2) АВ, то ВА – симметричность.
3) АВ и ВС, то АС – транзитивность.
1) n→2n, 2,4,6,… — четные натуральные
2) n→2n-1, 1,3,5,…- нечетные натуральные.
Свойства счетных множеств.
1. Бесконечные подмножества счетного множества счетны.
Доказательство. Т.к. А – счетно, то А: х1,х2,… — отобразили А в N.
ВА, В: →1,→2,… — поставили каждому элементу В в соответствиенатуральное число, т.е. отобразили В в N. Следовательно В – счетно. Ч.т.д.
2. Объединение конечной (счетной) системы счетных множеств – счетно.
1. Множество целых чисел Z – счетно, т.к. множество Z можно представить как объединение счетных множеств А и В, где А: 0,1,2. и В: -1,-2,-3,…
2. Множество упорядоченных пар (т.е. (1,3)≠(3,1)).
3 (!). Множество рациональных чисел – счетно.

Q=. Можно установить взаимно однозначное соответствие между множеством несократимых дробейQ и множеством упорядоченных пар:

. Т.о. множество Q равномощно множеству .
Множество – множество всех упорядоченных пар – счетно. Следовательно и множество – счетно, а значит и Q – счетно.
Определение. Иррациональным числом называется произвольная бесконечная десятичная непериодическая дробь, т.е. 0,12…
Множество всех десятичных дробей образуют множество вещественных (действительных) чисел.
Множество иррациональных чисел – несчетно.
Теорема 1. Множество вещественных чисел из промежутка (0,1) – несчетное множество.
Доказательство. Допустим противное, т.е. что все числа интервала (0,1) можно занумеровать. Тогда, записывая эти числа в виде бесконечных десятичных дробей, получим последовательность:
Рассмотрим теперь вещественное число х=0,b1b2…bn…, где b1— любая цифра, отличная от а11, (0 и 9), b2 — любая цифра, отличная от а22, (0 и 9),…, bn — любая цифра, отличная от ann, (0 и 9).
Т.о. х(0,1), но хxi (i=1,…,n) т.к. в противном случае, bi=aii. Пришли к противоречию. Ч.т.д.
Теорема 2. Любой промежуток вещественной оси является несчетным множеством.
Теорема 3. Множество действительных (вещественных) чисел – несчетно.
Про всякое множество, равномощное множеству вещественных чисел говорят, что оно мощности континуума (лат. continuum – непрерывное, сплошное).

Пример. Покажем, что интервал обладает мощностью континуума.