Правило суммы нескольких векторов — основные сведения
Вектор в геометрии является таким отрезком, для которого задано направление, а также начало и конец, определенные граничными точками.
Обозначают вектор, например, таким образом: overrightarrow. В этом случае началом вектора является точка А, конец обозначен точкой В. Допускается и такое верное обозначение вектора: overrightarrow, которое можно встретить в задачах на сложение и вычитание.
Длина (или модуль) вектора A B → представляет собой длину отрезка АВ, который соответствует рассматриваемому вектору:
Нулевой вектор — это вектор со совпадающими началом и концом, то есть нулевым значением длины.
Коллинеарные вектора — вектора, расположенные на единой прямой, либо на прямых, которые являются параллельными.
Примеры коллинеарных векторов:
Если записанное ранее условие, при котором вектора коллинеарны, не выполняется, вектора называют неколлинеарными. В качестве примера можно представить следующие неколлинеарные вектора:
Пара векторов, которые коллинеарны друг другу, совпадают по направлению, являются сонаправленными.
На рисунке изображены сонаправленные вектора:
Если предыдущее условие, при котором вектора сонаправлены, не выполняется, то такие вектора называют противоположно направленными. Например, противоположно направлены следующие вектора:
В задачах на уроке можно встретить следующее обозначение того, как соотносятся между собой вектора:
a → ↑ ↑ c → , a → ↑ ↓ b → .
Равными векторами являются такие векторы, которые сонаправлены и равны по длине.
Правила нахождения суммы векторов
Формула сложения векторов a → = a x ; a y и b → = b x ; b y , которую можно применять в случае решения плоских задач:
a → + b → = a x + b x ; a y + b y .
Формула сложения векторов a → = a x ; a y ; a z и b → = b x ; b y ; b z , которую можно применять в случае решения пространственных задач:
a → + b → = a x + b x ; a y + b y ; a z + b z .
Формула сложения векторов a → = a x ; a y ; … ; a n и b → = b x ; b y ; … ; b n , которую можно применять в случае решения задач с n-мерными векторами:
a → + b → = a x + b x ; a y + b y ; … ; a n + b n .
Рассмотрим правила, которые целесообразно использовать при решении заданий в классе и самостоятельно на сложение коллинеарных векторов.
При сложении пары сонаправленных векторов требуется отмерить второй вектор от точки, которая является концом первого вектора. Результатом сложения является вектор с началом в точке, которая определяет начало первого вектора, и концом, совпадающим с конечной точкой второго вектора.
При сложении пары противоположно направленных векторов требуется отмерить второй вектор от точки, которая является началом первого вектора. Результатом сложения является вектор с началом в точке, совпадающей с началом для обоих векторов; длиной, равной разности длин векторов; направлением, совпадающим с направлением вектора, который обладает большей длиной.
Существует ряд правил, от знания которых будет зависеть то, насколько легко складываются вектора, не являющиеся коллинеарными.
Правило треугольника. Если даны два неколлинеарных вектора a → и b → , сумму которых нужно вычислить, то необходимо отмерить вектор b → от конечной точки, принадлежащей вектору a → . Результатом сложения таких векторов a → + b → является вектор с началом, расположенным в начальной точке вектора a → и концом, который совпадает с концом вектора b → .
Правило параллелограмма. Если даны два неколлинеарных вектора a → и b → , сумму которых нужно вычислить, то необходимо отмерить вектор b → от начальной точки, принадлежащей вектору a → . Результатом сложения векторов a → + b → является вектор, совпадающий с диагональю, проведенной в параллелограмме, который построен с помощью векторов a → и b → .
Действие по сложению векторов обладает рядом характерных свойств. Представим их описание:
- Наличие вектора, который является нейтральным: для какого-либо вектора a → выполняется следующее: a → + 0 → = a → .
- Наличие вектора, который является обратным: для какого-либо вектора a → выполняется следующее: a → + ( — a → ) = 0 → .
- Ассоциативность: для каких-либо векторов a → , b → и c → выполняется следующее: ( a → + b → ) + c → = a → + ( b → + c → ) .
- Коммутативность: для каких-либо векторов a → и b → выполняется следующее: a → + b → = b → + a → .
При сложении нескольких векторов следует откладывать их в определенной последовательности: каждый следующий нужно отмерять от точки, которая является концом предыдущего вектора. Результатом сложения данных векторов является вектор с началом, совпадающим с точкой, которая является началом первого вектора, и концом, расположенным в конце последнего вектора:
a 1 → + a 2 → + a 3 → + a 4 → = a → .
Примеры решения задач
Даны два вектора, сумму которых требуется найти:
a → = 1 ; 2 и b → = 4 ; 8 .
Воспользуемся формулой сложения векторов для плоских задач:
a → + b → = 1 + 4 ; 2 + 8 = 5 ; 10
Даны два вектора, сумму которых требуется вычислить:
a → = 1 ; 2 ; 5 и b → = 4 ; 8 ; 1 .
Воспользуемся формулой сложения векторов, применимой для решения пространственных задач:
a → + b → = 1 + 4 ; 2 + 8 ; 5 + 1 = 5 ; 10 ; 6
Даны два вектора, которые требуется сложить:
a → = 1 ; 2 ; 5 ; 9 и b → = 4 ; 8 ; 1 ; — 20 .
Воспользуемся формулой для решения задач с n-мерными векторами:
a → + b → = 1 + 4 ; 2 + 8 ; 5 + 1 ; 9 + ( — 20 ) = 5 ; 10 ; 6 ; — 11
Ответ: 5 ; 10 ; 6 ; — 11 .
Имеется некий прямоугольный треугольник ABC. В нем угол А составляет 90°, точка О обозначает центр окружности, описанной около рассматриваемого треугольника. Вектор А → В имеет координаты 1 ; 1 . Координаты вектора А → С р а в н ы — 1 ; 1 . Требуется определить, чему равна сумма координат вектора O C → .
Заметим, что в данном случае центр описанной окружности совпадает с серединой гипотенузы, так как вписанный треугольник является прямоугольным. В результате точка О расположена посередине ВС. Выполним соответствующий рисунок:
В данном случае, справедливо, что:
B C → = A C → — A B →
Определим сумму координат вектора O C → :
Имеется некая геометрическая фигура в виде многоугольника с четырьмя углами АВСD. На сторонах этого четырехугольника отмерены следующие вектора:
A B → , B C → , C D → , D A → .
Необходимо вычислить длину такого вектора в следующем порядке:
A B → + B C → + C D → + D A → .
Изобразим геометрическую фигуру, согласно условиям задачи:
A B → + B C → = A C → , A C → + C D → = A D →
В таком случае, можно записать, что:
A B → + B C → + C D → + D A → = A C → + C D → + D A → = A D → + D A → = A D → — A D → = 0 → .
Длина нулевого вектора, согласно определению, имеет нулевое значение. Исходя из альтернативного понятия, вектор представляет собой перемещение. В таком случае, A B → + B C → обозначает перемещение из A в B, а далее из B в C. В результате получается перемещение из A в C. В итоге:
A B → + B C → + C D → + D A → = 0 →
Вывод сделан на основании перемещения из точки А в точку А. Вектор обладает длиной, равной нулю и представляет собой 0 → .
На рисунке изображен параллелограмм ABCD. Диагонали данной фигуры, обозначенные, как AC и BD, имеют общую точку пересечения O.
A B → = a → , A D → = b →
O A → = x · a → + y · b →
Здесь x и y являются какими-то числами. Требуется определить число, которое равно:
O A → = 1 2 C A → = 1 2 ( C B → + B A → ) = 1 2 ( D A → + B A → ) = 1 2 ( — b → — a → ) = — 1 2 a → — 1 2 b → ⇒ x = — 1 2 , y = — 1 2 ⇒ x + y = — 1 .
На рисунке изображен некий параллелограмм ABCD. Точки K и L расположены на сторонах BC и CD соответственно. При этом выполняется следующее соотношение:
Точка L расположена на середине стороны CD.
A B → = a → , A D → = b →
K L → = x · a → + y · b →
Здесь х и y являются какими-то числами. Требуется вычислить такое число, которое равно:
K L → = K C → + C L → = 1 4 B C → + 1 2 C D → = 1 4 A D → + 1 2 B A → = 1 4 b → — 1 2 a → ⇒ x = — 1 2 , y = 1 4 ⇒ x + y = — 0 , 25 .
На рисунке изображен некий параллелограмм ABCD. Точки M и N расположены на сторонах фигуры, обозначенных, как AD и BC соответственно. При этом выполняется следующее условие:
A B → = a → , A D → = b → .
M N → = x · a → + y · b →
Здесь x и y являются какими-то числами. Требуется определить число, которое равно:
M N → = M A → + A B → + B N → = 2 5 D A → + A B → + 3 4 B C → = — 2 5 A D → + A B → + 3 4 B C → = — 2 5 b → + a → + 3 4 b → = a → + 7 20 b → ⇒ x = 1 , y = 7 20 ⇒ x · y = 0 , 35 .
На рисунке изображен некий параллелограмм ABCD. Точка P расположена на диагонали BD, точка Q принадлежит стороне фигуры CD. При этом выполняется следующее условие:
A B → = a → , A D → = b →
P Q → = x · a → + y · b → .
Здесь х и y являются какими-то числами. Необходимо вычислить значение числа, которое равно:
На рисунке изображена геометрическая фигура в виде правильного шестиугольника ABCDEF.
A B → = a → , A F → = b →
B C → = x · a → + y · b →
Здесь x и y являются какими-то числами. Требуется определить число, которое равно:
Согласно условию задания:
Заметим пересечение отрезков AD, BE и CF в точке O. Данная точка делит рассматриваемые отрезки на две равные части. В данном случае:
ABCO представляет собой параллелограмм
ABOF является параллелограммом.
B C → = A O → = A B → + B O → = A B → + A F → = a → + b → ⇒ x = 1 , y = 1 ⇒ x + y = 2 .
Координаты вектора
Прямоугольная система координат (декаротова система координат) — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.
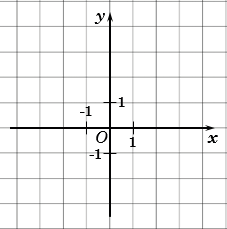
На рисунке выше оси и перпендикулярны. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом. В дальнейшем под длиной отрезка мы будем понимать это число. Так, единичный вектор — это вектор, длина которого равна 1.
Отложим от начала координат О единичные векторы и так, чтобы их направления совпадали с направлениями осей и соответственно.
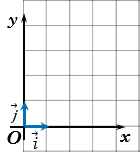
Векторы и называют координатными векторами.
Координатные векторы не коллинеарны, поэтому любой вектор можно разложить по координатным векторам, т.е. представить в виде , причем коэффициенты разложения и определяются единственным образом. Коэффициенты разложения вектора по координатным векторам называются координатами вектора в данной системе координат.
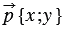
Координаты вектора записывают в фигурных скобках после обозначения вектора: .
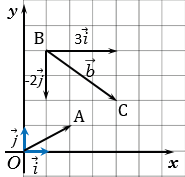
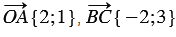
На рисунке выше .
Нулевой вектор можно представить в виде , следовательно, его координаты равны нулю: .
Если векторы и равны, то и . Значит, координаты равных векторов соответственно равны.
Правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число:
| 1 0 . Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов. |
Доказательство
Дано: , , .
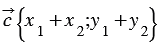
Доказать: .
Доказательство:
По условию и , тогда и .
Сложим последние два равенства и применим свойства сложения векторов и умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. . Что и требовалось доказать.
| 2 0 . Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. |
Доказательство
Дано: , , .
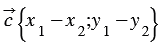
Доказать: .
Доказательство:
По условию и , тогда (1) и . (2)
Вычтем из равенства (1) равенство (2) и применим свойства сложения векторов и умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. . Что и требовалось доказать.
| 3 0 . Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. |
Доказательство
Дано: , — число, .
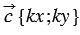
Доказать: .
Доказательство:
По условию , значит, .
Умножим последнее равенство на число и используя свойства умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. . Что и требовалось доказать.
Данные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Пример
Найти координаты вектора , если известно, что .
Решение:
По правилу 3 0 вектор будет иметь координаты , т.е. , вектор координаты , т.е. .
Так как , то координаты вектора можно найти по правилу 1 0 : , т.е. .
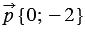
Ответ: .
сумма координат вектора
Координаты вектора Рассмотрим далее систему координат.
$ называются координатами данного вектора в данной системе координат, то есть [overrightarrow.
=\] Линейные операции над векторами Теорема 2 Теорема о сумме векторов: Координаты.
суммы векторов равны сумме соответствующих координат этих векторов.
координат этих векторов.
2. Контрольная работа на тему: операции над матрицами
Элементы аналитической геометрии Контрольная работа на тему: векторы, операции над векторами Пример №.
Суммой (разностью) матриц и называется матрица , элементы которой равны суммам (разностям) соответствующих.
Найдите сумму и разность матриц и .
Произведением матрицы размера на матрицу размера называется матрица размера , элементы которой равны сумме.
Найдем элементы матрицы : Для нахождения элемента находим сумму произведений элементов первой строки
3. Решение некоторых алгебраических задач с использованием вектора
Многие математические задачи допускают несколько вариантов решения. Часто первый избранный бывает далеко не самым удачным. Нахождение «наиболее простых», оригинальных путей решения нередко является результатом длительной и кропотливой работы. Умение решать задачу различными способами является одним из признаков хорошей математической подготовки. Существуют способы решения алгебраических задач методами, основанными на наглядно-геометрических интерпретациях. Понятие вектора является одним из фу.
Эксперты помогли более 1000 студентам по схожей теме
4. Линейная алгебра с элементами аналитической геометрии
Суммой векторов и является вектор , координаты которого равны суммам соответствующих координат векторов.
Геометрически можно показать, что для получения суммы векторов нужно совместить конец вектора с началом.
Суммой двух векторов одинаковой размерности n называется вектор Z = X + Y, компоненты которого равны.
сумме соответствующих компонент слагаемых векторов: zi = xi + yi, i = 1, 2, . . . n.
Линейные операции над векторами (сумма векторов и умножение вектора на число) удовлетворяют следующим
5. Как найти длину вектора
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной.
координатами этого вектора во введенной системе координат.
Найти: длину этого вектора. Решение. Введем на плоскости декартову систему координат $xOy$.
суммы этих координат.
Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие
6. Даны уравнения двух колебательных процессов Необходимо построить графики колебаний и с их помощью на
Для этого в системе координат хОу построим радиус-вектор, амплитудой, равной 1.8 и под углом в сторону.
положительного направления вращения векторов, то есть против направления движения часовой стрелки.
Аналогично построим радиус-вектор, соответствующий колебанию .Для поиска вектора, изображающего суммарное.
колебание , воспользуемся правилом параллелограмма сложения двух векторов.
По положению полученного вектора определяем амплитуду , измерив длину получившегося вектора и начальную
7. О возможности определения векторного произведения двух векторов в многомерном пространстве
Целью работы является определение векторного произведения двух векторов c = [a, b] в n-мерном евклидовом пространстве при n > 3, которое удовлетворяет общепринятому инвариантному определению, в соответствии с которым оно является вектором, модуль которого равен площади параллелограмма, построенного на векторах a и b, его направление перпендикулярно обоим векторам и векторы a, b и c образуют правую тройку векторов. В работе применяются ортонормированные базисы. Доказывается, что для двух ли.
8. Высшая математика: линейная алгебра
приставляется началом к концу предыдущего — замыкающий вектор дает сумму.
Вычитание выводится из сложения: Ь — а определяется как вектор, который в сумме с а дает Ь.
Второе вытекает из равенства проек у ции суммы векторов — сумме проек ций. lal Ilall) Отметим попутно.
Для обоснования (1.6) представим вектор ж в виде суммы где составляющая %l перпендикулярнавектору и.
При — «,»ом решает простое правило проекция суммы векторов равна сумме проекций: re = r ж cos (О) + ry
9. Координаты точки и координаты вектора. Как найти координаты вектора
$P=(2,2.5,1.5)$ Координаты вектора по двум точкам и формула нахождения Чтобы узнать, как найти вектор.
Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы.
(1) будут называться координатами этого вектора в заданной нами системе координат, то есть $overline.
=(m,n,l)$ Линейные операции над векторами Теорема 2 Теорема о сумме: Координаты суммы любого.
числа векторов определяются суммой их соответствующих координат.
10. Ротор. Теорема Стокс
Эту величину называют циркуляцией вектора по контуру Г.
Циркуляция = Циркуляция обладает свойством аддитивности, т.е. циркуляция по контуру Г будет равна сумме.
(1*) — (3*) можно получить из предыдущего путём циклической системы координат.
Таким образом, ротор вектора в декартовой системе координат будет иметь вид: Если известно, что ротор.
по замкнутому контуру равна потоку вектора rot через площадку S, ограниченную этим контуром.
11. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ ОПТИМАЛЬНОЙ ФИЛЬТРАЦИИ ПО МАП-КРИТЕРИЮ С ПРИМЕНЕНИЕМ ЧАСТИЧНЫХ СУММ РЯДА ЭДЖВОРТА
На основе непрерывного фильтра частиц и аппроксимации плотности вероятности частичными суммами ряда Эджворта сформирован статистический алгоритм приближенного решения задачи оптимальной фильтрации по критерию максимума апостериорной плотности вероятности. В предложенном алгоритме мода апостериорного распределения для каждой координаты ненаблюдаемого вектора состояния динамической системы неявно выражается через апостериорные центральные моменты до третьего, четвертого, пятого или шестого поря.
12. Физика
Fky = 0; k=1 n X Fkz = 0 (10) (11) k=1 (суммы проекций сил на оси координат) n X k=1 Mx (F~k ) = 0; n.
X My (F~k ) = 0; k=1 n X Mz (F~k ) = 0 (12) k=1 (суммы моментов сил относительно осей координат) 12.
Скорость произвольной точки А.Т.Т. равняется геометрической сумме вектора скорости полюса и скорости.
единичные векторы некоторой системы координат.
Обобщенной силой называется коэффициент перед вариацией обобщенной координаты в выражении для сумм элементарных
13. Направляющий вектор прямой
с координатами $(l;m)$, при этом вектор $overline$ — ненулевой.
Вектор $overline$ можно выразить через сумму векторов $overline$: $overline = overline.
Составьте уравнение прямой и выпишите координаты направляющего вектора.
=frac$ Ответ: координаты направляющего вектора $overline$ равны $(3;9)$.
Из этого уравнения получается, что координаты направляющего вектора равны $(6;7)$.
14. «Программирование на Cи с применением ассемблерных вставок» по дисциплине «Средства вычислительной техники»
Найдите сумму чисел, находящихся в регистрах EAX, EBX, ECX, накапливая ее в регистре EDX.
Найдите разность суммы чисел, находящихся в регистрах EAX, EBX, и числа из регистра ECX.
Сложите два вектора с целочисленными координатами (a1,a2) и (b1,b2).
15. ПЕРЕХОДНЫЕ ВЕРОЯТНОСТИ МАРКОВСКОГО ПРОЦЕССА НА ОТРЕЗКЕ, ЛЕЖАЩЕМ В ЧЕТВЕРТИ ПЛОСКОСТИ
Рассмотрен марковский процесс рождения и гибели квадратичного типа. Состояниями случайного процесса являются точки отрезка, лежащего в четверти плоскости. Назовем четвертью плоскости множество векторов с целыми неотрицательными координатами. Процесс задан инфинитезимальными характеристиками или плотностями переходных вероятностей. Эти характеристики определяются квадратичной функцией от координат — функцией на точках отрезка с целыми координатами. Граничные точки отрезка являются поглощающи.
Источник:
Вестник Московского государственного технического университета им. Н.Э. Баумана. Серия «Естественные науки»
16. Вычислить направляющие косинусы вектора
17. Линии на плоскости
Системы координат на плоскости 3. Переход от полярной системы координат к декартовой 3.1.
Линия в полярной системе координат 3.2. Линии в декартовой системе координат 4.
Прямая на плоскости в декартовой системе координат 5. Кривые второго порядка 5.1. Окружность 5.2.
18. Определение вероятностных моментов фазовых координат нелинейной модели конструкции
Рассмотрена задача стохастической динамики нелинейной конечно-элементной модели с использованием разложения решения по усеченному ортогональному базису собственных векторов статистически линеаризованной системы. Принято допущение, что нелинейности, присутствующие в системе, не приводят к принципиальному изменению ее динамического поведения, а только вносят существенную количественную поправку в вероятностные характеристики по отношению к линейной модели. Для того чтобы последняя не потеряла ф.
Планиметрия. Страница 8
. Сам вектор обозначается прописной буквой, например:
. Каждый вектор имеет определенную длину и направление. Например, вектора
имеют одинаковое направление. А вектора
Абсолютной величиной вектора или модулем вектора называется длина отрезка, представляющего собой вектор.
Если начало вектора совпадает с его концом, то такой вектор называется нулевым.
Если два вектора имеют одинаковое направление и равные абсолютные величины, то такие векторы называются равными.

Рис.1 Обозначение векторов.
Координаты вектора
Любой вектор имеет свои координаты. Координатами вектора называются числа x2-x1 и y2-y1. Например, координаты вектора
с начальной точкой А (1;1) и конечной точкой В (4;3) будут:
Координаты нулевого вектора равны нулю.
Абсолютная величина вектора — это его длина. А следовательно, ее можно определить как расстояние между двумя точками, начальной и конечной. Т.е.

Два вектора называются равными, если у них соответствующие координаты равны.

Рис.2 Координаты вектора.
2.Сложение векторов
Пусть заданы два вектора со своими координатами
(b1;b2). Тогда суммой двух векторов будет вектор с координатами
В векторной форме можно записать так:

Для сложения векторов используются два метода: метод треугольника и метод параллелограмма.
Для сложения векторов методом треугольника необходимо перенести вектор
параллельным переносом так, чтобы конец вектора
совпадал с началом вектора
. Тогда начало вектора
и конец вектора
и будет сумма векторов
По методу параллелограмма, если два вектора
имеют общее начало, то суммой двух векторов будет диагональ параллелограмма, построенного на этих векторах, т.е. вектор
Разностью двух векторов
называется такой вектор
, который нужно прибавить к вектору
, чтобы получить вектор

Рис.3 Сложение векторов.
3.Умножение вектора на число
Любой вектор с координатами (x;y) можно умножить на простое число, например λ. (Рис.3) Тогда произведением вектора на число λ будет называться вектор с координатами (λx;λy). Абсолютная величина вектора будет равна:

Для любых двух векторов
число λ можно вынести за скобку λ (
Если λ > 0, то направление вектора не изменяется, а если λ 2 и называется скалярным квадратом. Отсюда следует, что
Теорема. Скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними.
Доказательство. Пусть даны два вектора а и b и угол между ними α. Тогда квадрат суммы двух векторов равен:

Следовательно, скалярное произведение двух векторов не зависит от выбора системы координат, а зависит только от их абсолютных величин. (Рис.5)
Так как координаты вектора
(b cos α; b sin α), то скалярное произведение двух векторов
Рис.5 Скалярное произведение векторов.
Отсюда вытекает следующий вывод:
если два вектора перпендикулярны, то их скалярное произведение равно нулю.
если скалярное произведение двух ненулевых векторов равно нулю, то векторы перпендикулярны.
Репетитор: Васильев Алексей Александрович
Предметы: математика, физика, информатика, экономика, программирование.

2000 руб / 120 мин — подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин — индивидуально (базовый уровень). 2000 руб / 120 мин — студенты.
Тел. 8 916 461-50-69, email: alexey-it@ya.ru
6.Пример 1
Четырехугольник ABCD — параллелограмм. Докажите равенство векторов
Доказательство:
Пусть ABCD данный параллелограмм (Рис.6). Необходимо доказать, что вектора
параллельному переносу таким образом, чтобы точка А совпала с точкой D. При таком перемещении точка А смещается по прямой AD и переходит в точку D. Это значит, что точка В переместится по параллельной прямой ВС в точку С.
Таким образом, при параллельном переносе прямая АВ переходит в параллельную прямую DC, а вектор
переходит в вектор
. А это значит, что эти вектора равны.
Действительно, так как при перемещении прямая АВ переходит в параллельную прямую DC, а точка А переходит в точку D, то на луче DC можно отложить только один вектор, равный вектору

Рис.6 Задача. Четырехугольник ABCD — параллелограмм.
Пример 2
Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2). Докажите равенство векторов
Доказательство:
Найдем координаты векторов
Таким образом, координаты векторов следующие:
А так как равные вектора имеют равные соответствующие координаты и xAB = xCD, yAB = yCD, то вектора

Рис.7 Задача. Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2).
Пример 3
В треугольнике АВС проведена медиана AM. Докажите, что
Доказательство:
, равный и параллельный вектору
от точки С. И отложим вектор
, равный и параллельный вектору
от точки В (Рис.8).
Тодга получим параллелограмм, в котором вектор
, так же как вектор
. А так как диагонали параллелограмма пересекаются в точке М и делятся этой точкой пополам, то
Координаты вектора

Основываясь на разложении вектора по двум неколлинеарным векторам, на этом уроке вводят понятие координат вектора. Получают правила нахождения координат вектора выраженного суммой векторов, разностью векторов и произведением вектора на число. Рассматриваются примеры применения этих правил при определении координат любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока «Координаты вектора»
Ранее вы уже сталкивались с координатами, но указывали их для точек. При этом работали в прямоугольной координатной плоскости, для задания которой необходимо было провести две взаимно перпендикулярные прямые с выбранными на них направлениями (их называют координатными осями) и выбрать единицу измерения на каждой из осей.
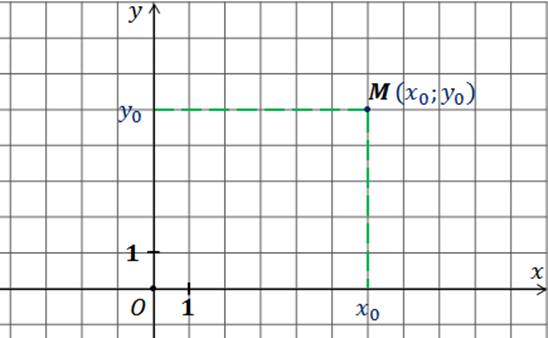
Это и позволяло определить координаты любой точки.
На этом уроке нам предстоит выяснить, что называют координатами вектора.
С прошлых занятий вам известно, что любой вектор на плоскости можно разложить по двум неколлинеарным векторам.
От точки О начала координат отложим векторы , длины которых равны единице (в дальнейшем будем называть такие векторы единичными), так, чтобы направление вектора совпадало с направлением оси x, а направление вектора совпадало с направлением оси y.

Тогда векторы будем называть координатными векторами. Понятно, что любой вектор можно разложить по векторам . Причём коэффициенты разложения, числа x и y, определяются единственным образом.
Так вот коэффициенты разложения вектора по координатным векторам называют координатами вектора в данной системе координат.
Координаты вектора будем записывать в фигурных скобках через точку с запятой. При этом первым будем записывать коэффициент разложения x, а вторым — y.

На одном из прошлых занятий мы разлаживали векторы, изображённые в координатной плоскости по векторам .
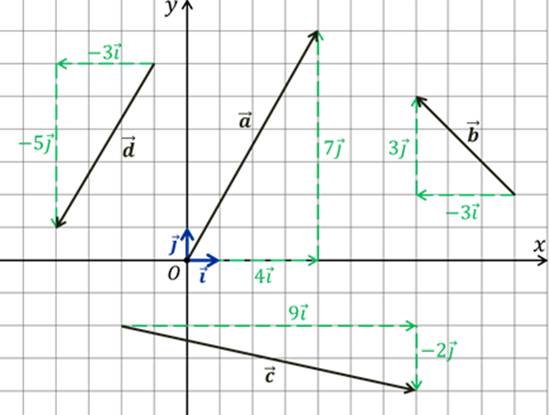
Пользуясь этими разложениями, запишем координаты данных векторов.
Итак, вектор имеет координаты .
Вектор имеет координаты .
Координатами вектора являются числа ..
Ну, а координатами вектора будут числа .

Обратите внимание, что такие координаты данные векторы будут иметь только в конкретной системе координат и при конкретных координатных векторах .

Коэффициенты разложения нулевого вектора по векторам равны нулю. Тогда получаем, что нулевой вектор имеет координаты 0 0, причём в любой системе координат и при любых координатных векторах.

Если векторы равны, то их разложения по векторам также будут равны, а значит, равны будут и коэффициенты разложения. Таким образом, получаем, что координаты равных векторов соответственно равны.
Рассмотрим ещё один особенный случай — противоположные векторы.
Их разложения противоположны. Значит, противоположны будут и соответственные координаты.
Можем подытожить, что координаты равных векторов соответственно равны, а координаты противоположных векторов соответственно противоположны.
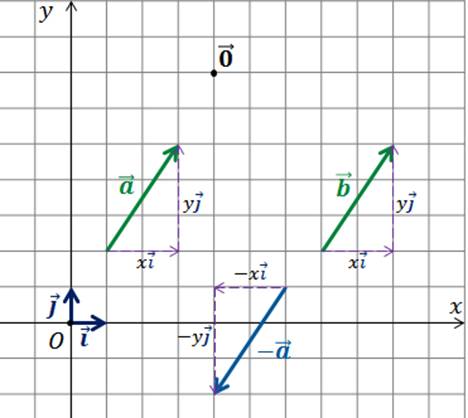
Пользуясь полученными выводами, для каждого из данных векторов запишем противоположный и укажем его координаты.
; ; ; ; .





Задача. Разложить векторы по координатным векторам и , указать их координаты.
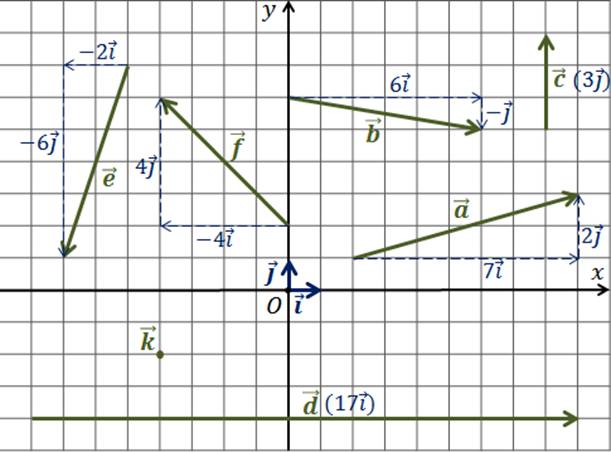
Начнём с вектора . Его разложение . Значит, его координатами будут числа 7 и 2.

Далее запишем разложение вектора . Коэффициенты разложения 6 и -1 являются его координатами.
Вектор . Коэффициенты разложения равны 0 и 3. Значит, вектор .
Следующим рассмотрим вектор . Значит, координаты вектора .
Далее обратим своё внимание на вектор . Тогда координаты данного вектора .
Запишем разложение вектора . Значит, он имеет координаты .
Последним рассмотрим вектор . Тогда получаем, .
Видим, что для определения координат вектора достаточно его разложения по координатным векторам. Поэтому при наличии разложения вектора можно сразу назвать его координаты. Главное — помнить, что в качестве первой координаты записывают коэффициент разложения при координатном векторе, коллинеарном оси x (в данном случае — это вектор ), а в качестве второй координаты — коэффициент разложения при координатном векторе, коллинеарном оси y (в данном случае — это вектор ).

Запишем координаты векторов, пользуясь их разложениями по координатным векторам .
Из разложения вектора видим, что он имеет координаты .
, то ;
, то ;
, то ;
, то .
А теперь, пользуясь только координатами данных векторов, построим их в прямоугольной координатной плоскости, откладывая каждый вектор от точки О начала координат.
Координатами вектора являются числа 8 и -1. Значит, чтобы переместиться из точки О на вектор , сначала нужно переместиться на вектор , а затем на вектор . Соединив точку О с конечной точкой, получим вектор .

Далее изобразим вектор . Для этого из точки О переместимся на вектор . Тем самым получим искомый вектор .
Чтобы из точки О переместиться на вектор сначала переместимся на вектор ,, а затем на вектор . Проведём вектор из точки О в конечную точку. Так мы получили вектор .

Далее построим вектор .
Последним построим вектор . Перемещение на этот вектор состоит из перемещений на вектор и на вектор . Перемещение из точки О в конечную точку и задаёт вектор
Так мы рассмотрели примеры построения вектора по его координатам.
Далее, пользуясь приобретёнными знаниями о координатах вектора, получим правила нахождения координат векторов, полученных уже известными вам действиями: сложением, вычитанием и умножением вектора на число.
Сначала рассмотрим сумму двух векторов , .
Пользуясь их координатами, можем записать разложения данных векторов по координатным векторам , .
Сложим полученные равенства . Пользуясь свойствами сложения векторов и произведения вектора на число, получаем, что координаты вектора суммы векторов и равны , .
Можем записать правило.
Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.
Найдём координаты векторов суммы, если вектор , , , .
Координаты вектора суммы и равны .
Координаты вектора суммы , , равны .
Теперь рассмотрим разность векторов -.
Из разложения вектора вычтем разложение вектора .

Получаем, что координаты вектора разности равны .
Запишем правило. Каждая координата разности двух векторов равна разности соответствующих координат данных векторов.
Разность векторов и имеет координаты .
Разность векторов и имеет координаты .

Далее получим координаты произведения вектора на число k.

Получаем, что координаты произведения равны .
Запишем правило. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Найдём координаты вектора 4. Они равны .
Координаты вектора 2,5 равны .
Вектор 3 имеет координаты .
Ну, а вектор имеет координаты .
Все три правила, полученные нами, в дальнейшем помогут определять координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Задача. Найти координаты векторов и по координатам данных векторов , , , .


Представим это выражение в виде суммы.
Вектор имеет координаты , или .
Вектор имеет координаты , или .
Координаты вектора . А вот координаты вектора .
Координаты вектора найдём как суммы соответствующих координат полученных векторов. В результате получаем, что имеет координаты
Далее найдём координаты вектора . Запишем второй множитель в виде суммы. Координаты векторов и . Вектор имеет координаты , или . Вектор .

Сумма полученных векторов будет иметь координаты .
Произведение этого вектора на 3 имеет координаты . Это и есть координаты вектора .
Подведём итоги урока. Сегодня, пользуясь уже известным правилом разложения вектора по двум неколлинеарным векторам, мы ввели понятие координатных векторов и дали определение координатам вектора. А также получили правила нахождения координат векторов суммы векторов, разности векторов и произведения вектора на число. Этих правила позволяют определять координаты векторов, представленных в виде алгебраической суммы данных векторов с известными координатами.
На следующем уроке мы найдём связь между координатами вектора и координатами его начала и конца.
Что такое сумма координат

Задания Д15 C4 № 505823
На диаметре AB полукруга взята точка С и в полукруге на отрезках AC и CB как на диаметрах построены два полукруга. Из точки C восставлен препендикуляр к AB и с обеих сторон от него построены два круга, касающиеся как этого перпендикуляра, так и обоих полукругов.
а) Докажите, что радиусы построенных кругов равны.
б) Найдите их радиусы, если AB = 12 и AC : CD = 1 : 3.
а) Введем координаты — направим ось y по перпендикуляру к AB, а ось x — по Пусть центры окружностей имеют координаты и тогда и а их радиусы — a и Центр большой окружности имеет координаты Пусть центр окружности, касающейся правой полуокружности, имеет координаты и радиус r (она касается вертикальной оси). Запишем условия касания с окружностями (расстояние между центрами равно сумме или разности радиусов)
Возводя последнее в квадрат, получаем
Возводя первое в квадрат и подставляя получаем то есть
Очевидно, если поменять местами в формуле a и b, ответ не изменится, но станет также ответом для картинки, отраженной относительно вертикальной оси. Поэтому два указанных радиуса равны.
б) Радиусы окружностей составят и Из формулы, полученной в первом пункте, имеем

Задания Д10 C2 № 505845
Дана правильная треугольная призма , стороны основания которой равны Найдите угол между прямыми и , если сумма длин всех сторон обоих оснований равна
1) Элементарно-геометрическим методом.
Достроим заданную призму до прямой четырехугольной призмы Соединим отрезками точки B и и
Ясно, что || — искомый.
По теореме Пифагора получим: Очевидно также, что также
По теореме косинусов будем иметь:
где — искомый угол.
Вычислим также по теореме косинусов.
2) Координатно-векторным методом.
Пусть — искомый угол. Тогда
Введем декартову систему координат (см.рисунок). Найдем координаты нужных точек:
Представим векторы в координатах: ,
Для отыскания угла воспользуемся понятием скалярного произведения двух векторов.

Задания Д15 C4 № 505975
Две окружности радиусов R и r (R > r) касаются внешним образом. Найдите радиусы окружностей, касающихся обеих данных окружностей и прямой, проходящей через центры данных.
Введем координаты так, чтобы линия центров этих окружностей была осью абсцисс, а ось ординат проходила через точку касания окружностей. Тогда центры окружностей будут и (выберем соответствующее направление оси). Пусть координаты центра искомой окружности Можно считать, что окружность лежит выше оси, поэтому Тогда, очевидно, ее радиус должен быть равен b.
Ясно, что начальных двух окружностей она касается внешним образом. Тогда расстояния между ее центром и центрами остальных окружностей равны сумма радиусов ее и остальных окружностей. Получаем систему уравнений
Вычитая уравнения, находим
Подставляя в первое уравнение, получаем
Поскольку поделим на него и домножим на знаменатель.

Задания Д15 C4 № 514882
Четырехугольник ABCD со взаимно перпендикулярными диагоналями АС и BD вписан в окружность.
а) Докажите, что квадрат диаметра окружности равен сумме квадратов противоположных сторон четырехугольника.
б) Найдите площадь четырехугольника ABCD, если известно, что
а) Будем считать, что окружность имеет радиус (введем новую единицу длины) и центр в начале координат, а диагонали четырехугольника параллельны координатным осям. Тогда обозначим координаты вершин так — Имеем:
что и требовалось доказать.
б) Из пункта а) следует, что поэтому и радиус окружности равен По теореме Птолемея:
По формуле для площади четырехугольника:

Задания Д10 C2 № 521486
В параллелепипеде ABCDA1B1C1D1 точка К — середина ребра АВ.
а) Докажите, что плоскость СКD1 делит объем параллелепипеда в отношении 7 : 17.
б) Найдите расстояние от точки D до плоскости СКD1, если известно, что ребра АВ, АD и АА1 попарно перпендикулярны и равны соответственно 6, 4 и 6.
а) Пусть T — середина тогда Значит, точка T лежит в плоскости и сечение — трапеция Вычислим теперь объем одной из частей (за V обозначен объем параллелепипеда).
откуда и следует утверждение задачи.
б) Введем координаты с началом в точке A и с осями направленными вдоль прямых соответственно. Тогда координаты точек будут такими: Написав уравнение плоскости, проходящей через них, получим Тогда расстояние от точки до этой плоскости составит

Задания Д10 C2 № 506009
В правильной треугольной пирамиде отношение бокового ребра к высоте пирамиды равно 2. Найдите отношение радиуса вписанного в пирамиду шара к стороне основания пирамиды.
Задачу решим несколькими методами.
а) Методом объемов.
Пусть — высота заданной правильной пирамиды,
SM — ее апофема, — медианы основания,
Поскольку а это значит, что т. е.
Поскольку центр вписанного шара равноудалена от всех граней заданной пирамиды, то это обстоятельство позволяет выразить радиус шара, вписанного в пирамиду, через объем пирамиды и площадь ее полной поверхности. Мы имеем возможность мысленно разбить заданную пирамиду на четыре пирамиды, основаниями которых будут служить грани заданной пирамиды, а высоты их будут равны радиусу искомого шара. Так как объем заданной пирамиды V будет равен сумме объемов пирамид, составляющих эту пирамиду, то понятно, что где r — искомый радиус.
б) Использование тангенса половинного угла.
Искомый центр вписанного шара будет лежать на SO (а это надо бы доказать!). Кроме того, центр вписанного шара есть точка пересечения биссектрис линейных углов двугранных углов, образуемых боковыми гранями и основанием заданной пирамиды. Таким образом, центр шара лежит на пересечении высоты пирамиды SO и биссектрисы угла Если это — точка то и есть искомый радиус.
Вычислив OM и SM, можно найти косинус угла Тогда по формуле тангенса половинного угла сможем вычислить и значение тангенса угла
в) Метод площадей.
В прямоугольном треугольнике SOD по теореме Пифагора имеем:
Будем иметь в виду, что центр вписанного шара (сферы) лежит на Обозначим эту точку Опустим из нее перпендикуляр к грани Ясно, что где r — радиус шара (сферы). Теперь соединим точку отрезком с точкой Треугольник SOD разбивается на два треугольника: и
г) Координатный метод исследования.
Поместим пирамиду в декартову систему координат, как показано на рисунке. Пусть Тогда
Для дальнейшего исследования этих расстояний нам вполне достаточно.
Будем иметь в виду, что центр вписанного шара (сферы) лежит на Обозначим эту точку Тогда радиус шара (сферы) равен
Зная, что точка удалена от грани ASCна то же расстояние, что и от основания ABC, для достижения цели найти искомый радиус, используем формулу расстояния от точки до плоскости.
Найдем координаты точек
В нашем случае очень легко составить уравнения плоскостей ASC и Ясно, что уравнение плоскости ABC заведомо имеет вид:
Составим уравнение плоскости ASC, имея в виду, что в этой же плоскости лежит также точка
В системе, приведенной ниже, первое уравнение учитывает принадлежность точки D, второе — принадлежность точки S, а третье — принадлежность точки
Таким образом, искомое уравнение имеет вид: или
Теперь нетрудно найти расстояние от точки до плоскости
д) Метод подобия.
В прямоугольном треугольнике SOD по теореме Пифагора имеем:
Будем иметь в виду, что центр вписанного шара (сферы) лежит на Обозначим эту точку Опустим из нее перпендикуляр к грани ASC. Ясно, что где r — радиус шара (сферы).
Теперь соединим точку отрезком с точкой
Прямоугольные треугольники и SOD подобны как имеющие общий острый угол. Значит, Будем иметь в виду, что В таком случае:

Тип 16 № 517502
Точки E и K — соответственно середины сторон CD и AD квадрата ABCD. Прямая BE пересекается с прямой CK в точке O.
а) Докажите, что вокруг четырёхугольника ABOK можно описать окружность.
б) Найдите AO, если сторона квадрата равна 1.
а) Треугольники BCE и CDK равны по двум катетам, следовательно,
то есть прямая BE перпендикулярна прямой CK. Тогда в четырёхугольнике ABOK: ∠BAK = ∠BOK = 90°. Поэтому вокруг него можно описать окружность.
б) Введём систему координат, как показано на рисунке. В этой системе
Уравнение прямой KC: уравнение прямой BE: Координаты точки O найдём из системы уравнений
Тогда расстояние между и равно
Приведём другое решение п. а).
Повернём треугольник BCE на 90° по часовой стрелке и параллельным переносом совместим точку B с точкой C. Тогда треугольник BCE наложится на CKD, прямая BE совпадет с прямой CK. Поскольку после поворота прямые совпали, до поворота угол между ними был 90°.
Приведём другое решение п. б).
Прямоугольные треугольники BCE и BAK равны по двум катетам, значит, то есть на хорды AO и AB описанной около четырёхугольника ABOK окружности опираются равные углы. Таким образом,
Приведём решение п. б) Андрея Плюхина.
Продолжим отрезок CK до точки F пересечения с прямой AB. Прямоугольные треугольники KDC и KAF равны по катету и острому углу, поэтому AF = ВС = 1, а точка A — середина BF.
Точка O принадлежит окружности с центром в точке A и диаметром BF, так как эта точка — вершина прямого угла, стягивающего диаметр BF. Следовательно, AO = AB = AF = 1 — радиус этой окружности.
Второй абзац этого решения можно заменить таким рассуждением: из суммы углов получаем, что угол FOB прямой, следовательно, АО является медианой прямоугольного треугольника и равна половине гипотенузы.
Сумма приращений координат
Главными геодезическими задачами на плоскости являются прямая и обратная задачи. Прямая геодезическая задача на плоскости формулируется следующим образом: по заданным координатам x1 и y1 точки 1, дирекционному углу α и длине d стороны 1-2 вычислить координаты точки 2 (рис. 8.1).

Рис. 8.1. Приращения координат
Вначале вычисляют приращения координат:

;

;
после чего находят координаты определяемой точки

;
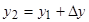
.
Контроль вычислений заключается в вычислении расстояния по формуле

.
Отклонение вычисленного расстояния d от заданного не должно превышать 1 см.
Обратная геодезическая задача на плоскости заключается в вычислении по заданным координатам двух точек (1 и 2) дирекционного угла и длины стороны 1-2.
Для ее решения находят приращения координат


.
После чего, игнорируя знаки приращений координат, вычисляют величину тангенса румба



.
Четверть румба определяется в соответствии со знаками приращений координат и (рис. 8.2). Зависимость между дирекционными углами и румбами определяется четвертью румба (рис. 8.3).

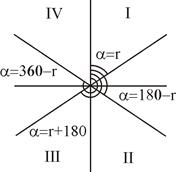
Рис. 8.2. Знаки Dx и Dy Рис. 8.3. Дирекционные углы
Контроль вычислений осуществляется по формулам

.
Расхождения в значениях расстояний не должны превышать 1 – 2 см.
Сумма приращений координат
Для получения теоретической суммы приращений координат разомкнутого теодолитного хода рассмотрим рис. 8.4.

Рис. 8.4. Сумма приращений координат
Из математики известно, что проекция суммы векторов на какую-либо ось равна сумме их проекций. Каждая сторона теодолитного хода может рассматриваться как вектор, представленный направлением и длиной. Поэтому проекция суммы сторон теодолитного хода на какую-либо ось равна сумме их проекций на эту ось. Для каждой стороны теодолитного хода приращения координат Dx и Dy равны проекциям этой стороны на соответствующую ось координат:

;

.
Из чертежа легко видеть, что сумма проекций сторон теодолитного хода на какую-либо ось координат будет равна проекции замыкающей AB на соответствующую ось, а проекция замыкающей равна разности координат исходных пунктов. Следовательно, можно написать равенства

;

.
В замкнутом теодолитном ходе

;

;
поэтому для замкнутого теодолитного хода теоретические суммы приращений координат будут равны

;

.
Вследствие неизбежных ошибок измерений горизонтальных углов и длин сторон теодолитного хода сумма вычисленных приращений координат обычно не равна теоретической сумме приращений. Разности между полученными суммами координат и их теоретическими значениями называют невязками по осям координат:

;

.






